Молекула водорода | это… Что такое Молекула водорода?
Моле́кула водоро́да — простейшая молекула, состоящая из двух атомов водорода. В её состав входят два ядра атомов водорода и два электрона. Вследствие взаимодействия между электронами и ядрами образуется ковалентная химическая связь. Кроме основной изотопной модификации H2, существуют разновидности, в которых один или оба атома протия заменены другими изотопами водорода — дейтерием или тритием: HD, HT, D2, DT, T2. Симметричность или несимметричность молекулы имеет значение при её вращении.
Содержание
|
Модели молекулы водорода
Рис.1.Модель водорода по Бору и осевая проекция электронного кольца
Н.Бор ещё в 1913 году дал описание модели молекулы водорода[1]. Согласно Бору, два внешних электрона, образующих молекулу, вращаются по одной и той же орбите вокруг линии, проходящей через ядра обоих атомов, и удерживают последние на определённом расстоянии друг от друга (рис.1). Боровская модель химической связи давала чёткую картину образования молекулярного водорода — динамическое равновесие системы, содержащей два протона, удерживающихся на определённом расстоянии друг от друга (d), притяжением кольца из двух электронов. При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.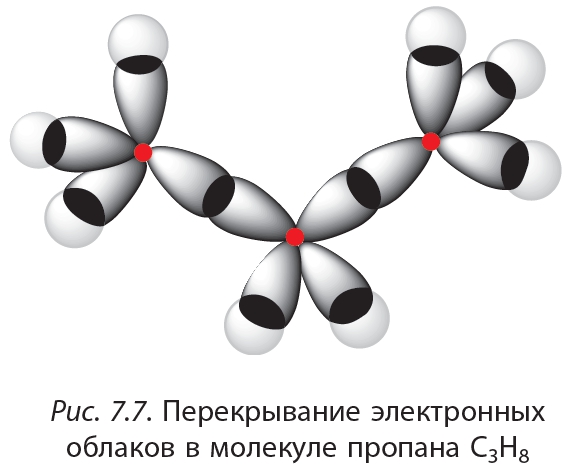
Также как и боровская модель атома, боровская модель молекулы водорода не отражала и не могла отражать волновую природу электрона и статистическую интерпретацию волновой функции. Здесь уместно дополнить боровскую модель молекулы водорода достижениями квантовой механики, аналогично боровской модели атома. В этом случае гипотетическое кольцо электронов в модели молекулы водорода трансформируется в геометрическое место расположения плотности вероятности нахождения связывающих электронов. Электронную пару следует представлять электронным облаком в форме кольца, баранки, тора. При этом предполагается, что электроны в торе удалены друг от друга на максимально возможное расстояние, а электронная плотность в молекуле водорода имеет минимум — «кулоновскую дырку» на линии, соединяющей ядра молекулы водорода. Наиболее вероятный радиус электронного тора (r
re2 = a02 — (d/2)2; re = 0,377 Å.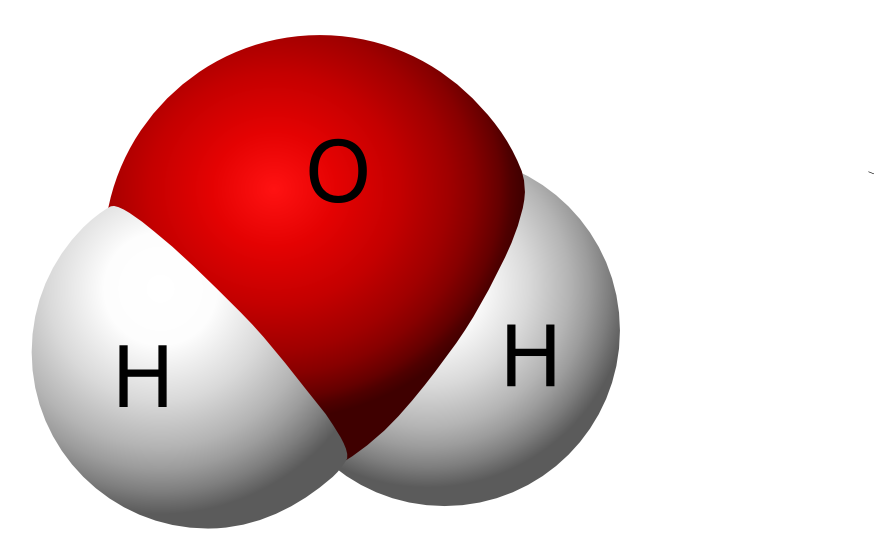
Рис.2.Контурная карта электронной плотности для молекулы водорода[2]
В теории молекулярных орбиталей, разработанной в 1927—1932 г.г. Ф.Хундом, Р.Малликеном и др., модель молекулы водорода описывали контурными картами электронной плотности (рис.2).
Карта строится как разность между электронной плотностью молекулы и несвязанных атомов. Сплошные линии контурной карты отражают области увеличения электронной плотности (в единицах заряда электрона). Пунктирные — области её уменьшения в молекуле по сравнению с электронной плотностью несвязанных атомов водорода, сближенных на равновесное расстояние.
Поскольку в теории молекулярных орбиталей учитывается лишь фермиевская корреляция электронов, поэтому электронная плотность в молекуле водорода сконцентрирована на линии, соединяющей ядра молекулы (см. рис.2).
Рис.3.Модель молекулы водорода в теории валентных связей
Квантово-механическую теорию ковалентной связи в молекуле водорода разработали в 1927 году Вальтер Гайтлер и Фриц Лондон.
Расчёт молекулы водорода в основном сводится к определению интеграла перекрытия атомных орбиталей.
Гамильтониан
Гамильтониан молекулы водорода H2 записывается в виде
- ,
где M — масса протона, m — масса электрона, — координаты ядер, — координаты электронов.
В адиабатическом приближении задача нахождения энергетических состояний молекулы водорода разбивается на два этапа. На первом этапе рассматривается только электронная подсистема, а ядра считаются зафиксированными в точках и .
Гамильтониан электронной подсистемы имеет вид
- ,
Гамильтониан молекулы водорода симметричен относительно переменных и , то есть не изменяется при смене нумерации электронов. Кроме того, он не зависит от спиновых переменных.
Волновые функции
Схематическое изображение симметричной волновой функции молекулы водорода и образования ковалентной связи
Схематическое изображение антисимметричной волновой функции молекулы водорода
Исходя из принципа тождественности частиц и учитывая то, что электроны являются фермионами, волновая функция молекулы водорода должна быть антисимметричной относительно перестановки электронов. Независимость гамильтониана от спиновых переменных позволяет выбрать её в виде произведения двух функций, одна из которых зависит только от координат и называется координатной волновой функцией, а вторая зависит только от спинов и называется спиновой функцией.
Существуют два возможных типа спиновых функций для двух электронов: с параллельными спинами и с антипараллельными спинами. Функции с параллельными спинами симметричны относительно перестановки электронов и образуют триплетные состояния, в которых суммарный спин равен единице. Функции с антипараллельными спинами образуют синглетные состояния с нулевым суммарным спином (см. Мультиплетность, Состояние (квантовая механика)). Они антисимметричны относительно перестановки электронов.
Поскольку волновая функция электрона должна быть антисимметричной относительно перестановки, она может быть произведением либо
- симметричной координатной функции на антисимметричную спиновую функцию, либо
- антисимметричной координатной функции на симметричную спиновую функцию.
Симметричную и антисимметричную координатные функции основного состояния в нулевом приближении теории возмущений можно построить исходя из волновых функций основного состояния атома водорода .
Первый член каждой из приведенных волновых функций отвечает локализации электрона, пронумерованного индексом 1 на атоме с индексом 1 и электрона, пронумерованного индексом 2 на атоме с индексом 2.
Энергия электронных состояний
Энергия электронных состояний находится усреднением гамильтониана на волновых функциях
- .
Для двух возможных волновых функций основного состояния она приобретает вид
- ,
где — расстояние между ядрами, — значение энергии основного состояния атома водорода, — интеграл перекрытия, который определяется выражением
- ,
— кулоновский интеграл, определяемый как
- ,
— обменный интерграл, равный
- .
Энергия молекулы водорода состоит из удвоенной энергии атома водорода, энергии кулоновского отталкивания между ядрами и членов, определяющих взаимодействие электронов между собой и с другим ядром.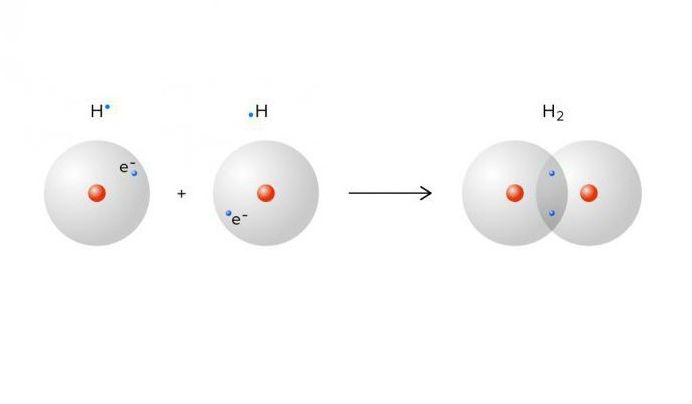
Величина — это средняя энергия кулоновского взаимодействия между двумя электронами и электронов с «чужим ядром». Величина определяет вклад в энергию обменного взаимодействия, которая не имеет аналога в классической механике. Именно этот член определяет существенное различие между синглетными и триплетными состояниями.
Зависимость энергии основного состояния от расстояния между ядрами
Ковалентная связь
Энергия взаимодействия атомов в молекуле водорода для синглетного(сплошная линия) и триплетного (пунктирная линия) состояний
Обменный интеграл для молеклы водорода в определённом диапазоне расстояний между атомами отрицательный. Вследствие этого, для синглетных состояний он обеспечивает дополнительное притягивание между ядрами атомов, а для триплетных — дополнительное отталкивание.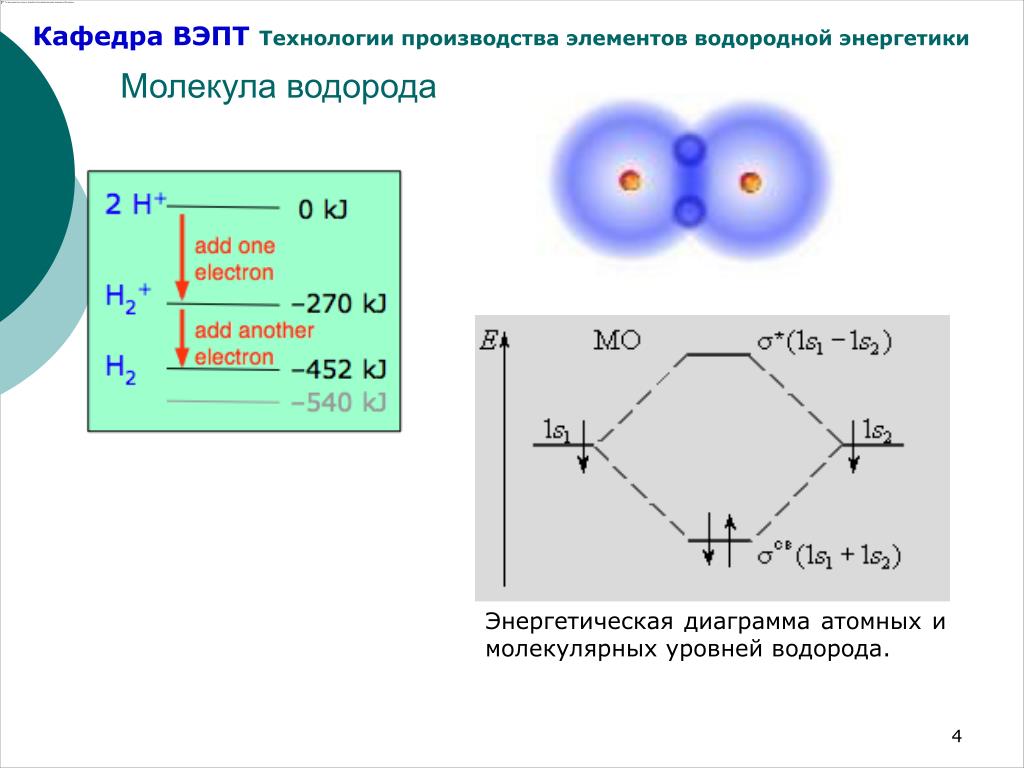 Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Насыщение ковалентной связи
Для параллельных спинов, то есть для триплетного состояния, дополнительный положительный вклад в энергию приводит к тому, что атому отталкиваются на любом расстоянии. Этим объясняется насыщение ковалентной связи. Молекула водорода может состоять только из двух атомов. Третий атом водорода не может образовать связь с молекулой потому, что его спин непременно будет параллельным одному из спинов электронов в составе молекулы. Параллельность спинов приводит к отталкиванию между ядрами на любом расстоянии.
Необходимо отметить, что на больших расстояниях между атомами они притягиваются в любых состояниях благодаря Ван-дер-Ваальсовому взаимодействию, которое, однако, намного слабее ковалентной связи. Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Движение ядер в молекуле водорода
Гамильтониан, описывающий относительное движение двух ядер в молекуле водорода имеет вид
- ,
где — приведённая масса двух ядер, — энергия синглетного электронного состояния, зависящая от расстояния между ядрами (определена в предыдущем разделе), — оператор углового момента, описывающий вращение молекулы.
Вращение
Оператор углового момента коммутирует с гамильтонианом, поэтому собственные функции гамильтониана можно выбрать общими с собственными функциями оператора углового момента, то есть сферические гармоники:
- .
Вклад вращения в энергию молекулы равен
- .
Этот вклад мал, потому, что массы ядер намного больше, чем массы электронов. Он зависит от расстояния между ядрами R. При колебаниях ядер это расстояние меняется, поэтому вращательное движение, строго говоря, невозможно отделить от колебательного. Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Вращательные уровни вырождены относительно магнитного квантового числа ml. Кратность вырождения 2l+1.
Колебания атомов
Вблизи минимума функцию можно разложить в ряд Тейлора, ограничившись только квадратичным членом.
- ,
где
Таким образом, задача об энергетических состояниях колебания ядер сводится к задаче квантового гармонического осциллятора. Следовательно, для низших колебательных и вращательных уровней энергия молекулы водорода равна
- ,
где — колебательное квантовое число.
Низшая энергия колебания отвечает нулевым колебаниям.
При больших значениях квантовых чисел n и l колебательное и вращательное движение разделить невозможно.
Таким образом, энергию молекулы при малых квантовых числах можно записать в виде трёх слагаемых — электронного, колебательного и вращательного:
Малым параметром задачи является отношение массы электрона к массе протона. Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
- .
Следовательно, электронный уровень расщепляется на несколько колебательных, каждый из которых, в свою очередь, расщепляется на вращательные. Поскольку энергии вращательных уровней близки, то в оптических спектрах они сливаются в полосы — образуется полосатый спектр, который наблюдается для молекулы HD. Для симметричной молекулы H2 переходы между орбитальными и колебательными уровнями запрещены правилами отбора, поэтому молекулярный протий не поглощает в инфракрасной области.
Пара- и ортоводород
Схематическое изображене спиновых изомеров водорода
Ядра атомов водорода, входящие в состав молекулы, являются протонами — фермионами со спином 1/2. По правилам сложения спинов ядерный спин молекулы может быть 0 или 1. Молекулы водорода с суммарным ядерным спином 0 называют параводородом, а молекулы с суммарным ядерным спином 1 и тремя возможными проекциями (−1, 0, 1) называют ортоводородом. В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
Характеристики молекулы водорода
Межъядерные расстояния и энергии диссоциации молекул водорода, его изотопов и молекулярного иона водорода[3]
| Молекула | Межъядерное расстояние,Å | Энергия диссоциации, Эв |
|---|---|---|
| H2 | 0,7416 | 4,477 |
| HD | 0,7414 | 4,512 |
| D2 | 0,7416 | 4,555 |
| DT | 0,7416 | 4,570 |
| T2 | 0,7416 | 4,588 |
| HT | 0,7416 | 4,524 |
| H2+ | 1,06 | 2,648 |
Константы реакции диссоциации молекулярного водорода (Kp) и степень превращения (α) в зависимости от абсолютной температуры[4]:
| T, к | 2000 | 3000 | 4000 | 5000 | 6000 | 8000 |
|---|---|---|---|---|---|---|
| Кр | 2,62 · 10-6 | 2,47 · 10-2 | 2,52 | 4,09 · 10 | 2,62 · 102 | 2,70 · 103 |
| α | 8,10 · 10-4 | 7,83 · 10-2 | 0,621 | 0,954 | 0,992 | 0,999 |
См.
- Молекулярный ион водорода
- Рекомбинация (химия)
- Боровская модель химической связи
- Кулоновская электронная корреляция
- Статистическая интерпретация волновой функции
- Теория молекулярных орбиталей
- Теория валентных связей
Примечания
- ↑ Бор Н. Избранные научные труды (статьи 1909-1925 г.г). — М.: Наука, 1973. — Т. 1. — С. 133. — 584 с.
- ↑ 1 2 Химический энциклопедический словарь / гл. редактор И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — С. 646. — 792 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1962. — Т. 1. — С. 338. — 1072 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1964. — Т. 3. — С. 24. — 1008 с.
Литература
- Білий М. У. Атомна фізика. — Київ: Вища школа, 1973. (укр.
 )
) - Федорченко А. М. Теоретична фізика. Квантова механіка, термодинаміка і статистична фізика. Т.2. — Київ: Вища школа, 1993.
- Юхновський І. Р. Основи квантової механіки. — Київ: Либідь, 2002.
- Ландау Л. Д., Лившиц Е. М. Теоретическая физика. т. ІІІ. Квантовая механика. Нерелятивистская теория. — М.: Наука, 1974.
Молекула водорода | это… Что такое Молекула водорода?
Моле́кула водоро́да — простейшая молекула, состоящая из двух атомов водорода. В её состав входят два ядра атомов водорода и два электрона. Вследствие взаимодействия между электронами и ядрами образуется ковалентная химическая связь. Кроме основной изотопной модификации H2, существуют разновидности, в которых один или оба атома протия заменены другими изотопами водорода — дейтерием или тритием: HD, HT, D2, DT, T2. Симметричность или несимметричность молекулы имеет значение при её вращении.
Содержание
|
Модели молекулы водорода
Рис.1.Модель водорода по Бору и осевая проекция электронного кольца
Н.Бор ещё в 1913 году дал описание модели молекулы водорода[1]. Согласно Бору, два внешних электрона, образующих молекулу, вращаются по одной и той же орбите вокруг линии, проходящей через ядра обоих атомов, и удерживают последние на определённом расстоянии друг от друга (рис.1). Боровская модель химической связи давала чёткую картину образования молекулярного водорода — динамическое равновесие системы, содержащей два протона, удерживающихся на определённом расстоянии друг от друга (d), притяжением кольца из двух электронов. При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.
При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.
Также как и боровская модель атома, боровская модель молекулы водорода не отражала и не могла отражать волновую природу электрона и статистическую интерпретацию волновой функции. Здесь уместно дополнить боровскую модель молекулы водорода достижениями квантовой механики, аналогично боровской модели атома. В этом случае гипотетическое кольцо электронов в модели молекулы водорода трансформируется в геометрическое место расположения плотности вероятности нахождения связывающих электронов. Электронную пару следует представлять электронным облаком в форме кольца, баранки, тора. При этом предполагается, что электроны в торе удалены друг от друга на максимально возможное расстояние, а электронная плотность в молекуле водорода имеет минимум — «кулоновскую дырку» на линии, соединяющей ядра молекулы водорода. Наиболее вероятный радиус электронного тора (re) определяется боровским радиусом a0 и межъядерным расстоянием (d)
Наиболее вероятный радиус электронного тора (re) определяется боровским радиусом a0 и межъядерным расстоянием (d)
re2 = a02 — (d/2)2; re = 0,377 Å.
Рис.2.Контурная карта электронной плотности для молекулы водорода[2]
В теории молекулярных орбиталей, разработанной в 1927—1932 г.г. Ф.Хундом, Р.Малликеном и др., модель молекулы водорода описывали контурными картами электронной плотности (рис.2).
Карта строится как разность между электронной плотностью молекулы и несвязанных атомов. Сплошные линии контурной карты отражают области увеличения электронной плотности (в единицах заряда электрона). Пунктирные — области её уменьшения в молекуле по сравнению с электронной плотностью несвязанных атомов водорода, сближенных на равновесное расстояние.[2]
Поскольку в теории молекулярных орбиталей учитывается лишь фермиевская корреляция электронов, поэтому электронная плотность в молекуле водорода сконцентрирована на линии, соединяющей ядра молекулы (см. рис.2).
рис.2).
Рис.3.Модель молекулы водорода в теории валентных связей
Квантово-механическую теорию ковалентной связи в молекуле водорода разработали в 1927 году Вальтер Гайтлер и Фриц Лондон. Выполненный ими расчёт волновых функций явился основой теории валентных связей. В этой теории модель молекулы водорода описывали перекрыванием атомных орбиталей атомов водорода (1S типа). Схема перекрывания электронных облаков, образующих сигма-связь молекулы водорода, совпадает с линией соединения атомных центров молекулы (рис.3).
Расчёт молекулы водорода в основном сводится к определению интеграла перекрытия атомных орбиталей.
Гамильтониан
Гамильтониан молекулы водорода H2 записывается в виде
- ,
где M — масса протона, m — масса электрона, — координаты ядер, — координаты электронов.![]()
В адиабатическом приближении задача нахождения энергетических состояний молекулы водорода разбивается на два этапа. На первом этапе рассматривается только электронная подсистема, а ядра считаются зафиксированными в точках и .
Гамильтониан электронной подсистемы имеет вид
- ,
Гамильтониан молекулы водорода симметричен относительно переменных и , то есть не изменяется при смене нумерации электронов. Кроме того, он не зависит от спиновых переменных.
Волновые функции
Схематическое изображение симметричной волновой функции молекулы водорода и образования ковалентной связи
Схематическое изображение антисимметричной волновой функции молекулы водорода
Исходя из принципа тождественности частиц и учитывая то, что электроны являются фермионами, волновая функция молекулы водорода должна быть антисимметричной относительно перестановки электронов. Независимость гамильтониана от спиновых переменных позволяет выбрать её в виде произведения двух функций, одна из которых зависит только от координат и называется координатной волновой функцией, а вторая зависит только от спинов и называется спиновой функцией.
Существуют два возможных типа спиновых функций для двух электронов: с параллельными спинами и с антипараллельными спинами. Функции с параллельными спинами симметричны относительно перестановки электронов и образуют триплетные состояния, в которых суммарный спин равен единице. Функции с антипараллельными спинами образуют синглетные состояния с нулевым суммарным спином (см. Мультиплетность, Состояние (квантовая механика)). Они антисимметричны относительно перестановки электронов.
Поскольку волновая функция электрона должна быть антисимметричной относительно перестановки, она может быть произведением либо
- симметричной координатной функции на антисимметричную спиновую функцию, либо
- антисимметричной координатной функции на симметричную спиновую функцию.
Симметричную и антисимметричную координатные функции основного состояния в нулевом приближении теории возмущений можно построить исходя из волновых функций основного состояния атома водорода .
Первый член каждой из приведенных волновых функций отвечает локализации электрона, пронумерованного индексом 1 на атоме с индексом 1 и электрона, пронумерованного индексом 2 на атоме с индексом 2. Второй член отвечает ситуации, когда первый электрон принадлежит второму атому, а второй — первому. При смене нумерации электронов первая (симметричная) функция не меняется, вторая (антисимметричная) — меняет знак.
Второй член отвечает ситуации, когда первый электрон принадлежит второму атому, а второй — первому. При смене нумерации электронов первая (симметричная) функция не меняется, вторая (антисимметричная) — меняет знак.
Энергия электронных состояний
Энергия электронных состояний находится усреднением гамильтониана на волновых функциях
- .
Для двух возможных волновых функций основного состояния она приобретает вид
- ,
где — расстояние между ядрами, — значение энергии основного состояния атома водорода, — интеграл перекрытия, который определяется выражением
- ,
— кулоновский интеграл, определяемый как
- ,
— обменный интерграл, равный
- .
Энергия молекулы водорода состоит из удвоенной энергии атома водорода, энергии кулоновского отталкивания между ядрами и членов, определяющих взаимодействие электронов между собой и с другим ядром. В зависимости от спинового состояния в формуле для следует выбирать знак «+» или знак «-». Знак «+» отвечает синглетному состоянию, знак «-» — триплетному.
В зависимости от спинового состояния в формуле для следует выбирать знак «+» или знак «-». Знак «+» отвечает синглетному состоянию, знак «-» — триплетному.
Величина — это средняя энергия кулоновского взаимодействия между двумя электронами и электронов с «чужим ядром». Величина определяет вклад в энергию обменного взаимодействия, которая не имеет аналога в классической механике. Именно этот член определяет существенное различие между синглетными и триплетными состояниями.
Зависимость энергии основного состояния от расстояния между ядрами
Ковалентная связь
Энергия взаимодействия атомов в молекуле водорода для синглетного(сплошная линия) и триплетного (пунктирная линия) состояний
Обменный интеграл для молеклы водорода в определённом диапазоне расстояний между атомами отрицательный. Вследствие этого, для синглетных состояний он обеспечивает дополнительное притягивание между ядрами атомов, а для триплетных — дополнительное отталкивание. Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Насыщение ковалентной связи
Для параллельных спинов, то есть для триплетного состояния, дополнительный положительный вклад в энергию приводит к тому, что атому отталкиваются на любом расстоянии. Этим объясняется насыщение ковалентной связи. Молекула водорода может состоять только из двух атомов. Третий атом водорода не может образовать связь с молекулой потому, что его спин непременно будет параллельным одному из спинов электронов в составе молекулы. Параллельность спинов приводит к отталкиванию между ядрами на любом расстоянии.
Необходимо отметить, что на больших расстояниях между атомами они притягиваются в любых состояниях благодаря Ван-дер-Ваальсовому взаимодействию, которое, однако, намного слабее ковалентной связи. Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Движение ядер в молекуле водорода
Гамильтониан, описывающий относительное движение двух ядер в молекуле водорода имеет вид
- ,
где — приведённая масса двух ядер, — энергия синглетного электронного состояния, зависящая от расстояния между ядрами (определена в предыдущем разделе), — оператор углового момента, описывающий вращение молекулы.
Вращение
Оператор углового момента коммутирует с гамильтонианом, поэтому собственные функции гамильтониана можно выбрать общими с собственными функциями оператора углового момента, то есть сферические гармоники:
- .
Вклад вращения в энергию молекулы равен
- .
Этот вклад мал, потому, что массы ядер намного больше, чем массы электронов. Он зависит от расстояния между ядрами R. При колебаниях ядер это расстояние меняется, поэтому вращательное движение, строго говоря, невозможно отделить от колебательного. Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Вращательные уровни вырождены относительно магнитного квантового числа ml. Кратность вырождения 2l+1.
Колебания атомов
Вблизи минимума функцию можно разложить в ряд Тейлора, ограничившись только квадратичным членом.
- ,
где
Таким образом, задача об энергетических состояниях колебания ядер сводится к задаче квантового гармонического осциллятора. Следовательно, для низших колебательных и вращательных уровней энергия молекулы водорода равна
- ,
где — колебательное квантовое число.
Низшая энергия колебания отвечает нулевым колебаниям.
При больших значениях квантовых чисел n и l колебательное и вращательное движение разделить невозможно.
Таким образом, энергию молекулы при малых квантовых числах можно записать в виде трёх слагаемых — электронного, колебательного и вращательного:
Малым параметром задачи является отношение массы электрона к массе протона. Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
- .
Следовательно, электронный уровень расщепляется на несколько колебательных, каждый из которых, в свою очередь, расщепляется на вращательные. Поскольку энергии вращательных уровней близки, то в оптических спектрах они сливаются в полосы — образуется полосатый спектр, который наблюдается для молекулы HD. Для симметричной молекулы H2 переходы между орбитальными и колебательными уровнями запрещены правилами отбора, поэтому молекулярный протий не поглощает в инфракрасной области.
Пара- и ортоводород
Схематическое изображене спиновых изомеров водорода
Ядра атомов водорода, входящие в состав молекулы, являются протонами — фермионами со спином 1/2. По правилам сложения спинов ядерный спин молекулы может быть 0 или 1. Молекулы водорода с суммарным ядерным спином 0 называют параводородом, а молекулы с суммарным ядерным спином 1 и тремя возможными проекциями (−1, 0, 1) называют ортоводородом. В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
Характеристики молекулы водорода
Межъядерные расстояния и энергии диссоциации молекул водорода, его изотопов и молекулярного иона водорода[3]
| Молекула | Межъядерное расстояние,Å | Энергия диссоциации, Эв |
|---|---|---|
| H2 | 0,7416 | 4,477 |
| HD | 0,7414 | 4,512 |
| D2 | 0,7416 | 4,555 |
| DT | 0,7416 | 4,570 |
| T2 | 0,7416 | 4,588 |
| HT | 0,7416 | 4,524 |
| H2+ | 1,06 | 2,648 |
Константы реакции диссоциации молекулярного водорода (Kp) и степень превращения (α) в зависимости от абсолютной температуры[4]:
| T, к | 2000 | 3000 | 4000 | 5000 | 6000 | 8000 |
|---|---|---|---|---|---|---|
| Кр | 2,62 · 10-6 | 2,47 · 10-2 | 2,52 | 4,09 · 10 | 2,62 · 102 | 2,70 · 103 |
| α | 8,10 · 10-4 | 7,83 · 10-2 | 0,621 | 0,954 | 0,992 | 0,999 |
См.
 также
также- Молекулярный ион водорода
- Рекомбинация (химия)
- Боровская модель химической связи
- Кулоновская электронная корреляция
- Статистическая интерпретация волновой функции
- Теория молекулярных орбиталей
- Теория валентных связей
Примечания
- ↑ Бор Н. Избранные научные труды (статьи 1909-1925 г.г). — М.: Наука, 1973. — Т. 1. — С. 133. — 584 с.
- ↑ 1 2 Химический энциклопедический словарь / гл. редактор И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — С. 646. — 792 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1962. — Т. 1. — С. 338. — 1072 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1964. — Т. 3. — С. 24. — 1008 с.
Литература
- Білий М. У. Атомна фізика. — Київ: Вища школа, 1973. (укр.
 )
) - Федорченко А. М. Теоретична фізика. Квантова механіка, термодинаміка і статистична фізика. Т.2. — Київ: Вища школа, 1993.
- Юхновський І. Р. Основи квантової механіки. — Київ: Либідь, 2002.
- Ландау Л. Д., Лившиц Е. М. Теоретическая физика. т. ІІІ. Квантовая механика. Нерелятивистская теория. — М.: Наука, 1974.
Молекула водорода | это… Что такое Молекула водорода?
Моле́кула водоро́да — простейшая молекула, состоящая из двух атомов водорода. В её состав входят два ядра атомов водорода и два электрона. Вследствие взаимодействия между электронами и ядрами образуется ковалентная химическая связь. Кроме основной изотопной модификации H2, существуют разновидности, в которых один или оба атома протия заменены другими изотопами водорода — дейтерием или тритием: HD, HT, D2, DT, T2. Симметричность или несимметричность молекулы имеет значение при её вращении.
Содержание
|
Модели молекулы водорода
Рис.1.Модель водорода по Бору и осевая проекция электронного кольца
Н.Бор ещё в 1913 году дал описание модели молекулы водорода[1]. Согласно Бору, два внешних электрона, образующих молекулу, вращаются по одной и той же орбите вокруг линии, проходящей через ядра обоих атомов, и удерживают последние на определённом расстоянии друг от друга (рис.1). Боровская модель химической связи давала чёткую картину образования молекулярного водорода — динамическое равновесие системы, содержащей два протона, удерживающихся на определённом расстоянии друг от друга (d), притяжением кольца из двух электронов. При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.
При этом модель Н.Бора отражала кулоновскую электронную корреляцию — оба электрона за счёт электростатического отталкивания находятся в диаметрально противоположных точках электронного кольца вокруг линии, проходящей через ядра обоих атомов молекулы водорода.
Также как и боровская модель атома, боровская модель молекулы водорода не отражала и не могла отражать волновую природу электрона и статистическую интерпретацию волновой функции. Здесь уместно дополнить боровскую модель молекулы водорода достижениями квантовой механики, аналогично боровской модели атома. В этом случае гипотетическое кольцо электронов в модели молекулы водорода трансформируется в геометрическое место расположения плотности вероятности нахождения связывающих электронов. Электронную пару следует представлять электронным облаком в форме кольца, баранки, тора. При этом предполагается, что электроны в торе удалены друг от друга на максимально возможное расстояние, а электронная плотность в молекуле водорода имеет минимум — «кулоновскую дырку» на линии, соединяющей ядра молекулы водорода. Наиболее вероятный радиус электронного тора (re) определяется боровским радиусом a0 и межъядерным расстоянием (d)
Наиболее вероятный радиус электронного тора (re) определяется боровским радиусом a0 и межъядерным расстоянием (d)
re2 = a02 — (d/2)2; re = 0,377 Å.
Рис.2.Контурная карта электронной плотности для молекулы водорода[2]
В теории молекулярных орбиталей, разработанной в 1927—1932 г.г. Ф.Хундом, Р.Малликеном и др., модель молекулы водорода описывали контурными картами электронной плотности (рис.2).
Карта строится как разность между электронной плотностью молекулы и несвязанных атомов. Сплошные линии контурной карты отражают области увеличения электронной плотности (в единицах заряда электрона). Пунктирные — области её уменьшения в молекуле по сравнению с электронной плотностью несвязанных атомов водорода, сближенных на равновесное расстояние.[2]
Поскольку в теории молекулярных орбиталей учитывается лишь фермиевская корреляция электронов, поэтому электронная плотность в молекуле водорода сконцентрирована на линии, соединяющей ядра молекулы (см. рис.2).
рис.2).
Рис.3.Модель молекулы водорода в теории валентных связей
Квантово-механическую теорию ковалентной связи в молекуле водорода разработали в 1927 году Вальтер Гайтлер и Фриц Лондон. Выполненный ими расчёт волновых функций явился основой теории валентных связей. В этой теории модель молекулы водорода описывали перекрыванием атомных орбиталей атомов водорода (1S типа). Схема перекрывания электронных облаков, образующих сигма-связь молекулы водорода, совпадает с линией соединения атомных центров молекулы (рис.3).
Расчёт молекулы водорода в основном сводится к определению интеграла перекрытия атомных орбиталей.
Гамильтониан
Гамильтониан молекулы водорода H2 записывается в виде
- ,
где M — масса протона, m — масса электрона, — координаты ядер, — координаты электронов.
В адиабатическом приближении задача нахождения энергетических состояний молекулы водорода разбивается на два этапа. На первом этапе рассматривается только электронная подсистема, а ядра считаются зафиксированными в точках и .
Гамильтониан электронной подсистемы имеет вид
- ,
Гамильтониан молекулы водорода симметричен относительно переменных и , то есть не изменяется при смене нумерации электронов. Кроме того, он не зависит от спиновых переменных.
Волновые функции
Схематическое изображение симметричной волновой функции молекулы водорода и образования ковалентной связи
Схематическое изображение антисимметричной волновой функции молекулы водорода
Исходя из принципа тождественности частиц и учитывая то, что электроны являются фермионами, волновая функция молекулы водорода должна быть антисимметричной относительно перестановки электронов. Независимость гамильтониана от спиновых переменных позволяет выбрать её в виде произведения двух функций, одна из которых зависит только от координат и называется координатной волновой функцией, а вторая зависит только от спинов и называется спиновой функцией.
Существуют два возможных типа спиновых функций для двух электронов: с параллельными спинами и с антипараллельными спинами. Функции с параллельными спинами симметричны относительно перестановки электронов и образуют триплетные состояния, в которых суммарный спин равен единице. Функции с антипараллельными спинами образуют синглетные состояния с нулевым суммарным спином (см. Мультиплетность, Состояние (квантовая механика)). Они антисимметричны относительно перестановки электронов.
Поскольку волновая функция электрона должна быть антисимметричной относительно перестановки, она может быть произведением либо
- симметричной координатной функции на антисимметричную спиновую функцию, либо
- антисимметричной координатной функции на симметричную спиновую функцию.
Симметричную и антисимметричную координатные функции основного состояния в нулевом приближении теории возмущений можно построить исходя из волновых функций основного состояния атома водорода .
Первый член каждой из приведенных волновых функций отвечает локализации электрона, пронумерованного индексом 1 на атоме с индексом 1 и электрона, пронумерованного индексом 2 на атоме с индексом 2. Второй член отвечает ситуации, когда первый электрон принадлежит второму атому, а второй — первому. При смене нумерации электронов первая (симметричная) функция не меняется, вторая (антисимметричная) — меняет знак.
Второй член отвечает ситуации, когда первый электрон принадлежит второму атому, а второй — первому. При смене нумерации электронов первая (симметричная) функция не меняется, вторая (антисимметричная) — меняет знак.
Энергия электронных состояний
Энергия электронных состояний находится усреднением гамильтониана на волновых функциях
- .
Для двух возможных волновых функций основного состояния она приобретает вид
- ,
где — расстояние между ядрами, — значение энергии основного состояния атома водорода, — интеграл перекрытия, который определяется выражением
- ,
— кулоновский интеграл, определяемый как
- ,
— обменный интерграл, равный
- .
Энергия молекулы водорода состоит из удвоенной энергии атома водорода, энергии кулоновского отталкивания между ядрами и членов, определяющих взаимодействие электронов между собой и с другим ядром. В зависимости от спинового состояния в формуле для следует выбирать знак «+» или знак «-». Знак «+» отвечает синглетному состоянию, знак «-» — триплетному.
В зависимости от спинового состояния в формуле для следует выбирать знак «+» или знак «-». Знак «+» отвечает синглетному состоянию, знак «-» — триплетному.
Величина — это средняя энергия кулоновского взаимодействия между двумя электронами и электронов с «чужим ядром». Величина определяет вклад в энергию обменного взаимодействия, которая не имеет аналога в классической механике. Именно этот член определяет существенное различие между синглетными и триплетными состояниями.
Зависимость энергии основного состояния от расстояния между ядрами
Ковалентная связь
Энергия взаимодействия атомов в молекуле водорода для синглетного(сплошная линия) и триплетного (пунктирная линия) состояний
Обменный интеграл для молеклы водорода в определённом диапазоне расстояний между атомами отрицательный. Вследствие этого, для синглетных состояний он обеспечивает дополнительное притягивание между ядрами атомов, а для триплетных — дополнительное отталкивание. Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Дополнительное притягивание обусловливает появление минимума электронной энергии на расстоянии приблизительно в 1,5 радиуса Бора (что соответствует приблизительно 75 пм). Этот минимум возникает только для синглетного состояния, то есть для антипараллельных спинов. Таким образом устанавливается ковалентная связь между атомами. Электроны двух атомов водорода «спариваются».
Насыщение ковалентной связи
Для параллельных спинов, то есть для триплетного состояния, дополнительный положительный вклад в энергию приводит к тому, что атому отталкиваются на любом расстоянии. Этим объясняется насыщение ковалентной связи. Молекула водорода может состоять только из двух атомов. Третий атом водорода не может образовать связь с молекулой потому, что его спин непременно будет параллельным одному из спинов электронов в составе молекулы. Параллельность спинов приводит к отталкиванию между ядрами на любом расстоянии.
Необходимо отметить, что на больших расстояниях между атомами они притягиваются в любых состояниях благодаря Ван-дер-Ваальсовому взаимодействию, которое, однако, намного слабее ковалентной связи. Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Ван-дер-Ваальсово взаимодействие не учитывается в приведенной теории, поскольку требует рассмотрения возбуждённых состояний высших, чем 1s-орбиталь.
Движение ядер в молекуле водорода
Гамильтониан, описывающий относительное движение двух ядер в молекуле водорода имеет вид
- ,
где — приведённая масса двух ядер, — энергия синглетного электронного состояния, зависящая от расстояния между ядрами (определена в предыдущем разделе), — оператор углового момента, описывающий вращение молекулы.
Вращение
Оператор углового момента коммутирует с гамильтонианом, поэтому собственные функции гамильтониана можно выбрать общими с собственными функциями оператора углового момента, то есть сферические гармоники:
- .
Вклад вращения в энергию молекулы равен
- .
Этот вклад мал, потому, что массы ядер намного больше, чем массы электронов. Он зависит от расстояния между ядрами R. При колебаниях ядер это расстояние меняется, поэтому вращательное движение, строго говоря, невозможно отделить от колебательного. Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Однако при малых l и при малых энергиях колебательного движения можно считать, что R равняется определённому среднему значению.
Вращательные уровни вырождены относительно магнитного квантового числа ml. Кратность вырождения 2l+1.
Колебания атомов
Вблизи минимума функцию можно разложить в ряд Тейлора, ограничившись только квадратичным членом.
- ,
где
Таким образом, задача об энергетических состояниях колебания ядер сводится к задаче квантового гармонического осциллятора. Следовательно, для низших колебательных и вращательных уровней энергия молекулы водорода равна
- ,
где — колебательное квантовое число.
Низшая энергия колебания отвечает нулевым колебаниям.
При больших значениях квантовых чисел n и l колебательное и вращательное движение разделить невозможно.
Таким образом, энергию молекулы при малых квантовых числах можно записать в виде трёх слагаемых — электронного, колебательного и вращательного:
Малым параметром задачи является отношение массы электрона к массе протона. Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
Электронное слагаемое не зависит от этого отношения, колебательное пропорционально , вращательное пропорционально . Поэтому
- .
Следовательно, электронный уровень расщепляется на несколько колебательных, каждый из которых, в свою очередь, расщепляется на вращательные. Поскольку энергии вращательных уровней близки, то в оптических спектрах они сливаются в полосы — образуется полосатый спектр, который наблюдается для молекулы HD. Для симметричной молекулы H2 переходы между орбитальными и колебательными уровнями запрещены правилами отбора, поэтому молекулярный протий не поглощает в инфракрасной области.
Пара- и ортоводород
Схематическое изображене спиновых изомеров водорода
Ядра атомов водорода, входящие в состав молекулы, являются протонами — фермионами со спином 1/2. По правилам сложения спинов ядерный спин молекулы может быть 0 или 1. Молекулы водорода с суммарным ядерным спином 0 называют параводородом, а молекулы с суммарным ядерным спином 1 и тремя возможными проекциями (−1, 0, 1) называют ортоводородом. В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
В состоянии термодинамического равновесия при комнатной температуре отношение между ортоводородом и параводородом составляет 3:1. Однако при низких температурах в состоянии термодинамического равновесия молекулы параводорода доминируют благодаря разным вращательным свойствам: параводород является симметричным ротатором, ортоводород — несимметричным ротатором. Переход ортоводорода в параводород — медленный процесс, и состояние термодинамического равновесия при низких температурах устанавливается долго.
Характеристики молекулы водорода
Межъядерные расстояния и энергии диссоциации молекул водорода, его изотопов и молекулярного иона водорода[3]
| Молекула | Межъядерное расстояние,Å | Энергия диссоциации, Эв |
|---|---|---|
| H2 | 0,7416 | 4,477 |
| HD | 0,7414 | 4,512 |
| D2 | 0,7416 | 4,555 |
| DT | 0,7416 | 4,570 |
| T2 | 0,7416 | 4,588 |
| HT | 0,7416 | 4,524 |
| H2+ | 1,06 | 2,648 |
Константы реакции диссоциации молекулярного водорода (Kp) и степень превращения (α) в зависимости от абсолютной температуры[4]:
| T, к | 2000 | 3000 | 4000 | 5000 | 6000 | 8000 |
|---|---|---|---|---|---|---|
| Кр | 2,62 · 10-6 | 2,47 · 10-2 | 2,52 | 4,09 · 10 | 2,62 · 102 | 2,70 · 103 |
| α | 8,10 · 10-4 | 7,83 · 10-2 | 0,621 | 0,954 | 0,992 | 0,999 |
См.
 также
также- Молекулярный ион водорода
- Рекомбинация (химия)
- Боровская модель химической связи
- Кулоновская электронная корреляция
- Статистическая интерпретация волновой функции
- Теория молекулярных орбиталей
- Теория валентных связей
Примечания
- ↑ Бор Н. Избранные научные труды (статьи 1909-1925 г.г). — М.: Наука, 1973. — Т. 1. — С. 133. — 584 с.
- ↑ 1 2 Химический энциклопедический словарь / гл. редактор И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — С. 646. — 792 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1962. — Т. 1. — С. 338. — 1072 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — М.-Л.: ГНТИ Химической литературы, 1964. — Т. 3. — С. 24. — 1008 с.
Литература
- Білий М. У. Атомна фізика. — Київ: Вища школа, 1973. (укр.
 )
) - Федорченко А. М. Теоретична фізика. Квантова механіка, термодинаміка і статистична фізика. Т.2. — Київ: Вища школа, 1993.
- Юхновський І. Р. Основи квантової механіки. — Київ: Либідь, 2002.
- Ландау Л. Д., Лившиц Е. М. Теоретическая физика. т. ІІІ. Квантовая механика. Нерелятивистская теория. — М.: Наука, 1974.
Водородная связь — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1660
Водородная связь представляет собой межмолекулярную силу (IMF), которая образует особый тип диполь-дипольного притяжения, когда атом водорода, связанный с сильно электроотрицательным атомом, существует вблизи другого электроотрицательного атома с неподеленной парой электронов. Межмолекулярные силы (IMF) возникают между молекулами. Другие примеры включают обычные диполь-дипольные взаимодействия и дисперсионные силы. Водородные связи, как правило, прочнее обычных диполь-дипольных и дисперсионных сил, но слабее истинных ковалентных и ионных связей.
Межмолекулярные силы (IMF) возникают между молекулами. Другие примеры включают обычные диполь-дипольные взаимодействия и дисперсионные силы. Водородные связи, как правило, прочнее обычных диполь-дипольных и дисперсионных сил, но слабее истинных ковалентных и ионных связей.
Доказательства водородной связи
Многие элементы образуют соединения с водородом. Если вы нанесете точки кипения соединений элементов группы 14 с водородом, вы обнаружите, что точки кипения увеличиваются по мере того, как вы спускаетесь по группе.
Рис. 1: Температуры кипения галогенидов 14-й группы.Повышение температуры кипения происходит из-за того, что молекулы становятся больше с большим количеством электронов, и поэтому дисперсионные силы Ван-дер-Ваальса становятся больше. Если вы повторите это упражнение с соединениями элементов групп 15, 16 и 17 с водородом, произойдет нечто странное.
Рисунок 2: Температуры кипения галогенидов элементов 15-17 групп. Хотя те же рассуждения применимы к группе 4 периодической таблицы, температура кипения соединения водорода с первым элементом в каждой группе аномально высока. В случаях \(NH_3\), \(H_2O\) и \(HF\) должны существовать какие-то дополнительные силы межмолекулярного притяжения, требующие значительно большей тепловой энергии для разрыва ММП. Эти относительно мощные межмолекулярные силы описываются как водородные связи.
В случаях \(NH_3\), \(H_2O\) и \(HF\) должны существовать какие-то дополнительные силы межмолекулярного притяжения, требующие значительно большей тепловой энергии для разрыва ММП. Эти относительно мощные межмолекулярные силы описываются как водородные связи.
Происхождение водородных связей
Молекулы, способные образовывать водородные связи, включают следующее:
Рисунок 3: Неподеленные пары, ответственные за водородные связи в \(NH_3\), \(H_2O\) и \(HF\). Сплошная линия представляет собой связь в плоскости экрана или бумаги. Точечные связи уходят обратно в экран или бумагу от вас, а клиновидные выходят к вам.Обратите внимание, что в каждой из этих молекул:
- Водород присоединен непосредственно к сильно электроотрицательным атомам, в результате чего водород приобретает сильно положительный заряд.
- Каждый из сильно электроотрицательных атомов приобретает высокий отрицательный заряд и имеет по крайней мере одну «активную» неподеленную пару.
 У неподеленных пар на уровне 2 электроны содержатся в относительно небольшом объеме пространства, что приводит к высокой плотности отрицательного заряда. Неподеленные пары на более высоких уровнях более рассеяны, что приводит к более низкой плотности заряда и меньшему сродству к положительному заряду.
У неподеленных пар на уровне 2 электроны содержатся в относительно небольшом объеме пространства, что приводит к высокой плотности отрицательного заряда. Неподеленные пары на более высоких уровнях более рассеяны, что приводит к более низкой плотности заряда и меньшему сродству к положительному заряду.
Если вы не знакомы с электроотрицательностью, вам следует перейти по этой ссылке, прежде чем продолжить. 9+\) водород настолько сильно притягивается к неподеленной паре, что создается впечатление, будто вы начинаете формировать координационную (дательную ковалентную) связь. Это не заходит так далеко, но притяжение значительно сильнее, чем обычное диполь-дипольное взаимодействие. Водородные связи имеют примерно одну десятую прочности средней ковалентной связи и постоянно разрываются и восстанавливаются в жидкой воде. Если вы сравните ковалентную связь между кислородом и водородом со стабильным браком, водородная связь имеет статус «просто хороших друзей». 9+\) атомов водорода и неподеленных пар, каждый из которых участвует в образовании водородных связей.
Вот почему температура кипения воды выше, чем у аммиака или фтористого водорода. В случае аммиака количество водородных связей ограничено тем фактом, что каждый атом азота имеет только одну неподеленную пару. В группе молекул аммиака не хватает неподеленных пар, чтобы удовлетворить все атомы водорода. Во фтороводороде проблема заключается в нехватке водорода. В воде две водородные связи и две неподеленные пары позволяют образовывать взаимодействия водородных связей в решетке молекул воды. Таким образом, вода считается идеальной системой с водородными связями.
Более сложные примеры водородных связей
Гидратация отрицательных ионов
Когда ионное вещество растворяется в воде, молекулы воды группируются вокруг разделенных ионов. Этот процесс называется гидратацией. Вода часто присоединяется к положительным ионам координационными (дательными ковалентными) связями. Он связывается с отрицательными ионами с помощью водородных связей.
Если вас интересует связь в гидратированных положительных ионах, вы можете перейти по этой ссылке, чтобы ознакомиться с координационной (дательной ковалентной) связью.
На схеме показаны потенциальные водородные связи, образованные ионом хлора Cl-. Хотя неподеленные пары в ионе хлорида находятся на уровне 3 и обычно недостаточно активны для образования водородных связей, в этом случае они становятся более привлекательными за счет полного отрицательного заряда хлора.
Рис. 5: Водородная связь между ионами хлора и водой.Каким бы сложным ни был отрицательный ион, всегда будут неподеленные пары, с которыми атомы водорода из молекул воды могут водородно связываться.
Водородная связь в спиртах
Спирт представляет собой органическую молекулу, содержащую группу -ОН. Любая молекула, в которой атом водорода присоединен непосредственно к кислороду или азоту, способна образовывать водородные связи. Водородные связи также возникают, когда водород связан со фтором, но группа HF не появляется в других молекулах. Молекулы с водородными связями всегда будут иметь более высокую температуру кипения, чем молекулы аналогичного размера, которые не имеют группы -ОН или -NH.
Водородная связь делает молекулы «более липкими», так что для их разделения требуется больше тепла (энергии). Это явление можно использовать для анализа температуры кипения различных молекул, определяемой как температура, при которой происходит фазовый переход от жидкости к газу.
Этанол, \(\ce{Ch4Ch3-O-H}\), и метоксиметан, \(\ce{Ch4-O-Ch4}\), имеют одинаковую молекулярную формулу, \(\ce{C2H6O}\).
У них одинаковое количество электронов и одинаковая длина. Притяжение Ван-дер-Ваальса (как дисперсионные силы, так и диполь-дипольное притяжение) в каждом из них будет одинаковым. Однако у этанола атом водорода присоединен непосредственно к кислороду; здесь у кислорода все еще есть две неподеленные пары, как у молекулы воды. Водородная связь может возникать между молекулами этанола, хотя и не так эффективно, как в воде. Водородная связь ограничена тем фактом, что в каждой молекуле этанола имеется только один водород с достаточным зарядом +.
В метоксиметане неподеленные пары кислорода все еще присутствуют, но атомов водорода недостаточно + для образования водородных связей.
За исключением некоторых довольно необычных случаев, атом водорода должен быть присоединен непосредственно к самому электроотрицательному элементу, чтобы возникла водородная связь. Температуры кипения этанола и метоксиметана показывают резкое влияние водородных связей на липкость молекул этанола:
этанол (с водородными связями) 78,5°С метоксиметан (без водородной связи) -24,8°С Водородная связь в этаноле подняла его температуру кипения примерно на 100°C. Важно понимать, что помимо притяжения Ван-дер-Ваальса существуют водородные связи. Например, все следующие молекулы содержат одинаковое количество электронов, а первые две имеют одинаковую длину цепи. Более высокая температура кипения бутан-1-ола обусловлена дополнительной водородной связью.
При сравнении двух спиртов (содержащих группы -ОН) оба имеют высокие температуры кипения из-за дополнительной водородной связи; однако значения не совпадают.
Температура кипения 2-метилпропан-1-ола не такая высокая, как у бутан-1-ола, потому что разветвление молекулы делает ван-дер-ваальсово притяжение менее эффективным, чем у более длинного бутан-1-ола.
Водородная связь в органических молекулах, содержащих азот
Водородная связь также возникает в органических молекулах, содержащих группы N-H; вспомните водородные связи, возникающие с аммиаком. Примеры варьируются от простых молекул, таких как CH 3 NH 2 (метиламин) в большие молекулы, такие как белки и ДНК. Две нити знаменитой двойной спирали в ДНК удерживаются вместе водородными связями между атомами водорода, присоединенными к азоту на одной цепи, и неподеленными парами на другой азот или кислород на другой.
Доноры и акцепторы
Для образования водородной связи должны присутствовать как донор водорода, так и акцептор. Донором в водородной связи обычно является сильно электроотрицательный атом, такой как N, O или F, который ковалентно связан с водородной связью.
Акцептор водорода представляет собой электроотрицательный атом соседней молекулы или иона, который содержит неподеленную пару, участвующую в водородной связи.
Почему возникает водородная связь?
Поскольку донор водорода (N, O или F) является сильно электроотрицательным, он притягивает ковалентно связанную электронную пару ближе к своему ядру и от атома водорода. Затем атом водорода остается с частичным положительным зарядом, создавая диполь-дипольное притяжение между атомом водорода, связанным с донором, и неподеленной электронной парой акцептора. Это приводит к образованию водородной связи (см. Взаимодействие между молекулами с постоянными диполями)
Типы водородных связей
Хотя водородные связи хорошо известны как тип IMF, эти связи также могут возникать внутри одной молекулы, между двумя идентичными молекулами или между двумя разнородными молекулами.
Внутримолекулярные водородные связи
Внутримолекулярные водородные связи возникают внутри одной единственной молекулы.
Это происходит, когда две функциональные группы молекулы могут образовывать водородные связи друг с другом. Для этого в одной молекуле должны присутствовать как донор водорода, так и акцептор водорода, и они должны находиться в непосредственной близости друг от друга в молекуле. Например, внутримолекулярная водородная связь возникает в этиленгликоле (C 2 H 4 (OH) 2 ) между двумя его гидроксильными группами из-за молекулярной геометрии.
Межмолекулярные водородные связи
Межмолекулярные водородные связи возникают между отдельными молекулами вещества. Они могут возникать между любым количеством одинаковых или разных молекул, если доноры и акцепторы водорода находятся в положениях, в которых они могут взаимодействовать друг с другом. Например, межмолекулярные водородные связи могут возникать между NH 3 только молекулы, только между H 2 молекулами O или между NH 3 и H 2 молекулами O.
Свойства и влияние водородных связей
О температуре кипения
Когда мы рассматриваем точки кипения молекул, мы обычно ожидаем, что молекулы с большей молярной массой будут иметь более высокие нормальные точки кипения, чем молекулы с меньшей молярной массой. Это, без учета водородных связей, связано с большими дисперсионными силами (см. Взаимодействие между неполярными молекулами). Более крупные молекулы имеют больше места для распределения электронов и, следовательно, больше возможностей для мгновенного дипольного момента. Однако, если мы рассмотрим приведенную ниже таблицу, то увидим, что это не всегда так.
Соединение Молярная масса Нормальная температура кипения \(H_2O\) 18 г/моль 373 К \(ВЧ\) 20 г/моль 292,5 К \(NH_3\) 17 г/моль 239,8 К \(H_2S\) 34 г/моль 212,9 К \(HCl\) 36,4 г/моль 197,9 К \(PH_3\) 34 г/моль 185,2 К Мы видим, что H 2 O, HF и NH 3 имеют более высокие точки кипения, чем одно и то же соединение, образующееся между водородом и следующим элементом, движущимся вниз по соответствующей группе, что указывает на то, что первые обладают большими межмолекулярными силами.
. Это потому, что Н 2 O, HF и NH 3 все имеют водородные связи, тогда как другие нет. Кроме того, \(H_2O\) имеет меньшую молярную массу, чем HF, но имеет больше водородных связей на молекулу, поэтому его температура кипения выше.
О вязкости
Тот же эффект, что и при температуре кипения в результате образования водородных связей, можно наблюдать и в отношении вязкости некоторых веществ. Вещества, способные образовывать водородные связи, как правило, имеют более высокую вязкость, чем те, которые не образуют водородных связей. Как правило, вещества, которые могут иметь несколько водородных связей, обладают еще более высокой вязкостью.
Факторы, препятствующие образованию водородной связи
Электроотрицательность
Водородная связь не может возникнуть без значительных различий в электроотрицательности между водородом и атомом, с которым он связан. Таким образом, мы видим такие молекулы, как PH 3 , которые не участвуют в водородных связях.
PH 3 имеет тригонально-пирамидальную молекулярную геометрию, как у аммиака, но в отличие от NH 3 не может образовывать водородные связи. Это связано со сходством электроотрицательностей фосфора и водорода. Оба атома имеют электроотрицательность 2,1, поэтому дипольный момент отсутствует. Это предотвращает получение атомом водорода частичного положительного заряда, необходимого для водородной связи с неподеленной электронной парой в другой молекуле. (см. Поляризуемость)
Размер атома
Размер доноров и акцепторов также может влиять на способность к образованию водородных связей. Это может объяснить относительно низкую способность Cl образовывать водородные связи. Когда радиусы двух атомов сильно различаются или велики, их ядра не могут достичь непосредственной близости при взаимодействии, что приводит к слабому взаимодействию.
Водородные связи в природе
Водородные связи играют решающую роль во многих биологических процессах и могут объяснить многие природные явления, такие как необычные свойства воды.
Помимо того, что они присутствуют в воде, водородные связи также важны в водной транспортной системе растений, вторичной и третичной структуре белков и спаривании оснований ДНК.
Растения
Когезионно-адгезионная теория транспорта в сосудистых растениях использует водородные связи для объяснения многих ключевых компонентов движения воды через ксилему растения и другие сосуды. Молекулы воды внутри сосуда водородно связываются не только друг с другом, но и с цепочкой целлюлозы, из которой состоит стенка растительной клетки. Поскольку сосуд относительно мал, притяжение воды к целлюлозной стенке создает своего рода капиллярную трубку, обеспечивающую капиллярное действие. Этот механизм позволяет растениям втягивать воду в свои корни. Кроме того, водородные связи могут создать длинную цепочку молекул воды, которая может преодолеть силу гравитации и подняться на большие высоты листьев.
Белки
Водородные связи в изобилии присутствуют во вторичной структуре белков, а также редко в третичной конформации.
Вторичная структура белка включает взаимодействия (в основном водородные связи) между соседними полипептидными остовами, которые содержат пары, связанные азотом и водородом, и атомы кислорода. Поскольку и N, и O сильно электроотрицательны, атомы водорода, связанные с азотом в одной полипептидной цепи, могут водородно связываться с атомами кислорода в другой цепи, и наоборот. Хотя они относительно слабые, эти связи обеспечивают существенную устойчивость вторичной белковой структуры, поскольку они повторяются много раз и работают коллективно.
В третичной структуре белка взаимодействия в основном происходят между функциональными R-группами полипептидной цепи; одно такое взаимодействие называется гидрофобным взаимодействием. Эти взаимодействия происходят из-за водородных связей между молекулами воды вокруг гидрофоба, что еще больше укрепляет конформацию белка.
Ссылки
- Brown, et al. Химия: центральная наука. 11-е изд. Река Аппер-Сэдл, Нью-Джерси: Пирсон / Прентис-Холл, 2008 г.
.- Чанг, Рэймонд. Общая химия: основные понятия. 3-е изд. Нью-Йорк: Макгроу Хилл, 2003 г.
- Петруччи и др. Общая химия: принципы и современные приложения. 9-е изд. Река Аппер-Сэдл, Нью-Джерси: Пирсон / Прентис-Холл, 2007.
.Hydrogen Bonding распространяется под лицензией CC BY-NC-SA 4.0, автором, ремиксом и/или куратором выступили Джим Кларк и Хосе Пьетри.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги
- автор @ Джим Кларк
- автор @ Хосе Пьетри
- водородная связь
3.3.2: Волновое поведение и связь в молекуле водорода
В начале 20-го века наше понимание света и материи развивалось очень быстро, но некоторые вещи все еще не имели смысла для людей. Все действительно начало получаться, когда ряд физиков начали думать о вещах по-другому. Одна из революционных вещей, которые они сделали, состояла в том, чтобы серьезно рассмотреть с помощью математических уравнений волновую природу света и материи.
В случае со светом идея восходит к середине 17 века. Кристиан Гюйгенс, голландский часовщик и астроном, полагал, что свет распространяется волнами, потому что он мог видеть свидетельство интерференции в свете, очень похожее на то, как рябь на пруду может интерферировать друг с другом, создавая новые узоры.
Другие ученые, такие как Ньютон, действительно думали, что свет состоит из мелких частиц. В некотором смысле оба были правы, и теперь мы думаем о частицах света, или фотонах, как об обладающих некоторыми свойствами волн.
Что мы знаем о волнах? Хорошими примерами являются волны на поверхности озера или океана. Вероятно, вы внимательно изучали их в 6-м классе, хотя, возможно, забыли некоторые детали. Итак, давайте еще раз посмотрим.
Возможно, вы стояли рядом с волновым резервуаром в музее науки и видели что-то похожее на это. Поверхность воды колеблется вверх и вниз. Есть 90 134 гребня 90 135, где вода скапливается в холмах, и 90 134 впадины 90 135, где вода ускользает в долины. Где-то посередине находится средний уровень воды, где поверхность оседала бы, если бы все было спокойно и волн вообще не было.
Мы также можем думать о волнах как о нулевых точках или узлах; это позиции на полпути между гребнем и впадиной.
Макс Планк и Альберт Эйнштейн более внимательно рассмотрели эту идею в начале 1900-х годов, когда они пытались определить отношения между электронами в материалах и их взаимодействие с электромагнитным излучением.
Электромагнитное излучение включает в себя такие вещи, как ультрафиолетовый и видимый свет.
Если мы стоим на берегу моря, первое, что мы замечаем в волнах, это их высота. Может быть, это действительно спокойный день, и волны почти плоские. Может быть, это действительно тяжелый день, и волны очень высокие. Характеристика волн, которую вы замечаете, называется амплитудой. Это высота волны от среднего уровня воды до гребня или, наоборот, глубина до впадины. В макроскопическом мире действительно важна амплитуда волн. Вам нужно знать, нормально ли стоять и смотреть на волны, или это становится слишком грубым, и вам следует искать более высокое место. Если вы не будете осторожны, на вас может обрушиться волна очень высокой амплитуды.
Волны в океане могут иметь большую или малую амплитуду, и это имеет физические последствия. Звуковые волны также могут иметь большую амплитуду (это громкие) или малую амплитуду (это тихие). Конечно, если бы амплитуда была очень-очень низкой, у нас почти не было бы волны (когда этот человек шепчет что-то, а вы его даже не слышите).
В наномире, мире фотонов и электронов, амплитуда волны — гораздо более тонкая вещь. Это не первое наше соображение. Гораздо важнее длина волны. Длина волны — это просто расстояние от одного гребня до другого или от одного впадины до другого.
Длина волны действительно важна, потому что, согласно анализу экспериментальных данных, проведенному Планком и Эйнштейном, именно она определяет энергию отдельного фотона или энергию отдельного электрона. Чем короче длина волны фотона или электрона, тем выше его энергия. Чем больше длина волны фотона или электрона, тем меньше его энергия. Это отношение является примером обратной пропорциональности: когда одно становится больше, другое становится меньше.
У волн есть дополнительный атрибут – частота. Мы можем думать о частоте как о том, как часто волна достигает гребня. В качестве альтернативы, если мы представим электромагнитную волну, проходящую мимо неподвижного объекта, частота будет описывать, как часто гребень проходит мимо объекта.
(Весь свет распространяется с одинаковой скоростью, примерно 3 x 10 8 м с -1 , поэтому нам не нужно беспокоиться о том, что это фактор.)
Частота обратно пропорциональна длине волны: чем длиннее длина волны, тем ниже частота. Следовательно, частота прямо пропорциональна энергии фотона или электрона. Чем выше частота, тем выше энергия.
Упражнение \(\PageIndex{1}\)
Какая волна из каждой пары имеет большую энергию?
- Ответить
В каждом случае волна с более высокой частотой и меньшей длиной волны будет иметь более высокую энергию. а) я; б) ii; в, ii; д) я.
Вернемся к первоначальному наблюдению Христиана Гюйгенса за интерференционными картинами света. Что это значит?
Предположим, две волны сходятся. Мы рассмотрим два разных случая. В первом случае две волны совпадают по фазе друг с другом. Это означает, что они оба достигают гребня одновременно, и их впадины также всегда выровнены.
Что происходит тогда? Вы можете себе представить, что гребни будут просто нарастать друг на друга, становясь выше, а впадины будут впадать друг в друга, становясь глубже. Амплитуда волн вместе увеличивается. Это конструктивное вмешательство.
Теперь предположим, что две волны не совпадают по фазе. Когда один достигает пика, другой достигает дна. В этом случае гребень одной волны попадает во впадину другой. Все выравнивается. Это деструктивное вмешательство.
Конструктивная интерференция и деструктивная интерференция также происходят с волнами на воде. Это приводит к множеству волнистых узоров, если вы бросите два камня в неподвижный пруд. Фотоны также могут создавать такие узоры, как и электроны.
Льюис предполагает, что два атома с неспаренными электронами могут делиться своими электронами для образования связи. В структуре Льюиса мы можем изобразить эти два электрона между символами двух атомов, чтобы показать, что образовалась связь. Квантовая механика предлагает количественное математическое представление о молекулах и, как считается, дает точную картину поведения атомов и молекул.
Теперь вместо того, чтобы ставить два атома рядом друг с другом и позволять двум точкам соединяться, образуя связь, как в структуре Льюиса, мы будем думать о связи с точки зрения квантовой механики.
- Два атома водорода расположены рядом друг с другом.
- Два атома окружены волнами, образованными их электронами.
- Если два атома расположены близко друг к другу, эти две волны перекрываются между двумя атомами.
Что происходит, когда волны перекрываются? Развиваются интерференционные картины. Представьте себе плоский спокойный пруд, в который вы с другом бросаете два маленьких камня на расстоянии нескольких футов друг от друга. Образовавшаяся рябь движется по кругу от двух точек, куда упали камни, и когда два набора волн встречаются друг с другом, возникают новые узоры. Круговые наборы волн объединяются, чтобы сформировать новые волны с новыми формами.
Когда волны встречаются, возникают две основные комбинации. Эти комбинации зависят от того, находятся ли две волны в фазе или в противофазе друг с другом.
- Если волны совпадают по фазе, так что пик одной волны приходится на вершину пика другой, а впадина одной волны совпадает с впадиной другой, возникает конструктивная интерференция. Волны складываются и становятся больше там, где они пересекаются.
- Если волны точно не совпадают по фазе, пик одной падает на впадину другой, и там, где они перекрываются, две волны компенсируются. Это деструктивное вмешательство.
Мы можем применить эти идеи к электронам в атомах, которые собираются вместе, чтобы образовать связь. В структурах Льюиса отдельные электроны на двух разных атомах образуют пары в связи между двумя атомами. Электроны должны быть объединены, чтобы образовать связь. Если электроны обладают волновыми свойствами, то при сближении этих атомов возникают интерференционные картины.
Прежде чем мы начнем, обратите внимание, что волны, с которыми мы будем иметь дело, выглядят немного иначе, чем стоячие волны, которые мы рассматривали ранее.
Эти волны будут трехмерными и займут разные области пространства. Вместо того, чтобы отображать информацию о фазе в виде пиков и впадин, мы собираемся использовать общепринятое соглашение о затенении, чтобы обозначить, смотрим ли мы на положительную часть (с точки зрения фазы) или на отрицательную часть волны. Например, мы можем показать гребни синим цветом, а впадины — красным, или мы можем показать один черный, а другой — белый. В стоячей волне фазы будут выглядеть так:
В атоме водорода электрон находится в сферической области вокруг ядра. Мы не сможем увидеть две отдельные фазы — гребень и впадину — в этой волне одновременно. Однако мы могли бы взглянуть на два разных атома водорода и проиллюстрировать, находятся ли их электроны в фазе или в противофазе друг с другом.
Когда эти два электрона встречаются и находятся в фазе друг с другом, возникает конструктивная интерференция. Они не будут полностью перекрываться; это атомы, и они занимают место. Однако они смогут располагаться довольно близко друг к другу, как бы сталкивая свои электроны.
Это конструктивное вмешательство произойдет посередине, между атомами.
Когда два электрона встречаются и находятся в противофазе, возникает деструктивная интерференция. Опять же, это произойдет посередине, между атомами.
Итак, в паре атомов водорода две волны могут объединиться, чтобы дать два возможных результата.
- В одном случае высота комбинированной волны наибольшая между двумя атомами, где они перекрываются и находятся в фазе. Амплитуда волны здесь больше.
- В другом случае комбинированная волна состоит из двух половин, находящихся в противофазе, и между двумя атомами, где они компенсируются, вообще нет волны; амплитуда этой волны равна нулю между двумя ядрами.
Эти две возможные комбинации дают два разных результата. Мы отслеживаем эти результаты, используя диаграмму взаимодействия молекулярных орбиталей. На диаграмме показано, что две орбитали могут объединяться двумя разными способами: синфазно или противофазно.
Диаграмма также говорит нам, что синфазная комбинация приводит к уменьшению энергии, когда два атома объединяются. Противофазная комбинация приводит к увеличению энергии, когда атомы собираются вместе.
Рисунок \(\PageIndex{1}\): Диаграмма взаимодействия молекулярных орбиталей для H 2 . Орбиталь атома водорода 1s показана на слева с сопутствующим энергетическим уровнем. То же самое показано на справа . В середине диаграммы две водородные 1s-орбитали могут комбинироваться двумя способами: синфазно и противофазно. Эти комбинации создают две новые орбитали (или электронные волны) с двумя новыми уровнями энергии.
Почему совпадающая по фазе комбинация имеет пониженную энергию, а противофазная – повышается?
Рассмотрим идею о том, что каждая из этих волн имеет длину волны, и что эта длина волны связана с кинетической энергией. Для 1s-электрона атома водорода мы действительно можем визуализировать только половину волны; эта полуволна в основном имеет размер атома водорода, поэтому общая длина волны будет равна двум атомам водорода (из-за отсутствия лучшего критерия).
Для противофазной комбинации мы можем визуализировать всю волну, как ее «пик» с одной стороны, так и «впадину» с другой. Два атома водорода не просто сидят рядом друг с другом, они на самом деле перекрываются, так что расстояние от одного конца волны до другого фактически несколько меньше, чем два атома водорода. Допустим, это полтора атома водорода в длину. Эта волна имеет более короткую длину волны, чем волны любого отдельного атома водорода, и поэтому имеет более высокую энергию.
Рисунок \(\PageIndex{2}\): Сравнение длин волн вдоль оси связи в диводороде.
В синфазном случае снова два атома водорода перекрываются. Но на этот раз мы можем визуализировать только половину волны; поэтому общая длина волны будет больше, чем два атома водорода. Может быть, это три атома водорода в длину. Эта волна имеет большую длину волны, чем электрон в отдельном атоме водорода, поэтому она имеет более низкую энергию.
- Комбинация атомных орбиталей дает новые молекулярные орбитали.
- Количество объединенных атомных орбиталей = количеству произведенных молекулярных орбиталей.
- Возможны комбинации в фазе (низкая энергия) и в противофазе (высокая энергия).
А теперь самое странное:
- Согласно квантовой механике, синфазные и противофазные комбинации происходят одновременно .
Куда на самом деле пойдут два электрона? Здесь справедлив процесс ауфбау, используемый для атомных электронных конфигураций. Два электрона могут находиться в одном и том же пространстве при условии, что они спарены по спину; один будет вращаться «вверх», а другой — «вниз». Оба электрона могут быть найдены на более низкой энергетической орбитали. Это означает, что оба электрона водорода теряют энергию, когда H 2 формы; Таким образом, образование молекулы водорода из двух атомов водорода является экзотермическим.
- Занятая орбиталь называется связывающей орбиталью; он отвечает за энергию связи в H 2 .
- Энергия связи относится к количеству энергии, выделяемой при образовании связи.
Что произойдет, если каждый атом водорода принесет с собой два электрона? Могут ли два иона гидрида образовать связь?
- В H 9 было бы четыре электрона.0108 2 2- молекула.
- Первые два электрона заняли бы нижнюю связующую орбиталь.
- Следующие два электрона займут верхнюю орбиту
- В целом, не было бы чистой потери энергии, поэтому связь не образовалась бы.
- Противофазная комбинация называется разрыхляющей орбиталью, потому что ее увеличение энергии компенсирует уменьшение энергии, которое происходит, когда электроны переходят на связывающую орбиталь.
- Размещение электронов на разрыхляющей орбитали ослабляет или разрывает связь.
Что квантовая механика говорит нам о связи, чего мы не можем узнать из структур Льюиса? Мы узнаем, что иногда электроны могут снижать свою кинетическую энергию, образуя связи.
Если это так, то связь будет сформирована. С другой стороны, если кинетическая энергия не может быть снижена, связь вообще не образуется.
- Ковалентные связи образуются, потому что электроны могут принимать более длинные волны.
- Электроны с большей длиной волны имеют меньшую кинетическую энергию.
Упражнение \(\PageIndex{2}\)
Добавьте несколько слов, поясняющих идеи, отраженные в этих рисунках.
- Ответить
Когда две s-орбитали объединяются в противофазе, возникает деструктивная интерференция.
Между атомами есть узел.
Энергия электронов увеличивается.
Когда две s-орбитали объединяются в фазе, возникает конструктивная интерференция.
Между атомами нет узла; электроны находятся между атомами.
Энергия электронов уменьшается.
Водород — что это такое? | Водородная энергия
Здесь, на Земле, огромное количество атомов водорода содержится в воде, растениях, животных и, конечно же, в людях.
Но хотя он присутствует почти во всех молекулах живых существ, его очень мало в виде газа — менее одной части на миллион по объему.
Водород может быть получен из различных ресурсов, таких как природный газ, ядерная энергия, биогаз и возобновляемые источники энергии , такие как солнечная энергия и ветер. Задача состоит в том, чтобы использовать водород в качестве газа в больших масштабах для топлива наших домов и предприятий.
Почему водород важен как экологически чистый источник энергии будущего?
Топливо — это химическое вещество, которое можно «сжечь» для получения полезной энергии. Горение обычно означает, что химические связи между элементами в топливе разрываются, и элементы химически соединяются с кислородом (часто из воздуха).
В течение многих лет мы использовали природный газ для отопления наших домов и предприятий, а электростанции — для выработки электроэнергии. В Великобритании 85% домов и 40% электричества в стране в настоящее время зависят от газа; в США 47% домохозяйств используют природный газ и 36% — электричество 1 .
Метан является основным компонентом «природного газа» нефтяных и газовых месторождений. Мы продолжаем использовать природный газ, потому что это легкодоступный ресурс, он экономически эффективен и является более чистой альтернативой углю — самому грязному ископаемому топливу, на которое мы исторически полагались для отопления и производства электроэнергии.
При сжигании природного газа выделяется тепловая энергия. Но побочным продуктом наряду с водой является углекислый газ, который при выбросе в атмосферу способствует изменение климата . Когда мы сжигаем водород, единственным побочным продуктом является водяной пар.
В чем разница между синим водородом и зеленым водородом?
Синий водород производится из невозобновляемых источников энергии одним из двух основных способов. Паровая конверсия метана является наиболее распространенным методом производства объемного водорода и составляет большую часть мирового производства. В этом методе используется реформинг-установка, в которой пар при высокой температуре и давлении реагирует с метаном и никелевым катализатором с образованием водорода и монооксида углерода.
Альтернативно, автотермический риформинг использует кислород и двуокись углерода или пар для реакции с метаном с образованием водорода. Недостатком этих двух методов является то, что они производят углерод в качестве побочного продукта, поэтому улавливание и хранение углерода (CCS) необходимо для улавливания и хранения этого углерода.
Зеленый водород производится с использованием электричества для питания электролизера, который отделяет водород от молекул воды. Этот процесс производит чистый водород без вредных побочных продуктов. Дополнительным преимуществом является то, что, поскольку в этом методе используется электричество, он также дает возможность направить любой избыток электричества, который трудно хранить (например, избыточную энергию ветра), на электролиз, используя его для создания газообразного водорода, который можно хранить для будущего. энергетические потребности.
Узнайте больше о цветовом спектре водорода
Водород уже используется в качестве топлива?
Да.
Уже есть автомобилей , которые работают на водородных топливных элементах. В Японии есть 96 общественных станций заправки водородом, что позволяет вам заправляться так же, как бензином или дизельным топливом, и в те же сроки, что и автомобиль на традиционном топливе. В Германии 80 таких водородных станций, а США занимают третье место с 42 станциями.
Водород также является захватывающим легким топливом для автомобильного, воздушного и морского транспорта. Международная служба доставки DHL уже располагает парком из 100 фургонов h3, способных проехать 500 км без дозаправки.
Каковы потенциальные тормоза для ускорения использования водорода в качестве экологически чистой энергии?
Чтобы водород стал жизнеспособной альтернативой метану, его необходимо производить в больших масштабах, экономично, а существующую инфраструктуру необходимо адаптировать.
Хорошая новость заключается в том, что водород можно транспортировать по газопроводам, сводя к минимуму нарушения и уменьшая объем дорогостоящей инфраструктуры, необходимой для строительства новой сети передачи водорода.
Также не будет необходимости в изменении культуры в нашей домашней жизни, поскольку люди привыкли использовать природный газ для приготовления пищи и отопления, и появляются эквиваленты водородной энергии .
Что делает National Grid для продвижения водорода в качестве альтернативного экологичного топлива?
Мы взяли на себя обязательство достичь чистый ноль к 2050 году, а это значит, что нам нужно начать готовиться к изменению использования газа в ближайшие годы. Один из способов, который мы предлагаем для этого, — водород.
В Великобритании действующая Национальная система передачи (NTS) транспортирует природный газ по всей стране, и люди, предприятия и промышленность полагаются на нашу сеть.
NTS представляет собой уникальную и сложную сеть, в которой используются стальные трубы для транспортировки природного газа под высоким давлением. Нам необходимо полностью понять влияние, которое воздействие водорода под высоким давлением может оказать на трубы, прежде чем сеть можно будет переоборудовать.


 )
) 1 Ковалентная связь
1 Ковалентная связь