как найти, формула расчёта, в чем измеряется
Содержание:
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В.
В таком случае выражение следует умножить на корень из трех или 1.73
Что это означает
В сетях переменного тока, которыми на сегодняшний день пользуется абсолютно весь мир, без активной и реактивной мощностей никак не обойтись – они взаимозависимы и даже необходимы. К активной электроэнергии относится напряжение, которое вырабатывается на ТЭС, ГрЭС, АЭС, мобильном генераторе, стоящем в гараже и т.д. – оно поступает к потребителю (на фабрики, заводы, к нам домой) и питает все электроприборы от сети ≈220-380 V. В это же время функция реактивной составляющей полного тока заключается в бесцельном блуждании от источника к потребителю и обратно. Так откуда же берётся эта, бесполезная на первый взгляд, субстанция?
Все дело в том, что в наших домах, на предприятиях и любых других электрифицированных объектах есть приборы с индуктивными катушками (для примера можно взять статор двигателя), где постоянно возникают магнитные поля. То есть, часть из них вращает ротор (якорь), а часть возвращается обратно и так до бесконечности, пока существует движение активной энергии. Это хорошо демонстрирует кружка свежего пива: с жидкостью человек выпивает лишь малую часть пены, а остальную оставляет в бокале либо сдувает на землю. Но эта самая пена является продуктом брожения (индукции), без которого пива, как такового, не будет вообще.
Это хорошо демонстрирует кружка свежего пива: с жидкостью человек выпивает лишь малую часть пены, а остальную оставляет в бокале либо сдувает на землю. Но эта самая пена является продуктом брожения (индукции), без которого пива, как такового, не будет вообще.
Сейчас уже можно подвести первый итог в понимании темы: если есть индуктивная нагрузка (а она есть всегда), то обязательно появится реактивный ток, потребляемый индукцией, которая сама его создает. То есть, индукция вырабатывает реактивную мощность, потом её потребляет, вырабатывает заново и так постоянно, но в этом кроется одна проблема. Для движения реактивной субстанции туда обратно, нужна активная энергия, которая расходуется из-за постоянного движения электронов по проводам (нагрев проводов).
Можно прийти к выводу, что активная мощность генератора, это полное противопоставление реактивной, на первый взгляд бесполезной мощности? Но это не так. Вспомните, сестры неразлучны между собой, так как любят друг друга, а пиво без пены никто не станет пить, да и забродить без неё напиток будет не в состоянии. То же можно сказать о реактивной мощности – без неё невозможно создание магнитных полей, так что с этой силой придется считаться. Но тут в дело пошли мозговые извилины изобретателей, которые решили сократить территориальное пространство (не гонять по проводам взад-вперед) этой, не совсем понятной, субстанции и вырабатывать её в непосредственной близости от объекта потребления.
То же можно сказать о реактивной мощности – без неё невозможно создание магнитных полей, так что с этой силой придется считаться. Но тут в дело пошли мозговые извилины изобретателей, которые решили сократить территориальное пространство (не гонять по проводам взад-вперед) этой, не совсем понятной, субстанции и вырабатывать её в непосредственной близости от объекта потребления.
Для наглядного примера можно взять всем известный электрический фен, в котором есть двигатель, вращающий вал с лопастями – он называется турбиной для подачи горячего воздуха. Так вот, чтобы разгрузить линию электропередач от бесполезной беготни реактива от станции к потребителю и обратно, в корпус прибора встраивают конденсатор нужной емкости. А представьте себе ту же электросварку или токарный цех с десятками мощных станков, – какой потенциал высвобождается реактивным током для увеличения КПД. Если говорить техническим языком, то установка конденсаторов или других статических компенсирующих элементов называется компенсацией реактивной мощности. Получается, что активная и реактивная мощность, это две неразрывно связанных между собой величины.
Получается, что активная и реактивная мощность, это две неразрывно связанных между собой величины.
Вырабатывать реактивную мощность могут также и генераторы на электростанциях любого типа. Для этого достаточно сменить ток возбуждения (перевозбуждения, недовозбуждения) и генератор окажется как поставщиком, так и потребителем этой величины. Но, это всего лишь законы физики, которые в данном случае не очень выгодны для людей, поэтому лучше всего переносить емкость накопления и отдачи, как можно ближе к источнику – в корпус прибора (агрегата) или в производственный цех.
Простое объяснение с формулами
Активная мощность (P)
Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть
P = U I
потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:
P = U I Cosθ
В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.
Формулы для активной мощности
P = U I – в цепях постоянного тока
P = U I cosθ – в однофазных цепях переменного тока
P = √3 UL IL cosθ – в трёхфазных цепях переменного тока
P = 3 UPh IPh cosθ
P = √ (S2 – Q2) или
P =√ (ВА2 – вар2) или
Активная мощность = √ (Полная мощность2 – Реактивная мощность2) или
кВт = √ (кВА2 – квар2)
Реактивная мощность (Q)
Также её мощно было бы назвать бесполезной или безваттной мощностью.
Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).
Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.
Реактивная мощность определяется, как
Q = U I sinθ
и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.
Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.
В чем измеряется активная мощность?
Активная мощность: обозначение P, единица измерения: Ватт Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный) Полная мощность: обозначение S, единица измерения: ВА (Вольт Ампер)
В чем разница между активной и реактивной мощности?
youtube.com/embed/psiEwq4DiTM» frameborder=»0″ allowfullscreen=»allowfullscreen»>Как узнать какая мощность в цепи переменного тока
Стоит указать, что это величина, которая прямо связывается с иными показателями. К примеру, она находится в прямой зависимости от времени, силы, скорости, вектора силы и скорости, модуля силы и скорости, момента силы и частоты вращения. Часто в формулах во время вычисления электромощности используется также число Пи с показателем сопротивления, мгновенным током, напряжением на конкретном участке электрической сети, активной, полной и реактивной силой. Непосредственно участник вычисления это амплитуда, угловая скорость и начальная сила тока с напряжением.
Формула мощности в цепи переменного тока
В однофазной цепи
Понять, какой мощностный показатель есть в однофазной цепи переменного тока, можно при помощи применения трансформатора тока. Для этого необходимо воспользоваться ваттметром, который включен через токовый трансформатор. Показания следует перемножить на трансформаторный коэффициент тока. В момент измерения мощности в высоком напряжении трансформатор тока необходим, чтобы заизолировать ваттметр и обеспечить безопасность пользователя. Параллельна цепь включается не непосредственным способом, а благодаря трансформатору напряжения. Вторичные обмотки с корпусами измерительных трансформаторных установок необходимо заземлять во избежание случайного изоляционного повреждения и попадания высокого напряжения на приборы.
Показания следует перемножить на трансформаторный коэффициент тока. В момент измерения мощности в высоком напряжении трансформатор тока необходим, чтобы заизолировать ваттметр и обеспечить безопасность пользователя. Параллельна цепь включается не непосредственным способом, а благодаря трансформатору напряжения. Вторичные обмотки с корпусами измерительных трансформаторных установок необходимо заземлять во избежание случайного изоляционного повреждения и попадания высокого напряжения на приборы.
Обратите внимание! Для определения параметров в сети необходимо амперметр перемножить на трансформаторный коэффициент тока, а цифры, полученные вольтметром, перемножить на трансформаторный коэффициент напряжения.
В однофазной цепи
Чему равна активная мощность трехфазной цепи?
Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз приемника. где — φ угол сдвига фаз между фазными напряжением и током.
Как рассчитать активную мощность трансформатора?
Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула: S = U I, где U – это напряжение сети, а I – это сила тока сети. Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда: S = U * I * cos φ.
Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда: S = U * I * cos φ.
Электроприборы, влияющие на качество потребления
Коэффициент мощности равен единице при подключении ламп и нагревателей. Он уменьшается до 0,7 и менее, когда в цепи добавляют преобладающие по потреблению энергии электромоторы, другие компоненты с реактивными составляющими.
Правильное применение определений и расчетов мощности помогает оптимизировать проект электрической сети с учетом особенностей подключаемых нагрузок. Приведенные выше сведения пригодятся на стадии определения параметров проводки, защитных автоматов. Комплексное использование этих знаний повысит надежность электроснабжения, предотвратит возникновение и развитие аварийных ситуаций.
Чем отличается активная мощность от реактивной – Все об электричестве
Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.
Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны.
Единица измерений активной мощности Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР).
Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.
Соотношение энергий
Электротехника используется активную составляющую в качестве измерения передачи энергии отдельными электрическими приборами. Рассмотрим, сколько мощности потребляют некоторые из них:
| Прибор | Мощность бытовых приборов, Вт/час |
| Зарядное устройство | 2 |
| Люминесцентная лампа ДРЛ | От 50 |
| Акустическая система | 30 |
| Электрический чайник | 1500 |
| Стиральной машины | 2500 |
| Полуавтоматический инвертор | 3500 |
| Мойка высокого давления | 3500 |
Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.
Генерация активной составляющей
Обозначение реактивной составляющей:
Это номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.
Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:
S = U I, где U – это напряжение сети, а I – это сила тока сети.
Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:
Схема симметричной нагрузки
Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:
S = U * I * cos φ.
Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ.
Это зависит от того, какие характеристики имеет cos φ.
Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная.
Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).
Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.
Расчет трехфазной сети
Максимальная и активная обозначается P, реактивная мощность – Q.
Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:
QL = ULI = I2xL
Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.
Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.
Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:
S = √P2 + Q2, и все это равняется U*I .
Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:
Сопротивление индуктивности: xL = ωL = 2πfL,
Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).
Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.
При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности.
Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы.
С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:
Диаграмма треугольников напряжений
К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:
cos φ = r/z = P/S
Для получения максимально точных результатов рекомендуется не округлять полученные данные.
Учитывая, что при резонансе токов реактивная мощность равняется 0:
Q = QL – QC = ULI – UCI
Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.
При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит:
- Значительно уменьшается нагрузка силовых трансформаторов;
- Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;
- У сигнальных и радиоустройств уменьшаются помехи;
- На порядок уменьшаются гармоники в электрической сети.
Активная электроэнергия
Активная составляющая полной мощности совершает полезную работу и преобразовывается в те виды энергии, которые нужны потребителю. У части бытовых и промышленных электроприборов в расчетах активная и полная мощность совпадают. Среди таких устройств – электроплиты, лампы накаливания, электропечи, обогреватели, утюги и гладильные прессы и прочее.
Если в паспорте указана активная мощность 1 кВт, то полная мощность такого прибора будет составлять 1 кВА.
Предыдущая
РазноеЭнергия конденсатора
Следующая
РазноеАвтоматические выключатели
Мощность цепи определяется по формуле. Реактивная мощность это
В цепях переменного тока различают три вида мощностей: активную Р, реактивную Q и полную S.
Активная мощность вычисляется по формуле:
Активную мощность потребляет резистивный элемент. Единица
измерения активной мощности называется Ватт (Вт), производная единица – килоВатт (кВт), равная 10 3 Вт.
Реактивная мощность вычисляется по формуле:
Реактивная мощность потребляется идеальным индуктивным и
емкостным элементами. Единица измерения реактивной мощности называется Вольт-Ампер реактивный (Вар), производная единица – килоВАр (кВАр), равная 10 3 ВАр.
Полная мощность потребляется полным сопротивлением и обозначается буквой S:
Единица измерения полной мощности называется ВА (Вольт-Ампер), производная единица – килоВольт-Ампер (кВА), равная 10 3 ВА.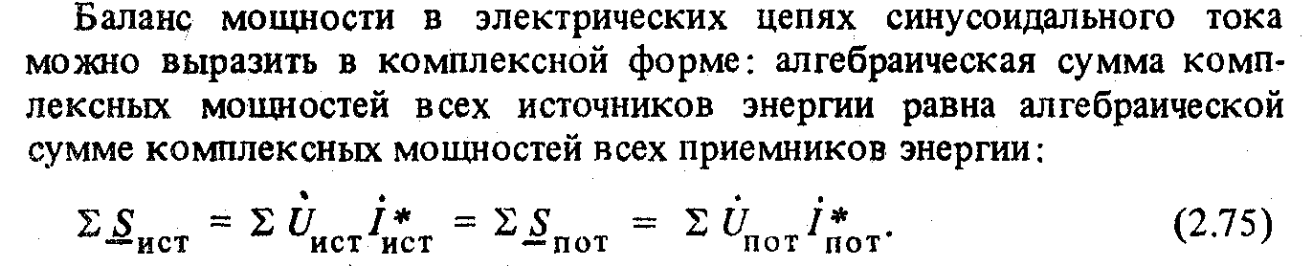
Проявляются различные виды мощности по-разному. Активная мощность необратимо преобразуется в другие виды мощности (например, тепловую, механическую). Реактивная мощность обратимо циркулирует в электрических цепях: энергия электрического поля конденсатора преобразуется в энергию магнитного поля, и наоборот. «Извлечь» реактивную мощность с «пользой для дела» невозможно.
Из формул (2.19) – (2.21) следует, что между активной, реактивной и полной мощностью имеет место соотношение:
Соотношение между P, Q и S можно интерпретировать как соотношение сторон прямоугольного треугольника (вспомните треугольник сопротивлений, треугольник напряжений – все эти треугольники подобны).
Из рис. 2.10 видно, что cosφ = (2.24)
Отсюда вытекает определение одной из основных характеристик цепей переменного тока – коэффициента мощности. Специального обозначения он не получил.
Специального обозначения он не получил.
Коэффициент мощности показывает, какую долю полной мощности составляет активная мощность.
Желательно, чтобы коэ ффициент мощности цепи был как можно больше, т.е. приближался к 1. Реально предприятия электрических сетей устанавливают такое ограничение для промышленных предприятий: соs φ = (0,92…..0,95). Достигать значений соs φ >0,95 рискованно, так как разность фаз φ при этом может скачком перейти от положительных значений к отрицательным, что вредно для
Если коэ ффициент мощности оказывается мал, его необходимо повышать. График функции соs φ имеет вид монотонно убывающей функции в интервале от 0 0 до 90 0 . Следовательно, увеличить соsφ – значит уменьшить разность фаз , то есть уменьшить (Х L -Х С).
Если влиять на (Х L -Х С), меняя С и L, то это приведет к увеличению тока в последовательной цепи и изменению режима работы оборудования, поэ тому такой способ практически не применяется.
ЛЕКЦИЯ 4 .
2.6 Цепь переменного тока с параллельным соединением ветвей.
Рассмотрим э лектрическую цепь с двумя параллельными
ветвями (рис. 2.11). Полученные выводы распространим на цепь с любым количеством ветвей. К цепи, содержащей две параллельные ветви, включающие активные, индуктивные и емкостные элементы (R 1 , L 1 , C 1 и R 2 , L 2 , C 2 cоответственно), подводится переменное напряжение U частоты f.
входящие в цепь элементы. цепи. Найти неизвестные элементы
Найти все токи и разности цепи (эта задача решена в лабора-
фаз. торной работе Ц-5)
Решим прямую задачу, то есть найдем токи I 1, I 2 и общий ток I .
Рис. 2.11.Э лектрическая цепь с двумя параллельными
Из второго закона Кирхгофа следует, что напряжения на параллельных участках цепи одинаковы:
U 1 = U 2 = U (2.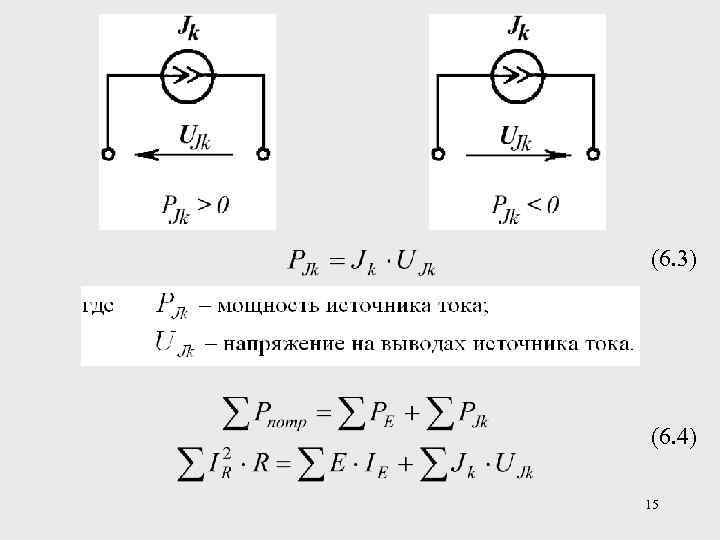 25)
25)
На основании закона Ома найдем токи I 1 и I 2:
; (2.26)
Найдем также разности фаз тока и напряжения для каждой ветви:
(2.27)
На основании первого закона Кирхгофа применительно к узлу А можно записать:
Таким образом, для определения тока I необходимо векторно сложить токи I 1 и I 2 . В качестве опорного вектора удобно выбрать вектор напряжения .
Мгновенная электрическая мощность
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
| где — тензор проводимости . |
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
Для пассивной линейной цепи, в которой соблюдается закон Ома , можно записать:
Если цепь содержит источник ЭДС , то отдаваемая им или поглощаемая на нём электрическая мощность равна:
где — ЭДС. |
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.
Мощность переменного тока
В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности , удобно обратиться к теории комплексных чисел . Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ
(сдвиг фаз) — аргументом.
Активная мощность
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока , φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи
 С полной мощностью
С полной мощностью Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.
Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Единица полной электрической мощности — вольт-ампер (V·A, В·А)
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода , кабели , распределительные щиты , трансформаторы , линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии.
Комплексная мощность
Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной.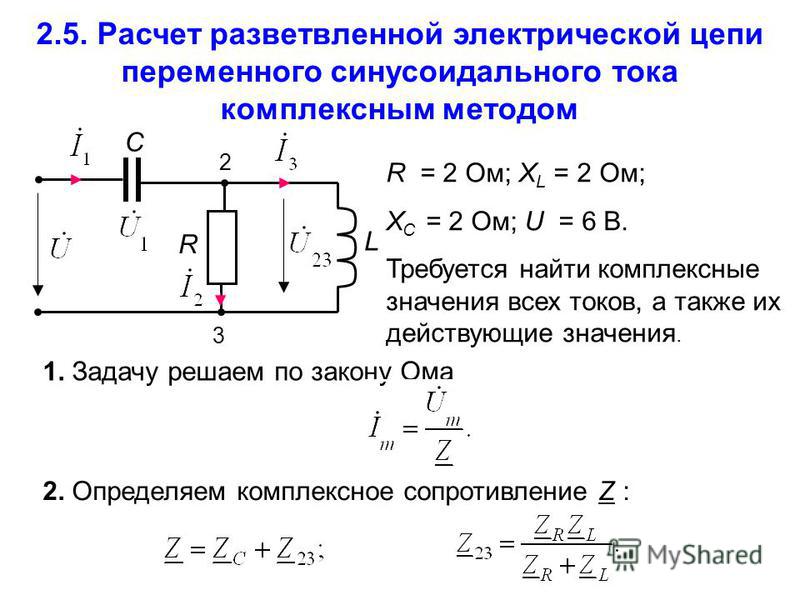
Связь неактивной, активной и полной мощностей
Величину неактивной мощности обозначим N . Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения:
Представим вектор тока i в виде суммы двух ортогональных составляющих i a и i p , которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть i a = λu , где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем
Запишем выражение для активной мощности P , скалярно умножив последнее равенство на u :
Отсюда находим
Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность.
Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность:
Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе.
Неактивная мощность иногда называется реактивной мощностью по Фризе.
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры , можно также использовать косвенный метод, с помощью вольтметра и амперметра .
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон — ГЭТ 153-86 Государственный специальный эталон единицы электрической мощности в диапазоне частот 40-2500 Гц. Институт-хранитель: ВНИИМ
Мощность некоторых электрических приборов
В таблице указаны значения мощности некоторых потребителей электрического тока:
Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная.
Литература
- ГОСТ 8.417-2002 Единицы величин
- ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации
- Бессонов Л. А. Теоретические основы электротехники.
 — М: Высшая школа, 1984.
— М: Высшая школа, 1984. - Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193-2009. — 146 с.
Дополнительная литература
- Агунов М. В., Агунов А. В., Вербова Н. М. Определение составляющих полной мощности в электрических цепях с несинусоидальными напряжениями и токами методами цифровой обработки сигналов // Электротехника, 2005, № 7, С. 45-48.
- Агунов А. В. Неактивные составляющие полной мощности в автономных электротехнических системах судостроения. Автореферат диссертации на соискание ученой степени кандидата технических наук. СПб., СПбГМТУ, 1997, 20 с.
- Агунов М. В. Энергетические процессы в электрических цепях с несинусоидальными режимами и их эффективность. Кишинев-Тольятти: МолдНИИТЭИ, 1997, 84 с.
- Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С.
 53-56.
53-56. - Агунов А. В. Управление качеством электроэнергии при несинусоидальных режимах. СПб., СПбГМТУ, 2009, 134 с.
- Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
- Агунов А. В. Статический компенсатор неактивных составляющих мощности с полной компенсацией гармонических составляющих тока нагрузки // Электротехника, 2003, № 2, С. 47-50. — см. Мощность электрическая … Большой Энциклопедический словарь
электрическая мощность — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN electric powerelectrical powerep … Справочник технического переводчика
Физическая величина, характеризующая скорость изменения (получения, потребления, передачи, преобразования, рассеяния и т. п.) электрической энергии. В электрических цепях постоянного тока электрическая мощность Р равна произведению силы тока I и… … Энциклопедия техники
электрическая мощность — 9 электрическая мощность: Физическая величина, характеризующая скорость передачи или преобразования электрической энергии de. Elektrische Leistung en. Electric power fr. Puissance électrique
Elektrische Leistung en. Electric power fr. Puissance électrique
Реактивная мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Если элемент цепи — резистор c электрическим сопротивлением R , то
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: . В цепях однофазного синусоидального тока , где U и I — действующие значения напряжения и тока , φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W , Вт ). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением . Единица активной мощности — ватт (W , Вт ). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I , умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ . Единица реактивной мощности — вольт-ампер реактивный (var , вар ). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ , более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I ; связана с активной и реактивной мощностями соотношением: , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0 , а при ёмкостной Q ). Единица полной электрической мощности — вольт-ампер (VA , ВА ).
Единица полной электрической мощности — вольт-ампер (VA , ВА ).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Измерения
- Для измерения электрической мощности применяются ваттметры и варметры , можно также использовать косвенный метод, с помощью вольтметра и амперметра .
- Для измерения коэффициента реактивной мощности применяют фазометры
Литература
- Бессонов Л. А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа,
Ссылки
См. также
- Список параметров напряжения и силы электрического тока
Wikimedia Foundation . 2010 .
Смотреть что такое «Реактивная мощность» в других словарях:
реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
[ГОСТ Р 52002 2003]… … Справочник технического переводчика
Электр. мощность в цепи переменного тока, расходуемая на поддержание вызываемых переменным током периодических изменений: 1) магнитного поля при наличии в цепи индуктивности; 2) заряда конденсаторов при наличии конденсаторов и проводов (напр.… … Технический железнодорожный словарь
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними: Q =… … Большой Энциклопедический словарь
РЕАКТИВНАЯ МОЩНОСТЬ — величина, характеризующая скорость обмена энергией между генератором переменного тока и магнитным (млн. электрическим) полем цепи, создаваемым электротехническими устройствами (индуктивностью и ёмкостью). Р. м. возникает в цепи при наличии сдвига … Большая политехническая энциклопедия
реактивная мощность — 3. 1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации
1.5 реактивная мощность (вар): Реактивная мощность сигналов синусоидальной формы какой либо отдельной частоты в однофазной цепи, определяемая как произведение среднеквадратических значений тока и напряжения и синуса фазового угла между ними.… … Словарь-справочник терминов нормативно-технической документации
реактивная мощность — reaktyvioji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Menamoji kompleksinės galios dalis, skaičiuojama pagal formulę Q² = S² – P²; čia Q – reaktyvioji galia, S – pilnutinė galia, P – aktyvioji galia. Matavimo vienetas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
реактивная мощность — reaktyvioji galia statusas T sritis fizika atitikmenys: angl. reactive power; wattless power vok. Blindleistung, f; wattlose Leistung, f rus. безваттная мощность, f; реактивная мощность, f pranc. puissance déwatée, f; puissance réactive, f … Fizikos terminų žodynas
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля. Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь
Для синусоидального тока равна произведению действующих тока I и напряжения U на синус угла сдвига фаз между ними:… … Энциклопедический словарь
реактивная мощность — reaktyvioji galia statusas T sritis automatika atitikmenys: angl. reactive power vok. Blindleistung, f; wattlose Leistung, f rus. реактивная мощность, f pranc. puissance réactive, f … Automatikos terminų žodynas
Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока (См. Переменный ток). Р. м. Q равна произведению действующих значений напряжения U и тока… … Большая советская энциклопедия
Книги
- Потери электроэнергии. Реактивная мощность. Качество электроэнергии: Руководство для практических расчетов , Железко Ю.С.. Прикладные науки. Техника. Промышленность…
Активная и реактивная электрическая мощность
| Классическая электродинамика |
| Электричество · Магнетизм |
| Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал |
| Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция |
| Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле |
| Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс |
| Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток |
См. также: Портал:Физика также: Портал:Физика |
Электрическое напряжение Сила тока Электрическая мощность
Электрическое сопротивление
Электри́ческая мо́щность
— физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение:
Вт
, международное:
W
).
Содержание
- 1 Мгновенная электрическая мощность 1.1 Дифференциальные выражения для электрической мощности
- 3.1 Активная мощность
youtube.com/embed/yP1V4Zzjl6Q?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Мгновенная электрическая мощность
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A {\displaystyle A} в точку B {\displaystyle B} , к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A {\displaystyle A} в точку B {\displaystyle B} . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:
Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:
U {\displaystyle U} — напряжение на участке A − B {\displaystyle A-B} (принимаем его постоянным на интервале Δ t {\displaystyle \Delta t} ), Q {\displaystyle Q} — количество зарядов, прошедших от A {\displaystyle A} к B {\displaystyle B} за время Δ t {\displaystyle \Delta t} , A {\displaystyle A} — работа, совершённая зарядом Q {\displaystyle Q} при движении по участку A − B {\displaystyle A-B} , P {\displaystyle P} — мощность.
Записывая вышеприведённые рассуждения, получаем:
P A − B = A Δ t {\displaystyle P_{A-B}={\frac {A}{\Delta t}}}
Для единичного заряда на участке A − B {\displaystyle A-B} :
P e ( A − B ) = U Δ t {\displaystyle P_{e(A-B)}={\frac {U}{\Delta t}}}
Для всех зарядов:
P A − B = U Δ t ⋅ Q = U ⋅ Q Δ t {\displaystyle P_{A-B}={\frac {U}{\Delta t}}\cdot {Q}={U}\cdot {\frac {Q}{\Delta t}}}
Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть I = Q Δ t {\displaystyle I={\frac {Q}{\Delta t}}} по определению, в результате получаем:
P A − B = U ⋅ I {\displaystyle P_{A-B}=U\cdot I} . {2}}{\sigma }}} ,
{2}}{\sigma }}} ,
где σ = d e f 1 ρ {\displaystyle \sigma \,{\overset {\underset {\mathrm {def} }{}}{=}}\,{\frac {1}{\rho }}} — удельная проводимость, величина, обратная удельному сопротивлению.
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
w = σ α β E α E β {\displaystyle w=\sigma _{\alpha \beta }E_{\alpha }E_{\beta }} ,
где σ α β {\displaystyle \sigma _{\alpha \beta }} — тензор проводимости.
В чем физический смысл активной, реактивной и полной мощностей? Назовите единицы измерения?
⇐ ПредыдущаяСтр 4 из 4
Активная мощность потребляется в активных сопротивлениях, и, в конечном итоге, за счет нее выполняется механическая работа или происходит нагревание резисторов. Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.
Реактивная мощность-эта та мощность, которая попросту «болтается в проводах». Она не потребляется активно цепью, но системы передачи оказываются ею загруженными.
Пусть приемник электроэнергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдвинутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением
| p(t) = u(t) ∙ i(t) = 2UI sin (ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ) | (5.1) |
и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.
Среднее значение p(t)
за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):
Активная мощность характеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и
Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и
газа и т. п.
Среднее значение от второго слагаемого мгновенной мощности (1.1) (пульсирует с двойной частотой) за время Т равно нулю, т. е. на ее создание не требуется каких-либо материальных затрат и поэтому она не может совершать полезной работы. Однако ее присутствие указывает, что между источником и приемником происходит обратимый процесс обмена энергией. Это возможно, если имеются элементы, способные накапливать и отдавать электромагнитную энергию – емкость и индуктивность. Эта составляющая характеризует реактивную мощность.
Полную мощность на зажимах приемника в комплексной форме можно представить следующим образом:
| . | (5.2) |
Единица измерения полной мощности S = UI – ВА.
Реактивная мощность – величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями (обменом) энергии между источником и приемником. Для синусоидального тока она равна произведению действующих значений тока I
Для синусоидального тока она равна произведению действующих значений тока I
и напряжения
U
на синус угла сдвига фаз между ними:
Q
=
UI
sinφ. Единица измерения – В∙Ар.
Реактивная мощность не связана с полезной работой ЭП и расходуется только на создание переменных электромагнитных полей в электродвигателях, трансформаторах, аппаратах, линиях и т. д.
Для реактивной мощности приняты такие понятия, как генерация, потребление, передача, потери, баланс. Считается, что если ток отстает по фазе от напряжения (индуктивный характер нагрузки), то реактивная мощность потребляется и имеет положительный знак, а если ток опережает напряжение (емкостный характер нагрузки), то реактивная мощность генерируется и имеет отрицательное значение.
Основными потребителями реактивной мощности на промышленных предприятиях являются асинхронные двигатели (60–65 % общего потребления), трансформаторы (20–25 %), вентильные преобразователи, реакторы, воздушные электрические сети и прочие приемники (10 %).
Передача реактивной мощности загружает электрические сети и установленное в ней оборудование, уменьшая их пропускную способность. Реактивная мощность генерируется синхронными генераторами электростанций, синхронными компенсаторами, синхронными двигателями (регулирование током возбуждения), батареями конденсаторов (БК) и линиями электропередачи.
Реактивная мощность, вырабатываемая емкостью сетей, имеет следующий порядок величин: воздушная линия 20 кВ генерирует 1 кВ∙Ар на 1 км трехфазной линии; подземный кабель 20 кВ – 20 кВ∙Ар/км; воздушная линия 220 кВ – 150 кВ∙Ар/км; подземный кабель 220 кВ – 3 МВ∙Ар/км.
Коэффициент мощности и коэффициент реактивной мощности.Векторное представление величин, характеризующих состояние сети, приводит к представлению реактивной мощности Q
вектором, перпендикулярным вектору активной мощности
Р
(рис. 5.2 ). Их векторная сумма дает полную мощность
S
.
Рис. 5.1. Треугольник мощностей
Согласно рис. 5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
5.1 и (5.2) следует, что S2 = Р2 + Q2; tgφ = Q/P; cosφ = P/S.
Основным нормативным показателем, характеризующим реактивную мощность, ранее был коэффициент мощности cosφ. На вводах, питающих промышленное предприятие, средневзвешенное значение этого коэффициента должно было находиться в пределах 0,92–0,95. Однако выбор соотношения P/S
в качестве нормативного не дает четкого представления о динамике изменения реального значения реактивной мощности. Например, при изменении коэффициента мощности от 0,95 до 0,94 реактивная мощность изменяется на 10 %, а при изменении этого же коэффициента от 0,99 до 0,98 приращение реактивной мощности составляет уже 42 %. При расчетах удобнее оперировать соотношением tgφ =
Q/P
, которое называют коэффициентом реактивной мощности.
Предприятиям, у которых присоединенная мощность более 150 кВт (за исключением «бытовых» потребителей), определены предельные значения коэффициента реактивной мощности, потребляемой в часы больших суточных нагрузок электрической сети – с 7 до 23 часов (Приказ Министерства промышленности и энергетики РФ от 22. 02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).
02.2007 г. № 49 «О порядке расчета значений соотношения потребления активной и реактивной мощности для отдельных энергопринимающих устройств потребителей электрической энергии, применяемых для определения обязательств сторон в договорах об оказании услуг по передаче электрической энергии»).
Контрольные вопросы лаб. работы № 2
Законы Кирхгофа.
Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.
В этом случае законы формулируются следующим образом.
Первый закон гласит, что суммарный ток, втекающий в любой узел цепи, равен нулю. Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.
Второй закон гласит, что суммарное напряжение по любому замкнутому контуру цепи, равно сумме ЭДС, которые в нём находятся.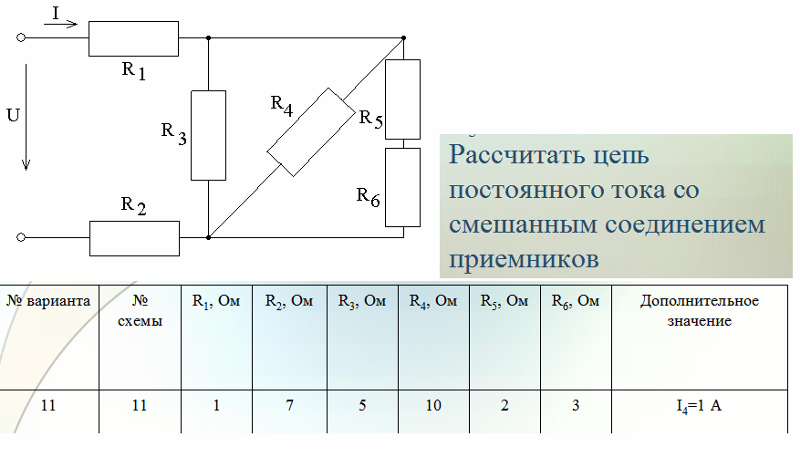 Если в контуре нет ЭДС, то суммарное напряжение равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, то она описывается m − (p − 1) уравнениями напряжений.
Если в контуре нет ЭДС, то суммарное напряжение равно нулю. Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, то она описывается m − (p − 1) уравнениями напряжений.
Законы Кирхгофа –правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа.
Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю.
Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.
Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2 входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения.
Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.
Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре.
Напряжение выражено как произведение тока на сопротивление (по закону Ома).
В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно:
Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3 совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно:
-E1+E2+E3=I1R1-I2R2-I3R3
На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа.
⇐ Предыдущая4
Рекомендуемые страницы:
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
P = I ⋅ U {\displaystyle P=I\cdot U} . {2}\cdot r} прибавляется к поглощаемой или вычитается из отдаваемой.
{2}\cdot r} прибавляется к поглощаемой или вычитается из отдаваемой.
Суть понятия
При протекании через проводник электрического тока вокруг него возникает электромагнитное поле. Образуется оно из-за движущихся элементарных частиц, обладающих зарядом. Магнитное поле считается основным признаком присутствия электрического. При изменении одного происходит изменение и другого. Если ток в проводнике пропадёт, то электромагнитное поле всё равно никуда не исчезнет, разве что потеряет свою интенсивность.
Основоположником теории поля стал английский физик Джеймс Клерк Максвелл. Именно он доказал связь между этими двумя явлениями, описав их в своей работе, изданной в 1857 году. Учёный обосновал, что электрическое поле не может отдельно существовать от магнитного. Величина этих полей связана с энергией, заключённой в них. Она постоянно передаётся из одной формы в другую, но при этом не исчезает.
Электромагнитное поле распространяется в виде излучения, или как выражаются учёные — пространственного возмущения. Это испускание свободно распространяется в любой физической среде. Характеризуется оно частотой, длиной и поляризацией (направлением) волны. А также одним из параметров излучения является количество энергии, переносимой волной (интенсивность).
Это испускание свободно распространяется в любой физической среде. Характеризуется оно частотой, длиной и поляризацией (направлением) волны. А также одним из параметров излучения является количество энергии, переносимой волной (интенсивность).
Численно интенсивность определяется как усреднённый период колебания волны, пронизывающей площадку, расположенную перпендикулярно ей. При этом она связана с плотностью энергии и скоростью распространения волны. Поток электромагнитной энергии находится с учётом вектора Пойтинга, который принимает во внимание плотность, интенсивность и напряжённость поля.
То есть математически, интенсивность описывается выражением: I (t) = 1/T ∫ {s (t)} dt, где S (t) — вектор Пойтинга. В простом понимании её смысл заключается в том, что количественная составляющая электроэнергии изменяется во времени, при этом скорость изменения зависит от напряжённости электрического поля и магнитной индукции.
Для обозначения именно электрической составляющей электромагнитного поля было введено понятие электрическая мощность.
Под ней понимают физическую величину, характеризующую передачу или преобразование электрической энергии.
Физическое определение
Основной характеристикой любого электрического прибора является мощность. Передача электричества от источника питания к нагрузке сопровождается преобразованием энергии из одного вида в другую. Выработанное электричество передаётся по электрической цепи (например, линии передачи) при этом происходит её частичное рассеивание. Другими словами, часть электричества превращается в иную энергию: тепловую, световую, механическую.
Это преобразование характеризуется интенсивностью, обозначающей, какое её количество перейдёт в другой вид за единицу времени. Интенсивность, с которой происходит трансформирование, и называют мощностью.
как найти, формула расчёта, в чем измеряется
Активная, реактивная и полная мощность напрямую связаны с током и напряжением в замкнутой электрической цепи, когда включены какие-либо потребители. Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного тока мощность разделяется на несколько составляющих, отмеченных выше. Вычисление каждой из них осуществляется с помощью формул.
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
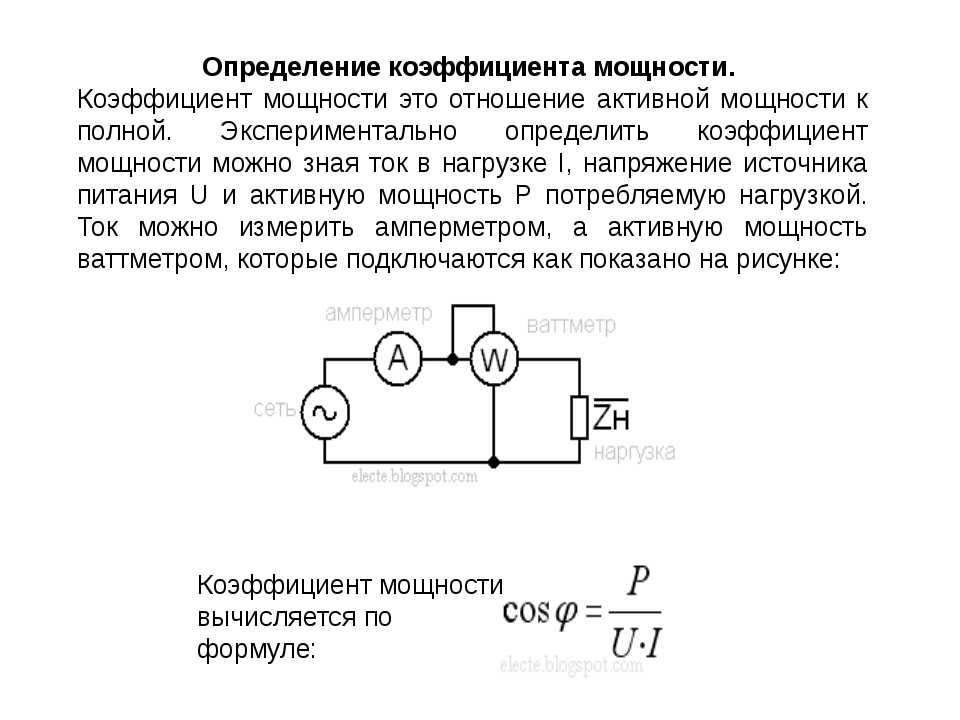
Как измеряют cosφ на практике
Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром . Также с этой задачей легко справится цифровой ваттметр.
Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
- Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору.
 Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит. - Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Как перевести амперы в киловаты?
Что такое делитель напряжения и как его рассчитать?
Способы вычисления потребления электроэнергии бытовыми приборами
Как рассчитать падение напряжения по длине кабеля в электрических сетях
Что такое фазное и линейное напряжение?
Как подобрать блок питания для светодиодной ленты по техническим характеристикам, расчёт мощности
Источник
Формула для полной мощности
Полная мощность = √ (Активная мощность 2 + Реактивная мощность 2 )
kUA = √(kW 2 + kUAR 2 )
Следует заметить, что:
- резистор потребляет активную мощность и отдаёт её в форме тепла и света.

- индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
- конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:
Источник
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.
Рис. 2. коэффициент мощности
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Реактивная составляющая
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Зачем нужна
Электричество передает энергию в проводник для осуществления технического процесса. Чтобы процесс происходил, переданная сила должна преобразовываться в тепло и напряжение. При этом электроэнергия должна поступать постоянно, что обеспечивается обеими разновидностями мощностной характеристики. Активно действующая дает полезную силу, а реактивно действующая ее поддерживает в электродвигательных, трансформаторных, печных, сварочных, дроссельных и осветительных установках.
При этом электроэнергия должна поступать постоянно, что обеспечивается обеими разновидностями мощностной характеристики. Активно действующая дает полезную силу, а реактивно действующая ее поддерживает в электродвигательных, трансформаторных, печных, сварочных, дроссельных и осветительных установках.
Косинус фи для различных потребителей – таблица
| Наименование электроприбора | cos φ |
| Бойлер | 1 |
| Болгарка | 0.8 |
| Вакуумный насос | 0.85 |
| Индукционные печи | 0.85 |
| Компрессор | 0.7 |
| Компьютер | 0.95 |
| Кофеварка | 1 |
| Лампы газоразрядные | 0.4-0.6 |
| Лампы люминисцентные | 0.95 |
| Лампы накаливания | 1 |
| Обогреватель | 1 |
| Перфоратор | 0.85 |
| Пылесос | 0.9 |
| СВЧ-печь | 1 |
| Стиральная машина | 0. 9 9 |
| Телевизор | 1 |
| Утюг | 1 |
| Фен | 1 |
| Холодильник | 0.95 |
| Электродрель | 0.85 |
| Электромоторы | 0.7-0.8 |
| Электроплита | 1 |
| Электросварка дуговая | 0.3-0.6 |
| Электрочайник | 1 |
Описание явлений
Мощностью называется скалярный вид физической величина, которая показывает, как передается или преобразуется электроэнергия. Бывает мощность постоянного и переменного тока. Что касается последнего, то делится на активную и реактивную.
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов.
Образуется при работе электроприборов.
Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значениям.
Пример расчета реактивной мощности асинхронного двигателя
В данной статье будет рассматриваться пример расчета реактивной мощности асинхронного двигателя.
Определить реактивную мощность асинхронного двигателя типа АИР132М2 с нагрузкой 100 и 50%.
Технические характеристики двигателя определяются по каталогу согласно таблице 1:
- Рн = 11 кВт – номинальная активная мощность;
- сosϕн = 0,89 – коэффициент мощности;
- Uн = 380В – номинальное напряжение при схеме соединения обмоток статора в треугольник;
- ηн = 0,884 – коэффициент полезного действия.
Таблица 1 — Технические характеристики электродвигателей типа АИР
Источник реактивной энергии
Чтобы понять природу появления этой энергии и то, как найти реактивную мощность, нужно уточнить, что любая электромагнитная или индукционная машина, которая работает на переменном токе, преобразует электричество в тепло. Чтобы это преобразование произошло, нужно магнитное поле. Оно, соответственно, формируется безваттной энергией. Причина в поглощении энергии индукционной цепи и отдаче ее обратно при спаде магнитного поля два раза за цикл мощностной частоты.
Чтобы это преобразование произошло, нужно магнитное поле. Оно, соответственно, формируется безваттной энергией. Причина в поглощении энергии индукционной цепи и отдаче ее обратно при спаде магнитного поля два раза за цикл мощностной частоты.
Расчет
Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:
S = U \ I, где U – это напряжение сети, а I – это сила тока сети.
Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:
Схема симметричной нагрузки
Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:
Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).
Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).
Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.
Расчет трехфазной сети
Максимальная и активная обозначается P, реактивная мощность – Q.
Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:
Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.
Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:
S = √P 2 + Q 2 , и все это равняется U*I .
Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:
Сопротивление индуктивности: xL = ωL = 2πfL,
Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).
Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.
При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:
Диаграмма треугольников напряжений
К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:
Для получения максимально точных результатов рекомендуется не округлять полученные данные.
Мощность генератора. Обозначения характеристик дизельных генераторов
Электрическая мощность – величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
При движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени.
В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток и напряжение в общем случае сдвинуты по фазе на некоторый угол, мгновенное значение мощности равно произведению мгновенных значений силы тока и напряжения. Кривую мгновенной мощности можно получить перемножением мгновенных значений тока и напряжения при различных углах. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику, в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику, в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Таким образом, мгновенная мощность может быть представлена в виде векторной суммы двух составляющих – активной и реактивной мощности.
Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую, электромагнитную). Единица измерения активной мощности – Ватт (Вт, W) .
Реактивная мощность – это энергия, перекачиваемая от источника на реактивные элементы приемника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесенная к этому периоду.
Генераторы переменного тока рассчитаны на определенный номинальный ток и определенное номинальное напряжение, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток генератора или пробою их изоляции. Поэтому каждый генератор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение. Произведение действующих значений тока и напряжения называется полной мощностью.
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередач), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Активная мощность дизельного генератора является характеристикой генератора, в то время как реактивная мощность является в большей степени характеристикой электрической цепи и зависит от наличия в цепи накопителей энергии, таких как катушка индуктивности или конденсатор.
Характеристика, которая показывает, насколько эффективно используется мощность в электрической цепи, называется коэффициентом мощности . Чем больше значение коэффициента мощности цепи, тем эффективнее используется мощность дизельного генератора.
Стандартное обозначение мощности дизельного генератора (например для генератора AIRMAN SDG 100 S ) выглядит так:
Это означает, что при коэффициенте мощности 0,8 и частоте переменного тока 50 Гц
Активная мощность генератора составит – 64 кВт,
Полная мощность генератора составит – 80 кВА
Необходимо понимать что указанные выше значения мощностей являются рабочими (номинальными ), т. е. дизельная электростанция способна выдавать такие мощности при постоянной работе. Максимально допустимые (пиковые) нагрузки на генератор будут выше номинальных в среднем на 15-20% в зависимости от производителя и модели.
е. дизельная электростанция способна выдавать такие мощности при постоянной работе. Максимально допустимые (пиковые) нагрузки на генератор будут выше номинальных в среднем на 15-20% в зависимости от производителя и модели.
Источник
Различия
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания.
Простое объяснение с формулами
Активная мощность (P)
Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть
потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением.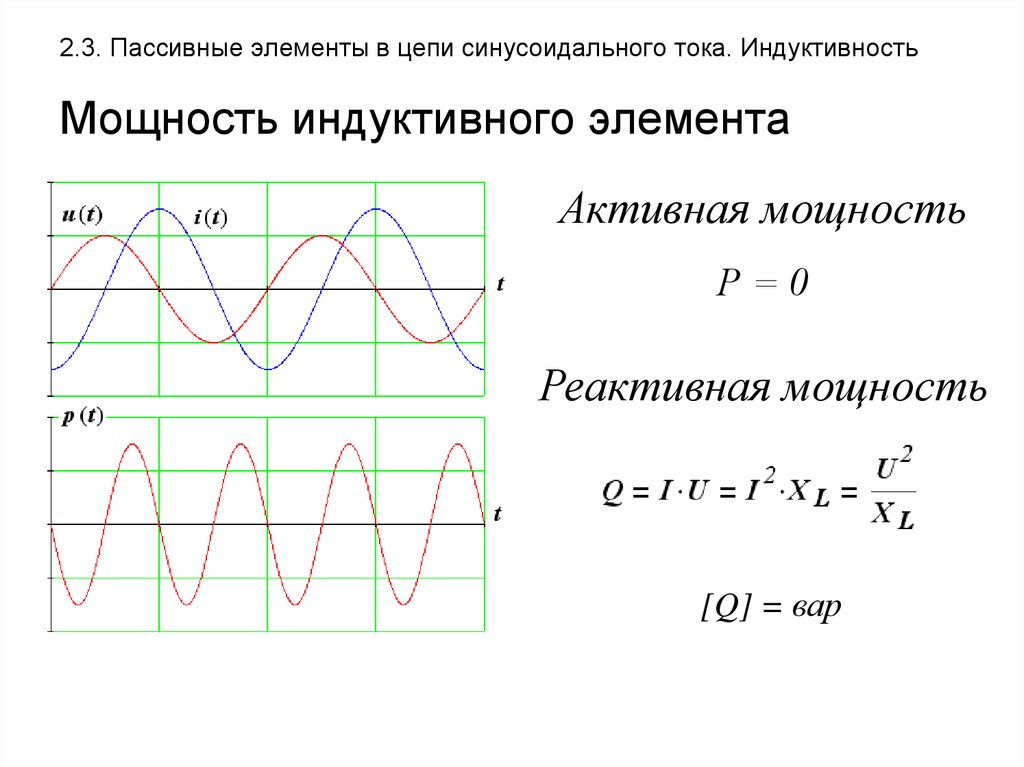 Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:
В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.
Формулы для активной мощности
P = U I — в цепях постоянного тока
Цепь синусоидального тока с резистором. Энергетический процесс. Мгновенная и средняя (активная) мощности.
Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону:
Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают . Период – это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду , единица частоты — герц (Гц).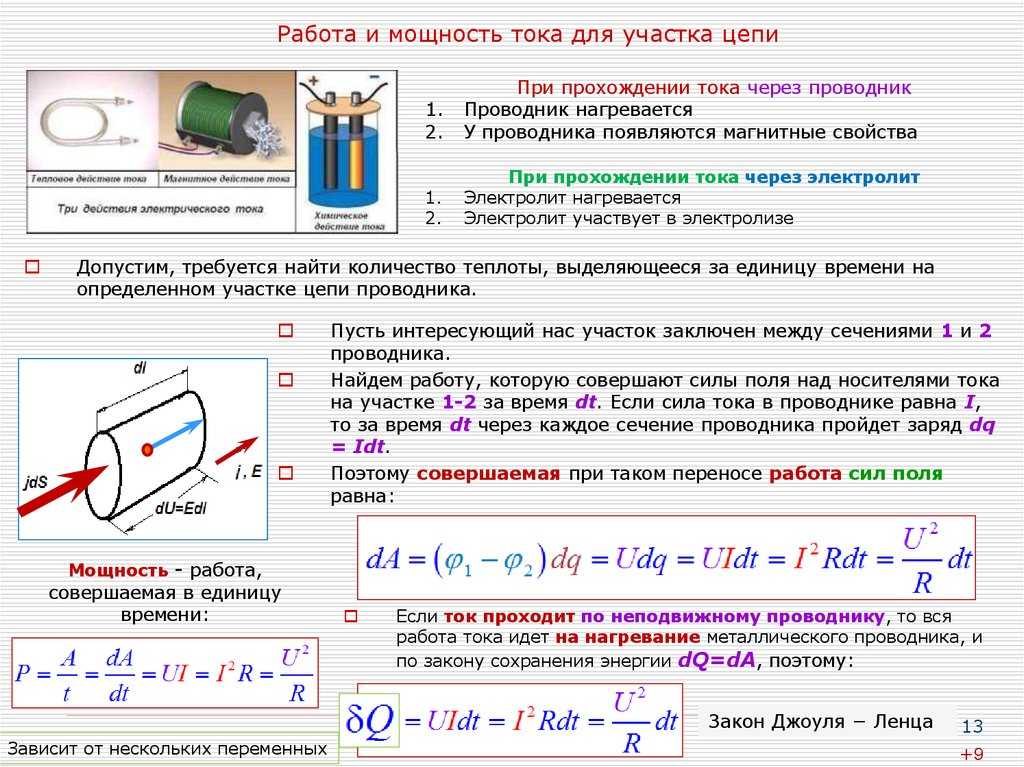
Угловая частота , единица угловой частоты рад/с или . Аргумент синуса, т.е. , называют фазой. Фаза характеризует состояние колебания в данный момент времени .
Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период
Большинство измерительных приборов амперметров и вольтметров показывают действующее значение измеряемой величины.
Резистор в цепи син. Тока.
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:
Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:
Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:
Активная мощность
Измеряется в W [Вт] Ватт.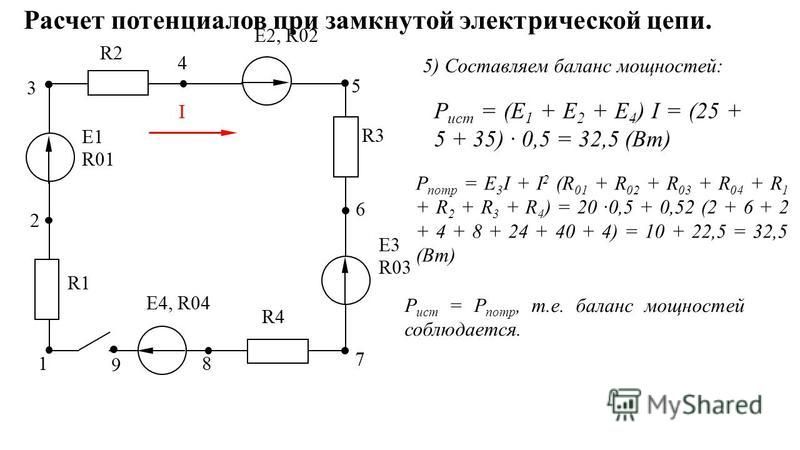
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U иI — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
У идеальной катушки отсутствует активное омическое сопротивление и отсутствует паразитная межвитковая ёмкость. Значит, постоянная времени для неё равна нулю (R/L).
Значит, постоянная времени для неё равна нулю (R/L).
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где Io = Uo/R − амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины Uo и Io = Uo/R называются амплитудными значениями напряжения и силы тока. Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока
Pпост =I2R,
то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
Iд = Io/√2.
Аналогично можно ввести действующее значение и для напряжения
Uд = Uo/√2.
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
P = UдIд = Iд2R = Uд2/R, Iд = Uд/R.
Индуктивное сопротивление, его зависимость от частоты.
32. Цепь синусоидального тока с индуктивностью.
Энергетический процесс.
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Для единичного заряда на участке A-B:
Для всех зарядов:
Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало.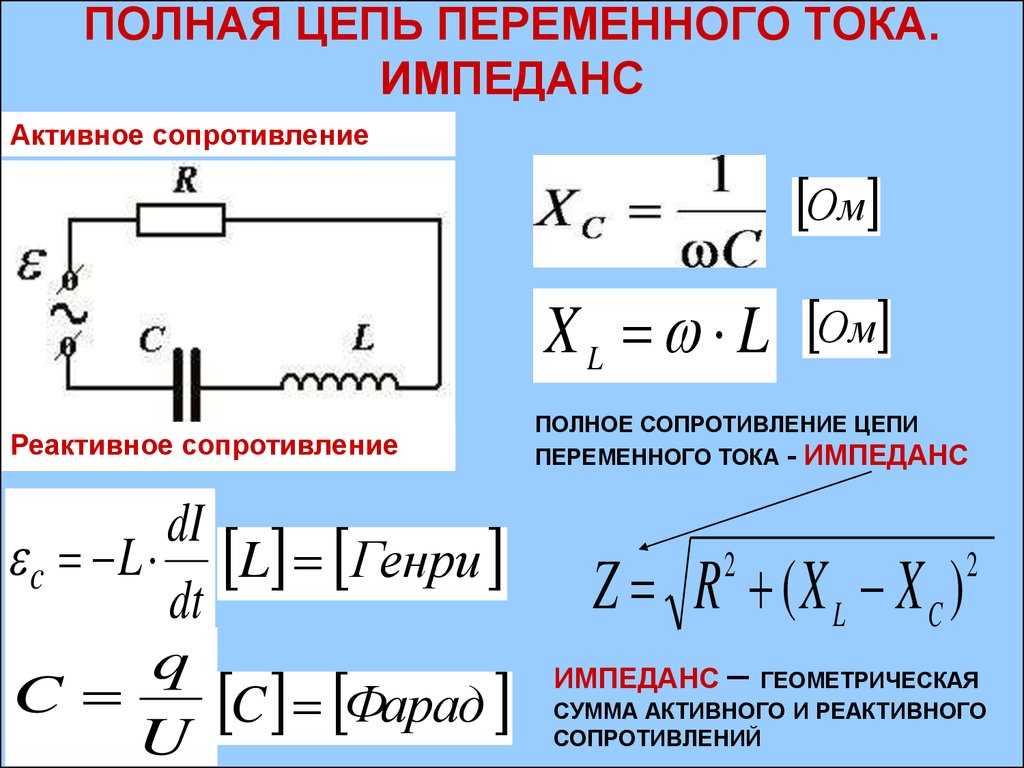 В итоге получаем следующее определение мгновенной электрической мощности:
В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:
Если участок цепи содержит резистор c электрическим сопротивлением R, то
Активная мощность
Единица измерения — ватт (W, Вт).
Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними.
Реактивная мощность
Единица измерения — вольт-ампер реактивный (var, вар)
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .
Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .
Билет 34
1)Треугольник сопротивлений получается из треугольника напряжений. Треугольники напряжений и сопротивлений подобны. Длины сторон треугольника сопротивлений определяются путем деления соответствующих напряжений на значение тока. При ф О сторона треугольника jx направлена влево от катета г — преобладает индуктивное сопротивление, при ф 0 сторона треугольника — jx направлена вправо — преобладает емкостное сопротивление.
Треугольник сопротивлений дает графическую интерпретацию связи между модулем полного сопротивления z и активным и реактивным сопротивлениями цепи; треугольник проводимости — интерпретацию связи между модулем полной проводимости у и ее активной и реактивной составляющими.
Треугольники напряжений (а) и сопротивлений (б)
Треугольник сопротивлений можно получить, уменьшив в / раз стороны треугольника напряжений.
UL образуют у треугольник напряжений для активно-индуктивной нагрузки.
Умножив все стороны треугольника напряжений на величину тока /, получим треугольник мощностей , в котором QL — реактивная мощность индуктивности, a Qc-реактивная мощность емкости.
Если все стороны треугольника напряжений разделить на величину тока, то получится подобный треугольник — треугольник сопротивлений , где длина гипотенузы соответствует полному сопротивлению г -; катет — активному сопротивлению.
2)
— полное сопротивление цепи.
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников(резисторов): R = R1 + R2.
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников: 1/R = 1/R1 + 1/R2.
3) Угол сдвига фаз называется электрическим углом.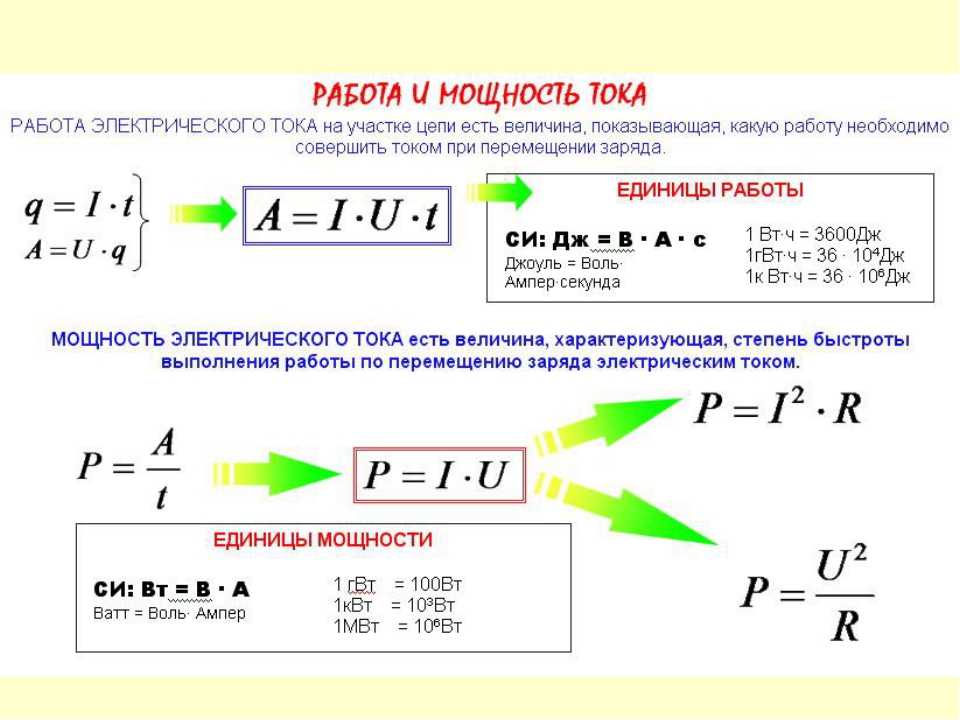 Он, так же как и геометрический угол, измеряется в градусах или радианах.
Он, так же как и геометрический угол, измеряется в градусах или радианах.
Угол сдвига фаз между током в одной цепи и напряжением в другой равен 1 / 4 периода.
Угол сдвига фаз между током и напряжением при резонансе равен нулю.
Угол сдвига фаз между током и напряжением зависит от соотношения между активным и реактивным сопротивлениями, включенными в цепь.
Угол сдвига фаз между напряжением и током для каждой гармоники получается различным, так как с изменением порядкового номера активное сопротивление г не изменяется, а реактивное сопротивление xkk ( uL — 1 / fecoC изменяется.
Угол сдвига фаз между током и напряжением определим из соотношения.
— полное сопротивление цепи
Определим угол сдвига фаз между напряжением источника и током в цепи:
arctg (xL — хсУг = arctg (3/4)
Билет 35
1)Реактивная мощность Q измеряется в вольт-амперах реактивных (вар), полная мощность S — в вольт-амперах (В·А)
Активная, реактивная и полная мощности связаны друг с другом соотношениями:
P = Scosφ; Q = Ssinφ
Из приведенных соотношений следует, что индуктивная цепь потребляет реактивную мощность: при отставании тока от напряжения φ > 0 и Q > 0. При емкостном характере цепи, наоборот, φ < 0 и Q < 0. Поэтому конденсаторы условно рассматривают как источники, а индуктивности — как потребители реактивной мощности. Реактивная мощность, таким образом, является характеристикой интенсивности обратимого обмена энергией между отдельными участками цепи, который является существенным при оценке потерь в соединительных проводах цепи.
При емкостном характере цепи, наоборот, φ < 0 и Q < 0. Поэтому конденсаторы условно рассматривают как источники, а индуктивности — как потребители реактивной мощности. Реактивная мощность, таким образом, является характеристикой интенсивности обратимого обмена энергией между отдельными участками цепи, который является существенным при оценке потерь в соединительных проводах цепи.
Полная мощность S определяет амплитуду колебаний мгновенной мощности p(t). Активную, реактивную и полную мощности можно непосредственно определить по комплексным напряжению и току на участке цепи.
Мгновенная мощность переменного тока
Сдвиг фаз φ зависит от соотношения между активным и реактивными сопротивлениями и тем самым от частоты ω. Поскольку напряжение и ток в цепи изменяются с частотой ω, то при подсчете работы тока нужно рассматривать настолько малый промежуток времени Δt, чтобы значения напряжения и тока можно было считать постоянными: ΔA = I(t)U(t)Δt
,где U(t) = Uocosωt, I(t) = Iocos(ωt − φ).
Отсюда получается следующее выражение для мгновенной мощности тока:
P(t) = ΔA/Δt = I(t)U(t).
Подставив сюда значения I(t) и U(t) из (1), получаем P(t) = UoIocosωt•cos(ωt − φ). (2)
Воспользовавшись тригонометрическим тождеством
сosα•cosβ = (1/2)[cos(α + β) + cos(α − β)],
перепишем в следующем виде: P(t) = (1/2)UoIo[cosφ + cos(2ωt − φ). (3)
Выражение для мгновенной мощности состоит из двух слагаемых: одно из них не зависит от времени, а второе осциллирует с удвоенной частотой 2ω. Это значит, что дважды за каждый период изменения приложенного напряжения изменяется направление потока энергии: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течение другой части возвращается обратно. Средний за период поток энергии положителен, т. е. энергия поступает в цепь от источника.
АКТИВНАЯ МОЩНОСТЬ, среднее за период значение мощности переменного тока; характеризует среднюю скорость преобразования электромагнитной энергии в др. формы (тепловую, механическую, световую и т. д.). Измеряется в ваттах. Для синусоидального тока равна произведению действующих (эффективных) значений тока I и напряжения U на косинус угла j сдвига фаз между ними: P = IUcosj.
формы (тепловую, механическую, световую и т. д.). Измеряется в ваттах. Для синусоидального тока равна произведению действующих (эффективных) значений тока I и напряжения U на косинус угла j сдвига фаз между ними: P = IUcosj.
— Активная мощность связана с полной
-Мгновенная, активная, реактивная и полная мощности.
2)
Треугольник мощностей
В цепях переменного тока различают три понятия мощности: активная Р, реактивная Q, полная S.
Соотношения между мощностями могут быть получены из треугольника мощностей, который образуется путем умножения всех сторон треугольника напряжений на значение тока I.
ТРЕУГОЛЬНИК МОЩНОСТЕЙ — графическое изображение активной, реактивной и полной мощностей в цепи переменного тока.
Треугольник мощностей получается из соотношения Р2 + Q2 = S2.
3)
Коэффициент мощности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Коэффициентом мощности или cos φ электрической сети называется отношение активной мощности к полной мощности нагрузки расчетного участка.
cos φ = P/S, где:
cos φ – коэффициент мощности;
Р — активная мощность Вт;
S — полная мощность ВА;
Коэффициент мощности можно определить как расчетным путем, так и измерить специальными приборами. Только в том случае, когда нагрузка имеет исключительно активный характер, cos φ равен единице. В основном же, активная мощность меньше полной и поэтому коэффициент мощности меньше единицы.
Следует учитывать, что низкий коэффициент мощности потребителя приводит:
*к необходимости увеличения полной мощности трансформаторов и электрических станций, а также к увеличению сечения питающих линий электропередач;
*к понижению коэффициента полезного действия вырабатывающих и трансформирующих элементов цепи;
*к увеличению потерь мощности и напряжения в проводах. При одних и тех же значениях мощности и напряжения уменьшение коэффициента мощности сопровождается увеличением тока в проводах, вследствие чего возрастают потери на нагрев, что, в свою очередь, приводит к падению напряжения в сети;
При одних и тех же значениях мощности и напряжения уменьшение коэффициента мощности сопровождается увеличением тока в проводах, вследствие чего возрастают потери на нагрев, что, в свою очередь, приводит к падению напряжения в сети;
Чем меньше коэффициент мощности сети, тем менее загружена сеть активной мощностью и тем меньше коэффициент полезного действия использования сети.
В связи с этим необходимо, чтобы как можно большую часть в полной мощности составляла именно активная мощность, а не реактивная, в этом случае коэффициент мощности будет ближе к единице.
Билет 36
1)
Емкостью обладают любые два тела способные нести на себе равные по величине и противоположные по знаку заряды, а называется емкостью отношение абсолютной величины заряда на одном из тел к напряжению между ними: С=q/u. Поскольку q и u пропорциональны друг другу, то С от них не зависит, а зависит от формы и геометрических размеров тел, их взаимного расположения и от свойств среды, в которой они находятся. Устройства, предназначенные для получения определенной величины емкости называются конденсаторами.
Устройства, предназначенные для получения определенной величины емкости называются конденсаторами.
Емкостное сопротивление обратно пропорционально частоте и величине ёмкости. С увеличением частоты возрастает скорость изменения напряжения, а значит и ток. При f=0 (постоянный ток) xC=∞, т.е. ёмкость не пропускает постоянный ток.
2) Конденсатор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:
Изменение заряда конденсатора в колебательном контуре происходит по закону:
q = 10-4cos10πt (Kл).
3) Мгновенные значения токов и других величин можно рассчитать , с применением метода наложения.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению электрической величины тока или напряжения
4) Векторная диаграмма изображается синхронно с временной диаграммой с параметрами сигналов, рассчитанными для момента времени, отмеченного визиром. Программа предоставляет возможность отобрать сигналы для просмотра.
Программа предоставляет возможность отобрать сигналы для просмотра.
Отсчет углов ведется относительно вертикальной верхней полуоси. Длина векторов пропорциональна модулям комплексов соответствующих сигналов. Если модуль вектора слишком мал, программа обозначает только его направление.
Таблица имен располагается в нижней части подокна и содержит список имен сигналов, выводимых в виде векторов, и их числовые параметры в данный момент времени: амплитуду в единицах сигнала и фазу в градусах. Размер таблицы ограничен и определяется размерами всего подокна.
А) временная; б) векторная; в)диаграмма цепи
39.1Цепь синусоидального тока с емкостью.
Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток
;
.
Из анализа выражений следует, что ток опережает напряжение по фазе на 90o.
Выражение в комплексной форме записи имеет вид:
,
где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления. 2)/R
2)/R
На индуктивном элементе: P=UIcos(π/2)
На емкостном элементе: P=UIcos(-π/2)
Реактивная мощность – характеризует интенсивность обменного процесса в цепи переменного тока. Q=UIsinφ=[ВАр]
Полная мощность: S=[ВА]
⇐ Предыдущая12345678910Следующая ⇒
Читайте также:
Мощность переменного тока — виды, формула, примеры вычисления » Kupuk.net
Показатель мощности переменного тока характеризует темп передачи или видоизменения электроэнергии. Мощность — величина, полученная от произведения силы тока и напряжения на выбранном участке цепи. В Международной СИ применяется обозначение Ватт (интернациональное — W, в России — Вт).
Общее понятие
Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
В переменной электрической цепи выделяется 3 вида мощности:
- активный P;
- реактивный Q;
- полного типа S.
В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Применяется концепция комплексных чисел для связывания всех трех видов мощности. Это понятие обозначает, что в переменной цепи нагрузка выражается подобным числом так, что активная разновидность представляется действительной составляющей. Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.
Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.
Активная мощность
Активная скорость преобразования выражается также через взаимное отношение силы потока, напряжения к значению активной составляющей сопротивления. В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.
Для определения среднего периодического размера используется активная мощность переменного тока, формула расчета P = U . I . cos φ (косинус), где:
Средний показатель мгновенной скорости преобразования в однофазной цепи берется в виде среднеквадратичного значения тока и напряжения с определенным углом сдвига. В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.
В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.
Проходящая мощность используется в качестве активной в концепции длинных магистралей для анализа электромагнитных течений, протяженность которых сопоставляется с размерностью волны. Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.
Реактивная характеристика
Для обозначения применяется дополнительно единица вольт-ампер реактивный (вар). В русских аналогах используется вар, а международные специалисты применяют var. В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.
В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.
Нахождение производится по формуле P = U . I . sin φ (синус), где:
При диапазоне показателя от 0 до 90º (ток отстает от напряжения, а нагрузка носит активно-индуктивный вид) синус φ будет иметь положительное значение. При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.
В физическом смысле реактивная нагрузка показывает энергию, которая перекачивается от источника тока на конденсаторы, индукторы, двигательные обмотки, а впоследствии возвращается к источнику за один колебательный период. Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.
Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.
Это обстоятельство рассматривается в условном контексте, т. к. почти все энергопотребляющие приборы, например, двигатели асинхронной работы, а также полезная нагрузка, подаваемая через трансформатор, относятся к активно-индуктивным видам. Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.
С помощью современных преобразователей производится компенсация реактивной нагрузки во избежание перегрузок и для увеличения коэффициента мощности электроустановок. Приборы более точно оценивают размер энергии, которая поступает в обратном направлении от индуктора к источнику переменного тока.
Полная нагрузка
Показатель используется в физике для описания потребляемой мощности, которая прилагается к подводящим агрегатам электросети с использованием резисторов. Суммируются параметры ЭДС распределительных щитков, кабелей, проводов, ЛЭП, трансформаторов.
Полную нагрузку можно рассчитать по формуле S = U . I, где:
Параметр темпа преобразований зависит от характеристик применяемого тока, а не от свойств фактически использованной нагрузки. По этой причине полная мощность распределительных электрощитов и трансформаторных агрегатов измеряется в вольт-амперах, а значение ватт к ней не применяется.
Работа в различных условиях
Модуль комплексного показателя интенсивности передвижения равняется показателю полной нагрузки.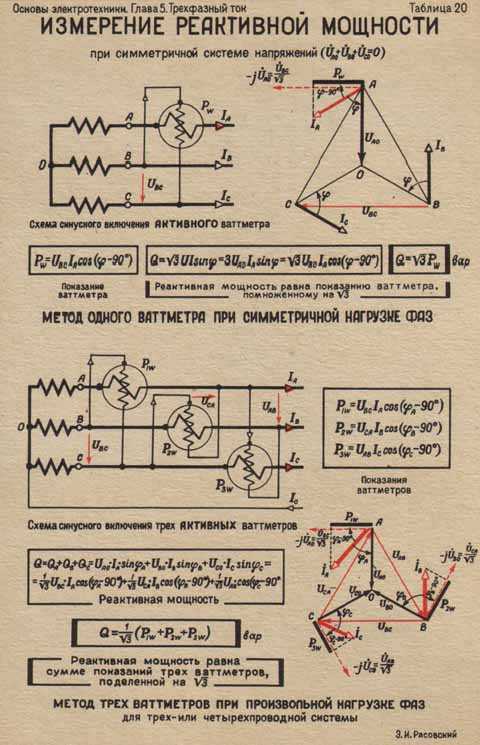 Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.
Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.
Измерение мощностных характеристик переменного потока электронов проводится при пропускании равного по значению тока по фазным проводникам. Показатели силы течения заряженных частиц с применением нулевого проводника имеют ничтожную размерность. Равномерная или симметричная фазовая нагрузка в трехфазной магистрали зависит от величины протекающих токов. Неравномерная или несимметричная нагрузка зависит от прохождения потока по нейтральным или нулевым кабелям. Общий мощностной уровень находится суммированием.
Если присутствует фазовый сдвиг между напряжением и силой тока, то он совпадает с углом смещения между векторными радиусами показателей электротока. В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.
В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.
Если в магистрали происходит сдвиг напряжения и переменного тока, то мощностные показатели представляются значением с отрицательным знаком, так как калькулятор перемножает положительные и отрицательные величины. Продолжительность периодов зависит от уровня смещения фаз. При этом длительность отрицательных нагрузок определяет характеристики сдвига. При расчетах используются показатели сопротивления, которые знакомы из физического закона Ома.
Коэффициент скорости преобразования
Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки.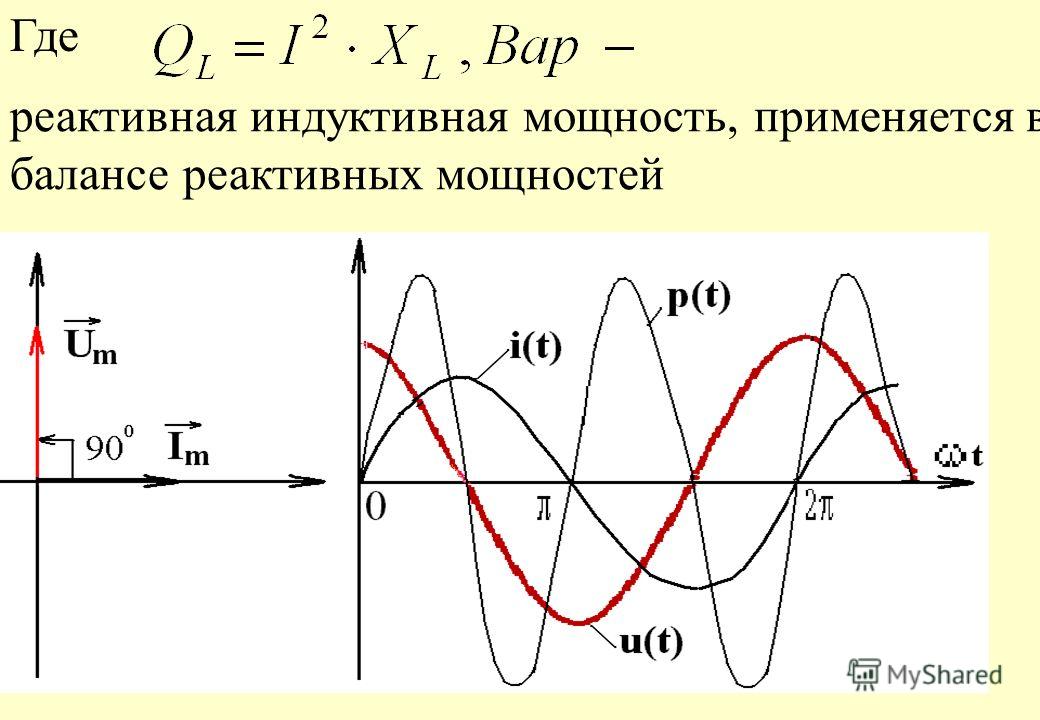 Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.
При математическом расчете числовой множитель интерпретируется в качестве косинуса угла между токовыми векторами и направлением приложения вольтажа. Поэтому при синусоидальных характеристиках размерность коэффициента может совпадать с косинусом угла. Если применяется только синусоидальный вольтаж, а ток используется несинусоидальный с нагрузкой без реактивного компонента, то числовой переходник равняется части нагрузки при первых искажениях потребительского тока.
Если реактивный элемент присутствует в нагрузке, то, помимо мощностного коэффициента, указывается характер работы (емкостно-активный или индуктивно-активный). Коэффициент в этих случаях отличается и является отстающим или опережающим значением.
Практическое применение и коррекция
Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.
Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.
Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Трехфазный калькулятор — Расчет мощности переменного тока фазовая цепь?
Добро пожаловать в трехфазный калькулятор , который может помочь вам:
- Расчет трехфазной мощности по напряжению, току, фазовому углу или коэффициенту мощности;
- Оценка других видов мощности по заданному виду мощности и фазовому углу или коэффициенту мощности; и
- Нахождение величин линии и других величин фаз по величине фазы, одному типу мощности и фазовому углу или коэффициенту мощности.

Наш трехфазный калькулятор представляет собой комплексный инструмент — он может определить значение тока, напряжения и мощности в вашей трехфазной цепи!
Кроме того, мы объясняем , как вывести уравнения трехфазной мощности в терминах линейных величин для звездообразных и дельта-систем.
Не только это, наш калькулятор также полезен для понимания:
- три типа питания в цепи переменного тока;
- различия между активной мощностью и полной мощностью ;
- Как кажущаяся мощность относится к электрической мощности; и
- Что вызывает реактивную мощность в цепи переменного тока, и преимущества прилагается.
Готов? Поехали!
🙋 В этом трехфазном калькуляторе мы имеем дело только с симметричными трехфазными цепями . Сбалансированная трехфазная цепь имеет одинаковые напряжения, токи и коэффициенты мощности во всех трех фазах. Если один из этих параметров отличается для каждой фазы, это Несимметричная трехфазная цепь .
Если один из этих параметров отличается для каждой фазы, это Несимметричная трехфазная цепь .
Что такое полная мощность в трехфазной цепи?
Полная мощность – это полная электрическая мощность в трехфазной цепи. Рассчитаем полную мощность трехфазной цепи через фазный ток и фазное напряжение как:
- S = 3 × V Ph × I Ph ,
где:
- S – полная мощность;
- В Ph – фазное напряжение; и
- I Ph – фазный ток.
💡 Полная мощность измеряется в вольт-ампер ( ВА ). Чтобы узнать больше о ВА и о том, почему он используется вместо ватт ( Вт ), взгляните на наш калькулятор кВА.
Как рассчитать полную мощность, используя линейное напряжение и силу тока?
В пересчете на линейное напряжение и линейный ток , полная мощность трехфазной цепи:
- S = √3 × V линия × I линия ,
где:
- В линия линейное напряжение; и
- I линия — ток линии.

💡 Хотите узнать о различиях между конфигурациями линейного и линейного напряжения применительно к трехфазным токам? Здесь вам поможет наш калькулятор преобразования ватт в ампер.
Что такое активная или реальная мощность?
Активная мощность – это фактическая мощность, которая действительно передается в нагрузку и рассеивается в цепи. Мы рассчитываем активную мощность как произведение полной мощности и коэффициента мощности.
- P = S × PF,
где:
- P – активная мощность; и
- PF — коэффициент мощности, равный
cos φ. Здесьφ— фазовый угол , — угол опережения или угол отставания фазы тока по отношению к фазе напряжения.
Таким образом, мы можем рассчитать активную мощность, используя две фазы:
- P = V ф × I ф × PF
Или, с точки зрения линейного напряжения и линейного тока:
- P = √3 × V линия × I линия × PF
💡 Активная мощность измеряется в Вт ( Вт ), так как указывает на полезную работу, проделанную в цепи.
Что такое реактивная мощность?
Резисторы поглощают электроэнергию и рассеивают ее в виде тепла или света, в то время как конденсаторы и катушки индуктивности возвращают мощность, полученную в одной половине цикла, в источник питания в следующей половине. Электрическая мощность, которая течет в цепь и из нее благодаря конденсаторам и катушкам индуктивности, представляет собой реактивную мощность или безваттную мощность ( Q ).
Рассчитаем реактивную мощность для трехфазной цепи как мощность, обусловленную синусоидальной составляющей фазного тока, т. е. произведение полной мощности ( S ) на синус фазового угла:
- Q = S × sin φ
Таким образом, в пересчете на количество фаз реактивная мощность равна:
- Q = 3 × V Ph × I Ph × sin φ
Формула реактивной мощности с точки зрения количества линий:
- Q = √3 × V линия × I линия × sin φ
💡 Реактивная мощность измеряется в вольт-амперах реактивных ( вар ).
💡 Чтобы узнать больше об электроэнергии, связанной с резистивной цепью, взгляните на наш калькулятор мощности резистора!
В чем разница между потребляемой мощностью при соединении по схеме «звезда» и «треугольник»?
При соединении звездой линейный ток и фазный ток одинаковы, а линейное напряжение равно √3 фазному напряжению.
- I строка = I фот
- В линия = √3 × В фаза
Линейное напряжение и фазное напряжение одинаковы при соединении треугольником , а линейный ток в √3 раза превышает фазный ток.
- I строка = √3 × I фот
- В строка = В фот
Следовательно, как для соединения треугольником, так и для соединения звездой, полная мощность равна:
- S = √3 × V линия × I линия
Таким образом, формула активной мощности при соединении по схеме «звезда» и «треугольник» будет следующей:
и формула реактивной мощности в обоих соединениях:
- Q = √3 × V строка × I строка × sin φ
⚠️ Хотя мы можем использовать одни и те же уравнения мощности для обеих трехфазных систем, параметры линии не совпадают.
Например, если фазное напряжение 400 В, фазный ток 10 А и фазовый угол 30 градусов:
- Соединение звездой:
- В L = √3 В фазы = 693 В
- I L = I ф = 10 А
- S = √3 В L I L = 12 кВА
- P = √3 В L I L cos φ = 10,4 кВт
- Q = √3 В L I L sin φ = 6 кВАр
- Соединение треугольником:
- В L = В ф = 400 В
- I L = √3 I ф = 17,3 A
- S = √3 В L I L = 12 кВА
- P = √3 В L I L cos φ = 10,4 кВт
- Q = √3 В L I L sin φ = 6 кВАр
Следовательно, соединения треугольником и звездой с одним и тем же фазным током, напряжением и углом имеют одинаковую мощность в своих цепях, хотя количество их линий различно.
Как рассчитать трехфазный ток?
Известный параметр | Формула для нахождения тока |
|---|---|
Полная мощность | |
Активная мощность | |
Реактивная мощность | |
3-фазный калькулятор Omni также является 3-фазным калькулятором тока для соединений треугольником и звездой (звездой). 🔥🔥 Смотрите!
💡 Знаете ли вы, что нулевой провод не нужен в сбалансированной трехфазной системе? Когда три нагрузки равны, обратный ток в нейтрали равен нулю. Следовательно, ток нейтрали в сбалансированной трехфазной системе равен нулю, и нулевой провод не нужен.
Следовательно, ток нейтрали в сбалансированной трехфазной системе равен нулю, и нулевой провод не нужен.
Как использовать трехфазный калькулятор для расчета мощности переменного тока?
❓ Пример: Реальная мощность трехфазного двигателя переменного тока 5 кВт . Если напряжение и ток двигателя равны 400 В и 8,6 А соответственно, определите коэффициент мощности системы треугольник?
Провести правильный расчет трехфазной мощности по приведенной выше задаче:
- Определить заданные параметры — активную мощность
= 5 кВт, фазное напряжение= 400 Ви линейный ток= 8,6 А. - Выберите тип соединения. По умолчанию тип трехфазного подключения трехфазного калькулятора Omni —
Delta (D). Поскольку в задаче не указан тип соединения, вы можете оставить этот вариант как есть. - Выберите соответствующую единицу измерения из раскрывающегося списка рядом с каждым параметром.

- Введите значения заданных параметров в соответствующие поля ввода.
Готово! Трехфазный калькулятор показывает значения других параметров:
- Фазный ток
=5 А; - Напряжение сети
= 400 В; - Фазовый угол
= 33 градуса; - Коэффициент мощности
= 0,84; - Полная мощность
= 5,96 кВА; и - Реактивная мощность
= 3,24 кВАр.
💡 Хотите узнать больше о трехфазных системах? Вам обязательно понравится наш конвертер дельта-звезда!
Часто задаваемые вопросы
В чем разница между активной мощностью и полной мощностью?
Существует много различий между активной и полной мощностью. Вот некоторые из них, перечисленные рядом в таблице для удобства сравнения.
Полная мощность | Активная мощность |
|---|---|
Известный как «воображаемая сила» | Известный как «реальная сила» |
Измеряется в вольт-амперах ( | Измерения в ваттах ( |
Теоретическая максимальная мощность, отдаваемая источником напряжения в течение определенного интервала времени | Доля электроэнергии, преобразованная в полезную работу |
Комбинация активной и реактивной мощностей | Компонент полной мощности |
Что вызывает реактивная мощность в цепи переменного тока?
В любой цепи переменного тока реактивная мощность вызывает фазовый сдвиг между кривыми напряжения и тока и уменьшает перекрытие между двумя кривыми. Это приводит к тому, что на нагрузку подается меньшая мощность.
Каковы преимущества реактивной мощности?
Важным преимуществом реактивной мощности является то, что она помогает поддерживать уровни напряжения для передачи активной мощности по линиям электропередачи. Линии электропередач действуют как конденсаторы при очень низких уровнях нагрузки и повышают напряжение. При высоких нагрузках линии электропередач поглощают реактивную мощность и снижают напряжение.
При высоких нагрузках линии электропередач поглощают реактивную мощность и снижают напряжение.
Как найти мощность, подводимую к двигателю, работающему при напряжении 4 кВ и токе 462 А?
Полная мощность представляет отдаваемую мощность. Чтобы найти точный ответ, умножьте напряжение ( 4 кВ ) на силу тока ( 462 А ), что дает 1848 кВА .
💡 Также ознакомьтесь с нашим калькулятором закона Ома, чтобы понять, как рассчитать электроэнергию, и нашим преобразователем мощности, чтобы узнать о различных единицах измерения мощности 🙂
Mehjabin Abdurrazaque
Тип подключения
Фазовый ток (Iₚₕ)
Фазовое напряжение (Vₚₕ)
Ток линии (Iₗᵢₙₑ)
Напряжение линии (Vₗᵢₙₑ)
Фазовый угол (φ)
Силовой коэффициент
Очевидная мощность (s)
Активная мощность (P)
Реактивная мощность (Q)
Ознакомиться с 83 похожими калькуляторами электромагнетизма0001
Треугольник силы | Треугольник мощности, напряжения, тока Треугольник мощности — это просто прямоугольный треугольник, сторона которого соответствует активной, реактивной и полной мощности. Компонент основания символизирует активную мощность, перпендикулярный компонент обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Компонент основания символизирует активную мощность, перпендикулярный компонент обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Треугольник мощности — это графическое представление реальной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
Уравнение степенного треугольника | Треугольник мощности PQS Расчет формулы треугольника мощности | Уравнение треугольника мощностейВ треугольнике мощностей активная мощность P, реактивная мощность Q и полная мощность S образуют прямоугольный треугольник. Следовательно,
гипотенуза 2 = основание 2 + перпендикуляр 2
S 2 = P 2 + Q 2
Здесь полная мощность (S) измеряется в вольт-амперах (ВА).
Активная мощность (P) измеряется в ваттах (Вт).
Реактивная мощность (Q) измеряется в реактивных вольт-амперах (ВАр).
- Треугольник мощности — это графическое представление активной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
- Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется как P и среднее значение активной мощности P .
- Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. T также известен как мощность без ватт. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается буквой Q.
- Полная мощность в цепи, как поглощаемая, так и рассеиваемая, называется полной мощностью.
 Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.
Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла. - Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина.
- Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Рассмотрим цепь RLC, соединенную последовательно, как указано выше.
Где, резистор с сопротивлением R.
индуктор с индуктивностью L.
конденсатор с емкостью C.
В — среднеквадратичное значение приложенного напряжения, а I — среднеквадратичное значение полного тока в цепи. Катушка индуктивности и конденсатор дают Х L и X C оппозиций соответственно в цепи. Теперь может быть три случая:
Катушка индуктивности и конденсатор дают Х L и X C оппозиций соответственно в цепи. Теперь может быть три случая:
Случай 1: X L > X C
Случай 2: X L < X C
Треугольник мощности получается из векторной диаграммы, если мы умножив каждый из векторов напряжения на I, мы получим три составляющие мощности.
Из векторного треугольника мы можем быстро получить треугольник мощности, умножив напряжения на I. Реальная мощность умножается на V R , что равно I 2 R. Реактивная мощность I умножается на (V C – V L ), что равно I 2 (X C – X L ). Полная мощность V = I 2 Z рассчитывается из активной мощности и реактивной мощности для обоих случаев. Здесь мы принимаем во внимание другую величину, комплексную мощность. Комплексная мощность представляет собой сумму активной мощности и реактивной мощности, представленных в комплексной форме, т. е. с величиной j.
е. с величиной j.
Следовательно, комплексная мощность
S = P – jQ когда X L < X C
S = P + jQ, когда X L > X C
, для случая реактивной, индуктивной, теперь меньше емкостного сопротивления. Следовательно, реактивная мощность отрицательна, и угол ϕ также отрицателен. Для случая 2 значение индуктивного сопротивления больше, чем значение емкостного сопротивления, реактивная мощность равна +ve, а угол ϕ также равен +ve.
Треугольник активной реактивной полной мощности | Мощность вольт ампер треугольник Треугольник активной и реактивной мощности . Треугольник истинной силы .Активная или истинная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется в виде P и среднего значения активной мощности P is,
P = VI = I 2 R
Треугольник реактивной мощности Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. Он также известен как без ватт мощность. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольт-амперах реактивной (кВАр) и обозначается Q.
Он также известен как без ватт мощность. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольт-амперах реактивной (кВАр) и обозначается Q.
Реактивная мощность Q = VI реактивная = I 2 X.
Треугольник полной мощностиПолная мощность в цепи, как поглощаемой, так и рассеиваемой, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла. 9{2} + (Реактивная\; мощность)2}[/Latex]
Для чисто резистивной цепи реактивная мощность отсутствует. Итак, кажущаяся мощность равна активной или истинной мощности.
Силовой треугольник для цепи переменного тока | Треугольник электрической мощности Цепи переменного тока могут иметь любую комбинацию R, L и C, и если мы хотим правильно рассчитать общую мощность, мы должны знать разность фаз между I и V. Форма волны тока а напряжение синусоидальное. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают. В этой ситуации формы волны называются «синфазными» друг с другом.
Форма волны тока а напряжение синусоидальное. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают. В этой ситуации формы волны называются «синфазными» друг с другом.
- В чисто резистивной цепи переменного тока I и V идеально совпадают по фазе. Следовательно, просто умножая их, мы можем получить мощность.
- Если в цепи имеется индуктивная или емкостная нагрузка, создается разность фаз. Даже если разница фаз незначительна, мощность переменного тока делится на две части: одну положительную и одну отрицательную. Отрицательная мощность не является математически отрицательной величиной; это просто означает, что в систему подается питание, но передачи энергии не происходит. Эта мощность известна как реактивная мощность. Положительная величина совершает некоторую реальную работу, поэтому ее классифицируют как реальную или активную мощность.
- Другая часть питания поступает в цепь от источника.
 Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина. Нам нужно применить некоторые специальные формулы, чтобы рассчитать переменный ток и параметры силового треугольника.
Треугольник мощности для емкостной нагрузкиЕмкостная нагрузка означает, что коэффициент мощности опережает ток по фазовому углу относительно напряжения.
Треугольник мощности для индуктивной нагрузки Индуктивная нагрузка показывает, что коэффициент мощности отстает, поскольку I отстает от V на фазовый угол.
Комплексная мощность есть не что иное, как представление мощности с использованием комплексных чисел. Действительная часть представляет собой активную мощность. Мнимая часть представляет собой реактивную мощность.
Предположим, что ток и напряжение в емкостной цепи равны I и V соответственно. Мы знаем, что для емкостной нагрузки I опережает V на фазовый угол. Примем этот угол за ϕ.
Допустим, напряжение на нагрузке V= ve jƟ и ток I = iej (Ɵ+ϕ) .
Мы знаем, мощность — это напряжение, умноженное на сопряженный ток.
Итак, комплексная мощность S = VI* = ve jƟ x ie -j(Ɵ+ϕ) = vie -jϕ
S = vi(cosϕ – jsinϕ) = vicosϕ – jvisinϕ = P – jQ [мы знаем активную мощность P = vicosϕ и реактивную мощность Q = visinϕ]
Для емкостной нагрузки I отстает от V на фазовый угол. Итак, напряжение на нагрузке V= ve jƟ и ток I = ie j(Ɵ-ϕ) .
So комплексная мощность
S = VI* = ve jƟ x ie-j (Ɵ-ϕ) = vie jϕ
S = vi(cosϕ + jsinϕ) = P vicosϕ + jvisinϕ
Трехфазный силовой треугольникПеременный ток может быть однофазным или трехфазным. Изменение амплитуды тока приводит к генерации синусоидальных волн. Для однофазного питания есть только одна волна. Трехфазные системы разделяют ток на три части. Три составляющие тока не совпадают по фазе на одну треть цикла каждая. Каждая текущая составляющая равна по величине, но противоположна по направлению двум другим конъюнктивным.
Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Треугольник импеданса и треугольник мощности Коэффициент мощности треугольника импеданса В цепях постоянного тока только сопротивление отвечает за противодействие току. Но в цепях переменного тока величина, называемая реактивным сопротивлением, также противодействует току. Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически. Итак, мы строим треугольник импеданса с гипотенузой Z (импеданс), основанием R (сопротивление) и реактивным сопротивлением X (индуктивное или емкостное реактивное сопротивление или оба). 9{2}}[/Latex]
Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически. Итак, мы строим треугольник импеданса с гипотенузой Z (импеданс), основанием R (сопротивление) и реактивным сопротивлением X (индуктивное или емкостное реактивное сопротивление или оба). 9{2}}[/Latex]
Коэффициент мощности [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности треугольника мощностиКоэффициент мощности в треугольнике мощности обозначается как отношение активной мощности к полной мощности, определяемое как косинус угла вектора.
Треугольник коррекции коэффициента мощности Коррекция коэффициента мощности — это метод повышения эффективности электрической цепи за счет снижения реактивной мощности. Коррекция коэффициента мощности достигается за счет параллельно соединенных конденсаторов, которые противодействуют эффектам, вызванным индуктивными элементами, и уменьшают фазовый сдвиг.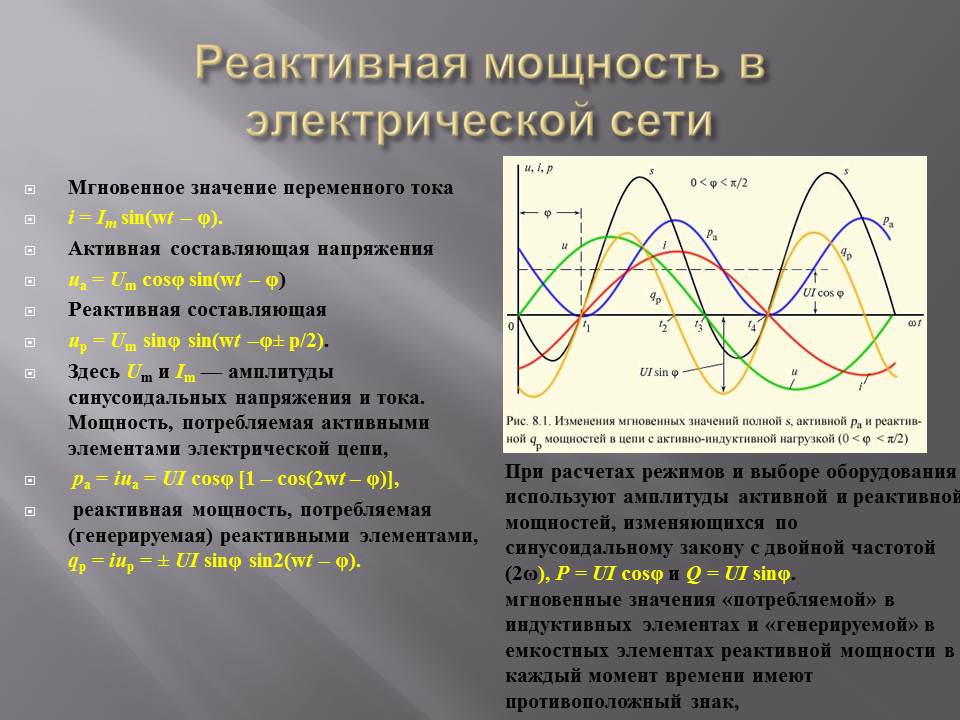
Коэффициент мощности для емкостной или индуктивной нагрузки [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности [Latex]= \frac{Real\; мощность {Очевидная \; power}[/Latex]
Треугольник энергии мощностиЭлектрическая энергия определяется как мощность системы, умноженная на общее время использования энергии.
Энергия E = P x T
Как нарисовать треугольник мощности? Генератор треугольника мощностейТреугольник мощностей строится с использованием активной мощности в качестве основания, реактивной мощности в качестве перпендикуляра и полной мощности в качестве гипотенузы.
Металлические треугольники на линиях электропередач Мы часто видим несколько треугольных петель, свисающих с линий электропередач. Они используются для обеспечения устойчивости строп при сильном ветре. Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]
Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]
Коэффициент мощности цепи = R/Z = 12/13 = 0,92
Пример треугольника мощностейQ. Нагрузка 20 кВт при коэффициент мощности 0,8 отстает. Найдите номинал конденсатора, чтобы он мог поднять значение коэффициента мощности до 0,95.
Здесь реальная мощность P = 20 кВт
Коэффициент мощности cosϕ 1 = 0,8
Мы знаем, что реактивная мощность должна быть уменьшена, чтобы получить увеличенный коэффициент мощности. Следовательно, фазовый угол также уменьшится. Предположим, что изначально фазовый угол был ϕ 1 , а после снижения реактивной мощности фазовый угол равен ϕ 2 . Итак, треугольник мощностей выглядит так-
Из диаграммы видно, что реактивная мощность уменьшилась до AB от переменного тока. Итак, нам нужно вычислить разницу AC и AB, и эта величина является требуемым номиналом конденсатора.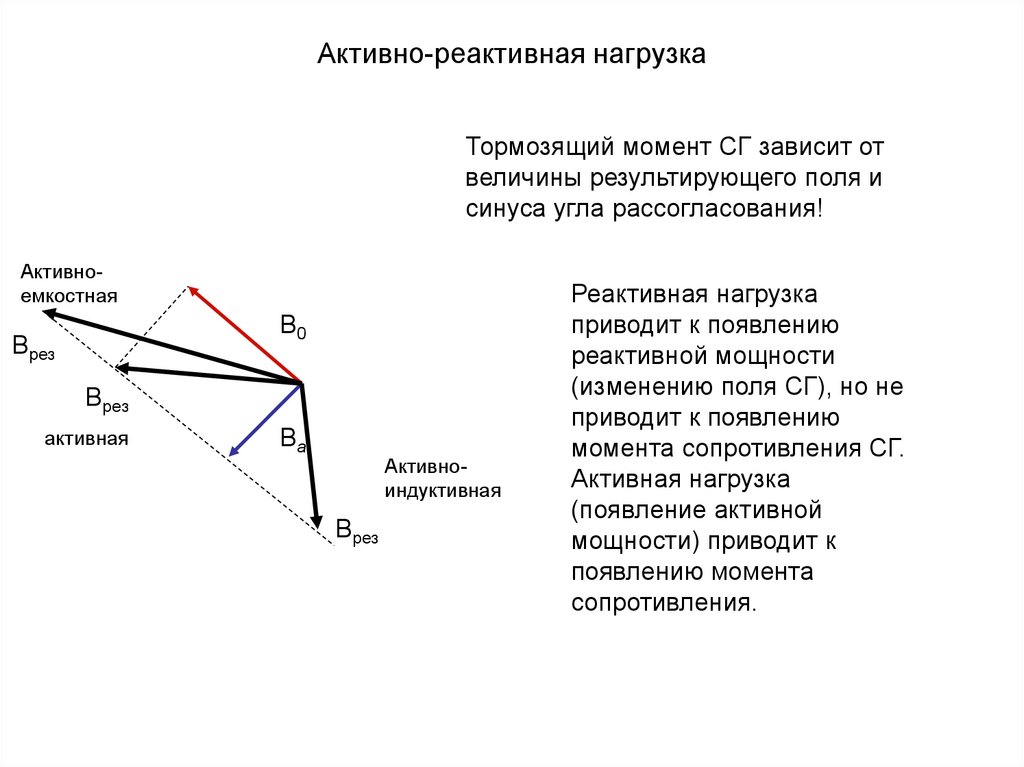
Здесь, OA = 20 кВт
Cos Вотство 1 = 0,8
Cos Вотство 2 = 0,95
Мы знаем, Cos Вотство 1 = OA/OC
SO, OC = 20/0,8 = 25 KVA
- 003
- – Истинная или активная мощность.
- – реактивная мощность.
- – полная мощность.
- Треугольники имеют большую площадь основания, что делает их очень жесткими. Эта жесткость помогает выдерживать боковые нагрузки.
- Треугольники имеют меньшую площадь, чем любой четырехугольник. Если бы форма была четырехугольной, то стоимость была бы больше. Треугольная форма снижает стоимость за счет исключения одной лишней стороны.
Подача энергии в системе переменного тока зависит от фазового угла между напряжением и током.
Фазовый угол также зависит от импеданса цепи, который вызывает изменение фазы.
При наличии разности фаз между напряжением и током реальная мощность, подаваемая на нагрузку, может быть довольно низкой. Вы можете определить, когда это произойдет, посмотрев на графики для вашей схемы.
- Тип тока
- Переменный ток — расчет однофазной мощности
- AC — расчет трехфазной мощности
- ДС
- Ток в амперах
- Тип напряжения
- Линейный
- Линия-нейтраль
- Напряжение (в вольтах)
- Введите коэффициент мощности
- Рассчитать; Перезагрузить; Менять;
- Результаты измерения мощности (милливатты)
- Результаты мощности (Вт)
- Результаты мощности (киловатт)
- Коэффициент мощности равен нулю (0), когда вся мощность является реактивной.
- Коэффициент мощности равен единице (1), когда вся мощность является реальной (без реактивной мощности).
ac = √ (OC 2 — OA 2 ) = 15 KVAR
COSЦ 2 = OA/OB
SO, OB = 20/0,95 = 21 KVA
AB = √ (OB 2. – OA 2 ) = 6,4 квар
Следовательно, BC = AC – AB = (15 – 6,4) = 8,6 квар
Часто задаваемые вопросы Сколько типов треугольника в степени степеней?Треугольник мощности состоит из трех типов мощности
Треугольник мощности представляет собой треугольное представление отношения между активной мощностью, реактивной мощностью и полной мощностью.
Например, в любом электроприборе общая вырабатываемая мощность представляет собой части активной и реактивной мощности.
Что такое треугольник мощности цепи переменного тока?Треугольник мощности цепи переменного тока может быть резистивным, емкостным или индуктивным, и треугольник состоит из трех видов мощностей, а полная мощность рассчитывается с помощью активной мощности и реактивной мощности.
Что такое треугольник мощности цепи RL?Цепь RL имеет треугольник мощности с активной мощностью = I 2 R, реактивной мощностью = I 2 X L , а полная мощность = I 2 Z, где X L — индуктивное реактивное сопротивление, а Z — полное сопротивление цепи.
Какая связь между KVA, KW и KVAr? КВА — это единица полной мощности, а кВт и квар — это единицы активной мощности и реактивной мощности соответственно. Следовательно, из концепции треугольника мощности можно сделать вывод, что кВА 2 = кВт 2 + кВАр0710 2 .
Следовательно, из концепции треугольника мощности можно сделать вывод, что кВА 2 = кВт 2 + кВАр0710 2 .
Для индуктивных и емкостных нагрузок коэффициент мощности играет жизненно важную роль при расчете реактивной мощности. Реактивная мощность — это часть активной мощности, которая уменьшается, а коэффициент мощности — это отношение истинной мощности к полной мощности. Коэффициент мощности, равный единице, указывает на то, что цепь имеет полностью резистивный характер.
Сколько ватт составляет 6 кВА?6 кВА = 6000 ВА
При единичном коэффициенте мощности 6 кВА = 1 x 6000 = 6000 Вт
Если коэффициент мощности другой, 6 кВА = 6 x (коэффициент мощности) Вт
Как преобразовать кВтч в кВАч?кВтч = кВАч X коэффициент мощности
Таким образом, кВАч = кВтч/коэффициент мощности
Сколько ватт составляет 1 кВА? Для чисто резистивной нагрузки реактивная мощность отсутствует. Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт
Таким образом, коэффициент мощности равен 1. Здесь 1 кВА = 1 Вт
. Если нагрузка емкостная или индуктивная, резистивная мощность не равна 0, поскольку коэффициент мощности представляет собой сопротивление/импеданс. Здесь 1 кВА = коэффициент мощности x 1 кВт
Почему электрические опоры имеют треугольную форму?По следующим причинам электрические опоры имеют треугольную форму.
Коэффициент мощности трансформатора зависит от характеристик нагрузки.
Если нагрузка чисто резистивная, коэффициент мощности равен единице или 1.
Если нагрузка емкостная, т. е. X C > X L , коэффициент мощности называется опережающим.
Если нагрузка индуктивная, т. е. X L > X C , коэффициент мощности называется отстающим.
В чем разница между KVA KWH KVAH и KVAR? | Треугольник мощности кВт КВА КВАРКВА означает киловольт-ампер. Это единица реальной или активной мощности.
KWH означает киловатт-час. Это используется для измерения того, сколько энергии (в киловаттах) потребляется за час.
KVAH означает киловольт-ампер-час. KVAH — это полная мощность, а KWH — это активная мощность. KVAH = KWH/коэффициент мощности
KVAR означает реактивный киловольт-ампер. Используется для измерения реактивной мощности. 9{2}}}[/Latex]
Какова единица измерения коэффициента мощности? Коэффициент мощности – это отношение активной мощности (кВт) к полной мощности (кВА), поскольку и числитель, и знаменатель являются мощностями, коэффициент мощности – это величина без единицы.
Используйте формулу фазового угла для понимания подачи мощности
Ключевые выводы
Поддерживайте высокий коэффициент мощности при работе с 3-фазным питанием в ваших системах переменного тока.
Работа с подачей энергии может быть опасной и сложной, особенно когда мы рассматриваем реактивное сопротивление в практических цепях переменного тока. Обеспечение реальной подачи мощности на резистивную нагрузку зависит от поддержания высокого коэффициента мощности в ваших цепях, что в свою очередь требует поддержания фазового угла в вашей системе близким к нулю. Время от времени вам нужно будет проверять угол сдвига фаз между напряжением и током в реактивной цепи, чтобы обеспечить достаточную подачу мощности на элемент нагрузки.
Обеспечение реальной подачи мощности на резистивную нагрузку зависит от поддержания высокого коэффициента мощности в ваших цепях, что в свою очередь требует поддержания фазового угла в вашей системе близким к нулю. Время от времени вам нужно будет проверять угол сдвига фаз между напряжением и током в реактивной цепи, чтобы обеспечить достаточную подачу мощности на элемент нагрузки.
Просто взглянув на разницу во времени между подаваемым напряжением и током на вашем компоненте нагрузки, вы можете определить фазовый угол, определяющий реальную подачу мощности. Затем вы можете использовать формулу фазового угла для реальной и полной мощности, чтобы определить коэффициент мощности в вашей системе. Затем вы можете определить, потребуется ли коррекция коэффициента мощности, которая будет зависеть от входного напряжения и мощности в системе.
Формула фазового угла
Фазовый угол цепи зависит от разности фаз между напряжением и током в цепи.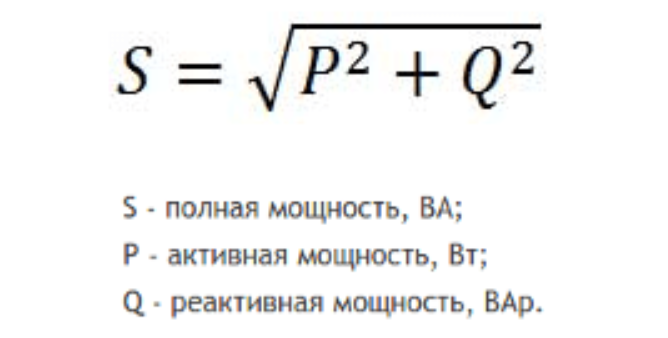 Предполагая, что у нас есть простая система LTI, состоящая только из резисторов, конденсаторов и катушек индуктивности, вы можете определить простое соотношение фазового угла между напряжением и током в каждом элементе схемы.
Предполагая, что у нас есть простая система LTI, состоящая только из резисторов, конденсаторов и катушек индуктивности, вы можете определить простое соотношение фазового угла между напряжением и током в каждом элементе схемы.
Разность фаз в различных цепях RLC графически показана на изображении ниже, где мы видим, что напряжение и ток смещены друг относительно друга во временной области. Здесь реактивное сопротивление элементов C и L создает разность фаз между напряжением и током. Эта разность фаз станет важной позже, когда вы захотите рассчитать реальную мощность, подаваемую на компонент нагрузки.
Комплексные напряжения и токи в различных цепях, а также их разности фаз.
Фазовый угол можно определить, просто взглянув на разницу во времени между кривыми напряжения и тока. Это равно разнице во времени между соседними пиками тока и напряжения, деленной на 180 градусов. В качестве альтернативы, если вы знаете импеданс в вашей цепи переменного тока, вы можете рассчитать разницу фаз, которую вы увидите между напряжением и током:
Формула фазового угла в терминах импеданса.
Обратите внимание, что это относится к цепям LTI, где фаза является постоянной величиной (т. е. не зависит от напряжения или тока). Для обычной сети RLC фазовый угол может быть функцией частоты, даже если цепь представляет собой систему LTI. Теперь, когда у нас есть четкое определение разности фаз в цепи переменного тока, мы можем определить реальную мощность, подаваемую на компонент нагрузки в цепи переменного тока.
Отдаваемая мощность и фазовый угол
Когда ток и напряжение имеют некоторую разность фаз между собой, мощность в цепи представляется комплексным числом S. Действительная и мнимая части комплексной мощности представляют реальную отдаваемую мощность и реактивную мощность соответственно. Следующая формула определяет комплексную мощность S, которая выражается через комплексный импеданс Z.
Комплексная мощность через комплексный импеданс.
Обратите внимание, что резистивные части цепи всегда рассеивают активную мощность, как мы сейчас увидим, а реактивные части получают только реактивную мощность. Физически реактивная мощность представляет собой мощность, ограниченную реактивным элементом в цепи (т. е. элементами L и C). Напротив, реальная мощность рассеивается в виде тепла в резистивных элементах.
Физически реактивная мощность представляет собой мощность, ограниченную реактивным элементом в цепи (т. е. элементами L и C). Напротив, реальная мощность рассеивается в виде тепла в резистивных элементах.
Если вы знаете фазовый угол из импеданса или разницы во времени между током и напряжением, то вы можете рассчитать реальную мощность, подаваемую на нагрузку. Это определяется ниже с точки зрения величины S и фазового угла:
Фактическая мощность, подаваемая на компонент нагрузки.
Чтобы рассчитать реактивную мощность, просто замените косинус на синус в приведенном выше уравнении. Обратите внимание на знак фазового угла в этом расчете, так как он покажет вам, когда мощность ограничивается реактивными элементами, а когда она рассеивается в резистивных элементах. Это различие между кажущейся мощностью и реальной мощностью становится более ясным, когда мы исследуем распределение тока и напряжения в последовательной цепи RLC, как показано на рисунке ниже.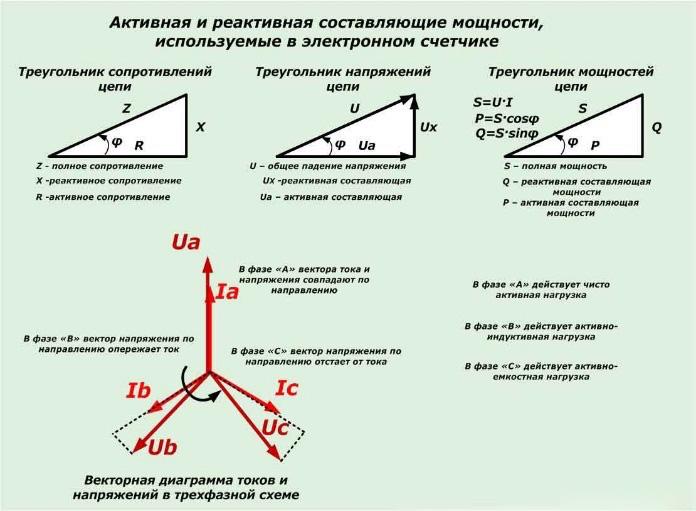
Распределение напряжения и тока в последовательной цепи RLC.
На этом изображении ток и индуктивность имеют напряжения, которые не совпадают по фазе друг с другом, поэтому общая реактивная мощность в LC-ветви цепи равна нулю. Другими словами, элементы C и L имеют противоположное реактивное поведение в разные моменты времени; один элемент генерирует реактивную мощность, а другой ограничивает ее.
Фазовый угол от активной и реактивной мощности
Другой важной величиной является полная мощность |S|, которая учитывает реальную и реактивную мощности вместе без фазовой постоянной. В другом случае вы можете уже знать реальную мощность Re[S] и кажущуюся мощность |S|, и вам нужно найти фазовый угол. Отношение этих двух величин известно как коэффициент мощности, который очень важен в регулируемых системах преобразования переменного тока в постоянный. Коэффициент мощности определяется по фазовому углу следующим образом:
Определение коэффициента мощности по фазовому углу.
В идеале коэффициент мощности системы преобразования мощности должен быть равен 1. Поскольку реальные схемы регуляторов имеют коэффициент мощности где-то около ~ 0,7, схема PFC обычно добавляется на этапе выпрямления AC-DC, чтобы обеспечить коэффициент мощности как можно ближе к 1. Вычисление фазового угла говорит вам, как вам нужно будет компенсировать низкий коэффициент мощности при проектировании ваших цепей.
После того, как вы использовали формулу фазового угла и определили, какой уровень коррекции коэффициента мощности вам нужен, вы можете создать макет платы с помощью лучшего программного обеспечения для компоновки и проектирования печатных плат с полным набором инструментов проектирования. Allegro PCB Editor включает в себя функции, необходимые для компоновки плат для любого приложения, включая системы преобразования энергии переменного тока. Затем вы можете использовать инструменты анализа Cadence для моделирования и анализа поведения вашей силовой электроники.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Калькулятор мощности переменного токадля однофазной и трехфазной сети — Blackhawk Supply
Измерения должны быть точными при выборе электрооборудования или при работе со схемами. Если вам не нравится считать кВт и Ампер вручную — у нас есть решение! Наш онлайн-калькулятор мощности переменного тока может помочь вам преобразовать электрическую мощность в ток и наоборот для однофазной и трехфазной электроэнергии.
Если вам не нравится считать кВт и Ампер вручную — у нас есть решение! Наш онлайн-калькулятор мощности переменного тока может помочь вам преобразовать электрическую мощность в ток и наоборот для однофазной и трехфазной электроэнергии.
Ниже мы научим вас пользоваться нашим калькулятором мощности и расскажем о формулах для этих измерений. Давайте погрузимся!
Как пользоваться калькулятором мощности?
Хотите перевести ампер в кВт (или наоборот) без математических расчетов? Без проблем!
Наш калькулятор однофазной и трехфазной мощности прост в использовании. Просто заполните поля необходимыми данными, включая тип тока, напряжение и коэффициент мощности. Калькулятор все сделает автоматически.
Калькулятор мощности переменного тока — кВт в амперах
Ампер (А или ампер) и киловатт (кВт) — это два разных параметра электричества. Что они имеют в виду?
Что они имеют в виду?
Ампер указывает количество тока, потребляемого нагрузкой. Киловатты – это количество энергии, потребляемой нагрузкой в любой момент времени. Короче говоря, амперами измеряется сила тока, а киловаттами измеряется мощность.
Как можно преобразовать ампер в киловатты для трехфазного, однофазного переменного тока (AC) или постоянного тока (DC)?
Киловатты не могут быть преобразованы в ампер напрямую. Величина тока или мощности зависит от коэффициента мощности, типа тока и типа напряжения.
Однако вы можете получить точные измерения, преобразовав эти показатели с помощью формул. Кроме того, вы можете использовать наш трехфазный преобразователь киловатт в ампер, а также калькулятор однофазной мощности и мощности постоянного тока.
Что такое однофазная электроэнергия?
Фаза означает распределение электрической нагрузки однофазным или трехфазным источником питания.
Однофазная электроэнергия обычно используется в бытовых целях, жилых домах и небольших офисах. Другими словами, он работает для приборов, которым требуется небольшое количество энергии (холодильники, светильники, обогреватели, телевизоры и тому подобное).
Другими словами, он работает для приборов, которым требуется небольшое количество энергии (холодильники, светильники, обогреватели, телевизоры и тому подобное).
Стандарт для однофазного распределения электроэнергии в США составляет 120 вольт переменного тока с частотой 60 герц. Каждый герц означает количество изменений электричества, происходящих в проводе каждую секунду. Следует отметить, что мощность переменного тока может переключать полярность, в отличие от мощности постоянного напряжения.
Как рассчитать однофазную мощность?
Вот формулы, которые можно использовать для расчета однофазной мощности.
Киловатты из Ампер
кВт = PF × A × V / 1000
В этой формуле мощность (в кВт) равна коэффициенту мощности нагрузки (PF), умноженному на фазный ток, измеренный в амперах (А), умноженному на среднеквадратичное напряжение (В) и деленному на 1000.
Ампер из киловатт
A = 1000 × кВт / (PF × V)
A означает фазный ток, равный кВт (мощности), умноженный на 1000, затем разделенный на коэффициент мощности (PF) умножается на среднеквадратичное напряжение (В).
Что такое трехфазное питание переменного тока?
Трехфазная электроэнергия является распространенным типом производства и распределения электроэнергии переменного тока, широко используемым для нагрузок более 1000 Вт. В отличие от однофазного источника питания, трехфазный источник питания требует меньше алюминия или меди, имеет более высокий КПД проводника и выдерживает большие силовые нагрузки. Это также обеспечивает большую общую плотность, оптимизируя тем самым потребление энергии.
Для более точного расчета мощности формула для трехфазных приложений должна учитывать тип конфигурации мощности. Двумя наиболее распространенными конфигурациями являются «треугольник» (используются только три провода) и «вей» (имеет четвертый нейтральный провод).
Трехфазное электропитание обычно используется в коммерческих и промышленных объектах с большими двигателями, производственным оборудованием, мощными кондиционерами и другими приложениями с большой нагрузкой.
Теперь к основной теме. Как перевести амперы в киловатты в трехфазных цепях переменного тока (и наоборот)?
Как рассчитать 3-х фазную мощность?
Вот уравнения, которые можно использовать для расчета трехфазной мощности. Имейте в виду, что формула трехфазной мощности будет отличаться для линейного и нейтрального напряжений.
Киловатты из ампер (линейное напряжение)
кВт = √3 × PF × A × V / 1000
Мощность (кВт) равна квадратному корню из трех (√3), умноженному на мощность коэффициент (PF), умноженный на ток (А), умноженный на линейное среднеквадратичное напряжение (В), деленное на 1000.
Киловатты от ампер (линейное напряжение)
кВт = 3 × PF × A × V / 1000
Вы можете рассчитать трехфазную мощность из ампер в кВт с линейным напряжением так же, как и с линейным напряжением. Единственное отличие состоит в том, что квадратный корень из трех (√3) заменяется числом три (3), а межфазное среднеквадратичное значение заменяется линейным среднеквадратичным значением напряжения в уравнении.
Ампер из киловатт (линейное напряжение)
A = 1000 × кВт / (√3 × PF × В)
Фазный ток (А) равен 1000-кратному количеству киловатт (кВт), деленному на квадратный корень из трех, умноженный на коэффициент мощности (PF), умноженный на линейное среднеквадратичное напряжение (В).
Ампер из киловатт (линейное напряжение)
A = 1000 × кВт / (3 × PF × В)
Для расчета трехфазного источника питания необходимо умножить 1000 на мощность ( кВт), деленное на три умножения на коэффициент мощности, умноженный на среднеквадратичное напряжение между фазой и нейтралью (В).
Что такое коэффициент мощности?
Теперь мы несколько раз упомянули коэффициент мощности (PF) в формулах. Он относится к отношению между реальной и кажущейся мощностью, рассеиваемой цепью переменного тока, к изделию с электрическим питанием.
Реальная мощность означает электрическую мощность, используемую устройствами, а кажущаяся мощность означает электроэнергию, подаваемую в цепь.
Значение коэффициента мощности изменяется от нуля до единицы в зависимости от резистивной и реальной нагрузки.
Как рассчитать коэффициент мощности?
Существует множество уравнений коэффициента мощности, основанных на типе мощности и тока. Давайте рассмотрим каждую формулу коэффициента мощности.
Коэффициент мощности для синусоидального тока равен абсолютному значению косинуса фазы полной мощности. Фазовый угол кажущейся мощности будет отмечен как φ в приведенных ниже формулах.
Для расчета реальной мощности в ваттах:
Вт = |ВА| × ПФ = |ВА| × |cos ф|
Фактическая мощность равна полной мощности в вольт-амперах (ВА), умноженной на коэффициент мощности.
Резистивная нагрузка импеданса
PF(резистивная нагрузка) = P / |S| = 1
Активная мощность резистивных импедансных нагрузок равна полной мощности (S) с коэффициентом мощности (PF), равным 1 (единице).
Вольт-ампер реактивный
Q = |VA| × |sin φ|
Реактивная мощность (Q) в вольт-амперах реактивная равна полной мощности в вольт-амперах (ВА), умноженной на синус фазового угла.
Однофазная мощность
PF = |cos φ| = 1000 × кВт / (В × А)
Чтобы рассчитать коэффициент мощности однофазной цепи, необходимо умножить 1000 на мощность в киловаттах (кВт), разделить на среднеквадратичное напряжение (В), умноженное на фазный ток в Ампер (А).
3-фазное питание (линейное)
PF = |cos φ| = 1000 × кВт / (√3 × В × A)
Расчет линейной трехфазной мощности для коэффициента мощности: 1000 умножить на мощность в киловаттах (кВт), затем разделить на квадратный корень из трех, умноженный на линейное среднеквадратичное напряжение (В), умноженное на фазный ток в амперах (А).
3-фазная мощность (линия-нейтраль)
PF = |cos φ| = 1000 × кВт / (3 × В × А)
Чтобы измерить коэффициент мощности для трехфазной мощности между фазой и нейтралью, умножьте 1000 на киловатты (кВт), а затем разделите среднеквадратичное значение напряжения между фазой и нейтралью в три раза. (V) умножить на ампер (A).
(V) умножить на ампер (A).
Преобразование кВт в Амперы
Вы хотите перевести киловатты в Амперы? Эти данные можно рассчитать по простой формуле (при условии, что вы знаете коэффициент мощности). Формула:
I = P / (√3 × PF × V)
В этом уравнении I обозначает силу тока (ампер), P обозначает относительную мощность (измеряется в ваттах), PF — коэффициент мощности, а V — напряжение.
Если ваша мощность измеряется в тысячах ватт, вам будет проще преобразовать данные в ватты, умножив их на 1000. Вам также необходимо убедиться, что ваше напряжение измеряется в киловольтах (кВ).
Приведем пример, используя приведенную выше формулу. Если ваш коэффициент мощности равен 0,8, и у вас есть мощность 1,5 кВт (1500 Вт) и постоянное напряжение 220 (В), расчет будет следующим:
I = 1500 / (√3 × 0,8 × 220) = 4,92 A
Вот так можно конвертировать ватты и киловатты в ампер.
Преобразование ампер в кВт
Теперь давайте сделаем обратное. Для преобразования ампер в киловатт используйте следующую формулу:
Для преобразования ампер в киловатт используйте следующую формулу:
P = √3 × PF × I × V
Маркировка здесь та же. P — мощность, коэффициент мощности — PF, I — ток (ампер), а V — напряжение.
В нашем следующем примере мы будем использовать такое же напряжение (220 В) и коэффициент мощности (0,8) и ток 4,92 А. Теперь переведем ампер в киловатты:
P = √3 × 0,8 × 4,92 × 220 = 1500 Вт = 1,5 кВт
Заключение
легкий. Однако использование формул для расчета 3-фазной полной мощности может занять немного времени.
Если вы хотите получить точные измерения без каких-либо хлопот, используйте наш онлайн-калькулятор мощности переменного тока, так как он поможет вам найти лучшие источники питания для ваших систем.
Blackhawk Supply предлагает широкий ассортимент климатического, сантехнического и электрического оборудования. Выбирайте реле, корпуса, трансформаторы, блоки питания и другие устройства!
Блоки питания
Провода
Трансформаторы
Корпуса
Что такое коэффициент мощности? — Силовая сторона
Представьте, что вы заказываете еду в новом ресторане в городе. Вы садитесь и
выберите что-нибудь из меню, и официант принесет вам тарелку с едой. Если
еда отличная, и вы едите все, это эффективный способ
утоление голода. Однако он становится менее эффективным, если вам не нравится
часть еды или она несъедобна. Эта часть еды еще готовится, варится,
и подается вам, но в конечном итоге возвращается на кухню несъеденным. Ты мог
подсчитайте долю еды, которую вы съели, по сравнению с размером
общая еда, которая покажет вам, насколько эффективен этот ресторан на встрече
твои нужды.
Вы садитесь и
выберите что-нибудь из меню, и официант принесет вам тарелку с едой. Если
еда отличная, и вы едите все, это эффективный способ
утоление голода. Однако он становится менее эффективным, если вам не нравится
часть еды или она несъедобна. Эта часть еды еще готовится, варится,
и подается вам, но в конечном итоге возвращается на кухню несъеденным. Ты мог
подсчитайте долю еды, которую вы съели, по сравнению с размером
общая еда, которая покажет вам, насколько эффективен этот ресторан на встрече
твои нужды.
В более общем плане, если учесть долю любого расходный материал, который удовлетворяет потребность, по сравнению с долей, которая вместо этого возвращается к источнику, неиспользованный, у вас есть мера того, насколько эффективно система соответствует что нужно. Когда вы применяете это к электрической цепи, где расходный материал электрической мощности, мерой эффективности является коэффициент мощности.
Эффективная электрическая цепь — это цепь, в которой нагрузка использует большую часть
подаваемой мощности для совершения работы. Принимая во внимание, что неэффективная электрическая цепь — это цепь, которая потребляет электрические
власть, но использует часть ее для выполнения непродуктивных действий. Во время каждого
цикл переменного тока, схема получает эту мощность от и возвращает ее к
источник питания. Сила
Коэффициент представляет собой отношение электрической мощности, потребляемой нагрузкой, по сравнению с
к общей мощности, подаваемой в цепь. Этот расчет говорит
Вы насколько эффективны электрические
цепь подает питание для совершения работы.
Принимая во внимание, что неэффективная электрическая цепь — это цепь, которая потребляет электрические
власть, но использует часть ее для выполнения непродуктивных действий. Во время каждого
цикл переменного тока, схема получает эту мощность от и возвращает ее к
источник питания. Сила
Коэффициент представляет собой отношение электрической мощности, потребляемой нагрузкой, по сравнению с
к общей мощности, подаваемой в цепь. Этот расчет говорит
Вы насколько эффективны электрические
цепь подает питание для совершения работы.
·
Активная сила Активный
сила — это имя, данное
к мощности, потребляемой электрической цепью, делающей что-то полезное, например питание
уличные фонари или запуск производственной линии. Активная мощность измеряется в ваттах (Вт) или в кратных им единицах, например
киловатты (кВт) и мегаватты (МВт). Устройство, работающее от электроэнергии, имеет
рейтинг, основанный на активном
мощность, которую он потребляет, например, лампочка мощностью 60 Вт или дуговая печь мощностью 500 кВт.
·
Реактивная мощностьРеактивный мощность — это термин, используемый для описания мощности, потребляемой электрической цепью для выполнения непродуктивных действий, таких как зарядка конденсатора или создание магнитного поля в асинхронном двигателе. Его единицей измерения является реактивный вольт-ампер (ВАР). В электрической цепи, устройства, производящие или потребляющие реактивные мощности, такие как шунтирующие реакторы и конденсаторы, имеют рейтинг реактивной мощности.
·
Полная мощность Видимый
мощность это общая
мощность, проходящая через электрическую
цепь, как активная, так и реактивная. Это важное значение, которое следует учитывать
при проектировании и расчете электрической цепи. Полная мощность измеряется в вольт-амперах (ВА). Вы часто будете видеть устройства
используется для производства или преобразования электрической мощности, номинальной в кВА или МВА. Примеры
может включать трансформатор мощностью 50 кВА или дизель-генератор мощностью 1000 кВА.
Вы можете подключить устройства мониторинга к критическим местам в электрической цепи, чтобы измерить напряжение и силу тока. Эти места включают выходы генератора, трансформатор соединения, а также большие, прерывистые или непредсказуемые нагрузки. Такой мониторинг устройство может использовать измеренные значения напряжения и тока для расчета активного, реактивная, полная мощность, и коэффициент мощности. Более передовые устройства, такие как анализатор мощности PQube 3, могут записывать эти данные со временем и генерировать регулярные отчеты.
Ведущий и отстающий коэффициент мощности Вернувшись в ресторан, в идеальном мире официант будет обслуживать
основное блюдо и гарниры одновременно. Это самый действенный метод
доставки вашей еды. Если гарниры подаются к вашему столу очень рано или
поздно, это снизит степень вашей удовлетворенности обслуживанием. Чем раньше сторона
блюда лидируют, или чем позже они отстают от основного блюда, тем менее приемлемы
ситуация становится. Точно так же переменный ток в электрической цепи
может опережать, отставать или соответствовать напряжению, и это влияет на коэффициент мощности.
Точно так же переменный ток в электрической цепи
может опережать, отставать или соответствовать напряжению, и это влияет на коэффициент мощности.
В идеальном электрическом цепь, где сопротивление нагрузки только резистивное, ток и напряжение проходят через нагрузку одновременно. Когда это происходит, кажущаяся мощность равна к активной мощности а коэффициент мощности один. Это также известно как единичный коэффициент мощности. Сила фактор также иногда описывается как опережающий или отстающий. С опережающий коэффициент мощности, ток опережает напряжение, и схема генерирует реактивную мощность. Это до к сопротивлению электрического цепь в основном емкостная, например, с подземными кабелями. С отстающий коэффициент мощности, наоборот, ток отстает от напряжения. Эта электрическая цепь потребление реактивной мощности, вызвано преимущественно индуктивной нагрузкой, такой как асинхронный двигатель.
Итак, мощность
Коэффициент просто выражается как отношение активной мощности к полной мощности. Чем ближе это отношение к единице,
чем больше кажущегося
мощность активна
мощность, подаваемая в нагрузку, и тем эффективнее электрическая цепь
является. Чем больше коэффициент мощности
опережает или отстает, тем больше отклонение коэффициента мощности от единицы, и тем больше мощность
требования к электрике
схема.
Чем ближе это отношение к единице,
чем больше кажущегося
мощность активна
мощность, подаваемая в нагрузку, и тем эффективнее электрическая цепь
является. Чем больше коэффициент мощности
опережает или отстает, тем больше отклонение коэффициента мощности от единицы, и тем больше мощность
требования к электрике
схема.
Получите дополнительную информацию о коэффициенте мощности, подписавшись на нашу рассылку, и будьте в курсе последних новостей из нашего блога.
Объяснение коэффициента мощности — Инженерное мышление
Объяснение коэффициента мощности Объяснение коэффициента мощности. В этом уроке мы рассмотрим коэффициент мощности. Мы узнаем, что такое коэффициент мощности, что такое хороший и плохой коэффициент мощности, как сравнивать коэффициент мощности, причины коэффициента мощности, почему и как исправить коэффициент мощности, а также некоторые примеры расчетов, которые помогут вам изучить электротехнику.
Прокрутите вниз, чтобы посмотреть БЕСПЛАТНОЕ руководство на YouTube
Итак, что такое коэффициент мощности?
Что такое коэффициент мощности Коэффициент мощности — безразмерное число, используемое в цепях переменного тока. Его можно использовать для обозначения отдельной единицы оборудования, например, асинхронного двигателя, или для обозначения потребления электроэнергии во всем здании. В любом случае он представляет собой соотношение между истинной мощностью и кажущейся мощностью. Формула PF = кВт / кВА. Итак, что это значит?
Его можно использовать для обозначения отдельной единицы оборудования, например, асинхронного двигателя, или для обозначения потребления электроэнергии во всем здании. В любом случае он представляет собой соотношение между истинной мощностью и кажущейся мощностью. Формула PF = кВт / кВА. Итак, что это значит?
Моя любимая аналогия для объяснения этого — аналогия с пивом.
Мы платим за пиво по стаканам, а внутри стакана и пиво, и пена. Чем больше у нас пива, тем меньше пены, поэтому мы получаем хорошее соотношение цены и качества. Если много пены, то пива мало, и мы не получаем хорошего соотношения цены и качества.
Коэффициент мощности аналогия с пивомПиво представляет нашу истинную мощность или наши кВт, киловатты. Это полезные вещи, которые мы хотим и в которых нуждаемся, это то, что делает работу.
Пена представляет собой нашу реактивную мощность или наши реактивные кВАр, киловольт-ампер. Это бесполезные вещи, они всегда будут, и мы должны платить за них, но мы не можем их использовать, поэтому мы не хотим их слишком много. (на самом деле у него есть применение и назначение, но позже мы поймем почему)
(на самом деле у него есть применение и назначение, но позже мы поймем почему)
Комбинация этих кВт и кВАр является нашей полной мощностью или нашей кВА. киловольт-ампер
.
Формула коэффициента мощностиКоэффициент мощности, таким образом, представляет собой отношение полезной мощности или фактической мощности в кВт, деленное на то, за что мы платим, в кВА. Таким образом, это говорит нам о том, какое соотношение цены и качества мы получаем за потребляемую мощность.
Треугольник мощности – коррекция коэффициента мощности Если мы очень кратко коснемся терминов электротехники, мы можем увидеть, что это выражается в виде треугольника мощности. В этом случае я нарисую его как ведущий фактор мощности, так как его легче визуализировать. Пиво или истинная мощность — это соседняя линия, затем у нас есть пена, которая представляет собой реактивную мощность на противоположной стороне, затем для стороны гипотенузы, которая является самой длинной стороной, у нас есть кажущаяся мощность, это под углом от истинного мощность, угол известен как тета.
По мере увеличения реактивной мощности или пенообразования увеличивается и полная мощность или кВА. Затем мы могли бы использовать тригонометрию для вычисления этого треугольника, я не буду в этой статье, поскольку я просто рассказываю об основах, поэтому мы просто увидим нужные вам формулы, но мы сделаем некоторые расчеты и рабочие примеры позже в этой статье.
Если мы посмотрим на типичный счет за электроэнергию для жилого дома, мы обычно увидим плату за количество использованных киловатт-часов, потому что коэффициент мощности и потребление электроэнергии будут очень низкими, поэтому электрические компании, как правило, не беспокоятся об этом.
Однако в коммерческих и промышленных счетах за электроэнергию, особенно в зданиях с интеллектуальными или интервальными счетчиками электроэнергии, мы, скорее всего, увидим платежи и информацию об использованном количестве кВт, кВтч, кВА и кВАрч. В частности, в больших зданиях часто также будет наблюдаться плата за реактивную мощность, но это зависит от поставщика электроэнергии.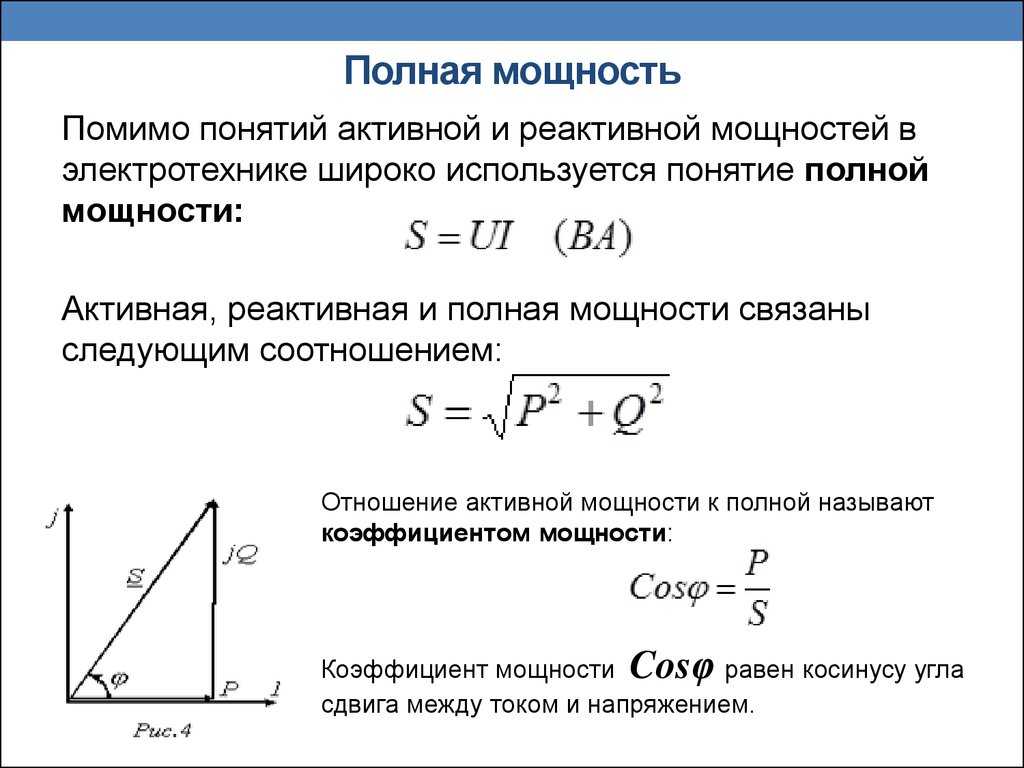
Причина, по которой они взимают штраф за это, заключается в том, что, когда крупные потребители имеют плохие коэффициенты мощности, они увеличивают ток, протекающий через электрическую сеть, и вызывают перепады напряжения, что снижает мощность распределения поставщиков и имеет эффект детонации для другие клиенты. Кабели рассчитаны на то, чтобы выдерживать определенное количество тока, протекающего через них. Таким образом, если многие крупные потребители подключаются с плохими коэффициентами мощности, то кабели могут быть перегружены, им будет сложно удовлетворить спрос и соглашения о пропускной способности, и ни один новый потребитель не сможет подключиться, пока они либо не заменят кабели, либо не установят дополнительные кабели.
Плата за реактивную мощность возникает, когда коэффициент мощности здания падает ниже определенного уровня, этот уровень определяется поставщиком электроэнергии, но обычно он начинается от 0,95 и ниже.
Идеальный коэффициент мощности должен быть равен 1,0, однако на самом деле этого почти невозможно достичь. Мы вернемся к этому позже в видео.
Мы вернемся к этому позже в видео.
В больших коммерческих зданиях общий коэффициент мощности, вероятно, относится к следующим категориям
Хороший коэффициент мощности обычно составляет от 1,0 до 0,95
Плохой коэффициент мощности — от 0,95 до 0,85
Плохой коэффициент мощности — любой ниже 0,85.
Коммерческие офисные здания обычно имеют значение между 0,98 и 0,92, промышленные здания могут иметь значение всего 0,7. Вскоре мы рассмотрим причины этого.
Сравнение коэффициента мощности асинхронного двигателяЕсли сравнить два асинхронных двигателя, оба имеют выходную мощность 10 кВт и подключены к трехфазной сети 415 В 50 Гц. У одного коэффициент мощности 0,87, у другого коэффициент мощности 0,9.2
Оба двигателя обеспечивают мощность 10 кВт, но первый двигатель имеет более низкий коэффициент мощности по сравнению со вторым, а это означает, что мы не получаем такого соотношения цены и качества.
Первый двигатель должен потреблять 11,5 кВА из электросети, чтобы обеспечить мощность 10 кВт.
Второй двигатель должен потреблять всего 10,9 кВА из электросети, чтобы обеспечить мощность 10 кВт.
Это означает, что первый двигатель имеет мощность 5,7 кВАр, а второй двигатель имеет мощность всего 4,3 кВАр. 92
Мы могли бы также найти коэффициент мощности из кВт и кВА, используя 10 кВт, деленные на 11,5 кВА
PF = кВт / кВА
Мы могли бы найти кВт из коэффициента мощности и кВА, используя получить 10
кВт = PF x кВА
Так что же является причиной плохого коэффициента мощности?
В большинстве случаев на коэффициент мощности влияют индуктивные нагрузки.
Чисто резистивная нагрузкаЕсли бы у нас была чисто резистивная нагрузка, такая как электрический резистивный нагреватель, то формы волн напряжения и тока были бы синхронизированы или очень близки. Они оба прошли бы свои точки максимума и минимума и прошли бы нулевую ось одновременно. Коэффициент мощности в этом случае равен 1, что идеально.
Если бы мы нарисовали векторную диаграмму, то напряжение и ток были бы параллельны, поэтому вся энергия, получаемая от источника электричества, идет на выполнение работы, в данном случае на создание тепла.
Если мы возьмем индуктивную нагрузку, такую как асинхронный двигатель, магнитное поле катушек сдерживает ток и приводит к фазовому сдвигу, при котором формы волны напряжения и тока не синхронизируются с током, и поэтому он проходит через нулевая точка после напряжения, это называется отстающим коэффициентом мощности.
Ранее в статье я сказал, что пена или кВАр бесполезны, это не совсем так, нам действительно нужна реактивная мощность для создания и поддержания магнитного поля, которое вращает двигатель. Реактивная мощность тратится впустую в том смысле, что мы не получаем от нее работы, но все же должны за нее платить, хотя она нам нужна, прежде всего, для выполнения работы. Ранее мы рассмотрели, как работают асинхронные двигатели, щелкните здесь, чтобы просмотреть этот учебник.
Если мы нарисуем векторную диаграмму для чисто индуктивной нагрузки, то ток будет под углом ниже линии напряжения, а это означает, что не все потребляемое электричество совершает работу.
Если мы взяли чисто емкостную нагрузку, то с индуктивной нагрузкой происходит обратное. Напряжение и ток не совпадают по фазе, за исключением того, что на этот раз напряжение сдерживается. Это приводит к опережающему коэффициенту мощности. Опять же, это будет означать, что не вся электроэнергия используется для выполнения работы, но мы должны платить за нее в любом случае.
Если бы мы нарисовали векторную диаграмму для чисто емкостной нагрузки, то линия тока располагалась бы под углом над линией напряжения, поскольку она опережает.
Корректировка плохого коэффициента мощности
Волновая диаграмма коррекции коэффициента мощностиЧто мы можем сделать, чтобы исправить плохой коэффициент мощности и плату за реактивную мощность? В большинстве случаев мы сталкиваемся с отстающим коэффициентом мощности, вызванным индуктивными нагрузками, но мы можем встретить и опережающий коэффициент мощности.
Чтобы скорректировать низкий коэффициент мощности, мы можем добавить в цепь конденсаторы или катушки индуктивности, которые вернут ток обратно в фазу и приблизит коэффициент мощности к 1. Если у нас есть запаздывающий коэффициент мощности, вызванный высокими индуктивными нагрузками в цепи, тогда мы добавляем конденсаторы, это наиболее распространено. Если у нас есть опережающий коэффициент мощности, вызванный высокими емкостными нагрузками, мы добавляем в цепь индуктивную нагрузку. Их необходимо рассчитать, и мы увидим несколько примеров расчетов в конце статьи.
Если у нас есть запаздывающий коэффициент мощности, вызванный высокими индуктивными нагрузками в цепи, тогда мы добавляем конденсаторы, это наиболее распространено. Если у нас есть опережающий коэффициент мощности, вызванный высокими емкостными нагрузками, мы добавляем в цепь индуктивную нагрузку. Их необходимо рассчитать, и мы увидим несколько примеров расчетов в конце статьи.
Зачем исправлять низкий коэффициент мощности?
Зачем исправлять плохой коэффициент мощности Низкий коэффициент мощности означает, что для выполнения той же работы вам нужно получать больше энергии от электрических сетей, а кабели должны быть больше, поэтому это будет стоить дороже. Если коэффициент мощности станет слишком низким, поставщик электроэнергии может взимать с вас штраф или плату за реактивную мощность. Низкий коэффициент мощности может вызвать потери в оборудовании, таком как трансформаторы, и привести к сильному выделению тепла. Это может привести к перепадам напряжения и даже сократить ожидаемый срок службы оборудования в экстремальных сценариях.


 В таком случае выражение следует умножить на корень из трех или 1.73
В таком случае выражение следует умножить на корень из трех или 1.73 — М: Высшая школа, 1984.
— М: Высшая школа, 1984. 53-56.
53-56. Под ней понимают физическую величину, характеризующую передачу или преобразование электрической энергии.
Под ней понимают физическую величину, характеризующую передачу или преобразование электрической энергии.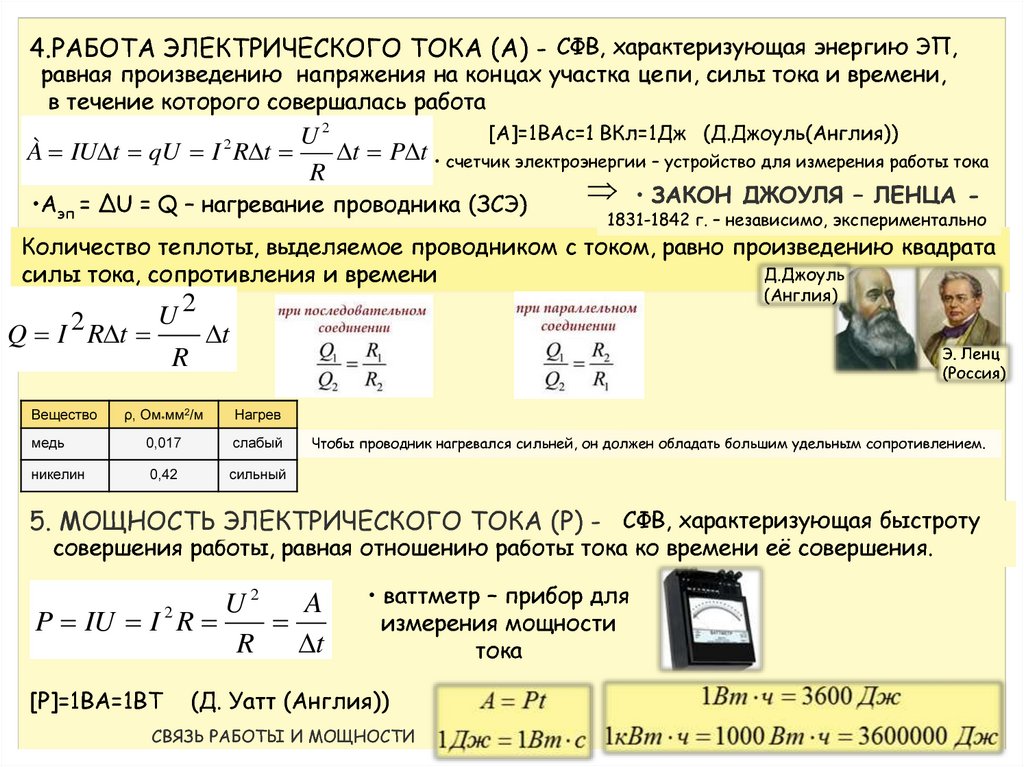 Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.

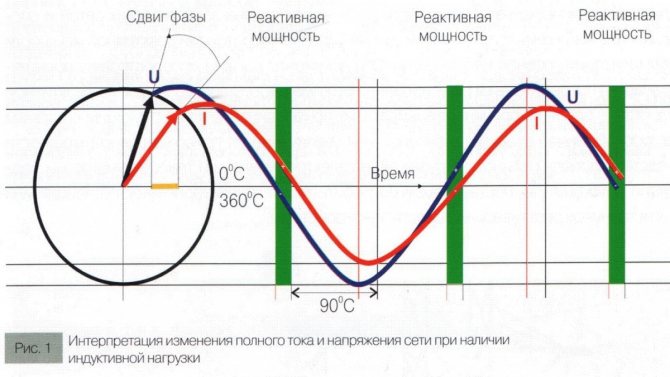


 д.)
д.) Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.
Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.  Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.