Вычисление — момент — инерция

Cтраница 1

Вычисление момента инерции относительно оси.  [1]

Вычисление моментов инерции во многих случаях можно упростить, используя соображения подобия и симметрии, теорему Гюйгенса-Штейнера, а также некоторые другие общие соотношения, о которых будет сказано ниже.  [2]

Вычисление моментов инерции во многих случаях можно упростить, используя соображения подобия и симметрии, теорему Гюйгенса — Штейнера, а также некоторые другие общие соотношения, о которых будет сказано ниже.  [3]

Вычисление моментов инерции по приведенной формуле сложно.  [4]

Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.

Само собой понятно, что момент в не следует смешивать с моментом инерции / относительно оси. В случае момента / массы dm умножаются на квадраты расстояний до этой оси, а в случае момента в — до неподвижной точки.  [5]

Вычисление момента инерции цилиндра относительно его поперечной оси симметрии.  [6]

Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. В случае непрерывного распределения масс эта сумма сводится к интегралу f г ат Само собой понятно, что момент в не следует смешивать с моментом инерции / относительно оси. В случае момента / массы dm умножаются на квадраты расстояний до.  [7]

Вычисление момента инерции произвольных тел представляет достаточно сложную задачу.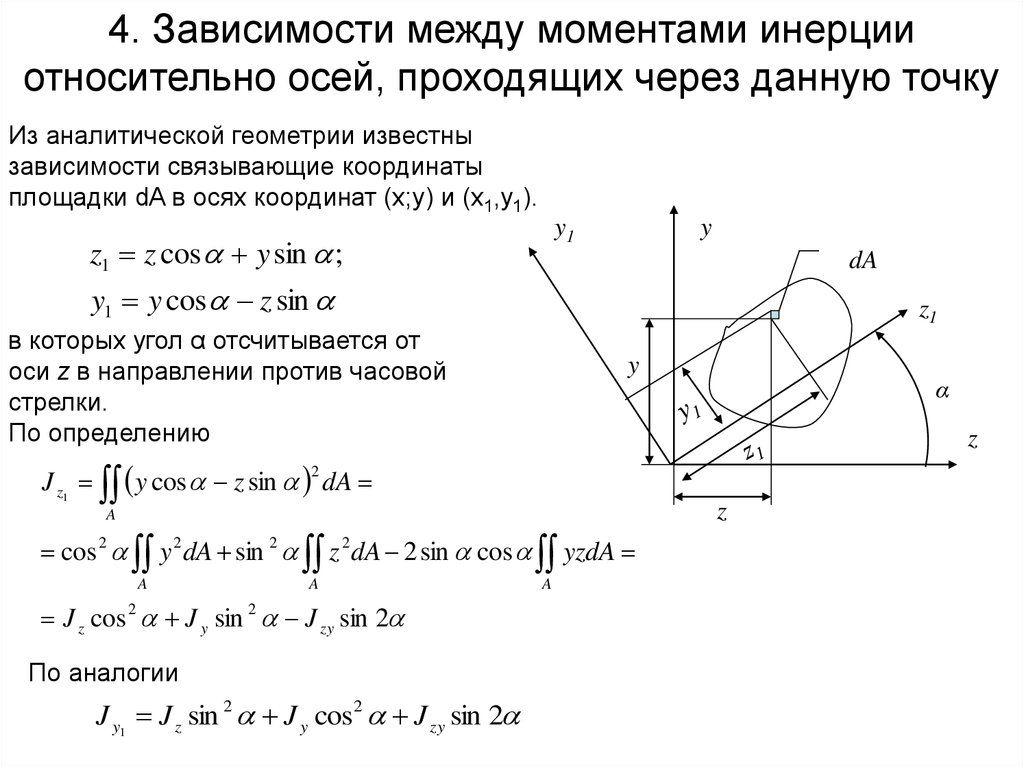 Сравнительно просто вычислить моменты инерции тел вращения.  [8]

Вычисление моментов инерции неоднородных тел ( а также однородных тел сложной геометрической формы) вызывает большие затруднения. Поэтому в современной технической практике методы экспериментального определения моментов инерции тел имеют весьма важное значение. Рассмотренные нами методы изучения движения твердого тела около неподвижной оси и основные теоремы механики дают научную основу для практического осуществления соответствующих установок.  [9]

Вычисление момента инерции твердого тела произвольной формы относительно той ли иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу.  [10]

Вычисление моментов инерции однородных тел правильной геометрической формы производится с помощью методов интегрального исчисления. В случае тел, не имеющих правильной формы, моменты инерции определяются или экспериментально или приближенно путем вычислений, для чего данное тело разбивают на несколько тел, имеющих правильную геометрическую форму.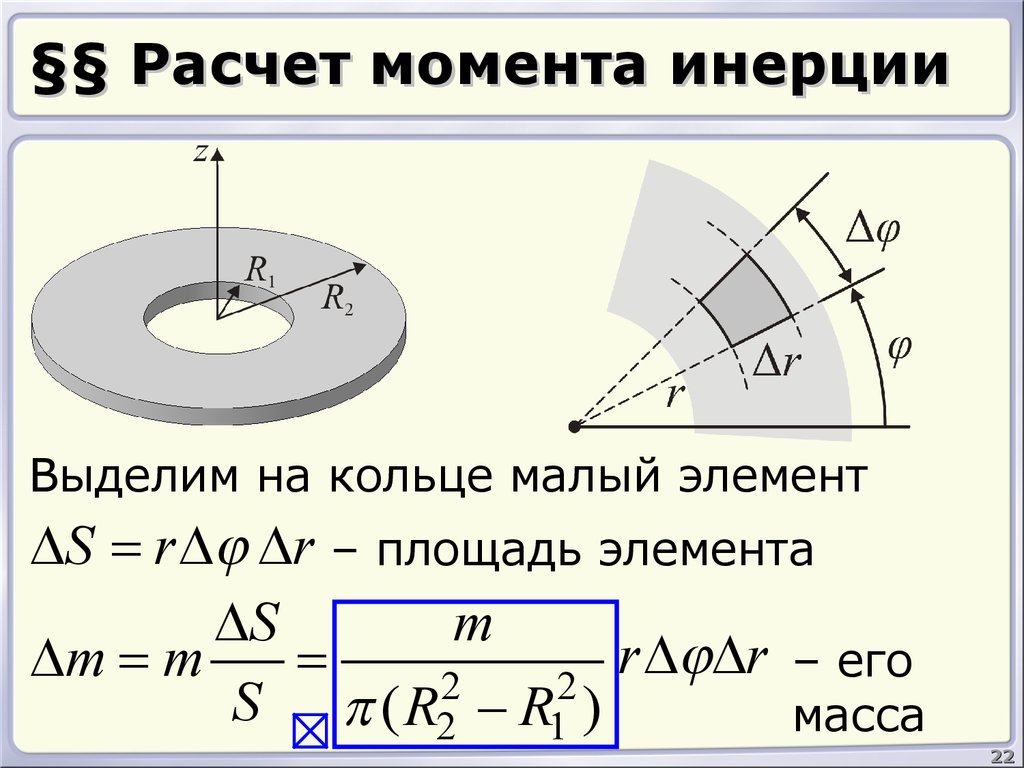

О способах экспериментального определения моментов инерции будет сказано ниже.  [11]

Вычисление моментов инерции неоднородных и однородных тел неправильной геометрической формулы в ряде случаев бывает сложным. Поэтому моменты инерции таких тел определяют обычно опытным путем. Опытное определение моментов инерции основывается на наблюдении того или иного вида вращения твердого тела вокруг неподвижной оси, так как момент инерции тела — это характеристика его инертности во вращательном движении.  [12]

Способ вычисления моментов инерции сложнь х сечений основан на том, что любой интеграл МОЖЕО рассматривать как сумму интегралов и, следовательно, момент инерции любого сечения вычислять ке. Поэтому для вычисления моментов инерции сложное сечение разбивается на ряд простых частей ( фигур) с таким расчетом, чтобы их геометрические характеристики можно было вычислить по известным формулам или найти по специальным справочным таблицам.  [13]

Способ вычисления моментов инерции сложных сечений основан на том, что любой интеграл можно рассматривать как сумму интегралов и, следовательно, момент инерции любого сечения вычислять как сумму моментов инерции отдельных его частей.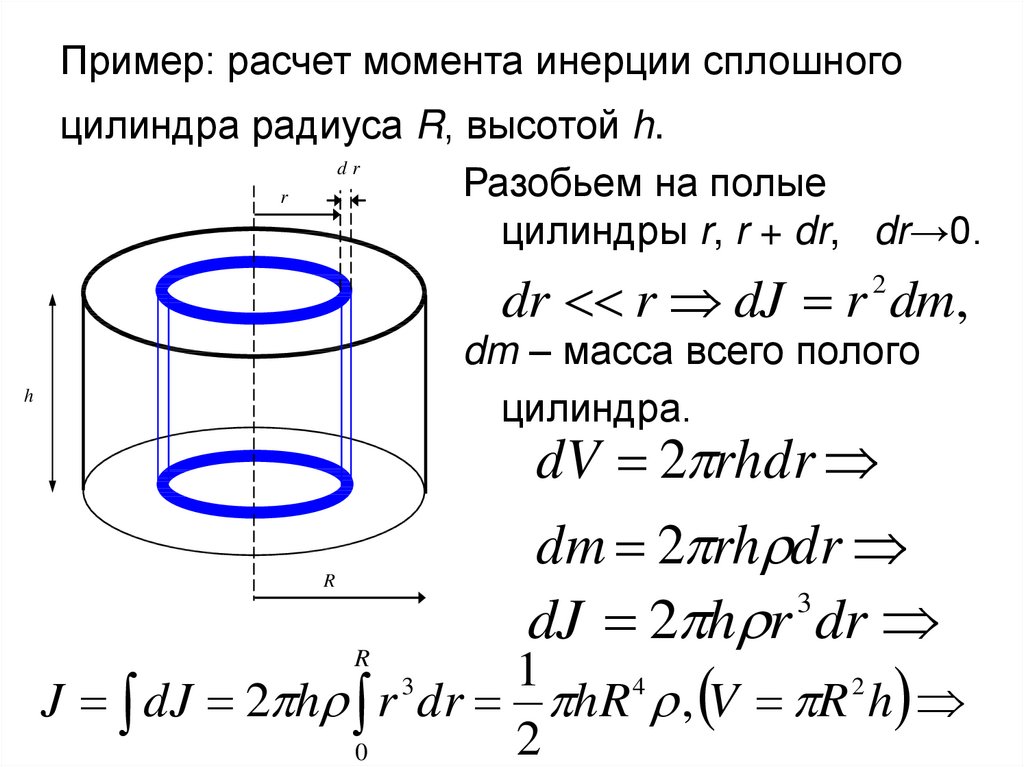

 [14]

При вычислении момента инерции обе части сечения считать жестко соединенными между собой. Какой ширины могла бы быть прорезь при той же величине наибольшего растягивающего напряжения, если бы она была расположена посредине ширины полосы.  [15]

Страницы:      1    2    3

Лабораторная работа № 23 определение момента инерции твердого тела и проверка теоремы штейнера

Цель работы:

Экспериментальное определение моментов инерции различных твердых тел с помощью измерения периода крутильных колебаний, и проверка теоремы Штейнера.

Оборудование:

Штатив со спиральной пружиной и приспособлением для крепления исследуемых тел, регистратор движения, электронный блок управления Cobra3, набор тел различной формы, компьютер.

Продолжительность работы– 4 часа.

Момент инерции — это величина, зависящая от распределения масс в теле и являющаяся мерой инертности тела при вращательном движении.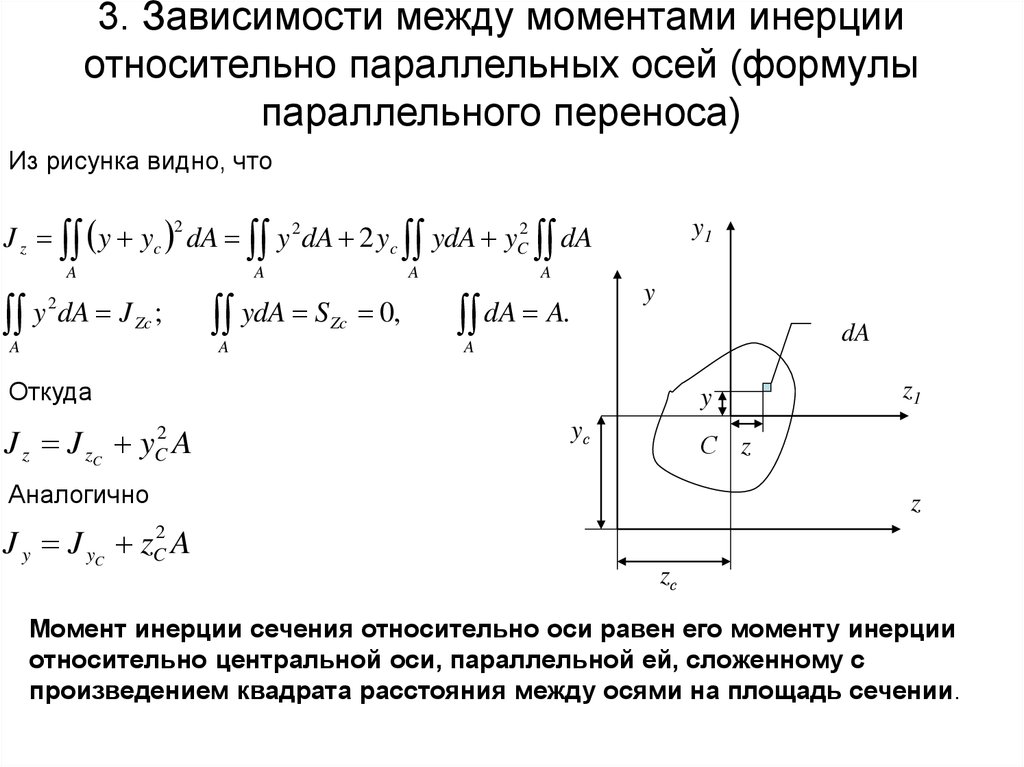 Момент инерции тела относительно оси вращения определяется выражением

(1)

где- элементарные («точечные») массы, на которые мысленно разбивается тело,- расстояния от этих масс до оси вращения (рис.1)

Рис.1. К определению момента инерции (ось перпендикулярна плоскости чертежа)

Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла

, (2)

где и- масса и объем элемента тела, находящегося на расстоянииот интересующей нас оси;- плотность тела. Интегрирование должно производиться по всему объему тела.

Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы. Если твердое тело представляет собой тонкое кольцо радиуса

Rи массыm, то момент инерции относительно оси, перпендикулярной плоскости кольца и проходящей через его центр равен (рис. 2).

. (3)

При вычислении момента инерции однородного цилиндра (или диска) относительно оси, совпадающей с его осью симметрии (рис.3), следует учесть, что величины в выражениине равны радиусу дискаR, а изменяются для разных элементарных массот 0 доR. После вычисления этой суммы (интегрирования) получим для момента инерции цилиндра

(4)

где — масса цилиндра.

Рис. 2. Момент инерции кольца	Рис. 3. Момент инерции цилиндра	Рис.4 Момент инерции шара

Вычисление по формуле (2) момента инерции шара массы m

и радиусаRотносительно оси, проходящей через центр шара (рис.4), дает результат:

. (5)

Другим типовым элементом конструкции твердых тел является стержень. Стержень массы m , имеющий длинуL , изображен на рис.5.

Рис.5 Схематическое изображение стержня

Момент инерции стержня, вычисленный относительно оси Z, проходящей через его центр масс, равен:

(6)

Если определен момент инерции относительно некоторой оси Z, проходящей через центр масс тела, то, оказывается, можно легко вычислить момент инерции относительно любой другой оси, параллельной оси Z. Правила этого расчета сформулированы в теореме Штейнера.

Согласно этой теоремы,момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс телаи параллельной данной оси, и произведения массы тела т на квадрат расстояния между осями:

(7)

С помощью формул (3) – (6) можно рассчитать именно величины I_с предметов различной формы. Если интересует, например, момент инерции стержня относительно осиZ₁, проходящей через один из его торцов ( рис.5 ), то, в соответствии с (7):

(8) Для тел неправильной формы интегралы (2) могут быть найдены численными методами.

Экспериментально определить момент инерции можно, например, с использованием механического устройства, создающего крутильные колебания исследуемого тела. В данной работе крутильные колебания создаются с помощью спиральной пружины. Один конец этой пружины жестко связан с основанием штатива, другой прикреплен к вертикальному валу, ось которого совпадает с осью вращения тела. Вал может вращаться относительно основания без трения. В верхнем торце вала имеется приспособление для крепления исследуемого тела.

При повороте тела на угол φ пружина закручивается, и возникает момент силM, который в широких пределах пропорционален углу закручивания:

(9)

где f– постоянная для данной пружины величина, называемая ее модулем кручения.

Если исследуемое тело повернуть на некоторый угол, а затем отпустить, в системе возникнут крутильные колебания, которые можно описать с помощью основного уравнения динамики вращательного движения:

или (10)

Уравнение (10) тождественно дифференциальному уравнению второго порядка вида:

(11)

Если (12)

Известно, что решением уравнения (11) является функция:

(13)

где — амплитуда, а- начальная фаза колебаний.

Последнее утверждение легко проверить, подставив функцию (13) в уравнение (11).

Таким образом, чтобы экспериментально определить момент инерции тела I , нужно измерить период колебанийи знать модуль крученияf.Как следует из (12):

(14)

Вращательная динамика — Момент Инерции Произвольной Формы

Ну, идея, которая у вас есть, интуитивно понятна и тоже в некотором смысле верна, но она должна быть более точной.

Эта тема обсуждается в учебниках по механике для студентов бакалавриата (например, Классическая механика Джона Р. Тейлора). Мои рассуждения следуют упомянутой выше книге (глава 10, стр. 372). Сначала я упомяну краткое изложение тензора момента инерции, а затем обращусь к вашей идее о кинетической энергии. Поскольку вы упомянули, что учитесь в старшей школе, я постараюсь быть максимально полным в своих объяснениях. Так как эта тема действительно требует большого количества расчетов, я настоятельно рекомендую вам сделать это в качестве упражнения.

Идея момента инерции заключается в следующем. Мы хотим найти связь между угловым моментом вращающегося тела (может состоять из многих частиц) и его угловой скоростью. По сути, мы хотим найти что-то вроде этого: $$ \vec{L} = (что-то) * \vec{\omega} $$

Вопрос в том, что это за (что-то) . В случае, когда объект вращается вокруг фиксированной оси и вокруг него существует вращательная симметрия, этот объект, который я называю (что-то) — это просто момент инерции, с которым вы знакомы, и это просто число. Но что, если объект не обладает вращательной симметрией? это (что-то) все еще число? Что ж, ответ на этот вопрос — то, что описал Триаттикус. Это матрица $3 \times 3$, называемая тензором инерции. Не пугайтесь слова тензор, просто думайте о нем как о матрице.

При заданном множестве маленьких кусочков масс $m_\alpha$ суммарный угловой момент равен сумме отдельных угловых моментов: $$ \vec{L} = \sum l_\alpha = \sum \vec{r}_\alpha \times m_\alpha \; \vec{v}_\альфа $$ 92 \vec{\omega} = I \vec{\omega} $$ Здесь я использовал векторную идентичность для $\vec{A}\times\vec{B}\times\vec{C} = (\vec{A}\cdot\vec{C})\vec{B}-( \vec{A}\cdot\vec{B})\vec{C}$.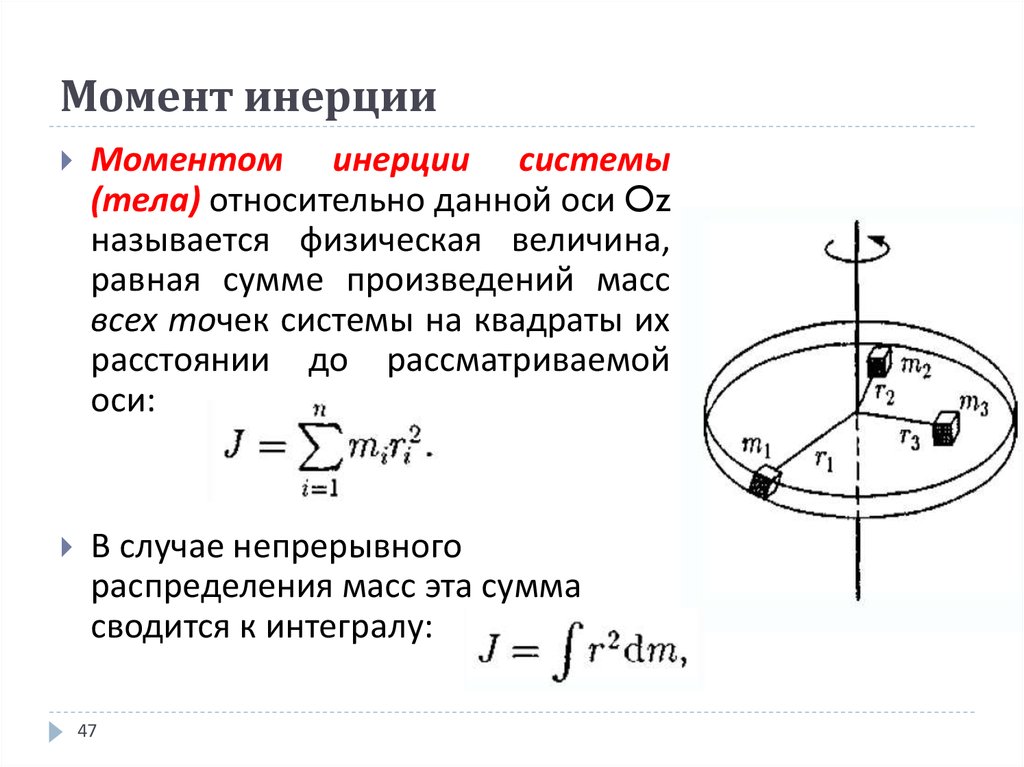

Однако это не очень общее. Ниже приведен лишь набросок того, что вы можете сделать, чтобы описать тело произвольной формы, и я рекомендую вам ознакомиться со ссылкой и сделать это самостоятельно, так как это хорошее упражнение. Это не слишком сложно и, на мой взгляд, доступно для старшеклассников.

Предположим, что $\vec{\omega} = (\omega_x,\omega_y,\omega_z) $, т.е. произвольно. Затем, $$ \vec{L} = \sum \vec{r}_\alpha \times m_\alpha \; \vec{v}_\alpha = m_\alpha \; \vec{r}_\alpha \times (\vec{\omega} \times \vec{r}_\alpha) $$ Примечание: ($\vec{v} = \vec{\omega} \times \vec{r}$)

Подставьте значения $\vec{\omega}$ и $\vec{r}_\alpha = (r_{\alpha,x},r_{\alpha,y},r_{\alpha,z})$

Использование свойств векторов. Затем сгруппируйте термины с индексами $\alpha$. Вы получите что-то вроде формы, упомянутой Триаттикусом. $$ \vec{L} = I \vec{\omega} $$ Где $I$ здесь $3 \times 3$ симметричная матрица, называемая тензором инерции.

Теперь мы использовали направления x,y,z для описания векторов и матрицы в нашей задаче, но мы не обязаны их использовать, и мы фактически можем использовать другой набор перпендикулярных осей. Оказывается, если у вас есть симметричная матрица, вы можете найти 3 направления, такие что этот тензор момента инерции является диагональной матрицей, т.е. есть только ненулевые члены на 11, 22, 33 позициях.

Вот где твоя интуиция была права. Если вы выбрали этот конкретный набор направлений (и написали $\omega$ с помощью этих новых единичных векторов), вы можете использовать написанную вами формулу!

Я уверен, что написал недостаточно, но если вам потребуются какие-либо разъяснения, пожалуйста, дайте мне знать.

динамика вращения — Момент инерции произвольной формы, представленный конечным числом сфер

Краткий обзор

Я пишу программное обеспечение для своих исследований (главным образом сосредоточенных на определении орбиты и оценке гравитационного поля вокруг тел неправильной формы). Для создания истинных эталонных моделей я использую модели формы астероида в формате многогранника, которые затем наполняю сферами (или кубами, но для упрощения описания проблемы я собираюсь ограничить свое описание только обсуждением сферы). Это позволяет мне очень легко рассчитать гравитационное поле для тел неправильной формы, просто рассматривая его как набор упакованных сфер и суммируя их гравитационные потенциалы.

Вопрос

Используя этот набор сфер, я также хотел бы создать момент инерции относительно центра масс, что позволит мне точно смоделировать вращение астероида. Каждая сфера в модели имеет свою уникальную массу и радиус (все они НЕ обязательно идентичны, но все они БУДУТ полными, так что никаких частичных сфер/кубов). Для простого представления этого, просто чтобы все было ясно, обратитесь к последнему разделу.

Мой первый подход состоял в том, чтобы просто рассмотреть момент инерции сферы: 92 + m_i \ y_i \ z_i$$

Однако он оформляется как непрерывный интеграл для сплошной среды. Хотя я понимаю, что непрерывный интеграл аналогичен конечной сумме, такой как то, что я описал выше, мне трудно понять, применимо ли это к набору сфер/кубов. Или если этот второй член в моей сумме ($m_i \ x_i \ y_i$) вообще нужно изменить.