|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 17Следующая ⇒ Определение 6. , , если a > 0, , если a < 0. Если или a = 0, то вектор считается равным нулевому вектору. Свойства операции умножения вектора на действительное число. 10. Произведение любого вектора на любое действительное число определено и однозначно. 20. 1 для любого вектора . 30. для любого вектора и любых действительных чисел a, b. Доказательство. Возможны случаи. 1) a = 0, или b = 0, или = . В этом случае равенство очевидно. 2) a ¹ 0, b ¹ 0 и ¹ . Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства. , . Следовательно, . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи. а) a и b одного знака (пусть a > 0, b > 0). , , следовательно, . Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны. б) a и b имеют разные знаки (пусть a > 0, b < 0). В этом случае a × b < 0. . . Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны. 40. и ( для любых векторов , и любых действительных чисел a, b. (Докажите это свойство самостоятельно).
Коллинеарные векторы Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой. Свойства коллинеарных векторов. 10. Нулевой вектор коллинеарен с любым вектором. 20. Противоположные векторы коллинеарны. 30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. 40. Если вектор умножить на действительное число, то получится вектор, коллинеарный данному. Следовательно, множество коллинеарных векторов замкнуто относительно операции умножения на действительное число. 50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число. Доказательство. Пусть векторы и коллинеарны. Если вектор = , то = 0 . Если = , то = 0 × . Если ¹ , ¹ и , то = . Если , то = — . Из двух последних свойств следуют следующие два свойства. 60. (Необходимое и достаточное условие коллинеарности двух векторов) Два вектора коллинеарны тогда и только тогда, когда хотя бы один из них можно представить в виде произведения другого на действительное число. 70. Если вектор не нулевой, то любой вектор, коллинеарный с вектором , можно представить в виде . Наконец, из всех приведённых свойств можно сделать вывод, что относительно сложения векторов и умножения вектора на действительное число множество коллинеарных векторов ведёт себя так же как множество всех геометрических векторов. Задача 2. Отрезок АВ точками С, Р, О, К, М, Т разбит на семь равных частей. Пусть
.
1.5. Компланарные векторы Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости. Свойства компланарных векторов. 10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. 20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения. 30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других. Доказательство. Þ Пусть векторы компланарны. Возможны два случая. 1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть и коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть . Тогда , т.е. вектор есть линейная комбинация векторов и .
Ü Пусть . По свойствам 10 и 20 следует, что вектор компланарен с векторами и . 40. Если векторы и не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации. 50. Из свойств 10 и 20 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них. Задача 3. АВСD и AB1C1D1 — два произвольных параллелограмма.
Векторные пространства Определение 8. Множество векторов V называется векторным пространством, если в нём определены две алгебраические операции: сложение векторов и умножение вектора на действительное число, удовлетворяющие следующим требованиям: 1. Множество V замкнуто относительно обеих операций. 2. для любых векторов и (коммутативный закон сложения). 3. для любых векторов (ассоциативный закон сложения). 4. Существует , такой, что для любого вектора . 5. Для любого вектора существует противоположный вектор (- ) такой, что + (- ) = . 6. 1 для любого вектора . 7. для любого вектора и любых действительных чисел a, b. 8. и ( для любых векторов , и любых действительных чисел a, b. (дистрибутивные законы сложения относительно умножения на действительное число). Примеры векторных пространств (следуют из предыдущего материала). 1. Множество всех геометрических векторов. 2. Множество всех компланарных векторов. 3. Множество всех коллинеарных векторов. 4. Множество, состоящее из одного нулевого вектора.
⇐ Предыдущая12345678910Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Особенности и правила умножения вектора на число
При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.
В статье будет показано, как умножать их на постоянные числа.
…
Основные понятия и определения
Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:
- Постоянная — любое обычное число, которое может принимать определённые фиксированные значения, быть положительным, отрицательным или нулевым. Обозначать будем латинской буквой С (от греческого слова constanta, то есть постоянная).
- Вектор — участок прямой, ограниченный двумя точками и имеющий заданное направление.
 Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD). - Вектора называются параллельными (коллинеарными), если они лежат на коллинеарных прямых или на одной прямой.
- Нулевым вектором называется такой, у которого конец и начало совпадают. Называется нуль-вектор и обозначается (0).
- Координатами (АВ) называются числа, равные его протяжённости относительно каждой из оси координат в Декартовой системе. Они находятся вычитанием из координат конца вектора координат его начала. Знак минус перед этим числом означает, что вектор направлен против направления данной оси.
- Модулем (АВ) называется длина отрезка АВ.
- Квадратный корень из числа или выражения условимся обозначать латинским буквосочетанием SQRT.
- (АВ) с координатами (x, y, z) будем обозначать как (АВ) (x, y, z).

Правила умножения вектора на число
Рассмотрим, как умножить вектор на число:
- Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
- Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
- Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
- Для умножения (АВ) (x, y, z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x, С*y, С*z).
Алгебраический и геометрический смысл действия
Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:
- Геометрический смысл: (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.

- Алгебраический смысл: (АВ) (x, y, z)*С — это новый (А1В1) с координатами равными (С*x, С*y, С*z).
- Физический смысл: уменьшение или увеличение в С раз силы действующей на тело или материальную точку.
Формулы умножения
При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:
- С*(АВ) (x, y, z) = (А1В1) (С*x, С*y, С*z).
- 0*(АВ) = (0).
Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57,63,28). Как изменится эта сила по координатам при её десятикратном увеличении?
Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:
10*(АВ) (57,63,28) = (А1В1) (10*57,10*63,10*28) = (А1В1) (570,630,280).
Вторую задачу возьмём аналогичную: как изменится сила, действующая на материальное тело, описываемая (АВ) (46,59,-43) при её увеличении в -0,5 раза.
Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:
-0,5*(АВ) (46,59,-43) = (А1В1) (-0,5*46,-0,5*59,-0,5*(-43)) = (А1В1) (-23,-29,5,21,5).
Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:
- 33*(CD) (11,10) = (C1D1) (33*11,33*10) = (C1D1) (363,330).
- -0,2*(АВ) (-0,3,25) = (А1В1) (-0,2*(-0,3), -0,2*25) = (А1В1) (0,06, -5).
- 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
- 0*(АВ) (65,-87) = (0).
Возможные действия с векторами
Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:
Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:
- модуль (АВ) (3,4) = SQRT (3 2+ 4 2) = SQRT (9 + 16) = SQRT25 = 5.
Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.
Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.
В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону. Что такое сравнение в литературе читайте в нашей статье.
Как умножить вектор на скаляр в питоне?
спросил
Изменено 2 года, 3 месяца назад
Просмотрено 2к раз
Я хочу умножить вектор на скаляр на цикл, т.е.: x1=[2,3,4,5] и я хочу умножить на 2, чтобы получить х1=2(х2) , х2=[4,6,8,10] .
Я попытался сделать это:
def multiplicar_vector (x1):
х2=[]
для я в x1:
х2[я] = (х1[я])*2
печать (x2)
Но это не работает.
- питон
1
Если вы хотите использовать чистый Python, вы, вероятно, будете использовать понимание списка.
x1 = [элемент * 2 для элемента в x2]
Это берет каждый элемент в x2 и умножает его на 2. Квадратные скобки указывают, что вы хотите составить список результатов. Это эквивалентно:
Квадратные скобки указывают, что вы хотите составить список результатов. Это эквивалентно:
х1 = []
для предмета в x2:
x1.append(элемент * 2)
На самом деле, большинство людей будут использовать numpy при работе с большим количеством векторов, так как это намного быстрее и проще.
импортировать numpy как np x1 = np.массив ([1, 2, 3, 4]) х2 = 2 * х1
0
Вы можете перебирать каждый элемент и умножать его
x1=[2,3,4,5] N=2 x2 = [x * N для x в x1] печать (x2)
Если вы хотите использовать предопределенный пакет. Преобразуйте свой тип вектора списка в тип векторного массива numpy и умножьте.
импортировать numpy как np х1=[2,3,4,5] N=2 мой_массив = np.массив (x1) x2 = мой_массив * N печать (x2)
0
Существует пакет Python, который делает это очень хорошо: numpy
import numpy as np x2 = np.массив (x1) * 2
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Умножение на скаляр — объяснение и примеры
Умножение на скаляр — это способ изменения величины или направления вектора. Проще говоря, это
Проще говоря, это
Напомним, что скаляр — это просто действительное число. Умножение вектора на скаляр вызывает изменение масштаба этого вектора.
В этом разделе мы обсудим следующие аспекты скалярного умножения:
- Что такое скалярное умножение?
- Как умножить вектор на скаляр?
- Умножение вектора на скаляр
Что такое скалярное умножение?
Скалярное умножение включает умножение заданной величины на скалярную величину. Если данная величина является скалярной, умножение дает другую скалярную величину. Но, если количество является вектором, умножение на скаляр дает выходной вектор.
Например, , умножение скаляра C на вектор даст другой вектор. Мы запишем эту операцию как:
C* A = C A
исходный вектор A . Его направление определяется значением C следующим образом:
- Если C > 0, то результирующий вектор C A будет иметь то же направление, что и вектор A.

- Если C <0, то результирующий вектор равен:
-C* A = – C A
Знак минус изменит направление результирующего вектора на противоположное относительно опорного вектора A. - Если C = 0, то умножение дает нулевой вектор как:
0* A = 0
Обратите внимание, что если C = 1, то умножение любого вектора на C сохраняет этот вектор неизменным.
1* А = А
Как умножить вектор на скаляр?
Предположим, что вектор P выражен как вектор-столбец:
P = (x1, y1).
Умножение на скаляр означает масштабирование каждого компонента вектора P на C следующим образом:
Теперь величину результирующего вектора можно найти так же, как мы можем найти величину вектора 92
Умножение вектора на скаляр
В этом разделе мы обсудим некоторые важные свойства скалярного умножения. Обратите внимание, что эти свойства верны независимо от того, умножается ли скаляр на вектор или на другой скаляр.
Обратите внимание, что эти свойства верны независимо от того, умножается ли скаляр на вектор или на другой скаляр.
Давайте сначала рассмотрим два вектора, A и B, и два скаляра, c и d. Тогда выполняются следующие свойства:
- |c A | = |с|*| А|. Величина результирующего масштабированного вектора равна абсолютному значению скаляра, умноженному на величину.
- Ассоциативное свойство: c(d B ) = (cd)* B
- Коммутативное свойство: c* A = A *c
- Распределительное свойство: (c + 90 d) 3 900 C * a + D * A
D * ( A + B ) = D * A + D * B
Примеры
. обсудите некоторые примеры и их пошаговые решения, чтобы помочь лучше понять скалярное умножение.
Пример 1
Автомобиль движется со скоростью V = 30 м/с в направлении на север. Определяет вектор, который в два раза больше этого вектора.
Решение
Из предоставленных данных мы имеем следующую информацию:
В = 30 м/с Север.
Чтобы определить вектор, равный удвоенному этому вектору, мы умножаем данный вектор на скалярное значение 2. Это дает нам:
2* В = 2 * (30 м/с)
2 V = 60 м/с, север
Поскольку данное скалярное значение положительное, направление V не изменяется . Однако он изменяет свою величину в два раза по сравнению с исходным значением. Таким образом, автомобиль будет продолжать двигаться на север с удвоенной начальной скоростью.
Пример 2
Дан вектор S = (2, 3), определить и нарисовать 2* S. Каковы модуль и направление вектора 2 S ?
Решение
Данный вектор S представляет собой вектор-столбец, а скалярная величина равна 2. Умножение вектора S на 2 дает нам:
Умножение вектора S на 2 дает нам:
2 *S = 2* (2, 3)
Умножение каждого из компонентов вектора S на 2 дает нам:
2 *S = (2*2, 2*3)
2 *S = (4, 6).
Далее определяем и сравниваем величины обоих векторов:
| С 92
|2 S | = √16 + 36
|2 S | = √52
|2 S | = √4*13
|2 S | = 2*(√13)
Из последнего уравнения ясно видно, что в результате скалярного умножения величина вектора S удвоилась. С . Видно, что направление вектора 2 S параллельно направлению вектора С . Это еще раз подтверждает, что масштабирование вектора положительной величиной изменяет только величину, но не направление.
Пример 3
Дан вектор S = (2, 3), определить и нарисовать -2* S. Найти модуль и направление вектора -2 S .
Найти модуль и направление вектора -2 S .
Решение
Данный вектор S является вектор-столбцом, а скалярная величина равна 2. Умножение вектора S на 2 дает нам: 92
|-2 S | = √16 + 36
|-2 S | = √52
|-2 S | = √4*13
|-2 S | = 2*(√13)
Из последнего уравнения ясно видно, что скалярное умножение удвоило величину вектора S . Также отрицательный знак не влияет на величину вектора -2 S.
На приведенном ниже изображении показаны два вектора S и -2 S. Видно, что направление вектора -2 S противоположен вектору S . Это дополнительно подтверждает, что масштабирование вектора отрицательной величиной не влияет на его величину (т. е. векторы 2 S и -2 S имеют одинаковую величину), но меняет направление на противоположное.
Пример 4
Дан вектор A = (-4, 6), определите и зарисуйте вектор 1/2* A .
Решение
Данный вектор A представляет собой вектор-столбец, а скалярная величина равна 1/2. Умножение вектора 92
|1/2 А | = √4 + 9
|1/2 А | = √13
Умножение на скаляр со значением, равным половине, таким образом, уменьшило величину исходного вектора наполовину.
На приведенном ниже рисунке показаны два вектора A, и ½ A. Оба вектора имеют одинаковое направление, но разные величины.
Пример 5
Дан вектор m = 5i + 6j +3 в ортогональной системе, определить результирующий вектор, если м умножается на 7.
Решение
В этом сценарии результирующий вектор можно получить, просто умножив заданный вектор на 7:
7 м = 7 *(5i + 6j +3)
7 м = (7*5i + 7*6j + 7*3)
7 м = 35i + 42j + 21
Результирующий вектор имеет в 7 раз большую величину, чем исходный вектор м но без изменения направления.



 Произведением ненулевого вектора на отличное от нуля действительное число a называется такой вектор (обозначение ), что
Произведением ненулевого вектора на отличное от нуля действительное число a называется такой вектор (обозначение ), что
 Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
 В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число. Пусть , , . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда , т.е. вектор есть линейная комбинация векторов и .
Пусть , , . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда , т.е. вектор есть линейная комбинация векторов и .
 Докажите, что
Докажите, что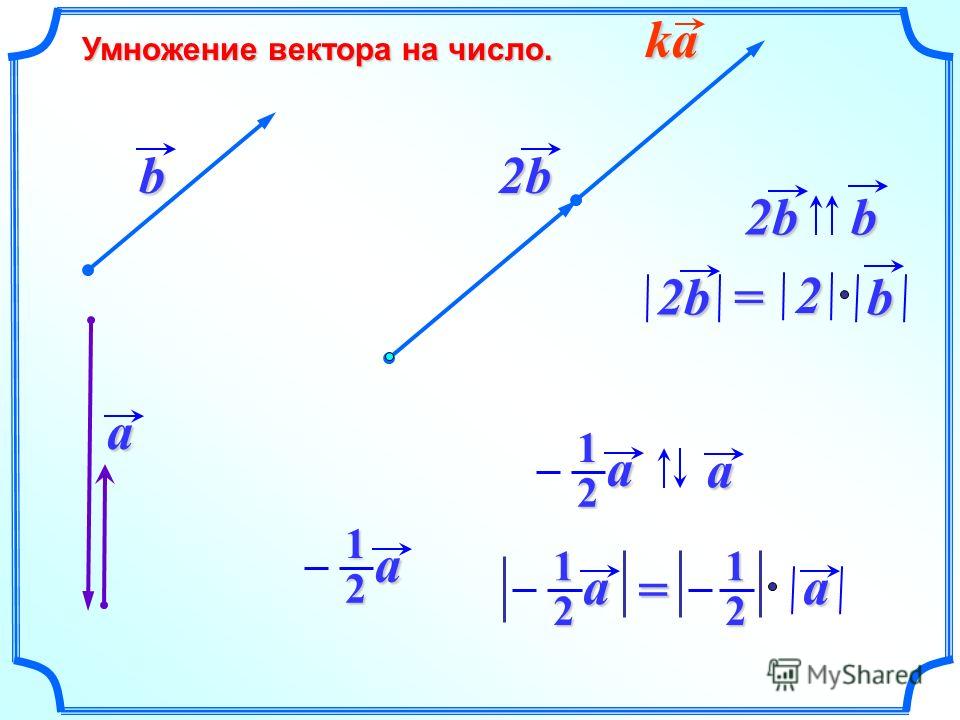
 ..
.. Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).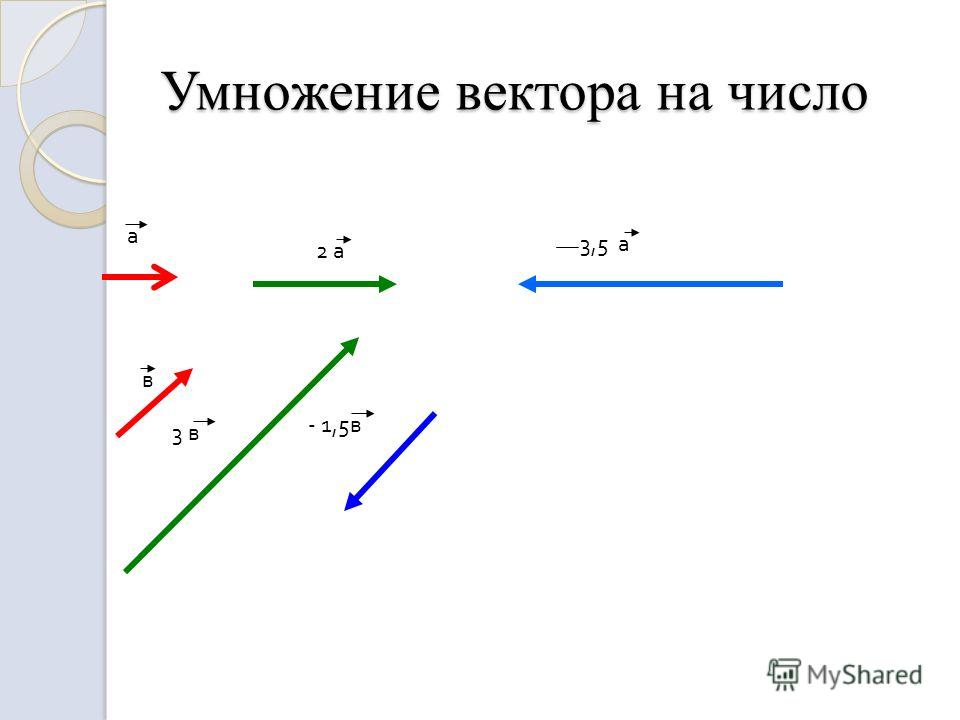

 массив (x1) * 2
массив (x1) * 2