Как определить емкость конденсатора? Емкость конденсаторов: определение, формулы, примеры.

Содержание

С использованием мультиметра и формул

Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.

Режим «Сх» в мультиметре

Менее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).

Рис. 2. Схема подключения конденсатора

Алгоритм измерения следующий:

1. Измерьте напряжение источника питания щупами контактов измерительного прибора.
2. Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
3. Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
4. Замерьте напряжение образованной цепи с помощью мультиметра.
5. Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
6. Вычислите 95% от полученного значения. Запишите показатели измерений.
7. Возьмите секундомер и включите его одновременно с убиранием закоротки.
8. Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
9. По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.

Рис. 3. Измерение с помощью тестера. Проверка

Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.

Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f– частота тока, а Xc– ёмкостное сопротивление.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение.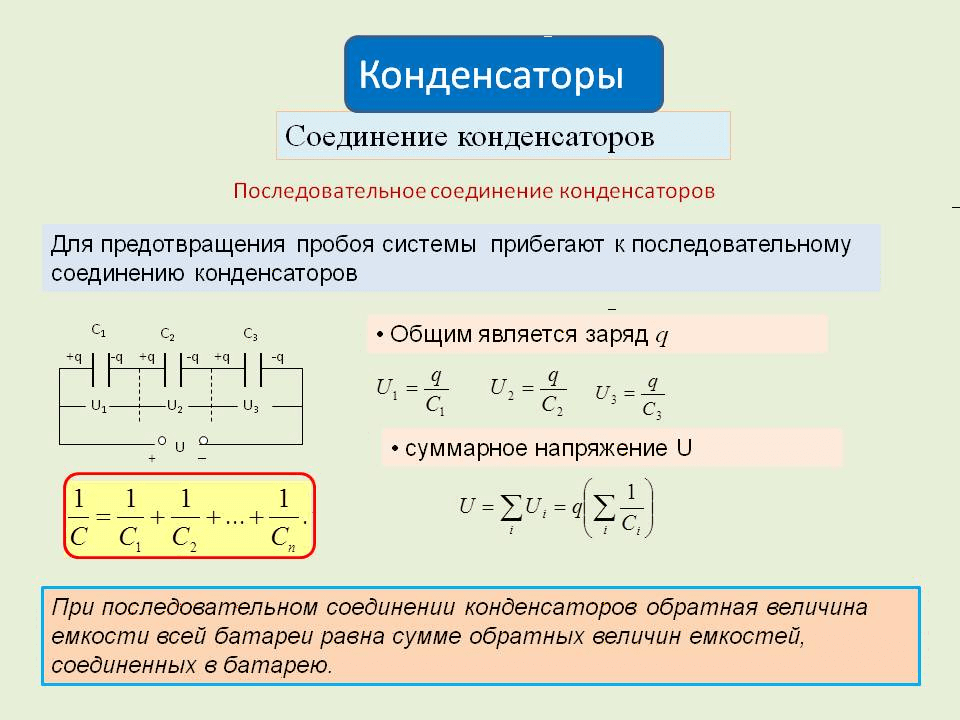 Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

• пикофарад — 10—12 Ф;
• нанофарад — 10—9 Ф;
• микрофарад — 10—6 Ф.

Вам это будет интересно  Удельное электрическое сопротивление металлических проводников

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

• А — площадь меньшей пластины;
• d — расстояние между ними;
• ε — абсолютная проницаемость используемого диэлектрического материала.

Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

• 1,0006 — воздух;
• 2,5—3,5 — бумага;
• 3—10 — стекло;
• 5—7 — слюда.

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

Осциллографом

С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = UR / UC* ( 1 / 2*π*f*R ).

Рис. 4. Простая схема

Алгоритм вычисления простой:

1. Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
2. Измерьте амплитуды напряжений на конденсаторе и на резисторе.
3. Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
4. Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.

При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.

Рисунок 5. Мостовая схема

Плоский конденсатор и его емкость

Плоским конденсатором называют конденсатор, который состоит из двух одинаковых пластин, которые параллельны друг другу. Пластины могут быть разной формы. На практике чаще всего можно встретить квадратные, прямоугольные и круглые пластины. Давайте рассмотрим простой плоский квадратный конденсатор.

Страница не найдена — РОО «Ассоциация победителей олимпиад»

Ваши ФИО*

Ваш email*

Ваш номер телефона*

Какой предмет вы хотели бы преподавать?*

Расскажите кратко о своих олимпиадных достижениях*

Приложите резюме*
Объём файлов не должен превышать 20 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваша электронная почта*

Из какого вы региона?*

Расскажите, как мы могли бы сотрудничать*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО*

Ваша электронная почта*

Ваш номер телефона*

Образовательное учреждение*

Расскажите кратко, какая у вас сложилась ситуация с олимпиадным движением в школе и какого результата вы ожидаете от сотрудничества с АПО*

Please leave this field empty.

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Ваш email

Каким предметом вы интересуетесь

Выберите наиболее подходящий статус Статус не выбранУченикРодительПредставитель школыПедагог

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ученика

Дата рождения ученика

Класс

Образовательное учреждение

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Выберите группу Группа не выбрана

Мотивационное письмо Объём файла не должен превышать 2 Мбайт / Доступные форматы: doc / docx / rtf / pdf / html / txt

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Образовательное учреждение

Город образовательного учреждения

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО

Телефон

Email

Проект / отдел

Должность

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

ФИО ребенка

Название образовательного учреждения

Город образовательного учреждения

ФИО родителя

Телефон родителя

Email родителя

Нажимая на кнопку, вы принимаете положение и согласие на обработку персональных данных.

Войти

---

Родитель

Буду покупать курсы для своего ребёнка Зарегистрироваться

---

Обучающийся

Сам буду проходить курсы Зарегистрироваться

---

Представитель школы

Буду заказывать услуги для своего образовательного учреждения и контролировать их исполнение Зарегистрироваться

19.

6 Конденсаторы, включенные последовательно и параллельно – College Physics

Глава 19 Электрический потенциал и электрическое поле

Резюме

• Выведите выражения для полной емкости при последовательном и параллельном подключении.
• Определите последовательное и параллельное соединение конденсаторов.
• Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых 9.0017 серии и параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.

На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]{C = \frac{Q}{V}}[/latex].

Обратите внимание на рис. 1, что противоположные заряды величиной [латекс]{Q}[/латекс] текут по обеим сторонам первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс]{В}[/латекс]. Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рисунок 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Å . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс]{С = \frac{Q}{V}}[/латекс] для [латекс]{В} [/latex] дает [latex]{V = \frac{Q}{C}}[/latex]. Таким образом, напряжения на отдельных конденсаторах равны [латекс]{V_1 = \frac{Q}{C_1}}[/latex], [латекс]{V_2 = \frac{Q}{C_2}}[/latex] и [ латекс]{V_3 = \frac{Q}{C_3}}[/латекс]. Общее напряжение представляет собой сумму отдельных напряжений:

[латекс] {V = V_1 + V_2 + V_3}.[/латекс]

Теперь, называя общую емкость [латекс]{C_S}[/латекс] последовательной емкостью, считайте, что

[латекс] {V =} [/латекс] [латекс] {\ гидроразрыва {Q} {C_S}} [/ латекс] [латекс] { = V_1 + V_2 + V_3}.

[/латекс]

Введя выражения для [латекс]{V_1}[/латекс], [латекс]{V_2}[/латекс] и [латекс]{V_3}[/латекс], мы получим

[латекс] {\ гидроразрыва {Q} {C_S} = \ гидроразрыва {Q} {C_1} + \ гидроразрыва {Q} {C_2} + \ гидроразрыва {Q} {C_3}}. [/латекс]

Отменяя [латекс]{Q}[/латекс], мы получаем уравнение для полной емкости последовательно [латекс]{C_S}[/латекс] равной

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_3}} [/латекс] [ латекс]{+ \cdots},[/латекс]

, где «…» указывает, что выражение справедливо для любого количества последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к тому, что общая емкость [латекс]{C_S}[/латекс] меньше любой из отдельных емкостей [латекс]{С_1}[/латекс], [латекс]{С_2}[/латекс]. ], …, как показано в следующем примере.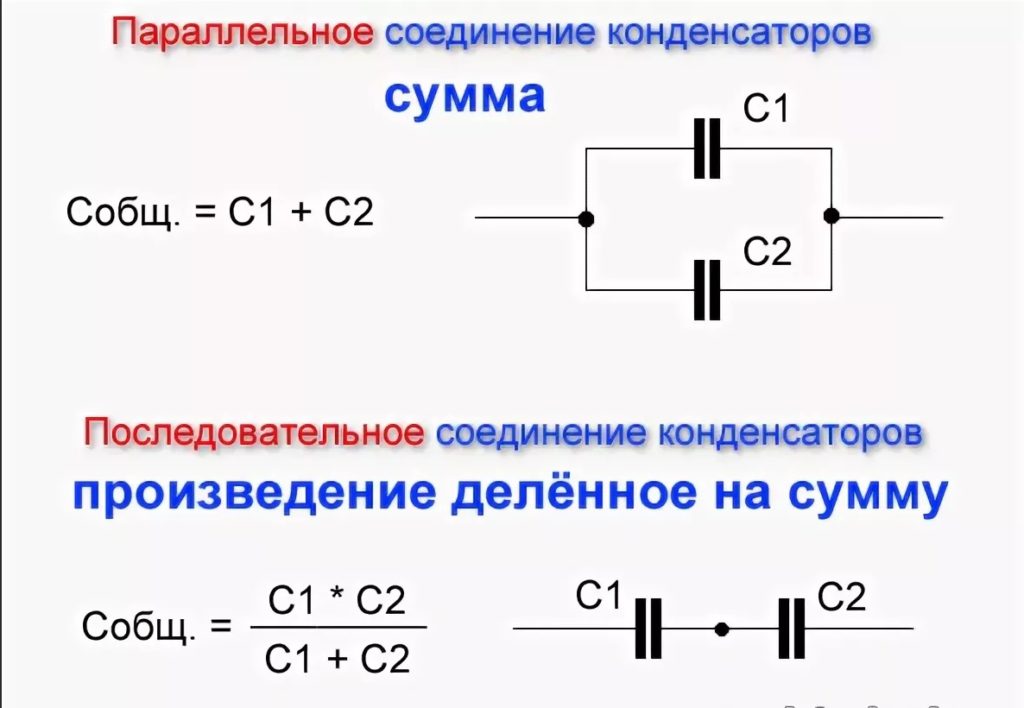

Полная последовательная емкость,

C _с

Полная последовательная емкость: [латекс] {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \frac{1}{C_3} + \cdots}[/latex]

Пример 1: Что такое последовательная емкость?

Найдите общую емкость трех последовательно соединенных конденсаторов, если их отдельные емкости равны 1000, 5000 и 8000 [латекс]\мк\текст{F}[/латекс].

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.

Решение

Ввод данных емкостей в выражение для [латекс]{\ гидроразрыва {1} {C_S}} [/латекс] дает [латекс] {\ гидроразрыва {1} {C_S} = \ гидроразрыва {1 {C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex].

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ мю \ текст {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{5.

000 \;\текст{F}}}[/латекс] [латекс]{+}[/латекс] [ латекс] {\ гидроразрыва {1} {8.000 \; \ му \ текст {F}}} [/ латекс]  [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1,325} {\ му \ текст { F}}}[/латекс]

Инвертирование для нахождения [латекс]{C_S}[/латекс] дает [латекс]{C_S = \frac{\mu \text{F}}{1,325} = 0,755 \;\mu \text{F}}[/ латекс].

Обсуждение

Суммарная последовательная емкость [латекс]{C_s}[/латекс] меньше наименьшей индивидуальной емкости, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {40} {40 \; \ мю \ текст {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{8}{40 \;\му \текст{F}}}[/латекс] [латекс]{+}[/латекс ] [латекс] {\ гидроразрыва {5} {40 \; \ му \ текст {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {53} {40 \; \mu \text{F}}},[/latex]

, так что

[латекс]{C_S =}[/латекс] [латекс]{\frac{40 \;\mu \text{F}}{ 53}}[/латекс] [латекс]{= 0,755 \; \mu \text{F}}. [/latex]

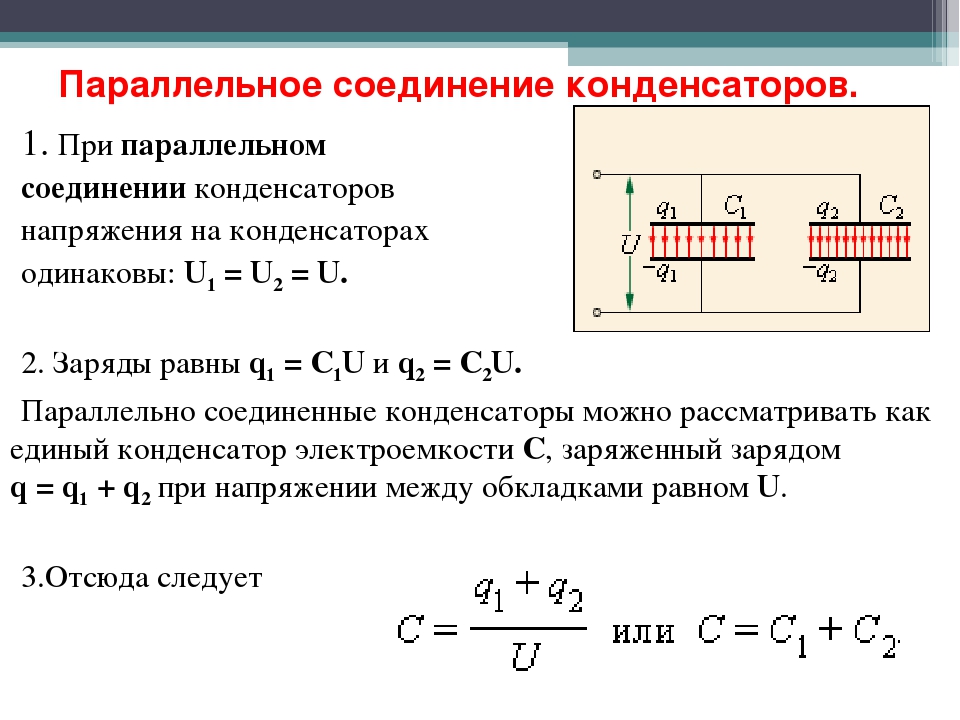
На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс]{\текст{С}_{\текст{р}}}[/латекс], сначала отметим, что напряжение на каждом конденсаторе равно [латекс]{В}[/латекс], такие же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд [латекс]{Q}[/латекс] представляет собой сумму отдельных сборов:

[латекс] {Q = Q_1 + Q_2 + Q_3}.[/латекс]

Рис. 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение [латекс]{Q = CV}[/латекс], мы видим, что общий заряд равен [латекс]{Q = C_{\text{p}}V}[/латекс], а отдельные заряды равны [латекс]{Q_1 = C_1 V}[/латекс] ,  [латекс]{Q_2 = C_2 V}[/латекс] , и [латекс]{Q_3 = C_3 V}[/латекс]. Ввод их в предыдущее уравнение дает

[латекс] {C_{\text{p}} V = C_1 V + C_2 V + C_3 V} .[/latex]

Исключая [латекс]{V}[/латекс] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс]{С_{\текст{р}}}[/латекс]:

[латекс] {C_{\text{p}} = C_1 + C_2 + C_3 \cdots}[/латекс].

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять «…” указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы

[латекс]{C_{\text{p}} = 1,000 \;\mu \text{F} + 5,000 \;\mu \text{F} + 8,000 \;\mu \text{F} = 14,000 \; \mu \text{F}}.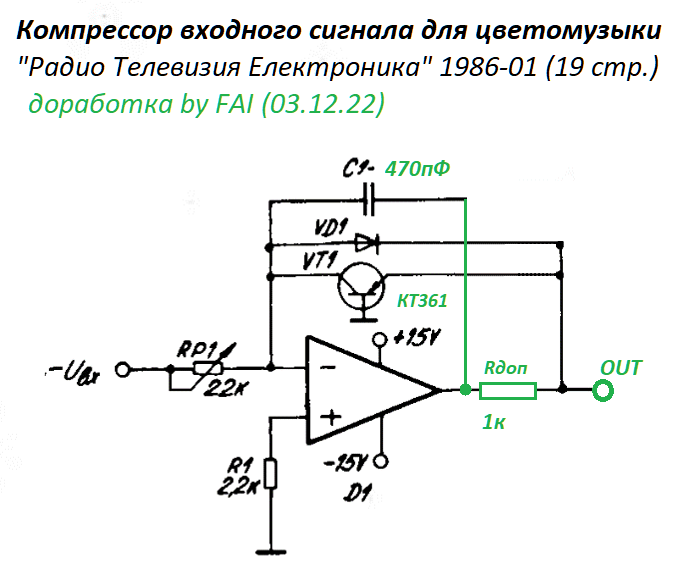 [/latex]

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рис. 2(b).

Суммарная емкость при параллельном подключении,

C _p [латекс] {C_{\text{p}}}[/latex]

Суммарная емкость при параллельном подключении [латекс]{C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/латекс]

Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.

Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ расположены последовательно; их эквивалентная емкость C _S меньше любого из них.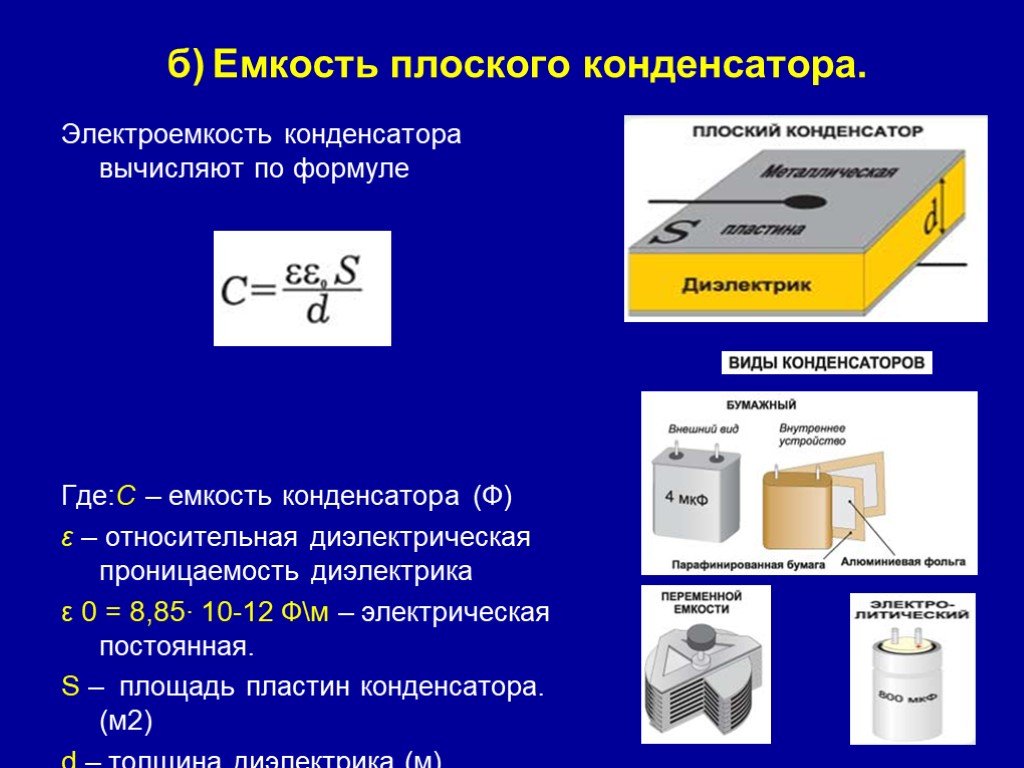 (c) Обратите внимание, что C _S находится параллельно с C ₃ . Полная емкость равна, таким образом, сумме C _S и С ₃ .

Смесь последовательных и параллельных емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ([latex]{C_1 = 1,000 \;\mu\text {F}}[/латекс], [латекс]{C_2 = 5.000 \;\mu \text{F}}[/латекс] и [латекс]{C_3 = 8.000 \;\mu \text{F}}[ /latex]) и округлить ответ до трех знаков после запятой.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] включены последовательно. Их комбинация, обозначенная на рисунке [латекс]{C_S}[/латекс], параллельна [латекс]{С_3}[/латекс].

Решение

Поскольку [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] соединены последовательно, их общая емкость определяется как [латекс]{\ гидроразрыва {1} {C_S } = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex]. Ввод их значений в уравнение дает

[латекс] {\ гидроразрыва {1} {C_1}} [/латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [ / латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ mu \ текст {F}}} [/ латекс] [латекс] {+} [/ латекс] [ латекс] {\ гидроразрыва {1} {5,000 \; \ му \ текст {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1,200} \ му \ текст { F}}}.[/латекс]

Инвертирование дает

[латекс] {C_{\text{S}} = 0,833 \;\mu \text{F}} .[/latex]

Эта эквивалентная последовательная емкость подключена параллельно третьему конденсатору; таким образом, общее количество равно сумме

[латекс]\begin{array}{r @{{}={}} l} {C_{\text{tot}}}\;= & {C_S + C_S} \\ [1em]= & {0,833 \;\mu \text{F} + 8,000 \;\mu \text{F}} \\[1em]= & {8,833 \;\mu \text{F}}. \end{array}[/latex]

Обсуждение

Этот метод анализа комбинаций конденсаторов по частям до тех пор, пока не будет получена сумма, может быть применен к большим комбинациям конденсаторов.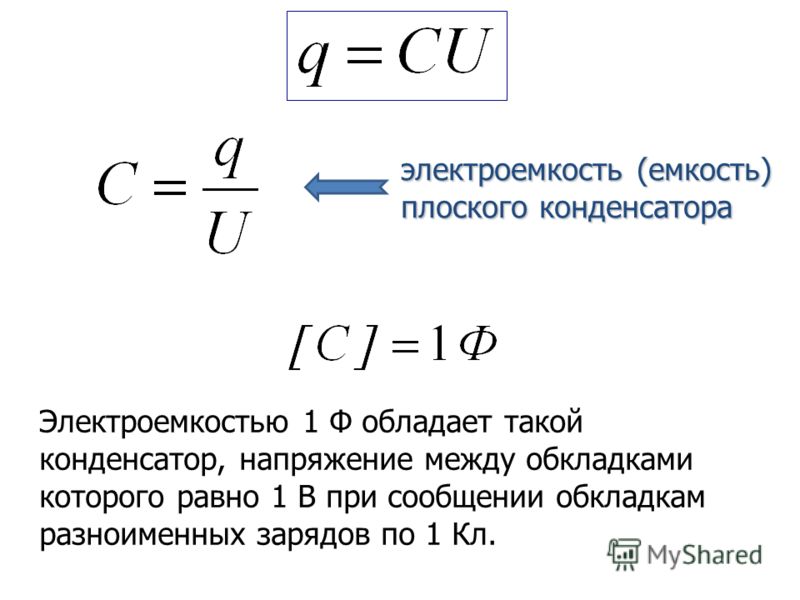

 

• Суммарная емкость последовательно [латекс] {\ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} C_3} + \cdots}[/латекс]
• Общая емкость при параллельном соединении [латекс] {C_{\text{p}} = C_1 + C_2 + C_3 + \cdots}[/latex]
• Если цепь содержит комбинацию конденсаторов, соединенных последовательно и параллельно, определите последовательные и параллельные части, вычислите их емкости, а затем найдите общую сумму.

 

 

Калькулятор конденсаторов

| Код конденсатора

Создано Лучано Мино

Последнее обновление: 10 июля 2022 г.

Содержание:

• Что такое конденсатор? Формула конденсатора
• Коды конденсаторов
• Допустимое отклонение конденсатора

Наш калькулятор конденсаторов найдет всех отсутствующих параметров конденсатора на основе вашего ввода .

С помощью этого инструмента вы можете получить код конденсатора , емкость , допуск , заряд и напряжение с легкостью. Этот калькулятор по существу работает как:

• Конденсаторный калькулятор;
• Калькулятор кода конденсатора;
• Вычислитель заряда конденсатора; и
• Калькулятор напряжения на конденсаторе.

Просто введите любой параметр, а наш калькулятор сделает все остальное!

Что такое конденсатор? Формула конденсатора

Мы рассказали обо всех возможностях этого инструмента, но они бесполезны, если мы не знаем, что такое конденсатор.

Конденсатор — это устройство, которое накапливает энергию посредством электрического поля . Как правило, в конденсаторах используются два проводника, разделенных диэлектрической средой, и существует множество различных форм конденсаторов (параллельные пластины, цилиндрические, сферические и т. д.).

Формула конденсатора выражает отношение между зарядом (QQQ), хранящимся в конденсаторе, его емкостью (CCC) и напряжением (VVV), используемым для удержания этого заряда:

C=QVC = \frac{Q}{V}C=VQ​

Используя эту формулу, мы можем рассчитать напряжение на конденсаторе, если мы знаем значение его емкости и количество хранящегося в нем заряда.

Коды конденсаторов

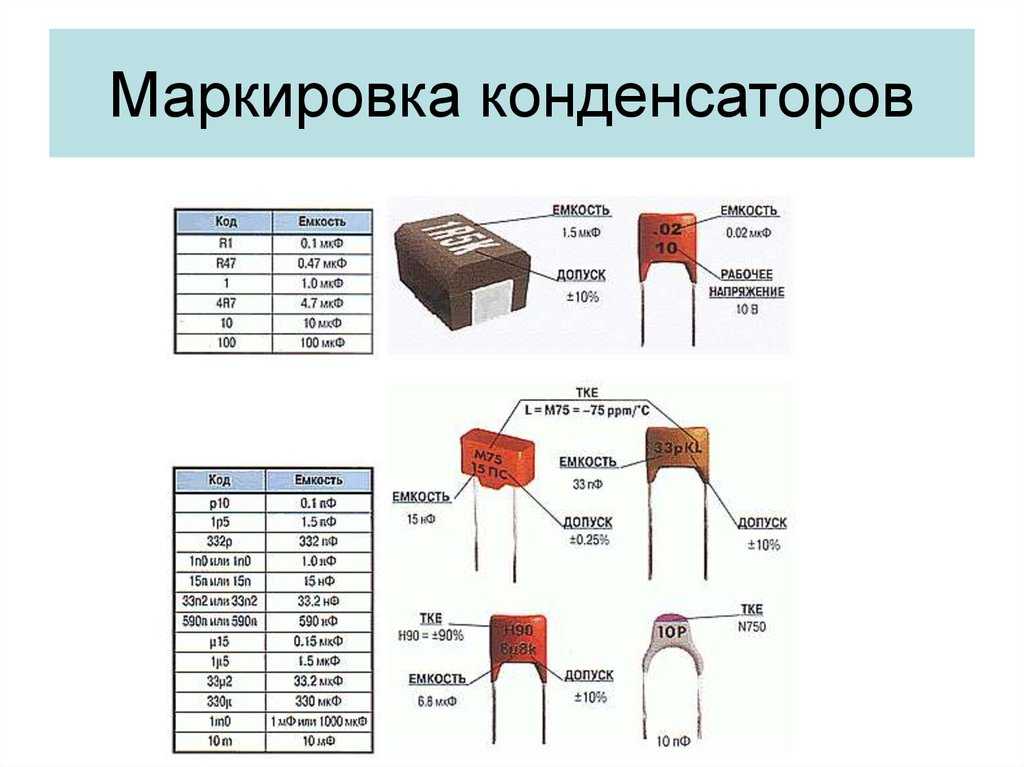
Мы используем коды для быстрой идентификации конденсаторов, используя два значения: их емкость и номинальное напряжение . Номинальное напряжение говорит нам о максимальном напряжении, которое конденсатор может выдержать при правильной работе.

Для конденсаторов емкостью более 100 мкФ , мы часто можем найти их значение, написанное прямо на нем ( 200 мкФ 25 В конденсатор имеет емкость 200 мкФ и работает с напряжениями до 25 В ).

Однако для более низких значений емкости мы используем трехзначный код конденсатора для идентификации:

• Первые и вторые цифры сообщают нам первые две значащие цифры емкости в пФ .
• Третья цифра — 9.0030 множитель . Это число указывает, в какой степени 10 мы должны умножить первую и вторую цифры, чтобы получить фактическое значение емкости.