Коэффициент трения
{\mu = \dfrac{F_{тр}}{mg}}
Найти коэффициент трения
через силу трения и массучерез угол наклона
Сила трения Fтр
микроньютонмиллиньютонньютонкилоньютонмеганьютонгиганьютонкилограмм-силакипдин
Масса m
микрограмммиллиграммграммкгцентнертонна
Ускорение свободного падения g
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
\mu = \dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9. 81 м/с²)
81 м/с²)
Формула коэффициента трения через угол наклона
\mu = \tg(\alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,33 | |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 | |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
\mu = \dfrac{F_{тр}}{mg} = \dfrac{50}{20 \cdot 9.81} = \dfrac{50}{196.2} \approx 0.25484
Ответ: \approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
\mu = \tg(\alpha) = \tg(30°) \approx 0.57735
Ответ: \approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Сила трения (10 класс)
СИЛА ТРЕНИЯ
10 класс
Учитель физики
Тихонова О.А.
Почему звучит скрипка, когда по струнам проводят смычком? Почему на мокрой дороге автомобилю сложнее затормозить? Вы стоите на абсолютно гладкой поверхности ледяного озера. Как сдвинуться с места? Как снять тесное кольцо с пальца?
Как сдвинуться с места? Как снять тесное кольцо с пальца?
Ответы на все эти вопросы можно получить, подробно изучив такую важную тему, как
закон силы трения.
Когда мы говорим «абсолютно гладкая поверхность» — это значит,
что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел. Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.
Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Она всегда меньше силы нормального давления.
Откуда берётся трение
Трение возникает по двум причинам:
- Все тела имеют шероховатости.
 Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения. - Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Виды силы трения
В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.
Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки. Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
- трение скольжения,
- трение покоя,
- трение качения.

Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения
сильно увеличиваются.
Сухое трение, возникающее при относительном покое тел;
Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону.
Сила трения покоя не может превышать некоторого максимального значения ( F тр ) max . Если внешняя сила больше ( F тр ) max , возникает относительное проскальзывание.
Сила трения покоя
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя.
Сила трения покоя
(υ = 0).
Сила трения скольжения
Всегда направлена в сторону, противоположную направлению движения;
Зависит от относительной скорости тел;
При изменении направления скорости изменяется и направление силы трения.
Сила возникающая при относительном движении контактирующих твёрдых тел, называется силой трения скольжения.
Сила трения качения
Возникает в случае, когда тело не скользит по поверхности, а катится;
Скорости тел в точке касания одинаковы и по модулю и по направлению.
Сила трения качения — это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Направление силы трения
Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.
Как рассчитать и измерить силу трения
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Сила реакции опоры обозначается N .
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
где μ — коэффициент трения, N — сила нормальной реакции опоры.
Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:
ПРИМЕР ЗАДАЧИ
На горизонтальном полу стоит ящик массой 20 кг.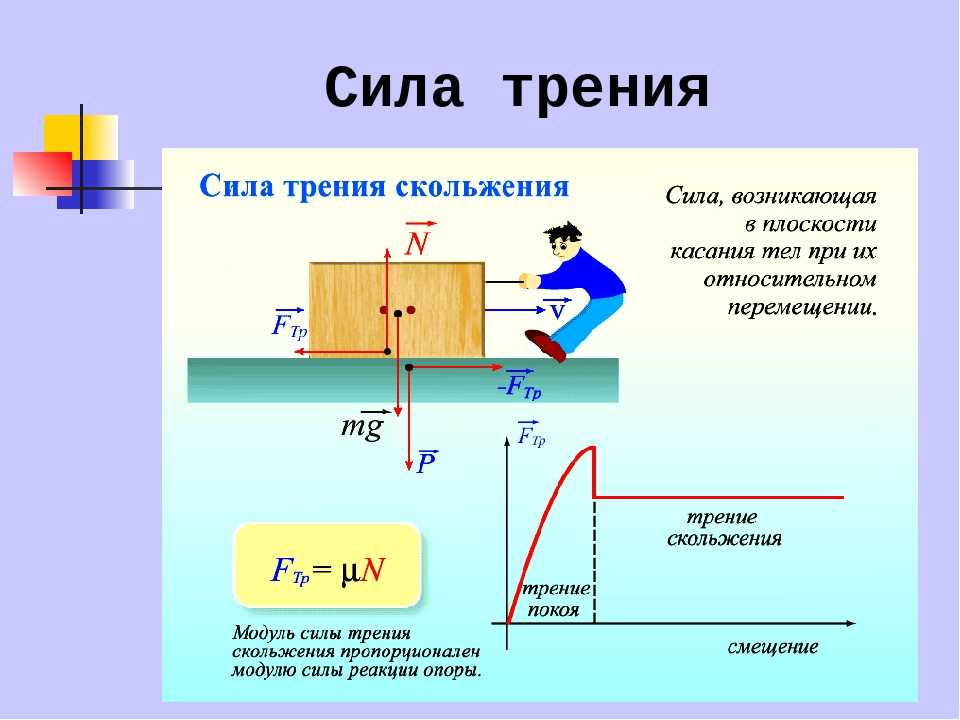 Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
РЕШЕНИЕ: Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
F тр.пок . = F = 36 (Н).
Подведём итоги
- Сила трения покоя меняется от нуля до максимального значения 0
- Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.макс
- Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N, где μ — коэффициент трения, N — сила нормальной реакции опоры.

- При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
- Коэффициент трения μ зависит от рода и степени обработки поверхностей 0 μ
- При одинаковых силе нормального давления и коэффициенте
трения сила трения качения всегда меньше силы трения скольжения.
Домашняя работа:
§ 36, 37.
Упр. стр. 117.
формула определения значения, обозначение в физике, измерительные действия
Физика
12.11.21
15 мин.
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения. Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия).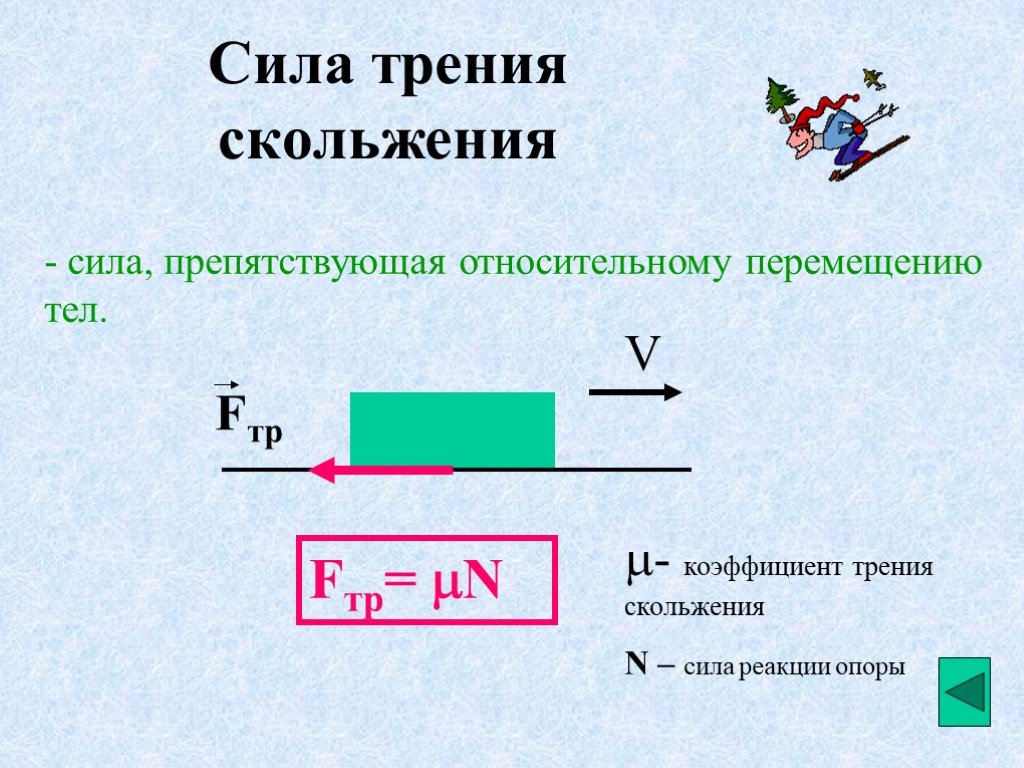 Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Оглавление:
- Краткое описание
- Сила трения скольжения
- Правила расчёта
- Измерительные манипуляции
- Основные характеристики
- Практическое значение
- Ключевые нюансы
Процесс взаимодействия тел при их относительном движении можно отобразить с помощью формулы трения скольжения. Коэффициент определяется только путём проведённых исследований. Изучением процессов трения занимается раздел физики, который называется трибологией (механикой фрикционного взаимодействия). Определяемый коэффициент является совокупной характеристикой пары материалов, которые не зависят от площади соприкосновения тел.
Краткое описание
Трение можно рассматривать как способ взаимодействия двух объектов.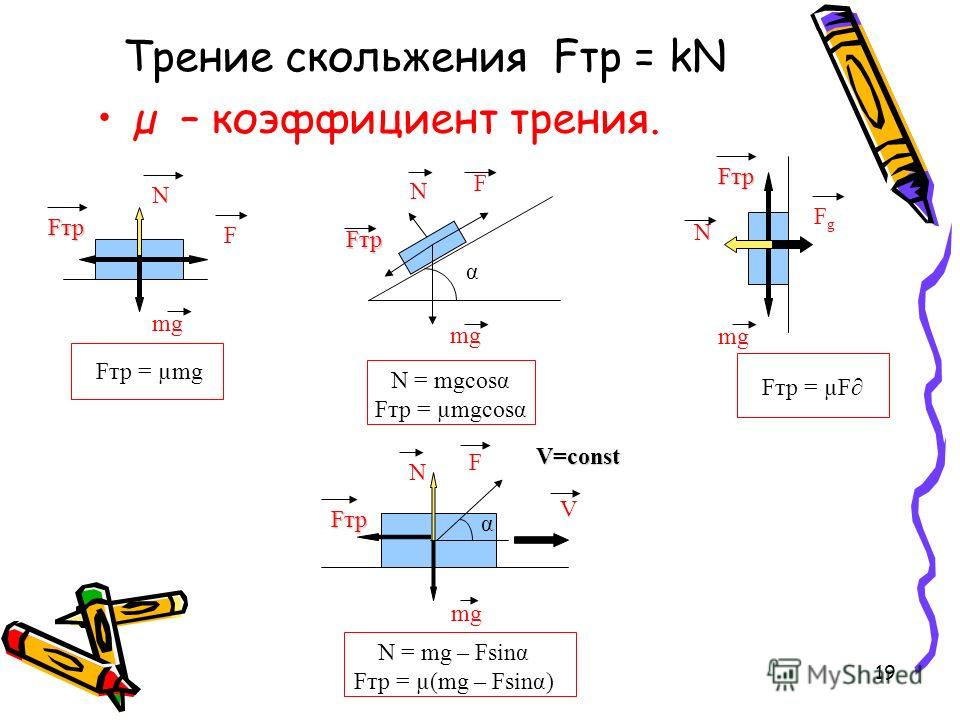 Но у этого процесса есть свои нюансы. Между двумя объектами трение возникает только в результате их соприкосновения с определённой площадью поверхности. Этот процесс попадает под действие третьего закона Ньютона.
Но у этого процесса есть свои нюансы. Между двумя объектами трение возникает только в результате их соприкосновения с определённой площадью поверхности. Этот процесс попадает под действие третьего закона Ньютона.
Например, если взять 2 небольших бруска из дерева и просто их передвигать, то в итоге можно наблюдать соприкосновение по площадям. Во время эксперимента можно заметить, что двигать предметами относительно друг друга гораздо сложнее, нежели совершать с ними какие-либо манипуляции в воздухе. Именно в этом случае в действие вступает закон трения.
В третьем законе Ньютона описано правило, которое касается того, что по модулю силы равны, но направлены совершенно в разные стороны. Получается, что сила μ является векторной величиной. Этот процесс имеет электромагнитную природу. Трение возникает в результате того, что молекулы и атомы тел, участвующих в соприкосновении, начинают взаимодействовать друг с другом. На этом правиле основано много задач по физике. Латинской буквой k или греческой μ обозначается коэффициент трения.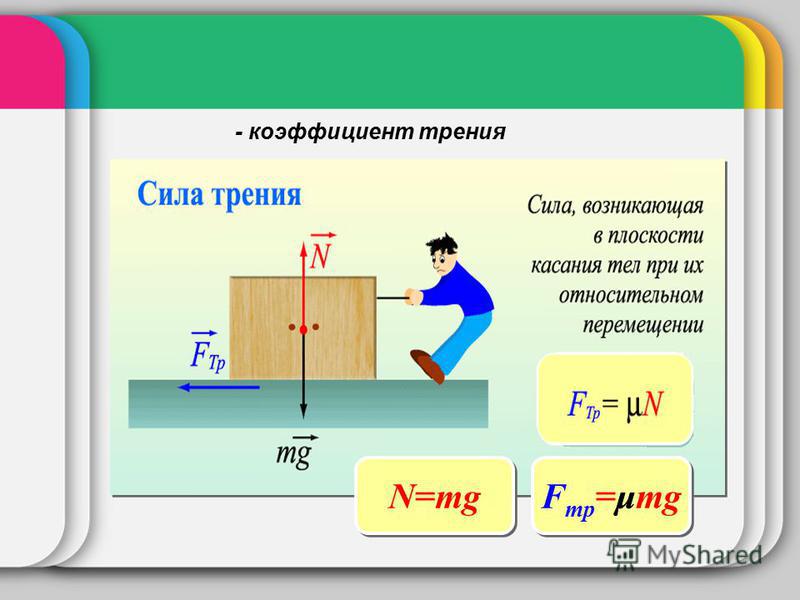
Сила трения скольжения
Коэффициент трения скольжения показывает отношение μ к силе давления на поверхность. Это правило изучают на уроках физики в 10 классе. Силы трения всегда воздействуют на объекты. Они возникают в результате соприкосновения твёрдых тел, газов и жидкостей, подчиняются закону Ньютона.
Для решения сложных задач нужно понимать, что направление силы трения противоположно движению объекта и факторам, которые стремятся изменить его положение. Исключений не предусмотрено. О процессе трения скольжения можно говорить только тогда, когда тело движется относительно другого объекта. Конечные результаты во многом зависят от следующих факторов:
- скорости движения;
- коэффициента трения скольжения (µ), от которого напрямую зависят свойства, а также состояние поверхностей соприкосновения;
- силы нормальной реакции опоры (N→).
Итоговый коэффициент во многом зависит от свойств задействованного материала.
Например, чем шероховатее будет поверхность, тем больше станет значение μ. У скользких оснований коэффициент окажется минимальным. Трение во многом зависит от скорости, но этим значением часто пренебрегают, если речь не идет о точных измерениях. По этой причине показатель μ является постоянным.
Правила расчёта
С максимальной точностью силу трения скольжения можно определить с помощью формулы F = µ* N. Значение N рассчитывается как производное массы тела на ускорение свободного падения. Учитывается также косинус угла к поверхности: N = m * g * cosa. Формула коэффициента трения скольжения выглядит следующим образом: µ = F/N.
На уроках физики можно узнать, что для основного количества всех пар материалов коэффициент рассчитывается во время опытов. Значение находится в пределах от 0,1 до 0,5. В такой ситуации μ будет являться переменной величиной.
В физике используются специальные таблицы, в которых указаны переменные величины для каждого из материалов.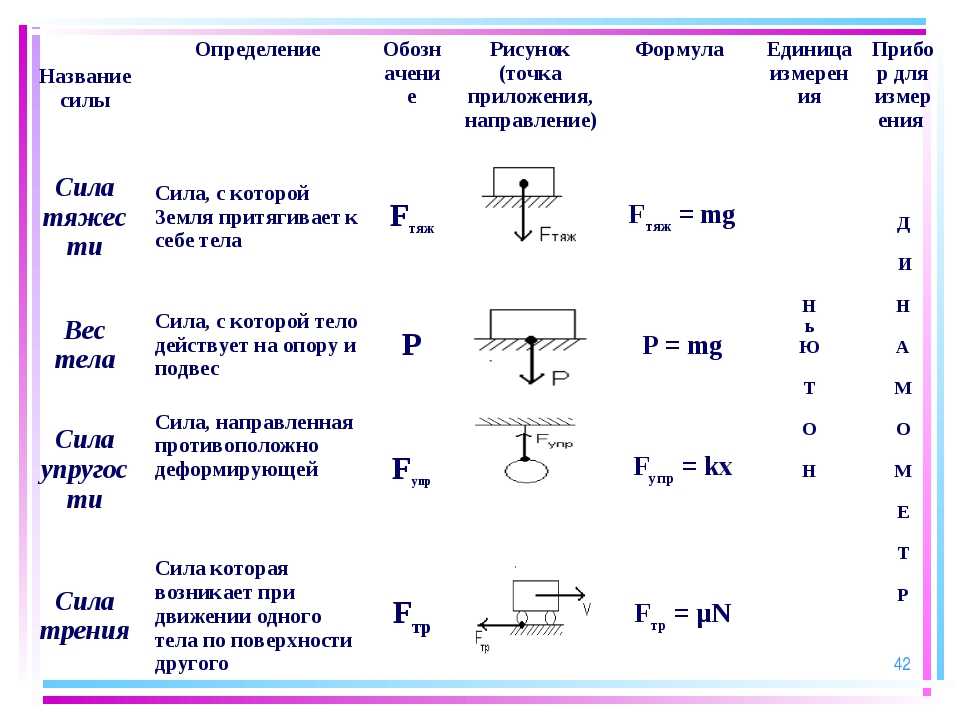 Но эти данные являются актуальными только при соблюдении определённых условий. Если нужно получить максимально точный результат, тогда следует самостоятельно выполнить расчёты для конкретной ситуации.
Но эти данные являются актуальными только при соблюдении определённых условий. Если нужно получить максимально точный результат, тогда следует самостоятельно выполнить расчёты для конкретной ситуации.
Измерительные манипуляции
Динамометр используется для измерения реальных показателей механической силы. Этот прибор включает в себя силовой элемент (пружину) и отчётное звено (линейку). Принцип использования стандартного пружинного динамометра прост. На прибор воздействует сила, которая растягивает либо сжимает упругое звено. Полученное значение фиксируется при помощи измерительной части.
Чтобы правильно найти величину μ, которая передаётся на брусок в процессе его движения по конкретной поверхности, нужно постараться прикрепить к объекту динамометр. Необходимо потянуть устройство за пружину в горизонтальной плоскости.
Чтобы полученный результат не имел погрешностей, нужно следить за тем, чтобы прибор перемещался максимально равномерно и с постоянной скоростью.
На анализируемую величину будут действовать сразу 2 силы, одна из которых препятствует движению бруска, а вторая старается снизить вероятность деформации пружины. Так как движение динамометра равномерное, силы имеют одинаковое значение и уравновешивают друг друга. На измерительной шкале регистрируется показатель упругости пружины, из-за чего полученная величина и будет искомой цифрой.
Проведённый опыт может доказать, что итоговое значение μ во многом зависит от веса задействованного объекта. Если применить дополнительный груз и повторить исследование, тогда можно заметить, что значение на линейке увеличится.
Основные характеристики
Сила трения может рассматриваться как процесс, который возникает в результате соприкосновения двух объектов и препятствует их относительному движению. Основными причинами трения являются специфическая шероховатость трущихся поверхностей и взаимодействие имеющихся молекул. Существует определённый характер фрикционного взаимодействия, который принято делить на несколько категорий:
Существует определённый характер фрикционного взаимодействия, который принято делить на несколько категорий:
- Граничное. В области контакта содержатся участки и слои разной природы (например, жидкость, оксидные плёнки). Это самый распространённый случай, когда дело касается скольжения.
- Сухое. Взаимодействующие твёрдые тела не разделены между собой дополнительными слоями. На практике крайне редко фиксируются ситуации, которые свойственны сухому трению. Для этого случая характерно наличие большого значения μ в состоянии покоя.
- Жидкостное. Задействованные тела разделены слоем твёрдого тела (например, порошок графита), газом либо жидкостью. Эта ситуация чаще всего фиксируется при трении качения. Твёрдые тела погружены в жидкость, а величина μ отличается вязкой средой.
- Смешанное. Зона контакта содержит участки жидкостного и сухого трения.
- Вязкоупругое.
 Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.
Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.
Многочисленные исследования показали, что для многих пар материалов итоговое значение µ не превышает 1. В противном случае можно говорить, что между контактирующими телами присутствует сила адгезии.
Для решения элементарных задач используется следующая формула: µ = (F + F adhesion)/ N. Значение μ измеряется стандартным образом, никакие дополнительные буквы для обозначения полученного результата не используются (указываются только цифры).
Практическое значение
Трение играет отрицательную роль во многих механизмах, например, в транспортных средствах, двигателях внутреннего сгорания, зубчатых шестеренках. Негативное значение сказывается на снижении коэффициента полезного действия механизма. Смазки, масла на синтетической и натуральной основе позволяют существенно уменьшить силу трения. На многих широко распространённых деталях присутствует защитное напыление.
Если речь идет о миниатюризации МЭМС (микроэлектромеханических систем) и НЭМС (наноэлектромеханических систем), тогда показатель μ будет существенно увеличиваться. Для решения этих проблем используется усовершенствованный подход в рамках трибологии.
Благодаря трению объекты могут перемещаться. Например, при ходьбе неизбежным является сцепление стопы с полом, из-за чего человек отталкивается от поверхности и движется дальше. Аналогичным образом происходит сцепление колёс транспортного средства с дорогой. Для повышения эксплуатационных характеристик автомобилей выпускаются инновационные формы и специальные разновидности резины для колёс. На спортивные машины устанавливают универсальные антикрылья, которые прижимают транспортное средство к трассе.
Ключевые нюансы
Сила трения имеет место и при качении какого-либо тела. Но этим параметром часто пренебрегают, так как итоговые показатели недостаточно велики, чтобы брать их в расчёт. Такой подход позволяет упростить процесс решения различных задач. Но даже в этом случае можно сохранить высокую степень точности итогового результата.
Такой подход позволяет упростить процесс решения различных задач. Но даже в этом случае можно сохранить высокую степень точности итогового результата.
Для закрепления полученных знаний можно изучить пример решения задачи по физике. На пол поставили ящик весом 7 кг. Между этим объектом и напольным покрытием значение μ составляет 0,3. К ящику прикладывают силу, которая соответствует 14 Н. Нужно совершить необходимые расчёты, чтобы понять, можно ли сдвинуть объект с места. Для определения силы реакции необходимо массу ящика умножить на ускорение:
- N = m * g.
- N = 10 кг * 9,8 м/с² = 98 кг * м/с² = 98 Н.
- F = k * N.
- F = 0,3 * 98 Н = 29,4 Н.
Полученный результат позволяет сделать вывод, что ящик останется на прежнем месте. Это связано с тем, что итоговое значение превышает усилия, приложенные к объекту: 29,4 Н > 14 Н.
Силы трения имеют большое значение в жизни людей и животных.
Благодаря этому явлению человек может ходить и держать в руках различные предметы. За счёт действия закона сцепления на скалах удерживаются огромные валуны и не падают в пропасть, а плетущиеся растения тянутся к солнечному свету и скрепляются с ближайшей опорой.
За счёт действия закона сцепления на скалах удерживаются огромные валуны и не падают в пропасть, а плетущиеся растения тянутся к солнечному свету и скрепляются с ближайшей опорой.
Люди и животные от природы умеют избавляться от негативного воздействия торможения. К примеру, всё тело рыбы покрыто специальной слизью, что позволяет существенно уменьшить трение о воду. Человек при работе с техникой научился использовать различные смазывающие материалы, благодаря чему увеличивается срок эксплуатации, а также качество работы устройства.
Сила трения тема по физике 7 класса
Трение — это сила, которая удерживает объекты от отдаления от нас при малейшем прикосновении, как шайба на столе для аэрохоккея. В этой статье мы обсудим значение силы трения, коэффициент трения с соответствующим символом, формулу трения и некоторые примеры расчета трения.
Сила трения — определение и значение
Сила трения — это сила, которая противодействует скользящему движению одного объекта / поверхности по другому объекту / поверхности.
Если вы толкаете коробку горизонтально, сопротивление, которое вы чувствуете, борясь с вами, — это сила трения. Трение напрямую связано с весом объекта и шероховатостью взаимодействующих поверхностей. Трение всегда действует параллельно поверхности, в направлении, противоположном скольжению, как показано на рисунке ниже. Существует два типа трения: статическое и кинетическое.
Статическое трение — это сила, которая противодействует движению, когда объект не движется. Представьте, что вы пытаетесь толкнуть большую тяжелую коробку. Если вы нажмете совсем немного, он вообще не сдвинется — статическая сила трения удерживает его на месте. Вы должны увеличивать силу нажатия, пока он, наконец, не начнет двигаться. До этого момента статическое трение сопротивляется вашему толчку. Именно в тот момент, когда коробка начинает двигаться, статическое трение больше не действует, и вступает в силу кинетическое трение.
Кинетическое трение — это сила, которая противодействует движению, когда объект движется. Это сила, которая заставляет объекты замедляться — в противном случае они продолжали бы скользить вечно. Если вы думаете о том, чтобы толкать эту большую, тяжелую коробку, вы можете подумать о том, что заставить коробку начать движение сложнее, чем поддерживать ее движение. Это связано с тем, что статическое трение обычно больше, чем кинетическое трение.
Это сила, которая заставляет объекты замедляться — в противном случае они продолжали бы скользить вечно. Если вы думаете о том, чтобы толкать эту большую, тяжелую коробку, вы можете подумать о том, что заставить коробку начать движение сложнее, чем поддерживать ее движение. Это связано с тем, что статическое трение обычно больше, чем кинетическое трение.
Трение возникает в результате действия межатомных электрических сил
Трение — это тип контактной силы, и, как таковой, оно возникает в результате межатомных электрических сил. В микроскопическом масштабе поверхности объектов не являются гладкими; они состоят из крошечных пиков и щелей. Когда пики скользят и сталкиваются друг с другом, электронные облака вокруг атомов каждого объекта пытаются оттолкнуться друг от друга. Также могут существовать молекулярные связи, которые образуются между частями поверхностей для создания адгезии, которая также препятствует движению. Все эти электрические силы вместе составляют общую силу трения, которая противодействует скольжению.
Коэффициент символа трения
Различные типы поверхностей вносят разный вклад в силу трения. Подумайте о том, насколько сложнее толкать коробку по бетону, чем толкать ту же коробку по льду. Способ, которым мы учитываем эту разницу, — это коэффициент трения. Коэффициент трения — это безразмерное число, зависящее от шероховатости (а также других качеств) двух взаимодействующих поверхностей. Было проведено много экспериментов для определения коэффициента трения при взаимодействии общих поверхностей.
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения и обозначается обычно латинской буквой k {\displaystyle k} или греческой буквой ? {\displaystyle \mu}. Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости.
Расчет силы трения
Сила трения высчитывается путем произведения реакции опоры N и коэффициента трения k. Формула силы трения будет иметь следующий вид:
F тр = k * N.
В некоторых формулах коэффициент трения k обозначается символом µ.
Написанные выше расчеты справедливы в самом простом случае, когда тело лежит на строго горизонтальной поверхности.
Если же движение происходит по наклонной плоскости, то расчеты силы трения несколько усложняются.
Каждая сила имеет единицы измерения Ньютонов,. Эта формула показывает, что величина силы трения зависит от коэффициента трения, как мы обсуждали выше, а также от величины нормальной силы. По мере увеличения коэффициента трения или нормальной силы сила трения увеличивается. Это интуитивно понятно — когда мы толкаем коробку, толкать труднее, когда поверхность более шероховатая и когда коробка тяжелее.
Уравнение статического трения
Значение «равно или меньше знака» в приведенном выше общем уравнении относится к статическому трению. Это потому, что если вы нажмете на коробку, а она не сдвинется с места, сила трения будет равна силе вашего толчка (потому что без ускорения сумма сил равна нулю). Поэтому, если вы нажмете на 5N сила, сила трения, сопротивляющаяся движению, будет равна 5N; если вы нажмете на 10N и он все еще не движется, сила трения будет равна 10N. Силой выступает F fs = ? s F n (? s – коэффициент статического трения, F n – нормальная сила).
Поэтому, если вы нажмете на 5N сила, сила трения, сопротивляющаяся движению, будет равна 5N; если вы нажмете на 10N и он все еще не движется, сила трения будет равна 10N. Силой выступает F fs = ? s F n (? s – коэффициент статического трения, F n – нормальная сила).
Чтобы найти максимально возможную силу, которую вы можете приложить, не перемещая коробку, или просто заставить коробку начать движение, вы должны установить силу трения, равную коэффициенту трения, умноженному на нормальную силу.
Кинетическое уравнение трения
Поскольку объект уже движется для применения кинетического трения, кинетическое трение не может быть меньше, чем коэффициент трения, умноженный на нормальную силу.
Сила трения — основные выводы
Сила трения противодействует скольжению между объектом и поверхностью.
Трение действует параллельно поверхности в направлении, противоположном движению (или попытке движения).
Трение является результатом межатомных электрических сил. Электронные облака между шероховатыми участками поверхностей могут отталкиваться друг от друга, а сцепление может препятствовать движению поверхностей, но все это приводит к силе трения, которая препятствует движению.
Электронные облака между шероховатыми участками поверхностей могут отталкиваться друг от друга, а сцепление может препятствовать движению поверхностей, но все это приводит к силе трения, которая препятствует движению.
Статическое трение препятствует скольжению, когда объекты не движутся, и может быть меньше, чем коэффициент статического трения, умноженный на нормальную силу.
Кинетическое трение противодействует скольжению при движении объектов и всегда равно коэффициенту кинетического трения, умноженному на нормальную силу.
Сохраните материал в вашей социальной сети, чтобы легко найти его:
Ответы на домашние задания:
- Квантовые числа и орбитали
- Необходимый элемент азот (факты, купить, физические свойства, применение) химия
- Преимущества изучения второго языка в раннем возрасте org/Article»>Емкость буфера и расчеты, химия. Что такое pH? Формула и уравнение pH.
- Виртуальная реальность: преимущества и недостатки
- Таблица с формулами вычисления интегралов
- Знаки препинания в русском языке схема расстановки
- Энтальпия связи и энергия связи
- Как улучшить математику моего ребенка?
- Какова функция регулирующих клапанов в системе ОВКВ?
- Как записать цифры в порядке убывания, таблица.
- Программное и аппаратное обеспечение компьютера
- Прописные буквы русского алфавита для первоклассников распечатать org/Article»>Грамматика в русском и английском языке
- Именно поэтому этот год, безусловно, будет годом законодательства
Интегрированный урок по физике 7 класс Сила трения. Трение покоя. Трение в природе и технике
Интегрированный урок по физике
7 класс
Тема: Сила трения. Трение покоя. Трение в природе и технике
Цель урока: познакомить обучающихся с силой трения, её видами и значением в жизни человека и природы.
Задачи:
в направлении личностного развития:
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• воспитание качеств личности, способность принимать самостоятельные решения;
• формирование мышления;
• развитие интереса к предмету «Физика».
в предметном направлении:
• познакомить учащихся с силой трения, её видами и значением в жизни человека и природы;
• формирования механизмов мышления, характерных для математической деятельности
в метапредметном направлении:
• развитие представлений о физике как форме описания и методе познания действительности;
• формирование общих способов интеллектуальной деятельности, характерных для физики и являющихся основой познавательной культуры.
Оборудование: деревянный брусок, гиря, штатив, динамометр демонстрационный, компьютер, мультимедиапроектор, экран, листы бумаги, корзинка, шаблон кластера, тест, анкета по рефлексии, тест.
Ход урока.
Организационный момент.
Актуализация. «Корзина идей».
Учитель: Когда-то чтобы добыть огонь, люди брали острую деревянную палочку, упирали её в деревянный брусок и быстро вращали. При достаточном упорстве через некоторое время появлялся дым, начиналось тление и возгорание образовавшихся опилок и подложенного, например, сухого мха.
Как вы считаете, о чем пойдет речь сегодня на уроке? На краю ваших парт лежат шаблон. Заполните первый столбик, запишите все, что знаете о силе трение.
(школьники зачитывают ответы).
«Знаю» | «Хочу узнать» | «Узнал (а)» |
Подумайте, чтобы вы хотели узнать о трении сегодня на уроке? (школьники зачитывают ответы, план урока записывается на доске).
Ученики: Мы сегодня узнаем, что такое сила трения, какие виды силы трения существуют, причины возникновения силы трения, а также научимся измерять силу трения с помощью динамометра. Узнаем про трение в природе и технике.
План
— Что такое трение?
— Причина возникновения силы трения.
— Виды трения.
— Как можно рассчитать силу трения?
— Измерение сил трения.
— Трение в природе и технике.
— Полезно трение или вредно?
Изучение нового материала
Учитель. С трением мы сталкиваемся на каждом шагу, но без трения не смогли бы сделать и шага. Невозможно представить себе мир без трения. В отсутствие трения Земля бы сотрясалась бы от непрерывных землетрясений, т.к. тектонические плиты постоянно сталкивались бы между собой. Все ледники сразу же скатились с гор, а по поверхности Земли носилась бы пыль прошлогоднего ветра. Как хорошо, что все-таки есть на свете сила трения! С другой стороны, трение между деталями машин приводит к износу и дополнительным расходам.
Презентации «Сила трения», «Трение в жизни растений и животных». (Работа учащихся в рамках ИОП по теме: «Сила»)
1.Силы трения – это силы, возникающие при соприкосновении движущихся тел с другими телами. 2. Природа силы трения Причиной возникновения силы трения является шероховатость поверхности. Выступающие части поверхностей задевают друг за друга и препятствуют движению тела. Другая причина трения – взаимное притяжение молекул соприкасающихся тел. На величину трения влияют: нагрузка, скорость перемещения тел, шероховатость их поверхностей, температура, наличие смазки. Наибольшее значение сила трения имеет в момент начала движения. 3.Виды трения Различают сухое и жидкое трение. Сухое трение покоя, скольжения и трение качения. Сила трения покоя удерживает гвоздь, вбитый в доску, не дает развязаться банту на ленте, удерживает нитку, которой сшиты два куска ткани. 4. Формула силы трения Сила трения обозначается буквой Fтр. Единица измерения – 1 Н. Формула, по которой можно рассчитать силу трения: Fтр = µmg, где µ — коэффициент трения, m – масса тела, g – ускорение свободного падения. 5. Измерение сил трения с помощью динамометра Первые исследования трения, о которых мы знаем, были проведены Леонардо да Винчи примерно 500 лет назад. Он измерял силу трения, действующую на деревянные параллелепипеды, скользящие по доске, причём, ставя бруски на разные грани, определял зависимость силы трения от площади опоры. Но работы Леонардо да Винчи стали известны уже после того, как классические законы трения были вновь открыты французскими учёными Амонтоном и Кулоном в XVII – XVIII веках. Демонстрация «Измерение силы трения покоя» 1.Положите на горизонтальную поверхность линейки деревянный брусок с тремя отверстиями на поверхности. На него положите груз массой 100 г. К крючку динамометра прицепите брусок. С помощью динамометра приведите брусок в равномерное движение. Зафиксируйте показания динамометра. Рассчитаем коэффициент трения скольжения. µ = Fтр/ mg 6. Трение в природе и технике Учитель: В жизни многих растений трение играет положительную роль. Например, лианы, хмель, горох, бобы и другие вьющиеся растения. Благодаря трению они цепляются за находящиеся поблизости опоры, удерживаются на них и тянутся к свету. Трение создается за счет того, что стебли многократно обвивают опоры и поэтому очень плотно прилегают к ним. У многих животных имеются различные органы, служащие для хватания (хобот слона, цепкие хвосты лазающих животных). Отгадайте загадки и объясните, как это связано с трением. 1. Она с лианы на лиану, А в передышку ест бананы. (Обезьяна). 2. В зелененьком домишке, много ребятишек, Усиками цепляются, к солнышку тянутся. (Горох) 3. Гроздь ягод на солнце наливается, а потом в корзину собирается. (Виноград). Ученики: Растениям, как репейник, трение помогает распространять семена, имеющие колючки с небольшими крючками на концах. Эти колючки зацепляются за шерсть животных и вместе с ними перемещаются. Семена же гороха, орехи благодаря своей шарообразной форме и малому трению качения перемещаются легко сами. У растений, имеющих корнеплоды, такие, как морковь, свекла, брюква, сила трения о грунт способствует удержанию их в почве. С ростом корнеплода давление окружающей земли на него увеличивается, а это значит, что сила трения тоже возрастает. Учитель: Вспомните известную сказку «Репка». — Почему не смог дед вытащить репку? Как выглядел бы мир без трения? Учитель: представьте, что пол в нашем классе стал очень скользким, например, как каток. Чтобы произошло? Ученики: Люди поминутно падали бы и не могли подняться. Ведь только трение (точнее: трение покоя) позволяет нам отталкиваться ногами, шагая вдоль по ровной дороге. Учиель: приведите примеры, когда нам необходимо трение в жизни. Ученики: Все узлы немедленно развязывались бы; ведь узлы держатся только благодаря трению одних частей верёвки, шнурка или бечёвки о другие. Все ткани расползались бы по ниткам, а нитки — в мельчайшие волокна. Шофёр не смог бы остановить свою машину? Ведь автомобиль тормозят тем, что прижимают к специальным барабанам, вращающимся вместе с колёсами, тормозные колодки (или ленты). В мире без трения нельзя было бы ничего толком построить или изготовить: все гвозди выпадали бы из стен, — ведь вбитый гвоздь держится только из-за трения о дерево. Все винты, болты, шурупы вывинчивались бы при малейшем сотрясении — они удерживаются только из-за наличия трения покоя. Учитель: Как вы считаете, а трение полезно или вредно? 7. Трение полезно или вредно? Послушайте внимательно стихотворение. 1-й ряд выписывает примеры того, когда трение полезно. 2 – й ряд выписывает примеры того, когда трение вредно. | |
Трение – наш друг и враг.
Что такое трение?
Трение – явление.
Враг оно нам или друг?
Это знают все вокруг:
Если б трение пропало,
Что б со всеми нами стало?
Мы ходить бы не смогли,
Оттолкнувшись от земли.
Если б взял ты что – то вдруг,
Оно выпало б из рук.
Помогает трение
Начинать движение
Всем машинам, тракторам
Мотоциклам, поездам.
Ну, а также тормозить
И их всех остановить.
Очень нужно тренье нам,
Всем растеньям и зверям!
Но притом приносит вред
И не мало разных бед:
В станках, приборах трутся части-
И это главное несчастье.
Ну, а все автомашины
Быстро снашивают шины!
И поэтому вопрос
Не настолько уж и прост:
Трение – друг нам или враг?
Ответ двоякий: так и так!
Проверка.
— Назовите примеры полезного трения.
— Приведите примеры, когда трение приносит вред.
Итак, благодаря трению происходит движение паровоза, автомобиля и т. д. Трение используется в ременных передачах, в тормозах и т. п., но оно же вызывает нагревание и износ различных частей механизмов и машин. Вредное влияние трения внешнего уменьшают смазкой, применяют шариковые и роликовые подшипники, заменяя трение скольжения трением качения.
Первичное закрепление.
1. Викторина.
1. Почему нагруженный автомобиль на размытой дороге буксует меньше, чем пустой?
(Нагруженный автомобиль оказывает большее давление на дорогу, вследствие этого сцепление колес с грунтом у него больше, чем у порожнего).
2. Почему спускаясь по канату, опасно быстро скользить? (Вследствие большого трения можно обжечь руки и ноги).
3. Перечислите все известные вам смазочные вещества. ( Машинное, авиационное, дизельное масла, солидол, нигрол, ружейное масло, технический вазелин, автол и др. )
)
4. Назовите пословицы и поговорки, связанные с трением. (Сухая ложка рот дерет; Идет как по маслу; скрипит как немазаная телега; скользкий как налим и т.д.)
5. Почему тротуары посыпают песком? (Тротуары посыпают песком, чтобы увеличить силу трения между подошвой обуви и льдом).
6. Зачем на подошвы спортивной обуви футболиста набивают кожаные шипы? (
2. Решение задач
1. С помощью динамометра равномерно перемещают брусок. Чему равна сила трения скольжения между бруском и столом, если динамометр показывает 0,5 Н?
2. На транспортере движется ящик с грузом (без скольжения). Куда направлена сила трения покоя между лентой транспортера и ящиком?
Повторение
1) Кластер по теме: «Трение»
Учащиеся составляют кластер. Проверка.
2) Работа с тестом.
Тест «Сила трения» пособие А.В. Постников «Проверка знаний учащихся по физике 7 — 8 класс», 1 вариант (отпечатанные варианты с листочками для ответов заранее заготовлены и положены на столы детей перед уроком)
Пример варианта № 1 (выбери правильный ответ)
1. Сани скатываются с горы под действием силы …, а, скатившись, останавливаются за счет силы … .
Сани скатываются с горы под действием силы …, а, скатившись, останавливаются за счет силы … .
а) трения…тяжести
б) упругости…трения
в) трения …упругости
г) тяжести…трения
2. При смазке трущихся поверхностей сила трения …
а) не изменяется
б) увеличивается
в) уменьшается
3. Совпадает ли сила трения с направлением скорости движения тела?
а) совпадает
б) направлена в сторону, противоположную скорости
4.Какие причины влияют на силу трения?
а) природа трущихся поверхностей
б) силы, прижимающие соприкасающиеся поверхности друг к другу
в) шероховатость соприкасающихся поверхностей
Рефлексия. Итог урока.
-Что нового узнали?
Мы с вами изучили темы, связанные с различным видом сил. Учащиеся третий столбик таблицы «Я узнал(а)».
Домашнее задание.
Подготовиться к контрольной работе. Тест.
1. Напишите формулу силы тяжести. | |
2. Единица измерения веса тела? | |
3. Каков вес тела массой 1 кг? | |
4. Какую величину измеряют с помощью динамометра? | |
5. Чему равна сила тяжести, массой 300 г? | |
6. Парашютист, масса которого 80 кг, равномерно движется. Чему равна сила сопротивления воздуха, действующая на него? | |
7. | |
8. Какая сила вызывает приливы и отливы в морях и океанах на Земле? | |
9. Если масса воды уменьшится в 3 раза, уменьшится ли ее вес? Как? | |
10. F1 = 3Н F2 = 5 Н Определите равнодействующую сил. |
Литература:
- http://www.bibliofond.ru/view.aspx?id=659048
Трение. Сила трения | 7 класс
Содержание
Давайте рассмотрим обычные и всем нам знакомые ситуации. Например, езду на велосипеде.
Когда велосипедист крутит педали — велосипед едет, а когда не крутит — велосипед начинает тормозить и вскоре останавливается.
Сани, скатившись с горы, постепенно теряют скорость и тоже останавливаются (рисунок 1).
Рисунок 1. Движение и остановка санокМы знаем, что причиной всякого изменения скорости движения (в данном случае уменьшения) является сила. Значит, и в рассмотренных примерах на каждое движущееся тело действовала сила.
Существуют разные уже изученные нами ранее силы: сила тяжести, сила упругости, вес тела. В приведенных выше примерах фигурировала сила трения. Именно о ней и пойдет речь на данном уроке.
Что такое сила трения?
Итак, разберем это понятие.
Сила трения — это сила, возникающая при взаимодействии двух тел и препятствующая их относительному движению.
Обозначается она буквой $F$ с индексом, то есть следующим образом: $F_{тр}$.
Взглянем на силу трения на примере движущихся саней (рисунок 2). Она направлена вдоль поверхностей соприкасающихся тел в сторону, противоположную скорости движения тела (саней) по неподвижной поверхности.
{"questions":[{"content":"Укажите правильное определение понятия <b>сила трения</b>.[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["сила, возникающая при взаимодействии двух тел и препятствующая их относительному движению","сила, возникающая при взаимодействии двух тел и способствующая их относительному движению","сила, возникающая при взаимодействии двух тел и никак не влияющая на их относительное движение"],"answer":[0]}}}]}Причины возникновения трения
В чем заключаются причины трения?
1. Шероховатость поверхностей телГладкие на ощупь тела тоже имеют неровности, бугорки и царапины.
С помощью современных лазерных микроскопов сейчас можно увидеть даже самые незаметные неровности. Например, на рисунке 3 вы можете увидеть изображение поверхность листа стали, прошедшего обработку. Для наших невооруженных глаз такой стальной лист будет казаться идеально гладким, но это не так.
Из-за этого, когда одно тело скользит или катится по поверхности другого, эти неровности цепляются друг за друга. Это создает силу, препятствующую движению.
2. Взаимное притяжение молекул соприкасающихся телДругая причина возникновения трения — взаимное притяжение молекул соприкасающихся тел. Если поверхности тел идеально гладкие, то при соприкосновении молекулы тел находятся очень близко друг к другу. В этом случае заметно проявляется притяжение между молекулами тел (рисунок 4).
Рисунок 4. Взаимное притяжение молекул при соприкосновении двух тел{"questions":[{"content":"В чем заключаются причины возникновения силы трения?[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["Шероховатость тел","Взаимное притяжение молекул соприкасающихся тел","притяжение всех тел друг к другу из-за всемирного тяготения","наличие у тел веса"],"answer":[0,1]}}}]}Изменение силы трения.
 Смазка
СмазкаСилу трения можно уменьшить во много раз, если ввести между трущимися поверхностями смазку. Ее слой разъединит поверхности трущихся тел (рисунок 5).
Как смазка влияет на силу трения?
В этом случае соприкасаются не поверхности тел, а слои смазки. Смазка же в большинстве случаев жидкая, а, как известно, трение жидких слоев меньше, чем твердых.
Например, на коньках малое трение при скольжении по льду объясняется также действием смазки. Смазкой в этом случае является вода, образующаяся между коньками и льдом тонким слоем.
Именно из-за маленького трения жидкости мы поскальзываемся на вымытом полу. А в технике благодаря меньшему трению жидкости в качестве смазки широко применяют различные масла.
youtube.com/embed/St24HbCMk2E?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>{"questions":[{"content":"Как можно уменьшить трение?[[choice-7]]","widgets":{"choice-7":{"type":"choice","options":["использовать смазку","отполировать поверхности соприкасающихся тел","плотнее прижать тела друг к другу","Сделать поверхности тел более шершавыми"],"answer":[0,1]}}}]}Виды трения
Какие виды трения вы знаете?
Если одно тело скользит по поверхности второго, то возникает особое трение — трение скольжения. Оно возникает, например, при движении саней или лыж по снегу, при скольжении коньков по льду (рисунок 6).
Если же первое тело не скользит, а катится по поверхности второго, то возникающее при этом трение называют иначе — трением качения.
Оно проявляется при перекатывании бревна или бочки по земле, при движении автомобиля, велосипеда и других транспортных средств на колесах (рисунок 7).
{"questions":[{"content":"Человек передвигает кресло, толкая его перед собой. В этот момент между креслом и полом возникает[[choice-11]]","widgets":{"choice-11":{"type":"choice","options":["трение скольжения","трения качения","трение передвижения"],"answer":[0]}}}]}Измерение силы трения
Силу трения можно не только изменить, применяя смазку, как было сказано ранее, но еще и измерить.
Как можно измерить силу трения?
Возьмем деревянный брусок и прикрепим к нему динамометр. Теперь будем его двигать, держа динамометр горизонтально (рисунок 8, а). Что покажет прибор?
На брусок в горизонтальном направлении действуют две силы. Это сила упругости пружины динамометра, направленная в cторону движения, и сила трения, направленная против движения.
Брусок движется равномерно, значит эти две силы компенсируют друг-друга (их равнодействующая равна 0). Следовательно, эти две силы равны по модулю, но имеют разные направления.
Следовательно, эти две силы равны по модулю, но имеют разные направления.
Таким образом, динамометр показывает силу, равную по модулю силе трения.
Измеряя силу, с которой динамометр действует на тело при равномерном движении, мы измеряем силу трения.
Как показать, что сила трения зависит от силы, прижимающей тело к поверхности?
Какие сани легче тащить: с грузом или без? Конечно, с грузом.
Также если мы положим на наш брусок какой-нибудь груз, и таким же образом измерим силу трения, то увидим, что она больше, чем у бруска без груза.
Чем больше сила, прижимающая тело к поверхности, тем больше возникающая при этом сила трения.
Как показать на опыте, что при равных нагрузках сила трения скольжения больше силы трения качения?
Положив брусок на круглые палочки (рисунок 8, б), мы измерим силу трения качения. Она будет меньше силы трения скольжения.
При равных нагрузках сила трения качения всегда меньше силы трения скольжения.
Именно поэтому мы повсеместно используем колесо, ведь оно помогает «заменить» силу трения скольжения на намного меньшую силу трения качения.
{"questions":[{"content":"Укажите, какие из приведенных высказываний верны.[[choice-13]]","widgets":{"choice-13":{"type":"choice","options":["Чем больше сила, прижимающая тело к поверхности, тем <b>больше</b> возникающая при этом сила трения","При равных нагрузках <b>сила трения качения</b> всегда меньше <b>силы трения скольжения</b>","При равных нагрузках <b>сила трения скольжения</b> всегда меньше <b>силы трения качения</b>","Чем больше сила, прижимающая тело к поверхности, тем <b>меньше</b> возникающая при этом сила трения"],"answer":[0,1]}}}]}Упражнение
Лыжник спускается с горы и далее скользит по горизонтальной лыжне. На рисунке 9 изобразите силу трения и точку ее приложения.
Рисунок 9. Движение лыжника со склонаПосмотреть ответ
Скрыть
На рисунке 10 изображена сила трения. Она возникает между соприкасающимися телами (лыжами и снежной поверхностью) и направлена в сторону, противоположную движению лыжника.
Она возникает между соприкасающимися телами (лыжами и снежной поверхностью) и направлена в сторону, противоположную движению лыжника.
5.1 Трение – Физика BCIT 0312 Учебник
Глава 5 Дополнительные применения законов Ньютона: трение, сопротивление и упругость
Резюме
- Обсудите общие характеристики трения.
- Описать различные виды трения.
- Рассчитайте величину статического и кинетического трения.
Трение — это сила, постоянно присутствующая вокруг нас, которая препятствует относительному движению между контактирующими системами, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
ТРЕНИЕ
Трение — это сила, противодействующая относительному движению между контактирующими системами.
Одной из самых простых характеристик трения является то, что оно параллельно поверхности контакта между системами и всегда в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением . Например, трение замедляет скольжение хоккейной шайбы по льду. Но когда объекты неподвижны, между ними может действовать статическое трение ; статическое трение обычно больше, чем кинетическое трение между объектами.
КИНЕТИЧЕСКОЕ ТРЕНИЕ
Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
Рисунок 1 представляет собой грубое графическое представление того, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для движения (кинетическое трение).
Когда между объектами нет движения, величина статического трения [латекс]\textbf{f}_{\textbf{s}}[/латекс] равна
[латекс] \boldsymbol {f _ {\ textbf {s}} \ leq \ mu _ {\ textbf {s}} \: N,} [/ латекс]
, где [латекс]\boldsymbol{\mu_{\textbf{s}}}[/латекс] — коэффициент статического трения, а [латекс]\textbf{N}[/латекс] — величина нормальной силы ( сила перпендикулярна поверхности).
ВЕЛИЧИНА СТАТИЧЕСКОГО ТРЕНИЯ
Величина статического трения[латекс]\boldsymbol{f_{\textbf{s}}}[/latex] равна
[латекс]\boldsymbol{f_{\textbf{s}}\leq \mu_{\textbf{s}}\:N,}[/latex]
, где[latex]\boldsymbol{\mu_{\textbf{s}}}[/latex] — коэффициент статического трения и[latex] ]\textbf{N}[/latex]является величиной нормальной силы.
Символ [латекс]\leq[/латекс] означает меньше или равно , подразумевая, что статическое трение может иметь минимальное и максимальное значение [латекс]\boldsymbol{\mu _{\textbf{s}}\ textbf{N}}. [/latex]Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до своего максимального предела. Как только приложенная сила превысит [латекс]\boldsymbol{f _{\textbf{s(max)}}},[/латекс] объект сдвинется. Таким образом
[/latex]Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до своего максимального предела. Как только приложенная сила превысит [латекс]\boldsymbol{f _{\textbf{s(max)}}},[/латекс] объект сдвинется. Таким образом
[латекс]\boldsymbol{f _{\textbf{s(max)}}=\mu _{\textbf{s}}\textbf{N}.}[/latex]
Когда объект движется, величина кинетического трения [латекс]\boldsymbol{f _{\textbf{k}}}[/латекс] определяется как
[латекс]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}\textbf{N},}[/latex]
, где[латекс]\жирныйсимвол{му_{\текстбф{к}}}[/латекс] — коэффициент кинетического трения. Система, в которой[latex]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}\textbf{N}}[/latex] описывается как система, в которой трение ведет себя просто .
ВЕЛИЧИНА КИНЕТИЧЕСКОГО ТРЕНИЯ
Величина кинетического трения [латекс]\boldsymbol{f _{\textbf{k}}}[/latex] определяется выражением
[латекс]\boldsymbol{f _{\textbf{k} }=\mu_{\textbf{k}}\textbf{N},}[/latex]
, где[latex]\boldsymbol{\mu_{\textbf{k}}}[/latex] — коэффициент кинетической трение.
Как видно из таблицы 1, коэффициенты кинетического трения меньше, чем их статические аналоги. То, что значения[latex]\boldsymbol{\mu}[/latex] в таблице 1 указаны только с одной или, самое большее, с двумя цифрами, является указанием на приблизительное описание трения, данное двумя приведенными выше уравнениями.
| [латекс]\textbf{Система}[/латекс] | [латекс]\textbf{Статическое трение}\boldsymbol{\mu _{\textbf{s}}}[/латекс] | [латекс]\textbf{Кинетическое трение}\boldsymbol{\mu _{\textbf{k}}}[/латекс] |
|---|---|---|
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь для льда | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Таблица 1. Коэффициенты статического и кинетического трения. Коэффициенты статического и кинетического трения. | ||
Приведенные ранее уравнения включают зависимость трения от материалов и нормальную силу. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с силой, параллельной полу), имеет массу 100 кг, то нормальная сила будет равна его весу,[латекс]\boldsymbol{\textbf{W}=mg =(100\textbf{кг})(92)=980\textbf{ N}},[/latex]перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить силу, параллельную полу, большую, чем[латекс]\boldsymbol{f _{\textbf{s(max)}}=\mu\textbf{N}=(0,45 )\:(980\textbf{ N})=440\textbf{ N}}[/latex], чтобы переместить ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н ([латекс]\boldsymbol{f _{\textbf{k}}=\mu _{\textbf{k} }\textbf{N}=(0,30)(980\textbf{ N})=290\textbf{ N}}[/latex]) будет поддерживать постоянную скорость. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
ЭКСПЕРИМЕНТ ДЛЯ ДОМА
Найдите небольшой пластиковый предмет (например, пищевой контейнер) и поставьте его на кухонный стол, слегка постукивая по нему. Теперь распылите воду на стол, имитируя легкий дождь. Что происходит теперь, когда вы нажимаете на объект того же размера? Теперь добавьте несколько капель масла (растительного или оливкового) на поверхность воды и дайте такой же кран. Что происходит сейчас? Эта последняя ситуация особенно важна для водителей, особенно после небольшого дождя. Почему?
Многие люди испытывали скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 2). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 2). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
К другим естественным смазочным материалам относятся слюна, вырабатываемая во рту для облегчения процесса глотания, и скользкая слизь, образующаяся между органами в организме, позволяющая им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания, и когда человек двигается. Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Пример 1. Упражнение на лыжах
Лыжник массой 62 кг скользит по заснеженному склону. Найдите коэффициент кинетического трения для лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой[латекс]\ textbf{N}[/latex]as[latex]\boldsymbol{f _{\textbf{k}}=\mu _{\textbf{k}}{N}}[/latex]; таким образом, коэффициент кинетического трения можно найти, если мы сможем найти нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. диаграмму «лыжник и свободное тело» на рис. 3.)
(См. диаграмму «лыжник и свободное тело» на рис. 3.)
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 1 для вощеной древесины. на снегу, но все же разумно, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой[латекс]\жирныйсимвол{м}[/латекс]скользит вниз по склону, образующему угол[латекс]\жирныйсимвол{мтета}[/латекс] с горизонтом, трение задается by[latex]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}mg\textbf{cos}\theta}. [/latex]Все объекты будут скользить по склону с постоянным ускорением под эти обстоятельства. Доказательство этого оставлено для задач и упражнений этой главы.
[/latex]Все объекты будут скользить по склону с постоянным ускорением под эти обстоятельства. Доказательство этого оставлено для задач и упражнений этой главы.
ЭКСПЕРИМЕНТ НА ЗАКАЗ
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в примере 1, кинетическое трение на склоне[латекс]\жирныйсимвол{f_{\textbf{k}}=\mu_{\textbf{k}}мг\textbf{cos}\theta}.[/latex] Компонент веса вниз по склону равен[latex]\boldsymbol{mg\textbf{sin}\theta}[/latex](см. диаграмму свободного тела на рисунке 3). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписывая это:
[латекс]\boldsymbol{f _{\textbf{k}}=Fg _{\textbf{x}}}[/latex]
[латекс]\boldsymbol{\mu _{\textbf{k}}мг \; \textbf{cos}\theta=mg \;\textbf{sin}\theta. }[/latex]
}[/latex]
Решение для[latex]\boldsymbol{\mu _{\textbf{k}}},[/latex]мы найдите, что
[латекс]\boldsymbol{\mu _{\textbf{k}}\:=}[/latex][латекс]\boldsymbol{\frac{mg \;\textbf{sin}\theta}{mg \ ;\textbf{cos}\theta}}[/latex][latex]\boldsymbol{=\:\textbf{tan}\theta.}[/latex]
Положите монету на книгу и наклоняйте ее, пока монета не скользит с постоянной скоростью по книге. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. Измерьте угол наклона относительно горизонтали и найдите[latex]\boldsymbol{\mu_{\textbf{k}}}.[/latex]Обратите внимание, что монета вообще не начнет скользить, пока угол больше[latex] ]\boldsymbol{\theta}[/latex] достигается, поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Обсудите, как это может повлиять на значение [latex]\boldsymbol{\mu _{\textbf{k}}}[/latex] и его неопределенность.
Мы обсудили, что, когда объект покоится на горизонтальной поверхности, существует нормальная сила, поддерживающая его, равная по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе.
Кроме того, простое трение всегда пропорционально нормальной силе.
УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ: СУБМИКРОСКОПИЧЕСКОЕ ОБЪЯСНЕНИЕ ТРЕНИЯ
Более простые аспекты трения, с которыми мы имели дело, — это его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
Рисунок 4 иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет крошечную часть от общей площади, поскольку соприкасаются только высокие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и оказывается, что трение пропорционально этой площади.
Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет крошечную часть от общей площади, поскольку соприкасаются только высокие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и оказывается, что трение пропорционально этой площади.
Но представление в атомном масштабе обещает объяснить гораздо больше, чем более простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. {12}}[/латекс]), и его трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления. известное с древних времен — трение.
{12}}[/латекс]), и его трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления. известное с древних времен — трение.
ИССЛЕДОВАНИЯ PHET: СИЛА И ДВИЖЕНИЕ
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте диаграмму всех сил свободного тела (включая силы тяжести и нормальные силы).
Рисунок 6. Силы и движение- Трение – контактная сила между системами, которая противодействует движению или попытке движения между ними. Простое трение пропорционально нормальной силе[латекс]\textbf{N}[/латекс], сталкивающей системы вместе.
 (Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина статического трения[латекс]\boldsymbol{f_{\textbf{s}}}[/латекс]между системами, стационарными относительно друг друга, определяется выражением
(Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина статического трения[латекс]\boldsymbol{f_{\textbf{s}}}[/латекс]между системами, стационарными относительно друг друга, определяется выражением[латекс]\boldsymbol{f _{\textbf{s}}\leq\mu\textbf{N},}[/латекс]
, где[латекс]\boldsymbol{\mu _{\textbf{s}}}[/латекс] — коэффициент статического трения, зависящий от обоих материалов.
- Кинетическая сила трения[латекс]\boldsymbol{f_{\textbf{k}}}[/латекс]между системами, движущимися друг относительно друга, определяется выражением
[латекс]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}\textbf{N},}[/latex]
, где [латекс]\boldsymbol{\mu_{\textbf{k}}}[/латекс] — коэффициент кинетического трения, который также зависит от обоих материалов.
Задачи и упражнения
1: Студент-физик готовит завтрак, когда замечает, что сила трения между его стальным шпателем и тефлоновой сковородкой составляет всего 0,200 Н. Зная коэффициент кинетического трения между двумя материалами, он быстро рассчитывает нормальную силу. Что это такое?
Зная коэффициент кинетического трения между двумя материалами, он быстро рассчитывает нормальную силу. Что это такое?
2: (a) При восстановлении двигателя своего автомобиля студент-физик должен приложить усилие 300 Н, чтобы вставить сухой стальной поршень в стальной цилиндр. Чему равна нормальная сила между поршнем и цилиндром? б) Какова величина силы, которую она должна была бы приложить, если бы стальные детали были смазаны маслом?
3: (a) Какова максимальная сила трения в коленном суставе человека, который поддерживает на этом колене 66,0 кг своей массы? (b) Во время напряженных упражнений на суставы можно воздействовать силой, в десять раз превышающей поддерживаемый вес. Какова максимальная сила трения при таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы изнашиваются, например, в результате травмы или артрита. Увеличение силы трения может привести к дальнейшему повреждению и боли. 93\textbf{ кг}}[/latex]грузовик поддерживается двумя ведущими колесами, какова величина максимального ускорения, которое он может развить на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянном кузове грузовика, скользить, если он будет двигаться с такой скоростью? (c) Решите обе задачи, предполагая, что грузовик имеет полный привод.
93\textbf{ кг}}[/latex]грузовик поддерживается двумя ведущими колесами, какова величина максимального ускорения, которое он может развить на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянном кузове грузовика, скользить, если он будет двигаться с такой скоростью? (c) Решите обе задачи, предполагая, что грузовик имеет полный привод.
6: Упряжка из восьми собак тянет нарты с вощеными деревянными полозьями по мокрому снегу (каша!). Собаки имеют среднюю массу 19,0 кг, а загруженные сани с всадником имеют массу 210 кг. (a) Рассчитайте величину ускорения, начиная с состояния покоя, если каждая собака прикладывает к снегу среднюю силу 185 Н, направленную назад. б) Чему равно ускорение саней после того, как они тронулись? (c) Для обеих ситуаций рассчитайте величину силы в сцеплении между собаками и санями.
7: Рассмотрим фигуриста массой 65,0 кг, которого толкают два других фигуриста, показанных на рис. 7. (a) Найдите направление и величину [латекс]\textbf{F}_{\textbf{tot}},[ /latex]суммарная сила, действующая на нее со стороны остальных, учитывая, что величины[latex]\boldsymbol{F_1}[/latex]и[latex]\boldsymbol{F_2}[/latex]составляют 26,4 Н и 18,6 Н соответственно. . (b) Каково ее начальное ускорение, если она изначально неподвижна и носит коньки со стальными лезвиями, направленные в направлении [латекс]\textbf{F}_{\textbf{tot}}?[/latex](c) Что ее ускорение предполагает, что она уже движется в направлении [латекс]\textbf{F}_{\textbf{tot}}?[/latex](Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между контактирующих поверхностей.)
. (b) Каково ее начальное ускорение, если она изначально неподвижна и носит коньки со стальными лезвиями, направленные в направлении [латекс]\textbf{F}_{\textbf{tot}}?[/latex](c) Что ее ускорение предполагает, что она уже движется в направлении [латекс]\textbf{F}_{\textbf{tot}}?[/latex](Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между контактирующих поверхностей.)
8: Покажите, что ускорение любого объекта вниз по склону без трения, образующему угол [латекс]\boldsymbol{\theta}[/latex]с горизонтом, равно[латекс]\boldsymbol{a =g \;\textbf{sin}\theta}.[/latex](Обратите внимание, что это ускорение не зависит от массы.)
9: Покажите, что ускорение любого объекта вниз по склону, где трение ведет себя просто (что где [латекс]\boldsymbol{f _{\textbf{k}}=\mu _{\textbf{k}}\textbf{N}}[/latex]) – [латекс]\boldsymbol{a=g(\ textbf{sin} \;\theta-\mu _{\textbf{k}}\textbf{cos} \;\theta}[/latex]). {\circ}}[/latex]с горизонталью) при следующих дорожных условиях. Предположим, что только половина веса автомобиля приходится на два ведущих колеса и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения. (Не обращайте внимания на прокатку.) (a) На сухом бетоне. (b) На мокром бетоне. (c) На льду, предполагая, что [латекс]\жирныйсимвол{\му _{\текстбф{с}}=0,100},[/латекс]то же, что и для обуви на льду. 95\textbf{ N}},[/latex]при условии, что двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. б) Какова величина силы в сцеплении между 37-м и 38-м вагонами (это сила, с которой каждый вагон действует на другой), если предположить, что все вагоны имеют одинаковую массу и что трение равномерно распределено между всеми вагонами и двигатели?
{\circ}}[/latex]с горизонталью) при следующих дорожных условиях. Предположим, что только половина веса автомобиля приходится на два ведущих колеса и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения. (Не обращайте внимания на прокатку.) (a) На сухом бетоне. (b) На мокром бетоне. (c) На льду, предполагая, что [латекс]\жирныйсимвол{\му _{\текстбф{с}}=0,100},[/латекс]то же, что и для обуви на льду. 95\textbf{ N}},[/latex]при условии, что двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. б) Какова величина силы в сцеплении между 37-м и 38-м вагонами (это сила, с которой каждый вагон действует на другой), если предположить, что все вагоны имеют одинаковую массу и что трение равномерно распределено между всеми вагонами и двигатели?
17: Рассмотрим альпиниста массой 52,0 кг на рис. 8. (a) Найдите натяжение веревки и силу, которую альпинист должен прикладывать ногами к вертикальной скале, чтобы оставаться неподвижным. Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, действующая на ее руки, незначительна. б) Каков минимальный коэффициент трения между ее туфлями и скалой?
8. (a) Найдите натяжение веревки и силу, которую альпинист должен прикладывать ногами к вертикальной скале, чтобы оставаться неподвижным. Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, действующая на ее руки, незначительна. б) Каков минимальный коэффициент трения между ее туфлями и скалой?
18: Участник зимних спортивных соревнований толкает глыбу льда весом 45,0 кг по замерзшему озеру, как показано на рис. 9(а). (a) Вычислите минимальную силу[латекс]\boldsymbol{F}[/латекс], которую он должен приложить, чтобы сдвинуть блок. б) Чему равно его ускорение после того, как оно начнет двигаться, если эта сила сохраняется?
19: Повторить упражнение 18, когда участник тянет блок льда с веревкой через плечо под тем же углом над горизонталью, как показано на рисунке 9.(б).
Рис. 9. Какой способ скольжения глыбы льда требует меньшего усилия — (а) толкание или (б) вытягивание под одним и тем же углом над горизонталью?
9. Какой способ скольжения глыбы льда требует меньшего усилия — (а) толкание или (б) вытягивание под одним и тем же углом над горизонталью?- трение
- сила, противодействующая относительному движению или попыткам движения между системами, находящимися в контакте
- кинетическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и движущихся относительно друг друга
- статическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и не движущихся относительно друг друга
- величина статического трения
- [латекс]\boldsymbol{f _{\textbf{s}}\leq\mu _{\textbf{s}}\textbf{N}},[/latex],где[латекс]\boldsymbol{\mu _{\textbf{ s}}}[/latex] — коэффициент статического трения, а [latex]\textbf{N}[/latex] — величина нормальной силы
- величина кинетического трения
- [латекс]\boldsymbol{f _{\textbf{k}}=\mu _{\textbf{k}}\textbf{N}},[/latex],где[латекс]\boldsymbol{\mu _{\textbf{k }}}[/latex]коэффициент кинетического трения 904:30
Сила трения: определение, символы и примеры
Трение — это сила, которая удерживает объекты от удаления от нас при малейшем прикосновении, как это делает шайба на столе для аэрохоккея. В этой статье мы обсудим значение силы трения, коэффициент трения с соответствующим символом, формулу трения и некоторые примеры расчета трения.
В этой статье мы обсудим значение силы трения, коэффициент трения с соответствующим символом, формулу трения и некоторые примеры расчета трения.
Сила трения – определение и значение
Сила трения – это сила, противодействующая скользящему движению одного объекта/поверхности по другому объекту/поверхности.
Если вы толкнете коробку горизонтально, то сопротивление, которое вы почувствуете, борясь с вами, будет силой трения. Трение напрямую связано с весом объекта и шероховатостью взаимодействующих поверхностей. Трение всегда действует параллельно поверхности, в направлении, противоположном скольжению, как показано на изображении ниже. Различают два вида трения: статическое и кинетическое.
Направление силы трения, Vecteezy
Статическое трение
Статическое трение — это сила, противодействующая движению, когда объект0017, а не
в движении. Представьте, что вы пытаетесь толкнуть большую тяжелую коробку. Если вы нажмете совсем немного, он вообще не сдвинется — сила трения покоя удерживает его на месте. Вы должны увеличить силу нажатия, пока он, наконец, не начнет двигаться. До этого момента статическое трение сопротивляется вашему толчку. Ровно в тот момент, когда коробка начинает двигаться, статическое трение перестает действовать, и вступает в действие кинетическое трение.
Если вы нажмете совсем немного, он вообще не сдвинется — сила трения покоя удерживает его на месте. Вы должны увеличить силу нажатия, пока он, наконец, не начнет двигаться. До этого момента статическое трение сопротивляется вашему толчку. Ровно в тот момент, когда коробка начинает двигаться, статическое трение перестает действовать, и вступает в действие кинетическое трение.Кинетическое трение
Кинетическое трение — сила, противодействующая движению объекта — это в движении. Это сила, которая заставляет объекты замедляться, иначе они будут скользить вечно. Если вы думаете о том, чтобы толкать эту большую тяжелую коробку, вы можете подумать о том, что заставить коробку двигаться труднее, чем удерживать ее в движении. Это связано с тем, что статическое трение обычно больше кинетического трения.
Трение в результате действия межатомных электрических сил
Трение является разновидностью контактной силы и, как таковое, является результатом межатомных электрических сил . В микроскопическом масштабе поверхности предметов не гладкие; они состоят из крошечных пиков и расщелин. Когда пики скользят и сталкиваются друг с другом, электронные облака вокруг атомов каждого объекта пытаются оттолкнуться друг от друга. Также могут быть молекулярные связи, которые образуются между частями поверхностей для создания адгезии, которая также борется с движением. Все эти электрические силы, вместе взятые, составляют общую силу трения, препятствующую скольжению.
В микроскопическом масштабе поверхности предметов не гладкие; они состоят из крошечных пиков и расщелин. Когда пики скользят и сталкиваются друг с другом, электронные облака вокруг атомов каждого объекта пытаются оттолкнуться друг от друга. Также могут быть молекулярные связи, которые образуются между частями поверхностей для создания адгезии, которая также борется с движением. Все эти электрические силы, вместе взятые, составляют общую силу трения, препятствующую скольжению.
Символ коэффициента трения
Разные типы поверхностей вызывают разное трение. Подумайте о том, насколько сложнее толкать ящик по бетону, чем по льду. Мы объясняем эту разницу коэффициентом трения . Коэффициент трения — безразмерное число, зависящее от шероховатости (а также других качеств) двух взаимодействующих поверхностей. Было проведено множество экспериментов для определения коэффициента трения при взаимодействии общих поверхностей.
Символ для коэффициента трения — это греческая буква mu:μ. Чтобы различать статическое трение и кинетическое трение, мы можем использовать нижний индекс «s» для статического, мкс, и «k» для кинетического, мкк.
Чтобы различать статическое трение и кинетическое трение, мы можем использовать нижний индекс «s» для статического, мкс, и «k» для кинетического, мкк.
Расчет силы трения
Трение рассчитывается по следующей формуле, где μ как коэффициент трения и FN как нормальная сила :
Ff≤μFn
Каждая сила выражается в ньютонах, Н. Эта формула показывает, что величина силы трения зависит от коэффициента трения, как мы обсуждали выше, а также от величины нормальной силы. По мере увеличения коэффициента трения или нормальной силы сила трения увеличивается. Это интуитивно понятно: когда мы толкаем коробку, толкать ее труднее, когда поверхность шероховатая, а коробка тяжелее.
Уравнение статического трения
Знак «равно или меньше» в приведенном выше общем уравнении характерен для статического трения. Это потому, что если вы толкаете коробку, а она не двигается, сила трения будет равна силе вашего толчка (поскольку без ускорения сумма сил равна нулю). Таким образом, если вы толкаете с силой 5 Н, сила трения, сопротивляющаяся движению, будет равна 5 Н; если вы нажмете 10 Н, а он все еще не двигается, сила трения будет 10 Н. Поэтому мы обычно пишем общее уравнение статического трения следующим образом:
Таким образом, если вы толкаете с силой 5 Н, сила трения, сопротивляющаяся движению, будет равна 5 Н; если вы нажмете 10 Н, а он все еще не двигается, сила трения будет 10 Н. Поэтому мы обычно пишем общее уравнение статического трения следующим образом:
Fs≤μsFn
Чтобы найти максимально возможную силу, которую вы можете приложить, не двигая коробку, или просто заставить коробку начать движение, вы должны установить силу трения, равную коэффициенту трения, умноженному на нормальную силу:
Fsmax=µsFn
Уравнение кинетического трения
Поскольку объект уже движется для применения кинетического трения, кинетическое трение не может быть меньше, чем коэффициент трения, умноженный на нормальную силу. Таким образом, уравнение кинетического трения просто следующее:
Fk=µkFn
Примеры формулы силы трения
Мы будем использовать несколько примеров, чтобы продемонстрировать, как использовать формулу трения, а также пример того, где формула не очень полезна и что делать вместо нее.
Пример 1. Сила трения о плоскую поверхность
Вы пытаетесь толкнуть 15-килограммовый ящик по ровному бетону. Коэффициент статического трения µs=0,6, а коэффициент кинетического трения µk=0,4.
Часть A
Какое усилие нужно приложить, чтобы коробка начала двигаться?
Диаграмма свободного тела для задачи 2, StudySmarter Originals
Мы хотим найти максимальную силу трения покоя, потому что она дает нам точку, в которой ящик едва начинает двигаться. Во-первых, мы рисуем диаграмму свободного тела , как на изображении выше, чтобы показать все силы, действующие на коробку. У нас есть наша толкающая сила, действующая вправо, сила трения, действующая против нее, — влево, гравитационная сила (вес), действующая вниз, и нормальная сила, действующая вверх. Поскольку коробка не ускоряется и в вертикальном направлении нет других сил, нормальная сила равна силе гравитации, которая представляет собой массу, умноженную на ускорение свободного падения. Мы можем подставить коэффициент статического трения и нормальную силу в уравнение максимального статического трения:
Мы можем подставить коэффициент статического трения и нормальную силу в уравнение максимального статического трения:
Fsmax=µsFnFsmax=0,6·15 кг·9,81 м/с2Fsmax=88,3 Н
Поскольку никакие другие силы не действуют на ящик, сила, которую вы должны приложить к ящику, равна найденной нами силе трения, поэтому вы нужно будет толкать с силой 88,3 Н.
Часть B
Если вы толкнете ту же коробку с силой 50 Н, какова будет сила трения?
Поскольку 50N меньше 88,3N, необходимых для перемещения ящика, ускорение равно нулю, а сумма сил будет равна нулю. Так как кроме вашего толчка и силы трения других сил нет, то сила трения тоже будет равна 50Н.
Часть C
Если вы толкаете коробку с силой 100 Н, какова сила трения?
Поскольку вы толкнули сильнее, чем сила, необходимая для перемещения ящика, теперь мы хотим использовать коэффициент кинетического трения, чтобы найти кинетическую силу трения:
Fk=µkFnFk=0,4·15 кг·9,81 м/с2Fk=58,9 N
Пример 2.
 Сила трения на наклонной плоскости
Сила трения на наклонной плоскостиA17kgbox неподвижно сидит на наклонной плоскости, как показано на рисунке ниже. Тета 30°, коэффициент трения μ=0,7.
Коробка на наклонной плоскости, StudySmarter Originals
Часть A
Какая сила трения действует на коробку?
В этом примере мы не будем использовать формулу силы трения. Поскольку коробка не движется, сила трения покоя может быть от 0 до макс. Если мы попытаемся использовать формулу, мы получим число для максимальной силы, но не будем знать, какова текущая сила трения. Вместо этого нам нужно использовать диаграмму свободного тела и Второй закон Ньютона 9.0018 (ΣF→=ma→) для определения силы трения. Мы наклоним систему координат, чтобы она соответствовала большинству сил, и воспользуемся принципом суперпозиции сил , чтобы разделить гравитационную силу на компоненты x и y для согласования с новой системой координат. Наша диаграмма свободного тела с этими настройками показана на изображении ниже.
Диаграмма свободного тела для примера 2 с новой системой координат и гравитационной силой, разделенной на компоненты x и y, StudySmarter Originals
Нормальная сила всегда направлена перпендикулярно поверхности, а гравитационная сила (вес) всегда направлена прямо вниз.
Поскольку мы хотим найти силу трения, которая находится на новой оси x, мы применим уравнение второго закона Ньютона в направлении x. Поскольку коробка не ускоряется, сумма сил в направлении x равна нулю:
-Ff+Fgx=0
Используйте тригонометрию, чтобы разбить гравитационную силу на компонент x:
Fgx=Fgsinθ
Заменяем Fg:
Ff=mgsinθ
Затем мы можем подставить наши числа:
Ff=17 кг·9,81 м/с2·sin(30)Ff=83,4 Н
Часть B
Какое усилие требуется чтобы начать двигать коробку вниз по склону?
Теперь мы можем вернуться к использованию формулы трения, так как мы хотим знать максимальное статическое трение: гравитационная сила:
Fn=FgcosθFsmax=0,7·17 кг·9,81 м/с2·cos(30)Fsmax=101,1 Н
На этот раз у нас есть сила помимо приложенной силы и силы трения; нам также необходимо учитывать гравитационную силу, действующую в направлении x. Мы можем использовать второй закон Ньютона в направлении x, и мы все равно можем предположить, что ускорение равно нулю, потому что оно еще не начало движение. Выбрав наклон вверх (слева) как отрицательный, а вниз (справа) как положительный, получим следующее:0,81 м/с2·sin(30)F=17,7 Н
Мы можем использовать второй закон Ньютона в направлении x, и мы все равно можем предположить, что ускорение равно нулю, потому что оно еще не начало движение. Выбрав наклон вверх (слева) как отрицательный, а вниз (справа) как положительный, получим следующее:0,81 м/с2·sin(30)F=17,7 Н
Сила трения — ключевые выводы
- Сила трения препятствует скольжению между объектом и поверхностью.
- Трение действует параллельно поверхности в направлении, противоположном движению (или попытке движения).
- Трение является результатом межатомных электрических сил. Электронные облака между шероховатыми частями поверхностей могут отталкиваться друг от друга, а адгезия может пытаться удерживать поверхности от движения, но все это складывается в силу трения, препятствующую движению.
- Общая формула трения Ff≤μFn.
- Статическое трение препятствует скольжению, когда объекты не движутся, и может быть меньше, чем коэффициент статического трения, умноженный на нормальную силу.

- Кинетическое трение препятствует скольжению при движении объектов и всегда равно коэффициенту кинетического трения, умноженному на нормальную силу.
5.1 Трение — Колледж физики 2e
Цели обучения
К концу этого раздела вы сможете:
- Обсудите общие характеристики трения.
- Описать различные виды трения.
- Рассчитайте величину статического и кинетического трения.
Трение — это постоянно присутствующая вокруг нас сила, которая противодействует относительному движению между соприкасающимися поверхностями, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
Трение
Трение – это сила, противодействующая относительному движению между соприкасающимися поверхностями.
Одной из самых простых характеристик трения является то, что оно параллельно поверхности контакта между поверхностями и всегда в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две поверхности соприкасаются и движутся относительно друг друга, то трение между ними называется кинетическим трением. Например, трение замедляет скольжение хоккейной шайбы по льду. Но когда объекты неподвижны, статическое трение может действовать между ними; статическое трение обычно больше, чем кинетическое трение между поверхностями.
Кинетическое трение
Если две поверхности соприкасаются и движутся друг относительно друга, то трение между ними называется кинетическим трением.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
Рис. 5.2 является грубым графическим представлением того, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Рисунок
5.2
Силы трения, такие как ff, всегда препятствуют движению или попытке движения между соприкасающимися поверхностями. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Для того чтобы объект двигался, он должен подняться туда, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что объясняет, например, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.
Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что объясняет, например, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.
Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для движения (кинетическое трение).
При отсутствии движения между объектами величина трения покоя fsfs равна
fs≤μsN,fs≤μsN,
5.1
где μsμs — коэффициент трения покоя, а NN — величина нормальной силы (сила, перпендикулярная поверхности).
Величина статического трения
Величина трения покоя fsfs равна
fs≤μsN,fs≤μsN,
5,2
где μsμs — коэффициент трения покоя, а NN — величина нормальной силы.
Символ ≤≤ означает, что меньше или равно , подразумевая, что трение покоя может иметь минимальное и максимальное значение µsNµsN. Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела. Как только приложенная сила превысит fs(max)fs(max), объект начнет двигаться. Таким образом
fs(max)=µsN.fs(max)=µsN.
5.3
Когда объект движется, величина кинетического трения fkfk определяется как
fk=µkN, fk=µkN,
5.4
, где µkµk — коэффициент кинетического трения. Система, в которой fk=µkNfk=µkN, описывается как система, в которой трение ведет себя просто .
Величина кинетического трения
Величина кинетического трения fkfk определяется как
fk=µkN,fk=µkN,
5,5
где μkμk — коэффициент кинетического трения.
Как видно из Таблицы 5.1, коэффициенты кинетического трения меньше, чем их статические аналоги. То, что значения μμ в таблице 5.1 указаны только с одной или, самое большее, с двумя цифрами, указывает на приблизительное описание трения, данное двумя приведенными выше уравнениями.
| Система | Статическое трение мкс мкс | Кинетическое трениеμkμk |
|---|---|---|
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь для льда | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,04 | 0,02 |
Стол
5. 1
Коэффициенты статического и кинетического трения
1
Коэффициенты статического и кинетического трения
Приведенные ранее уравнения включают зависимость трения от материалов и нормальной силы. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу, W=mg=(100 кг)(90,80 м/с2)=980 NW=мг=(100 кг)(9,80 м/с2)=980 Н, перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить параллельно полу силу, превышающую
fs(max)=µsN=0,45(980N)=440Nfs(max)=µsN=0,45(980N)=440Nдля перемещения ящика. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н
(fk=мкН=0,30980Н=290Нfk=мкН=0,30980Н=290Н)
будет поддерживать его движение с постоянной скоростью. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Коэффициент трения зависит от двух соприкасающихся поверхностей.
Домашний эксперимент
Найдите небольшой пластиковый предмет (например, пищевой контейнер) и поставьте его на кухонный стол, слегка постукивая по нему. Теперь распылите воду на стол, имитируя легкий дождь. Что происходит теперь, когда вы нажимаете на объект того же размера? Теперь добавьте несколько капель масла (растительного или оливкового) на поверхность воды и дайте такой же кран. Что происходит сейчас? Эта последняя ситуация особенно важна для водителей, особенно после небольшого дождя. Почему?
Многие люди испытывают скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 5.3). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 5.3). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Рисунок 5.3 Искусственная замена коленного сустава — это процедура, которая проводится уже более 20 лет. На этом рисунке мы видим послеоперационные рентгеновские снимки замены правого коленного сустава. (кредит: Майк Бэрд, Flickr)
Другие природные смазки включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания , и когда человек двигается. Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Пример 5.1
Упражнение на лыжах
Лыжник массой 62 кг скользит по заснеженному склону. Найдите коэффициент кинетического трения для лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой
NN как fk=µkNfk=µkN; таким образом, коэффициент кинетического трения можно найти, если мы сможем найти нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. диаграмму «лыжник и свободное тело» на рис. 5.4.)
5.4.)
Рисунок 5.4 Движение лыжника и трение параллельны склону, поэтому удобнее всего проецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). NN (нормальная сила) перпендикулярна склону, а ff (трение) параллельна склону, но ww (вес лыжника) имеет компоненты по обеим осям, а именно w⊥w⊥ и В//В//. NN равно по модулю w⊥w⊥, поэтому движение перпендикулярно склону отсутствует. Однако ff меньше W//W// по величине, так что ускорение вниз по склону (вдоль x оси).
То есть
N=w⊥=wcos25º=mgcos25º.N=w⊥=wcos25º=mgcos25º.
5,6
Подставив это в наше выражение для кинетического трения, мы получим
fk=µkmgcos25º, fk=µkmgcos25º,
5,7
, которое теперь можно решить для коэффициента кинетического трения µkµk.
Решение
Решение для µkµk дает
µk=fkN=fkwcos25º=fkmgcos25º. µk=fkN=fkwcos25º=fkmgcos25º.
µk=fkN=fkwcos25º=fkmgcos25º.
5,8
Подставляя известные значения в правую часть уравнения,
мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082.мкк=45,0 Н(62 кг)(9,80 м/с2)(0,906)=0,082.
5,9
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но все же приемлем, поскольку значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой мм скользит по склону, образующему угол θθ по горизонтали трение определяется формулой fk=µkmgcosθfk=µkmgcosθ. В этих условиях все объекты будут скользить вниз по склону с постоянным ускорением. Доказательство этого оставлено для задач и упражнений этой главы.
Домашний эксперимент
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в примере 5.1, кинетическое трение на склоне fk=µkmgcosθfk=µkmgcosθ. Компонент веса вниз по склону равен mgsinθmgsinθ (см. диаграмму свободного тела на рис. 5.4). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписывая это:
Как показано в примере 5.1, кинетическое трение на склоне fk=µkmgcosθfk=µkmgcosθ. Компонент веса вниз по склону равен mgsinθmgsinθ (см. диаграмму свободного тела на рис. 5.4). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Выписывая это:
fk=mgxfk=mgx
5.10
µkmgcosθ=mgsinθ.µkmgcosθ=mgsinθ.
5.11
Решая μkμk, находим, что
μk=mgsinθmgcosθ=tanθ.μk=mgsinθmgcosθ=tanθ.
5.12
Положите монету на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. Измерьте угол наклона относительно горизонтали и найдите µkµk. Обратите внимание, что монета вообще не начнет скользить, пока не будет достигнут угол, больший, чем θθ, поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Обсудите, как это может повлиять на значение µkµk и его неопределенность.
Обсудите, как это может повлиять на значение µkµk и его неопределенность.
Мы обсудили, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе.
Установление связей: субмикроскопические объяснения трения
До сих пор рассматривались более простые аспекты трения — его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
На рис. 5.5 показана одна макроскопическая характеристика трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет крошечную часть от общей площади, поскольку соприкасаются только высокие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и оказывается, что трение пропорционально этой площади.
Рисунок 5,5 Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь. Когда есть большая нормальная сила в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.
Но представление в атомном масштабе обещает объяснить гораздо больше, чем простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рис. 5.6 показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое будет обсуждаться далее в этой главе. Изменение напряжения сдвига заметно (более чем в 10121012 раз).
) и трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рис. 5.6 показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое будет обсуждаться далее в этой главе. Изменение напряжения сдвига заметно (более чем в 10121012 раз).
) и трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
Рисунок
5. 6
Наконечник зонда деформируется вбок под действием силы трения, когда зонд тащит по поверхности. Измерения того, как сила меняется для разных материалов, дают фундаментальное представление об атомной природе трения.
6
Наконечник зонда деформируется вбок под действием силы трения, когда зонд тащит по поверхности. Измерения того, как сила меняется для разных материалов, дают фундаментальное представление об атомной природе трения.
Исследования ФЕТ
Силы и движение
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте диаграмму всех сил свободного тела (включая силы тяжести и нормальные силы).
Трение: объяснение, обзор и примеры
Вы, наверное, уже слышали термин «трение». Это может вызвать образ скольжения по льду или выяснения того, как высоко вы можете наклонить свою папку, прежде чем карандаш скатится. Как оказалось, на самом деле это два разных типа трения: первое — кинетическое трение, а второе — статическое трение. В этой части мы узнаем о типах трения, роли коэффициента трения и о том, как использовать формулу силы трения.
В этой части мы узнаем о типах трения, роли коэффициента трения и о том, как использовать формулу силы трения.
Что мы рассматриваем
Что такое трение?Трение — это то, с чем вы, вероятно, уже знакомы, и у вас может быть какое-то его рабочее определение. В физике трение определяется как контактная сила, противодействующая движению. Контактная сила — это сила, которая требует соприкосновения объектов. Сопротивление движению может означать одно из двух: предотвращение начала движения чего-либо или замедление чего-либо, если оно уже движется. Это два отдельных типа трения.
Статическое и кинетическое трение
Статическое трение — это тип трения, который препятствует движению объекта. Кинетическое трение — это тип трения, который замедляет уже движущийся объект. Разница между статическим и кинетическим трением заключается в том, что кинетическое трение возникает, когда что-то скользит. Вероятно, вы можете вспомнить несколько разных примеров из своей жизни, связанных с этими различными типами трений, — возможно, вы даже начинаете понимать, насколько они важны. Без трения вы не сможете удержать телефон, малейшее прикосновение отправит любой предмет, скользящий по столу, на пол, и вы даже не сможете ходить.
Без трения вы не сможете удержать телефон, малейшее прикосновение отправит любой предмет, скользящий по столу, на пол, и вы даже не сможете ходить.
Теперь у нас есть рабочее определение двух типов трения, и мы немного знаем, когда их применять. Но есть еще две вещи, которые нам нужно знать, прежде чем мы сможем начать вычислять силы трения. Нам нужно знать, что такое коэффициент трения, и нам нужно точно знать, когда использовать каждый тип трения.
Что такое коэффициент трения?
Коэффициент трения — это константа, которая помогает нам понять величину силы трения, которую две поверхности прикладывают при движении или попытке пересечь друг друга. Обычно это некоторое значение между нулем и единицей (хотя в крайних случаях оно может быть и выше), которое, по сути, говорит нам, насколько велика будет сила трения по сравнению с нормальной силой. Более высокие коэффициенты трения соответствуют более высоким силам трения. Коэффициент трения изменяется в каждой ситуации и при каждом типе трения. В зависимости от ситуации, в которой вы находитесь, вы будете рассматривать коэффициент статического трения или коэффициент кинетического трения.
Коэффициент трения изменяется в каждой ситуации и при каждом типе трения. В зависимости от ситуации, в которой вы находитесь, вы будете рассматривать коэффициент статического трения или коэффициент кинетического трения.
Это может показаться странным и запутанным, но у вас тоже есть некоторый опыт в этом. Например, многие люди хранят чехлы на своих телефонах, потому что стеклянная подложка смартфонов имеет более низкий коэффициент статического трения, чем резиновый чехол. Так телефон легче выскользнет из руки, чем чехол. Если вы когда-нибудь пробовали передвигать большой предмет мебели по полу, то, вероятно, у вас есть некоторый опыт в том, зачем нужны оба коэффициента. Вы когда-нибудь замечали, что обычно легче заставить что-то двигаться, чем заставить этот же объект двигаться? Это связано с тем, что коэффициент статического трения (сила, удерживающая объект на месте) обычно выше, чем коэффициент кинетического трения (сила, действующая на движущийся объект).
Таблица общих коэффициентов трения
Позже мы более подробно рассмотрим, как найти коэффициент трения. А пока вот несколько общих примеров как коэффициента статического трения, так и коэффициента кинетического трения, а также то, как эти два значения имеют тенденцию различаться.
А пока вот несколько общих примеров как коэффициента статического трения, так и коэффициента кинетического трения, а также то, как эти два значения имеют тенденцию различаться.
| Система трения | Коэффициент статического трения | Коэффициент кинетического трения |
| Rubber on dry concrete | 1.0 | 0.7 |
| Rubber on wet concrete | 0.7 | 0.5 |
| Metal on wood | 0.5 | 0.3 |
| Shoes on wood | 0.9 | 0,7 |
| Обувь на льду | 0,1 | 0,03 |
, когда используете статическое трение против кинетического трения
. Коэффициент фрикции. Обычно мы используем статическое трение, когда что-то неподвижно, и кинетическую энергию, когда что-то движется. Однако вы не можете думать просто о чем-то движущемся, потому что если объект катится по поверхности, то никакая отдельная часть этого объекта не скользит по земле. Если объект скользит, мы имеем дело с кинетическим трением. Вы можете подумать, что это небольшая разница, но представьте, если бы вы использовали неправильный коэффициент при проектировании частей автомобиля. В такой ситуации, если ваши цифры будут правильными, это может предотвратить возникновение серьезных проблем. Итак, мы используем кинетическое трение, когда молекулы одного объекта будут скользить мимо молекул другого, и мы используем статическое трение в случаях, когда отдельные молекулы неподвижны друг относительно друга.
Если объект скользит, мы имеем дело с кинетическим трением. Вы можете подумать, что это небольшая разница, но представьте, если бы вы использовали неправильный коэффициент при проектировании частей автомобиля. В такой ситуации, если ваши цифры будут правильными, это может предотвратить возникновение серьезных проблем. Итак, мы используем кинетическое трение, когда молекулы одного объекта будут скользить мимо молекул другого, и мы используем статическое трение в случаях, когда отдельные молекулы неподвижны друг относительно друга.
Как и все в физике, у нас есть уравнение, позволяющее вычислить силу трения в любой ситуации. Хотя существует два разных типа трения, на самом деле вам нужно запомнить только одно уравнение:
| Формула трения F_{трение}= \mu F_{N} |
Здесь F_{трение} просто сообщает нам, что сила, которую мы рассчитываем, является силой трения, \mu — коэффициент трения, а N — нормальная сила. Теперь вы можете задаться вопросом, если есть только одно уравнение, как вы узнаете, какой коэффициент трения использовать? Ответ заключается в том, что решение часто зависит от вас.
Теперь вы можете задаться вопросом, если есть только одно уравнение, как вы узнаете, какой коэффициент трения использовать? Ответ заключается в том, что решение часто зависит от вас.
Как только вы определите, какой тип трения вы используете, вы можете добавить нижний индекс к коэффициенту трения, чтобы узнать, с каким из них вы работаете. Обычно коэффициент статического трения обозначается как \mu_{s}, а коэффициент кинетического трения обозначается как \mu_k. Теперь, когда мы знаем уравнение трения и как обозначить, с каким типом трения мы работаем, давайте приступим к решению некоторых задач.
Пример: как рассчитать силу трения
Тяжелый ящик толкают по заводскому полу. Нормальная сила, действующая на коробку, равна 50\text{ Н}, коэффициент кинетического трения равен 0,3, а коэффициент трения покоя равен 0,5. Чему равна сила трения о коробку?
Шаг 1: Определение типа трения Присутствует Нам были даны коэффициенты для обоих типов трения, но нам нужен только один. В данном случае наш ящик толкается, что подразумевает скользящее движение. Итак, нам нужно будет использовать коэффициент кинетическое трение для этой задачи.
В данном случае наш ящик толкается, что подразумевает скользящее движение. Итак, нам нужно будет использовать коэффициент кинетическое трение для этой задачи.
Теперь, когда мы знаем, с каким типом трения мы работаем, мы можем приступить к выполнению наших обычных шагов по решению проблемы, извлекая соответствующую информацию из проблемы.
- F_{N}=50\text{ N}
- \mu_{k}=0,3
В этом случае мы ищем силу трения, поэтому цель может быть записана как:
- F_{f}=\text{?}
Чтобы решить эту задачу, нам понадобится только наше уравнение трения. Мы заменим коэффициент кинетического трения, чтобы уравнение соответствовало вопросу, на который мы пытаемся ответить.
- F_{f}=\mu_{k}F_{N}
F_{f}=\mu_{k}F_{N}
F_{f}=0,3 \cdot 50\text{ Н}
F_{f}=15\text{N}
Пример: Как рассчитать коэффициент трения
Тот же самый ящик останавливается на том же заводском этаже. Нормальная сила, действующая на ящик, по-прежнему равна 50\text{ Н}, а сила трения на ящике теперь равна 25\text{ Н}. Каков коэффициент трения между коробкой и заводским полом?
Нормальная сила, действующая на ящик, по-прежнему равна 50\text{ Н}, а сила трения на ящике теперь равна 25\text{ Н}. Каков коэффициент трения между коробкой и заводским полом?
Вопрос остается открытым, поэтому мы можем искать коэффициент кинетического или статического трения. Поскольку наш ящик покоится, скользящего движения нет, и мы знаем, что будем искать коэффициент трения покоя .
Шаг 2. Определите, что вы знаетеВ этом случае мы ищем коэффициент статического трения, поэтому цель может быть записана как:
- \mu_{s}=\text{?}
Чтобы решить эту задачу, нам понадобится только наше уравнение трения. Мы заменим коэффициент статического трения, чтобы уравнение соответствовало вопросу, на который мы пытаемся ответить.
- F_{f}=\mu_{s}F_{N}
На этот раз мы не будем искать силу трения, но на следующем шаге мы изменим это уравнение.
Начнем с изменения нашего уравнения для определения коэффициента статического трения.
F_{f}=\mu_{s}F_{N}
\mu_{s}=\dfrac{F_{f}}{F_{N}}
Теперь мы подставим наши числа и начнем решать.
\mu_{s}=\dfrac{25\text{N}}{50\text{N}}
\mu_{s}=0,5
Обзор эксперимента: как найти коэффициент трения Теперь, когда вы знаете немного больше о трении и о том, как его рассчитать, вам может быть интересно, как мы измеряем силы трения и откуда вообще берутся коэффициенты трения. Ответ, как и многие вещи в науке, — это эксперимент. Во время эксперимента в лаборатории трения у вас есть объект или объекты, массу которых вы знаете (что позволяет вам рассчитать нормальную силу, действующую на этот объект). Отсюда вы можете понять, как измерить силу, необходимую для приведения неподвижного объекта в движение (измерение статического трения) или для удержания объекта в движении с постоянной скоростью (измерение кинетического трения). Измерение вашей силы трения вместе с нормальной силой на вашем объекте позволяет вам построить график, подобный приведенному ниже.
Измерение вашей силы трения вместе с нормальной силой на вашем объекте позволяет вам построить график, подобный приведенному ниже.
График зависимости силы трения от нормальной силы
На приведенном выше графике показана зависимость силы трения от нормальной силы, которая показывает силу трения по оси Y и нормальную силу по оси X. Это график, который вы могли бы построить, выполняя лабораторную работу по коэффициенту трения. Действительно важной и интересной частью этого графика является наклон. Если у вас есть правильное программное обеспечение, оно автоматически создаст линию тренда и предоставит вам наклон этой линии, как здесь.
Нахождение коэффициента трения с уклоном
Если вы помните, как вычислять наклон, вы знаете, что это фактически изменение значения y, деленное на изменение значения x. Итак, наклон этой линии здесь:
\text{slope}=\dfrac{\text{изменение силы трения}}{\text{изменение нормальной силы}}
Если бы мы взглянули на наше уравнение для силы трения, оно было бы таким:
\text{коэффициент трения}=\dfrac{\text{сила трения}}{\text{нормальная сила}}
Хотя наклон линии смотрит на изменение сил, в любой момент времени эти два уравнения будут практически одинаковыми. Это становится еще более очевидным, если смотреть на вещи в формате пересечения наклона, как показано ниже.
Это становится еще более очевидным, если смотреть на вещи в формате пересечения наклона, как показано ниже.
| y-value | slope | x-value | |
| y | = | m | x |
| F_{friction} | = | \мю | F_{N} |
Независимо от того, как вы это доказываете, наклон линии, созданной путем измерения силы трения на объекте относительно нормальной силы на этом объекте, эквивалентен коэффициенту трения между этими двумя материалами. Это верно для нахождения обоих типов трения.
Трение на наклонной плоскости Теперь, когда у нас есть четкое представление о трении на плоской поверхности, давайте посмотрим на что-то, движущееся вдоль или сидящее на наклонной плоскости. Вы действительно можете провести эксперимент с этим прямо сейчас. Возьмите любой небольшой предмет (стикеры, ручку, ластик, ключи и т. д.) и что-то плоское, что вы можете поднять за один конец, чтобы создать наклонную плоскость (книга, блокнот, блокнот, телефон и т. д.). .). Теперь поместите меньший объект на плоскую поверхность и медленно поднимайте одну сторону плоской поверхности, чтобы создать наклонную плоскость со все большим и большим углом. Объект сразу начал соскальзывать? Возможно нет. Вы должны были достичь определенной высоты, прежде чем это произошло, но почему? Ответ на этот вопрос, конечно же, заключается в трении.
Возьмите любой небольшой предмет (стикеры, ручку, ластик, ключи и т. д.) и что-то плоское, что вы можете поднять за один конец, чтобы создать наклонную плоскость (книга, блокнот, блокнот, телефон и т. д.). .). Теперь поместите меньший объект на плоскую поверхность и медленно поднимайте одну сторону плоской поверхности, чтобы создать наклонную плоскость со все большим и большим углом. Объект сразу начал соскальзывать? Возможно нет. Вы должны были достичь определенной высоты, прежде чем это произошло, но почему? Ответ на этот вопрос, конечно же, заключается в трении.
Диаграмма свободного тела с трением
Трение на наклонной плоскости работает так же, как трение на плоской поверхности с одним ключевым отличием. Угол наклонной плоскости повлияет на величину нормальной силы, которая, в свою очередь, повлияет на величину силы трения. Если вам нужна полная информация о том, как работают силы на наклонной плоскости, вы можете проверить здесь, но диаграмма ниже говорит нам все, что нам нужно знать прямо сейчас.
Угол наклона самолета эквивалентен углу между силой тяжести и нормальной силой. Значение этого заключается в том, что если наклон изменяется, то изменяется и этот угол, что приводит к изменению нормальной силы, а также силы трения. На приведенной выше диаграмме показана сила кинетического трения, но она работает одинаково для обоих типов трения.
Обычно для расчета нормальной силы используется уравнение F_{N}=mg. Однако в этом случае, поскольку у нас есть этот угол, нормальная сила будет F_{N}=mg\cos(\theta). Если вам не нравится тригонометрия и вы хотите просмотреть ее, это может быть хорошим ресурсом. Имея все это в виду, мы эффективно представляем уравнение для силы трения на наклонной плоскости как:
F_{f}=\mu F_{N}=\mu mg\cos{\theta}
Примечание: Могут быть случаи, когда вы хотите взять синус угла вместо косинуса угла. Мы будем придерживаться ситуаций, когда косинус угла будет работать всегда, но будьте готовы проанализировать проблемы, с которыми вы сталкиваетесь в классах, для которых угол будет работать лучше всего. 9{\circ} над горизонталью. Коэффициент кинетического трения между ящиком и плоскостью равен 0,2, а коэффициент трения покоя равен 0,7. Чему равна сила трения о коробку?
9{\circ} над горизонталью. Коэффициент кинетического трения между ящиком и плоскостью равен 0,2, а коэффициент трения покоя равен 0,7. Чему равна сила трения о коробку?
Нам были даны коэффициенты для обоих типов трения, но нам нужен только один. В этом случае наш ящик находится в состоянии покоя, поэтому движения нет. Итак, нам нужно будет использовать коэффициент трения покоя для этой задачи. 9{2}
Шаг 3. Определение цели- F_{f}=\text{?}
Чтобы решить эту проблему, нам понадобится только эта проблема. наше уравнение трения на наклонной плоскости. Мы подставим коэффициент статического трения, чтобы уравнение соответствовало вопросу, на который мы пытаемся ответить.
- F_{f}=\mu_{s}mg\cos\theta
F_{f}=\mu_{s}mg\cos\theta
9{\circ} над горизонталью. Человек имеет массу 100\text{ кг} и испытывает силу трения 30\text{ Н}. Чему равен коэффициент кинетического трения между санями и снегом?
Человек имеет массу 100\text{ кг} и испытывает силу трения 30\text{ Н}. Чему равен коэффициент кинетического трения между санями и снегом?
В этом случае нам сказали, что человек скатывается со снежного холма, что подразумевает скользящее движение. Итак, для этой задачи мы будем искать коэффициент кинетического трения .
Шаг 2. Определите, что вы знаете 9{2} Шаг 3. Определите цель- \mu_{k}=\text{?}
Хотя сейчас мы ищем коэффициент кинетическое трение вместо силы кинетического трения, мы начнем с того же уравнения и изменим его на следующем шаге.
- F_{f}=\mu_{k}mg\cos\theta
Начнем с изменения уравнения для определения коэффициента кинетического трения: 9{\ круг})}
\mu_{k}=0,04
Заключение Из этой статьи вы узнаете все, что вам нужно знать о трении, чтобы пройти любой курс физики в средней школе. Оба типа трения, статическое и кинетическое трение, формируют мир, в котором мы живем. В течение дня вы сможете найти бесчисленное количество примеров этой силы в своей жизни. Даже способность ходить или передвигаться в инвалидной коляске зависит от наличия трения. Эта сила будет продолжать проявляться в вашем физическом путешествии и возникнет, если вы решите продолжить какую-либо инженерную работу позже.
Оба типа трения, статическое и кинетическое трение, формируют мир, в котором мы живем. В течение дня вы сможете найти бесчисленное количество примеров этой силы в своей жизни. Даже способность ходить или передвигаться в инвалидной коляске зависит от наличия трения. Эта сила будет продолжать проявляться в вашем физическом путешествии и возникнет, если вы решите продолжить какую-либо инженерную работу позже.
Сила трения – определение, формула, типы, примеры и часто задаваемые вопросы
Сила трения – это противодействующая сила, когда две поверхности соприкасаются друг с другом, чтобы двигаться либо в одном, либо в противоположных направлениях. Поскольку трение — это сила, которая противодействует или сопротивляется движению объекта, который вступает в контакт и скользит друг относительно друга. Следовательно, сила трения является контактной силой. Трение – это сила, всегда противодействующая движению. Силы трения в основном зависят от текстуры поверхности объектов, которые соприкасались друг с другом, и от силы, действующей на них. Силы трения подразделяются на четыре различных типа: трение качения, скольжения, статическое и кинетическое трение. Еще одним важным видом трения является жидкостное трение.
Силы трения подразделяются на четыре различных типа: трение качения, скольжения, статическое и кинетическое трение. Еще одним важным видом трения является жидкостное трение.
Сила трения
Сила трения — это сила, возникающая, когда две поверхности соприкасаются друг с другом и скользят друг по другу.
Эти силы в основном зависят от шероховатости поверхности и величины силы, необходимой при их объединении. На объем силы трения влияют угол и положение объекта. Силы притяжения являются основной причиной трения между объектами.
Сила трения между двумя поверхностями всегда действует противоположно приложенной силе, как показано на рисунке выше. Текстура поверхности и величина силы, прижимающей их друг к другу, оказывают большое влияние на силу трения. Положение и угол объекта влияют на силу трения. Сила трения равна массе предмета, когда он прижат к другому предмету. Когда мы прижимаем предмет к поверхности другого предмета, сила трения увеличивается и превышает вес толкаемого предмета.
Максимальную силу трения, действующую на объект со стороны поверхности, можно легко рассчитать по следующей формуле:
- µ — коэффициент трения, а
- F норма относится к нормальной силе, действующей на указанный объект, заданной как F = mg (где m — масса, а g — ускорение свободного падения).
Единица силы трения
- Единицей силы трения является кг.м/с 2 или Ньютон (Н).
- Размерная формула силы трения [M L T -2 ].
Факторы, влияющие на силу трения
Величина силы трения зависит от следующих факторов, перечисленных ниже:
- Текстуры поверхности и сила, сталкивающая их вместе, оказывают большое влияние на эти силы.
- Величина силы трения зависит от положения и угла наклона объекта.
- Сила трения будет равна весу объекта, если его положить на другой объект.
- Сила трения увеличится и превысит вес предмета, если предмет будет прижат к поверхности.

Однако сила трения между двумя поверхностями не зависит от фактической площади контакта.
Виды сил трения
В зависимости от типа материала, находящегося в контакте, выделяют два основных типа сил трения:
Сухое трение
Когда два твердых тела вступают в контакт, как во время их движения (кинетическое трение), так и когда их нет, возникает реакция, известная как сухое трение (статическое трение).
Нормальная сила, приложенная между твердыми телами, определяет величину трения как в статическом, так и в кинетическом отношении. Различные коэффициенты трения используются для представления взаимодействия различных материалов. Отсюда следует, что при заданной нормальной силе между двумя веществами одни вещества оказывают большее сопротивление движению, чем другие.
В зависимости от типа движения между двумя объектами сила трения может быть классифицирована как:
Статическая сила трения – Статическое трение представляет собой величину сопротивления, которая существует между объектом и поверхностью, на которой он стоит.
Основное условие перемещения объекта, покоящегося на поверхности, заключается в приложении силы, превышающей силу трения, создаваемую поверхностью. Другое его название — , предельная сила трения . Статическое трение включает в себя такие вещи, как ходьба, скалолазание и другие действия.
Сила кинетического трения — Когда коробка скользит, возникает кинетическое трение за пределами точки прихода движения. Когда есть кинетическое трение, нормальная сила между коробкой и поверхностью, умноженная на кинетический коэффициент трения, будет равна величине силы трения, противодействующей движению. Хотя он также опирается на два соприкасающихся объекта, кинетический коэффициент трения почти всегда меньше статического коэффициента.
Сила трения качения – Трение качения определяется как сопротивление, возникающее, когда одно тело вынуждено катиться по поверхности другого. По сравнению с кинетическим трением оно значительно меньше.
Некоторые из применений, в которых можно легко увидеть трение качения, включают роликовые коньки, шариковые подшипники и т. д.
Сила трения скольжения — Когда один объект перетаскивается по поверхности другого, возникает трение скольжения. По сравнению со статическим трением оно слабее. Примеры трения скольжения включают перетаскивание блока, который находится на столе, письмо, игра на слайде и т. д.
Трение жидкости
Вещество, которое может течь и принимать форму сосуда, в котором оно хранится, называется жидкостью. Жидкостное трение — это термин, обозначающий сопротивление, которое жидкость или газ оказывают движущемуся объекту. Следовательно, говоря простыми словами, сила трения, создаваемая жидкостями, называется трением жидкости.
Сила сопротивления воздуха или сила сопротивления — это термин, используемый для описания силы трения, создаваемой воздухом. Жидкостное трение затрудняет ходьбу по бассейну с водой в разгар шторма.
Примеры силы трения
Вот несколько примеров из реальной жизни, когда мы сталкиваемся с различными типами силы трения, а именно: Трение скольжения. Величина трения между объектом и поверхностью уменьшается за счет льда, отложившегося на земле или земле. Отсутствие трения на поверхности позволяет предметам на ней легко скользить и скользить.
 Скалолазание зависит от трения, чтобы создать надежное сцепление между ногами или руками альпиниста и поверхностью скалы. Он помогает взобраться на скалу и удерживает руки и ноги альпиниста от соскальзывания.
Скалолазание зависит от трения, чтобы создать надежное сцепление между ногами или руками альпиниста и поверхностью скалы. Он помогает взобраться на скалу и удерживает руки и ноги альпиниста от соскальзывания.Часто задаваемые вопросы о силе трения
Вопрос 1: Определение силы трения.
Ответ:
Сила трения возникает, когда две поверхности соприкасаются друг с другом и скользят друг по другу.
Вопрос 2: Какие факторы влияют на силу трения?
Ответ:
На силу трения больше всего влияют два важных фактора:
- Природа двух соприкасающихся поверхностей и
- Природа силы, действующей на эти поверхности.
Вопрос 3: Как рассчитать силу трения?
Answer:
The frictional force can be calculated by using the following formula:
F frict = µ × F norm
where,
- µ is the coefficient of friction , и
- F норма относится к нормальной силе, действующей на указанный объект, заданной как F = mg (где m — масса, а g — ускорение свободного падения).
Вопрос 4: Какова единица силы трения?
Ответ:
Единицей силы трения в системе СИ является кг.м/с 2 или Ньютон (Н).
Вопрос 5: Объясните, как смазка уменьшает силу трения между объектами?
Ответ:
Смазочные материалы покрывают дефекты поверхности в местах контакта.
Таким образом, трение уменьшается, когда движущиеся объекты соприкасаются со смазкой.
Вопрос 6: Приведите два примера силы трения.
Ответ:
Ниже приведены два примера силы трения:
- Человек может ходить только при наличии силы трения между землей и ногами. Поскольку трение является контактной силой, оно существует между точками пересечения. Это помогает в создании прочной связи между ногой и землей.
- Сила, препятствующая движению альпиниста по скале, может ощущаться, когда он это делает. Сила трения — это термин, данный этой силе.
Вопрос 7: Как рассчитывается максимальное статическое трение?
Ответ:
Максимальная сила трения покоя равна произведению коэффициента трения покоя на нормальную силу, действующую на объект.
Вопрос 8: Какова работа силы трения?
Ответ:
Работа силы трения всегда отрицательна.
Похожие статьи
- Типы трения
- Разница между статическим и динамическим трением
- Давление
Трение | Физика | | Герой курса
Цели обучения
К концу этого раздела вы сможете:
- Обсуждать общие характеристики трения.
- Описать различные виды трения.
- Рассчитайте величину статического и кинетического трения.
Трение — это сила, постоянно присутствующая вокруг нас, которая противодействует относительному движению между контактирующими системами, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
Трение
Трение — это сила, противодействующая относительному движению между соприкасающимися системами.
Одной из самых простых характеристик трения является то, что оно параллельно поверхности контакта между системами и всегда в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением . Например, трение замедляет скольжение хоккейной шайбы по льду. Но когда объекты неподвижны, между ними может действовать статическое трение ; статическое трение обычно больше, чем кинетическое трение между объектами.
Кинетическое трение
Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
На рис. 1 показано грубое графическое изображение того, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Рисунок 1.
Силы трения, такие как f , всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Для того чтобы объект двигался, он должен подняться туда, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что объясняет, например, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.
Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для движения (кинетическое трение).
When there is no motion between the objects, the magnitude of static friction f s is f s ≤ μ s N , where μ s is коэффициент трения покоя и Н — величина нормальной силы (силы, перпендикулярной поверхности).
Величина статического трения
Magnitude of static friction f s is f s ≤ μ s N , where μ s is the coefficient of static friction and N is the magnitude of the нормальная сила.
Символ ≤ означает, что меньше или равно , подразумевая, что статическое трение может иметь минимальное и максимальное значение μ с Н . Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела. Как только приложенная сила превысит f s(max) , объект начнет двигаться. Таким образом, f s(max) = μ s N .
Как только приложенная сила превысит f s(max) , объект начнет двигаться. Таким образом, f s(max) = μ s N .
Когда объект движется, величина кинетического трения f k определяется выражением f k = μ k N , где μ k — коэффициент кинетического трения. Система, в которой f k = μ k N , описывается как система, в которой трение ведет себя просто .
Величина кинетического трения
Величина кинетического трения f k определяется как f k = μ k N , где μ k — коэффициент кинетического трения.
Как видно из таблицы 1, коэффициенты кинетического трения меньше, чем их статические аналоги. То, что значения μ в Таблице 1 указаны только с одной или, самое большее, с двумя цифрами, является указанием на приблизительное описание трения, данное двумя приведенными выше уравнениями.
То, что значения μ в Таблице 1 указаны только с одной или, самое большее, с двумя цифрами, является указанием на приблизительное описание трения, данное двумя приведенными выше уравнениями.
| Таблица 1. Коэффициенты статического и кинетического трения | ||
|---|---|---|
| Система | Статическое трение мк с | Кинетическое трение μ k |
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Туфли на дереве | 0,9 | 0,7 |
| Обувь для льда | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Приведенные ранее уравнения включают зависимость трения от материалов и нормальную силу. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу, Вт = мг = (100 кг)(9,80 м/с 2 ) = 980 Н, перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить силу, параллельную полу, большую, чем 440N, чтобы переместить ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н f k = μ k Н = (0,30)(980 Н) = 290 Н поддерживает движение с постоянной скоростью. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу, Вт = мг = (100 кг)(9,80 м/с 2 ) = 980 Н, перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить силу, параллельную полу, большую, чем 440N, чтобы переместить ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н f k = μ k Н = (0,30)(980 Н) = 290 Н поддерживает движение с постоянной скоростью. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Эксперимент на вынос
Найдите небольшой пластиковый предмет (например, пищевой контейнер) и поставьте его на кухонный стол, слегка постукивая по нему. Теперь распылите воду на стол, имитируя легкий дождь. Что происходит теперь, когда вы нажимаете на объект того же размера? Теперь добавьте несколько капель масла (растительного или оливкового) на поверхность воды и дайте такой же кран. Что происходит сейчас? Эта последняя ситуация особенно важна для водителей, особенно после небольшого дождя. Почему?
Многие люди испытали на себе скользкость ходьбы по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 2). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 2). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Рис. 2. Замена коленного сустава искусственным — процедура, которая проводится уже более 20 лет. На этом рисунке мы видим послеоперационные рентгеновские снимки замены правого коленного сустава. (кредит: Майк Бэрд, Flickr)
Другие природные смазки включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания , и когда человек двигается. Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Пример 1. Лыжные упражнения
Лыжник массой 62 кг скользит по заснеженному склону. Найдите коэффициент кинетического трения лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой Н как таким образом, коэффициент кинетического трения можно найти, если мы сможем найти нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. диаграмму «лыжник и свободное тело» на рис. 3.)
3.)
Рис. 3.
Движение лыжника и трение параллельны склону, поэтому все силы удобнее спроецировать на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны на слева от лыжника). N (нормальная сила) перпендикулярна склону, а f (трение) параллельно склону, но w (вес лыжника) имеет составляющие по обеим осям, а именно w ⊥ и W // . N равно по модулю w ⊥ , поэтому движение перпендикулярно склону отсутствует. Однако по модулю f меньше, чем W //, поэтому имеется ускорение вниз по склону (вдоль оси x ).
То есть N = w ⊥ = w cos 25º = мг cos 25º.
Подставив это выражение в выражение для кинетического трения, мы получим f k = μ k мг cos 25º, которое теперь можно найти для коэффициента кинетического трения 92)(0,906)}=0,082\\мкк=(62 кг)(9,80 м/с2)(0,906)45,0=0,082
.
Обсуждение
Этот результат немного меньше, чем коэффициент, указанный в таблице 5.1 для вощеной древесины на снегу, но все же приемлем, поскольку значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой м скользит по склону, образующему с горизонтом угол θ , трение определяется выражением f k = μ k мг cos θ. В этих условиях все объекты будут скользить вниз по склону с постоянным ускорением. Доказательство этого оставлено для задач и упражнений этой главы.
Эксперимент на вынос
Объект будет скользить по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано в примере 1, кинетическое трение на склоне f k = μ k мг cos θ. Компонент веса вниз по склону равен мг sin θ (см. диаграмму свободного тела на рисунке 3). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Запись об этом:
Компонент веса вниз по склону равен мг sin θ (см. диаграмму свободного тела на рисунке 3). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Запись об этом:
F K = FG x
μ K MG COS θ = K MG COS θ
.Решая для μ k , мы находим, что
μk=mgsinθmgcosθ=tanθ\displaystyle\mu _{\text{k}}=\frac{mg\sin\theta}{mg\cos \theta}=\tan\theta\\μk=mgcosθmgsinθ=tanθ
Положите монету на книгу и наклоняйте ее до тех пор, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. Измерьте угол наклона относительно горизонтали и найдите μ k . Обратите внимание, что монета вообще не начнет скользить до тех пор, пока угол больше θ , так как коэффициент статического трения больше, чем коэффициент кинетического трения. Обсудите, как это может повлиять на значение μ k и его неопределенность.
Обсудите, как это может повлиять на значение μ k и его неопределенность.
Мы обсудили, что, когда объект покоится на горизонтальной поверхности, существует нормальная сила, поддерживающая его, равная по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе.
Соединения: субмикроскопические объяснения трения
До сих пор рассматривались более простые аспекты трения — его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
На рисунке 4 показана одна макроскопическая характеристика трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет крошечную часть от общей площади, поскольку соприкасаются только высокие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и оказывается, что трение пропорционально этой площади.
Рисунок 4. Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь. Когда есть большая нормальная сила в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.
Но представление в атомном масштабе обещает объяснить гораздо больше, чем простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рис. 5 показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое будет обсуждаться далее в этой главе. Изменение напряжения сдвига заметно (более чем в 10 9 раз).1440 12 ) и трудно поддающееся теоретическому прогнозированию, но касательное напряжение дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. На рис. 5 показано, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена, и установлено, что она связана с напряжением сдвига, которое будет обсуждаться далее в этой главе. Изменение напряжения сдвига заметно (более чем в 10 9 раз).1440 12 ) и трудно поддающееся теоретическому прогнозированию, но касательное напряжение дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.
Рис. 5. Наконечник зонда деформируется вбок под действием силы трения, когда зонд тащит по поверхности. Измерения того, как сила меняется для разных материалов, дают фундаментальное представление об атомной природе трения.
Исследования PhET: Силы и движение
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте диаграмму всех сил свободного тела (включая силы тяжести и нормальные силы).
Нажмите, чтобы скачать. Запуск с использованием Java.
Резюме раздела
- Трение — это контактная сила между системами, которая противодействует движению или попытке движения между ними. Простое трение пропорционально нормальной силе N, сталкивающей системы друг с другом.
 (Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина трения покоя
(Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина трения покояfs{f}_{\text{s}}\\fs
между системами, стационарными относительно друг друга, равнаfs≤µsN{f}_{\text{s}}\le {\mu }_{\text{s}}N\\fs≤µsN
, гдемкс{\mu }_{\ text{s}}\\µs
— коэффициент статического трения, зависящий от обоих материалов. - Кинетическая сила трения
fk{f}_{\text{k}}\\fk
между системами, движущимися относительно друг друга, определяется выражениемfk=µkN{f}_{\text{k}}={ \mu }_{\text{k}}N\\fk=µkN
, гдеµk{\mu }_{\text{k}}\\µk
— коэффициент кинетического трения, который также зависит от обоих материалов.
Концептуальные вопросы
- Дайте определение нормальной силе. Каково его отношение к трению, когда трение ведет себя просто?
- Клей на куске ленты может оказывать воздействие. Могут ли эти силы быть разновидностью простого трения? Объясните, особенно учитывая, что лента может приклеиваться к вертикальным стенам и даже к потолку.

- Когда вы учитесь водить машину, вы обнаружите, что вам нужно немного отпустить педаль тормоза, когда вы останавливаетесь, иначе машина остановится рывком. Объясните это с точки зрения связи между статическим и кинетическим трением.
- Когда вы водите мелом по классной доске, он иногда скрипит, потому что быстро то соскальзывает, то прилипает к доске. Опишите этот процесс более подробно, объяснив, в частности, как он связан с тем, что кинетическое трение меньше статического трения. (Тот же процесс проскальзывания происходит, когда шины визжат по асфальту.)
Задачи и упражнения
Ответы на задачи в этом разделе выражайте с правильным количеством значащих цифр и правильными единицами измерения.
- Студент-физик готовит завтрак, когда замечает, что сила трения между его стальным шпателем и тефлоновой сковородой составляет всего 0,200 Н. Зная коэффициент кинетического трения между двумя материалами, он быстро вычисляет нормальную силу.
 Что это такое?
Что это такое? - При восстановлении двигателя своего автомобиля студент-физик должен приложить усилие 300 Н, чтобы вставить сухой стальной поршень в стальной цилиндр. а) Какова величина нормальной силы между поршнем и цилиндром? (б) Какова величина силы, которую она должна была бы приложить, если бы стальные детали были смазаны маслом?
- (а) Какова максимальная сила трения в коленном суставе человека, который поддерживает на этом колене 66,0 кг своей массы? (b) Во время напряженных упражнений на суставы можно воздействовать силой, в десять раз превышающей поддерживаемый вес. Какова максимальная сила трения при таких условиях? Силы трения в суставах относительно малы при любых обстоятельствах, за исключением случаев, когда суставы изнашиваются, например, в результате травмы или артрита. Увеличение силы трения может привести к дальнейшему повреждению и боли.
- Предположим, у вас есть 120-килограммовый деревянный ящик, стоящий на деревянном полу. а) Какую максимальную силу вы можете приложить горизонтально к ящику, не сдвигая его? (б) Если вы продолжите прикладывать эту силу, как только ящик начнет скользить, какова будет тогда величина его ускорения?
- (a) Если половина веса небольшого 1,00 × 10 3 кг грузового автомобиля приходится на два ведущих колеса, какова величина максимального ускорения, которое он может развить на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянном кузове грузовика, скользить, если он будет двигаться с такой скоростью? (c) Решите обе задачи, предполагая, что грузовик имеет полный привод.

- Упряжка из восьми собак тянет нарты с полозьями из вощеного дерева по мокрому снегу (каша!). Собаки имеют среднюю массу 19,0 кг, а загруженные сани с всадником имеют массу 210 кг. (a) Рассчитайте величину ускорения, начиная с состояния покоя, если каждая собака прикладывает к снегу среднюю силу 185 Н, направленную назад. (b) Какова величина ускорения, когда сани начинают двигаться? (c) Для обеих ситуаций рассчитайте величину силы в сцепке между собаками и санями.
- Предположим, что фигурист весом 65,0 кг толкается двумя другими фигуристами, показанными на рис. 6. (a) Найдите направление и величину
Ftot{\mathbf{F}}_{\text{tot}}\\Ftot
, общая сила, действующая на нее со стороны других, учитывая, что величиныF1{F}_{1}\\F1
иF2{F}_{2}\\F2
равны 26,4 Н и 18,6 Н, соответственно; (b) Каково ее начальное ускорение, если она изначально неподвижна и на ней есть коньки со стальными лезвиями, направленные в направленииFtot{\mathbf{F}}_{\text{tot}}\\Ftot
? (c) Каково ее ускорение, если предположить, что она уже движется в направленииFtot{\mathbf{F}}_{\text{tot}}\\Ftot
? (Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между соприкасающимися поверхностями. )
)Рисунок 6.
- Покажите, что ускорение любого объекта на склоне без трения, образующем с горизонтом угол θ , равно a = g sin θ . (Обратите внимание, что это ускорение не зависит от массы.)
- Покажите, что ускорение любого объекта на склоне, где трение ведет себя просто (то есть, где f k = μ k N ) равно a − μ k cos θ ). Заметим, что ускорение не зависит от массы и сводится к выражению из предыдущей задачи, когда трение становится пренебрежимо малым ( μ k =0).
- Рассчитайте замедление сноубордиста, поднимающегося по склону 5,0º, принимая во внимание коэффициент трения вощеной древесины по мокрому снегу. Ответ на вопрос 9 может быть полезен, но будьте осторожны, принимая во внимание тот факт, что сноубордист движется в гору. Подробно покажите, как вы выполняете шаги, описанные в Стратегии решения проблем.

- (a) Рассчитайте ускорение лыжника, спускающегося по склону с уклоном 10,0º, исходя из коэффициента трения вощеной древесины по мокрому снегу. б) Найдите угол склона, под которым этот лыжник мог бы двигаться с постоянной скоростью. Вы можете пренебречь сопротивлением воздуха в обеих частях, и вы найдете результат вопроса 9{-1}\mu _{\text{s}}\\θ=tan−1 мкс . Вы можете использовать результат предыдущей задачи. Предположим, что a = 0 и что статическое трение достигло своего максимального значения.
- Рассчитайте максимальное замедление автомобиля, движущегося по уклону 6 градусов (составляющему угол 6 градусов с горизонтом) при следующих дорожных условиях. Вы можете предположить, что вес автомобиля равномерно распределяется на все четыре шины и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время замедления. (Качение не учитывать.) Рассчитайте для автомобиля: (а) на сухом бетоне; (б) На мокром бетоне; (c) На льду, если предположить, что
мкс=0,100{\mu }_{\text{s}}=0,100\\мкс=0,100
, то же, что и для обуви на льду.
- Рассчитайте максимальное ускорение автомобиля, движущегося вверх по склону 4 градуса (составляющему угол 4 градуса с горизонтом) при следующих дорожных условиях. Предположим, что только половина веса автомобиля приходится на два ведущих колеса и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения. (Не обращайте внимания на прокатку.) (a) На сухом бетоне; (b) на мокром бетоне; (c) На льду, если предположить, что 9{5}N\\7,50×105N , если предположить, что двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. (b) Какова величина силы в сцеплении между 37-й и 38-й тележками (это сила, с которой каждая из машин действует на другую), если предположить, что все машины имеют одинаковую массу и что трение равномерно распределено между всеми машинами и двигатели?
- Рассмотрим альпиниста весом 52,0 кг на рис.
 7. (a) Найдите натяжение веревки и силу, которую альпинист должен прикладывать ногами к вертикальной скале, чтобы оставаться неподвижным. Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, прилагаемая ее руками, незначительна; б) Каков минимальный коэффициент трения между ее туфлями и скалой?
7. (a) Найдите натяжение веревки и силу, которую альпинист должен прикладывать ногами к вертикальной скале, чтобы оставаться неподвижным. Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, прилагаемая ее руками, незначительна; б) Каков минимальный коэффициент трения между ее туфлями и скалой?Рис. 7. Часть веса альпиниста приходится на веревку, а часть — на трение между ногами и скалой.
- Участник зимних спортивных соревнований толкает глыбу льда весом 45,0 кг по замерзшему озеру, как показано на рис. 8а. (a) Вычислите минимальную силу F, которую он должен приложить, чтобы сдвинуть блок с места; б) Чему равно его ускорение после того, как оно начнет двигаться, если эта сила сохраняется?
Рис. 8. Какой способ скольжения глыбы льда требует меньшего усилия — (а) толкать или (б) тянуть под одинаковым углом над горизонталью?
- Повторите вопрос 18 с участником, который тянет блок льда с помощью веревки через плечо под тем же углом над горизонталью, как показано на рисунке 8b.

Глоссарий
трение: сила, противодействующая относительному движению или попыткам движения между контактирующими системами
кинетическое трение: сила, противодействующая движению двух систем, находящихся в контакте и движущихся относительно друг друга
статическое трение: сила, противодействующая движению двух систем, находящихся в контакте и не движущихся относительно друг друга
величина статического трения:
fs≤µsN{f}_{\text{s}}\le {\mu }_{\text{s}}N\\fs≤µsN
, где
мкс{\mu }_{\text{s}}\\µs
— коэффициент статического трения, а N — величина нормальной силы
величина кинетического трения:
fk=µkN{f}_{\ text{k}}={\mu }_{\text{k}}N\\fk=µkN
, где
µk{\mu }_{\text{k}}\\µk
— коэффициент кинетического трения
Избранные решения задач и упражнений
1. 5,00 Н
5,00 Н
4. (а) 588 Н; (б) 1,96 м/с 2
6. (а) 3,29 м/с 2 ; (б) 3,52 м/с 2 ; (в) 980 Н, 945 Н
10. 1,83 м/с 2
14. (а) 4,20 м/с 2 ; (б) 2,74 м/с 2 ; (в) –0.195 м/с 2
16. (а) 1.03 × 106 Н; (б) 3,48 × 105 Н
18. (а) 51,0 Н; (b) 0,720 м/с 2
Лицензии и атрибуты
Контент по лицензии CC, совместно используемый ранее
- Колледж физики. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
- Интерактивное моделирование PhET . Предоставлено : Университет Колорадо в Боулдере. Расположен по адресу : https://phet.



 Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения. 

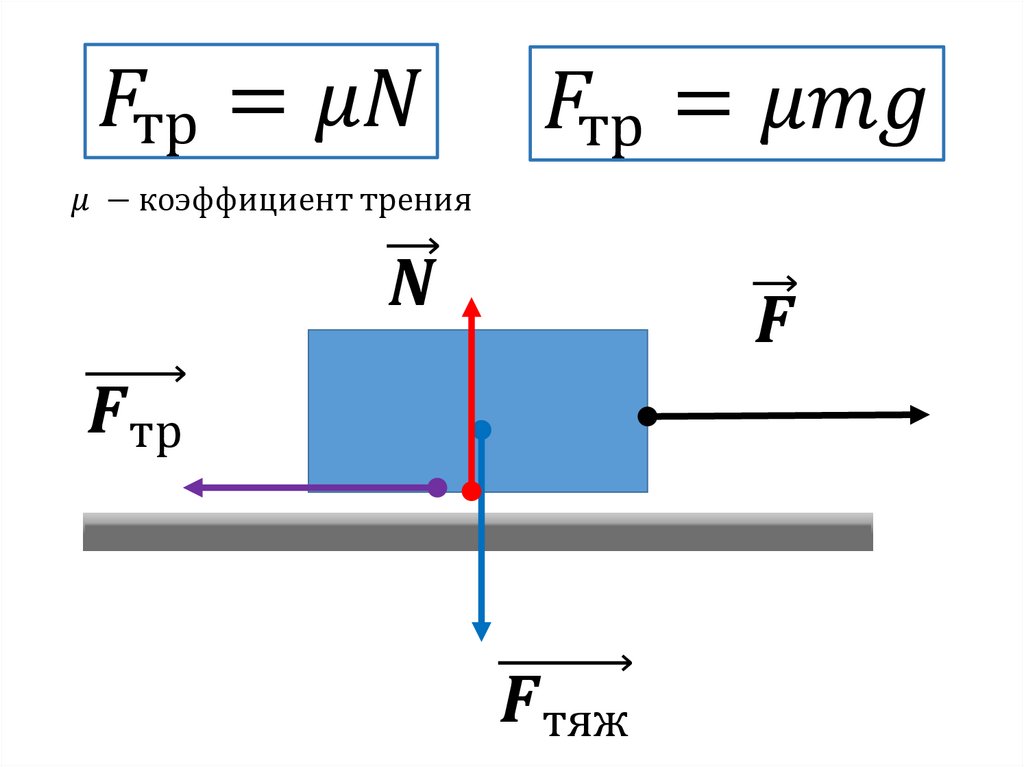

 Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.
Решающую роль играет внутреннее трение в смазывающем материале. Это фрикционное взаимодействие возникает при увеличении относительных скоростей перемещения.