Site Loader
Posted on 13.08.2023

Содержание

Построение таблиц истинности для логических выражений

Дата: 30.10.2020г

Класс: 8

Учитель: Муртазова Эльмира Вахитова

Ученики:_Мудаева Т., Дайтаева И

________________________________________________________________________________Автор учебника: Л. Л. Босова, А. Ю. Босова

Тема: «Построение таблиц истинности для логических выражений»

Цель урока: сформировать умения строить и заполнять таблицы истинности

Задачи:

  • Обучающие: изучить последовательность действий построения таблиц истинности, сформировать умение применять алгоритм заполнения таблиц истинности, научить находить значение логических выражений посредством построения таблиц истинности.

  • Развивающие: развивать логическое мышление и познавательный интерес к предмету, развивать внимание, память, речь учащихся.

  • Воспитательные: воспитывать культуру общения, формировать интеллектуальную и эмоциональную активность учащихся, воспитывать чувства ответственности за результаты своего труда.

Тип урока: урок изучения и первичного закрепления новых знаний.

План урока:

  • Организационный момент (2 мин.)

  • Повторение материала предыдущего урока, проверка ДЗ (5 мин.)

  • Объяснение нового материала (14 мин.)

  • Физкультминутка (2 мин.)

  • Закрепление разбор примера (5 мин.)

  • Задания для самостоятельной работы (8 мин.)

  • Подведение итогов, рефлексия (3 мин)

  • Домашнее задание (1 мин.)

Оборудование и программный материал:

ХОД УРОКА

I. Организационный момент

Здравствуйте ребята. Мы уже несколько уроков изучаем тему (главу) «Математические основы информатики». Слайд 1 И сегодня еще мы узнаем много нового. Вы готовы к этому?

Эпиграфом к уроку являются слова Б.Паскаля: “ВЕЛИЧИЕ ЧЕЛОВЕКА — В ЕГО СПОСОБНОСТИ МЫСЛИТЬ”. Слайд 2

На предыдущем уроке мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде формулы. В

Рыбу ловят сачком, или ловят крючком, или мухой приманивают, или червячком

А V В V С V В

Давайте вспомним основные определения и понятия, выполните задания в Якласс (4 слайд):

Задания в Якласс

1. Числовые выражения (1 Б.)

Определи, является ли высказыванием: 5⋅2

  • является высказыванием

  • не является высказыванием

2. Предложение (2 Б.)

«Капитанская дочь» — самое весёлое стихотворение.

нельзя однозначно определить

истинное

ложное

(Повесть)

3. Высказывания в геометрии (2 Б.)

Определи, высказывание является ложным или истинным.

 

Площадь прямоугольника с длинами сторон c и d равна c⋅d.

нельзя однозначно определить

истинное

ложное

4. Основные понятия (1 Б. )

Выбери верный ответ.

 

В алгебре логики высказывания обозначают буквами и называют ________________________.

логические переменные

истинное высказывание

геометрия логики

математическое предложение

III. Объяснение нового материала

На Слайде 5 логическое выражение: F = X ИЛИ Y И (НЕ Z). Записать данное выражение, заменяя логические связки на знаки, которые используются для записи логических операций.

(F = X + Y * ¬Z)

Давайте найдем значение данного выражения при значениях переменных Х=1;У=1; Z=0.

Для нахождения значения функции необходимо подставить значении переменных в формулу.

Ответ: F=1+1*(не 0)= 1+1*1=1.

Это единственное значение, которое может принять наша функция? (Нет).

От чего зависит значения функции? (От значений переменных X,Y, Z)

Из ранее изученного материала, нам известно, что для нахождения значения функции логической операции: инверсия, конъюнкция, дизъюнкция мы использовали таблицу истинности. А кто может сформулировать тему нашего урока:

Слайд 7 «ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ»

Запишем тему урока в тетрадь. Давайте вместе с вами постараемся дать определение понятию ТАБЛИЦА ИСТИННОСТИ.

Слайд 8 Таблица истинности – это таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний

Для того, что бы построить ТИ необходимо пользоваться определенным алгоритмом: см. учебник с.29

Приоритеты операций

  1. скобки

  2. отрицание

  3. конъюнкция

  4. дизъюнкция

Пример: Для формулы A* (B * С) построить таблицу истинности (слайд 9)

Следуя пунктам алгоритма получаем: (слайд 10)

1. посчитаем n: 3

2. посчитаем общее число логических операций в выражении: 3

3. установим последовательность выполнения логических операций с учетом скобок и приоритетов

4. определим число столбцов в таблице: 3 + 3 = 6

5. заполним шапку таблицы, включив в нее и операции в соответствии с последовательностью, установленной в п. 3

6. определим количество строк в таблице (не считая шапки таблицы) m = 2n : 23 = 8

7. выписать наборы входных переменных:

1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «1», а нижнюю «0»;

2.разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «1» и «0», начиная с группы «1»;

3.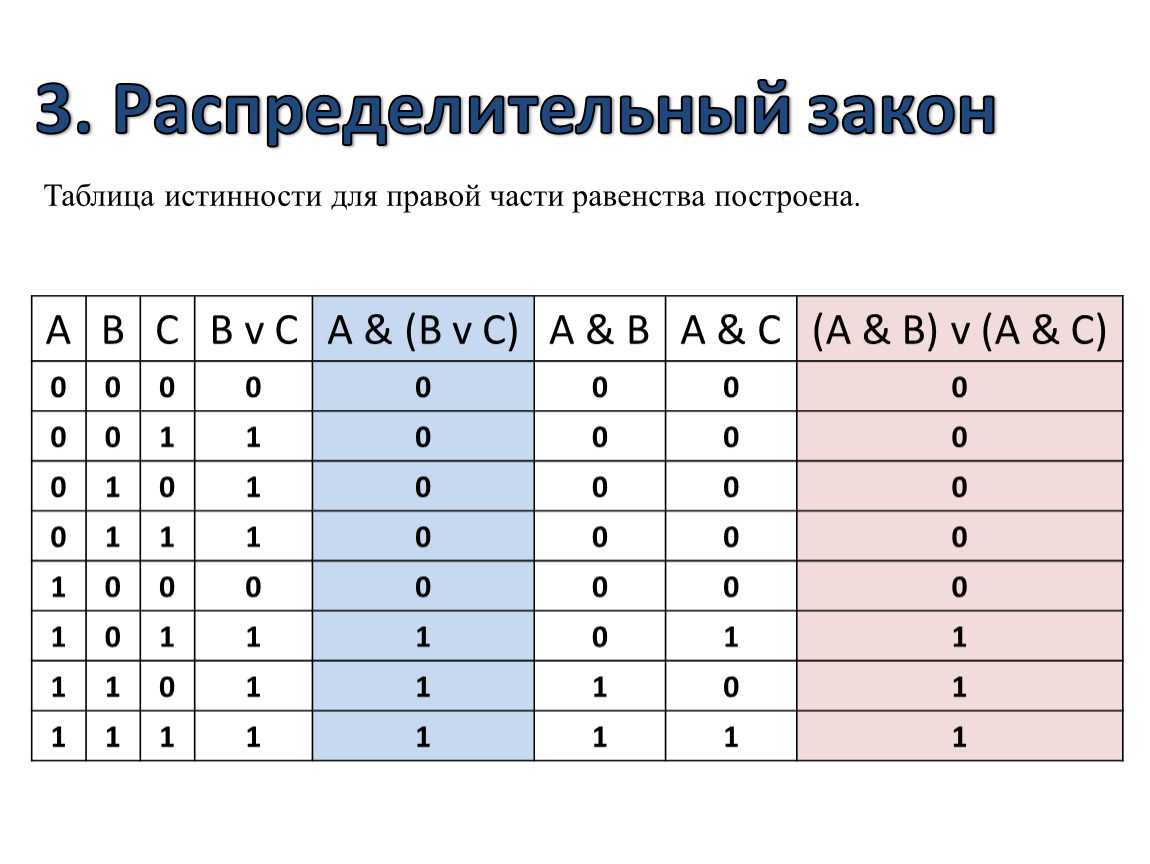 продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «1» или «0» до тех пор, пока группы «1» и «0» не будут состоять из одного символа.

8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

A

B

C

B*

A* (B *)

1

1

1

0

0

0

1

1

0

1

1

1

1

0

1

0

0

0

1

0

0

1

0

0

0

1

1

0

0

0

0

1

0

1

1

0

0

0

1

0

0

0

0

0

0

1

0

0

IV. Физкультминутка

Гимнастика для глаз (слайд 12)

V. Закрепление новых знаний

Построить таблицы истинности для следующих выражений:

Слайд 13-14

(Задания выведены на слайде)

VI. Контроль знаний (если останется время)

Слайд 15-16

Вариант 1

  1. Составить таблицу истинности для логического выражения

(А + В) * (¬А * А +В)

Вариант 2

  1. Составить таблицу истинности для логического выражения

(А * В) + (¬ В+А)

VII. Рефлексия

Слайд 16

Личностное осмысление каждым учеником результатов урока

    1. Что было наиболее трудным?

    2. Что удалось лучше всего?

Сегодня на уроке мы научились определять истинность составных высказываний, но больше с математической точки зрения, так как вам были даны не сами высказывания, а формулы, отображающие их. На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.

VIII. Домашнее задание

Слайд 17

Домашняя работа:

    1. §1.3.3

    2. Составить таблицы истинности для логических выражений



Слайд 18 спасибо за урок

Приложение 1

Вариант 1

  1. Составить таблицу истинности для логического выражения

(А + В) * (¬А * А +В)

Вариант 2

  1. Составить таблицу истинности для логического выражения

(А * В) + (¬ В+А)

Приложение 2

Домашняя работа: §1.3.3, №8,10



План-конспект дистанционного урока для 10 класса «Построение таблиц истинности для логических выражений» | Информатика

План-конспект дистанционного урока для 10 класса «Построение таблиц истинности для логических выражений»

Автор: Шабалин Виталий Леонидович

Организация: МБОУ г. Иркутска СОШ с угл. изучением отд. предметов №19

Населенный пункт: Иркутская область, г. Иркутск

Автор: Фокин Сергей Валентинович

Организация: МБОУ г. Иркутска СОШ с угл. изучением отд. предметов №19

Населенный пункт: Иркутская область, г. Иркутск

Формы, способы учебной деятельности:

Тип урока: урок открытие новых знаний.

Цель урока: создать условия для формирования у обучающихся умений построения таблиц истинности для логических выражений, содействовать развитию логического мышления, памяти обучающихся, повышению информационной культуры, через организацию совместной учебной деятельности обучающихся с учителем в условиях удаленного взаимодействия.

 

Планируемые результаты (формируемые УУД):

Личностные:

  1. Способствовать формированию желания выполнять учебные задания;
  2. Способствовать формированию устойчивой мотивации к обучению.

Познавательные:

  1. Умение выбирать наиболее эффективных способов решения задач в зависимости от конкретных условий;
  2. Построение табличных моделей для решения учебных заданий;
  3. Умение выполнять логические действия и операции.

Коммуникативные:

  1. Умение формулировать собственное мнение и позицию;
  2. Допускать возможность существования у людей различных точек зрения, в том числе не совпадающих с собственной;
  3. Общение в информационной среде.

Регулятивные:

  1. Умение планировать свои действия в соответствии с поставленной задачей и условиями ее реализации.

Предметные:

  1. Умение строить таблицы истинности;
  2. Использование понятийного аппарата раздела алгебры логики;
  3. Устанавливать истинность или ложность логической операции.

 

1 этап

Организационный момент

(2 мин)

Здравствуйте ребята!

Рад всех приветствовать на уроке.

Для контроля присутствия на уроке прошу в чате поставить плюсик в чате. Спасибо!

Подготовьте тетради и ручки.

 

Высказывание: «Человек, который смог сдвинуть гору, начинал с того, что перетаскивал с места на место мелкие камешки» (

Китайская поговорка)

 

Повторим правила поведения на дистанционном уроке:

  1. Отключить микрофоны
  2. Подготовить рабочую поверхность, убрать лишние предметы
  3. Общаться в чате и через микрофон уважительно, не перебивая собеседника
  4. Не писать в чат лишнюю информацию
  5. При желании ответить или задать вопрос необходимо нажать на кнопку на панели «Поднять руку»

2 этап

Мотивация к учебной деятельности (самоопределение)

(2 мин)

Для чего мы сегодня встретились?

Какие умения полученные на уроках информатики пригодятся в жизни?

 

Сегодняшняя тема урока находит свое отражение в профессиональной деятельности людей разной сферы: врачи, юристы, программисты, аналитики, экономисты и т. д. Полезна тем, кто собирается поступать в ВУЗы на направления области информатики. Также задания сегодняшней темы включены в ЕГЭ по информатике.

3 этап

Актуализация знаний и фиксация затруднений в деятельности

(3 мин)

Для чего повторять ранее изученные знания?

 

Какие логические операции вы знаете?

Назовите логические операции соответствующие таблицам на слайде (спрашивать детей согласны ли они с ответами ребят).

Назовите логические операции, которые соответствуют знаками для их обозначения.

Укажите правильный приоритет логических операций.

4 этап

Открытие новых знаний

(5 мин)

Для чего необходимо получать и добывать новые знания?

 

Как вы думаете, каким образом находить значение логического выражения, учитывая, что мы знаем, каким образом определяется значение известных нам логических операций.

 

На лайде отображен QR-код с темой урока. Отсканируйте код и назовите тему урока.

 

Запишите в тетрадь число и тему урока.

Сформулируйте и запишите цель урока. Прочитайте цель урока вслух. Чему еще мы должны научиться на уроке? (слушать друг друга, уважать мнение другого человека, вежливости, терпению)

 

Демонстрация учебника через документ-камеру. Посмотрите на таблицы истинности в учебнике. Скажите сколько строк в данной таблице?

(учебник 10 кл. 1 часть 162, 164, 166, 172)

От чего зависит количество строк в таблице истинности?

Почему именно такое количество строк?

Какой можно сделать вывод? (формула)

 

Формула необходимая для построения таблиц.

N=

N – количество строк в таблице

i – количество аргументов (переменных) в логическом выражении

 

(Проверить математические знания степени двойки)

5 этап

Первичное закрепление с проговариванием во внешней речи

(5 мин)

Рассмотрим логическое выражение.

Запишите его в тетрадь.

Какие логические операции видите?

Укажите приоритет операций.

Работаем на смарт доске Teams.

 

6 этап

Физминутка

(здоровьесберегающие технологии)

(2 мин)

Закройте глаза.

Откройте глаза.

Помаргайте.

Посморите вправо, влево, вверх, вниз.

Зажмурьте глаза.

Откройте глаза.

Посмотрите в окно.

7 этап

Самостоятельная работа с самопроверкой по эталону

(5 мин)

Самостоятельное решение логического выражения с помощью построения таблицы истинности.

Демонстрация экрана одного ученика (решение с помощь таблицы в MS Word)

 

 

Выполнить тест. (Критерии за тест)

8 этап

Рефлексия

(4 мин)

Что нового сегодня узнали на уроке?

Где пригодятся полученные знания?

Что было сложно на уроке?

Отметьте на мишени уровень участия в уроке. (слайд с мишенью)

 

Отметки за урок (за тест).

9 этап

Постановка домашнего задания

(2 мин)

Построить таблицу истинности для логического выражения. Выполнить решение на выбор: в MS Word, в MS Excel, в тетради.

 

Подготовить сообщение о человеке на фотографии. (Узнать кто это через поиск по картинке)

 

Все задания будут выложены в задании к уроку в Teams и в дневнике.ру.

10 Этап

Завершение

(2 мин)

Сегодняшний урок мы начали с поговорки:

 

«Человек, который смог сдвинуть гору, начинал с того, что перетаскивал с места на место мелкие камешки» (Китайская поговорка)

 

Вот и сегодня на уроке мы перенесли маленький камушек для достижения больших целей в вашей учебной жизни!

Спасибо Вам за урок до свидания!

 

Приложения:

  1. file0.docx. . 27,1 КБ
Опубликовано: 07.10.2022

Сведения об образовательной организации
Пользовательское соглашение Политика конфиденциальности

© 2010 – 2023, Всероссийский педагогический журнал «Современный урок»
ISSN: 2713 – 282X, УДК 371.321.1(051), ББК 74.202.701, Авт. знак С56
Лицензия на образовательную деятельность № 041875 от 29.12.2021
СМИ ЭЛ № ФС 77 – 65249 от 01.04.2016
Для писем: 125222, Москва, a/я 8
Телефон: +7 (925) 664-32-11
E-mail:  [email protected]

16+

4.3: Таблицы истинности — Mathematics LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    59946
    • Дарлин Диаз
    • Колледж Сантьяго-Каньон через Инициативу открытых образовательных ресурсов ASCCC

    Поскольку сложные логические операторы могут быть сложными для понимания, мы можем создать таблицу истинности, чтобы отслеживать, какие значения истинности для простых операторов делают сложное утверждение истинным и ложным.

    Определение: Таблица истинности

    Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.

    Пример \(\PageIndex{1}\)

    Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-то с фаэтоном».

    Решение

    Это сложное утверждение, состоящее из двух более простых условий: «является секционным» и «имеет шезлонг». Для простоты давайте использовать S для обозначения «является секционным», а C для обозначения «имеет шезлонг». Условие S выполняется, если кушетка секционная.

    Таблица истинности для этого будет выглядеть так:

    S С S или C
    Т Т Т
    Т Ф Т
    Ф Т Т
    Ф Ф Ф

    В таблице буква T используется для обозначения истины, а буква F — для ложности. В первой строке, если \(S\) истинно и \(C\) также истинно, то сложное утверждение «\(S\) или \(C\)» истинно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.

    Помните также, что или в логике не являются исключающими; если кушетка имеет обе функции, она соответствует условию.

    Чтобы еще больше сократить наши обозначения, мы собираемся ввести некоторые символы, которые обычно используются для и , или и вместо .

    Определение: Символы

    Символ \(⋀\) используется для и: A и B обозначается \(A ⋀ B\).

    Символ \(⋁\) используется для или: A или B обозначается \(A ⋁ B\)

    Символ ~ используется для not: not A обозначается ~\(A\)

    Вы можете запомнить первые два символа связывая их с формами объединения и пересечения. \(A ⋀ B\) будут элементами, которые существуют в обоих множествах, в \(A ⋂ B\). Точно так же \(A ⋁ B\) будут элементами, которые существуют в любом наборе, в \(A ⋃ B\).

    В предыдущем примере таблица истинности просто обобщала то, что мы уже знаем о том, как 9Выписка 0040 или работает. Ниже показаны таблицы истинности для основных утверждений и , или и , а не .

    Основные таблицы истинности

    А Б А ⋀ В
    Т Т Т
    Т Ф Ф
    Ф Т Ф
    Ф Ф Ф
    А Б А ⋁ В
    Т Т Т
    Т Ф Ф
    Ф Т Ф
    Ф Ф Ф
    А ~А
    Т Ф
    Ф Т

    Таблицы истинности очень полезны при анализе более сложных логических выражений.

    Пример \(\PageIndex{2}\)

    Создайте таблицу истинности для утверждения \(A ⋀\) ~\((B ⋁ C)\).

    Решение

    Помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для \(A\), \(B\) и \(C\). Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения \(B ⋁ C\).

    А Б С Б ⋁ С
    Т Т Т Т
    Т Т Ф Т
    Т Ф Т Т
    Т Ф Ф Ф
    Ф Т Т Т
    Ф Т Ф Т
    Ф Ф Т Т
    Ф Ф Ф Ф

    Далее мы можем найти отрицание \(B ⋁ C\), используя столбец \(B ⋁ C\), который мы только что создали.

    А Б С Б ⋁ С ~(В ⋁ С)
    Т Т Т Т Ф
    Т Т Ф Т Ф
    Т Ф Т Т Ф
    Т Ф Ф Ф Т
    Ф Т Т Т Ф
    Ф Т Ф Т Ф
    Ф Ф Т Т Ф
    Ф Ф Ф Ф Т

    Наконец, находим значения \(A\) и ~\((B ⋁ C)\)

    A Б С Б ⋁ С ~(В ⋁ С) А ⋀ ~(В ⋁ С)
    Т Т Т Т Ф Ф
    Т Т Ф Т Ф Ф
    Т Ф Т Т Ф Ф
    Т Ф Ф Ф Т Т
    Ф Т Т Т Ф Ф
    Ф Т Ф Т Ф Ф
    Ф Ф Т Т Ф Ф
    Ф Ф Ф Ф Т Ф

    Оказывается, это сложное выражение истинно только в одном случае: если А истинно, В ложно и С ложно.

    Попробуйте сейчас 1

    Создайте таблицу истинности для этого утверждения: (~\(A ⋀ B) ⋁\) ~\(B\)

    Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы совершаем действие в зависимости от значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой 9.0053 следствие .

    Определение: Импликации

    Импликации — это логические условные предложения, утверждающие, что высказывание \(p\), называемое антецедентом, подразумевает следствие \(q\).

    Импликации обычно записываются как \(p → q\)

    Импликации аналогичны условным операторам, которые мы рассматривали ранее; p \(→\) q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и кондиционалами заключается в том, что кондиционалы, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логические утверждения, предполагающие, что следствие должно логически следовать, если антецедент истинен.

    Пример \(\PageIndex{3}\)

    Английское утверждение «Если идет дождь, то облака — это небо» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.

    Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.

    Пример \(\PageIndex{4}\)

    Друг говорит вам, что «если вы загрузите это изображение на Facebook, вы потеряете работу». Возможны четыре исхода:

    1. Вы загружаете изображение и сохраняете свою работу
    2. Вы загрузили картинку и потеряли работу
    3. Вы не загружаете картинку и сохраняете свою работу
    4. Вы не загрузите картинку и потеряете работу

    Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.

    В традиционной логике импликация считается достоверной (истинной), если нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.

    Значения истинности для импликаций

    р q п → к
    Т Т Т
    Т Ф Ф
    Ф Т Т
    Ф Ф Т

    Пример \(\PageIndex{5}\)

    Построить таблицу истинности для утверждения \((m ⋀\) ~\(p) → r\)

    Решение

    Начнем с построения таблицы истинности для антецедента.

    м р ~р м ⋀ ~п
    Т Т Ф Ф
    Т Ф Т Т
    Ф Т Ф Ф
    Ф Ф Т Ф

    Теперь мы можем построить таблицу истинности импликации

    m р ~р м ⋀ ~п р (м ⋀ ~р) → г
    Т Т Ф Ф Т Т
    Т Ф Т Т Т Т
    Ф Т Ф Ф Т Т
    Ф Ф Т Ф Т Т
    Т Т Ф Ф Ф Т
    Т Ф Т Т Ф Ф
    Ф Т Ф Ф Ф Т
    Ф Ф Т Ф Ф Т

    В этом случае, когда \(m\) истинно, \(p\) ложно и \(r\) ложно, тогда антецедент \(m ⋀\) ~\(p\) будет быть истинным, но следствие ложным, что приводит к недействительному импликации; каждый другой случай дает правильное следствие.

    Для любого следствия есть три связанных утверждения, обратное , обратное и противоположное .

    Определение: родственные операторы

    Первоначальная импликация: «если p, то q» p → q

    Обратное: «если q, то p» q → p

    Обратное: «если не p, то не q» ~ p → ~ q

    Противоположное: «если не q, то не p» ~ q → 90 041 ~ р

    Пример \(\PageIndex{6}\)

    Рассмотрим снова верный вывод «Если идет дождь, значит, в небе облака».

    Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно.

    Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно.

    Противоположным было бы: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.

    Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.

    Значение Конверс Обратный Противоположный
    стр. q п → кв q → стр ~ p → ~ q ~ q → ~ p
    Т Т Т Т Т Т
    Т Ф Ф Т Т Ф
    Ф Т Т Ф Ф Т
    Ф Ф Т Т Т Т

    Определение: Эквивалентность

    Условное утверждение и его противоположность логически эквивалентны.

    Обратное и обратное утверждение логически эквивалентны.

    Эта страница под названием 4.3: Таблицы правды распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дарлин Диас (Инициатива открытых образовательных ресурсов ASCCC) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или Страница
        Автор
        Дарлин Диас
        Лицензия
        CC BY-NC-SA
        Версия лицензии
        4,0
        Программа OER или Publisher
        Программа ASCCC OERI
        Показать страницу TOC
        нет
      2. Теги
        1. общие таблицы истинности
        2. противопоставленный
        3. Конверс
        4. эквивалент
        5. следствие
        6. обратный
        7. source@https://www. sccollege.edu/OER/Documents/MATH 105/Математика для студентов, изучающих гуманитарные науки (2017).pdf
        8. символов
        9. таблицы истинности
        10. значения истинности

      Таблицы истинности и анализ аргументов: примеры | Математика для гуманитарных наук |

      Таблицы истинности

      Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным и ложным

      Таблица истинности

      Таблица, показывающая, каково результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.

      Пример 1

      Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Получите секционную 9-ку». 0040 или что-то с фаэтоном».

      Это сложное утверждение состоит из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты давайте использовать S для обозначения «является секционным» и C для обозначения «имеет шезлонг». Условие S верно, если кушетка секционная.

      Таблица истинности для этого будет выглядеть так:

      S С С или C
      Т Т Т
      Т Ф Т
      Ф Т Т
      Ф Ф Ф

      В таблице T используется для true, а F для false. В первой строке, если S верно и C также верно, то сложное утверждение « S или C » верно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию.

      Помните также, что или в логике не являются исключающими; если кушетка имеет обе функции, она соответствует условию.

      Чтобы еще больше сократить наши обозначения, мы собираемся ввести некоторые символы, которые обычно используются для и , или и вместо .

      Символы

      Символ ⋀ используется для и : A и B обозначается как A ⋀ B .

      Символ ⋁ используется для или : A или B обозначается A ⋁ B

      Символ ~ используется для , а не : не A обозначается ~ А

      Вы можете запомнить первые два символа, связав их с фигурами объединения и пересечения. A ⋀ B будут элементами, которые существуют в обоих множествах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.

      В предыдущем примере таблица истинности просто обобщала то, что мы уже знаем о том, как работают операторы или . Ниже показаны таблицы истинности для основных утверждений и , или и , а не .

      Основные таблицы истинности

      А Б А ⋀ В
      Т Т Т
      Т Ф Ф
      Ф Т Ф
      Ф Ф Ф
      А Б А ⋁ В
      Т Т Т
      Т Ф Т
      Ф Т Т
      Ф Ф Ф
      А ~А
      Т Ф
      Ф Т

      Таблицы истинности становятся действительно полезными при анализе более сложных логических выражений.

      Пример 2

      Составьте таблицу истинности для утверждения 9.0040 A ⋀ ~( B ⋁ C )

      Помогает работать изнутри наружу при создании таблиц истинности и создавать таблицы для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для A , B и C . Обратите внимание, что первый столбец содержит 4 T, за которыми следуют 4 F, второй столбец содержит 2 T, 2 F, затем повторяется, а последний столбец чередуется. Этот шаблон гарантирует рассмотрение всех комбинаций. Наряду с этими начальными значениями мы перечислим значения истинности для самого внутреннего выражения, Б ⋁ С .

      А Б С В ⋁ С
      Т Т Т Т
      Т Т Ф Т
      Т Ф Т Т
      Т Ф Ф Ф
      Ф Т Т Т
      Ф Т Ф Т
      Ф Ф Т Т
      Ф Ф Ф Ф

      Затем мы можем найти отрицание B ⋁ C , работая с столбцом B ⋁ C , который мы только что создали.

      А Б С В ⋁ С ~( Б ⋁ С )
      Т Т Т Т Ф
      Т Т Ф Т Ф
      Т Ф Т Т Ф
      Т Ф Ф Ф Т
      Ф Т Т Т Ф
      Ф Т Ф Т Ф
      Ф Ф Т Т Ф
      Ф Ф Ф Ф Т

      Наконец, мы находим значения А и ~( В ⋁ С )

      А Б С В ⋁ С ~( Б ⋁ С ) А ⋀ ~( В ⋁ С )
      Т Т Т Т Ф  Ф
      Т Т Ф Т Ф Ф
      Т Ф Т Т Ф Ф
      Т Ф Ф Ф Т Т
      Ф Т Т Т Ф Ф
      Ф Т Ф Т Ф Ф
      Ф Ф Т Т Ф Ф
      Ф Ф Ф Ф Т Ф

      Оказывается, это сложное выражение верно только в одном случае: если А истинно, В ложно и С ложно.

      Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Сейчас мы поговорим о более общей версии условного предложения, иногда называемой 9.0053 следствие .

      Последствия

      Импликации — это логические условные предложения, утверждающие, что утверждение p , называемое антецедентом, подразумевает следствие q .

      Импликации обычно записываются как p → q

      Последствия аналогичны условным операторам, которые мы рассматривали ранее; p → q обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие. Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.

      Пример 3

      Английское высказывание «Если идет дождь, то на небе облака» является логическим следствием. Это правильный аргумент, потому что если антецедент «идет дождь» истинен, то следствие «на небе облака» также должно быть истинным.

      Обратите внимание, что утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.

      Пример 4

      Друг говорит вам, что «если вы загрузите эту фотографию в Facebook, вы потеряете работу». Возможны четыре исхода:

      1. Вы загружаете изображение и сохраняете свою работу
      2. Вы загрузили картинку и потеряли работу
      3. Вы не загружаете картинку и сохраняете свою работу
      4. Вы не загрузите картинку и потеряете работу

      Есть только один возможный случай, когда ваш друг солгал — первый вариант, когда вы загружаете картинку и сохраняете свою работу. В последних двух случаях ваш друг ничего не сказал о том, что произойдет, если вы не загрузите изображение, поэтому вы не можете заключить, что его заявление недействительно, даже если вы не загрузили изображение и все равно потеряли работа.

      В традиционной логике импликация считается достоверной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.

      Значения истинности для импликаций

      р q р → q
      Т Т Т
      Т Ф Ф
      Ф Т Т
      Ф Ф Т

      Пример 5

      Постройте таблицу истинности для утверждения ( m ⋀ ~ p ) → r

      Начнем с построения таблицы истинности для антецедента.

      м стр ~ р м ⋀ ~ р
      Т Т Ф Ф
      Т Ф Т Т
      Ф Т Ф Ф
      Ф Ф Т Ф

      Теперь мы можем построить таблицу истинности для импликации

      м р ~ р м ⋀ ~ р р ( м ⋀ ~ р ) → р
      Т Т Ф Ф Т Т
      Т Ф Т Т Т Т
      Ф Т Ф Ф Т Т
      Ф Ф Т Ф Т Т
      Т Т Ф Ф Ф Т
      Т Ф Т Т Ф Ф
      Ф Т Ф Ф Ф Т
      Ф Ф Т Ф Ф Т

      В этом случае, когда m истинно, p ложно, а r ложно, тогда антецедент m ⋀ ~ p будет истинным, но следствие ложным, что приведет к недопустимому импликации; каждый другой случай дает правильное следствие.

      Для любой импликации есть три связанных утверждения: обратное, обратное и контрапозитивное.

      Связанные заявления

      Первоначальный вывод: «если p , то q »: p → q

      Обратное: «если q , то p »: q → p

      Обратное «если не p , то не q »: ~ p → ~ q

      Противоположное «если не q , то не p »: ~ 90 040 → ~

      Пример 6

      Рассмотрим снова верный вывод: «Если идет дождь, значит, в небе облака».

      Обратное: «Если на небе облака, значит, идет дождь». Это, конечно, не всегда верно.

      Обратное: «Если не идет дождь, то на небе нет облаков». Точно так же это не всегда верно.

      Противоположным было бы: «Если на небе нет облаков, значит, не идет дождь». Это утверждение верно и эквивалентно исходному выводу.

      Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.

      Значение Конверс Обратный Противоположный
      р q р → q q → стр ~ р → ~ q ~ q → ~
      Т Т Т Т Т Т
      Т Ф Ф Т Т Ф
      Ф Т Т Ф Ф Т
      Ф Ф Т Т Т Т

      Эквивалент

      Условное утверждение и его противоположность логически эквивалентны.

      Обратное и обратное утверждение логически эквивалентны.

      Аргументы

      Логический аргумент — это утверждение о том, что набор предпосылок поддерживает вывод. Существует два основных типа аргументов: индуктивные и дедуктивные аргументы.

      Типы аргументов

      Индуктивный 9Аргумент 0056 использует набор конкретных примеров в качестве посылок и использует их, чтобы предложить общий вывод.

      дедуктивный аргумент использует набор общих утверждений в качестве своих предпосылок и использует их, чтобы предложить конкретную ситуацию в качестве вывода.

      Пример 7

      Аргумент «когда я пошел в магазин на прошлой неделе, я забыл свой кошелек, и когда я пошел сегодня, я забыл свой кошелек. Я всегда забываю свою сумочку, когда иду в магазин» — это индуктивный аргумент.

      Помещения:

      Я забыл свой кошелек на прошлой неделе

      Я забыл свой кошелек сегодня

      Вывод:

      Я всегда забываю свой кошелек

      Обратите внимание, что посылки — это конкретные ситуации, а заключение — это общее утверждение. В данном случае это достаточно слабый аргумент, так как он основан всего на двух случаях.

      Пример 8

      Аргумент «каждый день в течение последнего года самолет пролетает над моим домом в 2 часа дня. Каждый день в 14:00 над моим домом будет летать самолет» — более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств.

      Оценка индуктивных аргументов

      Индуктивный аргумент никогда не сможет доказать истинность вывода, но он может предоставить как слабое, так и сильное доказательство того, что оно может быть истинным.

      Многие научные теории, такие как теория большого взрыва, никогда не могут быть доказаны. Вместо этого они представляют собой индуктивные аргументы, подкрепленные широким спектром доказательств. Обычно в науке идея считается гипотезой до тех пор, пока она не будет тщательно проверена, после чего она становится теорией. Все общеизвестные научные теории, такие как теория гравитации Ньютона, выдержали годы испытаний и доказательств, хотя иногда их необходимо корректировать на основе новых данных. Для гравитации это произошло, когда Эйнштейн предложил общую теорию относительности.

      Дедуктивный аргумент является более верным или нет, что облегчает его оценку.

      Оценка дедуктивных аргументов

      Дедуктивный аргумент считается действительным, если все посылки верны, а вывод логически следует из этих посылок. Другими словами, посылки истинны, и заключение обязательно следует из этих посылок.

      Пример 9

      Аргумент «Все кошки — млекопитающие, а тигр — кошка, значит, тигр — млекопитающее» — верный дедуктивный аргумент.

      Помещения:

      Все кошки млекопитающие

      Тигр кошка

      Вывод:

      Тигр — это млекопитающее

      Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, можно использовать диаграмму Венна. Из первой посылки мы можем заключить, что множество кошек является подмножеством множества млекопитающих. Из второй посылки нам говорят, что тигр находится в множестве кошек. Отсюда на диаграмме Венна видно, что тигр также находится внутри множества млекопитающих, так что вывод верен.

      Анализ аргументов с помощью диаграмм Венна

      [2]

      Чтобы проанализировать аргумент с помощью диаграммы Венна

      1. Нарисуйте диаграмму Венна на основе посылок аргумента
      2. Если помещения недостаточно для определения того, что определяет расположение элемента, укажите это.
      3. Аргумент действителен, если ясно, что вывод должен быть верным

      Пример 10

      Предпосылка:          Все пожарные знают CPR

      Предпосылка:          Джилл знает СЛР

      Вывод:     Джилл — пожарный

      Из первой посылки мы знаем, что все пожарные входят в группу тех, кто знает СЛР. Из второй посылки мы знаем, что Джилл является членом этого большего множества, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшего подмножества, то есть пожарных.

      Поскольку вывод не обязательно следует из посылок, это неверный аргумент, независимо от того, действительно ли Джилл является пожарным.

      Важно отметить, что для оценки обоснованности аргумента не важно, действительно ли Джилл пожарный; нас интересует только то, достаточно ли посылок для доказательства вывода.

      В дополнение к этим категориальным посылкам стиля в форме «все ___», «некоторые ____» и «нет ____», также часто встречаются посылки, являющиеся импликациями.

      Пример 11

      Помещение:          Если вы живете в Сиэтле, вы живете в Вашингтоне.

      Посылка:          Маркус не живет в Сиэтле

      Вывод:     Маркус не живет в Вашингтоне

      Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества людей, живущих в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.

      Пример 12

      Рассмотрим аргумент «Вы женатый мужчина, поэтому у вас должна быть жена».

      Это неверный аргумент, так как есть, по крайней мере, в некоторых частях мира, мужчины, которые женаты на других мужчинах, так что предпосылка не является недостаточной, чтобы подразумевать вывод.

      Некоторые аргументы лучше анализировать с помощью таблиц истинности.

      Пример 13

      Рассмотрим аргумент:

      Посылка:          Если вы купили хлеб, то вы пошли в магазин

      Посылка:          Вы купили хлеб

      Вывод:     Вы пошли в магазин

      Хотя мы надеемся, что этот пример является довольно очевидным обоснованным аргументом, мы можем проанализировать его, используя таблицу истинности, представив каждую из предпосылок символически. Затем мы можем рассмотреть импликацию о том, что посылки вместе подразумевают вывод. Если таблица истинности является тавтологией (всегда истинной), то аргумент действителен.

      Получим, что B означает «вы купили хлеб», а S — «вы пошли в магазин». Тогда аргумент принимает вид:

      Посылка:          B → S

      Посылка:          B

      Вывод:     S

      Чтобы проверить достоверность, мы смотрим, подразумевает ли комбинация обеих посылок заключение; правда ли, что [( B → S ) ⋀ B ] → S ?

      Б С В → С ( Б → С ) ⋀ Б [( Б → С ) ⋀ Б ] → С
      Т Т Т Т Т
      Т Ф Ф Ф Т
      Ф Т Т Ф Т
      Ф Ф Т Ф Т

      Поскольку таблица истинности для [( B → S ) ⋀ B ] → S всегда верна, это правильный аргумент.

      Анализ аргументов с использованием таблиц истинности

      Чтобы проанализировать аргумент с помощью таблицы истинности:

      1. Символически представить каждую посылку
      2. Создайте условный оператор, соединив все посылки с помощью и для формирования антецедента и используя заключение в качестве следствия.
      3. Создайте таблицу истинности для этого утверждения. Если это всегда истинно, то аргумент действителен.

      Пример 14

      Предпосылка:         Если я пойду в торговый центр, то я куплю новые джинсы

      Предпосылка:          Если я куплю новые джинсы, я куплю к ним рубашку

      Вывод:     Если мне нужно торговый центр, я куплю рубашку.

      Пусть M = я иду в торговый центр, J = я покупаю джинсы и S = я покупаю рубашку.

      Посылки и заключение можно сформулировать так:

      Посылка:           M → J

      Посылка:            J → S

      Вывод:    M → S

      Мы можем построить таблицу истинности для [( M → J ) ⋀ ( J → S )] → ( M → S )

      М Дж С М → Дж Дж → С ( М → Дж ) ⋀ ( Дж → С ) М → С [( M → J ) ⋀ ( J → S )] → ( M → S )
      Т Т Т Т Т Т Т Т
      Т Т Ф Т Ф Ф Ф Т
      Т Ф Т Ф Т Ф Т Т
      Т Ф Ф Ф Т Ф Ф Т
      Ф Т Т Т Т Т Т Т
      Ф Т Ф Т Ф Ф Т Т
      Ф Ф Т Т Т Т Т Т
      Ф Ф Ф Т Т Т Т Т

      Из таблицы истинности мы видим, что это правильный аргумент.

      alexxlab

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *