Если два вектора коллинеарны и сонаправлены, то их сумма представляет со­бой вектор, направленный в ту же сторону и равный по модулю сумме модулей векторов слагаемых.

Если два вектора коллинеарны и направле­ны в противоположные стороны, то их сумма будет представлять собой вектор, модуль которого равен разности модулей векторов слагае­мых, направленный в сторону того вектора-сла­гаемого, модуль которого больше.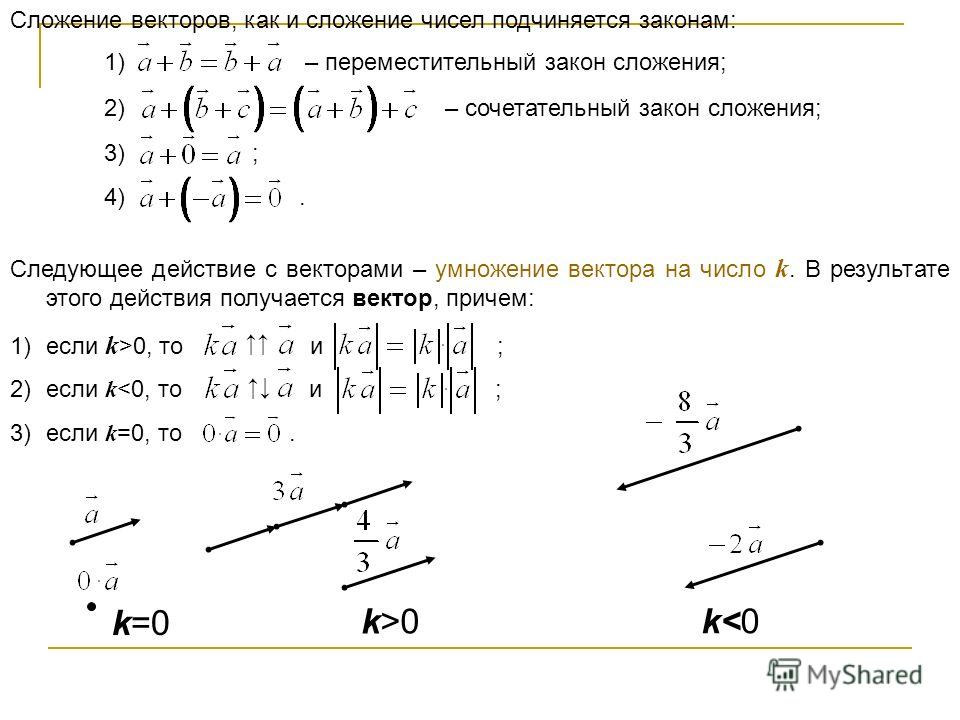

Сумма векторов может быть найдена и по правилу параллелограмма .

В этом случае параллельным переносом нуж­но совместить начала векторов а и в и построить на них параллелограмм. Тогда сумма а и в будет пред­ставлять собой диагональ этого параллелограмма.

2. Умножение вектора на скаляр.

Произведением вектора а на число k называют вектор в, коллинеарный век­тору а, направленный в сторону, что и вектор а, если k>0 и в направлен в проти­воположную сторону, если

Если два вектора коллинеарны, то они отличаются только скалярным мно­жителем.

Если к —1, то в—а. Вектор -а имеет модуль равный модулю вектора а, но на­правлен в противоположную сторону.

Два вектора, противоположно направленные и име­ющие равные длины, называются противоположными.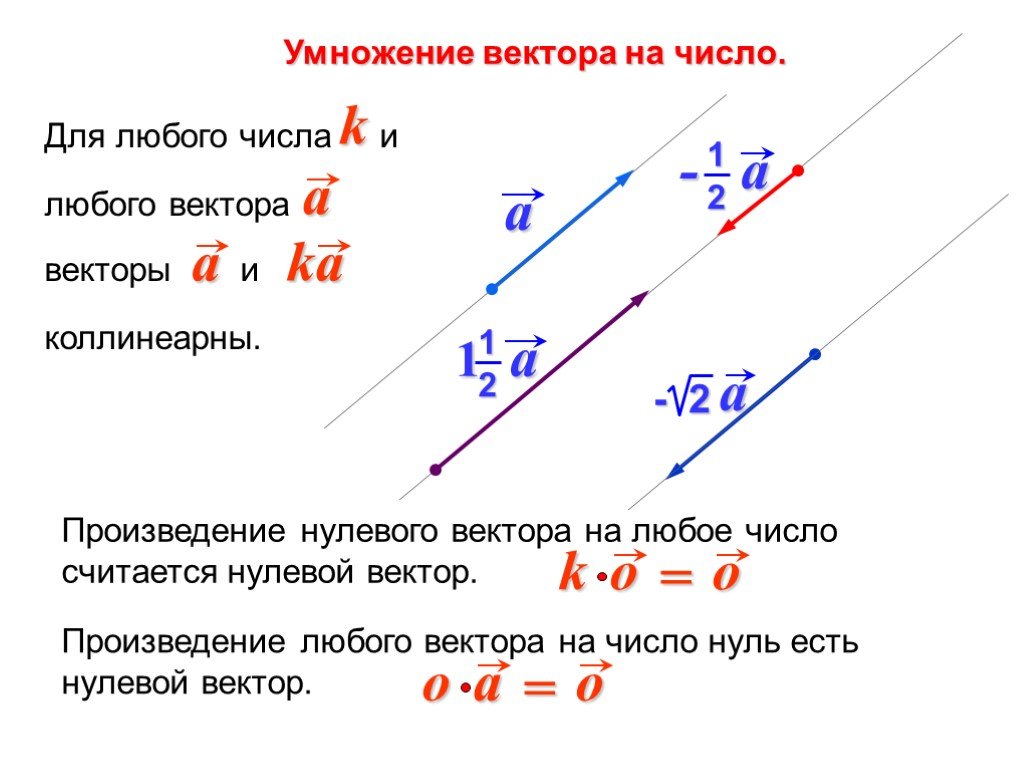 А~а представляют собой противоположные векторы.

3. Разность векторов.

Вычитание векторов есть действие, обратное сло­жению.

Разностью векторов в и а называют такой вектор h, который в сумме с векто­ром а дает вектор в.  h= в-а и h+a=e по определению одно и то же.

IV. Закрепление изученного

1. Какие величины называют скалярными, а какие — векторными?

2. Чем отличается векторная величина от скалярной?

3. Какие правила сложения векторов вы знаете?

4. Как производится сложение нескольких векторов?

5. Как определить разность двух векторов?

6. Какие вектора называются коллинеарными?

7. Как производится сложение и вычитание коллинеарных векторов?

V. Решение задач

1. Начало вектора а задано координатами точки А (2;2), конец В (6;5). Пост­роить вектор.

2. Эквивалентно замените силу Р=0,6 Н, приложенную в т. Л, двумя силами, действующими на ту же точку вдоль той же прямой, но противоположные сторо­ны. Меньшая из этих сил равна 1,1 Н. Каким должен быть модуль второй силы?

3. В одной точке приложены силы F, = 15 Н,Р₂=24 Н =19 H, f,= 20 Н. Определите их равнодействующую для случаев, когда

а) все данные силы действуют вдоль одной прямой в одну сторону.

б) все данные силы действуют вдоль одной прямой, первые две в одну сторо­ну, а вторые две — в сторону, противоположную первым.

Домашнее задание

§ 1-3 

Урок 4. Вектора и линейные операции над векторами

РАЗДЕЛ II. Поурочные разработки по физике к учебнику Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского

ВВЕДЕНИЕ

ФИЗИКА В ПОЗНАНИИ ВЕЩЕСТВА, ПОЛЯ, ПРОСТРАНСТВА И ВРЕМЕНИ

Урок 4. Вектора и линейные операции над векторами

Цель: познакомить с векторами и операциями над ними.

Ход урока

I. Повторение. Беседа

1. Что называется перемещением толчки?

2. Каков смысл модуля перемещения?

3. Что называется телом отсчета?

4. Какими способами можно задать положение точки?

5. Что называют радиус-вектором?

II. Изучение нового материала

Известно, что некоторые физические величины полностью характеризуются числом, которое выражает отношение этой величины к единице измерения.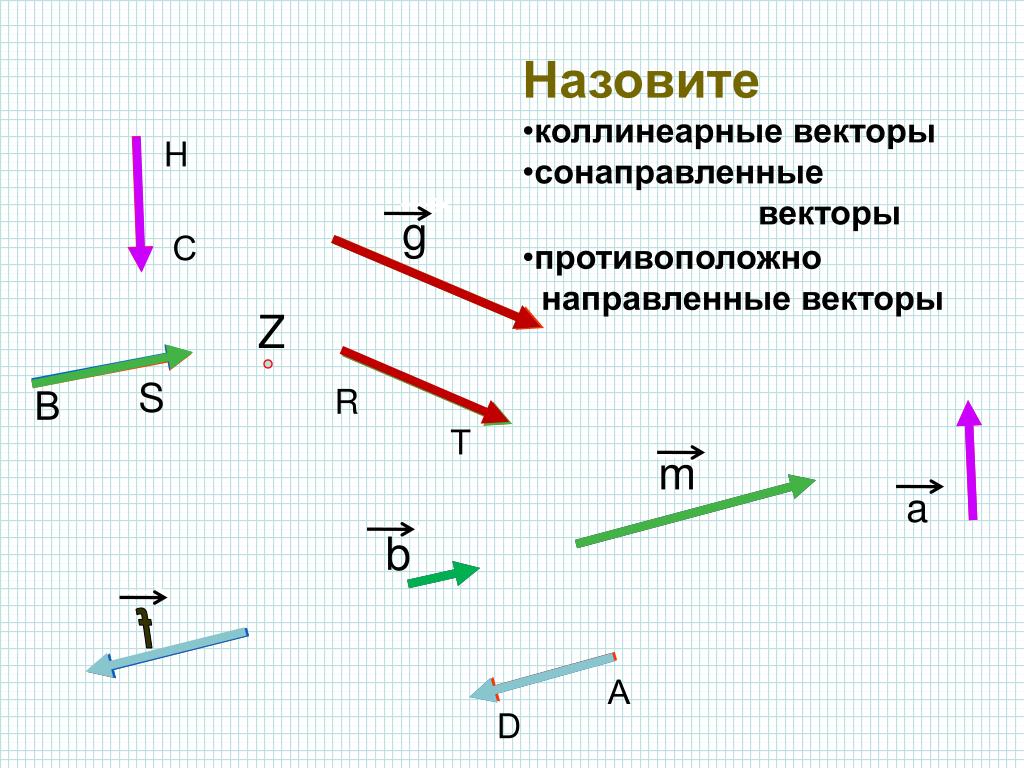 Такие величины называют скалярными.

— Приведите пример таких величин. (Примерами могут служить масса, температура, плотность, энергия.)

Для характеристики других физических величин, например скорости, силы, недостаточно знать число, измеряющее их величину, необходимо знать и их направление. Такие величины называют векторными. В физике они играют большую роль. Вектор — направленный отрезок прямой.

У вектора есть начало и конец. Начало вектора называют так же точкой его приложения.

Если точка А является началом вектора а, то мы будем говорить, что вектор а приложен к точке А (рис. 4).

Число, выражающее длину направленного отрезка, называют модулем вектора, и обозначают той же буквой, что и сам вектор, но без стрелки сверху.

Если начало вектора совпадает с его концом, такой вектор называют нулевым.

Вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 5).

Два вектора называют равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление.

Из определения равенства векторов вытекает утверждение: каковы бы ни были вектор а и т. Р, существует единственный вектор с началом в т. Р, равный вектору а.

В физике принципиальное значение имеют линия, вдоль которой направлен вектор, и точка приложения вектора.

1. Сумма векторов.

Пусть даны два вектора а и b. Для нахождения их суммы нужно вектор в перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора а. Тогда вектор, проведенный из начала вектора а в конец перенесенного вектора b, и будет являться суммой а и b. с = а + b = b + а — правило треугольника.

Если два вектора коллинеарны и сонаправлены, то их сумма представляет собой вектор, направленный в ту же сторону и равный по модулю сумме модулей векторов слагаемых.

Если два вектора коллинеарны и направлены в противоположные стороны, то их сумма будет представлять собой вектор, модуль которого равен разности модулей векторов слагаемых, направленный в сторону того вектора-слагаемого, модуль которого больше.

Сумма векторов может быть найдена и по правилу параллелограмма (рис. 6).

В этом случае параллельным переносом нужно совместить начала векторов а ив и построить на них параллелограмм. Тогда сумма а и b будет представлять собой диагональ этого параллелограмма.

2. Умножение вектора на скаляр.

Произведением вектора а на число k называют вектор b, коллинеарный вектору а, направленный в сторону, что и вектор а, если k 0 и в направлен в противоположную сторону, если k b = ka, причем модуль b = lklа.

Если два вектора коллинеарны, то они отличаются только скалярным множителем.

Если k = -1, то b = -а. Вектор -а имеет модуль равный модулю вектора а, но направлен в противоположную сторону.

Два вектора, противоположно направленные и имеющие равные длины, называются противоположными. А и -а представляют собой противоположные векторы.

3. Разность векторов.

Вычитание векторов есть действие, обратное сложению.

Пусть необходимо из вектора b вычесть вектор а и тем самым найти их разность, т. е. h = b — a. Чтобы найти вектор разности, нужно по правилу параллелограмма (или треугольника) сложить вектор b с вектором, противоположным вектору а, т. е. с вектором -а (рис. 7).

Разностью векторов b и а называют такой вектор h, который в сумме с вектором а дает вектор b. h = b — a и h + a = b по определению одно и то же.

III. Закрепление изученного

1. Какие величины называют скалярными, а какие — векторными?

2. Чем отличается векторная величина от скалярной?

3. Какие правила сложения векторов вы знаете?

4. Как производится сложение нескольких векторов?

5. Как определить разность двух векторов?

6. Какие вектора называются коллинеарными?

7. Как производится сложение и вычитание коллинеарных векторов?

IV. Решение задач

1. Начало вектора а задано координатами точки А (2;2), конец В (6;5). Построить вектор.

2. Эквивалентно замените силу F = 0,6 Н, приложенную в т. А, двумя силами, действующими на ту же точку вдоль той же прямой, но противоположные стороны. Меньшая из этих сил равна 1,1 Н. Каким должен быть модуль второй силы? (Ответ: 1,7 Н)

3. В одной точке приложены силы F₁ = 15 Н, F₂ = 24 Н, F₃ = 19 Н, F₄ = 20 Н. Определите их равнодействующую для случаев, когда

а) все данные силы действуют вдоль одной прямой в одну сторону.

б) все данные силы действуют вдоль одной прямой, первые две в одну сторону, а вторые две — в сторону, противоположную первым.

Домашнее задание

П. 5.

Умножение вектора на скалярный

★ ★ ★ ★ ★ [2 голоса]

Существует 4 урока в этом уроке по физике, покрывающим размножение вектора на Scalar . Учебник начинается с введения в Умножение вектора на скаляр , а затем следует список отдельных уроков, учебник предназначен для чтения по порядку, но вы можете пропустить определенный урок или вернуться, чтобы восстановить конкретный урок физики, необходимый для расширения ваших знаний по физике Умножение вектора на скаляр . Вы можете получить доступ ко всем урокам из этого руководства ниже.

В дополнение к учебнику по умножению вектора на скаляр на этой странице вы также можете получить доступ к следующим учебным ресурсам по векторам и скалярам для умножения вектора на скаляр

В этом учебнике по физике вы узнаете:

• Значение «Умножение вектора на скаляр»
• Как выразить деление вектора на скаляр в терминах умножения?
• Какие есть примеры умножения вектора на скаляр в физике?
• Как умножить вектор на скаляр в координатах?

Введение

В геометрии именно при обсуждении подобных фигур вы узнали, что две подобные фигуры одинаковы по форме, но их размеры различны. Например, два квадрата похожи, поскольку имеют одинаковые характеристики; они оба имеют 4 равные стороны, 4 прямых угла, 2 равные диагонали и т. д. Однако длина их соответствующих сторон различна. Посмотрите на рисунок:

Из правил подобия мы можем написать для вышеуказанных квадратов:

Квадрат 2 = 2 × Квадрат 1

Поскольку стороны второго квадрата в два раза длиннее сторон первого квадрата (6 см = 2 × 3 см) . (Не путайте величины соответствующих площадей поверхностей с размерами сторон. Площадь второго квадрата в 4 раза больше площади первого квадрата, но здесь мы просто написали «Квадрат 2 = 2 × Квадрат 1», а не « Площадь квадрата 2 = 2 × площадь квадрата 1″).

Понятно, что обе фигуры имеют одинаковые черты, кроме размеров. Например, их нижнее основание горизонтально; боковые стороны вертикальны в обоих квадратах и ​​так далее. Следовательно, мы можем сказать: «У подобных фигур все остальные признаки, кроме размеров, одинаковы». Это утверждение поможет вам понять умножение вектора на скаляр.

Пожалуйста, выберите конкретный урок «Умножение вектора на скаляр» из таблицы ниже, просмотрите видеоурок, распечатайте примечания к пересмотру или используйте практический вопрос, чтобы улучшить свои знания по этой теме физики.

Векторы и скаляры Учебный материал

Идентификатор учебника	Название учебника по физике	Учебник	Видео Учебник	Версия 3	6 Вопросы	70057
2. 3	Multiplication of a Vector by a Scalar
Lesson ID	Physics Lesson Title			Lesson	Video Lesson
2.3.1	Умножение вектора на положительную скалярную величину
2.3.2	Деление вектора на скалярную величину как умножение на обратную			Умножение вектора на отрицательную скалярную величину

★ ★ ★ ★ ★ [2 голоса]

Векторы и Скаларные расчеты.

• 2 D Vector Calculator
• Vector Calculator

Related Math Calculators by iCalculator

• 2D Vector Addition Calculator
• 2D Vector Angle Calculator
• 2D Vector Magnitude Calculator
• 2D Vector Scaler Product Calculator
• Angle between Two Калькулятор векторов

Физические калькуляторы

Вам также могут пригодиться следующие физические калькуляторы.

• Калькулятор сопротивления из-за температуры
• Калькулятор светимости гравитационных волн
• Калькулятор гравитационной потенциальной энергии
• Калькулятор теплопередачи при испарении
• Магнитная сила, действующая на движущийся заряд внутри однородного магнитного поля Калькулятор
• Калькулятор Боровского радиуса водородоподобных атомов вокруг длинного магнитного поля
• 90 Токонесущий провод
• Калькулятор энергии в релятивистских событиях
• Калькулятор эффекта Рамзауэра Таунсенда
• Калькулятор максимальной высоты снаряда
• Скорость потока в калькулятор PSI
• Калькулятор свойств жидкости
• Постоянный Q Калькулятор преобразования
• Угловая частота колебаний в калькуляторе RLC.
• Калькулятор общей средней мощности от колеблющегося диполя
• Калькулятор потока Фанно
• Калькулятор емкости куба

Векторы и скаляры. В этом уроке я буду описывать векторы… | Фархан Танвир Тушар | Open Physics Class

В этом уроке я буду описывать векторы и скалярные величины, их различия и различные типы векторов, включая единичные векторы.

Некоторые физические величины можно полностью описать одним числом, например, время, вес, длина и т. д. Эти величины называются скалярными величинами. Но в некоторых случаях одного номера недостаточно. Предположим, ваш дом находится в 5 км к северу от вашей школы. Кто-то спросил вас о местонахождении вашего дома, и вы сказали, что ваш дом находится в 5 км от вашей школы. Если он захочет найти ваш дом, вариантов для него бесконечно много. Он может пройти 5 км на восток или 5 км на запад или в любом другом направлении. Единственный способ, которым он может найти ваш дом, это если он пойдет на 5 км на север.

Итак, в данном случае «5 км» недостаточно для описания расстояния между вашим домом и школой. Также нужно указать направление. Эти типы величин называются векторными величинами. В этом случае значение в сочетании с направлением называется смещением. Другим примером векторной величины является сила. Сила имеет как величину, так и направление.

Вектор представлен стрелкой. Длина стрелки представляет собой величину или значение вектора, а направление стрелки — это направление вектора.

Вектор можно представить тремя способами. Во-первых, с двумя буквами и стрелкой над ними, где первая буква — начальная точка, а вторая — конечная. Во-вторых, с одной буквой со стрелкой над ней. В-третьих, жирным шрифтом. Величина или длина вектора представлена ​​абсолютным символом с вектором.

Два вектора могут быть равны, если они оба имеют одинаковую длину и одинаковое направление.

На предыдущем изображении оба A и B имеют одинаковую длину и одинаковое направление. Следовательно, векторы A и B равны. A и D также имеют одинаковую длину, но их направления противоположны. Итак, A и D не являются равными векторами. и C имеют одинаковое направление, но их длина различна. Итак, эти два вектора не равны.