Как производится умножение вектора на скаляр
Основы векторного исчисления
Вектором называется количественная характеристика, имеющая не только числовую величину, но и направление. Иногда говорят, что вектор это направленный отрезок.
Векторная система обозначений имеет два существенных преимущества.
1. Формулировки физических законов в векторной форме не зависят от выбора осей координат. Векторная система обозначений представляет собой такой язык, в котором формулировки имеют физическое содержание даже без введения системы координат.
2. Векторная система обозначений является компактной. Многие физические законы выражаются через векторные величины.
Определим основные операции, которые можно производить с векторами.
Равенство двух векторов
Два вектора 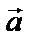 и
и 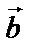
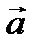 |
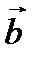 |
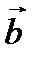 |
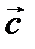 |
Сложение векторов
Суммой двух векторов называют вектор 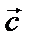 , проведенный из начальной точки вектора
, проведенный из начальной точки вектора 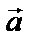 к конечной точке вектора
к конечной точке вектора 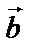 , если вектор
, если вектор  перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора
перенести параллельно самому себе так, чтобы его начало совпадало с концом вектора 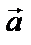
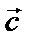 =
= 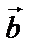 +
+ 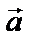 =
= 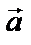 +
+ 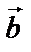 , если совместить начало векторов
, если совместить начало векторов 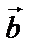
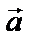 , то вектор
, то вектор 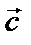 =
=  +
+ 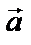 =
=  +
+ 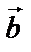 является диагональю параллелограмма, построенного на векторах
является диагональю параллелограмма, построенного на векторах 
 как на его сторонах и выходящий из общего начала. Сумма векторов не зависит от порядка, в котором складываются векторы.
как на его сторонах и выходящий из общего начала. Сумма векторов не зависит от порядка, в котором складываются векторы.Умножение вектора на скаляр
Произведением вектора 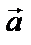 на число
на число 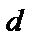 называется вектор
называется вектор 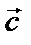 , длина которого равна длине первого вектора, умноженной на модуль числа, а направление либо совпадает с начальным вектором, либо противоположно.
, длина которого равна длине первого вектора, умноженной на модуль числа, а направление либо совпадает с начальным вектором, либо противоположно.
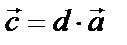
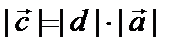 и
и 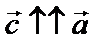 , если
, если 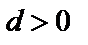 и
и 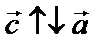 , если
, если 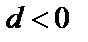 .
.
Произведение числа 0 на любой вектор дает нулевой вектор, который по сути таковым не является ибо он не имеет длины она равна “нулю” и не имеет направления в пространстве. Сумма двух векторов равна нулю тогда и только тогда, когда они равны по модулю и противоположны по направлению. Если
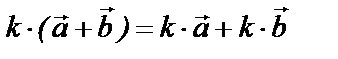 т. е. умножение вектора на скаляр дистрибутивно.
т. е. умножение вектора на скаляр дистрибутивно.Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9375 —  | 7304 —
| 7304 —  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В статье узнаете что такое вектор, векторные компоненты, единичный вектор, как складывать вектора, умножать вектора на скаляр, скалярное, векторное и смешанное произведение двух векторов.
Сохранение физической величины с вектором обычно означает совершенно иную ситуацию, чем просто сохранение ее скалярной длины. Постоянное значение импульса p (скаляр) может означать совершенно иную ситуацию, чем постоянный вектор p.

Вектор должен иметь три необходимые характеристики: значение (длина), направление, начало и конец.
Любое изменение любого из этих признаков — длины, направления или начало с концом — означает, что создан другой вектор. Два вектора равны тогда и только тогда, когда они имеют равную длину, направление и начало с концом.
Векторные компоненты
Компонентами вектора являются его проекции на оси системы координат.

Также в трехмерном пространстве векторы A называются векторами, которые являются проекциями этого вектора A на оси системы координат.
Имея вектор A, мы погружаем его в систему координат x, y, z. Векторы, являющиеся проекциями вектора A на оси системы, называются векторными компонентами вектора A. Вектор A является векторной суммой составляющих векторов Ax, Ay и Az .

Единичный вектор
Единичный вектор, имеющий то же направление, что и вектор, на который он ссылается, важен, но его длина всегда равна 1.

Единичные векторы осей координат. Мы также присваиваем единичные векторы оси системы отсчета. а) относится к правовращающей системе и б) к левосторонней системе.

Сложение векторов
Сумма вектора обычно не совпадает с суммой скалярных величин:

Добавление двух или более векторов друг к другу сводится к добавлению их компонентов, то есть проекций на опорные оси. Результирующий вектор называется случайным вектором. Для двух векторов результирующий вектор является диагональю параллелограмма, построенного на этих векторах. Метод параллелограмма.

В случае большего числа векторов результирующий вектор получается путем рисования одного из этих векторов, затем в конце первого вектора мы начинаем второй, в конце второго мы даем начало третьего и так далее. Полученный вектор является вектором, начало которого находится в начале первого из добавленных векторов. и его конец в конце последнего. При изменении порядка сложения результирующий вектор (красный) не меняет длину, направление:


Это правило добавления векторов также действует в трехмерном пространстве:

Умножение вектора на скаляр

Самым простым умножением, выполняемым на векторах, является умножение вектора на скаляр (число). Такое умножение не меняет направление вектора, но, как правило, меняет его длину и может изменить его конец (когда скаляр является отрицательным числом). Когда вектор A умножается на α-скаляр, мы получаем новый вектор B:

Скалярное произведение и векторное произведение двух векторов являются очень важными направления в физике и геометрии. Существует также смешанное произведение трех векторов.
Скалярное произведение двух векторов
Формально скалярное произведение векторов представляет собой точку, и ее значение определяется зависимостью

Скалярное произведение описывает способ, которым оба вектора видят друг друга, то есть как долго тень (проекция) отбрасывает каждый из векторов в своего партнера, когда угол между ними равен φ

B cos φ — длина тени, которую вектор B выбрасывает в вектор A. Аналогично, A cos φ — длина тени, которую вектор A выбрасывает в вектор B.
Когда длина проекции (тени) одного из векторов равна нулю, тогда длина проекции второго вектора равна нулю, то есть A • B = 0. Это означает, что эти векторы не работают в одном и том же направлении вообще. Работа, которую мы выполняем при движении автомобиля, зависит не только от приложенной силы F, но и от угла, который создает направление силы и направление пути.
Так как единичные векторы оси системы отсчета х, у и z, которые обозначают векторы ех, еYи еz, перпендикулярны друг к другу, то в виду того, что А • В = АВcosφ и что cos 0 = 1 и cos 90 o = 0, мы получаем произведение значений этих единичных векторов:

Выполнение аналогичного умножения на векторы A и B

мы получили новое выражение для скалярного произведения двух векторов A и B

Значение скалярного произведения двух векторов A и B можно записать в виде двух эквивалентных выражений:

Сравнивая оба выражения, мы находим выражение для угла между векторами A и B:

Векторное произведение двух векторов
Многие важные величины в науке и технике определяются вектором, который является произведением двух других векторов. В таких случаях произведение этих векторов, называемое векторным произведением , приводит к третьему вектору.
В этом случае задача состоит в том, чтобы определить все три особенности вектора C, являющегося произведением векторного произведения векторов A и B:
Произведение векторов A и B , приводящее к третьему вектору C, отмечено диагональным крестом

Направление
Вектор С такой, что вектор перпендикулярен к плоскости, образованной векторами A и B, которая перпендикулярна как к вектору A и B.

Длина
вектор С равен значению параллелограмма, построенного на векторах А и В. Числовой C = ABsin φ.

Начало и конец
Вектор С определяет правое направление движения шнека во время нанесения первого вектора, а именно А или B.
Изменение порядка применения векторов означает изменение знака векторного произведения.

Таким образом, действительное свойство векторного произведения выглядит следующим образом A*B= -B*A
В отличие от скалярного произведения, векторное произведение некоммутативно.

Мы встретимся с векторным произведением на протяжении всего курса физики. Это также часто встречается в механике, а также в науке об электричестве и магнетизме.
В повседневной жизни векторное произведение находится в виде момента силы во вращательном движении. Мы воздействуем на вращательное движение тем эффективнее, чем больше применяем момент силы.
При откручивании гайки гаечным ключом речь идет не только о силе F, но и о способе ее применения (длина рычага R и угол, который создает рычаг с направлением силы).

Все эти зависимости элегантно включены в одно выражение в виде векторного произведения:

Хотя составляющие вектора C, который является произведением векторного произведения векторов A и B, уже включены в его длину и направление, но имея данные составляющих векторов A и B, мы можем использовать их для определения компонентов вектора C в форме матрицы:

Удобнее всего рассчитать этот определитель, расширив относительно первой строки.
Смешанное произведение трех векторов
Смешанное произведение трех векторов является скалярным значением, равным значению детерминанта

Геометрическая интерпретация: смешанное произведение численно равно объему V параллелепипеда, растянутому по векторам A, B и C:

Циклическая корректировка векторов в смешанном произведении не меняет значение этого произведения, то есть:

Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Физика > Умножение векторов на скаляр
Умножение векторов на число: описание терминов и определения вектора и скаляра, как провести умножение векторов, свойства вектора и скаляра, пример с графиком.
При умножении вектора на скаляр меняется величина вектора, но не направление.
Задача обучения
- Обобщить взаимодействие между векторами и скалярами.
Основные пункты
- Вектор характеризуется величиной и направлением.
- Скаляр отображается лишь величиной.
- Умножение вектора на скаляр эквивалентно умножению вектора величины на скаляр.
Термины
- Вектор – количество, обладающее величиной и направлением (между двумя точками).
- Скаляр – количество с величиной (лишено направления).
- Величина – число вектора, указывающее на длину.
Обзор
Вектор и скаляры отображают разные типы физических величин, но иногда вынуждены контактировать. Конечно, они обладают разными размерами в пространстве, поэтому добавление невозможно. Однако вектор можно умножить на скаляр, а вот умножить скаляр на вектор не получится.
Чтобы проделать подобную операцию, следует умножать компоненты, а именно величины. Это создаст новый вектор с тем же направлением, но будет уже результатом двух величин.
Пример
Допустим, вы располагаете вектором А с определенными величиной и направлением. Если умножить его на скаляр с величиной 0.5, то новый вектор будет вдвое меньше изначального. Если же величина 3, то втрое больше. Чтобы разобраться детальнее, возьмем силу гравитации. Сила отображает вектор с величиной, зависящей от скаляра (масса), а направление идет вниз. Если массу удвоить, то сила тяжести также удвоится.

(I) – Умножение вектора А на скаляр (а = 0.5) создает вектор В, который вдвое длиннее.
(Ii) – Умножение вектора А на 3 утраивает его длину.
(Iii) – Удвоение массы (скаляр) удваивает и силу тяжести (вектор).
В физике умножение вектора на число приносит много пользы. Большая часть единиц в векторных величинах выступает внутренними скалярами, умноженными на вектор. К примеру, м/с для отображения скорости состоит их двух величин: скаляр длины в метрах и скаляр времени в секундах. Теперь вы знаете, как проводить умножение векторов.
Умножение векторов на скаляр
Физика > Умножение векторов на скаляр
Умножение векторов на число: описание терминов и определения вектора и скаляра, как провести умножение векторов, свойства вектора и скаляра, пример с графиком.
При умножении вектора на скаляр меняется величина вектора, но не направление.
Задача обучения
- Обобщить взаимодействие между векторами и скалярами.
Основные пункты
- Вектор характеризуется величиной и направлением.
- Скаляр отображается лишь величиной.
- Умножение вектора на скаляр эквивалентно умножению вектора величины на скаляр.
Термины
- Вектор – количество, обладающее величиной и направлением (между двумя точками).
- Скаляр – количество с величиной (лишено направления).
- Величина – число вектора, указывающее на длину.
Обзор
Вектор и скаляры отображают разные типы физических величин, но иногда вынуждены контактировать. Конечно, они обладают разными размерами в пространстве, поэтому добавление невозможно. Однако вектор можно умножить на скаляр, а вот умножить скаляр на вектор не получится.
Чтобы проделать подобную операцию, следует умножать компоненты, а именно величины. Это создаст новый вектор с тем же направлением, но будет уже результатом двух величин.
Пример
Допустим, вы располагаете вектором А с определенными величиной и направлением. Если умножить его на скаляр с величиной 0.5, то новый вектор будет вдвое меньше изначального. Если же величина 3, то втрое больше. Чтобы разобраться детальнее, возьмем силу гравитации. Сила отображает вектор с величиной, зависящей от скаляра (масса), а направление идет вниз. Если массу удвоить, то сила тяжести также удвоится.

(I) – Умножение вектора А на скаляр (а = 0.5) создает вектор В, который вдвое длиннее.
(Ii) – Умножение вектора А на 3 утраивает его длину.
(Iii) – Удвоение массы (скаляр) удваивает и силу тяжести (вектор).
В физике умножение вектора на число приносит много пользы. Большая часть единиц в векторных величинах выступает внутренними скалярами, умноженными на вектор. К примеру, м/с для отображения скорости состоит их двух величин: скаляр длины в метрах и скаляр времени в секундах. Теперь вы знаете, как проводить умножение векторов.
Умножение вектора на скаляр — Мегаобучалка
Векторная алгебра. Векторы.
П.1 основные определения.
Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…).
Определение 1. Вектором называется направленный отрезок с начальной точкой А и конечной В.
Начало вектора называется его точкой приложения.
Определение 2. Длиной вектора называется длина отрезка . Число, равное длине вектора, измеренного выбранной масштабной единицей, называется модулем.
Задать вектор – это значит задать его модуль и направление в пространстве.
Определение 3. Вектор называется единичным, если =1. Вектор называется нулевым или нуль-вектором, если . Нулевой вектор имеет любое направление.
Определение 4. Векторы и называются сонаправленными, если они параллельны (лежат на одной или параллельных прямых) и имеют одинаковое направление, если при этом направление не совпадает, то векторы называются противоположно направленными.
– сонаправлены. – противоположно направлены.
Определение 5.Векторы и называются равными, если .
Определение 6. Единичный вектор, имеющий одинаковое направление с вектором , называется ортом вектора и обозначается .
=1.
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором.
С помощью параллельного переноса векторы можно перемещать в любое место пространства.
П.2 Линейные действия над векторами.
Сложение векторов.
А) Правило треугольника: + = .
В) Правило параллелограмма: вектор направлен по диагонали параллелограмма, построенного на векторах и .
С) Для сложения трех векторов в пространстве существует правило параллелепипеда: + + = .
Свойства сложения: 1. + = +
2. + + = ( + )+ = + ( + )
3. + =
4. Если + + = , то
Вычитание векторов.
Определение 8.Противоположным вектором к вектору называется вектор , причем .
Вычесть вектор, значит прибавить противоположный (по правилу параллелограмма):
Или по правилу треугольника
Вывод из 1 и 2 :
векторы суммы и разности векторов направлены по диагоналям параллелограмма, построенного на векторах и .
Умножение вектора на скаляр.
Определение 9.Пусть λ – действительное число, тогда произведением числа λ на вектор называется вектор такой, что 1) 2) , если и , если .
, причем .
Умножение вектора на число – это растяжение или сжатие вектора с сохранением или с изменением на противоположное направления.
Свойства произведения: 1. 2. 3. 4.
5. λ ( + ) = λ + λ 6. 7. 8.
Определение 10. Векторы, лежащие на одной или параллельных прямых, называются коллинеарными.
коллинеарен любому вектору.
Теорема 1(о необходимом и достаточном условии коллинеарности векторов). Равенство , где λ – действительное число, справедливо тогда и только тогда, когда векторы и коллинеарны, при этом если , то , если , то , если λ = 0, то направление любое.
Доказательство.
Необходимость ( ). Пусть , тогда по определению 9 векторы и лежат на одной или параллельных прямых, совпадают или противоположны по направлению. Тогда. По определению 10, векторы и коллинеарны.
Достаточность ( ). Пусть векторы и коллинеарны, тогда по определению 10, они расположены на одной или параллельных прямых, при этом они совпадают или противоположны по направлению. Такие векторы можно получить, используя определение 9, т.е. , где λ – действительное число. (что и требовалось доказать)
Определение 11. Векторы, лежащие в одной плоскости, называются компланарными.
УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
Пусть даны вектор 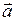 и скаляр
и скаляр 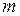 . При умножении вектора
. При умножении вектора 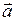 на скаляр
на скаляр 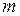 модуль вектора
модуль вектора 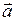 изменяется в
изменяется в 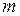 раз, а его направление остаётся прежним или меняется на противоположное в зависимости от того, будет скаляр положительным или отрицательным числом. В результате такого действия образуется новый вектор ma, который называется произведением вектора
раз, а его направление остаётся прежним или меняется на противоположное в зависимости от того, будет скаляр положительным или отрицательным числом. В результате такого действия образуется новый вектор ma, который называется произведением вектора 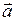 на скаляр
на скаляр 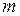 , т.е.
, т.е. 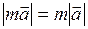 , где
, где 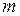 — абсолютная величина числа
— абсолютная величина числа 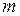 .
.
Введём понятие единичного вектора. Единичным вектором, или «ортом », направления 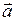 называется
называется 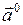 , имеющий направление вектора
, имеющий направление вектора 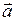 и модуль, равный единице:
и модуль, равный единице:  , тогда вектор
, тогда вектор 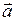 можно записать через единичный вектор следующим образом:
можно записать через единичный вектор следующим образом: 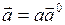 , где а – модуль вектора
, где а – модуль вектора 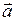 .
.
Любой вектор можно представить как произведение единичного вектора на модуль данного вектора. Например, дан вектор 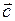 , пусть
, пусть 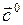 — единичный вектор, с – модуль вектора
— единичный вектор, с – модуль вектора 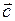 , тогда
, тогда 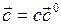 .
.
Проекция любого вектора, на какую либо ось равна его модулю, умноженному на косинус угла между положительным направлением оси проекции и направлением самого вектора. Из рисунка 5 следует, что
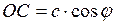 .
.

А теперь рассмотрим, что происходит в случае умножения вектора на положительный скаляр и на отрицательный скаляр.
Пусть у нас будут даны: вектор A и скаляр 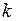 .
.
При умножении вектора A на положительный скаляр 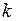 получаем новый вектор (
получаем новый вектор ( 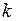 A), направление которого совпадает с направлением вектора A, а числовое значение отличается в
A), направление которого совпадает с направлением вектора A, а числовое значение отличается в 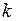 раз.
раз.
Пример 3: Определить импульс тела массой 2 кг, движущегося со скоростью 5 м/с.
Решение: Импульс тела равен:  кг · м/с и направлен в сторону
кг · м/с и направлен в сторону  (рис.6).
(рис.6).

При умножении вектора A на отрицательный скаляр 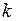 получаем новый вектор (
получаем новый вектор ( 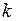 A), направление которого противоположно вектору A, а числовое значение отличается в
A), направление которого противоположно вектору A, а числовое значение отличается в 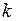 раз.
раз.
Пример 4: Заряд 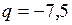 нКл помещён в электрическое поле с напряженностью
нКл помещён в электрическое поле с напряженностью 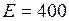 В/м. Найти модуль и направление силы, действующей на заряд.
В/м. Найти модуль и направление силы, действующей на заряд.
Решение: Сила, по определению, равна 
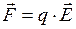 . Так как заряд отрицателен, то вектор силы направлен в сторону, противоположную
. Так как заряд отрицателен, то вектор силы направлен в сторону, противоположную 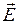 (рис.7). Модуль силы равен
(рис.7). Модуль силы равен 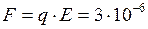 Н
Н 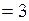 мкН.
мкН.

5. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Скалярным произведением двух векторов 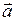 и
и 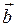 называется произведение их модулей на косинус угла между ними.
называется произведение их модулей на косинус угла между ними.
Скалярное произведение обозначается через ( 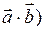 или
или 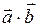 .
.
Итак, по определению скалярное произведение двух векторов 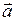 и
и 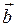 равно
равно
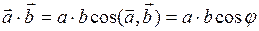 ,
,
где 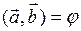 — угол между векторами
— угол между векторами 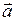 и
и 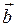 .
.
Скалярное произведение двух векторов есть скалярная величина, положительная или отрицательная, в зависимости от того, будет  больше или меньше нуля, т.е. острый или тупой угол образуют векторы
больше или меньше нуля, т.е. острый или тупой угол образуют векторы 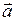 и
и 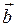 . Примером скалярного произведения является механическая работа
. Примером скалярного произведения является механическая работа 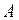 , равная произведению силы
, равная произведению силы 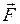 на вектор перемещения
на вектор перемещения 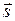 и косинус угла между ними, т.е.
и косинус угла между ними, т.е.
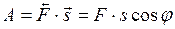 .
.
Если векторы параллельны, то скалярное произведение равно 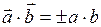 , так как
, так как  ;
; 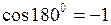 .
.
Если векторы перпендикулярны 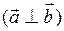 , то скалярное произведение векторов равно нулю:
, то скалярное произведение векторов равно нулю: 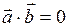 , так как
, так как 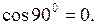
Пример5: Найти работу постоянной силы 20 Н, если перемещение тела 7,5 м , а угол 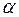 между силой и перемещением равен 1200.
между силой и перемещением равен 1200.
Решение: Работа силы равна, по определению, скалярному произведению силы и перемещения:
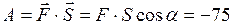 Дж
Дж
Дата добавления: 2016-09-06; просмотров: 5037;
Похожие статьи:
2. Линейные операции над векторами
К линейным операциям над векторами относятся следующие операции:
сложение векторов;
вычитание векторов;
умножение вектора на скаляр (действительное число).
2.1 Сложение векторов
Определение 2.1. Суммой двух векторов 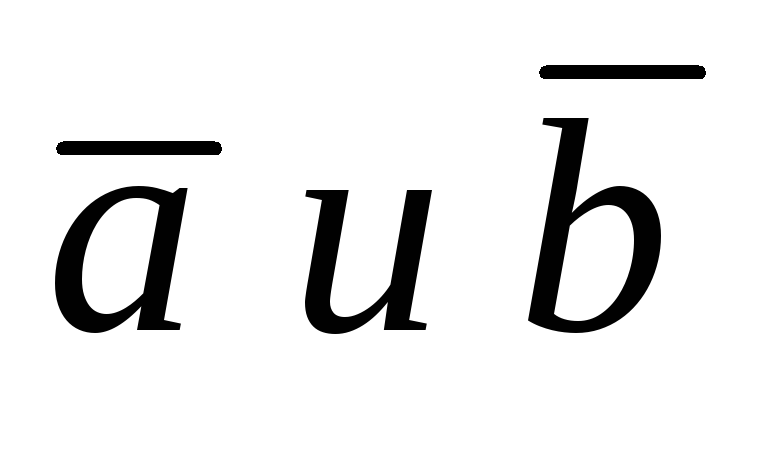 называется третий вектор
называется третий вектор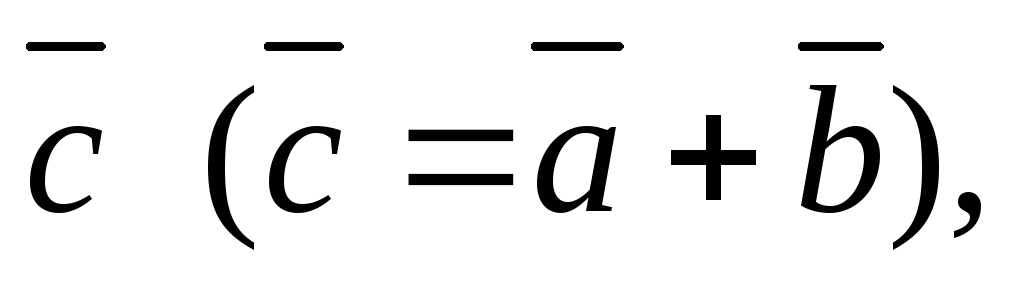 имеющий своим началом начало вектора
имеющий своим началом начало вектора ,
а концом – конец вектора
,
а концом – конец вектора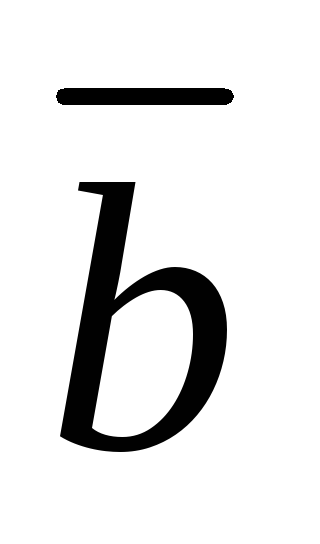 при условии, что начало вектора
при условии, что начало вектора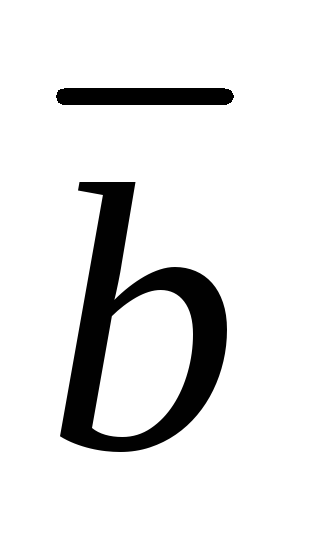 совпадает с концом вектора
совпадает с концом вектора (вектор
(вектор приведен к концу вектора
приведен к концу вектора )(рис. 2.1).
)(рис. 2.1).
Это определение сложения двух векторов носит название «правило треугольника.
Э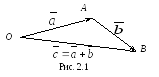 то
правило сложения векторов можно
распространить на любое их количество.
то
правило сложения векторов можно
распространить на любое их количество.
Правило. Чтобы сложить любое
количество векторов, следует расположить
их так, чтобы конец каждого предыдущего
вектора был началом следующего и
построить вектор 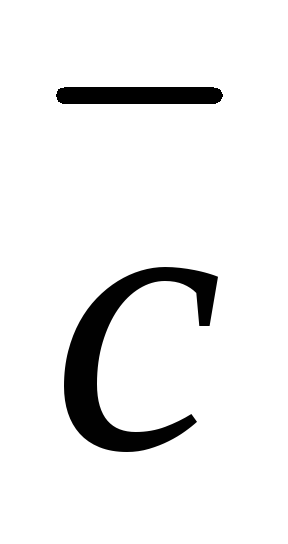 началом в начале первого и концом в
конце последнего вектора(рис. 2.2).
началом в начале первого и концом в
конце последнего вектора(рис. 2.2).
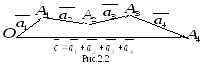
Наряду с правилом треугольника сложения векторов существует «правило параллелограмма»
О пределение
2.1*. Суммой
векторов
пределение
2.1*. Суммой
векторов  и
и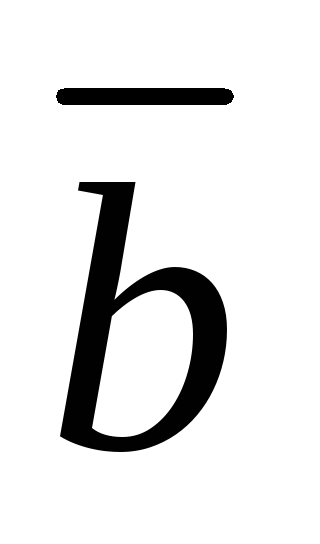 является вектор
является вектор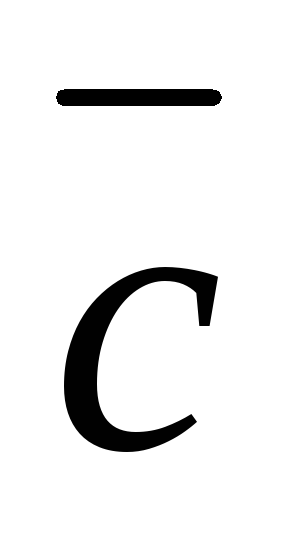 – вектор-диагональ параллелограмма,
построенного на векторах
– вектор-диагональ параллелограмма,
построенного на векторах и
и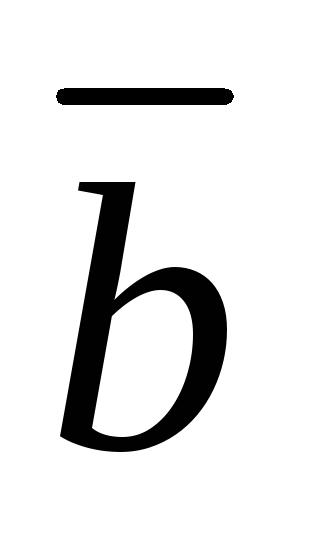 ,
причем векторы
,
причем векторы и
и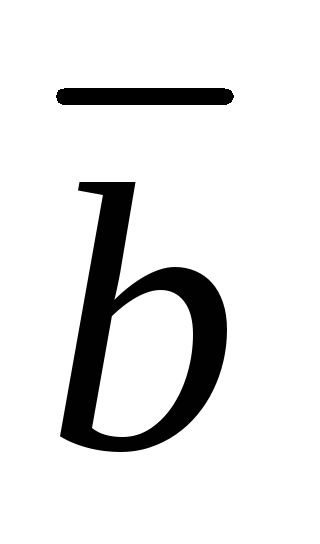 приведены к одному началу(рис. 2.3).
приведены к одному началу(рис. 2.3).
На рис 2.3 этой диагональю является
диагональ 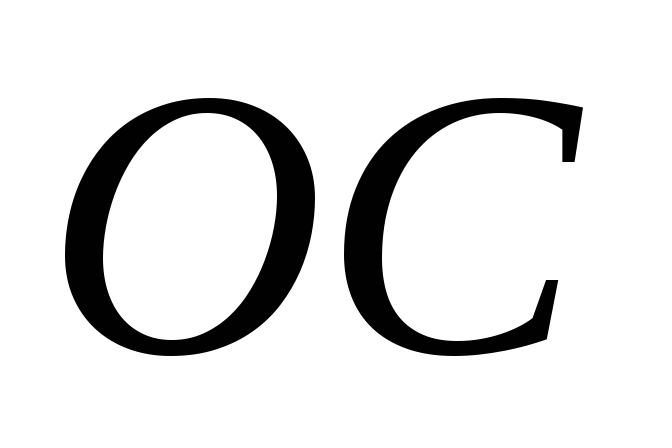 .
.
П о
правилу параллелограмма определяется
равнодействующая двух сил. Для нахождения
равнодействующей сил
о
правилу параллелограмма определяется
равнодействующая двух сил. Для нахождения
равнодействующей сил
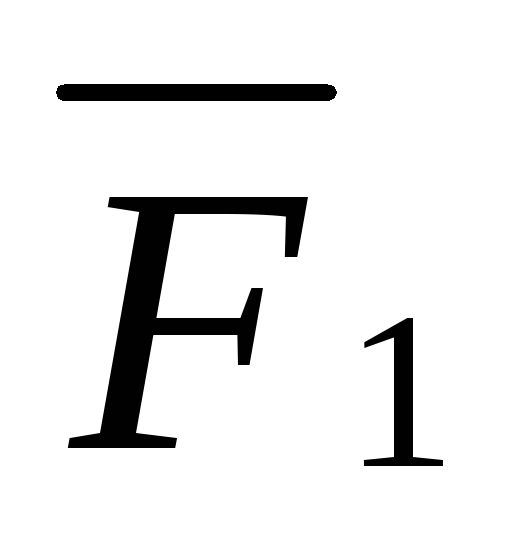 и
и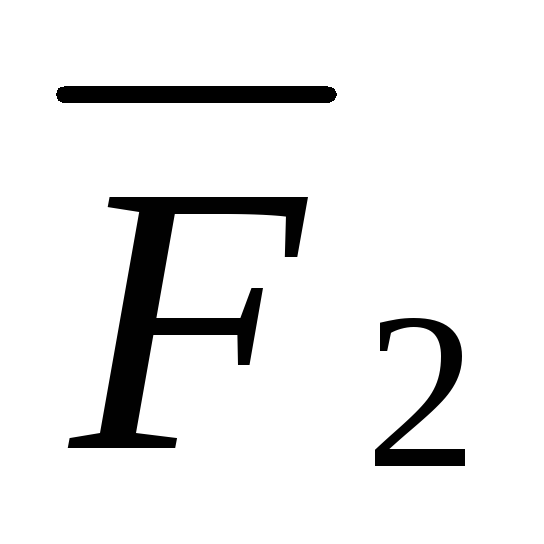 ,
,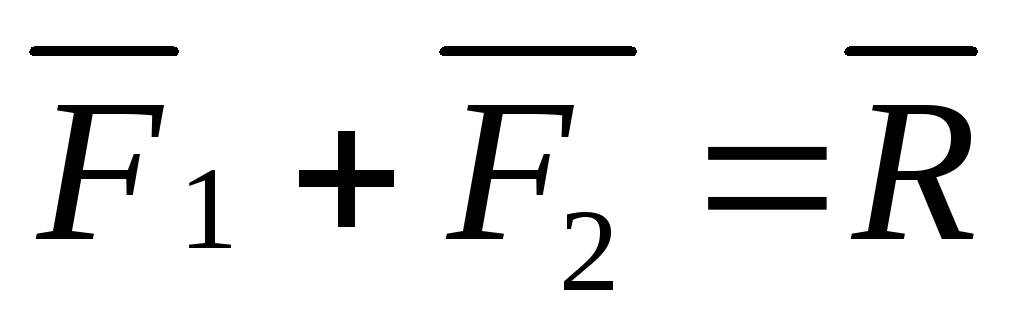 ,
приводим эти силы к точке
,
приводим эти силы к точке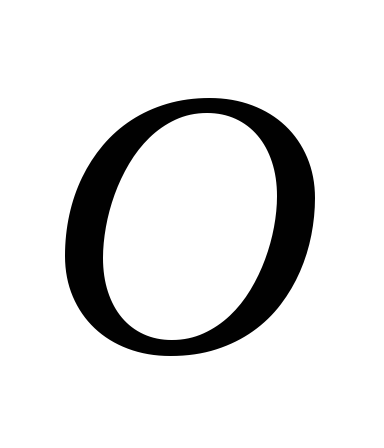 и строим на них параллелограмм.
Вектор-диагональ
и строим на них параллелограмм.
Вектор-диагональ параллелограмма и является равнодействующих
этих сил (рис. 2.4).
параллелограмма и является равнодействующих
этих сил (рис. 2.4).
Свойства сложения векторов
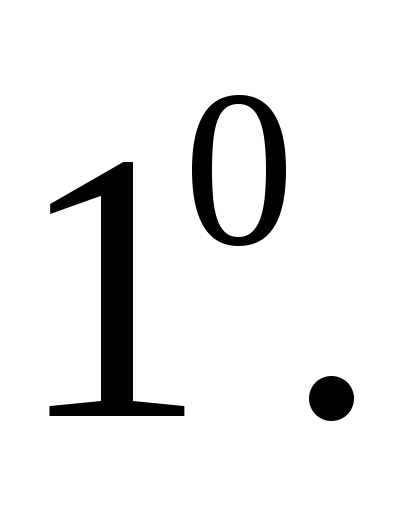
 –коммутативный (переместительный)
закон.
–коммутативный (переместительный)
закон.
Рис. 2.3 иллюстрирует справедливость
свойства. В самом деле: 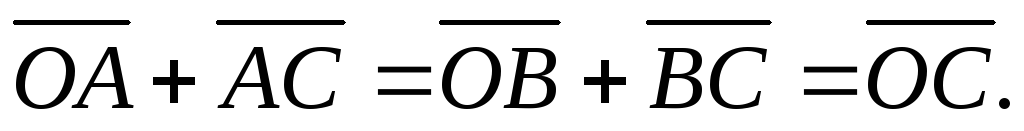

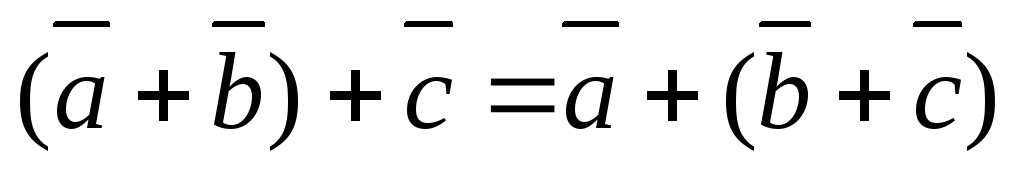 ‑ассоциативный (сочетательный)
закон.
‑ассоциативный (сочетательный)
закон.
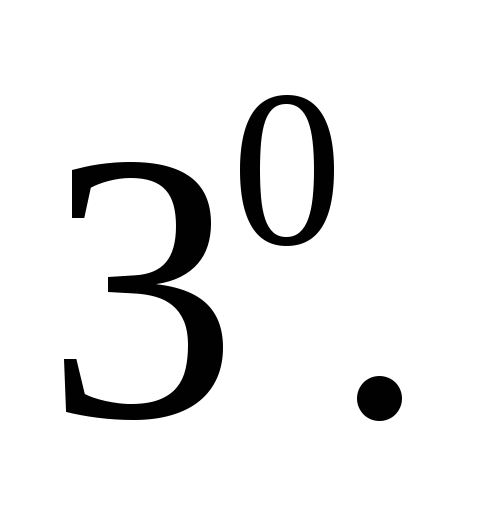
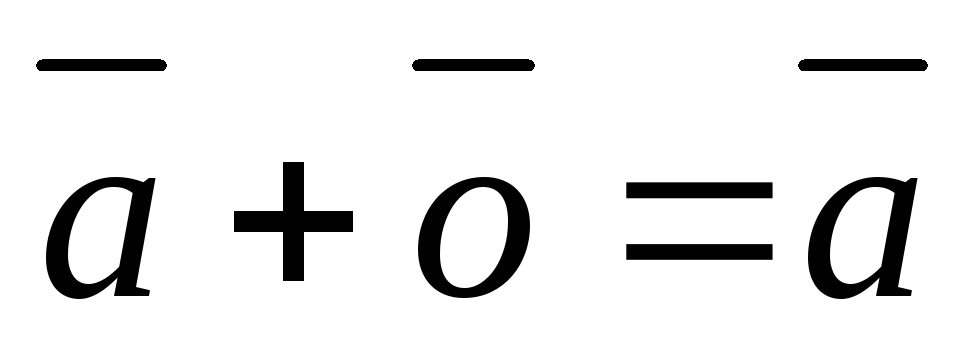 для любого вектора
для любого вектора  .
.
 Для любого вектора
Для любого вектора  :
: 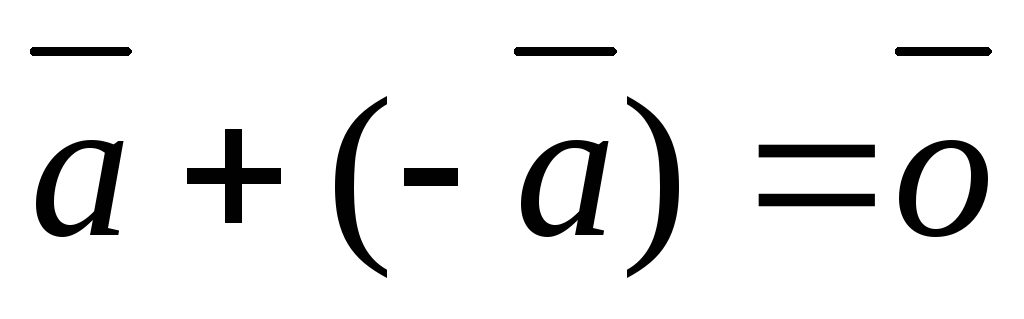 .
.
2.2 Вычитание векторов
Определение 2.2. Разностью
двух векторов  и
и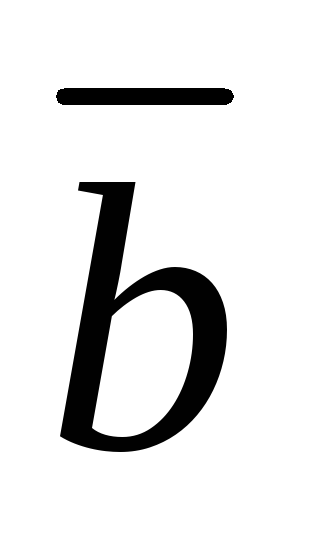 называется третий вектор
называется третий вектор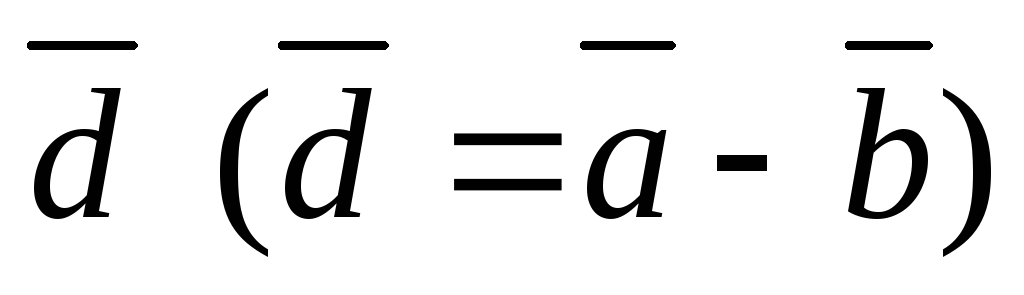 ,
такой, что
,
такой, что .
.
Покажем, как реализуется на практике сформулированное определение понятия разности.
Задача 2.1. Даны два вектора:
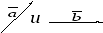
Найти: разность векторов  и
и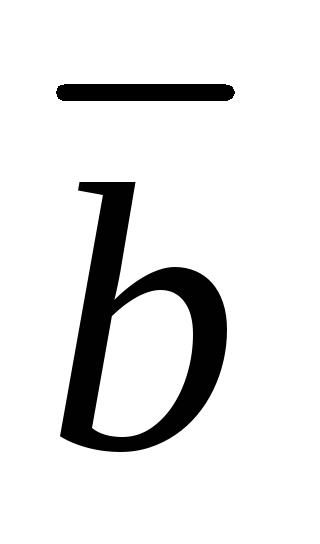 .
.
Р ешение.Приведем варианта два решения.
ешение.Приведем варианта два решения.
10. Из определения следует: чтобы
построить разность двух векторов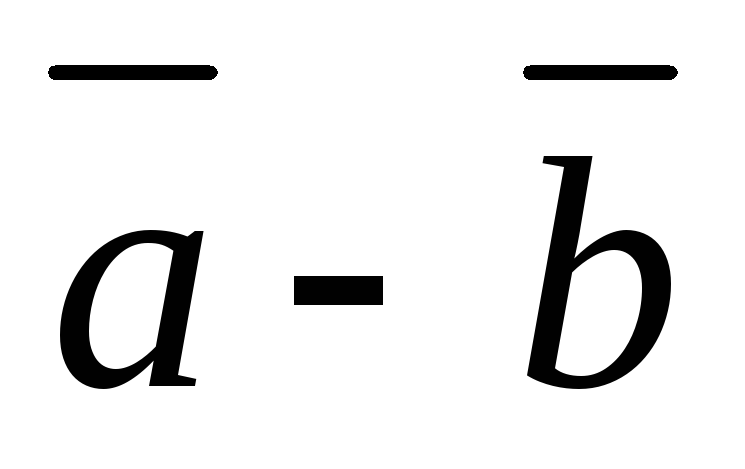 эти векторы надо привести к одному
началу, а затем построить вектор с
началом в конце вектора
эти векторы надо привести к одному
началу, а затем построить вектор с
началом в конце вектора и концом в конце вектора
и концом в конце вектора (рис. 2.5). Суммой векторов
(рис. 2.5). Суммой векторов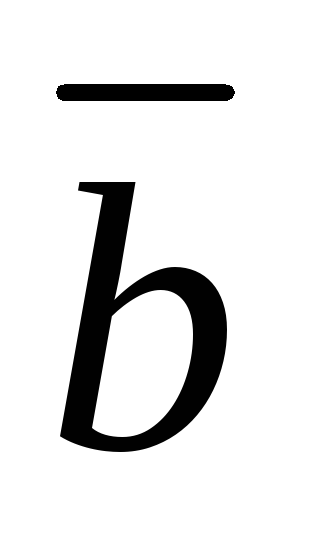 и
и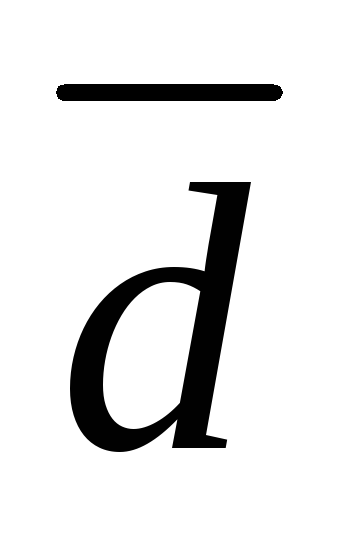 является вектор
является вектор  .
.
Обратимся к рис. 2.3. В параллелограмме OACB диагональOC является суммой векторов и
и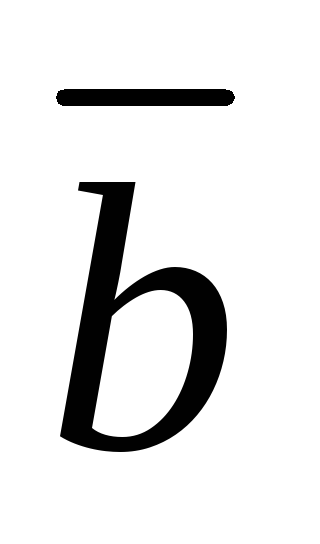 ,
а диагональBA –
разностью этих векторов.
,
а диагональBA –
разностью этих векторов.
2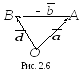 0.
Преобразуем равенство
0.
Преобразуем равенство 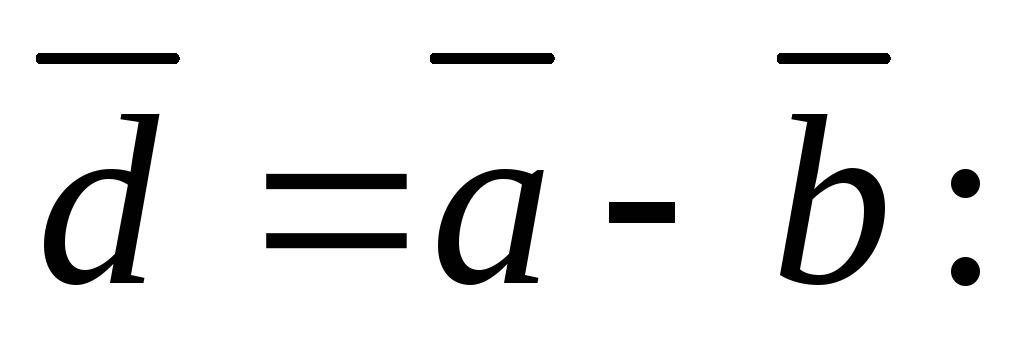
 .
Следовательно, вектор
.
Следовательно, вектор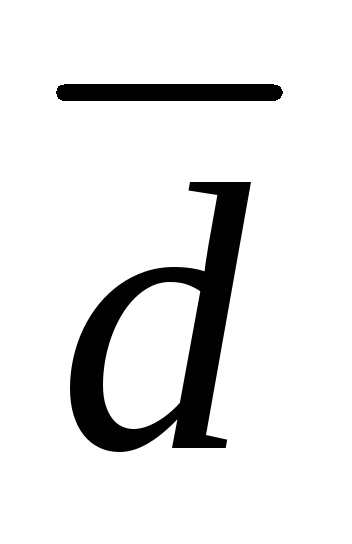 является суммой вектора
является суммой вектора и вектора
и вектора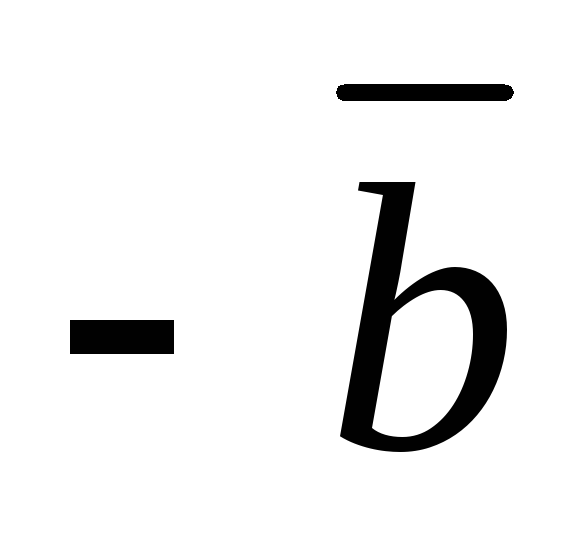 ,
противоположного вектору
,
противоположного вектору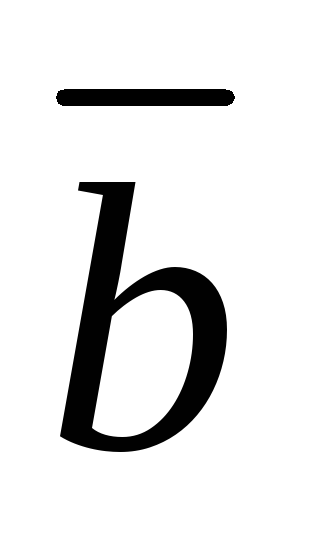 .
Отсюда следует построение искомой
разности векторов (рис. 2.6).
.
Отсюда следует построение искомой
разности векторов (рис. 2.6).
2.3. Умножение вектора на скаляр
О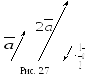 пределение
2.3. Произведением вектора
пределение
2.3. Произведением вектора  на скаляр
на скаляр называется вектор
называется вектор 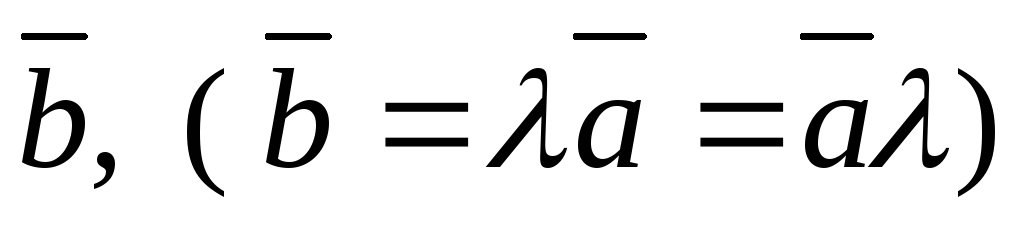 ,
удовлетворяющий двум условиям:
,
удовлетворяющий двум условиям:
Свойства умножения вектора на скаляр
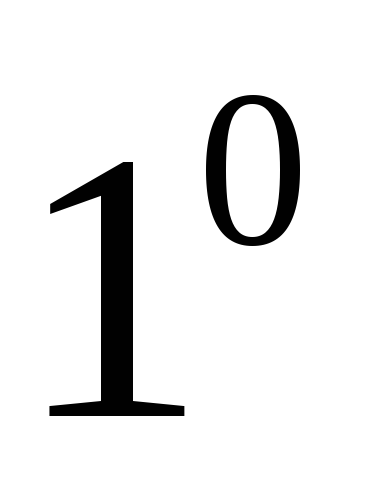 .
. ;
;
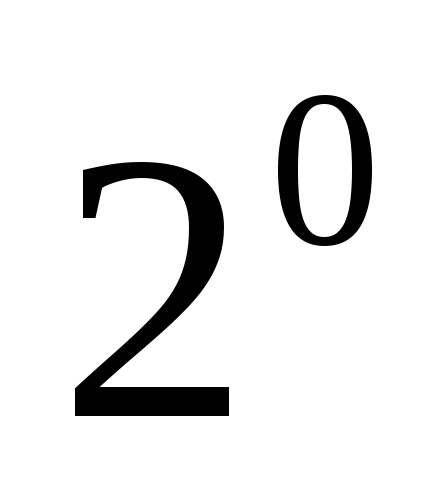 .
.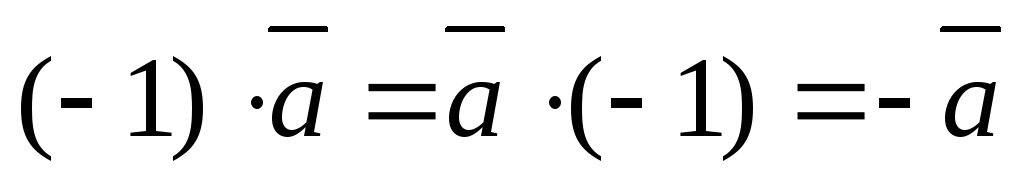 ;
;
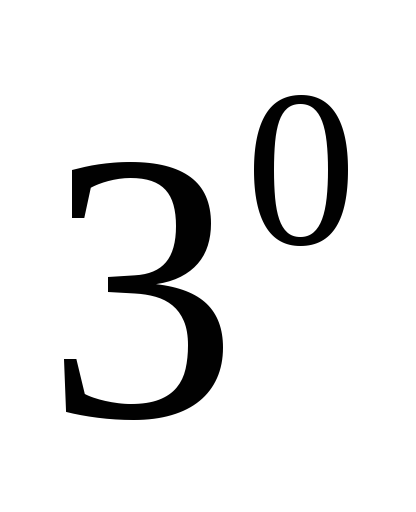 .
. 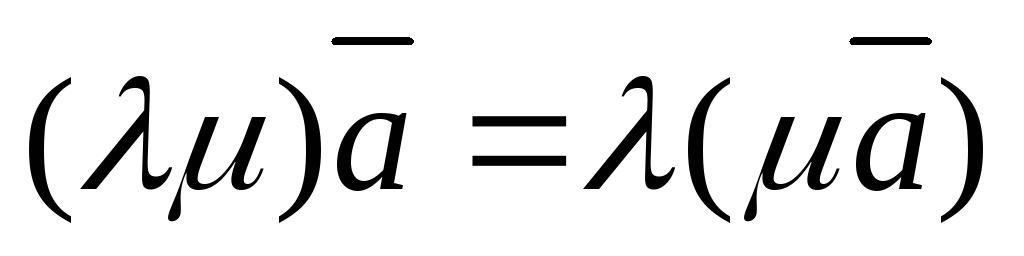 ассоциативный (сочетательный) закон по
отношению к скалярным множителям;
ассоциативный (сочетательный) закон по
отношению к скалярным множителям;
 .
. 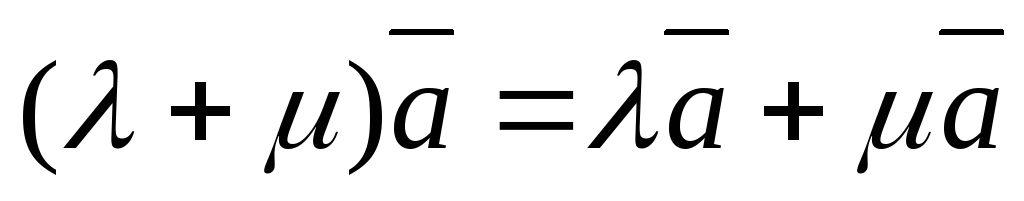 – дистрибутивный (распределительный)
закон по отношению к векторному множителю;
– дистрибутивный (распределительный)
закон по отношению к векторному множителю;
 .
. 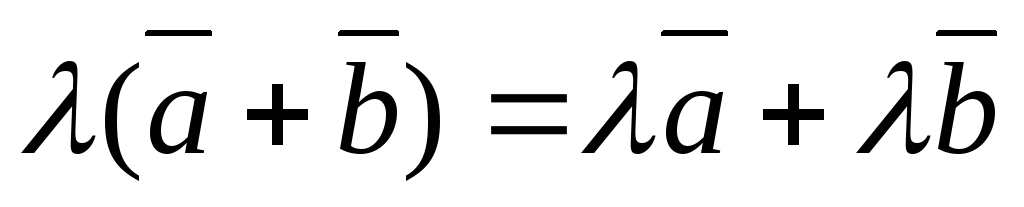 – дистрибутивный (распределительный)
закон по отношению к числовому множителю.
– дистрибутивный (распределительный)
закон по отношению к числовому множителю.
Замечание. Свойства сложения векторов и умножения вектора на число свидетельствуют о следующем: векторные одночлены и многочлены можно преобразовывать относительно этих операций по правилам преобразования алгебраических одночленов и многочленов.
В заключение рассмотрим пример использования изученных свойств на практике.
Задача 2.2.Даны два вектора  и
и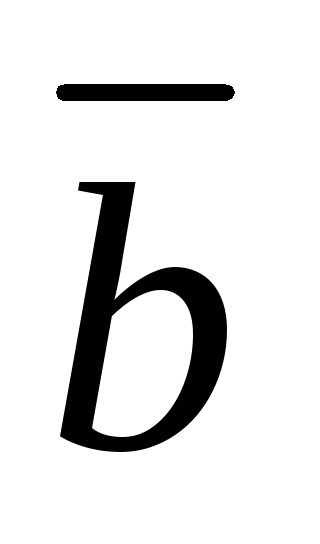 :
:

Найти: вектор 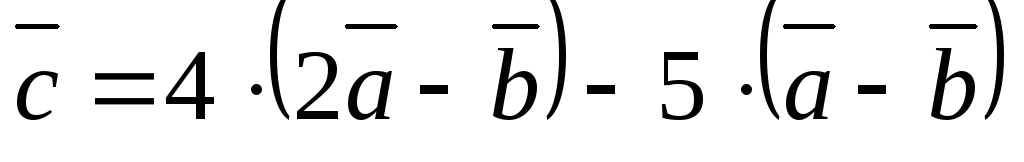 .
.
Решение.Преобразуем выражение
вектора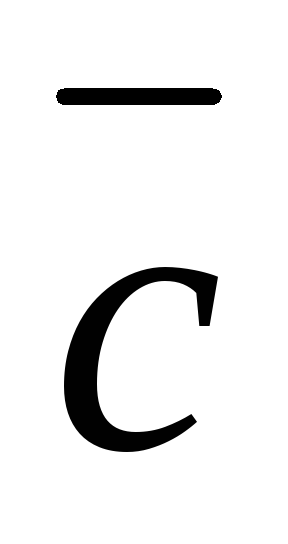 ,
используя свойства сложения векторов
и умножения вектора на скаляр:
,
используя свойства сложения векторов
и умножения вектора на скаляр:
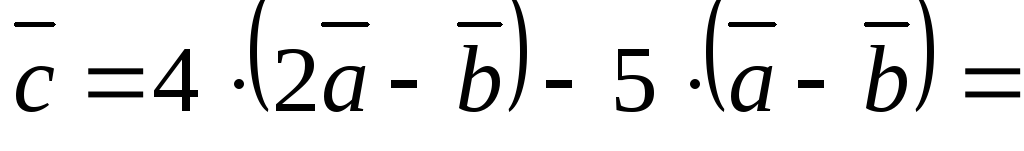
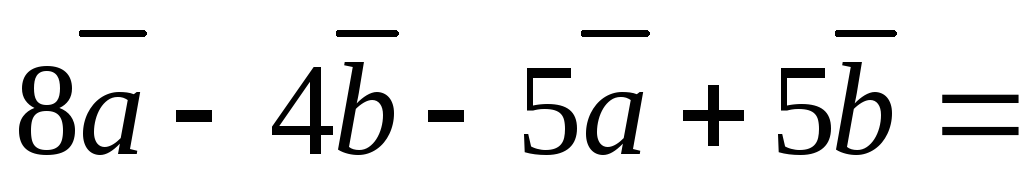
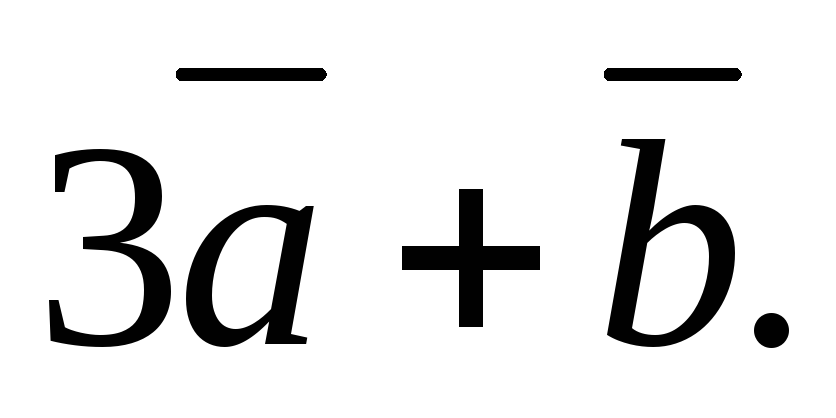
Полученную сумму построим по правилу треугольника (рис. 2.8).

