Условие коллинеарности векторов, когда векторы параллельны, свойства коллинеарных векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Определение 1Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→, μ∈R
Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).
По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay или ax=μ·bxay=μ·by
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Определение 4Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Пример 1Исходные данные: векторы a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1
Т. е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.
е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Пример 2Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.
Пример 3Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении pзаданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7
тогда λ=37, а p=λ·2⇔p=67 .
Ответ: при p=67 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Пример 4Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .
Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).
Пример 5Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)
Ответ: (352, 452,- 12)
Решение задач
от 1 дня / от 150 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Вектор (геометрия) | это… Что такое Вектор (геометрия)?
Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
Содержание
|
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности.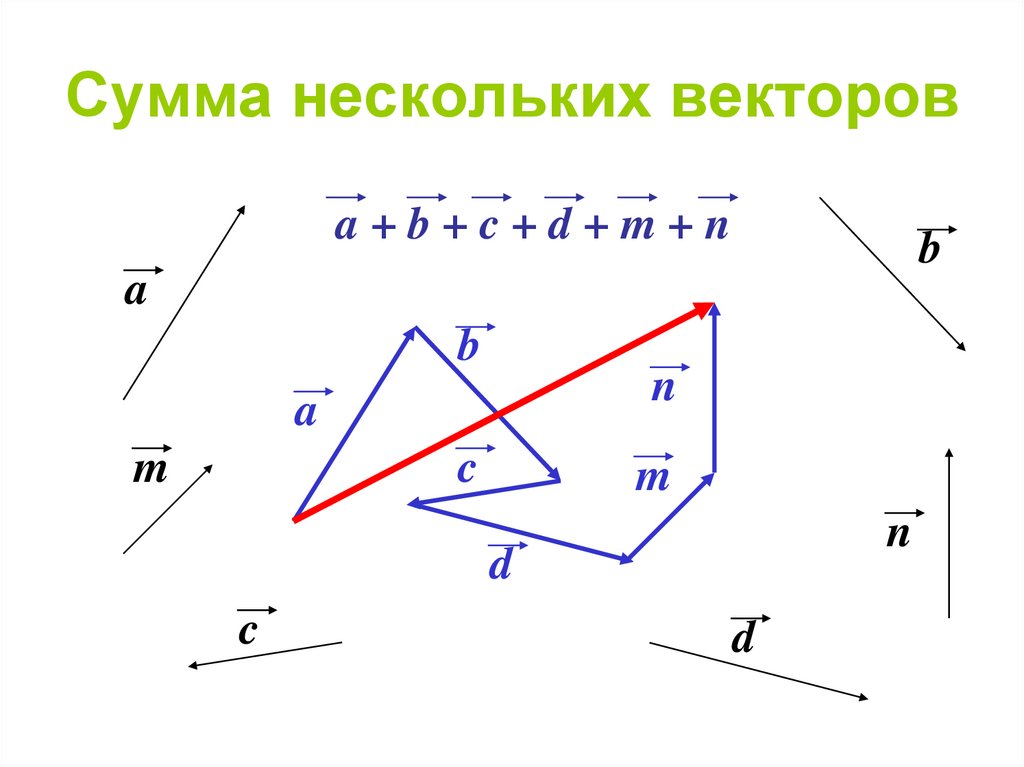
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют
- Вектор называют противоположным вектору .
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: .
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Определение. Говорят, что свободные векторы и равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы и , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
Определение. Говорят, что скользящие векторы и равны, если
- точки A,B,C,D располагаются на одной прямой,
- векторы и равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы и равны, если попарно совпадают точки A и C, B и D.
Операции над векторами
Сложение векторов
Два вектора u, v и вектор их суммы
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.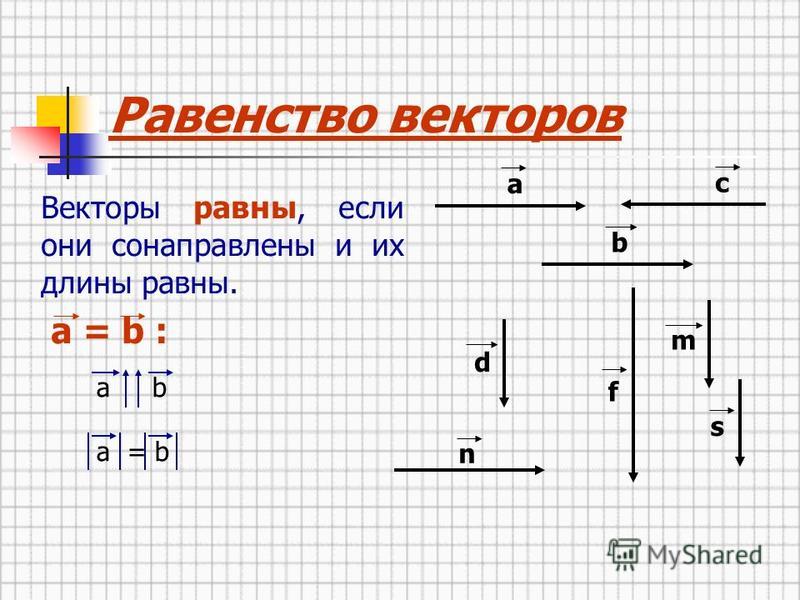
Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).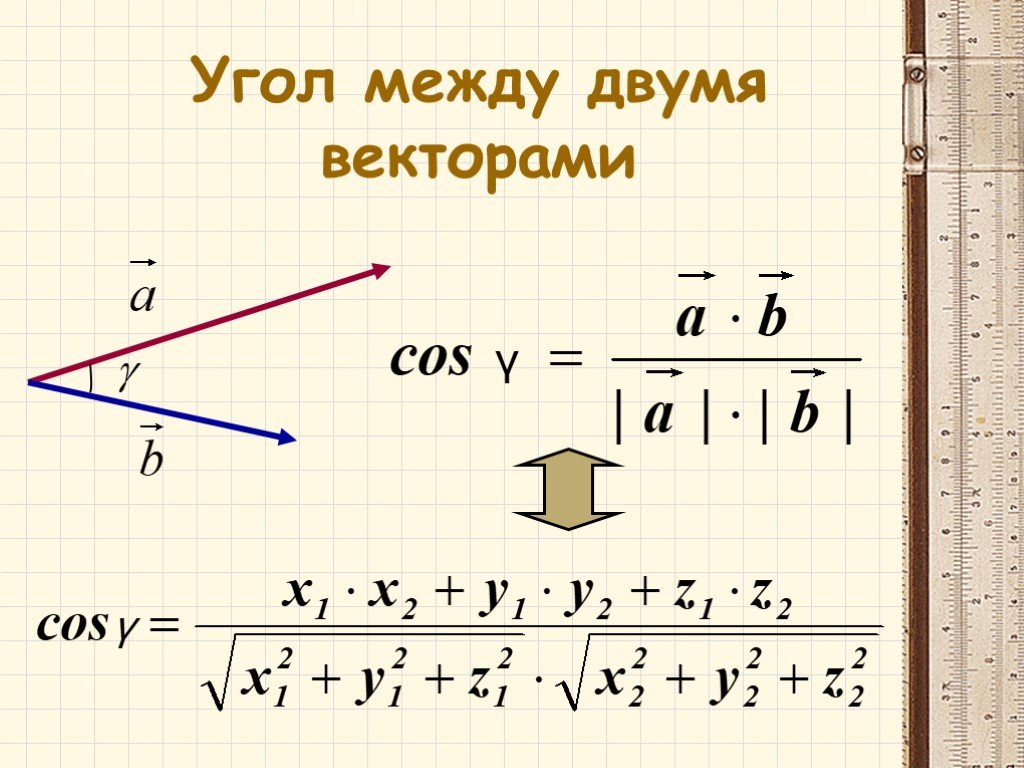
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Произведение вектора на число
Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .
Из определения произведения вектора на число легко вывести следующие свойства:
- если , то . Наоборот, если , то при некотором λ верно равенство ;
- всегда °, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Основная статья: Скалярное произведение
Скалярным произведением векторов и называют число, равное , где — угол между векторами и . Обозначения: или .
Обозначения: или .
Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
- — коммутативность.
- — дистрибутивность.
- — линейность по отношению к умножению на число.
- — норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
Векторное произведение
Основная статья: Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.

Обозначение:
Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Основная статья: Смешанное произведение
Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и :
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объем параллелепипеда, построенного на векторах .
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы коллинеарны, если x1 = λx2и y1 = λy2, где
См. также
- Нулевой вектор
- Вектор (алгебра)
- Радиус-вектор
- Тензор
- Момент силы
- Псевдовектор
Ссылки
- Г. С. М. Коксетер, С.
 П. Грейтцер. Новые встречи с геометрией, 1978
П. Грейтцер. Новые встречи с геометрией, 1978
Интуитивное объяснение векторов | Скайлер Дейл
Фото Франка В. на UnsplashПогрузитесь в линейную алгебру
В этом вступительном посте я дам определение векторам, обсужу некоторые способы их интерпретации, а затем предоставлю интуитивно понятное объяснение связанных с ними математических операций .
Начнем со знакомого упражнения из начальной школы. Мы построим точку (1,2) на сетке чисел X, Y, где X представляет горизонтальное направление, а Y представляет вертикальное направление.
Мы уже на пути к определению вектора. Ключевое отличие состоит в том, что вместо того, чтобы думать о мире с точки зрения «точек» на сетке, нам также нужно начать думать о «линиях».
В приведенном выше случае мы переместились из точки (0,0) в точку (1,2). Наш вектор — это просто линия, представляющая это движение:
Если вы внимательно посмотрите, то заметите, что наша линия имеет два ключевых свойства, которых нет у точки:
- Величина : Это синоним слова «длина».
 Мы также можем думать об этом как о том, «как далеко мы продвинулись».
Мы также можем думать об этом как о том, «как далеко мы продвинулись». - Направление: В отличие от нашей точки, наша линия на самом деле движется в определенном направлении.
Теперь мы можем дать формальное определение этому понятию. Согласно Мириам Вебстер, вектор — это:
«количество, имеющее величин и направлений и обычно представленное направленным отрезком линии, длина которого представляет величину, а ориентация в пространстве представляет направление».
Я предпочитаю простое определение: «линия в пространстве».
Обычный способ представления вектора состоит в том, чтобы наложить измерения X и Y друг на друга:
Простое представление двумерного вектораМы также можем расширить наше школьное понимание системы координат, выйдя за рамки двух измерений.
В воспринимаемом реальном мире у нас есть три измерения — левое/правое, переднее/заднее и верхнее/нижнее. Помашите рукой в воздухе и подумайте, как она двигалась в каждом из этих направлений. Теперь у вас есть представление о трехмерном векторе.
Помашите рукой в воздухе и подумайте, как она двигалась в каждом из этих направлений. Теперь у вас есть представление о трехмерном векторе.
Мы также можем попытаться визуализировать наш трехмерный вектор. Давайте возьмем наш исходный вектор (1,2) и добавим третье измерение, которое мы назовем Z и присвоим ему значение 1. Ниже приведен результирующий вектор (1,2,1):
На этой иллюстрации нет вполне отдают должное трем измерениям, потому что они отображаются на 2D-экране. И как только мы начинаем выходить за пределы трех измерений, человеческому мозгу становится очень сложно визуализировать. Если вы хотите попробовать, я рекомендую зайти на YouTube и проверить некоторые популярные попытки.
Но в то время как наша пространственная интерпретация ограничивается тремя измерениями, математическая или аналитическая интерпретация может пойти дальше. И мы также можем начать переходить от чисел к реальным сущностям реального мира, которые они могут представлять.
Давайте возьмем пример из набора данных радужной оболочки — популярного набора данных, используемого для введения классификации в машинное обучение:
Здесь у нас есть четыре «признака» или предиктора — длина чашелистика, ширина чашелистика, длина лепестка и ширина лепестка, которые мы можем используйте, чтобы предсказать нашу целевую переменную; тип цветка (обозначается как 0, 1 или 2).
Каждая из строк и столбцов в приведенной выше таблице может интерпретироваться как векторы. Например, мы можем представить нашу первую строку следующим образом:
Или, геометрически, мы можем думать об этом экземпляре цветка как о линии в пространстве, которая находится на расстоянии 5,1, 3,5, 1,4 и 0,2 единицы от начала координат в 4 разных направления.
Прежде чем мы перейдем к математике, я прошу вас остановиться и подумать о том, что мы только что обнаружили. Каждый набор данных, фиксирующий что-то реальное и осязаемое в мире, может быть переведен в линии в многомерном пространстве.
В этом разделе мы кратко познакомим вас с математическими операциями, связанными с векторами.
Прежде чем мы это сделаем, я быстро поделюсь своей философией изучения математики. Если вы строго не академик, цель математики — помочь нам решить реальные проблемы в мире . К сожалению, нам приходится уравновешивать это необходимостью получить начальное понимание основ. В этом посте у нас не будет времени для решения каких-либо реальных проблем, но я призываю вас не упускать из виду это как конечную цель.
В этом посте у нас не будет времени для решения каких-либо реальных проблем, но я призываю вас не упускать из виду это как конечную цель.
Добавление вектора
Численно: Мы добавляем каждое измерение к нашим двум векторам.
Пример: [1,2] + [1, -1] = [2, 1]
Геометрически: Складываем два вектора, помещая хвост одного вектора на начало другого вектора и затем рисуем линию от нашей начальной точки до нашей конечной точки.
Это интуитивно понятно, когда мы думаем о наших векторах как о представлениях «путешествия». Мы просто добавляем одно путешествие к другому, чтобы затем измерить наше общее путешествие.
Ниже мы показываем синий вектор [1,2] + красный вектор [1, -1] = зеленый вектор [2,1].
Вычитание вектора
Численно: Мы вычитаем каждое измерение из наших двух векторов.
Пример: [1,2]-[1, -1] = [0, 3]
Геометрически: Поскольку мы вычитаем, мы можем думать об этом как об изменении направления второго вектора на противоположное (красный), а затем поместите его хвост на голову первого вектора (синий), чтобы получить наш результат (зеленый):
Скалярное умножениеЧисленно: Мы умножаем каждое измерение нашего вектора на скалярное значение: [1,1] * 2 = [2, 2]
Геометрически: Наш начальный вектор [1,1] сохраняет свое направление, но «масштабируется» или увеличивается в множителе скалярного значения.
Величина вектора
Численно: Чтобы измерить величину или длину , , мы используем теорему Пифагора: извлекаем квадратный корень из сумм каждого квадрата элементов вектора. Ниже приведены несколько примеров:
Пример 1: Величина [1,2] = sqrt(1² + 2²) = sqrt(5) = 2,23
Пример 2: Величина [3,5,6] = sqrt(3² + 5² + 6²) = sqrt(9 + 25 + 36) = sqrt(70) = 8,36
Геометрически: Это не требует визуализации. Это просто длина вектора, который вы видите. Величина вектора часто представляется с помощью вертикальной черты: |V|.
Умножение на вектор (точечный продукт)Численно: Мы суммируем произведения каждого измерения в двух векторах. Результат всегда будет скалярным значением. Ниже приведены несколько примеров:
Пример 1: [1,2] · [2,3] = 1*2 + 2*3 = 8.
Пример 2: [1,2,3 ] · [2,3,4] = 1*2 + 2*3 + 3*4 = 20 .
Геометрически: Это немного сложно. Вместо прямой пространственной интерпретации давайте возьмем один вектор [0,1] (красный внизу) и найдем его скалярное произведение с несколькими другими векторами (синий внизу):
Выполняя это упражнение, я заметил несколько вещей:
- Скалярное произведение больше, когда направление синих векторов совпадает с направлением красного вектора.
- Скалярное произведение тем больше, чем больше величина синего вектора.
- Скалярное произведение равно 0, когда синий вектор перпендикулярен красному вектору.
Учитывая эти наблюдения, мое упрощенное объяснение скалярного произведения таково: скалярное произведение говорит нам, насколько две линии похожи по направлению; масштабируется по величине двух векторов.
Давайте теперь закрепим наше понимание, рассмотрев пример, где X имеет ненулевое значение в двух измерениях:
Каждое из приведенных выше скалярных произведений должно иметь смысл в контексте нашего объяснения выше.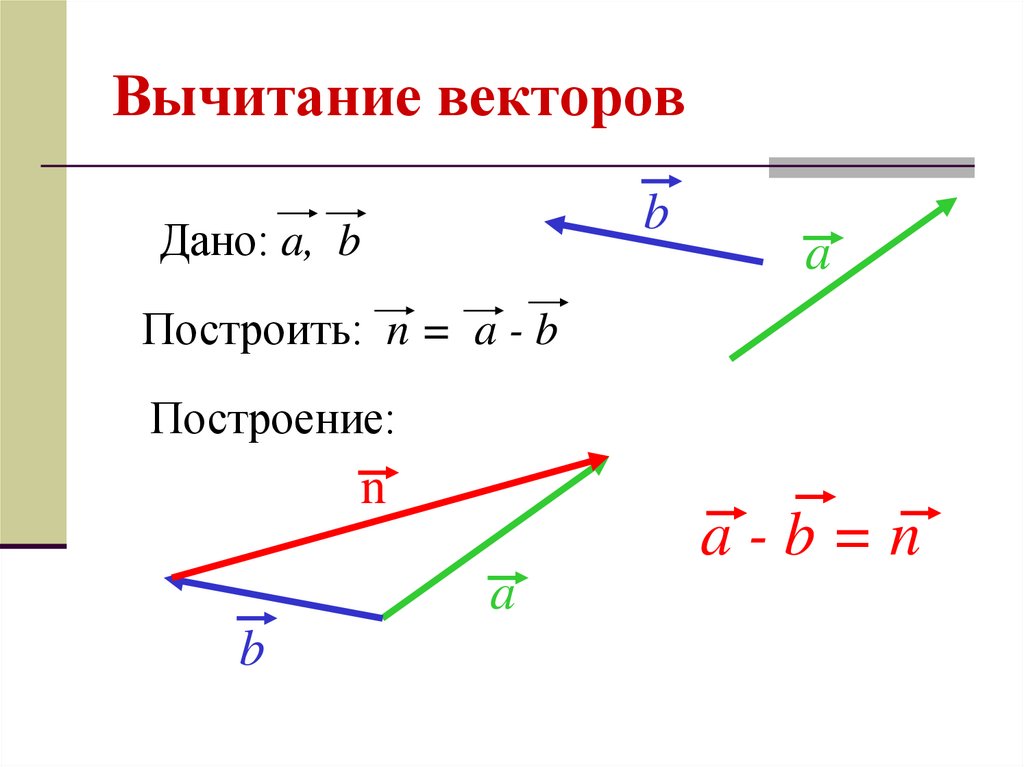
Почему у синего вектора [1.5, 2] скалярное произведение с нашим красным вектором больше, чем у синего вектора [2, 1]? Потому что он имеет большую величину и его направление больше похоже на наш красный вектор.
Почему у синего вектора [1, -1] есть скалярное произведение 0 с нашим красным вектором? Потому что два вектора ортогональны (под прямым углом друг к другу). Они указывают в разных направлениях.
До сих пор мы определяли вектор как линейное пространство с величиной и направлением. Мы узнали, что каждую строку или столбец в наборе данных можно представить геометрически как вектор в теоретически бесконечном числе измерений. Наконец, мы рассмотрели числовую и геометрическую интерпретацию основных векторных операций.
В следующем посте я дам определение матрицам и объясню их роль в линейной алгебре.
Понимание векторных вычислений — Математика средней школы
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Исчисление II — Интегралы » Параметрический, полярный и векторный » Вектор » Понимание векторных вычислений
Позвольте быть векторами. Определено все следующее, КРОМЕ:
Определено все следующее, КРОМЕ:
Возможные ответы:
Правильный ответ:
Объяснение:
Перекрестное произведение двух векторов (обозначенных буквой «x») требует двух векторов и приводит к другому вектору. Напротив, скалярное произведение (обозначаемое знаком «») между двумя векторами требует двух векторов и дает скаляр, а не вектор.
Если бы нам нужно было вычислить , нам пришлось бы сначала оценить , что привело бы к скаляру, потому что это скалярное произведение.
Однако, если у нас есть скалярное значение, мы не можем вычислить перекрестное произведение с другим вектором, потому что для перекрестного произведения требуется два вектора. Например, мы не можем найти векторное произведение между 4 и вектором <1, 2, 3>; перекрестное произведение определено только для двух векторов, а не скаляров.
Ответ .
Сообщить об ошибке
Найти величину вектора:
Возможные ответы:
Правильный ответ:
Объяснение:
Для решения величины вектора мы используем следующую формулу:
Отчет о ошибке
данный вектор и, соревнованный для.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти , нам нужно сложить компоненты вектора и компоненты вместе:
Сообщить об ошибке
Учитывая вектор и , решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти , нам нужно вычесть компоненты вектора и компоненты вместе:
Сообщить об ошибке
Учитывая вектор и , найдите .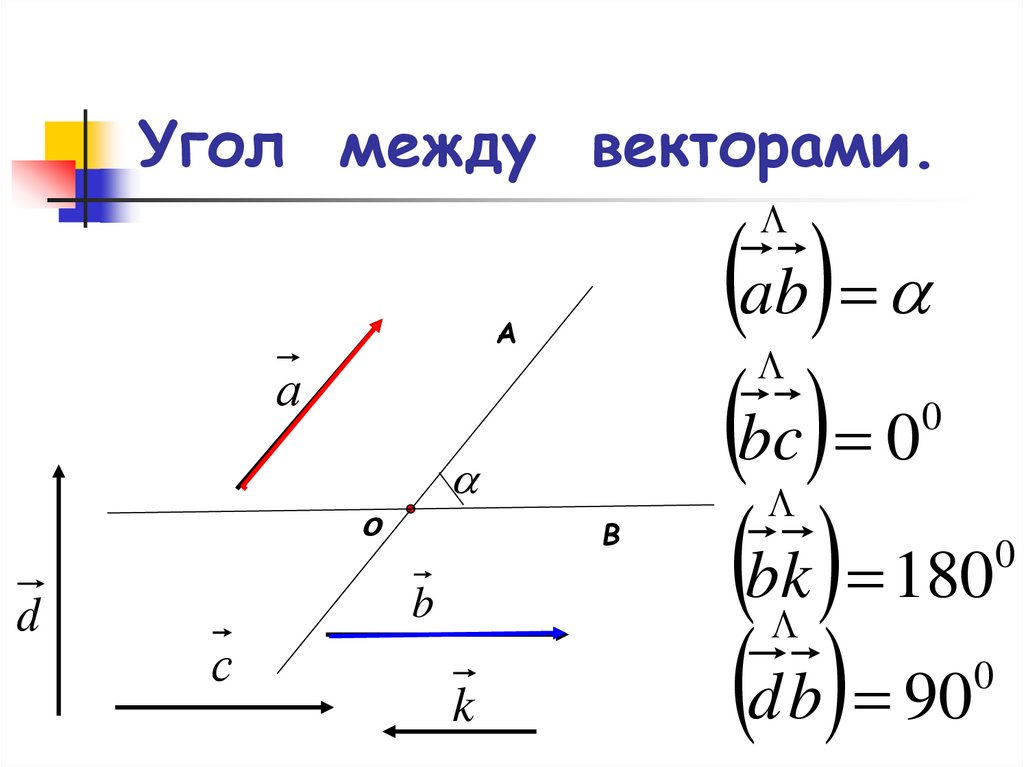
Возможных ответов:
Правильный ответ:
Объяснение:
Чтобы найти , нам нужно сначала умножить на вектор, чтобы найти, и умножить на вектор, чтобы найти ; затем нам нужно вычесть компоненты вектора и компоненты вместе:
Сообщить об ошибке
Найти единичный вектор .
Возможные ответы:
Правильный ответ:
Объяснение:
Для решения для единичного вектора необходимо использовать следующую формулу:
Вектор единиц:
. Является ли единичный вектор?
Возможные ответы:
да, потому что величина равна
нет, потому что величина не равна
предоставлено недостаточно информации
Правильный ответ:
да, потому что величина равна
Объяснение:
Чтобы проверить, является ли вектор единичным, мы должны найти его величину. Если величина равна 1, то вектор является единичным вектором:
Если величина равна 1, то вектор является единичным вектором:
равен единичному вектору.
Сообщить об ошибке
Данный вектор . Найдите направление (угол) вектора:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить направление вектора, мы используем следующую формулу:
=
с вектором
Сообщить об ошибке
Решите для вектора с учетом направления и величины .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти вектор с заданной величиной и направлением, мы используем следующую формулу:
Сообщить об ошибке
5
Сообщить об ошибке для заданного вектора и.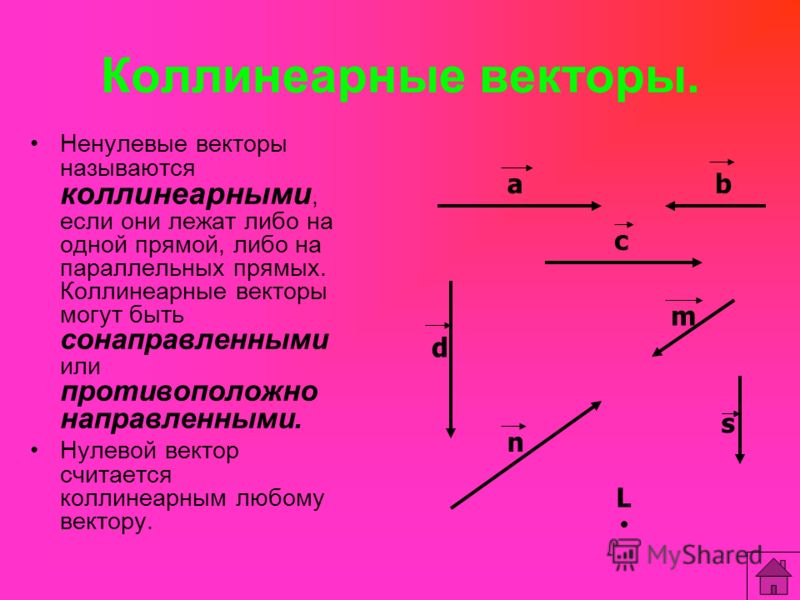



 П. Грейтцер. Новые встречи с геометрией, 1978
П. Грейтцер. Новые встречи с геометрией, 1978 Мы также можем думать об этом как о том, «как далеко мы продвинулись».
Мы также можем думать об этом как о том, «как далеко мы продвинулись».