Основное уравнение динамики вращательного движения, момент силы, момент инерции
Пусть к материальной точке массы m приложена сила 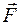 . Моментом силы
. Моментом силы 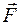 относительно оси вращения называют вектор, определяемый формулой
относительно оси вращения называют вектор, определяемый формулой
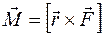 .
.
Модуль этого вектора равен
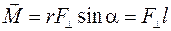 ,
, 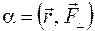 ,
,
где 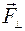 – составляющая силы в плоскости, перпендикулярной к оси вращения,
– составляющая силы в плоскости, перпендикулярной к оси вращения, 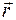 – вектор, проведенный от оси вращения к материальной точке (рис. 11, ось вращения проходит через точку
– вектор, проведенный от оси вращения к материальной точке (рис. 11, ось вращения проходит через точку
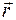 ),
), 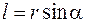 – плечо силы (кратчайшее расстояние от линии действия силы до оси вращения). Вектор
– плечо силы (кратчайшее расстояние от линии действия силы до оси вращения). Вектор 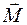 направлен вдоль оси вращения.
направлен вдоль оси вращения.
Выражение для модуля вектора 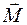 можно записать в другом виде, используя проекцию силы
можно записать в другом виде, используя проекцию силы 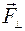
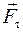 ). Именно
). Именно 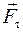 и вызывает вращательное движение материальной точки, создавая тангенциальное ускорение
и вызывает вращательное движение материальной точки, создавая тангенциальное ускорение
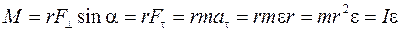
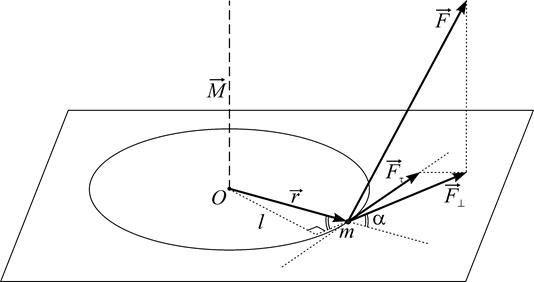 |
| Рис. 11. Момент сил, действующий на материальную точку массой |
Для абсолютно твердого тела, представляющего собой совокупность материальных точек массами dm, помимо векторной суммы моментов внешних сил 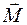 , действующих на его материальные точки, между материальными точками этого тела действуют также и внутренние силы. Однако согласно третьему закону Ньютона векторная сумма моментов внутренних сил относительно оси вращения равна нулю, и поэтому
, действующих на его материальные точки, между материальными точками этого тела действуют также и внутренние силы. Однако согласно третьему закону Ньютона векторная сумма моментов внутренних сил относительно оси вращения равна нулю, и поэтому
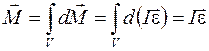 .
.
В итоге основной закон динамики вращательного движения для абсолютно твердого тела представляется в виде
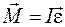 , ,
| (1) |
который формулируется следующим образом:
произведение момента инерции тела относительно оси вращения на вектор углового ускорения равно векторной сумме моментов действующих на тело внешних сил относительно этой оси вращения.
Сравнивая (1) с выражением второго закона Ньютона для поступательного движения 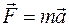 , можно заключить, что при вращательном движении роль силы
, можно заключить, что при вращательном движении роль силы
Маятник Обербека
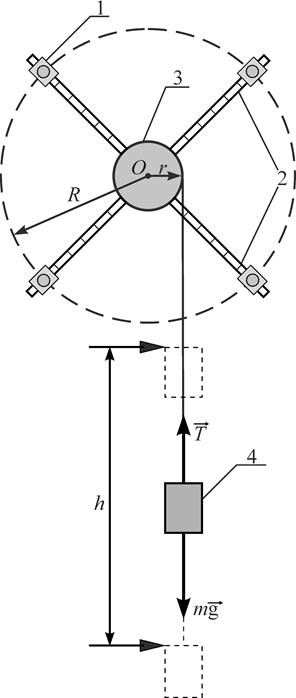 |
| Рис. 12. Маятник Обербека |
Для проверки законов вращательного движения в данной работе используется маятник Обербека, схема которого изображена на рис. 12.
Маятник Обербека состоит из четырех стержней 2, укрепленных на втулке под прямым углом друг к другу. На стержнях закрепляются грузы 1, перемещая которые, можно менять момент инерции тела. На одной оси с маятником находится шкив 3 радиусом
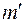 .
.
Если на барабан, вращающийся относительно оси, проходящей через точку O, намотать шнур с привязанным к его концу грузом массы m, то, будучи представлена самой себе, система придет в ускоренное движение.
Изменяя массу груза, подвешенного к нити, можно изменить вращающий момент сил. Перемещая грузы 2 вдоль стержней, можно менять момент инерции системы.
На груз будут действовать две силы: сила тяжести 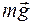 и натяжение нити
и натяжение нити 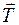 . Второй закон Ньютона для груза в проекции на ось, совпадающей с нитью будет иметь вид:
. Второй закон Ньютона для груза в проекции на ось, совпадающей с нитью будет иметь вид:
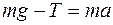 , ,
|
отсюда
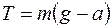 | (2) |
Ускорение груза a можно определить из законов кинематики, измеряя время t, за которое груз опустится на величину h, имея начальную скорость 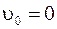 по формуле
по формуле
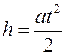 , ,
|
или
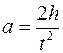 . .
| (3) |
Подставляя (3) в (2), найдем силу натяжения нити
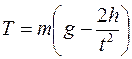 . .
| (4) |
Если радиус барабана r, то натянутая нить создает вращающий момент
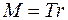 . .
| (5) |
Тогда основное уравнение динамики вращательного движения твердого тела (без учета сил трения) будет иметь вид
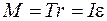
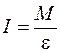 . .
| (6) |
Заменяя T из (4), получим
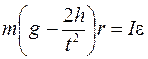 . .
| (7) |
Все точки барабана имеют одинаковое угловое ускорение ε. Точки, лежащие на ободе барабана, обладают касательным ускорением 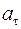 , равным ускорению груза a, т.к. нить нерастяжима, поэтому можно записать
, равным ускорению груза a, т.к. нить нерастяжима, поэтому можно записать
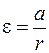 | (8) |
Подставляя (8) в (7) с учетом (3), получим
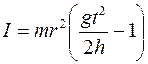 . .
|
Используя уравнения (4) и (5) можно записать
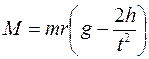 . .
| (9) |
Из (8) с учетом (3) под действием этого момента сил M маятник Обербека вращается с угловым ускорением
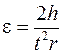 | (10) |
Приборы и принадлежности
– Маятник Обербека – 1 шт.
– Секундомер – 1 шт.
– Рулетка – 1 шт.
– Штангенциркуль – 1 шт.
– Набор грузов. – 1 шт.
Порядок выполнения работы
Динамика вращательного движения. Момент m силы f относительно какой-нибудь оси вращения определяется формулой
где l – кратчайшее расстояние от прямой, вдоль которой действует сила, до оси вращения.
Моментом инерции материальной точки относительно какой-нибудь оси вращения называется величина
где m – масса материальной точки и r – ее расстояние до оси вращения.
Моментом инерции твердого тела относительно его оси вращения
где интегрирование должно быть распределено навесь объем тела. Производя интегрирование можно получить момент инерции тела любой формы.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра
где R – радиус цилиндра и m – его масса.
Момент инерции полого цилиндра (обруча) с внутренним радиусом R1 и внешним R2 относительно оси цилиндра
для тонкостенного полого цилиндра R1≈ R2=R и J≈mR2.
Момент инерции однородного шара радиусом R относительно оси, проходящей через его центр,
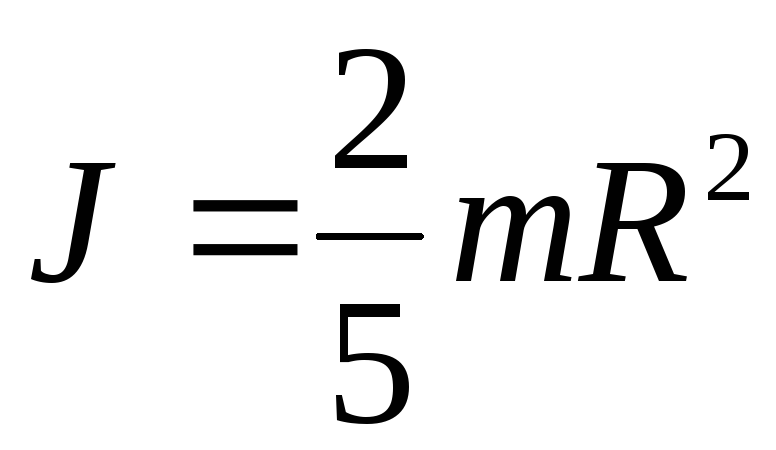 .
.
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно к нему,
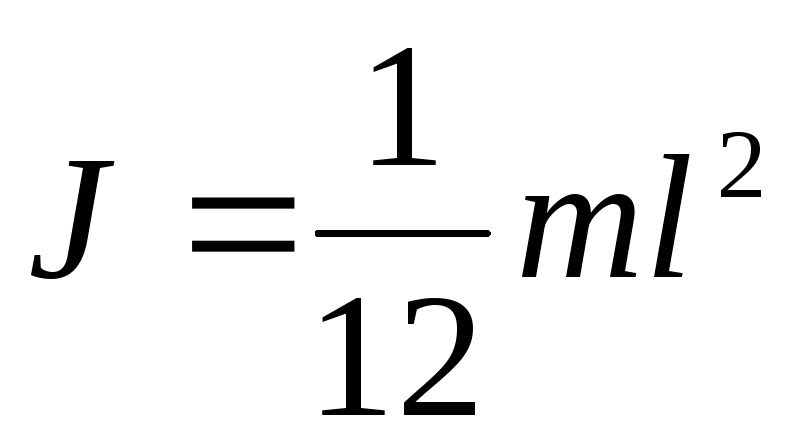 .
.
Если для какого-либо тела известен его момент инерции J0 относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельно первой, может быть найден по формуле Штейнера
где m – масса тела и D – расстояние от центра масс тела до оси вращения.
Основной закон динамики вращательного движения (закон сохранения момента импульса) выражается уравнением
где M – момент сил, приложенных к телу, L – момент импульса тела (J – момент инерции тела, ω – его угловая скорость). Если J=const, то
где ε – угловое ускорение, приобретаемое телом под действием момента сил M.
где J –момент инерции тела и ω – его угловая скорость.
Вывести формулу для момента инерции тонкого кольца радиусом R и массой m относительно оси симметрии. Ответ: J = mR2.
Определить момент инерции сплошного однородного диска радиусом R = 40 см и массой m = 1 кг относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Ответ: 0,12 кг·м2.
Определить момент инерции J тонкого однородного стержня длиной l = 50 см и массой m = 360 г относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длины. Ответ: 1) 3·10-2 кг·м2; 2) 1,75·10-2 кг·м2.
Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра. Ответ: В 1,07 раза.
Полная кинетическая энергия Т диска, катящегося по горизонтальной поверхности, равна 24 Дж. Определить кинетическую энергию Т1 поступательного и Т2 вращательного движения диска. Ответ: Т1 = 16 Дж, Т2 = 8 Дж.
Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену υ1=1,4 м/с, после удара υ’1=1 м/с. Определить выделявшееся при ударе количество теплоты Q. Ответ: Q=m(υ12— υ’12) = 0,48 Дж.
Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением ε вращается стержень, если на него действует момент сил М = 98,1 мН·м? Ответ: 2,35 рад/с2.
К ободу однородного сплошного диска массой m = 10 кг, насажанного на ось, приложена постоянная касательная сила F = 30 H. Определить кинетическую энергию диска через время t = 4 с после начала действия силы. Ответ: 1,44 кДж.
Маховое колесо, момент инерции которого J = 245 кг·м2, вращается с частотой n=20 об/с. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Ответ: 513 Н·м; 600.
Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению φ = А + Вt2 + Сt3 (В = 2 рад/с2, С = –0,5 рад/с3). Определить момент сил М для t = 3 с. Ответ: –0,1 Н·м.
Вентилятор вращается с частотой n = 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N = 50 оборотов, остановился. Работа А сил торможения равна 31,4 Дж. Определить: момент М сил торможения; 2) момент инерции J вентилятора. Ответ: 1) 0,1 Н·м; 2) 15,9 мН·м.
Маховик в виде сплошного диска, момент инерции которого J=150 кг·м2, вращается с частотой n = 240 об/мин. Через время t=1 мин, как на маховик стал действовать момент сил торможения, он остановился. Определить: 1) момент М сил торможения; 2) число оборотов маховика от начала торможения до полной остановки. Ответ: 1) 62,8 Н·м; 2) 120.
Сплошной однородный диск скатывается без скольжения по наклонной плоскости, образующей угол α с горизонтом. Определить линейное ускорение а центра диска. Ответ: a = 2/3gsinα.
К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 400 H. При вращении диска на него действует момент сил трения Мтр = 2 Н·м. Определить массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с2. Ответ: 24 кг.
Частота вращения no маховика, момент инерции J которого равен 120 кг·м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время t = π мин. Считая трение в подшипниках постоянным, определить момент М сил трения. Ответ: 16 Н·м.
Маховик в виде сплошного диска, момент инерции которого J=1,5 кг·м2, вращаясь при торможении равнозамедленно, за время t= 1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Определить: 1) угловое ускорение ε маховика; 2) момент М силы торможения; 3) работу торможения А. Ответ: 1) 0,21 рад/с2, 2) 0,047 Н·м; 3) 355 Дж.
Колесо радиусом R = 30 см и массой m = 3 кг скатывается по наклонной плоскости длиной 1 = 5 м и углом наклона α = 25°. Определить момент инерции колеса, если его скорость υ в конце движения составляла 4,6 м/с. Ответ: 0,259 кг·м2.
С наклонной плоскости, составляющей угол α = 30° к горизонту, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см. Ответ: 0,585 с.
На однородный сплошной цилиндрический вал радиусом R = 50 cм намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Определить: 1) момент инерции J вала; 2) массу М вала. Ответ: 1) 6,25 кг·м2; 2) 50 кг.
На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого J = 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой m = 0,5кг. До начала вращения барабана высота h груза над полом составляла 2,3 м. Определить: 1) время опускания груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол. Ответ: 1) 2 с; 2) 4,31 Н; 3) 1,32 Дж.
Через неподвижный блок в виде однородного сплошного цилиндра массой m = 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m1= 0,35 кг и m2 = 0,55 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) отношение T2/T1 сил натяжения нити. Ответ: 1) 1,96 м/с2; 2) 1,05.
Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, Wк = 60 Дж. Найти момент импульса L вала. Ответ: 3,8 кг·м2/с.
Карандаш длиной l=15 см, поставленный вертикально, падает на стол. Какую угловую скорость ω и линейную скорость υ будут иметь в конце падения середина и верхний конец карандаша? Ответ: ωс= ωк=14 рад/с; υс=1,05 м/с, υк=2,1 м/с.
Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε = 0,4 рад/с2. Определить кинетическую энергию маховика через время t2 = 25 с после начала движения, если через t1 = 10 с после начала движения момент импульса L1 маховика составлял 60кг·м2/с. Ответ: 1) Ек = 75 Дж.
Горизонтальная платформа массой m = 25 кг и радиусом R = 0,8 м вращается с частотой n1 = 18 мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J1 = 3,5 кг·м2 до J2 = 1 кг·м2. Ответ: 23 мин-1.
Человек, стоящий на скамье Жуковского, держит в руках стержень длиной l = 2,5 м и массой m = 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции J = 10 кг·м2 и вращается с частотой n1 = 12 мин-1. Определить частоту n2 вращения системы, если стержень повернуть в горизонтальное положение. Ответ: 8,5 мин-1.
Человек массой T = 60 кг, стоящий на краю горизонтальной платформы массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1=10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить, с какой частотой будет тогда вращаться платформа. Ответ: 20 мин-1.
Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определять, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы. Ответ: Возрастет в 1,43 раза.
Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом R = 1 м массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить работу, совершаемую человеком при переходе от края платформы к ее центру. Ответ: 65,8 Дж.
Однородный стержень длиной l = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Найти период колебаний Т стержня. Ответ: 1,16 с.
Обруч диаметром D = 56,5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период колебаний Т обруча. Ответ: 1,5 с.
Изучение законов вращения на крестообразном маятнике обербека
48
ЛАБОРАТОРНАЯ РАБОТА 1
Цель работы: исследование зависимость момента инерции маятника от расположения грузов, закрепленных на стержне маятника.
Приборы и принадлежности: маятник Обербека, набор грузов и перегрузов, штангенциркуль.
Теоретические сведения
В механике под твердым телом подразумевают абсолютно твердое тело, т. е. тело деформациями которого можно пренебречь. При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Быстроту вращения характеризуют углом поворота тела в единицы времени. Если за любые равные промежутки времени тело поворачивается на одинаковые углы, вращение называется равномерным. Величина, определяющая изменение угла поворота за единицу времени, называется угловой скоростью. Угловая скорость определяется по формуле
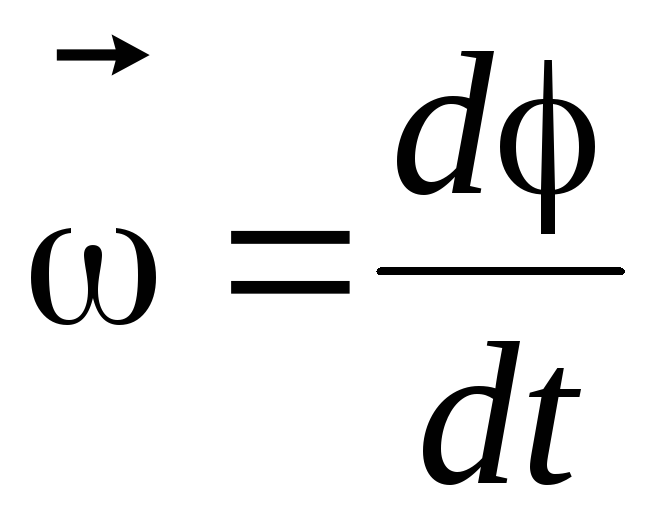 .
.
Единицей измерения угловой скорости является рад/с. При неравномерном вращении изменение угловой скорости со временем характеризуется угловым ускорением, которое вычисляется по формуле
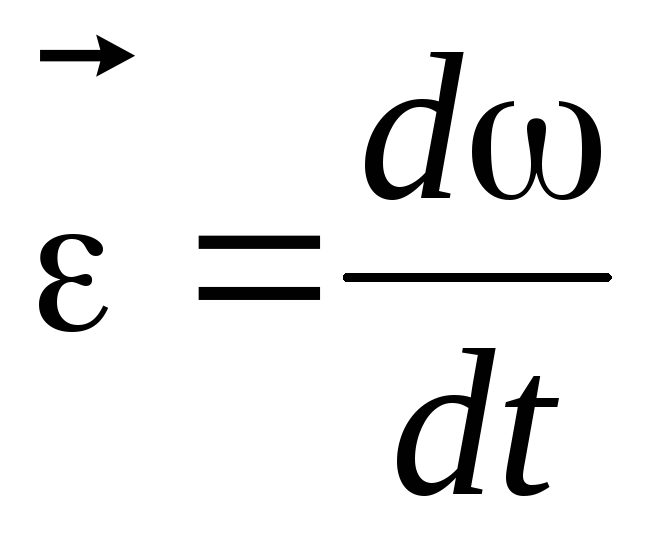 .
.
Единица
измерения углового ускорения является
рад/с2.
Угловая
скорость ωи
угловое ускорение ε связаны с линейной скоростью  и линейным (тангенциальным)
ускорением
и линейным (тангенциальным)
ускорением 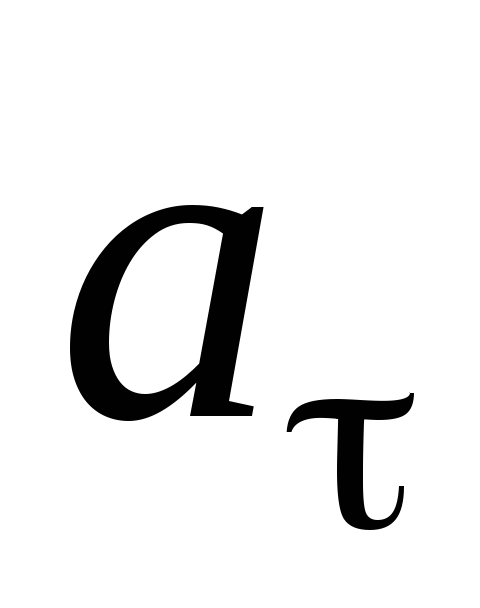 следующими соотношениям:
следующими соотношениям:
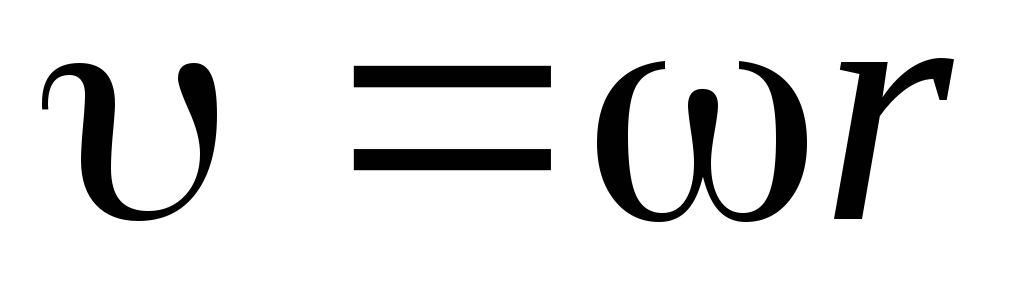 и
и 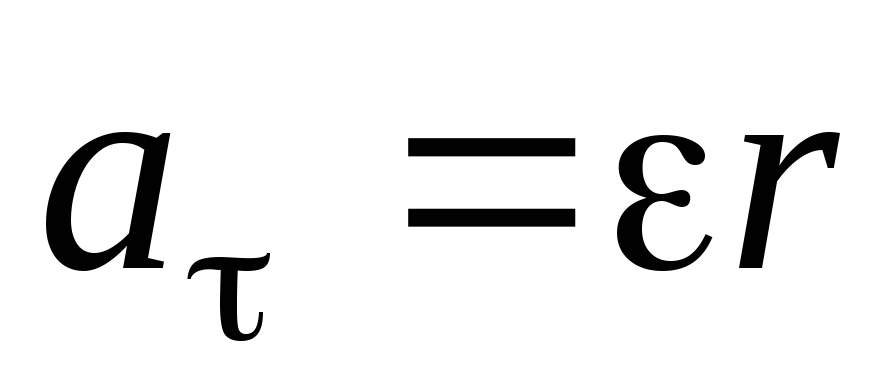 ,
(1)
,
(1)
где 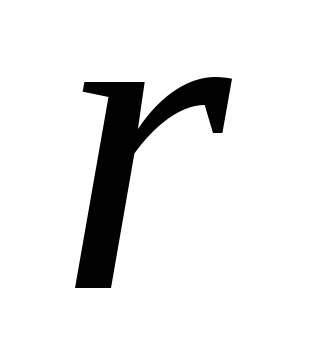 – расстояние от точек до оси вращения
– расстояние от точек до оси вращения
При
вращении тела вокруг неподвижной оси
изменение угловой скорости
и его движения зависит от действующего
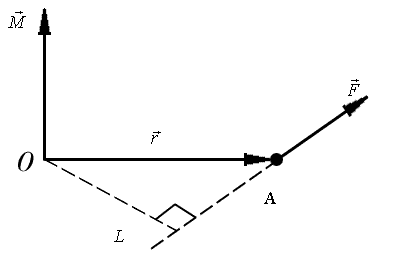
момента силы. Моментом силы 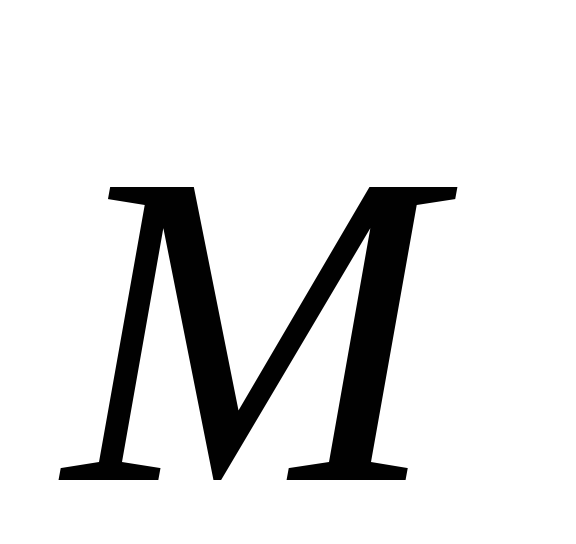 относительно неподвижной точки О
называется векторная
величина, определяемая векторным
произведением радиуса-вектора
относительно неподвижной точки О
называется векторная
величина, определяемая векторным
произведением радиуса-вектора 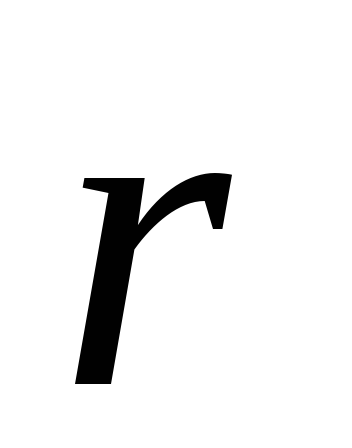 , проведенного
из точки О в точку А приложения
силы, на силу
, проведенного
из точки О в точку А приложения
силы, на силу  (рис.
1).
(рис.
1).
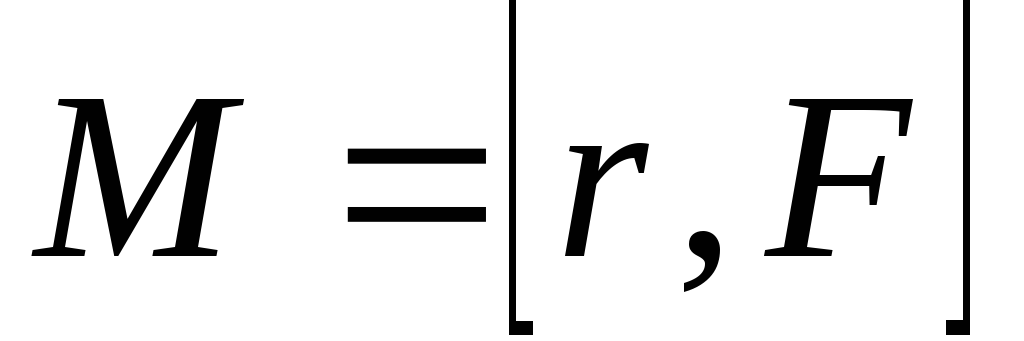 ,
,
где 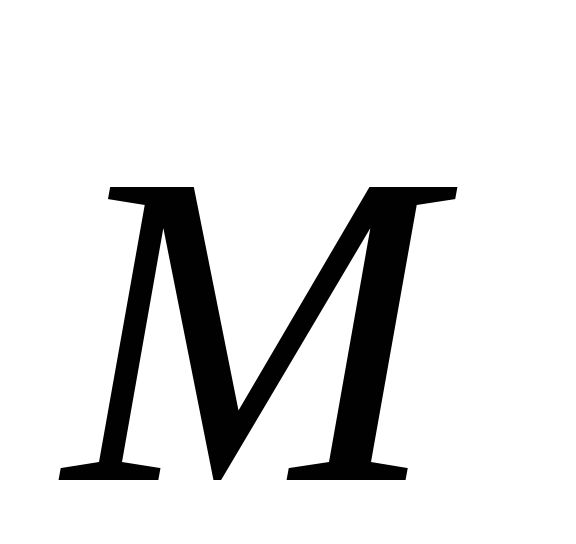 – псевдовектор, его направление совпадает
с направлением поступательного
движения правого винта при его вращении
от
– псевдовектор, его направление совпадает
с направлением поступательного
движения правого винта при его вращении
от 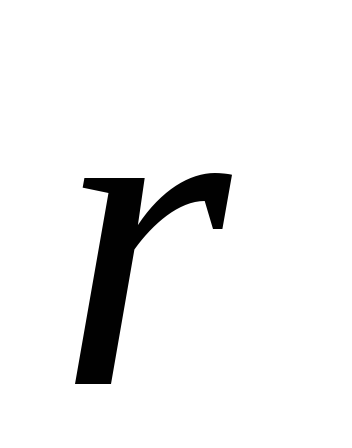 к
к  .
.
| |
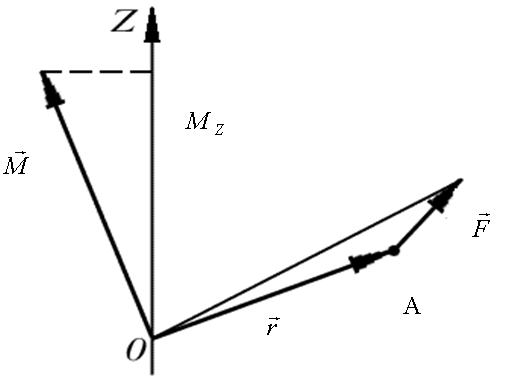
Рис. 1 | Рис.2 |
Модуль момента силы
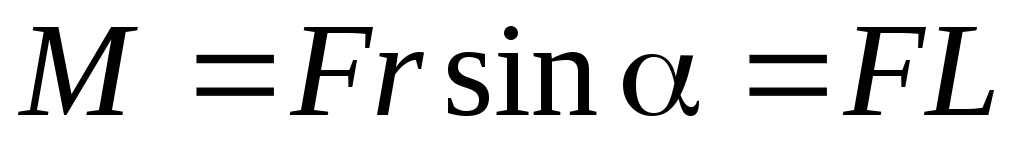 ,
,
где  – угол между
– угол между 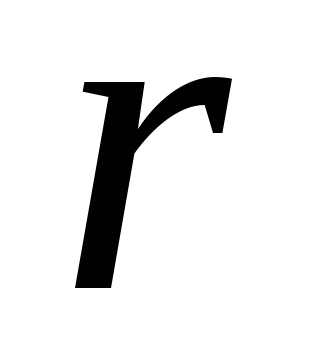 и
и 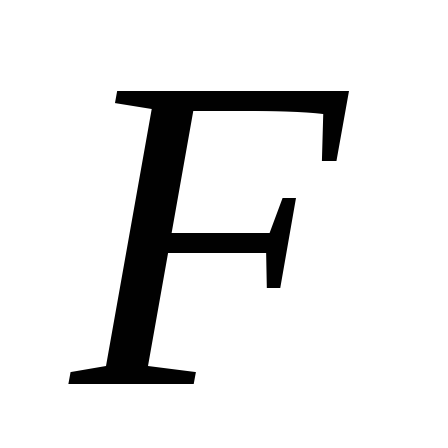 ;
; 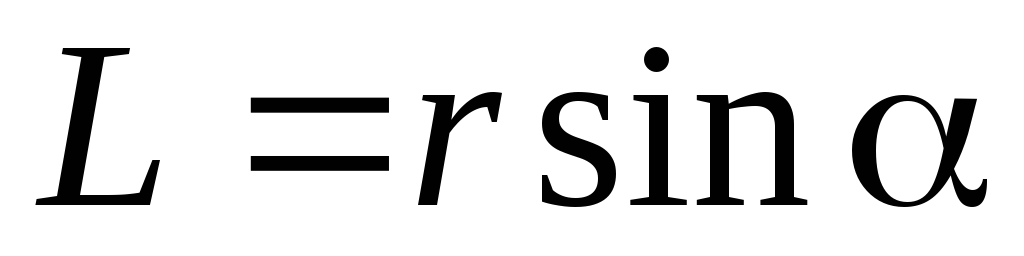 – плечо силы — кратчайшее расстояние
между линиями действия силы и точкой
О.
– плечо силы — кратчайшее расстояние
между линиями действия силы и точкой
О.
Моментом
силы относительно неподвижной оси  , называется
скалярная
величина
, называется
скалярная
величина 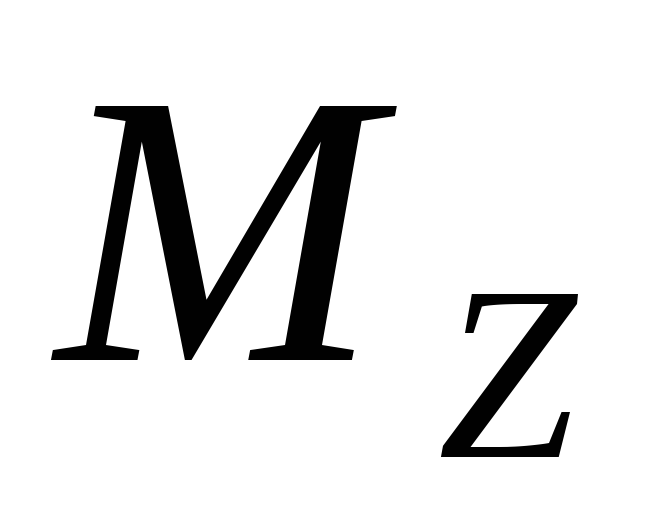 ,
равная проекции на эту ось вектора
момента силы
,
равная проекции на эту ось вектора
момента силы 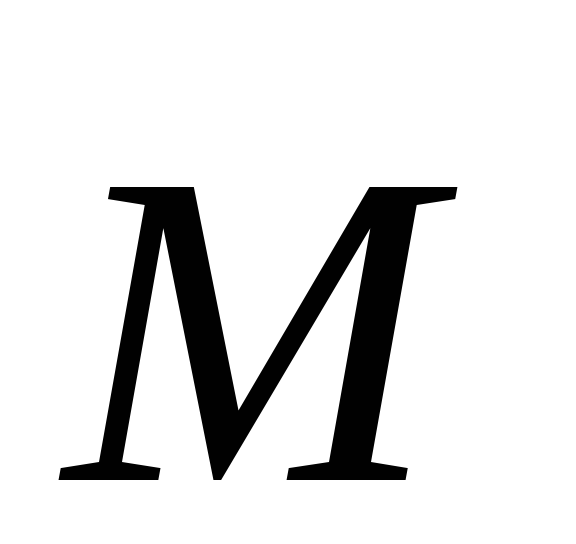 ,
определенного относительно произвольной
точки О, данной на оси
,
определенного относительно произвольной
точки О, данной на оси  (рис. 2). Значение момента
(рис. 2). Значение момента 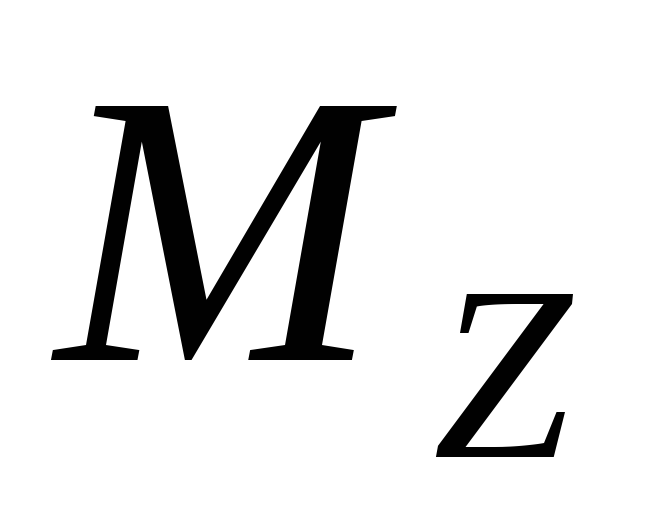 не зависит от
выбора положения точки О на оси
не зависит от
выбора положения точки О на оси  .
.
Равнопеременное вращательное движение тел характеризуется постоянным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению.
Зависимость углового ускорения от момента силы выражена в основном законе динамики вращательного движения
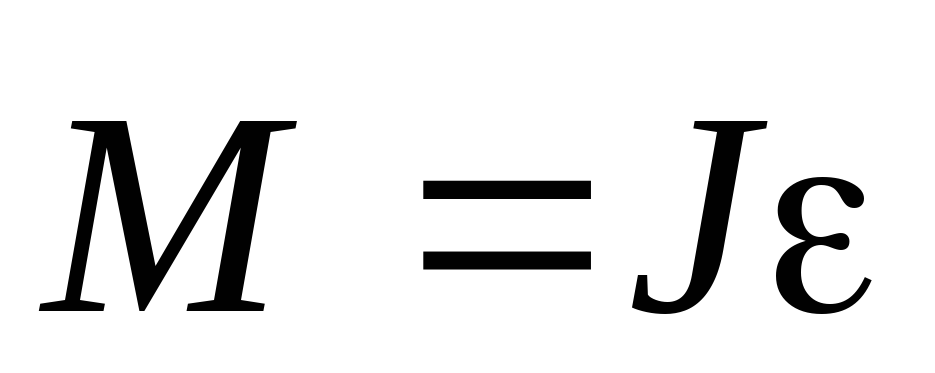 ,
(2)
,
(2)
где  — момент инерции тела.
— момент инерции тела.
Момент
инерции  материальной точки относительно
какой-либо оси
вращения называется скалярная величина,
равная произведению массы m
этой точки на квадрат
расстояния
материальной точки относительно
какой-либо оси
вращения называется скалярная величина,
равная произведению массы m
этой точки на квадрат
расстояния 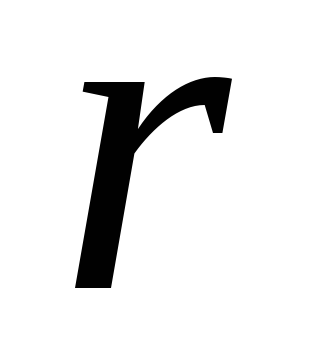 от точки до оси вращения:
от точки до оси вращения:
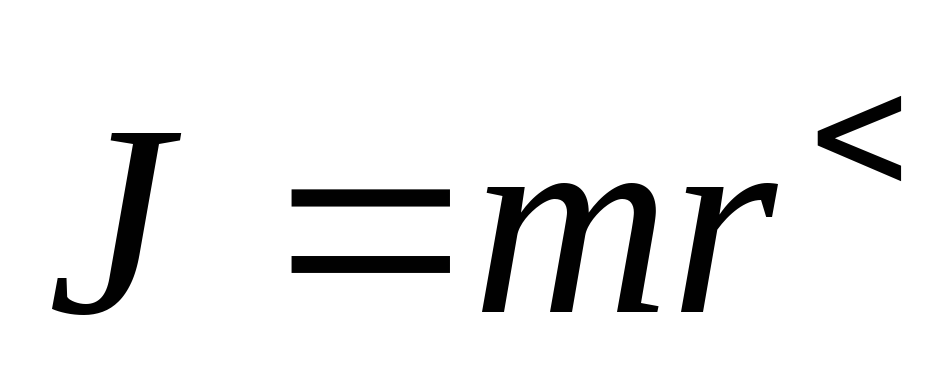 .
.
Моментом инерции тела относительно данной оси вращения называют сумму моментов инерции элементарных масс, на которые разбивается тело:
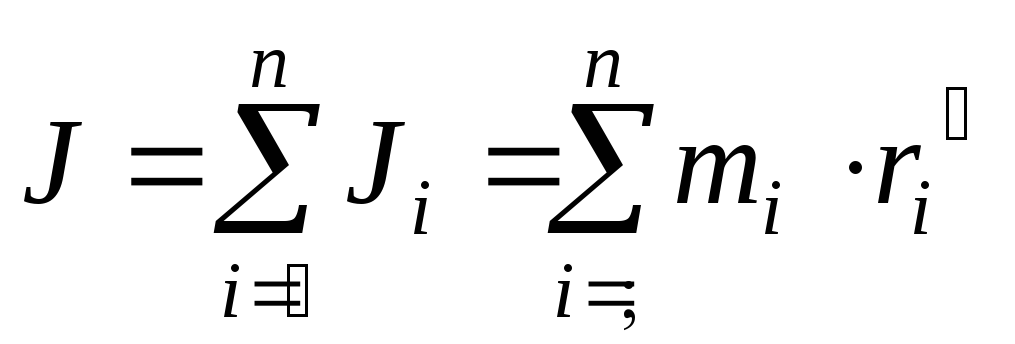 ,
,
где 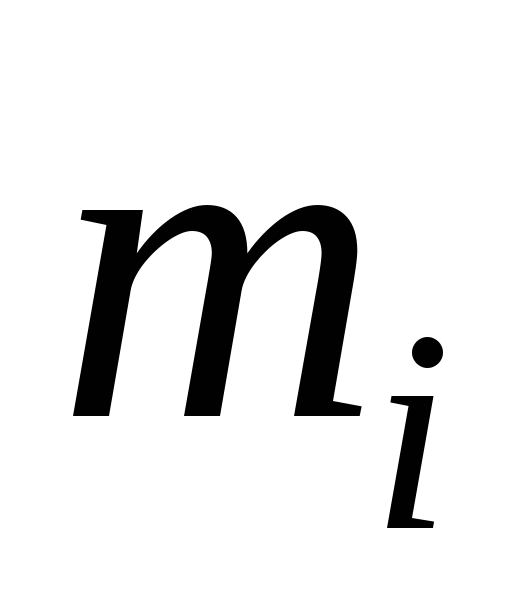 — элементарная масса;
— элементарная масса;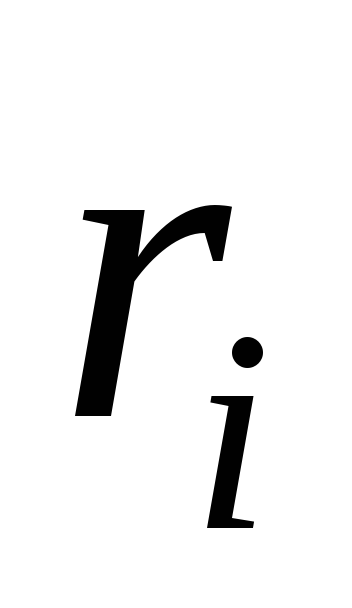 — расстояние от элементарной массы до
оси вращения.
— расстояние от элементарной массы до
оси вращения.
Если
известен момент инерции тела относительно
оси, проходящей
через его центр масс, то момент инерции
относительно любой другой
параллельной
оси определяется теоремой Штейнера:
момент инерции
тела  относительно
любой оси вращения равен моменту инерции относительно
параллельной оси, проходящей через
центр масс тела, сложенному
с произведением массы тела на квадрат
расстояния
относительно
любой оси вращения равен моменту инерции относительно
параллельной оси, проходящей через
центр масс тела, сложенному
с произведением массы тела на квадрат
расстояния 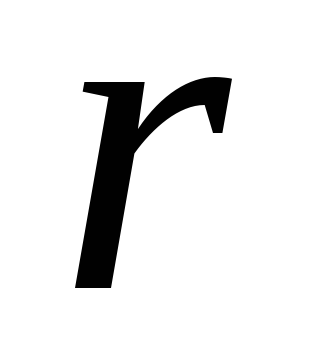 между
осями:
между
осями:
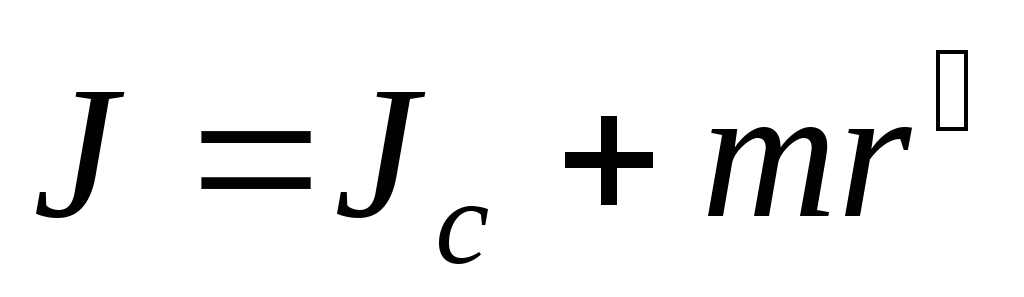 .
.
Законы вращения тел можно изучить с помощью маятника Обербека.
Рис.3 | Рассмотрим
движения механической системы
представленной на рис. 3.
Груз
массой m
движется с ускорением Диск
вращается равноускоренно под действием
натянутой нити, вызванной силой
натяжения нити |
Если
предположить, что нить невесомая, то на
диск маятника действует сила 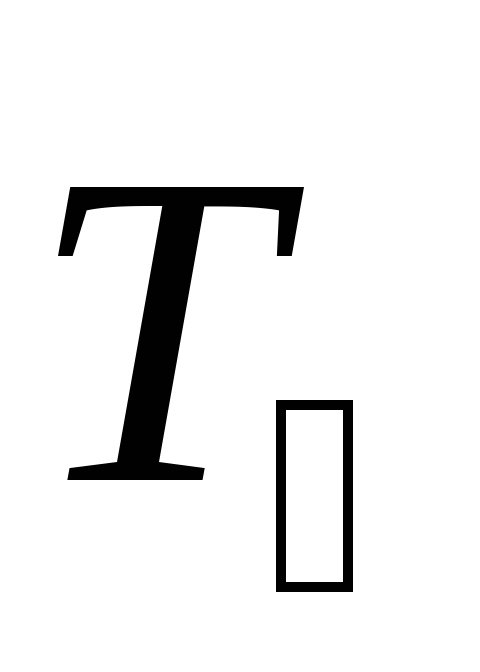 ,
равная по величине
,
равная по величине 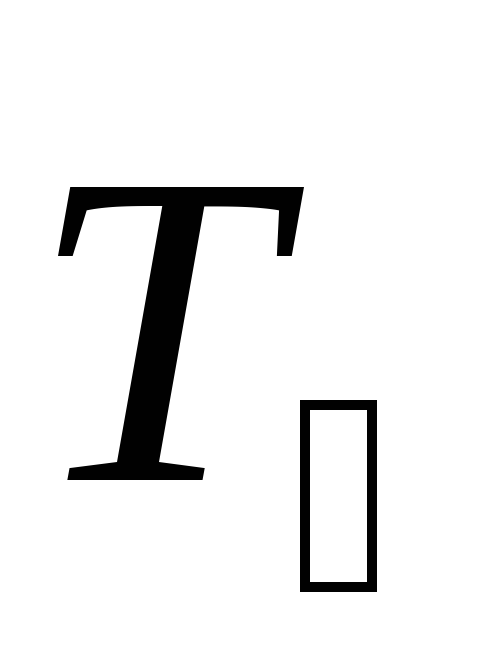 и противоположная ей по направлению
(следствие третьего закона Ньютона:
и противоположная ей по направлению
(следствие третьего закона Ньютона: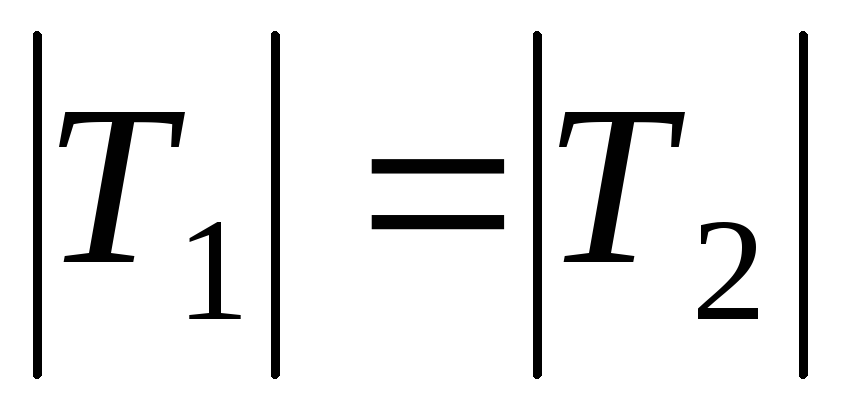 ).
Отсюда
).
Отсюда
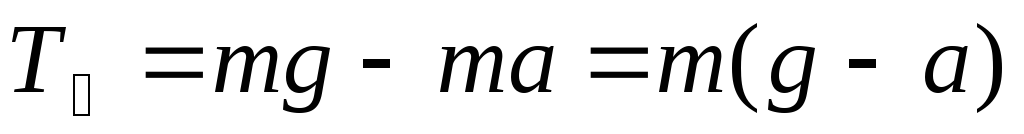 .
(3)
.
(3)
Сила
натяжения нити 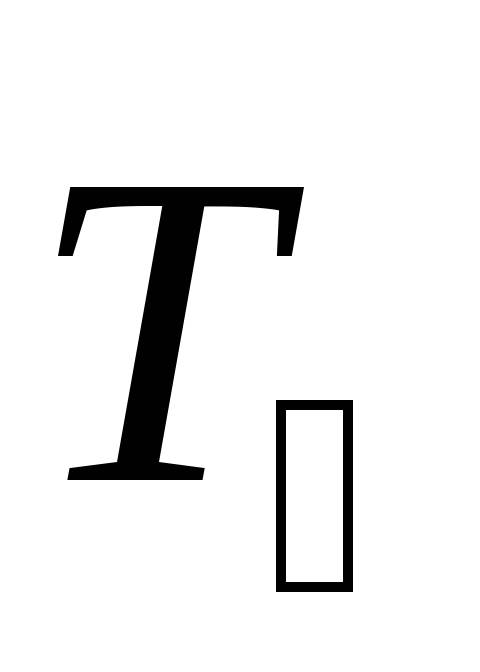 создает вращательный момент
создает вращательный момент 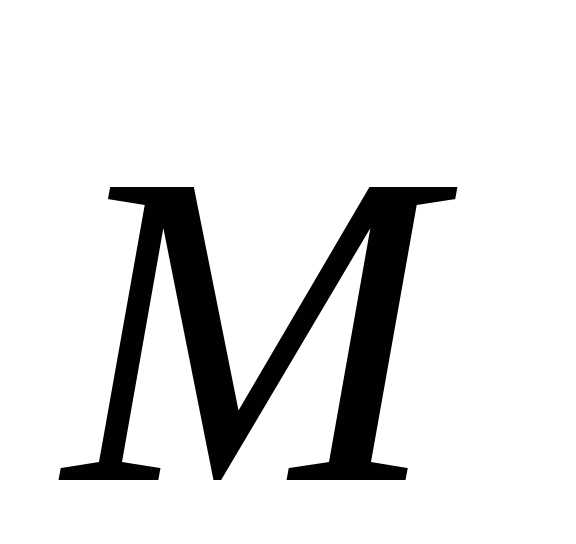 относительно горизонтальной осиO,
направленный вдоль этой оси «от нас» и
приводящий в движение маятник Обербека.
Величина момента силы равна
относительно горизонтальной осиO,
направленный вдоль этой оси «от нас» и
приводящий в движение маятник Обербека.
Величина момента силы равна
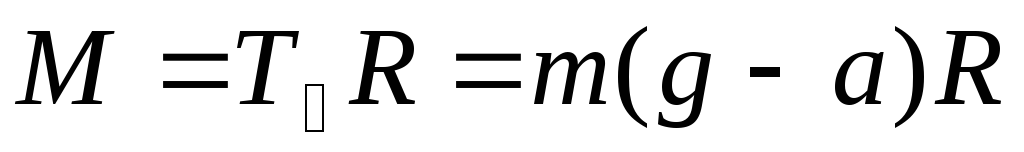 ,
(4)
,
(4)
где  – радиус диска, на который намотана
нить.
– радиус диска, на который намотана
нить.
Основной закон динамики вращательного движения (2) в скалярном виде и с учетом момента силы (4) примет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О, направление которой выбрано «от нас»):
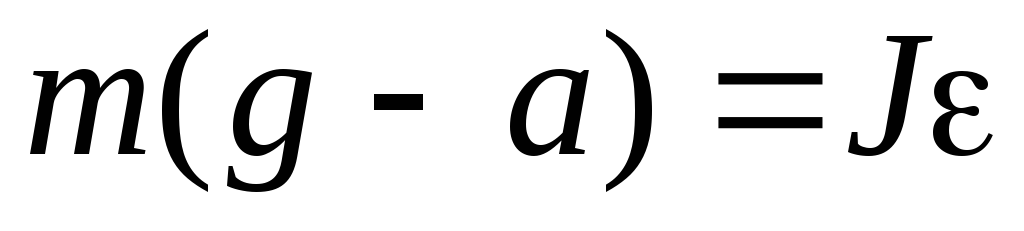 .
(5)
.
(5)
Используя
кинематическую связь линейного и
углового ускорения (1), а также уравнение
движения груза при нулевой начальной
скорости 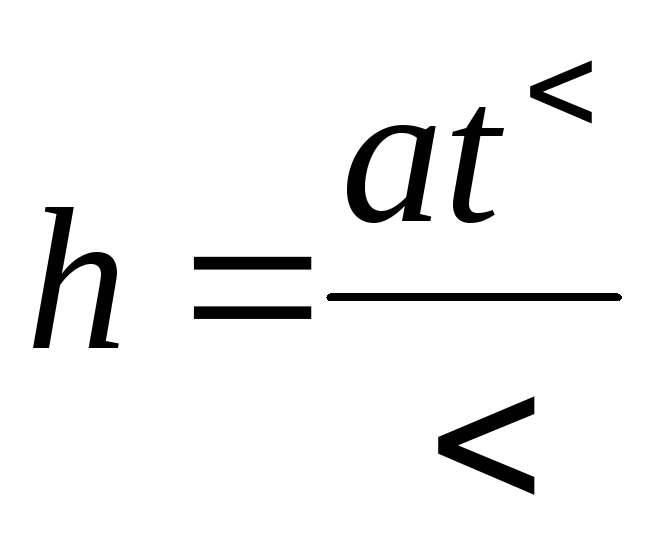 ,
выразим
,
выразим  через величины
через величины 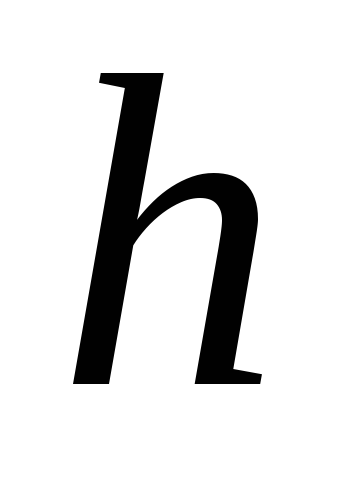 и
и  :
:
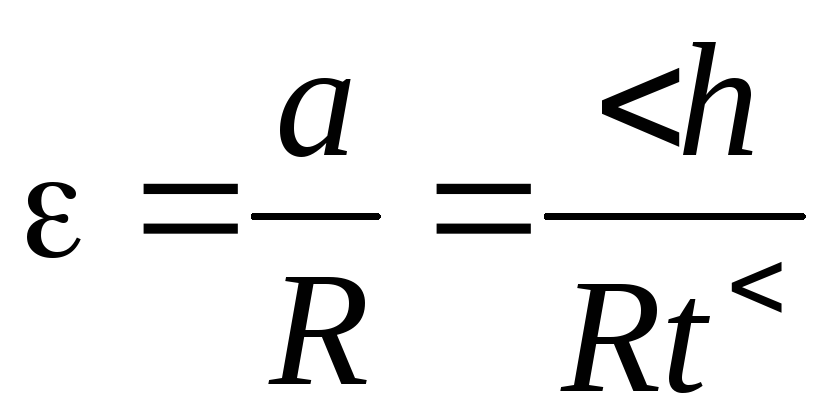 .
(6)
.
(6)
Преобразуем
уравнение (5), используя выражение (6) и 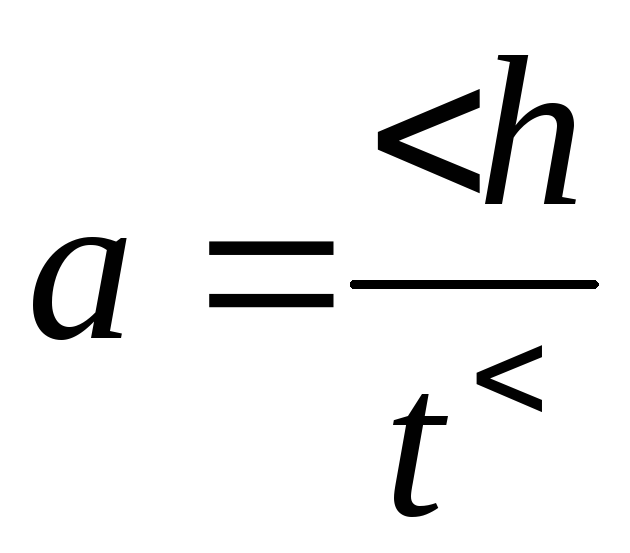 и получим момент инерции маятника
Обербека
и получим момент инерции маятника
Обербека
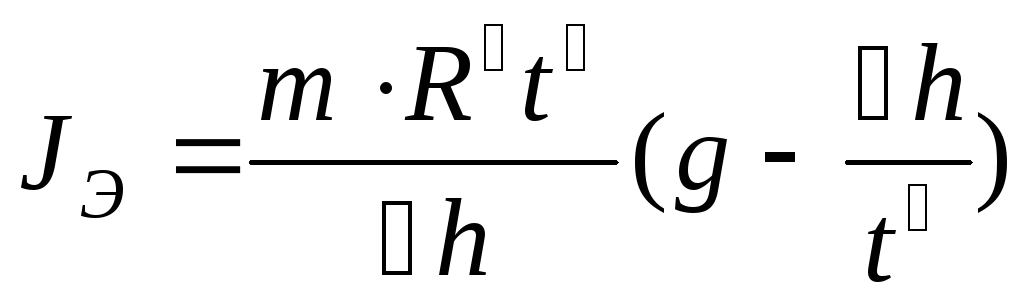 .
(7)
.
(7)
Эту зависимость можно использовать для экспериментальной оценки величины момента инерции маятника Обербека.
Теоретический
расчет момента инерции маятника Обербека
представляет сумму моментов инерций  — момента инерции диска радиусом
— момента инерции диска радиусом  ,
, 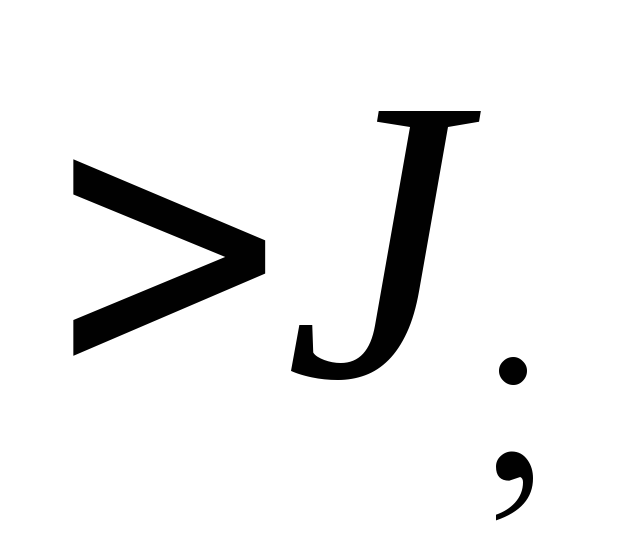 — моментов инерции четырех подвижных
грузов
— моментов инерции четырех подвижных
грузов 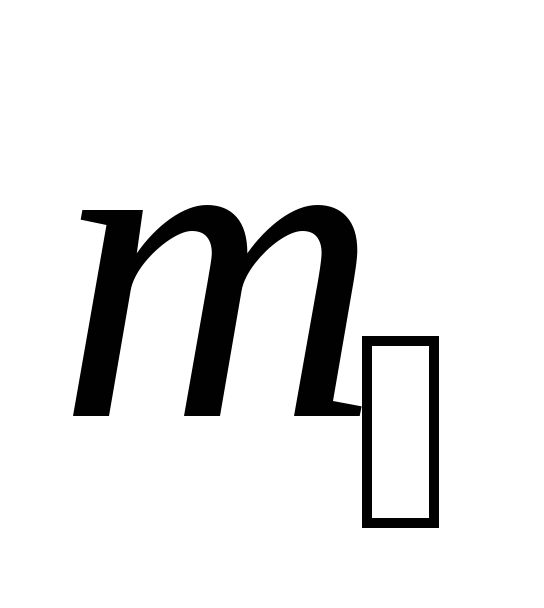 и
и  — момента инерции крестовины маятника
без груза
— момента инерции крестовины маятника
без груза 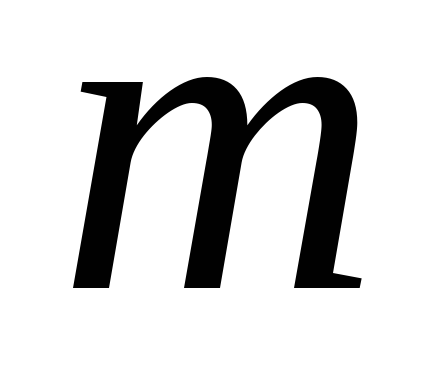 .
.
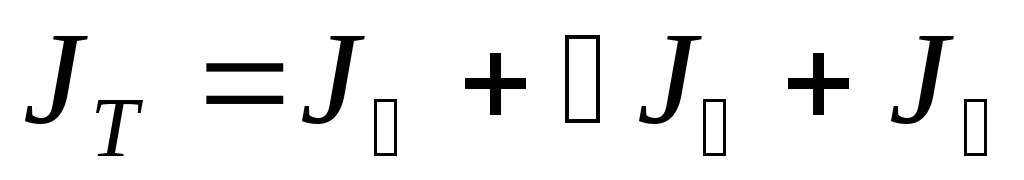 .
.
В связи с тем, что размеры грузов малы по сравнению с расстоянием от оси вращения до центров масс грузов, то грузы можно считать материальными точками. Для материальной точки момент инерции равен
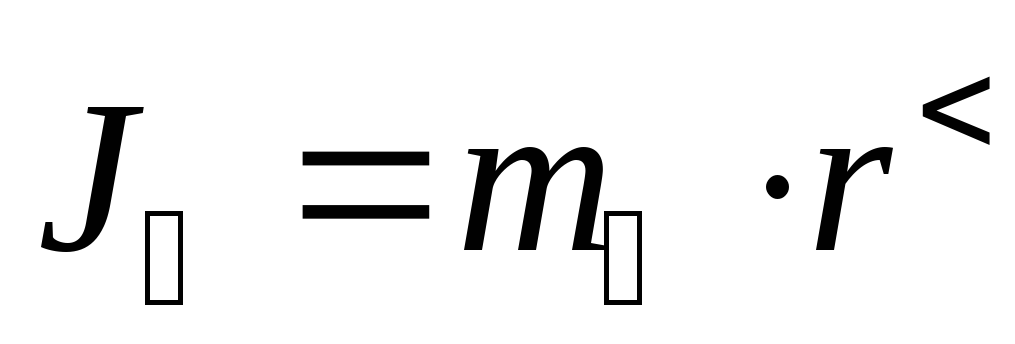 ,
,
где 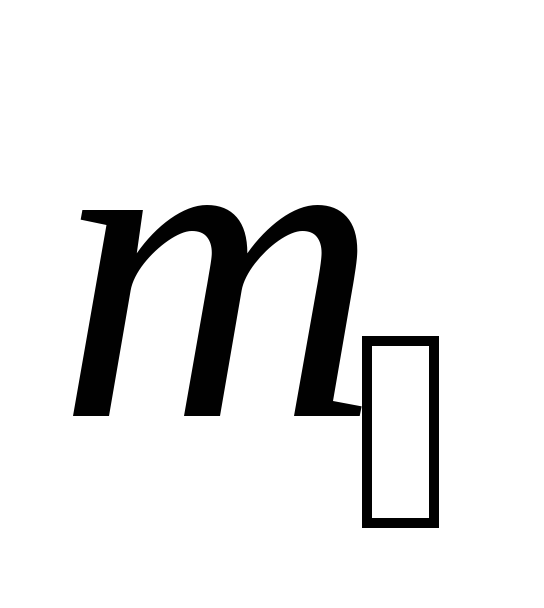 – масса груза на крестовине;
– масса груза на крестовине; 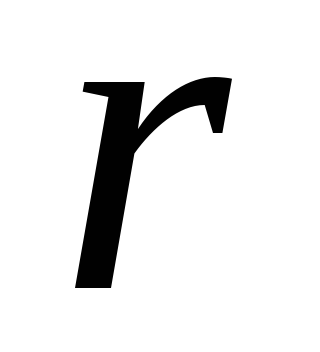 – расстояние от оси вращения до центра
грузов. Момент инерции крестовины
маятника без груза определяется как
– расстояние от оси вращения до центра
грузов. Момент инерции крестовины
маятника без груза определяется как
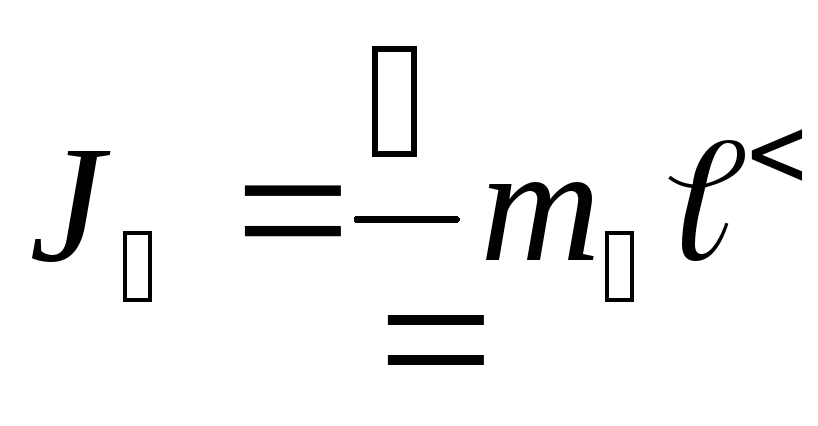 ,
,
где 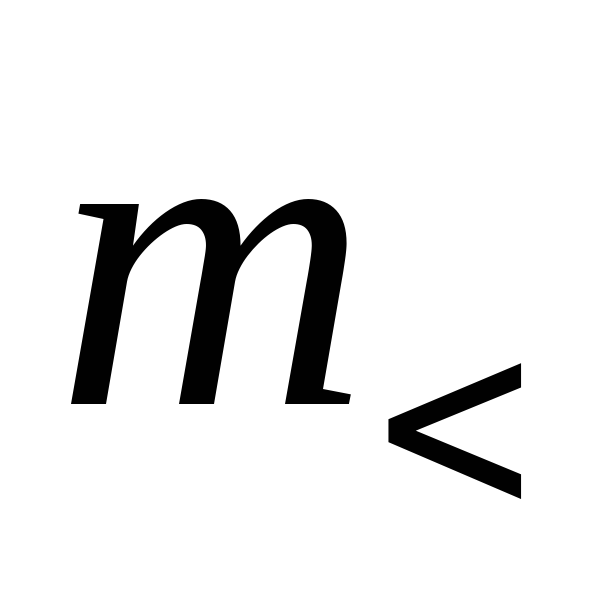 – масса стержня без груза;
– масса стержня без груза; 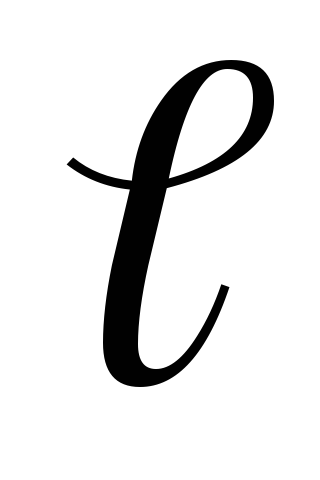 — длина стержня крестовины.
— длина стержня крестовины.
Таким образом, теоретический расчет момент инерции маятника можно представить следующей формулой
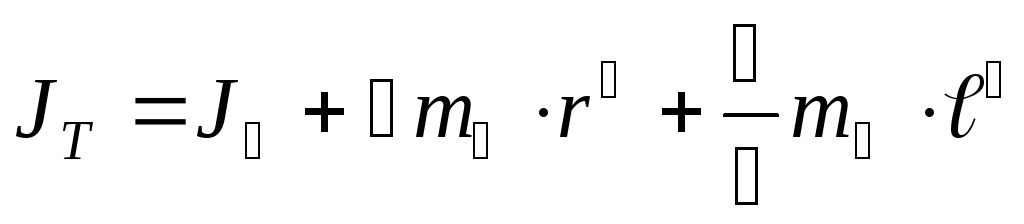 .
.
Расчет
разности моментов инерции 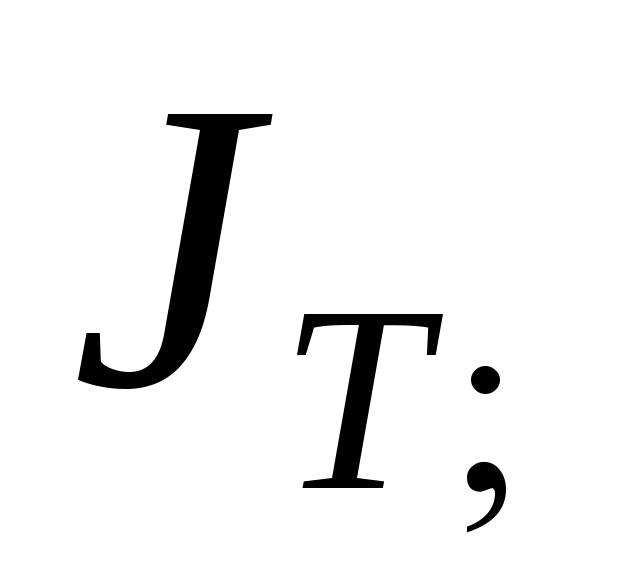 и
и 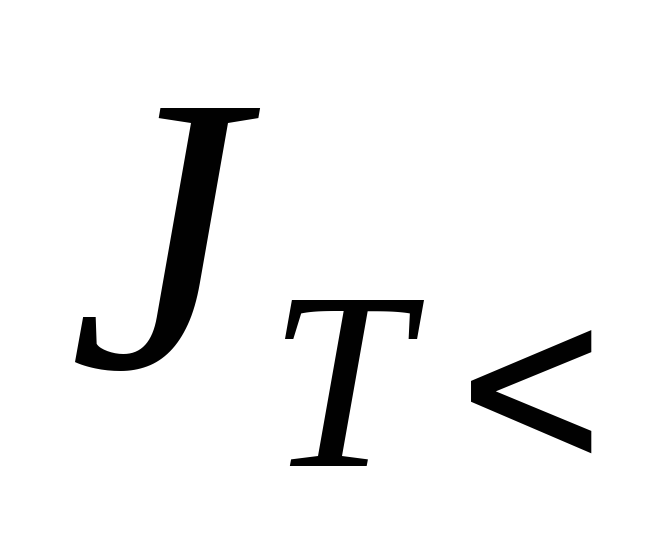 для двух различных расстояний
для двух различных расстояний 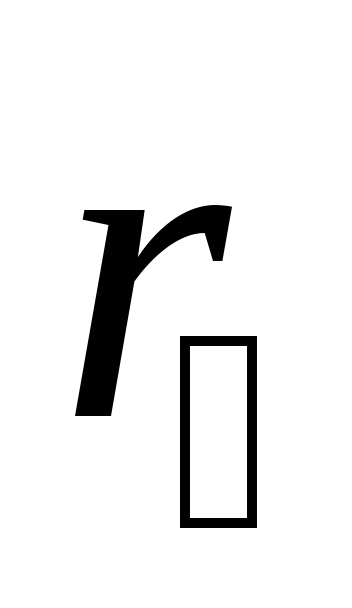 и
и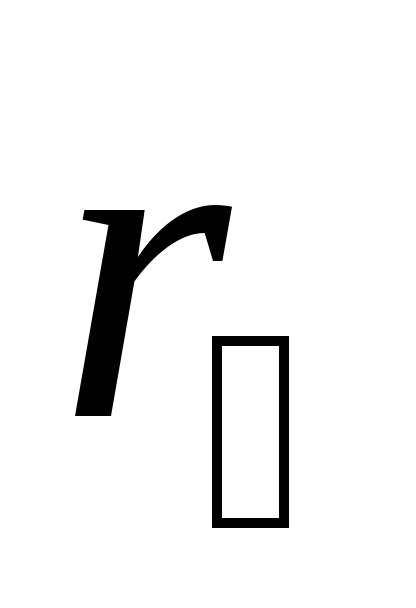 позволит исключить слагаемые
позволит исключить слагаемые  и
и 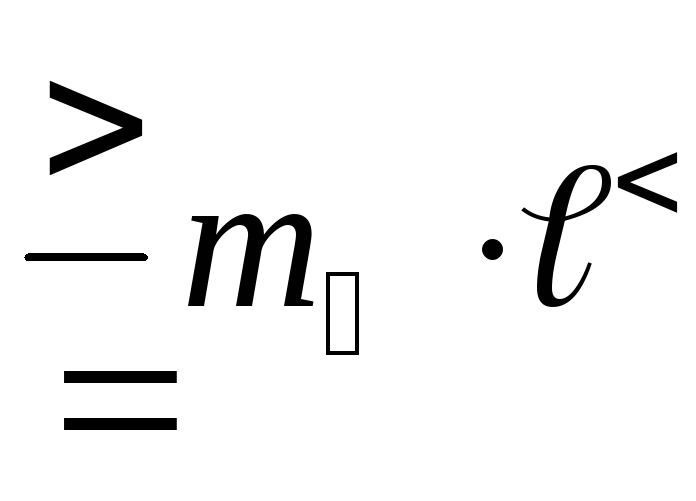 .
Тогда теоретический расчет момента
инерции маятника будет определяться
по формуле
.
Тогда теоретический расчет момента
инерции маятника будет определяться
по формуле
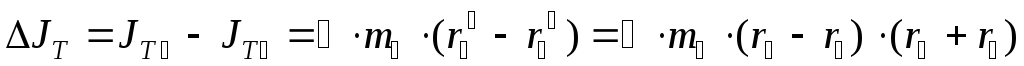 .
(8)
.
(8)
Расчет
момента инерции маятника 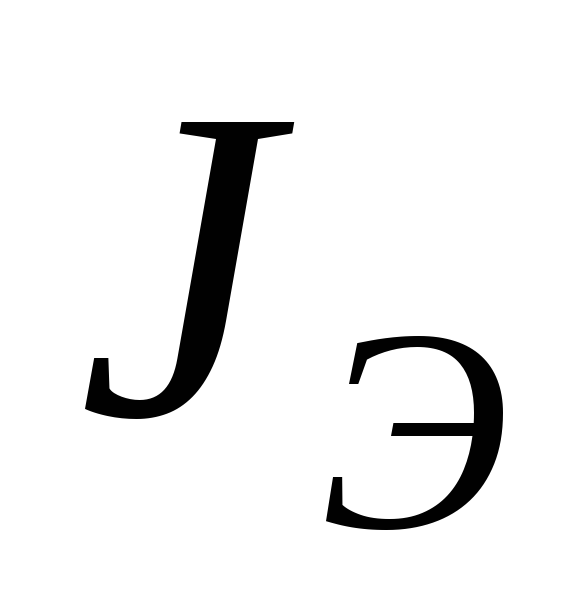 по формуле (7) при различных расположениях
грузов на крестовине можно теоретически
проверить величиной момента инерции
по формуле (7) при различных расположениях
грузов на крестовине можно теоретически
проверить величиной момента инерции  ,
рассчитанного по формуле (8).
,
рассчитанного по формуле (8).
Описание установки
Для
расчетов экспериментального 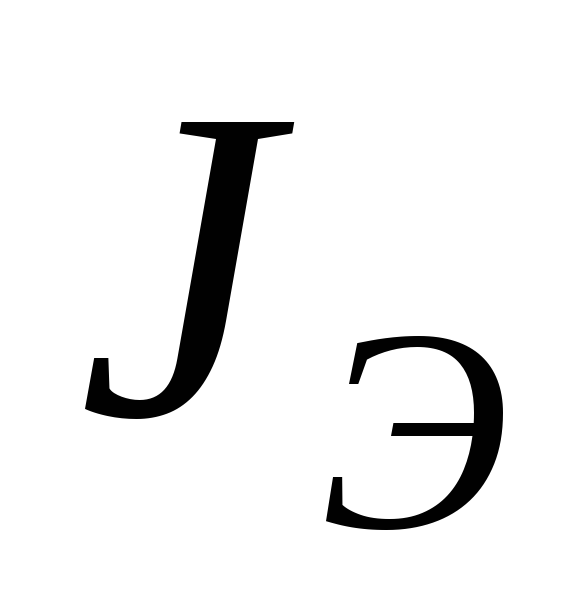 и теоретического
и теоретического  моментов инерции представлена установка
маятника Обербека (рис. 4, а).
Схематический
вид установки маятника Обербека показан
на рис. 4, б,
в.
моментов инерции представлена установка
маятника Обербека (рис. 4, а).
Схематический
вид установки маятника Обербека показан
на рис. 4, б,
в.
Маятник Обербека имеет вертикальную колонну 1, которая установлена на основании 2. На вертикальной колонне 1 прикреплены два кронштейна: нижний 3 является неподвижным, верхний 4 — подвижный и две неподвижные втулки: нижняя 5 и верхняя 6. Основание снабжено регулируемыми ножками 7, обеспечивающими горизонтальную установку прибора.
На верхней втулке 6 посредством основания 8 закреплен подшипниковый узел диска 9 и диск 10. Через диск перекидывается нить 11. Один конец нити прикреплен к двухступенчатому диску 12, а на втором конце закреплены грузы 13. На нижней втулке 5 посредством основания 14 прикреплен тормозной электромагнит 15, который удерживает систему крестовины вместе с грузами в состоянии покоя. Подвижный кронштейн 4 можно переместить вдоль колонны и фиксировать его в любом положении, определяя длину пути падающего груза. Для этого на колонне 1 нанесена миллиметровая шкала 16. На подвижном кронштейне 4 укреплен фотоэлектрический датчик 17. На неподвижном кронштейне 3 — фотоэлектрический датчик 18. К кронштейну 3 прикреплен кронштейн 19 с резиновым амортизатором, ограничивающим движение грузов.
Под
действием груза нить разматывается и
приводит маятник во вращательное
движение, которое предполагается
равноускоренным. Угловое
ускорение при этом тем меньше, чем больше
момент инерции системы относительно
оси вращения, величина которого зависит
от положения
перемещаемых грузов на крестовине.
Время
движения груза  измеряется электронным секундомером
18, расположенныму
основания прибора,
а остановка происходит по сигналу
фотодатчика. Груз опускается на расстояние
измеряется электронным секундомером
18, расположенныму
основания прибора,
а остановка происходит по сигналу
фотодатчика. Груз опускается на расстояние 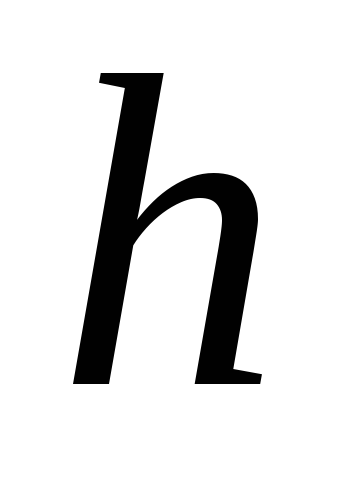 ,
измеряемое вертикально закрепленной
линейкой с сантиметровыми делениями.
,
измеряемое вертикально закрепленной
линейкой с сантиметровыми делениями.
| | |
а | б | в |
Рис. 4 | ||
Порядок выполнения работы
1.
Установить один перегруз на падающий
груз. Определить массу общего падающего
груза 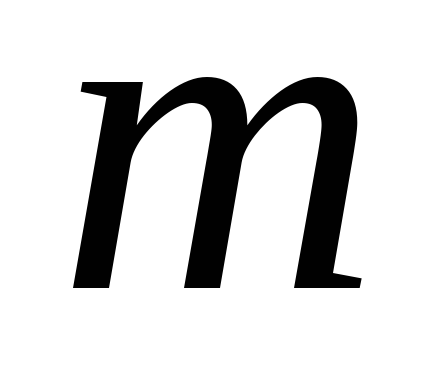 и записать в табл.
и записать в табл.
2.
Измерить с помощью штангенциркуля
диаметр диска. Рассчитайте радиус диска  и записать в табл..
и записать в табл..
3.
Укрепить на стержне крестовины грузы 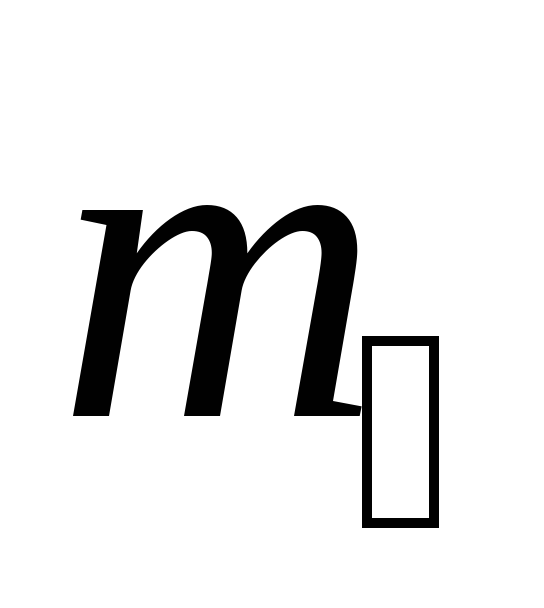 на одинаковых расстояниях
на одинаковых расстояниях 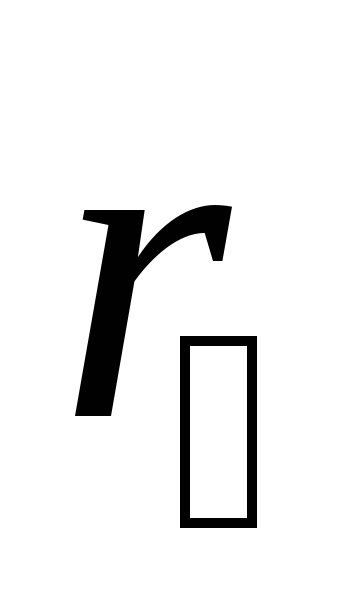 от оси вращения (в пределах от 5 до 15 см).
Определите это расстояние, используя
деления нанесенные на стержне (1 деление
=1 см) и записать в табл.
от оси вращения (в пределах от 5 до 15 см).
Определите это расстояние, используя
деления нанесенные на стержне (1 деление
=1 см) и записать в табл.
4.
Вращая маятник рукой, намотать нить на
диск и установить падающий груз на
высоте 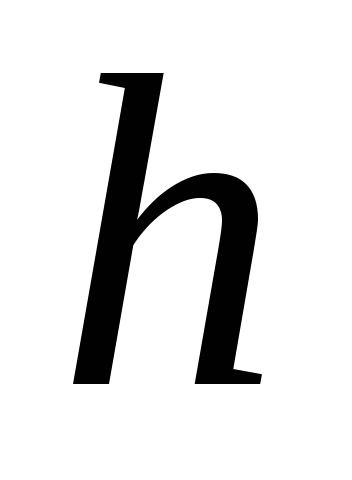 (в пределах от 30 до 40 см). Значение высоты
записать в таб.
(в пределах от 30 до 40 см). Значение высоты
записать в таб.
5.
Включить электронный секундомер. Нажать
кнопку «пуск» и одновременно запустить
вращение диска. В момент прохождения
грузом нижней точки секундомер
остановится. Записать время падения  груза в табл.
груза в табл.
6.
Провести прямые пятикратные измерения
времени падения груза  при
неизменной геометрии эксперимента
согласно п.п. 4-5. Результаты измерений
записать в табл. Рассчитать среднее
время падения.
при
неизменной геометрии эксперимента
согласно п.п. 4-5. Результаты измерений
записать в табл. Рассчитать среднее
время падения.
7.
Изменить расстояние 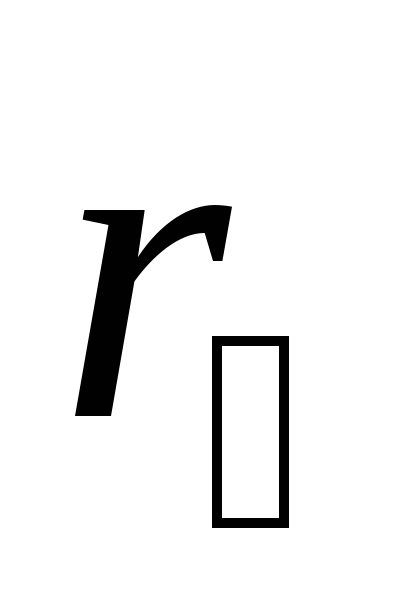 от оси вращения до грузов
от оси вращения до грузов 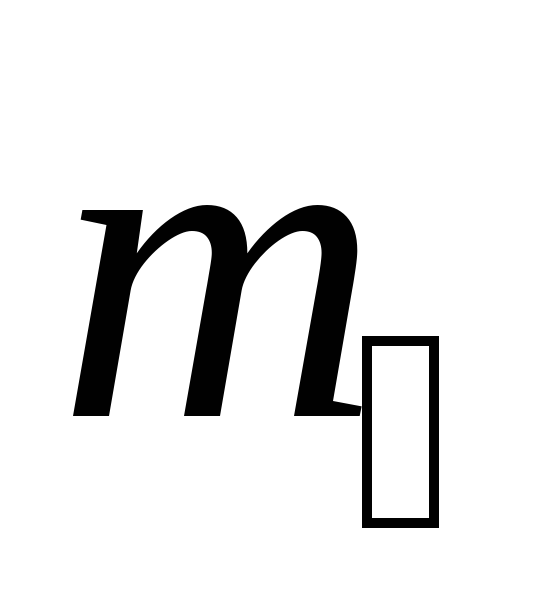 (в пределах от 20 до 25 см) и записать в
табл.
(в пределах от 20 до 25 см) и записать в
табл.
8.
Провести прямые пятикратные измерения
времени 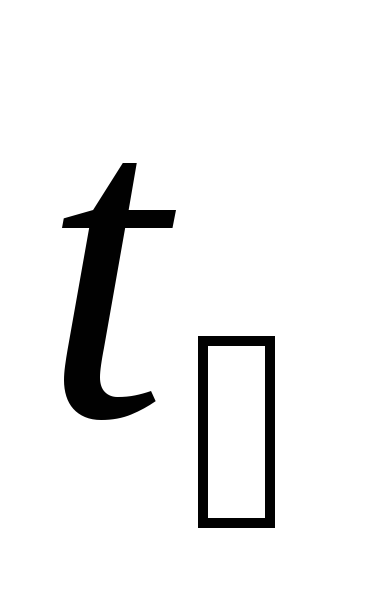 падения груза при неизменной геометрии
эксперимента согласно п.п. 4-5. Результаты
измерений записать в табл. Рассчитать
среднее время падения.
падения груза при неизменной геометрии
эксперимента согласно п.п. 4-5. Результаты
измерений записать в табл. Рассчитать
среднее время падения.
Таблица
N
 ,
г
,
г ,
г
,
г ,
см
,
см ,
см
,
см, см
 ,
c
,
c ,
см
,
см ,
c
,
c1
2
3
4
5
 =
= =
=
9.
Вычислить экспериментальные значения
моментов инерции маятника 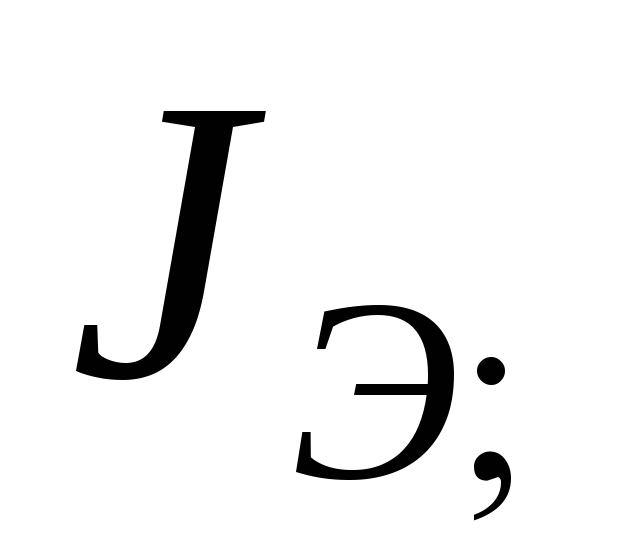 и
и 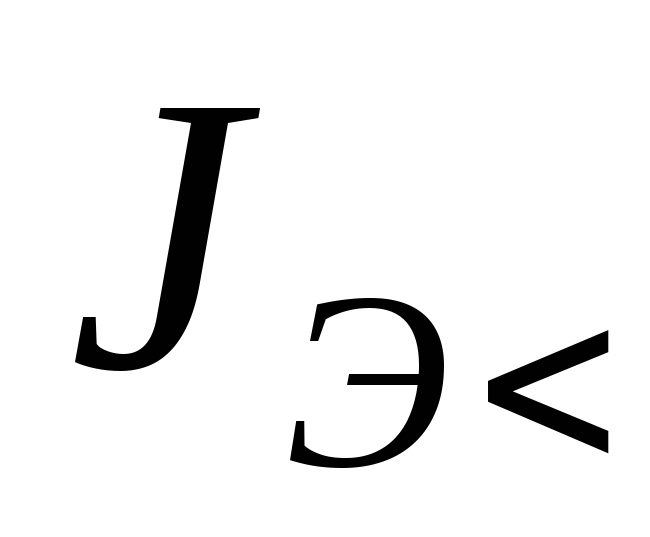 с
грузами на стержнях, расположенных на
разном расстоянии
с
грузами на стержнях, расположенных на
разном расстоянии 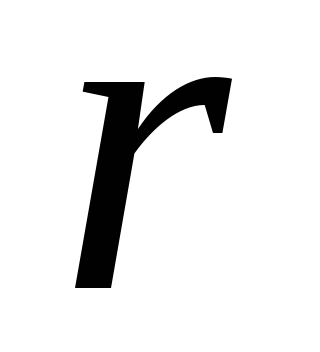 от оси вращения по формуле (7). В качестве
времени падения груза взять его среднее
значение.
от оси вращения по формуле (7). В качестве
времени падения груза взять его среднее
значение.
10.
Рассчитать теоретическое значение
момента инерции маятника 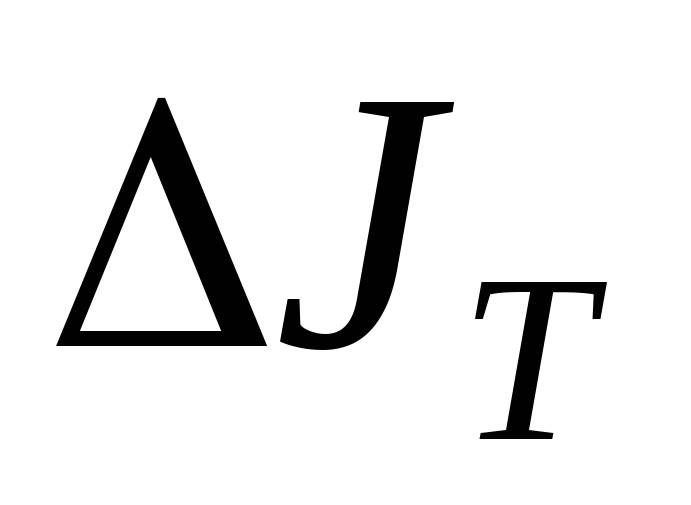 для
выбранных расстояний
для
выбранных расстояний 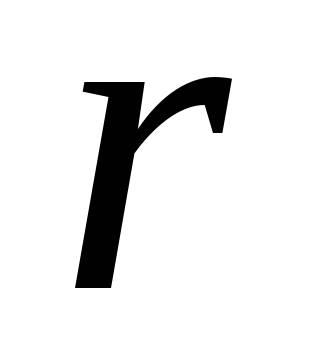 по
формуле (8).
по
формуле (8).
11. Сравнить полученные результаты и найдите относительную погрешность измерения момента инерции по формуле
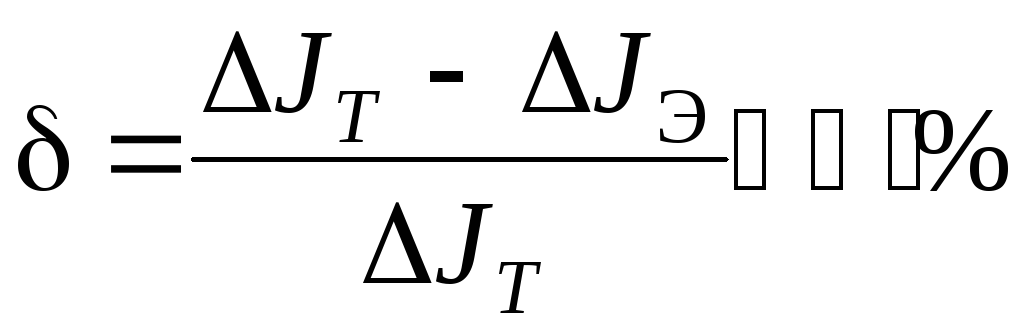 ,
,
где 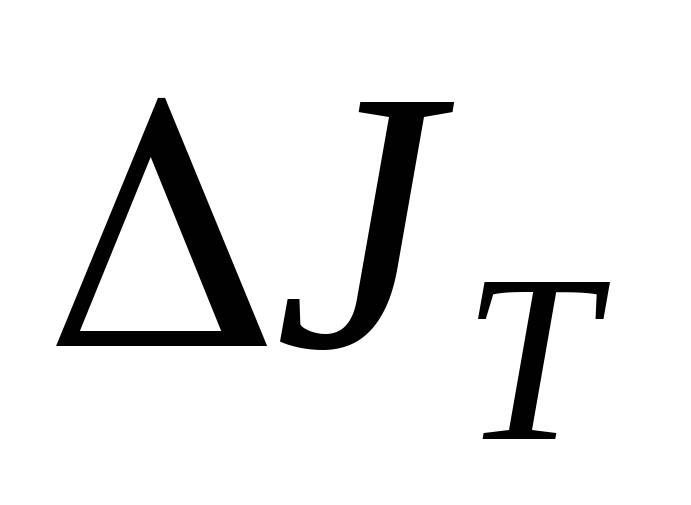 — теоретическое изменение моментов
инерции при разных расстояниях;
— теоретическое изменение моментов
инерции при разных расстояниях; 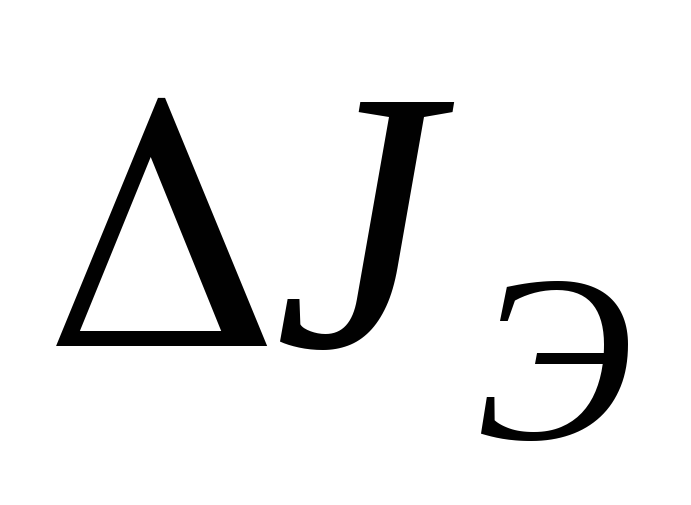 — экспериментальное
изменение моментов инерции при разных
расстояниях.
— экспериментальное
изменение моментов инерции при разных
расстояниях.
Контрольные вопросы
1. Дать определение абсолютно твердого тела и вращательного движения.
2. Дать определение средней и мгновенной угловых скоростей, средней и мгновенной угловых ускорений. Единицы измерения угловой скорости и углового ускорения. Как определяется направления векторов угловой скорости и углового ускорения? Какова связь между линейными и угловыми скоростями и ускорениями?
3. Почему движение падающего груза и вращение маховика являются равноускоренными?
4. Вывести основной закон динамики вращательного движения.
5. Что называется моментом силы тела относительно неподвижной точки вращения? Как определяется его направление? В каких единицах он измеряется?
6. Какая сила сообщает вращающий момент маятнику? Как направлен момент этой силы?
7. Что называется моментом инерции материальной точки и тела? В каких единицах он измеряется? Каков физический смысл момента инерции тела.
8. Сформулируйте и объясните теорему Штейнера.
ЛАБОРАТОРНАЯ РАБОТА №2
Определение средней силы натяжения нитей в момент «рывка» при движении маяника Максвелла
Постановка задачи. Определить среднюю силу натяжения нитей в маятнике Максвелла при его равноускоренном движении и во время «рывка», когда маятник достигает нижней точки траектории. Масса маятника m, радиус вала r; путь h маятник проходит за время (рис 10.1).
Указания
к решению. Из
рис. 10.2. видно, что скорость центра масс
маятника Максвелла начинает уменьшаться,
начиная с момента, когда нити полностью
раскручены и точка их закрепления
находится в положении В1.
В момент, когда точки закрепления нитей
занимают положение В2,
скорость центра масс оказывается равной
нулю, а когда точки закрепления нитей
займут положение В3 (нити начинают наматываться на вал),
скорость центра маятника изменит свое
направление, причем 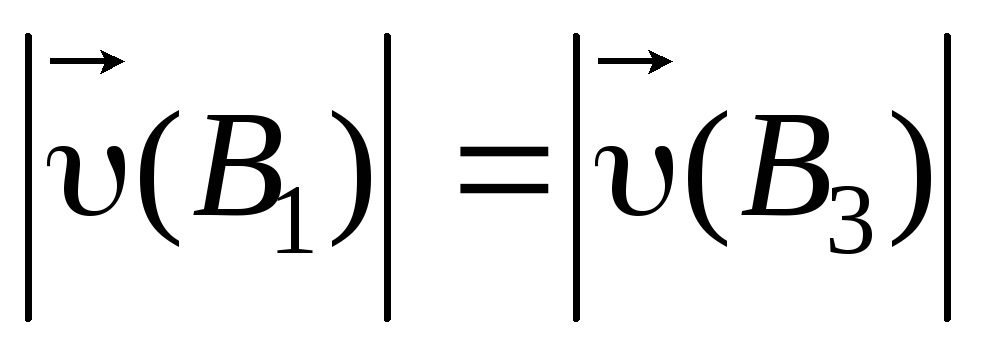 .
Отсюда следует, что за время половины
оборота вала импульс сил, действующих
на маятник, равен
.
Отсюда следует, что за время половины
оборота вала импульс сил, действующих
на маятник, равен
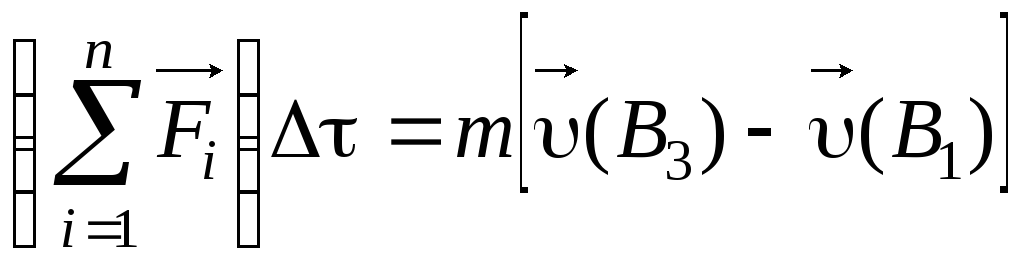 .
.
Здесь 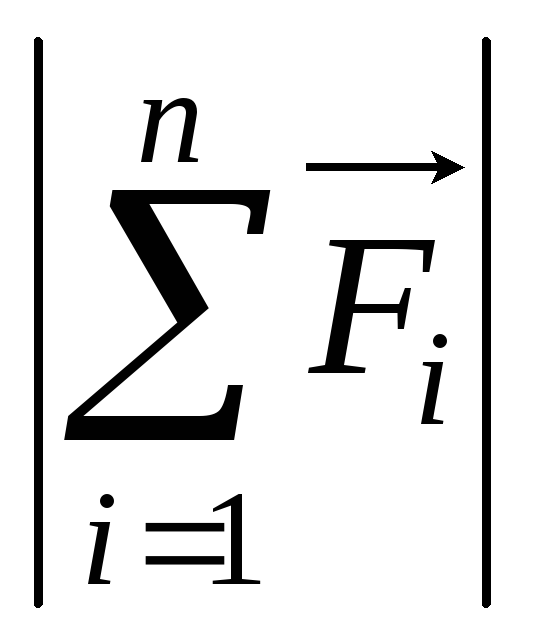 —
среднее значение суммарной силы,
действующей на маятник в процессе
изменения направления движения. В
результате получим
—
среднее значение суммарной силы,
действующей на маятник в процессе
изменения направления движения. В
результате получим
(2Тср—mg)=2m. (10.20)
Здесь (В1)= (В3)= ; Тср— средняя сила натяжения нити за время «рывка»; время половины оборота, когда происходит «рывок», приближенно равно
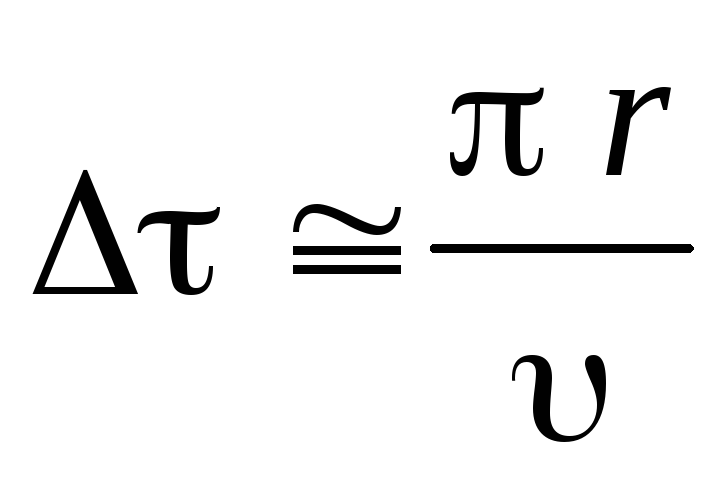 .
(0.21)
.
(0.21)
Здесь r – радиус вала; — максимальная скорость центра масс маятника.
Движение маятника Максвелла описывается системой уравнений.
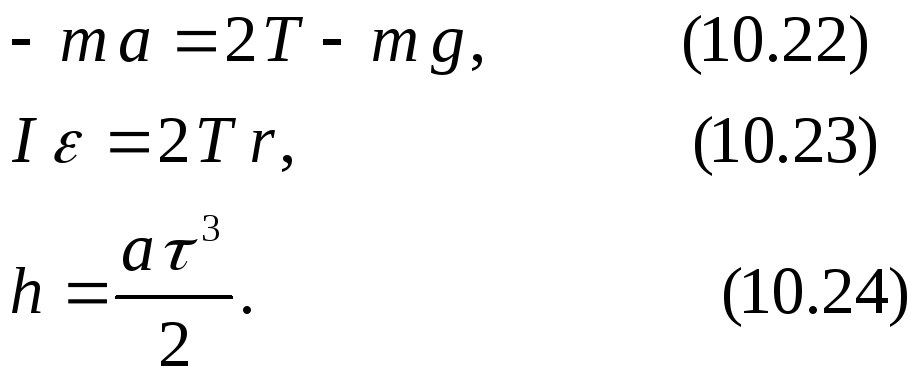
Из (10.22) и (10.23) следует, что при движении маятника Максвелла сила натяжения нити равна
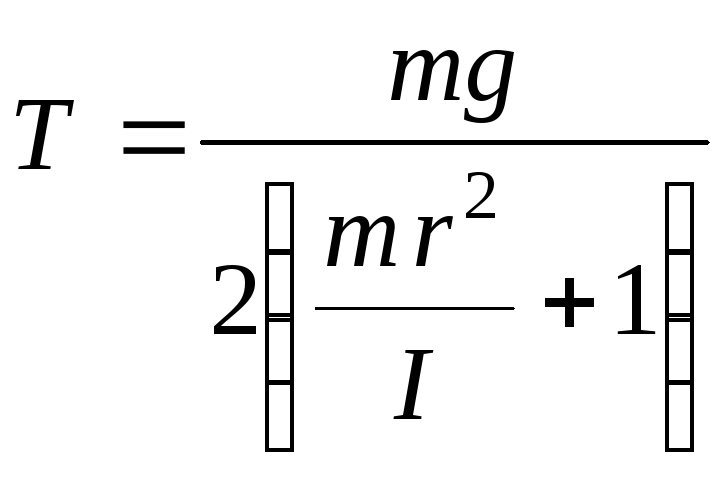 ,
(10.25)
,
(10.25)
где момент инерции маятника I определяется соотношением (10.15). Максимальную скорость центра масс маятника (маятник в нижнем положении) определим из (10.24)
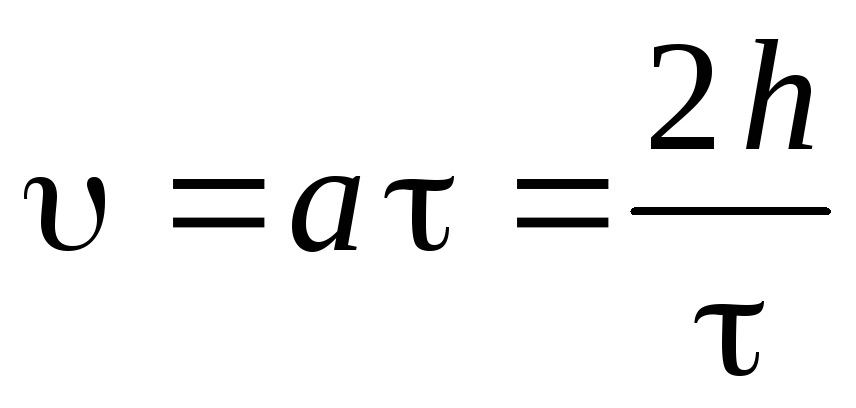 .
(10.26)
.
(10.26)
Из (10.20), (10.21) и (10.26) следует, что средняя сила натяжения нити при «рывке» приблизительно равна
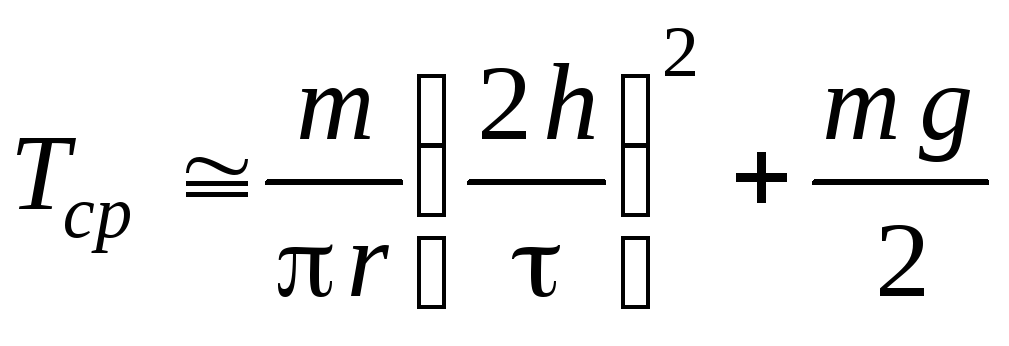 .
(10.27)
.
(10.27)
Описание экспериментальной установки
Схема
экспериментальной установки представлена
на рис.10.3. На вертикальной стойке 1
закреплены кронштейны 2 и 3. На кронштейне
2 смонтирован электромагнит 4 и устройство
5 для крепления и регулировки длины
нитей подвеса. Маятник представляет
собой диск 6, жестко скрепленный с
цилиндрическим валом 7. На диск насаживается
съемное кольцо. Маятник фиксируется в
верхнем положении электромагнитом 4.
На стойке 1 закреплена миллиметровая
шкала, позволяющая определить расстояние,
на которое опускается центр масс маятника
Максвелла при его д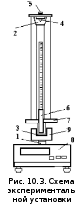 вижении.
Время движения маятника от верхнего до
нижнего положения измеряется с помощью
миллисекундомера 8 с цифровой индекцией.
Включение миллисекундомера осуществляется
нажатием клавиши ПУСК, расположенной
на нижней панели прибора. Одновременно
отключается от источника питания
электромагниты, удерживающие маятник
в верхнем положении, начинается движении
маятника вниз. Остановка счета времени
осуществляется при помощи фотоэлектрического
датчика 9 в момент пересечения магнитом
оптической оси фотодатчика. Фотодатчик
закреплен на нижнем кронштейне 3;
кронштейн 3 может перемещаться вдоль
вертикальной стойки 1.
вижении.
Время движения маятника от верхнего до
нижнего положения измеряется с помощью
миллисекундомера 8 с цифровой индекцией.
Включение миллисекундомера осуществляется
нажатием клавиши ПУСК, расположенной
на нижней панели прибора. Одновременно
отключается от источника питания
электромагниты, удерживающие маятник
в верхнем положении, начинается движении
маятника вниз. Остановка счета времени
осуществляется при помощи фотоэлектрического
датчика 9 в момент пересечения магнитом
оптической оси фотодатчика. Фотодатчик
закреплен на нижнем кронштейне 3;
кронштейн 3 может перемещаться вдоль
вертикальной стойки 1.
§36. Вращение твердого тела. Момент силы
∑ mi wi = ∑ Fi | (35.3) |
где справа получается результирующая всех внешних сил, действующих но тело. Сумму, стоящую в левой части уравнения (35.3), можно заменить произведением массы тела m на ускорение его центра инерции wc. Действительно, радиус-вектор центра инерции по определению (см. (23.1)) равен
rc = ∑ mi wi .
m
Продифференцировав это соотношение дважды по времени и учитывая, что rc=wc, a ri=wi, можно написать:
mwc = ∑ mi wi . | (35.4) |
Следовательно, |
|
mwc = ∑Fi . | (35.5) |
откуда вытекает, что центр инерции твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил.
Уравнение (35.5) дает возможность установить движение центра инерции твердого тела, если известна масса тела и действующие на него силы. В случае поступательного движения это уравнение будет определять ускорение не только центра инерции, но и любой другой точки тела.
Чтобы выяснить, чем определяется характер вращения тела вокруг неподвижной оси, рассмотрим следующий опыт. Возьмем тело в виде легкой крестовины, на концах которой закреплены равные массивные грузы m (рис. 87).
В центре крестовины укрепим ступенчатый шкив. Крестовину вместе со шкивом наденем на ось, позаботившись о том, чтобы трение при вращении вокруг этой оси было пренебрежимо мало.
Рис. 87.
Прикрепим к одной из ступеней шкива конец нити, обмотаем ее вокруг шкива и, перебросив свободный конец нити через блок, подвесим к нему груз P. Если отпустить груз P. крестовина пойдет во вращение со все возрастающей угловой скоростью ω, причем вращение будет равномерно-ускоренным.
Варьируя величину груза P, радиус шкива l, массу грузов m и их расстояние R от оси вращения» исследуем, как эти факторы влияют на величину углового ускорения β . Результаты
подобного исследования сводятся к тому, что угловое ускорение β 1) прямо пропорционально натяжению нити l и радиусу шкива l;
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
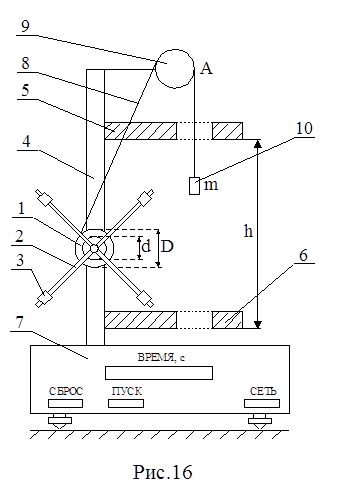
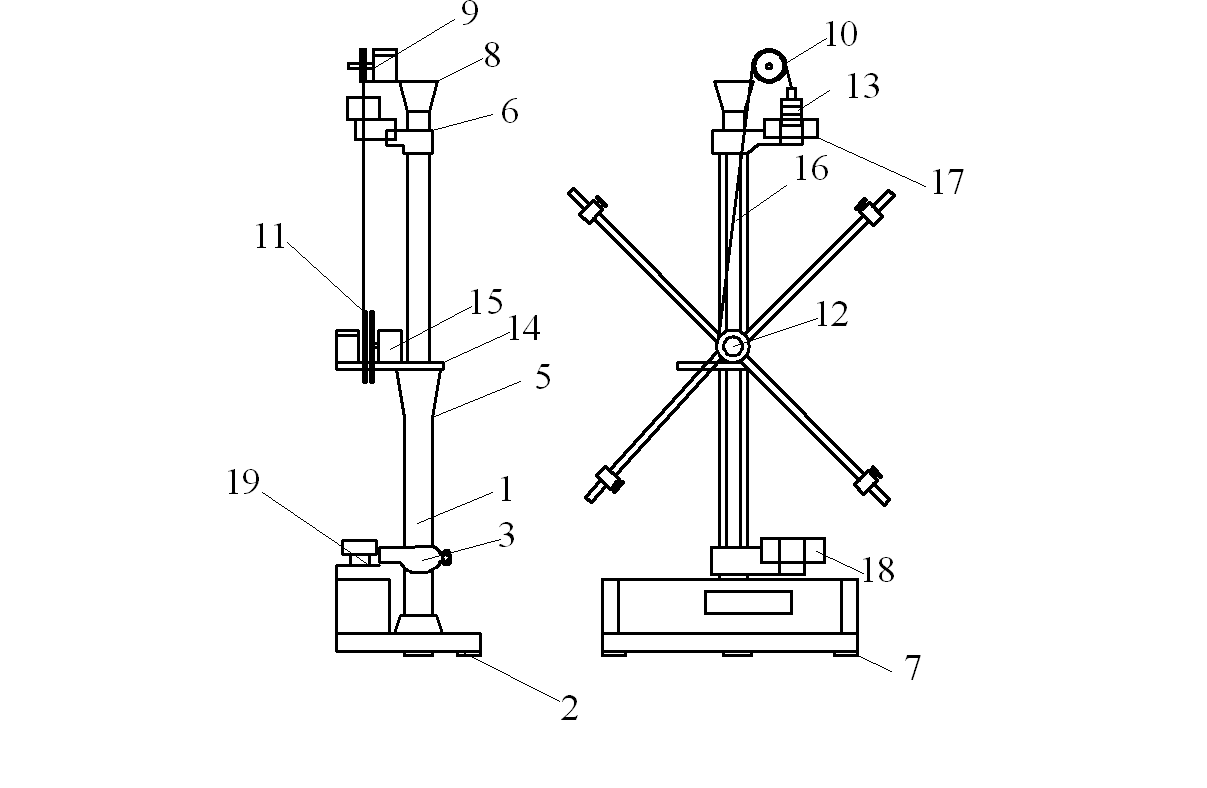
Экспериментальная установка показана на рис.16.
Маятник Обербека состоит из четырех спиц, укрепленных на втулке под прямым углом друг к другу. На втулке закреплены два шкива 1 с разными диаметрами D и d. Втулка со спицами и шкивами может свободно вращаться относительно горизонтальной оси. Вдоль каждой спицы 2 можно перемещать грузик 3, закрепляя его на расстоянии R от оси вращения. Маятник Обербека и два кронштейна 5 и 6 крепятся к вертикальной стойке 4. Если на шкив 1 намотать нить 8, к ее концу присоединить груз 10 массой m и перекинуть нить через неподвижный блок 9, то, нажимая кнопку «ПУСК», измерить время ускоренного движения груза 10 на расстоянии h с помощью секундомера 7 экспериментальной установки.
 Так как начальная скорость груза равна нулю, то
Так как начальная скорость груза равна нулю, то 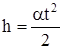 ,
,
где t — время движения груза. Тогда ускорение груза, направленное вниз, равно
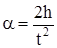 . (13)
. (13)
На груз действует его сила тяжести 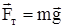 и сила натяжения нити
и сила натяжения нити 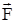 . Если на вертикальной оси координат положительное направление выбрать вниз, то проекция второго закона Ньютона
. Если на вертикальной оси координат положительное направление выбрать вниз, то проекция второго закона Ньютона 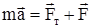 на эту ось имеет вид:
на эту ось имеет вид: 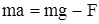 . Отсюда сила натяжения нити равна
. Отсюда сила натяжения нити равна
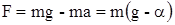 .
.
Момент силы натяжения, действующий на маятник Обербека, относительно горизонтальной оси z соответственно равен 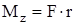 , где r — радиус шкива. Тогда
, где r — радиус шкива. Тогда
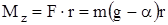 . (14)
. (14)
Под действием момента силы маятник вращается с угловым
ускорением e. Если нить, навитая на шкив, не проскальзывает, то ускорение нити, равное ускорению груза, равно тангенциальному ускорению точек обода шкива 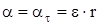 . Отсюда
. Отсюда
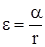 . (15)
. (15)
Подставляя формулы (14) и (15) в формулу (12), найдем общий момент инерции маятника Обербека относительно горизонтальной оси z, проходящей через центр масс маятника
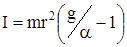 . (16)
. (16)
Подставляя формулу (13) в формулу (16) и учитывая, что
r = d/2, получим формулу для определения момента инерции маятника Обербека относительно оси вращения:
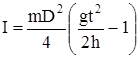 . (17)
. (17)
Если момент инерции крестовины со шкивами относительно оси вращения обозначить Iкр, то общий момент инерции маятника относительно этой оси равен
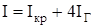 . (18)
. (18)
Момент инерции IГ одного цилиндрического грузика относительно оси вращения находим с помощью формулы (10) и теоремы Штейнера (11):
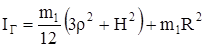 , (19)
, (19)
где m1 — масса грузика, r, Н — радиус и высота цилиндрического грузика,
R — расстояние центра масс каждого грузика до оси вращения. Подставляя формулу (19) в формулу (18), получим момент инерции маятника относительно оси вращения в виде:
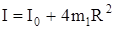 , (20)
, (20)
где 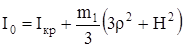 .
.
Согласно формуле (20) меняя расстояние R центров грузиков до оси вращения, изменяем общий момент инерции I маятника Обербека.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Найдите массу m падающего груза и диаметры D и d шкивов. Установите и измерьте определенную высоту h падающего груза. Запишите найденные результаты в таблицу 1.
2. С помощью кнопки «СЕТЬ» включите экспериментальную установку.
3. Поместите на спицы маятника 4 грузика с массами m1 на одинаковом расстоянии R1 от центра шкива и добейтесь безразличного равновесия. Измерьте R1 и запишите в таблицу 1.
4. В один слой намотайте нить на шкиве с большим диаметром D. Отпустите крестовину и измерьте время падения t1D груза m с высоты h, нажимая кнопку «ПУСК». После измерения нажмите кнопку «СБРОС». Повторите эти измерения не менее пяти раз. Результаты запишите в таблицу 1.
5. Повторите измерения п.4, наматывая нить на шкив меньшего диаметра d, определяя время t1d.
6. Повторите измерения п.п.3¸5 для других расстояний R2, R3 и R4 грузиков до оси вращения. Результаты измерений запишите в таблицу 1.
7. Для каждого расстояния R и диаметра шкива найдите средние значения времени падения 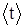 груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.
груза, а также полуширину доверительного интервала Dt. По формуле (15) вычислите момент инерции I маятника Обербека в каждом случае.
Таблица 1
| m = ; D = ; d = ; h = ; | ||||||||
| №№ наблюдений | R1 = | R2 = | R3 = | R4 = | ||||
| t1D | t1d | t2D | t1d | t3D | t3d | t4D | t4d | |
Среднее время 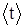 | ||||||||
Полуширина доверительного интервала 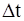 | ||||||||
| Момент инерции I | ||||||||
Полуширина доверительного интервала 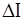 | ||||||||
| Угловое ускорение e | ||||||||
| Полуширина доверительного интервала De |
8. Полуширину доверительного интервала 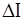 момента инерции маятника определите с помощью формулы:
момента инерции маятника определите с помощью формулы:
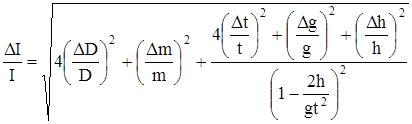 . (21)
. (21)
9. Для каждого диаметра шкива постройте график зависимости 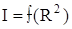 .
.
10. По формулам (13) и (15) вычислите угловое ускорение 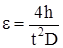 для различных R и постройте график зависимости
для различных R и постройте график зависимости 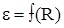 для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы:
для каждого диаметра шкива. Пренебрегая погрешностями измерения D и h, найдите полуширину De доверительного интервала с помощью формулы: 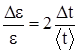 .
.
11. Для одного расстояния R1 по формулам (13), (14) и (15) оцените, как меняется угловое ускорение e при изменении момента силы, вызванном изменением радиуса r шкива.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте цель лабораторной работы.
2. Напишите основной закон динамики вращательного движения твердого тела относительно неподвижной оси.
3. Дайте определение момента силы относительно точки (центра).
4. Дайте определение момента силы относительно оси.
5. Найдите момент силы относительно оси Z, если модуль момента этой силы относительно точки О, лежащей на оси, равен М0 = 10 Нм, а направление момента образует с осью Z угол: 1) g = 30°; 2) g = 150°.
6. Модуль радиуса-вектора, проведенного из начала координат О в точку приложения силы, равен r = 30 см, а направление образует с направлением силы угол
a = 120°. Найдите плечо этой силы относительно начала координат О.
7. Определите момент силы относительно точки, если модуль силы равен
F = 10 Н, а плечо h = 2 см.
8. Дайте определение момента инерции тела относительно оси.
9. По какой формуле можно вычислить момент инерции относительно оси:
1) системы материальных точек; 2) произвольного тела ?
10. На каком расстоянии от оси находится материальная точка массой
m = 20 г, если ее момент инерции относительно этой оси равен I = 200 мг×м2 ?
11. Моменты инерции относительно оси трех тел по отдельности равны
I1 = 10 кг×м2; I2 = 20 кг×м2; I3 = 30 кг×м2. Найдите момент инерции системы этих тел относительно той же оси.
12. Какую массу имеет прямой круглый однородный цилиндр с радиусом основания R = 10 см, если момент инерции цилиндра относительно оси, проходящей через его центр масс параллельно боковой поверхности, равен
I = 0,25 кг×м2 ?
13. Сформулируйте теорему Штейнера.
14. Момент инерции однородного шара радиусом R = 6 см относительно оси, проходящей через центр шара, равен Iс. На каком расстоянии от центра шара должна находится ось, чтобы момент инерции шара относительно ее оказался равным 2Iс ?
15. Определите угловое ускорение твердого тела, вращающегося
относительно неподвижной оси Z под действием момента силы
Mz = 12 мН×м, если момент инерции тела относительно этой оси Iz = 0,48 кг×м2.
16. Нарисуйте эскиз маятника Обербека.
17. Как можно менять момент инерции маятника Обербека ?
18. Момент какой силы сообщает маятнику Обербека угловое ускорение ?
19. Почему момент силы тяжести крестовины равен нулю ?
20. Какие силы действуют на груз, подвешенный к маятнику Обербека ?
21. Как найти силу натяжения нити, на которой подвешен груз ?
22. Как определить ускорение груза, подвешенного к маятнику Обербека ?
23. Как найти угловое ускорение крестовины ?
24. Выведите формулу экспериментального определения момента инерции маятника Обербека.
25. Какие величины постоянны при выполнении эксперимента в данной лабораторной работе ?
26. Как применить теорему Штейнера для теоретической оценки момента инерции маятника Обербека ?
27. Как меняется угловое ускорение маятника Обербека при удалении грузиков крестовины от оси вращения ?
28. Меняется ли натяжение нити в зависимости от расстояния грузиков крестовины от оси вращения?
29. Как меняется угловое ускорение крестовины при изменении радиуса r ее шкива ?
30. Выведите формулу вычисления доверительного интервала DI при экспериментальном определении момента инерции I маятника Обербека.
Угловое ускорение маховика и момент сил натяжения нити для опытов с различными массами грузов
Контрольные вопросы для допуска к работе
1. Что называется моментом инерции? В каких единицах он измеряется?
2.От чего зависит момент инерции твердого тела массой m относительно данной оси вращения Z?
3.Каков физический смысл момента инерции твердого тела?
4.Как определяется момент инерции материальной точки, системы материальных точек, твердого тела относительно оси?
5. Дайте определение момента силы относительно неподвижного полюса, относительно неподвижной оси.
6. Как рассчитывается теоретическое значение момента инерции маховика относительно оси вращения? Какие параметры для этого надо знать? Какими величинами можно пренебречь?
7.Каким образом в работе определяется работа сил трения в подшипниках вала?
8. Каков будет характер движения макового колеса при отсутствии трения?
9.Почему груз в эксперименте поднимается на высоту, меньшую первоначальной ?
10.Какие силы создают вращающие моменты в установке, каковы направления моментов этих сил?
11.Является ли движение грузов равноускоренным?
12.Как определить линейное ускорение грузов и угловое ускорение колеса?
Задание на срс. Проработать следующие вопросы и задания к сдаче отчета
1.Какой закон положен в основу вывода расчетной формулы?
2.Запишите основное уравнение динамики вращательного движения и
охарактеризуйте входящие в него величины.
3.Получите формулу для расчета момента инерции маховика по данным эксперимента, пренебрегая трением в подшипниках вала.
4.Рассчитайте момент инерции сплошного однородного кольца относительно оси, перпендикулярной плоскости кольца и проходящей через его центр.
5.Сформулируйте закон изменения механической энергии.
6.Выведите
формулу погрешности 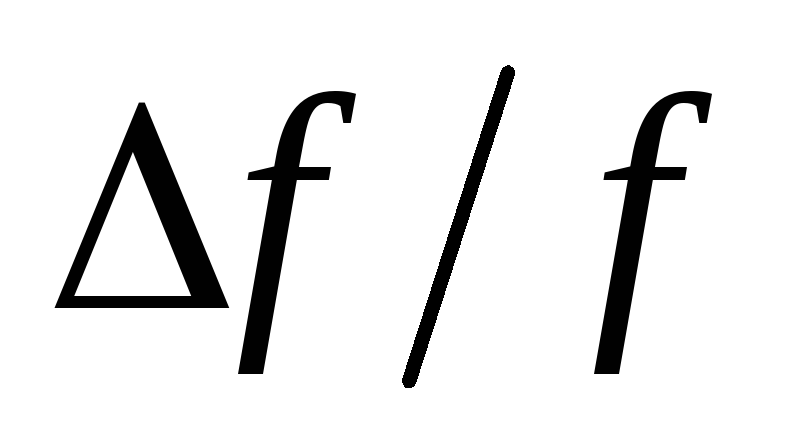 для силы трения.
для силы трения.
7.Определите относительную погрешность формулыдля основного закона вращательного движения Iε=M.
Лабораторная работа № 1.8 в определение момента инерции тела с помощью крутильного маятника и проверка теоремы штейнера
Цель работы: определение момента инерции различных тел методом крутильных колебаний.
Приборы и принадлежности: кронштейн с закрепленной нитью к нему трифилярный подвес, исследуемые тела, набор вспомогательных тел, секундомер, штангенциркуль, весы.
Теоретическая часть
Если тело, подвешенное на упругой нити, вывести из положения равновесия путем поворота вокруг вертикальной оси на угол m и предоставить самому себе, то в системе возникнут крутильные колебания. При малых m эти колебания можно считать гармоническими:
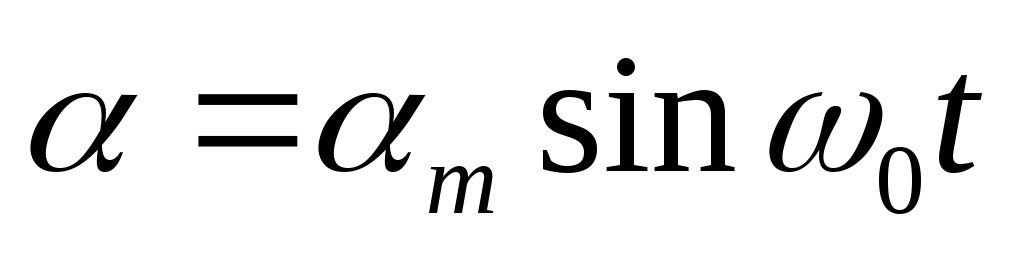 . (1)
. (1)
Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела, когда угол отклонения от положения равновесия изменится по закону синуса или косинуса. Например,
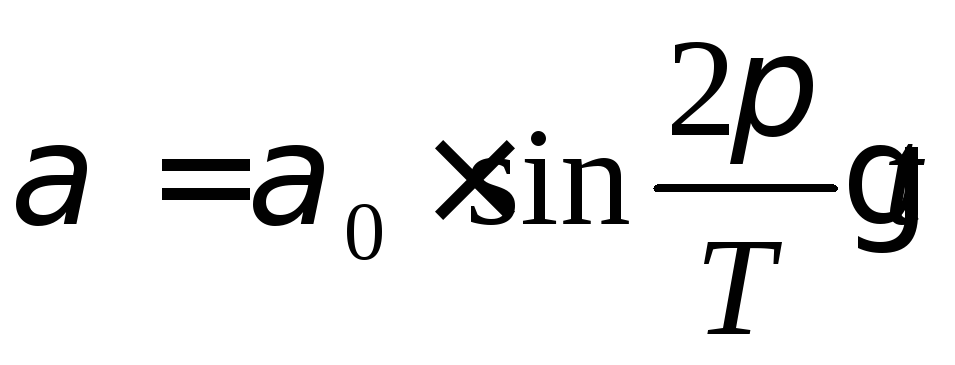 (2)
(2)
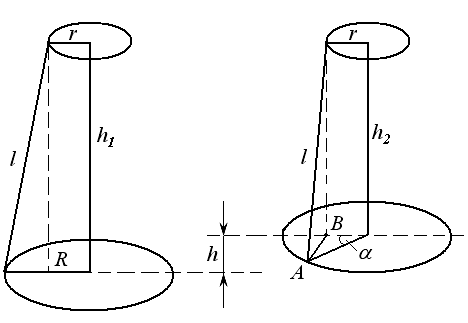
Момент инерции различных тел могут быть измерены методом крутильных колебаний с помощью, так называемого трифиляьрного подвеса. Трифилярный подвес состоит из диска массой m радиуса R (рис.1), подвешанного на трех симметрично расположенных металлических нитях.
| На
верху эти нити симметрично закреплены
по краям диска меньшего радиуса r. При повороте нижнего диска на небольшой
угол |
Рис. 1 |
положение,
центр тяжести системы несколько
приподнимается по оси вращения. Нижний
диск начнет совершать крутильные
колебания, период которых будет зависеть
от момента инерции системы. Пусть при
вращении диск поднялся на высоту 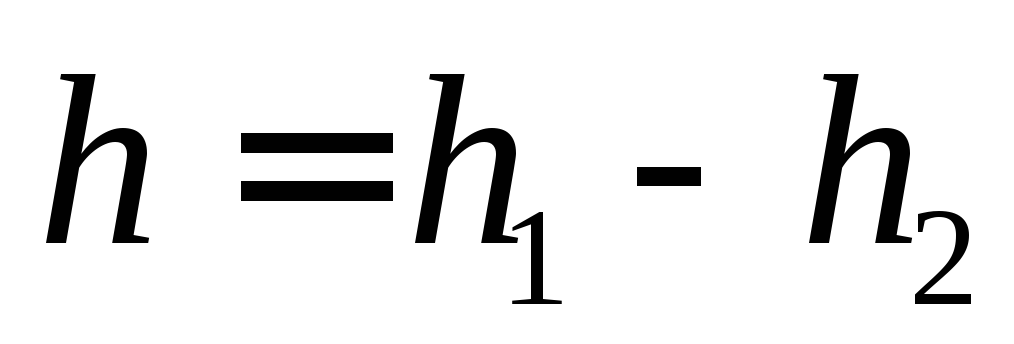 (рис.1) Тогда приращение потенциальной
энергии равно
(рис.1) Тогда приращение потенциальной
энергии равно
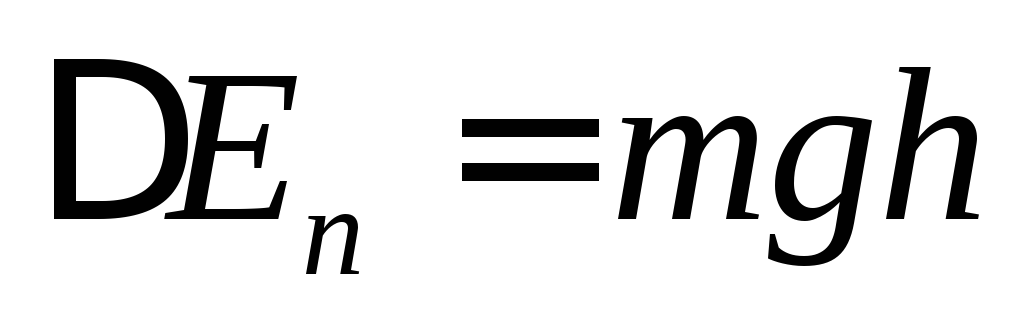 . (3)
. (3)
При вращении диска в другую сторону потенциальная энергия переходит в кинетическую энергию вращательного движения
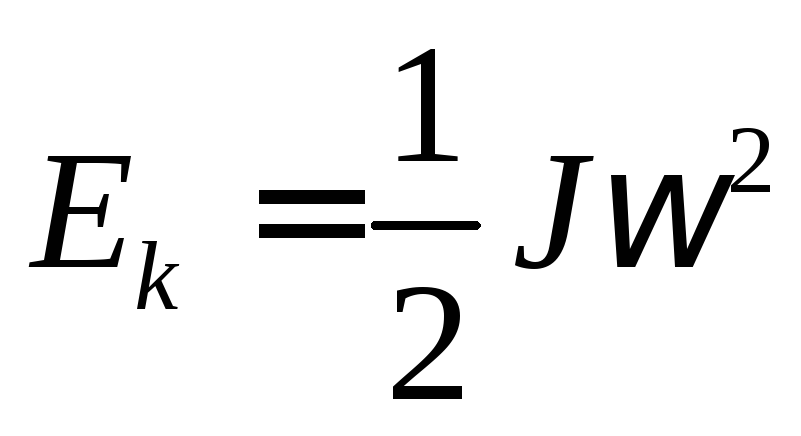 . (4)
. (4)
В момент прохождения положения равновесия кинетическая энергия принимает максимальное значение. Пренебрегая трением, можно записать:
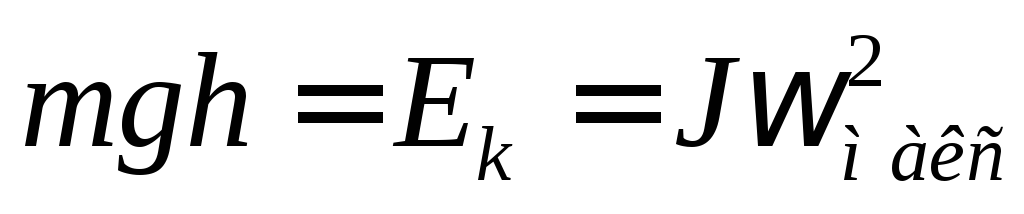 . (5)
. (5)
Угловую скорость диска можно найти взяв производную от α см.формулу (2):
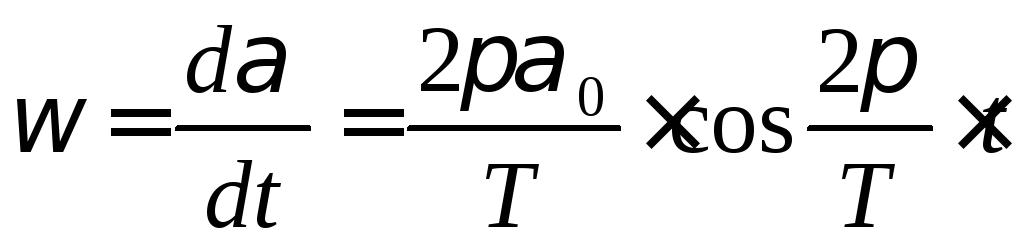
Очевидно
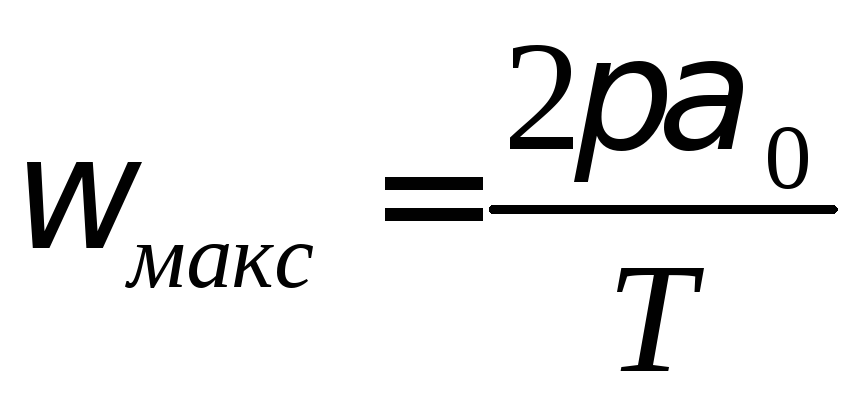 (6)
(6)
Найдем
величину h при повороте диска на угол 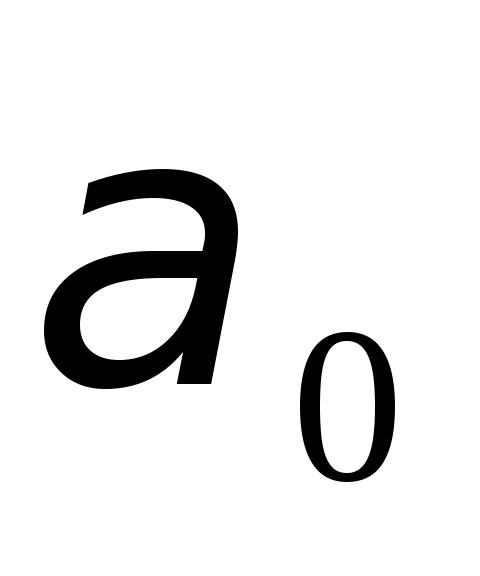 ,
считая, чтоh1+ h2≈2l:
,
считая, чтоh1+ h2≈2l:
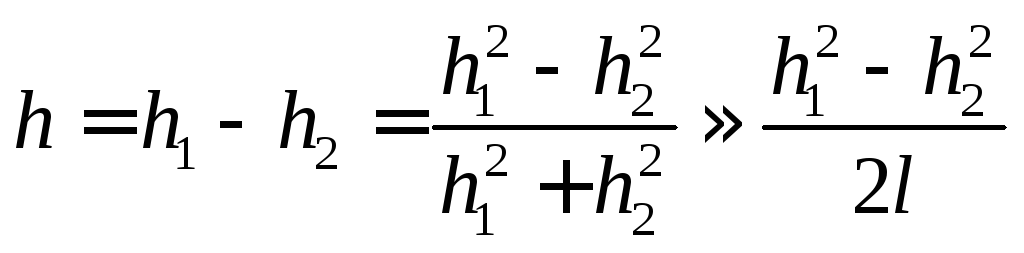 . (7)
. (7)
Из рис.1 ясно, что
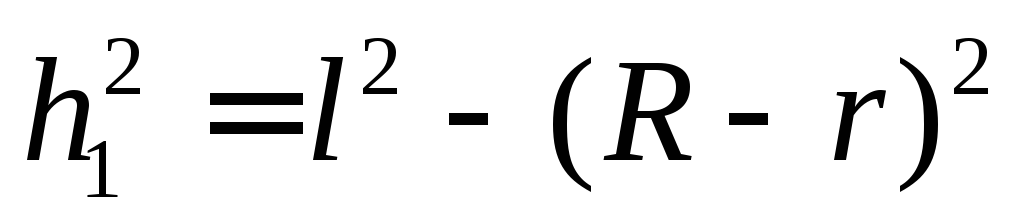 и
и 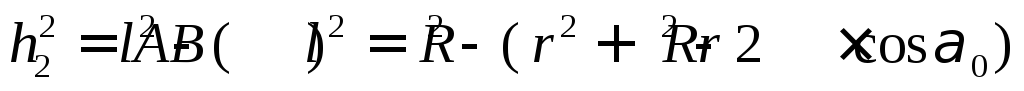 .
.
Подставляя
значение 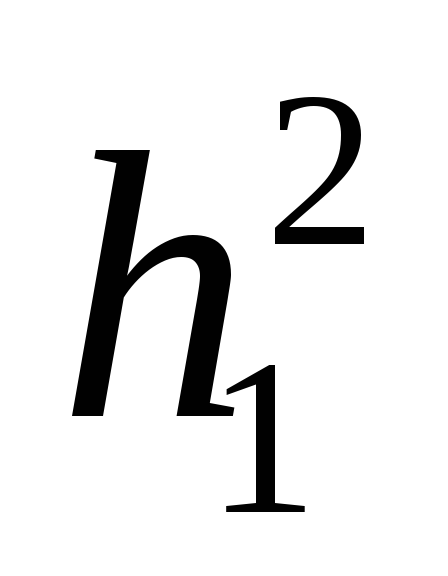 и
и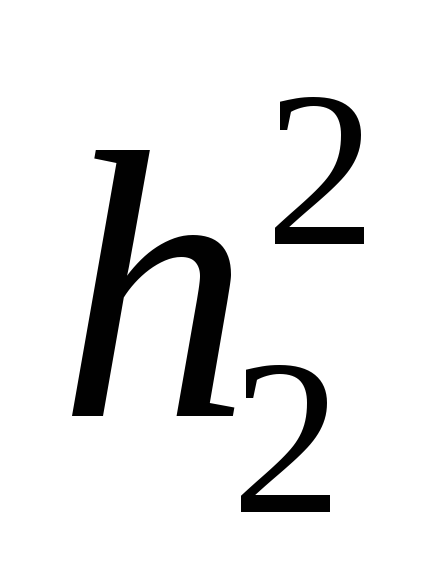 в (7), получим:
в (7), получим:
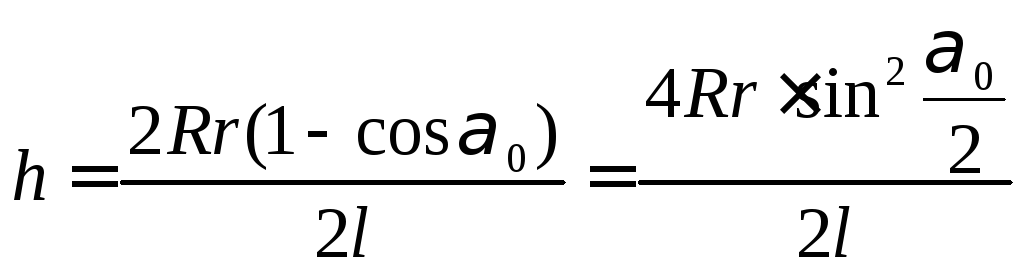 .
.
Вследствие малости угла α0 синус можно заменить аргументом:
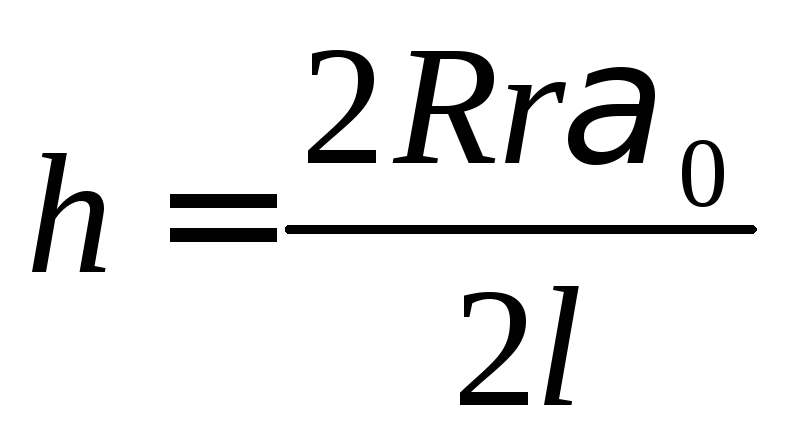 .
(8)
.
(8)
Подставляя выражения (3-24) и (3-26) в формулу (3-23) получим окончательно:
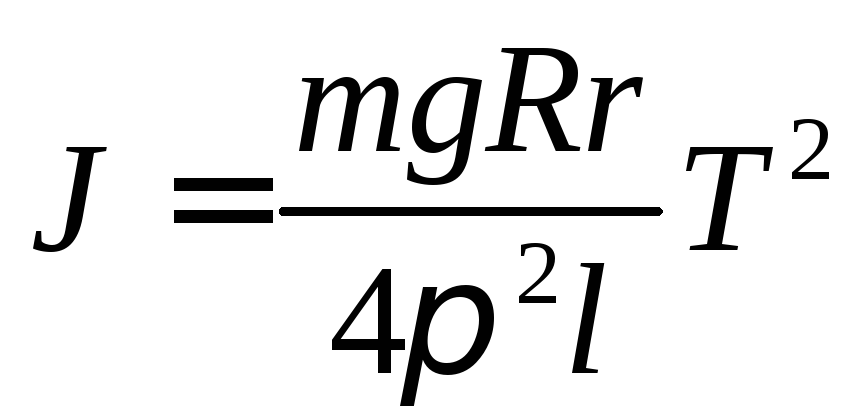 .
(9)
.
(9)


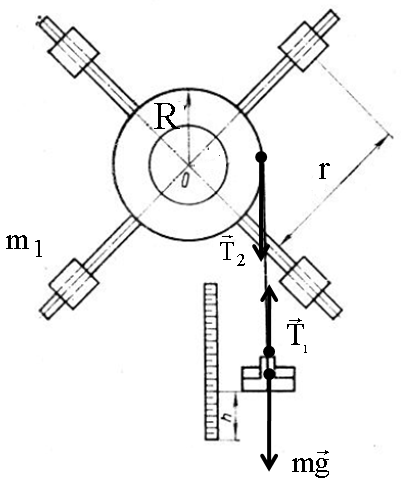
 под действием результирующей силы
тяжести
под действием результирующей силы
тяжести 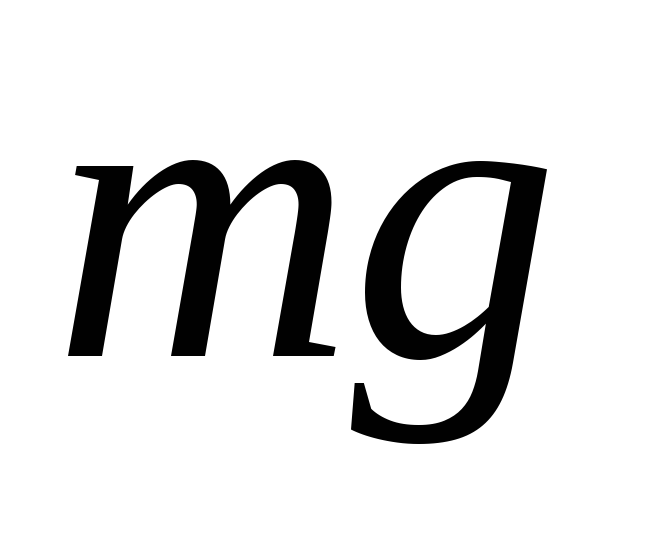 и силы натяжения нити
и силы натяжения нити  (рис. 3). Запишем для груза второй закон
Ньютона в проекции на направление
движения:
(рис. 3). Запишем для груза второй закон
Ньютона в проекции на направление
движения: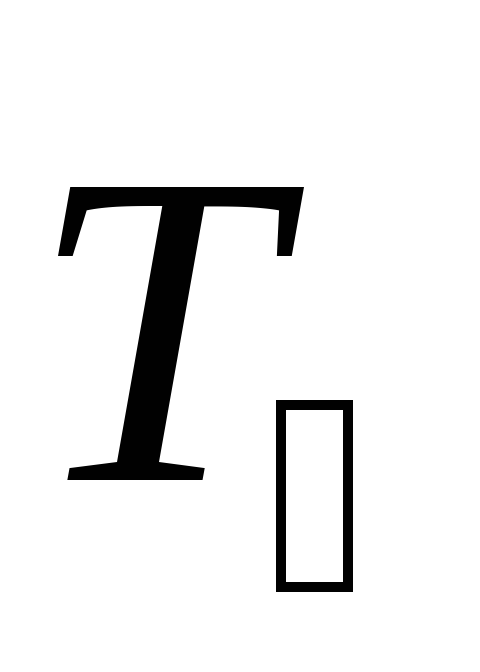 .
Сила натяжения передается нитью от
груза к диску вращающегося маятника.
.
Сила натяжения передается нитью от
груза к диску вращающегося маятника.
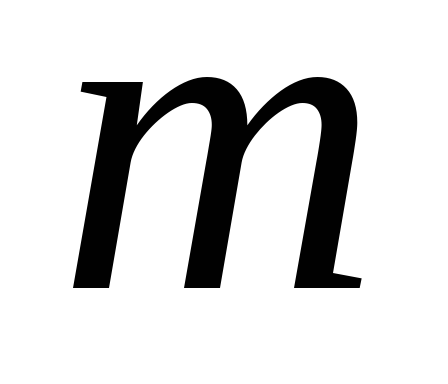 ,
г
,
г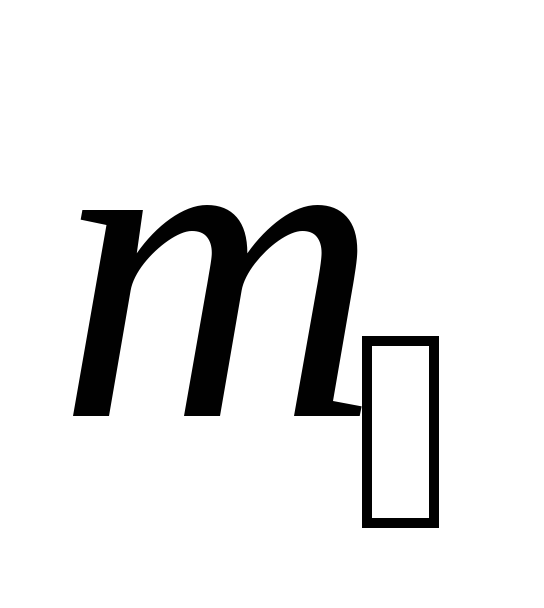 ,
г
,
г ,
см
,
см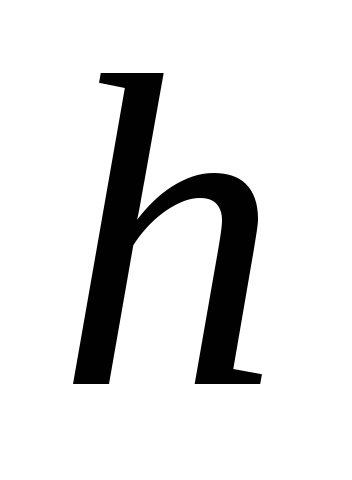 ,
см
,
см ,
c
,
c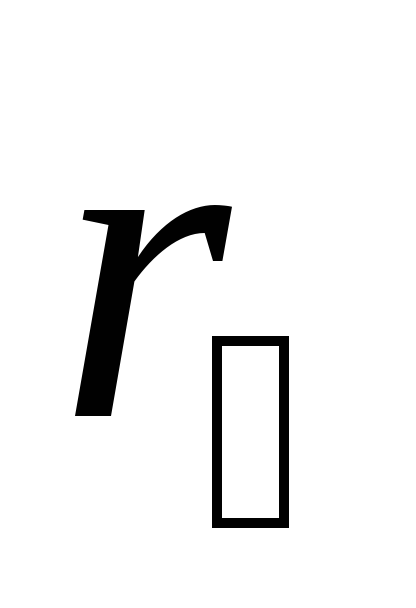 ,
см
,
см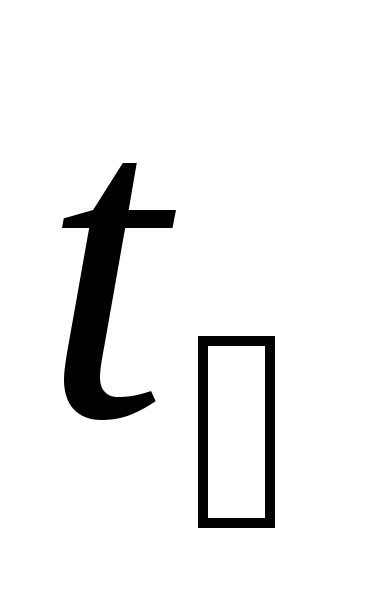 ,
c
,
c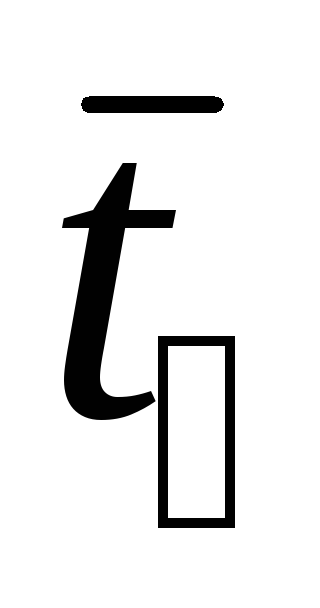 =
=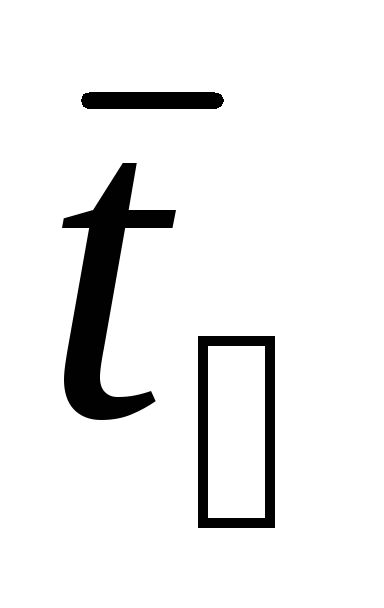 =
=
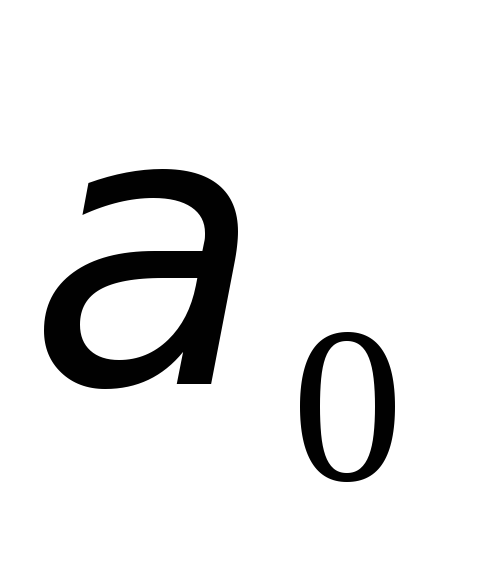 вокруг вертикальной оси, перпендикулярной
к плоскости диска и проходящей через
его центр, все три нити принимают
наклонное
вокруг вертикальной оси, перпендикулярной
к плоскости диска и проходящей через
его центр, все три нити принимают
наклонное