Расчет резонансной частоты катушки

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи. Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. Обладает способностью накапливать и отдавать электрическую энергию. Обладает способностью накапливать и отдавать магнитную энергию. Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Расчет колебательного контура
• Частота собственного резонанса катушки
• Калькулятор
• Резонансная частота: формула
• Расчёт резонансной частоты контура
• Как найти резонансную частоту
• Расчет резонансной частоты контура
• Частота собственного резонанса катушки
• Конвертер величин
• Цепи синусоидального тока. Резонансные цепи: Методические указания к лабораторным работам

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Катушка Мишина. Правильное измерение резонансной частоты катушки.

Расчет колебательного контура

На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса.

Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках. Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия.

При этом большинство инженеров с этой целью пытались уменьшить эту самую «межвитковую» паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких нестыковок.

В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Давайте проведем исследование однослойной спиральной катушки в программе HFSS.

В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки.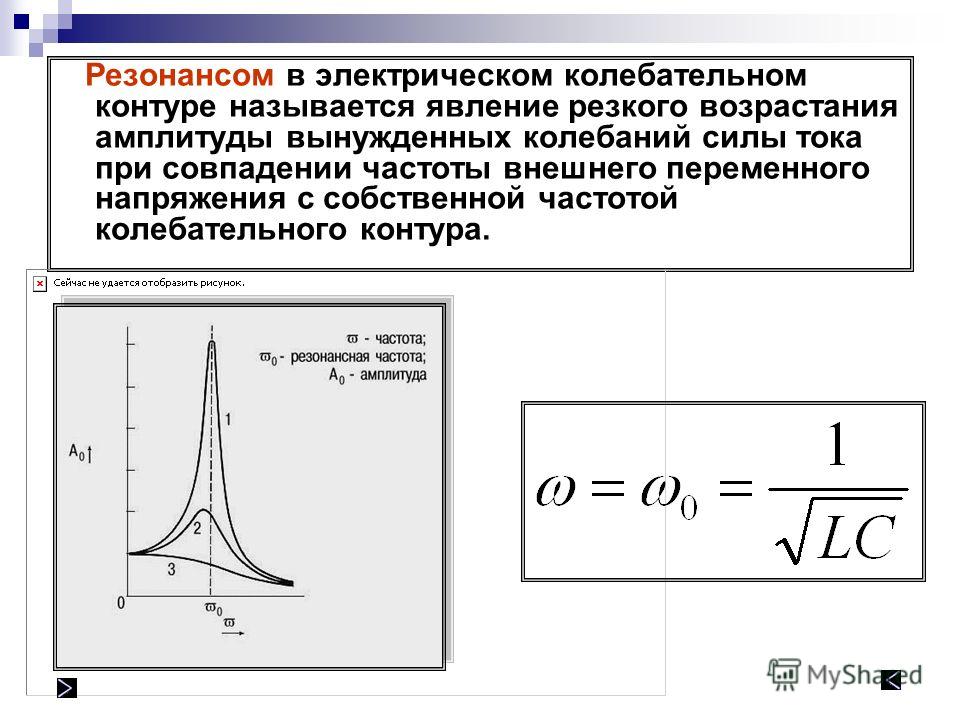

При такой сегментации для успешного расчета требуется не менее Гб оперативной памяти компьютера.

Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс — полуволновой. В результате исследования мы получили графики импеданса на зажимах источника относительно частоты.

Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца.

Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью.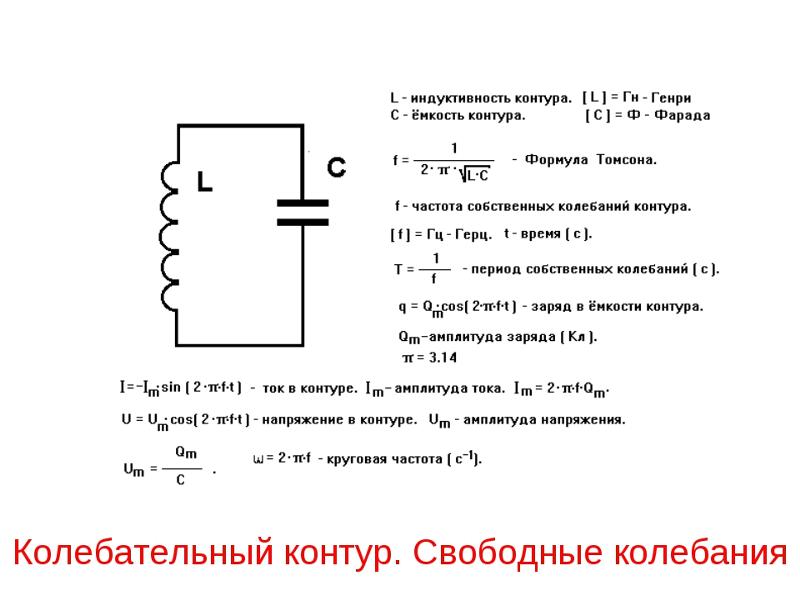 И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны.

Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками. В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными ЭМ волнами, распространяющимися вдоль провода спирали.

Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны. Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.

Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.

В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси.

Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:. Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна «добирается» до другого конца катушки быстрее чем непосредственно вдоль провода.

Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности.

Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам Поэтому увеличение частоты собственного резонанса сводится к увеличению значения v ax.

Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем. У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования: На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать.

В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод.

В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки.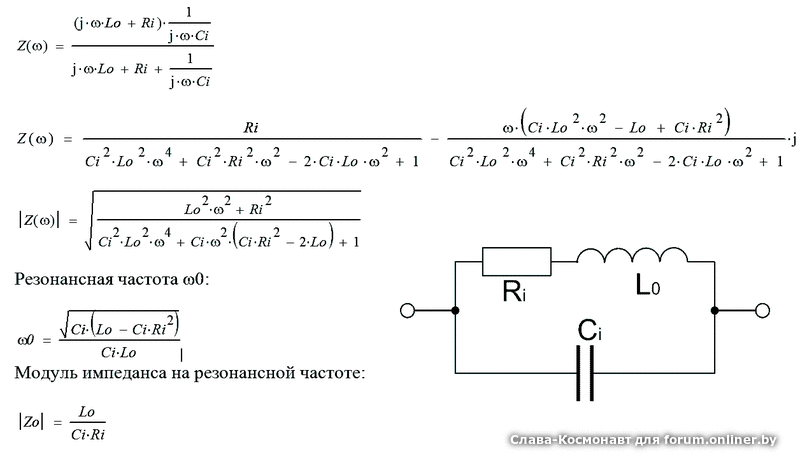

Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий.

Именно по этой причине О. Хевисайд и предложил в г. Как положительную реактивность. Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки.

Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только v ax , но и погонная емкость и погонная индуктивность и, как следствие — величины собственной индуктивности и собственной емкости катушки в целом.

Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона.

Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл , что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области.

Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый матан , что и делает Coil Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И. Гончаренко об анодном дросселе коротковолнового передатчика [2].

На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий. Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка.

Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем рассчитать частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:.

Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты «голой катушки в вакууме», то есть одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях.

Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе! Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью.

Однако численные методы решения уравнений Максвелла чем в принципе и занимается HFSS приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil32 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями.

При этом не учитывается влияние экрана, каркаса и других факторов. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат.

На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.

S: В заключении хотелось бы добавить несколько слов о концепции » Двух независимых резонансов в катушке — волновом и LC-резонансе «. Эта концепция зиждется на трех ложных в своей основе предпосылках и поэтому в корне неверна:. Имя обязательное. E-Mail обязательное.

Частота собственного резонанса катушки

By Юриг , May 28, in Разное. Подскажите пожалуйста, как посчитать резонансную частоту плоской катушки? Какие параметры необходимо знать для подсчета резонанса. Если можно, то напишете пожалуйста формулу. Мы принимаем формат Sprint-Layout 6!

Собственная паразитная ёмкость катушек индуктивности, Онлайн рачёт Несмотря на кажущуюся простоту, точный расчёт этого параметра — это вовсе: приблуда для определения собственной резонансной частоты катушки.

Калькулятор

Практический расчет последовательного или параллельного LC контура. Доброго дня уважаемые радиолюбители! Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. Конечно я уверен, что это делается без всяких нехороших даже грязных мыслей подслушать кого-нибудь, а в благих целях. Вот тут вам придет на помощь знание нижеприведенной статьи. LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах.

Резонансная частота: формула

Резонанс в последовательно параллельных цепях. В простых реактивных схемах с небольшим сопротивлением или отсутствием такового, на резонансной частоте проявляются эффекты радикального изменения импеданса. Импеданс параллельной LC цепи колебательного контура в состоянии резонанса достигает бесконечного значения. Импеданс последовательной LC цепи в состоянии резонанса достигает нулевого значения.

Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура.

Расчёт резонансной частоты контура

Random converter. Калькулятор определяет импеданс и фазовый сдвиг для соединенных параллельно идеальных катушки индуктивности и конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота. Рассчитать импеданс , катушки индуктивности мкГн и конденсатора пФ на частоте 1 МГц. В этом примере показана цепь с очень высоким импедансом, приблизительно равным кОм.

Как найти резонансную частоту

Портал QRZ. RU существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Мы стараемся размещать только релевантную рекламу, которая будет интересна не только рекламодателям, но и нашим читателям. Отключив Adblock, вы поможете не только нам, но и себе. Знакомство с трансформатором Н.

Расчет точки совмещения LC-резонанса и режима стоячих волн в катушке распостранения волны от резонансной частоты и параметров катушки.

Расчет резонансной частоты контура

На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса. Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках.

Частота собственного резонанса катушки

ВИДЕО ПО ТЕМЕ: Намотка и замер резонансной частоты катушки

Программа для расчета элементов колебательного контура. Написать данную программу, как всегда подталкивают определенные обстоятельства. Программа написана для того чтобы автоматизировать процесс расчета элементов колебательного контура. Данная программа универсальна и позволяет выполнять расчеты величины индуктивности контура для заданной вами частоты — рис.

Собственная ёмкость — это паразитный параметр катушки индуктивности.

Конвертер величин

Программа «Калькулятор» представляет собой электротехнический калькулятор, позволяющий рассчитывать параметры колебательных контуров, определять индуктивности обособленных проводников и катушек различных типов, а также производить вычисления активных и реактивных сопротивлений. Помимо этого, в программу интегрирован поиск аналогов отечественных и зарубежных транзисторов и микросхем, а также модуль, содержащий справочные данные по SMD транзисторам и дающий возможность определять по цветовой маркировке номинал и класс точности резисторов и дросселей. В каждом из них, в свою очередь, можно выбрать необходимый шаблон для вычислений. Шаблон для расчёта последовательного и параллельного колебательных контуров позволяет при задании резонансной частоты и ёмкости либо индуктивности определить недостающий параметр. При выборе расширенного режима расчёта контура дополнительно появляется возможность задать параметры волны, а также рассчитать физические параметры катушки индуктивности. К примеру, в последнем случае задаются два из трёх параметров — длина проводника, диаметр его сечения и индуктивность, а третий рассчитывается автоматически.

Цепи синусоидального тока. Резонансные цепи: Методические указания к лабораторным работам

По идее, если бы был конденсатор, то проблем не возникло бы, но суть в том, что во вторичной катушке в роли конденсатора для колебательного контура выступает собственная емкость катушки. Как ее найти, не имея индикаторов индуктивности и генераторов частот? Vurtwinz wrote:.

Резонансная емкость — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Резонансная емкость и резонансная частота определяются в момент настройки контура в резонанс по соответствующим шкалам измерительного блока и генератора высокой частоты.  [1]

Неточность определения резонансной емкости зависит от погрешности градуировки шкалы, погрешности считывания и погрешности фиксации экстремального уровня напряжения на конденсаторе.  [2]

Как определить резонансную емкость конденсаторной батареи, если известны индуктивность катушки и частота тока в цепи.  [3]

Сх и С2 — резонансные емкости, соответствующие температурам и t % и круговой частоте со.  [4]

Эффективная магнитная проницаемость — отношение резонансной емкости катушки с сердечником к резонансной емкости катушки без сердечника.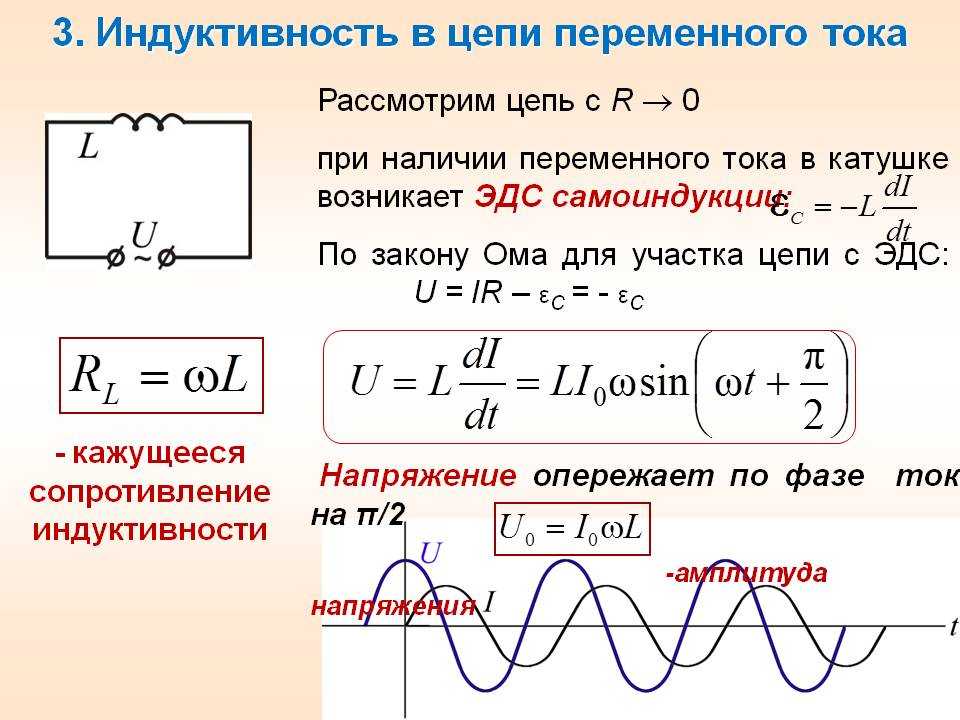  [5]

Положительной особенностью рассматриваемой схемы является то, что резонансная емкость теоретически не зависит от величины сопротивления, шунтирующего конденсатор. При резонансе достигается максимум напряжения.  [6]

Основные технические характеристики.  [7]

Кроме измерения добротности, прибор позволяет измерять индуктивность, межвитковую и резонансную емкость катушек, резонансную частоту контуров, а также определять значения активной и реактивной составляющих комплексного сопротивления. В последнем случае ( при Q lOO) измерение осуществляется по приращению добротности, что повышает разрешающую способность измерителя и точность измерений.  [8]

Феррорезонансный стабилизатор состоит из насыщенного Тр и ненасыщенного Тр2 трансформаторов и резонансной емкости С. Ненасыщенный трансформатор с воздушным зазором имеет линейную характеристику и работает из-за наличия воздушного зазора на ненасыщенном участке кривой намагничивания.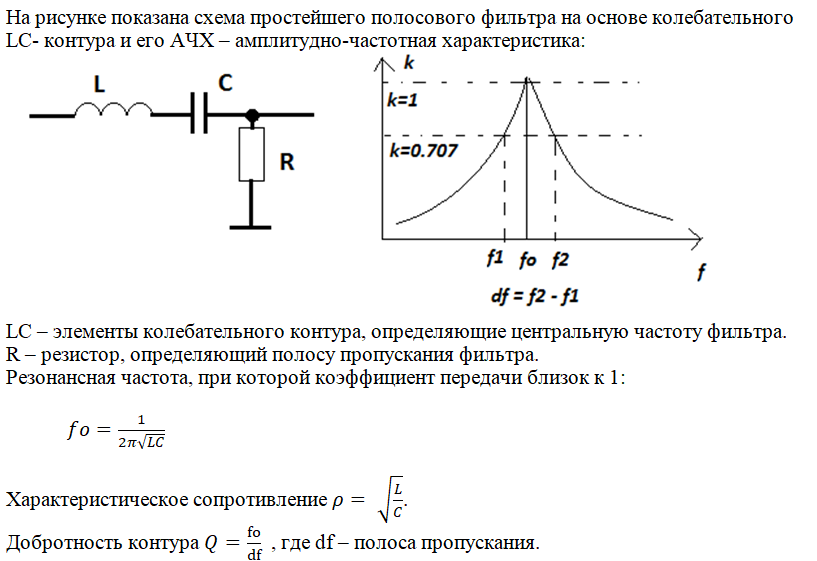 Ненасыщенный трансформатор имеет первичную w и вторичную w2 об — мотки, насыщенный трансформатор — первичную w, резонансную zwp и вторичную w2 обмотки, Параллельно включенные конденсатор и резонансная обмотка представляют собой нелинейное звено стабилизатора. Вторичные обмотки насыщенного и ненасыщенного трансформаторов соединяются в несимметричную звезду и подключаются к трехфазной мостовой схеме выпрямления. При изменении напряжения сети и тока нагрузки происходит перераспределение напряжения между первичными, а следовательно, и вторичными обмотками трансформаторов и изменение угла сдвига фаз между ними. Благодаря этому напряжение на выходе моста остается скомпенсированным.  [9]

Эффективная магнитная проницаемость — отношение резонансной емкости катушки с сердечником к резонансной емкости катушки без сердечника.  [10]

Погрешность определения tg6 и QOTH зависит от погрешности измерения добротности и резонансной емкости куметра.  [11]

Простейшая схема измерителя.| Эквивалентная схема катушки индуктивности.  [12]

Погрешность установки частоты лежит в пределах 1 %, а погрешность определения резонансной емкости зависит от погрешностей градуировки шкалы, считывания и определения экстремального уровня напряжения на конденсаторе. Значение последней при малых добротностях контура может составлять несколько процентов.  [13]

Если резонанс на k — й гармонике достигается изменением емкости ( индуктивности), то резонансная емкость С ( индуктивность Lk) в k раз меньше емкости ( индуктивности), при которой наблюдается резонанс на частоте основной гармоники.  [14]

Если резонанс на fc — й гармонике достигается изменением емкости ( индуктивности), то резонансная емкость Ck ( индуктивность 1) в k раз меньше емкости ( индуктивности), при которой наблюдается резонанс на частоте основной гармоники.  [15]

Страницы:      1    2    3

Coil32 — Частота собственного резонанса

В первые дни эпохи радио было обнаружено, что спиральная катушка индуктивности не является идеальной катушкой индуктивности. На определенной частоте он находится в резонансном режиме даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки емкостной. Для объяснения этого явления принято, что помимо собственной индуктивности реальная катушка имеет собственную емкость (предположительно между соседними витками) и катушку представляют как модель из сосредоточенных RLC-элементов, где L — индуктивность, C — собственная емкость, а R учитывает различные потери в катушке. Такая модель имеет только одну резонансную частоту, называемую собственной резонансной частотой катушки (СРЧ). Эта модель стала классической моделью реальной катушки во всех учебниках.

Поскольку в большинстве практических применений катушка работает на частотах намного ниже SRF, целью разработчика является обеспечение этого условия. Большинство инженеров с этой целью пытались уменьшить эту «межвитковую паразитную емкость». В случае, если катушка работает на частотах, близких к SRF, как например в винтовом резонаторе или катушках Тесла, RLC-модель дает некорректные результаты, но в таких случаях были разработаны альтернативные алгоритмы расчета и все конструкторы остались довольны и не очень перебрался в уме о причинах таких несоответствий.

В цифровую эпоху появились приложения, дающие возможность с высокой степенью точности моделировать любые высокочастотные устройства, так называемые электромагнитные симуляторы. Существуют мощные пакеты, такие как CST Studio, HFSS и многие другие. Проверим однослойную спиральную катушку в HFSS. В первой модели поместите катушку над идеально проводящей поверхностью и возбудите ее портом с сосредоточенными параметрами с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Моделирование будет производиться в режиме «Проектирование ВЧСС» методом конечных элементов. Второй виток моделируем методом «Проектирование ВЧСС-ИЭ» методом моментов. Возбуждаем катушку через короткие выводы от того же сосредоточенного порта. Поскольку в этой модели катушка не заземлена, первый резонанс является полуволновым.
В результате исследования нами получены графики импеданса на зажимах источника в зависимости от частоты. Графики показывают, что спиральная катушка имеет много резонансов. Отсюда следует вывод, что катушка представляет собой не единый LC-контур со своей собственной индуктивностью и паразитной собственной емкостью как сосредоточенными элементами, а линию передачи с распределенными параметрами. Тот факт, что линия передачи состоит из одного провода, не должен сбивать с толку. Вы знаете, что явление резонанса наблюдается даже в одном проводе, это показывает пример диполя. Существование волновых явлений в проводах свидетельствует о том, что электромагнитное взаимодействие распространяется с конечной скоростью. И катушка в этом отношении недалеко ушла от диполя, потому что, несмотря на свои небольшие размеры, длина провода, на который она намотана, имеет размеры, сравнимые с длиной волны.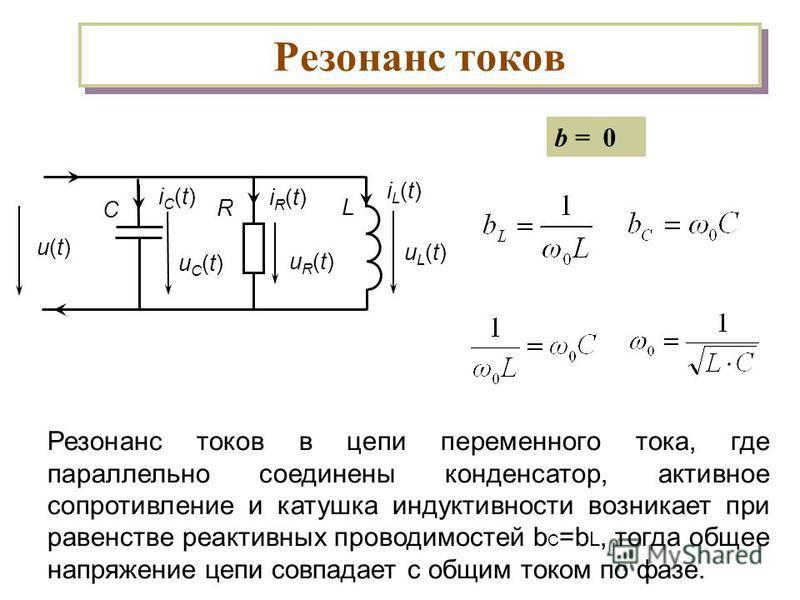 Собственную резонансную частоту диполя можно довольно легко определить, зная его длину. Для катушки это не так просто.

---

В учебниках по электродинамике можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися по спиральному проводу. Такие волноводы используются в качестве замедляющих структур в спиральных антеннах и лампах бегущей волны. В таких волноводах длина одного витка и шаг намотки сравнимы с длиной волны. Фазовая скорость волны вдоль оси винтового волновода значительно ниже скорости света, и его применение в качестве замедляющей структуры основывается на этом.

[1]

Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, так как ЭМ-волна распространяется практически только по проволоке спирали.

---

В катушке длина каждого витка, длина намотки и шаг намотки намного меньше длины волны. В этом случае, помимо основной моды вдоль проволоки, существуют высшие моды непосредственно вдоль оси спирали. Другими словами, ЭМ волна распространяется не только по длине провода, но и часть ее «перескакивает с витка на виток». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:

[2]

где:

• λ ₀ — длина волны рабочей частоты в свободном пространстве
• Д , р — диаметр и шаг обмотки
• с — скорость света

Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — это тот же спиральный волновод с медленными волнами, но работающий в другом режиме.
Из-за наличия высших мод электромагнитной волны частота первого резонанса катушки всегда выше, чем частота, рассчитанная по длине провода. По этой причине более высокочастотные резонансы не кратны первому и друг другу.
Короткие катушки имеют последующие резонансы, которые отделены от первых намного выше по частоте, что вы можете видеть в результатах моделирования HFSS: На частотах значительно ниже первой резонансной частоты пространственная задержка много меньше периода колебаний ЭМ поле. Поле вокруг катушки представляет собой статическое поле соленоида и скоростью распространения волны вдоль его оси можно пренебречь. В этом случае модель RLC с сосредоточенными параметрами будет полностью рабочей и точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это не статическая емкость между витками. Катушки всех трех моделей работают в этом режиме на КВ диапазоне и ниже. Однако на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитной связи, и катушку следует рассматривать только как винтовой волновод. В этом случае модель RLC неверна. Более того, это приводит к неправильному пониманию механизма резонансных явлений в катушке.
Катушка как набор сосредоточенных RLC-элементов и катушка как схема с распределенными параметрами — это две разные модели реальной катушки. Первая модель основана на предположении, что плотность тока во всех витках одинакова, поэтому она ограничена и применима только на низких частотах, вторая является полной и применима на любой частоте.

Особенно хотелось бы отметить следующее обстоятельство. На низких частотах, где, как мы видели, справедлива RLC-модель, можно считать, что индуктивность и собственная емкость катушки не зависят от частоты и определяются только геометрией обмотки. Это известный факт, зафиксированный, например, в формуле Нагаоки. Но на самом деле параметры винтовой линии передачи зависят от частоты. Не просто v _ax , а емкость и индуктивность на единицу длины. Лишь на низких частотах эта зависимость незначительна, однако на частотах, близких к первому резонансу, значения индуктивности и собственной емкости катушки начинают заметно «плавать» по частоте.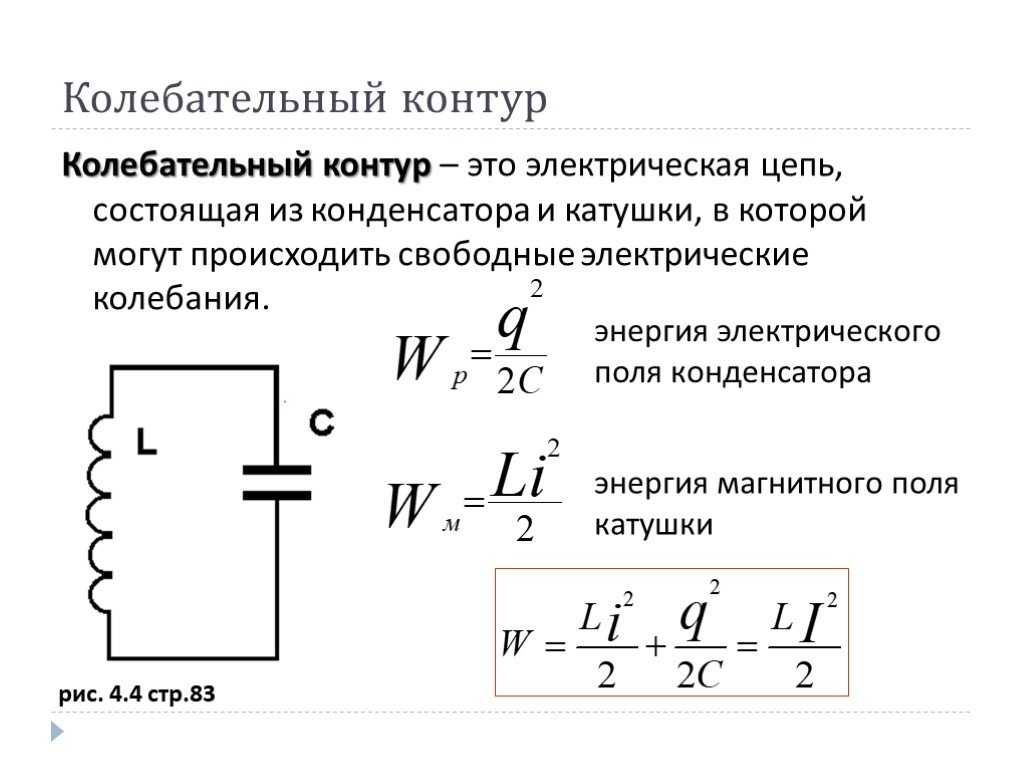 В итоге мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не подходят для расчета собственной резонансной частоты по формуле Томсона. Расчет даст неверный результат! Поэтому для расчета резонансной частоты катушки необходимо использовать более сложный численный метод из [1]. Во-вторых, любой предмет вблизи катушки, в том числе измерительный щуп, влияет на параметры линии передачи. В этом случае частота собственного резонанса отодвигается от своего фактического значения для «свободной» катушки.

Если конструктору необходимо создать катушку с минимальными размерами и с максимальной собственной резонансной частотой, то наилучшей будет намотка с расстоянием между витками, равным диаметру провода, и с отношением l/D ≈ 1 ..1,5. На практике следует придерживаться следующего простого правила: если общая длина провода катушки меньше четверти длины волны на самой высокой рабочей частоте, катушка будет работать ниже своего первого резонанса.

Каталожные номера:

1. САМОРЕЗОНАНС И СОБСТВЕННАЯ ЕМКОСТЬ СОЛЕНОИДНЫХ КАТУШЕК  — применимая теория, модели и методы расчета. Дэвид В. Найт1 (G3YNH)
2. АВТОРЕЗОНАНС В КАТУШКАХ и миф о собственной емкости. Алан Пейн (G3RBJ)
3. ВЧ-катушки, спиральные резонаторы и усиление напряжения с помощью когерентных пространственных мод. К.Л. Corum и JF Corum (PDF)

 

Формула резонансной частоты — GeeksforGeeks

Резонансная частота определяется как частота контура, когда значения емкостного сопротивления и индуктивного сопротивления становятся равными. Она определяется как частота, при которой тело или система достигает наивысшей степени колебаний. Резонансный контур состоит из параллельно соединенных конденсатора и катушки индуктивности. Он в основном используется для создания заданной частоты или для учета определенной частоты в сложной цепи. Резонансная частота существует только тогда, когда цепь является чисто резистивной.

Формула

Формула резонансной частоты представляет собой обратную величину произведения удвоенного числа пи и квадратного корня из произведения индуктивности и емкости. Он представлен символом f _или . Его стандартной единицей измерения является герц или секунда (Гц или с ^-1 ), а его размерная формула определяется как [M ⁰ L ⁰ T ^-1 ].

f _o = 1/2π√(LC)

где,

f _o – резонансная частота,

L – индуктивность цепи,

C – емкость цепи.

Вывод

Предположим, у нас есть цепь, в которой резистор, катушка индуктивности и конденсатор соединены последовательно под источником переменного тока.

Значение сопротивления, индуктивности и емкости равно R, L и C. 

Теперь известно, что полное сопротивление цепи Z определяется выражением,

0002 Z = R + jωL – j/ωC

Z =R + j (ωL – 1/ωC)

Для выполнения условия резонанса цепь должна быть чисто резистивной. Следовательно, мнимая часть импеданса равна нулю.

ωl — 1/ωc = 0

ωl = 1/ωc

ω ² = 1/LC

Положение ω = 1/2πf _O , мы получаем

(1/2πf _O ), мы получаем

(1/2πf _O ). ² = 1/LC

f _o = 1/2π√(LC)

Отсюда выводится формула для резонансной частоты.

Проблемы с образцами

Задача 1. Рассчитайте резонансную частоту для схемы индуктивности 5 ч и емкости 3 F.

Решение:

Мы имеем

L = 5

C =

L = 5

C =

L = 5

C =

L = 5

C =

L = 5

C =

L = 5

C = 3

Используя формулу, которую мы имеем,

f _о = 1/2π√(LC)

= 1/ (2 × 3,14 × √(5 × 3))

= 1/24,32

90,0042 = 1/24,32

2 Гц

Задача 2. Вычислить резонансную частоту для цепи с индуктивностью 3 Гн и емкостью 1 Ф.

Решение:

Мы имеем,

L = 3

C = 1

Используем формулу, которую мы имеем,

F _O = 1/2π√ (LC)

= 1/1/ (2 × 3,14 × √(3 × 1))

= 1/10,86

= 0,092 Гц

Решение:

Имеем,

L = 4

C = 2,5

Используя формулу, которую мы имеем,

f _o = 1/2π√(LC)

= 1/(2 × 3,14 × √(4 × 2,5))

= 1/60,38

= 0,159 Гц

Задача 4.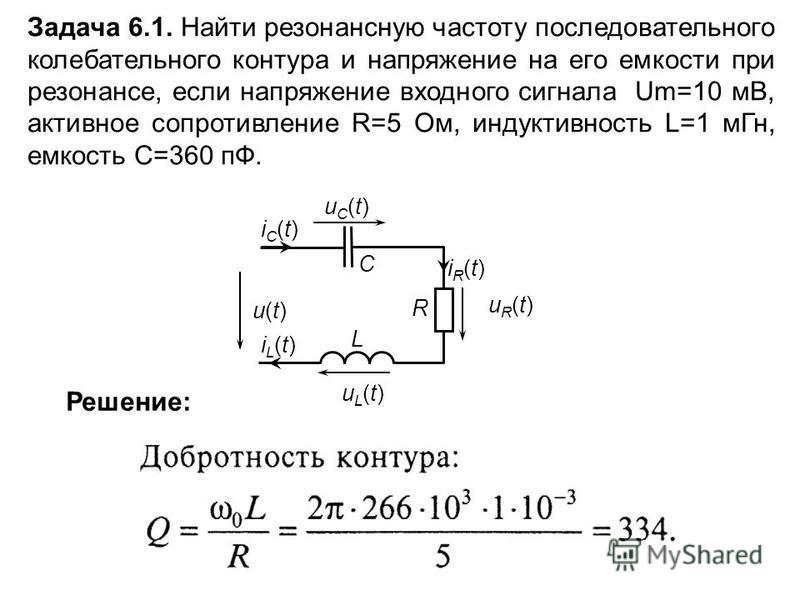 Рассчитайте индуктивность цепи, если емкость равна 4 Ф, а резонансная частота равна 0,5 Гц.

Решение:

Имеем,

f _o = 0,5

C = 4

Используя формулу имеем, f

3

_o = 1/2π√(LC)

=> L = 1/4π ² Cf _o ²

= 1/ (4 × 3,14 × 3,14 × 900,3 × 0,5 0,5 = 1/39,43

= 0,025 Гн

Задача 5. Вычислить индуктивность цепи, если емкость равна 3 Ф, а резонансная частота равна 0,023 Гц.

Решение:

Имеем,

f _o = 0,023

C = 3

Используя формулу имеем,

F _O = 1/2π√ (LC)

=> L = 1/4π ² CF _O ²

= 1/(4 × 3.14 × 3.14 × 3 × 0,023 × 0,023 )

= 1/0,0199

= 50,25 Гн

Задача 6. Вычислить емкость цепи, если индуктивность равна 1 Гн, а резонансная частота равна 0,3 Гц.