7. Направление силы Ампера
А 1 | В однородном магнитном поле находится рамка, по которой начинает течь ток (см. рисунок). Сила, действующая на верхнюю сторону рамки, направлена
| |||||||||||
А 2 | В однородном
магнитном поле находится рамка, по
которой начинает течь ток (см.
| |||||||||||
А 3 | Квадратная рамка
расположена в однородном магнитном
поле в плоскости линий магнитной
индукции так, как показано на рисунке.
Направление тока в рамке показано
стрелками. | |||||||||||
| ||||||||||||
А 4 | Круговой виток с током, расположенный горизонтально, помещен в магнитное поле, линии индукции которого перпендикулярны плоскости витка (см. рисунок). Под действием сил Ампера виток | |||||||||||
1) растягивается | ||||||||||||
2) сжимается | ||||||||||||
3) перемещается вниз | ||||||||||||
4) перемещается вверх | ||||||||||||
А 5 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле, вектор магнитной индукции
которого
направлен верти-кально вверх (см. | 2 4 + 1 3 | ||
сверху). Куда направлена вызванная этим полем сила Ампера, действующая на проводник 4-1? | ||||
1) Горизонтально вправо 2) Горизонтально влево 3) Вертикально вверх 4) Вертикально вниз | ||||
А 6 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле, вектор магнитной индукции
которого
направлен вертикально вверх (см. | 1 4 2 3 + — | ||
вид сверху). Куда направлена вызванная этим полем сила Ампера, действующая на проводник 1-2? | ||||
1) Горизонтально вправо 3) Вертикально вверх | 2) Горизонтально влево 4) Вертикально вниз | |||
А 7 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле, вектор магнитной индукции
которого
направлен вертикально вниз (см. | 1 4 2 3 + — | ||
вид сверху) Куда направлена вызванная этим полем сила Ампера, действующая на проводник 3-4? | ||||
1) Горизонтально вправо 3) Вертикально вверх | 2) Горизонтально влево 4) Вертикально вниз | |||
А 8 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле, вектор магнитной индукции
которого
направлен вертикально вниз (см. | 2 4 + 1 — 3 |
вид сверху) Куда направлена вызванная этим полем сила Ампера, действующая на проводник 1-4? | ||
1) Горизонтально вправо | 2) Горизонтально влево 4) Вертикально вниз | |
А 9 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле. | 1 2 3 + — |
Куда направлена вызванная этим полем сила Ампера, действующая на проводник 1-2? | ||
1) Горизонтально вправо 3) Вертикально вверх | 2) Горизонтально влево 4) Вертикально вниз | |
А 10 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле. | 1 4 2 3 + — |
Куда направлена вызванная этим полем сила Ампера, действующая на проводник 4-1? | ||
1) Горизонтально вправо 3) Вертикально вверх | 2) Горизонтально влево 4) Вертикально вниз | |
А 11 | Электрическая
цепь, состоящая из четырёх прямолинейных
горизонтальных проводников (1-2, 2-3,
3-4, 4-1) и источника постоянного тока,
находится в однородном магнитном
поле. | 1 4 2 3 + — | ||
вызванная этим полем сила Ампера, действующая на проводник 3-4? | ||||
1) Горизонтально вправо 3) Вертикально вверх | 2) Горизонтально влево 4) Вертикально вниз | |||
А 12 | Силовые
линии магнитного поля идут слева
направо параллельно плоскости листа,
проводник с электрическим током
перпендикулярен плоскости листа, а
ток течет в плоскость листа. | |||
1) вправо 2) влево | 3) вверх 4) вниз | |||
А 13 | На проводник с током, лежащий в плоскости листа, по которому течет ток снизу вверх, действует сила Ампера, направленная из листа. Это может происходить, если северный полюс стержневого магнита поднесли | |||
1) слева | 2) справа | |||
3) с передней стороны листа | 4) с обратной стороны листа | |||
А 14 | Как взаимодействуют два параллельных друг другу проводника, если электрические токи в них противоположны по направлению? | |||
1) Сила взаимодействия равна нулю 2) Проводники притягиваются 3) Проводники отталкиваются 4) Проводники поворачиваются в одинаковом направлении | ||||
А 15 | Как взаимодействуют два параллельных друг другу проводника, если электрические токи в них совпадают по направлению? | |||
1) Сила взаимодействия равна нулю 2) Проводники притягиваются 3) Проводники отталкиваются 4) Проводники поворачиваются в одинаковом направлении | ||||
А 16 | Как взаимодействуют два параллельных друг другу проводника, если в первом случае электрический ток в них идет в одном направлении, а во втором случае – в противоположных направлениях? | |||
1) В обоих случаях притягиваются друг к другу 2) В обоих случаях отталкиваются друг от друга 3) В первом случае притягиваются, а во втором случае отталкиваются друг от друга 4) В первом случае отталкиваются, а во втором случае притягиваются друг к другу | ||||
А 17 | Два
параллельных проводника, по которым
течет ток в одном направлении,
притягиваются. | |||
1) токи непосредственно взаимодействуют друг с другом 2) электрические поля зарядов в проводниках непосредственно взаимодействуют друг с другом 3) магнитные поля токов непосредственно взаимодействуют друг с другом 4) магнитное поле одного проводника с током действует на движущиеся заряды во втором проводнике | ||||
А 18 | Как направлена сила Ампера, действующая на проводник № 1 со стороны двух других (см. рисунок), если все проводники тонкие, лежат в одной плоскости, параллельны друг другу и расстояния между соседними проводниками одинаковы? (- сила тока) | 1 2 3 | ||
1) К нам 2) От нас | 3) Вверх 4) Вниз | |||
А 19 | На
проводник № 2 со стороны двух других
действует сила Ампера (см. | 1 2 3 | ||
1) направлена вверх | 2) направлена вниз | |||
3) направлена от нас | 4) равна нулю | |||
А 20 | На
проводник № 3 со стороны двух других
действует сила Ампера (см. рисунок).
Все проводники тонкие, лежат в одной
плоскости, параллельны друг другу, и
расстояния между соседними провод-никами
одинаковы. | 1 2 3 | ||
1) направлена вверх | 2) направлена вниз | |||
3) направлена от нас | 4) равна нулю | |||
С 1 | По прямому горизонтальному проводнику длиной 1 м с площадью поперечного сечения , подвешенному с помощью двух одинаковых невесомых пружинок жесткостью 100 Н/м, течет ток 10 А. На какой угол от вертикали отклонятся пружины при включении вертикального магнитного поля с индукцией 0,1 Тл, если абсолютное удлинение каждой из пружинок при этом составляет ? (Плотность материала проводника ) | |||
Решение задач на определение силы Ампера — презентация
Первый слайд презентации: Решение задач на определение силы Ампера
План урока:
Выполните тест «Магнитное поле-2» (на стене в группе)
Подготовьтесь к решению задач – выполните разминку. Если не совсем понятно решение – посмотрите видеоролик «комментарии к разминке»
Попробуйте самостоятельно решить задачи 4-12 (в случае затруднений постепенно открывайте решение). Напишите, какие задачи вызвали наибольшее затруднение (устроим видеоразбор )
Изучите новый материал (слайды ) и попробуйте решить задачи (слайды ).
Домашнее задание.
Если не совсем понятно решение – посмотрите видеоролик «комментарии к разминке»
Попробуйте самостоятельно решить задачи 4-12 (в случае затруднений постепенно открывайте решение). Напишите, какие задачи вызвали наибольшее затруднение (устроим видеоразбор )
Изучите новый материал (слайды ) и попробуйте решить задачи (слайды ).
Домашнее задание.
Изображение слайда
Слайд 2: Разминка
Изображение слайда
Слайд 3: Разминка 1
На тонких проволоках подвешена катушка. Если по катушке пропустить ток, то она притягивается к магниту. В чем причина наблюдаемого вами явления? Ответ: Катушка с током — это электромагнит. Левый конец катушки — южный полюс (правило буравчика), а разноименные полюсы притягиваются.
Изображение слайда
Слайд 4: Разминка 2
На тонких проволоках подвешены две катушки. Почему они притягиваются (или отталкиваются), если по ним пропускать электрический ток?
Ответ: Электрический ток каждой из катушек взаимодействует с магнитным полем, создаваемым другой катушкой. В данном случае катушки будут отталкиваться.
Почему они притягиваются (или отталкиваются), если по ним пропускать электрический ток?
Ответ: Электрический ток каждой из катушек взаимодействует с магнитным полем, создаваемым другой катушкой. В данном случае катушки будут отталкиваться.
Изображение слайда
Слайд 5: Разминка 3
Почему, если замкнуть цепь, алюминиевый стержень М придет в движение (покатится)? В какую сторону он покатится? Ответ: На проводник MN с током будет действовать сила со стороны магнитного поля подковообразного магнита. Стержень покатится вправо.
Изображение слайда
Слайд 6: Разминка
Перед вами два совершенно одинаковых стальных стержня. Один из них намагничен. Как определить, какой стержень намагничен, не имея в своем распоряжении никаких вспомогательных средств?
Ответ: Поднести конец одного из стержней к середине другого. Намагниченный стержень не будет притягивать ненамагниченный.
Намагниченный стержень не будет притягивать ненамагниченный.
Изображение слайда
Слайд 7
Изображение слайда
Слайд 8: Задача 4
С какой силой действует однородное магнитное поле индукцией 2,5 Тл на проводник длиной 50 см, расположенный под углом 30˚ к вектору индукции, при силе тока в проводнике 0,5 А? Дано: В=2,5 Тл, ∆ l =0,5 м, α =30˚, I =0,5 А, F -? На проводник действует сила Ампера: F=B∙|I|∙∆ l∙sin α Подставив числовые данные, получим: F= 2,5 Тл∙0,5 А∙0,5 м ∙sin 30˚= =0,3125 Н Ответ: F =0,3125 Н
Изображение слайда
Слайд 9: Задача 5: Цепь находится в однородном магнитном поле и состоит из четырех прямолинейных проводников.
 Куда направлена сила Ампера, действующая на проводник 1-2?
Куда направлена сила Ампера, действующая на проводник 1-2?
За направление силы тока принято направление движения положительно заряженных частиц. Значит, ток в цепи течет по направлению часовой стрелки ( в проводнике 1-2 сверху – вниз) По правилу левой руки сила Ампера направлена горизонтально вправо.
Изображение слайда
Слайд 10: Задача 6
На проводник № 2 со стороны двух других проводников действует сила Ампера. Все проводники лежат в одной плоскости и параллельны. Расстояния между соседними проводниками одинаковы. Чему равна сила Ампера, действующая на проводник № 2 со стороны двух других? Силы Ампера действующие на второй проводник со стороны двух других равны по модулю и противоположны по направлению, значит, их суммарное воздействие равно нулю.
Изображение слайда
Слайд 11: Задача 7
Участок проводника длиной 10 см находится в магнитном поле индукцией 50 мТл. Сила тока, протекающего по проводнику, 10 А. Какую работу совершает сила Ампера при перемещении проводника на 8 см в направлении своего действия? Проводник расположен перпендикулярно линиям магнитной индукции.
Работа силы Ампера равна произведению модуля силы на перемещение под действием этой силы.
Дано: В=50 мТл, ∆ l =0,1 м, α =90˚, I =10А, а=0,08м, А-?
Сила Ампера: F=B∙|I|∙∆l∙sin α, значит, ее работа вычисляется по формуле: А=а∙ F= а∙ B∙|I|∙∆l∙sin α
Подставляя числовые данные, получим: А=0,004 Дж=4 мДж
Сила тока, протекающего по проводнику, 10 А. Какую работу совершает сила Ампера при перемещении проводника на 8 см в направлении своего действия? Проводник расположен перпендикулярно линиям магнитной индукции.
Работа силы Ампера равна произведению модуля силы на перемещение под действием этой силы.
Дано: В=50 мТл, ∆ l =0,1 м, α =90˚, I =10А, а=0,08м, А-?
Сила Ампера: F=B∙|I|∙∆l∙sin α, значит, ее работа вычисляется по формуле: А=а∙ F= а∙ B∙|I|∙∆l∙sin α
Подставляя числовые данные, получим: А=0,004 Дж=4 мДж
Изображение слайда
Слайд 12: Задача 8
Электрическая цепь, состоящая из четырех проводников, находится в однородном магнитном поле, вектор магнитной индукции которого направлен горизонтально вправо. Куда направлена сила Ампера, действующая на проводник 1-2 ?
Направление тока в цепи – против часовой стрелки (в проводнике 1-2 сверху – вниз). По правилу левой руки сила Ампера направлена вертикально вверх (перпендикулярно плоскости чертежа, к нам).
По правилу левой руки сила Ампера направлена вертикально вверх (перпендикулярно плоскости чертежа, к нам).
Изображение слайда
Слайд 13: Задача 9
Прямолинейный проводник длиной 0,4 м помещен в однородное магнитное поле перпендикулярно линиям магнитной индукции. Определите индукцию магнитного поля, если при силе тока 2 А на проводник действует сила 4 Н. Сила Ампера: F=B∙|I|∙∆l∙sin α sin α =1, значит, Ответ: В=5 Тл
Изображение слайда
Слайд 14: Задача 10
Какова сила тока, проходящего по прямолинейному проводнику, расположенному перпендикулярно однородному магнитному полю, если на активную часть проводника длиной 40 см действует сила 20 Н при индукции магнитного поля 10 Тл.
Используется закон Ампера. Ответ: 5 А
Ответ: 5 А
Изображение слайда
Слайд 15: Задачи 11, 12
Прямолинейный проводник с током помещен в однородное магнитное поле с индукцией 2 Тл. Определите силу, с которой действует магнитное поле на проводник, если его длина 10 см, сила тока в проводнике 5 А и проводник составляет с направлением индукции магнитного поля угол 30 0 Ответ: 0,5 Н Определите длину активной части прямолинейного проводника, помещенного в однородное магнитное поле с индукцией 400 Тл, если при силе тока 2,5 А на него действует сила 100 Н. Проводник расположен под углом 30 0 к линиям индукции магнитного поля. Ответ: 0,2 м
Изображение слайда
Слайд 16: Силы, действующие на рамку с током
Силы 1 и 3 лишь растягивают рамку, а пара сил 2 и 4 стремится повернуть рамку вокруг оси ОХ, причем сила Ампера действует на сторону в, а плечом является а /2
Изображение слайда
Слайд 17: Вращающий момент, действующий на рамку с током
Изображение слайда
Слайд 18: Задача 13
Рамка площадью 100 см 2 помещена в однородное магнитное поле с индукцией 0,5 Тл. Найдите максимальный вращающий момент сил, действующих на рамку, если сила тока в ней 1000 А.
Воспользоваться формулой для определения вращающего момента: M= I∙S∙B∙sin α
Подставить числовые значения, переведенные в систему СИ: М=1000 А∙10 -2 м 2 ∙0,5 Тл∙1=5 Н∙м
Найдите максимальный вращающий момент сил, действующих на рамку, если сила тока в ней 1000 А.
Воспользоваться формулой для определения вращающего момента: M= I∙S∙B∙sin α
Подставить числовые значения, переведенные в систему СИ: М=1000 А∙10 -2 м 2 ∙0,5 Тл∙1=5 Н∙м
Изображение слайда
Слайд 19: Задача 14
Квадратная рамка со стороной 5 см, имеющая 10 витков, находится в однородном магнитном поле с индукцией 0,1 Тл. Плоскость рамки составляет угол 0° с направлением магнитного поля. Определите вращающий момент сил, действующих на рамку, если сила тока в рамке равна 4 А. Воспользоваться формулой для определения вращающего момента: M= I∙S∙B∙sin α Площадь рамки равна 25 см 2 = 2,5∙10 -3 м 2 Подставить числовые значения, переведенные в систему СИ: М=4 А∙2,5∙10 -3 м 2 ∙0,1 Тл∙1=0,01 Н∙м
Изображение слайда
Слайд 20: Задача 15
Рассчитайте силу тока, протекающего по плоскому контуру площадью 5 см 2, находящемуся в однородном магнитном поле с индукцией 0,5 Тл, если максимальный вращающий момент, действующий на контур со стороны поля, равен 0,25 мН∙м. Ответ: I = 1 A
Ответ: I = 1 A
Изображение слайда
Слайд 21: Задача 16
Чему равна индукция магнитного поля, если на прямоугольную рамку, сила тока в которой 0,5 А, действует максимальный вращающий момент 10 -2 Н∙м? Размеры рамки 20 х 30 см 2. Ответ: В = 0,33 Тл
Изображение слайда
Слайд 22: Задача 17
Какова индукция однородного магнитного поля, если на прямоугольную рамку (20 х 30 мм 2 ), помещенную в поле, действует максимальный вращающий момент 0,003 Н∙м? Рамка состоит из 100 витков, сила тока в рамке 5 А. Ответ: В = 0, 01 Тл
Изображение слайда
Последний слайд презентации: Решение задач на определение силы Ампера: Домашнее задание
( 11 кл ) § 4, 5 — повторить
Конспект презентации. Тест «МАГНИТНОЕ ПОЛЕ-2»
Тест «МАГНИТНОЕ ПОЛЕ-2»
Изображение слайда
12.6: Закон Ампера — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4425
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как закон Ампера связывает магнитное поле, создаваемое током, со значением тока
- Рассчитайте магнитное поле длинного прямого провода, тонкого или толстого, по закону Ампера
Фундаментальное свойство статического магнитного поля заключается в том, что, в отличие от электростатического поля, оно не является консервативным. Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от \(\vec{B}\) и известен как Закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
Консервативное поле — это такое поле, которое совершает одинаковую работу над частицей, перемещающейся между двумя разными точками, независимо от выбранного пути. Магнитные поля таким свойством не обладают. Вместо этого существует связь между магнитным полем и его источником, электрическим током. Он выражается через линейный интеграл от \(\vec{B}\) и известен как Закон Ампера . Этот закон также может быть выведен непосредственно из закона Био-Савара. Теперь рассмотрим этот вывод для частного случая бесконечного прямого провода.
На рисунке \(\PageIndex{1}\) показана произвольная плоскость, перпендикулярная бесконечному прямому проводу, ток которого I направлен за пределы страницы. Линии магнитного поля представляют собой окружности, направленные против часовой стрелки и центрированные на проводе. Для начала рассмотрим \(\oint \vec{B} \cdot d\vec{l}\) над замкнутыми путями М и Н . Обратите внимание, что один путь ( M ) охватывает провод, а другой ( N ) нет. Поскольку силовые линии круглые, \(\vec{B} \cdot d\vec{l}\) является произведением B и проекции dl на окружность, проходящую через \(d\vec{l }\). Если радиус этого конкретного круга равен r , проекция равна \(rd\theta\) и
Поскольку силовые линии круглые, \(\vec{B} \cdot d\vec{l}\) является произведением B и проекции dl на окружность, проходящую через \(d\vec{l }\). Если радиус этого конкретного круга равен r , проекция равна \(rd\theta\) и
\[\vec{B} \cdot d\vec{l} = Br \, d\theta.\]
Рисунок \(\PageIndex{1}\): Ток I длинного прямого провода направлен за пределы страницы. Интеграл \(\oint d\theta\) равен \(2\pi\) и 0 соответственно для путей M и N.С \(\vec{B}\), заданным уравнением 12.4.1,
\[\oint \vec{B} \cdot d\vec{l} = \oint \left(\frac{\mu_0 I}{2\pi r}\right) \, r \, d\theta = \ frac{\mu_0 I}{2\pi} \oint d\theta.\]
Для пути M , который циркулирует по проводу, \(\oint_M d\theta = 2\pi\) и
\[\oint_M \vec{B} \cdot d\vec{l} = \mu_0 I.\]
Путь N , с другой стороны, циркулирует как через положительный (против часовой стрелки), так и через отрицательный (по часовой стрелке) \(d\theta\) (см. рисунок \(\PageIndex{1}\)), и поскольку он замкнут, \(\oint_N d\тета = 0\). Таким образом, для пути Н ,
рисунок \(\PageIndex{1}\)), и поскольку он замкнут, \(\oint_N d\тета = 0\). Таким образом, для пути Н ,
\[\oint_N \vec{B} \cdot d\vec{l} = 0.\]
Распространение этого результата на общий случай есть закон Ампера.
Закон Ампера
По произвольному замкнутому контуру,
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I\]
где I — полный ток, проходящий через любой открытый поверхность S , периметр которой является путем интегрирования. Необходимо учитывать только токи внутри пути интегрирования.
Чтобы определить, является ли конкретный ток I положительный или отрицательный, согните пальцы правой руки в направлении пути интегрирования, как показано на рисунке \(\PageIndex{1}\). Если I проходит через S в том же направлении, что и ваш вытянутый большой палец, I положителен; если I проходит через S в направлении, противоположном вашему вытянутому большому пальцу, это отрицательно.
Стратегия решения задач: закон Ампера
Чтобы рассчитать магнитное поле, создаваемое током в проводах, выполните следующие действия:
- Определите симметрию тока в проводе(ах). Если симметрии нет, используйте закон Био-Савара для определения магнитного поля.
- Определите направление магнитного поля, создаваемого проводом(ами), по правилу правой руки 2.
- Выберите петлю пути, в которой магнитное поле либо постоянно, либо равно нулю.
- Рассчитать ток внутри контура.
- Вычислить линейный интеграл \(\oint \vec{B} \cdot d\vec{l}\) вокруг замкнутого контура.
- Приравнять \(\oint \vec{B} \cdot d\vec{l}\) к \(\mu_0 I_{enc}\) к \(\mu_0 I_{enc}\) и найти \(\vec {В}\).
Использование закона Ампера для расчета магнитного поля, создаваемого проводом
Использование закона Ампера для расчета магнитного поля, создаваемого постоянным током I в бесконечно длинном тонком прямом проводе, как показано на рисунке \(\PageIndex{ 2}\).
Стратегия
Рассмотрим произвольную плоскость, перпендикулярную проводу, с током, направленным за пределы страницы. Возможные компоненты магнитного поля в этой плоскости \(B_r\) и \(B_{\theta}\) показаны в произвольных точках на окружности радиусом r с центром на проводе. Поскольку поле цилиндрически симметрично, ни \(B_r\), ни \(B_{\theta}\) не меняются в зависимости от положения на этой окружности. Также из симметрии радиальные линии, если они есть, должны быть направлены либо все внутрь, либо все наружу от провода. Это означает, однако, что должен существовать чистый магнитный поток через произвольный цилиндр, концентричный проводнику. Радиальная составляющая магнитного поля должна быть равна нулю, поскольку \(\vec{B}_r \cdot d\vec{l} = 0\). Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Следовательно, мы можем применить закон Ампера к круговому пути, как показано на рисунке.
Решение
По этому пути \(\vec{B}\) постоянна и параллельна \(d\vec{l}\), поэтому
\[\oint \vec{B} \cdot d \vec{l} = B_{\theta} \oint dl = B_{\theta}(2\pi r).\]
Таким образом, закон Ампера сводится к
\[B_{\theta}(2\pi r ) = \mu_0 I.\]
Наконец, поскольку \(B_{\theta}\) является единственным компонентом \(\vec{B}\), мы можем опустить индекс и написать
\[B = \frac{\mu_0 I}{2\pi r}.\]
Это согласуется с приведенным выше расчетом Био-Савара.
Значимость
Закон Ампера хорошо работает, если у вас есть путь интегрирования, по которому \(\vec{B} \cdot d\vec{l}\) дает результаты, которые легко упростить. Для бесконечного провода это легко работает с круговым путем вокруг провода, так что магнитное поле не учитывается при интегрировании. Если зависимость от пути кажется сложной, вы всегда можете вернуться к закону Био-Савара и использовать его для нахождения магнитного поля.
Пример \(\PageIndex{2}\): Расчет магнитного поля толстой проволоки по закону Ампера
Радиус длинного прямого провода на рисунке \(\PageIndex{3}\) равен a , и по проводу течет ток \(I_0\), равномерно распределенный по его поперечному сечению. Найдите магнитное поле как внутри, так и снаружи провода.
Рисунок \(\PageIndex{3}\): (a) Модель токоведущего провода радиусом a и током \(I_0\). (b) Поперечное сечение того же провода, показывающее радиусы х и петлю Ампера радиусом х .Стратегия
Эта задача имеет ту же геометрию, что и пример \(\PageIndex{1}\), но замкнутый ток изменяется по мере того, как мы перемещаем путь интегрирования снаружи провода внутрь провода, где он не захватывает весь ток прилагается (см. рисунок \(\PageIndex{3}\)).
Решение
Для любого кругового пути радиусом r с центром на проводе
\[\oint \vec{B} \cdot d\vec{l} = \oint Bdl = B\oint dl = B(2\pi r). \]
\]
Согласно закону Ампера это равно полному току, проходящему через любую поверхность, ограниченную путем интегрирования. 92} (r \leq a).\]
Вне провода ситуация идентична ситуации бесконечного тонкого провода из предыдущего примера; то есть
\[B = \frac{\mu_0 I_0}{2\pi r} (r \geq a).\]
Вариант B с r показан на рисунке \(\ Индекс страницы{4}\).
Рисунок \(\PageIndex{4}\): Изменение магнитного поля, создаваемого током \(I_0\) в длинном прямом проводе радиусом a .Значение
Результаты показывают, что по мере увеличения радиального расстояния внутри толстой проволоки магнитное поле увеличивается от нуля до известного значения магнитного поля тонкой проволоки. Вне провода поле падает независимо от того, толстый провод или тонкий.
Этот результат аналогичен тому, как закон Гаусса для электрических зарядов ведет себя внутри равномерного распределения зарядов, за исключением того, что закон Гаусса для электрических зарядов имеет равномерное распределение заряда по объему, тогда как закон Ампера здесь имеет однородную область распределения тока. Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Кроме того, спад вне толстого провода подобен тому, как спадает электрическое поле вне линейного распределения заряда, поскольку оба случая имеют одинаковую геометрию, и ни один случай не зависит от конфигурации зарядов или токов, когда петля находится снаружи. распространение.
Использование закона Ампера с произвольными путями
Используйте закон Ампера для оценки \(\oint \vec{B} \cdot d\vec{l}\) для текущих конфигураций и путей на рисунке \(\PageIndex{5}\ ).
Рисунок \(\PageIndex{5}\): Текущие конфигурации и пути для примера \(\PageIndex{3}\).Стратегия
Закон Ампера гласит, что \(\oint \vec{B} \cdot d\vec{l} = \mu_0 I\), где I — это полный ток, проходящий через замкнутый контур. Самый быстрый способ вычислить интеграл — вычислить \(\mu_0 I\), найдя чистый ток через контур. Положительные токи текут по большому пальцу правой руки, если ваши пальцы скручиваются в направлении петли. Это подскажет нам знак ответа.
Решение
(a) Ток, протекающий вниз по контуру, равен току, выходящему из контура, поэтому чистый ток равен нулю. {-6} T \cdot m.\) 9{-6} T \cdot m\).
{-6} T \cdot m.\) 9{-6} T \cdot m\).
Значение
Если бы все токи закручивались таким образом, что один и тот же ток входил бы в петлю и выходил из нее, то суммарный ток был бы равен нулю и магнитное поле отсутствовало бы. Вот почему провода в электрическом шнуре расположены очень близко друг к другу. Токи, протекающие к устройству и от устройства по проводу, равны нулевому общему току, протекающему через петлю Ампера вокруг этих проводов. Следовательно, никакие блуждающие магнитные поля не могут присутствовать в проводах с током.
Упражнение \(\PageIndex{1}\)
Рассмотрите возможность использования закона Ампера для расчета магнитных полей конечного прямого провода и круглой проволочной петли. Почему это не полезно для этих расчетов?
- Ответить
В этих случаях интегралы вокруг петли Ампера очень сложны из-за отсутствия симметрии, поэтому этот метод бесполезен.
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс и многие другие авторы. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс и многие другие авторы. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 12.6: Закон Ампера распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Закон Ампера
- Закон Ампера
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
Ампер: Настоящее | NIST
Несмотря на значительные проблемы, присущие прежнему официальному определению ампера, эту единицу измерения можно было измерять с достаточно низкой неопределенностью почти для всех нынешних целей, за исключением самых передовых исследований. Однако это обычно означало полный отказ от существующего определения SI.
К счастью, физика предоставила удобный альтернативный метод в виде закона Ома, сформулированного немецким ученым Георгом Омом в 1827 году. Он описывает пропорциональные отношения между тремя тесно связанными электрическими единицами: ампер, вольт и ом.
NIST также занимается научными измерениями ома, единицы сопротивления. С системой квантового сопротивления Холла (QHR) NIST показаны (задний ряд) Рэнд Элмквист, Марлин Крафт, Шамит Паягала (Университет медицины, JQI) и Кванг Мин Ю (KRISS, Южная Корея) и (передний ряд) Дин Джарретт. и Джордж Джонс.
и Джордж Джонс.
Если эти единицы незнакомы, может быть полезно думать о них, как если бы они были элементами системы водоснабжения. Амперы соответствуют объему воды, выходящей из трубы, вольты — давлению воды, а омы — диаметру трубы, определяющему ее сопротивление потоку.
Электрический ток выражается одним из самых простых и наиболее полезных уравнений в науке: I = V/R, где I – ток, V – напряжение, а R – сопротивление. (I, как символ тока, происходит от французской фразы intensité de courant , или сила тока.)
Итак, используя закон Ома, если известны напряжение и сопротивление в цепи, то ток можно определить по формуле.
Марлин Крафт из NIST регулирует соединения на токовом шунтирующем резисторе, который датируется 1899 годом. Слева показана система измерения постоянного тока NIST на 3000 ампер. Каждый из трех блоков питания выдает максимум 1000 А.
Конечно, это выглядит совершенно наоборот. В конце концов, в системе СИ семь основных единиц, включая ампер, предназначены для использования в различных математических комбинациях для определения 22 производных единиц, включая вольт и ом.
В конце концов, в системе СИ семь основных единиц, включая ампер, предназначены для использования в различных математических комбинациях для определения 22 производных единиц, включая вольт и ом.
Тем не менее, на практике производные вольты и омы использовались для измерения основных ампер.
Для этого есть отличная причина: и вольт, и ом были известны с гораздо большей точностью, чем ампер. Это потому, что их значения уже были основаны на константах, полученных из фундаментальных эффектов в области квантовой физики. В результате вольт может быть реализован с погрешностью около 6 частей на миллиард, а ом до 2 частей на 10 миллиардов.
Этот источник шума квантового напряжения (QVNS) обеспечивает принципиально точный сигнал напряжения, который можно сравнить с шумом напряжения от электронов в резисторе.
Кредит: Дэн Шмидт/NIST
Но есть одна загвоздка. Закон Ома не совсем соответствует, скажем, законам движения Ньютона. То есть I = V/R нельзя вывести из других законов физики. Вместо этого он представляет собой, казалось бы, неизменную взаимосвязь между тремя электрическими величинами, измеренную различными методами по всему миру в течение последних двух столетий. (Такая формула называется «эмпирическим» законом, потому что она полностью основана на данных наблюдений.) На сегодняшний день кажется, что закон Ома успешно описывает измерения, сделанные с погрешностями в диапазоне частей на десять миллионов. Согласно одному отчету, он все еще удерживает нанопроволоки в один атом высотой и в четыре атома шириной.
То есть I = V/R нельзя вывести из других законов физики. Вместо этого он представляет собой, казалось бы, неизменную взаимосвязь между тремя электрическими величинами, измеренную различными методами по всему миру в течение последних двух столетий. (Такая формула называется «эмпирическим» законом, потому что она полностью основана на данных наблюдений.) На сегодняшний день кажется, что закон Ома успешно описывает измерения, сделанные с погрешностями в диапазоне частей на десять миллионов. Согласно одному отчету, он все еще удерживает нанопроволоки в один атом высотой и в четыре атома шириной.
Пока все хорошо. Но современная метрология потребует еще более низких неопределенностей. Более того, одна из давних целей исследований электрических единиц — выяснить, продолжает ли закон Ома работать вплоть до квантово-механического масштаба атомов и даже меньших объектов.
В настоящее время это невозможно. Но переопределение ампера на основе элементарного заряда в конечном итоге позволит проверить закон Ома в наименьших измерениях в соотношении, называемом «треугольник квантовой метрологии».


 рисунок).
Сила, действующая на нижнюю сторону
рамки, направлена
рисунок).
Сила, действующая на нижнюю сторону
рамки, направлена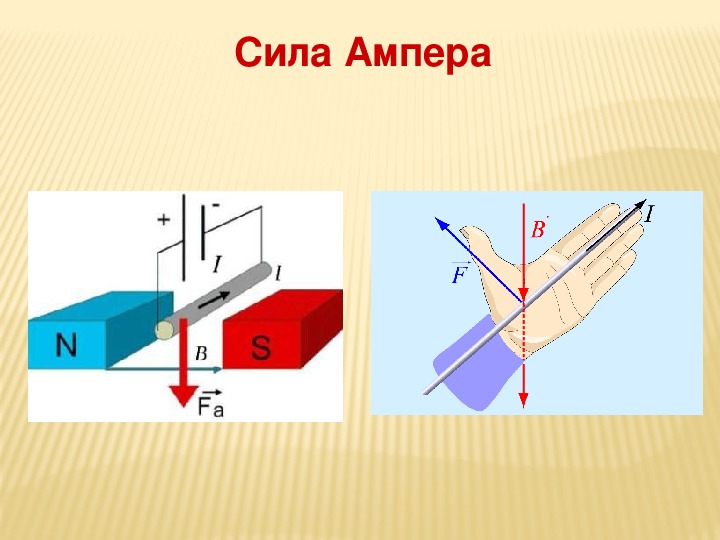 Как направлена сила,
действующая на сторону
рамки со стороны магнитного поля?
Как направлена сила,
действующая на сторону
рамки со стороны магнитного поля? рисунок, вид
рисунок, вид рисунок,
рисунок,

 Вектор магнитной индукции
направлен горизонтально вправо (см.
рисунок, вид сверху)
Вектор магнитной индукции
направлен горизонтально вправо (см.
рисунок, вид сверху) Вектор магнитной индукции
направлен горизонтально влево (см.
рисунок, вид сверху)
Вектор магнитной индукции
направлен горизонтально влево (см.
рисунок, вид сверху) Вектор магнитной индукции
направлен горизонтально влево (см.
рисунок, вид сверху). Куда направлена
Вектор магнитной индукции
направлен горизонтально влево (см.
рисунок, вид сверху). Куда направлена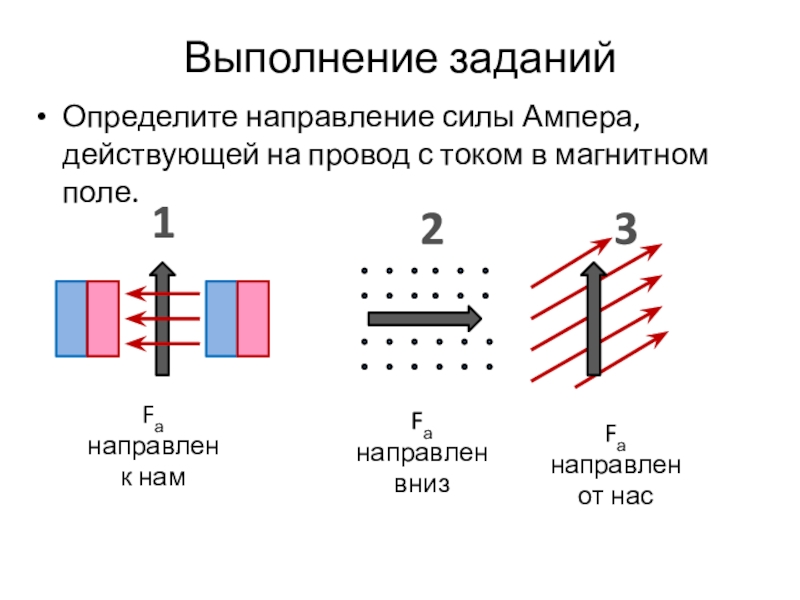 Сила
Ампера, действующая на проводник,
направлена
Сила
Ампера, действующая на проводник,
направлена Это объясняется тем,
что
Это объясняется тем,
что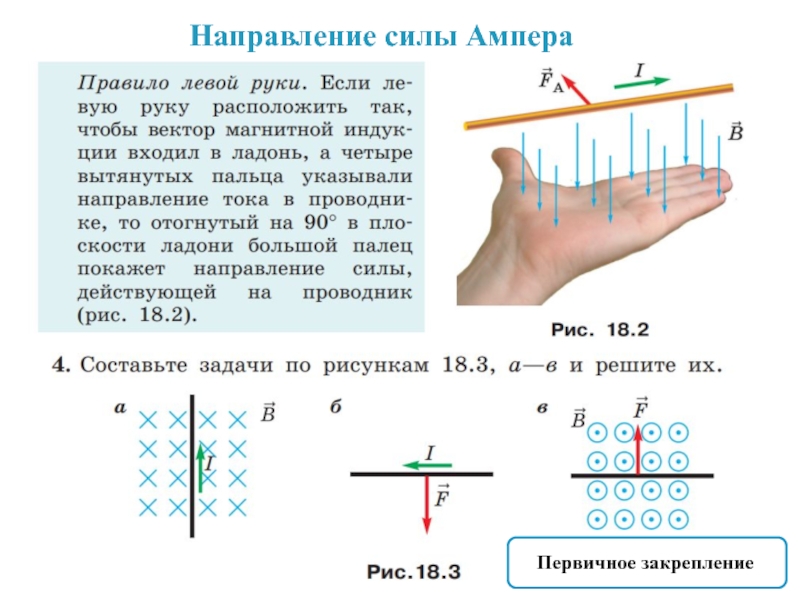 рисунок).
Все проводники тонкие, лежат в одной
плоскости, параллельны друг другу, и
расстояния между соседними провод-никами
одинаковы.
—
сила тока. Сила Ампера в этом случае
рисунок).
Все проводники тонкие, лежат в одной
плоскости, параллельны друг другу, и
расстояния между соседними провод-никами
одинаковы.
—
сила тока. Сила Ампера в этом случае —
сила тока. Сила Ампера в этом случае
—
сила тока. Сила Ампера в этом случае org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2