(курс 68 ч.) Алгебра логики
Планирование уроков на учебный год (по учебнику Н.Д. Угриновича)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику Н.Д. Угриновича) | Алгебра логики
Содержание урока
Логика
Логическое умножение (конъюнкция)
Логическое сложение (дизъюнкция)
Логическое отрицание (инверсия)
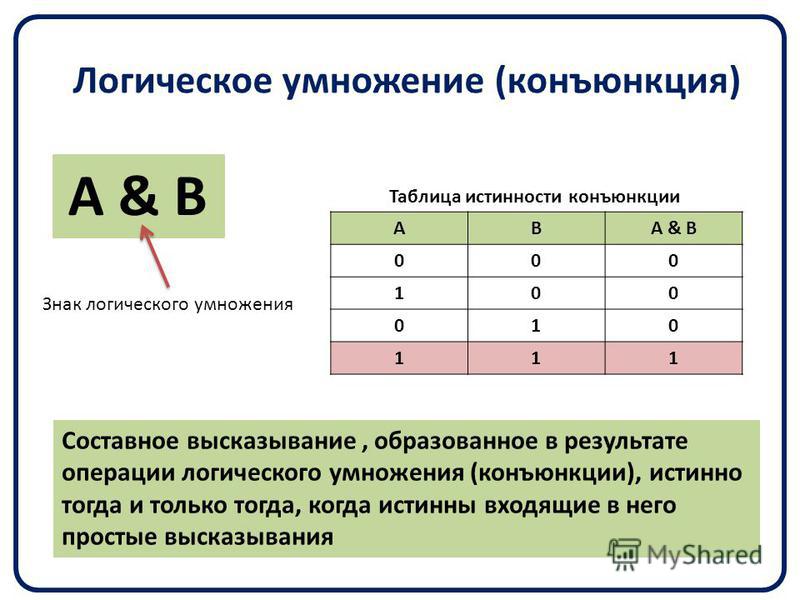
Логическое умножение (конъюнкция)
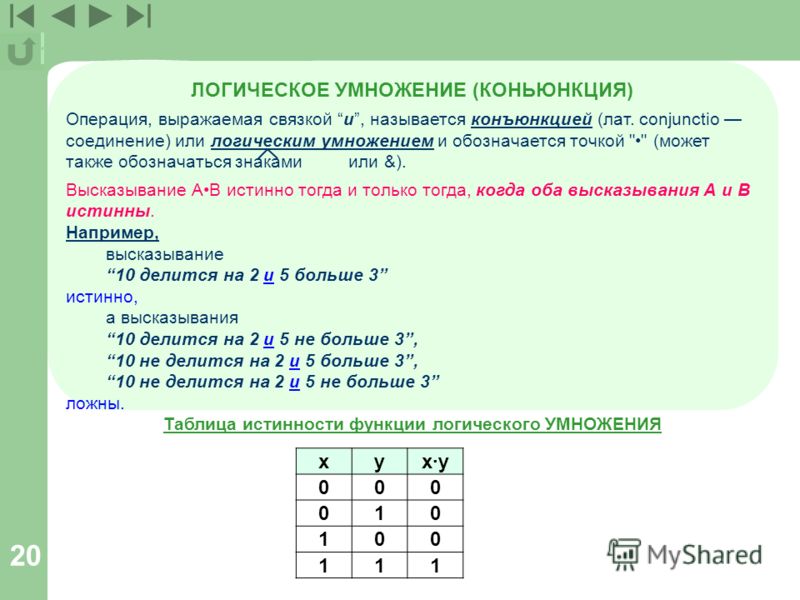
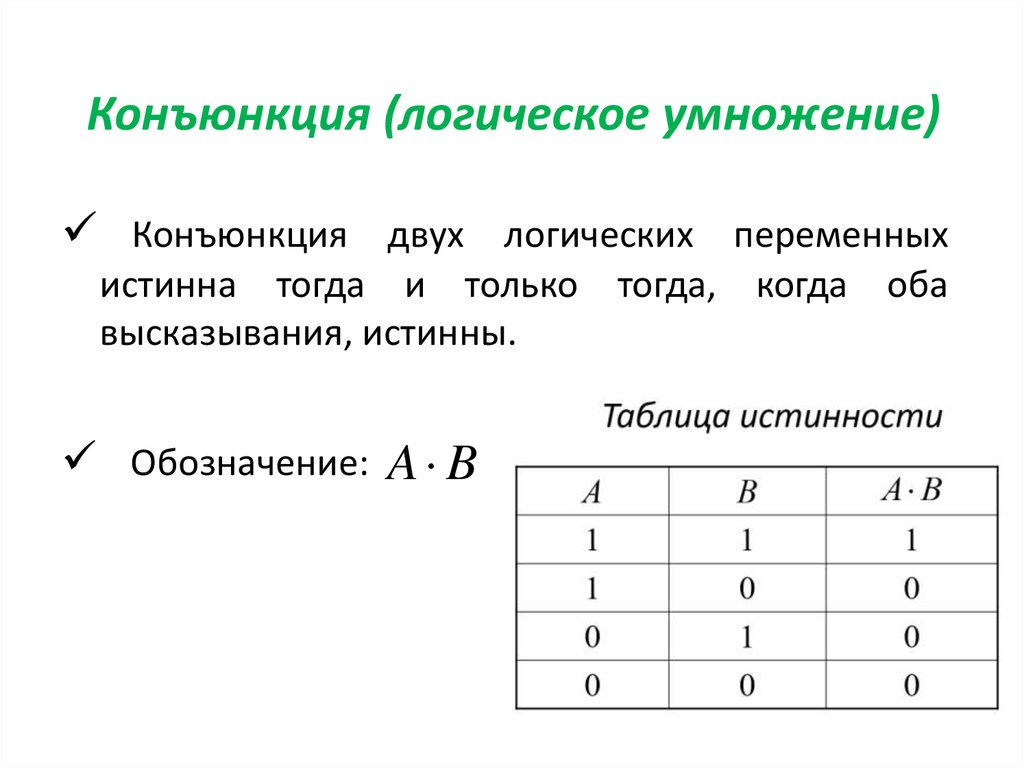
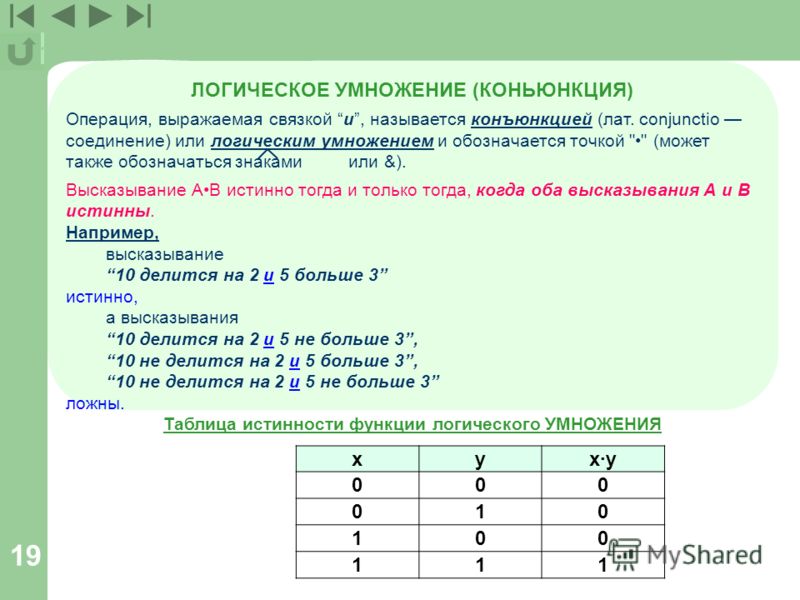
Логическое умножение (конъюнкция). Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.
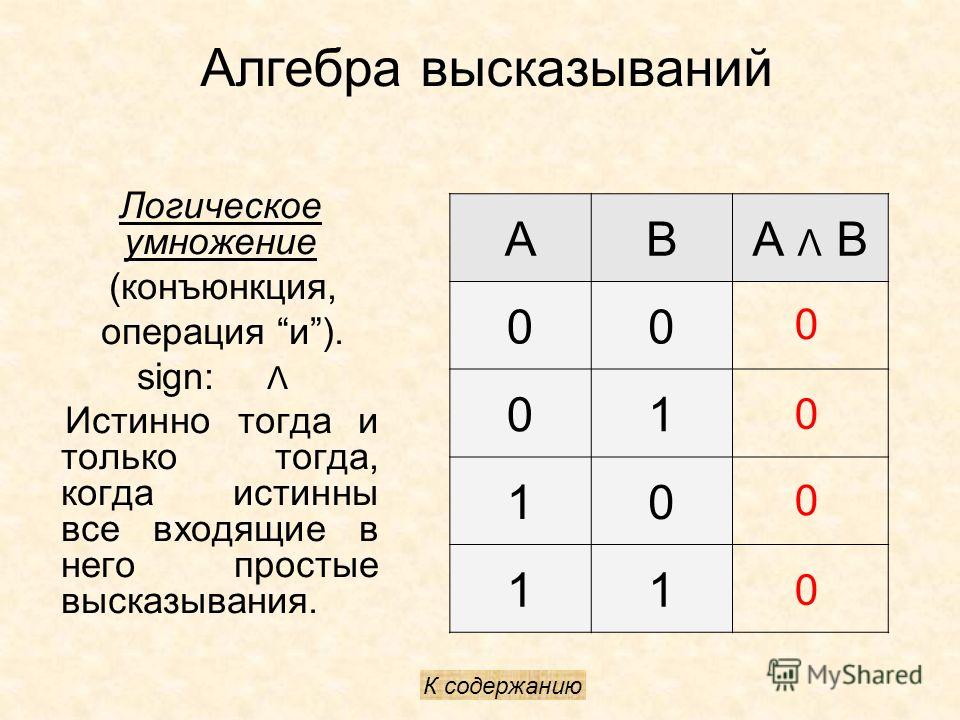
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны входящие в него простые высказывания.
Из приведенных ниже четырех составных высказываний, образованных с помощью операции логического умножения, истинно только четвертое, так как в первых трех составных высказываниях хотя бы одно из простых высказываний ложно:
(1) «2 х 2 = 5 и 3 х 3 = 10» (2) «2 х 2 = 5 и 3 х 3 = 9» (3) «2 х 2 = 4 и 3 х 3 = 10» (4) «2 х 2 = 4 и 3 х 3 = 9»
Перейдем теперь от записи высказываний на естественном языке к их записи на формальном языке алгебры логики. Операцию логического умножения (конъюнкцию) принято обозначать значком
А & В. (3.1)
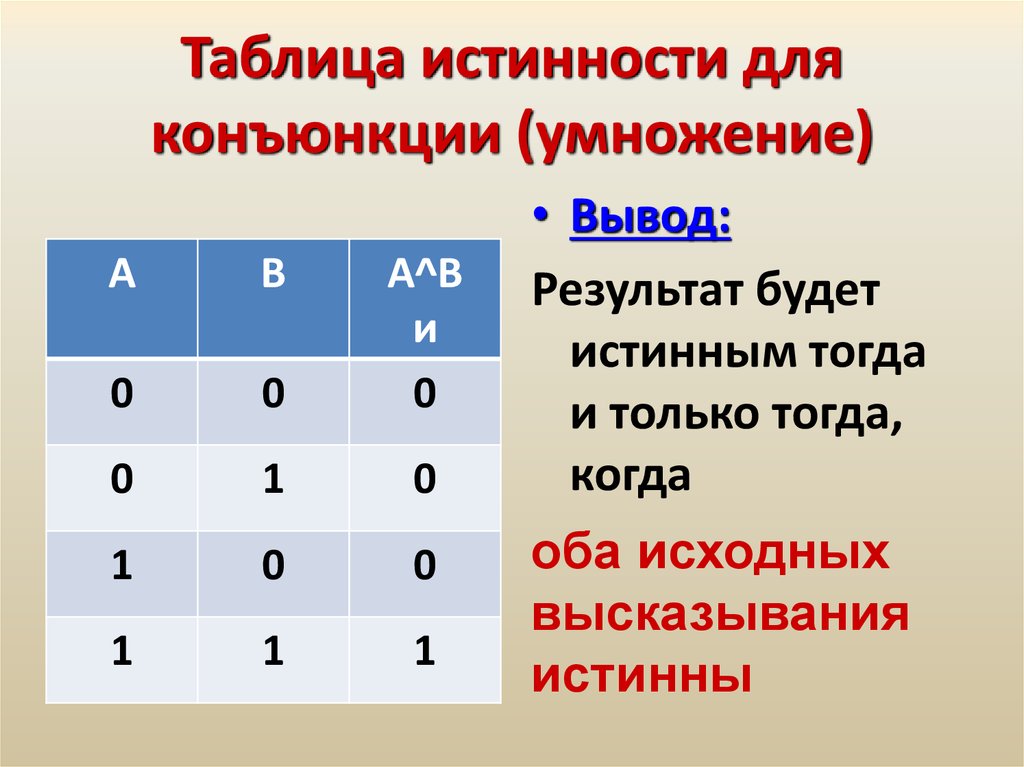
Значение операции логического умножения задается с помощью таблицы истинности. Таблица истинности показывает, какие значения дает логическая операция при всех возможных наборах ее аргументов. Результатом операции логического умножения является значение «истина» (1) тогда и только тогда, когда оба аргумента принимают значения «истина» (1) (табл.
3.1).
Таблица 3.1. Таблица истинности конъюнкции (логического умножения)
Таблица истинности задает логическую функцию, аргументы которой — логические переменные (принимают значение либо О, либо 1), а значение функции — результат логической операции над этими переменными (тоже значение либо 0, либо 1).
По таблице истинности легко определить истинность составного высказывания, образованного с помощью операции логического умножения.
Рассмотрим, например, составное высказывание «2 х 2 = 4 и 3 х 3 = 10».
Первое простое высказывание истинно (А = 1), а второе высказывание ложно (B = 0), по таблице истинности логического умножения определяем, что данное составное высказывание ложно.
Cкачать материалы урока
Тест по теме Основы логики и логические основы компьютера
Тест по теме «Основы логики и логические основы компьютера»
Вариант 1
1.
Как называется логическое умножение?
а) инверсия
б) дизъюнкция
в) конъюнкция
г) импликация
2. Какое из обозначений не применяется для инверсии
а) НЕ
б) │
в) ¬
г) NOT
А | Б | ? |
0 | 0 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
1 | 1 | 1 |
3. У какой из логических функций следующая таблица истинности:
а) инверсия
б) конъюнкция
в)дизъюнкция
г) импликация
4.
Запишите на языке алгебры логики высказывание: «Эта зима нехолодная и снежная»
а) А и Б
б) А
в) ¬ (А v Б)
г) ¬ А и Б
5. А = 0, Б = 1. В какой из ниже записанных формул результатом будет 1 (истина)?
а) ¬ Б
б) А и Б
в) ¬ (А или Б)
г) ¬ А или ¬ Б
6. Высказывание … истинно, когда А ложно, и ложно, когда А истинно
а)
б)
в) А →В
г)
7. Высказывание … ложно, тогда и только тогда, когда оба высказывания А и В ложны.
а)
б)
в)
г) А →В
8. Высказывание А ↔В истинно, тогда и только тогда, когда
а) А истинно, а В ложно
б) А и В совпадают
в) А ложно, а В истинно
г) А и В истинны
9. Определите, какому закону алгебры логики соответствует логическое тождество
а) сочетательный закон
б) переместительный закон
в) распределительный закон
г) закон идемпотенции
10.
Как будет выглядеть логическое выражение в упрощенном
виде ?
а)1
б)
в)
г)
11. Часть электронной логической схемы, которая реализует элементарную логическую функцию – это …
а) логическая схема компьютера
б) логический элемент компьютера
в) электронный элемент компьютера
г) триггер
12. Такой структурной схемой обозначается
а) конъюнктор
б) дизъюнктор
в) вентиль не
г) инвертор
13. Реализует дизъюнкцию двух и более логических значений …
а) вентиль
б) схема И
в) схема ИЛИ
г) схема НЕ
14. Равносильны или нет следующие переключательные схемы ?
а) да б) нет
15.
Алеша, Боря и Гриша нашли в земле сосуд. Каждый из них высказал по два предположения.
Алеша: » Это сосуд греческий, V века».
Боря: » Это сосуд финикийский, III века».
Гриша: » Это сосуд не греческий, IV века».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух своих предположений. Где и в каком веке был изготовлен сосуд?
а) Сосуд изготовлен в Греции в IV веке.
б) Сосуд изготовлен в Финикии в III веке.
в) Сосуд изготовлен в Финикии в V веке.
г ) Сосуд изготовлен в Греции в V веке.
16. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:
Россия — «Проект не наш, проект не США»;
США — «Проект не России, проект Китая»;
Китай — «Проект не наш, проект России».
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду. Определите, представителями каких стран являются откровенный, скрытный и осторожный министры
а) Откровеннее был российский министр, осторожнее — китайский, скрытнее — министр США
б) Откровеннее был министр США, осторожнее — российский, скрытнее — китайский министр
в) Откровеннее был китайский министр, осторожнее — российский, скрытнее — министр США
г ) Откровеннее был китайский министр, осторожнее — министр США, скрытнее — российский министр
Итоговый тест по теме «Основы логики и логические основы компьютера»
Вариант 2
1. Как называется логическое сложение?
а) инверсия
б) дизъюнкция
в) конъюнкция
г) импликация
2. Какое из обозначений не применяется для конъюнкции?
а) И
б) AND
в) v
г) &
А | Б | ? |
0 | 0 | 1 |
1 | 0 | 0 |
0 | 1 | 1 |
1 | 1 | 1 |
3.
У какой из логических функций следующая таблица истинности:
а) инверсия
б) конъюнкция
в)дизъюнкция
г) импликация
4. Запишите на языке алгебры логики высказывание: «Сегодня светит солнце, и мы пойдем кататься на коньках и лыжах»
а) А и (В и С)
б) (А и В) или С
в) А и В
г) А
5. А = 1, Б = 0. В какой из ниже записанных формул результатом будет 0 (ложь)?
а) ¬ (Б или А)
б) А v Б
в) ¬ (А и Б)
г) А и ¬ Б
6. Высказывание … истинно, тогда и только тогда, когда оба высказывания А и В истинны.
а)
б)
в)
г) А →В
7. Высказывание А →В ложно тогда и только тогда, когда …
а) А истинно, а В ложно
б) А и В совпадают
в) А ложно, а В истинно
г) А и В истинны
8.
Высказывание А ↔В истинно, тогда и только тогда, когда
а) А истинно, а В ложно
б) А ложно, а В истинно
в) А и В совпадают
г) А и В истинны
9. Определите, какому закону алгебры логики соответствует логическое тождество
а) сочетательный закон
б) закон идемпотенции
в) переместительный закон
г) распределительный закон
10. Как выглядит функция проводимости в упрщенном виде?
а)
б)
в)
г)
11 . Реализует конъюнкцию двух и более логических значений …
а) вентиль
б) схема И
в) схема ИЛИ
г) схема НЕ
12. Такой структурной схемой обозначается
а) конъюнктор
б) дизъюнктор
в) вентиль не
г) инвертор
13. Электронная схема, применяемая в регистрах компьютера для запоминания одного разряда двоичного кода это …
а) вентиль
б) логическая схема
в) триггер
г) электронная схема
14.
Как выглядит функция проводимости к заданной переключательной
схеме ?
а)
б)
в)
г)
15. В соревнованиях по гимнастике на первенство школу участвуют Алла, Валя, Таня и Даша. Болельщики высказали предположения о возможных победителях:
1-й болельщик : «Первой будет Таня, Валя будет второй».
2-й болельщик : «Второй будет Таня, Даша — третьей».
3-й болельщик : «Алла будет второй, Даша — четвертой».
По окончании соревнований оказалось, что в каждом предположении только одно из высказываний истинно, другое же ложно. Какое место на соревнованиях заняла каждая из девочек, если все они оказались на разных местах?
а) Алла– 1место, Даша– 2 место, Таня – 3 место, Валя– 4 место.
б) Таня – 1место, Алла – 2 место, Даша – 3 место, Валя – 4 место.
в) Валя– 1место, Таня– 2 место, Даша – 3 место, Алла –4 место.
г) Таня — 1место, Валя– 2 место, Даша – 3 место, Алла –4 место
16.
На конгрессе встретились четверо ученых: физик, биолог, историк и математик. Каждый ученый владел двумя языками из четырех (русским, английским, французским и итальянским), но не было такого языка, на котором могли бы разговаривать все четверо. Есть только один язык, на котором могли вести беседу сразу трое. Никто из ученых не владеет и французским и русским языками. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. Физик, биолог и математик не могут разговаривать на одном языке. Какими двумя языками владеет каждый ученый?
а) Физик– английский и французский, Биолог – французкий и итальянский, Историк- русский и английский, математик – английский и итальянский
б) Физик – французкий и итальянский, Биолог – английский и французский, Историк- русский и итальянский, математик – английский и итальянский.
в) Физик –– английский и итальянский, Биолог – французкий и итальянский, Историк- русский и итальянский, математик – английский и итальянский.
г) Физик – французкий и русский, Биолог – английский и французский, Историк- русский и итальянский, математик – английский и итальянский.
404: Страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Поиск- Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs.com.
- Посетите нашу домашнюю страницу и просмотрите наши технические темы
Просмотр по категории
Сеть
- неэкранированная витая пара (UTP)
Неэкранированная витая пара (UTP) — это повсеместно распространенный тип медных кабелей, используемых в телефонной проводке и локальных сетях (LAN).
- Оптимизация WAN (ускорение WAN)
Оптимизация глобальной сети, также известная как ускорение глобальной сети, представляет собой набор технологий и методов, используемых для улучшения …
- Многопротокольная коммутация по меткам (MPLS)
Безопасность
- трехфакторная аутентификация (3FA)
Трехфакторная аутентификация (3FA) — это использование учетных данных для подтверждения личности из трех отдельных категорий аутентификации…
- кибершпионаж
Кибершпионаж (кибершпионаж) — вид кибератаки, которую злоумышленники осуществляют против предприятия или правительства…
- управление доступом на основе ролей (RBAC)
Управление доступом на основе ролей (RBAC) — это метод ограничения доступа к сети на основе ролей отдельных пользователей в пределах .
ИТ-директор
- системы, основанные на знаниях (KBS)
Системы, основанные на знаниях (KBS), — это компьютерные программы, которые используют централизованное хранилище данных, известное как база знаний, для …
- Закон Сарбейнса-Оксли
Закон Сарбейнса-Оксли от 2002 года — это федеральный закон, устанавливающий широкомасштабные аудиторские и финансовые правила для публичных компаний.
- устав проекта
Устав проекта — это формальный краткий документ, в котором указывается, что проект существует, и предоставляется руководителям проекта письменные полномочия на…
HRSoftware
- вовлечения сотрудников
Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.
- кадровый резерв
Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.
- разнообразие, равенство и инклюзивность (DEI)
Разнообразие, равенство и инклюзивность — термин, используемый для описания политики и программ, которые способствуют представительству и …
Обслуживание клиентов
- представитель по развитию продаж (SDR)
Представитель по развитию продаж (SDR) — это лицо, занимающееся поиском, перемещением и квалификацией потенциальных клиентов через …
- индикатор уровня обслуживания
Индикатор уровня обслуживания (SLI) — это метрика, указывающая, какую меру производительности получает клиент в данный момент времени.
- платформа клиентских данных (CDP)
Платформа данных о клиентах (CDP) — это тип программного приложения, которое обеспечивает единую платформу информации о клиентах, которая .
..
..Почему знак + обычно используется как логический оператор ИЛИ?
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 11 тысяч раз
Несколько дней назад меня спросили, почему довольно часто используется + вместо символа v в качестве логического оператора ИЛИ в цифровой логике.
Его аргумент заключался в том, что совершенно нелогично использовать + для ИЛИ, потому что это, скорее всего, будет интерпретировано как И из общего использования/контекста.
Из Wiki: В логике и математике или — это функциональный оператор истинности, также известный как (включительно) дизъюнкция и чередование.
или +.
Логическая связка, представляющая этот оператор, также известна как «или» и обычно записывается как 9.0126 v Я провел небольшое исследование и выяснил происхождение знака против . Оно происходит от латинского слова «vel», что означает «или».
Одна вещь, которая добавляет путаницы, заключается в том, что + означает «и» с исторической точки зрения. Согласно этому и этому было изобретено около 1360 г. как и аббревиатура от латинского «et» («и»), напоминающая знак «плюс».
Однако я понятия не имею, кто придумал + в булевой алгебре и почему он предпочтительнее против в контексте цифровой логики/инженерии.
- цифровая логика
- булева алгебра
\$\конечная группа\$
9
\$\начало группы\$
Одно слово: Дистрибутивность
Умножение является дистрибутивным над сложением, и поэтому логическое И дистрибутивное над логическим ИЛИ.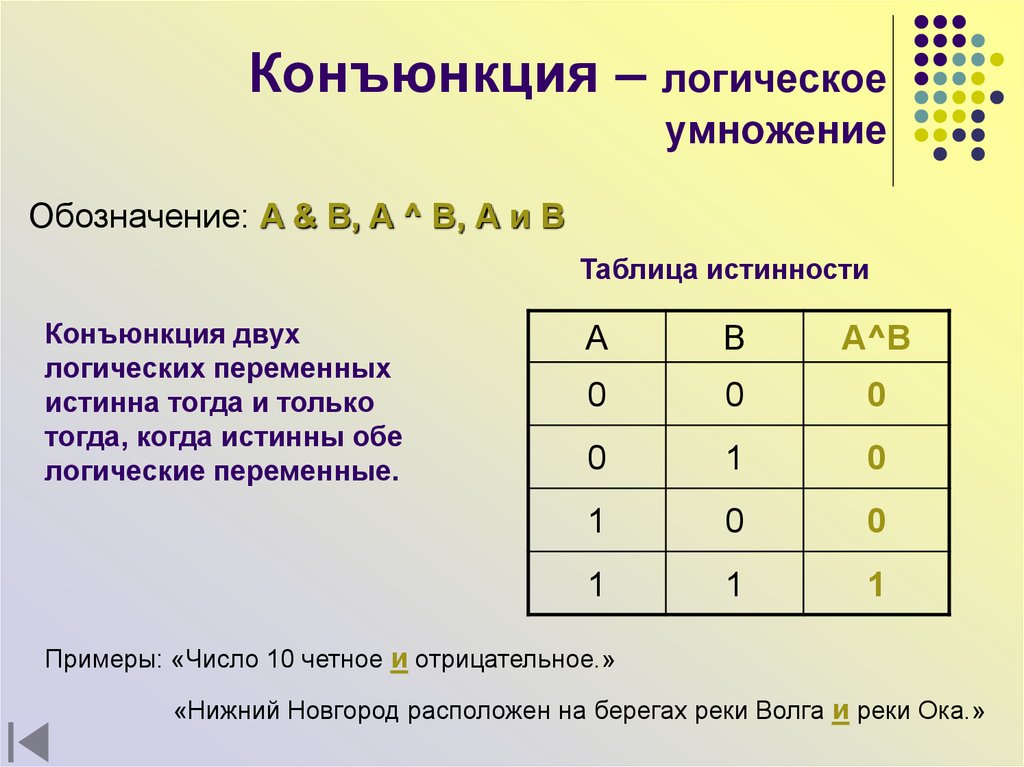
С другой стороны, умножение часто используется без символа ( 2a вместо 2*a ), и логическое И очень похоже. Если и A, и B должны быть истинными, написать AB просто и интуитивно понятно.
Очень удобен при построении таблиц истинности и алгоритмов на их основе.
$$f = A + BC$$
даже человек с небольшим опытом с первого взгляда заметит, что f может иметь место, когда A истинно, или когда оба B и 9 И или наоборот? Даже если вы их не забудете, читать будет намного понятнее и легче, если использовать только символы умножения и сложения, тем более что их невозможно спутать. В булевой логике нет ни сложения, ни умножения, поэтому их символы можно использовать повторно.
Тот факт, что 1 * 0 = 0 и 1 + 0 = 1 , и в булевой алгебре мы выбрали 1 как истину, а 0 как ложь, также помогает определить, какой оператор есть какой. Символы в математике — это просто символы.
У них есть значение, потому что мы присвоили им значение, поэтому лучше, если мы выберем символы, которые легко запомнить, и их использование в других областях аналогично.
\$\конечная группа\$
2
\$\начало группы\$
Один из аргументов, который я всегда использовал для логических знаков И и ИЛИ, — это их отношение к математическим операциям, которые они представляют.
Начнем с логического И. Его часто представляют в виде знака умножения, например *. Итак, если у вас есть длинное выражение, такое как s1*s2*s3*s4…. и одна из переменных принимает значение 0 или логическую ложь, тогда все выражение примет значение 0, что вполне нормально для умножения. , потому что 1*1*0*1… равно 0,
С другой стороны, когда мы используем знак +, который обычно обозначает сложение для представления логического ИЛИ, мы имеем аналогичный случай.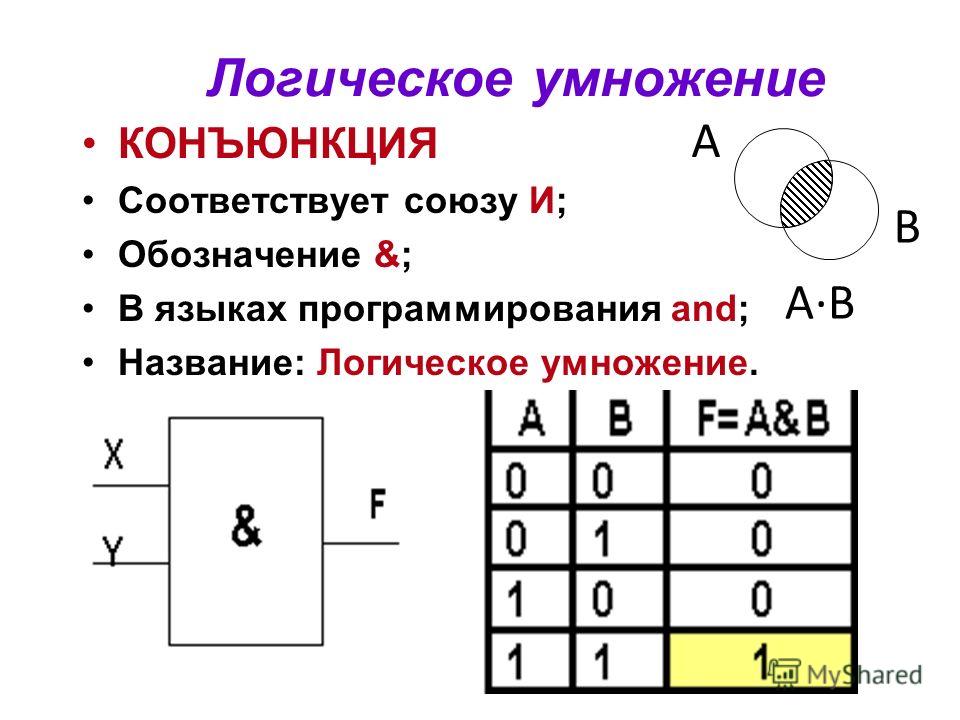
Если у нас есть несколько переменных, объединенных ИЛИ, то мы снова имеем случай s1+s2+s3+s4… Если хотя бы одна из переменных отлична от нуля, то результат также будет ненулевым, т.е. логично (ИМХО), когда мы сравниваем ИЛИ с дополнением. Например, 0+0+1+0… равно 1. Одна точка, где это прерывается, заключается в том, что у нас больше единиц, результат все еще один. Один из способов мышления, который я использовал для этого, состоит в том, чтобы просто помнить, что один представляет существование, так что если что-то существует, и вы добавляете к этому больше существования, оно все равно будет существовать.
\$\конечная группа\$
2
\$\начало группы\$
Майкл Шредер «Краткая история обозначений алгебры Буля», Nordic Journal of Philosophical Logic 2 (1): 41-62 (1997), приписывает использование + для представления включительно-или Лейбницу в его «Элементах исчисления» и обсуждает использование Булем обозначений, а также некоторые другие обозначения.
