CS307: Введение в компьютерную графику

При автоматической настройке задействовано значительное количество 3D-геометрии. камера. (Еще больше задействовано использование мыши для перетаскивания камеры к другой точке зрения, но мы пока отложим это.) Нам также нужно чтобы понять некоторую геометрию векторов, чтобы сделать вычисления для материала и освещение.

Итак, мы собираемся атаковать его сейчас. Это чтение объясняет соответствующую математику. Наиболее важной частью нижеследующего является понимание скалярного произведения. Скалярный продукт используется несколькими способами в модель освещения, поэтому чем вам с ней удобнее, тем лучше. Мы не будем использовать кросс-произведения в материале и освещении, но позже в семестр, и здесь он вполне подходит, но если вы заблудитесь в понимая перекрестный продукт, не волнуйтесь.

Векторная математика

Интуитивно и геометрически вектор представляет собой стрелку . Это имеет длину и направление .

В системе координат мы может представить вектор как тройку чисел $(\Delta x, \Delta y, \Дельта г)$.

Конечно, тройка чисел также используется для представляют точек . Есть ли разница? Да. Точка имеет местоположение , но не длину и вектор имеет длина , но не местоположение. Вы можете получить одно от другого, хоть. Если у нас есть две точки, A и B, мы можем найти вектор из A в B с помощью вычитания: \[ \vecIII{\Delta x}{\Delta y}{\Delta z} = \vec{v} = В — А = \vecIII{b_x}{b_y}{b_z} — \vecIII{a_x}{a_y}{a_z} = \vecIII{b_x-a_x}{b_y-a_y}{b_z-a_z} \]

Векторы и точки в однородных координатах

Интересно, мы можем отличить векторы от точек в однородных координатах

, о котором мы узнали в контекст аффинных преобразований. Очки имеют $w=1$, и (как вы можете см. из вычитания выше) векторы имеют $w=0$: \[ \vecIV{\Delta x}{\Delta y}{\Delta z}{0} = \vec{v} = В — А = \vecIV{b_x}{b_y}{b_z}{1} — \vecIV{a_x}{a_y}{a_z}{1} \]

Скалярный продукт

Обозначение $v\cdot w$ означает произведение точек или скалярное произведение или (иногда) внутреннее произведение двух векторов, $v$ и $w$. В абстрактной математике мы можем говорить о выборе внутреннего произведение в векторном пространстве, и этот внутренний продукт должен удовлетворять определенным характеристики:

• $v\cdot w\in\Re$. То есть скалярное произведение двух векторов — это просто действительное число, скаляр (не вектор).
• $\forall\ v, v\cdot v=0 \mathrm{~iff~} v=\vec{0}$. то есть точка произведение вектора на самого себя равно нулю тогда и только тогда, когда вектор является нулевой вектор. В 3D нулевой вектор равен (0,0,0).
• (коммутативность) $v \cdot w = w \cdot v$. То есть порядок вектора значения не имеют.
• (линейность) $v \cdot (au+bw) = a(v\cdot u) + b(v \cdot w)$. Который есть скалярное произведение вектора $v$ на линейную комбинацию двух другие векторы, $u$ и $w$, совпадают с линейной комбинацией два точечных произведения. 9{n} v_i w_i \]

  На самом деле, поскольку мы используем только 3 измерения, $x$, $y$ и $z$: \[ v \cdot w = v_x w_x + v_y w_y + v_z w_z \]

  Вы можете легко проверить, что это определение скалярного произведения удовлетворяет требуемые свойства.

  Обратите внимание, что вычисление одного элемента матричного умножения — это то же самое, что и скалярное произведение: результирующий элемент является скалярным произведением строка из первой матрицы со столбцом из второй матрицы.

  Пример

  Предположим, у нас есть следующие два вектора: \[ \begin{выравнивание*} v &=& (1,2,3) \\ ш &=& (6,5,4) \\ \end{выравнивание*} \]

  Скалярное произведение этих векторов равно: \[ v \cdot w = 1\ast6+2\ast5+3\ast4 = 6+10+12 = 28 \]

  Обратите внимание, что скалярное произведение двух векторов является скаляром : действительное число, а не вектор.

  Длина

  Учитывая скалярное произведение, мы можем определить длину вектора: \[ |v| = \sqrt{v\cdot v} \]

  Это всего лишь наш старый друг, замаскированная теорема Пифагора! Почему? Поскольку скалярное произведение вектора на самого себя в конечном итоге приводит к квадрату каждого элемент и суммировать их.

  Обратите внимание, что мы можем масштабировать (уменьшать или увеличивать) любой вектор (кроме нулевого). 2} = \sqrt{4+9+36} = \sqrt{49} = 7 \]

  Если мы нормализуем $v$, что мы получим? Пусть $w=v/|v|$, получаем \[w = (2,3,6)/7 = (2/7,3/7,6/7) \ приблизительно (0,28,0,43,0,86) \]

  Легко проверить, что $|w|=1$. Вектор $w$ точно такой же направление как $v$, но это одна единица длины.

  Углы между векторами

  Угол между двумя векторами $v$ и $w$ можно найти с помощью следующая формула: \[ \cos(\theta) = \frac{v\cdot w}{|v||w|} \]

  , который мы также можем представить как: \[ \cos(\theta) = \frac{v}{|v|} \cdot \frac{w}{|w|} \]

  Другими словами, это просто скалярное произведение двух единичных векторов. То есть, если оба из двух векторов $v$ и $w$ нормализованы (длина одна единица), формула косинуса угла между ними принимает вид следующее, что удивительно просто: \[ \cos(\theta) = v\cdot w \]

  Это хорошая новость, потому что скалярное произведение вычисляется очень быстро: в 3D, это всего лишь 3 умножения и 2 сложения. Получается, что косинус угол часто требуется в компьютерной графике, поэтому возможность вычислить его так просто чрезвычайно ценно. На самом деле бывают случаи, когда хвост виляет собакой: используется косинус угла, потому что он такой быстрый вычислить. Он часто используется в расчетах освещения. 92} = \sqrt{81+36+4} = \sqrt{121} = 11 \]

  Следовательно, косинус угла между $v$ и $w$ равен: \[ \cos(\theta) = \frac{v\cdot w}{7\ast 11} = \frac{2\ast9+3\ast6+6\ast2}{77} = \frac{18+18+12}{77} = \ гидроразрыва {48} {77} \ приблизительно 0,62 \]

  Если по какой-то причине нам нужен фактический угол, мы можем вычислить дугу косинус, но нам это почти никогда не понадобится. (Этот угол составляет около 51 градусов.)

  Пример 2

  Предположим, у нас есть векторы $x=(1,0,0)$ и $y=(0,1,0)$. То есть эти являются единичными векторами, которые указывают в направлении осей X и Y. Это легко видеть, что скалярное произведение между ними равно нулю.

  Что это значит? Если косинус угла равен нулю, то угол — прямой угол (девяносто градусов). То есть эти два вектора перпендикулярно . (Мы не удивлены, что они перпендикулярны, но приятно видеть, что расчет это подтверждает.) В линейном В алгебре термин ортогональный используется для векторов, которые перпендикуляр. На гиковском языке мы говорим, что две вещи «ортогональны». если одно не влияет на другое. Это имеет смысл, потому что мы можем перевести объект на кратное вектору $x$, не затрагивая его Y координаты, и переведем ее на кратные вектору $y$ без влияет на его координату X.

  Пример 3

  Что мы можем сказать об угле $\theta$ между векторами: \[ \begin{выравнивание*} v &=& (2,3,6)\\ и &=& (-6,10,-3)\\ \end{выравнивание*} \]

  Косинус угла находится по формуле: \[ \cos(\theta) = \frac{(2,3,6)\cdot(-6,10,-3)}{|v||u|} = \frac{-12+30-18}{|v||u|} = \frac{0}{|v||u|} = 0 \]

  Итак, эти векторы перпендикулярны (ортогональны).

  Применение закона косинусов

  В этом разделе доказывается, что скалярное произведение нормализованных векторов равно угол между ними.

  Можете пропустить, если вам не интересно. два вектора, v и w, и их разность, v-w, которая стрелка между конечными точками 9п v_i w_i}{|v| |ш|} \]

  , но этот числитель — просто скалярное произведение $v$ и $w$, поэтому \[ \cos(\theta) = \frac{v\cdot w}{|v| |ш|} \]

  Перекрестное произведение

  Как мы знаем, скалярное произведение двух векторов дает скаляр . Перекрестное произведение дает вектор : тот, который перпендикулярен оба из них. В 3D перекрестное произведение равно: \[ \begin{выравнивание*} \vec{n} &=& \vec{v}\times\vec{w} \\ &=& \vecIII{v_x}{v_y}{v_z}\times\vecIII{w_x}{w_y}{w_z} \\ &=& \vecIII{v_yw_z-v_zw_y}{v_zw_x-v_xw_z}{v_xw_y-v_yw_x} \end{выравнивание*} \]

  Обратите внимание, что порядок имеет значение: $v \times w = — w \times v$. Заметьте также, что при вычислении $n_x$ вы используете только члены из компонентов Y и Z, и аналогично для $n_y$ и $n_z$. Есть хороший графический способ запомнить способ вычислить это. Глядя на следующие цифры, умножьте термины, соединенные линиями, и вычесть одну строку из другой. Для Х и Z, вы вычитаете большую диагональ (с наклоном вправо) из малой диагонали, а для Y вы вычитаете их в обратном порядке (или просто отрицать результат). Как вычислить перекрестный продукт

  Направление перекрестного произведения

  В каком направлении указывает вектор? Для этого нам понадобится правило правой руки : направьте пальцы правой руки в направлении первого вектора, проведите их ко второму, и ваш большой палец указывает в направлении поперечного произведения. В качестве альтернативы укажите большой палец в направлении первого вектора, указательный в направлении направлении второго, а средний палец в направлении перекрестный продукт.

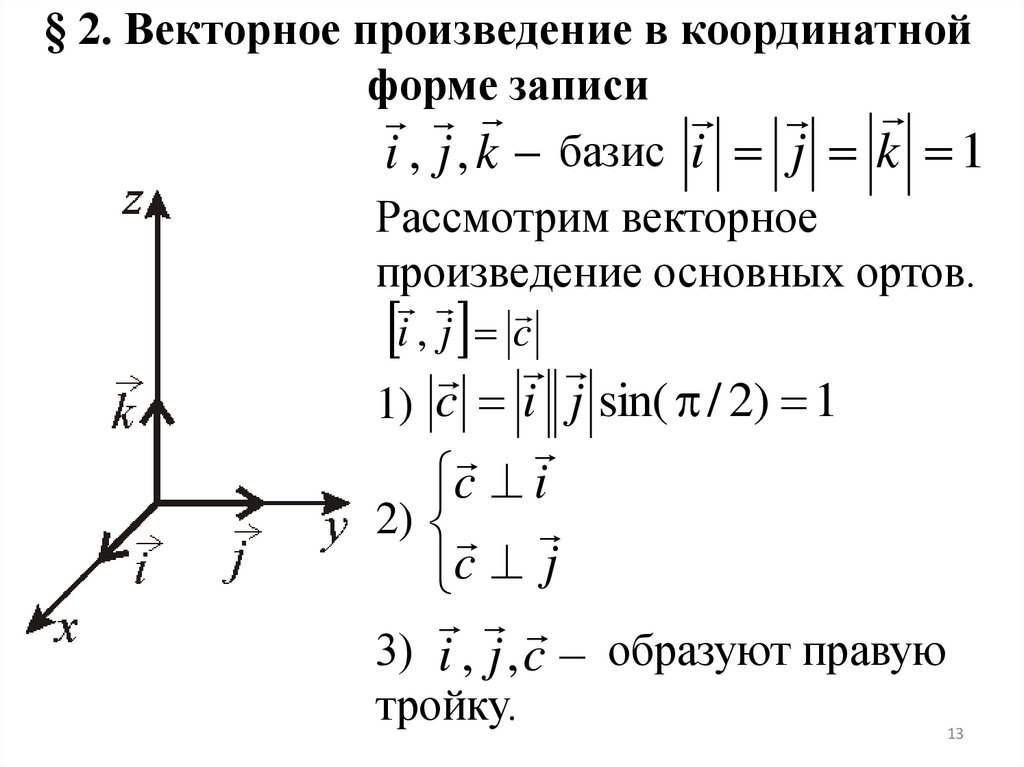
  Интересно, что $z=x\times y$, $x = y \times z$ и $y = z \times x$. Который — нормированный вектор, параллельный оси $z$, (0,0,1) — крест произведение векторов для оси $x$ (1,0,0) и оси $y$ (0,1,0).

  Длина поперечного произведения

  Длина перекрестного произведения, деленная на длины двух vectors дает синус угла между двумя векторами: \[ \sin(\theta) = \frac{|v\times w|}{|v| |ш|} \]

  Пример перекрестного продукта

  Найдите векторное произведение следующих двух векторов: \[ \begin{выравнивание*} v &=& (2,3,6)\\ ш &=& (9,6,2)\\ \end{выравнивание*} \]

  Напишем векторы вертикально, чтобы найти результат. \[ \begin{выравнивание*} \vec{n} &=& \vec{v}\times\vec{w} \\ &=& \vecIII{2}{3}{6}\times\vecIII{9}{6}{2} \\ &=& \vecIII{3\ast2-6\ast6}{9\ast6-2\ast2}{2\ast6-9\ast3} \\ &=& \vecIII{6-36}{54-4}{12-27} \\ &=& \vecIII{-30}{50}{-15} \\ \end{выравнивание*} \] 92 = 5929/5929\]

  Ух ты!

  Векторы нормалей

  Вектор, перпендикулярный поверхности, такой как плоскость или Сфера, как говорят, нормалей к ней . Поэтому он называется нормальный вектор. (Другие векторы не являются аномальными .)

  Векторы нормалей для поверхностей имеют решающее значение в расчетах освещения, потому что вектор нормали сообщает нам ориентацию поверхности, а ориентация важна для того, как свет падает на поверхность и где он отражает к.

  Обычный способ найти вектор нормали к плоскости — найти два вектора которые лежат в плоскости и берут их векторное произведение. Чтобы найти нормальный вектор для поверхности, найти плоскость, касательную в нужной точке, и найти вектор нормали к этой плоскости. Мы увидим примеры этого позже в курсе.

  Координаты и векторы в пространстве

  Координаты и векторы в пространстве

  Координатная геометрия даже полезнее в космосе, чем на плоскости, поскольку она намного сложнее рисовать фигуры в 3D для точной визуализации.

  Обозначение:

  Векторы будут записаны в виде строк или столбцов, если только векторные операции обеспокоены. Если в картину входят матрицы, то есть разница между векторы-строки (матрицы-строки) и векторы-столбцы (матрицы-столбцы).

  • Обычно пишут O или иногда 0 для нулевого вектора .
  • В 2-местном часто пишут O или 0 для (0, 0), I или i для (1, 0) и J или j для (0, 1).
  • В 3-х пробельный часто пишут O или 0 для (0, 0, 0), I или i для (1, 0, 0) и J или j для (0, 1, 0), K или k для (0, 0, 1).
  • В n-пространстве даже при n = 1, 2 или 3 записываются векторы e ₁ , …, e _n , где ek — вектор в n-пространстве со всеми элементами = 0 кроме 1 в записи k.

  Сложение векторов и скалярное умножение

  В этих заметках предполагается, что механика и базовая геометрия векторных сложение и умножение вектора на скаляр (т. е. действительное число) понял.

  Центры масс и параметризация линий и Самолеты

  Линии и плоскости могут быть описаны в координатной геометрии с помощью параметризации. Эта тема изучалась в Math 444. Дается обзор и несколько упражнений. по ссылке выше.

  Уравнения прямых и плоскостей

  Линии и плоскости также являются решениями систем линейных уравнений. Эта секция вводит тему.

  Основы многоточечного продукта

  Здесь приведены основные сведения о скалярном произведении: определение, алгебраические свойства, связь с косинусом и критерий скалярного произведения для ортогональных векторов.

  Крест Основные сведения о продукте

  Этот сайт Texas A&M определяет векторное произведение и показывает некоторые основные свойства.