Как найти силу тока протекающего через лампу
Как найти силу тока
С проблемой определения силы тока сталкиваются и при решении задач, и в повседневной жизни. Вычислить этот параметр для проводника или электрической цепи можно не только путем проведения измерений, но и при помощи формул.
В проводнике
Основными величинами, характеризующими электрический ток, являются сила, напряжение и сопротивление. Взаимосвязь между ними была установлена экспериментальным путем в 1826 году Георгом Омом. В последствии она была сформулирована в виде закона, который и был назван в честь ученого.
Определение
Закон Ома: сила тока в участке цепи или проводнике обратно пропорциональна сопротивлению и прямо пропорциональна напряжению.
Рассчитать силу тока в проводнике также можно, если разделить мощность на напряжение.
При протекании тока происходит нагревание проводника. И по количеству выделившегося тепла на основании закона Джоуля-Ленца возможно провести вычисление силы тока.
В цепи
Реальный источник тока всегда обладает своим внутренним сопротивлением.
Определение
Закон Ома для полной цепи формулируется так: сила тока в полной цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна сумме внутреннего и внешнего сопротивления.
Формулы
Закон Ома для участка цепи:
\(I=\frac UR\)
где R — сопротивление проводника, а U — напряжение.
Закон Ома для полной цепи:
\(I=\frac\Sigma{R+r}\)
где ε — электродвижущая сила источника тока, R + r — сумма сопротивлений источника и внешней нагрузки.
Формула, для определения силы тока по мощности и напряжению:
\(I=\frac PU\)
где P — мощность, а U — напряжение.
Определение
Закон Джоуля-Ленца: при протекании по проводнику тока происходит выделение тепла (Q), которое равно произведению квадрата силы тока (I) на время (t), которое он протекал и на сопротивление проводника (R).
Математически формула выглядит так:
\(Q=I^2Rt\)
Исходя из нее можно вывести еще одну формулу для расчета силы тока:
\(I=\sqrt{\frac Q{Rt}}\)
Параметры постоянного тока
Как и всякая физическая величина, постоянный электрический ток характеризуется целым рядом параметров, имеющих непосредственное к нему отношение и отношение к взаимосвязанным с ним величинам.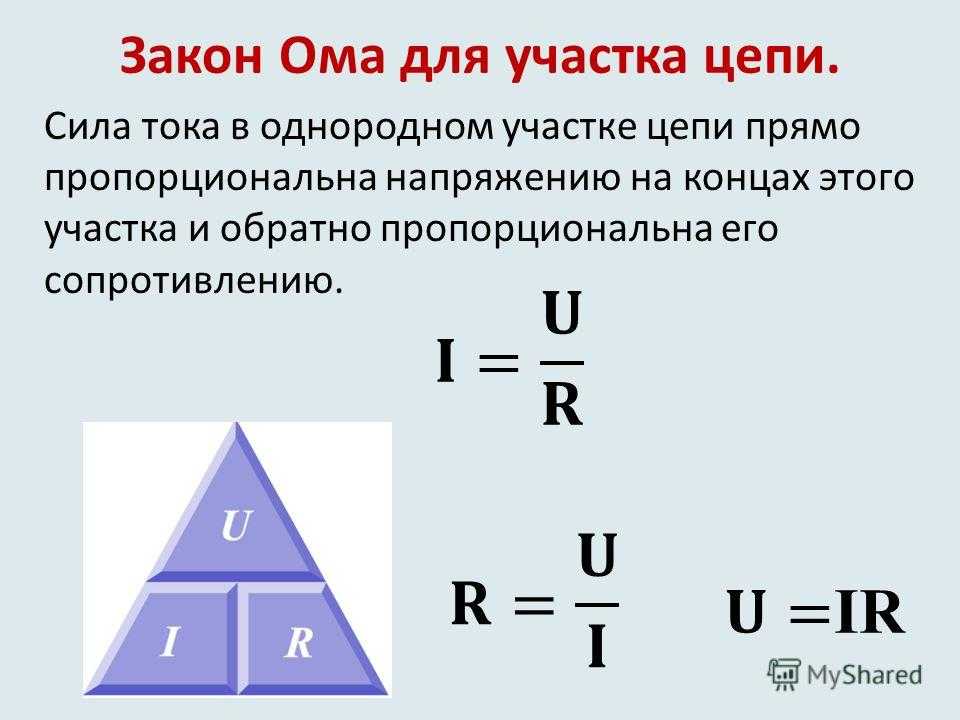
Величина постоянного тока (сила тока)
Прежде чем говорить о силе тока, определимся с таким понятием, как электрический заряд, выражающий способность тел участвовать в электромагнитных явлениях типа создания электромагнитного поля и электромагнитного взаимодействия.
Впервые это понятие было введено в конце XVIII века французским учёным Шарлем Кулоном, сформулировавшим тогда же свой знаменитый закон о силе взаимодействия между точечными зарядами в зависимости от разделяющего их расстояния. В честь него единица измерения электрического заряда (количества электричества) стала называться «Кулон» (Кл).
Только опираясь на понятие электрического заряда, можно говорить о величине (силе) тока, формула расчёта которого (для равномерного движения зарядов) выглядит следующим образом:
I = Q/t
Что можно выразить следующими словами: сила тока прямо пропорциональна количеству зарядов, проходящих через поперечное сечение проводника за единицу времени. Здесь:
- I – ток, измеряемый в амперах (Андре Мари-Ампер – ещё один французский физик, внёсший значительный вклад в теорию электромагнетизма).

- Q – электрический заряд, измеряемый в кулонах или ампер-часах (А·ч). 1 А·ч = 3600 Кл.
- t – единица времени.
Для измерения силы тока используются амперметры, включаемые последовательно с источником электрического тока.
Плотность тока
Ещё одно важное понятие, необходимое в целях правильного выбора токопроводящего сечения линий электропередачи. Плотность тока это:. j = I/S
j = I/S
Где: I – сила тока в амперах. S – площадь поперечного сечения в м2. J – плотность тока в А/м2 или А/мм2.
Электродвижущая сила (ЭДС)
Электродвижущая сила (ЭДС) – это величина, характеризующая работу первичного источника электрической энергии по созданию постоянного электрического тока.
E = A/Q
E – электродвижущая сила (ЭДС), измеряемая в вольтах (Алессандро Вольта – известнейший итальянский физик). A – работа, измеряемая в джоулях (Джеймс Прескотт Джоуль – английский физик, внёсший значительный вклад в развитие термодинамики).
Электрическое напряжение
Электрическое напряжение – это величина, показывающая работу эффективного электрического поля, затраченную на перенос единичного пробного заряда из точки A в точку B.
UAB = φA – φB + EAB
φA – φB – разница потенциалов между точками A и B. EAB – электродвижущая сила, возникающая на искомом участке цепи постоянного тока. Здесь все величины измеряются в вольтах. Для определения величины напряжения применяются вольтметры, подключаемые параллельно участку измерения напряжения.
Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
R=r1+r2+r3
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).
Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=Iх U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А. Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств. Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
§ 37. Сила тока. Единицы силы тока
Действия электрического тока, которые были описаны в § 35, могут проявляться в разной степени — сильнее или слабее. Опыты показывают, что интенсивность (степень действия) электрического тока зависит от заряда, проходящего по цепи в 1 с.
Когда свободная заряженная частица — электрон в металле или ион в растворе кислот, солей или щелочей — движется по электрической цепи, то вместе с ней происходит и перемещение заряда. Чем больше частиц переместится от одного полюса источника тока к другому или просто от одного конца участка цепи к другому, тем больше общий заряд q, перенесённый частицами.
Ампер Андре Мари (1775-1836)
Французский физик и математик, создал первую теорию, которая выражала связь электрических и магнитных явлений. Ввёл в физику понятие «электрический ток».
Электрический заряд, проходящий через поперечное сечение проводника в 1 с, определяет силу тока в цепи. Значит, сила тока равна отношению электрического заряда q, прошедшего через поперечное сечение проводника, ко времени его прохождения t, т. е.
I = q/t
где I — сила тока.
На Международной конференции по мерам и весам в 1948 г. было решено в основу определения единицы силы тока положить явление взаимодействия двух проводников с током. Ознакомимся сначала с этим явлением на опыте.
Ознакомимся сначала с этим явлением на опыте.
На рисунке 60 изображены два гибких прямых проводника, расположенных параллельно друг другу. Оба проводника подсоединены к источнику тока. При замыкании цепи по проводникам протекает ток, вследствие чего они взаимодействуют — притягиваются или отталкиваются, в зависимости от направления токов в них.
Рис. 60. Взаимодействие проводников с током
Силу взаимодействия проводников с током можно измерить
Эта сила, как показывают расчёты и опыты, зависит от длины проводников, расстояния между ними, среды, в которой находятся проводники, и, что самое важное для нас, от силы тока в проводниках. Если одинаковы все условия, кроме силы токов, то, чем больше сила тока в каждом проводнике, тем с большей силой они взаимодействуют между собой. Представим теперь себе, что взяты очень тонкие и очень длинные параллельные проводники
Расстояние между ними 1 м, и находятся они в вакууме. Сила тока в них одинакова
Представим теперь себе, что взяты очень тонкие и очень длинные параллельные проводники.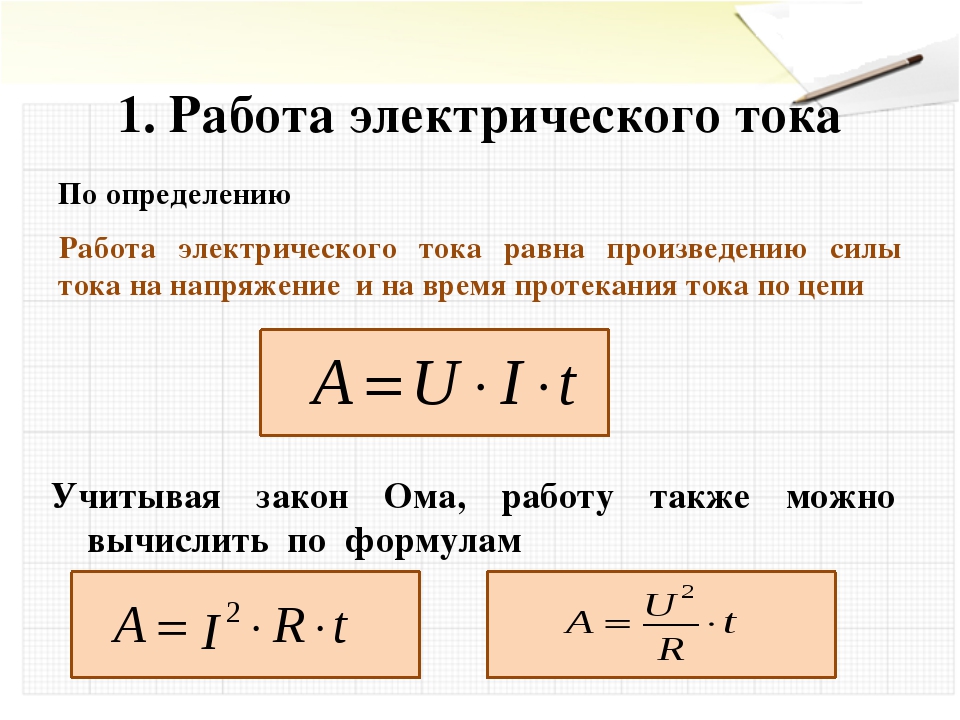 Расстояние между ними 1 м, и находятся они в вакууме. Сила тока в них одинакова.
Расстояние между ними 1 м, и находятся они в вакууме. Сила тока в них одинакова.
За единицу силы тока принимают силу тока, при которой отрезки таких параллельных проводников длиной 1 м взаимодействуют с силой 2 • 10-7 Н (0,0000002 Н).
Эту единицу силы тока называют ампером (А). Так она названа в честь французского учёного Андре Ампера.
Применяют также дольные и кратные единицы силы тока: миллиампер (мА), микроампер (мкА), килоампер (кА).
1мА = 0,001 А;
1 мкА = 0,000001 А;
1кА=1000А.
Чтобы представить себе, что такое ампер, приведём примеры: сила тока в спирали лампы карманного фонаря 0,25 А = 250 мА. В осветительных лампах, используемых в наших квартирах, сила тока составляет от 7 до 400 мА (в зависимости от мощности лампы).
Через единицу силы тока — 1 А определяется единица электрического заряда — 1 Кл, о которой было сказано в § 28.
Так как I = q/t, то q = It. Полагая I = 1 А, t = 1 с, получим единицу электрического заряда — 1 Кл.
1 кулон = 1 ампер • 1 секунду,
или
1Кл = 1А • 1с = 1А • с.
За единицу электрического заряда принимают электрический заряд, проходящий сквозь поперечное сечение проводника при силе тока 1 Аза время 1 с.
Из формулы q = It следует, что электрический заряд, проходящий через поперечное сечение проводника, зависит от силы тока и времени его прохождения. Например, в осветительной лампе, в которой сила тока равна 400 мА, сквозь поперечное сечение спирали за 1 мин проходит электрический заряд, равный 24 Кл.
Электрический заряд имеет также другое название — количество электричества.
Сила тока в различных потребителях электроэнергии
Вопросы
- От чего зависит интенсивность действий электрического тока?
- Какой величиной определяется сила тока в электрической цепи?
- Как выражается сила тока через электрический заряд и время?
- Что принимают за единицу силы тока? Как называется эта единица?
- Какие дольные и кратные амперу единицы силы тока вы знаете?
- Как выражается электрический заряд (количество электричества) через силу тока в проводнике и время его прохождения?
Упражнение 24
- Выразите в амперах силу тока, равную 2000 мА; 100 мА; 55 мА; 3 кА.

- Сила тока в цепи электрической плитки равна 1,4 А. Какой электрический заряд проходит через поперечное сечение её спирали за 10 мин?
- Сила тока в цепи электрической лампы равна 0,3 А. Сколько электронов проходит через поперечное сечение спирали за 5 мин?
Где может пригодиться этот закон Джоуля-Ленца?
В электротехнике есть понятие длительно допустимого тока протекающего по проводам. Это такой ток, который провод способен выдержать длительное время (то есть, бесконечно долго), без разрушения провода (и изоляции, если она есть, потому что провод может быть и без изоляции). Конечно, данные вы теперь можете взять из ПУЭ (Правила устройства электроустановок), но получали эти данные исключительно на основе закона Джоуля-Ленца.
В электротехнике так же используются плавкие предохранители. Их основное качество – надёжность срабатывания. Для этого используется проводник определенного сечения. Зная температуру плавления такого проводника можно вычислить количество теплоты, которое необходимо, чтобы проводник расплавился от протекания через него больших значений тока, а вычислив ток, можно вычислить и сопротивление, которым такой проводник должен обладать. В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.
В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.
А ещё, помните, мы говорили про . Там на примере лампочки я рассказывал парадокс, что более мощная лампа в последовательном соединении светит слабее. И наверняка помните почему: падение напряжения на сопротивлении тем сильнее, чем меньше сопротивление. А поскольку мощность — это , а напряжение очень сильно падает, то и выходит, что большое сопротивление выделит большое количество тепла, то есть, току придется больше потрудиться, чтобы преодолеть большое сопротивление. И количество тепла, которое выделит ток при этом можно посчитать с помощью закона Джоуля-Ленца. Если брать последовательное соединение сопротивлений, то использовать лучше выражение через квадрат тока, то есть, изначальный вид формулы:
А для параллельного соединения сопротивлений, поскольку ток в параллельных ветвях зависит от сопротивления, в то время, как напряжение на каждой параллельной ветви одинаковое, то формулу лучше всего представить через напряжение:
Примерами работы закона Джоуля-Ленца вы все пользуетесь в повседневной жизни – в первую очередь это всевозможные нагревательные приборы. Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.
В общем, несмотря на кажущуюся простоту, закон Джоуля-Ленца играет в нашей жизни очень огромную роль. Этот закон дал большой толчок для теоретических расчётов: выделение тепла токами , вычисление конкретной температуры дуги, проводника и любого другого электропроводного материала, потери электрической мощности в тепловом эквиваленте и т.д.
Вы можете спросить, а как перевести Джоули в Ватты и это довольно частый вопрос в интернете. Хотя вопрос несколько неверный, читая далее, вы поймёте почему. Ответ довольно прост: 1 дж = 0.000278 Ватт*час, в то время, как 1 Ватт*час = 3600 Джоулей. Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.
Думаю, что теперь вам не составит труда применить закон Джоуля-Ленца в практике и теории, если таковое потребуется и даже сделать перевод Джоулей в Ватты и наоборот. А благодаря пониманию, что закон Джоуля-Ленца это произведение электрической мощности на время, вы сможете более легко его запомнить и даже, если вдруг забыли основную формулу, то помня всего лишь закон Ома можно снова получить закон Джоуля-Ленца. А я на этом с вами прощаюсь.
А я на этом с вами прощаюсь.
Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.
Как зависит сила тока в проводнике от сопротивления этого проводника
Различные действия тока, такие, как нагревание проводника, магнитные и химические действия, зависят от силы тока. Изменяя силу тока в цепи, можно регулировать эти действия. Но чтобы управлять током в цепи, надо знать, от чего зависит сила тока в ней. Мы знаем, что электрический ток в цепи — это упорядоченное движение заряженных частиц в электрическом поле. Чем сильнее действие электрического поля на эти частицы, тем, очевидно, и больше сила тока в цепи. Но действие поля характеризуется физической величиной — напряжением. Поэтому можно предположить, что сила тока зависит от напряжения. Установим, какова эта зависимость, на опыте.
Установим, какова эта зависимость, на опыте.
На рисунке изображена электрическая цепь, состоящая из источника тока — аккумулятора, амперметра, спирали из никелиновой проволоки, ключа и параллельно присоединенного к спирали вольтметра. Замыкают цепь и отмечают показания приборов. Затем присоединяют к первому аккумулятору второй такой же аккумулятор и снова замыкают цепь. Напряжение на спирали при этом увеличится вдвое, и амперметр покажет вдвое большую силу тока. При трех аккумуляторах напряжение на спирали увеличивается втрое, во столько , же раз увеличивается сила тока. Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нем. Другими словами, сила тока в проводнике прямо пропорциональна напряжению на концах проводника. На рисунке показан график зависимости силы тока в проводнике от напряжения между концами этого проводника. На графике в условно выбранном масштабе по горизонтальной оси отложено напряжение в вольтах, а по вертикальной — сила тока в амперах.
Зависимость силы тока от напряжения мы уже установили. На основании опытов было показано, что сила тока в проводнике прямо пропорциональна напряжению на концах проводника
Следует обратить внимание, что при проведении опыта сопротивление проводника не менялось, одна и та же спираль служила участком цепи, на котором измеряли напряжение и силу тока. При проведении физических опытов, в которых определяют зависимость одной величины от другой, все остальные величины должны быть постоянными, если они будут изменяться, то установить зависимость будет сложнее
Поэтому, определяя зависимость силы тока от сопротивления, напряжение на концах проводника надо поддерживать постоянным. Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту. На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различными сопротивлениями. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже в таблице приведены результаты опытов с тремя различными проводниками: В первом опыте сопротивление проводника 1 Ом и сила тока в цепи 2 А. Сопротивление второго проводника 2 Ом, т.е. в два раза больше, а сила тока в два раза меньше. И наконец, в третьем случае сопротивление цепи увеличилось в четыре раза и во столько же раз уменьшилась сила тока. Напомним, что напряжение на концах проводников во всех трех опытах было одинаковое, равное 2 В. Обобщая результаты опытов, приходим к выводу: сила тока в проводнике обратно пропорциональна сопротивлению проводника.
За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже в таблице приведены результаты опытов с тремя различными проводниками: В первом опыте сопротивление проводника 1 Ом и сила тока в цепи 2 А. Сопротивление второго проводника 2 Ом, т.е. в два раза больше, а сила тока в два раза меньше. И наконец, в третьем случае сопротивление цепи увеличилось в четыре раза и во столько же раз уменьшилась сила тока. Напомним, что напряжение на концах проводников во всех трех опытах было одинаковое, равное 2 В. Обобщая результаты опытов, приходим к выводу: сила тока в проводнике обратно пропорциональна сопротивлению проводника.
Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома по имени немецкого ученого Ома, открывшего этот закон в 1827 г. Закон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению: I=U/R здесь I — сила тока в участке цепи, U — напряжение на этом участке, R — сопротивление участка. Закон Ома — один из основных физических законов. На рисунке зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах показана графически. На этом графике по горизонтальной оси в условно выбранном масштабе отложены сопротивления проводников в омах, по вертикальной — сила тока в амперах. Из формулы I=U/R — следует, что U=IR и R=U/I . Следовательно, зная силу тока и сопротивление, можно по закону Ома вычислить напряжение на участке цепи, а зная напряжение и силу тока — сопротивление участка. Сопротивление проводника можно определить по формуле R=U/I , однако надо понимать, что R — величина постоянная для данного проводника и не зависит ни от напряжения, ни от силы тока. Если напряжение на данном проводнике увеличится, например, в 3 раза, то во столько же раз увеличится и сила тока в нем, а отношение напряжения к силе тока не изменится.
Закон Ома — один из основных физических законов. На рисунке зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах показана графически. На этом графике по горизонтальной оси в условно выбранном масштабе отложены сопротивления проводников в омах, по вертикальной — сила тока в амперах. Из формулы I=U/R — следует, что U=IR и R=U/I . Следовательно, зная силу тока и сопротивление, можно по закону Ома вычислить напряжение на участке цепи, а зная напряжение и силу тока — сопротивление участка. Сопротивление проводника можно определить по формуле R=U/I , однако надо понимать, что R — величина постоянная для данного проводника и не зависит ни от напряжения, ни от силы тока. Если напряжение на данном проводнике увеличится, например, в 3 раза, то во столько же раз увеличится и сила тока в нем, а отношение напряжения к силе тока не изменится.
Источник
Вариант 2
1. Сила тока, идущего по проводнику, равна 2 А. Какой заряд проходит по проводнику за 10 минут?
1) 0,2 Кл
2) 5 Кл
3) 20 Кл
4) 1200 Кл
2. При увеличении напряжения U на участке электрической цепи сила тока I в цепи изменяется в соответствии с графиком (см. рисунок). Электрическое сопротивление на этом участке цепи равно
При увеличении напряжения U на участке электрической цепи сила тока I в цепи изменяется в соответствии с графиком (см. рисунок). Электрическое сопротивление на этом участке цепи равно
1) 2 Ом
2) 0,5 Ом
3) 2 мОм
4) 500 Ом
3. Если увеличить в 2 раза напряжение между концами проводника, а его длину уменьшить в 2 раза, то сила тока, протекающего через проводник
1) не изменится
2) уменьшится в 4 раза
3) увеличится в 4 раза
4) увеличится в 2 раза
4. Сопротивление участка цепи, изображенного на рисунке, равно
1) 11 Ом
2) 6 Ом
3) 4 Ом
4) 1 Ом
5. На цоколе лампы накаливания написано: «150 Вт, 220 В». Найдите силу тока в спирали при включении в сеть с номинальным напряжением
1) 0,45 А
2) 0,68 А
3) 22 А
4) 220 000 А
6. Проволочная спираль, сопротивление которой в нагретом состоянии равно 55 Ом, включена в сеть с напряжением 127 В. Какое количество теплоты выделяет эта спираль за 1 минуту?
1) 17,595 кДж
2) 20 кДж
3) 230 кДж
4) 658,5 кДж
7. Установите соответствие между физическими величинами и единицами измерения этих величин. К каждой позиции первого столбца подберите соответствующую позицию второго.
Установите соответствие между физическими величинами и единицами измерения этих величин. К каждой позиции первого столбца подберите соответствующую позицию второго.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) Сила тока
Б) Сопротивление
В) Работа электрического тока
ЕДИНИЦЫ ИЗМЕРЕНИЯ
1) Джоуль
2) Ватт
3) Вольт
4) Ампер
5) Ом
Запишите выбранные цифры под соответствующими буквами.
8. Электродвигатель подъемного крана подключен к источнику тока напряжением 380 В, при этом сила тока в обмотке 20 А. Определите КПД подъемного крана, если он поднимает груз массой 1 т на высоту 19 м за 50 с.
PunKot › Блог › Замер мультиметром напряжения аккумулятора и утечки тока в авто
Недавно я столкнулся с проблемами с аккумулятором — машина не заводится.Аккумулятор я купил новый, но все же захотел проверить машину — а вдруг утечка где есть. Захотеть-то — захотел, но как это сделать? Нашел в интернете я информацию и решил поделиться со всеми.Для этого нам понадобится мультимер. Самый распространенный и недорогой выглядит примерно так:
Самый распространенный и недорогой выглядит примерно так:
Для понятности я нашел картинку, где расписаны все значения мультиметра
Итак, приступим.1) Замер напряжения аккумулятораДля измерения напряжение с помощью мультиметра, необходимо включить его в режим измерения постоянного напряжения, при этом диапазон установить выше максимального значения напряжения на заряженном аккумуляторе, заряженный аккумулятор имеет около 12,7 вольт, поэтому выбираем — DCV, 20 вольт. Далее нужно подключить черный щуп мультиметра на минус аккумулятора, красный щуп на плюс АКБ и снять показания с дисплея мультиметра.
Теперь перейдем к утечке тока.В любой машине есть минимальный ток утечки (порядка 50-80мА.)Охранная сигнализация обычно потребляет около 20–25 мА, память контроллера системы впрыска – 5 мА, память магнитолы – 3 мА, так же потребляет ток приборка и блок центрального замка. В итоге получается около 60мА. С такими затратами тока аккумулятор прослужит несколько лет, не подводя хозяина. Но если утечка тока составляет больше чем 60-80мА, тогда аккумулятор будет быстро садится.
Но если утечка тока составляет больше чем 60-80мА, тогда аккумулятор будет быстро садится.
2) Замер утечки токаДля начала нужно Мультиметр поставить в режим измерения тока на 10 или 20 Ампер.
Как определить утечку тока в разрыв массы:Снимаем «-» клемму с АКБОдин из провод амперметра подключаем к «-» АКБДругой на снятый провод (полярность на цифровом мультиметре не имеет значения)
Как определить утечку тока в разрыв плюса:Отключите плюсовую клемму от аккумулятораПодключите амперметр минусовой клеммой — к контактной клемме автомобиляПлюсовой клеммой — к АКБ
Технология определения утечки тока:Подготовьте автомобиль к тестированию (отключите магнитолу, габариты, освещение в салоне и т.д.)Через минуту подключите амперметр в разрыв цепи и снимите показания (особенность автосигнализаций такова, что они становятся на охрану не раньше чем через минуту)Как увидели на амперметре ток утечки, то начинаем вытаскивать и ставить обратно по порядку предохранители и реле — станет понятно какая цепь дает утечку, когда ток придет в норму.
Надеюсь моя запись поможет кому-то и избавит от необходимости листать интернет в поисках информации.Здесь рассмотрены только основные моменты работы с мультиметром и аккумулятором авто. А возможности мультиметра очень обширны, не зря его назвали МУЛЬТИ, что значит много.
Работа тока
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Эту работу принято называть работой тока.
Если за промежуток времени Δt через поперечное сечение произвольного участка проводника проходит заряд Δq, то электрическое поле за это время совершит работу (см. § 1.19)
А = AqU,
где U — напряжение на концах проводника. Так как сила тока
Работа тока на участке цепи равна произведению силы тока, напряжения на этом участке и времени, в течение которого совершалась работа.
Согласно закону сохранения энергии эта работа должна быть равна изменению энергии рассматриваемого участка цепи. Поэтому энергия, выделяемая на данном участке цепи за время Δt, равна работе тока .
Если в формуле (2.7.1) выразить либо напряжение через силу тока (U = IR), либо силу тока через напряжение то получим еще две формулы для работы тока:
Формула (2.7.1) является универсальной, так как для ее вывода мы пользовались только законом сохранения энергии, который справедлив во всех случаях. Формулы (2.7.2) и (2.7.3) получены из формулы (2.7.1) с помощью закона Ома для однородных участков цепи. Поэтому эти формулы справедливы только в том случае, когда работа тока полностью идет на увеличение внутренней энергии проводника.
Формулой (2.7.2) удобно пользоваться при последовательном соединении проводников, так как сила тока в этом случае одинакова во всех проводниках. Формула (2.7.3) удобна при параллельном соединении проводников, так как напряжение на всех проводниках одинаково.
Переменный ток | Формулы по физике
Электродвижущая сила переменного тока
Найти
Известно, что:
εBSω =
Вычислить ‘ε’Электродвижущая сила переменного тока
Найти
Известно, что:
eε_msinωt =
Вычислить ‘e’Максимальная сила переменного тока
Найти
Известно, что:
I_mε_mR =
Вычислить ‘I_m’Действующее (эффективное) значение силы переменного тока
Известно, что:
I_efI_m =
Вычислить ‘I_ef’Средняя мощность переменного тока
Найти
Известно, что:
p_средI_mR =
Вычислить ‘p_сред’Действующее (эффективное) значение напряжения переменного тока
Найти
Известно, что:
U_efU_m =
Вычислить ‘U_ef’Напряжение переменного тока
Найти
Известно, что:
UU_mcosωt =
Вычислить ‘U’Максимальная сила переменного тока
Найти
Известно, что:
I_mU_mCω =
Вычислить ‘I_m’Ёмкостное сопротивление
Найти
Известно, что:
X_cCω =
Вычислить ‘X_c’Сила и ёмкостное сопротивление переменного тока
Найти
Известно, что:
IUX_c =
Вычислить ‘I’Сила и индуктивное сопротивление переменного тока
Найти
Известно, что:
IUX_L =
Вычислить ‘I’Индуктивное сопротивление
Найти
Известно, что:
X_LωL =
Вычислить ‘X_L’Закон Ома для цепи переменного тока
Найти
Известно, что:
XRX_LX_C =
Закон Ома для цепи переменного тока
Найти
Известно, что:
XRωLC =
Вычислить ‘X’Сдвиг фаз между током и напряжением переменного тока
Найти
Известно, что:
φX_LX_CR =
Вычислить ‘φ’Резонанс в цепи переменного тока
Известно, что:
UILC =
Вычислить ‘U’Первая формула трансформатора: напряжение
Найти
Известно, что:
U1U2N1N2 =
Вычислить ‘U1’Вторая формула трансформатора: сила тока
Найти
Известно, что:
I1I2N2N1 =
определение определение силы электрического тока
Электричество давно стало незаменимым спутником всего человечества. Но для большинства обывателей оно представляет собой какое-то абстрактное понятие, с которым сложно разобраться и тем более понять. Но нет нечего сложного для усвоения. Простыми словами электричество можно охарактеризовать как упорядоченное перемещение заряженных частиц.
Но для большинства обывателей оно представляет собой какое-то абстрактное понятие, с которым сложно разобраться и тем более понять. Но нет нечего сложного для усвоения. Простыми словами электричество можно охарактеризовать как упорядоченное перемещение заряженных частиц.
Определяющими характеристиками электрической энергии являются напряжение, сила тока и сопротивление. Рассмотрим более подробно что это за характеристики их определения, способы измерений и вычислений.
Определение силы электрического тока в электроцепи
Электрический ток, как говорилось выше, представляет собой упорядоченное перемещение заряженных частиц от одного электрода к другому. В металлах это электроны, в жидкостях – ионы, а их количество принято именовать зарядом. Одной из ключевых характеристик электротока является его сила или собственно отношение общего количества заряда к временному отрезку за который он проходит через отдельный участок.
Следовательно, определение силы тока в электроцепи или его величины можно выразить формулой:
I=q/t
q – количество заряда, а t – промежуток времени за которое он проходит этот определенный участок. В системе измерений СИ для определения единицы силы тока применяется ампер (сокращенно – «А»).
В системе измерений СИ для определения единицы силы тока применяется ампер (сокращенно – «А»).
Зависимость силы тока от напряжения и сопротивления
Когда разговор заходит о токе, то наиболее часто речь идет о напряжении. В системе СИ оно обозначается в вольтах (В). Для общего понимания определения напряжения рассмотрим физику формирования электричества в общем. В двух словах это процесс выглядит следующим образом. Из одного места извлекаются электроны, тем самым создавая разряжение. В другой точке они накапливаются, образуя избыток, который стремится занять освободившееся место. Таким образом образуются отрицательный и положительный потенциал, разница между ними и будет являться искомым напряжением в электрической сети. Для определения величины напряжения применяется специальный измерительный прибор – вольтметр.
Для того чтобы определить силу тока, зная напряжение, необходимо ввести еще одно понятие – сопротивление электроцепи. Оно в упрощенном понимании представляет собой некую силу, затрудняющую движение электронов от одного электрода к другому. Измеряется сопротивление в омах. Определить его величину можно омметром. Воедино понятия напряжение, силы тока и сопротивления связывает закон Ома. Он является одним из основополагающих при расчете любой электрической схемы.
Измеряется сопротивление в омах. Определить его величину можно омметром. Воедино понятия напряжение, силы тока и сопротивления связывает закон Ома. Он является одним из основополагающих при расчете любой электрической схемы.
Величина силы тока. Определение в зависимости от напряжения и сопротивления.
Закон Ома относительно применения к участку цепи определяет силу тока как величину пропорционально обратную сопротивлению и прямо сопоставимую разности потенциалов. Соответствующая формула выглядит следующим образом:
I=U/R, в которой: R (Ом)– сопротивление на участке электрической схемы, а U(В) – напряжение или разность потенциалов на электродах.
Из уравнения видно, что при наличии стабильного напряжения в электроцепи сила тока будет снижаться при увеличении нагрузочного сопротивления. Эта закономерность привела к тому, что последовательное включение потребителей применяется очень редко. При параллельном включении нагрузки величина силы тока на отельных участках может быть разной (в зависимости от сопротивления), но на входе, в точке соединения она останется прежней.
Сила тока и его плотность
Одно из важных понятий в электротехнике является плотность электрического тока, которая характеризуется его силой по отношению к площади приложения. В системе СИ плотность тока обозначается буквой «J», единица измерения — А/мм2. Общий вид формулы следующий:
J= I/S, где I – сила в амперах, а S – площадь поперечного сечения провода в квадратных мм.
Следовательно, с точки зрения физики, плотность тока — это количество заряда, перемещаемого через единицу площади за определенное время Одним словом эта величина описывает степень электрической нагрузки на проводник и является одной из определяющих при выборе кабельной продукции соответствующего диаметра.
Плотность играет важную роль, т.к. любой элемент сети в т.ч. и токопроводящий провод обладает собственным сопротивлением. Следствием потери тока является нагрев проводника. Значительные потери могут привести к перегреву, вплоть до расплавления изоляции или материала жил.
В заключение отметим, что данные определения силы тока, через основные характеристики носят общий характер. В частных случаях используются дополнительные данные которые влияют на точность вычислений, но не искажают обобщенного представления о физики электричества и взаимосвязи значений.
В частных случаях используются дополнительные данные которые влияют на точность вычислений, но не искажают обобщенного представления о физики электричества и взаимосвязи значений.
Закон ома все формулы
Главная » Разное » Закон ома все формулы
Закон Ома — формулировка простыми словами, определение
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.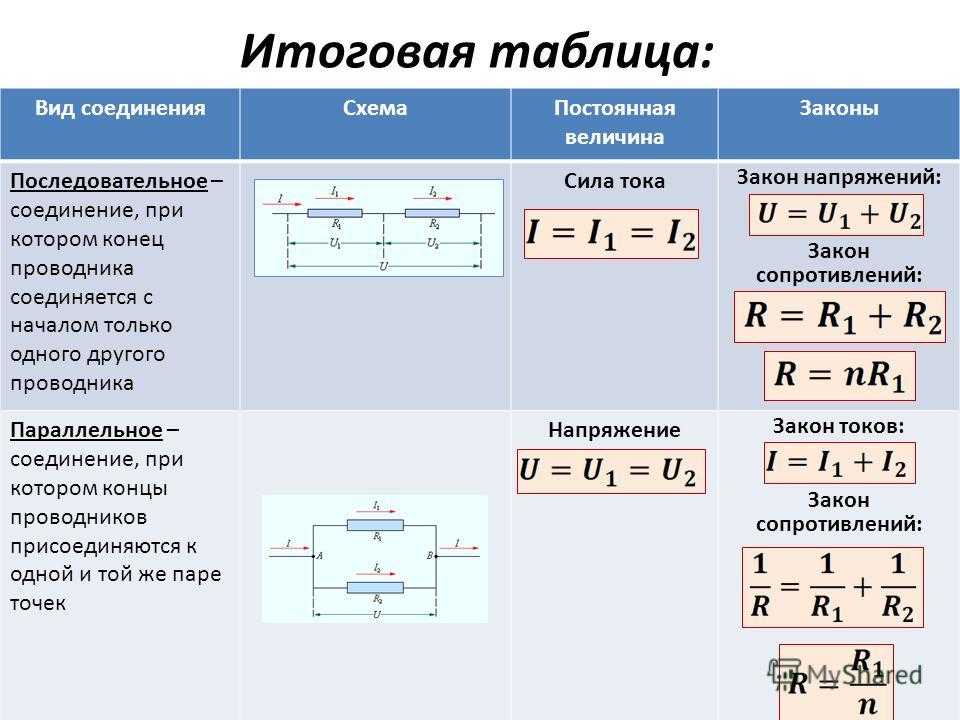
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника
— это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Таблица удельных сопротивлений различных материалов
Материал | Удельное сопротивление ρ, Ом · мм2/м |
Алюминий | 0,028 |
Бронза | 0,095–0,1 |
Висмут | 1,2 |
Вольфрам | 0,05 |
Железо | 0,1 |
Золото | 0,023 |
Иридий | 0,0474 |
Константан (сплав NiCu + Mn) | 0,5 |
Латунь | 0,025–0,108 |
Магний | 0,045 |
Манганин (сплав меди марганца и никеля — приборный) | 0,43–0,51 |
Медь | 0,0175 |
Молибден | 0,059 |
Нейзильбер (сплав меди, цинка и никеля) | 0,2 |
Натрий | 0,047 |
Никелин (сплав меди и никеля) | 0,42 |
Никель | 0,087 |
Нихром (сплав никеля, хрома, железа и марганца) | 1,05–1,4 |
Олово | 0,12 |
Платина | 0,107 |
Ртуть | 0,94 |
Свинец | 0,22 |
Серебро | 0,015 |
Сталь | 0,103–0,137 |
Титан | 0,6 |
Хромаль | 1,3–1,5 |
Цинк | 0,054 |
Чугун | 0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее.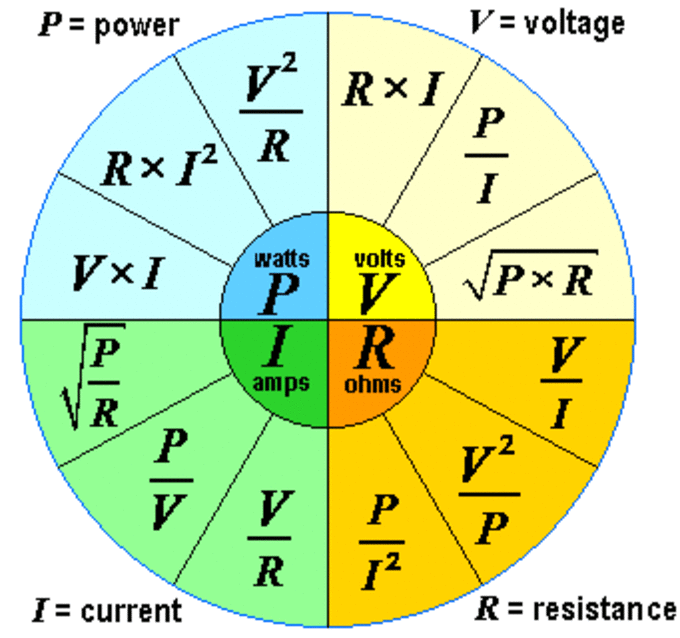 В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.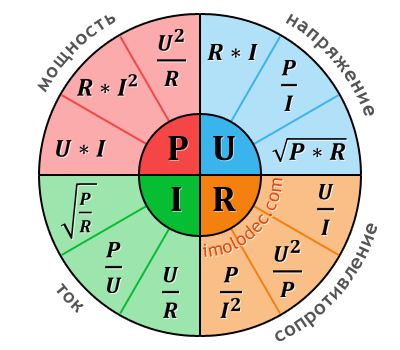
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.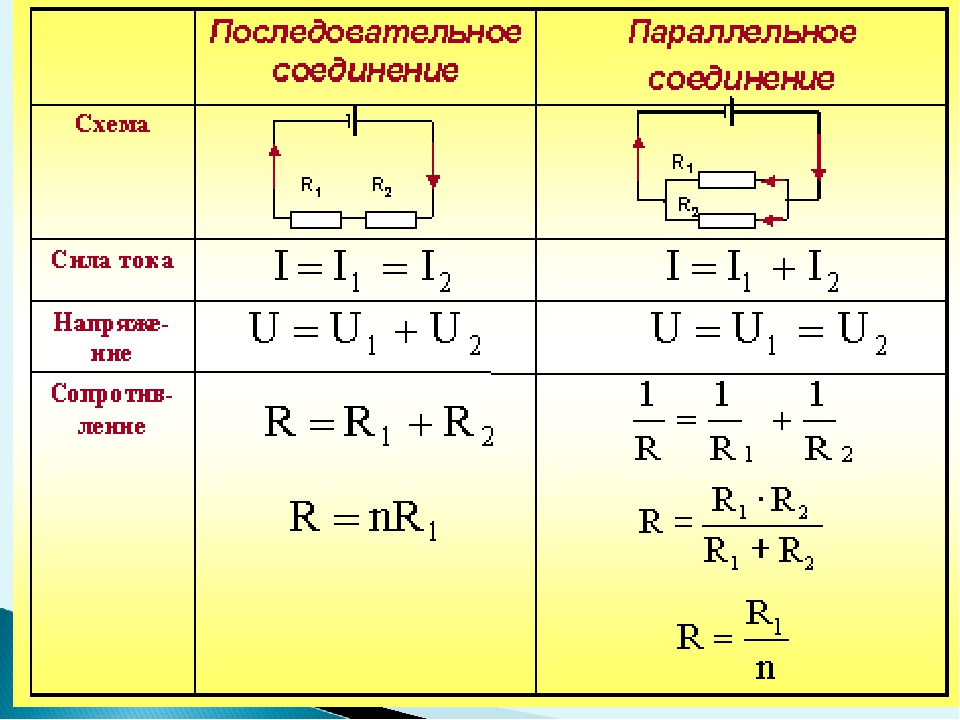
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
Закон Ома для полной цепи I — сила тока [A] ε — ЭДС [В] R — сопротивление нагрузки [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно.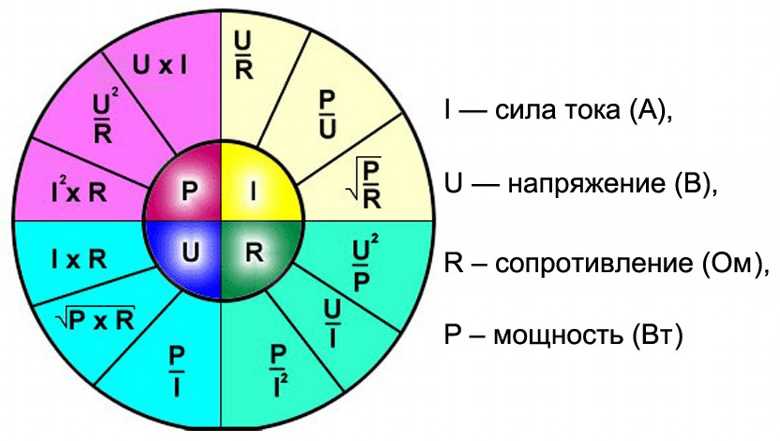
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
| Fluke
Talk to a Fluke sales expert
Связаться с Fluke по вопросам обслуживания, технической поддержки и другим вопросам»
What is your favorite color?
Имя *
Фамилия *
Электронная почта *
Компания *
Номер телефона *
Страна * — Пожалуйста, выберите значение -United States (Estados Unidos)CanadaAfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAzerbaijanBahamasBahrainBangladeshBarbadosБеларусь (Belarus)Belgien/Belgique (Belgium)BelizeBeninBermudaBhutanBoliviaBonaireBosnia and HerzegovinaBouvet IslandBotswanaBrasil (Brazil)British Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCape VerdeCayman IslandsCentral African RepublicČeská republika (Czech Republic)ChadChile中国 (China)Christmas IslandCittà Di VaticanCocos (Keeling) IslandsCook IslandsColombiaComorosCongoThe Democratic Republic of CongoCosta RicaCroatiaCyprusCôte D’IvoireDanmark (Denmark)Deutschland (Germany)DjiboutiDominicaEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEspaña (Spain)EstoniaEthiopiaFaroese FøroyarFijiFranceFrench Southern TerritoriesFrench GuianaGabonGambiaGeorgiaGhanaGilbralterGreeceGreenlandGrenadaGuatemalaGuadeloupeGuam (USA)GuineaGuinea-BissauGuyanaHaitiHeard Island and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIraqIrelandIsraelIslas MalvinasItalia (Italy)Jamaica日本 (Japan)JordanKazakhstanKenyaKiribati대한민국 (Korea Republic of)KuwaitKyrgyzstanLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMéxico (Mexico)MicronesiaMoldovaMonacoMongoliaMontenegroMonserratMoroccoMozambiqueMyanmarNamibiaNauruNederland (Netherlands)Netherlands AntillesNepalNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorge (Norway)Norfolk IslandNorthern Mariana IslandsOmanÖsterreich (Austria)PakistanPalauPalestinePanamaPapua New GuineaParaguayPerú (Peru)PhilippinesPitcairn IslandPuerto RicoРоссия (Russia)Polska (Poland)Polynesia (French)PortugalQatarRepública Dominicana (Dominican Republic)RéunionRomânia (Romania)RwandaSaint HelenaSaint Pierre and MiquelonSaint Kitts and NevisSaint LuciaSaint Vincent and The GrenadinesSan MarinoSao Tome and PrincipeSaudi ArabiaSchweiz (Switzerland)SenegalSerbiaSeychellesSierra LeoneSingaporeSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and The South Sandwich IslandsSouth SudanSri LankaSudanSuomi (Finland)SurinameSvalbard and Jan MayenSverige (Sweden)SwazilandTaiwanTajikistanTanzaniaThailandTimor-LesteTokelauTogoTongaTrinidad and TobagoTunisiaTürkiye (Turkey)TurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUnited States Minor Outlying IslandsUruguayUzbekistanVanuatuVirgin Islands (British)Virgin Islands (USA)VenezuelaVietnamWallis and FutunaWestern SaharaWestern SamoaYemenZambiaZimbabwe
Почтовый индекс *
Интересующие приборы
iGLastMSCRMCampaignID
?Отмечая галочкой этот пункт, я даю свое согласие на получение маркетинговых материалов и специальных предложений по электронной почте от Fluke Electronics Corporation, действующей от лица компании Fluke Industrial или ее партнеров в соответствии с политикой конфиденциальности.
consentLanguage
Политика конфиденциальности
Формула закона Ома
ОПРЕДЕЛЕНИЕ
Сила тока в проводнике равна разности потенциалов (напряжению) между концами проводника, делённой на сопротивление проводника.
Здесь – сила тока, – напряжение, – сопротивление. Это равенство называют законом Ома для участка цепи.
Единица измерения силы тока – А (ампер).
Указанная формула верна для участка цепи, в котором напряжение постоянно (сила тока тоже будет постоянной). Для полной цепи формула усложняется:
Где – электродвижущая сила (ЭДС) источника питания, – внутреннее сопротивление источника питания, а – сопротивление всех внешних элементов цепи. Это равенство называют законом Ома для полной цепи. Из этой формулы следует, что ЭДС источника равна сумме падений напряжения в самом источнике и во внешней цепи.
Примеры решения задач по теме «Закон Ома»
ПРИМЕР 1
| Задание | Найти силу тока, если напряжение на участке цепи с сопротивление 5 кОм равно 100 В. |
| Решение | Напомним, что 5 кОм = 5 000 Ом. Подставим численные значения в формулу:
|
| Ответ | Сила тока в цепи равна 0,02 ампера. |
| Понравился сайт? Расскажи друзьям! | |||
Закон Ома для участка цепи. Определение, формула расчета, калькулятор
В 1827 году Георг Ом опубликовал свои исследования, которые составляют основу формулы, используемую и по сей день. Ом выполнил большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.
Этот закон является эмпирическим, то есть основанный на опыте. Обозначение «Ом» принято в качестве официальной единицы СИ для электрического сопротивления.
Закон Ома для участка цепи гласит, что электрический ток в проводнике прямо пропорционален разности потенциалов в нем и обратно пропорционален его сопротивлению. Принимая во внимание, что сопротивление проводника (не путать с удельным сопротивлением) величина постоянная, можно оформить это следующей формулой:
Принимая во внимание, что сопротивление проводника (не путать с удельным сопротивлением) величина постоянная, можно оформить это следующей формулой:
где
- I — тока в амперах (А)
- V — напряжение в вольтах (В)
- R — сопротивления в омах (Ом)
Для наглядности: резистор имеющий сопротивление 1 Ом, через который протекает ток силой в 1 А на своих выводах имеет разность потенциалов (напряжение) в 1 В.
Немецкий физик Кирхгоф (известен своими правилами Кирхгофа) сделал обобщение, которое больше используется в физике:
Набор для Arduino
Cтартовый набор Keyestudio Super с платой V4.0 для Arduino…
где
- σ – проводимость материала
- J — плотность тока
- Е — электрическое поле.
Закон Ома и резистор
Резисторы являются пассивными элементами, которые оказывают сопротивление потоку электрического тока в цепи. Резистор, который функционирует в соответствии с законом Ома, называется омическим сопротивлением. Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.
Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.
Формула Ома остается справедливой и для цепей с переменным напряжением и током. Для конденсаторов и катушек индуктивности закон Ома не подходит, так как их ВАХ (вольт-амперная характеристика) по сути, не является линейной.
Формула Ома действует так же для схем с несколькими резисторами, которые могут быть соединены последовательно, параллельно или иметь смешанное соединение. Группы резисторов, соединенные последовательно или параллельно могут быть упрощены в виде эквивалентного сопротивления.
В статьях о параллельном и последовательно соединении более подробно описано как это сделать.
Немецкий физик Георг Симон Ом опубликовал в 1827 свою полную теорию электричества под названием «теория гальванической цепи». Он нашел, что падение напряжения на участке цепи является результатом работы тока, протекающего через сопротивление этого участка цепи.
Это легло в основу закона, который мы используем сегодня. Закон является одним из основных уравнений для резисторов.
Закон Ома — формула
Формула закона Ома может быть использована, когда известно две из трех переменных. Соотношение между сопротивлением, током и напряжением может быть записано по-разному. Для усвоения и запоминания может быть полезен «треугольник Ома».
или
или
Ниже приведены два примера использования такого треугольного калькулятора.
| Имеем резистор сопротивлением в 1 Ом в цепи с падением напряжения от 100В до 10В на своих выводах. Какой ток протекает через этот резистор? Треугольник напоминает нам, что: | |
Имеем резистор сопротивлением в 10 Ом через который протекает ток в 2 Ампера при напряжении 120В. Какое будет падение напряжения на этом резисторе? Использование треугольника показывает нам, что:Таким образом, напряжение на выводе будет 120-20 = 100 В. |
Закон Ома — мощность
Когда через резистор протекает электрический ток, он рассеивает определенную часть мощности в виде тепла.
Мощность является функцией протекающего тока I (А) и приложенного напряжения V (В):
где
- Р — мощность в ваттах (В)
В сочетании с законом Ома для участка цепи, формулу можно преобразовать в следующий вид:
или
Идеальный резистор рассеивает всю энергию и не сохраняет электрическую или магнитную энергию. Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной.
Окружающие условия могут снизить или повысить это значение. Например, если окружающий воздух горячий, то способность рассеять излишнее тепло у резистора снижается, и на оборот, при низкой температуре окружающего воздух рассеиваемая способность резистора возрастает.
На практике, резисторы редко имеют обозначение номинальной мощности. Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.
Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.
Ниже приведена круговая диаграмма, которая поможет вам быстро определить связь между мощностью, силой тока, напряжением и сопротивлением. Для каждого из четырех параметров показано, как вычислить свое значение.
Закон Ома — калькулятор
Данный онлайн калькулятор закона Ома позволяет определить взаимосвязь между силой тока, электрическим напряжением, сопротивлением проводника и мощностью. Для расчета введите любые два параметра и нажмите кнопку расчет:
Для закрепления понимания работы закона Ома, приведем несколько задач для самостоятельного решения.
Основные электрические законы. Базовые формулы и расчеты
В предыдущей статье мы познакомились с основными электрическими понятиями, такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.
Закон Ома
Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома. В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:
«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».
Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.
Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:
В предыдущей статье мы проводили аналогию между электричеством и водой, и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:
На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).
Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.
Последовательное подключение – последовательная цепь
При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).
А закон Ома в последовательной цепи будет иметь вид:
При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:
Параллельное подключение – параллельная цепь
При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.
Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:
При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».
Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:
Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:
Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.
Электрическая мощность
Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:
Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно подобрать и заменить проволоку.
Применив закон Ома, можно рассчитать мощность и по другой формуле:
При расчетах надо учитывать, что часть потребляемой электроэнергии расходуется на нагрев и преобразуется в тепло. При работе греются не только электрообогреватели, но и телевизоры, и компьютеры и другая бытовая техника.
И в завершение, в качестве бонуса, вот такая шпаргалка, которая поможет определить любой из основных электрических параметров, по уже известным.
формулировка простыми словами, формула для первого, второго и третьего
Есть такие формулы и законы, которые люди узнают еще в школе, а помнят всю жизнь. Обычно это несложные уравнения, состоящие из двух-трех физических величин и объясняющие какие-то фундаментальные вещи в науке, основу основ. Закон Ома как раз такая штука.
Закон Ома: кто придумал, определение
Закон Ома — это основной закон электродинамики, который выводит взаимосвязь между ключевыми понятиями электрической цепи: силой тока, напряжением и сопротивлением.
Данную взаимозависимость выявил немецкий физик Георг Симон Ом в 1826 году. Несмотря на то, что этот закон является истинным законом природы, точность которого была многократно проверена и доказана позже, публикация работы Ома в 1827 году прошла незамеченной для научной общественности. И лишь в 1830-х гг., когда французский физик Пулье пришел к тем же самым выводам, что и Ом, работа немецкого ученого была оценена по достоинству.
И лишь в 1830-х гг., когда французский физик Пулье пришел к тем же самым выводам, что и Ом, работа немецкого ученого была оценена по достоинству.
Установление закономерностей между основными параметрами электроцепи имеет огромное значение для науки. Ведь оно позволило количественно измерить свойства электрического тока.
Источник: rusenergetics.ru
Формулировки и основные формулы
Закон Георга Ома формулируется так: сила тока в проводнике прямо пропорциональна напряжению в проводнике и обратно пропорциональна сопротивлению этого проводника.
Пояснения к закону:
- Чем выше напряжение в проводнике, тем выше будет и сила тока в этом проводнике.
- Чем выше сопротивление проводника, тем меньше будет сила тока в нем.
Обозначение основных параметров, характеризующих электроцепь, известны всем с уроков физики в школе:
- I — сила электротока;
- U — напряжение;
- R — сопротивление.

Объяснение закона Ома в классической теории
Формула закона, известная всем со школьных лет, выглядит так:
\(I=\frac UR\)
Из нее легко выводятся формулы для определения \(U\):
\(U\;=I\times R\)
и для определения \(R\):
\(R=\frac UI\)
Единицами измерения силы тока являются амперы, напряжения — вольты, сопротивление измеряется в омах.
Данный закон верен для линейного участка цепи, на котором зафиксировано стабильное сопротивление.
Источник: dzgo.ru
Закон Ома для полной (замкнутой) цепи
Замкнутой или полной называется такая электрическая цепь, по которой проходит электроток.
Описание формулы этого закона для полной цепи выглядит так:
\(I=\frac\epsilon{R+r}\)
где \(\epsilon\) — это электродвижущая сила или напряжение источника питания, которое не зависит от внешней цепи;
\(R\) — сопротивление внешней цепи;
\(r\) — внутреннее сопротивление источника.
Источник: multiurok.ru
Использование закона Ома при параллельном и последовательном соединении
При последовательном соединении элементы цепи подключаются друг за другом последовательно. Так как такая электрическая цепь является неразветвленной, сила тока на каждом ее участке будет одинаковая. Пример последовательного соединения — лампочки в новогодней гирлянде.
При последовательном соединении элементов основные параметры электроцепи рассчитываются следующим образом:
- Сила тока по формуле:
\(I=I_1=I_2=I_3\)
Где \(I\) — общая сила тока в электроцепи, \(I_1\) — сила тока первого участка, \(I_2\) — сила тока второго участка, \(I_3\) — сила тока третьего участка.
- Напряжение по формуле:
\(U=U_1+U_2+U_3\)
Где \(U\) — общее напряжение, \(U_1\) — напряжение первого участка, \(U_2\) — напряжение второго участка, \(U_3\) — напряжение третьего участка.
- Сопротивление согласно формуле:
\(R=R_1+R_2+R_3\)
Где \(R\) — общее сопротивление в цепи, \(R_1\) — сопротивление первого участка, \(R_2\) — сопротивление второго участка, \(R_3\) — сопротивление третьего участка.
Подключая элементы в цепь параллельно, получают разветвленную электрическую цепь. Примером такого соединения является стандартная разводка электричества по квартире, когда в комнате одновременно можно включить несколько предметов бытовой техники и верхнее освещение.
При параллельном соединении элементов основные параметры электроцепи рассчитываются следующим образом:
\(I=I_1+I_2+I_3\)
Где \(I\) — общая сила тока в электроцепи, \(I_1, I_2, I_3\) — сила тока первого, второго и третьего участков соответственно.
\(U=U_1=U_2+U_3\)
Где \(U\) — общее напряжение, \(U_1, U_2, U_3\) — напряжение первого, второго и третьего участков соответственно.
- Сопротивление:
\(R=\frac{R_1\times R_2\times R_3}{R_1+R_2+R_3}\)
Где \(R\) — общее сопротивление в цепи, \(R_1, R_2, R_3\) — сопротивление первого, второго и третьего участков соответственно.
Закон Ома для переменного и постоянного тока
Для цепи постоянного тока правильными будут уже озвученные нами взаимосвязи основных параметров электроцепи:
Источник: en.ppt-online.org
При подключении к электроцепи источника переменного тока, сила электротока в цепи будет определяться по формуле:
\(I=\frac UZ\)
где \(Z\) — полное сопротивление или импеданс, который состоит из активной \((R)\) и реактивных составляющих (\(X_C\) — сопротивление емкости и \(X_L\) — сопротивление индуктивности).
Реактивное сопротивление цепи зависит:
- от значений реактивных элементов,
- от частоты электротока;
- от формы тока в цепи.
Источник: fizikaotfizika.ru
Закон Ома для однородного и неоднородного участка цепи
Закон Ома для однородного участка электроцепи представляет собой классическое выражение зависимости силы от напряжения и сопротивления:
\(I=\frac UR\)
В этом случае основной характеристикой проводника является сопротивление. От внешнего вида проводника зависит, как выглядит его кристаллическая решетка и какое количество атомов примесей содержит. От проводника зависит поведение электронов, которые могут ускоряться или замедляться.
От внешнего вида проводника зависит, как выглядит его кристаллическая решетка и какое количество атомов примесей содержит. От проводника зависит поведение электронов, которые могут ускоряться или замедляться.
Поэтому \(R\) зависит от вида проводника, точнее, от его сечения, длины и материала и определяется по формуле:
\(R=p\times\left(\frac lS\right)\)
где \(p\) — удельное сопротивление, \( l\) — это длина проводника, а \(S\) — площадь его сечения.
Под неоднородным участком цепи постоянного тока подразумевается такой промежуток цепи, на который помимо электрических зарядов воздействуют другие силы.
Источник: grabachapter.com
Как можно было убедиться, закон, открытый Георгом Омом, прост только на первый взгляд. Разобраться во всех тонкостях самостоятельно под силу далеко не каждому. Если столкнулись с трудностями в учебе и сложными для понимания темами, обращайтесь за помощью к образовательному ресурсу Феникс. Хелп. Квалифицированные эксперты помогут сдать в срок самую сложную работу.
Хелп. Квалифицированные эксперты помогут сдать в срок самую сложную работу.
Электрический ток — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Электрический ток. Сила тока. Сопротивление
К оглавлению…
В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:
Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.
Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):
Если же ток равномерно меняется с течением времени от значения I1 до значения I2, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:
Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:
При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:
Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:
где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.
Сопротивление проводника зависит и от его температуры:
где: R0 – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.
Диод в цепи постоянного тока
Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:
Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.
Закон Ома. Последовательное и параллельное соединение проводников
К оглавлению…
Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.
Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.
У каждого способа есть свои закономерности.
1. Закономерности последовательного соединения:
Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
2. Закономерности параллельного соединения:
Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:
Электроизмерительные приборы
Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.
Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.
Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.
ЭДС. Закон Ома для полной цепи
К оглавлению…
Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:
Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.
Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:
Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.
Несколько источников ЭДС в цепи
Если в цепи присутствует несколько ЭДС подключенных последовательно, то:
1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:
Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.
2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:
В обоих случаях общее сопротивление источников увеличивается.
При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:
В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.
Работа и мощность тока. Закон Джоуля-Ленца
К оглавлению…
Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):
Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж.Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:
Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).
Энергобаланс замкнутой цепи
К оглавлению…
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
К оглавлению. ..
..
Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.
Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.
Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.
Это явление называется электролитической диссоциацией.
Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Электрический ток в газах и в вакууме
К оглавлению…
Электрический ток в газах
В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.
Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.
Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).
Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.
Электрический ток в вакууме
Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.
Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.
Что такое закон Ома?
Закон Ома — это формула, выражающая математическое соотношение между напряжением, током и сопротивлением в электрической цепи.
Закон Ома — это формула, которая выражает математическую зависимость между напряжением, током и сопротивлением в электрической цепи.
Для студентов-электронщиков закон Ома (U = IR) так же важен, как уравнение относительности Эйнштейна (E = mc²) для физиков.
U = I x R
В развернутом виде это означает напряжение = ток x сопротивление , т.е. вольт = ампер x ом , т.е. В = A x Ом .
Этот закон, открытый немецким физиком Георгом Омом (1789-1854), описывает основные величины цепей:
| Размер | Символ в законе Ома | Единица измерения | Единица измерения (аббревиатура ) В Circuits | Для любопытных: | |||
|---|---|---|---|---|---|---|---|
| напряжение | U | U | Вольт (V) | Вольт (V) | Вольт, что триггеры поток электронов | U = электромологическая сила (ранее использованный срок) | |
| Текущий | I | I | Ampere (A) | Электронный расход | I = Текущий | ||
| Сопротивление | R | Ом (Ω) | Ом (Ω) | ОМС | ω = Греческая омега |
Если известны два из этих значений, техники могут преобразовать закон Ома для вычисления третьего. Достаточно изменить пирамиду следующим образом:
Достаточно изменить пирамиду следующим образом:
Если нам известны напряжение (U) и ток (I), и мы хотим знать сопротивление (R), мы строим R из пирамиды и вычисляем полученную формулу ( см. первую пирамиду слева вверху).
Совет: Поскольку вы не можете измерить сопротивление цепи во время ее работы, закон Ома очень полезен, когда вам нужно его рассчитать. Вместо того, чтобы отключать цепь для измерения сопротивления, технический специалист может рассчитать R из приведенного выше преобразования закона Ома.
Если мы уже знаем напряжение (U) и сопротивление (R), но хотим узнать ток (I), мы наносим I из пирамиды и вычисляем два других символа (см. среднюю пирамиду выше).
А если мы знаем ток (I) и сопротивление (R), но хотим знать напряжение (U), то умножаем нижние половинки пирамиды на себя (см. первую пирамиду справа).
Попробуйте некоторые примеры расчетов на основе простой последовательной цепи только с одним источником напряжения (батарея) и сопротивлением (лампочка). В каждом из примеров известны два значения. Вычислите третью часть закона Ома.
В каждом из примеров известны два значения. Вычислите третью часть закона Ома.
Пример 1: напряжение (U) и сопротивление (R) известны.
Какой ток в цепи?
I = U / R = 12 В / 6 Ом = 2 А
Пример 2: напряжение (U) и ток (I) известны.
Каково сопротивление лампы?
R = U / I = 24 В / 6 A = 4 Ом
Пример 3: ток (I) и сопротивление (R) известны. Сколько напряжение?
Какое напряжение в цепи?
U = I x R = (5 А) (8 Ом) = 40 В
Когда Ом опубликовал свою формулу в 1827 году., его основной вывод заключался в том, что величина электрического тока, протекающего через проводник, составляет и прямо пропорциональна приложенному к нему напряжению. Другими словами, один вольт напряжения требуется для того, чтобы ток в один ампер проходил через сопротивление в один ом.
Что можно проверить с помощью закона Ома?
Закон Ома можно использовать для проверки статических значений компонентов схемы, уровней тока, источников напряжения и падений напряжения. Например, если измерительный прибор обнаруживает более высокий ток, чем обычно, это может быть уменьшение сопротивления или увеличение напряжения, что приводит к высокому напряжению в этой точке цепи.Это может указывать на проблемы с питанием или цепью.
Например, если измерительный прибор обнаруживает более высокий ток, чем обычно, это может быть уменьшение сопротивления или увеличение напряжения, что приводит к высокому напряжению в этой точке цепи.Это может указывать на проблемы с питанием или цепью.
Если измеренный ток в цепях постоянного тока ниже обычного, возможно падение напряжения или увеличение сопротивления цепи. Причинами повышенного сопротивления могут быть нестабильные или ослабленные соединения, коррозия и/или поврежденные компоненты.
Потребители в цепи потребляют электроэнергию. Приемниками могут быть любые элементы: мелкие электроприборы, компьютеры, предметы быта или большой двигатель.Большинство этих элементов (приемников) имеют паспортную табличку или информационную наклейку. Эти паспортные таблички содержат маркировку безопасности и множество справочных параметров.
Технические специалисты могут прочитать стандартные значения напряжения и силы тока на заводской табличке компонента. Если в ходе измерений технические специалисты обнаружат, что на их цифровом мультиметре или токоизмерительных клещах не отображаются обычные значения, они могут использовать закон Ома, чтобы определить, какая часть цепи выходит из строя и в чем может быть проблема.
Базовое знание цепей
Цепи, как и вся материя, состоят из атомов. Атомы состоят из субатомных частиц:
- протонов (положительно заряженных),
- нейтронов (без заряда),
- электронов (отрицательно заряженных).
Атомы в полной мере сохраняют силы притяжения между ядром атома и электронами на его внешних оболочках. Под действием напряжения атомы в цепи начинают перестраиваться, и их частицы создают потенциал притяжения, называемый разностью потенциалов.Свободные электроны притягиваются протонами и их движение создает поток электронов (ток). Любой материал в цепи, препятствующий этому потоку, считается сопротивлением.
Источник: Digital Multimeter Principles, Glen A. Mazur, American Technical Publishers.
Связанные статьи
.
Закон Ома
Закон Ома описывает ситуацию простейшего случая зависимость между напряжением, приложенным к проводнику (сопротивлению), и током ток через этот проводник.
Формулировка закона Ома
Коэффициент силы тока, протекающего через проводник для питья между его одеял является постоянным.
Возвышение по закону Ома — Пост 1
I — интенсивность сила тока (в системе СИ в амперах — А)
U — напряжение между концами проводника (в системе СИ в вольтах — В)
Ра к Закону Ома — Пост 2
В противном случае закон Ома также можно сформулировать в условное обозначение:
I ~ U (I пропорциональна U)
Ток, протекающий через проводник, пропорциональна приложенному напряжению.
Вольтовая характеристика заполняющего проводника Закон Ома
Вольтовая характеристика заполняющего проводника Закон Ома — прямая.
Интерпретация закона Ома
Закон Ома говорит нам, что интенсивность потока через токопровод точно «передаёт» после изменения напряжения. Когда напряжение увеличивается вдвое, то поток, вызванный этим напряжением ток будет в два раза выше при увеличении напряжения 5 раз, сила этого тока должна возрасти в 5 раз по отношению к к начальному значению.
Другими словами:
Ток, являющийся следствием приложенного напряжения, ведет себя пропорционально своей причине.
Некоторый материал удовлетворяет закону Ома — в основном металлами и керамикой. Однако есть много веществ, которым законы Ома не удовлетворяют, т. е. интенсивность течения они вызывают изменение тока непропорционально напряжению.
Когда выполняется закон Ома?
Закон Ома является законом материи (не универсальным), что означает, что e Работает только для определенных материалов — веществ.Кроме того этот закон сушится только при определенных напряжениях и при определенных напряжениях внешние условия (например, температура должна быть постоянной).
Закон Ома в значительной степени выполняется металлами и материалами керамический. Однако есть много веществ, для которых законы Ома не подчиняются. то есть сила тока, проходящего через них, изменяется некоторым образом непропорционально напряжению. Кроме того, закон Ома был применим существенно зависит от диапазона напряжения — например. в типичных ситуациях с малышами ток напряжения пропорционален напряжению, но после передачи в диапазоне высоких напряжений пропорциональность будет нарушаться. На чертеже характеристики материалов, которые не соответствуют, представлены ниже Закон Ома.
в типичных ситуациях с малышами ток напряжения пропорционален напряжению, но после передачи в диапазоне высоких напряжений пропорциональность будет нарушаться. На чертеже характеристики материалов, которые не соответствуют, представлены ниже Закон Ома.
Чертеж — пример характеристик НЕ соответствующих законодательству материалов Ом.
Материалы и не соответствующие законам Ома
К материалам, подчиняющимся закону Ома, относятся следующие проводники:
| металлы (напр.Медь, Золото, Серебро, Железо) | |
| Некоторые керамики | |
| Большинство электролитов |
NO Соответствует закону Ом:
| полупроводники | |
газы (хотя в определенных диапазонах напряжения они могут быть совместимы с этим закон). |
.
Закон Ома
Закон Ома
Сила электрического тока, протекающего по проводнику, прямо пропорциональна величине электрического напряжения на его концах и обратно пропорциональна сопротивлению проводника.
Интересные статьи по физике: Делитель напряжения Мост Уитстона
В приведенной выше схеме амперметр А фактически измеряет сумму тока I и тока, протекающего через вольтметр V, Однако из-за того, что внутреннее сопротивление вольтметра (по сравнению с сопротивлением R) очень велико (обычно несколько сотен кОм), ток, протекающий через вольтметр, ничтожен.
Закон Ома выражается формулой:
После преобразования этой формулы можно получить другие, эквивалентные формулы:
Закон Ома — пример упражнения
На клеммах резистора было измерено напряжение 4В. Каково его сопротивление R, если при этом известно, что через него протекает 2А?
Решение
Используя закон Ома, получаем:
R = U / I = 4V / 2A = 2 Ω
Постоянный ток
Закон Кулона
Подключение конденсатора
См.
 статьи, которые могут вас заинтересовать
статьи, которые могут вас заинтересоватьДобавить комментарий3: 9000 на статье.
Комментарии пользователей (5)
2012-08-23 16:36:54 Йорг писал(а):
Очень полезная статья.Спустя десятилетия после выпуска некоторые вещи забываются. Особенно, если вы механик, а не электрик.Спасибо за статью.
10.10.2012 17:26:38 Anonymous писал(а):
Это все шаблоны трансформировались?
2012-11-22 08:35:13 DAwid123 писал(а):
Так же было бы полезно отметить буквы в формуле
2013-01-02 17:36:27 gugus писал(а) :
полезно
2013-03-17 20:52:47 marek писал(а):
здравствуйте помогите пожалуйста выбрать пусковую катушку для 2.2кВт 3-х фазного двигателя чтоб МГ работал на 220Вт пока все катушки взрываются из игры спасибо
.
Схемы электрического тока
Модели электрического тока
ЭДС (электродвижущая сила элемента)
— характеризует элемент с точки зрения способности совершать работу по перемещению заряда
Источник SEM представляет собой устройство, в котором неэлектрическая энергия может непрерывно преобразовываться в электрическую.
Интенсивность электрического тока
есть отношение электрического заряда, протекающего через поперечное сечение проводника, ко времени, за которое этот заряд прошел.
Закон Ома
сила тока (I), протекающего по проводнику, прямо пропорциональна напряжению (U), приложенному к его концам.
Электрическое сопротивление проводника
представляет собой постоянное отношение напряжения к току для этого проводника при данной температуре
Зависимость сопротивления проводника от геометрических размеров
Электрическое сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади поверхности его поперечного сечения и зависит от типа материала проводника сделан из
Зависимость сопротивления проводника от температуры
Закон Ома для всей цепи
Ток, протекающий в цепи, прямо пропорционален электродвижущей силе и обратно пропорционален полному сопротивлению цепи.
Измерение напряжения (вольтметр)
Измерение напряжения производится вольтметром, который подключается параллельно точкам цепи. Вольтметр должен иметь очень высокое сопротивление по отношению к сопротивлениям других элементов цепи.
Диапазон измерения вольтметра изменяется путем включения последовательно с вольтметром высоких сопротивлений.
Измерение тока (амперметр)
Измерение тока производится амперметром, включенным последовательно в цепь. Амперметр должен иметь как можно меньшее сопротивление.
Для изменения диапазона шкалы амперметра к нему параллельно подключены сопротивления, называемые шунтами.
Закон Кирхгофа I
Сумма сил токов, втекающих в узловую точку, равна сумме сил токов, вытекающих из этой точки.
Второй закон Кирхгофа
Алгебраическая сумма электродвижущих сил (ЭДС) и падений напряжения в замкнутой цепи равна нулю.
Последовательное соединение резисторов
При последовательном соединении приемников эквивалентное сопротивление равно сумме сопротивлений отдельных приемников
Особенности подключения: через каждый резистор в соединении протекает ток одинаковой силы.Сумма падений напряжения на резисторах соединения равна напряжению, приложенному к соединению. Эта комбинация используется для увеличения сопротивления.
Параллельное соединение резисторов
При параллельном соединении приемников обратная величина эквивалентного сопротивления равна сумме обратной величины сопротивлений отдельных приемников.
Особенности соединения: на каждом сопротивлении, входящем в соединение, одинаковое падение напряжения, равное приложенному к соединению напряжению.Сумма сил токов, протекающих через соединительные элементы, равна силе тока, протекающего в соединение. Комбинация используется для уменьшения сопротивления. Полученное сопротивление ниже наименьшего, входящего в соединение.
Полученное сопротивление ниже наименьшего, входящего в соединение.
Вывод формулы эквивалентного сопротивления последовательного соединения
Из второго закона Кирхгофа следует
Вывод формулы для эквивалентного сопротивления параллельного соединения
Из первого закона Кирхгофа следует
Последовательное соединение источников напряжения
Отрицательный полюс первого источника соединяется с положительным полюсом второго источника, отрицательный полюс второго источника соединяется с положительным полюсом следующего источника и так далее.Результирующая электродвижущая сила этой системы представляет собой сумму электродвижущих сил отдельных источников напряжения. Внутреннее сопротивление системы представляет собой сумму индивидуальных сопротивлений источников
Параллельное соединение источников напряжения
Положительные полюса всех источников подключаются к одному выводу системы, а отрицательные полюса — к другому. Электродвижущая сила системы равна электродвижущей силе одиночного источника. Обратная величина сопротивления внутреннего соединения равна сумме обратной величины внутреннего сопротивления отдельных источников.
Электродвижущая сила системы равна электродвижущей силе одиночного источника. Обратная величина сопротивления внутреннего соединения равна сумме обратной величины внутреннего сопротивления отдельных источников.
Работа постоянного тока
Работа постоянного тока, протекающего по проводнику, равна произведению напряжения (U), силы (I) протекающего тока и времени протекания (t)
Вывод формулы для работы постоянного тока
Работа постоянного тока, выраженная током
Работа постоянного тока, протекающего по проводнику, равна произведению квадрата силы тока на сопротивление проводника и время протекания
Мощность постоянного тока
Мощность постоянного тока, протекающая по проводнику, равна произведению напряжения (U) и силы (I) протекающего тока
Мощность постоянного тока, выраженная через ток
Мощность постоянного тока, протекающего по проводнику, равна произведению квадрата силы этого тока (I) на сопротивление проводника (R)
Вт
Единицей мощности в СИ является ватт (Вт) или джоуль в секунду, если заменить джоуль электрическими единицами, то
т. е. ватт это мощность постоянного тока 1А (ампер) при напряжении 1В (вольт)
е. ватт это мощность постоянного тока 1А (ампер) при напряжении 1В (вольт)
Киловатт-час (кВтч)
Киловатт-час (кВтч) – единица работы электрического тока, которая соответствует работе постоянного тока мощностью 1 кВт (киловатт) в течение 1 часа (часа).Один киловатт-час эквивалентен 3600 Дж (Джоулям).
Закон Джоуля
Количество тепловой энергии (Q), выделяющейся в проводнике, по которому протекает электрический ток, равно произведению напряжения на концах проводника (U), силы протекающего тока (I) и времени протекания ( т)
Эффективность электрического устройства
Мерой КПД электрических устройств является отношение полезной мощности к потребляемой (вкладываемой) мощности.
2008- 2012 © www.epomoce.pl
Политика конфиденциальности
Информация:
Уважаемый пользователь Интернета! Чтобы иметь возможность предоставлять вам все более качественные редакционные материалы и услуги, нам необходимо ваше согласие на адаптацию маркетингового контента к вашему поведению. Благодаря этому согласию мы можем поддерживать наши услуги.
Благодаря этому согласию мы можем поддерживать наши услуги.
Мы используем файлы cookie в функциональных целях, чтобы облегчить пользователям использование веб-сайта и создать анонимную статистику веб-сайта. Нам необходимо ваше согласие на их использование и сохранение в памяти устройства.
Вам должно быть не менее 16 лет, чтобы дать согласие на профилирование, файлы cookie и ремаркетинг. Отсутствие согласия никоим образом не ограничивает содержание нашего веб-сайта. Вы можете отозвать свое согласие в любое время в Политике конфиденциальности.
Мы всегда заботимся о вашей конфиденциальности. Мы не увеличиваем объем наших полномочий.
НЕТ СОГЛАСИЯ .Закон
Ом. История и модель
Закон Ома — это формула, выражающая математическую зависимость между током, напряжением и сопротивлением в электрической цепи. Это экспериментальный закон и в некоторых материалах (в основном в металлах) он достаточно точно выполняется для заданных условий протекания тока. Какова история этого закона? Какой узор?
Какова история этого закона? Какой узор?
Посмотрите видео: «Почему девочки лучше учатся в школе?»
1.Что такое Закон Ома?
Закон Ома провозглашает пропорциональность тока, протекающего по проводнику, напряжению между концами проводника . Он был открыт в 1825-1826 годах немецким учителем математики, впоследствии физиком, профессором Мюнхенского и Нюрнбергского технологического университетов Георгом Симоном Омом.
2. История закона Ома
В 1822 году Гемфри Дэви опубликовал результаты проведения электрического тока в металлах .В результате этих испытаний проводимость металлических проводов обратно пропорциональна их длине и прямо пропорциональна площади поперечного сечения. Этот исследователь также упорядочивал проводники по их способности проводить электричество.
Некоторое время спустя тогдашний школьный учитель математики Джордж Саймон Ом изучил зависимость электрического тока от размеров проводника и приложенного напряжения от 1825, но его работа была сложной и неясной, и поэтому не получила большого признания .
«Они не спят, потому что делают домашнее задание». Начался очередной учебный год
Полдня в школе, потом внеклассные занятия, а вечером домашняя работа. Родители выщипывают зарубки для маленького
прочитать статью
В 1826 году Ом представил результаты своих исследований в форме, аналогичной известной сегодня, утверждая, что ток, протекающий в проводнике, пропорционален приложенному напряжению .Однако прошло еще несколько лет, прежде чем научное сообщество приняло его утверждения.
Между 1845 и 1847 годами другой исследователь, Густав Кирхгоф, провел теоретический анализ течения и связал его плотность с электрическим полем внутри проводника. В 1900 г. Пауль Друде сформулировал свою модель проводимости металлов, объяснив пропорциональность тока напряжению, установленную экспериментально Омом.
Теперь известно, что многие материалы ведут себя не так, как утверждает Ом.Не соблюдается пропорциональность напряжения и тока и не всегда соблюдается закон Ома. Электронные компоненты и материалы, для которых выполняется закон Ома, называются линейными (или омическими), а те, для которых — нелинейными (или неомическими).
Электронные компоненты и материалы, для которых выполняется закон Ома, называются линейными (или омическими), а те, для которых — нелинейными (или неомическими).
Закон Ома не является всеобщим законом природы , а лишь справедливым соотношением для материалов определенного класса, с ограниченным диапазоном токов и напряжений. Однако этот закон имеет большое историческое и практическое значение.Это было первое количественное математическое описание электрического тока .
«Школьные вызовы. Как грамотно поддержать ребенка во взрослении?» — Издательство «Само седно».
Моника Грегорчук, Барбара Колтысь «Школьные вызовы.Как разумно поддержать взросление ребенка?» Книга
прочитать статью
3. Формула закона Ома
Для проводников напряжение между его концами пропорционально току, протекающему по проводнику. При определенной температуре коэффициент пропорциональности постоянен и мы называем его сопротивлением проводника.
Для проводника сопротивлением R, по которому протекает ток силой I, напряжение U между его концами равно:
U = I x R
Единицей сопротивления является Ω [Ом].
Сопротивление может быть связано с геометрией проводника. Для проводника длиной l и сечением S сопротивление составит:
R = p x l / S
, где р — удельное сопротивление, зависящее от материала, из которого изготовлен проводник.
Этот закон определяет сопротивление как коэффициент отношения напряжения к току . Он зависит от температуры, и для металлов он будет расти линейно с ней. Если при определенной температуре Т0 сопротивление будет равно R0, то при температуре ΔТ оно будет:
RΔT = R0 + R0⋅α⋅ΔT
где α — температурный коэффициент сопротивления
Для полупроводниковых материалов сопротивление будет уменьшаться экспоненциально при повышении температуры.
При комнатной температуре удельное сопротивление между стеклами составляет 1,7⋅10–8 Ом·м, а стекло в 1018 раз больше.
.
Закон Ома
Закон Ома гласит, что ток электрический (I), протекающий через проводник, прямо пропорционален напряжению (U), приложенному к концам этого проводника. Этот закон справедлив только в том случае, если температура проводника остается постоянной.
Закон Ома для постоянного тока можно записать в виде:
U = RI,
где R — электрическое сопротивление проводника.
Электрическое сопротивление , являющееся коэффициентом пропорциональности в уравнении Ома , зависит только от свойств данного проводника, но не от приложенного к его концам напряжения и протекающего по нему тока.
Сопротивление проводника зависит от трех факторов, т.е. площади поперечного сечения проводника (S), его длины (l) и т.н. удельное сопротивление (ρ), которое зависит от температуры и типа материала, из которого изготовлен проводник.
Формула для сопротивления выглядит следующим образом:
Единицей электрического сопротивления является ом, который равен .
Удельное сопротивление — характеристическая величина для типа проводника, представляет собой следующую температурную функцию:
где: ρ 0 — удельное сопротивление при 273К, α — температурный коэффициент сопротивления (постоянная величина для данного материала), T — температура.
Из последнего
.
::: В гостях ::: — Ты главный!
Дизайн – будьте в курсе
| я | — | текущий |
| В | — | электрический заряд |
| У | — | электрическое напряжение |
| Ε | — | источник тока электродвижущей силы (SEM) |
| Р | — | электрооборудование |
| р | — | Внутреннее оборудование SEM |
| т | — | время |
| р | — | тип проводника s — проводимость материала l — длина проводника |
| С | — | сечение провода |
| Вт | — | работа с электрическим током |
| Р | — | электроэнергия |
| Т | — | температура |
Увеличение тока. Количество груза Q, которое течет за время t
Количество груза Q, которое течет за время t
Увеличение интенсивности по закону Ома
Модель на базе
Надлежащая проводимость материал, можно узнать геометрические размеры и электропроводность электрическая из однородного блока данного материала:
,
где: G — электропроводность электрическая, S — площадь поперечного сечения элемента, l — длина блока.
Проводящие блоки правильная СИ в системе сименс на метр (1 См/м)
Увеличение электрического сопротивления проводника, температура которого увеличилась на D Тл, где R 0 сопротивление при начальной температуре, а это температурный коэффициент сопротивления
Увеличение SEM, где W — работа, выполненная источником для перемещения груза Q
Уравнение, выражающее закон Ома для замкнутой цепи
U = e-IrWzr к реальному напряжению rda
Р = Р 90 129 1 90 130 + Р 90 129 2 90 130 +… + Р н 90 130
Расширение запасного сопротивления для n последовательно соединенных резисторов
Увеличение заменяющего сопротивления для n резисторов, соединенных параллельно
Вт = UIt
Р = Вт/т
П = УИ.
.
Как найти силу тока — по формуле в резисторе, цепи, проводнике, зная мощность, ищем внутреннее сопротивление в электрической цепи
Чтобы правильно построить электрические цепочки в физике необходим расчёт параметров электроэнергии. Поскольку цель использования электрического тока в электротехнической технике – выполнение током работы, то появляется вопрос о поиске значения силы тока.
Однако, помимо этого следует понимать различие между разными видами электрической мощности, а также знать несколько способов для их вычисления.
Содержание
Определения
Сила тока – физическая величина, являющаяся одной из главных характеристик электрического тока. Она определяется таким понятием как: направленное движение электрических частиц. Другими словами, сила тока равна заряду, который за одну единицу времени прошёл через сечение проводника. Обозначается сила тока: [ I ] и исчисляется в Амперах (А).
Электрическая мощность — физическая величина, которая показывает с какой скоростью преобразуется или передаётся энергия электричества. Данная величина – характеристика производительности прибора. Обозначается: [ P ] и измеряется в Ватт (Вт).
Интересно! Впервые «Ватт» стали использоваться только в 1882 году. Ранее данный термин заменялся «лошадиными силами» (которые, в некоторых сферах, таких как автомобилестроение, используются и сейчас).
Формулы
Для нахождения силы тока
Сила тока рассчитывается по следующим формулам:
I = q/t
- q – заряд, который проходит через сечение проводника,
- t – время в секундах.
Закон Ома:
I = P/U
- P – электрическая мощность,
- U – электрическое напряжение.
I = U/R
- U – электрическое напряжение,
- R – электрическое сопротивление.
Следствие закона Джоуля-Ленца:
I = корень из Q/Rt
- R – электрическое сопротивление,
- Q – количество теплоты,
- t – время.
Для мощности электрического тока
P = A/t
- A – работа, которую выполняет электроприбор,
- t – время.
P = UxI
- U – электрическое напряжение,
- I – сила тока.

P = U2/R
- U – электрическое напряжение,
- R – электрическое сопротивление.
Нахождение силы тока при помощи приборов
Помимо формул, в некоторых случаях, гораздо удобнее использовать вычислительные приборы. Самое главное: правильно их использовать. При измерении следует соблюдать определенные правила и помнить о технике безопасности.
Амперметр
Амперметр – самый распространённый прибор для применения его в электрической цепи.
Единственным недостатком данного прибора является его собственное маленькое сопротивление, из-за чего он может сгореть или просто выключиться, если ему придется измерять силу тока, на которую он не рассчитан. Именно поэтому считается, что универсальность амперметра сильно ограничена.
Если появляется необходимость измерить постоянный ток, то для измерения прибором придется разорвать цепь, а также не забыть про полярность подключения. Данный процесс не всегда удобен и как следствие иногда вычисление по формулам является более предпочтительным.
Данный процесс не всегда удобен и как следствие иногда вычисление по формулам является более предпочтительным.
Существует несколько видов амперметров, каждый из которых используется локально, то есть в определенных электрических цепочках. Наиболее популярными стали: тепловой, электромагнитный, магнитноэлектрический, электродинамический и индукционный амперметр.
Правила при работе с амперметром
- Клемму амперметра, на которой изображен «плюс» – соединяем с проводом, который идет от положительного полюса. Клемма с «минусом» – наоборот.
- Подключать амперметр в электрическую цепь, при отсутствии потребителя тока, нельзя.
- Подключается амперметр в цепи последовательно.
Мультиметром
Мультиметр является многофункциональным прибором, то есть он может измерять ток и постоянных, и переменных токов. Его подключение аналогично амперметру (при условии измерения силы тока).
Прежде чем включить мультиметр внутри цепи, важно проверить режим измерения, а также выбрать пределы измерения гораздо больше силы, которую Вы ожидаете увидеть (современные мультиметры имеют цифровое табло).
При нахождении значения переменного тока переключите прибор на нужный режим и записывайте значения только после того, как цифры на дисплее перестанут мигать.
Единицы измерения на практике
Единицы измерения, приведенные в формулах, порой могут оказаться неудобным на практике, и оттого считаются «теоретическими». Например, в паспортах различных электроприборах (лампочек, телевизоров) Вы не увидите электрическую мощность в Ваттах. Это связано с тем, что если преобразовать формулу, то мы получим, что один Ватт – это 1 Джоуль/1 секунду.
И такое выражение крайне неудобное, ведь электроприборы потребляют ток в течение долгого времени: несколько минут, часов, дней, а расчет электричества по электросчетчику проводится раз в месяц!
Такие расчеты не оправданы и, как следствие, на практике время стали выражать не в секундах, а в часах, из-за чего электрический ток больше не выражается в Ваттах, а в ватт-час (ВтхЧ) или киловатт-час (кВтхЧ).
Из-за введения разных терминов (единиц измерения) мощности, следует разобраться как отличать килоВатт от килоВатт в час. Понятие первое показывает непосредственную мощность электротехники. Другими словами, в виде числа показывает способность прибора преобразовывать энергию электричества. КилоВатт в час – это то, сколько килоВатт за единицу времени (один час) может потребить, например, лампочка.
Сама мощность прибора никак не зависит от времени, однако то, какую мощность он может потребить – напрямую зависит от времени.
Узнать мощность электротехники, без использования формул или специальных приборов, можно взглянув на паспорт (инструкцию) выбранного объекта или на наклейку на нем.
- Телевизор в среднем потребляет до 200 Вт.
- Компьютер – 550 Вт.
- Электрический чайник – 1200 Вт.
- Тостер – 1200 Вт.
- Электрообогреватель – 1400 Вт.
- Микроволновая печь (СВЧ) – 1800 Вт.
- Электроплита – 2500 Вт.

Связь мощности тока с действием тока в электрической цепи
Определить нагрузку на прибор в электрической цепи можно с помощью сравнения мощности тока и номинальной мощности электротехники.
В случае, если мощность самого тока меньше, то его недостаточно или он в целом не проявляется. Это значит, что, если подключить мощный прибор – работать он не начнет.
Обратная ситуация, если сила тока слишком велика, то слабые приборы просто сгорят.
С помощью приведенных выше формул можно находить неизвестные переменные, которые используются в вычислительных задачах, связанных с электричеством. Самые распространенные величины в таких задачах: сопротивление, мощность, напряжение.
Каждый электроприбор имеет свою электрическую мощность и рассчитан на определенную силу тока. При избытке – прибор может сломаться, а при недостатке – не будет работать.
Иногда удобней будет использовать вычислительные «помощники», такие, как амперметр и мультиметр. Они изобретены для того, чтобы измерить силу тока в цепи, однако важно помнить об особенностях их использования.
Они изобретены для того, чтобы измерить силу тока в цепи, однако важно помнить об особенностях их использования.
Фото определения силы тока
Автор статьи:
2) Актуализация знаний
Вопросы 1.что такое электрический ток? 2.каков физический смысл понятия — сила тока? 3.что характеризует напряжение, каков физический этого понятия? 4.что такое сопротивление? 5. каков механизм возникновения сопротивления? 3) Выявление проблемы
1.что общего между этими 3-мя величинами?
2.Ребята, как вы думаете, к какой проблеме, связанной с этими величинами, мы подошли? на какой вопрос мы должны найти ответ? На экране слайд: проблема Учитель: определили ПРОБЛЕМУ которой будем заниматься: какова зависимость между силой тока, напряжением и сопротивлением?
У. 4)Постановка гипотезы Ребята, выдвигаем ГИПОТЕЗУ каков же характер зависимости 1) силы тока от напряжения У. Вспомните математику: как называется такая зависимость
На экране – слайд ГИПОТЕЗА Учитель. Гипотеза требует экспериментального подтверждения, в науке принимается за истину лишь экспериментально доказанное утверждение. Как докажем выдвинутую гипотезу?
5)Эксперимент У. Из каких элементов должна состоять электрическая цепь? У. кто желает собрать цепь на интерактивной доске У. Остальные начертите схему цепи в тетрадях Учитель проходит между рядами, проверяет схемы У. (Таблица проецируется на экран.
У. Как увеличим напряжение в 2 раза?
У. На интерактивной доске собираем цепь с теми же элементами, но добавляем ещё один источник тока.
У. Увеличьте напряжение в три раза, показания амперметра и вольтметра занесите в таблицу.
У. Чертим график зависимости силы тока от напряжения по данным из таблицы. Учитель проверяет, таблицу, графики учащихся.
У. Делаем вывод, как зависит сила тока от . напряжения? какой получился график?
У. Начинаем работу над второй частью гипотезы, как выяснить экспериментально, какова зависимость силы тока от сопротивления. У. Как можно изменить сопротивление в данной цепи.
У.
У. Занесите показания амперметра и значение сопротивления в таблицу. Сопротивление лампы 5 Ом
У. Начертите график зависимости силы тока от сопротивления У. как называется полученная кривая, графиком какой функции является эта прямая. У. Анализируем полученные результаты: как зависит сила тока от сопротивления? Какая зависимость?
6) Вывод У. Делаем вывод по двум экспериментам сразу, подтвердилась ли гипотеза предложенная вами. Нужно сформулировать – как зависит сила тока от напряжения и от сопротивления
У. Утверждение к которому вы пришли –закон Ома для участка цепи. Вы открыли для себя этот закон сегодня, впервые он был открыт Георгом Симоном Омом в 1826 году.
7) Исторические сведения Послушаем исторические сведения об открытии этого закона
8) У. физкультминутка
9) Практическое значение закона Ома Слайд У.закон Ома имеет огромное практическое значение в электротехнике, радиотехнике. 1)применяя этот закон можно найти любую из трех величин, зная две другие. 2) можно регулировать силу тока, изменяя сопротивление и напряжение. Решение задачи 10)Закрепление. Задачи в виде таблиц проецируются на экран
11)Рефлексия
блиц-тест(проецируется на экран) 1)Напряжение на участке цепи 2,4 В, сопротивление 3 Ома, найти силу тока. А) 4 А Б) 7,2 А В) 6 А Г) 0,8 А 2) Как увеличить силу тока в 3 раза при постоянном напряжении. А)увеличить сопротивление в 3 раза Б) уменьшить сопротивление в 3 раза В) увеличить сопротивление 1,5 раза Г) уменьшить сопротивление 1,5раза 3) При напряжении 1,2 кВ сила тока в цепи одной из секций телевизора равна 50 мА. Чему равно сопротивление цепи в этой секции. А)2400 ОМ В)240 Ом Г)600 Ом Д) 24000
4) Требуется увеличить в 4 раза силу тока в цепи при возросшем вдвое сопротивлении. Что нужно для этого делать
А)уменьшить напряжение 4 раза Б)увеличить напряжение в 4 раза В)уменьшить напряжение в 8 раз У. Меняйтесь тетрадями, проверяйте работу друг друга. Правильные ответы : Г Б Д Г Ставим оценки « 5 » -нет ошибок, « 4» — 1 ошибка, « 3»- 2 ошибки 12)Итог У.Что нового вы узнали сегодня на уроке ? У. Сформулируйте закон Ома.
У. Ребята, на каждом уроке мы открываем новые законы. и мир вокруг нас становится ярче, интересней. Пусть ваши умы будут готовы к открытиям, постижению истины.
|
Отвечают на поставленные вопросы, при необходимости уточняют и дополняют друг друга.
1.они характеризуют одно явление – электрический ток
2.есть ли связь между этими величинами? Какая зависимость между этими величинами?
1.сопротивление зависит от вещества, геометрических размеров проводника, от силы тока и напряжения сопротивление не будет зависеть. 2.напряжение — работа источника при перенесении единичного заряда. от сопротивления работа зависит, от силы тока — нет . 3.количество заряда проходящее через поперечное сечение за единицу времени будет зависеть и от напряжения, и от сопротивления
1)О. О. Это –прямая пропорциональность, сила тока прямо пропорциональна напряжению 2)О. При увеличении сопротивления сила тока уменьшится, при уменьшении-увеличится О. Это — обратная пропорциональность, сила тока обратно пропорциональна сопротивлению
О. Для доказательства прямой зависимости силы тока от напряжения: собрать электрическую цепь, изменять напряжение при постоянном сопротивлении, измерять силу тока и напряжение с помощью амперметра и вольтметра.
О. В цепи- источник тока, лампа, амперметр, вольтметр.
Ученик собирает цепь на интерактивной доске. (слайд )
Значение силы тока и напряжения заносят в таблицу
О. Два источника тока нужно соединить последовательно
Ученик собирает цепь на доске. На местах чертят схему, показания амперметра и вольтметра записывают в таблицу. Ученик собирает цепь с тремя источниками, показания измерительных приборов заносятся в таблицу.
Чертят график
О. При увеличении напряжения в 2 раза сила тока тоже увеличивается в 2 раза. При увеличении напряжения в 3 раза, сила тока увеличивается в три раза О.График –прямая. О.Гипотеза о зависимости силы тока от напряжения подтвердилась: Сила тока прямо пропорциональна напряжению. Первая часть гипотезы доказана экспериментально,(на экране слайд)
О. Оставляя неизменным напряжение, меняем сопротивление
О. Если соединить 2 лампы последовательно, сопротивление увеличится в 2 раза. О. Для увеличения сопротивления в 3 раза, соединяем 3 лампы последовательно.
1-й ученик собирает электрическую цепь с одной лампой. Снимают показания амперметра, заносят в таблицу (слайд) 2-й и 3-й ученики собирают электрическую цепь с 2-мя и 3-мя лампами. Все ученики снимают показания амперметра при разных сопротивлениях, заносят в таблицу в тетрадях
О.График данной зависимости – гипербола, график функции обратной пропорциональности.
О. При увеличении сопротивления в 2 раза сила тока уменьшилась в 2 раза, при увеличении в 3 раза-уменьшилась в 3 раза, это-обратная пропорциональность.
О. Эксперимент подтвердил нашу гипотезу
О. сила тока прямо пропорциональна напряжению, обратно пропорциональна сопротивлению.
Ученики пишут закон Ома в тетрадях (слайд)
Ученица. Исторические сведения.(Слайд )
Закон Ома был открыт 1826 году. Электрический ток только начали изучать, не было источников тока, амперметров, вольтметров. В качестве источника тока Ом взял термоэлемент, состоящий из меди и висмута, спаянные в двух местах.
Физкультминутку проводит ученик, заранее подготовленный.
Ученики решают задачи, по желанию выходят к доске, заполняют таблицу.
Ученики отвечают на вопросы теста
Учащиеся решают задачи, пишут ответы в виде ряда букв на полях тетради
О. О. Ученики формулируют закон Ома.
|
1. Theory — Electronics Cookbook [Book]
Хотя эта книга в основном посвящена практике, а не теории, есть несколько теоретических аспектов электроники, которых почти невозможно избежать.
В частности, если вы понимаете взаимосвязь между напряжением, током и сопротивлением, многие другие вещи будут иметь гораздо больше смысла.
Точно так же связь между мощностью, напряжением и током возникает снова и снова.
Проблема
Вы хотите понять, что означает текущий в электронике.
Решение
Как следует из слова «ток», значение тока в электронике близко к значению тока в реке. Вы можете думать о силе тока в трубе как о количестве воды, проходящей через точку трубы каждую секунду. Это может быть измерено во многих галлонах в секунду.
В электронике ток — это количество заряда, переносимого электронами, проходящими точку в проводе в секунду (Рисунок 1-1). Единицей силы тока является ампер, сокращенно ампер или обозначение единицы измерения А.
Рис. 1-1. Ток, протекающий по проводу
Обсуждение
Для многих цепей один целый ампер представляет собой довольно большой ток, поэтому единиц мА (миллиампер, тысячная доля ампера) вы увидите много.
См. также
Список единиц и префиксов единиц, таких как мА, см. в Приложении D.
Чтобы узнать больше о токе в цепи, см. Рецепт 1.4.
Проблема
Вы хотите понять, что означает напряжение в электронике.
Решение
В Рецепте 1.1 вы читаете, какова скорость потока заряда. Этот ток не будет течь, если на него что-то не повлияет. В водопроводной трубе это может быть связано с тем, что один конец трубы выше другого.
Чтобы понять напряжение, полезно представить его как высоту в системе водопроводных труб. Как и высота, она относительна, поэтому высота трубы над уровнем моря определяет не то, насколько быстро вода течет по трубе, а то, насколько выше один конец трубы над другим (Рисунок 1-2).
Как и высота, она относительна, поэтому высота трубы над уровнем моря определяет не то, насколько быстро вода течет по трубе, а то, насколько выше один конец трубы над другим (Рисунок 1-2).
Рис. 1-2. Напряжение по аналогии с высотой
Напряжение может относиться к напряжению на проводе (от одного конца до другого), а в других ситуациях оно может относиться к напряжению от одной клеммы батареи к другой. Общей чертой является то, что для того, чтобы напряжение имело смысл, оно должно относиться к двум точкам; более высокое напряжение — это положительное напряжение, отмеченное знаком +.
Это разница в напряжении, которая создает ток в проводе. Если нет разницы в напряжении между одним концом провода и другим, то ток не течет.
Единицей измерения напряжения является вольт. Батарейка типа АА имеет напряжение около 1,5 В на клеммах. Arduino работает от 5 В, а Raspberry Pi работает от 3,3 В, хотя для него требуется питание 5 В, которое снижается до 3,3 В.
Обсуждение
Иногда кажется, что напряжение используется для обозначения одной точки электронной схемы, а не разницы между двумя точками. В таких случаях напряжение означает разницу между напряжением в одной точке цепи и на земле. Земля (обычно сокращенно GND) — это локальное опорное напряжение, относительно которого измеряются все остальные напряжения в цепи. Это, если хотите, 0В.
В таких случаях напряжение означает разницу между напряжением в одной точке цепи и на земле. Земля (обычно сокращенно GND) — это локальное опорное напряжение, относительно которого измеряются все остальные напряжения в цепи. Это, если хотите, 0В.
См. также
Чтобы узнать больше о напряжениях, см. Рецепт 1.5.
Проблема
Вы хотите понять, как напряжение на чем-то управляет током, протекающим через это.
Решение
Используйте закон Ома.
Закон Ома гласит, что ток, протекающий через провод или электронный компонент (I), равен напряжению на этом проводе или компоненте (V), деленному на сопротивление компонента (R). Другими словами:
I=VR
Если вы хотите рассчитать напряжение, то эту формулу можно изменить следующим образом:
V=I×R
И, если вы знаете ток, протекающий через резистор, и напряжение на резисторе, вы можете вычислить сопротивление с помощью:
R=VI
Обсуждение
Сопротивление – это способность вещества сопротивляться протеканию тока. Провод должен иметь низкое сопротивление, потому что вы обычно не хотите, чтобы электричество, протекающее по проводу, было без необходимости затруднено. Чем толще провод, тем меньше его сопротивление для данной длины. Таким образом, несколько футов тонкого провода, который вы можете обнаружить, соединяя аккумулятор с лампочкой (или, что более вероятно, со светодиодом) в фонарике, могут иметь сопротивление от 0,1 Ом до 1 Ом, в то время как такая же длина толстого кабеля розетки переменного тока для чайника может имеют сопротивление всего несколько миллиом (мОм).
Провод должен иметь низкое сопротивление, потому что вы обычно не хотите, чтобы электричество, протекающее по проводу, было без необходимости затруднено. Чем толще провод, тем меньше его сопротивление для данной длины. Таким образом, несколько футов тонкого провода, который вы можете обнаружить, соединяя аккумулятор с лампочкой (или, что более вероятно, со светодиодом) в фонарике, могут иметь сопротивление от 0,1 Ом до 1 Ом, в то время как такая же длина толстого кабеля розетки переменного тока для чайника может имеют сопротивление всего несколько миллиом (мОм).
Чрезвычайно распространено желание ограничить величину тока, протекающего через часть цепи, путем добавления некоторого сопротивления в виде специального компонента, называемого резистором.
На рис. 1-3 показан резистор (зигзагообразная линия) и указаны ток, протекающий через него (I), и напряжение на нем (V).
Рис. 1-3. Напряжение, ток и сопротивление
Предположим, что нам нужно подключить батарею на 1,5 В к резистору на 100 Ом, как показано на Рисунке 1-4. Греческая буква Ω (омега) используется для обозначения единицы сопротивления («Ом»).
Греческая буква Ω (омега) используется для обозначения единицы сопротивления («Ом»).
Рис. 1-4. Батарея и резистор
Согласно закону Ома, ток равен напряжению на резисторе, деленному на сопротивление резистора (можно предположить, что сопротивление проводов равно нулю).
Итак, I = 1,5/100 = 0,015 А или 15 мА.
См. также
Чтобы понять, что происходит с током, протекающим через резисторы и провода в цепи, см. Рецепт 1.4.
Чтобы понять взаимосвязь между током, напряжением и мощностью, см. Рецепт 1.6.
Проблема
Вы хотите понять, какой ток будет протекать через любую точку цепи.
Решение
Используйте Текущий закон Кирхгофа.
Проще говоря, закон тока Кихгофа гласит, что в любой точке цепи ток, втекающий в эту точку, должен равняться току, вытекающему из нее.
Обсуждение
Например, на Рисунке 1-5 два резистора соединены параллельно и питаются от батареи (обратите внимание на условное обозначение батареи слева на Рисунке 1-5).
Рис. 1-5. Резисторы, включенные параллельно
В точке X ток I будет течь в точку X от батареи, но есть две ответвления от X. Если резисторы одинакового номинала, то через каждую ветвь будет протекать половина тока .
В точке Y два пути воссоединяются, поэтому два тока I/2, втекающие в Y, будут объединены для создания тока I, вытекающего из Y. .
Дальнейшее обсуждение резисторов, включенных параллельно, см. в рецепте 2.5.
Проблема
Вы хотите понять, как складываются напряжения в цепи.
Решение
Используйте закон напряжения Кирхгофа.
Этот закон гласит, что все напряжения между различными точками цепи в сумме равны нулю.
Обсуждение
На рис. 1-6 показаны два последовательно соединенных резистора с батареей. Предполагается, что оба резистора имеют одинаковое значение.
Рис. 1-6. Резисторы серии
На первый взгляд неясно, как применяется закон Кирхгофа для напряжения, пока вы не посмотрите на полярность напряжения. Слева батарея подает V вольт, которые равны по величине, но противоположны по направлению (и, следовательно, по знаку) двум напряжениям V/2 на каждом резисторе.
Слева батарея подает V вольт, которые равны по величине, но противоположны по направлению (и, следовательно, по знаку) двум напряжениям V/2 на каждом резисторе.
Другой способ взглянуть на это состоит в том, что V должно быть уравновешено двумя напряжениями V/2. Другими словами, V = V/2 + V/2 или V – (V/2 + V/2) = 0,
См. также
Такое расположение пары резисторов также используется для уменьшения напряжения (см. рецепт 2.6).
Текущий закон Кирхгофа см. в Рецепте 1.4.
Задача
Вы хотите знать, что означает мощность в электронике.
Решение
В электронике мощность — это скорость преобразования электрической энергии в другую форму энергии (обычно в тепло). Измеряется в джоулях энергии в секунду, которая также известна как ватт (Вт).
Когда вы подключаете резистор, как показано на Рисунке 1-4 Рецепта 1.3, резистор будет выделять тепло, и если это значительное количество тепла, то резистор станет горячим. Вы можете рассчитать количество энергии, преобразованной в тепло, используя формулу:
Вы можете рассчитать количество энергии, преобразованной в тепло, используя формулу:
P = I x V
Другими словами, мощность в ваттах — это напряжение на резисторе (в вольтах), умноженное на протекающий через него ток в амперах. . В примере на Рисунке 1-4, где напряжение на резисторе составляет 1,5 В, а ток через него рассчитан как 15 мА, генерируемая тепловая мощность составит 1,5 В x 15 мА = 22,5 мВт.
Обсуждение
Если известны напряжение на резисторе и сопротивление резистора, то можно объединить закон Ома и P=IV и использовать формулу:
P=V2R
При V=1,5 В и R 100 Ом мощность составляет 1,5 В x 1,5 В / 100 Ом = 22,5 мВт.
См. также
Закон Ома см. в рецепте 1.3.
Проблема
Вы слышали, что электричество бывает двух видов: постоянный ток (DC) и переменный ток (AC), и хотите узнать разницу.
Решение
Во всех рецептах до этого момента предполагается DC. Напряжение постоянное и, как правило, то, что вы ожидаете от батареи.
Переменный ток подается через настенные розетки, и хотя его можно снизить до более низкого напряжения (см. Рецепт 3.9), обычно он имеет высокое (и опасное) напряжение. В США это означает 110 В, а в большинстве других стран мира 220 В или 240 В.
Обсуждение
Что превращает переменный в переменный ток, так это тот факт, что направление тока в переменном токе меняется на противоположное много раз в секунду. На рис. 1-7 показано, как меняется напряжение в настенной розетке переменного тока в США.
Рис. 1-7. Переменный ток
Первое, на что следует обратить внимание, это то, что напряжение следует форме синусоиды, плавно увеличиваясь до тех пор, пока не превысит 150 В, затем снижается от 0 В до примерно -150 В, а затем снова поднимается, что занимает около 16,6 тысячных секунды ( миллисекунд или мс) для завершения одного полного цикла.
Соотношение между периодом переменного тока (время, необходимое для одного полного цикла) и частотой переменного тока (количество циклов в секунду):
частота = 1 период
Единицей частоты является герц (сокращенно Гц), поэтому вы можете видеть, что переменный ток, показанный на рис. 1-7, имеет период 16,6 мс, что составляет 0,0166 секунды. Таким образом, вы можете рассчитать частоту как:
1-7, имеет период 16,6 мс, что составляет 0,0166 секунды. Таким образом, вы можете рассчитать частоту как:
частота = 1 период = 10,0166≈60 Гц
Вам может быть интересно, почему переменный ток от розетки описывается как 110 В, когда на самом деле ему удается колебаться в диапазоне более 300 В от пика к пику. Ответ заключается в том, что цифра 110 В — это эквивалентное постоянное напряжение, способное обеспечить такое же количество энергии. Это называется среднеквадратичным значением напряжения и представляет собой пиковое напряжение, деленное на квадратный корень из 2 (что примерно равно 1,41). Таким образом, в предыдущем примере пиковое напряжение 155 В при делении на 1,41 дает примерно 110 В RMS.
См. также
Дополнительную информацию об использовании переменного тока см. в главе 7.
Мощность, рассеиваемая резистором? Надежность цепи и примеры расчетов
В электронике термин «рассеивание» довольно распространен, и те, кто работает в этой отрасли, слишком хорошо его знают или, по крайней мере, должны знать. Я говорю должен, потому что очевидно, что это не всегда так. Что ж, я подробнее остановлюсь на том, почему я сразу сказал «должен». Но пока давайте сосредоточимся на теме диссипации.
Я говорю должен, потому что очевидно, что это не всегда так. Что ж, я подробнее остановлюсь на том, почему я сразу сказал «должен». Но пока давайте сосредоточимся на теме диссипации.
Возьмем, к примеру, полностью заряженный конденсатор, такой как конденсатор емкостью 3,0 фарад, используемый в аудиосистеме. В этом случае, если вы снимаете конденсатор для хранения, замены или проведения технического обслуживания системы, вы определенно хотите, чтобы конденсатор рассеял свой заряд.
Это был пункт, который не смог понять один джентльмен, даже после того, как предоставил ему подробные детали вместе с необходимыми шагами. Однако несоблюдение надлежащих протоколов разрядки плюс катание конденсатора в багажнике плюс WD-40 равняется событию, которое могло бы вдохновить одну из моих любимых групп (The Power Station) на написание одной из моих любимых песен (Some Like it Hot). Кроме шуток, в его багажнике горела жара, и по сей день его прозвище все еще «дым-дым-дым».
Что такое рассеиваемая мощность?
Рассеяние мощности определяется как процесс, при котором электронное или электрическое устройство выделяет тепло (потери или потери энергии) в качестве нежелательного производного от его основного действия. Как и в случае с центральными процессорами, рассеивание мощности является основной проблемой в компьютерной архитектуре.
Кроме того, рассеивание мощности в резисторах считается естественным явлением. Факт остается фактом: все резисторы, являющиеся частью цепи и имеющие на ней падение напряжения, будут рассеивать электрическую мощность. Более того, эта электрическая мощность преобразуется в тепловую энергию, и поэтому все резисторы имеют номинальную мощность. Кроме того, номинальная мощность резистора — это классификация, которая характеризует максимальную мощность, которую он может рассеивать, прежде чем он достигнет критического отказа.
Как вы, наверное, знаете, мощность выражается в ваттах (Вт), а формула мощности: P (мощность) = I (ток) x E (напряжение). Что касается законов физики, если есть увеличение напряжения (E), то ток (I) также будет увеличиваться, и, в свою очередь, будет увеличиваться рассеиваемая мощность резистора. Однако, если вы увеличите значение резистора, ток уменьшится, а также уменьшится рассеиваемая мощность резистора. Эта корреляция следует закону Ома, который устанавливает формулу тока как I (ток) = V (напряжение) ÷ R (сопротивление).
Что касается законов физики, если есть увеличение напряжения (E), то ток (I) также будет увеличиваться, и, в свою очередь, будет увеличиваться рассеиваемая мощность резистора. Однако, если вы увеличите значение резистора, ток уменьшится, а также уменьшится рассеиваемая мощность резистора. Эта корреляция следует закону Ома, который устанавливает формулу тока как I (ток) = V (напряжение) ÷ R (сопротивление).
Расчет мощности, рассеиваемой резистором
В области электроники рассеиваемая мощность также является параметром измерения, который количественно определяет выделение тепла в цепи из-за неэффективности. Другими словами, рассеиваемая мощность является мерой того, сколько мощности (P = I x E) в цепи преобразуется в тепло. Как я упоминал ранее, у каждого резистора есть номинальная мощность, и с точки зрения конструкции это позволяет разработчикам оценить, будет ли конкретный резистор соответствовать их конструктивным требованиям в схеме. Итак, теперь давайте подробнее рассмотрим, как рассчитать этот критический параметр конструкции.
Во-первых, согласно закону Ома,
В (напряжение) = I (ток) × R (сопротивление)
I (ток) = V (напряжение) ÷ R (сопротивление)
P (мощность) = I (ток) × V (напряжение)
Следовательно, для расчета мощности, рассеиваемой резистором, формулы следующие:
P (рассеиваемая мощность) = I2 (ток) × R (сопротивление)
или
P (рассеиваемая мощность) = V2 (напряжение) ÷ R (сопротивление)
Итак, используя приведенную выше принципиальную схему в качестве справки, мы можем применить эти формулы для определения мощности, рассеиваемой резистором.
Напряжение = 9 В
Сопротивление = 100 Ом
I (ток) = 9 В ÷ 100 Ом или I (ток) = 90 мА
P (мощность) = 90 мА × 9 В или P (мощность) = 0,81 Вт или 810 мВт
P (рассеиваемая мощность) = V2 (напряжение) ÷ R (сопротивление)
или
P (рассеиваемая мощность) = 92 ÷ 100
или
P (рассеиваемая мощность) = 81 ÷ 100 или P (мощность рассеиваемая мощность) = 810 мВт
Рассеиваемая мощность: хорошо или плохо?
Вообще говоря, нет; тем не менее, есть некоторые случаи, когда рассеивание тепла является хорошей вещью. Возьмем, к примеру, электрические нагреватели, в которых используется резистивная проволока, такая как нихром. Нихром является уникальным нагревательным элементом благодаря своей экономичности, устойчивости к потоку электронов, прочности, гибкости, стойкости к окислению, стабильности при высоких температурах.
Возьмем, к примеру, электрические нагреватели, в которых используется резистивная проволока, такая как нихром. Нихром является уникальным нагревательным элементом благодаря своей экономичности, устойчивости к потоку электронов, прочности, гибкости, стойкости к окислению, стабильности при высоких температурах.
Кроме того, еще одним примером благоприятного рассеяния тепла являются лампы накаливания, которые используются в качестве экономичных обогревателей. В целом, при нормальных условиях рассеивание тепла нежелательно, но в тех редких случаях, когда оно имеет место, оно будет заключаться в усилиях по контролю рассеивания тепла, а не в его сдерживании.
Вот некоторые важные моменты, на которые следует обратить внимание при рассмотрении рассеиваемой мощности.
Убедитесь, что номинальная мощность резистора соответствует требованиям вашей схемы.
Обязательно перепроверьте, зависит ли рейтинг вашей микросхемы от использования радиаторов.

Если вы проектируете печатные платы, убедитесь, что ваши дорожки достаточно велики, чтобы поддерживать низкое сопротивление и избегать чрезмерного нагрева.
При проектировании схемы переключения убедитесь, что время переключения максимально короткое.
Чтобы сократить время переключения, сделайте скорость нарастания как можно более крутой, уменьшив емкость на линии. Кроме того, в области электроники скорость нарастания определяется как изменение тока, напряжения или других электрических величин в единицу времени.
Резисторы — это многогранные компоненты, доступные для ваших цепей.
Как дизайнеры, вы постоянно сталкиваетесь с постоянно возникающими проблемами при проектировании электронных схем. Одним из наиболее важных аспектов проектирования является поиск правильных компонентов, отвечающих потребностям вашей схемы. Кроме того, обнаружение этих компонентов также означает, что они должны безопасно функционировать в пределах заданных параметров напряжения, мощности и тока. Поэтому расчет таких параметров, как рассеиваемая мощность, имеет решающее значение для общей схемы.
Кроме того, обнаружение этих компонентов также означает, что они должны безопасно функционировать в пределах заданных параметров напряжения, мощности и тока. Поэтому расчет таких параметров, как рассеиваемая мощность, имеет решающее значение для общей схемы.
Стратегии рассеивания мощности и использование резисторов в ваших цепях более чем эффективны с набором инструментов Cadence для проектирования и анализа. Решая любую задачу компоновки в Allegro PCB Designer, вы получаете быстрые, чистые и готовые к производству проекты.
Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
11.2 Закон Ома | Электрические цепи
11.2 Закон Ома (ESBQ6)
temp textТри основные величины электрических цепей: ток, напряжение (потенциал) разница) и сопротивление . Резюме:
Электрический ток, \(I\), определяется как скорость потока заряда через цепь.

Разность потенциалов или напряжение, \(В\), представляет собой количество энергии на единицу заряда, необходимое для перемещения этого заряд между двумя точками цепи.
Сопротивление, \(R\), является мерой того, насколько «тяжело» пропускать ток через элемент схемы.
Теперь посмотрим, как эти три величины связаны друг с другом в электрических цепях.
Важная зависимость между током, напряжением и сопротивлением в цепи была открыта Георгом Саймон Ом и называется Закон Ома .
- Закон Ома
Количество электрического тока через металлический проводник при постоянной температуре в цепи равно пропорциональна напряжению на проводнике и может быть описана как
\(I = \frac{V}{R}\)где \(I\) — ток через проводник, \(V\) — напряжение на проводнике и \(R\) это сопротивление проводника.
 Другими словами, при постоянной температуре сопротивление
проводник постоянен, не зависит от приложенного к нему напряжения или протекающего через него тока.
Другими словами, при постоянной температуре сопротивление
проводник постоянен, не зависит от приложенного к нему напряжения или протекающего через него тока.
Закон Ома говорит нам, что если проводник имеет постоянную температуру, ток, протекающий через проводника прямо пропорциональна напряжению на нем. Это означает, что если мы нанесем напряжение на по оси абсцисс графика и ток по оси у графика, мы получим прямую.
Градиент прямолинейного графика связан с сопротивлением проводника как \[\frac{I}{V} = \frac{1}{R}\] Это можно преобразовать с точки зрения постоянного сопротивления как: \[R = \frac{V}{I}\]
временный текстЗакон Ома
Цель
Для определения зависимости между током, протекающим через резистор, и потенциалом
разность (напряжение) на одном и том же резисторе.
Аппарат
4 элемента, 4 резистора, амперметр, вольтметр, соединительные провода
Метод
Этот эксперимент состоит из двух частей. В первой части мы будем варьировать приложенное напряжение на резисторе. и измерьте результирующий ток в цепи. Во второй части мы будем варьировать ток в цепи и измерьте результирующее напряжение на резисторе. После получения обоих наборов измерений, мы рассмотрим взаимосвязь между током и напряжением на резистор.
Изменение напряжения:
Настройте цепь в соответствии со схемой 1), начиная с одной ячейки.
Нарисуйте следующую таблицу в своем лабораторном журнале.

Количество ячеек
Напряжение, В (\(\text{В}\))
Ток, I (\(\text{A}\))
\(\текст{1}\)
\(\текст{2}\)
\(\текст{3}\)
\(\текст{4}\)
Попросите учителя проверить цепь перед включением питания.

Измерьте напряжение на резисторе с помощью вольтметра и ток в цепь с помощью амперметра.
Добавьте еще одну ячейку \(\text{1,5}\) \(\text{V}\) в схему и повторите измерения.
Повторяйте, пока у вас не будет четырех ячеек и вы не заполните таблицу.
Изменение тока:
Установите цепь в соответствии со схемой 2), начиная с 1 резистора в схема.
Нарисуйте следующую таблицу в своем лабораторном журнале.

Напряжение, В (\(\text{В}\))
Ток, I (\(\text{A}\))
Попросите учителя проверить вашу схему перед включением питания.

Измерьте ток и измерьте напряжение на одном резисторе.
Теперь добавьте еще один резистор последовательно в цепь и измерьте ток и снова напряжение только на исходном резисторе. Продолжайте добавлять резисторы, пока не иметь четыре последовательно, но не забудьте измерить напряжение только на исходном резистор каждый раз. Введите значения, которые вы измеряете, в таблицу.
Анализ и результаты
Используя данные, которые вы записали в первую таблицу, постройте график зависимости силы тока от напряжения. С напряжение — это переменная, которую мы напрямую изменяем, это независимая переменная и будет отложено по оси \(х\).
 Ток является зависимой переменной и должен быть
отложено по оси \(y\).
Ток является зависимой переменной и должен быть
отложено по оси \(y\).Используя данные, записанные во второй таблице, нарисуйте график зависимости напряжения от силы тока. В этом случай, когда независимой переменной является ток, который должен быть нанесен на ось \(х\), и напряжение является зависимой переменной и должно быть нанесено на ось \(y\).
Выводы
Изучите график, который вы построили из первой таблицы. Что происходит с током через резистор при увеличении напряжения на нем? то есть увеличивается или уменьшается?
Изучите график, который вы построили из второй таблицы. Что происходит с напряжением на резистор, когда ток увеличивается через резистор? то есть увеличивается или уменьшается?
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.

Вопросы и обсуждения
- Для каждого из ваших графиков рассчитайте градиент и на его основе определите сопротивление оригинальный резистор. Получаете ли вы одно и то же значение, когда вычисляете его для каждого из ваших графиков?
Как бы вы нашли сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \(R_0\)?
Моделирование: 242K
Закон Ома
Учебник Упражнение 11.1
Постройте график напряжения (по оси x) и тока (по оси y).
Какой тип графика вы получаете (прямая линия, парабола, другая кривая)
прямолинейный
Рассчитать градиент графика.
Градиент графика (\(m\)) представляет собой изменение тока, деленное на изменение напряжение:
\начать{выравнивать*} m & = \ гидроразрыва {\ Delta I} {\ Delta V} \\ & = \frac{(\text{1,6}) — (\text{0,4})}{(\text{12}) — (\text{3})} \\ & = \текст{0,13} \конец{выравнивание*}
Подтверждают ли результаты ваших экспериментов закон Ома? Объяснять.
Да. Прямолинейный график получается, когда мы строим график зависимости напряжения от силы тока.
Как бы вы нашли сопротивление неизвестного резистора, используя только мощность? питание, вольтметр и известный резистор \(R_{0}\)?
Вы начинаете с подключения известного резистора в цепь с блоком питания. Теперь ваша очередь прочитайте напряжение источника питания и запишите его.
Затем последовательно соедините два резистора. Теперь вы можете измерить напряжение для каждого из резисторов.
Итак, мы можем найти напряжения для двух резисторов. Теперь отметим, что:
\[V = ИК\]
Таким образом, используя это и тот факт, что для последовательно соединенных резисторов ток одинаков
везде в цепи мы можем найти неизвестное сопротивление.
\начать{выравнивать*} V_{0} & = IR_{0} \\ I & = \frac{V_{0}}{R_{0}} \\ V_{U} & = IR_{U} \\ I & = \frac{V_{U}}{R_{U}} \\ \frac{V_{U}}{R_{U}} & = \frac{V_{0}}{R_{0}} \\ \следовательно, R_{U} & = \frac{V_{U}R_{0}}{V_{0}} \конец{выравнивание*}
Омические и неомические проводники (ESBQ7)
Проводники, которые подчиняются закону Ома, имеют постоянное сопротивление при изменении напряжения на них или
ток через них увеличивается. Эти проводники называются омическими проводниками . График
ток по отношению к напряжению на этих проводниках будет прямой линией. Некоторые примеры омических
проводниками служат резисторы цепи и нихромовая проволока.
Как вы видели, когда мы говорим о законе Ома, упоминается постоянная температура . Этот Это связано с тем, что сопротивление некоторых проводников изменяется при изменении их температуры. Эти типы проводники называются неомическими проводниками , потому что они не подчиняются закону Ома. Лампочка есть типичный пример неомического проводника. Другими примерами неомических проводников являются диоды и транзисторы.
В лампочке сопротивление нити накала будет резко увеличиваться по мере ее нагревания от помещения
температуры до рабочей температуры. Если мы увеличим напряжение питания в реальной цепи лампы,
В результате увеличение тока вызывает повышение температуры нити накала, что увеличивает ее
сопротивление. Это эффективно ограничивает увеличение тока. В этом случае напряжение и ток не
подчиняться закону Ома.
Явление изменения сопротивления при изменении температуры свойственно почти всем металлам, из которых состоит большинство проводов. Для большинства применений эти изменения сопротивления достаточно малы, чтобы игнорируется. При применении металлических нитей накаливания, температура которых сильно повышается (примерно до \(\text{1 000}\) \(\text{℃}\) и начиная с комнатной температуры) изменение довольно велико.
В общем случае для неомических проводников график зависимости напряжения от силы тока не будет прямолинейным, что указывает на непостоянство сопротивления при всех значениях напряжения и тока.
Включен рекомендуемый эксперимент для неформальной оценки. В этом эксперименте учащиеся получат
данные о токе и напряжении для резистора и лампочки и определить, что подчиняется закону Ома. Ты сможешь
нужны лампочки, резисторы, соединительные провода, источник питания, амперметр и вольтметр. Учащиеся должны
Обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Учащиеся должны
Обнаружить, что резистор подчиняется закону Ома, а лампочка — нет.
Омические и неомические проводники
Цель
Определить, подчиняются ли два элемента цепи (резистор и лампочка) закону Ома
Аппарат
4 элемента, резистор, лампочка, соединительные провода, вольтметр, амперметр
Метод
Две цепи, показанные на приведенных выше схемах, одинаковы, за исключением того, что в первой имеется резистор, а во втором лампочка. Настройте обе схемы выше, начиная с 1 клетка. Для каждого контура:
Измерьте напряжение на элементе цепи (резистор или лампочка) с помощью вольтметр.
Измерьте ток в цепи с помощью амперметра.

Добавьте еще одну ячейку и повторяйте измерения, пока в вашей схеме не будет 4 ячеек.
Результаты
Нарисуйте в своей книге две таблицы, которые выглядят следующим образом. У вас должна быть одна таблица для измерения первой цепи с резистором и другая таблица для второй цепи измерения с лампочкой.
Количество ячеек | Напряжение, В (\(\text{В}\)) | Ток, I (\(\text{A}\)) |
\(\текст{1}\) | 904:30 | |
\(\текст{2}\) | ||
\(\текст{3}\) | ||
\(\текст{4}\) |
Анализ
Используя данные в ваших таблицах, нарисуйте два графика \(I\) (\(y\)-ось) и \(V\) (\(x\)-ось), один
для резистора и один для лампочки.
Вопросы и обсуждения
Внимательно изучите свои графики и ответьте на следующие вопросы:
Как должен выглядеть график зависимости \(I\) от \(V\) для проводника, подчиняющегося закону Ома?
Один или оба ваших графика выглядят так?
Какой вывод можно сделать о том, подчиняются ли резистор и/или лампочка сопротивлению Ома? Закон?
Является ли лампочка омическим или неомическим проводником?
Использование закона Ома (ESBQ8)
Теперь мы готовы увидеть, как закон Ома используется для анализа цепей.
Рассмотрим цепь с ячейкой и омическим резистором R. Если резистор имеет сопротивление \(\text{5}\) \(\text{Ω}\) и напряжение на резисторе \(\text{5}\) \(\text{V}\), то мы можем использовать Закон для расчета тока, протекающего через резистор. Наша первая задача — нарисовать схему диаграмма. При решении любой задачи с электрическими цепями очень важно составить схему схему, прежде чем делать какие-либо расчеты. Принципиальная схема для этой задачи выглядит следующим образом:
Уравнение для закона Ома: \[R = \frac{V}{I}\]
, который можно преобразовать в: \[I = \frac{V}{R}\]
Ток, протекающий через резистор:
\начать{выровнять*} I &= \frac{V}{R} \\ &= \frac{\text{5}\text{V}}{\text{5}\Omega} \\ &= \текст{1}\текст{ А} \конец{выравнивание*}
временный текстРабочий пример 1: Закон Ома
Изучите электрическую схему ниже:
Сопротивление резистора равно \(\text{10}\) \(\text{Ом}\) и ток, протекающий через
резистор \(\text{4}\) \(\text{A}\). Чему равна разность потенциалов (напряжение) на
резистор?
Чему равна разность потенциалов (напряжение) на
резистор?
Определите, как подойти к проблеме
Нам дано сопротивление резистора и ток, проходящий через него, и нас просят рассчитать напряжение на нем. Мы можем применить закон Ома к этой проблеме, используя: \[R = \frac{V}{I}.\]
Решите задачу
Измените приведенное выше уравнение и подставьте известные значения для \(R\) и \(I\), чтобы решить для \(В\). \начать{выравнивать*} R &= \frac{V}{I} \\ R \times I&= \frac{V}{I} \times I\\ V &= I \times R \\ &= \текст{10} \раз \текст{4} \\ &= \текст{40}\текст{В} \end{выравнивание*}
Напишите окончательный ответ
Напряжение на резисторе равно \(\text{40}\) \(\text{V}\).
Закон Ома
Учебник Упражнение 11.2
Рассчитать сопротивление резистора с разностью потенциалов \(\text{8}\) \(\text{V}\) через него, когда через него протекает ток \(\text{2}\) \(\text{A}\). Перед расчетом нарисуйте принципиальную схему.
Сопротивление неизвестного резистора:
\начать{выравнивать*} R & = \frac{V}{I} \\ & = \ гидроразрыв {8} {2} \\ & = \text{4}\text{ Ом} \конец{выравнивание*}
Какой ток будет течь через резистор \(\text{6}\) \(\text{Ом}\) при наличии
разность потенциалов \(\text{18}\) \(\text{V}\) на его концах? Нарисуйте схему
схему перед расчетом.
Сопротивление неизвестного резистора:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \фракция{18}{6} \\ & = \текст{3}\текст{А} \конец{выравнивание*}
Чему равно напряжение на резисторе \(\text{10}\) \(\text{Ом}\) при токе \(\text{1,5}\) \(\text{A}\) течет через него? Нарисуйте электрическую схему, прежде чем делать расчет.
Сопротивление неизвестного резистора:
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{1,5})(10) \\ & = \текст{15}\текст{В} \конец{выравнивание*}
Перебор резисторов, включенных последовательно и параллельно (ESBQ9)
В 10 классе вы узнали о резисторах и познакомились со схемами, в которых резисторы были соединены в
последовательно и параллельно. В последовательной цепи есть один путь, по которому течет ток. Параллельно
цепи существует несколько путей, по которым течет ток.
В последовательной цепи есть один путь, по которому течет ток. Параллельно
цепи существует несколько путей, по которым течет ток.
Когда в цепи имеется более одного резистора, мы обычно можем рассчитать общее суммарное сопротивление. сопротивления всех резисторов. Это известно как эквивалент сопротивления .
Эквивалентное последовательное сопротивление
В цепи, где резисторы соединены последовательно, эквивалентное сопротивление равно сумме сопротивления всех резисторов.
- Эквивалентное сопротивление в последовательной цепи,
Для n последовательно соединенных резисторов эквивалентное сопротивление:
\[R_{s} = R_{1} + R_{2} + R_{3} + \ldots + R_{n}\]
Применим это к следующей схеме.
Резисторы включены последовательно, поэтому:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} + R_{3} \\ & = \text{3}\text{ Ω} + \text{10}\text{ Ω} + \text{5}\text{ Ω} \\ & =\текст{18}\текст{ Ом} \end{выравнивание*}Моделирование: 242Р
Видео: 242S
Эквивалентное параллельное сопротивление
В цепи, где резисторы соединены параллельно, эквивалентное сопротивление определяется выражением
следующее определение.
- Эквивалентное сопротивление в параллельной цепи
Для \(n\) резисторов, включенных параллельно, эквивалентное сопротивление составляет:
\[\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \ldots + \frac{1}{R_{n}}\]
Применим эту формулу к следующей схеме.
Чему равно полное (эквивалентное) сопротивление в цепи?
\начать{выравнивать*} \frac{1}{R_{p}} & = \left( \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3} } \Правильно) \\ & = \left( \frac{1}{\text{10}\text{ Ω}} + \frac{1}{\text{2}\text{ Ω}} + \frac{1}{\text{1}\text{ Ω}} \right) \\ & = \left( \frac{\text{1}\text{ Ω} + \text{5}\text{ Ω} + \text{10}\text{ Ω}}{\text{10}\text{ Ω}} \right) \\ & = \left( \frac{\text{16}\text{Ω}}{\text{10}\text{Ω}} \right) \\ R_{p} & = \text{0,625}\text{ Ом} \end{выравнивание*}Видео: 242T
Видео: 242 В
Последовательное и параллельное сопротивление
Учебник Упражнение 11. 3
3
Два резистора \(\text{10}\) \(\text{кОм}\) соединены последовательно. Рассчитать эквивалентное сопротивление.
Поскольку резисторы включены последовательно, мы можем использовать:
\[R_{s} = R_{1} + R_{2}\]
Эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} \\ & = \text{10}\text{кОм} + \text{10}\text{кОм} \\ & = \text{20}\text{кОм} \конец{выравнивание*}
Два резистора соединены последовательно. Эквивалентное сопротивление равно \(\text{100}\)
\(\текст{Ω}\). Если один резистор равен \(\text{10}\) \(\text{Ом}\), рассчитайте
значение второго резистора.
Поскольку резисторы включены последовательно, мы можем использовать:
\[R_{s} = R_{1} + R_{2}\]
Эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} \\ R_{2} & = R_{s} — R_{1} \\ & = \text{100}\text{ Ом} — \text{10}\text{ Ом} \\ & = \text{90}\text{ Ом} \конец{выравнивание*}
Два резистора \(\text{10}\) \(\text{кОм}\) соединены параллельно. Рассчитать эквивалентное сопротивление.
Поскольку резисторы подключены параллельно, мы можем использовать:
\[\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}\]
Эквивалентное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{\text{100}} + \frac{1}{\text{10}} \\ & = \frac{1 + 10}{\text{100}} \\ & = \frac{11}{\text{100}} \\ R_{p} & = \text{9,09}\text{ кОм} \конец{выравнивание*}
Два резистора соединены параллельно. Эквивалентное сопротивление равно \(\text{3,75}\)
\(\текст{Ω}\). Если один резистор имеет сопротивление \(\text{10}\) \(\text{Ом}\),
каково сопротивление второго резистора?
Эквивалентное сопротивление равно \(\text{3,75}\)
\(\текст{Ω}\). Если один резистор имеет сопротивление \(\text{10}\) \(\text{Ом}\),
каково сопротивление второго резистора?
Поскольку резисторы подключены параллельно, мы можем использовать:
\[\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}\]
Эквивалентное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ \frac{1}{R_{2}} & = \frac{1}{R_{p}} — \frac{1}{R_{1}} \\ & = \frac{1}{\text{3,75}} — \frac{1}{\text{10}} \\ & = \frac{\text{10} — \text{3,75}}{\text{37,5}} \\ & = \ гидроразрыва {\ текст {6,25}} {\ текст {37,5}} \\ R_{2} & = \text{6}\text{ Ом} \конец{выравнивание*}
Рассчитайте эквивалентное сопротивление в каждой из следующих цепей:
а) Резисторы включены параллельно, поэтому мы используем:
\[\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}\]
Эквивалентное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{\text{3}} + \frac{1}{\text{2}} \\ & = \frac{\text{2} + \text{3}}{\text{6}} \\ & = \ гидроразрыва {\ текст {5}} {\ текст {6}} \\ R & = \text{1,2}\text{ Ом} \конец{выравнивание*}
b) Резисторы подключены параллельно, поэтому мы используем:
\[\frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}\]
Эквивалентное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}} \\ & = \frac{1}{\text{2}} + \frac{1}{\text{3}} + \frac{1}{\text{4}} + \frac{1}{\text{ 1}} \\ & = \frac{\text{6} + \text{4} + \text{3} + \text{12}}{\text{12}} \\ & = \ гидроразрыва {\ текст {25}} {\ текст {12}} \\ R & = \text{0,48}\text{ Ом} \конец{выравнивание*}
c) Резисторы включены последовательно, поэтому мы используем:
\[R_{s} = R_{1} + R_{2}\]
Эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} \\ & = \text{2}\text{ Ом} + \text{3}\text{ Ом} \\ & = \text{5}\text{ Ом} \конец{выравнивание*}
d) Резисторы включены последовательно, поэтому мы используем:
\[R_{s} = R_{1} + R_{2} + R_{3} + R_{4}\]
Эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} + R_{3} + R_{4} \\ & = \text{2}\text{ Ω} + \text{3}\text{ Ω} + \text{4}\text{ Ω} + \text{1}\text{ Ом} \\ & = \text{10}\text{ Ом} \конец{выравнивание*}
Использование закона Ома в последовательных и параллельных цепях (ESBQB)
Используя определения эквивалентного сопротивления резисторов, включенных последовательно или параллельно, мы можем проанализировать
некоторые схемы с этими настройками.
Рассмотрим цепь, состоящую из трех резисторов и одна ячейка, соединенная последовательно.
Первый принцип, который нужно понять о последовательных цепях, заключается в том, что величина тока одинакова. через любой компонент в цепи. Это связано с тем, что существует только один путь для движения электронов. в последовательной цепи. По тому, как подключен аккумулятор, мы можем сказать, в каком направлении ток пойдет. Мы знаем, что ток течет от положительного к отрицательному по соглашению. Общепринятый ток в этой цепи будет течь по часовой стрелке из точки А в точку В, затем в точку С, в точку D и обратно в А.
Мы знаем, что в последовательной цепи ток должен быть одинаковым во всех компонентах. Итак, мы можем написать:
\[I = I_{1} = I_{2} = I_{3}. \]
\]Мы также знаем, что общее напряжение цепи должно быть равно сумме напряжений по всем три резистора. Итак, мы можем написать:
\[V = V_{1} + V_{2} + V_{3}\]Используя эту информацию и то, что мы знаем о расчете эквивалентного сопротивления резисторов в серии, мы можем подойти к некоторым проблемам схемы.
Рабочий пример 2: Закон Ома, последовательная цепь
Рассчитайте ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как решить проблему
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторов в цепи и нам нужно найти общее сопротивление.
Найти общее сопротивление в цепи
Поскольку резисторы соединены последовательно, общее (эквивалентное) сопротивление R равно:
\[R = R_{1} + R_{2}\]
Следовательно,
\начать{выравнивать*} R & = \текст{2} + \текст{4} \\ & = \text{6}\text{ Ом} \конец{выравнивание*}
Применить закон Ома
\begin{align*} R & = \frac{V}{I} \\ R \times \frac{I}{R} & = \frac{V}{I} \times \frac{I}{R} \\ I & = \frac{V}{R} \\ & = \ гидроразрыв {12} {6} \\ & = \текст{2}\текст{А} \конец{выравнивание*}
Запишите окончательный ответ
В цепи протекает ток \(\text{2}\) \(\text{A}\).
Рабочий пример 3: Закон Ома, последовательная цепь
Два омических резистора (\(R_{1}\) и \(R_{2}\)) соединены последовательно с ячейкой. Найди сопротивление \(R_{2}\), учитывая, что ток, протекающий через \(R_{1}\) и \(R_{2}\), равен \(\text{0,25}\) \(\text{A}\) и что напряжение на ячейке равно \(\text{1,5}\) \(\текст{V}\). \(R_{1}\) =\(\text{1}\) \(\text{Ω}\).
Нарисуйте схему и вставьте все известные значения.
Определите, как подойти к проблеме.
Мы можем использовать закон Ома, чтобы найти полное сопротивление R в цепи, а затем вычислить неизвестное сопротивление с использованием:
\[R = R_{1} + R_{2}\]
, потому что он находится в последовательной цепи.
Найти общее сопротивление
\начать{выравнивать*} R & = \frac{V}{I} \\ & = \frac{\text{1,5}}{\text{0,25}} \\ & = \text{6}\text{ Ом} \конец{выравнивание*}Найдите неизвестное сопротивление
Мы знаем, что:
\[R = \текст{6}\текст{Ом}\]
и тот
\[R_{1} = \text{1}\text{Ом}\]
Начиная с
\[R = R_{1} + R_{2}\] \[R_{2} = R — R_{1}\]
Следовательно,
\[R_{1} = \text{5}\text{Ом}\]
Рабочий пример 4: Закон Ома, последовательная цепь
Для следующей цепи рассчитайте:
падение напряжения \(V_1\), \(V_2\) и \(V_3\) на резисторах \(R_1\), \(R_2\), и \(R_3\)
сопротивление \(R_3\).

Определить, как подойти к задаче
Нам известны напряжение на ячейке и ток в цепи, а также сопротивления двух из трех резисторов. Мы можем использовать закон Ома для расчета напряжения падение на известных резисторах. Так как резисторы включены последовательно, напряжение равно \(V = V_1 + V_2 + V_3\), и мы можем вычислить \(V_3\). Теперь мы можем использовать эту информацию для найти напряжение на неизвестном резисторе \(R_3\).
Рассчитать падение напряжения на \(R_1\)
Используя закон Ома: \начать{выравнивать*} R_1 &= \frac{V_1}{I} \\ I \cdot R_1 &= I \cdot \frac{V_1}{I} \\ V_1 &= {I}\cdot{R_1}\\ &= 2 \cdot 1 \\ V_1 &= \text{2}\text{V} \конец{выравнивание*}
Рассчитайте падение напряжения на \(R_2\)
Опять же, используя закон Ома: \начать{выравнивать*} R_2 &= \frac{V_2}{I} \\ I \cdot R_2 &= I \cdot \frac{V_2}{I} \\ V_2 &= {I}\cdot{R_2}\\ &= 2 \cdot 3 \\ V_2 &= \text{6}\text{V} \конец{выравнивание*}
Рассчитать падение напряжения на \(R_3\)
Поскольку падение напряжения на всех вместе взятых резисторах должно быть таким же, как падение напряжения через ячейку в последовательной цепи мы можем найти \(V_3\), используя: \начать{выравнивать*} В &= В_1 + В_2 + В_3\\ V_3 &= V — V_1 — V_2 \\ &= 18 — 2 — 6 \ V_3&= \text{10}\text{V} \конец{выравнивание*}
Найдите сопротивление \(R_3\)
Мы знаем напряжение на \(R_3\) и ток через него, поэтому мы можем использовать закон Ома для рассчитать значение сопротивления: \начать{выравнивать*} R_3 &= \frac{V_3}{I}\\ &= \фракция{10}{2} \\ R_3&= \text{5 } \Омега \конец{выравнивание*}
Напишите окончательный ответ
\(V_1 = \text{2}\text{ V}\)
\(V_2 = \text{6}\text{ V}\)
\(V_3 = \text{10}\text{ V}\)
\(R_1 = \text{5} \Omega\)
временный текстПараллельные цепи
Рассмотрим цепь, состоящую из одной ячейки и трех резисторов, соединенных параллельно.
Первый принцип, который нужно понять о параллельных цепях, заключается в том, что напряжение одинаково на всех элементах цепи. Это потому, что есть только два набора электрически общие точки в параллельной цепи и напряжение, измеренное между наборами общих точек всегда должны быть одинаковыми в любой момент времени. Итак, для показанной схемы верно следующее:
\[V = V_{1} = V_{2} = V_{3}.\]Второй принцип параллельной цепи заключается в том, что все токи через каждый резистор должны суммироваться до полного тока в цепи:
\[I = I_{1} + I_{2} + I_{3}.\]Используя эти принципы и наши знания о том, как рассчитать эквивалентное сопротивление параллельных резисторов, теперь мы можем подойти к некоторым проблемам схемы, связанным с параллельными резисторами.
Рабочий пример 5: Закон Ома, параллельная схема
Рассчитайте ток (I) в этой цепи, если оба резистора имеют омическую природу.
Определите, что требуется
Нам необходимо рассчитать ток, протекающий в цепи.
Определите, как решить проблему
Поскольку резисторы имеют омическую природу, мы можем использовать закон Ома. Однако есть два резисторов в цепи и нам нужно найти общее сопротивление.
Найдите эквивалентное сопротивление в цепи
Поскольку резисторы соединены параллельно, общее (эквивалентное) сопротивление R равно:
\[\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}.\] \начать{выравнивать*} \frac{1}{R} &= \frac{1}{R_1} + \frac{1}{R_2} \\ &= \frac{1}{2} + \frac{1}{4} \\ &= \фракция{2+1}{4} \\ &= \фракция{3}{4} \\ \text{Следовательно, } R &= \text{1,33 } \Omega \конец{выравнивание*}
Применение закона Ома
\начать{выравнивать*} R&= \frac{V}{I} \\ R \cdot \frac{I}{R} &= \frac{V}{I} \cdot \frac{I}{R} \\ I &= \frac{V}{R}\\ I &= V \cdot \frac{1}{R}\\ &= (12) \влево(\frac{3}{4}\вправо) \\ &= \текст{9}\текст{А} \конец{выравнивание*}Напишите окончательный ответ
Ток, текущий в цепи, равен \(\text{9}\) \(\text{A}\).
Рабочий пример 6: Закон Ома, параллельная схема
Два омических резистора (\(R_1\) и \(R_2\)) подключены параллельно ячейке. Найди сопротивление \(R_2\), учитывая, что ток, протекающий через ячейку, равен \(\text{4,8}\) \(\text{A}\) и что напряжение на ячейке равно \(\text{9}\) \(\текст{V}\).
Определите, что требуется
Нам нужно рассчитать сопротивление \(R_2\).
Определите, как подойти к проблеме
Так как резисторы омические и нам известны напряжение на ячейке и ток через ячейку, мы можем использовать закон Ома, чтобы найти эквивалентное сопротивление в цепи. \начать{выравнивать*} R & = \frac{V}{I} \\ & = \ гидроразрыва {9}{\текст{4,8}} \\ & = \text{1875} \\Омега \конец{выравнивание*}
Рассчитайте значение для \(R_2\)
Поскольку мы знаем эквивалентное сопротивление и сопротивление \(R_1\), мы можем использовать формулу
для резисторов параллельно найти сопротивление \(R_2\). \начать{выравнивать*}
\frac{1}{R} & = \frac{1}{R_1} + \frac{1}{R_2}
\конец{выравнивание*}
Перестановка для решения для \(R_2\):
\начать{выравнивать*}
\frac{1}{R_2} & = \frac{1}{R} — \frac{1}{R_1} \\
& = \frac{1}{\text{1875}} — \frac{1}{3}\\
& = \текст{0,2} \\
R_2 & = \frac{1}{\text{0,2}} \\
& = \text{5} \\Омега
\end{выравнивание*}
\начать{выравнивать*}
\frac{1}{R} & = \frac{1}{R_1} + \frac{1}{R_2}
\конец{выравнивание*}
Перестановка для решения для \(R_2\):
\начать{выравнивать*}
\frac{1}{R_2} & = \frac{1}{R} — \frac{1}{R_1} \\
& = \frac{1}{\text{1875}} — \frac{1}{3}\\
& = \текст{0,2} \\
R_2 & = \frac{1}{\text{0,2}} \\
& = \text{5} \\Омега
\end{выравнивание*}
Напишите окончательный ответ
Сопротивление \(R_2\) равно \(\text{5}\) \(\Omega\)
temp textРабочий пример 7: Закон Ома, параллельная схема
Аккумулятор на 18 В подключен к двум параллельным резисторам \(\text{4}\) \(\Omega\) и
\(\text{12}\) \(\Omega\) соответственно. Вычислите ток через ячейку и через
каждый из резисторов.
Вычислите ток через ячейку и через
каждый из резисторов.
Сначала нарисуйте схему, прежде чем делать какие-либо расчеты
Определите, как подойти к проблеме
Нам нужно определить ток через ячейку и каждый из параллельных резисторов. У нас есть дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.
Рассчитать ток через ячейку
Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалент сопротивление остальной части цепи. Резисторы включены параллельно, поэтому: \начать{выравнивать*} \frac{1}{R} &= \frac{1}{R_1} + \frac{1}{R_2} \\ &= \frac{1}{4} + \frac{1}{12} \\ &= \фракция{3+1}{12} \\ &= \фракция{4}{12} \\ R &= \frac{12}{4} = \text{3} \\Omega \конец{выравнивание*} Теперь, используя закон Ома, найдем ток через ячейку: \начать{выравнивать*} R &= \frac{V}{I} \\ I &= \frac{V}{R} \\ &= \фракция{18}{3} \\ Я &= \text{6}\text{ А} \end{выравнивание*}
Теперь определите ток через один из параллельных резисторов
Мы знаем, что для чисто параллельной цепи напряжение на ячейке такое же, как и
напряжение на каждом из параллельных резисторов. Для этой схемы:
\начать{выравнивать*}
V &= V_1 = V_2 = \text{18}\text{V}
\конец{выравнивание*}
Начнем с расчета тока через \(R_1\) по закону Ома:
\начать{выравнивать*}
R_1 &= \frac{V_1}{I_1} \\
I_1 &= \frac{V_1}{R_1} \\
&= \фракция{18}{4} \\
I_1 &= \text{4,5}\text{ А}
\end{выравнивание*}
Для этой схемы:
\начать{выравнивать*}
V &= V_1 = V_2 = \text{18}\text{V}
\конец{выравнивание*}
Начнем с расчета тока через \(R_1\) по закону Ома:
\начать{выравнивать*}
R_1 &= \frac{V_1}{I_1} \\
I_1 &= \frac{V_1}{R_1} \\
&= \фракция{18}{4} \\
I_1 &= \text{4,5}\text{ А}
\end{выравнивание*}
Рассчитайте ток через другой параллельный резистор
Мы можем снова использовать закон Ома, чтобы найти ток в \(R_2\): \начать{выравнивать*} R_2 &= \frac{V_2}{I_2} \\ I_2 &= \frac{V_2}{R_2} \\ &= \фракция{18}{12} \\ I_2 &= \text{1,5}\text{ А} \конец{выравнивание*} Альтернативный метод вычисления \(I_2\) состоял бы в том, чтобы использовать тот факт, что токи через каждый из параллельных резисторов должны в сумме составлять общий ток через клетка: \начать{выравнивать*} I &= I_1 + I_2 \\ I_2 &= I — I_1 \\ &= 6 — 4,5 \\ I_2 &= \text{1,5}\text{ А} \end{выравнивание*}
Напишите окончательный ответ
Ток через ячейку равен \(\text{6}\) \(\text{A}\).
Ток через резистор \(\text{4}\) \(\Omega\) равен \(\text{4,5}\) \(\text{A}\).
Ток через резистор \(\text{12}\) \(\Omega\) равен \(\text{1,5}\) \(\text{A}\).
Закон Ома в последовательных и параллельных цепях
Учебник Упражнение 11.4
Рассчитать номинал неизвестного резистора в цепи:
Сначала мы используем закон Ома для расчета полного последовательного сопротивления:
\начать{выравнивать*} R & = \frac{V}{I} \\ & = \ гидроразрыва {9} {1} \\ & = \text{9}\text{ Ом} \конец{выравнивание*}
Теперь мы можем найти неизвестное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} + R_{3} + R_{4} \\ R_{4} & = R_{s} — R_{1} — R_{2} — R_{3} \\ & = 9- 3 — 3 — 1\ & = \text{2}\text{ Ом} \конец{выравнивание*}
Рассчитайте значение тока в следующей цепи:
Сначала найдем полное сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} + R_{3} \\ & = \текст{1} + \текст{2,5} + \текст{1,5} \\ & = \text{5}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыв {9} {5} \\ & = \текст{1,8}\текст{А} \конец{выравнивание*}
Три резистора сопротивлением \(\text{1}\) \(\text{Ом}\), \(\text{5}\)
\(\text{Ω}\) и \(\text{10}\) \(\text{Ω}\) соответственно, связаны в
серия с аккумулятором \(\text{12}\) \(\text{V}\). Рассчитать значение тока в
схема.
Рассчитать значение тока в
схема.
Рисуем схему:
Теперь находим общее сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{2} + R_{3} \\ & = \текст{1} + \текст{5} + \текст{10} \\ & = \text{16}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыва {12} {16} \\ & = \текст{0,75}\текст{А} \конец{выравнивание*}
Рассчитайте ток через элемент, если оба резистора имеют омическую природу.
Сначала находим общее сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{\text{1}} + \frac{1}{\text{3}} \\ & = \frac{3 + 1}{\text{3}} \\ & = \frac{4}{\text{3}} \\ & = \text{0,75}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать ток:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{9}{\text{0,75}} \\ & = \текст{12}\текст{А} \конец{выравнивание*}
Рассчитаем номинал неизвестного резистора \(R_{4}\) в цепи:
Сначала найдем полное сопротивление:
\начать{выравнивать*} R & = \frac{V}{I} \\ & = \frac{24}{\text{2}} \\ & = \text{12}\text{ Ом} \конец{выравнивание*}
Теперь мы можем вычислить неизвестное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \frac{1}{R_{4}}\\ \frac{1}{R_{4}} & = \frac{1}{R_{p}} — \frac{1}{R_{1}} — \frac{1}{R_{2}} — \frac{1}{R_{3}}\\ & = \frac{1}{\text{12}} — \frac{1}{\text{120}} — \frac{1}{\text{40}} — \frac{1}{\text{60}} \\ & = \frac{10 — 1 — 3 — 2}{\text{120}} \\ & = \frac{4}{\text{120}} \\ & = \text{30}\text{ Ом} \конец{выравнивание*}
значение тока через аккумулятор
Рисуем принципиальную схему:
Для расчета значения тока через аккумулятор сначала нужно вычислить эквивалентное сопротивление:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}\\ & = \frac{1}{\text{1}} + \frac{1}{\text{5}} + \frac{1}{\text{10}} \\ & = \frac{10 + 2 + 1}{\text{10}} \\ & = \frac{13}{\text{10}} \\ & = \text{0,77}\text{ Ом} \конец{выравнивание*}
Теперь мы можем рассчитать ток через аккумулятор:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{20}{\text{0,77}} \\ & = \текст{26}\текст{А} \конец{выравнивание*}
значение тока в каждом из трех резисторов.
Для параллельной цепи напряжение на ячейке равно напряжению на каждой резисторов. Для этой схемы:
\[V = V_{1} = V_{2} = V_{3} = \text{20}\text{V}\]
Теперь мы можем рассчитать ток через каждый резистор. Начнем с \(R_{1}\):
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{20}{\text{1}} \\ & = \текст{20}\текст{А} \конец{выравнивание*}
Далее вычисляем ток через \(R_{2}\):
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{20}{\text{5}} \\ & = \текст{4}\текст{А} \конец{выравнивание*}
И, наконец, вычисляем ток через \(R_{3}\):
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \frac{20}{\text{10}} \\ & = \текст{2}\текст{А} \конец{выравнивание*}
Вы можете проверить, что они составляют общий ток.
Последовательные и параллельные сети резисторов (ESBQC)
Теперь, когда вы знаете, как обращаться с простыми последовательными и параллельными цепями, вы готовы заняться схемотехникой. которые объединяют эти две установки, такие как следующая схема:
Рисунок 11.1: Пример последовательно-параллельной сети. Пунктирные прямоугольники обозначают параллельные участки цепи. Относительно легко разработать такие схемы, потому что вы используете все, что у вас уже есть.
познакомился с последовательной и параллельной схемой. Разница лишь в том, что вы делаете это поэтапно. На рисунке 11.1 схема состоит из 2 параллельных частей.
которые затем последовательно с ячейкой. Чтобы определить эквивалентное сопротивление цепи, вы начинаете с
рассчитать общее сопротивление каждой из параллельных частей, а затем сложить эти сопротивления в
серии. Если бы все резисторы на рис. 11.1 имели
сопротивления \(\text{10}\) \(\text{Ω}\), мы можем вычислить эквивалентное сопротивление всего
схема. 9{-1} \\
&= \текст{5} \, \Омега
\конец{выравнивание*}
Если бы все резисторы на рис. 11.1 имели
сопротивления \(\text{10}\) \(\text{Ω}\), мы можем вычислить эквивалентное сопротивление всего
схема. 9{-1} \\
&= \текст{5} \, \Омега
\конец{выравнивание*}
Теперь вы можете рассматривать схему как простую последовательную цепь следующим образом:
Следовательно, эквивалентное сопротивление равно: \начать{выравнивать*} R &= R_{p1} + R_{p2} \\ &= 5 + 5 \\ &= 10 \, \Омега \конец{выравнивание*}
Эквивалентное сопротивление цепи на рис. 11.1 равно \(\text{10}\) \(\text{Ω}\).
временный текстПоследовательные и параллельные сети
Учебник Упражнение 11.5
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{4} + \frac{1}{2} \\ & = \ гидроразрыва {3} {4} \\ R_{p} & = \text{1,33}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с двумя последовательно соединенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{3} + R_{p} \\ & = \текст{2} + \текст{1,33} \\ & = \text{3,33}\text{ Ом} \конец{выравнивание*}
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ & = \frac{1}{1} + \frac{1}{2} \\ & = \ гидроразрыва {3} {2} \\ R_{p} & = \text{0,67}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с тремя последовательными резисторами, поэтому мы можем рассчитать эквивалентное сопротивление:
\начать{выравнивать*} R_{s} & = R_{3} + R_{4} + R_{p} \\ & = \текст{4} + \текст{6} + \текст{0,67} \\ & = \text{10,67}\text{ Ом} \конец{выравнивание*}
Начнем с определения эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{3} + \frac{1}{5} + \frac{1}{1} \\ & = \ гидроразрыва {23} {15} \\ R_{p} & = \text{0,652}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с двумя последовательно соединенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{4} + R_{p} \\ & = \текст{2} + \текст{0,652} \\ & = \text{2,652}\text{Ом} \конец{выравнивание*}
ток \(I\) через ячейку.
Чтобы найти ток \(I\), сначала нужно найти эквивалентное сопротивление. Мы начинаем путем расчета эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{3} + \frac{1}{5} + \frac{1}{1} \\ & = \ гидроразрыва {23} {15} \\ R_{p} & = \text{0,652}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с двумя последовательно соединенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{4} + R_{p} \\ & = \текст{2} + \текст{0,652} \\ & = \text{2,652}\text{Ом} \конец{выравнивание*}
Таким образом, ток через элемент:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыва {\ текст {12}} {\ текст {2652}} \\ & = \текст{4,52}\текст{А} \конец{выравнивание*}
ток через резистор \(\text{5}\) \(\text{Ω}\).
Ток через параллельную комбинацию резисторов равен \(\text{4,52}\) \(\текст{А}\). (Ток одинаков при последовательном соединении резисторов и мы можем рассматривать весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через параллельную комбинацию резисторов (не забудьте использовать эквивалентное параллельное сопротивление, а не эквивалентное сопротивление цепи):
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{4,52})(\текст{0,652}) \\ & = \текст{2,95}\текст{ В} \конец{выравнивание*}
Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это
также является напряжением на резисторе \(\text{5}\) \(\text{Ω}\).
Итак, теперь мы можем рассчитать ток через резистор:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыва {\ текст {2,95}}{\текст{5}} \\ & = \текст{0,59}\текст{А} \конец{выравнивание*}
Если ток, протекающий через ячейку, равен \(\text{2}\) \(\text{A}\) и все резисторы являются омическими, рассчитайте напряжение на ячейке и каждом из резисторов, \(R_1\), \(R_2\) и \(R_3\) соответственно.
Чтобы найти напряжение, нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{2} + \frac{1}{4} \\ & = \ гидроразрыва {3} {4} \\ R_{p} & = \text{1,33}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с двумя последовательно соединенными резисторами, поэтому мы можем рассчитать эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{p} \\ & = \текст{4,66} + \текст{1,33} \\ & = \text{5,99}\text{ Ом} \конец{выравнивание*}
Итак, напряжение на ячейке:
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{2})(\текст{5,99}) \\ & = \текст{12}\текст{В} \конец{выравнивание*}
Ток через параллельную комбинацию резисторов равен \(\text{2}\) \(\text{A}\). (Ток одинаков через последовательные комбинации резисторов, и мы можем рассмотреть
весь параллельный набор резисторов как один последовательный резистор.)
(Ток одинаков через последовательные комбинации резисторов, и мы можем рассмотреть
весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение на каждом из резисторов. Начнем с поиска напряжение на \(R_{1}\):
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{2})(\текст{4,66}) \\ & = \текст{9,32}\текст{В} \конец{выравнивание*}
Теперь находим напряжение на параллельной комбинации:
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{2})(\текст{1,33}) \\ & = \текст{2,66}\текст{В} \конец{выравнивание*}
Поскольку напряжение на каждом резисторе в параллельной комбинации одинаковое, это
также напряжение на резисторах \(R_{2}\) и \(R_{3}\).
ток через элемент
Чтобы найти ток нам сначала нужно найти эквивалентное сопротивление. Мы начинаем с расчет эквивалентного сопротивления параллельной комбинации:
\начать{выравнивать*} \frac{1}{R_{p}} & = \frac{1}{R_{2}} + \frac{1}{R_{3}} \\ & = \frac{1}{1} + \frac{1}{1} \\ & = 2\\ R_{p} & = \text{0,5}\text{ Ом} \конец{выравнивание*}
Теперь у нас есть схема с двумя последовательно соединенными резисторами, поэтому мы можем вычислить эквивалент сопротивление:
\начать{выравнивать*} R_{s} & = R_{1} + R_{4} + R_{p} \\ & = \текст{2} + \текст{1,5} + \текст{0,5} \\ & = \text{4}\text{ Ом} \конец{выравнивание*}
Таким образом, ток через элемент:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыва {\ текст {10}} {\ текст {4}} \\ & = \текст{2,5}\текст{А} \конец{выравнивание*}
падение напряжения на \(R_4\)
Ток через все резисторы равен \(\text{2,5}\) \(\text{A}\). (Ток есть
то же самое через последовательные комбинации резисторов, и мы можем рассмотреть весь
параллельный набор резисторов как один последовательный резистор.)
(Ток есть
то же самое через последовательные комбинации резисторов, и мы можем рассмотреть весь
параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти напряжение через \(R_{4}\):
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{2,5})(\текст{1,5}) \\ & = \текст{3,75}\текст{В} \конец{выравнивание*}
ток через \(R_2\)
Ток через все резисторы равен \(\text{2,5}\) \(\text{A}\). (Ток есть то же самое через последовательные комбинации резисторов, и мы можем рассмотреть весь параллельный набор резисторов как один последовательный резистор.)
Используя это, мы можем найти ток через \(R_{2}\).
Сначала нам нужно найти напряжение на параллельной комбинации:
\начать{выравнивать*} V & = I \cdot R \\ & = (\текст{2,5})(\текст{0,5}) \\ & = \текст{1,25}\текст{В} \конец{выравнивание*}
Теперь мы можем найти ток через \(R_{2}\), используя тот факт, что напряжение равно одинаково на каждом резисторе в параллельной комбинации:
\начать{выравнивать*} I & = \frac{V}{R} \\ & = \ гидроразрыва {\ текст {1,25}} {\ текст {1}} \\ & = \текст{1,25}\текст{А} \конец{выравнивание*}
Уметь рассчитать сопротивление зная мощность и напряжение.
 Расчеты.
Расчеты.Само электричество невидимо, хотя от этого его опасность не меньше. Даже наоборот: оттого и опаснее. Ведь если бы мы это видели, как мы видим, например, льющуюся из-под крана воду, то наверняка избежали бы многих неприятностей.
Вода. Вот она, водопровод, а вот и закрытый кран. Ничего не течет, не капает. Но мы знаем точно: внутри вода. И если система работает исправно, то эта вода находится под давлением. 2, 3 атмосферы или сколько там? Неважно. Но давление есть, иначе система бы не работала. Где-то гудят насосы, гоняя воду в систему, создавая это самое давление.
Но провод у нас электрический. Где-то далеко, на другом конце, тоже гудят генераторы, вырабатывающие электричество. И в проводе от этого тоже давление… Нет-нет, никакого давления, конечно, вот в этом проводе напряжение . Он тоже измеряется, но в своих единицах: в вольтах.
Давление в трубах на стены воды, не двигаясь, ожидая, когда появится выход, чтобы хлынуть туда мощным потоком. А в проводе молча ждут напряжения, когда выключатель замкнут, чтобы потоки электронов двинулись выполнять свое предназначение.
А в проводе молча ждут напряжения, когда выключатель замкнут, чтобы потоки электронов двинулись выполнять свое предназначение.
И вот открылся кран, потекла струя воды. По всей трубе течет, двигаясь от насоса к расходному клапану. И как только контакты переключателя замыкались, по проводам текли электроны. Что это за движение? это текущий . Электроны текущие . И это движение, этот ток тоже имеет свою единицу измерения: ампер.
А еще есть сопротивление . Для воды это, образно говоря, размер отверстия на выходе. Чем больше отверстие, тем меньше сопротивление движению воды. В проводах почти то же самое: чем больше сопротивление провода, тем меньше ток.
Вот как-то так, если образно представить основные характеристики электричества. А с точки зрения науки все строго: есть так называемый закон Ома. Он звучит так: I = U / R .
I — сила тока. Измеряется в амперах.
U — натяжение. Измеряется в вольтах.
R — сопротивление. Измеряется в омах.
Измеряется в омах.
Есть еще одно понятие — мощность, Вт. Тоже просто: Вт = U * I . Измеряется в ваттах.
Собственно, это вся необходимая и достаточная для нас теория. Из этих четырех единиц измерения в соответствии с приведенными выше двумя формулами можно вывести ряд других:
| № | Задача | Формула | Пример |
| 1 | Узнать силу тока, если известны напряжение и сопротивление. | И = У/Р | I = 220 В / 500 Ом = 0,44 А. |
| 2 | Узнать мощность, если известны ток и напряжение. | Ш = У * Я | Вт = 220 В * 0,44 А = 96,8 Вт. |
| 3 | Узнайте сопротивление, если известны напряжение и сила тока. | Р = У/Я | R = 220 В / 0,44 А = 500 Ом. |
| 4 | Узнайте, известны ли ток и сопротивление. | У = И * Р | U = 0,44 А * 500 Ом = 220 вольт. |
| 5 | Узнайте мощность, если известны сила тока и сопротивление. | Ш = И 2 * Р | Вт = 0,44 А * 0,44 А * 500 Ом = 96,8 Вт. |
| 6 | Узнайте, известны ли напряжение и сопротивление. | Ш = У 2 / Р | Вт = 220 В * 220 В / 500 Ом = 96,8 Вт. |
| 7 | Узнайте ток, когда известны мощность и напряжение. | И = Ш/У | I = 96,8 Вт / 220 В = 0,44 А. |
| 8 | Узнать напряжение, если известны мощность и ток. | У=В/Я | U = 96,8 Вт / 0,44 А = 220 В. |
| 9 | Узнайте сопротивление, если известны мощность и напряжение. | Р = У 2 / Ш | R = 220 В * 220 В / 96,8 Вт = 500 Ом. |
| 10 | Узнайте сопротивление, если известны мощность и ток. | Р = В/Я 2 | R = 96,8 Вт / (0,44 А * 0,44 А) = 500 Ом. |
Вы говорите: — Зачем мне все это? Формулы, цифры… Расчетами заниматься не буду.
А я отвечу: — Читай предыдущую статью. Как можно быть уверенным, не зная простейших истин и расчетов? Хотя на самом деле в бытовом практическом плане наиболее интересна только формула 7, где ток определяется при известном напряжении и мощности. Как правило, эти 2 значения известны, и результат (сила тока) совершенно необходим для определения допустимых сечений проводов и для выбора защит.
Есть еще одно обстоятельство, о котором следует упомянуть в контексте данной статьи. В электроэнергетике используется так называемый «переменный» ток. То есть те самые электроны движутся в проводах не всегда в одном направлении, они постоянно его меняют: вперед-назад-вперед-назад… И эта смена направления движения — 100 раз в секунду.
Подождите, а ведь везде говорят, что частота 50 герц! Да все верно. Частота измеряется числом периодов в секунду, но в каждом периоде ток дважды меняет свое направление. Другими словами, в одном периоде имеется два пика, характеризующих максимальное значение тока (положительный и отрицательный), и именно в этих вершинах происходит изменение направления.
Другими словами, в одном периоде имеется два пика, характеризующих максимальное значение тока (положительный и отрицательный), и именно в этих вершинах происходит изменение направления.
Не будем вдаваться в подробности, но все же: почему переменная, а не d.C.?
Вся проблема в передаче электроэнергии на большие расстояния. Тогда вступает в силу неумолимый закон Ома. При больших нагрузках, если напряжение 220 вольт, сила тока может быть очень большой. Для передачи электроэнергии с таким током потребуются провода очень большого сечения.
Выход один: поднять напряжение. Седьмая формула гласит: I = W/U . Совершенно очевидно, что если подать напряжение 220 вольт вместо 220 000 вольт, то ток уменьшится в 1000 раз. А это значит, что сечение проводов можно взять гораздо меньше.
Поиск по сайту.
Вы можете изменить поисковую фразу.
Электрический ток можно сравнить с тем, как течет вода в трубе, а напряжение с уровнем этой воды. Электрический ток, проходя по трубе, совершает определенную работу. Исходя из определения, мощность – это работа в единицу времени или скорость выполнения работы.
Исходя из определения, мощность – это работа в единицу времени или скорость выполнения работы.
За секунду определенное количество электричества проходит по цепи через поперечное сечение цепи. Это понятие будет называться текущей силой. Следовательно, между мощностью, током и напряжением будет прямо пропорциональная зависимость.
Формулы для расчета тока
Измеренная электрическая мощность в ваттах (Вт). Ток в 1А и при напряжении 1В имеет мощность 1Вт. Для того чтобы узнать, как определить мощность тока, необходимо воспользоваться следующей формулой: P = U*I(A), где U, I – напряжение электрического поля и сила тока соответственно, а P – его мощность.
Чтобы понять, как правильно использовать формулу, рассмотрим небольшой пример. Допустим, к резистору 150В приложено напряжение и к нему приложен ток 0,2А. Какой резистор развивает мощность? Р = 150 * 0,2 = 30 Вт.
Есть еще один способ расчета мощности электрического тока. Если известны сопротивление цепи и сила тока, то необходимо воспользоваться законом Ома (применима формула для отрезка цепи): U = I * R (B)
Теперь подставим формулу (B) в формулы (А) и получить формулу (В): P = I 2 R(B). Предположим, что через реостат, сопротивление которого равно 5 Ом, проходит с силой 0,5А ток. Определить мощность, которая теряется в реостате? Р = 0,5 2 * 5 = 1,25 Вт.
Предположим, что через реостат, сопротивление которого равно 5 Ом, проходит с силой 0,5А ток. Определить мощность, которая теряется в реостате? Р = 0,5 2 * 5 = 1,25 Вт.
Если ток нам неизвестен, но известны напряжение и сопротивление, то можно определить и мощность. Из закона Ома I = U/R, тогда по формуле (А) сила тока равна: P = U 2 /R(Г)
Реостат имеет сопротивление 5 Ом, а напряжение в нем 2,5В , то мощность по формуле (D) будет: P = 2,5 2/5 = 1,25Вт. Зная любые две величины из формулы закона Ома (если учитывать участок цепи), всегда можно определить текущую мощность.
Вспоминая определение мощности, можно написать другую формулу для ее расчета: P = A/t(D), где P – мощность, A – работа электрического тока, t – время, за которое эта работа готово.
Выбирая в магазине тот или иной бытовой прибор, мы часто задаемся вопросом, сколько денег нам придется заплатить за его использование. Особенно это касается обогревателя, работающего от электричества. Иногда, используя сварочный аппарат или электродвигатель, мы даже не подозреваем, сколько он потребляет электроэнергии. Но откуда нам знать нужные нам цифры, если данные об устройствах неизвестны.
Но откуда нам знать нужные нам цифры, если данные об устройствах неизвестны.
Потребляемая мощность электроприборов: таблица с показателями
Для расчетов необходимы элементарные знания электродинамики из школьного курса, связанные с мощностью, напряжением, током. Для того чтобы рассчитать потребляемую мощность устройства, необходимо знать величину напряжения, а также мощность источника. Мощность (P) можно рассчитать, умножив ток на электрическое напряжение в сети.
Силой тока принято называть величину электрического заряда, проходящего через данный участок сети в единицу времени. Физическая величина, характеризуемая электрическим полем, создающим ток — это напряжение.
Используются следующие метрики:
- В качестве несистемной единицы измерения мощности иногда используют несколько вольт-ампер;
- В этом случае усилие указано в автоматических выключателях.
Это действительно максимальное значение, при котором срабатывает выключатель.
Определение мощности источника питания: методы расчета
Для этого вам потребуется значение тока, обозначаемое как (I), и напряжение, обозначаемое как (V) источника питания. Чтобы вычислить мощность (P), необходимо перемножить эти два значения. Эта сила тока представляет собой количество заряда, которое проходит через определенную поверхность в течение определенного периода времени. Напряжение – переменная величина, характеризующая электрическое поле, создаваемое током.
Приблизительная мощность устройства равна произведению напряжения на силу тока. Формула имеет вид P = I x V.
Обычно:
- Сила тока указывает на автоматические выключатели;
- Указанное значение является максимальным током, при котором включается выключатель;
- Значение напряжения и силы тока обычно указывают на корпус электроприбора или тэн.
Если его там нет, вам следует поискать его в документации.
Как рассчитать потребляемую мощность устройства
Показатель силы тока, а также напряжения некоторых распространенных электроприборов имеется в специализированных справочниках. Если у вас их нет, то дайте запрос и поищите в интернете, или интернет-ресурсах.
Если у вас их нет, то дайте запрос и поищите в интернете, или интернет-ресурсах.
Ток рассчитывается по аналогичной формуле, как и напряжение. Для этого имеющиеся количества необходимо разделить.
Например, нужно рассчитать, сколько энергии потребляет телевизор, потолочный вентилятор или микроволновая печь, при этом на корпусе устройства указан такой показатель, как их сила тока. Для выполнения расчета необходимо найти напряжение и сопротивление вентилятора. Вы можете найти его в Интернете или у производителя. После этого, подставив в формулы значения, можно легко рассчитать мощность вентилятора.
Что нужно знать о мощности:
- Мощность — это скорость преобразования, передачи или потребления энергии. Обычно вы платите за электроэнергию в соответствии с потребленной мощностью.
- Измеряется мощность в ваттах (Вт).
- Мощность прибора — это показатель энергии, потребляемой прибором.
- Номинальная мощность – это требуемая величина, необходимая для корректной работы устройства.

- Ток постоянный и переменный. Переменный ток может различаться по величине или направлению. Питается электричеством. Определение — постоянный ток не меняется ни по направлению, ни по величине. Источник этого тока можно назвать батареей или батареей.
Пусковая мощность – это единица измерения, необходимая для запуска двигателя или компрессора.
Рассмотрим, как работает измеритель мощности в розетке
Если вам нужно узнать, какой мощностью обладает объект, вы можете измерить ток и напряжение с помощью мультиметра, а затем перемножить их. Существуют также устройства, определяющие мощность. Их называют ваттметрами. Индикатор питания вычисляет встроенный калькулятор, и индикатор тут же появляется на его дисплее.
Как пользоваться ваттметром и мультиметром:
- Включаем прибор в розетку 220В;
- В ваттметр вставляем штекер того прибора, который нам нужно измерить;
- Ждем, когда на дисплее появится нужный индикатор.

На задней панели устройства есть отсек для батареек, обычно идущих в комплекте. На табличке рядом с ним есть информация с характеристиками ваттметра, его номером, а также вилкой. Снаружи есть дисплей. Управление осуществляется 4-мя кнопками, возле которых находится розетка для подключения бытовой техники, оборудования и техники.
При включении устройства на его экране появляются три информационные строки, как счетчик: одна графическая и две цифровые строки.
Четвертой кнопкой Значение можно переключать и определять следующие измеряемые параметры:
- Напряжение сети;
- Мощность, потребляемая подключенным устройством;
- Ток, потребляемый устройством.
При установленном предельном значении по напряжению и току одна из характеристик устройства подаст сигнал. Это означает перегрузку.
Можно ли рассчитать потребляемую мощность, зная примерную мощность
При самостоятельном расчете не стоит забывать о малой мощности, которую потребляют некоторые устройства, даже когда они не работают, но подключены к розетке. Это тоже надо учитывать. Многие устройства снабжены индикатором или имеют светодиод, который также может потреблять некоторую мощность.
Это тоже надо учитывать. Многие устройства снабжены индикатором или имеют светодиод, который также может потреблять некоторую мощность.
Осведомленность о энергопотреблении устройства позволяет значительно экономить электроэнергию.
Расчеты производятся следующим образом:
- При расчете мощности по формуле получается примерное значение.
- В том случае, когда вам нужен точный коэффициент мощности, лучше использовать ваттметр. Любая мощность, будь то электрическая, тепловая или механическая, измеряется в ваттах. Для того, чтобы иметь возможность экономить электроэнергию, важно знать их мощность, потребляемую приборами.
- Чтобы вычислить разницу между двумя степенями, одно из этих значений нужно вычесть из другого.
Когда вы оплачиваете счета за электроэнергию, вы фактически платите за каждый потребленный киловатт. Чтобы перевести ватт в киловатты, нужно один показатель в ваттах разделить на 1000, а затем полученное значение в киловаттах умножить на количество часов, отработанных прибором. В результате вы получаете требуемое значение, существующее как (кВтч). Если умножить его на стоимость 1 киловатта электроэнергии, то можно узнать, сколько придется платить за эксплуатацию прибора. Например, если в вашем доме или квартире всего 10 лампочек и 100 ватт — мощность, потребляемая каждой лампой, то произведя расчет, мы получим 10 х 100, в итоге выйдет 1000 ватт — суммарная мощность всех ламп. Если 1000 Вт разделить на 1000, то получится 1 кВт. Теперь нетрудно подсчитать, что если, лампочки горели 2000 часов в год, а один киловатт в час стоит 6 рублей. То есть за год надо заплатить 12 000 руб.
В результате вы получаете требуемое значение, существующее как (кВтч). Если умножить его на стоимость 1 киловатта электроэнергии, то можно узнать, сколько придется платить за эксплуатацию прибора. Например, если в вашем доме или квартире всего 10 лампочек и 100 ватт — мощность, потребляемая каждой лампой, то произведя расчет, мы получим 10 х 100, в итоге выйдет 1000 ватт — суммарная мощность всех ламп. Если 1000 Вт разделить на 1000, то получится 1 кВт. Теперь нетрудно подсчитать, что если, лампочки горели 2000 часов в год, а один киловатт в час стоит 6 рублей. То есть за год надо заплатить 12 000 руб.
Электроприборы: потребляемая мощность (видео)
Мощность, потребляемую любым агрегатом, можно проверить ваттметром, либо рассчитать самостоятельно в домашних условиях по простой формуле. Необходимо знать этот показатель силы тока, измеряемой в А (амперах), а также величину напряжения, учитываемую в вольтах (В). Эти важные расчеты электроэнергии позволят вам сэкономить электроэнергию, а значит и стоимость коммунальных платежей для потребителя.
Оптимальным источником энергии для обогрева испарительного бака является квартирная электрическая сеть напряжением 220 В. Можно просто использовать для этой цели бытовую электрическую плиту. Но, при нагреве на электроплите, много энергии тратится на бесполезный нагрев самой плиты, а также излучает во внешнюю среду, от нагревательного элемента, не совершая при этом полезной работы. Эта, затрачиваемая энергия, может достигать приличных значений — до 30-50%, от общей затраченной мощности на обогрев куба. Поэтому использование обычных электроплит нерационально с точки зрения экономии. Ведь за каждый лишний киловатт энергии приходится платить. Наиболее эффективно использование заложенной в испарительную способность эл. Нагревательные элементы. При такой конструкции вся энергия расходуется только на нагрев куба + излучение его стенок наружу. Стены куба, для уменьшения теплопотерь, необходимо утеплить. Ведь затраты лучистого тепла, от стен самого куба, тоже могут составлять до 20 и более процентов от всей потребляемой мощности, в зависимости от его размера. Для использования в качестве ТЭНов, встраиваемых в бак, вполне подойдет от электронагревателей, от бытовых электрочайников или других подходящих по размерам. Мощность таких обогревателей может быть разной. На корпусе выбиты наиболее часто используемые ТЭНы мощностью 1,0 кВт и 1,25 кВт. Но есть и другие.
Для использования в качестве ТЭНов, встраиваемых в бак, вполне подойдет от электронагревателей, от бытовых электрочайников или других подходящих по размерам. Мощность таких обогревателей может быть разной. На корпусе выбиты наиболее часто используемые ТЭНы мощностью 1,0 кВт и 1,25 кВт. Но есть и другие.
Следовательно, мощность 1-го ТЭНа может не соответствовать по параметрам нагрев куба и быть больше или меньше. В таких случаях для получения необходимой мощности нагрева можно использовать несколько нагревателей, соединенных последовательно или последовательно-параллельно. Коммутация различных комбинаций подключения ТЭНов, выключатель от бытового электрического. пластин, можно получить разную мощность. Например, имея восемь встроенных ТЭНов, по 1,25 кВт каждый, в зависимости от комбинации включения можно получить следующую мощность.
- 625 Вт
- 933 Вт
- 1,25 кВт
- 1,6 кВт
- 1,8 кВт
- 2,5 кВт
Этого диапазона вполне достаточно для регулировки и поддержания нужной температуры при дистилляции и ректификации. Но можно получить разную мощность, добавляя количество режимов переключения и используя разные комбинации включения.
Но можно получить разную мощность, добавляя количество режимов переключения и используя разные комбинации включения.
Последовательное подключение 2-х обогревателей по 1,25 кВт и подключение их к сети 220В, суммарно дает 625 Вт. Параллельное подключение, суммарно дает 2,5 кВт.
Каталог кэша не найден! Каталог кэша не найден! Каталог кэша не найден!
Нам известно напряжение, действующее в сети, это 220В. Далее мы также знаем мощность нагревателя, выбитого на его поверхности, это 1,25кВт, значит нам нужно знать ток протекающий в этой цепи. Зная напряжение и мощность, узнаем из следующей формулы.
Сила тока = мощность, деленная на напряжение сети.
Записывается так: I = P/U .
Где I — сила тока.
P — мощность в ваттах.
U — напряжение в вольтах.
При расчете мощности, указанной на корпусе обогревателя в кВт, необходимо перевести ее в ватты.
1,25 кВт = 1250 Вт . Подставляем известные значения в эту формулу и получаем силу тока.
Подставляем известные значения в эту формулу и получаем силу тока.
I = 1250 Вт / 220 = 5,681 А
R = U / I, где
R — сопротивление в Омах
U — напряжение в вольтах
I — сила тока
Подставляем известные значения сопротивления в формулу и находим ТЭН.
R = 220/5,681 = 38,725 Ом.
R > = R1 + R2 + R3 и т. д.
Таким образом, два последовательно соединенных ТЭП имеют сопротивление, равное 77,45 Ом. Теперь нетрудно подсчитать мощность, выделяемую этими двумя нагревателями.
P = U 2 / R Где,
P — мощность в ваттах
U 2 — напряжение в квадрате, в вольтах
R — общее сопротивление последнего. Cpd. ДЕСЯТКИ
P = 624,919 Вт , округлить до значения 625 Вт .
В таблице 1.1 приведены значения для последовательного соединения нагревателей.
Таблица 1. 1.
1.
| Номер ТЭН | Мощность (Вт) | Сопротивление (Ом) | Напряжение (АТ) | Сила тока (А) |
| 1 | 1250 000 | 38 725 | 220 | 5,68 |
| Последовательное соединение | ||||
| 2 | 625 | 2 ТЭС = 77,45 | 220 | 2,84 |
| 3 | 416 | 3 ТЭС = 1 16 175 | 220 | 1,89 |
| 4 | 312 | 4 ТЭС = 154,9 | 220 | 1,42 |
| 5 | 250 | 5 TES = 193 625 | 220 | 1,13 |
| 6 | 208 | 6 ТЭС = 232,35 | 220 | 0,94 |
| 7 | 178 | 7 TES = 271 075 | 220 | 0,81 |
| 8 | 156 | 8 ТЭС = 309,8 | 220 | 0,71 |
В таблице 1. 2 приведены значения для параллельного подключения нагревательных элементов.
2 приведены значения для параллельного подключения нагревательных элементов.
Таблица 1.2.
| Номер ТЭН | Мощность (Вт) | Сопротивление (Ом) | Напряжение (АТ) | Сила тока (А) |
| Параллельное соединение | ||||
| 2 | 2500 | 2 ТЭС = 19,3625 | 220 | 11,36 |
| 3 | 3750 | 3 TES = 12,9083 | 220 | 17,04 |
| 4 | 5000 | 4 ТЭС = 9,68125 | 220 | 22,72 |
| 5 | 6250 | 5 ТЭС = 7,7450 | 220 | 28,40 |
| 6 | 7500 | 6 ТЭС = 6,45415 | 220 | 34,08 |
| 7 | 8750 | 7 ТЭС = 5,5321 | 220 | 39,76 |
| 8 | 10000 | 8 TES = 4840 | 220 | 45,45 |
Еще один немаловажный плюс, который дает последовательное подключение Это уменьшенный в несколько раз ток, протекающий через них, и соответственно небольшой нагрев корпуса ТЭНа, благодаря чему брага не пригорает при перегонке и не вносит неприятный дополнительный привкус и запах в конечном продукте. Также срок службы ТЭНов при таком включении будет практически вечным.
Также срок службы ТЭНов при таком включении будет практически вечным.
Расчеты выполнены для ТЭНов мощностью 1,25 кВт . Для нагревателей разной мощности суммарную мощность необходимо пересчитывать по закону Ом, по приведенным выше формулам.
Течение тока по проводнику можно сравнить с течением реки по трубе. Неправильный расчет сечения кабеля приводит к перегреву и короткому замыканию или к неоправданным затратам. Очень важно проводить расчеты на этапе проектирования, так как выход из строя скрытой проводки и последующая замена связаны со значительными затратами.
Основное назначение проводников – доставка электрической энергии потребителям в необходимом количестве. Поскольку в нормальных условиях эксплуатации сверхпроводников нет, приходится учитывать сопротивление материала проводника.
Расчет необходимого сечения жил и кабелей в зависимости от суммарной мощности потребителей основан на многолетнем опыте эксплуатации. Общий ход расчетов:
- П = (П1 + П2 +.
 .ПН)*К*Дж;
.ПН)*К*Дж; - выберите необходимое сечение по таблице 1.
P — мощность всех потребителей, подключенных к расчетной ветке, в Ваттах.
P1, P2, PN — мощность первого потребителя, второго, n-го соответственно, в Ваттах.
Таблица 1. Сечения проводов всегда следует выбирать в большую сторону (+)
Реактивная и активная мощность прибора
Мощность потребителей указывается в документах на оборудование. Обычно в паспортах оборудования активная мощность указывается вместе с реактивной мощностью.
Устройства с активным типом нагрузки преобразуют всю получаемую электрическую мощность с учетом КПД в полезную работу: механическую, тепловую или в ином ее виде. К приборам с активной нагрузкой относятся лампы накаливания, обогреватели, электроплиты. Для таких устройств расчет тока и напряжения следующий:
P = U * I
P — мощность в Вт
U — напряжение в В
I — ток в А
При нулевом смещении фаз мощность P = U * I всегда имеет положительное значение. Такой график фаз силы тока I и напряжения U имеют устройства с активным видом нагрузки
Такой график фаз силы тока I и напряжения U имеют устройства с активным видом нагрузки
Устройства с реактивным видом нагрузки способны аккумулировать энергию, поступающую от источника, а затем возвращать. Такой обмен происходит за счет смещения синусоидального тока и синусоидального напряжения.
При наличии фазового смещения между синусоидой тока и синусоидой напряжения мощность P = U * I может быть отрицательной. Устройство с реактивной мощностью возвращает накопленную энергию обратно в источник
К устройствам с реактивной мощностью относятся электродвигатели, электронные устройства всех размеров и назначений, а также трансформаторы.
Реактивная мощность имеет зависимость от угла сдвига фаз между синусоидами напряжения и тока. Угол сдвига фаз выражается через cosφ. Для нахождения полной мощности используется следующая формула:
P = P p / cosφ
P p — реактивная мощность в Вт
Обычно в паспортных данных прибора указывают реактивную мощность и cosφ.
Пример: в паспорте перфоратора указана реактивная мощность 1200Вт и cosφ=0,7. Следовательно, общая потребляемая мощность составит:
P = 1200/0,7 = 1714Вт
Если cosφ найти не удалось, то для подавляющего большинства бытовых приборов cosφ можно принять равным 0,7.
Коэффициенты одновременности и резерва
К — безразмерный коэффициент одновременности, показывает, сколько потребителей одновременно может быть включено в сеть. Редко бывает так, что все устройства одновременно потребляют электроэнергию. Одновременная работа телевизора и музыкального центра маловероятна. Из установившейся практики К можно принять равным 0,8. Если вы планируете использовать всех клиентов одновременно, K следует установить равным 1.
J Безразмерный запас прочности. Характеризует создание резерва мощности для будущих потребителей. Прогресс не стоит на месте, каждый год появляются новые и удивительные новые и полезные электроприборы. Ожидается, что к 2050 году прирост потребления электроэнергии составит 84%. Обычно J принимают в пределах от 1,5 до 2,0.
Обычно J принимают в пределах от 1,5 до 2,0.
Расчет сечения провода геометрическим методом
Во всех электротехнических расчетах принимается площадь поперечного сечения проводника — сечение жилы. Измеряется в мм 2.
Часто необходимо научиться правильно рассчитывать сечение провода по диаметру жилы провода. В этом случае имеется простая геометрическая формула для монолитного провода круглого сечения:
S = π * R 2 = π * D 2/4 , или наоборот
D = √ (4 * S / π)
Для проводников прямоугольного сечения:
S = h*m
S — площадь жилы в мм 2
R — радиус жилы в мм
D — диаметр жилы в мм
h, m — ширина и высота соответственно в мм
π — число пи, равное 3,14
При приобретении многожильного провода, в котором одна жила состоит из набора многожильных проводов круглого сечения расчет ведется по формуле:
S = N * D 2 / 1,27
N — количество жил в жиле
Провода, имеющие жилы из нескольких жил, жил, обычно имеют лучшую проводимость, чем монолитные. Это связано с особенностями протекания тока по круглому проводнику.
Это связано с особенностями протекания тока по круглому проводнику.
Электрический ток — это движение одноименных зарядов по проводнику. Одноименные заряды отталкиваются, поэтому плотность распределения заряда смещается к поверхности проводника.
Еще одним преимуществом многожильных проводов является их гибкость и механическая стойкость. Монолитные провода дешевле и используют их в основном для стационарной прокладки.
Пример расчета сечения по мощности
Задача: суммарная мощность потребителей на кухне 5000Вт (имеется в виду перерасчет мощности всех реактивных потребителей). Все потребители подключены к однофазной сети 220В и питаются от одной ветки.
Таблица 2. Если в дальнейшем планируется подключение дополнительных потребителей, в таблице представлены необходимые мощности общебытовых приборов (+)
Коэффициент одновременности К принимается равным 0,8. Кухня — это место постоянных инноваций, мало ли чего, коэффициент запаса J = 2,0. Общая расчетная мощность:
Общая расчетная мощность:
P = 5000 * 0,8 * 2 = 8000Вт = 8кВт
Используя значение расчетной мощности, найдите ближайшее значение в Таблице 1.
Ближайшим подходящим значением сечения жилы для однофазной сети является медная жила сечением 4 мм 2 . Аналогичное сечение провода с алюминиевой жилой 6 мм 2 . Для одножильной проводки минимальный диаметр составляет 2,3 мм и 2,8 мм соответственно. В случае многожильного варианта суммируется сечение отдельных проводов.
Расчет сечения по току
Расчет сечения по току и мощности кабелей и проводов даст более точные результаты. Такие расчеты позволяют оценить общее влияние на проводники различных факторов, в том числе тепловой нагрузки, марки проволоки, типа прокладки, условий эксплуатации и т. д.
Весь расчет осуществляется на следующих этапах:
- выбор мощности для всех потребителей;
- расчет токов, проходящих через проводник;
- выбор подходящего сечения по таблицам.
Для этого варианта потребляемый ток потребителей с напряжением принимается без учета поправочных коэффициентов. Они будут учтены при суммировании тока.
Они будут учтены при суммировании тока.
Формулы расчета тока
Для тех, кто забыл школьный курс физики, предлагаем основные формулы в виде графической схемы в качестве наглядной шпаргалка:
«Классическое колесо» наглядно демонстрирует взаимосвязь формул и взаимозависимость характеристики электрического тока
Запишем зависимость силы тока I от мощности P и напряжения сети U:
I = P/U л
I — ток получен в амперах
P — мощность в ваттах
U l — линейное напряжение в вольтах.
Линейное напряжение в общем случае зависит от источника электроснабжения, бывает одно- и трехфазным. Взаимосвязь линейного и фазного напряжений:
U л = U * cosφ при однофазном напряжении
U л = U * √3 * cosφ при трехфазном напряжении
Для бытовых электропотребителей принимают cosφ = 1, поэтому линейное напряжение можно переписать:
U l = 220В для однофазного напряжения
U L = 380В для трехфазного напряжения
I = (I1+I2+. ..IN)*K*J
..IN)*K*J
I — полный ток в амперах
I1..IN — сила тока каждого потребителя в амперах
К — коэффициент одновременности.
Дж – коэффициент безопасности.
Коэффициенты K и J имеют те же значения, которые использовались при расчете общей мощности.
Возможен случай, когда в трехфазной сети через разные фазные проводники протекает ток неодинаковой силы. Это происходит при одновременном подключении к трехфазному кабелю однофазных и трехфазных потребителей. Например, питается трехфазный автомат и однофазное освещение.
Возникает естественный вопрос: как в таких случаях рассчитывать сечение многожильного провода? Ответ прост — расчеты производятся на максимально загруженном ядре.
Выбор подходящего сечения из таблиц
В правилах эксплуатации электроустановок (ПЭС) имеется ряд таблиц для выбора необходимого сечения жилы кабеля.
Проводимость проводника зависит от температуры. Для металлических проводников сопротивление увеличивается с повышением температуры. При превышении определенного порога процесс становится самоподдерживающимся: чем выше сопротивление, тем выше температура, выше сопротивление и т. д. Проводник не перегорает и не вызывает короткого замыкания.
При превышении определенного порога процесс становится самоподдерживающимся: чем выше сопротивление, тем выше температура, выше сопротивление и т. д. Проводник не перегорает и не вызывает короткого замыкания.
В следующих двух таблицах показаны сечения проводников в зависимости от токов и способа их прокладки.
Кабель отличается от провода тем, что все жилы, снабженные собственной изоляцией, скручены в пучок и заключены в общую изоляционную оболочку.
Таблица 3. Сначала необходимо выбрать способ прокладки проводов, от этого зависит насколько эффективно происходит охлаждение (+)
Таблица 4. Открытый способ указан для всех значений сечения проводника, но на практике сечения менее 3 мм2 открыто не прокладывают из соображений механической прочности (+)
При использовании таблиц к допустимому многолетнему току коэффициенты равны:
- 0,68 при 5-6 проживших;
- 0,63 если выжило 7-9;
- 0,6 если жило 10-12.

Понижающие коэффициенты применяются к значениям токов из столбца «открыто».
Нулевая и заземляющая жилы в число жил не входят.
По нормам ПЭС выбор сечения нулевой жилы по допустимому длительному току производится не менее 50% фазного провода.
В следующих двух таблицах представлена зависимость допустимого продолжительного тока при прокладке в земле.
Таблица 5. Зависимость допустимого продолжительного тока для медных кабелей при прокладке в воздухе или в земле
Токовые нагрузки при открытой прокладке и при углублении в землю различны. Они считаются равными, если прокладка в грунте осуществляется с помощью лотков.
Таблица 6. Зависимость допустимого длительного тока для алюминиевых кабелей для прокладки в воздухе или в земле
Для прокладки временных линий электроснабжения (несущих, если для частного использования) применяется следующая таблица.
Таблица 7. Допустимый длительный ток при использовании переносных шланговых шнуров, переносных шланговых и шахтных тросов, прожекторных тросов, гибких переносных проводов. Применяются только медные жилы
Применяются только медные жилы
При прокладке кабелей в земле помимо теплоотводящих свойств необходимо учитывать удельное сопротивление, что отражено в следующей таблице
Таблица 8. Поправочный коэффициент в зависимости от вида и удельного сопротивления грунта на допустимый длительный ток, при расчете сечения кабеля (+)
Расчет и выбор медных жил до 6мм 2 или алюминиевых до 10мм 2 осуществляется как для длительного тока. В случае больших сечений можно применить понижающий коэффициент:
0,875 * √T pv
T pv — отношение продолжительности включения к продолжительности цикла. Продолжительность включения принимается не более 4 минут. При этом цикл не должен превышать 10 минут.
Пример расчета сечения токопровода
- трехфазный деревообрабатывающий станок мощностью 4000 Вт;
- сварочный аппарат трехфазный мощностью 6000Вт;
- бытовая техника в доме общей мощностью 25 000 Вт;
Подключение осуществляется пятижильным кабелем (три фазных провода, один нулевой и один заземляющий), проложенным в земле.
Изоляция кабельно-проводниковой продукции рассчитывается на конкретное значение рабочего напряжения. Следует учитывать, что указанное изготовителем рабочее напряжение его изделия должно быть выше напряжения в сети
Шаг 1. Рассчитываем линейное напряжение трехфазного подключения:
U l = 220 * √3 = 380В
Шаг № 2. Бытовые приборы, станки и сварочные аппараты имеют реактивную мощность, поэтому мощность машин и оборудования составит:
Р тэ = 25000 / 0,7 = 35700Вт
Побор = 10000 / 0,7 = 14300Вт
Этап №3 . Ток необходимый для подключения бытовых приборов:
I тек = 35700/220 = 162А
Шаг № 4 . Ток, необходимый для подключения оборудования:
I обор = 14300/380 = 38А
Шаг №5 . Требуемый ток для подключения бытовых приборов рассчитывается из расчета на одну фазу. По условию задачи выделяют три фазы. Следовательно, ток можно разделить на фазы. Для простоты примем равномерное распределение:
I te = 162/3 = 54А
Шаг № 6. Ток на фазу:
Ток на фазу:
I ф = 38 + 54 = 92А
Шаг №7. Техника и бытовая техника работать одновременно не будут, кроме этого заложим резерв равный 1,5. После применения поправочных коэффициентов:
I ф = 92 * 1,5 * 0,8 = 110 А
Шаг № 8. Несмотря на то, что в кабеле 5 жил, учитываются только трехфазные жилы. По Таблице 8 в графе трехжильный кабель в земле находим, что сила тока в 115А соответствует сечению жилы 16мм 2 .
Шаг № 9 . По таблице 8 применяют поправочный коэффициент в зависимости от характеристик земельного участка. Для нормального типа заземления коэффициент равен 1.
Шаг № 10 . Не обязательно рассчитайте диаметр жилы:
D = √(4*16/3,14) = 4,5мм
Если расчет производился только по мощности, без учета особенностей прокладки кабеля, сечение жилы будет 25 мм 2 . Расчет силы тока более сложен, но иногда позволяет сэкономить значительные средства, особенно если речь идет о многожильных силовых кабелях.
Расчет падения напряжения
Любой проводник, кроме сверхпроводников, имеет сопротивление. Поэтому при достаточной длине кабеля или провода происходит падение напряжения. Стандарты PES требуют, чтобы сечение жилы кабеля было таким, чтобы падение напряжения составляло не более 5%.
В первую очередь это касается низковольтных кабелей малого сечения. Расчет падения напряжения следующий:
R = 2 * (ρ * L) / S
U пад = I * R 9
R — сопротивление проводника, Ом жилы, Ом*мм 2 /м
S — сечение жилы, мм 2
U пад — падение напряжения, В
U % — падение напряжения по отношению к U лин, %
Таблица 9. Удельное сопротивление обычных металлических жил (+)
Пример расчета несущей
Желающим подключить бытовой сварочный аппарат к сети филиала следует учитывать текущее сито, на которое рассчитан используемый кабель. Не исключено, что суммарная мощность рабочих инструментов может быть выше. Оптимальный вариант — подключение потребителей к отдельным ответвлениям
Оптимальный вариант — подключение потребителей к отдельным ответвлениям
Шаг 1. Рассчитываем сопротивление медного провода, пользуясь таблицей 9:
R = 2 * (0,0175 * 20) / 1,5 = 0,47 Ом
Шаг №2 Ток, протекающий по проводнику:
I = 7000/220 = 31,8 А
Шаг № 3. Падение напряжения на проводе:
U pad = 31,8 * 0,47 = 14,95 В Шаг № 4
Рассчитайте процент падения напряжения:
U% = (14,95/220) * 100 = 6,8%
Вывод: для подключения сварочного аппарата требуется проводник с большим сечением.
Видеоматериалы по подбору жил
Расчет сечения жилы по формулам:
Рекомендации специалистов по выбору кабельно-проводниковой продукции:
Приведенные расчеты справедливы для медных и алюминиевых жил промышленного назначения. Для других типов проводников предварительно рассчитывается суммарная теплоотдача. На основании этих данных рассчитывается максимальный ток, способный протекать по проводнику, не вызывая чрезмерного нагрева.
Интеграция сверхмягкой органической солнечной батареи на теле насекомых-киборгов с неповрежденной подвижностью
Abstract
Насекомые-киборги были предложены для таких применений, как поиск и спасение в городах. Устройства для сбора энергии, устанавливаемые на теле, имеют решающее значение для расширения диапазона активности и функциональности насекомых-киборгов. Однако их выходная мощность ограничена менее чем 1 мВт, что значительно ниже, чем требуется для беспроводного управления движением. Площадь и нагрузка устройства сбора энергии значительно ухудшают подвижность крошечных роботов. Здесь мы описываем интеграцию ультрамягкого органического модуля солнечной батареи в насекомых-киборгов, который сохраняет их способности к движению. Наша количественная стратегия проектирования системы, разработанная с использованием комбинации ультратонкой пленочной электроники и адгезивно-неадгезивной прокладочной структуры для выполнения основных движений насекомых, успешно достигла фундаментального движения перемещения и самовосстановления. Установленный на корпусе сверхтонкий модуль органических солнечных элементов обеспечивает выходную мощность 17,2 мВт. Мы демонстрируем его осуществимость, демонстрируя подзарядку беспроводного управления движением насекомых-киборгов.
Установленный на корпусе сверхтонкий модуль органических солнечных элементов обеспечивает выходную мощность 17,2 мВт. Мы демонстрируем его осуществимость, демонстрируя подзарядку беспроводного управления движением насекомых-киборгов.
Введение
Киборги, являющиеся интеграцией машин и организмов, могут использоваться не только для замены дефектных частей тела организма, но и для реализации функций, превышающих нормальные возможности организма 1 . Достижения в области электроники привели к увеличению интеграции организмов и машин. Миниатюризация и производство полупроводниковых чипов с низким энергопотреблением с помощью микро- и нанотехнологий привели к созданию киборгов малых организмов. В частности, насекомые-киборги с небольшими интегральными схемами для контроля их поведения были предложены для таких приложений, как поиск и спасение в городах, мониторинг окружающей среды и осмотр опасных зон 9.2670 2,3,4,5,6,7 . Интеграция тонкой и мягкой электроники в организмы может упростить их использование в многочисленных приложениях 8,9,10,11 . Растягивающаяся электроника позволяет интегрировать устройства на трехмерные криволинейные поверхности с подвижными соединениями 12,13 .
Растягивающаяся электроника позволяет интегрировать устройства на трехмерные криволинейные поверхности с подвижными соединениями 12,13 .
Эволюция электроники, которая может быть интегрирована с организмами, увеличила потребность в разработке устройств электропитания с более высокой плотностью мощности. Ограничения по объему и весу аккумуляторов для непривязанных роботов можно преодолеть с помощью стратегий подзарядки, таких как возвращение роботов в назначенные места для подзарядки до того, как их аккумуляторы разрядятся 14 и беспроводное питание аккумуляторов 15,16 . Устройство сбора энергии, установленное на роботе, может расширить спектр его деятельности 17,18 . Биотопливный элемент, вырабатывающий энергию из тела насекомого, является перспективным устройством для сбора энергии 19 . На сегодняшний день 333 мкВт — это самая высокая выходная мощность, достигаемая с помощью ферментативных биотопливных элементов. Зарядка аккумулятора и управление цепью были достигнуты для этой выходной мощности для ходячих тараканов 20,21 .
Зарядка аккумулятора и управление цепью были достигнуты для этой выходной мощности для ходячих тараканов 20,21 .
Расширенные функции, такие как беспроводное управление движением киборгов-насекомых, требуют устройств сбора энергии, которые могут генерировать несколько милливатт или выше. Солнечная батарея может генерировать мощность 10 мВт см 92 670 –2 92 671 или выше в условиях солнечного света на открытом воздухе; эта технология может генерировать максимальную выходную мощность, доступную на открытом воздухе 22 . Жесткий кремниевый солнечный элемент, установленный на неподвижном насекомом, используется для зарядки литий-полимерных аккумуляторов 23,24 . Новые солнечные элементы, в том числе органические 25 , перовскит 26 и ячейки с квантовыми точками 27 могут достигать высокой мощности на единицу веса из-за их уменьшенной толщины подложки и пассивации, что полезно для достижения интеграции с живыми мелкими насекомыми. Ультратонкие органические солнечные элементы, имеющие общую толщину менее 5 мкм, могут обеспечить КПД преобразования энергии (КПД) 15,8%, что дает удельную мощность 33,8 Вт г –1 28 .
Ультратонкие органические солнечные элементы, имеющие общую толщину менее 5 мкм, могут обеспечить КПД преобразования энергии (КПД) 15,8%, что дает удельную мощность 33,8 Вт г –1 28 .
Однако достижение выходной мощности 10 мВт или выше с помощью сборщиков энергии, установленных на живых подвижных насекомых для беспроводного управления движением, остается сложной задачей. Для интеграции устройств в мелких животных с ограниченной площадью поверхности и переноски грузов 29 , конструкция устройства и стратегия интеграции солнечных элементов большой площади необходимы для получения достаточной выходной мощности и одновременного поддержания основных поведенческих способностей насекомых. Поскольку выходная мощность солнечного элемента пропорциональна площади, как нагрузка устройства, так и контакт между устройством и подвижными соединениями значительно ухудшают возможности движения.
В этой статье мы сообщаем о перезаряжаемом насекомом-киборге, в котором используется сверхмягкий органический модуль солнечной батареи, не нарушающий основных двигательных способностей насекомого, и демонстрируем подзарядку беспроводного управления движением со всеми компонентами, интегрированными в насекомое. Комбинация ультратонкой пленочной электроники и клейкой-неклейкой прокладочной структуры на брюшке насекомого продемонстрировала более 80% успеха в попытках самовосстановления. Эффект прикрепления пленки к основному движению был определен количественно с использованием аппроксимированной модели нагрузки на изгиб. Ультратонкий модуль органических солнечных элементов достиг выходной мощности 17,2 мВт на изогнутом брюшке насекомого, которое заряжало литий-полимерный аккумулятор для работы модуля управления беспроводным передвижением.
Комбинация ультратонкой пленочной электроники и клейкой-неклейкой прокладочной структуры на брюшке насекомого продемонстрировала более 80% успеха в попытках самовосстановления. Эффект прикрепления пленки к основному движению был определен количественно с использованием аппроксимированной модели нагрузки на изгиб. Ультратонкий модуль органических солнечных элементов достиг выходной мощности 17,2 мВт на изогнутом брюшке насекомого, которое заряжало литий-полимерный аккумулятор для работы модуля управления беспроводным передвижением.
Результаты и обсуждение
Структура перезаряжаемого насекомого-киборга
Gromphadorhina portentosa ( G. portentosa , мадагаскарский шипящий таракан) была использована в этом исследовании. Электронные компоненты крепились на спинной стороне насекомого (рис. 1а, б). Беспроводной модуль управления движением, состоящий из цепей беспроводной связи, схем контроллера напряжения стимуляции, повышающих цепей и литий-полимерной батареи, был установлен на грудной клетке с поддержкой трехмерного (3D) напечатанного мягкого рюкзака, который повторял изогнутую поверхность. грудной клетки (рис. 1в). Модуль органического солнечного элемента толщиной 4 мкм был прикреплен к брюшной полости. Мощность, генерируемая сверхтонким органическим солнечным элементом при имитации солнечного света (100 мВт см –2 ) был повышен до 4,2 В с помощью повышающей схемы для зарядки аккумулятора, и аккумулятор подавал питание на модуль управления беспроводным движением. Сигналы управления локомоцией передавались с внешнего сервера по беспроводной сети с помощью Bluetooth (рис. 1г). Сигналы стимуляции подавались на церки через провода для беспроводного управления движением насекомого (дополнительная рис. 1). Церки — парные придатки на самых задних сегментах брюшка. При электрическом раздражении правого церка насекомое совершало поворотно-правую локомоцию и наоборот.
грудной клетки (рис. 1в). Модуль органического солнечного элемента толщиной 4 мкм был прикреплен к брюшной полости. Мощность, генерируемая сверхтонким органическим солнечным элементом при имитации солнечного света (100 мВт см –2 ) был повышен до 4,2 В с помощью повышающей схемы для зарядки аккумулятора, и аккумулятор подавал питание на модуль управления беспроводным движением. Сигналы управления локомоцией передавались с внешнего сервера по беспроводной сети с помощью Bluetooth (рис. 1г). Сигналы стимуляции подавались на церки через провода для беспроводного управления движением насекомого (дополнительная рис. 1). Церки — парные придатки на самых задних сегментах брюшка. При электрическом раздражении правого церка насекомое совершало поворотно-правую локомоцию и наоборот.
a Фотография насекомого-киборга с использованием G. portentosa . Масштабная линейка, 10 мм. b Схемы киборгов. c Схема крепления жестких компонентов к грудной клетке с помощью напечатанного на 3D-принтере рюкзака. d Принципиальная схема системы беспроводного модуля управления движением и аккумуляторных источников питания.
portentosa . Масштабная линейка, 10 мм. b Схемы киборгов. c Схема крепления жестких компонентов к грудной клетке с помощью напечатанного на 3D-принтере рюкзака. d Принципиальная схема системы беспроводного модуля управления движением и аккумуляторных источников питания.
Полноразмерное изображение
Мягкий рюкзак, идеально ложащийся на криволинейные поверхности, со стабилизированным креплением компонентов на грудной клетке. Рюкзак был разработан с использованием точной 3D-модели G. portentosa (дополнительный рис. 2) и 3D-печати из эластичного полимера. Столбчатая структура внизу соответствует форме изогнутой поверхности (рис. 1с, дополнительный рис. 3). Благодаря мягкому материалу и столбчатой структуре рюкзак, разработанный с использованием конструкции, извлеченной из отдельного насекомого, может выдерживать разницу в форме, существующую между отдельными насекомыми, и обеспечивать хорошее сцепление (дополнительный рис. 4). Прилипание рюкзака, прикрепленного к грудной клетке, сохранялось даже через месяц в среде размножения, что подтверждало, что рюкзак прилипал к телу в течение длительного времени. Напротив, адгезия между жесткими компонентами с использованием обычного метода адгезии с использованием пчелиного воска, отслаивающегося от грудной клетки после 30 мин при комнатной температуре окружающей среды (примерно 20 °C) 2 .
Напротив, адгезия между жесткими компонентами с использованием обычного метода адгезии с использованием пчелиного воска, отслаивающегося от грудной клетки после 30 мин при комнатной температуре окружающей среды (примерно 20 °C) 2 .
Способность насекомых к движению с тонкими пленками
Была разработана стратегия крепления ультратонких пленок на брюшке, которая не мешала основному движению насекомых. Наблюдение за поперечным сечением живота показало, что каждый сегмент частично перекрывался во время деформации живота (дополнительный рисунок 5 и дополнительный фильм 1). Ход каждого сегмента составлял до 2,5 мм. Свободу движений живота реализовывали с помощью комбинированной технологии ультратонких полимерных пленок и адгезивно-неадгезивной прокладочной структуры, допускающей изгибание пленки (рис. 2а). После прикрепления пленок к животу смоляным клеем клей может быть естественным образом удален с той части, которая перекрывает другие сегменты при деформации, и пленка имеет полую структуру, которая избирательно прилипает только к той части, которая не перекрывается. Эта клейко-неадгезивная перемежающаяся структура оставляет место для того, чтобы пленка изгибалась вверх по мере движения сегмента (дополнительный рис. 6 и дополнительный фильм 1). Аналогичный изгиб наружу наблюдался с париленовыми пленками различной толщины с использованием трехмерной модели, имитирующей брюшные сегменты (дополнительная рис. 7).
Эта клейко-неадгезивная перемежающаяся структура оставляет место для того, чтобы пленка изгибалась вверх по мере движения сегмента (дополнительный рис. 6 и дополнительный фильм 1). Аналогичный изгиб наружу наблюдался с париленовыми пленками различной толщины с использованием трехмерной модели, имитирующей брюшные сегменты (дополнительная рис. 7).
a Схематическое изображение поперечного сечения брюшных сегментов с тонкими пленками, прикрепленными с помощью адгезивно-неадгезивной прокладочной структуры. Чередующаяся структура позволяет изгибать тонкие пленки наружу во время деформации брюшной полости. b , c Изображения преодоления препятствия вблизи начальной точки ( b ) и вблизи конечной точки ( c ). Масштабные линейки, 10 мм. d Коробчатые диаграммы времени прохождения при различных состояниях брюшной полости. Слева: свободное состояние без пленки, в центре: брюшная полость зафиксирована толстой пленкой, справа: париленовая пленка толщиной 3 мкм была приклеена к брюшной полости с чередующейся структурой. Центральная линия, медиана; пределы ящика, верхний и нижний квартили; усы, 1,5-кратный межквартильный размах; баллы, выбросы. e , f Фотографии попытки самовосстановления в перевернутом положении насекомого ( e ) и после успешной попытки ( ф ). Масштабные линейки, 10 мм. г Расчетная нагрузка на изгиб пленок, прикрепленных к животу, в зависимости от толщины пленки. Красные кружки и синие квадраты представляют париленовую пленку ( E = 4,0 ГПа) и пленку PDMS ( E = 3,3 МПа) соответственно. h Вероятность успешного восстановления в зависимости от нагрузки на изгиб. Красные кружки и синие квадраты представляют парилен и пленку PDMS. i Вероятность успешного выпрямления при различных заболеваниях грудной и брюшной полости. Планки ошибок в ч и i представляют собой стандартные отклонения для каждого условия.
Центральная линия, медиана; пределы ящика, верхний и нижний квартили; усы, 1,5-кратный межквартильный размах; баллы, выбросы. e , f Фотографии попытки самовосстановления в перевернутом положении насекомого ( e ) и после успешной попытки ( ф ). Масштабные линейки, 10 мм. г Расчетная нагрузка на изгиб пленок, прикрепленных к животу, в зависимости от толщины пленки. Красные кружки и синие квадраты представляют париленовую пленку ( E = 4,0 ГПа) и пленку PDMS ( E = 3,3 МПа) соответственно. h Вероятность успешного восстановления в зависимости от нагрузки на изгиб. Красные кружки и синие квадраты представляют парилен и пленку PDMS. i Вероятность успешного выпрямления при различных заболеваниях грудной и брюшной полости. Планки ошибок в ч и i представляют собой стандартные отклонения для каждого условия.
Изображение в натуральную величину
Эффективность стратегии прикрепления тонкой пленки была количественно оценена путем измерения времени, необходимого для преодоления препятствия (рис. 2b, c и дополнительный фильм 2). Фиксированный живот увеличивал необходимое время преодоления препятствий (медианные значения от 2,4 до 4,2 с) (рис. 2г). В то время как пленка толщиной 3 мкм с адгезивно-неадгезионной прокладочной структурой достигла примерно такого же времени прохождения, как и без прикрепленной пленки (медиана 2,2 с). Это показывает, что фиксация каждого сегмента значительно ухудшает эту деформируемость и ограничивает движение, и что стратегия тонкопленочного прикрепления эффективно обеспечивает свободу движений.
2b, c и дополнительный фильм 2). Фиксированный живот увеличивал необходимое время преодоления препятствий (медианные значения от 2,4 до 4,2 с) (рис. 2г). В то время как пленка толщиной 3 мкм с адгезивно-неадгезионной прокладочной структурой достигла примерно такого же времени прохождения, как и без прикрепленной пленки (медиана 2,2 с). Это показывает, что фиксация каждого сегмента значительно ухудшает эту деформируемость и ограничивает движение, и что стратегия тонкопленочного прикрепления эффективно обеспечивает свободу движений.
Эффективность была дополнительно подтверждена путем оценки способности к самовосстановлению в положении вверх ногами на земле (рис. 2д, е). Вероятность восстановления G. portentosa без прикрепленных пленок составила 99%, что согласуется с предыдущими результатами 30 . Тонкие пленки с различными модулями Юнга и толщиной были прикреплены к брюшкам G. portentosa . Когда париленовые пленки (модуль Юнга 4,0 ГПа) прикреплялись к животу с помощью адгезивно-неадгезивной прокладочной структуры, показатели успеха выпрямления составляли 96 и 81% для пленок толщиной 5 и 10 мкм соответственно. Для пленок толщиной 15 и 20 мкм вероятность успеха снизилась до 46 и 16% соответственно (дополнительный фильм 3). Аналогичная тенденция наблюдалась, когда мягкий полидиметилсилоксан (PDMS, модуль Юнга 3,3 МПа) был прикреплен к животу (дополнительный рисунок 8 и дополнительный фильм 4). Напротив, показатель успешности выпрямления составил 10 %, когда париленовая пленка толщиной 2 мкм была приклеена к брюшной полости без промежуточной структуры. Эти результаты подтверждают, что сочетание достаточно тонкой пленки и чередующейся структуры сохраняет подвижность насекомых (дополнительная рис. 9).). Кроме того, мы подтвердили, что париленовые пленки толщиной 3 мкм с чередующейся структурой, закрепленные на насекомом, не отпадали в течение как минимум 3 дней.
Для пленок толщиной 15 и 20 мкм вероятность успеха снизилась до 46 и 16% соответственно (дополнительный фильм 3). Аналогичная тенденция наблюдалась, когда мягкий полидиметилсилоксан (PDMS, модуль Юнга 3,3 МПа) был прикреплен к животу (дополнительный рисунок 8 и дополнительный фильм 4). Напротив, показатель успешности выпрямления составил 10 %, когда париленовая пленка толщиной 2 мкм была приклеена к брюшной полости без промежуточной структуры. Эти результаты подтверждают, что сочетание достаточно тонкой пленки и чередующейся структуры сохраняет подвижность насекомых (дополнительная рис. 9).). Кроме того, мы подтвердили, что париленовые пленки толщиной 3 мкм с чередующейся структурой, закрепленные на насекомом, не отпадали в течение как минимум 3 дней.
Численные отношения между состоянием брюшной полости и вероятностью успешного самовосстановления были детализированы с использованием аппроксимированной модели нагрузки на изгиб. Деформацию пленки из-за удара брюшного сегмента можно аппроксимировать короблением простой колонны, закрепленной с обоих концов 31 . Изгибающая нагрузка может быть получена из толщины пленки и модуля Юнга прикрепляемой пленки (уравнения (1–3) в методах и дополнительный рисунок 10). Нагрузки на изгиб были получены в зависимости от толщины пленки как для париленовой пленки, так и для пленки PDMS с использованием заданных параметров формы брюшного сегмента (дополнительная таблица 1) (рис. 2g). Взаимосвязь между нагрузкой на изгиб и вероятностью восстановления показала постоянство для обеих пленок, что подтвердило справедливость приближения (рис. 2h). Нагрузка на изгиб менее 0,05 Н обеспечивала вероятность успеха 80%, тогда как дальнейшее увеличение вызывало резкое снижение скорости. Таким образом, сила, с которой брюшные сегменты G. portentosa может генерировать диапазон от 0,05 до 0,1 N, что согласуется с ранее зарегистрированными значениями силы ног при восстановлении 32 . Мы провели повторные попытки самовосстановления для одного и нескольких человек. Некоторые люди показали высокий уровень успеха для нескольких таких попыток, тогда как другие показали 0% или очень низкий уровень успеха, подтверждая четкие индивидуальные различия.
Изгибающая нагрузка может быть получена из толщины пленки и модуля Юнга прикрепляемой пленки (уравнения (1–3) в методах и дополнительный рисунок 10). Нагрузки на изгиб были получены в зависимости от толщины пленки как для париленовой пленки, так и для пленки PDMS с использованием заданных параметров формы брюшного сегмента (дополнительная таблица 1) (рис. 2g). Взаимосвязь между нагрузкой на изгиб и вероятностью восстановления показала постоянство для обеих пленок, что подтвердило справедливость приближения (рис. 2h). Нагрузка на изгиб менее 0,05 Н обеспечивала вероятность успеха 80%, тогда как дальнейшее увеличение вызывало резкое снижение скорости. Таким образом, сила, с которой брюшные сегменты G. portentosa может генерировать диапазон от 0,05 до 0,1 N, что согласуется с ранее зарегистрированными значениями силы ног при восстановлении 32 . Мы провели повторные попытки самовосстановления для одного и нескольких человек. Некоторые люди показали высокий уровень успеха для нескольких таких попыток, тогда как другие показали 0% или очень низкий уровень успеха, подтверждая четкие индивидуальные различия. Большие полосы погрешностей представляют собой граничную область, которая зависит от мышечной силы человека.
Большие полосы погрешностей представляют собой граничную область, которая зависит от мышечной силы человека.
Качественный анализ попыток самовосстановления подтвердил, что фундаментальное движение было достигнуто, даже когда гибкая электроника была интегрирована в насекомых (рис. 2i, дополнительный фильм 5). Когда модуль органического солнечного элемента толщиной 4 мкм был прикреплен к брюшку таракана, были достигнуты 100% успешные попытки самовыравнивания, что подтвердило, что сверхтонкий модуль органического солнечного элемента обеспечивал движение насекомых. В отличие от приклеивания тонкой пленки на брюшную полость, прикрепление толстой пленки (толщиной 100 мкм) с поддержкой рюкзака к грудной клетке оказывает незначительное влияние на способность к самовосстановлению. Показатель успеха был 93%, когда на грудной клетке была толстая пленка, тогда как на животе пленки не было. При наложении на брюшную полость пленок толщиной 3 мкм и 10 мкм эффективность составила 80 и 13% соответственно. Таким образом, результаты экспериментов с различными условиями подтверждают, что относительно толстая пленка может быть установлена на грудную клетку G. portentosa для достижения основного движения, в то время как для брюшной полости требуется пленка с определенной мягкостью и разработанной стратегией прикрепления, позволяющей достаточную для движения деформацию.
Таким образом, результаты экспериментов с различными условиями подтверждают, что относительно толстая пленка может быть установлена на грудную клетку G. portentosa для достижения основного движения, в то время как для брюшной полости требуется пленка с определенной мягкостью и разработанной стратегией прикрепления, позволяющей достаточную для движения деформацию.
Производительность ультратонкого модуля органических солнечных элементов
Ультратонкий модуль органических солнечных элементов обеспечивает высокую выходную мощность до 17,2 мВт за счет максимизации эффективной площади изогнутой формы поверхности брюшка G. portentosa (рис. 3a). ). Брюшко G. portentosa было аппроксимировано пятиугольником площадью 777 мм 2 (дополнительная рис. 11). Модуль имеет трехрядное соединение с учетом КПД повышающего преобразователя (рис. 3б). Эффективная площадь модуля составила 3,96 см 2 , что соответствовало апертуре 51% площади живота. Поскольку тело насекомого имеет трехмерную криволинейную поверхность, интенсивность света, которую может получить каждая клетка, зависит от угла 25,33 . На основании боковой и задней формы 3D-модели углы дорсальной поверхности G. portentosa по отношению к вертикали были установлены как θ и δ соответственно (рис. 3в). Уменьшение интенсивности света в каждой области, т. е. cos θ * cos δ было оценено как по θ , так и по δ в каждой области (рис. 3d, дополнительная рис. 12). Модуль был спроектирован так, чтобы свести к минимуму снижение интенсивности из-за зависимости поверхности от угла. На рис. 3д показаны вольт-амперные характеристики ( I – В ) модуля органического солнечного элемента. Плоский ультратонкий модуль органических солнечных элементов имеет ток короткого замыкания ( I SC ) 28,3 мА, напряжение холостого хода ( В OC ) 1,98 В и коэффициент заполнения (FF) 0,564, что привело к максимальной выходной мощности 31,5 мВт и PCE 7,96% (дополнительная таблица 2).
Поскольку тело насекомого имеет трехмерную криволинейную поверхность, интенсивность света, которую может получить каждая клетка, зависит от угла 25,33 . На основании боковой и задней формы 3D-модели углы дорсальной поверхности G. portentosa по отношению к вертикали были установлены как θ и δ соответственно (рис. 3в). Уменьшение интенсивности света в каждой области, т. е. cos θ * cos δ было оценено как по θ , так и по δ в каждой области (рис. 3d, дополнительная рис. 12). Модуль был спроектирован так, чтобы свести к минимуму снижение интенсивности из-за зависимости поверхности от угла. На рис. 3д показаны вольт-амперные характеристики ( I – В ) модуля органического солнечного элемента. Плоский ультратонкий модуль органических солнечных элементов имеет ток короткого замыкания ( I SC ) 28,3 мА, напряжение холостого хода ( В OC ) 1,98 В и коэффициент заполнения (FF) 0,564, что привело к максимальной выходной мощности 31,5 мВт и PCE 7,96% (дополнительная таблица 2). Модуль, прикрепленный к напечатанной на 3D-принтере модели изогнутой поверхности, имеет I SC 22,8 мА, напряжение холостого хода ( В OC ) 1,92 В и FF 0,394, что приводит к максимальная выходная мощность 17,2 мВт. Снижение тока на изогнутой поверхности оценивается в 0,78 раза по сравнению с плоским состоянием, что согласуется с фактическим значением тока при подключении к трехмерной поверхности (рис. 3e, дополнительная таблица 3 и дополнительный рис. 13). Уменьшение FF связано с уменьшением сопротивления шунта из-за увеличения тока утечки в процессе присоединения (дополнительный рис. 14 и дополнительная таблица 2).
Модуль, прикрепленный к напечатанной на 3D-принтере модели изогнутой поверхности, имеет I SC 22,8 мА, напряжение холостого хода ( В OC ) 1,92 В и FF 0,394, что приводит к максимальная выходная мощность 17,2 мВт. Снижение тока на изогнутой поверхности оценивается в 0,78 раза по сравнению с плоским состоянием, что согласуется с фактическим значением тока при подключении к трехмерной поверхности (рис. 3e, дополнительная таблица 3 и дополнительный рис. 13). Уменьшение FF связано с уменьшением сопротивления шунта из-за увеличения тока утечки в процессе присоединения (дополнительный рис. 14 и дополнительная таблица 2).
a Конструкция модуля органических солнечных элементов, вид сверху. Красные пунктирные линии показывают эффективную площадь модуля. Масштабная линейка, 5 мм. b Структура модуля. c Виды брюшной полости сбоку и сзади, показывающие изменения угла падения света в каждой области. d Расчетное распределение изменений интенсивности света в брюшной полости. e Ток-напряжение ( I – V ) кривые модуля солнечной батареи, измеренные при AM 1,5 G с мощностью 100 мВт см –2 . Черная и красная сплошные линии представляют измеренную производительность на плоской сцене и изогнутой поверхности, напечатанной на 3D-принтере, соответственно. Пунктирная синяя линия представляет смоделированную кривую распределения изменения интенсивности света. f Нормализованное изменение PCE с отслеживанием времени теста MPP. Черные треугольники и красные квадраты представляют собой модуль, измеренный на плоской платформе и изогнутой поверхности, напечатанной на 3D-принтере, соответственно. Графики представляют собой средние значения, полученные из 5 отдельных модулей, а планки погрешностей представляют собой стандартное отклонение.
d Расчетное распределение изменений интенсивности света в брюшной полости. e Ток-напряжение ( I – V ) кривые модуля солнечной батареи, измеренные при AM 1,5 G с мощностью 100 мВт см –2 . Черная и красная сплошные линии представляют измеренную производительность на плоской сцене и изогнутой поверхности, напечатанной на 3D-принтере, соответственно. Пунктирная синяя линия представляет смоделированную кривую распределения изменения интенсивности света. f Нормализованное изменение PCE с отслеживанием времени теста MPP. Черные треугольники и красные квадраты представляют собой модуль, измеренный на плоской платформе и изогнутой поверхности, напечатанной на 3D-принтере, соответственно. Графики представляют собой средние значения, полученные из 5 отдельных модулей, а планки погрешностей представляют собой стандартное отклонение.
Изображение в полный размер
Ультратонкий солнечный элемент имеет вес на эффективную площадь приблизительно 5 г м –2 28 , что соответствует мощности на вес 15,9 и 8,69 Вт г –1 для больших модуль площади на плоском состоянии и на 3D-криволинейной поверхности. Плотность мощности на эффективную площадь соответствует 4,34 мВт см –2 . Меньшее значение модуля на изогнутых поверхностях, напечатанных на 3D-принтере, по сравнению с заявленными гибкими органическими солнечными элементами (в которых самая высокая плотность мощности на эффективную площадь составляла 17,5 мВт см 9 ).2670 –2 ) 34 возникла из-за снижения производительности, когда ультратонкие устройства были изогнуты до трехмерной формы. Выходная мощность, генерируемая модулем мягкого солнечного элемента на насекомом, может быть улучшена за счет подавления износа, вызванного процессом, улучшения нестабильности при непрерывном освещении светом и изменения конструкции с учетом конкретной изогнутой поверхности целевых насекомых. Потенциальные подходы включают использование материала активного слоя с большой оптимальной толщиной 35 , исследование стабильных межфазных материалов 36 , а также использование более механически прочных материалов для слоев инжекции заряда и прозрачных электродов 37 , а также использование материалов активного слоя с более высокой эффективностью преобразования энергии 38 .
Плотность мощности на эффективную площадь соответствует 4,34 мВт см –2 . Меньшее значение модуля на изогнутых поверхностях, напечатанных на 3D-принтере, по сравнению с заявленными гибкими органическими солнечными элементами (в которых самая высокая плотность мощности на эффективную площадь составляла 17,5 мВт см 9 ).2670 –2 ) 34 возникла из-за снижения производительности, когда ультратонкие устройства были изогнуты до трехмерной формы. Выходная мощность, генерируемая модулем мягкого солнечного элемента на насекомом, может быть улучшена за счет подавления износа, вызванного процессом, улучшения нестабильности при непрерывном освещении светом и изменения конструкции с учетом конкретной изогнутой поверхности целевых насекомых. Потенциальные подходы включают использование материала активного слоя с большой оптимальной толщиной 35 , исследование стабильных межфазных материалов 36 , а также использование более механически прочных материалов для слоев инжекции заряда и прозрачных электродов 37 , а также использование материалов активного слоя с более высокой эффективностью преобразования энергии 38 .
Мы провели испытание на стабильность работы мягких органических модулей солнечных элементов как в плоском, так и в прикрепленном виде на 3D-модели (рис. 3е). Оба модуля на плоской и трехмерной модели демонстрируют одинаковую стабильность работы при отслеживании точки максимальной мощности (MPPT) смоделированного солнечного света, демонстрируя приемлемую стабильность на искривленных поверхностях. Более быстрая деградация модулей большой площади по сравнению с одиночной ячейкой малой площади связана с путем утечки тока большей эффективной площади 28 .
Зарядка беспроводной системы управления движением живого насекомого-киборга
Характеристики зарядки подтвердили, что ультратонкий модуль органических солнечных элементов, прикрепленный к напечатанной на 3D-принтере модели G. portentosa , может успешно питать литий-полимерную батарею. Напряжение от модуля солнечной батареи на вход повышающего преобразователя было зафиксировано на уровне 0,95 В, чтобы модуль мог работать вблизи точки максимальной выходной мощности. Повышающий преобразователь увеличил напряжение с 0,95 до 4,2 В, а выход использовался для зарядки аккумулятора (рис. 1г). Выходное напряжение батареи увеличилось с 3,13 до 4,33 В после зарядки в течение 938 мин, что подтвердило завершение зарядки от разряженной до полной (рис. 4а).
Повышающий преобразователь увеличил напряжение с 0,95 до 4,2 В, а выход использовался для зарядки аккумулятора (рис. 1г). Выходное напряжение батареи увеличилось с 3,13 до 4,33 В после зарядки в течение 938 мин, что подтвердило завершение зарядки от разряженной до полной (рис. 4а).
a Зарядка аккумулятора с помощью модуля органических солнечных элементов. Напряжение между батареями было построено как функция времени во время зарядки модулем органического солнечного элемента, прикрепленным к изогнутой поверхности, напечатанной на 3D-принтере, при AM 1,5 G при 100 мВт см –2 . b Изменения напряжения во внешнем сервере (вверху) и модуле моделирования (внизу). Когда переключатель был включен, сигнал передавался с внешнего сервера на схемы стимуляции, и генерировались волны стимуляции. c Многократные экспозиции и соответствующие им траектории передвижения. Синие и красные линии обозначают выключение и включение стимуляции соответственно. Масштабная линейка, 100 мм. d Траектория пяти попыток управления движением.
Синие и красные линии обозначают выключение и включение стимуляции соответственно. Масштабная линейка, 100 мм. d Траектория пяти попыток управления движением.
Изображение в натуральную величину
Разработанные выходные сигналы для стимуляции контролировались по беспроводной сети с помощью модуля с незначительной задержкой сигнала. На рис. 4b показаны выходные сигналы для электрической стимуляции во время беспроводной связи. Когда переключатель на внешнем сервере был включен, схема стимуляции на приемнике создавала выходное напряжение прямоугольной формы с размахом напряжения 3,3 В, частотой 50 Гц и коэффициентом заполнения 50%. Время задержки включения и выключения составляло от 0,10 до 0,12 с.
Наконец, перезарядка и беспроводное управление движением были реализованы с использованием живых насекомых-киборгов, содержащих электронные компоненты (дополнительный фильм 6). Беспроводной модуль управления движением, литий-полимерный аккумулятор, ультратонкий органический модуль солнечной батареи и стимулирующие провода были прикреплены к спинной стороне G. portentosa (рис. 1а, б). Во-первых, мы подтвердили, что стимуляция не применялась до зарядки аккумулятора. После того, как смоделированное солнечное освещение было применено к модулю органических солнечных элементов на G. portentosa в течение 30 мин, управление движением при повороте направо проводилось по беспроводной связи (рис. 4с). Сигналы стимуляции передавались по беспроводной связи в течение 2,1 мин с заряженной батареей. В течение этого периода неоднократно предпринимались попытки управления локомоцией, что подтверждало, что беспроводное управление неоднократно выполнялось успешно (рис. 4г).
portentosa (рис. 1а, б). Во-первых, мы подтвердили, что стимуляция не применялась до зарядки аккумулятора. После того, как смоделированное солнечное освещение было применено к модулю органических солнечных элементов на G. portentosa в течение 30 мин, управление движением при повороте направо проводилось по беспроводной связи (рис. 4с). Сигналы стимуляции передавались по беспроводной связи в течение 2,1 мин с заряженной батареей. В течение этого периода неоднократно предпринимались попытки управления локомоцией, что подтверждало, что беспроводное управление неоднократно выполнялось успешно (рис. 4г).
Для обеспечения свободы движений крайне важно разделить компоненты между грудным и брюшным сегментами и обеспечить свободу брюшных сегментов. Эффективность этой схемы была количественно подтверждена оценкой движений насекомого 9.2670 39 . Попытки самовосстановления насекомого увенчались успехом, когда прикрепленная тонкая пленка с адгезивно-неадгезионной прокладочной структурой была достаточно мягкой, чтобы не нарушать силу деформации мышц насекомых. Такие деформации брюшка наблюдались у многих насекомых 40,41 ; поэтому стратегия монтажа гибкой электроники, предложенная в этом исследовании, может быть адаптирована к другим видам насекомых. Учитывая деформацию грудной клетки и брюшка во время основного движения, гибридные электронные системы из жестких или гибких элементов на грудной клетке и сверхмягких устройств на брюшке представляют собой эффективные конструкции насекомых-киборгов.
Такие деформации брюшка наблюдались у многих насекомых 40,41 ; поэтому стратегия монтажа гибкой электроники, предложенная в этом исследовании, может быть адаптирована к другим видам насекомых. Учитывая деформацию грудной клетки и брюшка во время основного движения, гибридные электронные системы из жестких или гибких элементов на грудной клетке и сверхмягких устройств на брюшке представляют собой эффективные конструкции насекомых-киборгов.
Хотя жесткие схемы, используемые в этом исследовании, недостаточно тонкие и легкие, чтобы обеспечить полную степень свободы G . portentosa , их толщина и вес могут быть уменьшены за счет использования точных и гибких схем с органическими полупроводниками 9 и Si схем, изготовленных на пластиковых пленках 42,43 . Как показано в этом исследовании, контур общей толщиной до 100 мкм может обеспечить почти полное основное движение за Г . портентоса . Уменьшение толщины печатных плат на грудной клетке должно стать будущим направлением перезаряжаемых насекомых-киборгов.
Поскольку насекомые постоянно перемещаются, следует рассмотреть возможность уменьшения угловой зависимости выработки энергии. Потенциальный подход заключается в изготовлении нанорешетчатых структур на подложке или функциональных слоях 25,33 . Интервал несветового освещения был необходим для эксперимента по зарядке, чтобы предотвратить Г . portentosa температура тела из-за слишком высокого подъема, а тараканы, как правило, ведут ночной образ жизни и обладают светобоязнью. Интегрируя систему управления движением, фотодиоды и датчики температуры, можно создать алгоритм, который стимулирует таракана оставаться под светом во время режима зарядки системы, принимая во внимание жизнеобеспечение. Измеренная потребляемая мощность беспроводной системы управления движением составила 73,3 мВт. Аккумулятора (40 мАч) после полной зарядки хватало примерно на 2 часа. В текущей системе большая часть потребляемой мощности приходится на беспроводную связь. Регулируя интервалы связи, батарея может работать дольше.
В заключение, мы разработали стратегию проектирования для установки электроники на насекомых путем систематической оценки двигательных способностей и продемонстрировали зарядку и беспроводное управление движением на живых насекомых-киборгах. Две критически важные стратегии, а именно достижение достаточной мягкости и структура, обеспечивающая движение сегмента, минимизируют ограничение свободы суставов тела. Ультратонкий модуль органических солнечных батарей подтвердил эффективность стратегии, заряжая батарею на живых подвижных насекомых. Разделенные функции компонентов грудной клетки и брюшной полости позволили устойчиво использовать насекомых-киборгов без каких-либо ограничений. Эта стратегия эффективна для других насекомых и компонентов устройства. Подход, представленный в данном исследовании, способствует расширению спектра деятельности и реализует разнообразные функции насекомых-киборгов.
Методы
Экспериментальные животные и среда разведения
Взрослые особи G. portentosa (старше 16 недель после рождения) использовались в этом исследовании. Их тела можно разделить на голову, грудь и брюшко. При виде сверху голова в основном прикрыта грудной клеткой. Грудная клетка и брюшко дополнительно делятся на три и восемь сегментов соответственно. Церки представляют собой парные придатки на самых задних сегментах брюшка и служат органами чувств. Самец G. portentosa можно отличить по наличию на груди двух роговидных выступов. Чтобы обеспечить одинаковые условия тестирования поведенческих способностей, в эксперименте использовались только особи женского пола для оценки их способности к самовосстановлению с пленкой или рюкзаком, прикрепленным к спинной стороне. Коммерчески доступные щепки коры были разложены в ящике для размножения шириной 43 см, глубиной 35 см и высотой 27 см для размножения от 40 до 200 колоний. Температуру разведения регулировали от 25 до 30 °С с помощью нагревательного мата. Два раза в неделю вводили соответствующее количество желе из насекомых и корма для тараканов.
portentosa (старше 16 недель после рождения) использовались в этом исследовании. Их тела можно разделить на голову, грудь и брюшко. При виде сверху голова в основном прикрыта грудной клеткой. Грудная клетка и брюшко дополнительно делятся на три и восемь сегментов соответственно. Церки представляют собой парные придатки на самых задних сегментах брюшка и служат органами чувств. Самец G. portentosa можно отличить по наличию на груди двух роговидных выступов. Чтобы обеспечить одинаковые условия тестирования поведенческих способностей, в эксперименте использовались только особи женского пола для оценки их способности к самовосстановлению с пленкой или рюкзаком, прикрепленным к спинной стороне. Коммерчески доступные щепки коры были разложены в ящике для размножения шириной 43 см, глубиной 35 см и высотой 27 см для размножения от 40 до 200 колоний. Температуру разведения регулировали от 25 до 30 °С с помощью нагревательного мата. Два раза в неделю вводили соответствующее количество желе из насекомых и корма для тараканов.
3D модель
G . портентозаЗамороженную самку G. portentosa поместили на небольшой поворотный стол, и было получено 45 изображений путем вращения образца с интервалом 8°. Изображения были импортированы в программное обеспечение для фотограмметрии (3DF Zephyr, OPT Technologies) для создания точной 3D-модели.
Измерение формы живота
Клейкий эластомерный лист (Y-4905J, 3 M™) был плотно прикреплен к животу женщины G. portentosa образец для заполнения брюшной полости. К листам эластомера прикрепляли бумагу для предотвращения деформации при расслаивании. Форма была определена с помощью листов расслоившегося эластомера, а затем приближена к пятиугольнику с общей площадью 777 мм 2 .
Подтверждение движения брюшной полости и формы сегмента
Наблюдение поперечного сечения было выполнено для подтверждения движения брюшной полости G. portentosa . Образец, замороженный при –18 °C, CO 2 Станок для лазерной обработки (FABOOL Laser CO2, Smart DIYs Inc. ) использовали для разрезания G. portentosa от центра грудной клетки до брюшной полости. Наблюдения проводились с использованием микроскопа (Dino-Lite Edge, Opto Science). Диапазон движения измеряли с помощью поперечного наблюдения. Брюшную полость разобрали на сегменты для измерения глубины сегмента, ширины, толщины и радиуса кривизны.
) использовали для разрезания G. portentosa от центра грудной клетки до брюшной полости. Наблюдения проводились с использованием микроскопа (Dino-Lite Edge, Opto Science). Диапазон движения измеряли с помощью поперечного наблюдения. Брюшную полость разобрали на сегменты для измерения глубины сегмента, ширины, толщины и радиуса кривизны.
Дизайн и изготовление рюкзака
Для обеспечения стабильного прилегания жестких компонентов к грудной клетке рюкзак был спроектирован так, чтобы покрывать первый-третий грудные сегменты 3D-модели Г . портентоса . Рюкзак был изготовлен на стереолитографическом 3D-принтере (Form3, Formlabs) из эластичного полимера (Elastic 50 A, Formlabs). Интерфейс между рюкзаком и поверхностью насекомого был разделен на столбцы. Столбчатые структуры были прикреплены к первому-третьему грудным сегментам с помощью суперклея (LOCTITE, LBR-005). Благодаря мягкости и столбчатой структуре рюкзак правильно прилегает к разным людям, подтверждая адекватную интеграцию цепей в Г . portentosa вид.
portentosa вид.
Прикрепление тонких пленок к брюшку
Клей для кожи на основе смолы (Spirit Gum, Mitsuyoshi) равномерно наносили на брюшко и прикрепляли тонкую пленку к поверхности насекомого. Клей был жидким и проявлял некоторую адгезионную прочность даже до отверждения. Во время отверждения клея часть клея, где сегменты перекрывались, соскабливалась в результате естественного движения насекомых, в результате чего образовывалась полая структура чередования клея и неклея.
Преодоление препятствия
В качестве препятствия на землю была помещена деревянная призма правильной треугольной формы со стороной и высотой 45 и 80 мм. Температура пола в исходном положении G. portentosa была установлена на 80 °C, а температура пола препятствия и за препятствием была установлена на комнатную температуру (в диапазоне от 23 до 25 °C), чтобы вызвать движение обхода. немедленно. Время прохождения определялось путем измерения времени с момента, когда голова G. portentosa прошел через ближайший торец препятствия до того момента, когда брюшко значительно превысило верхнюю вершину. Мы собрали в общей сложности 5 человек с 10 испытаниями от каждого человека для каждого состояния.
portentosa прошел через ближайший торец препятствия до того момента, когда брюшко значительно превысило верхнюю вершину. Мы собрали в общей сложности 5 человек с 10 испытаниями от каждого человека для каждого состояния.
Попытки самовосстановления
G. portentosa держали в перевернутом положении, а затем отпускали на землю, покрытую переработанной бумагой. Если животное выпрямлялось из перевернутой ориентации в течение 60 с, случай считался успешным. Те же самые попытки неоднократно проводились с различными людьми и состояниями пленки/компонента как на животе, так и на грудной клетке. Мы собрали в общей сложности не менее 3 человек, по крайней мере, по 5 испытаний от каждого человека для каждого состояния. См. дополнительную таблицу 4 для получения подробной информации о размере выборки. 92}}$$
(1)
где n – константа, определяемая закреплением обоих концов листа (в случае закрепления обоих концов, n = 4), E – модуль Юнга листа, I — момент инерции площади, определяемой формой поперечного сечения листа, а L — естественная длина между закрепленными концами. 3{ {{\mathrm{b}}}}}}{{12}}$$ 92}}$$
3{ {{\mathrm{b}}}}}}{{12}}$$ 92}}$$
(3)
Хотя деформация между двумя брюшными сегментами является вертикальным отклонением, она приближается к изгибу простой колонны с ходом сегмента как L , поскольку вертикальное отклонение достаточно маленький (дополнительные рисунки 5 и 9). Сила, необходимая для деформации изгиба при постоянном ходе брюшного сегмента ( L = 2,5 мм) и ширина пленки на брюшном сегменте ( b = 25 мм) рассчитывались с использованием модуля Юнга и толщины в качестве переменных (дополнительная таблица 1). ).
Материалы для модуля органического солнечного элемента
Прекурсор (ECRIOS VICT-Cz) для прозрачной полиимидной подложки был получен от Mitsui Chemicals. Фторированные полимеры (Novec1700, 3M) и их растворители (Novec 7100, 3M) были приобретены у 3M. Дегидраты ацетата цинка, этаноламин, 2-метоксиэтанол и хлорбензол были приобретены у FUJIFILM Wako Pure Chemical Corporation. Этоксилированный полиэтиленимин (PEIE) и 1-хлорнафталин были приобретены у Sigma-Aldrich. Поли[4,8-бис(5-(2-этилгексил)тиофен-2-ил)бензо[1,2-b;4,5-b’]дитиофен-2,6-диил-альт-(4-октил -3-фтортиено[3,4-b]тиофен)-2-карбоксилат-2-6-диил] (PBDTTT-OFT) получали от TORAY. 2,2′-((2Z,2′Z)-(((4,4,9,9-тетракис(4-гексилфенил)-4,9-дигидро-синдацено[1,2-b:5,6-b’]дитиофен-2,7-диил)бис(4-((2-этилгексил)окси) )тиофен-5,2-диил))бис(метанилиден))бис(5,6-дифтор-3-оксо-2,3-дигидро-1 H -инден-2,1-диилиден))дималононитрил (IEICO -4F) был куплен в 1-Material. Все материалы использовали в том виде, в каком они были получены, без дополнительной очистки.
Поли[4,8-бис(5-(2-этилгексил)тиофен-2-ил)бензо[1,2-b;4,5-b’]дитиофен-2,6-диил-альт-(4-октил -3-фтортиено[3,4-b]тиофен)-2-карбоксилат-2-6-диил] (PBDTTT-OFT) получали от TORAY. 2,2′-((2Z,2′Z)-(((4,4,9,9-тетракис(4-гексилфенил)-4,9-дигидро-синдацено[1,2-b:5,6-b’]дитиофен-2,7-диил)бис(4-((2-этилгексил)окси) )тиофен-5,2-диил))бис(метанилиден))бис(5,6-дифтор-3-оксо-2,3-дигидро-1 H -инден-2,1-диилиден))дималононитрил (IEICO -4F) был куплен в 1-Material. Все материалы использовали в том виде, в каком они были получены, без дополнительной очистки.
Изготовление модуля органического солнечного элемента
Сначала стеклянные подложки обрабатывали кислородной плазмой в течение 10 мин при мощности 300 Вт (PC-300, Samco). Затем слой фторированного полимера (Novec 1700:7100 = 1:8) наносили центрифугированием (MS-B100, Микса) на стекло размером 50 мм × 50 мм при 4000 об/мин в течение 1 мин. Далее подложку из фторированного стекла нагревали в инертной печи при 80 °С в течение 10 мин. Перед нанесением методом центрифугирования предшественника прозрачного полиимида слой стекло/фторированный полимер обрабатывали кислородной плазмой в течение 5 с при мощности 50 Вт. Прекурсор наносили методом центрифугирования на подложку при 2000 об/мин в течение 1 мин с образованием пленки толщиной примерно 2,4 мкм. Прозрачную полиимидную пленку отверждали реакцией имидирования при 250°С в течение 2 ч в инертной печи в атмосфере азота (DN411I, Yamato Scientific). Прозрачный электрод из оксида индия-олова (ITO) толщиной 100 нм наносили на подложку с помощью распылительной установки (SIH-1010, ULVAC, Inc.). Электрод ITO был сформирован с помощью фотолитографии, и слои Cr толщиной 3,5 нм и Au толщиной 100 нм были нанесены на электрод ITO в качестве поддерживающих проволок. PEIE, хелатированный Zn 2+ (PEI-Zn) использовали в качестве электрон-транспортного слоя 28,37 . Раствор предшественника PEI-Zn готовили путем растворения 70 мг дигидрата ацетата цинка в 1 мас.
Перед нанесением методом центрифугирования предшественника прозрачного полиимида слой стекло/фторированный полимер обрабатывали кислородной плазмой в течение 5 с при мощности 50 Вт. Прекурсор наносили методом центрифугирования на подложку при 2000 об/мин в течение 1 мин с образованием пленки толщиной примерно 2,4 мкм. Прозрачную полиимидную пленку отверждали реакцией имидирования при 250°С в течение 2 ч в инертной печи в атмосфере азота (DN411I, Yamato Scientific). Прозрачный электрод из оксида индия-олова (ITO) толщиной 100 нм наносили на подложку с помощью распылительной установки (SIH-1010, ULVAC, Inc.). Электрод ITO был сформирован с помощью фотолитографии, и слои Cr толщиной 3,5 нм и Au толщиной 100 нм были нанесены на электрод ITO в качестве поддерживающих проволок. PEIE, хелатированный Zn 2+ (PEI-Zn) использовали в качестве электрон-транспортного слоя 28,37 . Раствор предшественника PEI-Zn готовили путем растворения 70 мг дигидрата ацетата цинка в 1 мас. % PEIE в 2-метоксиэтаноле. Для формирования пленки PEI-Zn раствор прекурсора подвергали центрифугированию при 3500 об/мин в течение 45 с, а затем подвергали термическому отжигу при 180 °C в течение 30 мин на воздухе. PBDTTTT-OFT (10 мг) и IEICO-4F (15 мг) в хлорбензоле (970 мкл) нагревали при 70 °C в течение 2 часов. К раствору добавляли добавку 1-хлорнафталин (30 мкл) и перемешивали при 70°С в течение 5 мин. Раствор наносили центрифугированием в окружающем воздухе при 1400 об/мин в течение 60 с, чтобы сформировать объемный фотоактивный слой гетероперехода. Ненужные участки осторожно удаляли с помощью ватного тампона, смоченного в хлороформе, для последовательного соединения каждой субячейки. Высушенные образцы помещали в вакуумный испаритель и наносили дырочно-транспортирующий слой оксида молибдена (MoO X , 7,5 нм) и анод Ag (100 нм) последовательно осаждали путем термического испарения при температуре <3 × 10 −4 Па. пассивирующий слой. Модуль солнечного элемента имеет три последовательных и два параллельных субэлемента с эффективной площадью 22 × 3 мм.
% PEIE в 2-метоксиэтаноле. Для формирования пленки PEI-Zn раствор прекурсора подвергали центрифугированию при 3500 об/мин в течение 45 с, а затем подвергали термическому отжигу при 180 °C в течение 30 мин на воздухе. PBDTTTT-OFT (10 мг) и IEICO-4F (15 мг) в хлорбензоле (970 мкл) нагревали при 70 °C в течение 2 часов. К раствору добавляли добавку 1-хлорнафталин (30 мкл) и перемешивали при 70°С в течение 5 мин. Раствор наносили центрифугированием в окружающем воздухе при 1400 об/мин в течение 60 с, чтобы сформировать объемный фотоактивный слой гетероперехода. Ненужные участки осторожно удаляли с помощью ватного тампона, смоченного в хлороформе, для последовательного соединения каждой субячейки. Высушенные образцы помещали в вакуумный испаритель и наносили дырочно-транспортирующий слой оксида молибдена (MoO X , 7,5 нм) и анод Ag (100 нм) последовательно осаждали путем термического испарения при температуре <3 × 10 −4 Па. пассивирующий слой. Модуль солнечного элемента имеет три последовательных и два параллельных субэлемента с эффективной площадью 22 × 3 мм. Общая эффективная площадь составила 396 мм 2 , что соответствовало 51% светосилы абдоминальной области G. portentosa 9.2231 (777 мм 2 ).
Общая эффективная площадь составила 396 мм 2 , что соответствовало 51% светосилы абдоминальной области G. portentosa 9.2231 (777 мм 2 ).
Характеристика модуля
Вольт-амперные ( I – В ) характеристики OPV были записаны при AM 1,5 G (100 мВт см −2 , с калибровкой интенсивности с использованием кремниевого эталонного солнечного элемента) с использованием SourceMeter (Series2400, Keithley) в условиях окружающей среды в лаборатории.
Беспроводной модуль управления движением и аккумулятор
Беспроводной модуль управления движением состоял из трех жестких компонентов, а именно: схемы генерации стимулирующего напряжения, схемы беспроводной связи и повышающего преобразователя. Для получения статуса включения/выключения с внешнего сервера использовался модуль беспроводной связи с nRF24L01 + (Nordic Semiconductor). В качестве схемы генерации импульсного напряжения использовалась плата Arduino Pro mini. Для электростимуляции G. portentosa управление широтно-импульсной модуляцией было запрограммировано для получения сигнала с напряжением 3,3 В, частотой 50 Гц и коэффициентом заполнения 50%. ИС для сбора энергии (модуль повышающего преобразователя низкого напряжения LTC3105 250 мВ, Strawberry Linux Co., Ltd.) была установлена для стабильной зарядки батареи с использованием выходного сигнала модуля органических солнечных элементов. Выходная мощность модуля органического солнечного элемента фиксировалась на уровне 0,95 В с помощью контроллера точки максимальной мощности с резистором 100 кОм, а повышающий преобразователь повышал напряжение до 4,2 В. В качестве аккумуляторная батарея. Габаритные размеры этих компонентов составляли Ш 18,0 мм × Д 37,2 мм ×В 18,3 мм, а вес 8,14 г, и они были прикреплены к грудной клетке с помощью напечатанного на 3D-принтере рюкзака.
Для электростимуляции G. portentosa управление широтно-импульсной модуляцией было запрограммировано для получения сигнала с напряжением 3,3 В, частотой 50 Гц и коэффициентом заполнения 50%. ИС для сбора энергии (модуль повышающего преобразователя низкого напряжения LTC3105 250 мВ, Strawberry Linux Co., Ltd.) была установлена для стабильной зарядки батареи с использованием выходного сигнала модуля органических солнечных элементов. Выходная мощность модуля органического солнечного элемента фиксировалась на уровне 0,95 В с помощью контроллера точки максимальной мощности с резистором 100 кОм, а повышающий преобразователь повышал напряжение до 4,2 В. В качестве аккумуляторная батарея. Габаритные размеры этих компонентов составляли Ш 18,0 мм × Д 37,2 мм ×В 18,3 мм, а вес 8,14 г, и они были прикреплены к грудной клетке с помощью напечатанного на 3D-принтере рюкзака.
В качестве платы микрокомпьютера использовался внешний сервер Arduino Uno. Коммуникационный модуль, оснащенный nRF24L01 + (Nordic Semiconductor), использовался в качестве беспроводного модуля для связи. Кроме того, Arduino Uno с кнопочным переключателем использовался для управления состоянием включения/выключения. Состояние этой кнопки передавалось на модуль насекомого через модуль беспроводной связи. Внешний сервер был подключен к ПК для получения постоянного напряжения 5 В.
Кроме того, Arduino Uno с кнопочным переключателем использовался для управления состоянием включения/выключения. Состояние этой кнопки передавалось на модуль насекомого через модуль беспроводной связи. Внешний сервер был подключен к ПК для получения постоянного напряжения 5 В.
Тест зарядки
Литий-полимерный аккумулятор разряжен до 3,2 В с помощью электрохимической измерительной системы (HZ-7000, Hokuto Denko). Модуль органического солнечного элемента, прикрепленный к напечатанной на 3D-принтере модели G. portentosa , был подключен к аккумулятору. Смоделированный свет 1-Sun непрерывно подавался на модуль непосредственно сверху, а напряжение между батареями контролировалось с помощью измерителя источника (Series2400, Keithley).
Установка электрических компонентов на насекомое
Поверхности грудного и брюшного сегментов G. portentosa равномерно зачистили наждачной бумагой. Рюкзак, напечатанный на 3D-принтере, был прикреплен к первому-третьему грудным сегментам с помощью суперклея (LOCTITE, LBR-005). Беспроводной модуль управления движением и батарея были прикреплены к рюкзаку с помощью двусторонней ленты (Nystack™ NW-5, Nichiban Co., Ltd.). Сбоку пятого сегмента брюшка и церок делали отверстия с помощью иглы для насекомых (№ 1, Shiga Insect Spreading Co., Ltd.) или скальпеля. Серебряные микропровода были соединены с отверстиями и зафиксированы с помощью эпоксидной смолы, отверждаемой ультрафиолетом (UV-LED полимер star drop hard, Padico). Ультратонкий органический модуль солнечных батарей был прикреплен ко всему животу с помощью клея на основе смолы для кожи (Spirit Gum, Mitsuyoshi). И аноды, и катоды были подключены к повышающим преобразователям с помощью анизотропной токопроводящей ленты (ECATT 9).703, 3 М) и серебряные микропровода.
Беспроводной модуль управления движением и батарея были прикреплены к рюкзаку с помощью двусторонней ленты (Nystack™ NW-5, Nichiban Co., Ltd.). Сбоку пятого сегмента брюшка и церок делали отверстия с помощью иглы для насекомых (№ 1, Shiga Insect Spreading Co., Ltd.) или скальпеля. Серебряные микропровода были соединены с отверстиями и зафиксированы с помощью эпоксидной смолы, отверждаемой ультрафиолетом (UV-LED полимер star drop hard, Padico). Ультратонкий органический модуль солнечных батарей был прикреплен ко всему животу с помощью клея на основе смолы для кожи (Spirit Gum, Mitsuyoshi). И аноды, и катоды были подключены к повышающим преобразователям с помощью анизотропной токопроводящей ленты (ECATT 9).703, 3 М) и серебряные микропровода.
Демонстрация перезарядки и беспроводного управления движением насекомого-киборга
На G. portentosa был направлен имитированный свет 1-Sun для перезарядки разряженной батареи с использованием модуля солнечной батареи. Общая продолжительность освещения составляла 30 мин. Для каждого 10-минутного освещения был установлен 2-минутный интервал, чтобы предотвратить слишком высокое повышение температуры тела G. portentosa . После процесса подзарядки был проведен тест на беспроводную электрическую стимуляцию. При электростимуляции правого церка насекомое совершало поворотно-правую локомоцию. Время, в течение которого сервер управления и модуль электрической стимуляции обменивались данными, измерялось для оценки общей энергии, обеспечиваемой батареей модулем органических солнечных элементов. Чтобы подтвердить, достигла ли электрическая стимуляция эффективного контроля, траектория заднего конца G. portentosa записали с помощью видеокамеры и проанализировали с помощью MATLAB (The MathWorks).
Для каждого 10-минутного освещения был установлен 2-минутный интервал, чтобы предотвратить слишком высокое повышение температуры тела G. portentosa . После процесса подзарядки был проведен тест на беспроводную электрическую стимуляцию. При электростимуляции правого церка насекомое совершало поворотно-правую локомоцию. Время, в течение которого сервер управления и модуль электрической стимуляции обменивались данными, измерялось для оценки общей энергии, обеспечиваемой батареей модулем органических солнечных элементов. Чтобы подтвердить, достигла ли электрическая стимуляция эффективного контроля, траектория заднего конца G. portentosa записали с помощью видеокамеры и проанализировали с помощью MATLAB (The MathWorks).
Доступность данных
Исходные данные приводятся в настоящем документе.
Наличие кода
Весь код модуля стимуляции указан в дополнительной информации.
Ссылки
- «>
Tran-Ngoc, P. T. et al. Гибридная компьютерно-насекомая система для автономной поисково-спасательной операции. Препринт на https://arxiv.org/abs/2105.10869 (2021 г.).
Латиф Т., Уитмайр Э., Новак Т. и Бозкурт А. Датчики локализации звука для поисково-спасательных биороботов. IEEE Sens. J. 16 , 3444–3453 (2016).
Артикул Google ученый
Цао, Ф. и др. Биологический микропривод: поэтапное и замкнутое управление движением ног насекомых с помощью электрической стимуляции мышц. PLoS One 9 , e105389 (2014 г.).
Артикул Google ученый
«>Сато, Х. и Махарбиз, М. М. Последние разработки в области дистанционного радиоуправления полетом насекомых. Фронт. Неврологи. 4 , 199 (2010).
Артикул Google ученый
Tsang, W.M. et al. Интерфейс насекомое-машина: гибкий нейронный зонд, усиленный углеродными нанотрубками. J. Neurosci. Методы 204 , 355–365 (2012).
КАС Статья Google ученый
Гао, В. и др. Полностью интегрированные массивы носимых датчиков для мультиплексного анализа пота на месте.
 Природа 529 , 509–514 (2016).
Природа 529 , 509–514 (2016).КАС Статья Google ученый
Kim, Y. et al. Биоинспирированный гибкий органический искусственный афферентный нерв. Наука 360 , 998–1003 (2018).
КАС Статья Google ученый
Квон, К. и др. Накожная платформа для беспроводного мониторинга скорости потока, совокупной потери и температуры пота в режиме реального времени. нац. Электрон. 4 , 302–312 (2021).
Артикул Google ученый
Lee, S. et al. Наномеш-датчик давления для контроля манипуляций пальцами без сенсорных помех. Наука 370 , 966–970 (2020).
КАС Статья Google ученый
Мацухиса, Н.
 и др. Высокочастотные и растяжимые полимерные диоды. Природа 600 , 246–252 (2021).
и др. Высокочастотные и растяжимые полимерные диоды. Природа 600 , 246–252 (2021).КАС Статья Google ученый
Jung, D. et al. Высокопроводящая и эластичная наномембрана для кожной электроники. Наука 1026 , 1022–1026 (2021).
Артикул Google ученый
Джун, С., Ли, С. и Йих, Ю. Проблемы с доставкой и подзарядкой систем погрузочно-разгрузочных работ с использованием автономных мобильных роботов. евро. Дж. Опер. Рез. 289 , 1153–1168 (2021).
Артикул Google ученый
Курс А. и др. Беспроводная передача энергии через сильно связанные магнитные резонансы. Наука 317 , 83–86 (2007).
КАС Статья Google ученый
«>Ши Б., Ли З. и Фан Ю. Имплантируемые устройства для сбора энергии. Доп. Матер. 30 , 1801511 (2018).
Артикул Google ученый
Джафферис, Н. Т., Хелблинг, Э. Ф., Карпельсон, М. и Вуд, Р. Дж. Беспривязный полет микромасштабного летательного аппарата с машущими крыльями размером с насекомое. Природа 570 , 491–495 (2019).
КАС Статья Google ученый
Cosnier, S., le Goff, A. & Holzinger, M. Биотопливные клетки на основе глюкозы, имплантированные в организм человека для питания искусственных органов: обзор.
 Электрохим. коммун. 38 , 19–23 (2014).
Электрохим. коммун. 38 , 19–23 (2014).КАС Статья Google ученый
Shoji, K. et al. Насекомое с биотопливным элементом и его применение для беспроводного зондирования. Биосенс. Биоэлектрон. 78 , 390–395 (2016).
КАС Статья Google ученый
Сёдзи К., Морисима К., Акияма Ю., Накамура Н. и Оно Х. Автономный мониторинг окружающей среды с помощью биогибридного робота с автономным питанием. В 2016 IEEE Int. конф. Мехатрон. Автом . 629–634 (2016).
Лю, Ю., Фарр, М. и Сальваторе, Г. А. Лаборатория на коже: обзор гибкой и растягиваемой электроники для носимого мониторинга состояния здоровья. ACS Nano 11 , 9614–9635 (2017).
КАС Статья Google ученый
«>Латиф, Т. и Бозкурт, А. Линия, следующая за биоботами наземных насекомых. В Proc. Анну. Междунар. конф. IEEE инж. Мед. и биол. Соц . 972–975 (2012).
Парк, С. и др. Сверхгибкая электроника с автономным питанием благодаря органическим фотоэлектрическим элементам с нанорешетками. Природа 561 , 516–521 (2018).
КАС Статья Google ученый
Kaltenbrunner, M. et al. Гибкие перовскитовые солнечные элементы с высокой удельной мощностью и контактами из оксида хрома и металла для повышения стабильности на воздухе. Нац. Матер. 14 , 1032–1039 (2015).
КАС Статья Google ученый
«>Xiong, S. et al. Ультратонкие и эффективные органические фотогальваники с повышенной стабильностью на воздухе за счет подавления диффузии цинковых элементов. Доп. науч. 9 , 2105288 (2022).
КАС Статья Google ученый
Фулл, Р. и Ан, А. Статические силы и моменты, возникающие в ноге насекомого: сравнение трехмерной компьютерной модели скелетно-мышечной системы с экспериментальными измерениями.
 Дж. Экспл. биол. 198 , 1285–1298 (1995).
Дж. Экспл. биол. 198 , 1285–1298 (1995).КАС Статья Google ученый
Ли, К., Вёрль, Т., Лам, Х.К. и Фулл, Р.Дж. Тараканы используют различные стратегии для самостоятельного выбора положения на земле. Дж. Экспл. биол. 222 , jeb186080 (2019).
Артикул Google ученый
Тимошенко С. и Гир Дж. М. Теория упругой устойчивости . (Книжная компания McGraw-Hill, Inc., 1961).
Фулл, Р., Ямаути, А. и Джиндрич, Д. Максимальное производство силы одной ногой: тараканы выпрямляются на фотоэластичном желатине. Дж. Экспл. биол. 198 , 2441–2452 (1995).
КАС Статья Google ученый
Такакува, М. и др. Ультратонкая подложка со структурированной нанорешеткой для сверхгибких органических фотоэлектрических элементов.
 Маленькие методы 4 , 1
Маленькие методы 4 , 12 (2020).
КАС Статья Google ученый
Цзэн Г. и др. Создание гибких органических солнечных элементов с эффективностью 17,5% за счет химической сварки серебряных нанопроводных электродов на атомном уровне. Дж. Ам. хим. соц. 144 , 8658–8668 (2021).
Артикул Google ученый
Вохра, В. и др. Эффективные перевернутые полимерные солнечные элементы с благоприятной молекулярной ориентацией. нац. Фотон. 9 , 403–408 (2015).
КАС Статья Google ученый
Li, Y. et al. Органические фотоэлектрические элементы, не содержащие фуллерена, с собственным сроком службы более 30 лет. Нац. коммун. 12 , 5419 (2021).
КАС Статья Google ученый
«>Zhu, L. et al. Однопереходные органические солнечные элементы с эффективностью более 19 % благодаря усовершенствованной морфологии сети из двойных волокон. Нац. Матер. 21 , 656–663 (2022).
КАС Статья Google ученый
Ритцман Р. Э., Куинн Р. Д. и Фишер М. С. Конвергентная эволюция и передвижение по сложной местности с помощью насекомых, позвоночных и роботов. Структура членистоногих. Дев. 33 , 361–379 (2004).
Артикул Google ученый
Лян Ю. и др. Кинематика платформы Стюарта объясняет трехмерное движение абдоминальной структуры медоносной пчелы.
 J. Наука о насекомых. 19 , 1–6 (2019).
J. Наука о насекомых. 19 , 1–6 (2019).Артикул Google ученый
Францевич Л. Кинематика выпрямления жуков (Insecta: Coleoptera). Структура членистоногих. Дев. 33 , 221–235 (2004).
Артикул Google ученый
Ким, Д.-Х. и другие. Растворимые пленки фиброина шелка для ультратонкой конформной биоинтегральной электроники. Нац. Матер. 9 , 511–517 (2010).
КАС Статья Google ученый
Yokota, T. et al. Соответствующий имидж-сканер для биометрической аутентификации и измерения основных показателей жизнедеятельности. нац. Электрон. 3 , 113–121 (2020).
Артикул Google ученый
Уорвик, К. Мораль киборга, ценности киборга, этика киборга. Инф. по этике. Технол. 5 , 131–137 (2003).
Артикул Google ученый
Эриксон, Дж. К., Эррера, М., Бустаманте, М., Шингиро, А. и Боуэн, Т. Эффективные параметры стимула для направленного передвижения мадагаскарского биобота шипящего таракана. PLoS One 10 , e0134348 (2015 г.).
Артикул Google ученый
Хуан Дж., Чжоу Ю., Нин З. и Гарави Х. Беспроводная передача энергии и сбор энергии: Текущее состояние и перспективы на будущее. 9Проводной IEEE 2230. коммун. 26 , 163–169 (2019).
Артикул Google ученый
Латиф, Т., Уитмайр, Э., Новак, Т. и Бозкурт, А. К беззащитным границам для биороботов насекомых, работающих на солнечной энергии. В Proc. Анну. Междунар. конф. IEEE инж. Мед. и биол. Соц . 1670–1673 (2014).
Zhang, X., Öberg, V. A., Du, J., Liu, J. & Johansson, E. M. J. Чрезвычайно легкие и сверхгибкие солнечные элементы с квантовыми точками, преобразующими инфракрасный свет, с высокой выходной мощностью на единицу веса с использованием гибочный прочный серебряный электрод на основе нанопроволоки, обработанный раствором. Энергетика Окружающая среда. науч. 11 , 354–364 (2018).
КАС Статья Google ученый
Qin, F. et al. Прочный полимерный межфазный слой, хелатированный ионами металла, для сверхгибких органических солнечных элементов, не содержащих фуллерен. нац. коммун. 11 , 4508 (2020).
КАС Статья Google ученый
Ссылки на скачивание
Благодарности
Эта работа была частично поддержана Японским обществом содействия развитию науки в рамках его грантов в поддержку научных исследований (KAKENHI) (№ JP18H05469) и Японским агентством по науке и технологиям. (JST) в рамках своей Программы адаптивной и беспрепятственной передачи технологий посредством целевых исследований и разработок (A-STEP) (№ A3015021R) и JST в рамках своей программы JST-Mirai (№ JPMJMI21I1). Мы благодарим Toray Industries, Inc. за поставку полимера PBDTTT-OFT. Мы благодарим Mitsui Chemicals за поставку прекурсоров прозрачного полиимида (ECRIOS ТМ ).
(JST) в рамках своей Программы адаптивной и беспрепятственной передачи технологий посредством целевых исследований и разработок (A-STEP) (№ A3015021R) и JST в рамках своей программы JST-Mirai (№ JPMJMI21I1). Мы благодарим Toray Industries, Inc. за поставку полимера PBDTTT-OFT. Мы благодарим Mitsui Chemicals за поставку прекурсоров прозрачного полиимида (ECRIOS ТМ ).
Информация об авторе
Авторы и организации
Center for Emergent Matter Science, RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan
Yujiro Kakei, ShumpeiShumpeiTomayounga, Tawajioyoung, in in Фукуда и Такао Сомея
Департамент интегративной бионауки и биомедицинской инженерии, Центр передовых биомедицинских наук, Университет Твинс Васэда, 2-2 Вакамацу-чо, Синдзюку-ку, Токио, 162-8480, Япония
Юдзиро Какей и Синдзиро Умэдзу
Факультет современного машиностроения, Университет Васэда, 3-4-1 Окубо, Синдзюку-ку, Токио, 169-8555, Япония
Шумпей Катаяма, Масахито Такакува и Шиндзиро
Кафедра прикладной химии и пищевых наук, Факультет экологических и информационных наук, Технологический университет Фукуи, 3-6-1 Гакуэн, Фукуи, 910-8505, Япония
Казуя Фурусава
Школа машиностроения и аэрокосмической техники, Наньянский технологический университет, N3.
 2 – 01-20, 65 Nanyang Drive, Сингапур, 637460, Сингапур
2 – 01-20, 65 Nanyang Drive, Сингапур, 637460, СингапурХиротака Сато
Лаборатория тонкопленочных устройств, RIKEN, 2-1 Hirosawa, Вако, Сайтама, 351-0198, Япония
Кендзиро Фукуда и Такао Сомейя
Электрическая и электронная инженерия и информационные системы, Токийский университет, 7-3-1 Хонго, Бункё-ку, Токио, 113-8656, Япония
Takao Someya
Авторы
- Yujiro Kakei
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shumpei Katayama
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shinyoung Lee
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Masahito Takakuwa
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Kazuya Furusawa
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shinjiro Umezu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Hirotaka Sato
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Kenjiro Fukuda
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Takao Someya
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Взносы
С. У., Х.С., К.Ф. и Т.С. задумал основную идею. Ю.К., С.К. и К.Ф. спроектировал и провел эксперименты. Ю.К., С.Л. и М.Т. изготовил модули органических солнечных батарей. Ю.К., С.К. и Ке.Ф. проанализировал данные. Ке.Ф. и Ка.Ф. рассчитал механику пленки, используя аппроксимационную модель. Ю.К., С.К., К.Ф. Т.С. написал рукопись. Ке.Ф. и Т.С. курировал проект.
У., Х.С., К.Ф. и Т.С. задумал основную идею. Ю.К., С.К. и К.Ф. спроектировал и провел эксперименты. Ю.К., С.Л. и М.Т. изготовил модули органических солнечных батарей. Ю.К., С.К. и Ке.Ф. проанализировал данные. Ке.Ф. и Ка.Ф. рассчитал механику пленки, используя аппроксимационную модель. Ю.К., С.К., К.Ф. Т.С. написал рукопись. Ке.Ф. и Т.С. курировал проект.
Авторы переписки
Переписка с Кендзиро Фукуда или Такао Сомейя.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и принадлежности к организациям.
Дополнительная информация
Дополнительная информация
Дополнительный фильм 1 | Поперечный разрез брюшных сегментов.
Дополнительный фильм 2 | Преодоление препятствия.

Дополнительный фильм 3 | Самовосстановление с париленовыми пленками на животе.
Дополнительный фильм 4 | Самовосстановление с пленками PDMS на животе.
Дополнительный фильм 5 | Самовосстановление при различных состояниях грудной клетки/брюшка.
Дополнительный фильм 6 | Беспроводное управление движением с помощью перезаряжаемой батареи.
Dataset for Figure 2
Dataset for Figure 3
Dataset for Figure 4
Dataset for SI figures
Rights and permissions
Open Access This article is licensed under a Creative Commons Международная лицензия Attribution 4.0, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате, при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и указать, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Перепечатки и разрешения
Об этой статье
Сверхпроводящие экраны за триумфом МРТ
Теперь, когда записанный звук стал повсеместным, мы почти не задумываемся об этом. Смартфоны, умные колонки, телевизоры, радиоприемники, проигрыватели дисков и автомобильные аудиосистемы — прочное и приятное присутствие в нашей жизни. В 2017 году опрос, проведенный компанией Nielsen, показал, что около 90 процентов населения США регулярно слушают музыку и что в среднем они делают это 32 часа в неделю.
За этим свободно текущим удовольствием стоят огромные отрасли, применяющие технологии для достижения давней цели воспроизведения звука с максимально возможным реализмом. Начиная с фонографа Эдисона и рупорных динамиков 1880-х годов, последующие поколения инженеров в погоне за этим идеалом изобретали и использовали бесчисленные технологии: триодные вакуумные лампы, динамические громкоговорители, картриджи магнитных фонографов, схемы полупроводниковых усилителей с множеством различных топологий, электростатические громкоговорители. , оптические диски, стерео и объемный звук. И за последние пять десятилетий цифровые технологии, такие как сжатие и потоковая передача звука изменили музыкальную индустрию.
И все же даже сейчас, после 150 лет разработки, звук, который мы слышим даже из высококачественной аудиосистемы, далеко не соответствует тому, что мы слышим, физически присутствуя на живом музыкальном представлении. В таком случае мы находимся в естественном звуковом поле и можем легко заметить, что звуки разных инструментов исходят из разных мест, даже когда звуковое поле пересекается смешанными звуками от нескольких инструментов. Есть причина, по которой люди платят значительные суммы, чтобы послушать живую музыку: это более приятно, захватывающе и может произвести большее эмоциональное воздействие.
Есть причина, по которой люди платят значительные суммы, чтобы послушать живую музыку: это более приятно, захватывающе и может произвести большее эмоциональное воздействие.
Сегодня исследователи, компании и предприниматели, включая нас самих, наконец приближаются к записанному звуку, который действительно воссоздает естественное звуковое поле. В группу входят крупные компании, такие как Apple и Sony, а также более мелкие фирмы, такие как Творческий. Netflix недавно сообщил о партнерстве с Sennheiser, в рамках которого сеть начала использовать новую систему Ambeo 2-Channel Spatial Audio для повышения звукового реализма таких телешоу, как «Очень странные дела» и «Ведьмак».
В настоящее время существует по меньшей мере полдюжины различных подходов к созданию высокореалистичного звука. Мы используем термин «звуковая сцена», чтобы отличить нашу работу от других аудиоформатов, таких как пространственное аудио или иммерсивное аудио. Они могут воспроизводить звук с большим пространственным эффектом, чем обычное стерео, но обычно они не включают подробных признаков местоположения источника звука, которые необходимы для воспроизведения действительно убедительного звукового поля.
Мы верим, что звуковая сцена — это будущее записи и воспроизведения музыки. Но прежде чем произойдет такая радикальная революция, необходимо будет преодолеть огромное препятствие: удобное и недорогое преобразование бесчисленных часов существующих записей, независимо от того, являются ли они монофоническими, стереофоническими или многоканальными с объемным звуком (5.1, 7.1). , и так далее). Никто точно не знает, сколько песен было записано, но, по данным концерна развлекательных метаданных Gracenote, сейчас на планете Земля доступно более 200 миллионов записанных песен. Учитывая, что средняя продолжительность песни составляет около 3 минут, это эквивалентно примерно 1100 годам музыки.
Измерение передаточной функции, связанной с головой
Чтобы обеспечить высокую степень пространственного реализма для слушателя, вам необходимо точно отобразить детали того, как уникальная форма головы, ушей и носовой полости этого слушателя влияет на то, как он или она слышит звук . Это делается путем определения передаточной функции, связанной с головой слушателя, которая достигается путем воспроизведения звуков под разными углами и записи того, как голова пользователя влияет на звуки в каждом положении.
Это делается путем определения передаточной функции, связанной с головой слушателя, которая достигается путем воспроизведения звуков под разными углами и записи того, как голова пользователя влияет на звуки в каждом положении.
Питер Ли
Это партий музыки. Любая попытка популяризировать новый аудиоформат, каким бы многообещающим он ни был, обречена на провал, если только она не включает в себя технологию, которая позволяет нам слушать весь этот существующий звук с той же легкостью и удобством, с которыми мы сейчас наслаждаемся стереомузыкой — в наши дома, на пляже, в поезде или в машине.
Мы разработали такую технологию. Наша система, которую мы называем 3D Soundstage, позволяет воспроизводить музыку в звуковой сцене на смартфонах, обычных или умных колонках, наушниках, наушниках, ноутбуках, телевизорах, звуковых панелях и в транспортных средствах. Он не только может преобразовывать моно- и стереозаписи в звуковую сцену, но и позволяет слушателю, не имеющему специальной подготовки, реконфигурировать звуковое поле в соответствии со своими предпочтениями с помощью графического пользовательского интерфейса. Например, слушатель может назначить расположение каждого инструмента и источника звука вокала и отрегулировать громкость каждого — изменяя относительную громкость, скажем, вокала по сравнению с инструментальным сопровождением. Система делает это, используя искусственный интеллект (ИИ), виртуальную реальность и цифровую обработку сигналов (подробнее об этом чуть позже).
Например, слушатель может назначить расположение каждого инструмента и источника звука вокала и отрегулировать громкость каждого — изменяя относительную громкость, скажем, вокала по сравнению с инструментальным сопровождением. Система делает это, используя искусственный интеллект (ИИ), виртуальную реальность и цифровую обработку сигналов (подробнее об этом чуть позже).
Чтобы убедительно воссоздать звук, исходящий, скажем, от струнного квартета в двух небольших динамиках, таких как те, что есть в наушниках, требуется большое техническое мастерство. Чтобы понять, как это делается, давайте начнем с того, как мы воспринимаем звук.
Когда звук достигает ваших ушей, уникальные характеристики вашей головы — ее физическая форма, форма наружного и внутреннего ушей и даже форма носовых полостей — изменяют звуковой спектр исходного звука. Кроме того, существует очень небольшая разница во времени прихода звука от источника к вашим ушам. По этому спектральному изменению и разнице во времени ваш мозг воспринимает местоположение источника звука. Спектральные изменения и разница во времени могут быть математически смоделированы как передаточные функции, связанные с головой (HRTF). Для каждой точки в трехмерном пространстве вокруг вашей головы есть пара HRTF, одна для левого уха, а другая для правого.
Спектральные изменения и разница во времени могут быть математически смоделированы как передаточные функции, связанные с головой (HRTF). Для каждой точки в трехмерном пространстве вокруг вашей головы есть пара HRTF, одна для левого уха, а другая для правого.
Таким образом, мы можем обработать фрагмент аудио, используя пару HRTF, одну для правого уха и одну для левого. Чтобы воссоздать первоначальный опыт, нам нужно было бы принять во внимание расположение источников звука относительно записывающих их микрофонов. Если мы затем воспроизведем этот обработанный звук, например, через пару наушников, слушатель услышит звук с исходными репликами и воспримет, что звук исходит из тех направлений, с которых он был первоначально записан.
Если у нас нет исходной информации о местоположении, мы можем просто назначить местоположения для отдельных источников звука и получить практически тот же опыт. Слушатель вряд ли заметит незначительные сдвиги в расположении исполнителя — более того, он может предпочесть свою собственную конфигурацию.
Даже сейчас, после 150 лет разработки, звук, который мы слышим даже из высококачественной аудиосистемы, далеко не соответствует тому, что мы слышим, физически присутствуя на живом музыкальном представлении.
Существует множество коммерческих приложений, использующих HRTF для создания пространственного звука для слушателей, использующих головные телефоны и наушники. Одним из примеров является Spatialize Stereo от Apple. Эта технология применяет HRTF для воспроизведения звука, чтобы вы могли воспринимать пространственный звуковой эффект — более глубокое звуковое поле, более реалистичное, чем обычное стерео. Apple также предлагает версию с отслеживанием головы, в которой используются датчики на iPhone и AirPods для отслеживания относительного направления между вашей головой, на которую указывают AirPods в ушах, и вашим iPhone. Затем он применяет HRTF, связанные с направлением вашего iPhone, для создания пространственных звуков, чтобы вы воспринимали, что звук исходит от вашего iPhone. Это не то, что мы бы назвали звуком звуковой сцены, потому что звуки инструментов все еще микшируются. Вы не можете воспринимать, что, например, скрипач находится слева от альтиста.
Это не то, что мы бы назвали звуком звуковой сцены, потому что звуки инструментов все еще микшируются. Вы не можете воспринимать, что, например, скрипач находится слева от альтиста.
Однако у Apple есть продукт, который пытается обеспечить звук звуковой сцены: Apple Spatial Audio. Это значительное улучшение по сравнению с обычным стереозвуком, но, на наш взгляд, у него все еще есть несколько проблем. Во-первых, он включает в себя Dolby Atmos, технологию объемного звука, разработанную Dolby Laboratories. Spatial Audio применяет набор HRTF для создания пространственного звука для наушников и наушников. Однако использование Dolby Atmos означает, что вся существующая стереофоническая музыка должна быть переработана для этой технологии. Ремастеринг миллионов песен, уже записанных в моно и стерео, практически невозможен. Еще одна проблема с Spatial Audio заключается в том, что он может поддерживать только наушники, но не динамики, поэтому он бесполезен для людей, которые склонны слушать музыку дома и в машине.
Так как же наша система обеспечивает реалистичный звук звуковой сцены? Мы начинаем с использования программного обеспечения для машинного обучения, чтобы разделить звук на несколько изолированных дорожек, каждая из которых представляет один инструмент или певца, или одну группу инструментов или певцов. Этот процесс разделения называется повышающим микшированием. Затем продюсер или даже слушатель, не имеющий специальной подготовки, может рекомбинировать несколько дорожек, чтобы воссоздать и персонализировать желаемое звуковое поле.
Рассмотрим песню с участием квартета, состоящего из гитары, баса, ударных и вокала. Слушатель может решить, где «найти» исполнителей, и настроить громкость каждого в соответствии со своими личными предпочтениями. Используя сенсорный экран, слушатель может виртуально расположить источники звука и положение слушателя в звуковом поле для достижения приятной конфигурации. Графический пользовательский интерфейс отображает фигуру, представляющую сцену, на которую наложены значки, указывающие на источники звука — вокал, ударные, бас, гитары и т. д. В центре есть значок головы, указывающий положение слушателя. Слушатель может коснуться и перетащить значок головы, чтобы изменить звуковое поле в соответствии со своими предпочтениями.
д. В центре есть значок головы, указывающий положение слушателя. Слушатель может коснуться и перетащить значок головы, чтобы изменить звуковое поле в соответствии со своими предпочтениями.
Перемещение значка головы ближе к барабанам делает звук барабанов более заметным. Если слушатель переместит значок головы на значок, представляющий инструмент или певца, слушатель услышит этого исполнителя как соло. Дело в том, что, позволяя слушателю переконфигурировать звуковое поле, 3D Soundstage добавляет новые измерения (если вы простите за каламбур) к наслаждению музыкой.
Преобразованный звук звуковой сцены может быть двухканальным, если он предназначен для прослушивания через наушники или обычную систему с левым и правым каналами. Или он может быть многоканальным, если он предназначен для воспроизведения на многоканальной системе. В этом последнем случае звуковое поле звуковой сцены может быть создано двумя, четырьмя или более динамиками. Количество отдельных источников звука в воссозданном звуковом поле может быть даже больше, чем количество динамиков.
Этот многоканальный подход не следует путать с обычным объемным звуком 5.1 и 7.1. Обычно они имеют пять или семь отдельных каналов и динамик для каждого, а также сабвуфер («.1»). Несколько динамиков создают более захватывающее звуковое поле, чем стандартная стереофоническая установка с двумя динамиками, но им все же не хватает реализма, возможного при записи настоящей звуковой сцены. При воспроизведении через такую многоканальную настройку наши записи 3D Soundstage обходят 5.1, 7.1 или любые другие специальные аудиоформаты, включая стандарты многодорожечного сжатия звука.
Несколько слов об этих стандартах. Недавно были разработаны новые стандарты для лучшей обработки данных для улучшенных приложений объемного звука и иммерсивного звука. К ним относится стандарт 3D-аудио MPEG-H для иммерсивного пространственного звука с кодированием пространственных аудиообъектов (SAOC). Эти новые стандарты пришли на смену различным многоканальным аудиоформатам и соответствующим им алгоритмам кодирования, таким как Dolby Digital AC-3 и DTS, которые были разработаны несколько десятилетий назад.
При разработке новых стандартов экспертам пришлось учитывать множество различных требований и желаемых характеристик. Люди хотят взаимодействовать с музыкой, например, изменяя относительную громкость различных групп инструментов. Они хотят транслировать разные виды мультимедиа, по разным сетям и через разные конфигурации динамиков. SAOC был разработан с учетом этих функций, что позволяет эффективно хранить и транспортировать аудиофайлы, сохраняя при этом возможность для слушателя настраивать микс в соответствии со своим личным вкусом.
Однако для этого требуется множество стандартизированных методов кодирования. Для создания файлов SAOC использует кодировщик. Входными данными кодировщика являются файлы данных, содержащие звуковые дорожки; каждая дорожка представляет собой файл, представляющий один или несколько инструментов. Кодер по существу сжимает файлы данных, используя стандартные методы. Во время воспроизведения декодер в вашей аудиосистеме декодирует файлы, которые затем преобразуются обратно в многоканальные аналоговые звуковые сигналы с помощью цифро-аналоговых преобразователей.
Наша технология 3D Soundstage обходит это. В качестве входных данных мы используем моно-, стерео- или многоканальные файлы аудиоданных. Мы разделяем эти файлы или потоки данных на несколько дорожек изолированных источников звука, а затем преобразуем эти дорожки в двухканальный или многоканальный выход в зависимости от предпочтительных конфигураций слушателя для подключения наушников или нескольких громкоговорителей. Мы используем технологию искусственного интеллекта, чтобы избежать многодорожечной перезаписи, кодирования и декодирования.
На самом деле, одна из самых больших технических проблем, с которыми мы столкнулись при создании системы 3D Soundstage, заключалась в написании программного обеспечения для машинного обучения, которое разделяет (или микширует) обычную моно-, стерео- или многоканальную запись на несколько изолированных дорожек в реальном времени. . Программное обеспечение работает на нейронной сети. Мы разработали этот подход для разделения музыки в 2012 году и описали его в патентах, выданных в 2022 и 2015 годах (номера патентов США: 11 240 621 B2 и 9). ,131,305 В2).
,131,305 В2).
Слушатель может решить, где «найти» исполнителей, и может отрегулировать громкость каждого в соответствии со своими личными предпочтениями.
Типичная сессия состоит из двух компонентов: обучение и повышающее микширование. В учебном сеансе большая коллекция смешанных песен вместе с их изолированными инструментальными и вокальными треками используется в качестве входных и целевых выходных данных для нейронной сети соответственно. В обучении используется машинное обучение для оптимизации параметров нейронной сети, чтобы выходные данные нейронной сети — набор отдельных треков изолированных инструментальных и вокальных данных — соответствовали целевому выходу.
Нейронная сеть очень слабо смоделирована на основе мозга. Он имеет входной слой узлов, которые представляют собой биологические нейроны, а затем множество промежуточных слоев, называемых «скрытыми слоями». Наконец, после скрытых слоев есть выходной слой, где появляются окончательные результаты. В нашей системе данные, подаваемые на входные узлы, представляют собой данные микшированной звуковой дорожки. По мере того как эти данные проходят через уровни скрытых узлов, каждый узел выполняет вычисления, в результате которых получается сумма взвешенных значений. Затем над этой суммой выполняется нелинейная математическая операция. Этот расчет определяет, передаются ли и как аудиоданные от этого узла узлам следующего уровня.
По мере того как эти данные проходят через уровни скрытых узлов, каждый узел выполняет вычисления, в результате которых получается сумма взвешенных значений. Затем над этой суммой выполняется нелинейная математическая операция. Этот расчет определяет, передаются ли и как аудиоданные от этого узла узлам следующего уровня.
Этих слоев десятки. По мере того, как аудиоданные переходят от слоя к слою, отдельные инструменты постепенно отделяются друг от друга. В конце выходного слоя каждая отдельная звуковая дорожка выводится на узел выходного слоя.
В любом случае, это идея. Пока нейронная сеть обучается, вывод может быть неверным. Это может быть не изолированная инструментальная дорожка — например, она может содержать звуковые элементы двух инструментов. В этом случае индивидуальные веса в схеме взвешивания, используемой для определения того, как данные передаются от скрытого узла к скрытому узлу, настраиваются, и обучение запускается снова. Это итеративное обучение и настройка продолжаются до тех пор, пока результат не будет более или менее точно соответствовать целевому результату.
Как и в случае с любым набором обучающих данных для машинного обучения, чем больше количество доступных обучающих выборок, тем эффективнее будет обучение. В нашем случае для обучения нам понадобились десятки тысяч песен и их отдельных инструментальных треков; таким образом, общие наборы обучающих музыкальных данных исчислялись тысячами часов.
После обучения нейронной сети, получив на вход песню со смешанными звуками, система выводит несколько разделенных дорожек, пропуская их через нейронную сеть, используя систему, установленную во время обучения.
После разделения записи на составные дорожки следующим шагом является их повторное микширование в запись звуковой сцены. Это достигается процессором сигналов звуковой сцены. Этот процессор звуковой сцены выполняет сложную вычислительную функцию для генерации выходных сигналов, которые управляют динамиками и создают звук звуковой сцены. Входные данные для генератора включают изолированные дорожки, физическое расположение динамиков и желаемое расположение слушателя и источников звука в воссозданном звуковом поле. Выходы процессора звуковой сцены представляют собой многодорожечные сигналы, по одному на каждый канал, для управления несколькими динамиками.
Выходы процессора звуковой сцены представляют собой многодорожечные сигналы, по одному на каждый канал, для управления несколькими динамиками.
Звуковое поле может находиться в физическом пространстве, если оно создается динамиками, или в виртуальном пространстве, если оно создается наушниками. Функция, выполняемая в процессоре звуковой сцены, основана на вычислительной акустике и психоакустике и учитывает распространение звуковых волн и интерференцию в желаемом звуковом поле, а также HRTF для слушателя и желаемого звукового поля.
Например, если слушатель собирается использовать наушники, генератор выбирает набор HRTF на основе конфигурации желаемых местоположений источников звука, а затем использует выбранные HRTF для фильтрации дорожек изолированных источников звука. Наконец, процессор звуковой сцены объединяет все выходы HRTF для создания левой и правой дорожек для наушников. Если музыка будет воспроизводиться на колонках, то нужно как минимум две, но чем больше колонок, тем лучше звуковое поле. Количество источников звука в воссоздаваемом звуковом поле может быть больше или меньше количества динамиков.
Количество источников звука в воссоздаваемом звуковом поле может быть больше или меньше количества динамиков.
Мы выпустили наше первое приложение звуковой сцены для iPhone в 2020 году. Оно позволяет слушателям настраивать, слушать и сохранять музыку звуковой сцены в режиме реального времени — обработка не вызывает заметной временной задержки. Приложение под названием 3D Musica преобразует стереофоническую музыку из личной музыкальной библиотеки слушателя, облака или даже потоковой музыки в звуковую сцену в режиме реального времени. (Для караоке приложение может удалить вокал или вывести любой изолированный инструмент.)
Ранее в этом году мы открыли веб-портал,
3dsoundstage.com, который предоставляет все функции приложения 3D Musica в облаке, а также интерфейс прикладного программирования (API), делающий эти функции доступными для поставщиков потоковой музыки и даже для пользователей любого популярного веб-браузера. Теперь любой может слушать музыку в звуковой сцене практически на любом устройстве.
Когда звук достигает ваших ушей, уникальные характеристики вашей головы — ее физическая форма, форма наружного и внутреннего ушей и даже форма носовых полостей — изменяют звуковой спектр исходного звука.
Мы также разработали отдельные версии программного обеспечения 3D Soundstage для автомобилей, домашних аудиосистем и устройств, чтобы воссоздать трехмерное звуковое поле с использованием двух, четырех и более динамиков. Помимо воспроизведения музыки, мы возлагаем большие надежды на эту технологию в видеоконференциях. У многих из нас был утомительный опыт посещения видеоконференций, на которых мы плохо слышали других участников или не понимали, кто говорит. С помощью звуковой сцены звук можно настроить так, чтобы каждого человека было слышно из определенного места в виртуальной комнате. Или же «местоположение» можно просто назначить в зависимости от положения человека в сетке, типичной для Zoom и других приложений для видеоконференций. По крайней мере, для некоторых видеоконференцсвязь будет менее утомительной, а речь станет более разборчивой.
Так же, как звук перешел от моно к стерео и от стерео к объемному и пространственному звуку, теперь он начинает переходить к звуковой сцене. В те ранние эпохи аудиофилы оценивали звуковую систему по ее точности, основанной на таких параметрах, как полоса пропускания, гармонические искажения, разрешение данных, время отклика, сжатие данных без потерь или с потерями и другие факторы, связанные с сигналом. Теперь звуковая сцена может быть добавлена как еще одно измерение достоверности звука — и, осмелимся сказать, самое фундаментальное. Для человеческого уха влияние звуковой сцены с ее пространственными репликами и захватывающей непосредственностью гораздо важнее, чем постепенное улучшение точности воспроизведения. Эта исключительная функция предлагает возможности, ранее недоступные даже самым состоятельным меломанам.
Технологии способствовали предыдущим революциям в аудиоиндустрии, и теперь они запускают еще одну. Искусственный интеллект, виртуальная реальность и цифровая обработка сигналов подключаются к психоакустике, чтобы дать аудиоэнтузиастам возможности, которых у них никогда не было.




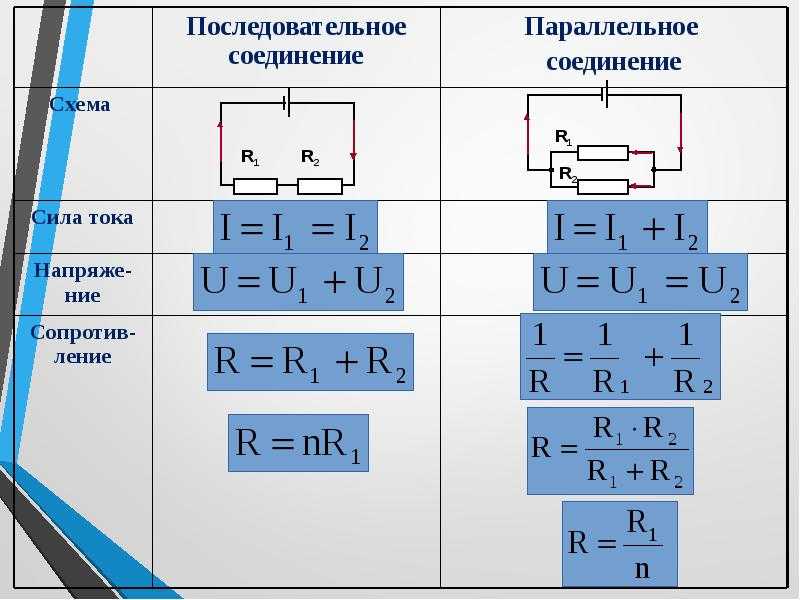 Это легло в основу закона, который мы используем сегодня. Закон является одним из основных уравнений для резисторов.
Это легло в основу закона, который мы используем сегодня. Закон является одним из основных уравнений для резисторов. 