Методика решения задач по теоретической механике
Методика решения задач по теоретической механике
ОглавлениеПРЕДИСЛОВИЕЧасть первая. СТАТИКА Предмет статики. Связи и реакции связей 1. Абсолютно гладкая опорная поверхность 2.  3. Опора на ребро 4. Гибкое тело (нить, канат, цепь) 5. Цилиндрический шарнир 6. Сферический шарнир 7. Стержневая опора 8. Шероховатая опорная поверхность 9. Неподвижная жесткая заделка I. ПЛОСКАЯ СИСТЕМА СИЛ 1-1. Равновесие трех сил 1-3. Равновесие какого угодно числа сил ГЛАВА II. ПАРАЛЛЕЛЬНЫЕ СИЛЫ ГЛАВА III. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ ГЛАВА IV. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ 4-2. Решение задач на равновесие тела при наличии идеальных связей (трение отсутствует) 4-3. Решение задач на опрокидывание 4-4. Решение задач на равновесие тел при наличии трения 4-5. Решение задач на равновесие системы сочлененных тел ГЛАВА V. ГРАФИЧЕСКАЯ СТАТИКА 5-4. Метод сквозных сечений 5-5. Метод вырезывания узлов II. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ ГЛАВА VI. СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ В ОДНОЙ ТОЧКЕ Глава VII. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ ГЛАВА VIII.  РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛГЛАВА IX. ЦЕНТР ТЯЖЕСТИ Часть вторая. КИНЕМАТИКА 10-1. Предмет кинематики. Основные положения 10-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки 10-3. Решение задач с помощью составления закона движения точки 11-2. Решение задач при нахождении скорости и ускорения по заданному закону движения точки в координатной форме 11-3. Решение задач на составление закона движения точки в координатной форме и нахождение скорости и ускорения движения по данным задачи 11-4. Решение задач при нахождении скорости и ускорения движущейся точки в случае естественного способа задания движения 11-5. Решение задач на составление закона движения точки в естественной форме и нахождение скорости и ускорения по данным задачи 11-6. Решение задач на определение wz, wn и p по заданному закону движения точки в координатной форме ГЛАВА XII.  ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. ПРЕОБРАЗОВАНИЕ ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА12-2. Решение задач на нахождение кинематических элементов по заданному закону вращения тела 12-3. Решение задач на составление закона вращения тела и нахождение кинематических элементов по данным задачи 12-4. Решение задач в случае преобразования простейших движений твердого тела V. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ ДВИЖЕНИЙ ТОЧКИ 13-1. Основные положения теории сложного движения точки 13-2. Решение задач с помощью формулы сложения скоростей точки 14-1. Решение задач с помощью формулы сложения ускорений при переносном поступательном движении 14-2. Решение задач с помощью формулы сложения ускорений точки при переносном вращательном движении вокруг неподвижной оси VI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 15-1. Основные положения теории плоскопараллельного движения твердого тела 15-2. Решение задач при нахождении скоростей точек плоской фигуры с помощью формулы распределения скоростей 15-3.  Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей Решение задач при определении скоростей точек плоской фигуры с помощью нахождения мгновенного центра скоростей16-1. Решение задач при нахождении ускорений точек плоской фигуры с помощью формулы распределения ускорений 16-2. Решение задач на нахождение мгновенного центра ускорений плоской фигуры ГЛАВА XVII. СЛОЖЕНИЕ ПЛОСКИХ ДВИЖЕНИЙ ТЕЛА (СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ) Часть третья. ДИНАМИКА 18-1. Основные положения. Дифференциальные уравнения движения материальной точки 18-2. Первая основная задача динамики материальной точки 18-3. Вторая основная задача динамики материальной точки (обратная первой) ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ 19-1. Теорема об изменении количества движения точки 19-3. Теорема об изменении кинетической энергии точки ГЛАВА XX. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ XIII. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 21-1.  Теорема о движении центра инерции системы Теорема о движении центра инерции системы21-2. Теорема об изменении количества движения системы 21-3. Теорема об изменении момента количества движения системы 21-4. Теорема об изменении кинетической энергии системы ГЛАВА XXII. ПРИНЦИПЫ МЕХАНИКИ 21-1. Принцип Даламбера 22-2. Принцип возможных перемещений 22-3. Принцип Даламбера-Лагранжа (Общее уравнение динамики системы) |
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| Traper |
| ||
03/11/15 |
| ||
| |||
| Pphantom |
| ||
09/05/12 | |||
| |||
| Pphantom |
| |||||
09/05/12 |
| |||||
| ||||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| Traper |
| ||
03/11/15 |
| ||
| |||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
| artur_k |
| ||
08/11/12 |
| ||
| |||
| Traper |
| ||
03/11/15 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| amon |
| |||
04/09/14 |
| |||
| ||||
| andrey67k |
| ||
03/11/15 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Определение, Формула, Количество I StudySmarter
Силы имеют как величину, так и направление и поэтому считаются векторами . Величина силы определяет, какая сила воздействует на объект.
Величина силы определяет, какая сила воздействует на объект.
Как действует сила
Сила действует на объекты, когда они взаимодействуют друг с другом. Сила перестает существовать, когда прекращается взаимодействие. Направление движения объекта также является направлением, в котором движется сила. Объекты в покое или в равновесии имеют противодействующие силы, удерживающие их на месте.
Итак, силы могут вызывать движение объектов и заставлять объекты оставаться в покое. Ваша интуиция подсказывает вам, что если вы хотите, чтобы объект сдвинулся влево, вы толкаете его влево.
В этом разделе мы познакомимся с понятием равнодействующей силы. Когда на частицу объекта действует ряд сил, результирующая сила представляет собой сумму всех сил, действующих на объект.
Примеры векторов
Вот несколько примеров того, как силы могут быть выражены в виде векторных величин.
Если к объекту приложены две силы F1=23 Н и F2=-34 Н, какова результирующая сила?
Ответ:
Сначала нанесите свои силы на график, чтобы увидеть их направление.
Рисунок 1. Пример равнодействующей силы
Если частица в точке 0 притягивается силами 1 и 2, вы можете предположить, что результирующая сила будет находиться где-то около пунктирной линии посередине двух сил на диаграмме выше. Однако вопрос подразумевает, что мы должны найти точную результирующую силу. Кроме того, другие вопросы могут быть не такими простыми, как этот.
Результирующий вектор = 23+-34
=-17
Это означает, что сила притянется при -17, как показано ниже.
Рисунок 2. Результирующая сила
Силы могут тянуть частицу со всех углов с одинаковой величиной, а результирующая сила равна 0. Это будет означать, что частица будет находиться в равновесии.
Рисунок 3. Результирующая сила
Рисунок 3. Результирующая сила
Как показано ниже, вычислите величину и направление результирующего вектора, который образуется при суммировании двух векторов.
Рисунок 4. Результирующая сила
Ответ:
Мы разбиваем каждый вектор на составные части и складываем компоненты вместе, чтобы получить результирующий вектор в компонентной форме. Затем мы найдем величину и направление этого вектора.
Итак, мы определяем компоненты x и y каждого вектора силы.
Пусть x компонент F1beF1x.
И компонент y F1beF1y.
F1x=F1cos𝛳
F1x=200Ncos(30°)
F1x=173.2N
Теперь давайте проделаем то же самое с компонентом y.
F1y=F1sin𝜃
F1y=200Nsin(30°)
F1y=100N
Теперь у нас есть компоненты x и y F1
F1=173.2i+100j
i и j используются для обозначения единичных векторов . i для векторов по оси x и j для векторов по оси y.
Повторим процесс для F2.
F2x=F2cos𝜃
F2x=300Ncos(135°)[45° — базовый угол, но нам нужен угол относительно положительной оси x, который равен 135°].
F2x=-212.1N
И сделайте то же самое для компонента y:
F2y=F2sin𝜃
F2y=300Nsin(135°)
F2y=212.1N 900 05
F2=-212.1i+212.2j
Теперь, когда у нас есть обе силы в виде компонентов, мы можем сложить их, чтобы получить результирующую силу.
FR=F1+F2
Мы сложим компоненты x, затем компоненты y.
F2=[173,2-212,1]i+[100+212,1]j
F2=-38,9i+312,1j
Нанесите это на график
Рисунок 5. Величина силы
Перемещение на 38,9 единиц по оси X и 312,1 единиц по оси Y. Это относительно больше, чем длина оси X. Гипотенуза образованного треугольника будет величиной, и она была помечена c. Воспользуемся теоремой Пифагора, чтобы найти c.
Здесь написано a2+b2=c2
Таким образом, a2+b2=c
Так как c здесь то же самое, что и FR,
F2=(-38,9)2+(312,1)2
F2=314,5N 9000 5
Это величина результирующего вектора.
Чтобы найти направление, нам нужно вернуться к графику и обозначить угол, обозначенный как θR.
θR=tan-1(312.138.9)
θR = 82,9 °
Если вам нужен угол, который положителен к оси x, вы вычтите 𝜃R из 180, так как все они лежат на прямой.
𝜃 + 82,9 = 180
𝜃 = 180 — 82,9
𝜃 = 97,1°
Теперь у нас есть величина и направление равнодействующей силы.
Сила как вектор — ключевые выводы
- Сила имеет как величину, так и направление.
- Объекты движутся в направлении чистой силы.
- Результирующая сила — это единственная сила, оказывающая на частицу такое же воздействие, как если бы к ней было приложено много сил.
- При нахождении равнодействующей силы вы складываете все силы, действующие на частицу.
Часто задаваемые вопросы о силе как векторе
Числовое значение силы показывает ее величину, а знак перед ним указывает ее направление.
Это диаграмма свободного тела, изображающая величину и направление сил, действующих на объект.
Их можно изобразить на графике. Его величина представлена длиной стрелки, а его направление представлено направлением стрелки.
Вектор силы представляет собой представление силы, которая имеет как величину, так и направление. Однако векторы не имеют сил.
Final Force as a Vector Quiz
Force as a Vector Quiz — Teste dein Wissen
Вопрос
Что такое вектор силы?
Показать ответ
Ответ
Вектор силы представляет собой представление силы, которая имеет величину и направление
Показать вопрос
Вопрос
Является ли крутящий момент вектором?
Показать ответ
Ответ
Крутящий момент является векторной величиной. Его направление зависит от направления силы на оси вращения.
Его направление зависит от направления силы на оси вращения.
Показать вопрос
Вопрос
Как найти направление вектора силы?
Показать ответ
Ответ
По функции арктангенса. Он равен углу, образованному с осью x или с осью y, в зависимости от приложения.
Показать вопрос
Вопрос
Может ли величина быть отрицательной?
Показать ответ
Ответ
Величина всегда является положительным значением.
Показать вопрос
Вопрос
Что такое диаграмма вектора силы?
Показать ответ
Ответ
Это диаграмма свободного тела, изображающая величину и направление сил, действующих на тело.
Показать вопрос
Вопрос
Что такое диаграмма вектора результирующей силы?
Показать ответ
Ответ
Диаграмма, представляющая сумму векторных сил, действующих на объект.
Показать вопрос
Вопрос
Что вызывает движение объектов и может заставить объекты оставаться в покое?
Показать ответ
Ответ
Показать вопрос
Вопрос
Когда силы притягивают частицу со всех сторон с одинаковой величиной, значение вашей равнодействующей силы будет …
Показать ответ
Ответ
Показать вопрос
Вопрос
Объекты всегда движутся в направлении чистой силы
Показать ответ
Ответ
Показать вопрос
Вопрос
Какова величина силы?
Показать ответ
Ответ
Величина силы определяет, какая сила воздействует на объект.
Показать вопрос
Вопрос
Вектор всегда содержит ___ и ___
Показать ответ
Ответ
Величина и направление
Показать вопрос
Вопрос
Результирующая величина любых двух векторов получается путем сложения величин каждого вектора вместе.
Показать ответ
Ответ
Показать вопрос
Разложение сил
Ранее в Уроке 1 подробно обсуждался метод разложения вектора на его компоненты. На том уроке было сказано, что любой вектор, направленный под углом к привычной оси координат, можно считать состоящим из двух частей, каждая из которых направлена вдоль одной из осей, либо горизонтально, либо вертикально. Части одного вектора называются компоненты и описывают влияние этого единственного вектора в заданном направлении. Одним из примеров, который был приведен во время Урока 1, был пример, когда Фидо тянули собачьей цепью. Если цепочку тянуть вверх и вправо, то на Фидо действует сила натяжения вверх и вправо. Эта единственная сила может быть разложена на две составляющие: одна направлена вверх, а другая вправо. Каждый компонент описывает влияние этой цепочки в заданном направлении. Вертикальная составляющая описывает восходящее влияние силы на Фидо, а горизонтальная составляющая описывает правонаправленное влияние силы на Фидо.
Части одного вектора называются компоненты и описывают влияние этого единственного вектора в заданном направлении. Одним из примеров, который был приведен во время Урока 1, был пример, когда Фидо тянули собачьей цепью. Если цепочку тянуть вверх и вправо, то на Фидо действует сила натяжения вверх и вправо. Эта единственная сила может быть разложена на две составляющие: одна направлена вверх, а другая вправо. Каждый компонент описывает влияние этой цепочки в заданном направлении. Вертикальная составляющая описывает восходящее влияние силы на Фидо, а горизонтальная составляющая описывает правонаправленное влияние силы на Фидо.
Задача определения величины влияния отдельного вектора в заданном направлении включает использование тригонометрических функций. Использование этих функций для определения компонентов одного вектора также обсуждалось в Уроке 1 этого раздела. В качестве краткого обзора давайте рассмотрим использование SOH CAH TOA для определения составляющих силы, действующей на Фидо. Предположим, что цепь действует на Фидо с силой 60 Н под углом 40 градусов к горизонтали. Быстрый набросок ситуации показывает, что для определения вертикальной составляющей силы можно использовать функцию синуса, а для определения горизонтальной составляющей силы можно использовать функцию косинуса. Решение этой проблемы показано ниже.
В качестве краткого обзора давайте рассмотрим использование SOH CAH TOA для определения составляющих силы, действующей на Фидо. Предположим, что цепь действует на Фидо с силой 60 Н под углом 40 градусов к горизонтали. Быстрый набросок ситуации показывает, что для определения вертикальной составляющей силы можно использовать функцию синуса, а для определения горизонтальной составляющей силы можно использовать функцию косинуса. Решение этой проблемы показано ниже.
В качестве другого примера использования SOH CAH TOA для разделения одного вектора на два его компонента рассмотрим диаграмму справа. Сила 400 Н приложена под углом 60 градусов (направление 300 градусов) для перемещения железнодорожного вагона на восток по железнодорожному полотну. На схеме изображен вид сверху ситуации. Сила, приложенная к автомобилю, имеет как вертикальную (на юг), так и горизонтальную составляющую (на восток). Чтобы определить величины этих двух компонентов, необходимо использовать функции синуса и косинуса. Задача становится более ясной, если начать с диаграммы ситуации с отмеченным углом и отмеченной гипотенузой. Как только треугольник построен, становится очевидным, что функция синуса должна быть использована для определения вертикальная (южная) составляющая и функция косинуса должны быть использованы для определения горизонтальной (восточной) составляющей. Треугольник и сопутствующие работы показаны ниже.
Задача становится более ясной, если начать с диаграммы ситуации с отмеченным углом и отмеченной гипотенузой. Как только треугольник построен, становится очевидным, что функция синуса должна быть использована для определения вертикальная (южная) составляющая и функция косинуса должны быть использованы для определения горизонтальной (восточной) составляющей. Треугольник и сопутствующие работы показаны ниже.
Каждый раз, когда вектор силы направлен под углом к горизонтали, можно использовать тригонометрические функции для определения компонентов этого вектора силы. Чтобы убедиться, что вы понимаете использование SOH CAH TOA для определения компонентов вектора, попробуйте решить следующие три практические задачи. Чтобы просмотреть ответы, нажмите на кнопку.
На трех приведенных выше диаграммах раскрывается важная концепция. Обратите внимание, что на каждой диаграмме сила имеет одинаковую величину; меняется только угол с горизонтом. По мере увеличения угла, который сила образует с горизонталью, составляющая силы в горизонтальном направлении (F x ) уменьшается. Принцип имеет некоторый смысл; чем больше сила направлена вверх (угол с горизонталью увеличивается), тем меньше сила способна оказывать влияние в горизонтальном направлении. Если вы хотите перетащить Fido горизонтально, то вам следует приложить усилия как можно ближе к горизонтальному направлению; вы не стали бы тянуть цепочку Фидо вертикально, если хотите тянуть его горизонтально.
По мере увеличения угла, который сила образует с горизонталью, составляющая силы в горизонтальном направлении (F x ) уменьшается. Принцип имеет некоторый смысл; чем больше сила направлена вверх (угол с горизонталью увеличивается), тем меньше сила способна оказывать влияние в горизонтальном направлении. Если вы хотите перетащить Fido горизонтально, то вам следует приложить усилия как можно ближе к горизонтальному направлению; вы не стали бы тянуть цепочку Фидо вертикально, если хотите тянуть его горизонтально.
Одним из важных применений этого принципа является парусный спорт. Парусники сталкиваются с силой сопротивления ветра из-за удара движущихся молекул воздуха о парус. Эта сила сопротивления ветра направлена перпендикулярно лицевой стороне паруса и поэтому часто направлена под углом к направлению движения парусника. Фактическое направление этой силы зависит от ориентации паруса. Чтобы определить влияние силы сопротивления ветра в направлении движения, эту силу необходимо разложить на две составляющие: одну в направлении движения парусника и другую в направлении, перпендикулярном движению парусника. См. схему справа. На диаграмме ниже показаны три различных направления паруса. Если предположить, что сила сопротивления ветра в каждом случае одинакова, то в каком случае будет оказываться наибольшее влияние на направление движения парусника? То есть в каком случае наибольшая составляющая силы направлена параллельно курсу лодок?
См. схему справа. На диаграмме ниже показаны три различных направления паруса. Если предположить, что сила сопротивления ветра в каждом случае одинакова, то в каком случае будет оказываться наибольшее влияние на направление движения парусника? То есть в каком случае наибольшая составляющая силы направлена параллельно курсу лодок?
Многие считают, что парусник не может двигаться против ветра. По их мнению, если ветер дует с севера на юг, парусная лодка не сможет двигаться с юга на север. Это просто неправда. Парусники могут двигаться «против ветра» и обычно делают это с помощью метода, известного как лавирование по ветру . Верно сказать, что парусная лодка никогда не сможет плыть против ветра, направив свою лодку прямо против ветра. Как видно на диаграмме справа, если лодка движется прямо против ветра, то сила ветра направлена против ее курса. В таком случае составляющая силы в направлении движения парусника отсутствует. То есть нет никакой «движущей силы». С другой стороны, если лодка идет под углом к ветру, то силу ветра можно разложить на две составляющие. В двух ориентациях парусника, показанных ниже, составляющая силы в направлении, параллельном курсу парусника, будет толкать лодку под углом к ветру. Лавируя против ветра, парусник обычно движется под углом 45 градусов, лавируя вперед и назад по ветру.
То есть нет никакой «движущей силы». С другой стороны, если лодка идет под углом к ветру, то силу ветра можно разложить на две составляющие. В двух ориентациях парусника, показанных ниже, составляющая силы в направлении, параллельном курсу парусника, будет толкать лодку под углом к ветру. Лавируя против ветра, парусник обычно движется под углом 45 градусов, лавируя вперед и назад по ветру.
Следующие задачи сосредоточены на понятиях, обсуждаемых в этом уроке. Ответьте на каждый вопрос, а затем нажмите кнопку, чтобы просмотреть ответ.
1. На схеме справа изображена сила, образующая угол с горизонтом. Эта сила будет иметь горизонтальную и вертикальную составляющие. Какой из приведенных ниже вариантов лучше всего описывает направление горизонтальной и вертикальной составляющих этой силы?
2.




 Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил Главный вектор системы сил
Главный вектор системы сил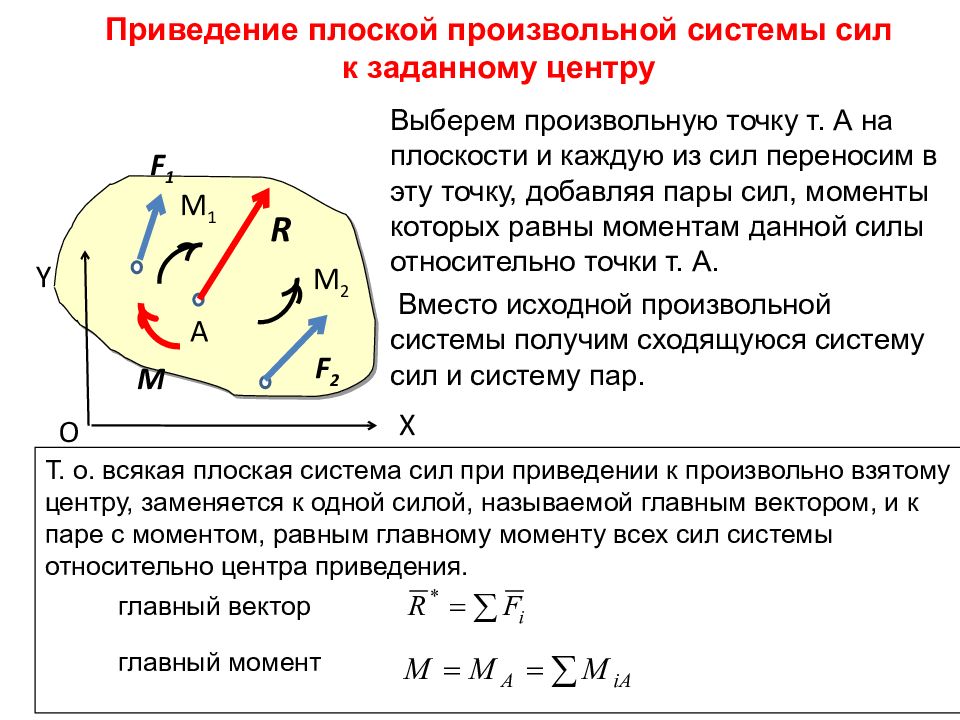 Главный вектор системы сил
Главный вектор системы сил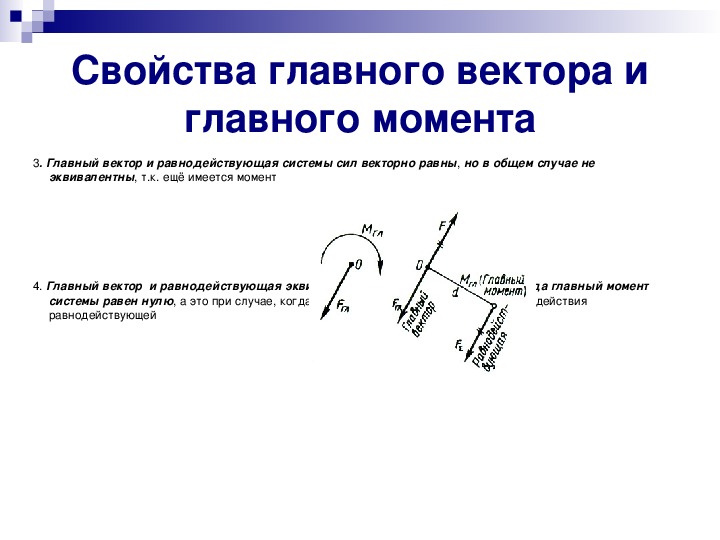 Главный вектор системы сил
Главный вектор системы сил
 Эти онлайн задачники, как бы сказать помягче, и верные ответы могут запороть, и к культуре правильных решений не приучают.
Эти онлайн задачники, как бы сказать помягче, и верные ответы могут запороть, и к культуре правильных решений не приучают. Иоффе СПб
Иоффе СПб . соотношение сторон в прямоугольном треугольнике в школе плохо дают..(((
. соотношение сторон в прямоугольном треугольнике в школе плохо дают..(((