Открытое образование — Электромагнетизм

Курс «Электромагнетизм» является разделом курса общей физики, в котором излагаются систематизированные знания об основных понятиях и законах электромагнетизма как обобщений опытных фактов, выраженных в математической форме. Изучаются и демонстрируются основополагающие эксперименты, лежащие в основе фундаментальных законов электричества, магнетизма и электродинамики. Разбираются теоретические модели взаимодействия электрических и магнитных полей с веществом и анализируются области их применимости. Разъясняются современные технологии, в основе которых лежат законы электромагнетизма. Дисциплина вырабатывает у студентов основы естественнонаучного мировоззрения и является базой для дальнейшего изучения общепрофессиональных и специальных дисциплин.

Форма обучения заочная (дистанционная). Еженедельные занятия будут включать просмотр тематических видеолекций, снабженных видеозаписями лекционных экспериментов, и выполнение тестовых заданий с автоматизированной проверкой результатов. Важным элементом изучения дисциплины является самостоятельное решение физических задач. Решение должно будет содержать строгие и логически верные рассуждения, приводящие к верному ответу.

Курс рассчитан на бакалавров 1 года обучения. Требуется знание физики и математики в объёме средней школы (11 классов).

Лекция 1. Электромагнитное взаимодействие и его место среди других взаимодействий в природе. Развитие физики электричества в работах М.В.Ломоносова. Электрический заряд. Микроскопические носители заряда. Опыт Милликена. Закон сохранения электрического заряда. Электростатика. Закон Кулона и его полевая трактовка. Вектор напряженности электрического поля. Принцип суперпозиции электрических полей.

Лекция 1. Поток вектора напряженности электрического поля. Электростатическая теорема Остроградского–Гаусса, ее представление в дифференциальной форме. Потенциальность электростатического поля. Потенциал. Нормировка потенциала. Связь вектора напряженности электростатического поля и потенциала.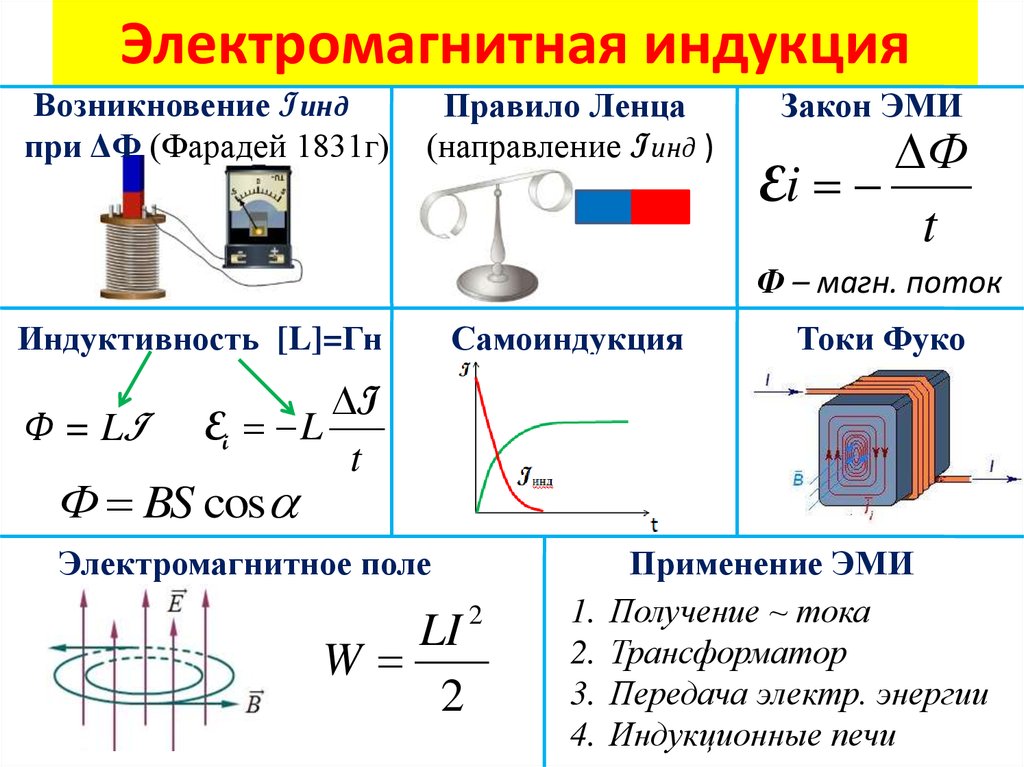 Работа сил электростатического поля. Потенциал системы зарядов.

Лекция 3. Циркуляция вектора напряженности электрического поля. Теорема о циркуляции, ее представление в дифференциальной форме. Уравнения Пуассона и Лапласа. Электрический диполь. Потенциал и напряженность поля диполя.

Лекция 4. Проводники в электростатическом поле. Электростатическая индукция. Напряженность поля у поверхности и внутри проводника. Распределение заряда по поверхности проводника. Электростатическая защита. Связь между зарядом и потенциалом проводника. Электроемкость. Конденсаторы. Емкость плоского, сферического и цилиндрического конденсаторов. Проводящий шар в однородном электростатическом поле.

Лекция 5. Диэлектрики. Свободные и связанные заряды. Вектор поляризации. Связь вектора поляризации со связанными зарядами. Вектор электрической индукции в диэлектрике. Диэлектрическая восприимчивость и диэлектрическая проницаемость и вещества. Материальное уравнение для векторов электрического поля. Теорема Остроградского – Гаусса для диэлектриков. Ее дифференциальная форма. Граничные условия для векторов напряженности и электрической индукции. Диэлектрический шар в однородном электрическом поле.

Лекция 6. Энергия системы электрических зарядов. Энергия взаимодействия и собственная энергия. Энергия электростатического поля и ее объемная плотность. Энергия электрического диполя во внешнем поле. Пондеромоторные силы в электрическом поле и методы их вычислений. Связь пондеромоторных сил с энергией системы зарядов.

Лекция 7. Электронная теория поляризации диэлектриков. Локальное поле. Неполярные диэлектрики. Формула Клаузиуса – Моссотти. Полярные диэлектрики. Функция Ланжевена. Поляризация ионных кристаллов. Электрические свойства кристаллов. Пироэлектрики. Пьезоэлектрики. Прямой и обратный пьезоэлектрический эффект и их применение. Сегнетоэлектрики. Доменная структура сегнетоэлектриков. Гистерезис. Точка Кюри. Применение сегнетоэлектриков.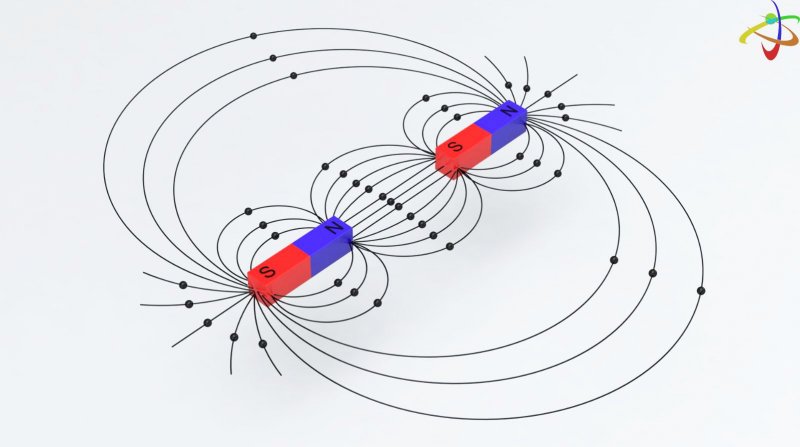

Лекция 8. Постоянный электрический ток. Сила и плотность тока. Линии тока. Электрическое поле в проводнике с током и его источники. Уравнение непрерывности. Условие стационарности тока. Электрическое напряжение. Закон Ома для участка цепи. Электросопротивление. Закон Ома в дифференциальной форме. Удельная электропроводность вещества.

Лекция 9. Токи в сплошных средах. Заземление. Работа и мощность постоянного тока. Закон Джоуля – Ленца и его дифференциальная форма. Сторонние силы. Электродвижущая сила. Закон Ома для замкнутой цепи. Разветвленные цепи. Правила Кирхгофа. Примеры их применения.

Лекция 10. Магнитостатика. Взаимодействие токов. Элемент тока. Закон Био – Савара – Лапласа и его полевая трактовка. Вектор индукции магнитного поля. Действие магнитного поля на ток. Закон Ампера. Теорема о циркуляции вектора индукции магнитного поля. Дифференциальная форма теоремы о циркуляции. Вихревой характер магнитного поля. Уравнение div B = 0. Понятие о векторном потенциале. Релятивистская природа магнитных взаимодействий.

Лекция 11. Элементарный ток и его магнитный момент. Магнитное поле элементарного тока. Элементарный ток в магнитном поле. Магнитное поле движущегося заряда. Взаимодействие движущихся зарядов. Сила Лоренца. Эффект Холла.

Лекция 12. Поток вектора магнитной индукции (магнитный поток). Коэффициент самоиндукции (индуктивность). Коэффициент взаимной индукции двух контуров. Потенциальная функция тока. Силы, действующие на контур с током. Взаимодействие двух контуров с током.

Лекция 13. Электромагнитная индукция. Закон электромагнитной индукции Фарадея и его дифференциальная форма. Правило Ленца. 

Лекция 14. Магнетики. Понятие о молекулярных токах. Вектор намагниченности вещества и его связь с молекулярными токами. Вектор напряженности магнитного поля. 

Лекция 15. Классификация магнетиков. Диамагнетики, парамагнетики и ферромагнетики. Классическое описание диамагнетизма. Ларморова прецессия. 

Лекция 16. Ферромагнетики. Спонтанная намагниченность и температура Кюри. Доменная структура. Гистерезис намагничивания, кривая Столетова. 

Лекция 17. Квазистационарные токи. Условия квазистационарности. Переходные процессы в RC- и LC-цепях. 

Лекция 18. Вынужденные колебания в контуре. Процесс установления вынужденных колебаний. 

Лекция 19. Резонанс напряжений. Напряжения и токи при резонансе. 

Лекция 20. Техническое применение переменных токов. Генераторы и электродвигатели. Трехфазный ток. 

Лекция 21. Высокочастотные токи. Скин-эффект. Толщина скин-слоя. 

Лекция 22. Классическая теория электронной проводимости Друде – Лоренца. 

Лекция 23. Полупроводники. 

В результате освоения дисциплины студент должен знать основные явления электричества и магнетизма, методы их теоретического описания и способы их использования в физических приборах, уметь решать задачи из раздела «Электромагнетизм» раздела курса общей физики.

Компетенции, необходимые для освоения дисциплины: ОНК-1, ПК-1; Компетенции, формируемые в результате освоения дисциплины: ПК-2; ОНК-5.

Физика. Электромагнетизм — то, что изменило нашу жизнь

12 сентября 2020, 14:30 12 сентября 2020, 15:30 12 сентября 2020, 16:30 12 сентября 2020, 17:30 12 сентября 2020, 18:30 12 сентября 2020, 19:30 12 сентября 2020, 20:30 12 сентября 2020, 21:30 12 сентября 2020, 22:30 12 сентября 2020, 23:30 13 сентября 2020, 00:30

Что такое электромагнетизм и как он работает? Притяжение и магнетизм – одно и то же? Как мы используем электромагнетизм в быту?
В гостях Юрий Олегович Михайловский, популяризатор науки, учитель физики Хорошколы.

• Смотрим всё

Электромагнетизм | Физика для идиотов

Содержимое

Для электромагнетизма все, что вам нужно знать, это то, что происходит, когда у вас есть + или — заряды, что происходит, когда они приближаются и что происходит, когда они перемещаются.

Вот и все! Для всех неквантовых ЭМ нужны всего 5 формул. 4 уравнения Максвелла и уравнение Лоренца описывают все электричество, магнетизм, свет, звук, излучение, фактически большую часть физики:

(1)  

(2)  

(3)  

(4)  

(5)  

Насколько плохой может быть тема, если вы можете описать ее всего с помощью 5 уравнений, вы, вероятно, сможете уместить их все на обратной стороне пивной подставки. Теперь, когда вы увидели заключение, мы можем перейти к началу и подробно прочитать всю историю. Если вы не изучаете университетский курс, вы можете не знать точно, что означает или делает уравнение, но этот сайт объяснит их позже, сначала давайте вернемся к основам.

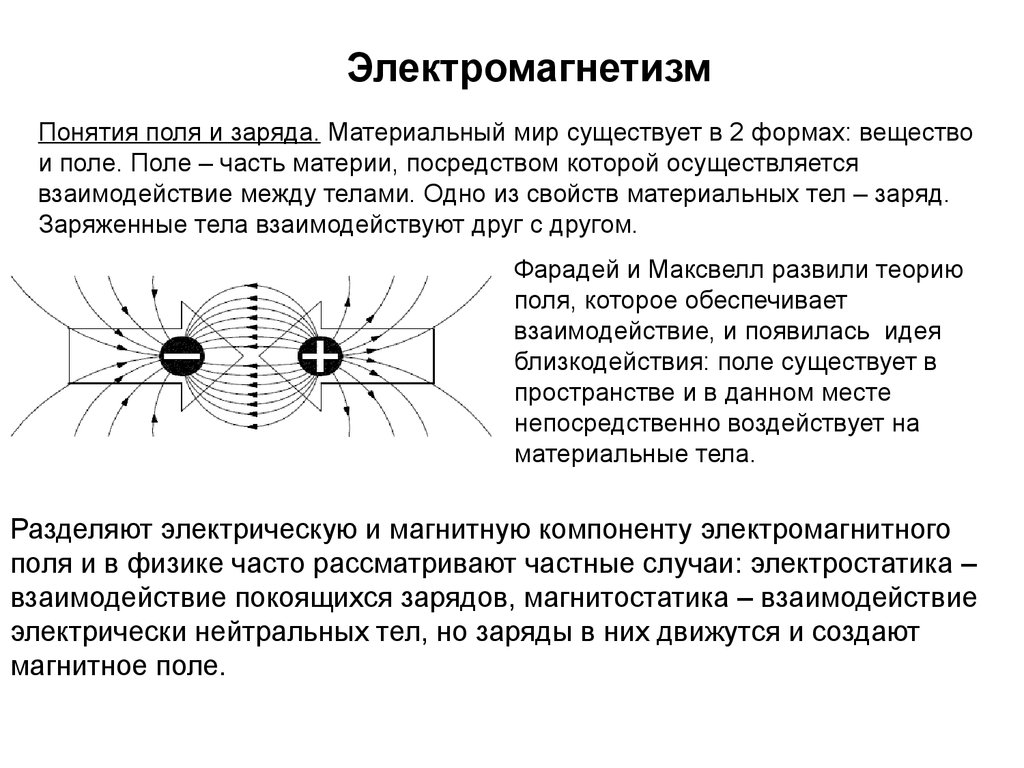
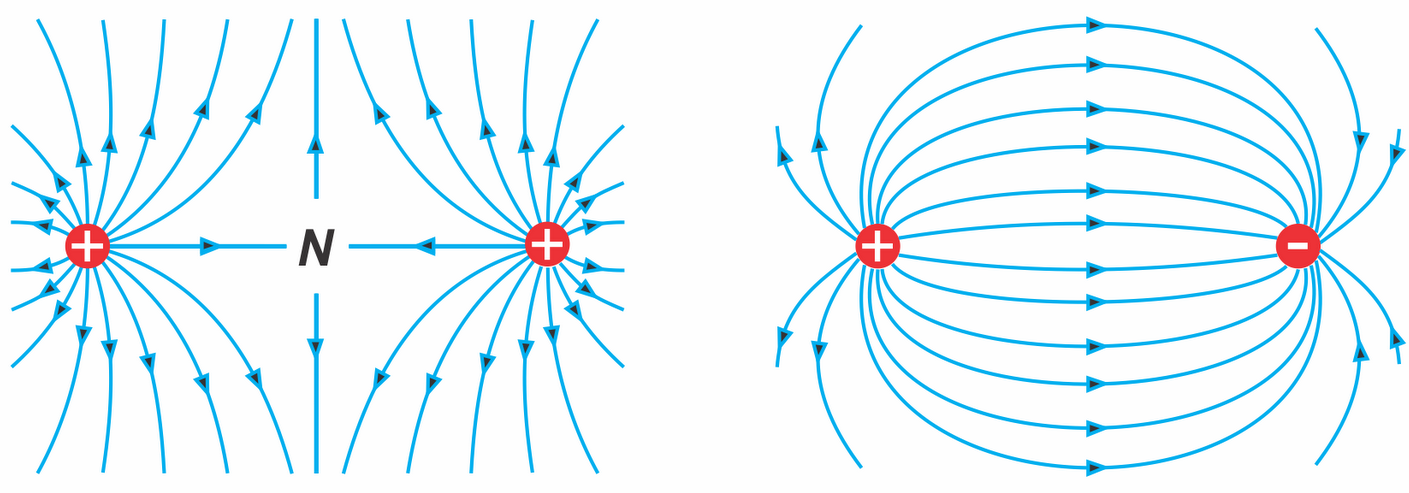
Заряд бывает двух типов: положительный и отрицательный, и измеряется в кулонах (C). Если у вас есть заряд сам по себе, он излучает поле во всех направлениях. Поле от заряда представлено буквой E, как и в E-электричестве. Если вы поместите другой заряд в поле, оно испытает силу. Одноименные заряды отталкиваются, а разноименные притягиваются.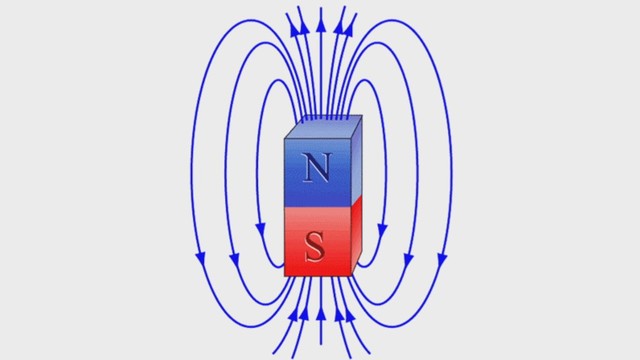 Чем больше заряд, тем сильнее сила, и чем дальше заряды, тем слабее сила, как и следовало ожидать. Это отношение может быть представлено законом Кулона;

   

и

   

s — это два заряда и расстояние между ними в квадрате. Другой бит — это просто константа, которая примерно равна

00000. (Точный вывод этого закона можно найти здесь). Из них вы можете видеть, что сила равна полю, умноженному на любой заряд, который вы приложили. Используя это, вы можете вычислить поле или силу между частицами, атомами или чем-то еще, имеющим заряд, при условии, что они не движутся. Как только вы начинаете движение заряда, происходят другие вещи.

Как только заряд начинает двигаться, он создает новое поле. Новое поле — это магнетизм, и оно представлено буквой B, как в B-магматизме?

Причина, по которой это B, просто в том, что он был вторым в алфавитном списке:

• Электромагнитный векторный потенциал: A
• Магнитная индукция: B
• Суммарный электрический ток: C
• Электрический рабочий объем: D
• Электродвижущая сила: E
• Механическая сила: F
• Скорость в точке: G
• Сила магнитного поля: H

(это также объясняет, откуда H для тех, кто заинтересован).

Итак, теперь ваша частица, или атом, или что-то еще имеет 2 выходных поля. Полное уравнение, описывающее, как оба поля действуют на частицу, выглядит так:

   

, известное как сила Лоренца. Символ не означает умножения, в данном контексте он означает перекрестное произведение. По сути, это короткий способ записи «умножить на синус угла между». Это потому, что поле толкает в 90°, в каком бы направлении он ни указывал И в каком бы направлении вы ни двигались. Теперь, если вы не выполняете ЭМ выше уровня A, вы можете забыть все о направлениях и углах и просто написать

   

Если мы расширим вышеизложенное выражение у нас есть

   

Но мы уже можем описать один из этих битов, это просто закон Кулона. Кроме того, на уровне A или ниже ситуация, вероятно, будет упрощена, поэтому вам нужно будет рассматривать только поля и отдельно. Таким образом, вам, вероятно, придется использовать только одну из следующих двух формул,

   

   

Очевидно, это сила и заряд, а также два ранее описанных поля и скорость движущегося заряда.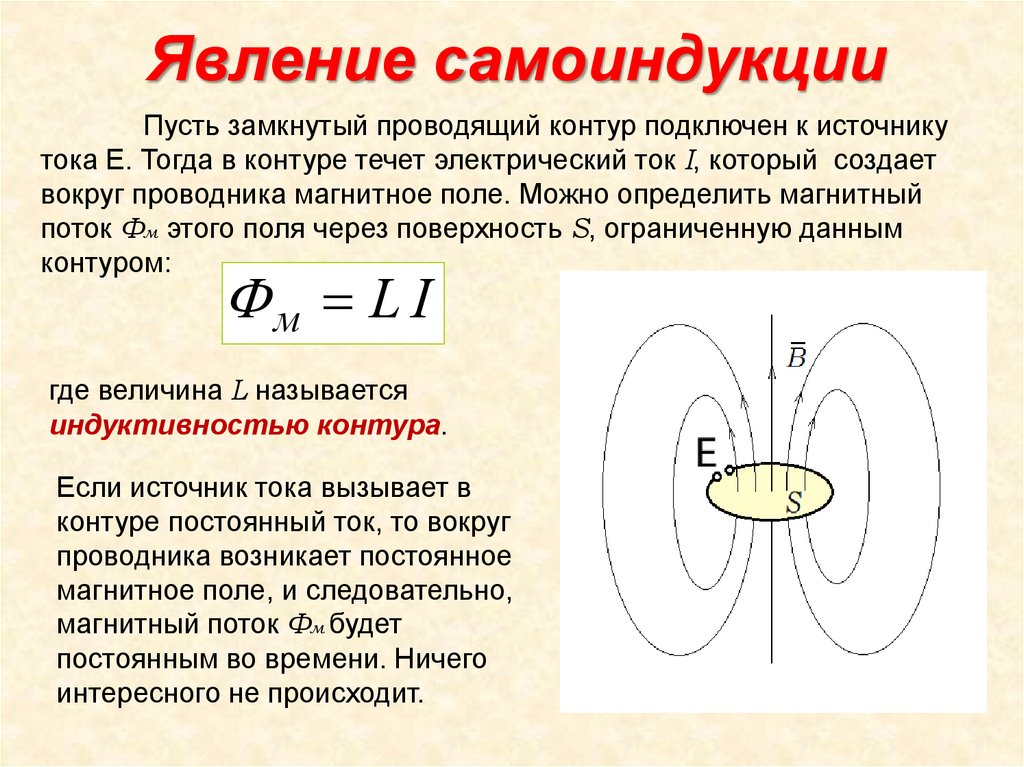

Электрическое поле измеряется в единицах СИ ньютонов на кулон () или, что эквивалентно, вольт на метр (). Магнитное поле измеряется в единицах СИ Тесла (Тл), что эквивалентно Веберам на квадратный метр () или вольт-секундам на квадратный метр ()

Теперь я не большой поклонник схем, никогда не был, теперь, надеюсь, я’ Я буду достаточно профессионален, чтобы моя неприязнь к ним не отразилась в этом разделе, но если это произойдет, я заранее извиняюсь. Если я действительно начну бороться со своей ненавистью, мне, возможно, придется вызвать второго писателя

Цепи A в основном просто серия движущихся зарядов со случайным объектом или устройством, которые влияют на поток. Теперь, когда я скажу, что электроны движутся вокруг, большинство людей подумает, что их скорость близка к скорости света, но это неправильно. Настоящие электроны движутся ОЧЕНЬ медленно, это волна движется быстро. Как сказано выше, одинаковые заряды отталкиваются, поэтому поместите один электрон рядом с другим, и они разойдутся.

С током в проводе у вас в основном есть трубка электронов, и вы добавляете один к одному из концов, это заставляет следующий электрон двигаться вниз, который, в свою очередь, толкает следующий и так далее. Таким образом, у вас есть эффект мексиканской волны, который движется быстро, но сами электроны движутся медленно.

Схемы обычно содержат всевозможные объекты и устройства в зависимости от того, для чего они предназначены, и в зависимости от того, как вы их настроите в схеме, зависит, как вы будете выполнять все свои расчеты.

Что есть что?

Если вы установите все компоненты в замкнутый цикл, например

, то мы скажем, что все компоненты относятся к серии . Если вы настроите их с путями ветвления, такими как

, тогда мы скажем, что компоненты находятся в Параллельный . Вы также можете создавать цепи, которые представляют собой смесь последовательных и параллельных секций, например,

Ампер, Вольт и Ом (о боже!) (А).

Амперы эквивалентны количеству заряда, прошедшего за определенное время, поэтому 2 кулона за 6 секунд будут эквивалентны 0,3А. Это, как и большинство вещей в физике, можно выразить в красивой формуле, которую вы должны выучить:

   

Еще одна важная идея в цепях — напряжение или разность потенциалов. Вольты — это в основном разница электрического потенциала в двух разных точках. Электрический потенциал между двумя точками определяется как

   

, где расстояние между и . Это в основном поле, умноженное на расстояние.

Другой важной идеей, когда речь заходит о цепях, является сопротивление. Сопротивление в основном является мерой того, какое сопротивление противостоит электрическому току. Почти все объекты или устройства в цепи вызывают сопротивление, и для расчета общего сопротивления в цепи вы используете одно или несколько из этих правил

   

   

Одним из наиболее важных и фундаментальных уравнений в цепях является закон Ома, и он связывает ток, напряжение и сопротивление.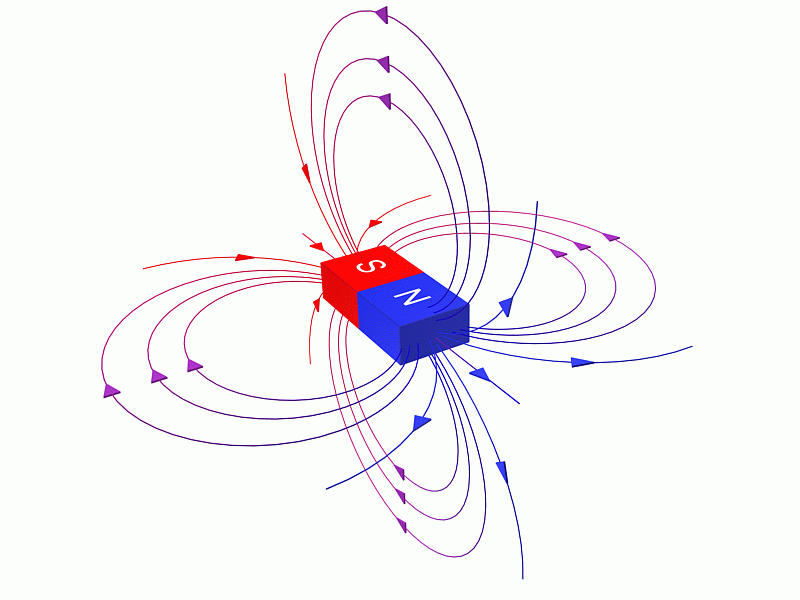

   

Вот оно. Классический ЭМ не идет дальше этого. Эти 4 являются фундаментальным уравнением для ВСЕХ полей в ЭМ. Это может занять некоторое время, чтобы прийти в себя, но как только вы это сделаете, все должно иметь смысл.

   

   

   

   

Если вы не знаете об интеграции и дифференциации, я предлагаю вам перейти к разделу «Интеграция» или «Дифференциация», я попытаюсь объяснить это здесь, но в основном сосредоточусь на физике.

Закон Гаусса

Хорошо, тогда сначала у нас есть Закон Гаусса.

   

Это говорит о том, что интеграл электрического поля через замкнутую область равен общему заряду внутри области, деленному на . является константой, называемой «Проницаемость свободного пространства», и проявляется во всей физике вместе с «Проницаемостью свободного пространства». Это уравнение означает, что вы можете взять ЛЮБУЮ замкнутую поверхность и найти поле, проходящее через нее, при условии, что вы можете заниматься математикой. Обычно вы не можете. Однако есть ряд случаев, когда это приятно и легко. Случаи, когда поле равномерно выходит прямо через поверхность. Случаев

• A Сферическая поверхность вокруг точки или сферы
• A Цилиндрическая поверхность вокруг бесконечной проволоки
• A Регулярная поверхность на сечении бесконечной плоскости

Я допускаю, что это звучит расплывчато и абстрактно, поэтому я продемонстрирую это с помощью диаграммы.

Это поверхности Гаусса. В основном с этими поверхностями все, что вы пытаетесь сделать, это облегчить жизнь. Вы просто убедитесь, что поверхность всегда находится на одном и том же расстоянии от источника заряда и что поле всегда проходит на 90 градусов. Затем вы можете решить интеграл с закрытыми глазами, это так просто. Левая часть закона Гаусса равна Е, умноженной на поверхность выбранной вами формы.

• Сферическая поверхность становится , где радиус сферы.
• Цилиндрическая поверхность становится , где  и — длина и радиус цилиндра.
• Обычная поверхность становится , где площадь выше и ниже бесконечной поверхности (вам нужен коэффициент 2, так как поле идет выше и ниже поверхности на 90 градусов).

Итак, закон Гаусса для сферы принимает вид

   

   

     

Который ранее был представлен как закон Кулона, теперь вы знаете, откуда он взялся. Закон Гаусса для бесконечной линии заряда всего лишь

   

   

   

. Если у вас есть бесконечная линия заряда, то общий заряд на ней бесконечен, и нет никакого способа узнать, какая часть этого бесконечного заряда будет у вас внутри вашей гауссовой поверхности. Вот тут-то и возникает значение заряда на единицу длины, поэтому, если = 4 см и у вас есть 5 метров, то заряд составляет всего 20С. Вот и все, просто значение заряда.

Для бесконечной поверхности закон Гаусса становится

   

Еще раз был добавлен новый символ, но он такой же, как и раньше. это просто плата за единицу площади, поэтому, если = 5 см и у вас есть площадь 100 м, общая стоимость составляет 500 C.

Заряженное кольцо

Допустим, у вас есть заряженное кольцо, и вам нужно знать создаваемое им поле. Мы снова будем использовать один из самых важных инструментов в физике, упрощая задачу. Во-первых, мы будем смотреть только на поле вдоль оси кольца, иначе все становится слишком сложным и не стоит усилий. Теперь давайте просто возьмем очень маленькую часть кольца и скажем, что это сфера. На самом деле это не так, но чем меньше мы делаем секцию, тем больше мы можем сделать ее похожей на точечный заряд. Итак, у вас есть что-то вроде этого

Вы хотите найти поле в точке по оси от кольца полного заряда и радиуса. Маленькая квадратная часть вверху — это то, что вы принимаете за заряженную сферу. Теперь мы не знаем, сколько заряда находится в этом маленьком разделе, поскольку вы можете сделать его любого размера, который вы хотите, поэтому мы просто называем заряд небольшим количеством . Итак, теперь у нас есть

   

Теперь, если подумать, каждый бит кольца выше оси, толкающей вниз, будет иметь такой же бит ниже оси, толкающей вверх. Это также будет одинаково для левой и правой и всех других частей кольца. Таким образом, вся сила от кольца будет действовать только вдоль оси. Чтобы отработать только этот бит, нам нужно использовать некоторый триггер. Нам нужно умножить поле на , чтобы получить осевую составляющую.

   

Как вы можете знать или не знать, также может быть описано (используя SOH CAH TOA) следующим соотношением для нашей ситуации: Итак, теперь у нас есть

   

Однако мы можем не знать, что это такое. Мы знаем радиус диска , и расстояние мы от диска, . Используя немного старого Пифагора, мы можем переписать в терминах и

   

Итак, теперь наше уравнение выглядит так

           

Теперь мы хотим избавиться от этого , поэтому мы интегрируем

           

Теперь мы знаем из диаграммы в начале, что общий заряд на диске равен , поэтому, если мы сложим все маленькие биты общего должно быть , так что интеграл просто .

   

Вот оно, поле с заряженного диска.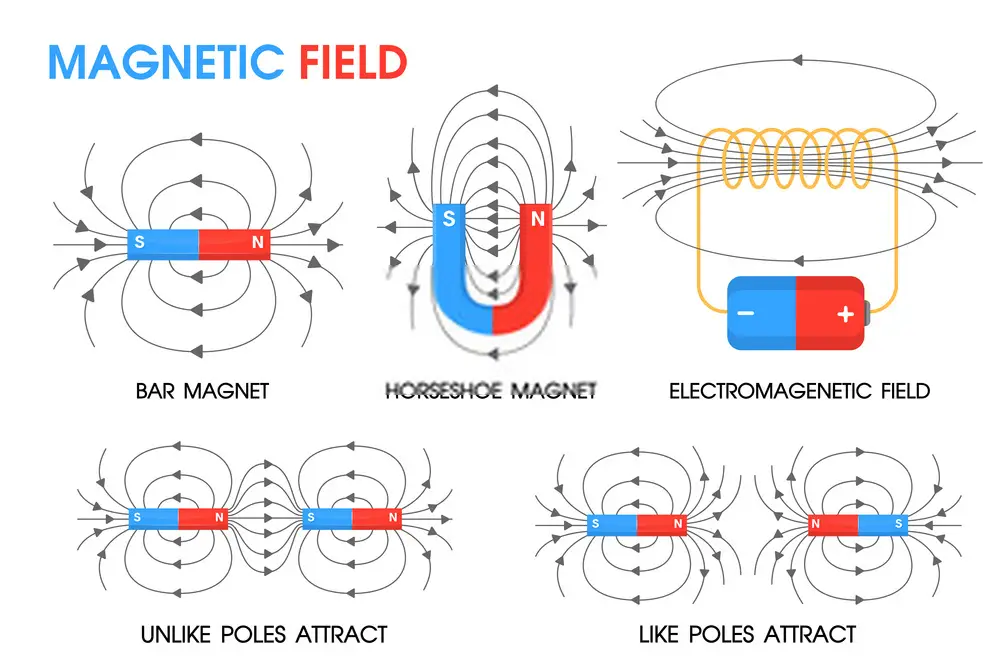 Все, что вам нужно, это поле с точки зрения и некоторые знания триггеров, и вы сможете это реализовать. Я мог бы просто дать вам окончательное решение, но таким образом вы сможете увидеть, откуда оно взялось, а затем, если вы его забудете, вы сможете разработать его из первых принципов, как указано выше.

Закон Гаусса для магнетизма

Это просто и красиво, но имеет некоторые важные последствия. Закон Гаусса для магнетизма:

   

Он подобен обычному закону Гаусса в том смысле, что он описывает поле, на этот раз магнитное поле, . Он говорит, что интеграл от B по замкнутой поверхности равен нулю. Ничего. Каждая линия поля, выходящая за пределы поверхности, имеет эквивалент, входящий внутрь. Общего поля не существует. Это означает, что невозможно получить источники Магнитного поля. В то время как электроны и протоны являются источником поля, от которого расходятся или сходятся силовые линии, магнитного аналога не существует. Линии магнитного поля всегда представляют собой замкнутые петли, без начала и без конца.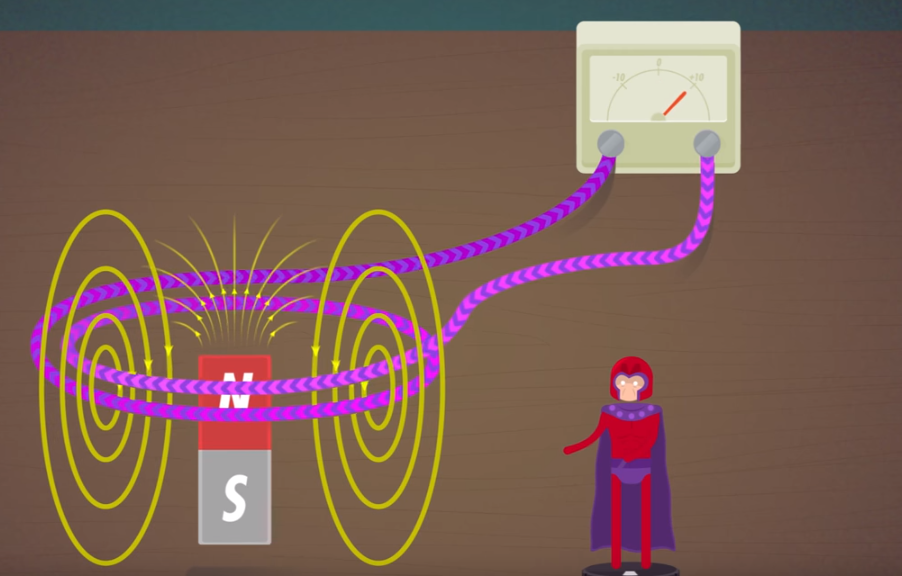 Это, конечно, не помешало людям подготовиться на случай, если мы найдем магнитный монополь.

Это уравнение может показаться красивым, и так оно и есть, но само по себе оно совершенно бесполезно. Обычно результат 0 в физике очень важен, он означает, что может происходить что-то особенное, здесь он показывает, что магнитных монополей не существует.

Закон Фарадея

Теперь все становится сложнее, здесь у нас есть закон Фарадея,

   

Я проведу вас через каждую часть, чтобы показать вам, что это на самом деле означает. Сначала у нас есть левая сторона, которая проста. Это так же, как закон Гаусса, только интеграл по другой вещи. Вместо того, чтобы находить полное поле через поверхность, теперь мы находим полное поле вокруг замкнутого контура. Это все, что отличается от левой стороны, больше никаких поверхностей, только замкнутые петли. Теперь о правой стороне. Во-первых, у нас есть минус, отметив, что это сложно. Почему он там, будет объяснено позже.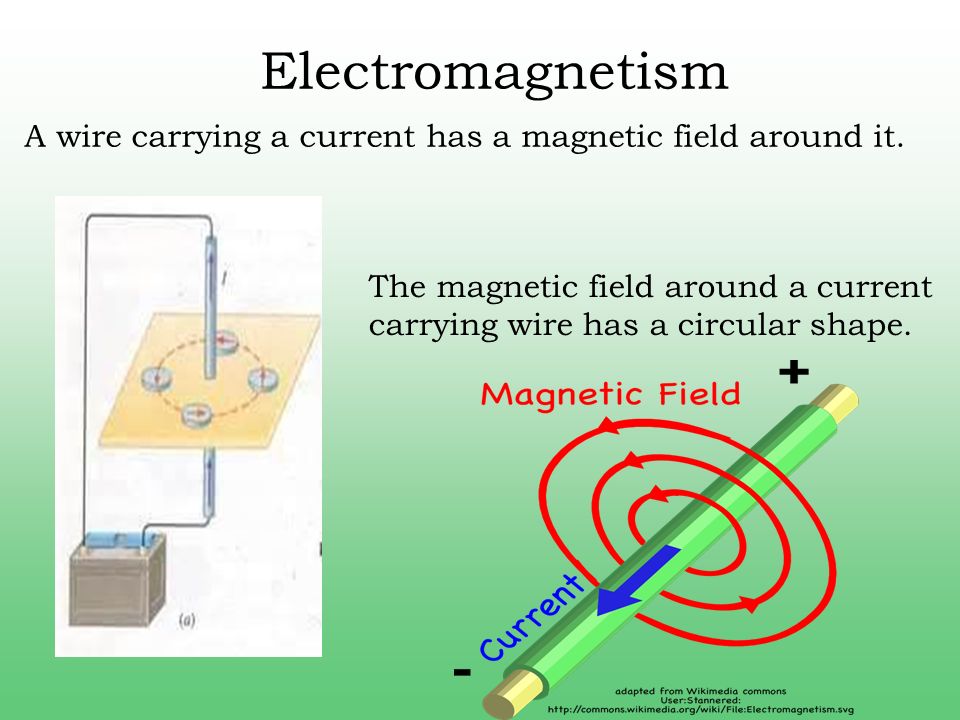 Далее у нас есть еще один интеграл, и он выглядит ужасно. Символ в основном означает небольшое изменение. Так  является изменением , и является изменением , где  является временем. Целое — это скорость изменения , насколько оно изменяется () в данный момент времени (). И это интегрируется по области. это область внутри замкнутого контура, если вы нарисуете какую-нибудь случайную волнистую вещь, убедившись, что линия не пересекает сама себя и что она соединяется сама с собой, тогда длина вокруг линии будет вашей, а область внутри линии — вашей. Простой да? Таким образом, общая сумма по циклу просто равна минусу изменения в цикле.

Что произойдет, если нет ? Ну нет , значит , ноль, что делает интеграл равным 0, значит нет . Что произойдет, если у вас есть константа ? Что ж, снова  равно 0. Значит,  равно нулю, что делает интеграл равным 0, так что снова нет . Вы можете создать поле только из изменяющегося поля.

Значение знака минус связано с тем, что поля создают поля, а поля создают поля (как показано в законах Фарадея и Ампера).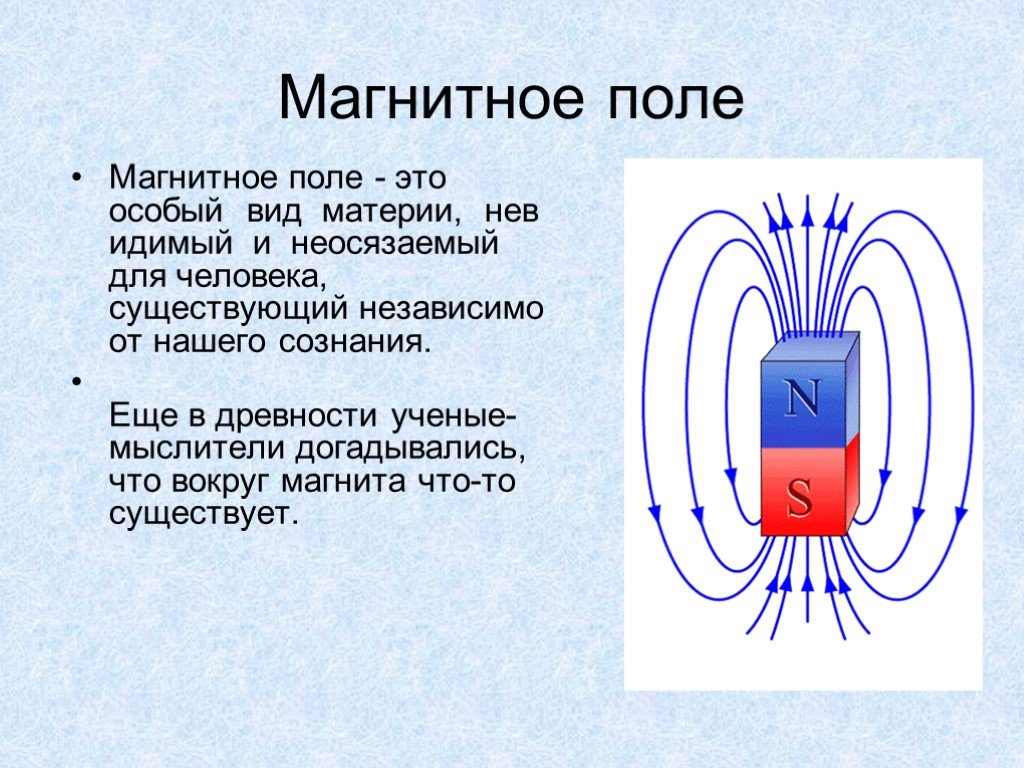 Если бы минуса не было, то поля продолжали бы накапливаться и накапливаться, в конечном итоге давая бесконечную энергию, а это недопустимо!

Закон Ампера-Максвелла

Последним из уравнений Максвелла является закон Ампера-Максвелла. Как первые два закона были похожи, так и последние два, в этом порядке для них есть шаблон, который может облегчить их запоминание. над областью, над областью, вокруг петли и теперь, наконец, вокруг петли. Уравнение:

   

Левая часть, простая, интеграл от B по замкнутому контуру. Правая сторона, не так просто. Сначала давайте проигнорируем немного, я вернусь к этому. В остальном он очень похож на закон Фарадея. У вас есть еще одно изменяющееся поле, интегрированное в область, но на этот раз это . На этот раз вместо умножения на минус 1 вы умножаете на . Опять же, это две очень важные величины в физике, по отдельности и вместе взятые. Они находятся в самом сердце ЭМ. Таким образом, ваше магнитное поле вокруг контура просто равно изменяющемуся полю Е, проходящему через него раз на , но тогда вам придется немного добавить. Это бит. Это просто ток, проходящий через петлю за время , потому что, как сказано в Перемещении вещей, если у вас есть движущийся заряд, то есть ток, вы получаете магнитное поле. Таким образом, вы должны добавить два бита вместе. Красный.

Помимо написания уравнений Максвелла, приведенных выше, в так называемой интегральной форме, вы также можете записать их в дифференциальной форме, например: одна из двух вышеупомянутых форм действительно упрощение. И интегральная форма, и дифференциальная форма являются векторными уравнениями, и они избавляют вас от необходимости выписывать полные 8 уравнений Максвелла для полей и во всех трех измерениях.

[su_spoiler title=”8 ‘Оригинальные’ уравнения Максвелла” style=”fancy”]

   

   

   

   

   

   

   

   

[/su_spoiler]

Ну мало ли что можно также компактизируйте четыре векторных уравнения Максвелла в два тензорных уравнения, например так: Они определены как

(6)  

(7)  

где – скорость света. То и просто скажу где в векторе или матрице смотреть, но сбивает с толку у некоторых начало с 0, так и (не путать с кубом). То же самое с , так и

Электромагнетизм — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

252

На данном этапе вы понимаете примерно столько же о классификации взаимодействий, сколько физики понимали примерно в 1800 году. По-видимому, существует три принципиально разных типа взаимодействий: гравитационное, электрическое и магнитное. Многие типы взаимодействий, которые на первый взгляд кажутся разными — липкость, химическое взаимодействие, энергия, запасаемая лучником в луке, — на самом деле одинаковы: это проявления электрических взаимодействий между атомами.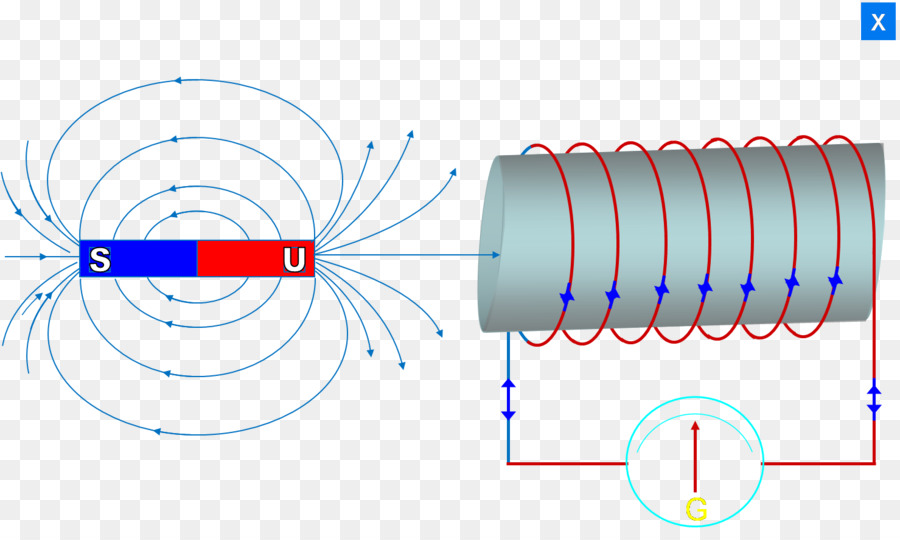 Есть ли способ еще больше сократить список? Перспективы сначала кажутся туманными. Например, мы обнаруживаем, что если потереть кусок меха о резиновую палочку, мех не притягивает и не отталкивает магнит. У меха есть электрическое поле, а у магнита есть магнитное поле. Они совершенно разные и, кажется, не влияют друг на друга. Точно так же мы можем проверить, изменяет ли намагничивание кусок железа его вес. Вес, кажется, не меняется на сколько-нибудь измеримую величину, поэтому магнетизм и гравитация кажутся не связанными.

Так обстояли дела до 1820 года, когда датский физик Ганс Христиан Эрстед читал лекцию в Копенгагенском университете и хотел показать своим студентам демонстрацию, которая проиллюстрировала бы передовые достижения исследований. Он генерировал ток в проводе, замыкая батарею, и держал провод рядом с магнитным компасом. Идея заключалась в том, чтобы привести пример того, как можно искать ранее не обнаруженную связь между электричеством (электрическим током в проводе) и магнетизмом. Никогда не знаешь, насколько можно верить в эти драматические легенды, но история ² , что эксперимент, который он ожидал получить отрицательным, вместо этого оказался положительным: когда он держал провод рядом с компасом, ток в проводе заставлял компас крутиться!

Подобные эксперименты проводились и раньше, но только со статическим электричеством, а не с движущимся электрическим током. Например, они подвесили батареи так, чтобы они могли свободно вращаться в магнитном поле Земли, и не обнаружили никакого эффекта; поскольку батарея не была подключена к полной цепи, ток не протекал. С собственной установкой Эрстеда h эффект производился только тогда, когда «цепь была замкнута, но не разомкнута, как несколько очень знаменитых физиков тщетно пытались несколько лет назад». ³

Рисунок 1 . Когда цепь неполная, ток по проводу не течет, и магнит не затрагивается. Он указывает направление магнитного поля Земли. 2. Цепь замыкается, и по проводу течет ток.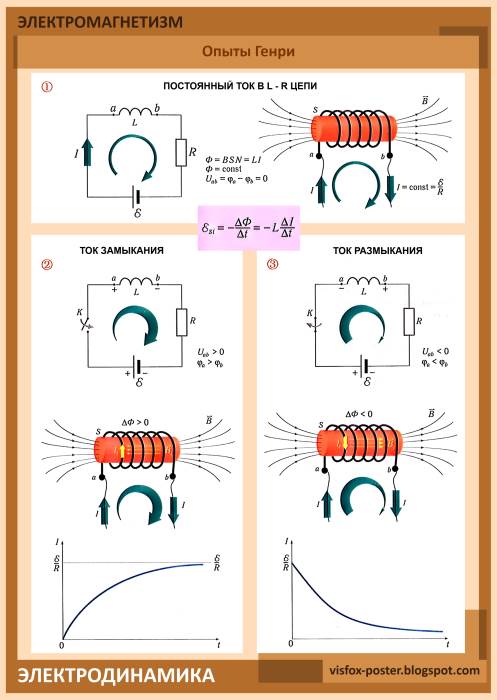 Проволока оказывает сильное воздействие на магнит, который поворачивается почти перпендикулярно ему. Если бы поле Земли можно было полностью убрать, компас указывал бы точно перпендикулярно проводу; это направление поля провода.

В конце концов Эрстед пришел к выводу, что магнетизм представляет собой взаимодействие между движущимися зарядами и другими движущимися зарядами, то есть между одним током и другим. Он предположил, что постоянный магнит содержит токи в микроскопическом масштабе, которые просто невозможно измерить с помощью амперметра. Сегодня это кажется нам естественным, поскольку мы привыкли представлять атом как крошечную солнечную систему с электронами, кружащимися вокруг ядра. Как показано на рисунке 1, намагниченный кусок железа отличается от ненамагниченного куска, потому что атомы в ненамагниченном куске перемешаны в случайных ориентациях, тогда как атомы в намагниченном куске, по крайней мере, частично организованы так, чтобы смотреть в определенном направлении.

Рисунок i : Схематическое изображение ненамагниченного материала 1 и намагниченного материала 2.

На рисунке j показан концептуально простой, но не очень практичный пример. Если вы попробуете это с обычной вакуумной лампой, такой как телевизор или компьютерный монитор, тока в проводе, вероятно, будет недостаточно для получения видимого эффекта. Более практичным методом является поднесение магнита к экрану. У нас все еще есть взаимодействие между движущимися зарядами и движущимися зарядами, но вращающиеся электроны в атомах в магните теперь играют роль, которую играют движущиеся заряды в проводе на рисунке j. Внимание: если вы делаете это, убедитесь, что на вашем мониторе есть кнопка размагничивания! Если нет, то ваш монитор может быть навсегда испорчен.

Рисунок j : Магнетизм — это взаимодействие между движущимися зарядами и движущимися зарядами. Движущиеся заряды в проводе притягивают движущиеся заряды в пучке заряженных частиц в вакуумной трубке.

Для теории относительности требуется магнетизм

Итак, магнетизм — это взаимодействие между движущимися зарядами и движущимися зарядами. но как это может быть? Теория относительности говорит нам, что движение — это вопрос мнения. Рассмотрим фигуру k. На этом рисунке и на рисунке 1 темная и светлая окраска частиц отражает тот факт, что одна частица имеет один тип заряда, а другая — другой.

Рисунок k ./ Один наблюдатель видит электрическое поле, а другой видит и электрическое поле, и магнитное.

Наблюдатель k/2 видит две частицы, летящие в пространстве бок о бок, поэтому они будут взаимодействовать как электрически (просто потому, что они заряжены), так и магнитно (потому что это заряды в движении). Но наблюдатель, движущийся вместе с ними, k/1, сказал бы, что они оба покоятся, и ожидал бы только электрического взаимодействия. Это кажется парадоксом. Однако магнетизм приходит не для того, чтобы разрушить относительность, а чтобы восполнить ее.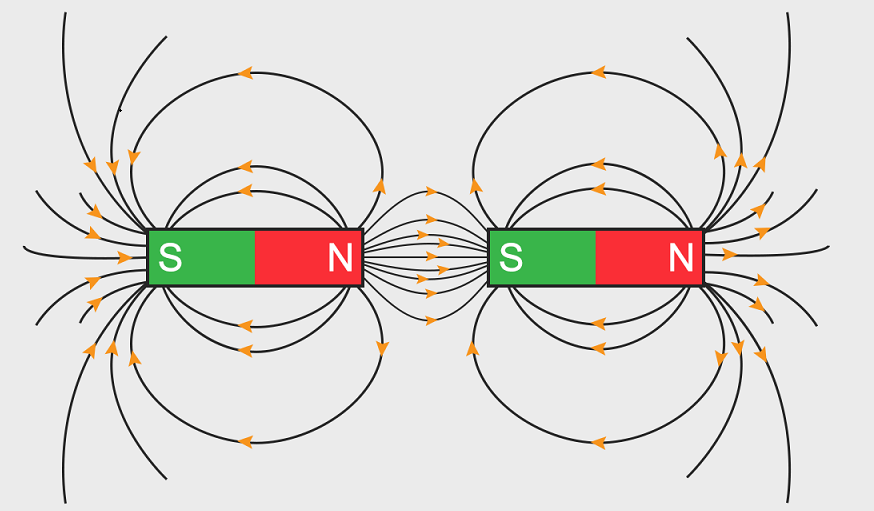 Магнитные взаимодействия должно существовать согласно теории относительности. Чтобы понять, как это может быть, рассмотрим, как время и пространство ведут себя в теории относительности. Наблюдатели в разных системах отсчета расходятся во мнениях относительно длины измерительных стержней и скорости часов, но законы физики действительны и непротиворечивы в любой системе отсчета. Точно так же наблюдатели в разных системах отсчета расходятся во мнениях относительно того, какие существуют электрические и магнитные поля, но соглашаются в отношении конкретных физических явлений. Наблюдатель в системе отсчета k/1 говорит, что вокруг частиц существуют электрические поля, и предсказывает, что с течением времени частицы начнут ускоряться навстречу друг другу, в конце концов столкнувшись. Она объясняет столкновение электрическим притяжением между частицами. Другой наблюдатель, k/2, говорит, что частицы движутся. Этот наблюдатель также предсказывает, что частицы будут сталкиваться, но объясняет их движение с точки зрения как электрического поля, так и магнитного поля. 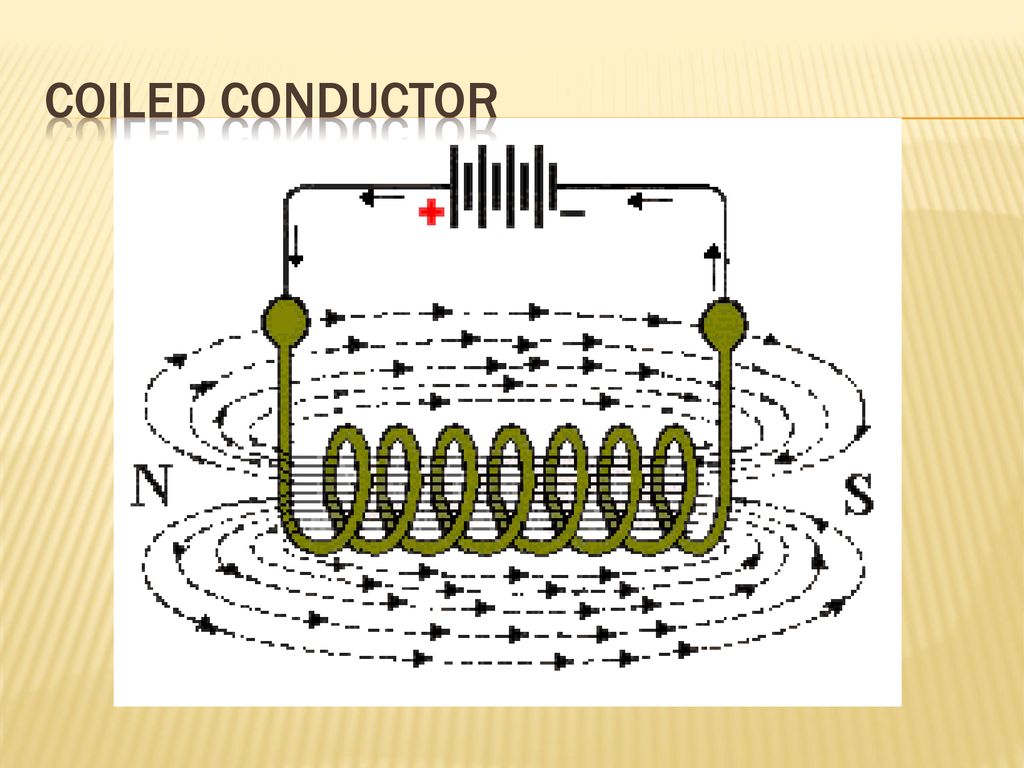Как мы вскоре увидим, магнитное поле равно требовал , чтобы поддерживать согласованность между предсказаниями, сделанными в двух системах отсчета.

Чтобы увидеть, как это работает на самом деле, нам нужно найти хороший простой пример. Например, число k равно , а не , потому что во второй системе отсчета движущиеся заряды создают поля, которые со временем меняются в любом заданном месте, например, когда V-образный след катера омывает буй. Примеры, подобные рисунку j, проще, потому что существует постоянный поток зарядов, и все поля остаются неизменными с течением времени. На рис. 1/1 показана упрощенная и идеализированная модель рисунка j. Заряд сам по себе подобен одной из заряженных частиц в луче вакуумной трубки на рисунке j, и вместо проволоки у нас есть две длинные линии зарядов, движущихся в противоположных направлениях. Обратите внимание, что, как обсуждалось в вопросе для обсуждения C на стр. 106, токи двух зарядных линий не уравновешиваются. Темные шары представляют собой частицы с одним типом заряда, а светлые шары — с другим типом заряда. Из-за этого общий ток в «проводе» в два раза больше, чем был бы, если бы мы убрали одну линию.

Как модель фигуры j, фигура l/1 частично реалистична, частично нереалистична. В реальном куске медной проволоки действительно есть заряженные частицы обоих типов, но оказывается, что частицы одного типа (протоны) заперты на месте, тогда как только часть другого типа (электроны) могут свободно перемещаться. двигаться. Модель также показывает, что частицы движутся простым и упорядоченным образом, как автомобили на двухполосной дороге, тогда как в действительности большинство частиц организованы в атомы меди, а также существует большое количество случайного теплового движения. Нереалистичные особенности модели не являются проблемой, потому что цель этого упражнения состоит только в том, чтобы найти одну конкретную ситуацию, которая показывает, что магнитные эффекты должны существовать на основе теории относительности.

Какую электрическую силу испытывает одинокая частица на рисунке l/1? Поскольку плотность «движения» по обеим сторонам «дороги» одинакова, общая электрическая сила на одинокую частицу равна нулю.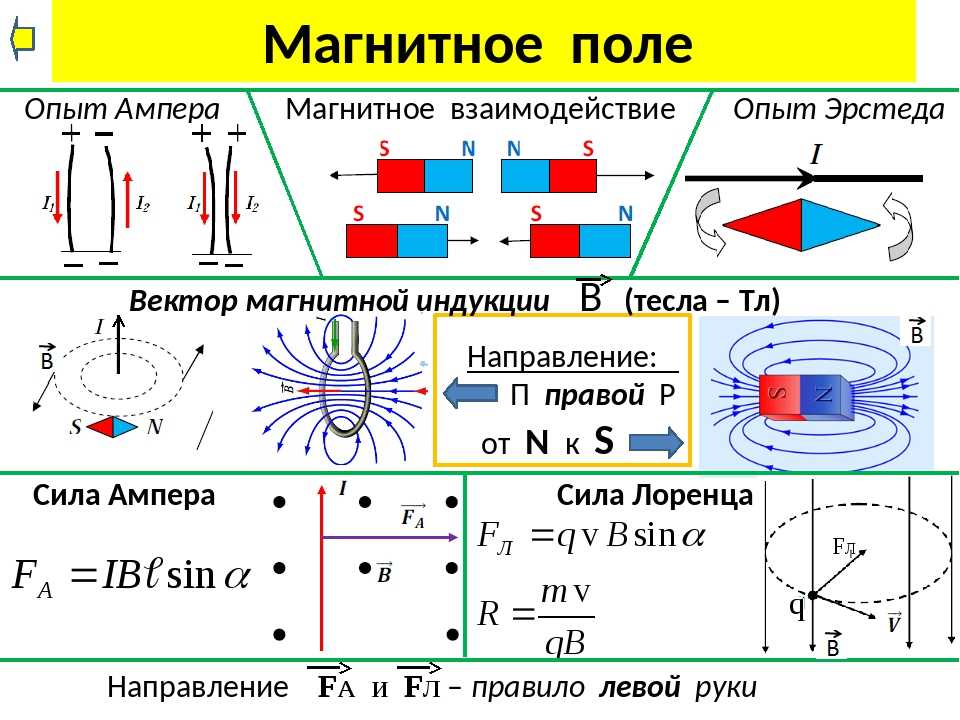 Каждая «машина», притягивающая одинокую частицу, находится в паре с партнером на другой стороне дороги, который ее отталкивает. Если бы мы не знали о магнетизме, мы бы подумали, что дело в этом: одинокая частица вообще не чувствует никакой силы от проволоки.

Рис. l: Модель заряженной частицы и провода с током в двух разных системах отсчета. Релятивистское сокращение длины сильно преувеличено. Сила, действующая на одинокую частицу, чисто магнитная в 1 и чисто электрическая в 2.

На рис. 1/2 показано, что мы увидели бы, если бы наблюдали все это из системы отсчета, движущейся вместе с одиноким зарядом. Вот тут-то и появляется теория относительности. Согласно теории относительности, движущиеся объекты кажутся сжатыми для наблюдателя, который не движется вместе с ними. Обе линии заряда находятся в движении в обеих системах отсчета, но в системе 1 они двигались с одинаковыми скоростями, поэтому их сокращения были равны. Однако в кадре 2 их скорости не равны. Темные заряды движутся медленнее, чем на кадре 1, поэтому на кадре 2 они менее сжаты. Заряды светлого цвета двигаются быстрее, поэтому их сжатие теперь сильнее. «Машины» по обеим сторонам «дороги» больше не парные, поэтому электрические силы, действующие на одинокую частицу, больше не компенсируются, как это было в случае 1/1. Одинокая частица притягивается к проволоке, потому что частицы, притягивающие ее, более плотны, чем частицы, отталкивающие ее. Кроме того, притяжение, ощущаемое одиноким зарядом, должно быть чисто электрическим, поскольку одинокий заряд в этой системе отсчета покоится, а магнитные эффекты возникают только между движущимися зарядами и другими движущимися зарядами.

Теперь наблюдатели на кадрах 1 и 2 расходятся во многом, но соглашаются по конкретным событиям. Наблюдатель 2 увидит, как одинокая частица дрейфует к проводу из-за электрического притяжения провода, постепенно ускоряясь и в конце концов ударяясь о провод. Если 2 видит это столкновение, то 1 тоже должен.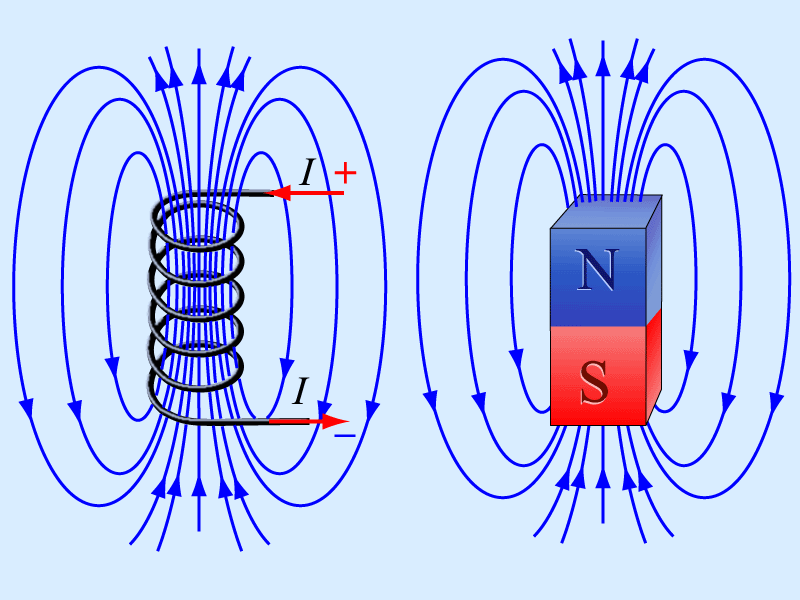 Но я знаю, что полная электрическая сила, действующая на одинокую частицу, точно равна нулю. Должен быть какой-то новый тип силы. Она изобретает название для этого нового типа силы: магнетизм. Это был особенно простой пример, потому что в одной системе отсчета сила была чисто магнитной, а в другой — чисто электрической. В общем случае наблюдатель в одной системе отсчета будет измерять смесь электрического и магнитного полей, а наблюдатель в другой системе отсчета, движущийся относительно первой, скажет, что в том же объеме пространства содержится другая смесь.

Таким образом, мы приходим к выводу, что электрические и магнитные явления не разделены. Это разные стороны одной медали. Мы называем электрические и магнитные взаимодействия вместе электромагнитными взаимодействиями. В нашем списке фундаментальных взаимодействий в природе теперь два пункта вместо трех: гравитация и электромагнетизм.

FigureFgm: Магнитные взаимодействия с участием только двух частиц одновременно.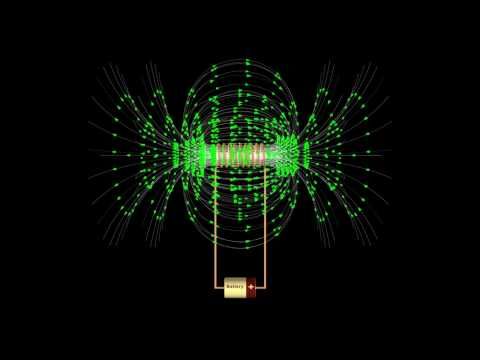 На этих рисунках, в отличие от рисунка 1/1, наряду с магнитными есть и электрические силы. Электрические силы здесь не показаны. Не запоминайте эти правила!

Основные правила магнитного притяжения и отталкивания, показанные на рисунке m, не так просты, как законы гравитации и электричества. Правила m/1 и m/2 следуют непосредственно из нашего предыдущего анализа рисунка 1. Правила 3 ​​и 4 получаются путем изменения типа заряда нижней частицы. Например, правило 3 похоже на правило 1, за исключением того, что нижний заряд теперь имеет противоположный тип. Это превращает притяжение в отвращение. (Мы знаем, что переворачивание заряда меняет взаимодействие на противоположное, потому что именно так это работает с электрическими силами, а магнитные силы — это просто электрические силы, рассматриваемые в другой системе отсчета.)

Пример 1: магнитный флюгер, расположенный рядом с током

На рисунке n показан магнитный флюгер, состоящий из двух зарядов, которые вращаются по кругу вокруг оси стрелки.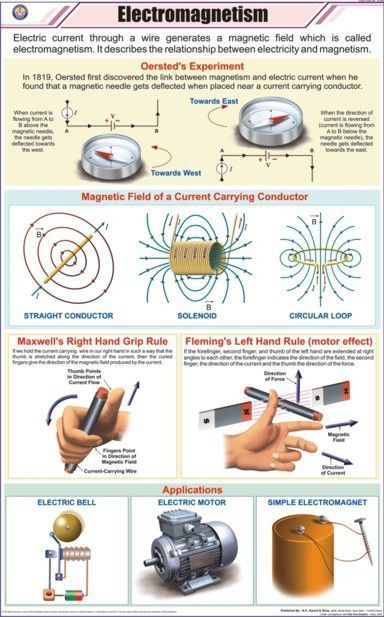 (Магнитное поле не заставляет их вращаться; в первую очередь для их вращения необходим двигатель.)

Рисунок n: Пример 1

Стрелка флюгера стремится выровняться в направлении, перпендикулярном проводу. Это его предпочтительная ориентация, потому что заряд, близкий к проводу, притягивается к проводу, а заряд, находящийся далеко от провода, отталкивается от него.

Магнитные поля

Как определить магнитное поле? Когда два объекта гравитационно притягиваются друг к другу, их гравитационная энергия зависит только от расстояния между ними, и кажется интуитивно разумным, что мы определяем стрелки гравитационного поля как дорожный знак, который гласит: «Этот путь понизит гравитационную энергию». Та же идея прекрасно работает для электрического поля. Но что, если две заряженные частицы взаимодействуют магнитным образом? Их взаимодействие зависит не только от расстояния, но и от их движений.

Нам нужно найти какое-то направление в пространстве, чтобы мы могли сказать: «Это направление магнитного поля здесь». Естественным и простым методом является определение направления магнитного поля в соответствии с направлением, которое указывает компас. Исходя из этого определения, мы можем, например, провести эксперименты, чтобы показать, что магнитное поле провода с током образует круговую структуру, o.

РИСУНОК o: Магнитное поле закручивается вокруг провода по кругу. В каждой точке пространства магнитный компас показывает направление поля.

Но правильное ли это определение? В отличие от определений направлений гравитационных и электрических полей, здесь используется особый инструмент, созданный человеком. Однако сравните цифру h с цифрой n. Обратите внимание, что оба этих инструмента выстраиваются вдоль линии, перпендикулярной проводу. На самом деле, как бы вы ни старались, вам никогда не удастся изобрести какое-либо другое электромагнитное устройство, которое будет согласовываться с любой другой линией. Все, что вы можете сделать, это сделать такой, который указывает точно в противоположном направлении, но вдоль той же линии. Например, вы можете использовать краску, чтобы поменять местами цвета, обозначающие концы стрелки магнитного компаса, или вы можете построить флюгер, как на цифре n, но вращающийся как левый винт, а не как правый. Флюгер и компас не так уж и отличаются, как кажется. На рис. p показаны их скрытые сходства.

Рисунок p : 1. Стрелка магнитного компаса представляет собой не что иное, как стержневой магнит, который может свободно вращаться в ответ на магнитное поле Земли. 2. Карикатура на структуру стержневого магнита на атомном уровне. Каждый атом очень похож на флюгер на рисунке n.

Природа пытается нам что-то сказать: в направлении, которое указывает компас, действительно есть что-то особенное. Определение направления магнитного поля с точки зрения этого конкретного устройства не так произвольно, как кажется. Единственный произвол заключается в том, что мы могли бы построить целый самосогласованный набор определений, начав с определения магнитного поля как направленного в противоположном направлении.

Пример 2: Выравнивание стержневых магнитов «голова к хвосту»

• Если вы позволите двум стержневым магнитам, подобным показанному на рисунке p, взаимодействовать, каким образом они выстроятся в линию, лицом к лицу или лицом к лицу? хвост?
• Каждый стержневой магнит содержит огромное количество атомов, но это не будет иметь значения для нашего результата; мы можем представить это как взаимодействие между двумя отдельными атомами. Если уж на то пошло, давайте смоделируем атомы в виде флюгеров, как на рисунке n. Предположим, мы поставили два таких флюгера рядом, чтобы их стрелки были направлены от нас. С нашей точки зрения, они оба вращаются по часовой стрелке. Когда один из зарядов левого флюгера опускается с правой стороны, один из зарядов правого флюгера поднимается с левой стороны. Эти два заряда расположены близко друг к другу, поэтому их магнитное взаимодействие в этот момент очень сильное. Их взаимодействие отталкивающее, так что это неустойчивое расположение двух флюгеров.

С другой стороны, предположим, что левый флюгер направлен в сторону от is, а его партнер справа указывает на нас. С нашей точки зрения, мы видим, что тот, что справа, вращается против часовой стрелки. В тот момент, когда их подопечные подходят как можно ближе, они оба уже на пути вверх. Их взаимодействие привлекательно, так что это стабильное расположение.

Возвращаясь от нашей модели к первоначальному вопросу о стержневых магнитах, мы обнаруживаем, что стержневые магниты имеют тенденцию выравниваться головой к хвосту. Это легко проверяется опытным путем.

Рисунок q: Сила, действующая на заряженную частицу, движущуюся через магнитное поле, перпендикулярна как полю, так и направлению ее движения. Зависимость правая для одного типа заряда и левая для другого типа.

Если вы вернетесь назад и примените это определение ко всем примерам, с которыми мы сталкивались до сих пор, вы обнаружите, что существует общее правило: сила, действующая на заряженную частицу, движущуюся через магнитное поле, перпендикулярна как полю, так и его направление движения. Сила, перпендикулярная направлению движения, — это как раз то, что требуется для кругового движения, поэтому мы обнаруживаем, что заряженная частица в вакууме будет двигаться по кругу вокруг стрелок магнитного поля (или, возможно, по штопору, если она также имеет какое-то движение). вдоль направления поля). Это означает, что магнитные поля имеют тенденцию захватывать заряженные частицы.

Рисунок r: Пучок электронов вращается вокруг стрелок магнитного поля.

На рисунке r показан этот принцип в действии. Пучок электронов создается в вакуумной трубке, в которой осталось небольшое количество газообразного водорода. Несколько электронов ударяются о молекулы водорода, создавая свет и позволяя нам увидеть траекторию луча. Магнитное поле создается путем пропускания тока (метра) через круглые витки проволоки перед и за трубкой. На нижнем рисунке при включенном магнитном поле сила, перпендикулярная направлению движения электронов, заставляет их двигаться по окружности.

Пример 3: Солнечные пятна

Солнечные пятна, подобные приведенному выше, представляют собой места, где магнитное поле Солнца необычайно сильное. Заряженные частицы задерживаются там на месяцы. Этого времени достаточно, чтобы солнечное пятно значительно остыло, и оно не нагревается снова, потому что более горячий окружающий материал удерживается теми же магнитными силами.

Рисунок : Это солнечное пятно является продуктом действия магнитных полей Солнца. Самая темная область в центре размером с нашу планету.

Пример 4: Полярное сияние и жизнь на поверхности Земли

Сильное магнитное поле, по-видимому, является одной из предпосылок существования жизни на поверхности планеты. Энергичные заряженные частицы от Солнца захватываются магнитным полем нашей планеты и безвредно спускаются по спирали к поверхности Земли на полюсах. Помимо защиты, это создает полярное сияние, или «северное сияние».

Астронавты, отправившиеся на Луну, около недели находились вне защитного поля Земли и за это время получили значительные дозы радиации. Проблема будет гораздо более серьезной для астронавтов в полете на Марс, который займет не менее пары лет.