Физики увидели рекордно быстрый переменный ток

Физики из Института квантовой оптики общества Макса Планка добились рекордной частоты колебаний электрического тока благодаря использованию интенсивных лазерных полей. Она составила почти 6 петагерц — время одного колебания по меньшей мере на порядок меньше, чем время колебания волны света оптического диапазона. Ученые надеются, что новая техника анализа таких высокочастотных колебаний позволит следить за динамикой электронов на атомном масштабе. Исследование опубликовано в журнале Nature, кратко о нем сообщает пресс-релиз Общества Макса Планка.

Скорость работы микроэлектронных чипов зависит от большого количества параметров: времени включения и отключения транзисторов, размеров чипа и других. Среди фундаментальных ограничений, влияющих на длительность элементарных операций, можно также выделить частоту с которой может меняться сигнал. Поскольку электрический ток возникает благодаря действию электрических полей, чем быстрее меняется вектор напряженности поля, тем больших частот можно добиться.

Естественным источником быстрых изменений в электромагнитных полях является свет. Так, колебания света оптического диапазона соответствуют частотам порядка сотен терагерц. Используя высокоинтенсивное лазерное излучение, физики ранее уже приближались к частоте колебаний электрического тока в один петагерц. В новой работе авторам удалось перешагнуть через эту границу.

Физики изучали природу нелинейных эффектов, возникающих при облучении тонких слоев оксида кремния лазерными импульсами высокой интенсивности. В работе ученые развивали напряженность электрического поля вплоть до 10 гигавольт (миллиардов вольт) на метр. В такой ситуации резко менялись свойства окиси кремния — так, ее проводимость увеличивалась в квинтиллион раз, с уровня 10^-14 — 10^-16 до десятков обратных ом·метров (сименсов). Сами электроны при этом начинали когерентно колебаться — с одной частотой и постоянной разностью фаз колебаний между частицами.

Для того, чтобы определить частоту колебаний электронов, физики исследовали ультрафиолетовое излучение, которое испускали частицы. Это гораздо проще, чем пытаться напрямую визуализировать движения электронов. Оказалось, что период их колебаний составлял менее одной фемтосекунды — 470 аттосекунд. Это соответствует 5,8 петагерца. Максимальные частоты колебаний, зарегистрированные в эксперименте, достигали 8 петагерц, что почти в десять раз превышает предыдущий зафиксированный рекорд.

На масштабе единиц и десятков фемтосекунд происходят процессы разрыва химических связей. С помощью современных методов исследования ученые имеют возможность отслеживать такие явления — недавно мы сообщали о наблюдениях за распадом молекулы ацетилена на два фрагмента. Научная группа добилась рекордного разрешения в 0,6 фемтосекунд — 600 аттосекунд. Улучшение разрешения до единиц и десятков аттосекунд позволит увидеть детали более быстрых процессов — например, переноса электронов.

Владимир Королёв

Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

Решение задач по теме «Механические колебания и волны.

Звук» (Ерюткин Е.С.) 9 класс онлайн-подготовка на Ростелеком

 

 

Здравствуйте! Наш завершает тему «Механические колебания и волны», поэтому он будет посвящен контрольной работе. Наша контрольная работа так и называется «Механические колебания и волны. Звук». Мы рассмотрим различные задачи, посвященные этой теме. Первая задача, которую будем рассматривать, посвящена колебаниям обыкновенного нитяного маятника, звучит она следующим образом.

 

 

Задача 1

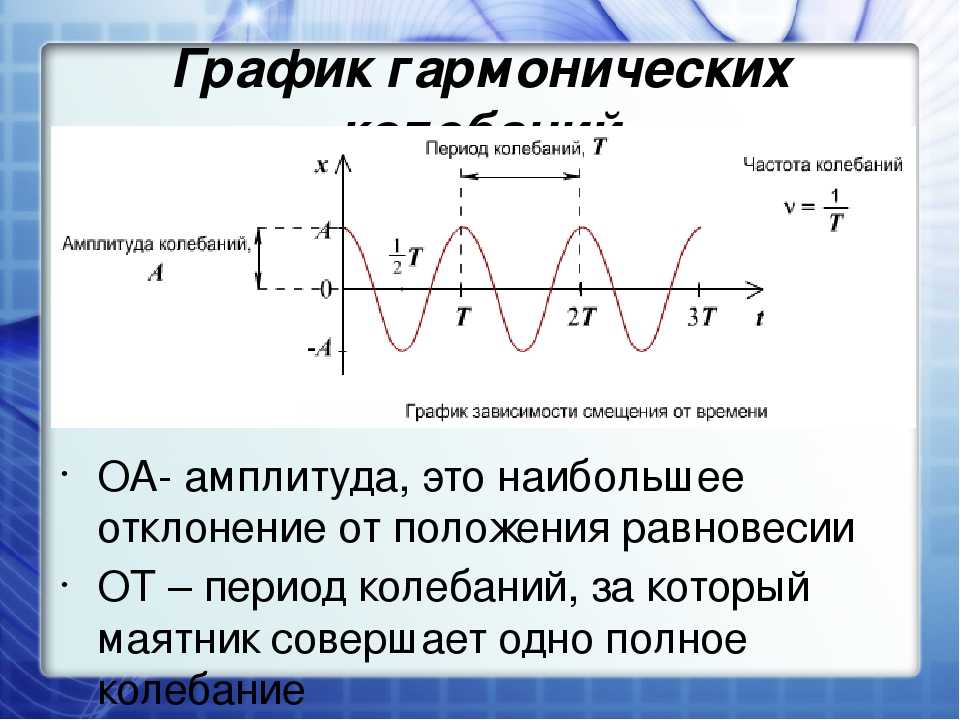
По представленному графику определите амплитуду и период колебаний нитяного маятника.

Решение:   Ответ:  А = 10-2 м, Т = 1 с.

Мне бы хотелось отметить, что такого рода задачи часто встречаются в контрольных работах.

Именно по графику определить характеристики колебаний. Давайте обратимся к записи, посмотрим на график и ответим на поставленный вопрос.

 

Итак, в данном случае график представлен на рисунке и выглядит он следующим образом. Сначала мы должны отметить точку равновесия. В данной точке тело когда находилось, оно находилось в положении равновесия. Дальше начинается движение маятника. С течением времени у нас смещение произошло сначала в одну сторону, затем в другую. Таким образом, мы представляем себе движение маятника в сочетании с осью времени. Мы знаем, что амплитудой является максимальное смещение от положения равновесия. Посмотрите, в данном случае смещение произошло на 1, на 1 в одну сторону относительно положения равновесия. И относительно положения равновесия в другую сторону тоже на 1. Если вы посмотрите, то смещение, обозначенное буквой х, измеряется в сантиметрах. По всему представленному графику смещение в данном случае максимальное постоянно, равно 1, т.е. 1 см. Это и есть амплитуда колебаний.

Обратите внимание: необходимо сразу записать, что А = 1 см, или в системе интернациональной А = 1 см = 10^{-2 м.}

Чтобы определить период колебаний, нам надо рассмотреть все колебания, представленные на этом графике. Что такое одно полное колебание? Это когда тело сходило в противоположную точку и вернулось обратно. Этот промежуток времени будет соответствовать периоду колебаний маятника. Таких движений за указанное время маятник совершил 2, таким образом, мы должны отметить, что число колебаний равно 2, а время этих колебаний составляет 2 с. Воспользуемся уравнением для определения периода колебаний: .

Обязательно необходимо записать ответ этой задачи. Ответ: А = 10^-2 м, Т = 1 с.

Следующая задача, которую мы будем разбирать, – задача, посвященная колебаниям пружинного маятника. Звучит текст этой задачи следующим образом.

 

Задача 2

Пружинный маятник совершил за 4 с 16 полных колебаний. Необходимо определить период и частоту колебаний этого маятника.

Давайте посмотрим на краткую запись этой задачи и рассмотрим ее решение. Посмотрите, краткое условие следующее.

Дано:	Решение:
N =16	Ответ: Т = 0,25 с, ν = 4 Гц.
t = 4 c
Найти: n — ? T — ?

 

Решение этой задачи тоже достаточно простое. Мы воспользуемся уравнением, которое дает возможность определить период, тем более, что мы рассматривали его уже в предыдущей задаче – . .

Что касается частоты, то в данном случае мы можем воспользоваться не одной, а двумя формулами. По выбору, кому какая формула больше нравится, как удобней вычислять эту величину. Можно воспользоваться уравнением, которое связывает у нас частоту и период. Посмотрите, мы записали это уравнение: . А мы определим частоту, используя те данные, которые у нас есть, т.е. формулу используем определения частоты .

Обязательно надо сказать об ответе. Ответ: Т = 0,25 с, ν = 4 Гц.

Здесь мне бы хотелось обратить внимание на одну особенность, соответствующую механическим колебаниям. В данном случае получается довольно любопытная ситуация, что если мы частоту умножим на период, то получим 1. Обратите внимание на то, что для механических колебаний это довольно характерная особенность.

 

Следующая задача, которую мы рассмотрим, будет посвящена волнам. В данном случае условие задачи звучит следующим образом.

 

Задача 3

Длина океанической волны составляет 270 м, период составляет 13,5 с. Определите скорость распространения волн.

Такая задача, связанная с механическими волнами, в частности, с волнами океаническими. Давайте посмотрим на запись и на ее решение. Она тоже не будет представлять собой какой-либо сложности. Конечно, при условии, что мы помним уравнение для вычисления указанных величин. Итак, посмотрите.

 

Дано:	Решение:
l = 270 м	Ответ: .
Т = 13,5 с
Найти: V = ?

 

Если мы помним, что надо определить скорость распространения волн, то в решении мы должны записать следующее уравнение: V = l * ν. Рассматривая вот это уравнение, мы можем записать следующее: скорость распространения волны может быть определена как . Если вместо частоты мы подставим выражение , то получим уравнение, которое здесь записано: . Подставляя теперь цифры, мы получим .

Обратите внимание на запись ответа. Ответ: . Тоже хотелось бы обратить ваше внимание на то, какова скорость распространения океанических волн. Ведь = 72 км/ч. Так что обратите внимание, какая величина этой скорости.

 

Следующая задача, которую мы рассмотрим, относится к звуковым волнам. Текст задачи звучит следующим образом.

 

Задача 4

Определите, во сколько раз будет отличаться длина звуковой волны при переходе из воздуха в воду. Считать, что скорость распространения звука в воздухе 340 м/с, в воде 1450 м/с.

Давайте посмотрим на краткую запись и на решение задачи. Посмотрите, в данном случае условие небольшое.

Дано:	Решение:
	ν1 =  ν2   Т1 = Т2     ;    Ответ: n ≈ 4,3 раза.
Найти:

Определить нам надо, во сколько раз изменилась длина волны при переходе. Надо разделить длину волны в воде к длине волны в воздухе. Итак, что предпримем? Обращаю внимание, что здесь после слова «решение» написано достаточно важное выражение ν₁ = ν₂. Когда мы обсуждали это явление, мы говорили, что волна переходит из одной среды в другую, но при этом сохраняется частота колебаний. Меняется, скорость меняется, длина волны меняется, а частота колебания частиц остается прежней. Посмотрите, в данном случае мы записываем, что частота колебаний частиц волны в воздухе ν₁ = ν₂ частоте колебаний частиц, которые составляют волну в воде. Обратите внимание: если частоты равны, то будут равны и периоды колебаний этих частиц ν

1 = ν₂ Þ Т₁ = Т₂. Дальше, мы используем уравнение, которое нам встречалось в предыдущей задаче

l= V * Т. Записываем длину волны для воздуха l₁ = V₁ * Т и для воды l₂ = V₂ * Т. Почему в данном случае мы обозначили период Т и Т, т.е. без индексов? Разговор идет о том, что периоды у нас одинаковые, поэтому мы их обозначили одной величиной, одной буквой. Теперь разделим .

В этом случае период колебаний сократится, и мы получаем значение отношения длин волн .

Мы обозначили это отношение буквой n и в ответе записываем следующее, что n≈4,3 раза. Во столько будет отличаться длина волны.

 

Следующая задача, которую мы рассмотрим, будет посвящена также звуку, и мы должны обязательно рассмотреть вопрос, связанный с эхом. Итак, условия задачи следующие.

 

Задача 5

В результате выстрела было услышано эхо через 20 с после произведенного выстрела. Определите расстояние до преграды, если скорость звука составляла . В данной задаче мы должны учесть, что эхо – это отраженная волна, значит, звук дошел до преграды и вернулся обратно к наблюдателю, т.е. как раз в то место, где и был произведен выстрел. Итак, давайте посмотрим на решение задачи. Посмотрите, пожалуйста, мы запишем, что время от момента выстрела до того момента, когда было услышано эхо, 20 с. Скорость звука составляло. Определить надо расстояние S до преграды.

Дано:	Решение:
t = 20 c	S1 = V * t;       Ответ: S=3400 м = 3,4 км.
Найти:  S — ?

Давайте определимся с тем, что именно за это время, за 20 с, волна прошла определенное расстояние. Это расстояние мы определим простым способом: как расстояние, пройденное телом за определенное время с постоянной скоростью. В данном случае у нас волна, поэтому мы определяем S₁ = V * t, полное расстояние, прошедшее волной. Теперь мы должны отметить то, что это расстояние мы должны разделить обязательно пополам, . Почему? Дело в том, что эхо – это отраженная волна. Значит, волна звуковая дошла до преграды и вернулась обратно, следовательно, . Теперь подставив сюда значение для вычисления , мы получаем расстояние до преграды .

Ответ, который мы здесь запишем: S=3400 м = 3,4 км. Расстояние достаточно большое, но выстрел – это достаточно громкий звук, и интенсивности его хватит, чтобы дойти до преграды и вернуться обратно.

 

В заключение контрольной работы мы рассмотрим задачу из ЕГЭ. Условие будет таким. Указан маятник, который совершает колебания между точками 1 и 3, как показано на рисунке. Надо определить, в каких точках кинетическая энергия маятника является минимальной. Обращаю ваше внимание, что эта задача связана с превращением энергии при колебательных процессах. Такая задача и выбирается в ЕГЭ. Давайте посмотрим на это условие и решим эту задачу.

 

Задача 6

В каких точках кинетическая энергия маятника является минимальной?

 

Рисунок

1. В точках 1 и 2.

2. В точках 1 и 3.

3. В точках 2 и 3.

4. Во всех точках одинаково.

Ответ: пункт 2.

Во-первых, нам надо рассмотреть сам рисунок. Представленный рисунок указывает цифру 2 – это положение равновесия нитяного маятника. И две крайних точки, точка 1 и 3. В условии задачи сказано, что именно между точками 1 и 3 совершаются колебания маятника. Дальше представлены 4 ответа. В каждом – определенный вид ответа, нам надо выбрать правильный. Давайте обсудим это решение. Кинетическая энергия – это энергия движения. Стало быть, это энергия тела в тот момент, когда тело обладает скоростью. В данном случае тело в точке 1 и в точке 3 на некоторую долю секунды замирает и обладает только потенциальной энергией относительно выбранной системы отсчета.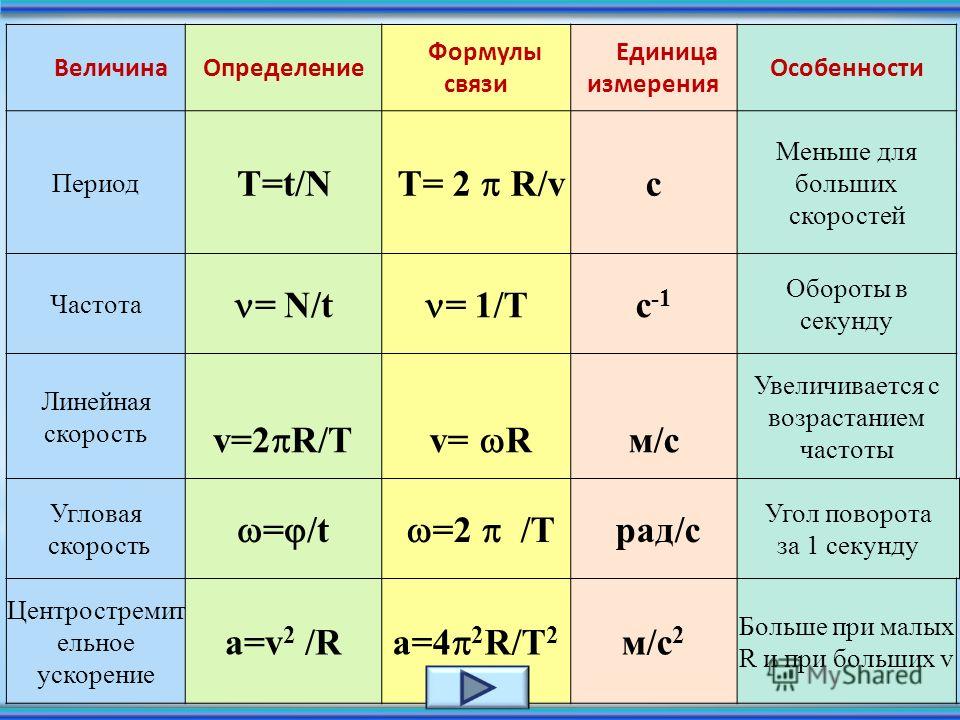 Так что в точке 1 и 3 кинетическая энергия будет минимальна, т.е. она будет равна 0. Мы должны выбрать ответ из указанных, там, где именно эти цифры. Посмотрите, в первом ответе говорится точка 1 и 2, вторая точка в данном случае не подходит. Второй ответ: в точках 1 и 3. Соответствует правильному ответу. Ответ так и надо записать: пункт 2. Если мы посмотрим в пункт 3, там указывается точка 2 и 3, и в последнем, четвертом, говорится, что везде энергия одинакова. Конечно, эти ответы являются в данном случае неправильными.

Итак, мы рассмотрели контрольную работу, вариант контрольной работы, и следующий урок будет посвящен новой теме – электромагнитным явлениям. Тема закончена. До свидания.

 

Частота и период — AP Physics 1

Все ресурсы AP Physics 1

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept

AP Physics 1 Справка » Электричество и волны » Волны » Частота и период

Какова длина волны , если ее скорость равна ?

Возможные ответы:

Правильный ответ:

Пояснение:

Связь между длиной волны и скоростью определяется уравнением;

Вопрос дает нам скорость волны и ее частоту. Используя эти значения, мы можем найти длину волны.

Сообщить об ошибке

Маятник длиной  с шариком массы отпущен под углом  от точки равновесия. Какая из следующих регулировок приведет к увеличению частоты колебаний?

Возможные ответы:

, увеличивая начальный угол

, увеличивая массу шарика

, увеличивая длину

, уменьшая массу шарика

Уменьшение длины

Правильный ответ:

Уменьшая длину

. Объяснение:

Период колебаний маятника на струне:

Период обратно пропорционален частоте.

Расчет частоты колебаний.

Единственный параметр, от которого зависит частота, — это длина. Уменьшение длины увеличивает частоту.

Сообщить об ошибке

Длина волны луча света, проходящего через вакуум, составляет . Каков период этой волны?

Возможные ответы:

Правильный ответ:

Пояснение:

В этом вопросе нам дана длина волны света в вакууме. Поскольку мы знаем, что скорость света в вакууме равна , мы можем сначала вычислить частоту света, а затем использовать это значение для расчета его периода.

Для начала нам нужно использовать следующее уравнение для определения частоты.

Затем, используя это значение, мы можем рассчитать период, заметив, что период является обратной величиной частоты.

И для полноты картины стоит отметить, что период означает количество времени, которое требуется для прохождения одной длины волны, что в данном случае составляет очень, очень малую долю секунды!

Сообщить об ошибке

Волны регулярно бьются о борт пирса. В течение 1 минуты волны, ударившиеся о борт пирса. Рассчитайте период волн за это время в секундах.

Возможные ответы:

Невозможно определить.

Правильный ответ:

Объяснение:

Чтобы вычислить период , нам нужно найти частоту, , с которой волны ударяются о причал. Нам говорят, что волны ударяются в окно. Следовательно,

. Затем мы можем рассчитать период на основе этой информации.

Сообщить об ошибке

Как период маятника реагирует на четырехкратное увеличение его длины?

Возможные ответы:

Разрезан пополам.

Увеличивает вдвое.

Уменьшается на .

Увеличивается на .

Правильный ответ:

Увеличивается вдвое.

Объяснение:

Уравнение для периода маятника выглядит следующим образом:  При учетверении длины можно вынуть квадратный корень из четырех, что удваивает период.

Сообщить об ошибке

Строка дает следующие частоты: , , и .

Какова основная частота этой струны?

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку производимые частоты различаются на , мы знаем, что основная частота должна быть разницей. Это потому, что основная частота — это самая первая и самая низкая частота, которую можно воспроизвести.

Следовательно, правильный ответ .

Сообщить об ошибке

Буй качается в океане во время шторма. От самой низкой точки до самой высокой точки буй поднимается в общей сложности на . За последние 20 минут буй переместился вверх и вниз в общей сложности на .

Какова частота колебаний буя?

Возможные ответы:

Правильный ответ:

Объяснение:

Всего буй перемещается на . Из задачи вы знаете, что буй перемещается в общей сложности на  с каждой длиной волны (10 метров вверх и 10 метров вниз). Это означает, что за 20 минут буй прошел циклы. Чтобы найти частоту, вы делите общее количество циклов на общее количество прошедшего времени в секундах:

Сообщить об ошибке

Если длина волны света равна , каков период этой волны?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы ответить на этот вопрос, важно понимать взаимосвязь между длиной волны и периодом. Кроме того, поскольку нам говорят, что это световая волна, важно также знать скорость, с которой распространяется свет.

Во-первых, мы можем показать уравнение, которое связывает длину волны и скорость волны.

Более того, мы можем связать частоту волны с ее периодом, оба из которых обратно пропорциональны друг другу.

Используя эти два выражения, мы можем объединить их в следующее выражение.

Далее мы можем изменить уравнение, чтобы выделить переменную, представляющую период волны.

Наконец, нам просто нужно подставить значение длины волны, данное нам в основе вопроса, вместе со скоростью света, чтобы получить ответ.

Этот ответ говорит нам о том, что для прохождения одной длины волны света через заданную точку требуется очень, очень короткое время!

Сообщить об ошибке

Частота звуковой волны, проходящей через воду, должна быть рекордной , каков период волны?

Возможные ответы:

Правильный ответ:

Объяснение:

Частота просто представлена ​​как инверсия периода, как показано ниже

, где f — частота, а T — период. Чтобы решить уравнение для периода, мы просто обращаем обратную зависимость

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы AP Physics 1

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept

17.

2 Скорость звука, частота и длина волны – College Physics: OpenStax

Глава 17 Физика слуха

Сводка

• Определение высоты тона.
• Опишите взаимосвязь между скоростью звука, его частотой и длиной волны.
• Опишите влияние звука на скорость его распространения в различных средах.
• Опишите влияние температуры на скорость звука.

Рисунок 1. При взрыве фейерверка световая энергия воспринимается раньше звуковой. Звук распространяется медленнее, чем свет. (кредит: Доминик Алвес, Flickr)

Звук, как и все волны, распространяется с определенной скоростью и обладает свойствами частоты и длины волны. Вы можете наблюдать прямое свидетельство скорости звука, наблюдая за фейерверком. Вспышка взрыва видна задолго до того, как слышен его звук, что подразумевает как то, что звук распространяется с конечной скоростью, так и то, что он намного медленнее света. Вы также можете непосредственно ощущать частоту звука. Восприятие частоты называется шаг . Длина волны звука непосредственно не ощущается, но косвенные свидетельства обнаруживаются в соотношении размеров музыкальных инструментов с их высотой звука. Маленькие инструменты, такие как пикколо, обычно издают высокие звуки, в то время как большие инструменты, такие как туба, обычно издают низкие звуки. Высокий тон означает малую длину волны, а размер музыкального инструмента напрямую связан с длиной волны звука, который он производит. Таким образом, небольшой инструмент создает коротковолновые звуки. Аналогичные аргументы утверждают, что большой инструмент создает длинноволновые звуки.

Соотношение скорости звука, его частоты и длины волны такое же, как и для всех волн:

[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс]

, где[latex]\boldsymbol{v_{\textbf{w}}}[/latex]– скорость звука,[latex]\boldsymbol{f}[/latex]– его частота, а[latex]\boldsymbol{ \lambda}[/latex] — его длина волны. Длина волны звука — это расстояние между соседними идентичными частями волны, например, между соседними сжатиями, как показано на рис. 2. Частота такая же, как у источника, и представляет собой количество волн, проходящих через точку на единицу. время.

Рисунок 2. Звуковая волна исходит от источника, колеблющегося с частотой f , распространяется с частотой v _w и имеет длину волны λ 2 .

Таблица 1 показывает, что скорость звука сильно различается в разных средах. Скорость звука в среде определяется сочетанием жесткости среды (или сжимаемости в газах) и ее плотности. Чем жестче (или менее сжимаема) среда, тем выше скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения прямо пропорциональна жесткости колеблющегося объекта. Чем больше плотность среды, тем медленнее скорость звука. Это наблюдение аналогично тому факту, что частота простого гармонического движения обратно пропорциональна массе колеблющегося объекта. Скорость звука в воздухе мала, потому что воздух сжимаем. Поскольку жидкости и твердые тела относительно жесткие и их очень трудно сжать, скорость звука в таких средах обычно выше, чем в газах.

Средний	v w (м/с)
Газы при 0ºC
Воздух	331
Углекислый газ	259
Кислород	316
Гелий	965
Водород	1290
Жидкости при 20ºC
Этанол	1160
Меркурий	1450
Вода пресная	1480
Морская вода	1540
Ткань человека	1540
Твердые вещества (продольные или объемные)
Вулканизированная резина	54
Полиэтилен	920
Мрамор	3810
Стекло, пирекс	5640
Свинец	1960
Алюминий	5120
Сталь	5960
Таблица 1. Скорость звука в различных средах.

Землетрясения, по существу звуковые волны в земной коре, являются интересным примером того, как скорость звука зависит от жесткости среды. Землетрясения имеют как продольную, так и поперечную составляющую, и они распространяются с разной скоростью. Объемный модуль гранита больше, чем его модуль сдвига. По этой причине скорость продольных волн или волн давления (Р-волн) при землетрясениях в граните значительно выше скорости поперечных или сдвиговых волн (S-волн). Оба компонента землетрясений распространяются медленнее в менее жестком материале, таком как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны, соответственно, имеют скорость от 2 до 5 км/с, причем обе они быстрее в более твердом материале. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору. Время между P- и S-волнами обычно используется для определения расстояния до их источника, эпицентра землетрясения.

Скорость звука зависит от температуры в данной среде. Для воздуха на уровне моря скорость звука равна

.

[латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}},[/латекс]

, где температура (обозначается как[латекс]\жирныйсимвол{Т})[/латекс]выражается в единицах Кельвина. Скорость звука в газах связана со средней скоростью частиц в газе,[латекс]\жирныйсимвол{v_{\textbf{среднеквадратичное значение}}},[/латекс]и что 9{\circ}\textbf{C}}[/latex] это 343 м/с, увеличение менее чем на 4%. На рис. 3 показано, как летучая мышь использует скорость звука для определения расстояния. Эхо также используется в медицинской визуализации.

Рисунок 3. Летучая мышь использует звуковое эхо, чтобы ориентироваться и ловить добычу. Время возвращения эха прямо пропорционально расстоянию.

Одним из наиболее важных свойств звука является то, что его скорость почти не зависит от частоты. Эта независимость, безусловно, верна на открытом воздухе для звуков в слышимом диапазоне от 20 до 20 000 Гц. Если бы эта независимость не была истинной, вы бы наверняка заметили ее, например, в музыке, которую играет марширующий оркестр на футбольном стадионе. Предположим, что высокочастотные звуки распространяются быстрее — тогда чем дальше вы находитесь от группы, тем больше звук низкочастотных инструментов будет отставать от высокочастотных. Но музыка всех инструментов доносится с ритмом, не зависящим от расстояния, поэтому все частоты должны распространяться почти с одинаковой скоростью. Напомним, что

[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда}.[/латекс]

В данной среде при фиксированных условиях [латекс]\boldsymbol{v _{\textbf{w}}}[/латекс]постоянна, так что существует связь между[латекс]\жирныйсимвол{f}[/латекс] и[латекс]\жирныйсимвол{\лямбда};[/латекс]чем выше частота, тем меньше длина волны. См. рис. 4 и рассмотрим следующий пример.

Рисунок 4. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером. 9{\circ}\textbf{C}}[/latex]воздух. (Предположим, что значения частоты точны до двух значащих цифр.)

Стратегия

Чтобы найти длину волны по частоте, мы можем использовать [латекс]\жирныйсимвол{v_{\textbf{w}}=f\lambda}. [/latex]

Решение

1. Идентификация известных. Значение для[латекс]\жирныйсимвол{v_{\textbf{w}}},[/латекс]задается как

   [латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{T}{273\textbf{ К}}}}.[/латекс]

2. Преобразуйте температуру в кельвины, а затем введите температуру в уравнение

   [латекс]\boldsymbol{v _{\textbf{w}}=(331\textbf{м/с})}[/latex][латекс]\boldsymbol{\sqrt{\frac{303\textbf{K}} {273\textbf{ K}}}}[/latex][latex]\boldsymbol{=348,7\textbf{ м/с}}.[/latex]

3. Решите зависимость между скоростью и длиной волны для [латекс]\жирныйсимвол{\лямбда}:[/латекс]

   [латекс]\boldsymbol{\lambda\:=}[/латекс][латекс]\boldsymbol{\frac{v _{\textbf{w}}}{f}}. [/latex]

4. Введите скорость и минимальную частоту, чтобы получить максимальную длину волны:

   [латекс]\boldsymbol{\lambda _{\textbf{max}}\:=}[/latex][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20\textbf{Гц}} }[/латекс][латекс]\boldsymbol{=17\textbf{м}}.[/латекс]

5. Введите скорость и максимальную частоту, чтобы получить минимальную длину волны:

   [латекс]\boldsymbol{\lambda _{\textbf{мин}}=}[/латекс][латекс]\boldsymbol{\frac{348,7\textbf{м/с}}{20 000\textbf{Гц}}}[ /латекс][латекс]\жирныйсимвол{=0,017\textbf{м}=1,7\текстбф{см}}.[/латекс]

Обсуждение

Поскольку произведение [латекс]\boldsymbol{f}[/latex], умноженное на [латекс]\boldsymbol{\lambda}[/latex], равно константе, чем меньше[латекс]\boldsymbol{ f}[/latex]есть, тем больше должен быть [латекс]\boldsymbol{\lambda}[/latex], и наоборот.

Скорость звука может изменяться при переходе звука из одной среды в другую. Однако частота обычно остается неизменной, потому что она похожа на возбужденное колебание и имеет частоту исходного источника. Если [латекс]\boldsymbol{v_{\textbf{w}}}[/latex]изменяется, а [латекс]\boldsymbol{f}[/latex]остается прежним, то длина волны[латекс]\boldsymbol{\lambda} [/latex] должен измениться. То есть, потому что[latex]\boldsymbol{v_{\textbf{w}}=f\lambda}[/latex]чем выше скорость звука, тем больше его длина волны для данной частоты.

Установление связей: домашнее исследование — Голос как звуковая волна

Подвесьте лист бумаги так, чтобы верхний край бумаги был зафиксирован, а нижний край мог двигаться. Вы можете приклеить верхний край бумаги к краю стола. Аккуратно подуйте возле края нижней части листа и обратите внимание, как движется лист. Говорите тихо, а затем громче, чтобы звуки касались края нижней части бумаги, и отмечайте, как движется лист. Объясните эффекты.

Зависимость скорости звука[латекс]\boldsymbol{v_{\textbf{w}}},[/latex]его частоты[латекс]\boldsymbol{f},[/latex]и его длины волны[латекс]\ жирныйсимвол{\lambda}[/латекс]равно

[латекс]\boldsymbol{v_{\textbf{w}}=f\лямбда},[/латекс]

, что является одним и тем же соотношением для всех волн.