Определение электродвижущей силы источника тока методом компенсации
Цель работы: измерить электродвижущую силу источника тока методом компенсации.
Приборы и оборудования: установка для измерения электродвижущей силы источника тока методом компенсации.
Теоретическое сведение
Электрическим
током называют направленное движение
электрических зарядов. Электрический
ток принято характеризовать силой тока 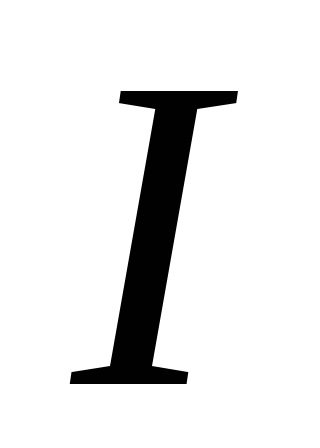 – скалярной величиной, определяемой
электрическими зарядами
– скалярной величиной, определяемой
электрическими зарядами  ,
проходящими через поперечное сечение
проводника за единицу времени
,
проходящими через поперечное сечение
проводника за единицу времени  :
:
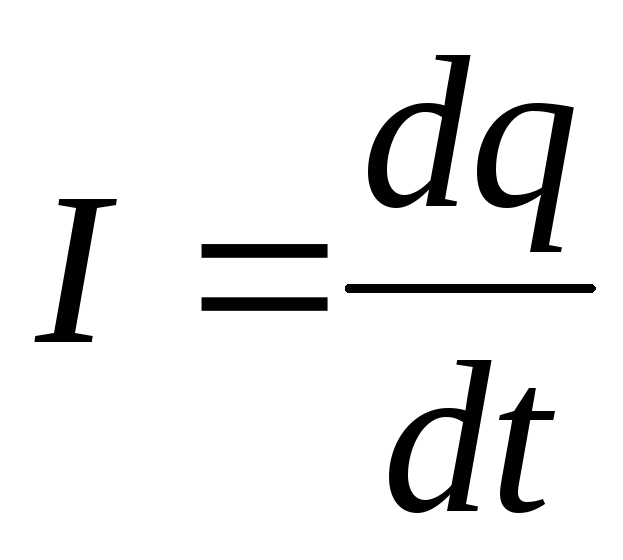
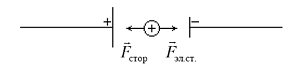
Единица измерения силы тока – ампер (А). Если за любые равные промежутки времени через поперечное сечение проводника проходит одинаковое количество электричества (электрический заряд), то такой ток называют постоянным. Условно за направление электрического тока в проводнике принимают направление движения положительных зарядов (рис. 1а).
Физическая
величина, определяемая силой тока,
проходящего через единицу
площади поперечного сечения проводника 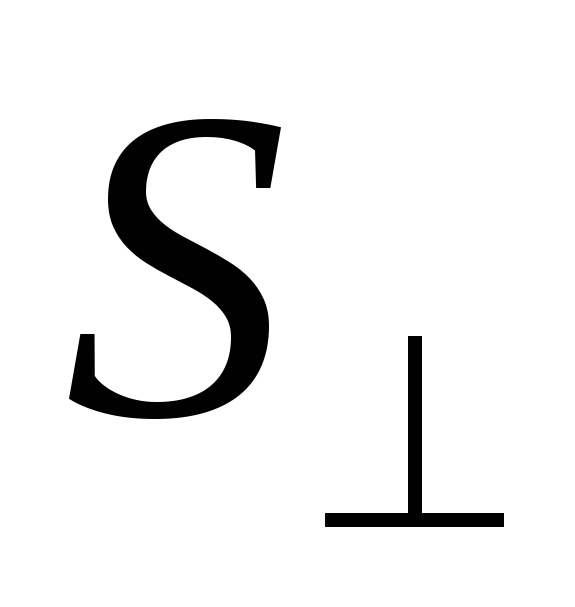 ,
перпендикулярного направлению
тока, называется плотностью тока
,
перпендикулярного направлению
тока, называется плотностью тока 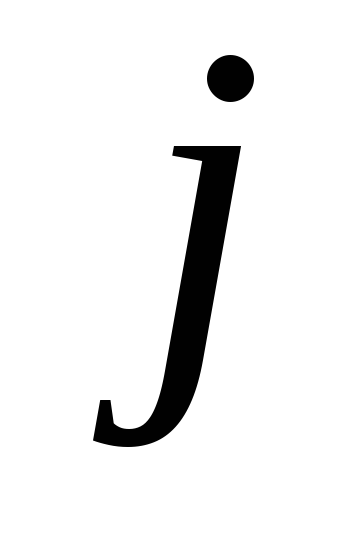
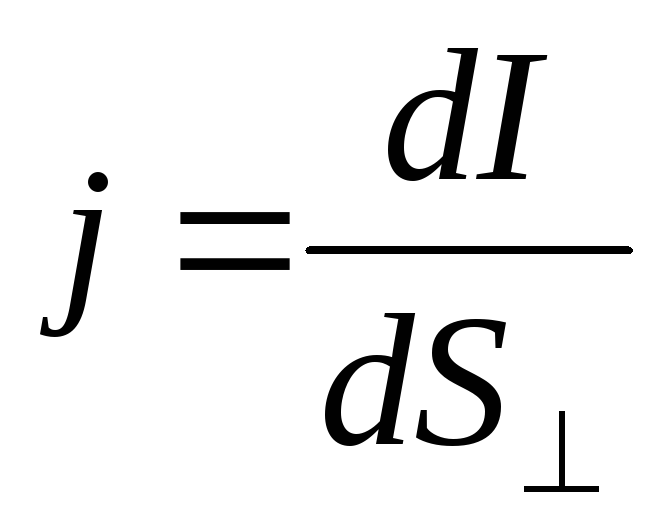 .
(2)
.
(2)
Плотность
тока является вектором 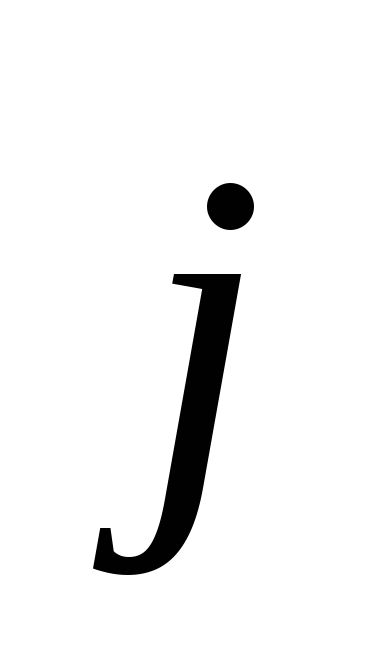 ,
направление которого совпадает с
упорядоченным
движением положительных зарядов.
,
направление которого совпадает с
упорядоченным
движением положительных зарядов.
В 1826
г. экспериментально установлен закон
Ома для однородного участка электрической
цепи (эл. схема на рис. 1б или участки ad,
dc,
cb
на рис.1а ), который гласит, что сила тока
в однородном
проводнике прямо пропорциональна
напряжению 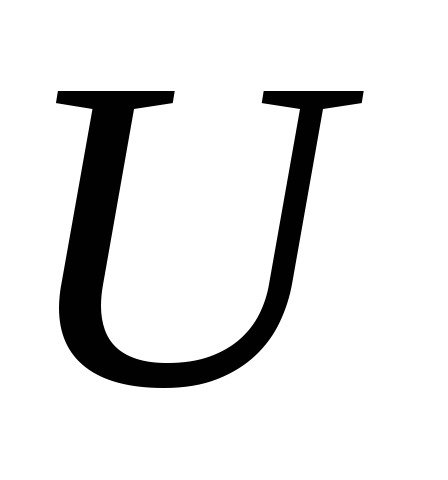
 :
: 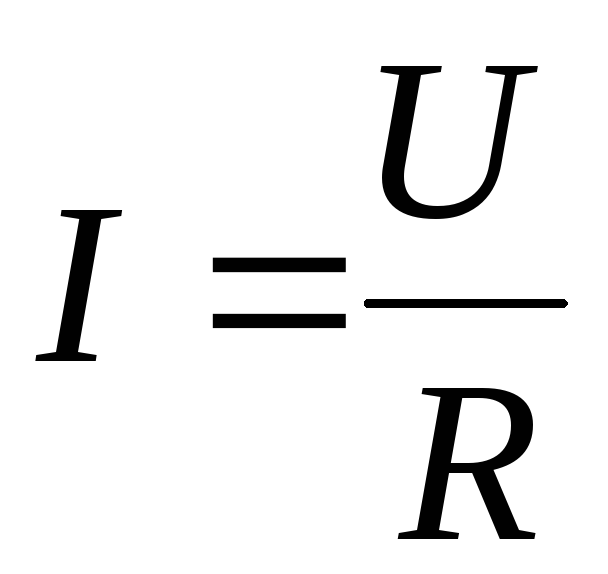 ,
(3)
,
(3)
Сопротивление проводника зависит от материала, из которого изготовлен проводник, его линейных размеров и формы:
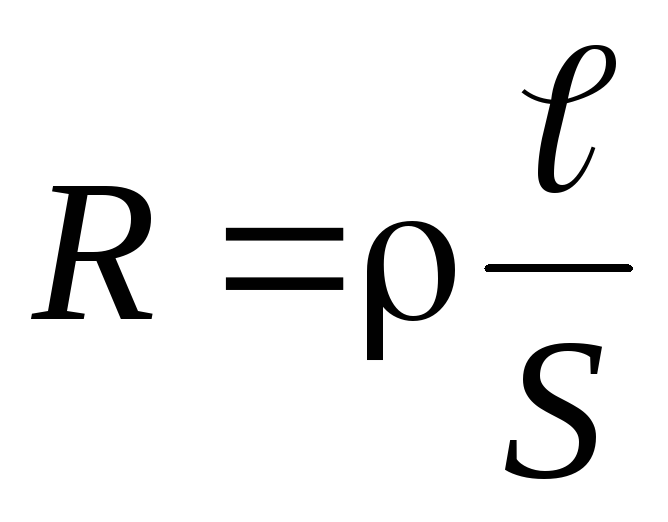 ,
(4)
,
(4) где  — удельное электрическое сопротивление,
характеризующий
материал проводника;
— удельное электрическое сопротивление,
характеризующий
материал проводника; 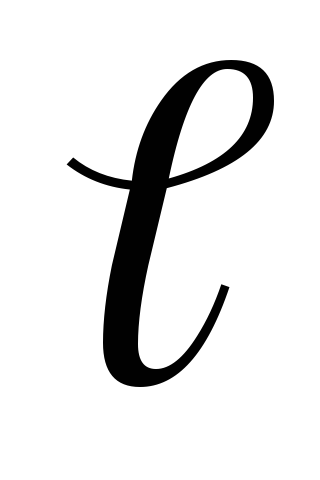 —
длина проводника;
—
длина проводника; 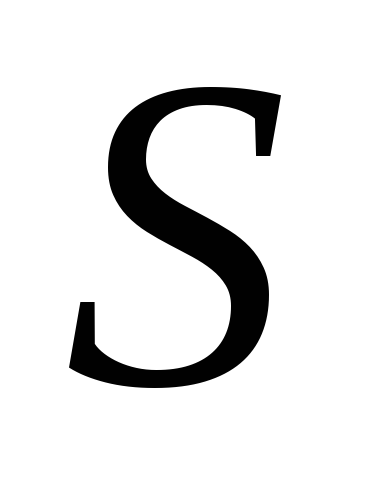 — площадь
поперечного сечения проводника. Единица
измерения удельного электрического
сопротивления – Ом∙м. 1 Ом·м —
— площадь
поперечного сечения проводника. Единица
измерения удельного электрического
сопротивления – Ом∙м. 1 Ом·м —
Если в выражение (4) подставить в закон Ома для однородного участка электрической цепи (3), то получим
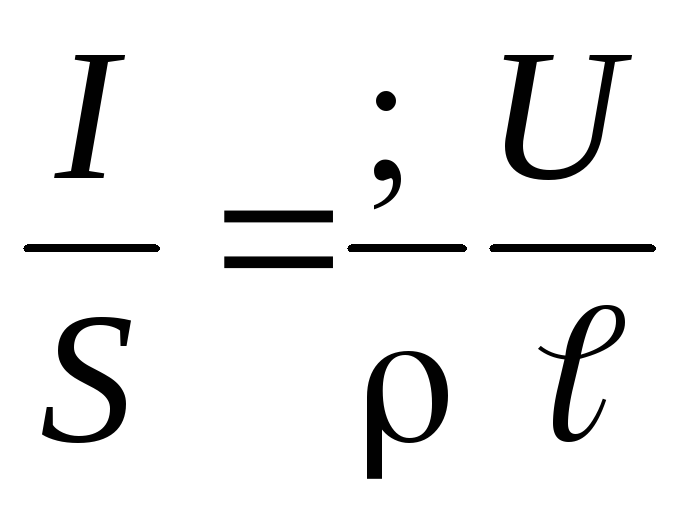 .
(5)
.
(5)
Учитывая, что
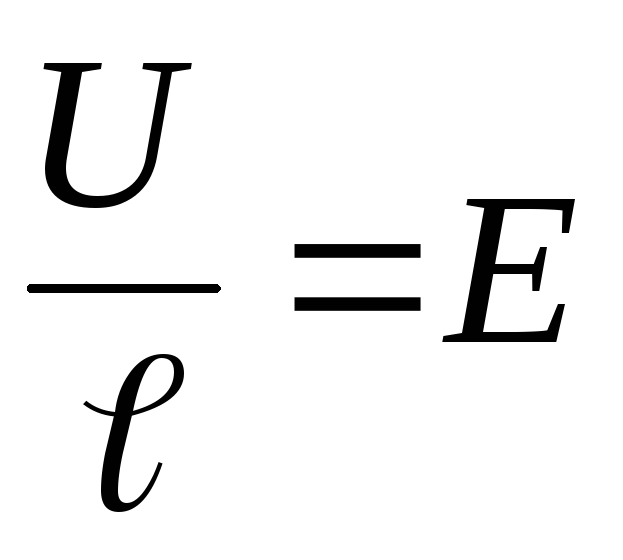 и
и 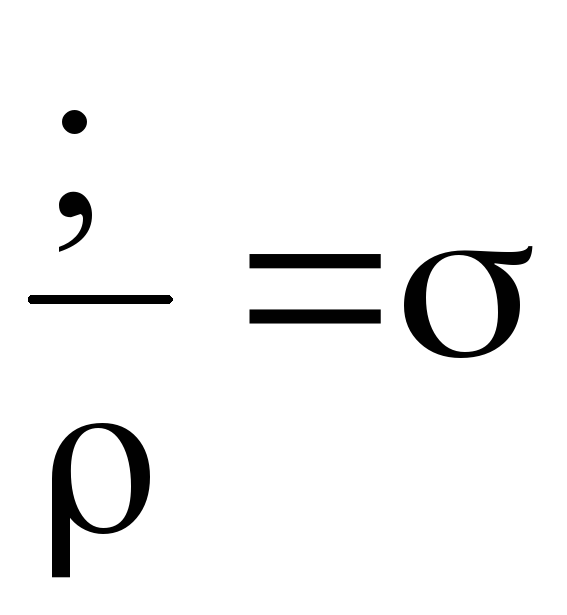 ,
,
а также применив формулу (2), уравнение (5) преобразуем в выражение, которое представляет собой закон Ома в дифференциальной форме для однородного участка электрической цепи:
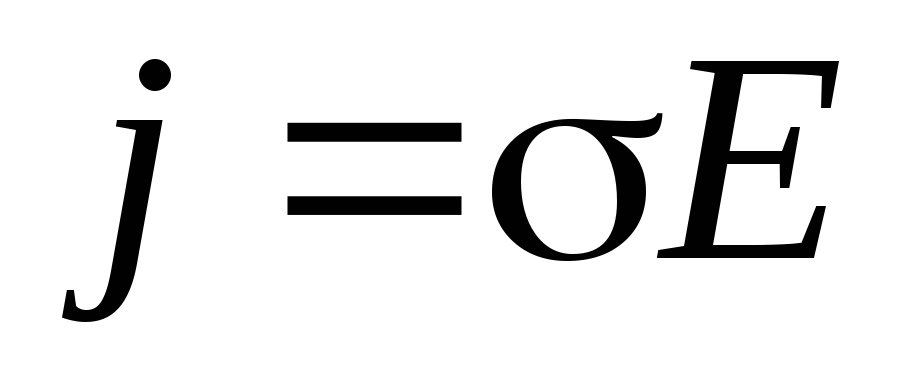 ,
,
где  — напряженность электростатического
поля внутри проводника;
— напряженность электростатического
поля внутри проводника;  — удельная электрическая проводимость
материала проводника.
— удельная электрическая проводимость
материала проводника.
В
виду того, что носители положительного
заряда в каждой точке движутся в
направлении вектора 
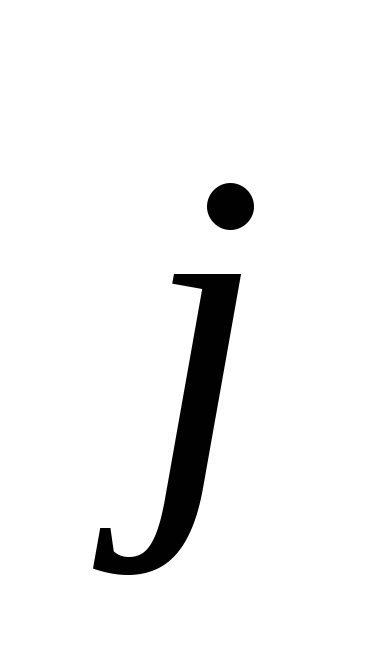 и
и  совпадают. Поэтому закон
Ома для однородного участка электрической
цепи
в
дифференциальном
виде запишется как
совпадают. Поэтому закон
Ома для однородного участка электрической
цепи
в
дифференциальном
виде запишется как 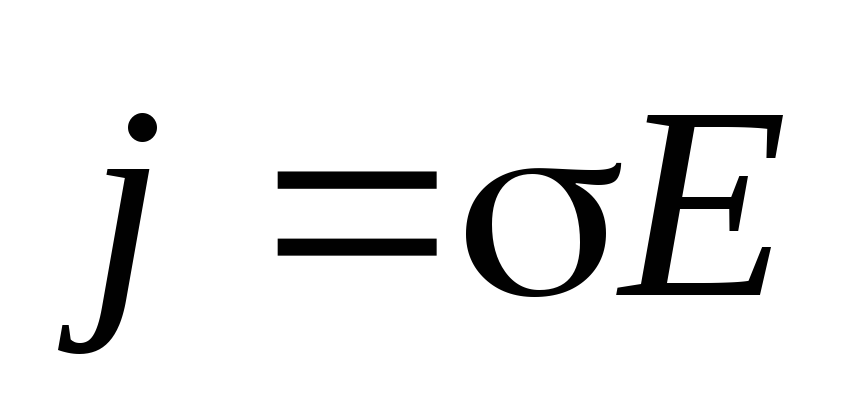 .
.
Для того, чтобы поддерживать ток в проводнике достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда считаем положительными) непрерывно отводить приносимые положительные заряды, а к концу с большим потенциалом непрерывно их подводить, т.е. необходимо установить круговорот положительных зарядов, при котором они двигались бы по замкнутой траектории.
В замкнутой электрической цепи есть участки, на которых положительные заряды движутся в сторону возрастания потенциала, т.е. против электростатического поля. Перемещение таких зарядов возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними. Природа сторонних сил различная, т.к. их появление обусловлено переменными магнитными полями, а также химическими, диффузионными, световыми процессами, происходящими в источниках тока.
 по
перемещению единичного положительного
заряда
по
перемещению единичного положительного
заряда  :
: 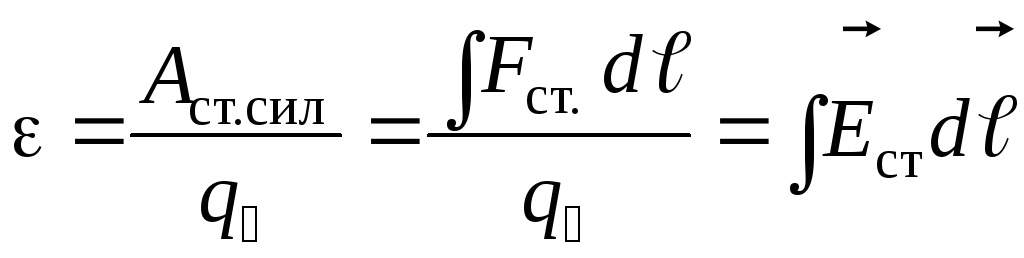 ,
,
где 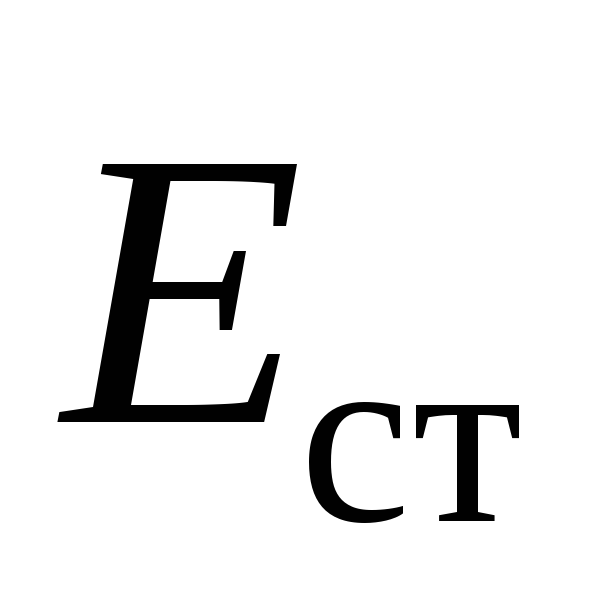 — вектор напряженности поля сторонних
сил;
— вектор напряженности поля сторонних
сил; 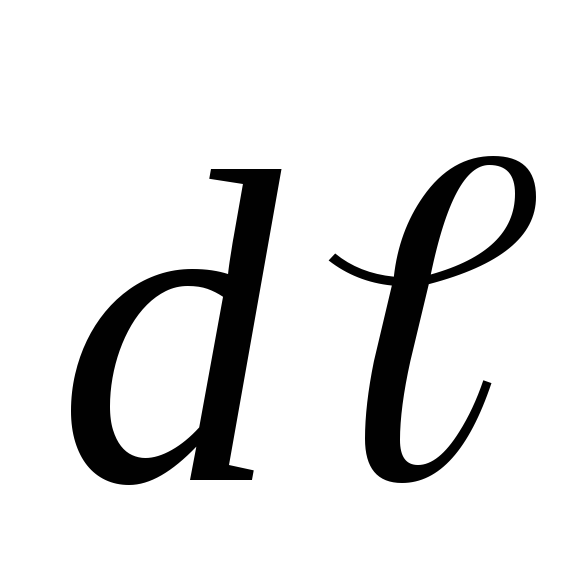
Если источник тока замкнуть на внешнюю нагрузку, равномерно распределенную по контуру, то потенциал будет падать по линейному закону по мере удаления от положительного электрода батареи (рис. 2).
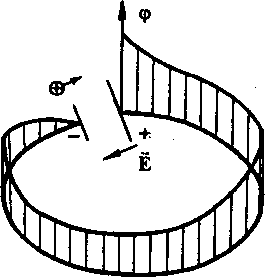
Рис. 2
Превращение
энергии
электрического тока во внутреннюю
вызывает нагревание проводника. Дж.
Джоуль и Э. Ленц экспериментально
установили, что количество тепла,
выделяющегося в проводнике, пропорционально
квадрату
силы тока в проводнике 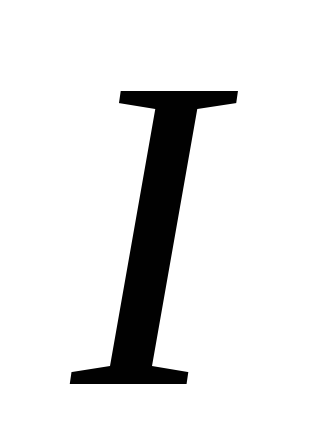
 и времени течения
тока
и времени течения
тока  .
.. (6)
Используя закон Джоуля-Ленца, выведен закон Ома для неоднородного участка электрической цепи, в котором учтено действие электростатических и сторонних сил на движущийся положительный заряд.
Согласно закону сохранения энергии количество тепла, выделенного в неоднородной электрической цепи (эл. схема на рис. 1в), равно сумме работы сил электрического поля и работы сторонних сил источника тока:
 ,
(7)
,
(7)
где 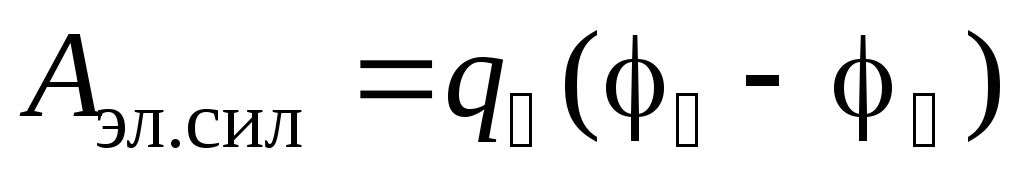 — работа сил электростатического поля;
— работа сил электростатического поля; 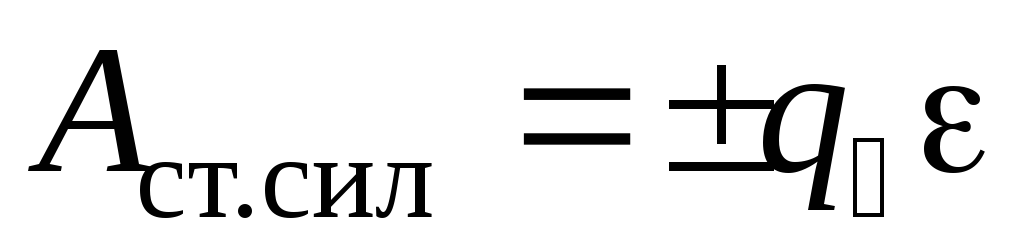 — работа сторонних сил. Сторонние силы
совершают положительную работу по
перемещению положительного заряда,
если направления сторонних сил
— работа сторонних сил. Сторонние силы
совершают положительную работу по
перемещению положительного заряда,
если направления сторонних сил 
|
Рис. 3. |
Учитывая,
что общее сопротивление на неоднородном
участке электрической цепи складывают
из внешнего  и внутреннего
и внутреннего 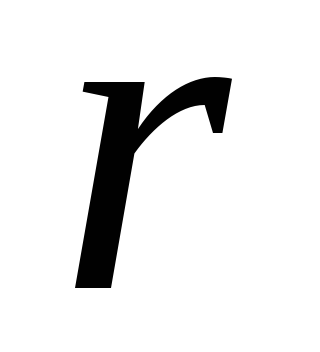 сопротивлений,
и приравняв выражения (6), (7) получим
сопротивлений,
и приравняв выражения (6), (7) получим
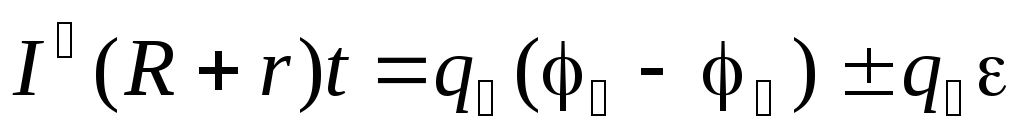 .
.
Принимая во внимание формулу (1), преобразуем выражение в вид:
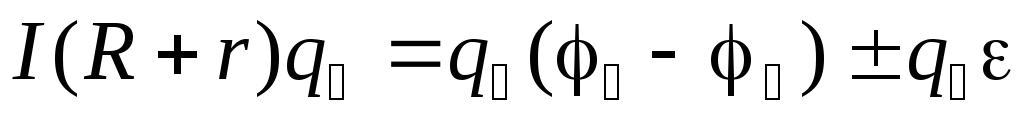 .
(8)
.
(8)
Сократим
полученное выражение на заряд 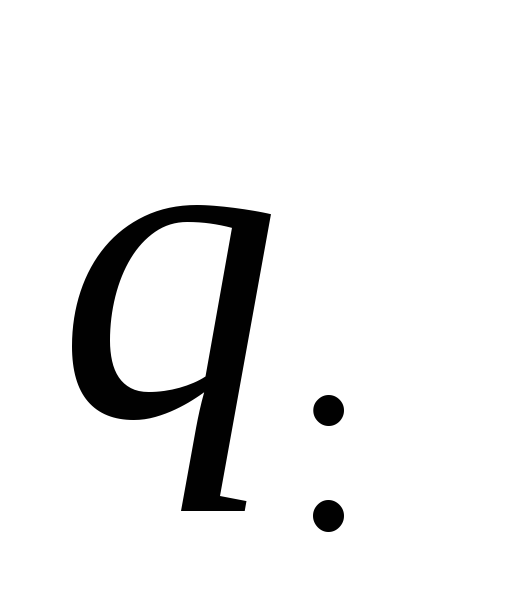 и получим закон
Ома для неоднородного участка электрической
цепи
и получим закон
Ома для неоднородного участка электрической
цепи
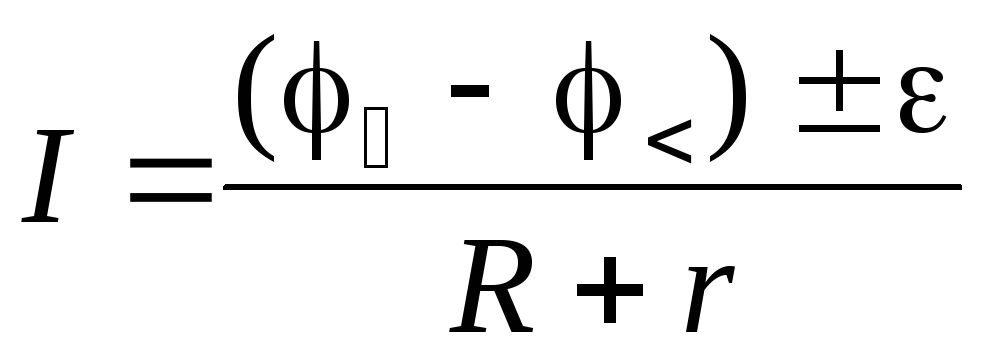 .
.
При
использовании этого закона необходимо
учитывать правило знаков: направление
обхода участка цепи задает индексация
потенциалов.
ЭДС
источника тока  берут со знаком «плюс», если направления
сторонних
сил
берут со знаком «плюс», если направления
сторонних
сил  и обхода
участка электрической цепи совпадают
(рис. 4а), в противном случае – наоборот
(рис. 4б).
и обхода
участка электрической цепи совпадают
(рис. 4а), в противном случае – наоборот
(рис. 4б).
Если
цепь замкнута, т.е. 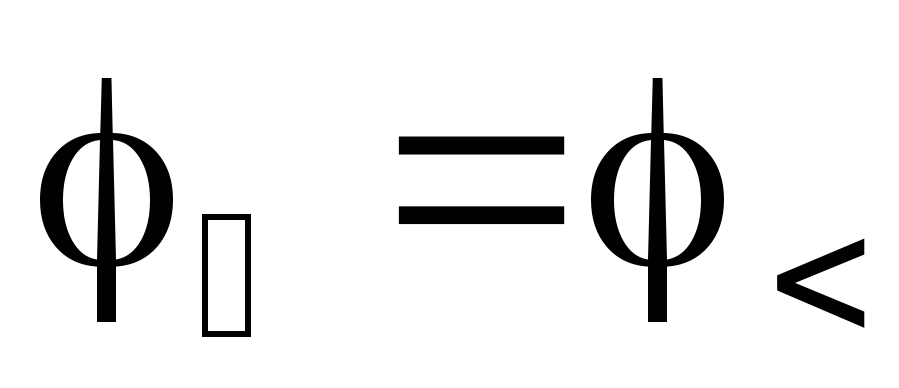 и
и 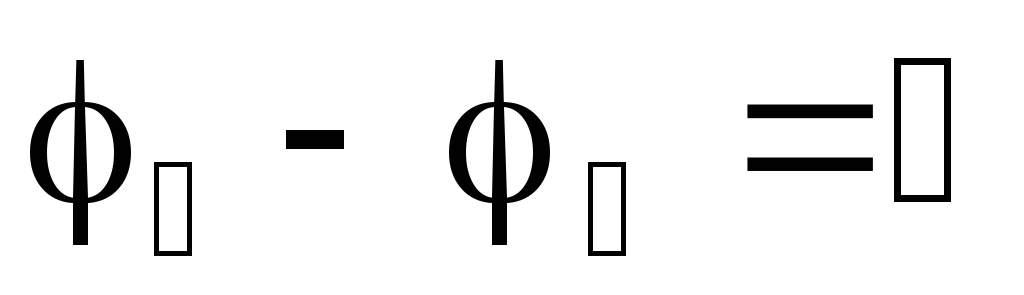 ,
то получим закон
Ома для замкнутой электрической цепи
(эл. схема на рис. 1а).
,
то получим закон
Ома для замкнутой электрической цепи
(эл. схема на рис. 1а).
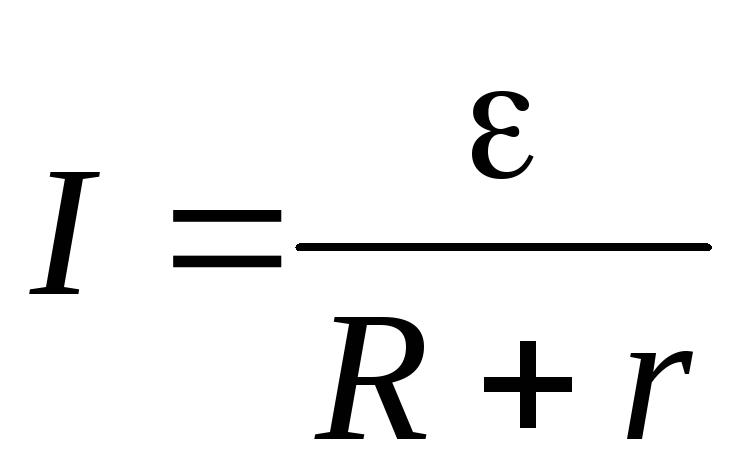
На практике ЭДС
источника тока  невозможно непосредственно измерить
с помощью обычного вольтметра, т.к.
вольтметр измеряет только разность
потенциалов
невозможно непосредственно измерить
с помощью обычного вольтметра, т.к.
вольтметр измеряет только разность
потенциалов 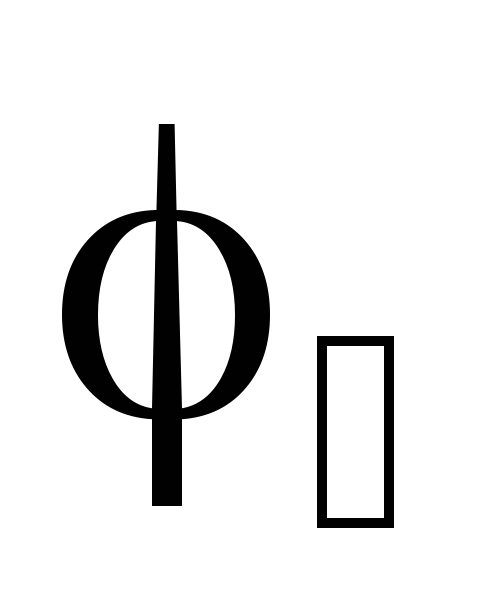 и
и 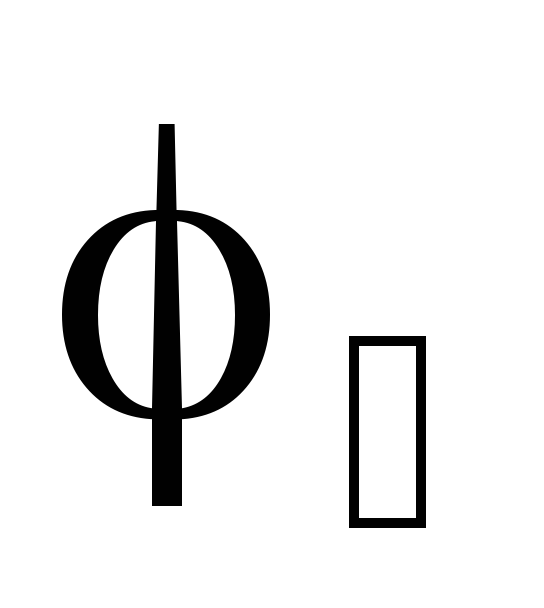 на
клеммах источника. Из выражения (8)
следует, что ЭДС источника тока
на
клеммах источника. Из выражения (8)
следует, что ЭДС источника тока  возможно найти через разность потенциалов
на клеммах источника (
возможно найти через разность потенциалов
на клеммах источника (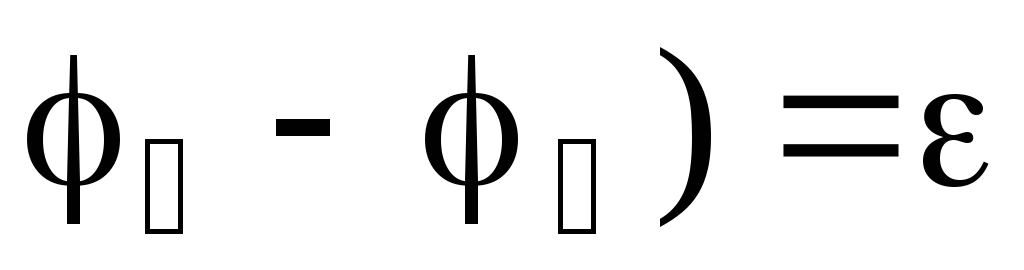 ,
если сила тока на участке электрической
цепи равна нулю. Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до
,
если сила тока на участке электрической
цепи равна нулю. Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до 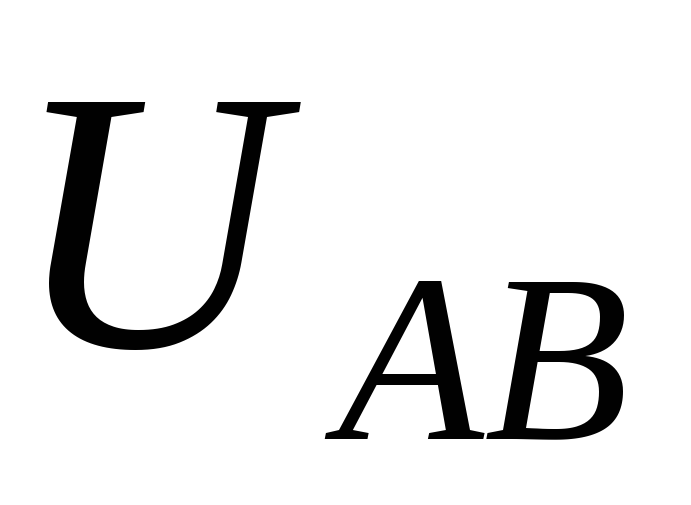 (
(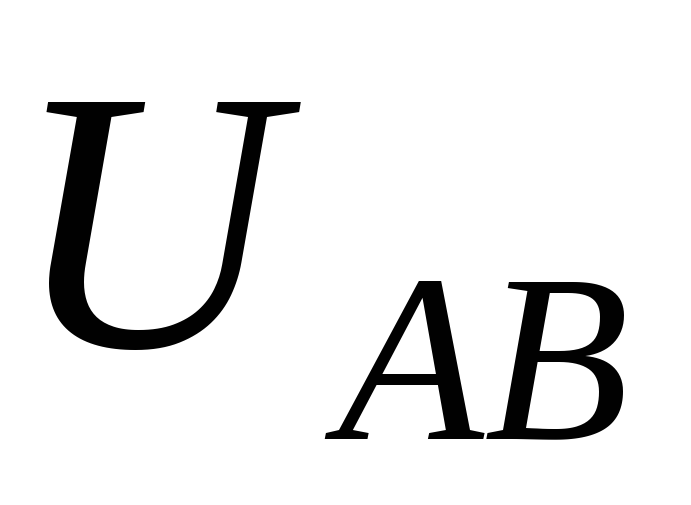 по абсолютной величине всегда меньше
ЭДС вспомогательного источника).
по абсолютной величине всегда меньше
ЭДС вспомогательного источника).
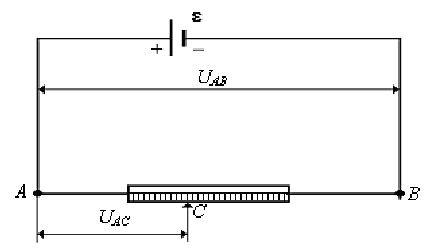
Рис. 5.
Сущность метода
компенсации заключается в том, что
измеряемую ЭДС неизвестного источника
тока  (рис. 5) компенсируют напряжением на
участке потенциометра (реохорда).
Компенсацию достигают, перемещая контакт
потенциометра С (рис. 6) до тех пор, пока
гальванометр Г не покажет нулевого
значения силы тока.
(рис. 5) компенсируют напряжением на
участке потенциометра (реохорда).
Компенсацию достигают, перемещая контакт
потенциометра С (рис. 6) до тех пор, пока
гальванометр Г не покажет нулевого
значения силы тока.
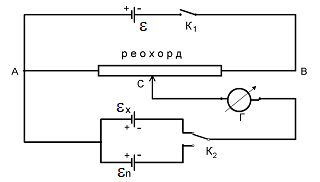
Рис. 6.
Обозначим величины
потенциалов на концах реохорда через 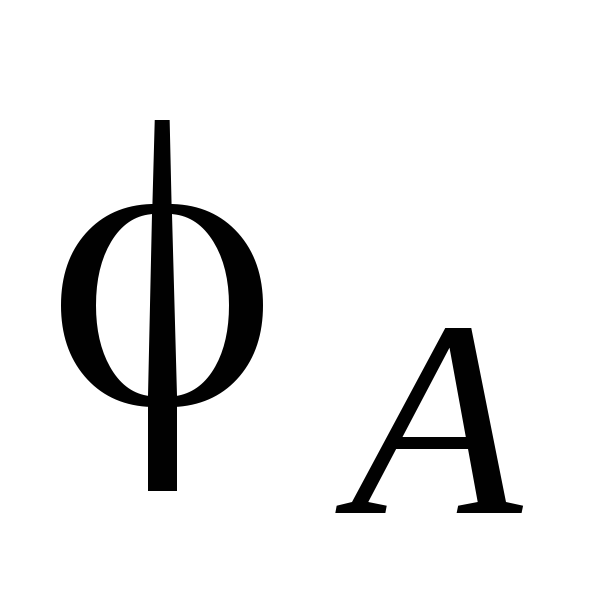 и
и 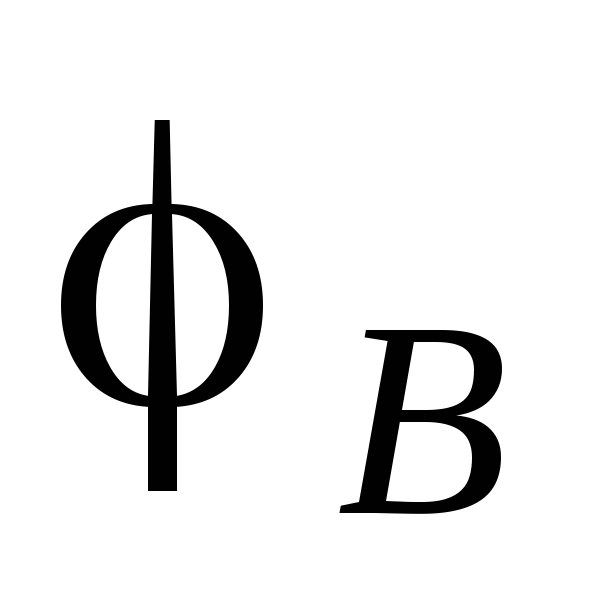 ,
потенциалы на концах источника тока —
через
,
потенциалы на концах источника тока —
через 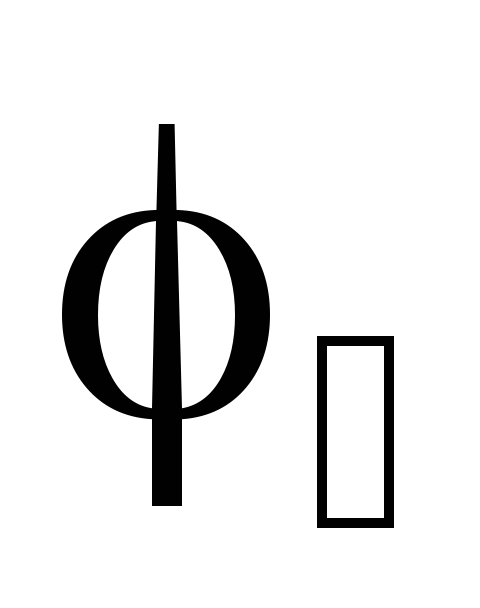 и
и 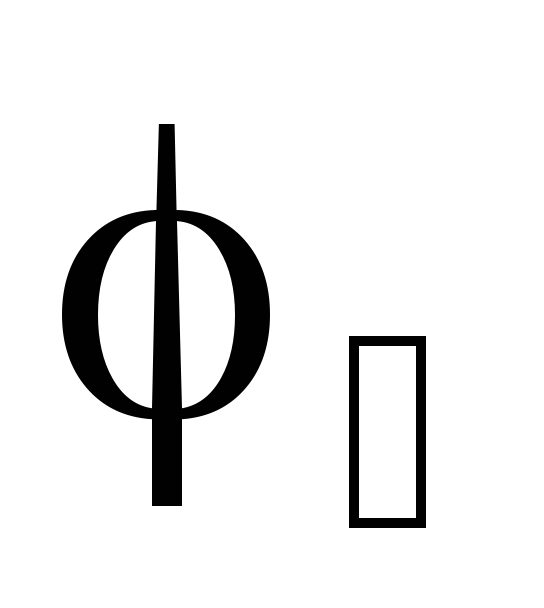 .
Пусть при определенном положении
контакта С на потенциометре ток не идет
через гальванометр Г и источник тока с
ЭДС
.
Пусть при определенном положении
контакта С на потенциометре ток не идет
через гальванометр Г и источник тока с
ЭДС 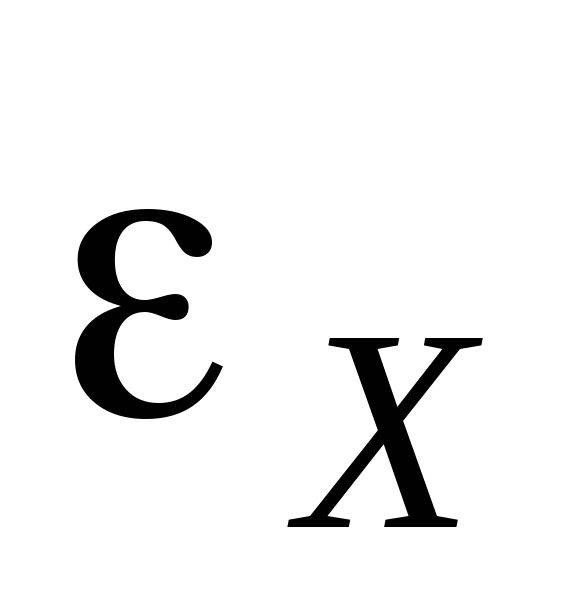 ,
то
,
то 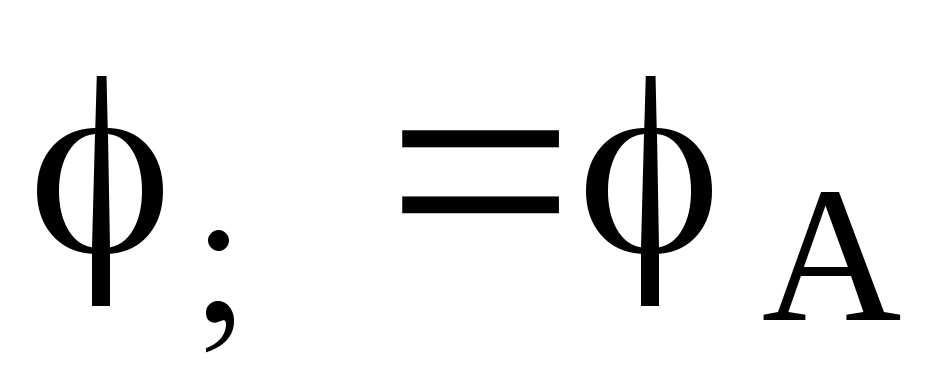 и
и 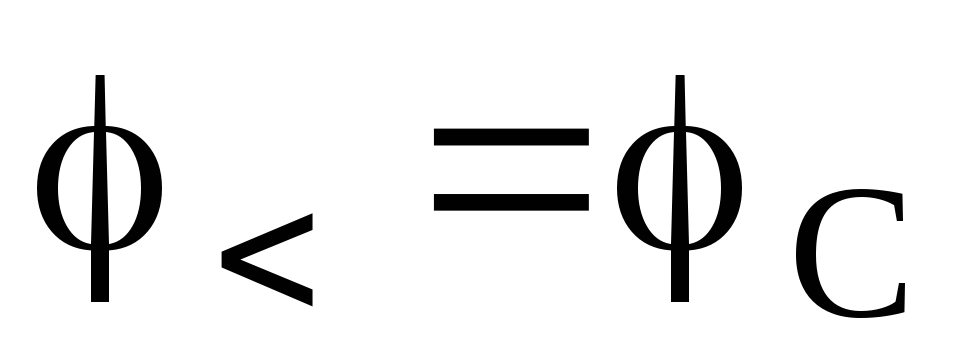 ,
поэтому
,
поэтому
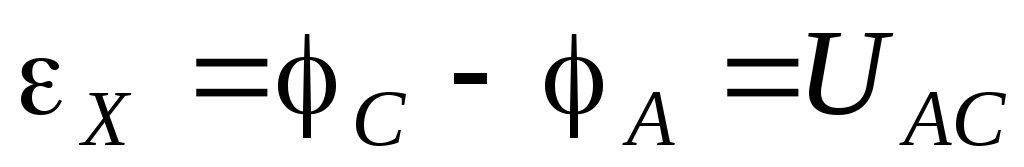 .
(9)
.
(9)
Согласно закону Ома
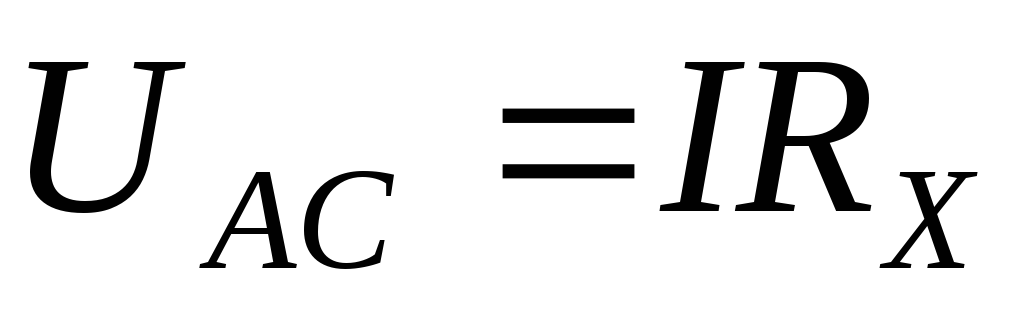 ,
(10)
,
(10)
где 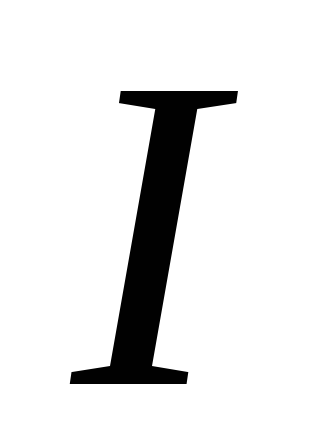 — сила тока в потенциометре,
— сила тока в потенциометре, 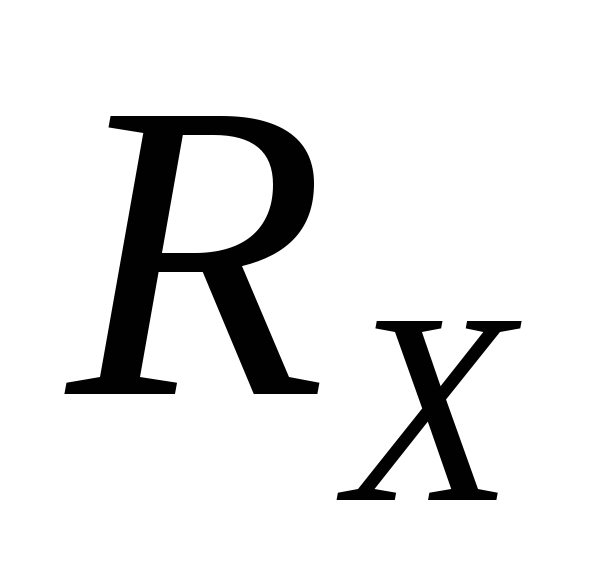 — сопротивление участка АС.
— сопротивление участка АС.
Приравняв выражения (9) и (10) получим
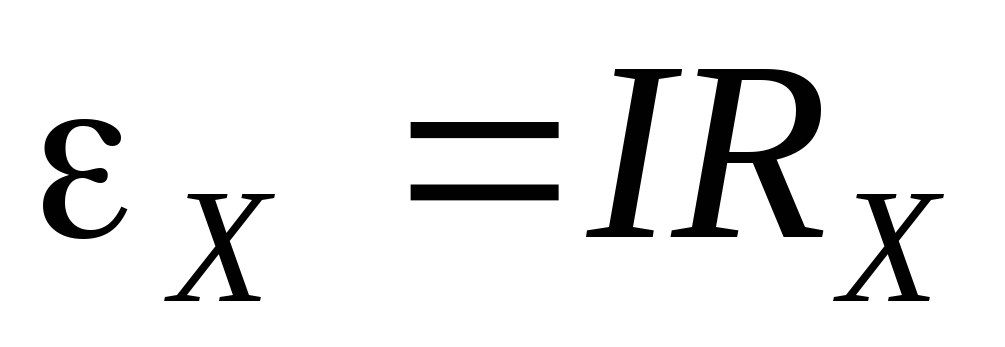 .
.
Чтобы не производить
для определения неизвестного ЭДС
источника тока 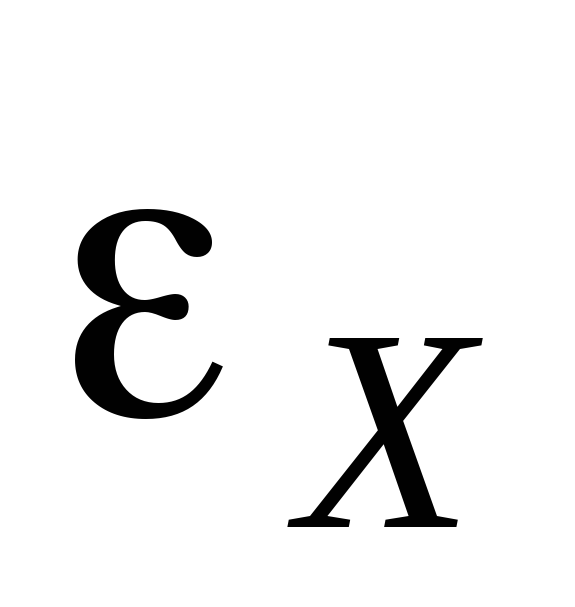 измерения силы тока
измерения силы тока 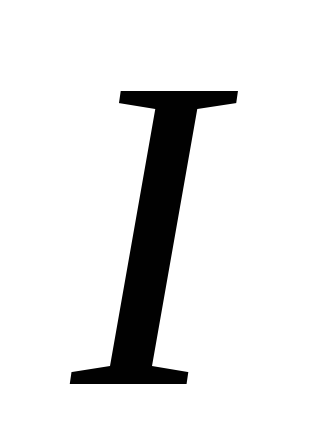 и сопротивления
и сопротивления 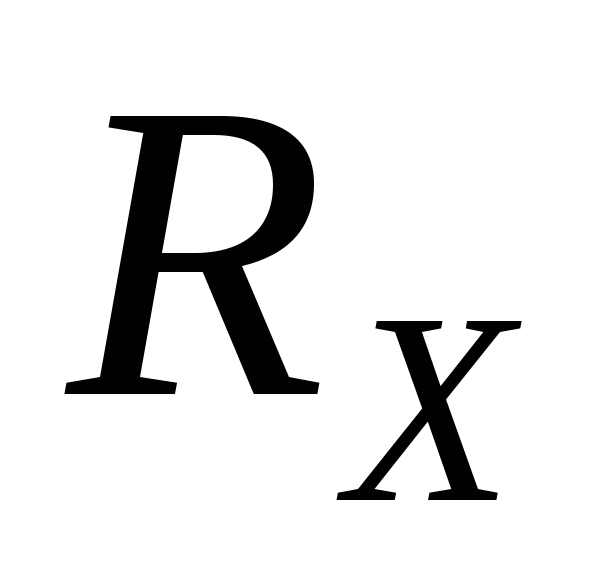 ,
прибегают к сравнению неизвестной ЭДС
,
прибегают к сравнению неизвестной ЭДС 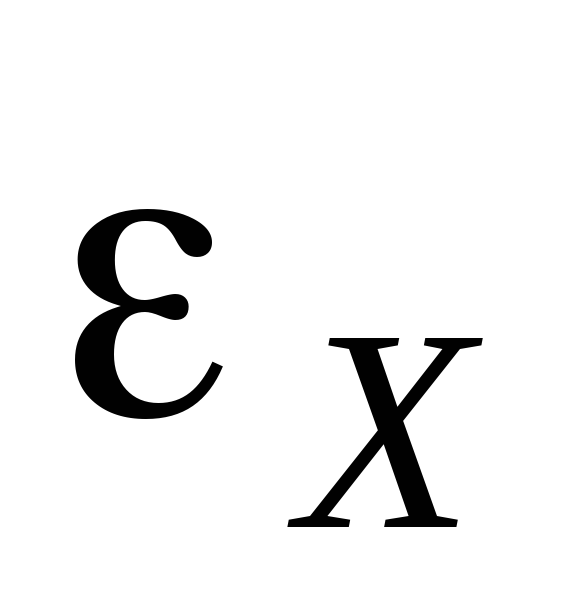 с
известной
с
известной 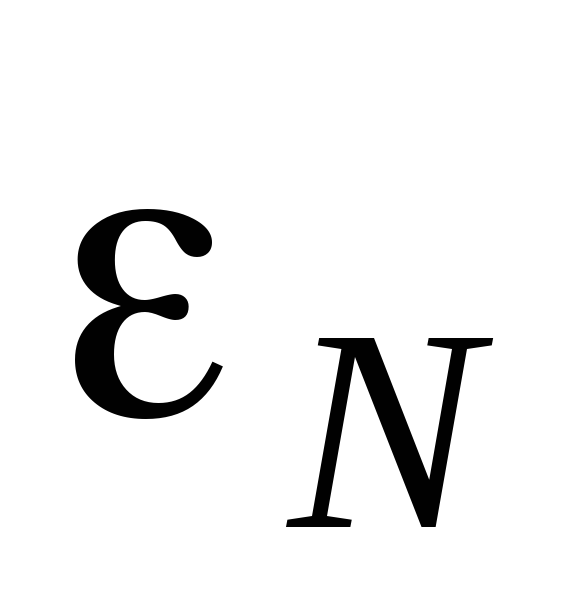 .
Для этого включают вместо источника с
ЭДС
.
Для этого включают вместо источника с
ЭДС 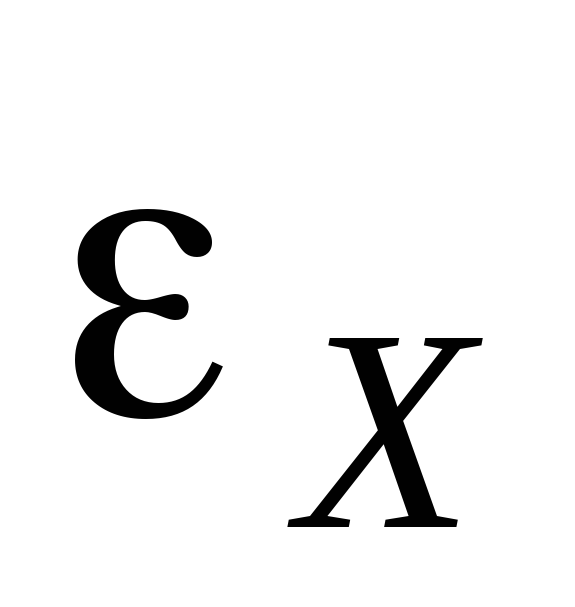 (рис. 6) источник с известной ЭДС
(рис. 6) источник с известной ЭДС 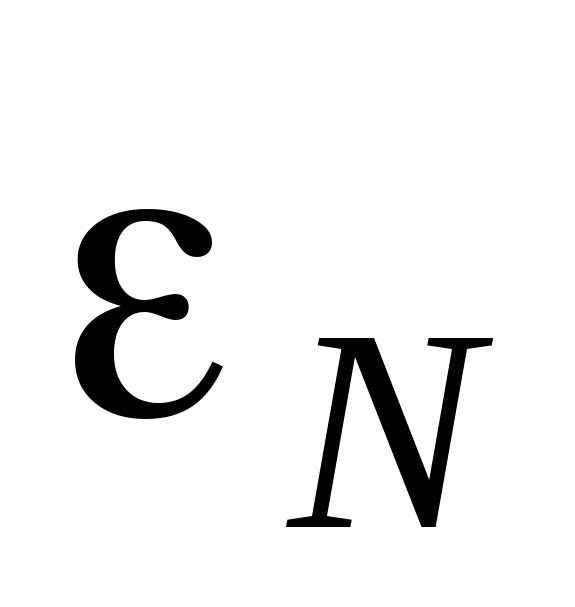 (ЭДС нормального источника тока). Вновь
достигают компенсации, перемещая
подвижный контакт С до нулевого показания
гальванометра. Вследствие этого ЭДС
источника тока определяют как
(ЭДС нормального источника тока). Вновь
достигают компенсации, перемещая
подвижный контакт С до нулевого показания
гальванометра. Вследствие этого ЭДС
источника тока определяют как
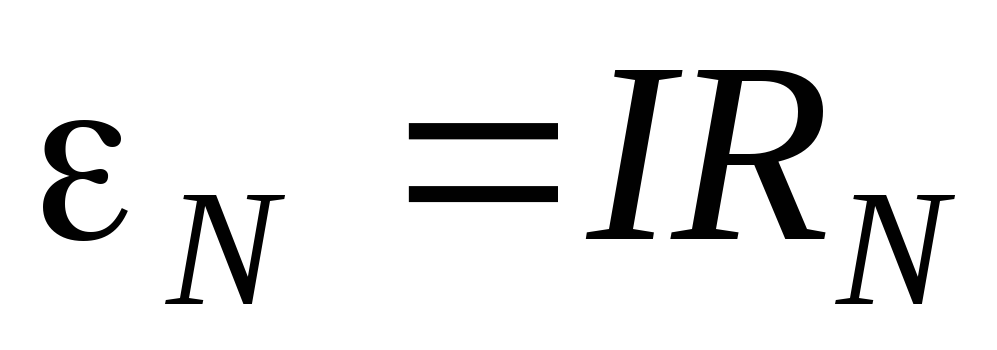 .
(11)
.
(11)
В условиях
компенсации ток течет только по цепи,
включающей потенциометр. При этом сила
тока будет одинакова. Разделим равенства
(10) на (11), сократив на силу тока 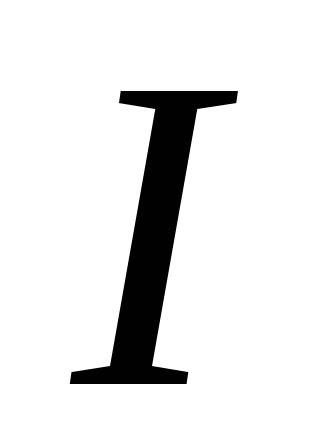 ,
получим условие:
,
получим условие:
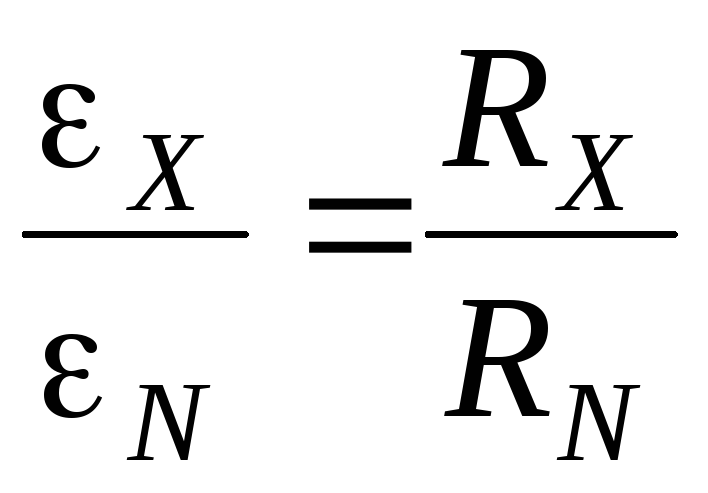 .
(12)
.
(12)
В виду того потенциометр изготовлен из однородного провода, электрическое сопротивление которого определяют по формуле (4), то подставим данную формулу в выражение (12) и выразим ЭДС исследуемого источника тока
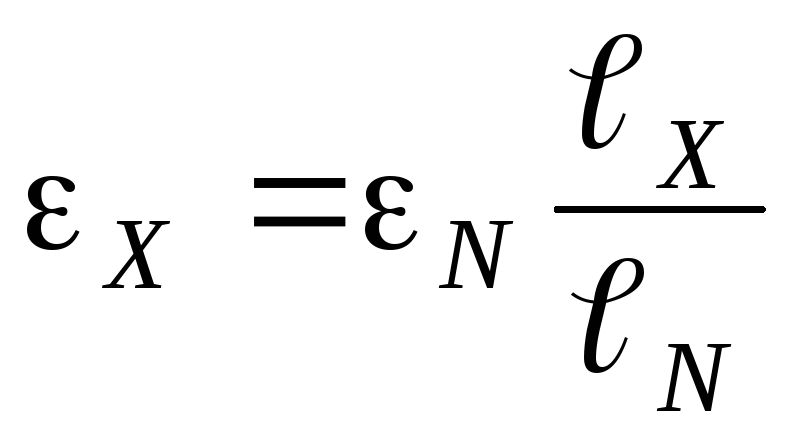 ,
(13)
,
(13)
где 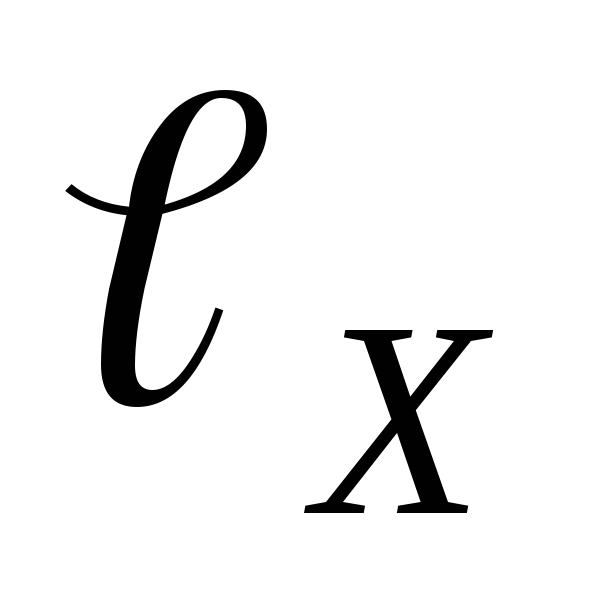 и
и 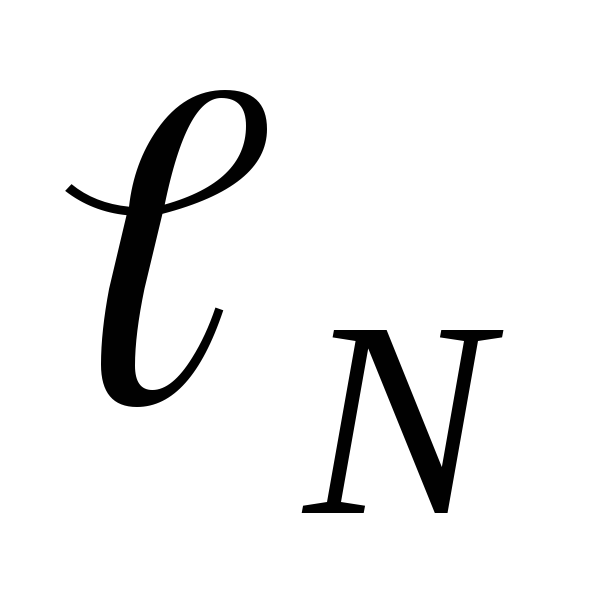
длины участков, на которых происходит
компенсация ЭДС неизвестного источника
тока
длины участков, на которых происходит
компенсация ЭДС неизвестного источника
тока 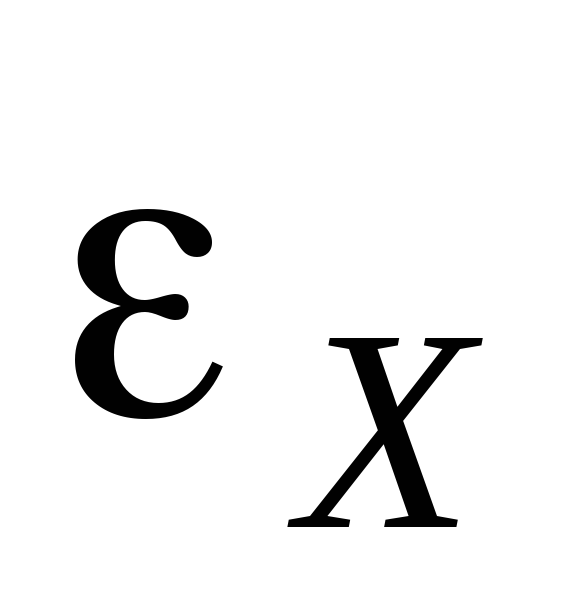 и нормального источника тока
и нормального источника тока 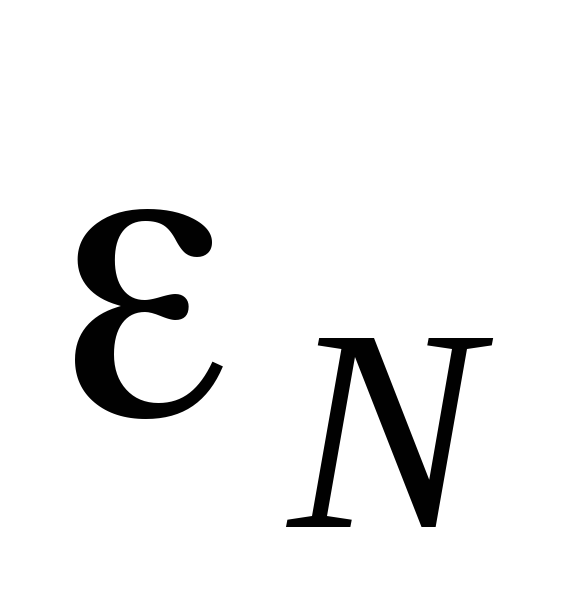 соответственно.
соответственно.
Необходимо также учитывать, что нормальные элементы быстро выходят из строя при пропускании через них больших токов, поэтому в цепь гальванометра вводят дополнительное сопротивление, ограничивающее силу тока через нормальный элемент и гальванометр.
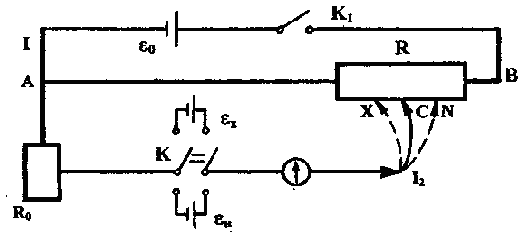
Описание установки
|
Рис. 7. |
Порядок выполнения работы
Включить электрическую цепь с помощью ключа К1 (рис. 7). Переключатель К поставить в положение соответствующее подключению источника
 .
.Передвигая свободный контакт по реохорду найти такое положение, при котором ток через гальванометр будет равен нулю (стрелка гальванометра должна показывать нуль).
Измерить длину участка
 по сантиметровой линейке, на котором
происходит компенсация ЭДС неизвестного
источника тока. Результаты измерений
занести в табл. 1. Повторить измерения
5 раз согласно п.2.
по сантиметровой линейке, на котором
происходит компенсация ЭДС неизвестного
источника тока. Результаты измерений
занести в табл. 1. Повторить измерения
5 раз согласно п.2.
Таблица 1
i
 ,
см
,
см
 ,
см
,
см
1
2
3
4
5
 ,
см
,
см
 ,
см
,
см
Замкнуть ключ К на нормальный элемент
 и повторить измерения по п.2, 3. Значение
длины участка
и повторить измерения по п.2, 3. Значение
длины участка  ,
на котором происходит компенсация ЭДС
нормального элемента, занести в таблицу
1.
,
на котором происходит компенсация ЭДС
нормального элемента, занести в таблицу
1.Рассчитать средние значения длин участков потенциометра
 ,
,  на которых
происходит компенсация ЭДС неизвестного
и нормального источника токов и средние
квадратичные отклонения от средних
значений этих величин.
на которых
происходит компенсация ЭДС неизвестного
и нормального источника токов и средние
квадратичные отклонения от средних
значений этих величин.По формуле (13), подставляя в нее средние значения
 ,
,  и
и  (см. на установке), определить средние
значения ЭДС неизвестного источника
тока.
(см. на установке), определить средние
значения ЭДС неизвестного источника
тока.Вычислить доверительную границу общей погрешности для длин
 и
и  ,
на которых происходит компенсация ЭДС
неизвестного и нормального источников
тока по формулам
,
на которых происходит компенсация ЭДС
неизвестного и нормального источников
тока по формулам
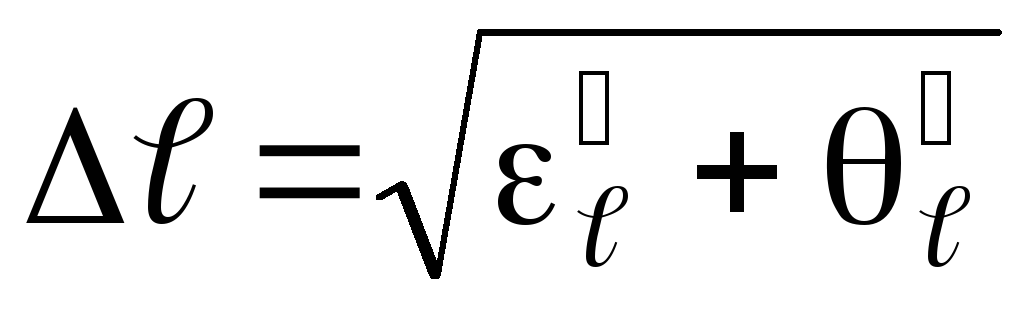 ,
,
где 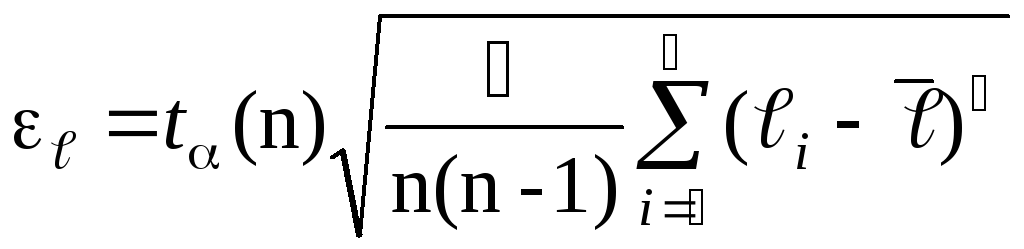 ,
, 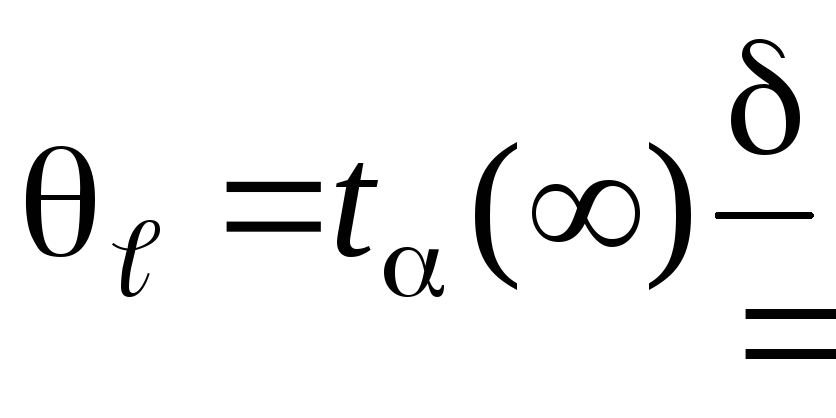 ,
,  — диаметр проволоки реохорда (0,4 мм).
— диаметр проволоки реохорда (0,4 мм).
Рассчитать относительную ошибку измерений длин, на которых происходит компенсация ЭДС источников токов по формуле
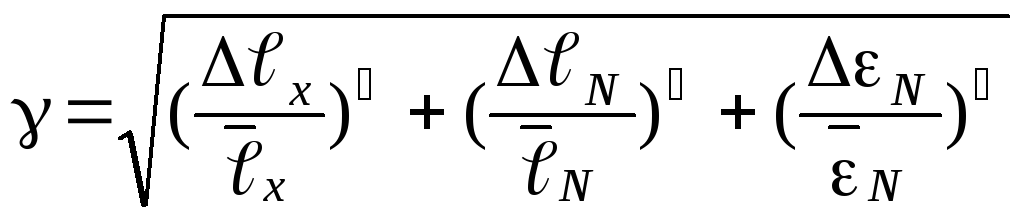 ,
,
где
величина 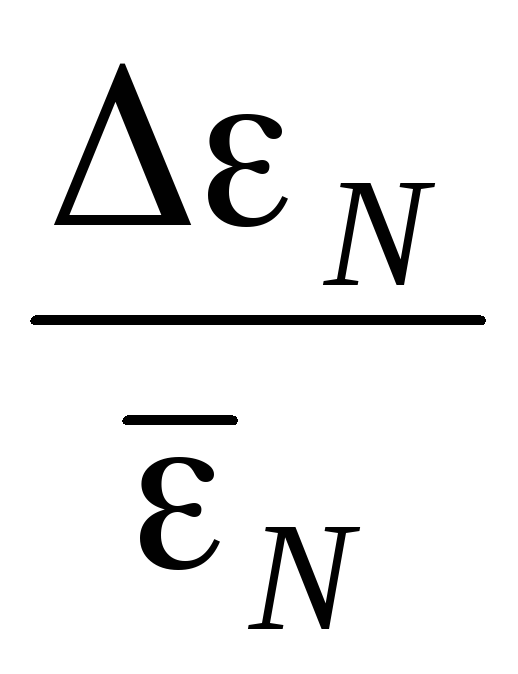 указана на установке.
указана на установке.
Определить абсолютную ошибку измерений для ЭДС неизвестного источника тока по формуле
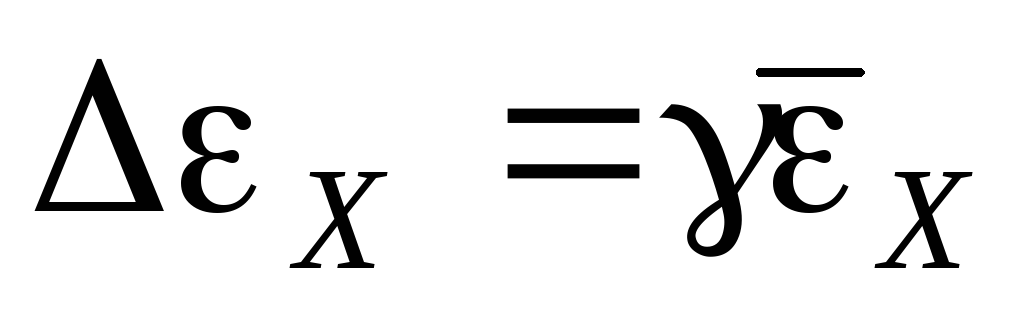
Записать окончательный результат измерения в виде
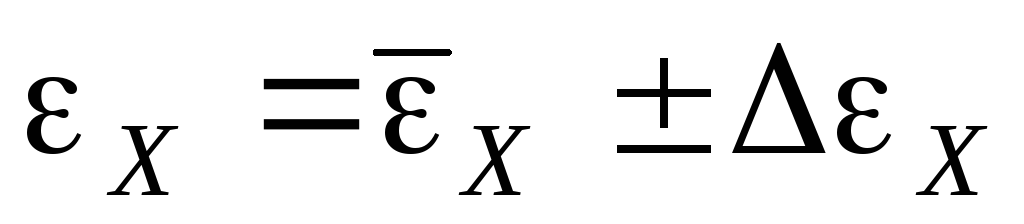 ,
при
,
при 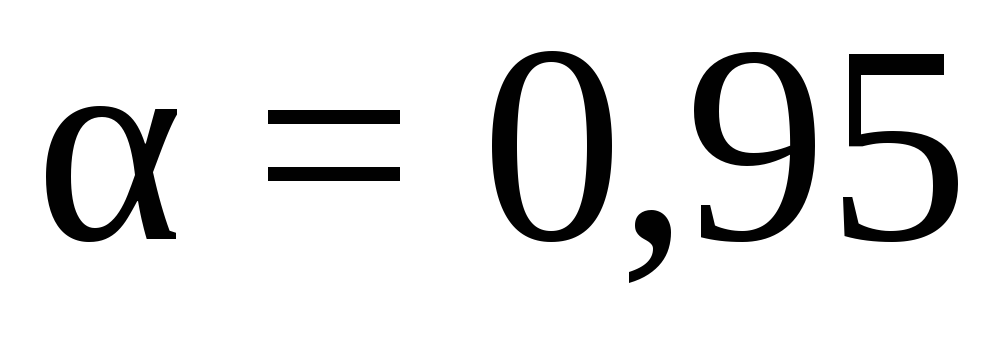 .
.
Контрольные вопросы
Что такое электрический ток, сила тока, плотность тока?
Вывести закон Ома для неоднородного участка электрической цепи и получит из него закон Ома для полной замкнутой и однородного участка электрической цепи.
Каков физический смысл ЭДС? Что такое сторонние силы? Каково их назначение?
4 Чем компенсируется неизвестная ЭДС при достижении нулевого показания гальванометра?
5. Если в схеме компенсации источник заменить другим источником с такой же ЭДС, но с большим внутренним сопротивлением, то в какую сторону следует сместить движок реохорда для восстановления компенсации?
ЛАБОРАТОРНАЯ РАБОТА 5
От чего зависит эдс. Эдс и напряжение источника электрической энергии
Для того чтобы разобраться что такое электродвижущая сила источника электрической энергии, необходимо вспомнить, что представляет собой электрический ток и за счёт чего происходит его движение в электрической цепи.
Известно, электрический ток движется в цепи за счёт разницы потенциалов. Для того чтобы движение тока не прекращалось, нужно непрерывно обеспечивать эту разницу потенциалов между полюсами источника напряжения, к которому подключена цепь.
Подобное явление можно сравнить с трубкой, которая соединена с двумя резервуарами с водой. Если в этих резервуарах будет разный уровень воды, то она непременно начнёт перетекать через трубку из одного сосуда в другой и наоборот; так если разница в уровне воды между сосудами будет постоянной, то и движение воды не прекратиться.
Данный пример помогает понять, что происходит в электрической цепи. Электрическая энергия, действующая внутри источника, постоянно поддерживает электрический ток. Таким образом, обеспечивается непрерывная работа.
Понятие «Электродвижущая сила»
В данном случае, электродвижущая сила (ЭДС) – это сила, которая поддерживает разницу потенциалов на разных полюсах источника энергии, она вызывает и поддерживает движение тока, а также преодолевает внутренне сопротивление проводника и т. д.
Ток может протекать по проводнику столь же долго, сколь существует разница потенциалов. Свободные электроны приходят в постоянное движение между телами, которые соединены в электрическую цепь.
Электродвижущая сила – величина физическая, т. е., её можно измерить и использовать как одну из характеристик электрической цепи. В источниках постоянного, либо переменного тока ЭДС характеризует работу непотенциальных сил. Это работа сторонних или непотенциальных сил в замкнутом контуре, когда они перемещают одиночный электрический заряд вдоль всего контура.
Возникновение электродвижущей силы
Существует различные виды источников электрической энергии. Каждый из них можно охарактеризовать по-разному, у каждого вида свои принципиальные особенности. Эти особенности влияют на возникновение электродвижущей силы, причины данного явления весьма специфичны, т. е. зависят от вида источника.
В чём же главная суть различий? К примеру, если мы берём химические источники электрической энергии, такие как аккумуляторы, другие гальванические элементы, то электродвижущая сила становится результатом химической реакции. Если рассмотреть генераторы, то здесь причиной является электромагнитная индукция, а в различных термических элементах основой является тепловая энергия. От этого возникает электрический ток.
Измерение электродвижущей силы
Электродвижущая сила измеряется в вольтах, также как и напряжение. Эти величины связаны между собой. Однако ЭДС можно измерять на отдельном участке электрической цепи, тогда будут измеряться работы не всех сил, действующих на этом контуре, а только те, которые есть на отдельно взятом участке цепи.
Разность потенциалов, являющуюся причиной возникновения и прохождения тока по цепи, также можно назвать напряжением. Однако, если ЭДС – работа сторонних сил, которая совершается при перемещении единичного заряда, то она не может быть охарактеризована с помощью разницы потенциалов, т. е., напряжения, так как работа зависит от траектории движения заряда, эти силы непотенциальны. В этом различие таких понятий как напряжение и электродвижущая сила.
Данная особенность учитывается при измерении ЭДС и напряжения. В обоих случаях используют вольтметры. Для того чтобы измерить ЭДС нужно при разомкнутой внешней цепи подключить вольтметр к концам источника энергии. Если требуется измерить напряжение на выбранном участке электрической цепи, то вольтметр должен быть подключён параллельно к концам конкретного участка.
ЭДС и напряжение источника электрической энергии могут быть независимо от величины электрического тока в цепи; в разомкнутой цепи ток равен нулю. Однако если генератор или аккумулятор будут работать, то они возбуждают ЭДС, а значит, между концами возникает напряжение.
Элемент электрической цепи, предназначенный для получения электроэнергии, принято называть источником электрической энергии. В источнике происходит преобразование в электрическую энергию других: видов энергии.
На практике применяют следующие основные источники: электромеханические генераторы (электрические машины для преобразования механической энергии в электрическую), электрохимические источники (гальванические элементы, аккумуляторы), термоэлектрогенераторы (устройства прямого преобразования тепловой энергии в электрическую), фотоэлектрогенераторы (преобразователи лучистой энергии в электрическую).
Принципы преобразования тепловой, лучистой и химической энергии в электрическую изучаются в курсе физики.
Общим свойством всех источников является
то, что в них происходит разделение положительного
и отрицательного зарядов и образуется электродвижущая сила (ЭДС). Что такое ЭДС?
В простейшей электрической цепи на перемещение заряда q по контуру замкнутой цепи (рис. 2.8) затрачивается работа источника А и.
Источник затрачивает одинаковую работу на перемещение каждой единицы заряда. Поэтому с увеличением q прямо пропорционально растет А и, а их отношение A и /q, называемое электродвижущей силой , остается неизменным:
E = A и /q. (2.12)
ЭДС численно равна работе, которую совершает источник, проводя заряд 1 Кл по замкнутому контуру цепи (1).
Единица ЭДС, как и напряжения,- вольт (В).
Благодаря ЭДС в электрической цепи поддерживается определенное значение тока.
Так как ЭДС не зависит от q, а ток I = q/t , то ЭДС источника не зависит от тока (2).
При изменении тока изменяется мощность источника Р и. Используя выражения P и =A и /t , A и = qE и q = It,
получаем формулу для расчета мощности источника:
Р и = EI. (2.13)
Таким образом, при изменении сопротивления приемника изменяется ток цепи, мощность источника и мощность приемника. При этом соблюдается положение (5) и непрерывно действует постоянная ЭДС, создающая ток.
В соответствии с балансом мощности
P и =P+P в,
где Р — мощность приемника; Р в — потери на внутреннем сопротивлении R B источника (потерями в соединительных проводах пренебрегаем).
Подставляя в это уравнение значение мощности из формул (2.10), (2.13), используя положение (3) получаем:
EI=UI+UJ;
E=U+U в (2.14)
(действие равно сумме противодействий).
В замкнутой цепи ЭДС встречает противодействие суммы падений напряжений на участках цепи.
Используя выражение (2.14) и закон Ома, получаем
E = IR + IR B . (2.15)
В этом уравнении Е и R B как параметры источника постоянные. При изменении сопротивления приемника R изменяет свое значение ток. Ток в цепи имеет строго определенное значение, необходимое для создания падений напряжений на участках цепи, уравновешивающих ЭДС (3). Аналогично в механике скорость движения тел такая, при которой вызванное этой скоростью противодействие сил трения уравновешивается действием сил, двигающих тело.
Из уравнения (2.15) ток
I = E/(R + R B). (2.16)
Эта формула отражает закон Ома для всей цепи: сила тока в цепи прямо пропорциональна ЭДС источника.
Следует отметить, что уравнение (2.14) является частным случаем второго закона Кирхгофа, который формулируется так: алгебраическая сумма ЭДС любого замкнутого контура электрической цепи равна алгебра
Урок 31. Лабораторная работа № 08. Измерение ЭДС и внутреннего сопротивления источника тока.
Лабораторная работа № 8
Тема: «Определение электродвижущей силы и внутреннего сопротивления источника тока».
Цель: научиться определять электродвижущую силу и внутреннее сопротивление источника электрической энергии.
Оборудование: 1. Амперметр лабораторный;
2. Источник электрической энергии;
3. Соединительные провода,
4. Набор сопротивлений 2 Ом и 4 Ом;
5. Переключатель однополюсный; ключ.
Теория.
Возникновение разности потенциалов на полюсах любого источника является результатом разделения в нем положительных и отрицательных зарядов. Это разделение происходит благодаря работе, совершаемой сторонними силами.
Силы неэлектрического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q внутри источника тока к величине этого заряда, называется электродвижущей силой источника (ЭДС):
ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда.
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах [В].
Чтобы измерить ЭДС источника, надо присоединить к нему вольтметр при разомкнутой цепи.
Источник тока является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Это сопротивление называют внутренним сопротивлением источника и обозначают r.
Если цепь разомкнута, то работа сторонних сил превращается в потенциальную энергию источника тока. При замкнутой цепи эта потенциальная энергия расходуется на работу по перемещению зарядов во внешней цепи с сопротивлением R и во внутренней части цепи с сопротивлением r , т.е. ε = IR + Ir.
Если цепь состоит из внешней части сопротивлением R и внутренней сопротивлением r, то, согласно закону сохранения энергии, ЭДС источника будет равна сумме напряжений на внешнем и внутреннем участках цепи, т.к. при перемещении по замкнутой цепи заряд возвращается в исходное положение , где IR – напряжение на внешнем участке цепи, а Ir — напряжение на внутреннем участке цепи.
Таким образом, для участка цепи, содержащего ЭДС:
Эта формула выражает закон Ома для полной цепи: сила тока в полной цепи прямо пропорциональна электродвижущей силе источника и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи.
ε и r можно определить опытным путем.
Часто источники электрической энергии соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε1 + ε2 + ε3
2. Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников rбатареи= r1 + r2 + r3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε1, а сопротивление rбатареи= nr1
3. Сила тока в такой цепи по закону Ома
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС. Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε1= ε2 = ε3
2. Сопротивление батареи меньше, чем сопротивление одного источника rбатареи= r1/n
3. Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Ход работы.
1. Начертите таблицу:
|
№ опыта |
Источник электрической энергии ВУП, В |
1-й отсчет |
2-й отсчет |
Э.Д.С. ε , В |
Внутреннее сопротивление, r , Ом |
||
|
R1, Ом |
Сила тока I1 , А |
R2, Ом |
Сила тока I2 , А |
||||
|
1
|
1 |
1 |
|
2 |
|
|
|
2. Рассмотрите шкалу амперметра и определите цену одного деления.
3. Составьте электрическую цепь по схеме, изображенной на рисунке 1. Переключатель поставить в среднее положение.
Рисунок 1.
4. Замкнуть цепь, введя меньшее сопротивление R1. Записать величину силы тока I1. Разомкнуть цепь.
5. Замкнуть цепь, введя большее сопротивление R2. Записать величину силы тока I2. Разомкнуть цепь.
6. Вычислить значение ЭДС и внутреннего сопротивления источника электрической энергии.
Закон Ома для полной цепи для каждого случая: и
Отсюда получим формулы для вычисления ε и r:
7. Результаты всех измерений и вычислений запишите в таблицу.
8. Сделайте вывод.
9. Ответьте на контрольные вопросы.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Раскройте физический смысл понятия «электродвижущая сила источника тока».
2. Определить сопротивление внешнего участка цепи, пользуясь результатами полученных измерений и законом Ома для полной цепи.
3. Объяснить, почему внутреннее сопротивление возрастает при последовательном соединении аккумуляторов и уменьшается при параллельном в сравнении с сопротивлением r0 одного аккумулятора.
4. В каком случае вольтметр, включенный на зажимы генератора, показывает ЭДС генератора и в каком случае напряжение на концах внешнего участка цепи? Можно ли это напряжение считать также и напряжением на концах внутреннего участка цепи?
Вариант выполнения измерений.
Опыт 1. Сопротивление R1=2 Ом, сила тока I1=1,3 А.
Сопротивление R2=4 Ом, сила тока I2=0,7 А.
Лаб№1(корект
Цель работы:
Получение навыков экспериментального исследования цепей постоянного тока.
Основные теоретические положения и ответы на вопросы полготовки:
1. Формулировки законов Ома и Кирхгофа.
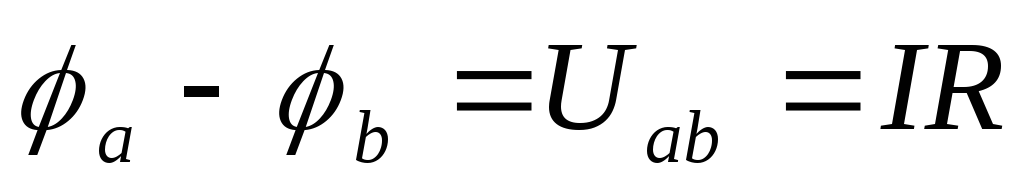 закон
Ома для участка цепи;
закон
Ома для участка цепи;
Разность потенциалов на участке цепи равна падению напряжения.
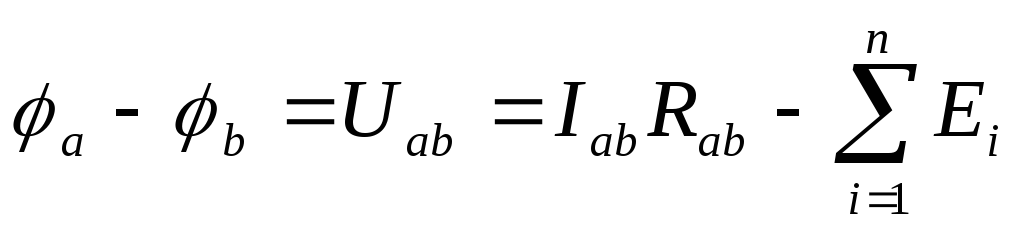 Обобщенный
закон Ома;
Обобщенный
закон Ома;
Разность потенциалов на участке цепи равна падению напряжения за вычетом алгебраической суммы ЭДС.
Первый закон Кирхгофа:
алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;
сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов.

Второй закон Кирхгофа:
1) алгебраическая
сумма падений напряжения в любом
замкнутом контуре равна алгебраической
сумме ЭДС вдоль того же контура; 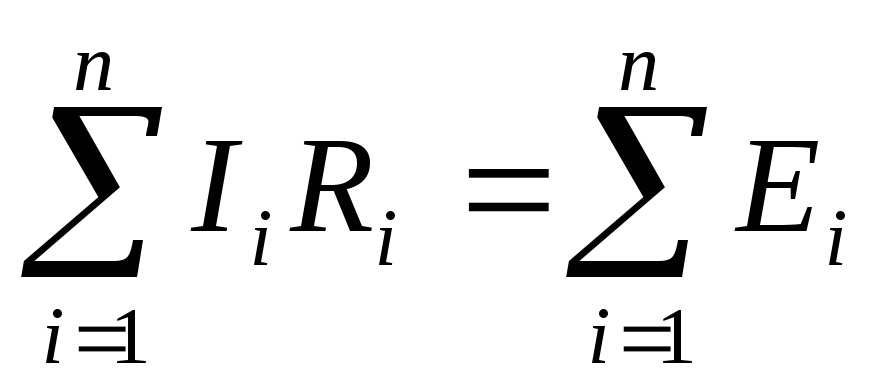
2) алгебраическая
сумма напряжений вдоль любого замкнутого
контура равна нулю; 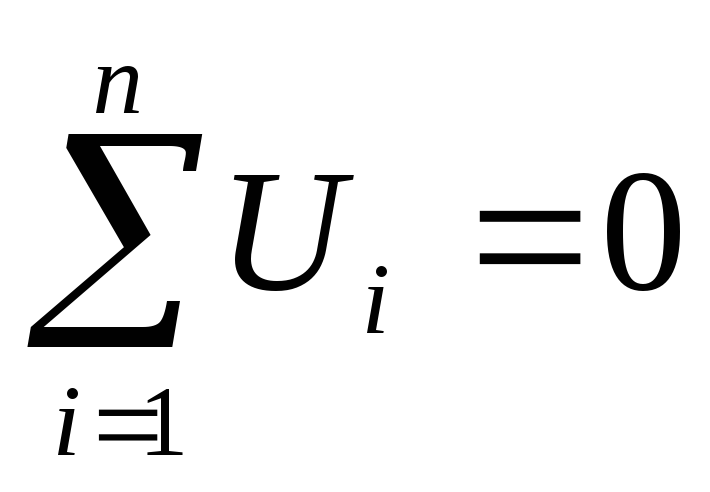
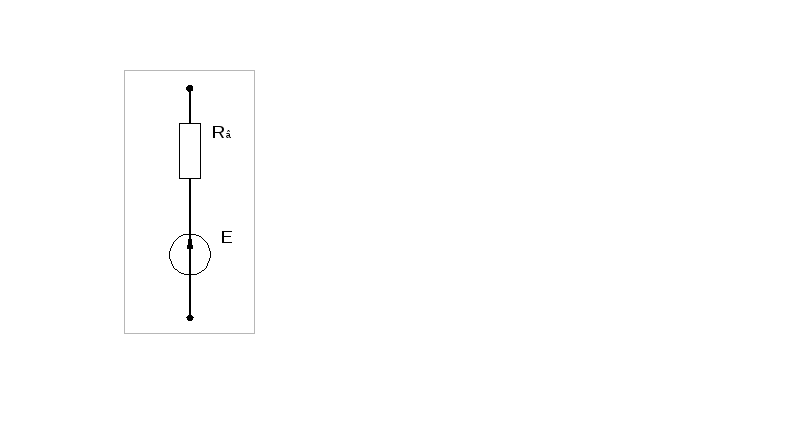
Особенности применения законов Кирхгофа при анализе цепей с источниками тока:
Е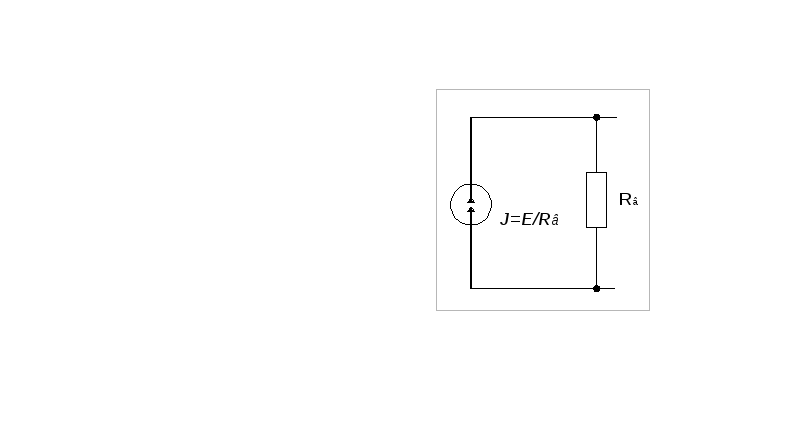
 сли
попытаться составить уравнение по
второму закону Кирхгофа в форме
сли
попытаться составить уравнение по
второму закону Кирхгофа в форме 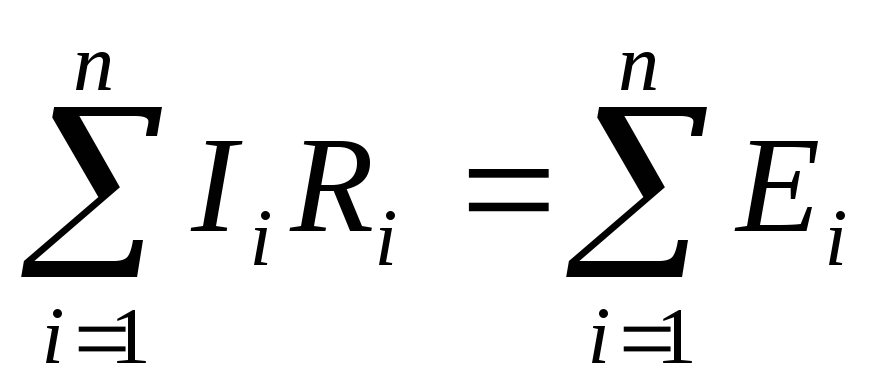 для контура, в который входит источник
тока, то в него вошли бы бесконечно
большие слагаемые и оно не имело бы
смысла.
для контура, в который входит источник
тока, то в него вошли бы бесконечно
большие слагаемые и оно не имело бы
смысла.
Какой источник энергии называется источником напряжения (ЭДС) и какой источником тока? Привести электрические схемы реальных и идеальных источников напряжения и тока.
Источником ЭДС называется источник, у которого внутреннее сопротивление Rв=0, а вольтамперная характеристика имеет вид прямой линии.
Источником тока называется идеализированный источник питания, который создает ток I, не зависящий от сопротивления нагрузки, к которой он присоединен, а его ЭДС Еит и внутреннее сопротивление Rит равны бесконечности.
Каким образом экспериментально определить ЭДС источника напряжения?
Так как ЭДС численно равно разности потенциалов на зажимах источника в режиме холостого хода, то его можно измерить вольтметром.
Как с помощью вольтметра определить величину и знак потенциала любой точки цепи по отношению к точке, потенциал которой принят равным нулю?
Один зажим устанавливается в точку с нулевым потенциалом, а другим определяется потенциалы других точек относительно точки с нулевым потенциалом
Что такое потенциальная диаграмма цепи, как ее получить экспериментально?
П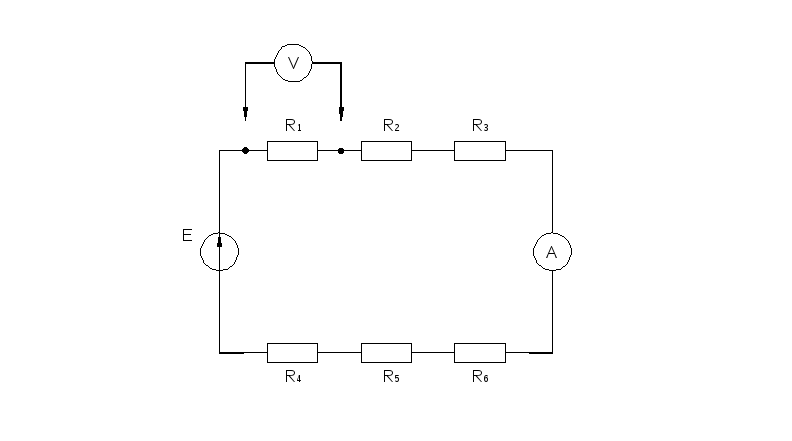 од потенциальной
диаграммой понимают график распределения потенциала
вдоль какого-либо участка цепи или
замкнутого контура. Производятся
измерения потенциалов всех точек, а
затем наносятся на координатную ось.
од потенциальной
диаграммой понимают график распределения потенциала
вдоль какого-либо участка цепи или
замкнутого контура. Производятся
измерения потенциалов всех точек, а
затем наносятся на координатную ось.
Порядок выполнения работы:
1) Собрать цепь
2) Измерить ток в цепи, ЭДС, сопротивление всех резисторов и напряжения на них, заполнить следующую таблицу:
Ток в цепи I=21,5мА; ЭДС E=20 В | |||||||
Резистор | R1(01) | R2(02) | R3(03) | R4(04) | R5(05) | R6(06) | |
Напряжение, В | U | 1,09 | 1,63 | 2,18 | 3,24 | 4,46 | 6,44 |
Сопротивление(экс), Ом | R | 50,6 | 75,5 | 100,9 | 150,4 | 207,6 | 299,4 |
Проводимость, Ом-1 | G | 0,0198 | 0,0132 | 0,0099 | 0,0066 | 0,0066 | 0,0033 |
Сопротивление(рас), Ом | R | 50,7 | 75,8 | 101,3 | 150,7 | 207,4 | 299,5 |
3) Проведем теоретические расчеты
сопротивлений, используя закон Ома 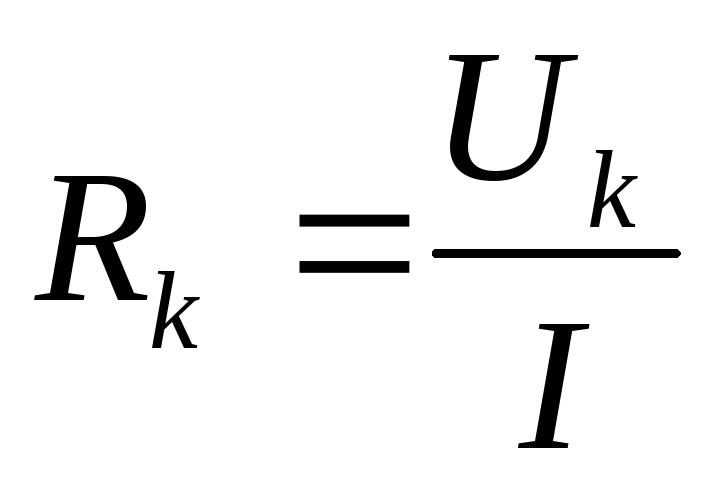 :
:
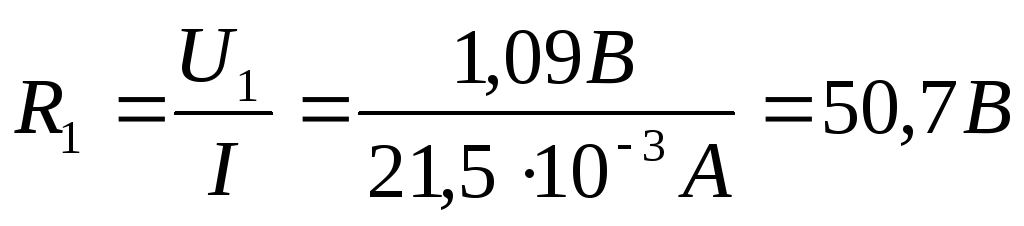
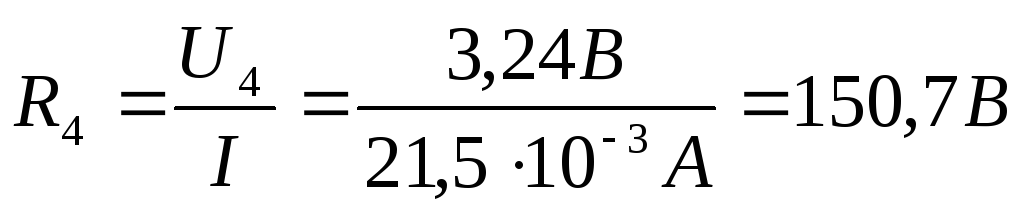
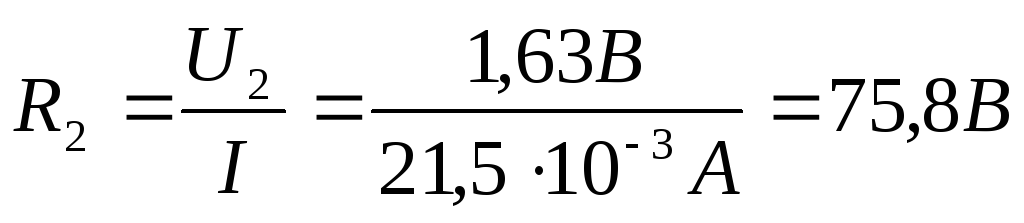
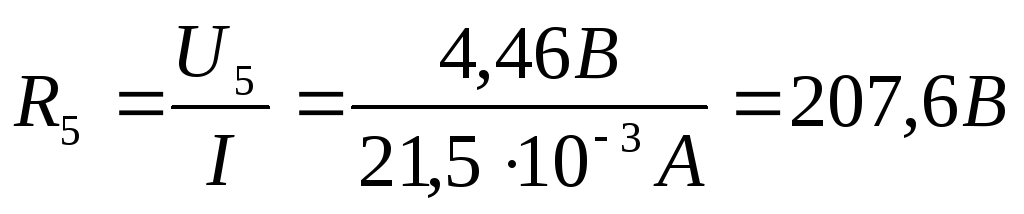
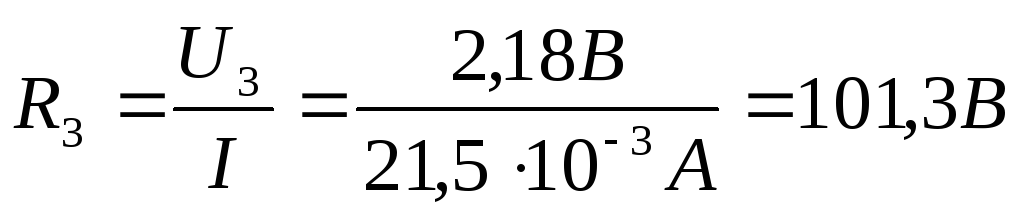
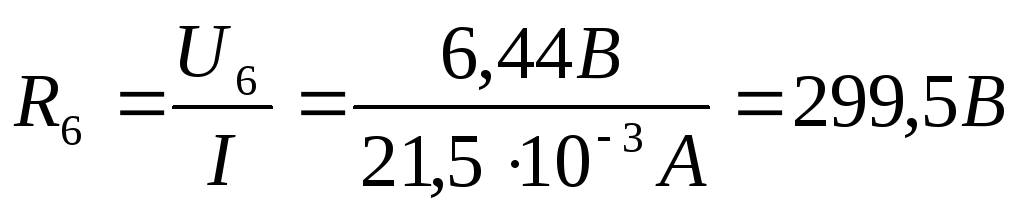
4) Проведем расчеты проводимости 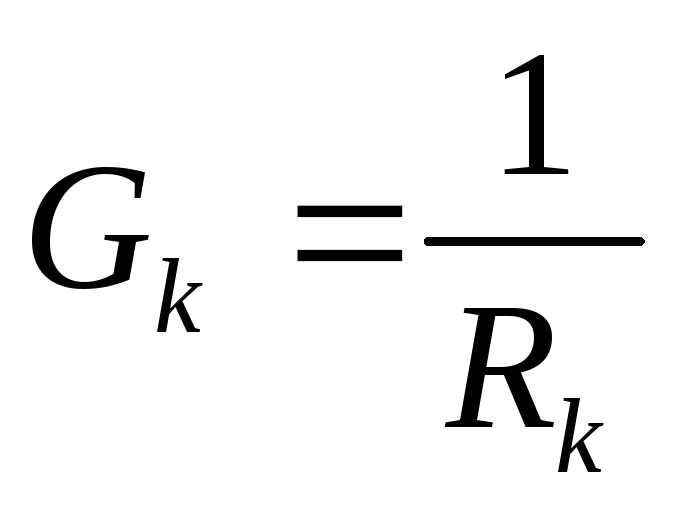
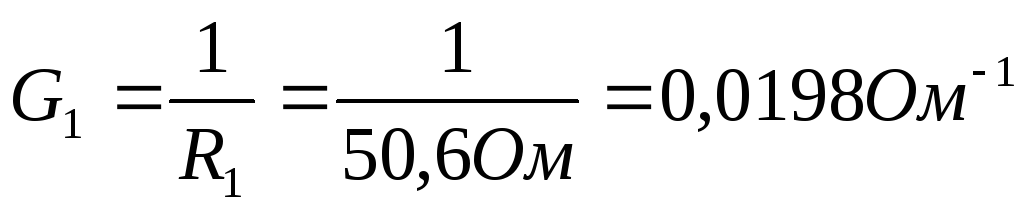
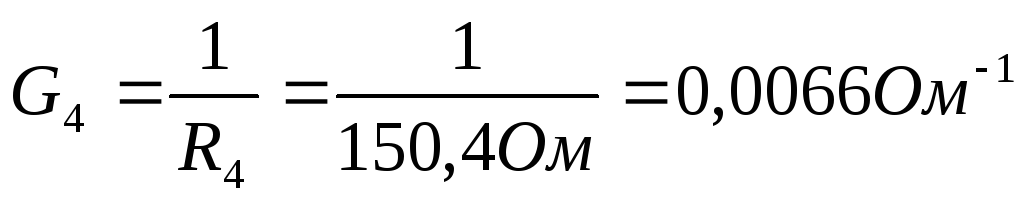
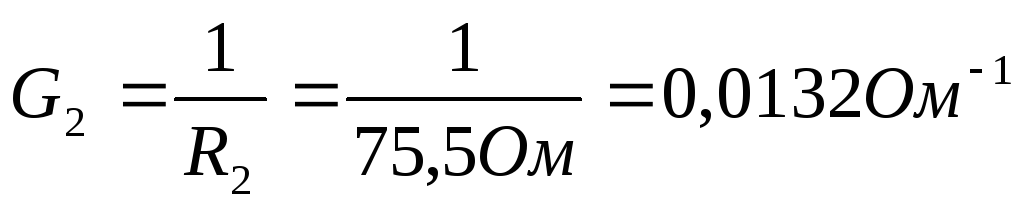
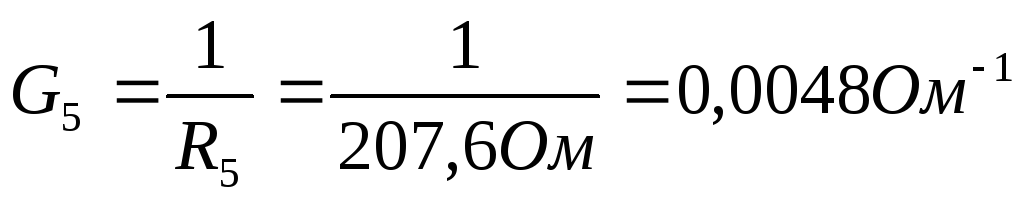
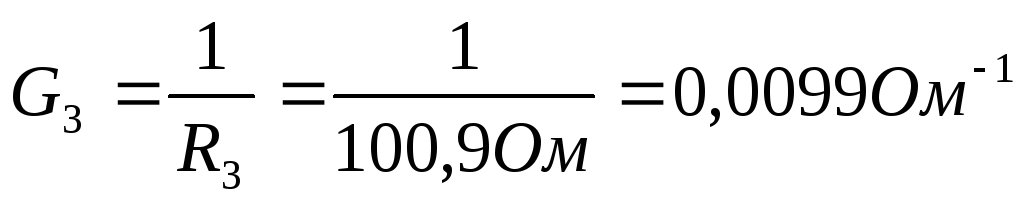
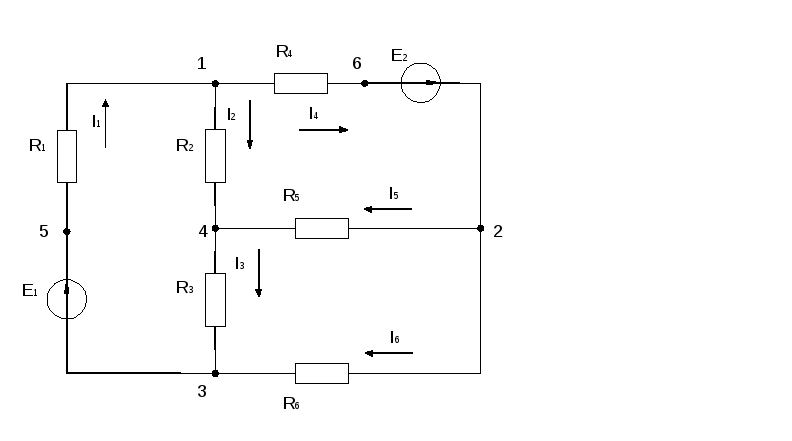
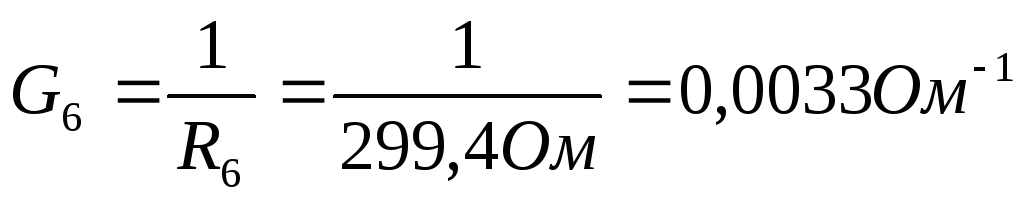
5) Согласно изображенной схеме соберем цепь. При сборке предусмотрим клеммы для подключения измерительных приборов. Амперметр подключим в соответствии с выбранными направлениями токов.
6) Измерим токи в ветвях и напряжения на всех резисторах.
I1, А
I2, А
I3, А
I4, А
I5, А
I6, А
0,121
0,057
0,078
0,0635
0,0205
0,0433
U1, В
U2, В
U3, В
U4, В
U5, В
U6, В
6,4
4,55
8,6
9,3
4,3
12,9
7) Приняв условно потенциал 3-го узла за нуль. Измерим потенциалы всех точек, указанных на схеме.
φ1, В
φ2, В
φ3, В
φ4, В
φ5, В
φ6, В
14
14,8
0
8,3
21
5,8
8) Рассчитаем токи в ветвях, используя метод контурных токов:
При использовании МКТ считается что в каждом независимом контуре протекает свой контурный ток и уравнения составляются по второму закону Кирхгофа для контурных токов.
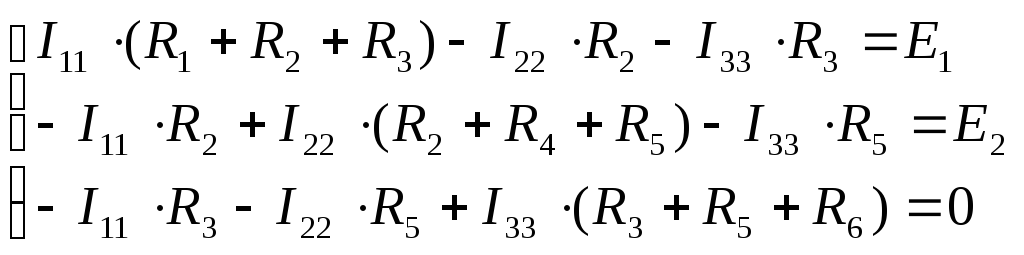 по
данным таблицы составим матрицу, за
неизвестные, приняв контурные токи.
по
данным таблицы составим матрицу, за
неизвестные, приняв контурные токи.
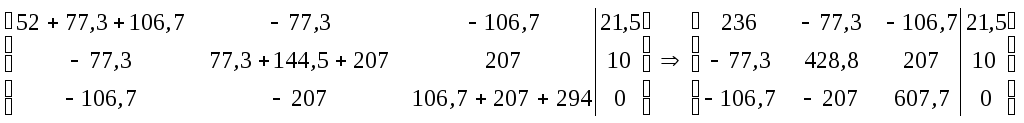
Решим данную матрицу методом Крамера
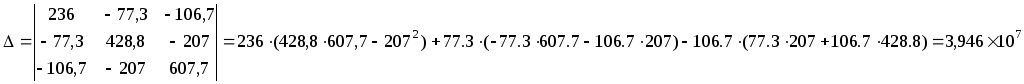
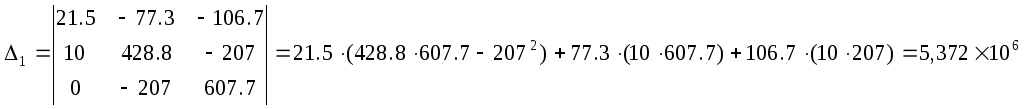
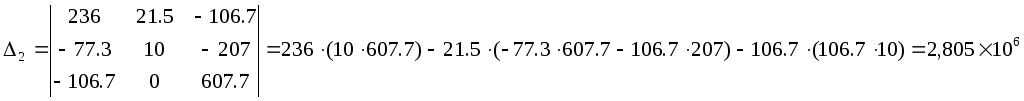

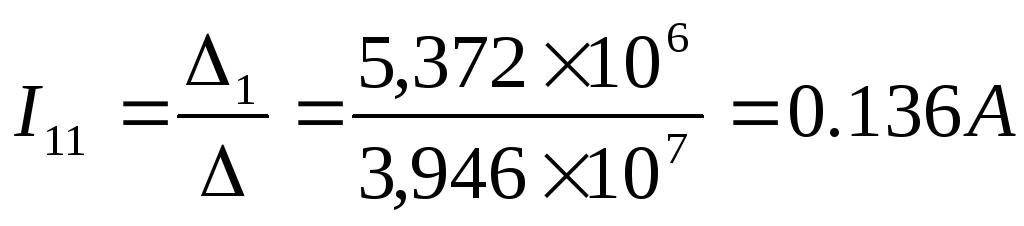
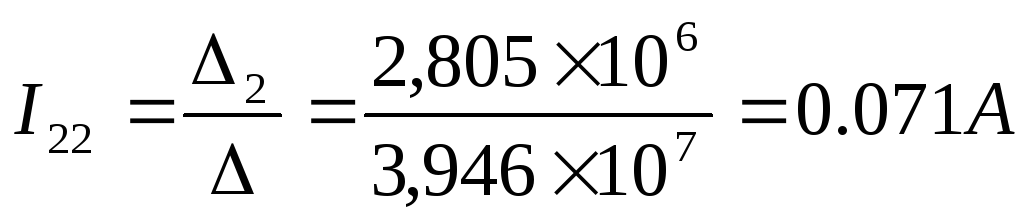
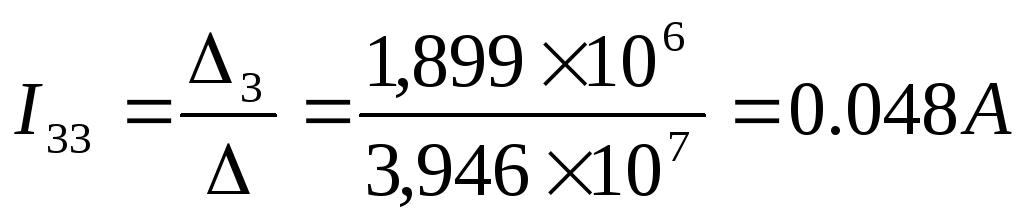
Теперь выразим токи в ветвях через контурные:
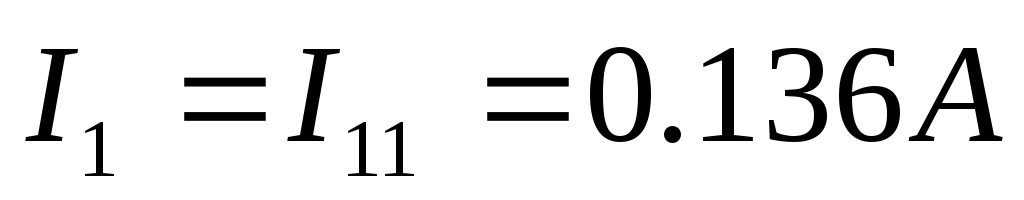
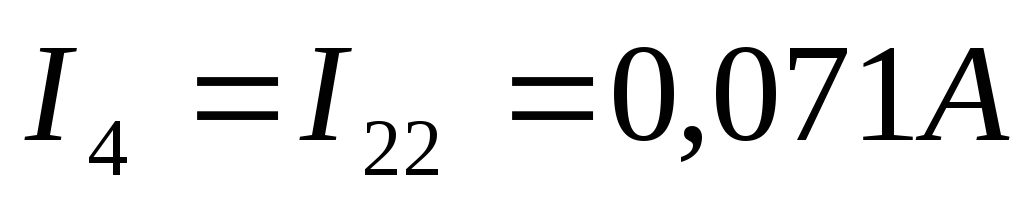
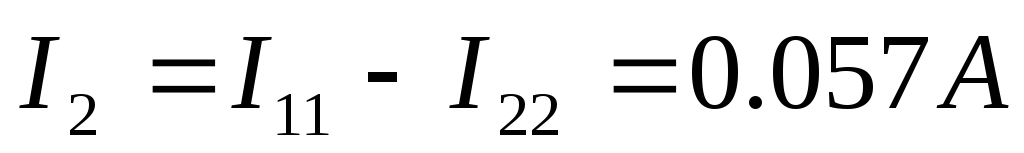
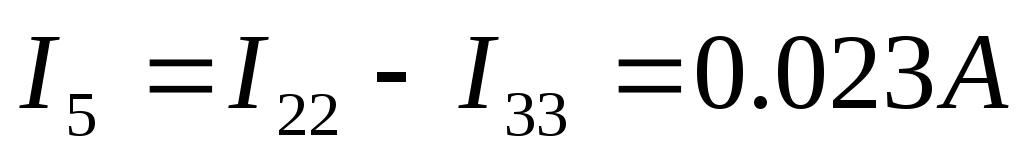
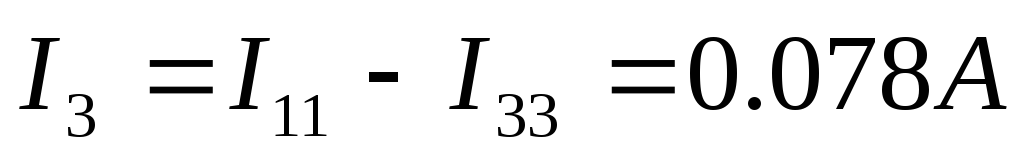
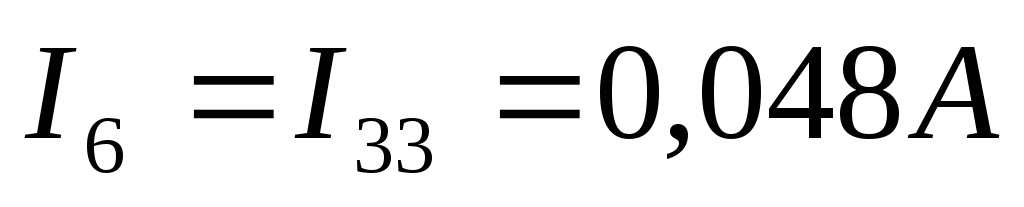
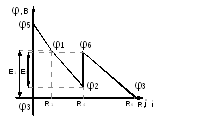
9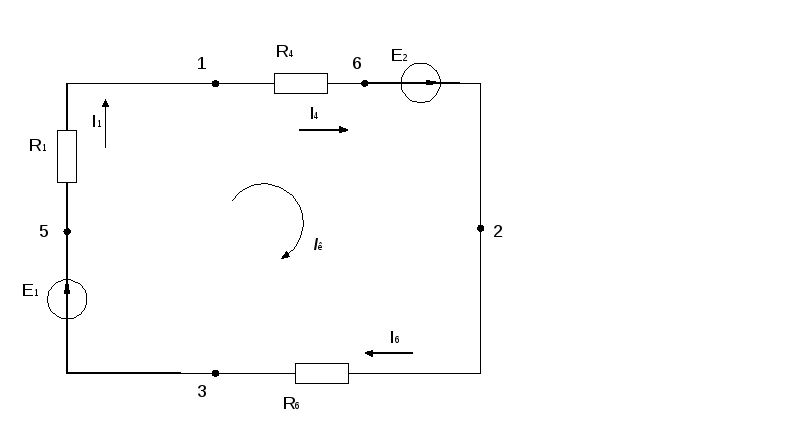 ) Построим потенциальную диаграмму для
внешнего контура исследуемой цепи:
) Построим потенциальную диаграмму для
внешнего контура исследуемой цепи:
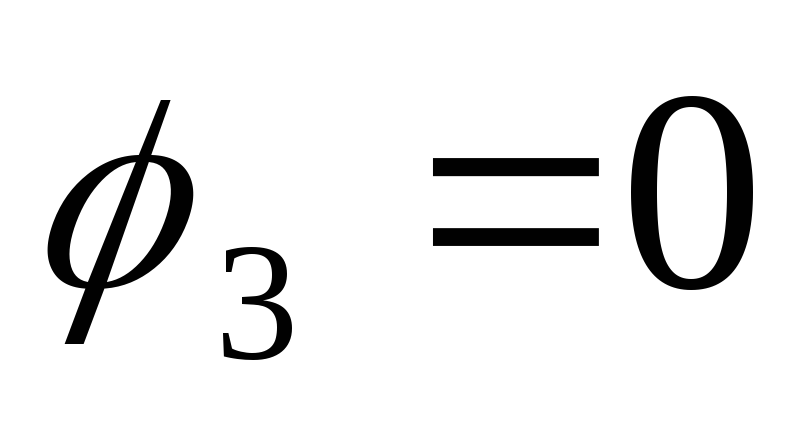
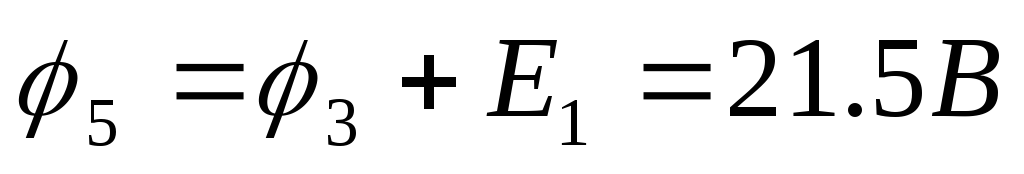
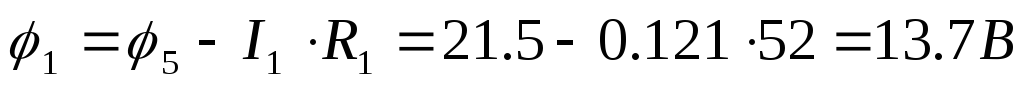
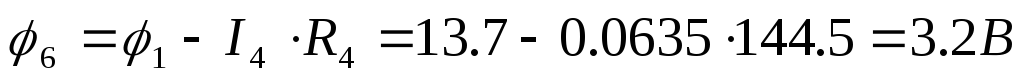
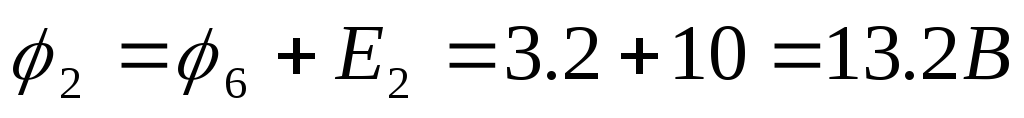
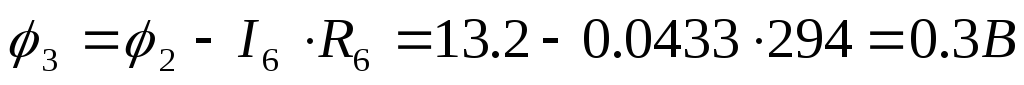
10) Проверим выполнение I – го закона Кирхгофа для данной цепи:
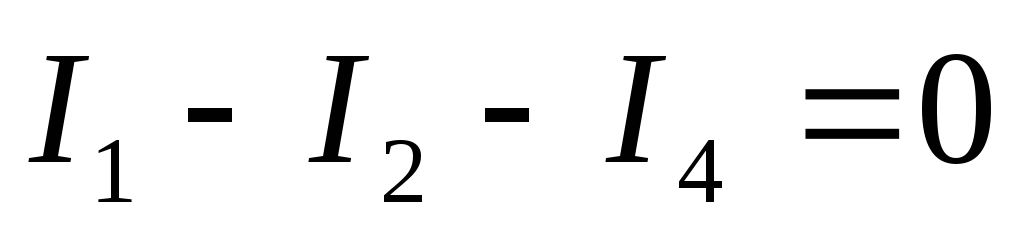
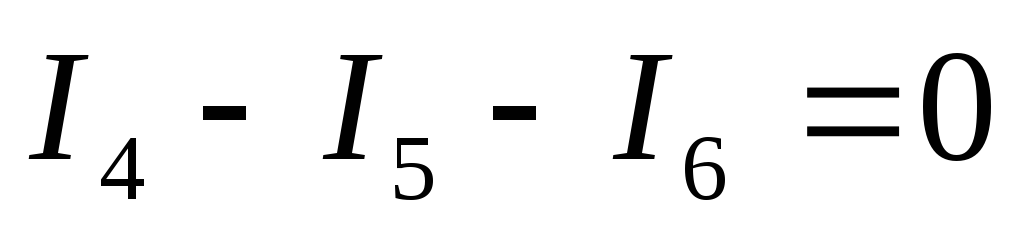
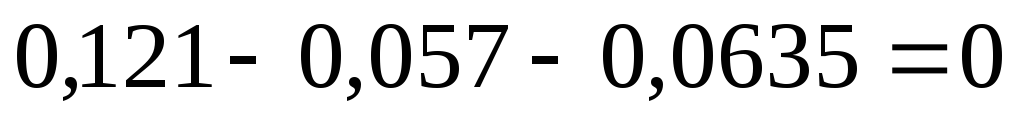
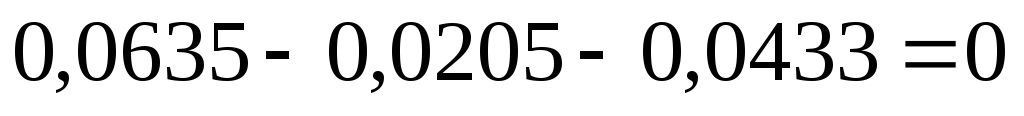
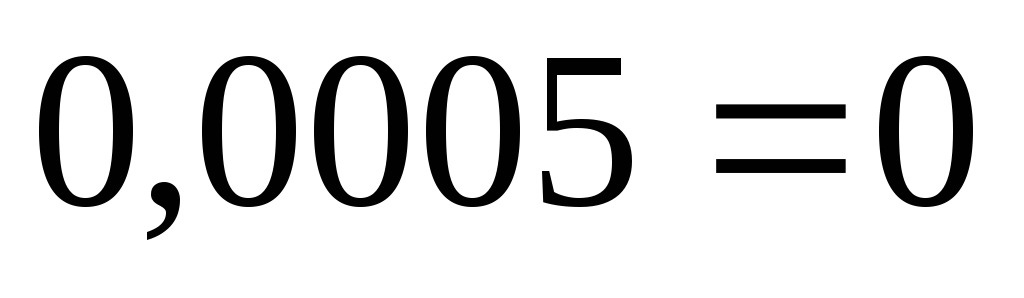
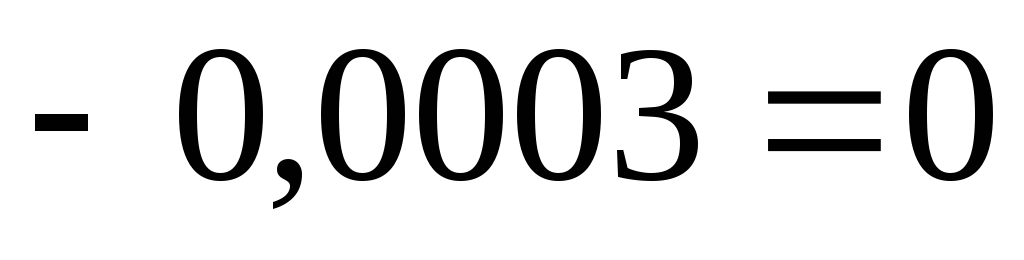
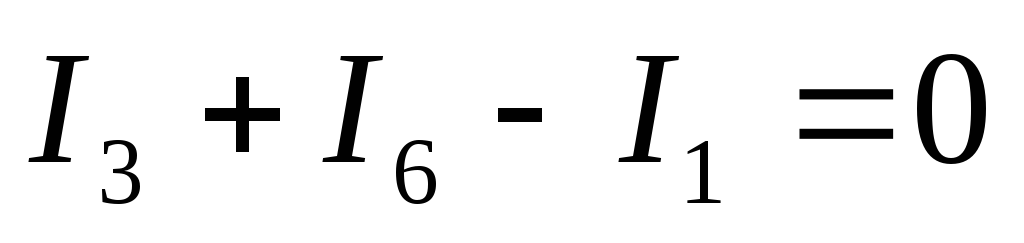
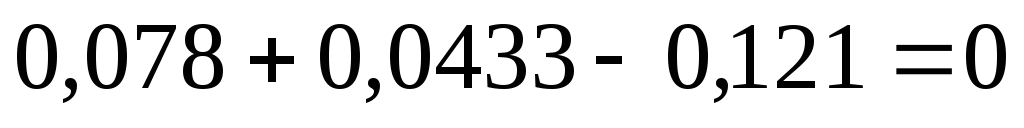
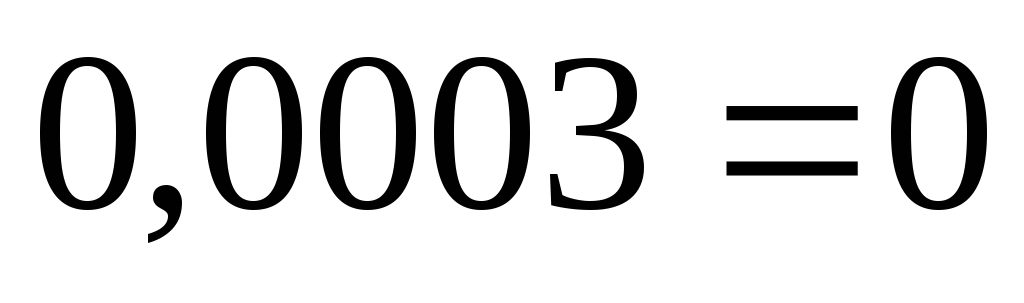
11) Рассчитаем для каждого узла погрешность измерения токов:
Узлы
1
2
3
Сумма токов, мА
0,5
0,3
0,3
Максимальный ток в узле, мА
121
63,5
121
Погрешность σ1, %
0,4
0,5
0,25
Расчеты будем проводить по следующей формуле:
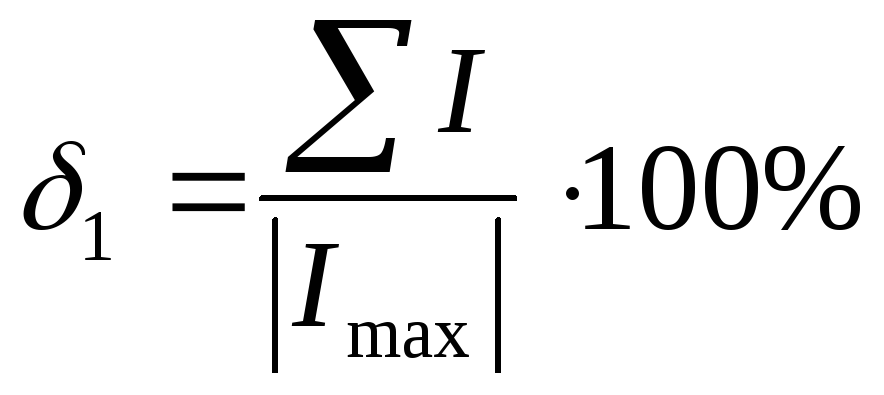
12) Проверим выполнение II – го закона Кирхгофа для данной цепи. Рассчитаем для каждого контура погрешность измерения напряжений по следующей формуле:
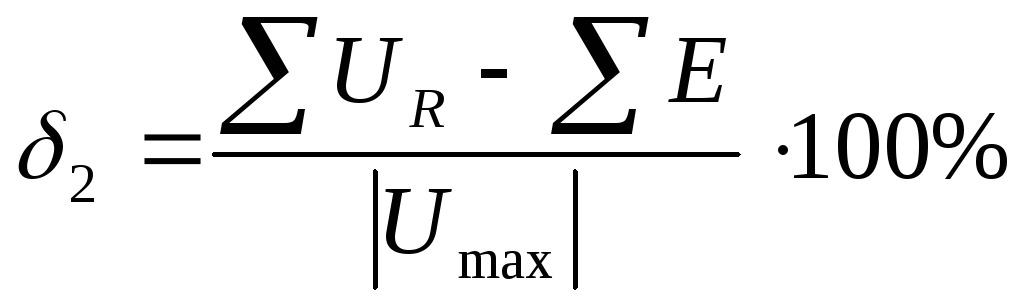
Результаты занесем в таблицу:
Контуры
1
2
3
Сумма напряжений, В
1,95
,95
1,95
Максимальное напряжение в контуре, В
8,6
9,3
12,9
Погрешность σ2, %
23
10
15
1: 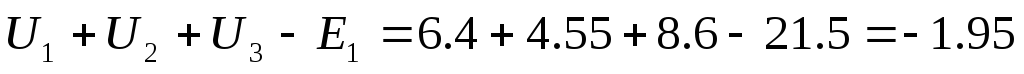 2:
2: 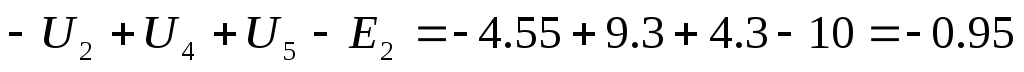
3: 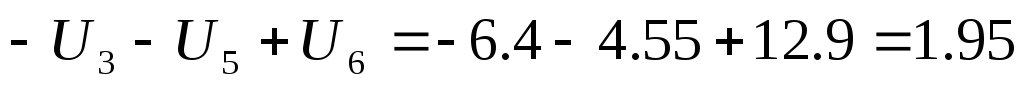
Задание 1. Измерение ЭДС источника тока вольтметром

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Общие сведения
Источники тока – это устройства, преобразующие различные виды энергии в электрическую энергию. Химические источники тока вырабатывают электрический ток за счёт энергии окислительно-восстановительных реакций химических реагентов (аккумуляторы, гальванические элементы). Физическими источниками тока называют устройства, преобразующие тепловую, механическую и электромагнитную энергию в электрическую энергию – электромашинные, термоэлектрические генераторы, солнечные батареи и др.
Источник постоянного тока имеет два вывода, между которыми создается определенная разность потенциалов – напряжение. При подключении к источнику внешней нагрузки, через нее начинает протекать электрический ток. В нагрузке, как правило, происходит преобразование получаемой от источника электрической энергии в другие ее виды: механическую (в электродвигателях), световую (в электролампах), тепловую (в электронагревателях) и т. д.
Напряжение на выводах источника тока всегда в той или иной степени зависит от мощности, отдаваемой в нагрузку.
Основными характеристиками источника тока являются электродвижущая сила Е и внутреннее сопротивление r.
Электродвижущая сила источника тока (ЭДС) есть работа сторонних (неэлектростатических) сил по перемещению единичного положительного заряда по замкнутой цепи:
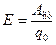
Сторонние силы, перемещая заряд q0 от отрицательного к положительному полюсу источника тока, совершают работу против электростатических сил. Поэтому ЭДС, в отличие от напряжения U, направлена от отрицательного полюса к положительному.
ЭДС измеряется в вольтах и численно равна напряжению на выводах источника при разомкнутой внешней цепи.
Внутреннее сопротивление источника тока обусловлено совокупностью физических эффектов, ограничивающих мощность, отдаваемую источником в нагрузку.
К таким эффектам относится, например: малая площадь контактирующих друг с другом химических реагентов в аккумуляторах; конечная скорость вращения лопастей турбогенераторов; ограниченное значение падающего потока световой энергии в солнечных батареях и др. Определенный вклад в ограничение отдаваемой мощности вносит и активное сопротивление отдельных конструктивных элементов источника тока.
Внутреннее сопротивление условно можно представить в виде резистора c сопротивлением r включенного последовательно с источником (рис. 1).
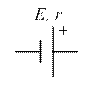 | 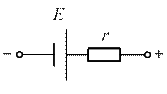 |
| а | б |
Рис. 1 – Графическое обозначение источника тока (а)
и его эквивалентная схема (б)
Однако, следует понимать, что внутреннее сопротивление не сосредоточено в каком-то одном элементе и является неотъемлемым конструктивным свойством источника тока как целого. Внутреннее сопротивление не может быть измерено непосредственно с помощью омметра и вычисляется по результатам косвенных измерений.
В большинстве случаев, внутреннее сопротивление можно считать постоянной, не зависящей от тока источника величиной.
Энергетическими характеристиками источника тока являются мощность и КПД:
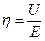
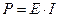
где U – напряжение на источнике; I – ток источника.
Задание 1. Измерение ЭДС источника тока вольтметром
ЭДС равна разности потенциалов на выводах источника тока при разомкнутой внешней цепи. Идеальный вольтметр, имеющий бесконечное входное сопротивление, покажет точное значение ЭДС источника в пределах класса точности.
Любой реальный вольтметр потребляет от источника некоторую мощность, необходимую для работы измерительной цепи и имеет конечное значение входного сопротивления.
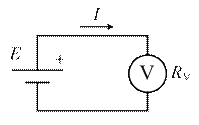
Рис. 2 – Измерение ЭДС вольтметром
Если к источнику тока подключить вольтметр (рис. 2), то в цепи потечет ток:
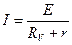
Этот ток создает на вольтметре падение напряжения:
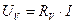
Подставив первое уравнение во второе и проведя элементарные преобразования, получим
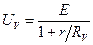
Показания вольтметра будут тем ближе к значению ЭДС, чем меньше отношение 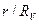 . Для измерений в пределах инженерной погрешности необходимо соблюдать условие
. Для измерений в пределах инженерной погрешности необходимо соблюдать условие 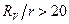 . Влияние входного сопротивления вольтметра на результат измерения можно считать несущественным при
. Влияние входного сопротивления вольтметра на результат измерения можно считать несущественным при 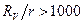 .
.
Для измерений в данной лабораторной работе используется цифровой мультиметр, имеющий в режиме вольтметра входное сопротивление RV = 1 МОм.
Определение ЭДС и внутреннего сопротивления источника электрической энергии
Цель работы:Научиться экспериментальным путем определять ЭДС, и внутреннее сопротивление источника тока.
Приборы и оборудование:Источники электрической энергии, амперметр (до 2А с делением до 0,1А), вольтметр (постоянного до 3А с делением до 0,3В), магазин (сопротивления до 10 Ом) ключ, соединительные провода.
ТЕОРИЯ:
Для поддержания тока в проводнике необходимо, чтобы разность потенциалов (напряжение) на его концах была неизменной. Для этого используется источник тока. Разность потенциалов на его полюсах образуется вследствие разделения зарядов на положительные и отрицательные. Работу по разделению зарядов выполняют сторонние силы (не электрического происхождения).
Величина, измеряемая работой, совершенной сторонними силами при перемещении единичного положительного электрического заряда внутри источника тока, называется электродвижущей силой источника тока (ЭДС) и выражается в вольтах.
Когда цепь замыкается, разделенные в источнике тока заряды образуют электрическое поле, которое перемещает заряды по внешней цепи; внутри же источника тока заряды движутся навстречу полю под действием сторонних сил. Таким образом, энергия, запасенная в источнике тока, расходуется на работу по перемещению заряда в цепи с внешним R и внутренним r сопротивлениями.
; или ;
ХОД РАБОТЫ
1. Собрать электрическую цепь как показано на схеме.
2. Измерить ЭДС источника электрической энергии замкнув его на вольтметр (схема).
3. Измерить силу тока и падение напряжения на заданном сопротивлении.
| № | Е | U | I | R | r | rcр |
| 1. | ||||||
| 2. | ||||||
| 3. |
4. Вычислить внутреннее сопротивление по закону Ома для всей цепи.
5. Произвести опыты с другими сопротивлениями и вычислить внутреннее сопротивление элемента.
6. Вычислить среднее значение внутреннего сопротивления элемента.
7. Результаты всех измерений и вычислений записать в таблицу.
8. Найти абсолютную и относительную погрешность.
9. Сделать вывод.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Укажите условия существования электрического тока в проводнике.
2. Какова роль источника электрической энергии в электрической цепи?
3. От чего зависит напряжение на зажимах источника электрической энергии?
ЛАБОРАТОРНАЯ РАБОТА № 7
ОПРЕДЕЛЕНИЕ ЭЛЕКТРОХИМИЧЕСКОГО ЭКВИВАЛЕНТА МЕДИ.
Цель работы: научиться на практике рассчитывать электрохимический эквивалент меди.
Оборудование:Весы с разновесом, амперметр, часы.,источник электрической энергии, реостат, ключ, медные пластины (электроды), соединительные провода, электролитическая ванна с раствором медного купороса.
Теория
Процесс, при котором молекулы солей, кислот и щелочей при растворении в воде или других растворителях распадаются на заряженные частицы (ионы), называется электролитической диссоциацией, получившийся при этом раствор с положительными и отрицательными ионами называется электролитом.
Если в сосуд с электролитом поместить пластины (электроды), соединенные с зажимами источника тока (создать в электролите электрическое поле), то положительные ионы будут двигаться к катоду, а отрицательные — к аноду. Следовательно, в растворах кислот, солей и щелочей электрический заряд будет перемещаться вместе с частицами вещества. У электродов при этом происходит окислительно-восстановительные реакции, при которых на них выделяется вещество. Процесс прохождения электрического тока через электролит, сопровождающийся химическими реакциями называется электролизом.
Для электролиза справедлив закон Фарадея: масса выделившегося вещества на электроде прямо пропорциональна заряду, прошедшему через электролит:
m=kq (1)
m=kIt (2)
где k-электрохимический эквивалент-количествовещества, выделенное при прохождении через электролит 1 Кл электричества. Измерив силу тока в цепи, время его прохождения и массу выделившегося на катоде вещества можно определить электрохимический эквивалент (1с выражается в кг/Кл).
k=m/It (3)
где m-масса меди, выделившейся на катоде; I-сила тока в цепи; t- время пропускания тока в цепи.
Содержание и метод выполнения работы.
Соберите электрическую цепь по схеме.
1. Одну из пластин, которая будет катодом, (если пластина мокрая, ее надо подсушить) тщательно взвесить с точностью до 10мг и записать результат в таблицу.
2. Вставить электрод в электролитическую ванну и составить электрическую цепь согласно схеме.
3. Отрегулировать реостатом ток, чтобы величина его не превышала 1А на 50см2 погруженной части катодной пластины.
4. Замкнуть цепь на 15-20 минут.
5. Разомкнуть цепь, вынуть катодную пластинку, смыть с нее остатка раствора и высушить под рукосушителем.
6. Взвесить высушенную пластину с точностью до 10мг.
7. Значение тока, время опыта, увеличение в массе катодной пластину записать в таблицу и определить электрохимический эквивалент.
| № опыта | I, А | Масса катода | Масса отлож. вещества | Время | Электрохимич. эквивалент | |
| до опыта | после опыта | |||||
Оценка погрешностей.
.
Относительная погрешность: .
Оцените в процессе проведения работы наибольшие допустимые ошибки при измерении массы, тока и времени. Вычислите относительную погрешность, найдите максимальную допустимую погрешность при определении k.
, следовательно .
После этого дается результат в виде: .
Сравните полученный результат с табличным.
Контрольные вопросы.
1. Что такое электролитическая диссоциация, электролиз?
2. До каких пор будет происходить электролиз медного купороса, если оба электрода медные? Оба электрода угольные?
3. Быстрее или медленнее пойдет электролиз, если один из медных электродов заменить цинковым?
эдс | Электроника как хобби
Это практический урок по теме «напряжение» в котором мы узнали каким образом появляется сама напряжённость.
Нам понадобится: 3 резистора на 25 Ом и 1 на 50 Ом, мультиметр и две батарейки типа АА.
И так, ЭДС создаёт напряжённость на участках цепи в зависимости от их сопротивления. Чем больше сопротивление участка тем большее напряжение достанется ему от ЭДС.
Значит, если в цепи все участки имеют равное сопротивление, то и их напряжённость будет равна.
- Соберите схему 1.
схема 1 Равная напряженность
Как видите все резисторы имеют номинал в 25 Ом и следовательно ЭДС должно создать на них одинаковую напряжённость.
Измерьте напряжение на каждом резисторе, оно должно быть одинаковым с учетом погрешности резисторов сопротивление которых не всегда идеально его номиналу.
2. Замените R3 на резистор в 50 Ом и измерьте напряжение на нём и на остальных резисторах. И тут уже более наглядно видна зависимость напряжённости участка от его сопротивления.
схема 2 Разная напряжённость участков цепи
3. Уберите из цепи один резистор в 25 Ом и измерьте напряжение на оставшихся резисторах. Так как резистор в 50 Ом вдвое больше по сопротивлению чем 25 Ом то и на нем будет вдвое больше напряжение.
схема 3 зависимость напряжения от сопротивления участка цепи
Вывод: ЭДС распределяется по цепи в зависимости от сопротивления её участков, чем большее сопротивление участка относительно других участков тем большее напряжение будет на нём.


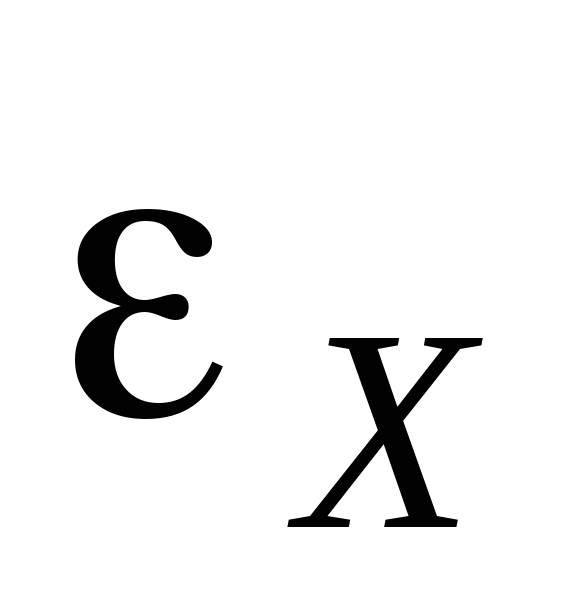 .
.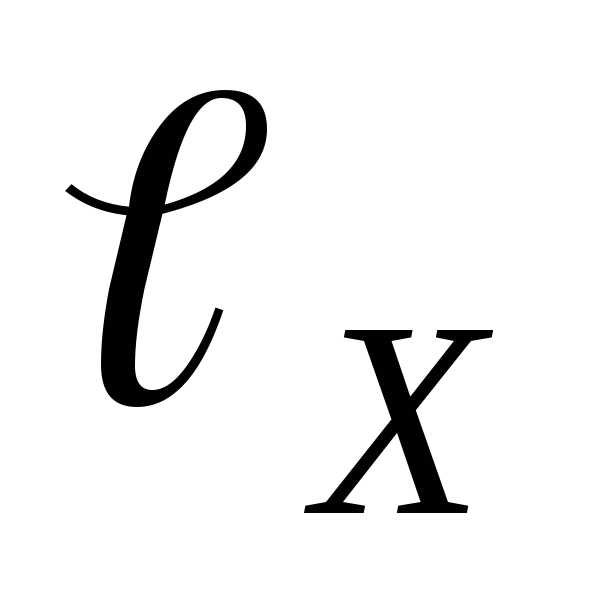 по сантиметровой линейке, на котором
происходит компенсация ЭДС неизвестного
источника тока. Результаты измерений
занести в табл. 1. Повторить измерения
5 раз согласно п.2.
по сантиметровой линейке, на котором
происходит компенсация ЭДС неизвестного
источника тока. Результаты измерений
занести в табл. 1. Повторить измерения
5 раз согласно п.2.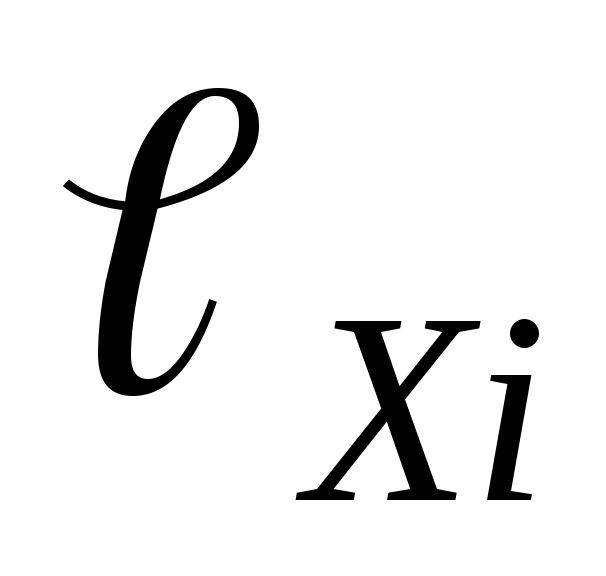 ,
см
,
см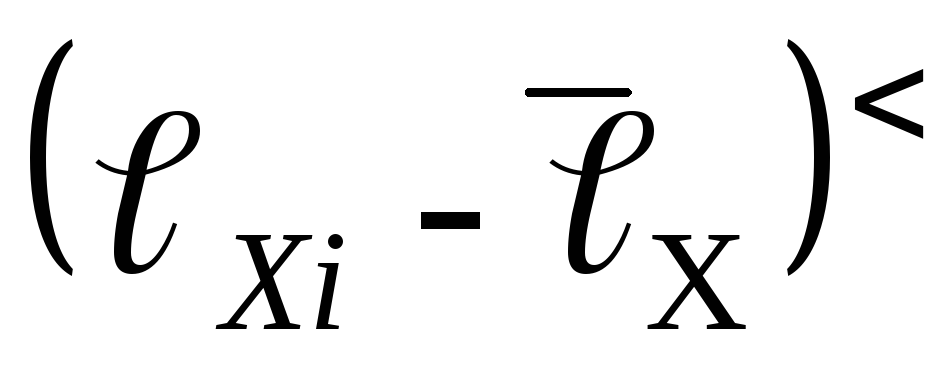
 ,
см
,
см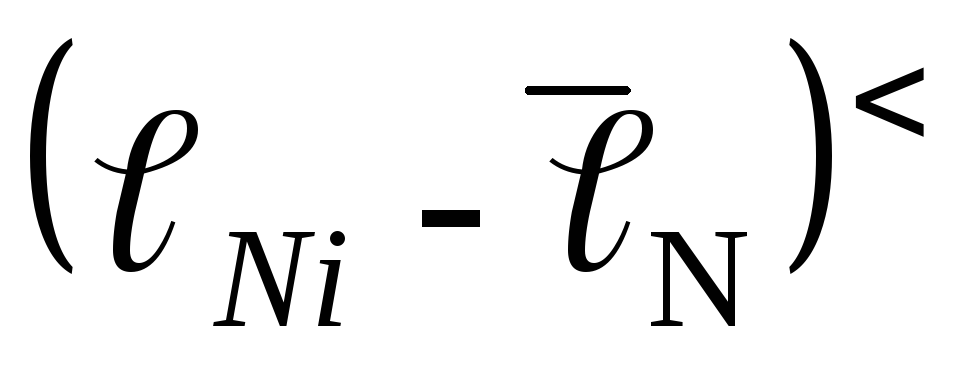
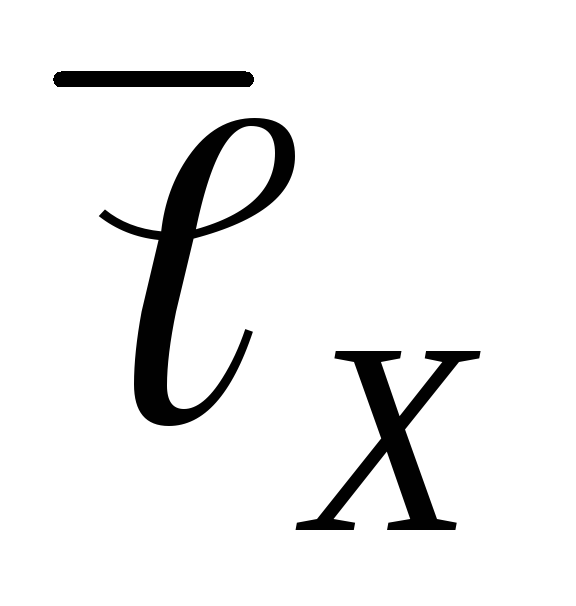 ,
см
,
см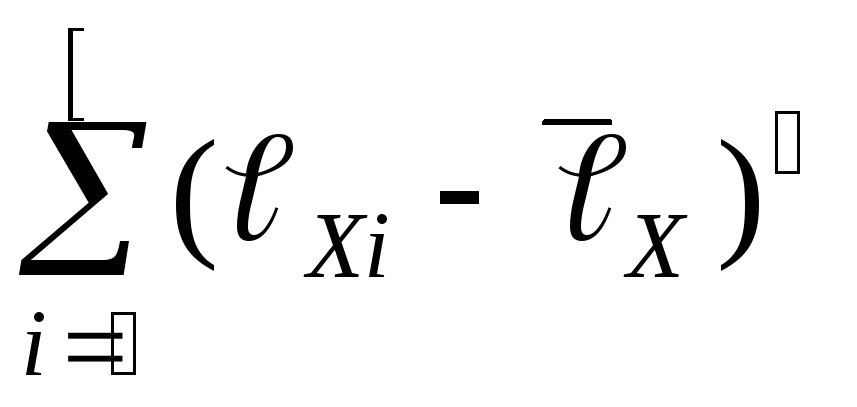
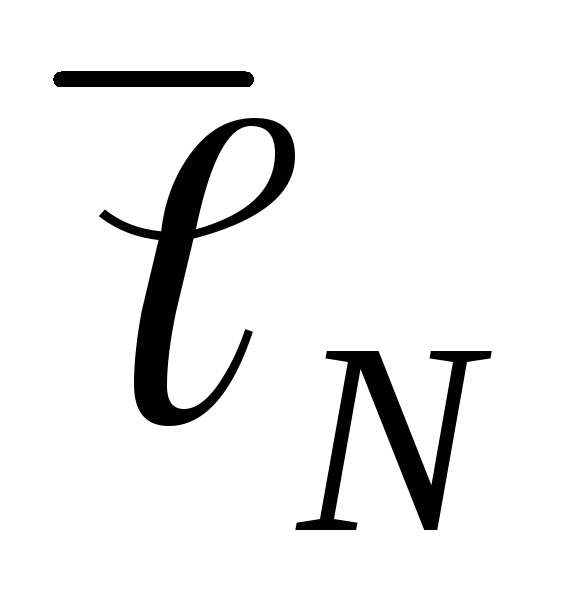 ,
см
,
см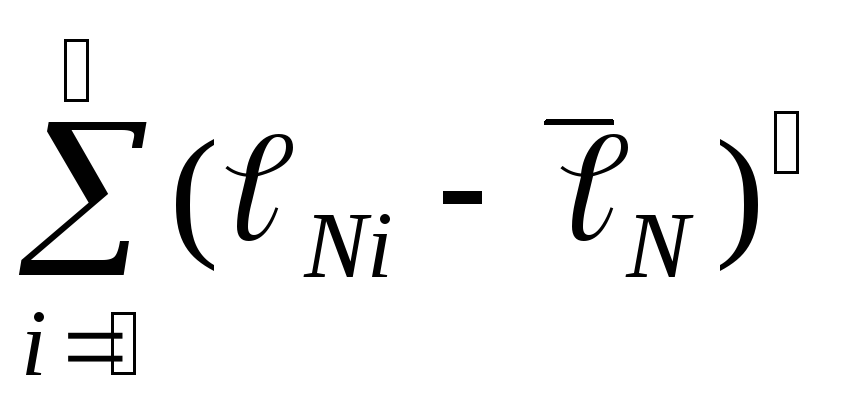
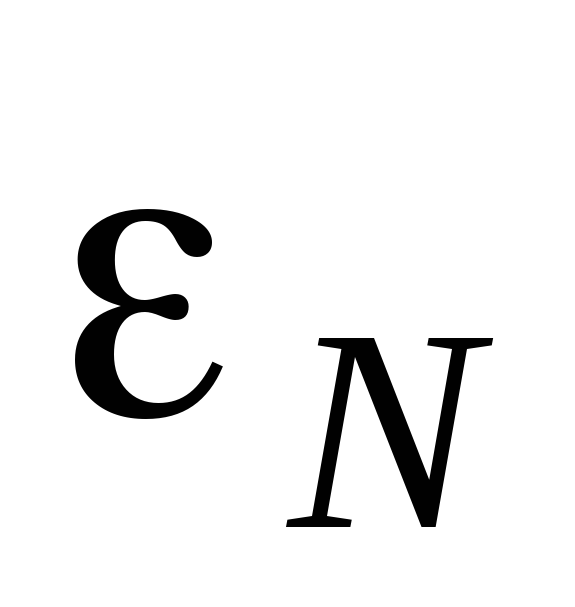 и повторить измерения по п.2, 3. Значение
длины участка
и повторить измерения по п.2, 3. Значение
длины участка 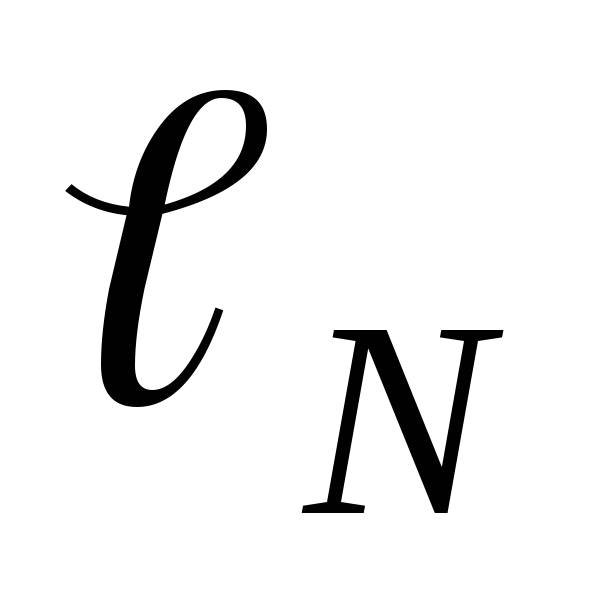 ,
на котором происходит компенсация ЭДС
нормального элемента, занести в таблицу
1.
,
на котором происходит компенсация ЭДС
нормального элемента, занести в таблицу
1.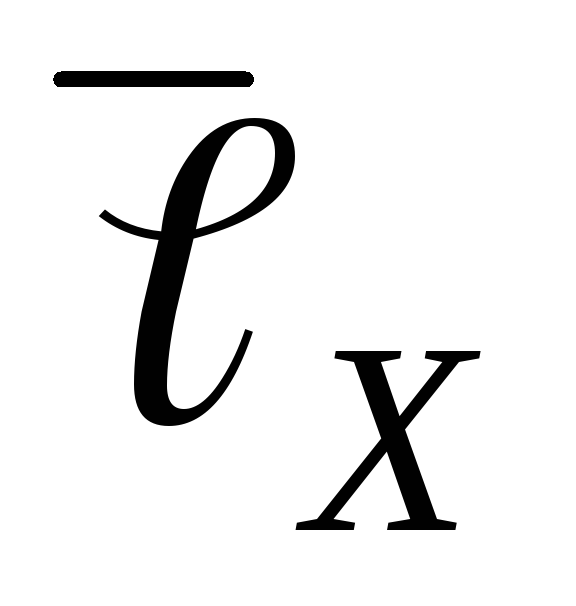 ,
, 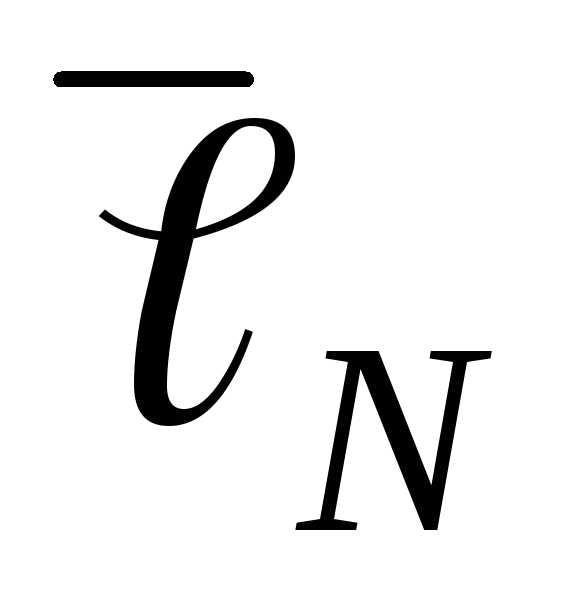 на которых
происходит компенсация ЭДС неизвестного
и нормального источника токов и средние
квадратичные отклонения от средних
значений этих величин.
на которых
происходит компенсация ЭДС неизвестного
и нормального источника токов и средние
квадратичные отклонения от средних
значений этих величин.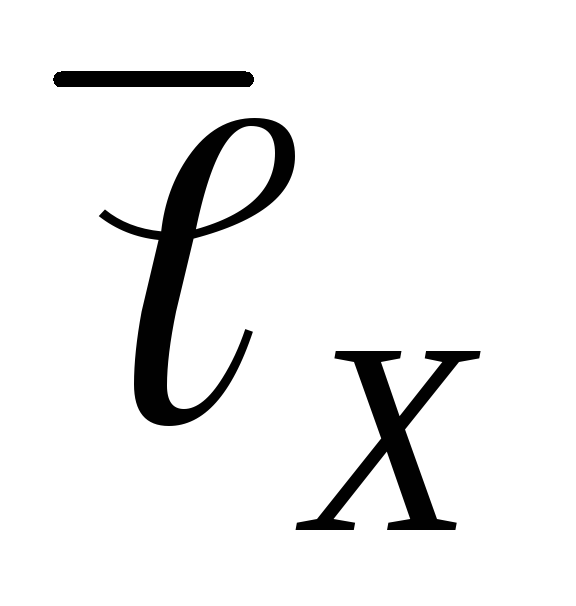 ,
, 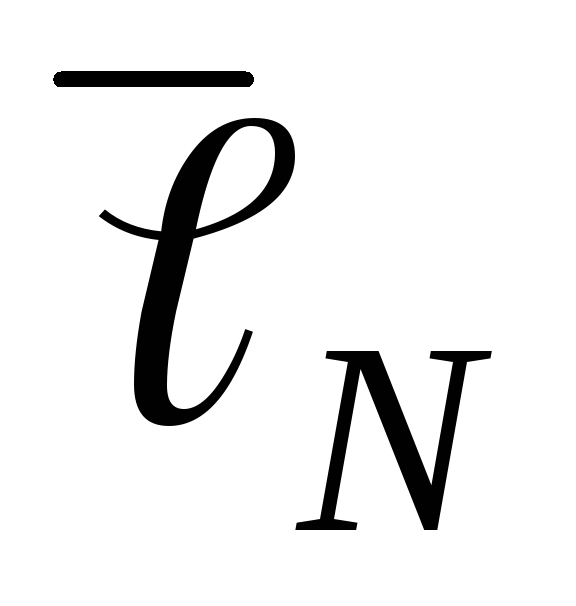 и
и 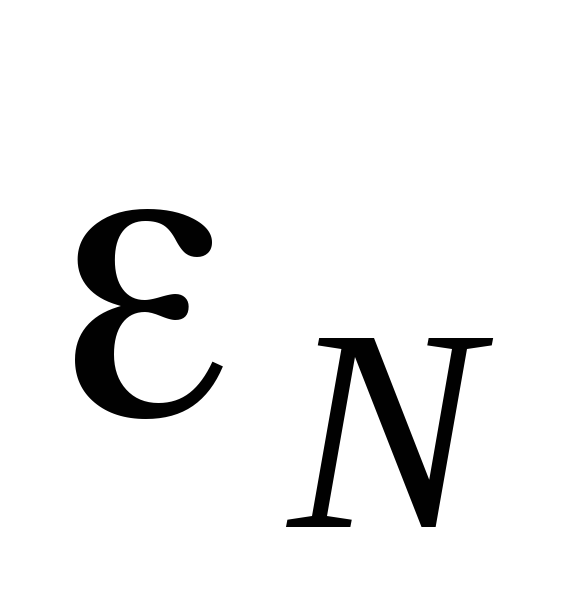 (см. на установке), определить средние
значения ЭДС неизвестного источника
тока.
(см. на установке), определить средние
значения ЭДС неизвестного источника
тока.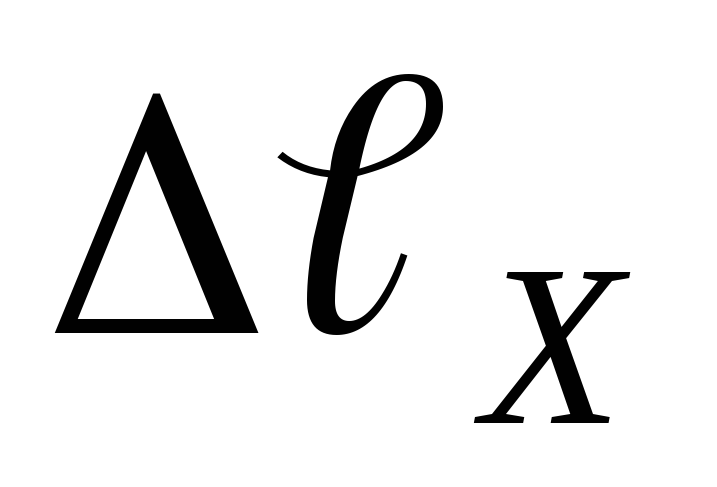 и
и 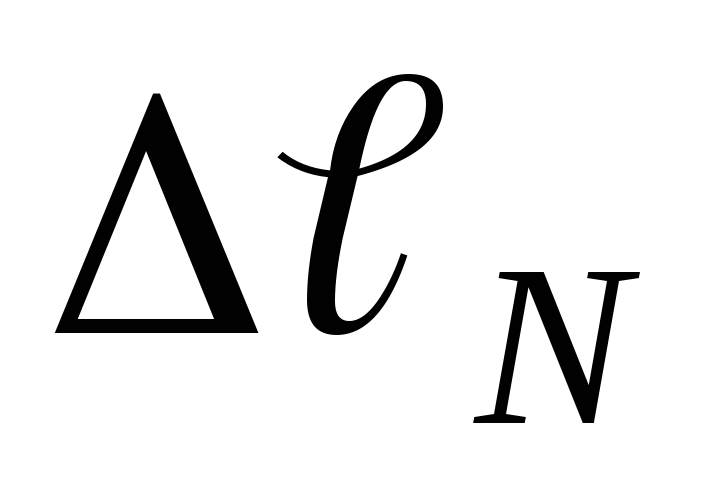 ,
на которых происходит компенсация ЭДС
неизвестного и нормального источников
тока по формулам
,
на которых происходит компенсация ЭДС
неизвестного и нормального источников
тока по формулам