создание, сложение, вычитание, умножение и деление
В простом смысле вектор можно рассматривать, как одномерный массив. Что касается Python, вектор – это одномерный массив списков. Он занимает элементы таким же образом, как и список Python.
Давайте теперь разберемся с созданием вектора в Python.
Содержание
- Создание вектора
- Основные операции с вектором
- 1. Выполнение операции сложения в векторе
- 2. Выполнение вычитания двух векторов
- 3. Выполнение умножения двух векторов
- 4. Выполнение операции деления
- 5. Векторное точечное произведение
Создание вектора
Модуль NumPy в Python используется для создания вектора. Мы используем метод numpy.array() для создания одномерного массива, то есть вектора.
Синтаксис:
numpy.array(list)
Пример 1: горизонтальный вектор.
import numpy as np lst = [10,20,30,40,50] vctr = np.array(lst) vctr = np.array(lst) print("Vector created from a list:") print(vctr)
Вывод:
Vector created from a list: [10 20 30 40 50]
Пример 2: вертикальный вектор.
import numpy as np
lst = [[2],
[4],
[6],
[10]]
vctr = np.array(lst)
vctr = np.array(lst)
print("Vector created from a list:")
print(vctr)
Вывод:
Vector created from a list: [[ 2] [ 4] [ 6] [10]]
Основные операции с вектором
Создав вектор, давайте теперь выполним некоторые базовые операции с этими векторами!
Вот список основных операций, которые можно выполнять с вектором:
- сложение;
- вычитание;
- умножение;
- деление;
- скалярное произведение и т.
 д.
д.
1. Выполнение операции сложения в векторе
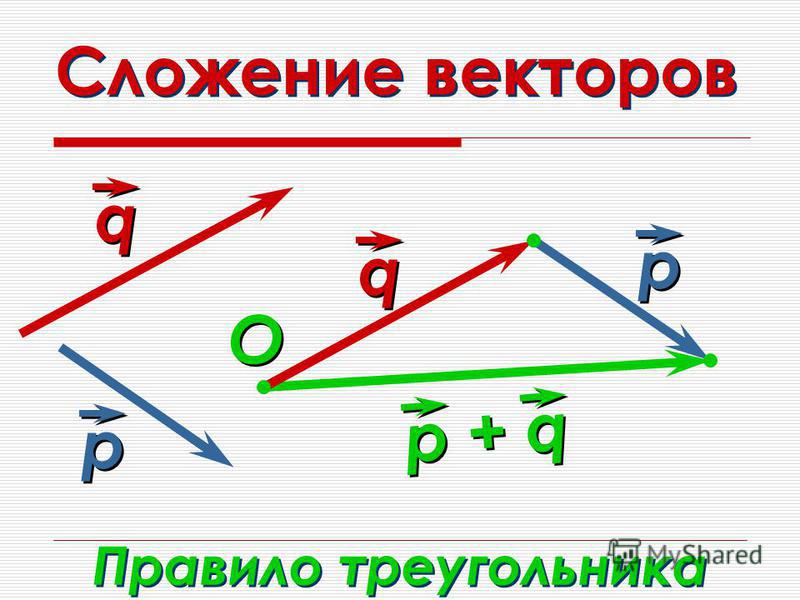
Ниже мы выполнили операцию сложения векторов над векторами. Операция сложения будет выполняться element-wise manner, т.е. поэлементно, и, кроме того, результирующий вектор будет иметь такую же длину, что и два аддитивных вектора.
Синтаксис:
vector + vector
Пример:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,2,3,4,5]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_add = vctr1+vctr2
print("Addition of two vectors: ",vctr_add)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Addition of two vectors: [11 22 33 44 55]
2.
 Выполнение вычитания двух векторов
Выполнение вычитания двух векторовАналогичным образом, при вычитании также будет применяться поэлементный метод, и в дальнейшем элементы вектора 2 будут вычитаться из вектора 1.
Давайте посмотрим на его реализацию.
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,2,3,4,5]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_sub = vctr1-vctr2
print("Subtraction of two vectors: ",vctr_sub)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Subtraction of two vectors: [ 9 18 27 36 45]
3. Выполнение умножения двух векторов
При умножении вектора элементы вектора 1 умножаются на элементы вектора 2, а вектор произведения имеет ту же длину, что и векторы умножения.
Попробуем представить себе операцию умножения:
x = [10,20] и y = [1,2] — два вектора. Таким образом, вектор произведения будет v [],
v [0] = x [0] * y [0] v [1] = x [1] * y [1]
Взгляните на приведенный ниже код:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,2,3,4,5]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_mul = vctr1*vctr2
print("Multiplication of two vectors: ",vctr_mul)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 2 3 4 5] Multiplication of two vectors: [ 10 40 90 160 250]
4. Выполнение операции деления
При делении результирующий вектор является значениями частного после выполнения операции деления над двумя векторами.
Для лучшего понимания рассмотрим приведенный ниже пример.
x = [10,20] и y = [1,2] – два вектора. Таким образом, результирующий вектор v будет таким:
v [0] = x [0] / y [0] v [1] = x [1] / y [1].
Давайте теперь реализуем вышеуказанную концепцию.
Пример:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [10,20,30,40,50]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_div = vctr1/vctr2
print("Division of two vectors: ",vctr_div)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [10 20 30 40 50] Multiplication of two vectors: [ 1 1 1 1 1 ]
5. Векторное точечное произведение
В векторном скалярном произведении мы поэлементно производим суммирование произведения двух векторов.
Давайте посмотрим ниже.
вектор c = x. у = (х1 * у1 + х2 * у2)
Пример:
import numpy as np
lst1 = [10,20,30,40,50]
lst2 = [1,1,1,1,1]
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_dot = vctr1.dot(vctr2)
print("Dot product of two vectors: ",vctr_dot)
Вывод:
Vector created from a list 1: [10 20 30 40 50] Vector created from a list 2: [1 1 1 1 1] Dot product of two vectors: 150
Как найти разность векторов — интернет энциклопедия для студентов
ФОРМУЛА
Чтобы найти разность векторов\(\
\overline{a}-\overline{b}
\), заданных на плоскости координатами \(\
\overline{a}=\left(a_{x} ; a_{y}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y}\right)
\) , необходимо вычесть из координат первого вектора соответствующие координаты второго, т.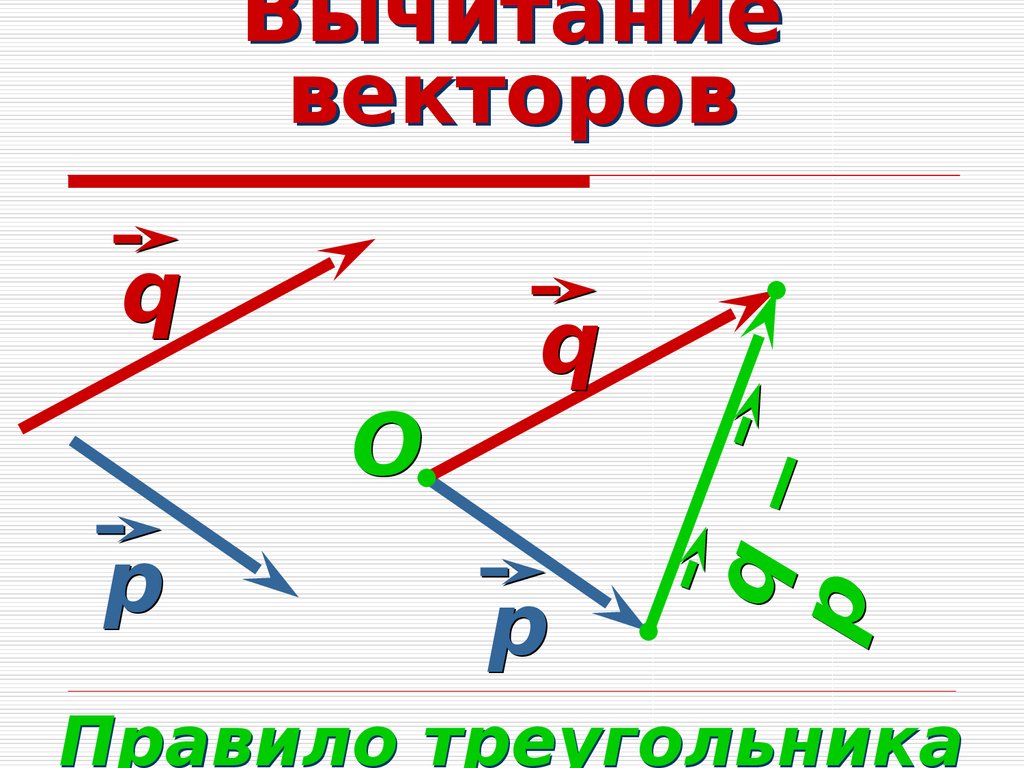
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y}\right) \)
Если векторы заданы в пространстве, то есть \(\ \tilde{a}=\left(a_{x} ; a_{y} ; a_{z}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \)тогда их различие
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}\right) \)
ПРИМЕР
ПРИМЕР
\(\ \overline{a}-\overline{b}-\overline{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)= \)
\(\ =(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Как найти сумму векторов Как найти вектор по точкам Периодические десятичные дроби Понятие десятичной дроби
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Вычитание векторов– объяснение и примеры
Существует много параллелей между скалярами и векторами, и вычитание векторов не является исключением.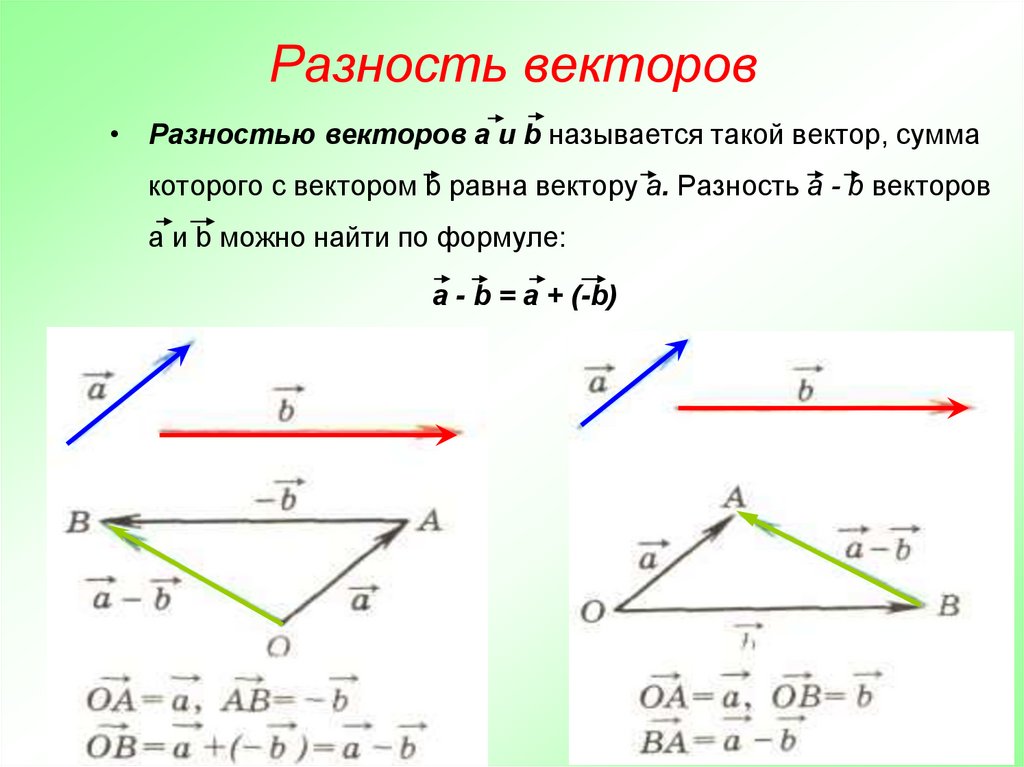 В частности, вычитание вектора:
В частности, вычитание вектора:
«Сложение вектора с отрицательным значением другого вектора».
Из приведенного выше определения ясно, что вычитание векторов означает просто сложение отрицательных векторов. Поэтому перед изучением вычитания векторов важно просмотреть отрицательные векторы.
Как известно, отрицательный вектор получается умножением данного вектора на -1. Это меняет направление вектора.
Допустим, — это вектор, направленный слева направо. Умножение вектора A на -1 дает нам -A, , что является отрицательным значением вектора A. Хотя величины двух векторов A и – A останутся прежними, отрицательный вектор – A будет направлен справа налево.
В этом разделе мы дополнительно обсудим следующие аспекты вычитания векторов:
- Как вычитать векторы
- Вычитание векторов графически
Как вычитать векторы
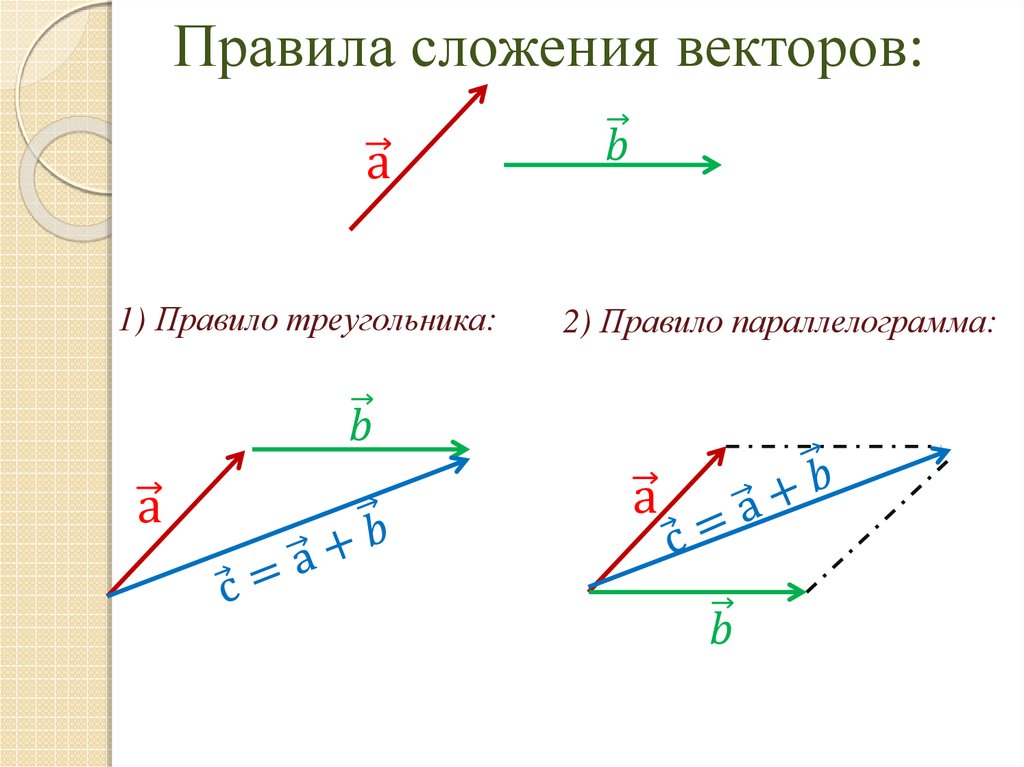
Мы знаем, что два вектора, A, и B, , можно сложить вместе, используя сложение векторов, и результирующий вектор можно сложить. как R = A + B . Точно так же, если нам нужно вычитание двух векторов, A и B математически выражается как:0005
как R = A + B . Точно так же, если нам нужно вычитание двух векторов, A и B математически выражается как:0005
R = A + (- B )
Таким образом, вычитание двух векторов аналогично сложению вектора A и отрицательного вектора B (т. е. B ). Векторы B и – B будут иметь одинаковую величину, но направление -B’ s будет противоположно направлению вектора B.
Вычитание векторов также работает, когда два вектора заданы в компонентной форме. или как векторы-столбцы. Если A = (ax1, ay1) и B = (bx1, by1), тогда разница между ними составляет:
R = A – B
Где горизонтальная и вертикальная составляющие результирующего вектора R могут быть выражены как :
Rx = ax1 – bx1
и
Ry = ay1 – by1.
Таким образом, результирующий вектор можно вычислить, просто вычислив разность соответствующих горизонтальных и вертикальных составляющих двух исходных векторов.
Вычитание векторов графически
Графически правило «голова к хвосту», используемое при сложении векторов, может быть адаптировано для вычитания векторов. Например, рассмотрим два вектора P и Q , как показано на рисунке ниже. Обратите внимание, что вектор – Q получается путем изменения направления Q.
Затем мы складываем векторы P и – Q , используя прямое правило:
Во-первых, нарисовать вектор P, , а затем поместите вектор – Q так, чтобы его хвост соединился с головой вектора P . Теперь, чтобы найти сумму P и – Q , нарисуйте результирующий вектор R так, чтобы он соединял хвост вектора P с головой вектора – Q , как показано на рисунке ниже.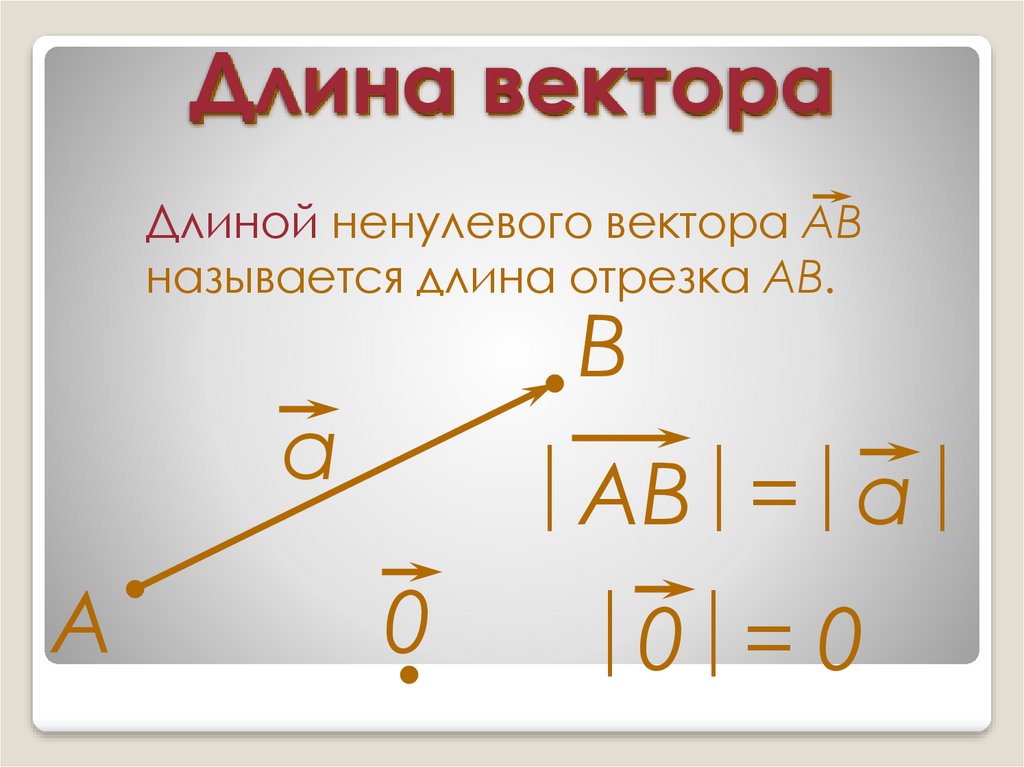 .
.
Математически результирующий вектор может быть выражен как:
R = P – Q
Примеры
В этом разделе мы будем практиковать вычитание векторов с различными примерами и их пошаговыми решениями, используя различные методы, описанные выше.
Пример 1
Графически вычтите заданные векторы A и B, показанные на изображении ниже, используя метод «голова к хвосту».
Решение
Сначала нарисуем отрицательную сторону вектора B , изменив его направление на противоположное, т. е. -B . Далее складываем векторы A и – B , применяя прямой метод.
Сначала мы размещаем заданные векторы A и – B так, чтобы хвост вектора -B соединился с головой вектора A , как показано на рисунке ниже. Далее, чтобы найти их сумму, рисуем результирующий вектор R так, чтобы он соединял хвост вектора A с головой вектора – B . Математически результирующая может быть выражена как:
Математически результирующая может быть выражена как:
R = A + (- B )
Пример 2
Учитывая два вектора AB = (3, 2) и до н.э. векторы. Затем определите модуль и угол результирующего вектора, заданного как:
S = AB + (- BC )
Сначала определите отрицательный вектор
0003 BC , умножив его на -1:
-BC = (-2, -2).
Далее, чтобы найти результирующий вектор S, Мы добавляем векторы AB и- до н.э. следующим образом:
S = AB + (- до н.э. , 2) + (-2, -2)
S = (1, 0).
Величина результирующего вектора S может быть найдена с помощью следующих уравнений:
| С 92
| С | = √ 1
| С | = 1 единица
Угол результирующего вектора S можно найти следующим образом:
Φ = tan -1 (Sy/Sx)
Φ = tan -1 (0/1)
φ = TAN -1 (0)
φ = 0 градусов
Пример 3
Учитывая два вектора S = 10 М, φ = 30 градусов и T = 20m, φ = 60 м. градусов. Вычтите два вектора, затем вычислите величину и угол результирующего вектора, используя метод компонентов.
градусов. Вычтите два вектора, затем вычислите величину и угол результирующего вектора, используя метод компонентов.
Решение
Let R Будьте полученным вектором, равным сумме данных векторов S и — T. Это может быть выражен в виде:
R = S +. (- T )
Чтобы использовать компонентный метод, мы сначала разобьем заданные векторы на их соответствующие горизонтальную и вертикальную составляющие:
Sx = S Cos Φ
Sx = 10 Cos 30 Примерно)
Аналогично, для вертикального компонента:
SY = S SIN φ
SY = 10 SIN 30
SY = 5 M
Далее мы вычисляем компоненты вектора T:
TX = T COS φ
TY = T SIN φ
Где
TX = 20 COS 60
TX = 10M
TY = 20 SIN 60
TY = 17,320 (приблизительно)
TY = 17,320 (приблизительно) мы можем вычислить вектор разности, вычислив разность отдельных компонентов x и y S и — T Vector AS:
RX = SX + ( -TX )
RX = 8,660 + (-10)
RX = -1,34 M
RX = -1,34 M
RX = -1,34 M
RY = SY + ( -Ty )
RY = 5 + (-17,32)
RY = -12,32 M
Результирующий вектор R может быть выражен в виде столбца.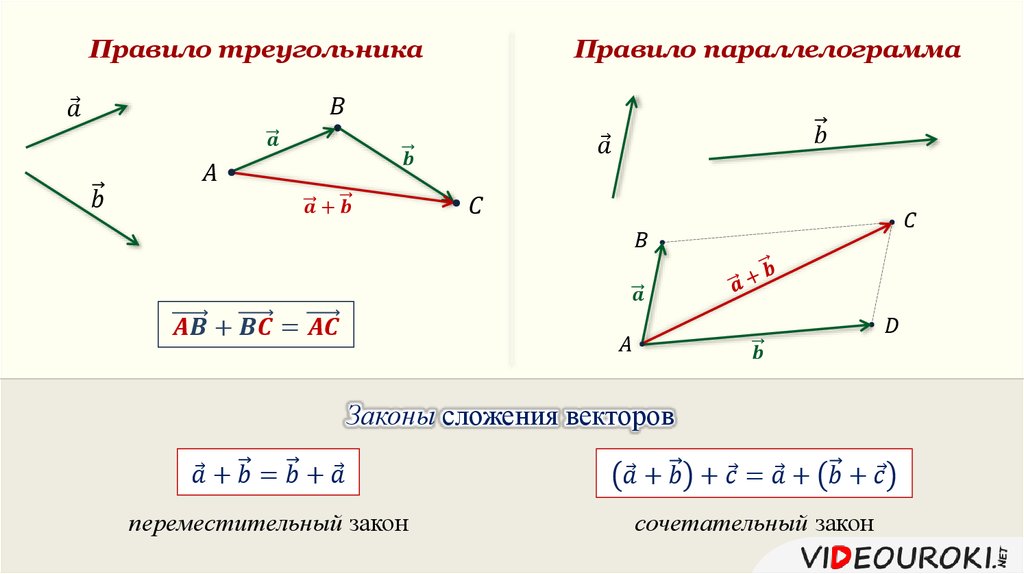 :
:
R = (-1,34, -12,32).
92|Р| = 12,392 M
φ = TAN -1 ( RY / RX )
φ = TAN -1 (-12,32 / -1,34)
φ = 83,79 град (приблизительно)
00055055555051, , результирующий вектор суммы может быть выражен как:R = 12,392 м, Φ = 83,79 градуса
Пример 4
Определить результирующий вектор суммы для двух векторов ) и – B = (2,-1).
Решение
Данные векторы уже находятся в своих составных формах, поэтому сначала определяем их углы.
для вектора A:
φ = TAN -1 ( AY / AX )
φ = TAN -1 (-1 / -5)
φ = 11,309 градуи (-1 / -5)
.
Для вектора – B:
Φ = tan -1 ( By / Bx )
Φ = tan -1 (-1/2)
φ = -26,56 градусов
Далее мы находим результирующий вектор, добавив отдельные компоненты:
S = A + ( — B )
SX = AX + ( — SX = AX + ( — SX = AX + ( — BX ) SX = -5 + 2 SX = -3 SY = AY + ( -BY ) SY = -1 -1 Sy = -2 Результирующий вектор 92 |С| = 3,605 единиц φ = TAN -1 ( SY / SX ) φ = TAN -1 (-2 / -3) φ = 33,69 градуса Таким Суммарный вектор может быть выражен как: S = 3,605 единиц, Φ = 33,69 градуса Пример 5 Учитывая три вектора ,-4), и Y = (2,6), определяют вектор Z = A – X – Y . Раствор Z = A – X – Y Z = (-20, -1) – (5, -4 5 Z) – (2, 00 6 Z) – 90 0 0 3 2 Z = (-27 , -3) M = 10 м прямо на восток и N = 15 м прямо на север. Вычтите два вектора, а затем задайте величину и угол результирующего вектора. Ответы R = M + (- N ) |R| = 18,027 м (Приблизительно) А угол: Φ = tan -1 (15/10) Φ = 56,30 градусов Таким образом, результирующий вектор R равен R = 18,027 м , Φ = 56,30 градусов на северо-восток. B = M — A B = (10, 2, 5)-(5, 0, -4) B = (10-5, 2- 0, 5+4) B = (5, 2, 9) В этом уроке мы рассмотрим, как вычесть два вектора на языке программирования R с помощью нескольких примеров. Вы можете использовать оператор Если векторы имеют одинаковую длину, соответствующие элементы (элементы с одинаковым индексом) вычитаются вместе. Следующее изображение иллюстрирует это. Если векторы имеют разную длину, более короткий вектор будет переработан, чтобы соответствовать длине более длинного вектора. На следующем изображении показано, как это делается. Рассмотрим несколько примеров вычитания двух векторов в R. Сначала вычтем два числовых вектора одинаковой длины с помощью оператора Вывод: Здесь мы вычитаем два вектора длины три. Теперь давайте вычтем два числовых вектора разной длины. Вывод: Здесь мы вычитаем вектор v2 (длины 5) из вектора v1 (длины 3). Более короткий вектор используется повторно, чтобы вычислить разницу с более длинным вектором. Значения 1 и 2 перерабатываются в индексы четыре и пять соответственно. Обратите внимание, что мы получаем предупреждение о том, что длина более длинного вектора не кратна длине более короткого вектора. Вот почему более короткий вектор не был полностью переработан, только первые два значения были переработаны, чтобы соответствовать длине более длинного вектора. Давайте посмотрим на другой пример. Здесь длина более длинного вектора кратна длине более короткого вектора. Вывод: Мы получаем результирующий вектор длины шесть (такой же, как длина более длинного вектора).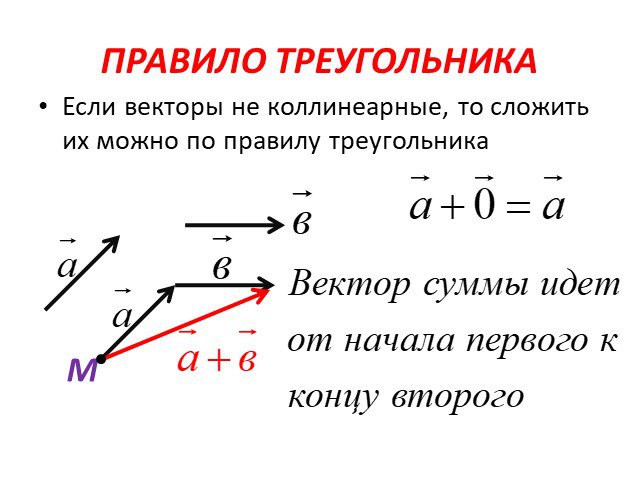
 Вычтите два вектора, затем задайте величину и угол результирующего вектора S .
Вычтите два вектора, затем задайте величину и угол результирующего вектора S .
Предыдущий урок | Главная страница | Следующий урок 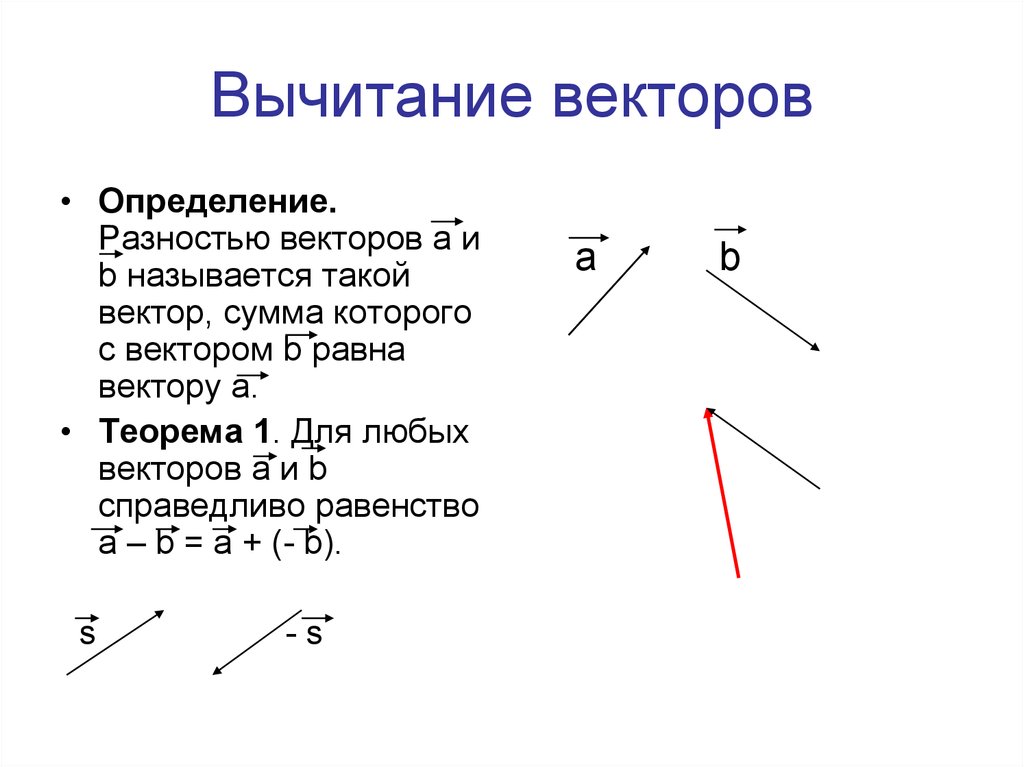 (приблизительно), а угол Φ = -29,05 градуса.
(приблизительно), а угол Φ = -29,05 градуса. Вычесть два вектора в R
Вычитание векторов в R
- для вычитания двух векторов в R. Арифметические операции над векторами выполняются поэлементно. То есть, когда вы вычитаете два вектора, соответствующие элементы вычитаются вместе.
Арифметические операции над векторами выполняются поэлементно. То есть, когда вы вычитаете два вектора, соответствующие элементы вычитаются вместе. Примеры
Вычитание двух числовых векторов одинаковой длины в R
- . # создаем два вектора
v1 <- с(1, 2, 3)
v2 <- с(0, 1, 2)
# вычесть v2 из v1
v <- v1 - v2
# отображаем результирующий вектор
печать (v)
[1] 1 1 1
 Результирующий вектор также имеет длину три, причем каждый элемент является результатом соответствующего поэлементного вычитания вектора v2 из вектора v1.
Результирующий вектор также имеет длину три, причем каждый элемент является результатом соответствующего поэлементного вычитания вектора v2 из вектора v1. Вычтите два числовых вектора разной длины в R
# создаем два вектора
v1 <- с(1, 2, 3)
v2 <- с(1, 1, 1, 1, 1)
# вычесть v2 из v1
v <- v1 - v2
# отображаем результирующий вектор
печать (v)
Предупреждающее сообщение в v1 - v2:
«более длинная длина объекта не кратна меньшей длине объекта»
[1] 0 1 2 0 1
 Вы можете видеть, что результирующий вектор имеет длину 5.
Вы можете видеть, что результирующий вектор имеет длину 5. # создаем два вектора
v1 <- с(1, 2, 3)
v2 <- с(1, 1, 1, 1, 1, 1)
# вычесть v2 из v1
v <- v1 - v2
# отображаем результирующий вектор
print(v)
[1] 0 1 2 0 1 2



 array(lst)
vctr = np.array(lst)
print("Vector created from a list:")
print(vctr)
array(lst)
vctr = np.array(lst)
print("Vector created from a list:")
print(vctr)
 д.
д.