момент инерции | это… Что такое момент инерции?
ТолкованиеПеревод
- момент инерции
3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси.
Источник: ГОСТ Р 52776-2007: Машины электрические вращающиеся. Номинальные данные и характеристики оригинал документа
2.25. Момент инерции — момент инерции (динамический) тела относительно оси, представляющий собой сумму (интегральную) произведений масс его отдельных частей на квадраты их расстояний от оси.
Примечание. Эта величина обозначается буквенным символом I и выражается в кг · м2.
Источник: ГОСТ 28173-89: Машины электрические вращающиеся. Номинальные данные и рабочие характеристики оригинал документа
Смотри также родственные термины:
3.
 18 момент инерции (динамический момент инерции) ротора:
18 момент инерции (динамический момент инерции) ротора:Определения термина из разных документов: момент инерции (динамический момент инерции) ротора
Источник: СТО 17330282.27.140.019-2008: Гидрогенераторы. Условия поставки. Нормы и требования
27. Момент инерции лопасти несущего винта относительно горизонтального и вертикального шарниров
Момент инерции лопасти
Момент инерции массы лопасти несущего винта и других агрегатов, совершающих вместе с лопастью маховое движение:
Определения термина из разных документов: Момент инерции лопасти несущего винта относительно горизонтального и вертикального шарниров
Источник: ГОСТ 22499-77: Аппараты винтокрылые. Механика полета в атмосфере. Термины, определения и буквенные обозначения оригинал документа
3.8 момент инерции механизма : Приведенный к валу электродвигателя момент инерции сочлененного с ним механизма.

Определения термина из разных документов: момент инерции механизма
Источник: СТО 70238424.29.160.30.002-2009: Электродвигатели. Организация эксплуатации и технического обслуживания. Нормы и требования
28. Момент инерции несущего винта
Jω
Суммарный момент инерции массы лопастей и всех кинематически связанных с ним агрегатов, приведенный к оси вращения несущего винта.
Примечание. Кинематически связанные с несущим винтом агрегаты определяются в каждом конкретном случае
Определения термина из разных документов: Момент инерции несущего винта
Источник: ГОСТ 22499-77: Аппараты винтокрылые. Механика полета в атмосфере. Термины, определения и буквенные обозначения оригинал документа
Момент инерции поперечного сечения распорного кольца, мм4 (см4)
Iк
Определения термина из разных документов: Момент инерции поперечного сечения распорного кольца, мм4
Источник: ГОСТ 25859-83: Сосуды и аппараты стальные.
 Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа
Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа74 момент инерции электропривода: Сумма моментов инерции всех движущихся масс электропривода при приведении их к скорости элемента приведения электропривода
Определения термина из разных документов: момент инерции электропривода
Источник: ГОСТ Р 50369-92: Электроприводы. Термины и определения оригинал документа
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
Игры ⚽ Нужно сделать НИР?
- момент затяжки М
- момент инерции (динамический момент инерции) ротора
Полезное
Момент инерции маятника Боба Калькулятор
✖Масса тела – это количество вещества в теле независимо от его объема или действующих на него сил.ⓘ Масса тела [M] | Ассарий (Библейская Roman)Масс-атомная единицаАттограммаЭвердюпуа драмБекан (Библейский иврит)КаратсантиграммДалтонДекаграммДециграммDenarius (Библейская Roman)Didrachma (Библейский греческий)Драхма (Библейский греческий)Масса электрона (Rest)ExagramFemtogramГаммаGerah (Библейский иврит)ГигаграммГигатонназернаграммГектограммЦентнер (Великобритания)Центнер (США)Масса ЮпитераКилограммКилограмм-сила в квадрате в секунду на метркилофунтКилотонна (метрическая)ЛЕПТОН (Библейская Roman)Масса ДейтронаМасса ЗемлиМасса нейтонаМасса протонаМасса СолнцамегаграммМегатоннамикрограммМиллиграммMina (Библейский греческий)Mina (Библейский иврит)масса мюонананограммунцияПеннивейтPetagramпикограммамасса ПланкафунтФунт (Troy или фармацевтическое)ПаундалФунт-сила в квадрате в секунду на футQuadrans (Библейская Roman)Четверть (Великобритания)Четверть (США)Квинтал (метрическая система)Скрупл (аптекарь)Шекель (библейский иврит)тихоходСолнечная массаСтоун (Великобритания)Камень (США)Талант (Библейский греческий)Талант (Библейский иврит)ТераграммаТетрадрахма (Библейский греческий)Тон (анализ) (Великобритания)Тон (анализ) (США)Тон (длинный)Тон (метрической размерности)Тон (короткометражный)Тонна | +10% -10% | |
✖Длина струны — это измерение длины нити маятника. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Момент инерции — это мера сопротивления тела угловому ускорению относительно данной оси. |
Грамм квадратный сантиметрГрамм квадратный миллиметрКилограмм квадратный сантиметрКилограмм квадратный метрКилограмм квадратный миллиметрКилограмм-сила, метр в квадрате, секундаУнция квадратный дюймУнция-сила, дюйм в квадрате, секундаФунт квадратный футфунт квадратный дюймФунт-сила-фут-квадрат-секундаФунт-сила, дюйм в квадрате, секундаСлаг Квадратный фут |
⎘ копия |
👎
Формула
сбросить
👍
Момент инерции маятника Боба Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.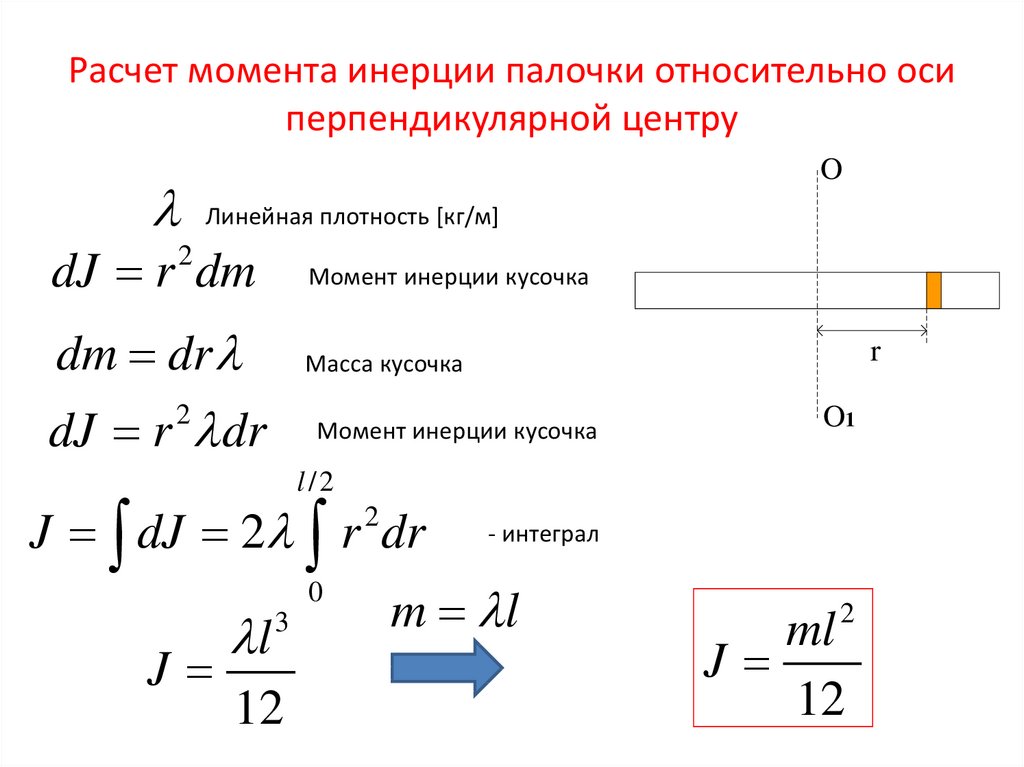 2)
2)
Проще говоря, что такое момент инерции?
Момент инерции, в физике, количественная мера инерции вращения тела — т. Е. Сопротивление, которое тело демонстрирует тому, чтобы его скорость вращения вокруг оси изменялась под действием крутящего момента (силы поворота). Ось может быть внутренней или внешней и может быть или не быть фиксированной.
Share
Copied!
вращательная динамика — Измеряется ли момент инерции массы до интересующей точки или всего объекта?
Задать вопрос
спросил
Изменено 5 лет, 5 месяцев назад
Просмотрено 126 раз
$\begingroup$
Я пытаюсь рассчитать количество кинетической энергии, которое будет иметь точка деревянного прямоугольника после того, как она раскачается и ударится обо что-то.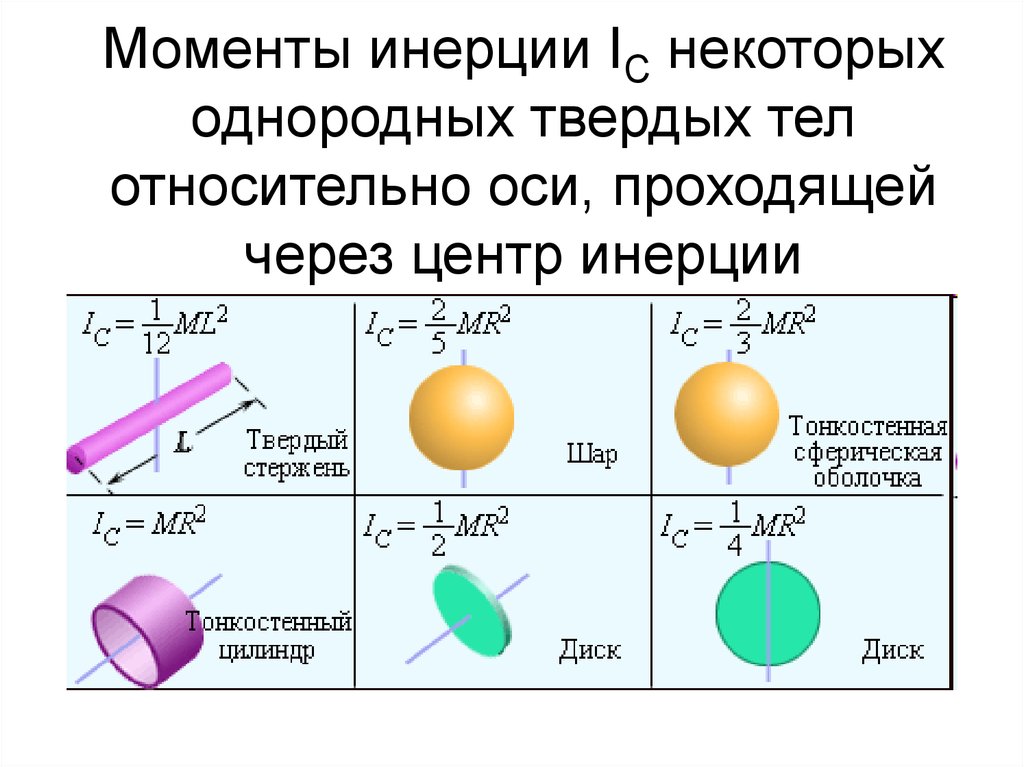
- динамика вращения
- момент инерции
$\endgroup$
$\begingroup$
Первое уравнение, которое у вас есть, это кинетическая энергия всего прямоугольника, и это уравнение нам нужно. Зная кинетическую энергию прямоугольника, вы можете найти угловую скорость каждой точки прямоугольника, поскольку они имеют одинаковую угловую скорость. Чтобы найти линейную скорость точки, расположенной на радиусе R от оси вращения, достаточно умножить угловую скорость на R.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Момент инерции
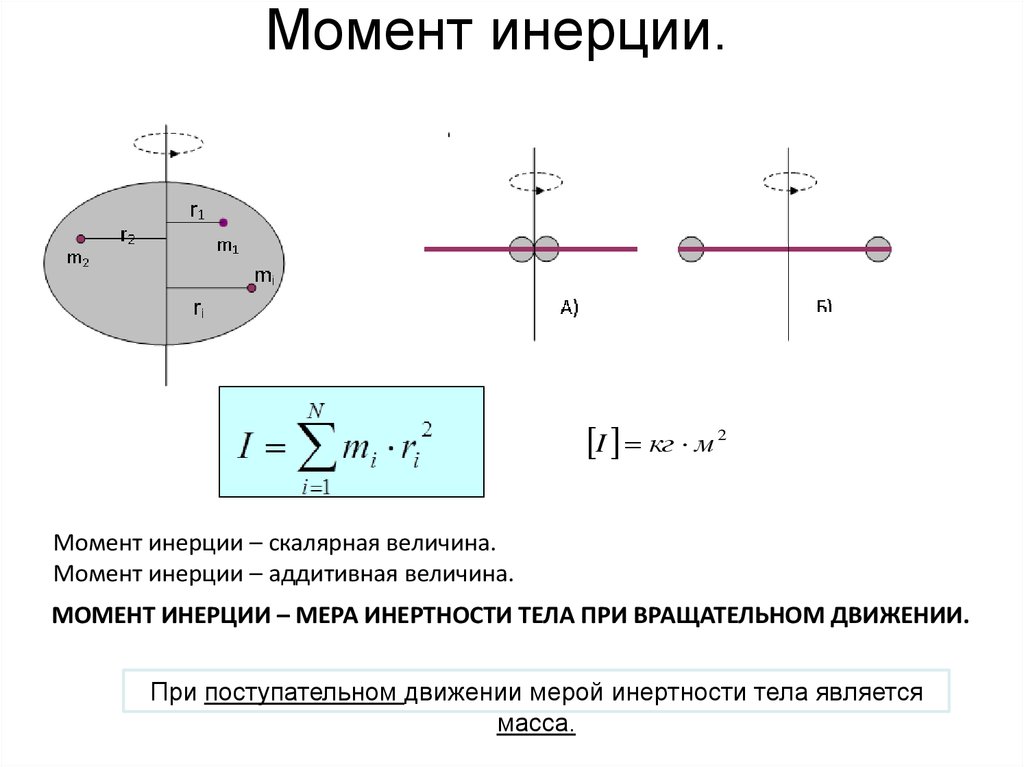
Момент инерции или момент инерции массы — это скалярная величина, которая измеряет сопротивление вращающегося тела вращению. Чем выше момент инерции, тем более устойчиво тело к угловому вращению. Тело обычно состоит из нескольких мелких частиц, образующих всю массу. Массовый момент инерции зависит от распределения каждой отдельной массы относительно перпендикулярного расстояния к оси вращения. Однако в физике мы обычно предполагаем, что масса объекта сосредоточена в одной точке, называемой центром масс.
Уравнение момента инерции
Математически момент инерции может быть выражен через его отдельные массы как сумма произведения каждой отдельной массы и квадрата перпендикулярного расстояния до оси вращения. Вы можете увидеть это в уравнении ниже. I — момент инерции, измеренный в килограммах на квадратный метр (кг·м2), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м).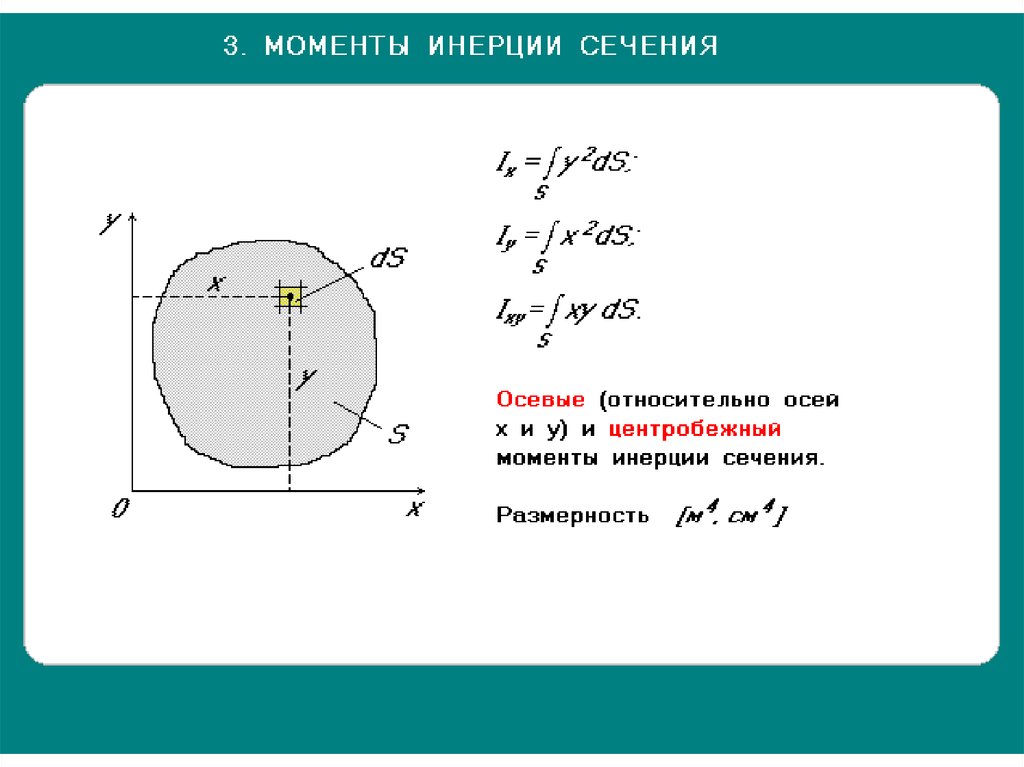
Мы также можем использовать приведенное ниже уравнение для объекта, масса которого предполагается сосредоточенной в одной точке. На изображении показано расстояние оси вращения r.
Диаграмма, показывающая расстояние до оси вращения r, Oğulcan Tezcan — StudySmarter Originals
Откуда взялся момент инерции?
Закон Ньютона гласит, что линейное ускорение объекта линейно пропорционально суммарной силе, действующей на него, когда масса постоянна. Мы можем сформулировать это с помощью приведенного ниже уравнения, где Ft — результирующая сила, m — масса объекта, а at — поступательное ускорение.
Точно так же мы используем крутящий момент для вращательного движения, который равен произведению вращательной силы и перпендикулярного расстояния до оси вращения. Однако поступательное ускорение при вращательном движении равно произведению углового ускорения α на радиус r.
Момент инерции является величиной, обратной массе во втором законе Ньютона для линейного ускорения, но он применяется к угловому ускорению. Второй закон Ньютона описывает момент силы, действующий на тело, который прямо пропорционален моменту инерции массы тела и его угловому ускорению. Как видно из приведенного выше вывода, крутящий момент T равен произведению момента инерции I и углового ускорения α.
Второй закон Ньютона описывает момент силы, действующий на тело, который прямо пропорционален моменту инерции массы тела и его угловому ускорению. Как видно из приведенного выше вывода, крутящий момент T равен произведению момента инерции I и углового ускорения α.
Чем больше толщина, тем больше момент инерции.
Примеры расчета момента инерции
Тонкий диск диаметром 0,3 м и суммарным моментом инерции 0,45 кг·м2 вращается вокруг своего центра масс. На внешней части диска находятся три камня массой 0,2 кг. Найдите полный момент инерции системы. Решение. Радиус диска равен 0,15 м. Мы можем рассчитать момент инерции каждого камня как Следовательно, общий момент инерции будет равен
Спортсмен сидит на вращающемся стуле, держа в каждой руке тренировочный вес 10 кг. Когда спортсмен будет чаще вращаться: когда он вытягивает руки далеко от тела или когда он отводит руки близко к телу? Решение Когда спортсмен вытягивает руки, момент инерции увеличивается по мере увеличения расстояния между весом и его ось вращения увеличивается. Когда спортсмен отводит руки, расстояние между отягощениями и осью вращения уменьшается, а также момент инерции. тело будет иметь меньшее сопротивление вращению.
Когда спортсмен отводит руки, расстояние между отягощениями и осью вращения уменьшается, а также момент инерции. тело будет иметь меньшее сопротивление вращению.
Очень тонкий диск диаметром 5 см вращается вокруг своего центра масс, а другой более толстый диск диаметром 2 см вращается вокруг своего центра масс. Какой из двух дисков имеет больший момент инерции?РешениеДиск большего диаметра будет иметь больший момент инерции. Как следует из формулы, момент инерции пропорционален квадрату расстояния до оси вращения, следовательно, чем больше радиус, тем больше момент инерции.
Момент инерции — ключевые выводыМомент инерции — это мера сопротивления вращающегося объекта вращению. Он зависит от массы и распределения ее массы вокруг оси вращения. Момент инерции является обратной величиной массы во втором законе Ньютона, применяемом для вращения. Момент инерции различен и специфичен для формы и оси каждого объекта.
Изображения
Инерция вращения. https://web2.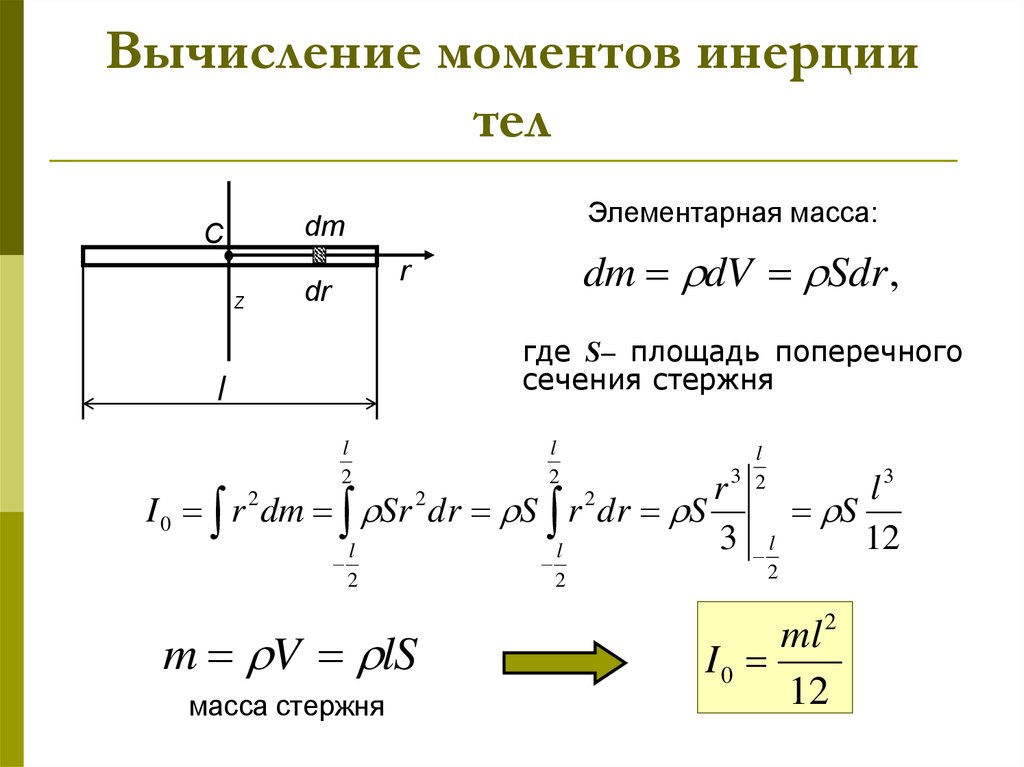


 18 момент инерции (динамический момент инерции) ротора:
18 момент инерции (динамический момент инерции) ротора: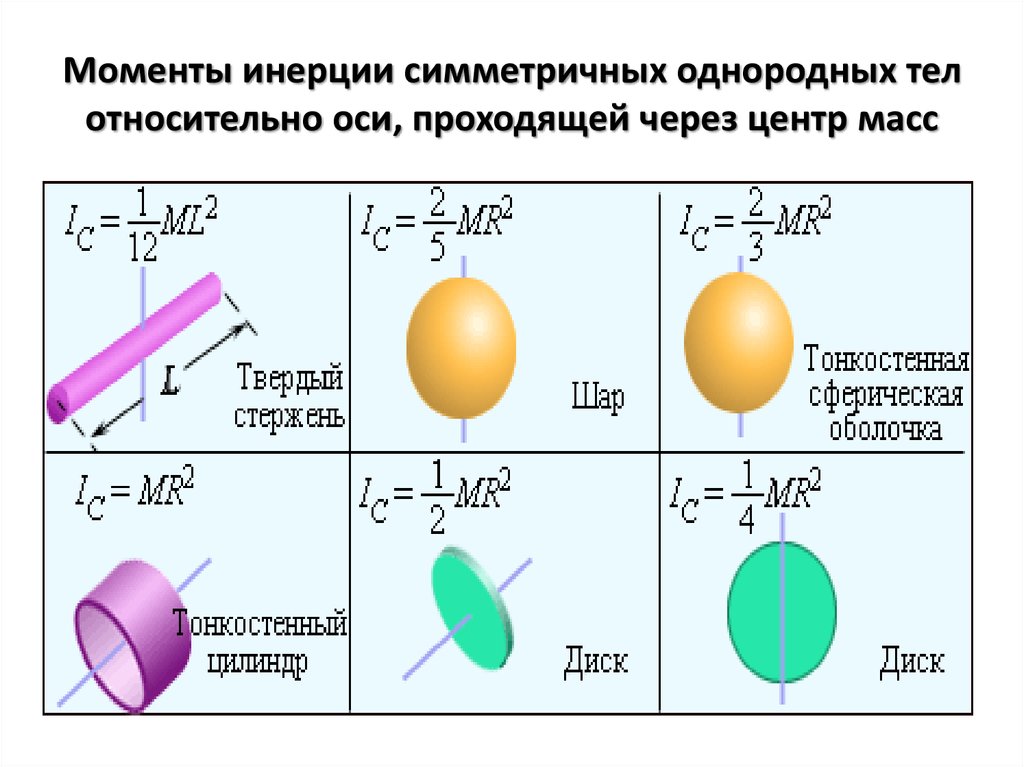
 Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа
Нормы и методы расчета на прочность при малоцикловых нагрузках оригинал документа ⓘ Длина строки [Lstring]
ⓘ Длина строки [Lstring] ⓘ Момент инерции маятника Боба [I]
ⓘ Момент инерции маятника Боба [I]