Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)
Среднеквадратичное значение (СКЗ). Действующее или эффективное значение
Истинное среднеквадратичное значение (ИСКЗ)
Root-mean-square (RMS) − среднеквадратичное значение – англ.
True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.
Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:
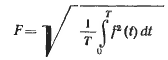 |
Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)
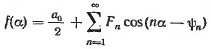 |
то действующее значение периодической несинусоидальной функции выражается формулой
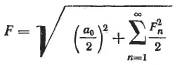 |
Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.
Например если, несинусоидальный ток выражается формулой:
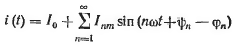 |
то среднеквадратичное значение тока равно:
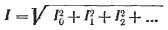 |
Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.
Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)
Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным. Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.
Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.
Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.
Замечания
Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:
UСКЗф = Uмаксф / (√2)
Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:
UСКЗл = Uмаксл / (√2)
Соотношение между фазным и линейным напряжением:
UСКЗл = UСКЗф * √3
Обозначения:
ф – линейное (напряжение)
л – фазное (напряжение)
СКЗ – среднеквадратичное значение
макс – максимальное или амплитудное значение (напряжения)
Примеры:
Фазному напряжению 220 В соответствует линейное напряжение 380 В
Фазному напряжению 230 В соответствует линейное напряжение 400 В
Фазному напряжению 240 В соответствует линейное напряжение 415 В
Фазное напряжение:
Напряжение в сети 220 В (СКЗ), — амплитудное значение напряжения около ±310 В
Напряжение в сети 230 В (СКЗ), — амплитудное значение напряжения около ±325 В
Напряжение в сети 240 В (СКЗ), — амплитудное значение напряжения около ±340 В
Линейное напряжение:
Напряжение в сети 380 В (СКЗ), — амплитудное значение напряжения около ±537 В
Напряжение в сети 400 В (СКЗ), — амплитудное значение напряжения около ±565 В
Напряжение в сети 415 В (СКЗ), — амплитудное значение напряжения около ±587 В
Ниже приведён обычный пример фазных напряжений в 3-фазной сети:
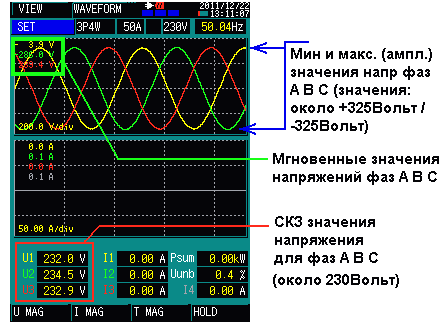 |
[1] Г.И. Атабеков Основы Теории Цепей с.176, 434 с.
Что означают RMS и True RMS? Здесь мы объясним вам различия


 Español
Español English
English Français
Français Italiano
Italiano Deutsch
Deutsch Русский
Русский
-
 Español
Español
 Français
Français Italiano
Italiano Deutsch
Deutsch Русский
Русский
-
РЕШЕНИЯ
- Антенны, Жилые здания, Дома
- SATCOM, Телепорты/Земные станции, OBvans/SNG/VSAT/Flyaways, TI
- Спутник, DTH, TVRO
- Трансляция, Покрытие сигнала, FSM
- Системы мониторинга 24/7
- Установка и обслуживание кабельного телевидения
-
- Анализаторы DOCSIS 3.1
- OBvans, SNG, Flyaway
- LTE помехи
- WIFI 2,4 ГГц и 5,7 ГГц
- IPTV & OTT
- Развертывание оптических сетей: FTTH, GPON
- Электронная лаборатория
-
- Электрические измерения
- Сертификация LAN
- Радиочастотное оборудование
- Термографическое оборудование
- образование
-
ПРОДУКЦИЯ
-
- Измерительное оборудование для телекоммуникаций
- Измерители эфирного, кабельного и спутникового телевидения
- Аксессуары для измерительных приборов
- Анализаторы для кабельного ТВ
- Генераторы несущих
- Системы мониторинга
- SATCOM, Телепорты/Земные станции, OBvans/SNG/VSAT/Flyaways, TI
- Анализаторы спектра, установленные в стойке
- Волоконно-оптические инструменты
- Источники света
- Оборудование для оптоволоконной сварки
- Оптические измерители сигнала
- Рефлектометры
- Аксессуары для оптического волокна
- Вспомогательные аксессуары для оптического волокна
-
- Модуляторы и Трансмодуляторы
- Кодеры HD
- Кодеры-модуляторы с HDMI CVBS входами
- Цифровые модуляторы для вещания
- MPEG Генераторы
- Трансмодуляторы из S/S2 — T/T2/ISDB-T/IP
- Digital To TV (DTTV)
- Комбайнеры / Усилители для DTTV
- Кодеры-модуляторы для DTTV
- IP стримеры для DTTV
- Модуляторы для DTTV
- Приемники для DTTV
- Трансмодуляторы для DTTV
- Другие элементы для DTTV
- Электроника
- Тепловизионная камера
- Блоки питания
- Генераторы сигналов специальной формы
- Цифровые мультиметры
- Осциллографы
-
- Радиочастотное оборудование
- Анализаторы RF спектра
- Анализаторы Wi-Fi сигналов
- РФ оборудование
- Электричество
- Люксметры
- Измерители сопротивления изоляции
- Измерители сопротивления
- Амперметры
- Шумомеры
- Тахометры
- Электрические измерители
- Обучающие системы
-
- ПОДДЕРЖКА
Важность использования RMS измерений для описания факторов, влияющих на качество электрической энергии
 Каждый из нас слышал, что занятие письмом под шум прибоя может оказывать лечебный эффект…
Каждый из нас слышал, что занятие письмом под шум прибоя может оказывать лечебный эффект…
Морские волны подобны синусоидальной волне переменного напряжения, которая используется в качестве эталонной при при определении качества питания. Отклонения от чисто синусоидальной формы волны могут быть обусловлены гармоническими составляющими, некратными гармониками, а также импульсными или колебательными переходными процессами. Изменения амплитуды синусоидального сигнала можно классифицировать следующим образом: падения, всплески и продолжительное перенапряжение либо пониженное напряжение. В то время как изменения в частоте питающего напряжения сравнительно редки и возникают при серьезных неполадках оборудования, чаще имеет место сдвиг фаз при провалах и всплесках. Для того чтобы охарактеризовать или описать синусоидальный сигнал, находящийся под воздействием описанных факторов, влияющих на качество электроэнергии, используются измерения истинных среднеквадратичных значений (Root Mean Squared — RMS). Являющиеся полезными во многих ситуациях, в ряде случаев такие измерения могут оказаться неадекватными либо вводить в заблуждение.
Что же представляют собой RMS?
Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.
Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла (см. рис. 1).

Рисунок 1. Форма волны на нагрузке однофазного источника питания с полноволновым измерителем.
RMS-значение чистого синусоидального сигнала составляет примерно 70,7% пикового значения. При искаженной форме волны это не верно, что является ответом на вопрос, почему приборы, измеряющие не в терминах истинных среднеквадратичных значений, могут выдавать совершенно различные результаты при различных степенях искажений и, следовательно, не могут использоваться при наличии гармоник. Те приборы, которые лишь вычисляют 71% от пикового значения будут давать неверный результат для формы тока, показанного на рис. 1. На рисунке изображена классическая форма токового сигнала однофазного источника питания с выпрямлением полной волны, присутствующего во многих электронных устройствах. Эта форма волны с гармоническими искажениями (THD) на уровне 108% имела пиковое значение 3,6 А и истинное среднеквадратичное значение 1,4 А, что не совпадает с рассчитанной величиной 0,707×3,6=2,55 А.
Невысокого качества анализаторы электроэнергии, которые настроены на RMS-значения, могут пропускать некоторые данные. Ряд приборов рассчитывают RMS-значения в ходе нескольких циклов. Весьма вероятно, что эти мониторы не зафиксируют многофазовый провал в течение одного цикла, изображенный на рис. 2.

Рисунок 2. Провал в течение одного цикла в двух фазах.
Такое искажение сигнала типично для случая, когда неполадка устраняется с помощью защитного предохранителя. На рис. 3 провал в течение одного цикла, возникший вследствие пробоя при пиковом напряжении (возможно из-за неисправности изоляции или удара молнии) будет давать различные RMS-значения на каждом из трех циклов.

Рисунок 3. Однофазный провал при пробое пиковым напряжением.
В зависимости от механизма включения триггера и пороговых значений, возможно необнаружение провала вплоть до третьего цикла, поскольку RMS-значение неисправных циклов может превышать порог срабатывания триггера. Неисправность, выражающаяся в сдвиге фаз, может иметь идентичные значения от одного цикла к следующему, несмотря на изменения амплитуды волны. Это происходит, когда используются электроанализаторы со многими механизмами включения триггера, например при переходных процессах или искажениях формы волны. Следует помнить, что хотя прибор не замечает таких неисправностей, это не значит, что они не существуют.
Справка
Консультативно-торговая компания «Энергометрика» поставляет компоненты автоматизации для: АСУ ТП, «интеллектуальное» здание, шкаф электрический, конденсаторная установка, системы учета параметров электроэнергии. SCADA системы.
Статья взята с сайта
www.energometrika.ru
Бюджетный вариант измерения TrueRMS / Habr
ВступлениеИзмерение trueRMS переменного напряжения — задача не совсем простая, не такая, какой она кажется с первого взгляда. Прежде всего потому, что чаще всего приходится измерять не чисто синусоидальное напряжение, а нечто более сложное, усложнённое наличием гармоник шумов.
Поэтому соблазнительно простое решение с детектором среднего значения с пересчётом в ср.кв. значения не работает там, где форма сигнала сильно отличается от синусоидальной или просто неизвестна.
Профессиональные вольтметры ср. кв. значения — это достаточно сложные устройства как по схемотехнике, так и по алгоритмам [1,2]. В большинстве измерителей, которые носят вспомогательный характер и служат для контроля функционирования, такие сложности и точности не требуются.
Также требуется, чтобы измеритель мог быть собран на самом простом 8-битном микроконтроллере.
Общий принцип измерения
Пусть имеется некое переменное напряжение вида, изображённого на рис. 1.
Квазисинусоидальное напряжение имеет некий квазипериод T.
Преимущество измерения среднеквадратичного значения напряжения в том, что в общем случае время измерения не играет большой роли, оно влияет только на частотную полосу измерения. Большее время даёт большее усреднение, меньшее даёт возможность увидеть кратковременные изменения.
Базовое определение ср. кв. значения выглядит вот таким образом:
где u(t) — мгновенное значение напряжения
T — период измерения
Таким образом, время измерения может быть, вообще говоря, любым.
Для реального измерения реальной аппаратурой для вычисления подинтегрального выражения необходимо проквантовать сигнал с некоторой частотой, заведомо превосходящей не менее, чем в 10 раз частоту квазисинусоиды. При измерении сигналов с частотами в пределах 20 кГц это не представляет проблемы даже для 8-битных микроконтроллеров.
Другое дело, что все стандартные контроллеры имеют однополярное питание. Поэтому измерить мгновенное переменное напряжение в момент отрицательной полуволны не представляется возможным.
В работе [3] предложено довольно остроумное решение, как внести постоянную составляющую в сигнал. Вместе с тем в том решении определение момента, когда стоит начать или закончить процесс вычисления ср. кв. значения представляется довольно громоздким.
В данной работе предлагается метод преодоления этого недостатка, а также вычисление интеграла с большей точностью, что позволяет снизить число точек выборки до минимума.
Особенности аналоговой части измерителя
На рис. 2 показано ядро схемы предварительной аналоговой обработки сигнала.
Сигнал поступает через конденсатор C1 на усилитель-формирователь, собранный на операционном усилителе DA1. Сигнал переменного напряжения замешивается на неинвертирующем входе усилителя с половиной опорного напряжения, которое используется в АЦП. Напряжение выбрано 2.048 В, поскольку в компактных устройствах часто используется напряжение питания +3.6 В и менее. В иных случаях удобно использовать 4.048 В, как в [3].
С выхода усилителя-формирователя через интегрирующую цепочку R3-C2 сигнал поступает на вход АЦП, который служит для измерения постоянной составляющей сигнала (U0). C усилителя-формирователя сигнал U’ — это измеряемый сигнал, сдвинутый на половину опорного напряжения. Таким образом, чтобы получить переменную составляющую, достаточно вычислить разность U’-U0.
Сигнал U0 используется также в качестве опорного для компаратора DA2. При переходе U’ через значение U0 компаратор вырабатывает перепад, который используется для формирования процедуры прерывания для сбора измерительных отсчётов.
Важно, что во многие современные микроконтроллеры встроены как операционные усилители, так и компараторы, не упоминая АЦП.
Базовый алгоритм
На рис. 3 дан базовый алгоритм для случая измерения величины переменного напряжения с основной частотой 50 Гц.
Запуск измерения может осуществляться по любому внешнему событию вплоть до кнопки, нажимаемой вручную.
После запуска в первую очередь измеряется постоянная составляющая во входном сигнале АЦП, а затем контроллер переходит в ожидание положительного перепада на выходе компаратора. Как только прерывание по перепаду наступает, контроллер делает выборку из 20 точек с временным шагом, соответствующим 1/20 квазипериода.
В алгоритме написано X мс, поскольку низкобюджетный контроллер имеет собственное время задержки. Чтобы измерение происходило в правильные моменты времени, необхоимо учитывать эту задержку. Поэтому реальная задержка будет меньше 1 мс.
В данном примере задержка соответствует измерениям квазисинусоид в диапазоне 50 Гц, но может быть любой в зависимости от квазипериода измеряемого сигнала в пределах быстродействия конкретного контроллера.
При измерениях ср.кв. значения напряжения произвольного квазипериодического сигнала, если априори неизвестно, что это за сигнал, целесообразно измерить его период, используя встроенный в контроллер таймер и тот же выход компаратора. И уже на основании этого замера устанавливать задержку при осуществлении выборки.
Вычисление среднеквадратичного значения
После того, как АЦП создал выборку, имеем массив значений U'[i], всего 21 значение, включая значение U0. Теперь, если применить формулу Симпсона (точнее, Котеса) для численного интергрирования, как наиболее точную для данного применения, то получим следующее выражение:
где h — шаг измерения, а нулевой компонент формулы отсутствует, поскольку он равег 0 по определению.
В результате вычисления мы получим значение интеграла в чистом виде в формате отсчётов АЦП. Для перевода в реальные значения полученное значение нужно промасштабировать с учётом величины опорного напряжения и поделить на интервал времени интегрирования.
где Uоп — опорное напряжение АЦП.
Если всё пересчитать в мВ, K приблизительно равняется просто 2. Масштабный коэффициент относится к разностям в квадратных скобках. После пересчёта и вычисления S делим на интервал измерения. С учётом множителя h фактически получаем деление на целое число вместо умножения на h с последующим делением на интервал времени измерения.
И в финале извлекаем квадратный корень.
И вот тут самое интересное и сложное наступает. Можно, разумеется, использовать плавающую точку для вычислений, поскольку язык C это допускает даже для 8-битных контроллеров, и производить вычисления непосредственно по приведённым формулам. Однако скорость расчёта упадёт существенно. Также можно выйти за пределы весьма небольшого ОЗУ микроконтроллера.
Чтобы такого не было, нужно, как верно указано в [3], использовать фиксированную точку и оперировать максимум 16-битными словами.
Автору эту проблему удалось решить и измерять напряжение с погрешностью Uоп/1024, т.е. для приведённого примера с точностью 2 мВ при общем диапазоне измерения ±500 мВ при напряжении питания +3.3 В, что достаточно для многих задач мониторинга процессов.
Программная хитрость состоит в том, чтобы все процессы деления, по возможности, делать до процессов умножения или возведения в степень, чтобы промежуточный результат операций не превышал 65535 (или 32768 для действий со знаком).
Конкретное программное решение выходит за рамки данной статьи.
Заключение
В данной статье рассмотрены особенности измерения среднеквадратичных значений напряжения с помощью 8-битных микроконтроллеров, показан вариант схемной реализации и основной алгоритм получения отсчётов квантования реального квазисинусоидального сигнала.
Ссылки
- Преобразователь среднеквадратического значения напряжения
- Цифровой вольтметр
- Метод измерения действующего значения напряжения с применением МК
Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)
Среднеквадратичное значение (СКЗ). Действующее или эффективное значение
Истинное среднеквадратичное значение (ИСКЗ)
Root-mean-square (RMS) − среднеквадратичное значение – англ.
True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.
Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:
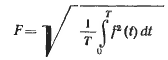 |
Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)
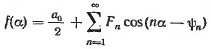 |
то действующее значение периодической несинусоидальной функции выражается формулой
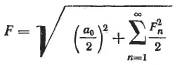 |
Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.
Например если, несинусоидальный ток выражается формулой:
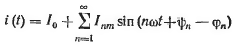 |
то среднеквадратичное значение тока равно:
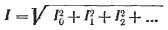 |
Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.
Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)
Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным. Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.
Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.
Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.
Замечания
Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:
UСКЗф = Uмаксф / (√2)
Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:
UСКЗл = Uмаксл / (√2)
Соотношение между фазным и линейным напряжением:
UСКЗл = UСКЗф * √3
Обозначения:
ф – линейное (напряжение)
л – фазное (напряжение)
СКЗ – среднеквадратичное значение
макс – максимальное или амплитудное значение (напряжения)
Примеры:
Фазному напряжению 220 В соответствует линейное напряжение 380 В
Фазному напряжению 230 В соответствует линейное напряжение 400 В
Фазному напряжению 240 В соответствует линейное напряжение 415 В
Фазное напряжение:
Напряжение в сети 220 В (СКЗ), — амплитудное значение напряжения около ±310 В
Напряжение в сети 230 В (СКЗ), — амплитудное значение напряжения около ±325 В
Напряжение в сети 240 В (СКЗ), — амплитудное значение напряжения около ±340 В
Линейное напряжение:
Напряжение в сети 380 В (СКЗ), — амплитудное значение напряжения около ±537 В
Напряжение в сети 400 В (СКЗ), — амплитудное значение напряжения около ±565 В
Напряжение в сети 415 В (СКЗ), — амплитудное значение напряжения около ±587 В
Ниже приведён обычный пример фазных напряжений в 3-фазной сети:
 |
[1] Г.И. Атабеков Основы Теории Цепей с.176, 434 с.
Основные понятия в электроизмерениях | РОБОТОША
Не всегда для проведения измерений требуется только правильно подключить измерительный прибор. Очень важно ответить себе на вопрос: зачем я это измеряю? Для измерения тока при проверке выделения тепла в проводе требуется один параметр, для измерения тока, чтобы определить уровень заряда конденсатора или батареи — совсем другой.
Параметры могут быть выражены в виде средней величины, среднеквадратического значения (RMS, Root Mean Square), мгновенного или пикового значения. Важен не только тип нагрузки, но также, имеем мы дело с переменным или постоянным током и как выглядит форма напряжения и тока. Тесно связаными с понятиями напряжения и тока являются мощность и энергия.
Мгновенные значения
Мгновенные ток , напряжение и мощность — это значения, соответствующие конкретному моменту времени . Любой сигнал состоит из бесконечного числа мгновенных значений. В случае с напряжением это записывается как .
Рассмотрим цепь, состоящую из последовательно соединененных резистора и катушки индуктивности, подключенных к источнику синусоидального напряжения с пиковым напряжением и частотой Гц.
Синусоидальное напряжение, как функцию времени, в этом случае, можно записать как:
(1)
Ток имеет максимальное значение и сдвинут на по отношению к напряжению:
(2)
Мощность, как функция времени, представляет собой соответствующие мгновенные значения напряжения и тока:
(3)
На рисунке ниже представлены графики напряжения, тока и мощности.
Для примера линией серого цвета показаны мгновенные значения для момента времени мс:
v (4.2) = 2.906 В
i (4.2) = 0.538 А
p (4.2) = 1.563 Вт
В определенный момент времени, мгновенные напряжение и ток всегда можно умножить, рассчитав мгновенную мощность.
Напряжение, ток и мощность как функции времени
Средние значения
Средние значения — это наиболее часто часто используемые параметры.
Если мультиметр устанавливается для измерения значений на постоянном токе, измеряются средние значения напряжения и тока. Кроме того, если мультиметр работает в режиме измерений постоянного тока, то для сигналов на переменном токе также будут измерены средние значения напряжения или тока. В случае симметричного переменного напряжения, мультиметр покажет , что является правильным значением.
Напряжение и ток
Среднее значение является суммой всех произведений мгновенных значений , деленное на число произведенных измерений. Если измерения производятся бесконечное число раз, то мы можем перейти к пределу, в котором промежуток времени измерения → 0 и сумма превратится в интеграл. В общем виде:
(4)
Для напряжения мы получим:
(5)
Мультиметр
Как упоминалось ранее, мультиметр, переведонный в режим измерений на постоянном токе, измеряет среднее значение напряжения или тока. В цифровых приборах, это среднее получается с помощью RC-фильтра. Входной сигнал непрерывно усредняется по постоянной времени . В виде формулы:
(6)
Усреднение напряжения RC-фильтром
Энергия и мощность
Уравнение (3) показывает, что результатом произведения мгновенного напряжения и тока является мгновенная мощность . Если просуммировать мгновенную мощность, умноженную на бесконечно малое время , то результатом будет энергия. Так как :
(7)
Действительно, энергия есть мощность, умноженная на время: , и энергетические пакеты можно всегда сложить для расчета полной энергии.
В качестве примера, опять возьмем последовательное соединение катушки индуктивности и резистора. На рисунке ниже черной линией показана динамика энергии во времени, рассчитанная в соответствии с уравнением (7).
Энергия как функция времени
Кривая мощности в случае напряжения и тока переменной полярности, также имеет периодическое изменение амплитуды с удвоенной частотой. Поскольку энергия рассеивается на сопротивлении, область серого цвета положительных значений кривой мощности больше, чем отрицательной области.
Значение энергии (черная линия) в любой момент времени равно площади под кривой мощности до этого момента. Хорошо видно, что энергия периодически возрастает сильнее, чем падает в результате амплитудной асимметрии кривой мощности относительно оси .
На рисунке показан период времени . Энергия внутри этого временного интервала , которая поступила в систему обозначена и вычисляется следующим образом:
(8)
Средняя мощность за определенный период времени равна общему количеству энергии, за это время, деленному на время измерений:
(9)
Если это подставить в уравнение (8), среднюю мощность можно вычислить для любой формы сигнала.
(10)
Это уравнение получено в соответствии с (4). Активная мощность всегда является средней мощностью.
Это уравнение для расчета средней рассеиваемой мощности всегда справедливо, потому что расчет основан на мгновенных значениях. Не имеет значения, является ток постоянным или переменным, как выглядит форма напряжения и тока и есть ли сдвиг фаз между напряжением и током.
Уравнение для расчета средней мощности лежит в основе метода, применяемого в измерителях мощности. Счетчики электроэнергии дома и на предприятиях работают в соответствии с уравнением (8), которое можно переписать в виде:
(11)
Верхний предел в интеграле — момент времени, в который счетчик энергии считывает значение.
Эффективные (RMS) значения
Среднеквадратическим (RMS), или эффективным значением является значение напряжения или тока, при котором на нагрузке рассеивается та же мощность, что и при постоянном напряжении или токе.
При переменном напряжении с эффективным значением 230В будет выделяться такое же количество тепла на нагрузке, как и при постоянном напряжении 230В. Действующее значение относится только к выделению тепла на резистивной нагрузке. Для примера, значение RMS тока полезно для измерения напряжения под нагрузкой в проводе (= резистивная), но не для измерения зарядного тока батареи или конденсатора (= поток электронов).
Среднеквадратическое значение
RMS является аббревиатурой от Root Mean Square, что буквально переводится как среднеквадратическое значение.
Над напряжением или током, как функциями времени, для вычисления значения RMS последовательно проводятся три математические операции: возведение в квадрат, усреднение и извлечение квадратного корня. Почему так?
Мощность, выделяемая на резисторе, подключенным к источнику напряжения:
(12)
Для мгновенных мощности и напряжения:
(13)
Вычисление средней мощности как функции времени показано в (10). можем подстваить из (13):
(14)
Так как — константа, то ее можно вынести за интеграл:
(15)
Перенеся напряжение в уравнении (12) в левую часть, мы можем расчитать напряжение по средней мощности и сопротивлению:
(16)
Затем, вычисленную среднюю мощность из (15), подставим в уравнение (16):
(17)
Сократив значения сопротивлений , получим:
(18)
Хорошо видно, что это уравнение состоит из трех частей: квадрата , среднего и квадратного корня.
В приведенных выше выкладках вычислялось значение напряжения на резисторе. Аналогично можно сделать и для тока через резистор:
(19)
Большинство мультиметров не может вычислить эффективное значение измеряемого напряжения. Чтобы узнать среднеквадратическое значение, обычно необходим специальный прибор.
На рисунке ниже показано, как вычисляет измеряемое напряжение прибор True RMS (истинные среднеквадратические значения). True RMS прибор, на практике, использует несколько иной метод работы, в котором необходим только один умножитель. Аналоговые умножители должны иметь очень низкий температурный дрейф и смещение, что делает эти инструменты достаточно дорогими.
Аналоговая схема получения RMS-значений
Кроме того, можно сделать расчет RMS программным путем с последовательных цифровых значений измеряемых напряжений. Этот подход обычно используется в мультиметрах и цифровых осциллографах.
Псевдо RMS
Большинство мультиметров не измеряет RMS-значений, когда выбран режим переменного тока. Тем не менее, они, кажется, дают эффективные значения при измерениях переменных напряжений и токов. Но отображаемые значения действительны только при измерениях синусоидального сигнала.
Простой прибор сначала выпрямляет измеряемый сигнал. Затем RC-фильтр нижних частот выделяет среднее значение, которое масштабируется таким образом, что прибор показывает эффективное значение. В виде уравнения:
(20)
Недостатком такого подхода является то, что это подходит только для синусоидальных сигналов. Для любой другой формы сигнала будет получено ошибочное эффективное значение.
Номинальная мощность?
Особенно в аудиотехнике широко используется термин «Номинальная мощность» или . Это по определению ошибочный термин.
Чуть выше, говоря про энергию и мощность, показано, что рабочая мощность рассчитывается из общего количества энергии, деленного на время за которое эта энергия измеряется, см. уравнение (9). Полная энергия определяется путем суммирования всех мгновенный пакетов энергии , см. уравнение (11). Это единственно правильный путь для расчета активной мощности.
Как выше указано, эффективное значение эквивалентно постоянному напряжению или току, при которых выделится такая же мощность на том же сопротивлении. Этот показатель рассчитывается как квадратный корень из среднего значения квадрата мгновенного напряжения (или тока). Нет причин думать, что эти три математические операции должны производиться для мгновенной мощности. Это было бы бессмысленное значение.
Чтобы проиллюстрировать это, приведу расчет для синусоидального напряжения с амплитудой В и частотой 1кГц.
Для представленного ниже графика сопротивление нагрузки Ом.
График напряжения и тока
Во-первых, вычислим эффективное напряжение для временной функции . В результате, имеем хорошо известное уравнение:
Далее, вычислим среднеквадратическое значение тока как функции времени . Оно равно:
Затем, вычислим тремя различными способами активную мощность, используя RMS-значения напряжения и тока:
Для проверки, вычислим среднюю мощность для временной функции :
И, наконец, попробуем формально подойти к задаче, и вычислить номинальную мощность:
Полученный результат (0.153Вт) значительно отличается от предыдущих трех (0.125Вт). Это подтверждает некорректность применения последней формулы.
В приведенном выше примере используются синусоидальные напряжение и ток. Но форма напряжения и тока, а также вид нагрузки и возможный фазовый сдвиг фазы принципиально не меняют ситуацию.
Активная мощность всегда является средней мощностью. Номинальная мощность — бессмысленное число.
Еще по этой теме
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
Среднеквадратическое отклонение — Википедия
Среднеквадрати́ческое отклоне́ние (среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние, станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. Обычно указанные термины означают квадратный корень из дисперсии случайной величины, но иногда могут означать тот или иной вариант оценки этого значения.
В литературе обычно обозначают греческой буквой σ{\displaystyle \sigma } (сигма).
Среднеквадратическое отклонение определяется как квадратный корень из дисперсии случайной величины: σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}}.
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.
На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.
В частности, если xi{\displaystyle x_{i}} — i-й элемент выборки, n{\displaystyle n} — объём выборки, x¯{\displaystyle {\bar {x}}} — среднее арифметическое выборки (выборочное среднее — оценка математического ожидания величины):
- x¯=1n∑i=1nxi=1n(x1+…+xn),{\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}),}
то два основных способа оценки стандартного отклонения записываются нижеследующим образом.
Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией[1]):
- S=1n∑i=1n(xi−x¯)2.{\displaystyle S={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}
Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.
Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии[1], в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):
- S0=nn−1S2=1n−1∑i=1n(xi−x¯)2.{\displaystyle S_{0}={\sqrt {{\frac {n}{n-1}}S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}
Само по себе, однако, S0{\displaystyle S_{0}} не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.
Обе оценки являются состоятельными[1].
Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки[2]. Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.
Правило трёх сигм (3σ{\displaystyle 3\sigma }) гласит: вероятность того, что любая случайная величина отклонится от своего среднего значения менее чем на 3σ{\displaystyle 3\sigma }, — P(|ξ−Eξ∣<3σ)≥89{\displaystyle P(|\xi -E\xi \mid <3\sigma )\geq {\frac {8}{9}}}.
Практически все значения нормально распределённой случайной величины лежат в интервале (μ−3σ;μ+3σ){\displaystyle \left(\mu -3\sigma ;\mu +3\sigma \right)}, где μ=Eξ{\displaystyle \mu =E\xi } — математическое ожидание случайной величины. Более строго — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.
Интерпретация величины среднеквадратического отклонения[править | править код]
Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.
На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.
Экономика и финансы[править | править код]
Среднее квадратическое отклонение доходности портфеля σ=D[X]{\displaystyle \sigma ={\sqrt {D[X]}}} отождествляется с риском портфеля.
В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.
Климат[править | править код]
Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.
Спорт[править | править код]
Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.
Пример вычисления стандартного отклонения оценок учеников[править | править код]
Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.
Пусть оценки учеников класса следующие:
- 2, 4, 4, 4, 5, 5, 7, 9.{\displaystyle 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9.}
Тогда средняя оценка равна:
- μ=2+4+4+4+5+5+7+98=5{\displaystyle \mu ={\frac {2+4+4+4+5+5+7+9}{8}}=5}
Вычислим квадраты отклонений оценок учеников от их средней оценки:
- (2−5)2=(−3)2=9(5−5)2=02=0(4−5)2=(−1)2=1(5−5)2=02=0(4−5)2=(−1)2=1(7−5)2=22=4(4−5)2=(−1)2=1(9−5)2=42=16{\displaystyle {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Среднее арифметическое этих значений называется дисперсией:
- σ2=9+1+1+1+0+0+4+168=4{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{8}}=4}
Стандартное отклонение равно квадратному корню дисперсии:
- σ=4=2{\displaystyle \sigma ={\sqrt {4}}=2}
Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:
- σ2=9+1+1+1+0+0+4+167≈4,57{\displaystyle \sigma ^{2}={\frac {9+1+1+1+0+0+4+16}{7}}\approx 4,57}
и стандартное отклонение равнялось бы:
- σ=4,57≈2,14{\displaystyle \sigma ={\sqrt {4,57}}\approx 2,14}
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
- ↑ 1 2 3 Ивченко Г. И., Медведев Ю. И. Введение в математическую статистику. — М. : Издательство ЛКИ, 2010. — §2.2. Выборочные моменты: точная и асимптотическая теория. — ISBN 978-5-382-01013-7.
- ↑ C. Patrignani et al. (Particle Data Group). 39. STATISTICS. — В: Review of Particle Physics // Chin. Phys. C. — 2016. — Vol. 40. — P. 100001. — DOI:10.1088/1674-1137/40/10/100001.
- Боровиков В. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов / В. Боровиков. — СПб.: Питер, 2003. — 688 с. — ISBN 5-272-00078-1..


 Español
Español English
English Français
Français Italiano
Italiano Deutsch
Deutsch