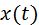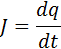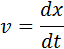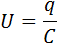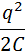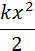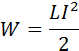Тема- Исследование электромагнитных колебаний в параллельном RLC контуре Выполнили- Тюлякова У
Работа добавлена на сайт samzan.ru: 2015-07-105
Г4=117
или ГИ
С1-72
Ф5080
C2
C1
C
L
R
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Отчет по лабораторной работе №3
Тема: Исследование электромагнитных колебаний в параллельном RLC контуре
Выполнили: Тюлякова У.Н.
Юшкевич М.А.
Задача
Для параллельного LC колебательного контура измерить и вычислить следующие величины:
- В режиме свободных затухающих колебаний: период колебаний, логарифмический декремент затухания, коэффициент затухания, постоянную времени затухания, добротность.
- В режиме вынужденных колебаний: резонансную частоту, полосу пропускания, добротность.
- Сравнить значения добротности, полученные в первом и втором случаях. Исследовать зависимость названных величин от параметров контура.
Установка
Таблица №1
Параметры контура | Порядковый номер наблюдения | 1 | 2 | 3 | Среднее T, мкс | Частота f, 106Гц | |
L = 215 мкГн С=0,022 мкФ R = 0 | Т, мкс | 13,6 | 14 | 13,5 | 13,7 | 0,073 | |
L = 215 мкГн С=0,022 мкФ R = 40 Ом | Т, мкс | 14 | 15 | 16 | 14 | 14,8 | 0,068 |
Таблица №2
Параметры контура: L = 215 мкГн, С = 0,022 мкФ, R = 40 Ом | |||||||
Порядковый номер амплитуды | 1 | 2 | 3 | Порядковый номер амплитуды | 1 | 2 | 3 |
(Y+), дел | 8 | 1 | (Y-), дел | 17 | 4 | 1 | |
| 1,386 | 0,693 | | 1,447 | 1,386 |
Таблица №3
Параметры контура | Порядковый номер наблюдения | 2 | 3 | 4 | 5 | среднее | |
L = 215 мкГн С=0,022 мкФ R = 0 | fрез, кГц | 70,644 | 71,319 | 70,386 | 70,045 | 70,476 | |
L = 215 мкГн С=0,022 мкФ R = 40 Ом | fрез, кГц | 69,928 | 67,903 | 65,706 | 67,746 | 67,911 |
Таблица №4
№ п.п. | f, кГц | U, дел | U/Uрез | f = f2 — f1, кГц | Q | ||||
R = 0 | R = 0 | R = 40 Ом | R = 0 | R = 40 Ом | |||||
1 | 50,604 | 50,613 | 3 | 6 | 0,086 | 0,545 | |||
2 | 55,801 | 55,706 | 5 | 7 | 0,143 | 0,636 | |||
3 | 60,783 | 60,783 | 8 | 8 | 0,229 | 0,727 | |||
4 | 65,581 | 65,740 | 18 | 10 | 0,514 | 0,909 | |||
5 | 70,606 | 70,606 | 35 | 11 | 1 | 1 | |||
6 | 75,927 | 75,782 | 15 | 11 | 0,429 | 1 | |||
7 | 80,134 | 80,543 | 10 | 10 | 0,286 | 0,909 | |||
8 | 85,007 | 85,316 | 8 | 10 | 0,229 | 0,909 | |||
9 | 90,039 | 89,475 | 6 | 9 | 0,171 | 0,818 | |||
10 | 95,407 | 8 | 0,727 | ||||||
11 | 100,182 | 8 | 0,727 | ||||||
12 | 105,009 | 7 | 0,636 | ||||||
13 | 110,269 | 7 | 0,636 | ||||||
14 | 114,753 | 7 | 0,636 | ||||||
15 | 120,043 | 6 | 0,545 |
Обработка результатов
Период затухающих колебаний: R = 0 T = 13,7 мкс
R = 40 Ом Т = 14,8 мкс
Частота затухающих колебаний: R = 0 f = 0,073 106 Гц
R = 40 Ом f = 0,068 106 Гц
Логарифмический декремент затухания: = 1,575
Коэффициент затухания: = /Т= 1,575/14,8мкс = 0,106106 Гц
Постоянная времени затухания: = 1/ = 1/1,106106 Гц = 0,904мкс
Добротность контура: Q = = 1,575 = 1,995
Погрешность периода затухающих колебаний (как погрешность прямых измерений):
Т =
Погрешность частоты затухающих колебаний (как погрешность прямых измерений):
f =
Погрешность коэффициента затухания (как погрешность косвенных измерений):
Погрешность постоянной времени затухания (как погрешность косвенных измерений):
Погрешность добротности контура (как погрешность косвенных измерений):
Резонансная кривая:
Полоса пропускания:
Добротность контура:
Погрешность резонансной частоты (погрешность прямых измерений)
Тема- Исследование электромагнитных колебаний в параллельном RLC контуре Выполнил- Ломакин А
Заказать написание уникльной работы
Работа добавлена на сайт TXTRef.ru: 2019-04-153
Г4=117
или ГИ
С1-72
Ф5080
C2
C1
C
L
R
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Отчет по лабораторной работе №3
Тема: Исследование электромагнитных колебаний в параллельном RLC контуре
Выполнил: Ломакин А.А.
Санкт-Петербург 2003г.
Задача
Для параллельного LC колебательного контура измерить и вычислить следующие величины:
- В режиме свободных затухающих колебаний: период колебаний, логарифмический декремент затухания, коэффициент затухания, постоянную времени затухания, добротность.
- В режиме вынужденных колебаний: резонансную частоту, полосу пропускания, добротность.
- Сравнить значения добротности, полученные в первом и втором случаях. Исследовать зависимость названных величин от параметров контура.
Установка
Измерения
Таблица №1
Параметры контура | Порядковый номер наблюдения | 1 | 2 | 3 | 4 | Среднее T, мкс | Частота f, 106Гц |
L = 215 мкГн С=0,022 мкФ R = 0 | Т, мкс | 13,6 | 14 | 13,5 | 13,7 | 13,7 | 0,073 |
L = 215 мкГн С=0,022 мкФ R = 40 Ом | Т, мкс | 14 | 15 | 16 | 14 | 14,8 | 0,068 |
Таблица №2
Параметры контура: L = 215 мкГн, С = 0,022 мкФ, R = 40 Ом | |||||||
Порядковый номер амплитуды | 1 | 2 | 3 | Порядковый номер амплитуды | 1 | 2 | 3 |
(Y+), дел | 8 | 2 | 1 | (Y-), дел | 17 | 4 | 1 |
| 1,386 | 0,693 | | 1,447 | 1,386 |
Обработка результатов
Период затухающих колебаний: R = 0 T = 13.7 мкс
R = 40 Ом Т = 14.8 мкс
Частота затухающих колебаний: R = 0 f = 73.0 кГц
R = 40 Ом f = 67.8 кГц
Логарифмический декремент затухания: = 1.575
Коэффициент затухания: = /Т= 1.575/14.8 = 10.6
Постоянная времени затухания: = 1/ = 1/0.106106 = 9.4 мкс
Добротность контура: Q = = 1.575 = 1.995
Погрешность периода затухающих колебаний (как погрешность прямых измерений):
Т = 0.1 мкс
Погрешность частоты затухающих колебаний (как погрешность прямых измерений):
f = 0.5 кГц
Погрешность коэффициента затухания (как погрешность косвенных измерений):
= 1.2 мкс
Погрешность постоянной времени затухания (как погрешность косвенных измерений):
= 1 мкс
Погрешность добротности контура (как погрешность косвенных измерений):
Q = 0.25
Заказать написание уникльной работыЛабораторная работа 2.22 ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНОГО LC-КОНТУРА Ю.И.Туснов
Лабораторная работа 35
 Лабораторная работа 35 Исследование резонанса в цепи переменного тока Методическое руководство Москва 04 г. Исследование резонанса в цепи переменного тока. Цель лабораторной работы Изучение зависимости
Лабораторная работа 35 Исследование резонанса в цепи переменного тока Методическое руководство Москва 04 г. Исследование резонанса в цепи переменного тока. Цель лабораторной работы Изучение зависимости
ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
 ЛАБОРАТОРНАЯ РАБОТА ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ Цель работы: исследование зависимости напряжения на емкости и тока в колебательном контуре от частоты вынужденных колебаний ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ Для
ЛАБОРАТОРНАЯ РАБОТА ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ Цель работы: исследование зависимости напряжения на емкости и тока в колебательном контуре от частоты вынужденных колебаний ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ Для
Тема 3.1 Электромагнитные колебания
 Тема 3. Электромагнитные колебания. Колебательный контур. Уравнение колебательного контура 3. Свободные незатухающие колебания в контуре 4. Свободные затухающие колебания в контуре 5. Вынужденные колебания
Тема 3. Электромагнитные колебания. Колебательный контур. Уравнение колебательного контура 3. Свободные незатухающие колебания в контуре 4. Свободные затухающие колебания в контуре 5. Вынужденные колебания
Лабораторная работа 2-32
 Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре. Цель работы:
Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре Лабораторная работа 2-32 Изучение вынужденных колебаний в последовательном колебательном контуре. Цель работы:
Механические колебания
 Механические колебания Гармонические колебания Колебаниями называются процессы (движения или изменения состояния), повторяющиеся во времени вблизи некоторого среднего положения. Положение, вблизи которого
Механические колебания Гармонические колебания Колебаниями называются процессы (движения или изменения состояния), повторяющиеся во времени вблизи некоторого среднего положения. Положение, вблизи которого
Лекц ия 28 Электромагнитные колебания
 Лекц ия 8 Электромагнитные колебания Вопросы. Электромагнитный колебательный контур. Незатухающие колебания. Формула Томсона. Затухающие колебания. Вынужденные колебания в контуре. Резонанс. Добротность
Лекц ия 8 Электромагнитные колебания Вопросы. Электромагнитный колебательный контур. Незатухающие колебания. Формула Томсона. Затухающие колебания. Вынужденные колебания в контуре. Резонанс. Добротность
ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики
 Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 01 ЛАБОРАТОРНАЯ
Ю. В. Тихомиров ЛАБОРАТОРНЫЕ РАБОТЫ по курсу физики С ЭЛЕМЕНТАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. ОПТИКА для студентов всех специальностей всех форм обучения МОСКВА — 01 ЛАБОРАТОРНАЯ
Когерентные колебания
 Л1 Когерентные колебания Определение Любые два гармонические колебания называют когерентными, если разность фаз этих колебаний не меняется с течением времени Рассмотрим два гармонические колебания с фазами
Л1 Когерентные колебания Определение Любые два гармонические колебания называют когерентными, если разность фаз этих колебаний не меняется с течением времени Рассмотрим два гармонические колебания с фазами
U m. 2) π. 1) 1, Дж 2) 5, Дж 3) 1, Дж 4) Дж
 Колебательный контур состоит из катушки индуктивности и конденсатора. В нём наблюдаются гармонические электромагнитные колебания с периодом Т = 5 мс. В начальный момент времени заряд конденсатора максимален
Колебательный контур состоит из катушки индуктивности и конденсатора. В нём наблюдаются гармонические электромагнитные колебания с периодом Т = 5 мс. В начальный момент времени заряд конденсатора максимален
Колебательные контуры
 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Мордовский Государственный университет им. Н.
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Мордовский Государственный университет им. Н.
ВЫНУЖДЕННЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
 ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра
, где I m амплитуда силы тока
 ЛАБОРАТОРНАЯ РАБОТА 8. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Цель работы: определение зависимости индуктивного и емкостного сопротивлений от частоты, а также определение угла сдвига фаз тока
ЛАБОРАТОРНАЯ РАБОТА 8. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Цель работы: определение зависимости индуктивного и емкостного сопротивлений от частоты, а также определение угла сдвига фаз тока
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
 ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ Состав работы: — лабораторный модуль 1 шт. — блок формирования импульсов 1 шт. — источник питания (МАРС) 1 шт. — осциллограф одноканальный (С1 94) 1 шт. — приборная полка
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ Состав работы: — лабораторный модуль 1 шт. — блок формирования импульсов 1 шт. — источник питания (МАРС) 1 шт. — осциллограф одноканальный (С1 94) 1 шт. — приборная полка
Тема 4.2. Цепи переменного тока
 Тема 4.. Цепи переменного тока Вопросы темы.. Цепь переменного тока с индуктивностью.. Цепь переменного тока с индуктивностью и активным сопротивлением. 3. Цепь переменного тока с ёмкостью. 4. Цепь переменного
Тема 4.. Цепи переменного тока Вопросы темы.. Цепь переменного тока с индуктивностью.. Цепь переменного тока с индуктивностью и активным сопротивлением. 3. Цепь переменного тока с ёмкостью. 4. Цепь переменного
5. Электрические колебания
 1 5 Электрические колебания 51 Колебательный контур Колебаниями в физике называют не только периодические движения тел но и всякий периодический или почти периодический процесс в котором значения той или
1 5 Электрические колебания 51 Колебательный контур Колебаниями в физике называют не только периодические движения тел но и всякий периодический или почти периодический процесс в котором значения той или
Л 2. Затухающие колебания
 Л Затухающие колебания 1 Колебательный контур Добавим в колебательный контур, состоящий из конденсатора C, индуктивности L и ключа К, Замкнем ключ — по закону Ома C IR L где введены обозначения D q C dq
Л Затухающие колебания 1 Колебательный контур Добавим в колебательный контур, состоящий из конденсатора C, индуктивности L и ключа К, Замкнем ключ — по закону Ома C IR L где введены обозначения D q C dq
Электромагнитные колебания
 И. В. Яковлев Материалы по физике MathUs.ru Электромагнитные колебания Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс,
И. В. Яковлев Материалы по физике MathUs.ru Электромагнитные колебания Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс,
Индуктивность в цепи переменного тока
 Лабораторная работа 7 Индуктивность в цепи переменного тока Цель работы: исследование зависимости сопротивления соленоида от частоты синусоидального тока, определение индуктивности соленоида, а также взаимной
Лабораторная работа 7 Индуктивность в цепи переменного тока Цель работы: исследование зависимости сопротивления соленоида от частоты синусоидального тока, определение индуктивности соленоида, а также взаимной
coswt, описывается уравнением
 4 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ Колебательным контуром называют электрическую цепь составленную из конденсаторов и катушек в которой возможен колебательный процесс перезарядки конденсаторов Этот процесс
4 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ Колебательным контуром называют электрическую цепь составленную из конденсаторов и катушек в которой возможен колебательный процесс перезарядки конденсаторов Этот процесс
1. Основные положения теории
 . Основные положения теории…. Предварительная подготовка… 6 3. Задание на проведение эксперимента… 6 4. Обработка результатов экспериментов… 5. Вопросы для самопроверки и подготовке к защите работы…
. Основные положения теории…. Предварительная подготовка… 6 3. Задание на проведение эксперимента… 6 4. Обработка результатов экспериментов… 5. Вопросы для самопроверки и подготовке к защите работы…
Лекция 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
 Лекция 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Колебательные процессы широко распространены в природе и технике. При движении маятника колеблется его центр тяжести. В случае переменного тока колеблются напряжение и
Лекция 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Колебательные процессы широко распространены в природе и технике. При движении маятника колеблется его центр тяжести. В случае переменного тока колеблются напряжение и
1. Основные положения теории
 . Основные положения теории…. Предварительная подготовка… 5 3. Задание на проведение эксперимента… 8 4. Обработка результатов экспериментов… 3 5. Вопросы для самопроверки и подготовке к защите
. Основные положения теории…. Предварительная подготовка… 5 3. Задание на проведение эксперимента… 8 4. Обработка результатов экспериментов… 3 5. Вопросы для самопроверки и подготовке к защите
10. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
 44 0 ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕКИЙ ТОК 0 Основные понятия и определения Переменным называется ток, который с течением времени изменяет свою величину Квазистационарным называется переменный ток, который во всех
44 0 ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕКИЙ ТОК 0 Основные понятия и определения Переменным называется ток, который с течением времени изменяет свою величину Квазистационарным называется переменный ток, который во всех
Лекция 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
 Лекция ЗАТУХАЮЩИЕ КОЛЕБАНИЯ Выше мы рассматривали колебания происходящие без потери энергии На практике всякая колебательная система непрерывно отдает часть энергии среде Вследствие этого колебания затухают
Лекция ЗАТУХАЮЩИЕ КОЛЕБАНИЯ Выше мы рассматривали колебания происходящие без потери энергии На практике всякая колебательная система непрерывно отдает часть энергии среде Вследствие этого колебания затухают
15. Электрические колебания
 5. Электрические колебания Вопросы. Дифференциальное уравнение, описывающее свободные колебания заряда конденсатора в колебательном контуре, имеет вид Aq + Bq = 0, где A и B известные положительные постоянные.
5. Электрические колебания Вопросы. Дифференциальное уравнение, описывающее свободные колебания заряда конденсатора в колебательном контуре, имеет вид Aq + Bq = 0, где A и B известные положительные постоянные.
Л20 Гармонические колебания
 Л Гармонические колебания Под колебаниями в физике понимают движения или состояния, обладающие той или иной степенью повторяемости во времени. Для колебаний характерно превращение одного вида энергии в
Л Гармонические колебания Под колебаниями в физике понимают движения или состояния, обладающие той или иной степенью повторяемости во времени. Для колебаний характерно превращение одного вида энергии в
C L. Рис. 1 W C = (2) W L
 Московский государственный технический университет им. Н.Э.Баумана Г.В.БАЛАБИНА ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ В КОНТУРЕ C Методические указания к лабораторной работе Э-6 по курсу общей физики Под редакцией Л.К.Мартинсона
Московский государственный технический университет им. Н.Э.Баумана Г.В.БАЛАБИНА ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ В КОНТУРЕ C Методические указания к лабораторной работе Э-6 по курсу общей физики Под редакцией Л.К.Мартинсона
Свободные электромагнитные колебания в контуре (Зеленин С.В.)
На данном уроке мы узнаем, что такое электромагнитные колебания, колебательный контур. Рассмотрим опыт с колебательным контуром и выясним, какие процессы происходят в нем за один период колебаний. В конце урока мы выведем формулу Томсона.
Успехи в изучении электромагнетизма в XIX веке привели к бурному развитию промышленности и техники, особенно это касается средств связи. Прокладывая линии телеграфа на большие расстояния, инженеры столкнулись с рядом необъяснимых явлений, которые побудили ученых к исследованиям. Так, в 50-х годах британский физик Уильям Томсон (лорд Кельвин) занялся вопросом о трансатлантической телеграфии. Учитывая неудачи первых практиков, он теоретически исследовал вопрос о распространении электрических импульсов вдоль кабеля. При этом Кельвин получил ряд важных выводов, которые в дальнейшем позволили осуществить телеграфирование через океан. Также в 1853 году британский физик выводит условия существования колебательного электрического разряда. Эти условия легли в основу всего учения об электрических колебаниях. На этом уроке и на других уроках данной главы мы рассмотрим некоторые основы теории электрических колебаний Томсона.
Периодические или почти периодические изменения заряда, тока и напряжения в цепи называются электромагнитными колебаниями. Также можно дать еще одно определение.
Электромагнитными колебаниями называются периодические изменения напряженности электрического поля (E) и магнитной индукции (B).
Для возбуждения электромагнитных колебаний необходимо иметь колебательную систему. Простейшая колебательная система, в которой могут поддерживаться свободные электромагнитные колебания, называется колебательным контуром.
На рисунке 1 представлен простейший колебательный контур – это электрическая цепь, которая состоит из конденсатора и проводящей катушки, подсоединенной к обкладкам конденсатора.
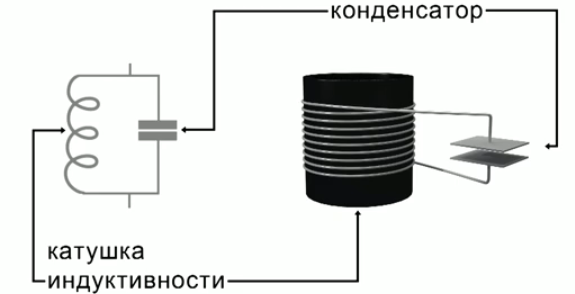
Рис. 1. Колебательный контур
В таком колебательном контуре могут протекать свободные электромагнитные колебания.
Свободными называются колебания, которые осуществляются за счет запасов энергии, накопленной самой колебательной системой, без привлечения энергии извне.
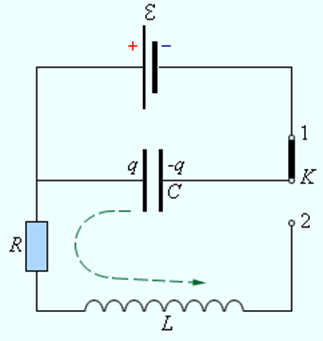
Рассмотрим колебательный контур, изображенный на рисунке 2. Он состоит из: катушки с индуктивностью L, конденсатора с емкостью C, лампочки (для контроля наличия тока в цепи), ключа и источника тока.При помощи ключа конденсатор может быть подключен либо к источнику тока, либо к катушке. В начальный момент времени (конденсатор не подключен к источнику тока) напряжение между его обкладками равно 0.
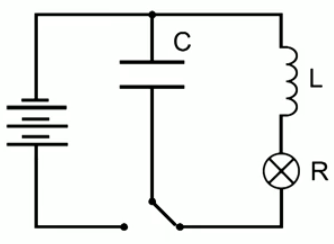
Рис. 2. Колебательный контур
Заряжаем конденсатор путем замыкания его на источник постоянного тока.
При переключении конденсатора на катушку лампочка на короткое время загорается, то есть конденсатор быстро разряжается.
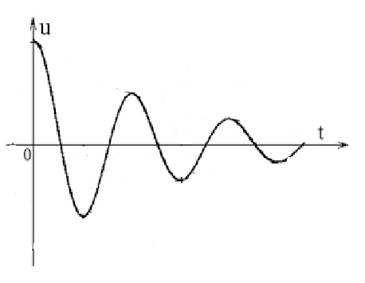
Рис. 3. График зависимости напряжения между обкладками конденсатора от времени при разрядке
На рисунке 3 изображен график зависимости напряжения между обкладками конденсатора от времени. На этом графике показан интервал времени с момента переключения конденсатора на катушку до момента, когда напряжение на конденсаторе равно нулю. Видно, что напряжение изменялось периодически, то есть в цепи протекали колебания.
Следовательно, в колебательном контуре протекают свободные затухающие электромагнитные колебания.
В начальный момент времени (перед тем как замкнули конденсатор на катушку) вся энергия была сосредоточена в электрическом поле конденсатора (см. Рис. 4 а).
При замыкании конденсатора на катушку он начнет разряжаться. Ток разряда конденсатора, проходя по виткам катушки, создает магнитное поле. Это означает, что происходит изменение магнитного потока, охватывающего катушку, и в ней возникает ЭДС самоиндукции, которая препятствует мгновенному разряду конденсатора, следовательно, ток разряда нарастает постепенно. С ростом тока разряда убывает электрическое поле в конденсаторе, но возрастает магнитное поле катушки (см. Рис. 4 б).
В момент, когда поле конденсатора исчезнет (конденсатор разрядится), магнитное поле катушки будет максимальным (см. Рис. 4 в).
Далее магнитное поле будет ослабевать и в цепи появится ток самоиндукции, который будет препятствовать убыванию магнитного поля, следовательно, этот ток самоиндукции будет направлен так же, как и ток разряда конденсатора. Это приведет к перезарядке конденсатора. То есть, на той обкладке, где вначале был знак плюс, появится минус, и наоборот. Направление вектора напряженности электрического поля в конденсаторе также поменяется на противоположное (см. Рис. 4 г).
Ток в цепи будет ослабевать за счет возрастания электрического поля в конденсаторе и полностью исчезнет, когда поле в конденсаторе достигнет максимального значения (см. Рис. 4 д).
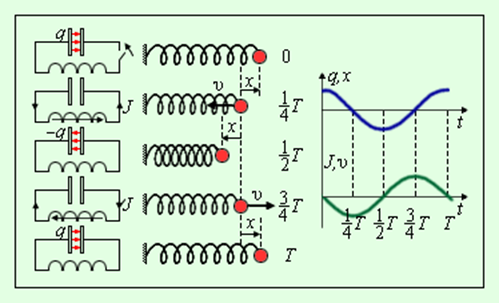
Рис. 4. Процессы, происходящие за один период колебаний
Далее конденсатор опять начнет разряжаться. Возникнет ток самоиндукции, который не даст конденсатору мгновенно разрядиться, и начнет возрастать магнитное поле (см. Рис. 4 е).
Когда электрическое поле конденсатора исчезнет, магнитное поле вновь достигнет своего максимума (см. Рис. 4 ж).
Начнется заряд конденсатора за счет тока индукции. По мере заряда ток будет ослабевать, а вместе с ним и магнитное поле (см. Рис. 4 з).
Когда конденсатор зарядится, ток в цепи и магнитное поле исчезнут. Система вернется в исходное состояние (см. Рис. 4 е).
Таким образом, мы рассмотрели процессы, происходящие за один период колебаний.
Значение энергии, сосредоточенной в электрическом поле конденсатора, в начальный момент времени вычисляется по формуле:
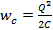 , где
, где
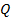 – заряд конденсатора; C – электроемкость конденсатора.
– заряд конденсатора; C – электроемкость конденсатора.
Через четверть периода вся энергия электрического поля конденсатора переходит в энергию магнитного поля катушки, которая определяется по формуле:
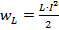 ,
,
где L – индуктивность катушки, I – сила тока.
Для произвольного момента времени сумма энергий электрического поля конденсатора и магнитного поля катушки является постоянной величиной (если пренебрегать затуханием):

Согласно закону сохранения энергии, полная энергия контура остается постоянной, следовательно, производная от постоянной величины по времени будет равна нулю:
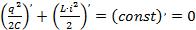
Вычисляя производные по времени, получим:
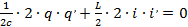
Учтем, что мгновенное значение тока – это первая производная заряда по времени:
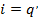
Следовательно:
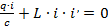
Если мгновенное значение тока – это первая производная заряда по времени, то производная тока по времени будет второй производной заряда по времени:
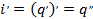
Следовательно:
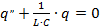
Мы получили дифференциальное уравнение, решением которого будет гармоническая функция (заряд гармонически зависит от времени):
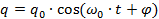 , где
, где
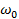 – циклическая частота колебаний, которая определяется значениями электроемкости конденсатора и индуктивности катушки:
– циклическая частота колебаний, которая определяется значениями электроемкости конденсатора и индуктивности катушки:
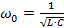
Поэтому колебание заряда, а значит, тока и напряжения в цепи, будут гармоническими.
Так как период колебаний связан с циклической частотой обратной зависимостью, то период равен:
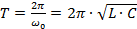
Данное выражение называется формулой Томсона.
Список литературы
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Lms.licbb.spb.ru (Источник).
- Home-task.com (Источник).
- Sch230.ru (Источник).
- Youtube.com (Источник).
Домашнее задание
- Что называют электромагнитными колебаниями?
- Вопросы в конце параграфа 28, 30 (2) – Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы) (Источник).
- Как осуществляется превращение энергии в контуре?
RLC-контур. Свободные колебания
RLC-контур
Кроме как в механических системах, к примеру, в таких, маятник или же грузило на пружине, свободные колебания могут возникать также и в электрических цепях, самым простым примером чего может послужить последовательный RLC-контур, изображенный на рис. 2.2.1.

Рисунок 2.2.1.Последовательный RLC-контур.
Находясь в положении 1, ключ К позволяет источнику зарядить конденсатор до некоего напряжения δ. Процесс разрядки ранее заряженного конденсатора провоцируется переключением ключа К во второе положение и происходит через катушку индуктивности L и резистор R. При выполнении определенных условий данный процесс может приобретать характер колебательного.
Для не содержащей внешнего источника тока замкнутой RLC-цепи закон Ома представляет из себя выражение:
JR+U=-LdJdt.
В данной формуле U=qC – напряжение на конденсаторе, q является обозначением заряда конденсатора, а J=dqdt – ток в цепи. Правой частью соотношения является выражение ЭДС самоиндукции катушки. В случае, когда заряд конденсатора q (t) берется как переменная величина, описывающее свободные колебания в RLC-контуре уравнение может быть приведено к виду:
q··+RLq·+1LCq=0.
Для начала рассмотрим такую ситуацию, в которой электромагнитные потери энергии в контуре равны нулю. В таком случае:
q··+ω02q=0.
Примем обозначение ω02=1LC. Данным чуть выше уравнением описывается процесс незатухающих свободных колебаний в LC- контуре. Внешне оно полностью эквивалентно уравнению свободных колебаний груза на пружине в условиях отсутствующих сил трения. Аналогичный свободным механическим и электрическим колебаниям процесс изображен на рисунке 2.2.2. На данной иллюстрации приводятся графики зависимости заряда смещения x (t) груза и q (t) конденсатора от положения равновесия, а также графики изменений
Отчет по лабораторной работе №: 14 Изучение свободных электромагнитных колебаний в lcr контуре
Санкт-Петербургский государственный Университет
информационных технологий, механики и оптики
СПб ГУИТМО
Отчет по лабораторной работе №: 14
Изучение свободных электромагнитных колебаний в
LCR – контуре.
Студент:
Группа №: 1704
Преподаватель: Сологуб В.В.
Санкт-Петербург
2004
Лабораторная работа № 14
Изучение свободных электромагнитных колебаний в LCR – контуре.
Цель работы:
Цель работы: Изучение характеристик свободного колебательного процесса, возбуждаемого импульсным воздействием в простом LCR контуре.
Приборы и оборудование:
1. Модули «ФПЭ-10/11», «ПИ» и два магазина сопротивления «МС».
2. Постоянное оборудование: источник питания «ИП», генератор ГЗ-112, осциллограф
С1-93 (С1-83), два цифровых вольтметра, комплект соединительных кабелей.
Теоретическая часть
Описание свободного колебательного процесса
Уравнение процесса. Характеристики затухания.
Простой колебательный контур состоит из последовательно соединенных индуктивности L, емкости С, и активного сопротивления R. Если предварительно
запасти энергию, например, зарядив конденсатор от внешнего источника
тока (рис.14.1), а затем подключить конденсатор к катушке индуктивности, то в образовавшемся изолированном контуре возникнут свободные электромагнитные колебания.
Действительно, при разряде конденсатора появляются изменяющиеся во времени ток и пропорциональное ему магнитное поле. Меняющееся магнитное поле порождает в контуре ЭДС самоиндукции E, которая по закону Ленца сначала замедляет скорость разряда конденсатора, а после того, как конденсатор полностью разрядится, продолжает поддерживать ток в прежнем направлении. В результате происходит перезарядка конденсатора.
Затем процесс разряда конденсатора продолжается, но в обратном направлении и т.д. Возникающие свободные колебания заряда q, тока и напряжений (7 на элементах контура совершаются с циклической частотой w, а колебания электрической и магнитной энергий с удвоенной частотой (максимумы энергий появляются дважды за период Т).
Вследствие джоулевых потерь в активном сопротивлении контура R часть энергии колебаний превращается в теплоту, что приводит к затуханию колебаний. При больших величинах R колебания могут вообще не возникнуть — наблюдается апериодический разряд конденсатора.
Найдем уравнение, описывающее свободные затухающие колебания в контуре.

По закону Кирхгофа для полной цепи имеем

С учетом соотношений (14.1) уравнение (14.2) для переменной U приобретает вид

Легко показать, что точно такой же вид имеют уравнения для заряда конденсатора q и тока I.
Затухание нарушает периодичность колебаний и строгое применение понятия периода и частоты к ним не применимо. Однако при малом затухании условно пользуются понятием периода как промежутка времени между последующими максимумами (или минимумами) колеблющейся величины. С учетом этой оговорки период свободных затухающих колебаний в контуре равен

С увеличением затухания период колебаний растет, обращаясь в бесконечность т.е. движение перестает быть периодическим. В данном случае напряжение на конденсаторе асимптотически приближается к нулю при t-> 0 и уже будет описываться функцией, отличной от вида (14.4). Такой процесс называется апериодическим. Переход к нему происходит при величине сопротивления контура

Фазовая плоскость
В ряде случаев удобно изучать колебательные и нелинейные процессы в системе координат (1Д) — «ток-напряжение». В механике аналогичными координатами являются скорость и перемещение. Плоскость таких координат носит название плоскости состояний
или фазовой плоскости, а кривая, изображающая зависимость этих координат называется фазовой кривой.
Рассмотрим фазовую кривую для процессов в LCR-контуре. Для нахождения силы тока продифференцируем функцию U(t) (14.4) по времени

Фазовая кривая I(U) описывается в параметрической форме системой из двух уравнений

 При R = 0 (о = 0) опережение тока по фазе составляет П/2 и фазовая кривая будет представлять собой эллипс, как в случае сложения двух взаимно перпендикулярных колебаний с постоянными амплитудами, сдвинутых по фазе на четверть периода.
При R = 0 (о = 0) опережение тока по фазе составляет П/2 и фазовая кривая будет представлять собой эллипс, как в случае сложения двух взаимно перпендикулярных колебаний с постоянными амплитудами, сдвинутых по фазе на четверть периода.
В реальной ситуации при наличии затухания (R > 0) амплитуды напряжения и тока в контуре непрерывно убывают, не повторяясь через период Т, и фазовая кривая получается незамкнутой (рис.14.4).
Методика измерений
Для наблюдения зависимости напряжения на конденсаторе контура от времени U(t) используется электрическая схема, изображенная на рис.14.5. Колебания в контуре возбуждаются короткими импульсами напряжения от преобразователя «ПИ»,
периодически повторяющимися с частотой V задающего генератора «PQ».

Контур соединен с генератором импульсов через разделительный конденсатор С (емкостью значительно меньшей емкости контура С). Для уменьшения влияния генератора на параметры контура.
Затухание контура определяется его полным эквивалентным сопротивлением R, которое включает в себя, в основном, сопротивление обмотки катушки, сопротивление потерь на
гистерезис в сердечнике катушки, внешнее сопротивление магазина Rm, а также сопротивление, вносимое в контур генератором импульсов. Сопротивление R заранее неизвестно и определяется из измерений характеристик затухания реального контура.
Порядок выполнения работы
Задание 1.
Измерение периода колебаний, логарифмического декремента и параметров контура.
1. Соберите электрическую схему согласно рис.14.5. Для получения возбуждающих импульсов на модуль «ПИ» подайте от генератора ГЗ-112 синусоидальное напряжение » 3,5 В. Установите частоту генератора V т 40… 70 Гц, задающую периодичность вырабатываемых импульсов. Длительность импульсов установите равную примерно 1…2 мс.
2. Включите приборы.
3. Получите устойчивую осциллограмму затухающих колебаний, в которой укладывается примерно 10-20 периодов. Режим синхронизации — внутренняя.
4. Измерьте период колебаний Т при минимальном внешнем сопротивлении R = 0 (гнезда магазина МС замкните проводом).
5. Измерьте амплитуды колебаний, отстоящих друг от друга на n = 5…15 периодов и вычислите логарифмический декремент по формуле (14.7а). Рассчитайте коэффициент затухания, добротность и время релаксации.
6. Повторите измерения по пп. 4 и 5 при других значениях вешнего сопротивления R в интервале от 1 до 10 Ом. (Для расширения пределов регулирования сопротивления при
возможности включите последовательно два магазина сопроивлений). Данные
измерений и вычислений занесите в таблицу 14.1.
7- Постройте график зависимости λ(RM). Поскольку период Т при малых затуханиях практически постоянен, то зависимость λ(RM) можно аппроксимировать линейной функцией.
8. Используя формулу

вычислите индуктивность L.
9. Модифицировав формулу (14.5), определите емкость контура
С. Данные занесите в таблицу 14.1.
10. Подберите сопротивление магазина R (качественно) при котором происходит переход к апериодическому режиму. Сравните полученное значение с рассчитанным по формуле
Результаты измерений
Rм, Ом | T, с | Ui, дел | Ui+n, дел |
0 | 0,60 | 2,4 | 0,90 |
3 | 0,60 | 2,4 | 0,85 |
6 | 0,58 | 2,4 | 0,75 |
9 | 0,59 | 2,3 | 0,65 |
12 | 0,60 | 2,3 | 0,55 |
15 | 0,60 | 2,3 | 0,50 |
18 | 0,60 | 2,25 | 0,30 |
20 | 0,60 | 2,2 | 0,28 |
Константы:
C=0,09 мкФ;
L=90 мГн;
n=10.
Расчеты
Rм, Ом | T, с | Ui, дел | Ui+n, дел | n | lambda | delta | Q | tau | L | C | R, Ом | |
0 | 0,60 | 2,4 | 0,90 | 10 | 0,098 | 0,163 | 32,0 | 6,1 | 47,1 | 0,000194 | 15,4 | |
3 | 0,60 | 2,4 | 0,85 | 10 | 0,104 | 0,173 | 30,3 | 5,8 | 53,2 | 0,000172 | 18,4 | |
6 | 0,58 | 2,4 | 0,75 | 10 | 0,116 | 0,201 | 27,0 | 5,0 | 53,3 | 0,000160 | 21,4 | |
9 | 0,59 | 2,3 | 0,65 | 10 | 0,126 | 0,214 | 24,9 | 4,7 | 56,9 | 0,000155 | 24,4 | |
12 | 0,60 | 2,3 | 0,55 | 10 | 0,143 | 0,238 | 22,0 | 4,2 | 57,4 | 0,000159 | 27,4 | |
15 | 0,60 | 2,3 | 0,50 | 10 | 0,153 | 0,254 | 20,6 | 3,9 | 59,7 | 0,000153 | 30,4 | |
18 | 0,60 | 2,25 | 0,30 | 10 | 0,201 | 0,336 | 15,6 | 3,0 | 49,7 | 0,000183 | 33,4 | |
20 | 0,60 | 2,2 | 0,28 | 10 | 0,206 | 0,344 | 15,2 | 2,9 | 51,5 | 0,000177 | 35,4 |
Строим график зависимости логарифмического декремента от сопротивления магазина:

По графику определяем эквивалентное сопротивление контура RK=15,4 Ом.
Расчет погрешностей
Найдём погрешность вычисления индуктивности и ёмкости.
Вычисление погрешности ΔL.
Lср=53,6.
№ опыта | L | L| | L) | L) | /N(N-1) | |
1 | 47,1 | 6,5 | 42,25 |
|
|
|
2 | 53,2 | 0,4 | 0,16 |
|
|
|
3 | 53,3 | 0,3 | 0,09 |
|
|
|
4 | 56,9 | 3,3 | 10,89 | 124,66 | 2,226 | 1,49 |
5 | 57,4 | 3,8 | 14,44 |
|
|
|
6 | 59,7 | 6,1 | 37,21 |
|
|
|
7 | 49,7 | 3,9 | 15,21 |
|
|
|
8 | 51,5 | 2,1 | 4,41 |
|
|
|
Коэффициент Стьюдента для 8 опытов при доверительной вероятности 95% равен 2,2.
ΔL = 1,49 · 2,2 3,3.
L = 100% · ΔL / L ср 6,2%
Аналогично найдём ΔC.
Cср=169,1 · 10-6
№ опыта | С 10-6 | С| | С) | С) | /N(N-1) | 10-6 |
1 | 194 | 24,9 | 620,01 | 1527 | 27,27 | 5,22 |
2 | 172 | 2,9 | 8,41 | |||
3 | 160 | 9,1 | 82,81 | |||
4 | 155 | 14,1 | 198,81 | |||
5 | 159 | 10,1 | 102,01 | |||
6 | 153 | 16,1 | 259,21 | |||
7 | 183 | 13,9 | 193,21 | |||
8 | 177 | 7,9 | 62,41 |
Коэффициент Стьюдента для 8 опытов при доверительной вероятности 95% равен 2,2.
ΔL = 5,22 · 10-6 · 2,2 11,5 · 10-6
L = 100% · ΔL / L ср 6,8%
Вывод
В результате проведения опытов мы нашли значения основных характеристик свободного колебательного процесса. Высчитанные с их использованием значения величин индуктивности и ёмкости контура позволяют говорить о качественных измерениях, так как погрешность получившихся результатов составила менее 7%.
Rlc-контур. Свободные колебания
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).
|
Рисунок 2.2.1. Последовательный RLC-контур |
Когда ключ K находится в положении 1, конденсатор заряжается до напряжения 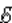 . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.
. После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
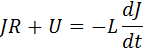
где 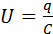 – напряжение на конденсаторе, q – заряд конденсатора,
– напряжение на конденсаторе, q – заряд конденсатора, 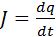 – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Если в качестве переменной величины выбрать заряд конденсатора q (t), уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду:
– ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Если в качестве переменной величины выбрать заряд конденсатора q (t), уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду:
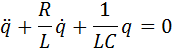
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
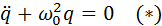
Здесь принято обозначение: 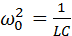 . Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения. Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период
. Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения. Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период 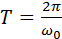 колебаний.
колебаний.
|
Рисунок 2.2.2. Аналогия процессов свободных электрических и механических колебаний |
Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1:
| Электрические величины | Механические величины | |
| Координата |
| |
| Ток в цепи |
| |
| Скорость |
| |
| Индуктивность | L | |
| Масса | m | |
| Величина, обратная электроемкости |
| |
| Жесткость | k | |
| Напряжение на конденсаторе |
| |
| Упругая сила | kx | |
| Энергия электрического поля конденсатора |
| |
| Потенциальная энергия пружины |
| |
| Магнитная энергия катушки |
|
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
q(t) = q0 cos(ωt + φ0). |
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
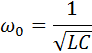
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q0 = C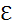 , φ0 = 0.
, φ0 = 0.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
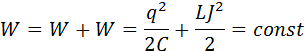
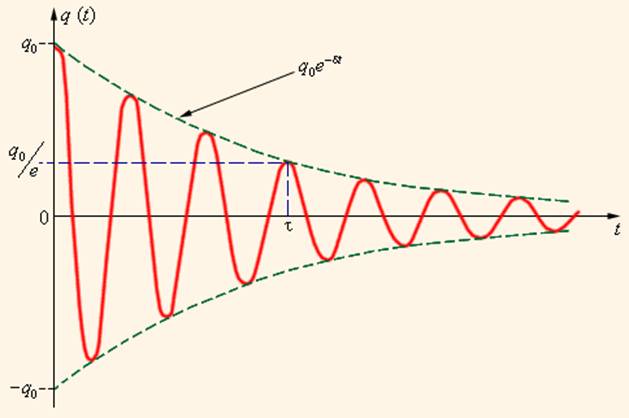
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).
|
Рисунок 2.2.3. Затухающие колебания в контуре |
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
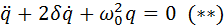
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
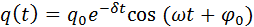
которая содержит множитель exp (–δt), описывающий затухание колебаний. Скорость затухания зависит от электрического сопротивления R контура. Интервал времени 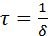 в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.
В § 2.4 части 1 было введено понятие добротности Q колебательной системы:
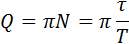
где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:
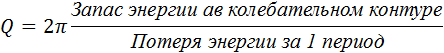
Для RLC-контура добротность Q выражается формулой
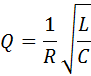
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω0 идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.
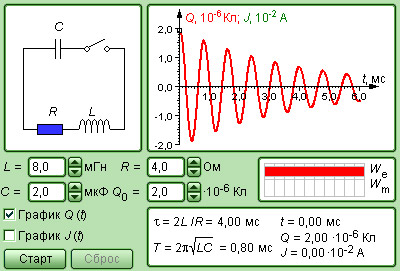 |
Модель. Свободные колебания в RLC-контуре |