Сложение по модулю 2 — Википедия
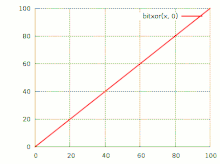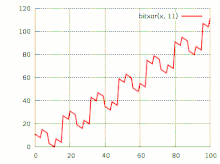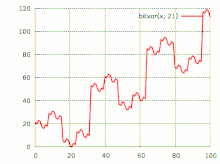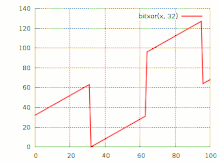 График побитового исключающего «или»
График побитового исключающего «или»Сложе́ние по мо́дулю 2 (исключа́ющее «или», XOR, строгая дизъюнкция, поразрядное дополнение, инвертирование по маске, жегалкинское сложение, логическое вычитание, логи́ческая неравнозна́чность) — булева функция, а также логическая и битовая операция, в случае двух переменных результат выполнения операции истинен тогда и только тогда, когда один из аргументов истинен, а другой — ложен. Для функции трёх (тернарное сложение по модулю 2) и более переменных — результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Сложение по модулю 2 называется «исключающим „или“» и «строгой дизъюнкцией» для отличения от «обычного» (неисключающего) логического «или» — нестрогой логической дизъюнкции. В теории множеств сложению по модулю 2 соответствует операция симметрической разности двух множеств.
Запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более 2 префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:
⊕2(a,b), a{\displaystyle \oplus _{2}(a,b),~a} ^ b, a⊕b,a⊕2b,a+2b,{\displaystyle b,~a\oplus b,a\oplus _{2}b,a+_{2}b,} a ≠ b, a≠b,(a,b)⊕2,a XOR b{\displaystyle a\neq b,(a,b)\oplus _{2},a~XOR~b}
В Юникоде есть символы для сложения по модулю 2: U+22BB ⊻ xor, U+2295 ⊕ circled plus и U+2A27 ⨧ plus sign with subscript two, U+2A52 ⩒ logical or with dot above, а также символ для суммы по модулю 2: U+2A0A ⨊ modulo two sum.
В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true>false{\displaystyle true>false}.
Таблицы истинности:
| a{\displaystyle a} | b{\displaystyle b} | a⊕b{\displaystyle a\oplus b} |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Правило: результат равен 0{\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1{\displaystyle 1}.
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a⊕b⊕c{\displaystyle a\oplus b\oplus c} |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Правило: результат равен 0{\displaystyle 0}, если нет операндов, равных 1{\displaystyle 1}, либо их чётное количество.
В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
- если
a=011001012{\displaystyle a=01100101_{2}}
b=001010012{\displaystyle b=00101001_{2}}
- то
a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}
Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.
Использование побитового исключающего «или» позволяет поменять местами значения целых переменных без использования дополнительной памяти.
В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:
- «результат истинен (равен 1), если A не равно B (A≠B)»;
- «если A не равно B (A≠B), то истина (1)».
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
- A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
- A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).
Операция ⊕{\displaystyle \oplus } исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция ∨{\displaystyle \lor } включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
В квантовых компьютерах аналог операции сложения по модулю 2 — вентиль CNOT.
Исключающее ИЛИ — это… Что такое Исключающее ИЛИ?
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи: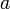 ^
^ 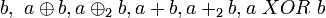 .
.
Булева алгебра
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества 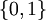 . Результат также принадлежит множеству
. Результат также принадлежит множеству 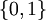 . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений
. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 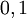 может использоваться любая другая пара подходящих символов, например
может использоваться любая другая пара подходящих символов, например 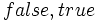 или
или 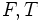 или «ложь», «истина».
или «ложь», «истина».
Правило: результат равен 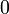 , если оба операнда равны; во всех остальных случаях результат равен
, если оба операнда равны; во всех остальных случаях результат равен 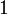 .
.
Таблица истинности:
Программирование
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 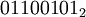 |
| b = | 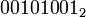 |
| то | |
| a ^ b = | 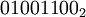 |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Связь с естественным языком
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
 истинно, если истинно
истинно, если истинно  или
или  , или оба сразу.
, или оба сразу. истинно, если истинно
истинно, если истинно  или
или  , но не оба сразу.
, но не оба сразу.
Операция 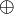 исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция
исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция 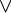 включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
См. также
Wikimedia Foundation. 2010.
Исключающее или — это… Что такое Исключающее или?
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи: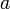
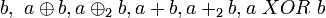 .
.Булева алгебра
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества 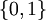 . Результат также принадлежит множеству
. Результат также принадлежит множеству 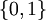 . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений
. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 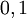 может использоваться любая другая пара подходящих символов, например
может использоваться любая другая пара подходящих символов, например 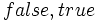 или
или 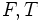 или «ложь», «истина».
или «ложь», «истина».
Правило: результат равен 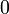 , если оба операнда равны; во всех остальных случаях результат равен
, если оба операнда равны; во всех остальных случаях результат равен 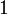 .
.
Таблица истинности:
Программирование
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 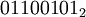 |
| b = | 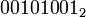 |
| то | |
| a ^ b = | 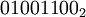 |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Связь с естественным языком
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
 истинно, если истинно
истинно, если истинно  или
или  , или оба сразу.
, или оба сразу. истинно, если истинно
истинно, если истинно  или
или  , но не оба сразу.
, но не оба сразу.
Операция 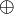 исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция
исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция 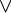 включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
См. также
Wikimedia Foundation. 2010.
Логический элемент Исключающее ИЛИ | HomeElectronics
Всем доброго времени суток! Сегодня мы рассмотрим последние два элемента, которые выполняют простейшие логические функции. Такими элементами являются Исключающее ИЛИ (Exclusive-OR, XOR) и Исключающее ИЛИ-НЕ (None Exclusive-OR, NXOR). Предыдущие статьи смотрите здесь, здесь, здесь и здесь.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Логический элемент Исключающее ИЛИ, как и ранее рассмотренные логические элементы имеет несколько равноправных входов и один выход, но не один из входных выводов не может заблокировать другие входы, установив выходной сигнал к уровню единицы или нуля. Исходя из сказанного, можно установить логику работы элемента Исключающее ИЛИ: высокий логический уровень на выходе появляется только тогда, когда только на одном из входов есть высокий уровень, а если на всех входах одновременно присутствуют сигналы логического нуля или логической единицы, то на выходе буде низкий уровень напряжения. Так же как и все остальные логические элементы элемент Исключающее ИЛИ может иметь инверсию на выходе, такой элемент называют Исключающее ИЛИ-НЕ. Логика работы такого элемента следующая: высокий уровень на выходе логического элемента Исключающее ИЛИ-НЕ появиться только в том случае, когда на всех входах одновременно присутствует сигналы лог. 0 или лог. 1. Таким образом таблица истинности логических элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет иметь следующий вид:
| Входные выводы | Тип логического элемента | ||
| 1 | 2 | Исключающее ИЛИ | Исключающее ИЛИ-НЕ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Элементы Исключающее ИЛИ из-за своего специфического функционала не имеют широкого применения, поэтому отдельных суффиксов в их обозначении не присутствует, они в основном входят в серию ЛП (например, К555ЛП5, КР1533ЛП12, К561ЛП2), в составе которой микросхемы с различным функционалом. Логические элементы Исключающее ИЛИ имеют своё графическое обозначение, которое приведено ниже.
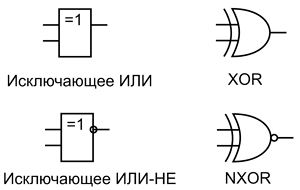

Условное графическое обозначение элементов Исключающее ИЛИ: DIN (слева) и ANSI (справа).
Применение элемента Исключающее ИЛИ
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию суммирования по модулю 2. Поэтому эти элементы иногда называют сумматорами по модулю два. Основное предназначение элементов Исключающее ИЛИ состоит в сравнении двух входных сигналов (когда на входы приходят два высоких или два низких логических уровня на выходе формируется лог. 0), очень часто данный элемент применяют для формирования задержки сигнала или формирования коротких импульсов.
Управляемый инвертор
Важное применение элементов Исключающее ИЛИ – управляемый инвертор. Опишем его работу. Один из входов используется как управляющий, а на другой поступает сигнал. Если на управляющем входе высокий логический уровень, то сигнал инвертируется, а если низкий, то не инвертируется. Чаще всего управляющий сигнал задаётся постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
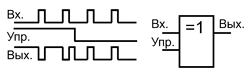

Элемент Исключающее ИЛИ в качестве управляемого инвертора.
Смешивание сигналов
В случае, когда имеется два сигнала и исключается их одновременный приход на элемент Исключающее ИЛИ, то он может быть использован для смешивания сигналов. Такое применение данного элемента может быть использовано в тех случаюх, когда остаются неиспользованными некоторые элементы Исключающее ИЛИ.
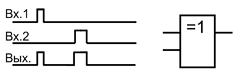
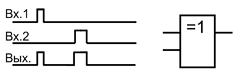
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов.
Формирование коротких импульсов
Второе важное применение данного элемента – выделение фронта и среза входного импульса, которое традиционно делали с помощью дифференцирующего RC-звена, с последующим усилением и формированием сигнала. Микросхема с элементами Исключающее ИЛИ упрощает данную задачу.
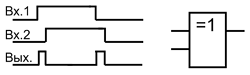

Выделения фронта и среза импульса.
Ниже представлена схема для выделения среза и фронта входящего импульса. Входной сигнал задерживается цепочкой элементов, а затем исходный сигнал и его задержаная копия поступают на входы элемента Исключающее ИЛИ. В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
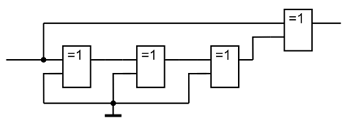

Схема реализующая выделение фронта и среза импульса.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Исключающее «или» — это… Что такое Исключающее «или»?
Сложе́ние по модулю 2 (исключа́ющее «ИЛИ», XOR, «сумма по модулю 2») — логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Это бинарная инфиксная операция, то есть она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи: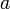 ^
^ 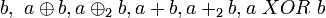 .
.
Булева алгебра
В булевой алгебре сложение по модулю 2 — это функция двух переменных (они же — операнды операции). Переменные могут принимать значения из множества 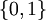 . Результат также принадлежит множеству
. Результат также принадлежит множеству 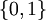 . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений
. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 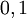 может использоваться любая другая пара подходящих символов, например
может использоваться любая другая пара подходящих символов, например 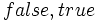 или
или 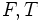 или «ложь», «истина».
или «ложь», «истина».
Правило: результат равен 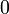 , если оба операнда равны; во всех остальных случаях результат равен
, если оба операнда равны; во всех остальных случаях результат равен 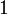 .
.
Таблица истинности:
Программирование
В языках C/C++ (а также Java, C#, Ruby, PHP, JavaScript и т. д.) эта операция обозначается символом «^», в языках Паскаль, Delphi, Ada — зарезервированным словом XOR, в языке ассемблера — одноименной логической командой. Сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 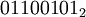 |
| b = | 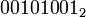 |
| то | |
| a ^ b = | 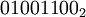 |
Выполнение операции XOR для значений логического типа (true, false) производится в разных языках программирования по-разному. Например в Delphi используется встроенный оператор XOR (пример: condition1 xor condition2). В языке C, начиная со стандарта С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов проихводится его побитовое применение. Перегрузка для стандартных типов невозможна, но операцию XOR над ними можно реализовать, исходя из принципа «исключающего ИЛИ». Выглядит это так:
(condition1 || condition2) && (condition1 != condition2)
(при этом нет разницы, применяются ли побитовые операторы & и |, или же логические && и ||)
Связь с естественным языком
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
 истинно, если истинно
истинно, если истинно  или
или  , или оба сразу.
, или оба сразу. истинно, если истинно
истинно, если истинно  или
или  , но не оба сразу.
, но не оба сразу.
Операция 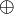 исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция
исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция 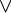 включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
См. также
Wikimedia Foundation. 2010.
Исключающее ИЛИ Википедия
График побитового исключающего «или»Сложе́ние по мо́дулю 2 (исключа́ющее «или», XOR, строгая дизъюнкция, поразрядное дополнение, инвертирование по маске, жегалкинское сложение, логическое вычитание, логи́ческая неравнозна́чность) — булева функция, а также логическая и битовая операция, в случае двух переменных результат выполнения операции истинен тогда и только тогда, когда один из аргументов истинен, а другой — ложен. Для функции трёх (тернарное сложение по модулю 2) и более переменных — результат выполнения операции будет истинным только тогда, когда количество аргументов, равных 1, составляющих текущий набор, — нечётное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Сложение по модулю 2 называется «исключающим „или“» и «строгой дизъюнкцией» для отличения от «обычного» (неисключающего) логического «или» — нестрогой логической дизъюнкции. В теории множеств сложению по модулю 2 соответствует операция симметрической разности двух множеств.
Обозначения
Запись может быть префиксной («польская запись») — знак операции ставится перед операндами, инфиксной — знак операции ставится между операндами и постфиксной — знак операции ставится после операндов. При числе операндов более 2 префиксная и постфиксная записи экономичнее инфиксной записи. Чаще всего встречаются следующие варианты записи:
В Юникоде есть символы для сложения по модулю 2: U+22BB ⊻ xor, U+2295 ⊕ circled plus и U+2A27 ⨧ plus sign with subscript two, U+2A52 ⩒ logical or with dot above, а также символ для суммы по модулю 2: U+2A0A ⨊ modulo two sum.
Свойства
Булева алгебра
В булевой алгебре сложение по модулю 2 — это функция двух, трёх и более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при этом необходимо доопределять старшинство, например, true>false{\displaystyle true>false}.
Таблицы истинности:
| a{\displaystyle a} | b{\displaystyle b} | a⊕b{\displaystyle a\oplus b} |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Правило: результат равен 0{\displaystyle 0}, если оба операнда равны; во всех остальных случаях результат равен 1{\displaystyle 1}.
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a⊕b⊕c{\displaystyle a\oplus b\oplus c} |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Правило: результат равен 0{\displaystyle 0}, если нет операндов, равных 1{\displaystyle 1}, либо их чётное количество.
Программирование
В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,
- если
a=011001012{\displaystyle a=01100101_{2}}
b=001010012{\displaystyle b=00101001_{2}}
- то
a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}
Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.
Использование побитового исключающего «или» позволяет поменять местами значения целых переменных без использования дополнительной памяти.
Связь с естественным языком
В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:
- «результат истинен (равен 1), если A не равно B (A≠B)»;
- «если A не равно B (A≠B), то истина (1)».
Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}.
Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:
- A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
- A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).
Операция ⊕{\displaystyle \oplus } исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ». Операция ∨{\displaystyle \lor } включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ». Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.
Квантовые вычисления
В квантовых компьютерах аналог операции сложения по модулю 2 — вентиль CNOT.
Ссылки
исключающее ИЛИ — это… Что такое исключающее ИЛИ?
- исключающее ИЛИ
исключающее ИЛИ
Логический оператор Функция «ИСКЛЮЧАЮЩЕЕ ИЛИ» (XOR) равна единице, если равен единице ТОЛЬКО один ее аргумент (МСЭ-Т Н.235.0, МСЭ-T H.235.6, МСЭ-Т Н.235).
[http://www.iks-media.ru/glossary/index.html?glossid=2400324]операция «исключающее ИЛИ»
Поразрядное сложение по модулю 2;
операция двоичной (булевой) алгебры, возвращающая в результате 1, если два значения различны, и 0, если два значения одинаковы.
[http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=1919]исключающее ИЛИ, сложение по модулю 2
(МСЭ-Т G.992.3).
[http://www.iks-media.ru/glossary/index.html?glossid=2400324]Тематики
- Булева алгебра, элементы цифровой техники
Синонимы
- операция «исключающее ИЛИ»
- сложение по модулю 2
EN
- exclusive OR
- exclusive-or
- modulo-2 addition
- XOR
Справочник технического переводчика. – Интент. 2009-2013.
- исключать
- исключающее картирование
Смотреть что такое «исключающее ИЛИ» в других словарях:
Исключающее ИЛИ — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
Исключающее «или» — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
Исключающее или — Сложение по модулю 2 (исключающее «ИЛИ», XOR, «сумма по модулю 2») логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …». Это бинарная инфиксная операция, то есть… … Википедия
выполнять операцию «исключающее ИЛИ» — выполнять операцию «исключающее ИЛИ» Сложение модулю 2. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики Булева алгебра, элементы цифровой техники EN exclusive OR … Справочник технического переводчика
побитовое исключающее ИЛИ — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики Булева алгебра, элементы цифровой техники EN bitwise xOR … Справочник технического переводчика
шифр на основе операции «исключающее ИЛИ» — шифр на основе операции «исключающее ИЛИ» Сложение по модулю 2. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN exclusive or cipher … Справочник технического переводчика
ИСКЛЮЧАЮЩЕЕ СУЖДЕНИЕ — изъемлющее суждение (в нематематической формальной логике), – суждение, в к ром выраженное в нем утверждение или отрицание чего либо относится ко всему объему логич. подлежащего, исключая нек рую выделенную и указанную в суждении часть… … Философская энциклопедия
И/или — и/или составной союз, использующийся в современных официально деловых (юридических, финансовых, государственных[1]), технических и иных текстах на русском языке. Указывает на возможность как одновременного наличия субъектов (признаков… … Википедия
функция исключающее НЕ-ИЛИ — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики Булева алгебра, элементы цифровой техники EN exclusive NOREXNOR … Справочник технического переводчика


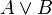 истинно, если истинно
истинно, если истинно 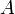 или
или 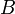 , или оба сразу.
, или оба сразу.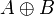 истинно, если истинно
истинно, если истинно