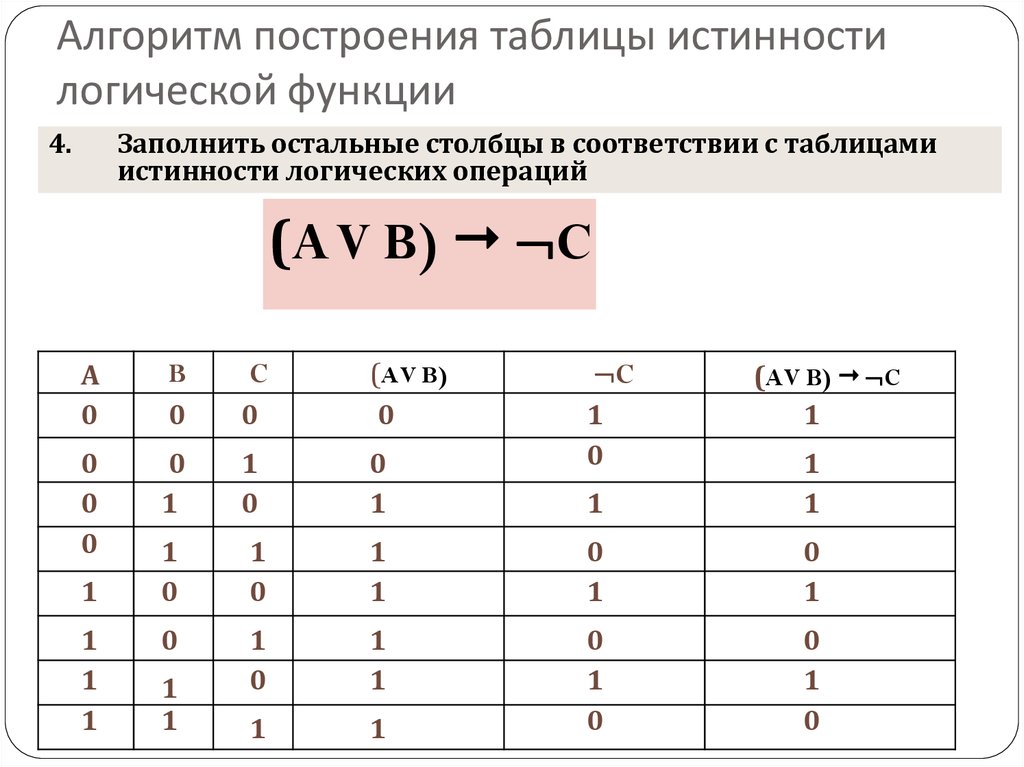
Использование таблиц истинности для решения логических задач
Учитель- Количество посещений 171
- Количество сохранений 3
- Количество комментариев 0
Описание
- Обзор:
- Учащиеся решают логические задачи, используя таблицы истинности, а затем реализуют их с помощью цифровых логических элементов (инженерное дело) или программного обеспечения (информатика).
- Тема:
- Информатика, Инжиниринг
- Уровень:
- Средняя школа, Высшая школа
- Оценки:
- 7 класс, 8 класс, 9 класс, 10 класс, 11 класс, 12 класс
- Тип материала:
- Деятельность/Лаборатория
- Автор:
- Джеффри Эрл
- Дата добавления:
- 04.
04.2019
04.2019- Лицензия:
- Creative Commons Attribution Некоммерческое использование
- Язык:
- Английский
- Формат носителя:
- Загружаемые документы, Текст/HTML
Стандарты
PA.SCI.3.4.10.C1 10 класс
Научная область: Технология и инженерное образование
Тема: Технология и инженерное проектирование
Стандарт: Применение компонентов процесса технологического проектирования.
Степень выравнивания: 3 Улучшенный (2 пользователя)
PA.BIT.15.4.12.H 9-12 классы
Область обучения: Компьютерные и информационные технологии
Стандарт: Программирование
Индикатор: Использование языков программирования для развития навыков логического мышления и решения проблем.
Степень выравнивания: 3 Улучшенный (1 пользователь)
Оценки
Средний балл (возможно 3 балла)
| Степень соответствия | 3 (2 пользователя) |
| Качество объяснения предмета | 3 (2 пользователя) |
| Полезность материалов, разработанных для поддержки обучения | 2 (2 пользователя) |
| Качество оценок | 2 (2 пользователя) |
| Качество технологической интерактивности | 2 (2 пользователя) |
| Качество учебных и практических упражнений | 3 (2 пользователя) |
| Возможности для более глубокого обучения | 2 (2 пользователя) |
- Комбинационная логика
- Цифровая электроника
- Цифровая логика
- Таблицы истинности
- Решение проблем
- Вычислительное мышление
Войдите, чтобы добавить теги к этому элементу.
Примечания к таблице истинности и логическим утверждениям
Таблица истинности логической функции содержит списки всех возможных значений, которые функция может получить для данного входа. Таблица истинности состоит из множества строк и столбцов, причем верхняя строка указывает логические переменные и их комбинации, а нижняя строка показывает конечную функцию с возрастающей сложностью. Таблица истинности логической системы представляет выходные данные системы для данного входа в виде строк и столбцов. Чтобы назвать столбцы таблицы истинности, используются входы и выходы со строками, представляющими все потенциальные входы и выходы схемы.
Что такое логические утверждения? Логическое утверждение — это утверждение, которое возвращает либо истину, либо ложь, т. е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.
Здесь он вернет либо истину, либо ложь в зависимости от оператора. Это декларативный тип оператора, который возвращает true или false.
Некоторые примеры логических утверждений:Примеры предложений, которые являются (или содержат) истинными утверждениями:
- «Том Круз — мужчина».
- «У треугольника три стороны».
- «Милан — столица Италии».
Примеры ложных предложений:
- «Все кулеры сделаны из чистого золота».
- «Два плюс два равно девять».
Примеры предложений, которые не являются (или не составляют) утверждениями: Эмоции, чувства, вопросы и т. д. не могут быть включены в логические утверждения.
- «Кто ты?»
- «Беги!»
- «Королева Англии мудра».
- «Пегас существует».
В логической функции есть три основные операции НЕ, ИЛИ и И:
- НЕ: Это также называется инверсией или отрицанием. Обозначается -. Это означает прямо противоположное или отрицательное значение.
- ИЛИ: Это также называется дизъюнкцией или сложением. Обозначается +. Это похоже на простое добавление значений. Функция возвращает истину, если хотя бы одно из ее значений истинно.
- И: Это также называется соединением или умножением. Он обозначается *. Это похоже на износ умножения для функции, возвращающей истину, оба значения должны быть истинными.
Обозначается -. Это означает прямо противоположное или отрицательное значение.Унарные логические операторы содержат только один логический оператор. Это может быть либо Логическая Истина, либо Логическая Ложь.
Таблица истинности для логического истинно: для каждого логического входа возвращает истинное значение.
Вход | Выход | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
T | T | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F | T | F | T | F | T | F | T | F | T | F | , | F. |
Input | Output |
T | F |
F | F |
Таблица истинности для комплимента: возвращает значение, прямо противоположное логическому входу.
Input | Output(~) |
T | F |
F | T |
В двоичных операциях есть два логических входа. Над этими операторами выполняются операции И, ИЛИ и НЕ.
Таблица истинности для операции ИЛИ: Возвращает истину, если хотя бы один из входов верен, и ложь, если оба входа ложны.
A | B | A OR B |
T | T | T |
T | F | Т |
Ф | T | T |
F | F | F |
Truth Table for AND Operation: it returns true only if both the inputs are true else false.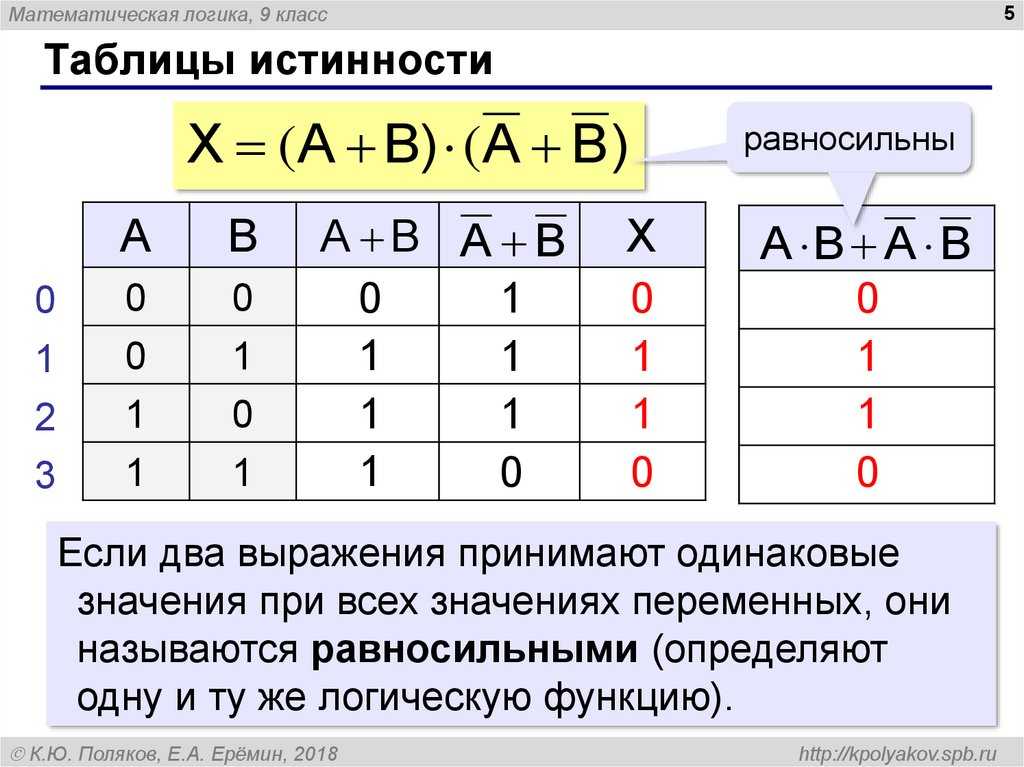
A | B | A AND B |
T | T | T |
T | F | F |
F | T | F |
F | F | F |
Значения функций могут быть 0 или 1. Где логический 0 означает ложь, а логическая 1 означает истину. Таким образом, применяются следующие правила:
Если A = 0, то -A = 1
Если A = 1, то -A = 0
A+B = 0, если A = 0 и B = 0
A+B = 1, за исключением случаев, когда A = 0 и B = 0
A*B = 1 если A = 1 и B = 1
A*B = 0, за исключением случаев, когда A = 1 и B = 1
Как оценить значения логической функции: Пример: показать процесс оценки значений логическая функция -(A+B) * -(A*B).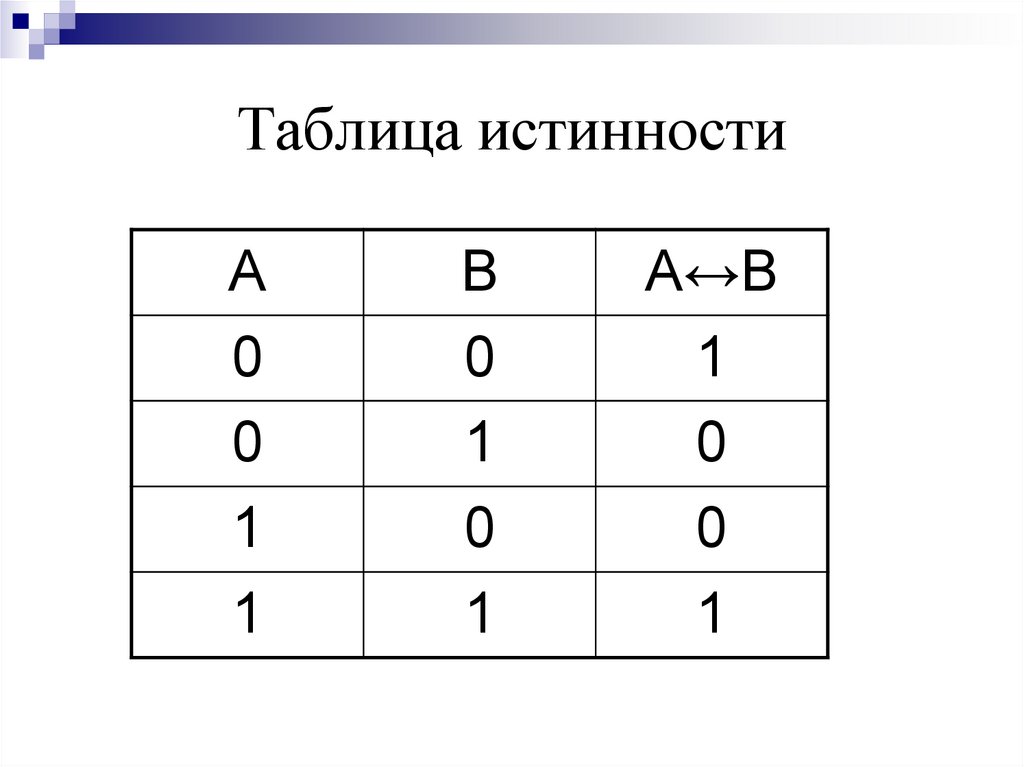
Он определяется путем разбиения на более мелкие составляющие функции и вычисления их значений для достижения последнего шага. Это последовательный процесс. Необходимо выполнить следующие шаги:-
- Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета двоичными числами: 00, 01, 10, 11.
- В третьем столбце значение (A+B) вычисляется с помощью операции ИЛИ. .
- В четвертом столбце минус (дополнение) третьего столбца берется, чтобы найти значения, связанные с функцией -(A+B)
- В пятом столбце мы вычисляем значения (A*B) с помощью AND операция.
- Мы находим отрицательное значение (A*B), чтобы вычислить значение -(A*B)
- В седьмом столбце мы находим И значений в четвертом столбце и шестом столбце, чтобы получить значение -(A+B) )*-(A*B)
Таким же образом мы вычисляем таблицу истинности и значения для всех функций.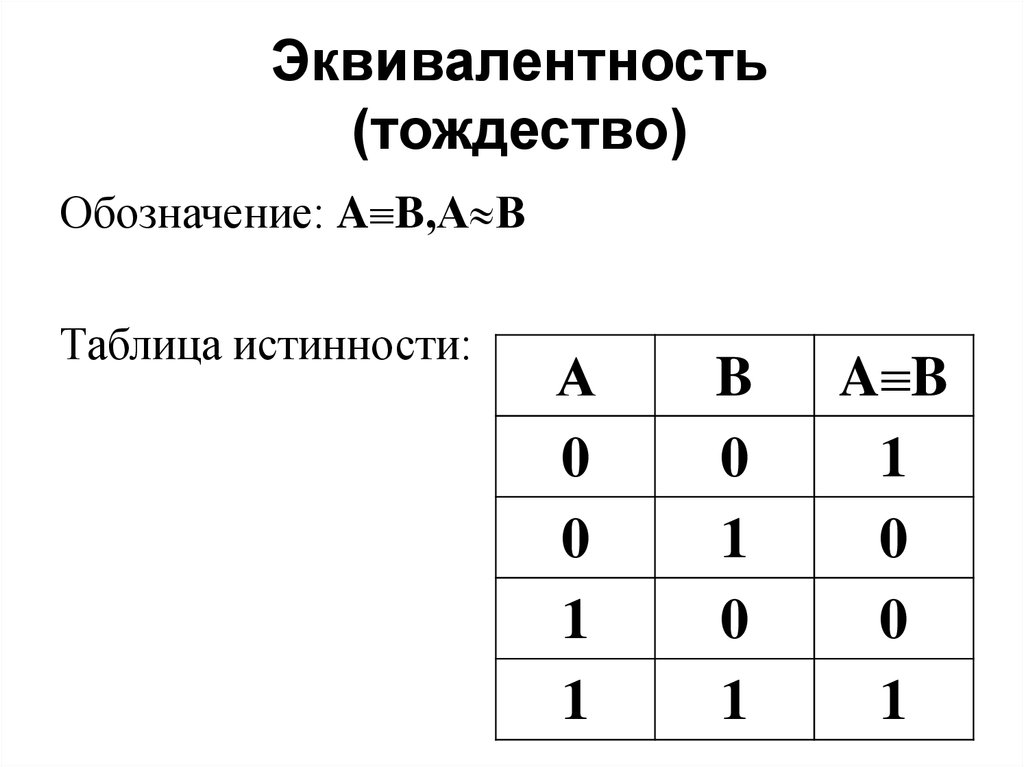
Ниже приведена таблица выражения для -(A+B) * -(A*B).
А | В | (А+В) | -(А+В) | (A*B) | -(A*B) | -(A+B) * -(A*B) | |||||
0 | 0 | 0 | 1 | 0 | 1 | 1 | |||||
0 | 1 | 1 | 0 | 0 | 1 | 0 | |||||
1 | 0 | 1 | 0 | 0 | 1 | 0 | |||||
1 | 1 | 1 | 0 | 1 | 0 | 0 | 9003 09 0 | 9003 09 | 9003 09 | .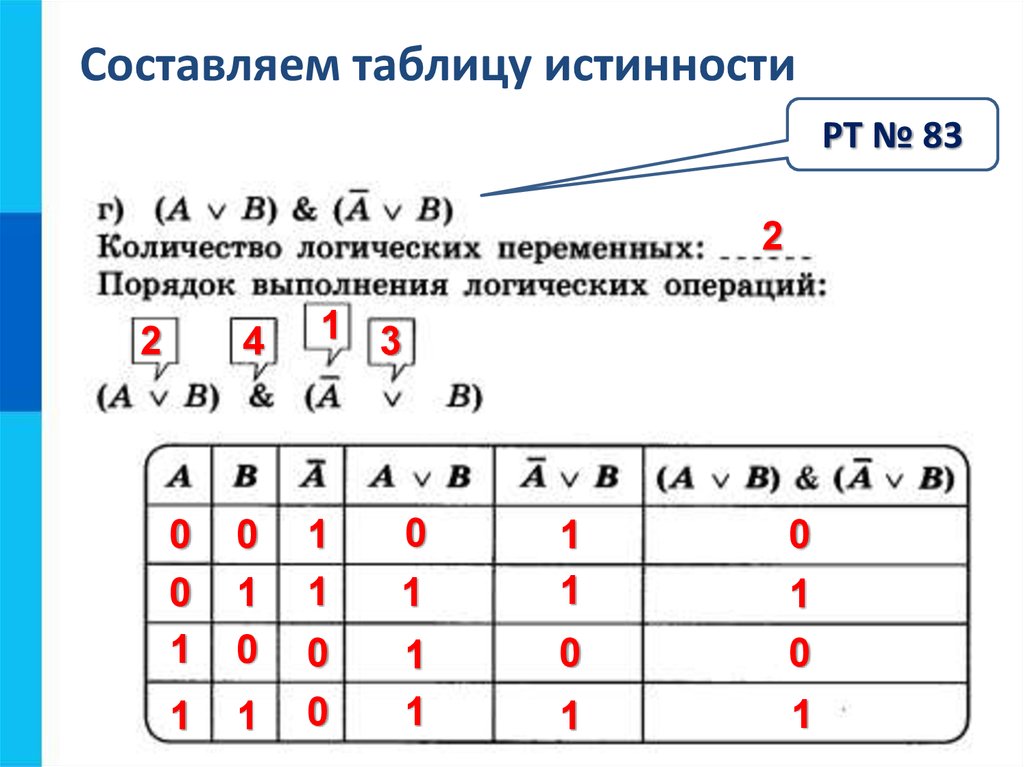 0131Крайний правый (седьмой) столбец содержит последнюю функцию, которая должна быть оценена. Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений. Применение таблиц истинности и логических утверждений:Для все более сложных логических функций компьютеры используются для построения таблиц истинности. Некоторые функции имеют большое количество входных переменных и состоят из нескольких составляющих функций; может получиться таблица с сотнями строк и столбцов. Мы можем использовать таблицы истинности, чтобы определить, верна ли структура логического аргумента. Они широко используются в логике запросов к базе данных, а также в их оптимизации. Кроме того, для приложений, связанных с общей логикой, таких как экспертные системы. Любой анализ, вероятно, должен реализовать их в той или иной форме. Кроме того, они используются в структурах базовых решений (IF, Case/Switch, IIF и т. д.  |
