Алгебра логики и таблицы истинности. (лекция 4)

Похожие презентации:

Основы логики. Таблица истинности. Равносильные логические выражения

Алгебра логики

Основные понятия алгебры логики

Логические операции и таблицы истинности

Логика высказываний. Таблицы истинности

Алгебра логики

Построение таблиц истинности для логических выражений

Логические основы компьютера. Формы человеческого мышления. Формальная логика

Логика высказываний

Элементы алгебры логики. Математические основы информатики. Таблицы истинности

1. Алгебра логики и таблицы истинности

Лекция № 4

2. Основные понятия

Логика — это наука о формах и способах мышления. Это
учение о способах их рассуждений и доказательств.
Понятие — это форма мышления, которая выделяет
существенные признаки предмета или класса предметов,
позволяющие отличать их от других.
Высказывание — это формулировка своего понимания
окружающего
мира.
Высказывание
является
повествовательным предложением, в котором что-либо
утверждается или отрицается.
Умозаключение — это форма мышления, с помощью которой
из одного или нескольких суждений может быть получено
новое суждение (знание или вывод).
Логическая переменная — это простое высказывание,
содержащее только одну мысль.
Ее символическое обозначение — латинская буква (например,
A,B,X,Y и т.д.).
Значением логической переменной могут быть только
константы ИСТИНА и ЛОЖЬ (1 и 0).
Составное высказывание — логическая функция, которая
содержит несколько простых мыслей, соединенных между
собой с помощью логических операций.
Ее символическое обозначение — F(A, B…)

5. Логические связки

A
№ Логическая
связка
Название
Обозначение
Высказывание
Математическая
запись
1
и
конъюнкция
логическое умножение
,
*, And
AиВ
A B,
A * B,
2
или
дизъюнкция
логическое сложение
+, Or
A или В
A B
A + B,
A Or B
3
не
инверсия,
логическое отрицание
¬,
Not
не А
¬А,
Not A
4
Если…то
импликация,
логическое следование
→,
Если A, то В
A→B
A B
5
тогда и
только
тогда
эквивалентность,
равносильность,
логическое тождество
,
,
А тогда и
только
тогда, когда
В
А В,
А В,
A B
A And B
А В
А В

6.

В
Дизъюнкция
А
В
AvB
Инверсия
А
¬А
Импликация
Эквивалентность
А
В А→В
А
В
А≡В
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
1
1
0
1
0
1
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
1
1
1
1
0
1
1
1
1
1
1
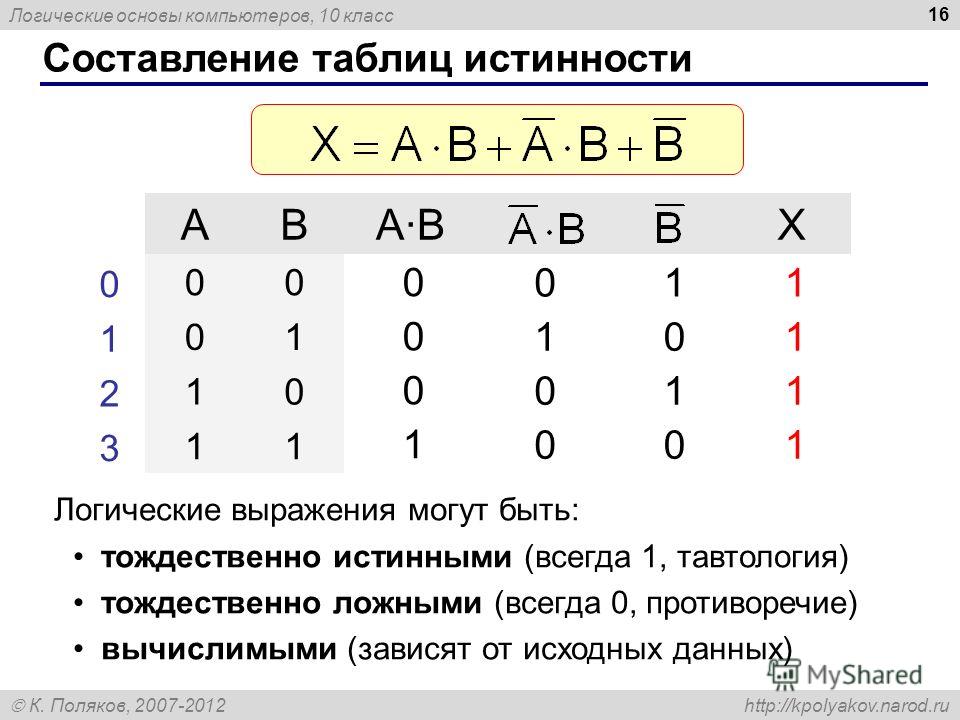
Вывод:
резу- Вывод: результат Вывод: результат Вывод: результат Вывод:
результат
льтат будет ис- будет ложным тог- будет
ложным, будет ложным тог- будет истинным тогтинным тогда и да и только тогда, если исходное
да и только тогда, да и только тогда,
только
тогда, когда оба исход- выражение
ис- когда из истинного когда оба высказыкогда оба исхо- ных высказывания тинно, и наоборот основания (А) сле- вания одновременно
дных высказы- ложны, и истиндует ложное след- либо ложны, либо
вания истинны ным в остальных
ствие (В)
истинны
случаях
Если составное высказывание (логическую функцию)
выразить в виде формулы, в которую войдут логические
переменные и знаки логических операций, то получится
логическое выражение, значение которого можно
вычислить. ), дизъюнкция (v),
импликация (→), эквивалентность (≡).

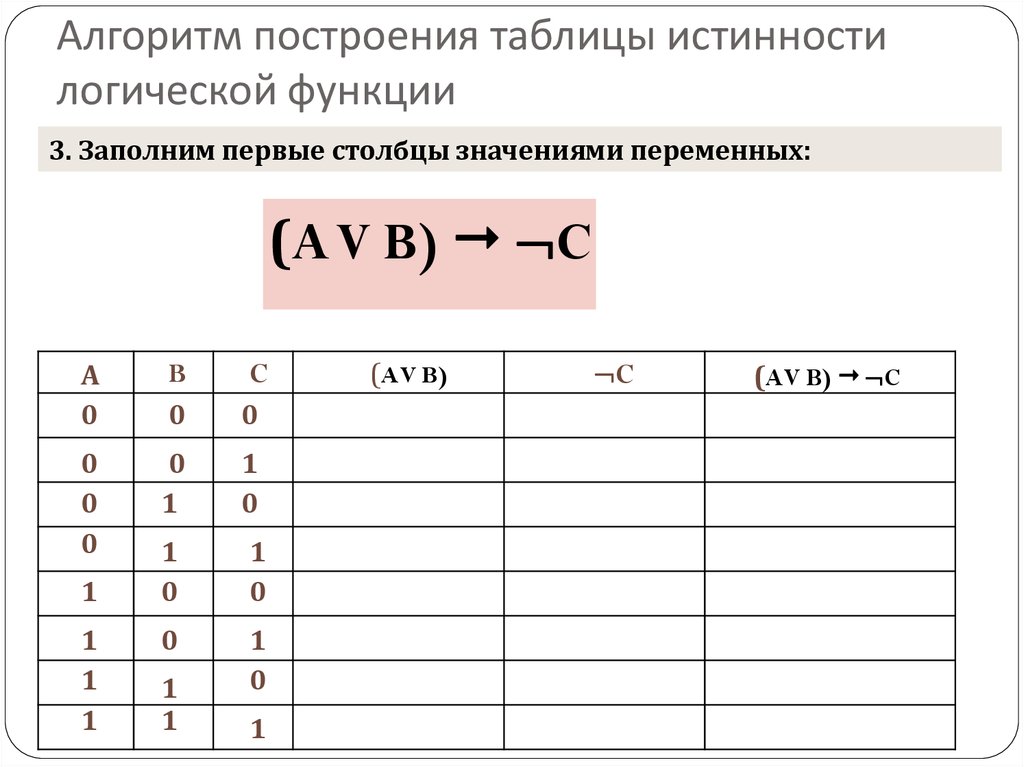
9. Для составления таблицы необходимо:

1.
2.
3.
4.
5.
Выяснить количество строк в таблице (вычисляется как
2n+1, где n — количество переменных).
Выяснить количество столбцов = количество переменных
+ количество логических операций.
Установить последовательность выполнения логических
операций.
Построить таблицу, указывая названия столбцов и
возможные наборы значений исходных логических
переменных.
Заполнить таблицу истинности по столбцам.

10. Пример 1

Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических
операций (v, &, ¬, v, ¬) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
(AvB)&(¬Av¬B)
А
В
AvB
¬А
¬В
¬Av¬B
(AvB)&(¬Av¬B)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0

11.

Логические схемыЭлементы, реализующие базовые логические операции,
назвали
базовыми
логическими
элементами
или
вентилями и характеризуются они не состоянием
контактов, а наличием сигналов на входе и выходе
элемента.
Их
названия
и
условные
обозначения
являются
стандартными и используются при составлении и
описании логических схем компьютера.

13. Правило построение логических схем

1) Определить число логических переменных.
2) Определить количество базовых логических
операций и их порядок.
3) Изобразить для каждой логической операции
соответствующий ей вентиль.
4)Соединить вентили в порядке выполнения
логических операций.

14. Пример 2

Пусть X = истина, Y = ложь. Составить
логическую схему для следующего
логического выражения: F = XvY&X.
Две переменные — X и Y.
2 1
Две логические операции: XvY&X.

15. Задание 1.

Составьте таблицы истинности для
следующих логических
выражений:
1. F = (X&¬Y)vZ.
2. F = X&YvX.
3. F = ¬(XvY)&(YvX).
4. F = ¬((XvY)&(ZvX))&(ZvY).
5. F = A&B&C&¬D.
6. F = (AvB)&(¬BvAvB)

18. Задание 2.

19. Задание 3.

Постройте логическую схему,
соответствующую логическому выражению, и
найдите значение логического выражения:
1. F=AvB&¬C, если А=1, В=1, С=1.
2. F=¬(AvB&C), если А=0, В=1, С=1.
3. F= ¬AvB&C, если А=1, В=0, С=1.
4. F=(AvB)&(CvB), если А=0, В=1, С=0.
5. F=¬(A&B&C), если А=0, В=0, С=1.
6. F=(A&B&C)v(B&Cv¬A), если А=1, В=1, С=0.
7. F=B&¬Av¬B&A, если А=0, В=0.

20. Задание 4.

Постройте логические выражения к
логическим схемам:

English     Русский Правила

Page not found — Сайт skobelevserg!

• Главная
• Информатика
• Практикумы
• Подготовка к ОГЭ
• Рабочие программы
• Используемая литература
• Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed.

This way to the home page.

• Главная
• Информатика
• • 5 класс (ФГОС)
  • • Информация вокруг нас
    • Компьютер — универсальная машина для работы с информацией
    • Ввод информации в память компьютера
    • Управление компьютером
    • Хранение информации
    • Передача информации
    • Кодирование информации
    • Текстовая информация
    • Представление информации в виде таблиц
    • Наглядные формы представления информации
    • Компьютерная графика
    • Обработка информации
  • 6 класс (ФГОС)
  • • Объекты окружающего мира
    • Компьютерные объекты
    • Отношения объектов и их множеств
    • Разновидности объектов и их классификация
    • Системы объектов
    • Персональный компьютер как система
    • Как мы познаем окружающий мир
    • Понятие как форма мышления
    • Информационное моделирование
    • Знаковые информационные модели
    • Табличные информационные объекты
    • Графики и диаграммы
    • Схемы
    • Что такое алгоритм
    • Исполнители вокруг нас
    • Формы записи алгоритмов
    • Типы алгоритмов
    • Управление исполнителем Чертежник
    • Компьютерный практикум
  • 7 класс (ФГОС)
  • • Информация и информационные процессы
    • Компьютер универсальное устройство для работы с информацией
    • Обработка графической информации
    • Обработка текстовой информации
    • Технология мультимедиа
  • 8 класс (ФГОС)
  • • Математические основы информатики
    • Основы алгоритмизации
    • Начала программирования
  • 9 класс (ФГОС)
  • • Моделирование и формализация
    • Алгоритмизация и программирование
    • Обработка числовой информации в электронных таблицах
    • Коммуникационные технологии
  • 10 класс (ФГОС)
  • • Информация и информационные процессы
    • Компьютер и его программное обеспечение
    • Представление информации в компьютере
    • Элементы теории множеств и алгебры логики
    • Современные технологии создания и обработки информационных объектов
  • 11 класс (ФГОС)
  • • Обработка информации в электронных таблицах
    • Алгоритмы и элементы программирования
    • Информационное моделирование
    • Сетевые информационные технологии
    • Основы социальной информатики
• Практикумы
• • Google формы
  • Основы работы в Microsoft PowerPoint
  • Создание анимации в презентациях
  • Основы работы в Microsoft Word
  • Основы работы в Microsoft Excel
  • Создание простейшей базы данных
  • Практикум по MS Excel
• Подготовка к ОГЭ
• Рабочие программы
• Используемая литература
• Об авторах
• • Блоги
  • Сайты

Логические вентили и таблицы истинности

Видео

Вступительное видео

https://www. youtube.com/watch?v=gI-qXk7XojAВидео не может быть загружено, так как отключен JavaScript: Булева логика и логические вентили: ускоренный курс Computer Science #3 (https://www.youtube.com/watch?v=gI-qXk7XojA)

 

 

NOT

NOT Gates

A NOT Gate — простейшая форма логического вентиля. Он просто берет один вход и инвертирует сигнал.

Таблица истинности шлюза NOT
Вход А	Выход
0	1
1	0

 

 

 

И

Элементы И

Элемент И — это элемент, который производит выход только в том случае, если оба входа включены.

И Таблица истинности шлюза
Вход А	Вход Б	Выход
0	0	0
0	1	0
1	0	0
1	1	1

 

ИЛИ

ИЛИ Ворота

Элемент ИЛИ — это тип элемента, который производит выход, если один (или оба) входа включены.

Таблица истинности шлюза ИЛИ
Вход А	Вход Б	Выход
0	0	0
0	1	1
1	0	1
1	1	1

 

NAND

NAND Gates

NAND Gate — это вентиль, который выключает оба, только если оба входа включены, в противном случае он остается включенным. Он состоит из вентиля И, входящего в вентиль НЕ.

Таблица истинности шлюза NAND
Вход А	Вход Б	Выход
0	0	1
0	1	1
1	0	1
1	1	0

ИЛИ-НЕ

Элементы ИЛИ-НЕ

Элемент ИЛИ-НЕ включается, только если оба входа отключены. Он состоит из вентиля ИЛИ, входящего в вентиль НЕ.

Таблица истинности шлюза NOR
Вход А	Вход Б	Выход
0	0	1
0	1	0
1	0	0
1	1	0

XOR

XOR Gates

AN XOR Gate включается только в том случае, если один (но не оба) входы включены.

Таблица истинности шлюза NOR
Вход А	Вход Б	Выход
0	0	0
0	1	1
1	0	1
1	1	0

Практика

Упражнение 1

Попробуйте соединить несколько логических элементов, чтобы посмотреть, что произойдет, используя симулятор ниже. Можете ли вы разработать входы и выходы для следующих примеров.

https://academo.org/demos/logic-gate-simulator/

Example 1

Example 2

Example 3

Example 4

 

Деятельность 2

Упражнение 2. Применение Logic Gates

Используя приведенную ниже ссылку, проверьте, сможете ли вы создать следующие системы:

Симулятор приложений Logic Gates

Система 1 — Вентиляторная система охлаждения.

Если главный выключатель системы включен, то вентилятор будет работать, когда:

• Каждые 5 секунд
• При нажатии кнопки ручного управления.

Система 2 — Базовая система сигнализации

Создайте систему, в которой при срабатывании любого из 3 датчиков (используйте 3 переключателя для обозначения датчиков) сигнальная лампочка будет мигать КРАСНЫМ.

Система 3 – Расширенная система сигнализации

Настройте систему так, чтобы:

• Тревога не срабатывала, если система не была поставлена ​​на охрану (используйте для этого другой переключатель)
• Сигнал тревоги должен попеременно мигать красным цветом и включаться сиреной каждую 1 секунду.

Система 4 – Светофор с кнопочным управлением.

Сделать светофор, который начинается с зеленого, затем переходит на желтый – красный – желтый – снова зеленый.

Подсказка. Вам понадобится флип-флоп!

Ресурсы

Конец тематического теста

Рабочий лист логических ворот

Старшая музыка — логическая песня

Knights против Knaves Starter

Logic Gates Kahoot

Think Maths Workshish

Logic Lab Activty

CS -Workged Workshish

Logicly Demo

Предыдущие экзаменационные вопросы

J15 Paper 11 Qn 7

N16 Paper 11 Qn5

N19 11 Qn3

21 Образец бумаги qn 5

J20 11 qn5a

J18 11 Qn4

тест

Символическая логика с таблицами истинности.

Мы рассмотрели основы символьной логики… | Бретт Берри | Математические приемы

Пример

Мы рассмотрели основы символьной логики в последнем посте . Теперь давайте воспользуемся этими навыками, решив оператор символьной логики.

Последнее сообщение

Введение в таблицы истинности и булевую алгебру

Таблица истинности — это небольшой удобный логический инструмент, который используется не только в математике, но также в информатике и… D)

Ключ к решению этой проблемы состоит в том, чтобы разбить ее на простейшие компоненты и решать по частям.

Шаги 1 и 2

Шаг 1: У нас есть 4 переменные, поэтому нам нужно 4 столбца. Нам также понадобится 16 рядов, так как их по два варианта для каждого.

Самый простой способ скомпоновать таблицу — использовать чередующийся шаблон T/F .

В первой колонке заполните первую половину буквой T, а вторую половину буквой F. Затем чередуйте T/F через каждые 8÷2 или 4 во второй колонке. Продолжайте следовать шаблону, чередуя T/F каждые 2 в третьем столбце и каждый второй пробел в последнем столбце. Это охватывает все возможные перестановки.

Шаг 2: Нам нужно ~B вместо B, поэтому переверните все значения истинности в столбце B. Если вы используете карандаш, вы можете стереть столбец B и просто заменить его на ~B.

Шаг 3: Далее нам нужно вычислить (A ∧ ~B) и (C ∨ D). Для этих вычислений мы добавим в нашу таблицу еще два столбца.

Для логической конъюнкции, т. е. оператора И, нам нужно, чтобы и A, и ~B были истинными, чтобы получить истинный результат. Для ИЛИ нам нужно, чтобы только один из C или D был True, чтобы получить True. Используйте эти знания, чтобы заполнить последние два столбца.

Шаг 3

Шаг 4: Это последний шаг! Добавьте еще один столбец в конец для нашего окончательного вычисления: (A ∧ ~ B) → (C ∨ D).

Мы знаем, что есть только один случай, когда импликация (→) ложна, и это когда T → F.