ОГЭ по информатике: Логические операции

Пример 1.

Для какого из приведённых чисел ложно высказывание: 

НЕ(число > 50) ИЛИ (число чётное)?
1) 9    2) 56     3) 123     4) 8

Решение. Сначала выполняем сравнения в скобках, затем операция НЕ, в последнюю очередь — операция ИЛИ.

1) Подставим число 9 в выражение:
НЕ (9 > 50) ИЛИ (9 чётное)
НЕ (ложь) ИЛИ (ложь) = истина ИЛИ ложь = истина

9 нам не подходит, так как по условию мы должны получить ложь.

2) Подставим число 56 в выражение:
НЕ (56 > 50) ИЛИ (56 чётное)
НЕ (истина) ИЛИ (истина) = ложь ИЛИ истина = истина

56 тоже не подходит.

3) Подставим 123:
НЕ (123 > 50) ИЛИ (123 чётное)
НЕ (истина) ИЛИ (ложь) = ложь 

ИЛИ ложь = ложь 

Число 123 подошло.

Эту задачу можно было решить и по-другому:
НЕ(число > 50) ИЛИ (число чётное)

Нам надо получить ложное значение. Мы видим, что операция ИЛИ будет выполняться в последнюю очередь. Операция ИЛИ даст ложь, когда оба выражения НЕ(число) и (число чётное) будут ложны.

Так как условие (число чётное) должно быть равно ложному значению, то сразу отвергаем варианты с числами 56, 8.

Далее, условие НЕ (число > 50) = ложь, соответственно условие (число > 50) = истина. Из двух оставшихся чисел 9 и 123 этому условию подходит число 123. 

Итак, можно решать прямой подстановкой, что долго и может дать ошибку при вычислении выражения; или же можно решать задачу быстро, проанализировав все простые условия.

Ответ: 3)

 

Пример 2

Для какого из приведённых чисел истинно высказывание:

НЕ(Первая цифра чётная) И НЕ(Последняя цифра нечётная)?

1) 6843       2)  4562       3) 3561       4) 1234

Сначала выполняем сравнения в скобках, затем операции НЕ над скобками, в последнюю очередь — операция И. Все это выражение должно принимать истинное значение.

Так как операция НЕ меняет смысл высказывания на противоположный, мы может переписать это сложное выражение так:

(Первая цифра нечётная)

И (Последняя цифра чётная) = истина 

Как известно, логическое умножение И дает истину только тогда, когда истинны все простые высказывания. Таким образом, оба условия должны быть истинными:

(Первая цифра нечётная) = истина       (Последняя цифра чётная) = истина

Как видно, подходит только число 1234

Ответ: 4)  

 

Пример 3

Для какого из приведённых имён истинно высказывание:
НЕ(Первая буква гласная) И (Количество букв > 5)?

1) Иван      2) Николай      3) Семён      4) Илларион

Перепишем выражение:
(Первая буква не гласная) И

 (Количество букв > 5) = истина 
(Первая буква согласная)  И (Количество букв > 5) = истина 

Оба условия должны выполняться (команда И дает истину когда оба входящих простых условия истинны).

Подходит имя «Николай» (первая буква не гласная и число букв 7>5).

Ответ: 2)

 

Пример 4

Для какого из приведённых значений числа X истинно высказывание:
НЕ (X > 5) И (X > 4)?

1) 4     2) 5     3) 6     4) 7

Первой выполняется операция НЕ, второй — И.

Перепишем выражение: (X ≤ 5) И (X > 4) = истина

Оба условия должны быть верными. Подходит число 5

Ответ: 2)

ОГЭ по информатике

Логические операции — урок. Информатика, 8 класс.

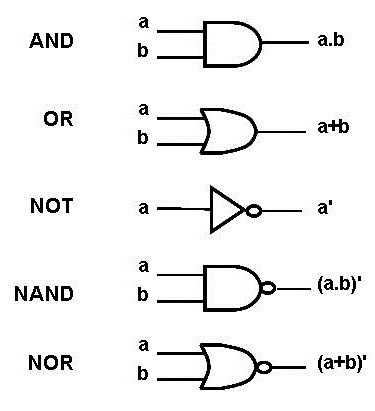
Сложные (составные) высказывания строятся из простых с помощью логических операций. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

 

Название логической операции	Логическая связка
Инверсия	«не»; «неверно, что»
Конъюнкция	«и»; «а»; «но»; «хотя»
Дизъюнкция	«или»

Конъюнкция

Рассмотрим два высказывания:

\(A\) = «Основоположником алгебры логики является Джордж Буль»,

\(B\) = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».

Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.

Например: A И B,AˆB,A⋅B,A&B.

Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

 

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы \(A\) и \(B\)), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: \(00, 01, 10, 11\). В последнем столбце записан результат выполнения логической операции для соответствующих операндов.

 

Обрати внимание!

Конъюнкцию также называют логическим умножением.

Дизъюнкция

Рассмотрим два высказывания:

\(A\) = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,

\(B\) = «Лейбниц является основоположником бинарной арифметики».

Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.

Например: A ИЛИ B;A∨B;A|B;A+B.

Дизъюнкция определяется следующей таблицей истинности:

 

Обрати внимание!

Дизъюнкцию также называют логическим сложением.

Инверсия

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Для записи инверсии используются следующие знаки: НЕ;¬;−

Например: НЕ А;¬А;А−.
Инверсия определяется следующей таблицей истинности:

 

 

Обрати внимание!

Инверсию также называют логическим отрицанием.

Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера».

Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».

Отрицанием высказывания «Все юноши \(8-х\) классов — отличники» является высказывание «Неверно, что все юноши \(8-х\) классов — отличники», другими словами, «Не все юноши \(8-х\) классов — отличники».

Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».

 

Любое сложное высказывание можно записать и виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки.

 

Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция.

 

Изменить порядок выполнения операций можно с помощью расстановки скобок.

 

Обрати внимание!

Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.

Источники:

Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний, 24 с.

Простейшие логические операции в информатике

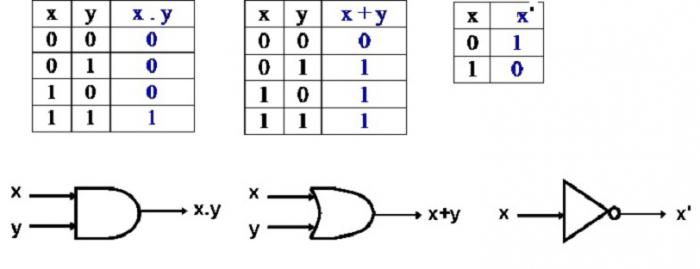
Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.

Отрицание

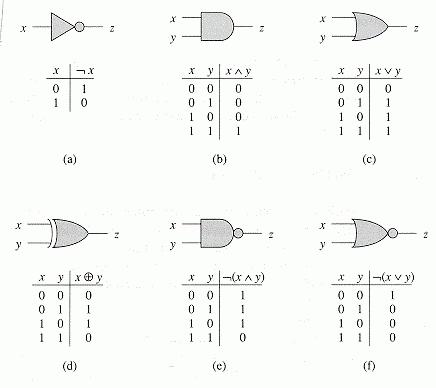
Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:

• отрицание;
• сложение;
• умножение;
• следование;
• равенство.

Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается «0», а правда «1».

Для каждого действия, как и в обычной математике, используются следующие знаки логических операций в информатике: ¬, v, &, ->.

Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.

Логическое отрицание — операция инверсии. Суть заключается в том, что если исходное выражение — истина, то результат инверсии — ложь. И наоборот, если исходное выражение — ложь, то результатом инверсии станет — правда.

При записи этого выражения используется следующее обозначение «¬A».

Приведём таблицу истинности — схему, которая показывает все возможные результаты операции при любых исходных данных.

Таблица истинности для инверсии

А	х	о
¬A	о	х

То есть, если у нас исходное выражение — истина (1), то его отрицание будет ложным (0). А если исходное выражение — ложь (0), то его отрицание — истина (1).

Сложение

Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение —

А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.

1. Е=1, Н=1 ,тогда Е v Н = 1. Если оба выражения истинны, тогда и их дизъюнкция также истинна.
2. Е=0, Н=1 ,в итоге Е v Н = 1. Е=1, Н=0 , тогда Е v Н= 1. Если хотябы одно из выражений истинно, тогда и результат их сложения будет истиной.
3. Е=0, Н=0 ,результат Е v Н = 0. Если оба выражения ложны, то их сумма также — ложь.

Для краткости создадим таблицу истинности.

Дизъюнкция

Е	х	х	о	о
Н	х	о	х	о
Е v Н	х	х	х	о

Умножение

Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком «&», либо буквой «И».

1. Е=1, Н=1 ,тогда Е & Н = 1. Если оба выражения истинны, тогда их конъюнкция — истина.
2. Если хотя бы одно из выражений — ложь, тогда результатом логического умножения также будет ложь.

• Е=1, Н=0, поэтому Е & Н = 0.
• Е=0, Н=1, тогда Е & Н = 0.
• Е=0, Н=0, итог Е & Н = 0.

Конъюнкция

Е	х	х	0	0
Н	х	0	х	0
Е & Н	х	0	0	0

Следствие

Логическая операция следования (импликация) — одна из простейших в математической логике. Она основана на единственной аксиоме — из правды не может следовать ложь.

1. Е=1, Н=, поэтому Е -> Н = 1. Если пара влюблена, то они могут целоваться — правда.
2. Е=0, Н=1, тогда Е -> Н = 1. Если пара не влюблена, то они могут целоваться — также может быть истиной.
3. Е=0, Н=0, из этого Е -> Н = 1. Если пара не влюблена, то они и не целуются — тоже правда.
4. Е=1, Н=0, результатом будет Е -> Н = 0. Если пара влюблена, то они не целуются — ложь.

Для облегчения выполнения математических действий также приведём таблицу истинности.

Импликация

Е	х	х	о	о
Н	х	о	х	0
Е -> Н	х	о	х	х

Равенство

Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как «…тогда и только тогда, когда…». Исходя из этой формулировки, напишем примеры для всех исходных вариантов.

1. А=1, В=1, тогда А≡В = 1. Человек пьёт таблетки тогда и только тогда, когда болеет. (истина)
2. А=0, В=0, в итоге А≡В = 1. Человек не пьёт таблетки тогда и только тогда, когда не болеет. (истина)
3. А=1, В=0, поэтому А≡В = 0. Человек пьёт таблетки тогда и только тогда, когда не болеет. (ложь)
4. А=0, В=1 ,тогда А≡В = 0. Человек не пьёт таблетки тогда и только тогда, когда болеет. (ложь)

Эквивалентность

А	х	о	х	о
В	х	о	0	х
А≡В	х	х	о	о

Свойства

Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.

А v В & ¬В -> В ≡ А

Порядок выполнения действий следующий.

1. ¬В
2. В&(¬В)
3. А v(В&(¬В))
4. (А v(В&(¬В)))->В
5. ((А v(В&(¬В)))->В)≡А

Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.

Решение примера

А	В	¬В	В&(¬В)	А v(В&(¬В))	(А v(В&(¬В)))->В	((А v(В&(¬В)))->В)≡А
х	о	х	о	х	х	х
х	х	о	о	х	х	х
о	о	х	о	о	х	о
о	х	о	о	о	х	о

Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.

Заключение

В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также — что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.

Логические операции «И», «ИЛИ». Информатика во 2-м классе

Цели:

Обучающие:

• познакомить с понятиями “логические операции “И” “ИЛИ”;
• научить оценивать простейшие высказывания с точки зрения истинности и ложности.

Развивающие:

• развитие логического мышления;
• развитие политехнических умений (работа на ПК).

Воспитывающие:

• воспитание познавательной потребности, интереса к предмету;
• воспитание дисциплинированности;
• выполнение установленных требований к уроку (контроль ТБ, правильностью посадки за ПК).

Подготовка к уроку.

1. На демонстрационном ПК загрузить:

• программу “Роботландия — 96”, задача “Перевозчик”;
• презентацию “Приложение к уроку”.

2. На всех компьютерах загрузить:

• программу “Роботландия – 96”, задача “Перевозчик”;
• презентацию “Приложение к уроку”.

Ход урока

1. Организационный этап урока.

а). Разминка. – Улыбнулись друг другу. Сказали добрые слова на букву И.

б). Скажите, с какими высказываниями вы познакомились на предыдущем уроке?

А сейчас повторим:

Истинные высказывания отметьте буквой “И”, а ложные- буквой “Л”.

• Все животные –домашние. (Л) (рис.1)
• Зимой падает иногда снег. (И) (рис. 2)

— Как вы думаете, вы всё узнали о логических операциях? Тема урока: логические действия “И” “ИЛИ”.

Сегодня мы отправляемся в удивительную страну “Логика”.

Но чтобы попасть в неё, мы должны пройти через ворота, где стоят два стража логические действия И и ИЛИ, и выполнить их задание.

Задание №1.

И Выбери круглый и съедобный. (рис. 3)

ИЛИ. Я не очень строгий страж и доволен, когда верно хотя бы одно моё высказывание.

Выбери круглый или съедобный. (рис. 4)

— Сколько предметов взяли?

Вывод: Логические операции: “И” - пересечение, “ИЛИ” — выбор, объединение. (Приложение 1)

2. Этап усвоения и закрепления.

Задание №25.

Разложи геометрические фигуры:

• Треугольники в белый круг,
• Маленькие фигуры в чёрный круг.

— Какие фигуры принадлежат обоим множествам?

Задания №26, №27, №28.

3. Оздоровительная минутка. (Для глаз, пальчиков и т. д. )

4. Этап обобщения полученных знаний.

Домашнее задание №36.

А) В задании надо провести стрелочки от предмета в область или нарисовать его в этой области.

Б) Выпиши множества:

• плавают и летают:
• плавают или летают:

5. Физкультминутка.

А сейчас отдохнём. Выполнив, условие и мы получаем результат.

Мы руками поведём —
Будто в море мы плывём.
1, 2, 3, 4 —
Вот мы к берегу приплыли.
Чтобы косточки рязмять,
Начнём наклоны выполнять —
Вправо и влево, назад и вперёд,

Влево и вправо, назад и вперёд.
Не забудем и присесть —
А теперь всем тихо сесть.

Выполнив условие физминутки, какой получаем результат? (Отдыхаем, расслабляемся).

— Все достигли этого результата?

6. Информационная минутка.

Компьютер в парикмахерской (Приложение 2)

• Сегодня я хочу начать нашу минутку с рассказа о посещении парикмахерской. В этой парикмахерской я бываю часто. Но в последний раз я увидела там что-то для себя неожиданное, а именно — компьютер. Как вы думаете, зачем его приобрели? (Как правило, дети отвечают, что он помогает считать зарплату. Но могут быть и правильные ответы, которые учителю необходимо прокомментировать.)
• Да, действительно, сегодня компьютер может даже помочь человеку выбрать прическу! Вот представьте, что девушка с длинными и светлыми волосами решила подстричь волосы или окрасить их в темный цвет, «но боится, что новая прическа окажется ей не к лицу. И вот тут-то на помощь приходит компьютер! Фотография клиента через специальное устройство, которое называется «сканер», передается в компьютер, и его лицо появляется на экране (при этом на доску можно вывесить нарисованное изображение). С помощью специальной программы к нему прикладываются различные прически. (Это тоже можно проделать на доске, предоставив право детям высказывать свое мнение: подходит или нет та или иная прическа. Как правило, дети активно включаются в обсуждение, что способствует повышению познавательной активности. )

Технологию подбора прически можно продемонстрировать разными способами, в зависимости от уровня техники и наличия программного обеспечения. Можно заранее отсканированное изображение (например, фотографию класса — вот будет сюрприз для детей!) отредактировать на глазах детей в графическом редакторе или воспользоваться специализированными программными продуктами. Но очень важно в конце информационной минутки напомнить ребятам, что графическое изображение переносится в компьютер с помощью сканера, и подчеркнуть преимущества моделирования причесок на компьютере (не надо проводить натурных экспериментов, результаты которых к тому же могут оказаться и неудачными).

7. Работа на компьютере. Игра “перевозчик”.

Давайте посмотрим, какие пары могут образовывать наши пассажиры, а какие нет. Из условия задачи следует:

Истинные высказывания:	Ложные высказывания:
коза И перевозчик вместе;	коза И капуста вместе;
коза одна;	волк И коза вместе.
волк И капуста вместе;
волк И перевозчик вместе;
волк один;
капуста И перевозчик вместе;
капуста одна.

8. Итог урока.

— Какая задача урока стояла перед нами?

— Выполнили ли мы её?

Спасибо за урок. До свидания.

Литература.

1. Адрес http://inf. 1september. ru/2000/2/art/bris1/htm.
2. Перевозкина Л. А. Методические рекомендации.
3. Приложение к журналу “Информатика и образование” №3-2001.

Информатика — Википедия

Информáтика (фр. Informatique; англ. Computer science) — наука о методах и процессах сбора, хранения, обработки, передачи, анализа и оценки информации с применением компьютерных технологий, обеспечивающих возможность её использования для принятия решений^[1].

Информатика включает дисциплины, относящиеся к обработке информации в вычислительных машинах и вычислительных сетях: как абстрактные, вроде анализа алгоритмов, так и конкретные, например разработка языков программирования и протоколов передачи данных.

Темами исследований в информатике являются вопросы: что можно, а что нельзя реализовать в программах и базах данных (теория вычислимости и искусственный интеллект), каким образом можно решать специфические вычислительные и информационные задачи с максимальной эффективностью (теория сложности вычислений), в каком виде следует хранить и восстанавливать информацию специфического вида (структуры и базы данных), как программы и люди должны взаимодействовать друг с другом (пользовательский интерфейс и языки программирования и представление знаний) и т. п.

Информатика занимается теоретическими основами информации и вычислений, а также практическими методами для реализации и применения этих основ

Термин нем. Informatik ввёл немецкий специалист Карл Штейнбух в статье Informatik: Automatische Informationsverarbeitung (Информатика: Автоматическая обработка информации) 1957 года^[2].

Термин «Computer science» («Компьютерная наука») появился в 1959 году в научном журнале Communications of the ACM^[3], в котором Луи Фейн (Louis Fein) выступал за создание Graduate School in Computer Sciences (Высшей школы в области информатики) аналогичной Гарвардской бизнес-школе, созданной в 1921 году^{[4][уточнить]}. Обосновывая такое название школы, Луи Фейн ссылался на Management science («Наука управления»), которая так же как и информатика имеет прикладной и междисциплинарный характер, при этом имеет признаки характерные для научной дисциплины. Усилия Луи Фейна, численного аналитика Джорджа Форсайта^[en] и других увенчались успехом: университеты пошли на создание программ, связанных с информатикой, начиная с Университета Пердью в 1962^[5].

Французский термин «informatique» введён в 1962 году Филиппом Дрейфусом, который также предложил перевод на ряд других европейских языков.

Термины «информология» и «информатика» предложены в 1962 году членом-корреспондентом АН СССР Александром Харкевичем. Основы информатики как науки были изложены в книге «Основы научной информации» 1965 года, которая была переиздана в 1968 году, под названием «Основы информатики»^[6].

Несмотря на своё англоязычное название (англ. Computer Science — компьютерная наука), большая часть научных направлений, связанных с информатикой, не включает изучение самих компьютеров. Вследствие этого были предложены несколько альтернативных названий^[7]. Некоторые факультеты крупных университетов предпочитают термин вычислительная наука (computing science), чтобы подчеркнуть разницу между терминами. Датский учёный Питер Наур предложил термин даталогия (datalogy)^[8], чтобы отразить тот факт, что научная дисциплина оперирует данными и занимается обработкой данных, хотя и не обязательно с применением компьютеров. Первым научным учреждением, включившим в название этот термин, был Департамент Даталогии (Datalogy) в Университете Копенгагена, основанный в 1969 году, где работал Питер Наур, ставший первым профессором в даталогии (datalogy). Этот термин используется в основном в скандинавских странах. В остальной же Европе часто используются термины, производные от сокращённого перевода фраз «автоматическая информация» (automatic information) (к примеру informazione automatica по-итальянски) и «информация и математика» (information and mathematics), например, informatique (Франция), Informatik (Германия), informatica (Италия, Нидерланды), informática (Испания, Португалия), informatika (в славянских языках) или pliroforiki (πληροφορική, что означает информатика) — в Греции. Подобные слова также были приняты в Великобритании, например, Школа информатики в Университете Эдинбурга^[9].

В русском, английском, французском и немецком языках в 1960-х годах была тенденция к замене термина «документация» терминами, имеющими в своей основе слово «информация»^[10]. В русском языке производной от термина «документация» стала документалистика и получили распространение термины научная и научно-техническая информация.

Во Франции термин официально вошёл в употребление в 1966 году^[11]. В немецком языке термин нем. Informatik имел вначале двойственное значение. Так, в ФРГ^[10] и Великобритании^[1] он был в значении «computer science», то есть означал всё, что связано с применением ЭВМ, а в ГДР, как и в основном по Европе, обозначал науку по французской и русской модели.

Эквиваленты в английском языке[править | править код]

Считается, что под терминами «informatics» в европейских странах и «информатика» в русском языке понимается направление, именуемое в английском языке «computer science». К другому направлению, посвящённому изучению структуры и общих свойств объективной (научной) информации, иногда называемому документалистикой (документальной информатикой) или автоматическим анализом документов^[1], близок термин «information science».

Принято считать, что в английский язык термин «informatics» независимо от остальных ввёл Уолтер Ф. Бауэр, основатель «Informatics Inc.». В США в настоящее время термин англ. informatics связан с прикладными вычислениями или обработкой данных в контексте другой области^[12], например в биоинформатике («bioinformatics») и геоинформатике («geoinformatics»).

Во многих словарях informatics и computer science приравниваются к информатике. В тезаурусе ЮНЕСКО «Информатика — Informatics» даётся как синоним к переводу «Computer science — Компьютерные науки»^[13].

Полисемия[править | править код]

Ряд учёных (специалистов в области информатики) утверждали, что в информатике существуют три отдельные парадигмы. Например, Питер Вегнер^[en] выделял науку, технологию и математику^[14]. Рабочая группа Питера Деннинга^[en] утверждала, что это теория, абстракция (моделирование) и дизайн^[15]. Амнон Х. Эден описывал эти парадигмы, как^[16]:

• рационалистическую парадигму, где информатика — это раздел математики, математика доминирует в теоретической информатике и в основном использует логический вывод,
• технократическую парадигму, используемую в инженерных подходах, наиболее важных в программной инженерии,
• и научную парадигму, где информатика — это ветвь естественных (эмпирических) наук, но информатика отличается тем, что в ней эксперименты проводятся над искусственными объектами (программами и компьютерами).

Полисемия в русском языке[править | править код]

В разные периоды развития информатики в СССР и России в понятие «информатика» вкладывался различный смысл. Информатика — это^[17]:

1. Теория научно-информационной деятельности. В рамках библиотечного дела под термином «научно-информационная деятельность» понимается «практическая работа по сбору, аналитико-синтетической переработке, хранению, поиску и предоставлению учёным и специалистам закрепленной в документах научной информации»^[18]. В 1952 г. в Москве был создан Институт научной информации Академии наук (переименованный позднее в ВИНИТИ). Цели его создания были более широкими, чем выполнение «научно-информационной деятельности» и А. А. Харкевич (директор Института проблем передачи информации АН СССР) предложил в письме А. И. Михайлову (директору ВИНИТИ) новое название: «„информология“ или „информатика“ („информация“ плюс „автоматика“)» ^[19]. Третье издание «Большой советской энциклопедии» (1970-е гг.) фиксирует значение информатики как дисциплины, изучающей «структуру и общие свойства научной информации, а также закономерности её создания, преобразования, передачи и использования в различных сферах человеческой деятельности»^[19].
2. Наука о вычислительных машинах и их применении (вычислительная техника и программирование). В 1976 г. профессорá Мюнхенского технического университета Ф. Л. Бауэр и Г. Гооз написали книгу «Информатика. Вводный курс», переведённую в том же году В. К. Сабельфельдом, учеником известного советского учёного Андрея Петровича Ершова, на русский язык. Они перевели «Informatik» словом «информатика» и определили как «науку, занимающуюся разработкой теории программирования и применения ЭВМ»^[19]. Термин «Informatik» Ф. Л. Бауэр и Г. Гооз объясняют как «немецкое название для computer science — области знания, которая сложилась в самостоятельную научную дисциплину в шестидесятые годы, прежде всего в США, а также в Великобритании. … В английском языке, по-видимому, останется „computer science“ (вычислительная наука), причем этот термин имеет уклон в область теории»^[20].
3. Фундаментальная наука об информационных процессах в природе, обществе и технических системах. В начале 1990-х гг. К. К. Колин (заместитель директора Института проблем информатики АН СССР) синтезировал толкования информатики, данные академиками А. П. Ершовым и Б. Н. Наумовым, а также проф. Ю. И. Шемакиным следующим образом: информатика — это наука «о свойствах, законах, методах и средствах формирования, преобразования и распространения информации в природе и обществе, в том числе при помощи технических систем». Предметная область информатики, по Колину, включает такие разделы: (1) теоретическая информатика; (2) техническая информатика; (3) социальная информатика, (4) биологическая информатика и (5) физическая информатика^[21].

Полагают^[17], что одновременное существование всех трёх значений у слова «информатика» затрудняет и мешает развитию данного научного направления.

Самые ранние основы того, что впоследствии станет информатикой, предшествуют изобретению современного цифрового компьютера. Машины для расчёта нескольких арифметических задач, такие как счёты, существовали с древности, помогая в таких вычислениях как умножение и деление.

Блез Паскаль спроектировал и собрал первый рабочий механический калькулятор, известный как калькулятор Паскаля, в 1642^[22].

В 1673 году Готфрид Лейбниц продемонстрировал цифровой механический калькулятор, названный «Stepped Reckoner»^[23]. Его можно считать первым учёным в области компьютерных наук и специалистом в области теории информации, поскольку, среди прочего, он ещё описал двоичную (бинарную) систему чисел.

В 1820 году Томас де Кольмар^[en] запустил промышленный выпуск механического калькулятора после того, как он создал свой упрощённый арифмометр, который был первой счётной машиной, достаточно прочной и надёжной для ежедневного использования. Чарльз Бэббидж начал проектирование первого автоматического механического калькулятора, его разностной машины, в 1822, что в конечном счёте подало ему идею первого программируемого механического калькулятора, его аналитической машины.

Он начал работу над этой машиной в 1834 году и менее чем за два года были сформулированы многие из основных черт современного компьютера. Важнейшим шагом стало использование перфокарт, сработанных на Жаккардовском ткацком станке ^[24], что открывало бесконечные просторы для программирования ^[25]. В 1843 году во время перевода французской статьи на аналитической машине Ада Лавлейс написала в одной из её многочисленных записок алгоритм для вычисления чисел Бернулли, который считается первой компьютерной программой ^[26].

Около 1885 года Герман Холлерит изобрёл табулятор, который использовал перфокарты для обработки статистической информации; в конечном итоге его компания стала частью IBM. В 1937 году, спустя сто лет после несбыточной мечты Бэббиджа, Говард Эйкен убедил руководство IBM, производившей все виды оборудования для перфорированных карт^[27] и вовлечённой в бизнес по созданию калькуляторов, разработать свой гигантский программируемый калькулятор ASCC/Harvard Mark I, основанный на аналитической машине Бэббиджа, которая, в свою очередь, использовала перфокарты и центральный вычислитель (central computing unit). Про готовую машину поговаривали: «мечта Бэббиджа сбылась»^[28].

В 1940-х с появлением новых и более мощных вычислительных машин термин компьютер стал обозначать эти машины, а не людей, занимающихся вычислениями (теперь слово «computer» в этом значении употребляется редко)^[29]. Когда стало ясно, что компьютеры можно использовать не только для математических расчётов, область исследований информатики расширилась с тем, чтобы изучать вычисления в целом. Информатика получила статус самостоятельной научной дисциплины в 1950-х и начале 1960-х годов^[30][31]. Первая в мире степень по информатике, Диплом Кэмбриджа по информатике, была присвоена в компьютерной лаборатории Кембриджского университета в 1953 году. Первая подобная учебная программа в США появилась в Университете Пердью в 1962 году^[32]. С распространением компьютеров возникло много новых самодостаточных научных направлений, основанных на вычислениях с помощью компьютеров.

Мало кто изначально мог предположить, что сами компьютеры станут предметом научных исследований, но в конце 1950-х годов это мнение распространилось среди большинства учёных ^[33]. Ныне известный бренд IBM в то время был одним из участников революции в информатике. IBM (сокращение от International Business Machines) выпустила компьютеры IBM 704^[34] и позже — IBM 709^[35], которые уже широко использовались одновременно с изучением и апробацией этих устройств. «Тем не менее работа с (компьютером) IBM была полна разочарований… при ошибке в одной букве одной инструкции программа „падала“ и приходилось начинать всё сначала»^[33]. В конце 1950-х годов информатика как дисциплина ещё только становилась^[36], и такие проблемы были обычным явлением.

Со временем был достигнут значительный прогресс в удобстве использования и эффективности вычислительной техники. В современном обществе наблюдается явный переход среди пользователей компьютерной техники: от её использования только экспертами и специалистами к использованию всем и каждым. Изначально компьютеры были весьма дорогостоящими и чтобы их эффективно использовать нужна была помощь специалистов. Когда компьютеры стали более распространёнными и доступными, тогда для решения обычных задач стало требоваться меньше помощи специалистов.

История информатики в СССР[править | править код]

Эта статья или раздел описывает ситуацию применительно лишь к одному региону, возможно, нарушая при этом правило о взвешенности изложения. Вы можете помочь Википедии, добавив информацию для других стран и регионов.

В школах СССР учебная дисциплина «Информатика» появилась в 1985 году одновременно с первым учебником А. П. Ершова «Основы информатики и вычислительной техники»^[37].

4 декабря отмечается День российской информатики, так как в этот день в 1948 году Государственный комитет Совета министров СССР по внедрению передовой техники в народное хозяйство зарегистрировал за номером 10 475 изобретение И. С. Брука и Б. И. Рамеева — цифровую электронную вычислительную машину M-1^[38].

Основные достижения[править | править код]

Несмотря на короткую историю в качестве официальной научной дисциплины, информатика внесла фундаментальный вклад в науку и общество. По сути, информатика, наряду с электроникой, является одной из основополагающих наук текущей эпохи человеческой истории, называемой информационной эпохой. При этом информатика является предводителем информационной революции и третьим крупным шагом в развитии технологий, после промышленной революции (1750—1850 н. э.) и неолитической революции (8000-5000 до н. э.).

Вклад информатики:

• Начало «цифровой революции», включающей информационную эпоху и интернет.
• Дано формальное определение вычислений и вычислимости, и доказательство того, что существуют алгоритмически неразрешимые задачи^[40].
• Введено понятие языка программирования, то есть средства для точного выражения методологической информации на различных уровнях абстракции^[41].
• В криптографии расшифровка кода «Энигмы» стала важным фактором победы союзных войск во Второй мировой войне^[39].
• Вычислительные методы обеспечили возможность практической оценки процессов и ситуаций большой сложности, а также возможность проведения экспериментов исключительно за счёт программного обеспечения. Появилась возможность углубленного изучения разума и картирования генома человека, благодаря проекту «Геном человека». Проекты распределенных вычислений, такие как Folding@Home, исследуют сворачивание молекул белка.
• Алгоритмическая торговля повысила эффективность и ликвидность финансовых рынков с помощью искусственного интеллекта, машинного обучения и других статистических и численных методов на больших диапазонах данных ^[42]. Частое использование алгоритмической торговли может усугубить волатильность^[43].
• Компьютерная графика и CGI повсеместно используются в современных развлечениях, особенно в области телевидения, кино, рекламы, анимации и видео-игр. Даже фильмы, в которых нет (явного) использования CGI, как правило, сняты на цифровые камеры и впоследствии обработаны или отредактированы в программах обработки видео.
• Моделирование различных процессов, например в гидродинамике, физике, электрике, электронных системах и цепях, а также для моделирования общества и социальных ситуаций (в частности, военных игр), учитывая среду обитания и др. Современные компьютеры позволяют оптимизировать, например, такие конструкции, как проект целого самолёта. Известным программным обеспечением является симулятор электронных схем SPICE, а также программное обеспечение для физической реализации новых (или модифицированных) конструкций, включающее разработку интегральных схем.
• Искусственный интеллект приобретает все большее значение, одновременно с этим становясь более сложным и эффективным. Существует множество применений искусственного интеллекта (ИИ), например роботы-пылесосы, которые можно использовать дома. ИИ также присутствует в видеоиграх, роботах огневой поддержки и противоракетных системах.

Информатика делится на ряд разделов. Как дисциплина, информатика охватывает широкий круг тем от теоретических исследований алгоритмов и пределов вычислений до практической реализации вычислительных систем в области аппаратного и программного обеспечения^[44][45]. Комитет CSAB^[en], ранее называемый «Советом по аккредитации вычислительных наук», включающий представителей Ассоциации вычислительной техники (ACM) и Компьютерного общества IEEE^[en] (IEEE-CS)^[46] — определил четыре области, важнейшие для дисциплины информатика: теория вычислений, алгоритмы и структуры данных, методология программирования и языков, компьютерные элементы и архитектура. В дополнение к этим четырём направлениям, комитет CSAB определяет следующие важные области информатики: разработка программного обеспечения, искусственный интеллект, компьютерные сети и телекоммуникации, системы управления базами данных, параллельные вычисления, распределённые вычисления, взаимодействия между человеком и компьютером, компьютерная графика, операционные системы, числовые и символьные вычисления^[44].

Теоретическая информатика[править | править код]

Огромное поле исследований теоретической информатики включает как классическую теорию алгоритмов, так и широкий спектр тем, связанных с более абстрактными логическими и математическими аспектами вычислений. Теоретическая информатика занимается теориями формальных языков, автоматов, алгоритмов, вычислимости и вычислительной сложности, а также вычислительной теорией графов, криптологией, логикой (включая логику высказываний и логику предикатов), формальной семантикой и закладывает теоретические основы для разработки компиляторов языков программирования.

Теория алгоритмов[править | править код]

По словам Питера Деннинга^[en], к фундаментальным вопросам информатики относится следующий вопрос: «Что может быть эффективно автоматизировано?»^[30] Изучение теории алгоритмов сфокусировано на поиске ответов на фундаментальные вопросы о том, что можно вычислить и какое количество ресурсов необходимо для этих вычислений. Для ответа на первый вопрос в теории вычислимости рассматриваются вычислительные задачи, решаемые на различных теоретических моделях вычислений. Второй вопрос посвящён теории вычислительной сложности; в этой теории анализируются затраты времени и памяти различных алгоритмов при решении множества вычислительных задач.

Знаменитая задача «P=NP?», одна из Задач тысячелетия^[47], является нерешённой задачей в теории алгоритмов.

Информация и теория кодирования[править | править код]

Теория информации связана с количественной оценкой информации. Это направление получило развитие благодаря трудам Клода Э. Шеннона, который нашёл фундаментальные ограничения на обработку сигнала в таких операциях, как сжатие данных, надёжное сохранение и передача данных^[48].

Теория кодирования изучает свойства кодов (системы для преобразования информации из одной формы в другую) и их пригодность для конкретной задачи. Коды используются для сжатия данных, в криптографии, для обнаружения и коррекции ошибок, а в последнее время также и для сетевого кодирования. Коды изучаются с целью разработки эффективных и надёжных методов передачи данных.

Алгоритмы и структуры данных[править | править код]

Алгоритмы и структуры данных, как раздел информатики, связаны с изучением наиболее часто используемых вычислительных методов и оценкой их вычислительной эффективности.

Теория языков программирования[править | править код]

В теории языков программирования, как подразделе информатики, изучают проектирование, реализацию, анализ и классификацию языков программирования в целом, а также изучают отдельные элементы языков. Эта область информатики, с одной стороны, в большой степени полагается на достижения таких наук как математика, программная инженерия и лингвистика, с другой стороны, сама оказывает большое влияние на их развитие. Теория языков программирования активно развивается, многие научные журналы посвящены этому направлению.

Формальные методы[править | править код]

Формальные методы — это своего рода математический подход, предназначенный для спецификации, разработки и верификации программных и аппаратных систем. Использование формальных методов при разработке программного и аппаратного обеспечения мотивировано расчётом на то, что, как и в других инженерных дисциплинах, надлежащий математический анализ обеспечит надёжность и устойчивость проекта. Формальные методы являются важной теоретической основой при разработке программного обеспечения, особенно в случаях, когда дело касается надёжности или безопасности. Формальные методы являются полезным дополнением к тестированию программного обеспечения, так как они помогают избежать ошибок, а также являются основой для тестирования. Для их широкого использования требуется разработка специального инструментария. Однако высокая стоимость использования формальных методов указывает на то, что они, как правило, используются только при разработке высокоинтегрированных и жизненно-важных систем^[en], где надёжность и безопасность имеют первостепенное значение. Формальные методы имеют довольно широкое применение: от теоретических основ информатики (в частности, логики вычислений, формальных языков, теории автоматов, программ и семантики) до систем типов и проблем алгебраических типов данных в задачах спецификации и верификации программного и аппаратного обеспечения.

Прикладная информатика[править | править код]

Прикладная информатика направлена на применение понятий и результатов теоретической информатики к решению конкретных задач в конкретных прикладных областях.

Искусственный интеллект[править | править код]

Это область информатики, неразрывно связанная с такими целеполагающими процессами, как решение задач, принятие решений, адаптация к окружающим условиям, обучение и коммуникация, присущими и людям, и животным. Возникновение искусственного интеллекта (ИИ) связано с кибернетикой и ведёт свой отсчёт с Дартмутской Конференции (1956). Исследования в области искусственного интеллекта (AI) с необходимостью были междисциплинарными, и основывались на таких науках, как: прикладная математика, математическая логика, семиотика, электротехника, философия сознания, нейрофизиология и социальный интеллект. У обывателей искусственный интеллект ассоциируется в первую очередь с робототехникой, но кроме этого ИИ является неотъемлемой частью разработки программного обеспечения в самых разных областях. Отправной точкой в конце 1940-х годов стал вопрос Алана Тьюринга: «Могут ли компьютеры думать?», и этот вопрос остаётся фактически без ответа, хотя «тест Тьюринга» до сих пор используется для оценки результатов работы компьютера в масштабах человеческого интеллекта.

Архитектура компьютера и компьютерная инженерия[править | править код]

Архитектура компьютера, или организация цифрового компьютера, является концептуальной структурой компьютерной системы. Она сосредоточена в основном на способе, при котором центральный процессор выполняет внутренние операции и обращается к адресам в памяти^[49]. Она часто включает в себя дисциплины вычислительной техники и электротехники, выбор и соединение аппаратных компонентов для создания компьютеров, которые удовлетворяют функциональным, производительным и финансовым целям.

Компьютерная инженерия связана с аппаратной частью вычислительной техники, например основами микропроцессорной техники, компьютерных архитектур и распределённых систем. Таким образом, она обеспечивает связь с электротехникой.

Анализ производительности компьютера[править | править код]

Анализ производительности компьютера — это изучение работы компьютеров с целью повышения пропускной способности, управления временем отклика, эффективного использования ресурсов, устранения узких мест и прогнозирования производительности при предполагаемых пиковых нагрузках^[50].

Компьютерная графика и визуализация[править | править код]

Компьютерная графика представляет собой изучение цифрового визуального содержания и включает в себя синтез и манипуляцию данными изображения. Это направление связано со многими другими областями информатики, в том числе с компьютерным зрением, обработкой изображений и вычислительной геометрией, также оно активно применяется в области спецэффектов и видео-игр.

Компьютерная безопасность и криптография[

Формулы и Задачи (Информатика 10)

Формулы

N = 2ⁱ

N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)

I = K * i

I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)

Q = N^L

Q — количество разных сообщений
N — количество символов
L — длина сообщения

Формула Хартли:

I = log₂N

I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений

---

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a₃a₂a₁a₀ = a₃ * p³ + a₂ * p² + a₁ * p¹ + a₀ * p⁰

Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

a₃a₂a₁a₀ = ((a₃ * p + a₂) * p + a₁) * p + a₀

p — основание системы счисления в котором представлено число.

Пример:

6375₁₀ = 6 * 10³ + 3 * 10² + 7 * 10¹ + 5 * 10⁰
6375₁₀ = ((6 * 10 + 3) * 10 + 7) * 10 + 5
1234₅ = 1 * 5³ + 2 * 5² + 3 * 5¹ + 4 * 5⁰ = 194₁₀
1234₅ = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 194₁₀

Развернутая запись дробного числа:

0,a₁a₂a₃a₄ = a₁*p^-1 + a₂*p^-2 + a₃*p^-3 + a₄*p^-4

Запись через схему Горнера:

0,a₁a₂a₃a₄ = p^-1 * (a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄)))
p * (0,a₁a₂a₃a₄) = a₁ + p^-1 * (a₂ + p^-1 * (a₃ + p^-1 * a₄))

p — основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10^-1 + 3 * 10^-2 + 7 * 10^-3 + 5 * 10^-4
0,6375 = 10^-1 * (6 + 10^-1 * (3 + 10^-1 * (7 + 10^-1 * 5)))
0,1234₅ = 1 * 5^-1 + 2 * 5^-2 + 3 * 5^-3 + 4 * 5^-4
0,1234₅ = 5^-1 * (1 + 5^-1 * (2 + 5^-1 * (3 + 5^-1 * 4)))

Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

1. информационная ёмкость символа: 256 = 2⁸      =>>      i = 8 бит = 1 байт
2. количество символов на странице:
   32 * 64 = 2⁵ * 26 = 2¹¹
3. общее количество символов:
   L = 10 * 2¹¹
4. информационный объём сообщения:
   I = L * i = 10 * 2¹¹ * 1 байт = 20 Кбайт

---

Системы счисления

  X10     X16     X8       X2
 0      0      0        0  1      1      1        1  2      2      2       10  3      3      3       11  4      4      4      100  5      5      5      101  6      6      6      110  7      7      7      111  8      8     10     1000  9      9     11     1001 10      A     12     1010 11      B     13     1011 12      C     14     1100 13      D     15     1101 14      E     16     1110 15      F     17     1111 16     10     20    10000 17     11     21    10001 18     12     22    10010 19     13     23    10011 20     14     24    10100 21     15     25    10101 22     16     26    10110 23     17     27    10111 24     18     30    11000 25     19     31    11001 26     1A     32    11010 27     1B     33    11011 28     1C     34    11100 29     1D     35    11101 30     1E     36    11110 31     1F     37    11111 32     20     40   100000

Логические операции

Логической операцией называется выбор решения (действия), исходя из  заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.

---

Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

A
0	1
1	0

Действие, связанное с операцией НЕ можно записать следующим образом:

---

Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).

Таблица истинности для операции И имеет вид:

A	B	X=A^B
0	0	0
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией И можно записать следующим образом:

X = AB = A*B = A ^ B

---

Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A	B	X=A v B
0	0	0
0	1	1
1	0	1
1	1	1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

X = A + B = A v B

---

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A	B	X=AB
0	0	0
0	1	1
1	0	1
1	1	0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

---

Действие, связанное с операцией Импликации можно записать следующим образом:

X = A → B

Таблица истинности Импликации имеет вид:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

---

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A	B	A Ξ B
0	0	1
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A Ξ B

---

   

Диаграммы Венна (круги Эйлера)

 

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.

маска сети	255.	255.	224.	0
IP-адрес	12.	16.	196.	10	— ip-адрес (узла, компьютера и т.п.)
IP-адрес	0000 1100.	0001 0000.	1100 0100.	0000 1010
маска сети	1111 1111.	1111 1111.	1110 0000.	0000 0000
адрес сети	0000 1100.	0001 0000.	110x xxxx.	xxxx xxxx	— эта часть относится к адресу сети — она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее:
адрес сети	0000 1100.	0001 0000.	1100 0000.	0000 0000	— полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем:
адрес сети	12.	16.	192.	0	— полный адрес сети (в десятичном виде)

 

Информатика: уроки, тесты, задания.

Информация по разделу

Информация вокруг нас

1. Как мы получаем информацию? Виды информации

2. Основные информационные процессы. Хранение, передача и обработка информации

Компьютер — универсальная машина для работы с информацией

1. Как устроен компьютер?

2. Техника безопасности, организация рабочего пространства

Ввод информации в память компьютера

1. Устройства ввода информации

2. Клавиатура и её использование

Управление компьютером

1. Программы и документы. Главное меню. Запуск программ

Хранение информации

1. Оперативная и долговременная память

Передача информации

1. Схема передачи информации. Электронная почта

Кодирование информации

1. В мире кодов

2. Метод координат

Текстовая информация

1. Текстовый редактор

Представление информации в форме таблиц

1. Структура таблицы

2. Табличный способ решения логических задач

Компьютерная графика

1. Графический редактор MS Paint

2. Устройства ввода графической информации