Масса и инертность

☰

Масса является мерой инертности. Чем больше масса тела, тем оно более инертно, то есть обладает большей инертностью. Закон инерции гласит, что если на тело не действуют другие тела, то оно остается в покое или совершает прямолинейное равномерное движение.

Когда тела взаимодействуют, например, сталкиваются, то покой или прямолинейное равномерное движение нарушаются. Тело может начать ускоряться или наоборот тормозить. Скорость, которую приобретет (или теряет) тело после взаимодействия с другим телом, кроме прочего зависит от соотношения масс взаимодействующих тел.

Так если катящийся мяч столкнется на своем пути с кирпичом, то он не просто остановится, а скорее всего изменит свое направление движения, отскочит. Кирпич же скорее всего останется на месте, может быть упадет. Но если на пути движения мяча будет картонная коробка, по размерам равная кирпичу, то мяч уже не отскочит от нее с той же скоростью, что от кирпича.

Мяч может вообще протащить ее впереди себя, продолжив движение, но замедлив его.

Мяч, кирпич и коробка имеют разные массы. Кирпич обладает большей массой, а, следовательно, он более инертный, поэтому мяч почти не может изменить его скорость. Скорее кирпич меняет скорость мяча на противоположную. Коробка менее инертна, поэтому ее проще сдвинуть, а сама она не может изменить скорость меча так, как это сделал кирпич.

Классический пример сравнения масс двух тел с помощью оценки их инертности таков. Две покоящиеся тележки скрепляют между собой, согнув и связав упругие пластины, припаянные к их концам. Далее пережигают связывающую нить. Пластины распрямляются, отталкиваясь друг от друга. Таким образом тележки тоже отталкиваются друг от друга и разъезжаются в противоположные стороны.

При этом существуют следующие закономерности. Если тележки имеют равные массы, то они приобретут равные скорости и до полного торможения отъедут от исходной точки на равные расстояния. Если тележки имеют разные массы, то более массивная (а значит более инертная) отъедет на меньшее расстояние, а менее массивная (менее инертная) отъедет на большее расстояние.

Причем существует связь масс и скоростей взаимодействующих тел, находящихся изначально в состоянии покоя. Произведение массы и приобретенной скорости одного тела равно произведению массы и приобретенной скорости другого тела после взаимодействия. Математически это можно выразить так:

m₁v₁ = m₂v₂

Эта формула говорит о том, что чем больше масса тела, тем меньше его скорость, и чем меньше масса, тем больше скорость тела. Масса и скорость одного тела находятся в обратно пропорциональной зависимости друг от друга (чем больше одна величина, тем меньше другая).

Обычно формулу записывают так (ее можно получить, преобразовав первую формулу):

m₁/m₂ = v₂/v₁

То есть отношение масс тел обратно пропорционально отношению их скоростей.

Используя данную закономерность можно сравнивать массы тел, измеряя приобретенные ими скорости после взаимодействия. Если, например, покоящиеся тела после взаимодействия приобрели скорости 2 м/с и 4 м/с, и известна масса второго тела (пусть будет 0,4 кг), то можно узнать массу первого тела: m1 = (v₂/v₁) * m₂ = 4 / 2 * 0,4 = 0,8 (кг).

Масса покоя или инертная масса?

Масса покоя или инертная масса?

УДК. 12:531.18+51]

Масса покоя или инертная масса?

Р. И. Храпко

Исключение из современных учебников физики инертной массы и замена ее массой покоя представляется ошибкой. Эта тема была поднята автором в статье [1,2]. Здесь приведены дополнительные рассуждения в подтверждение такого тезиса.

Конец 20-го века ознаменовался великой путаницей с физическим понятием «масса тела».

1. Масса покоя

В начале века, до создания теории относительности, было все ясно. Массой тела, m, называлось количество вещества тела, и в то же время масса являлась мерой инертности тела. Инертность тела определяет его «количество движения» при заданной скорости

v движения, то есть коэффициент пропорциональности в формуле

P = mv.     (1)

P — количество движения или, по-научному, импульс тела, а коэффициент m называется инертной массой.

Но массу как меру инертности тела можно определять и с помощью формулы

F = ma:     (2)

чем больше масса, тем меньше ускорение тела при заданной силе. Значение массы по формулам (1) и (2) получалось одно и то же, потому что формула (2) является следствием формулы (1), если инертная масса не зависит от времени и скорости.

То же значение массы можно было получить, взвесив тело, то есть измерив силу притяжения к земле или к любому другому заданному телу (масса которого обозначена M). В законе тяготения Ньютона фигурирует та же самая масса m,

,      (3)

но тут она называется гравитационной (пассивной) массой. В этом выражается эквивалентность инертной и гравитационной массы. Благодаря этой эквивалентности ускорение свободного падения, как известно, не зависит от природы и массы тела:

     (4)

2. Инертная масса

Однако при создании теории относительности выяснилось, что никакое тело нельзя разогнать до скорости света, потому что при приближении скорости тела к скорости света ускорение тела уменьшается до нуля, как бы ни была велика ускоряющая сила. Другими словами, выяснилось, что инертность тела возрастает до бесконечности при приближении его скорости к скорости света, хотя «количество вещества» тела, очевидно, остается при этом неизменным.

Выскажемся точнее по поводу увеличения инертности тела. Теория относительности показала, что импульс тела P при любых скоростях остается параллелен скорости v.

Поэтому формулу P = mv можно сохранить неизменной при больших скоростях, если принять, что коэффициент m, то есть инертная масса, увеличивается с ростом скорости по закону

,      (5)

то есть для импульса тела справедливо выражение

.      (6)

В этих формулах m₀ — это то значение массы рассматриваемого тела, о котором говорилось вначале, то есть значение, которое можно получить после того, как тело затормозят до достаточно малой скорости. Его называют массой покоя тела. Поэтому формулы (1), (2), (3) следовало бы записать так:

P = m₀v, F = m₀a, . Однако для малых скоростей, как видно из формулы (5), инертная масса равна массе покоя, m = m₀, и поэтому запись (1), (2), (3) в разделе «до теории относительности» корректна.

Для того, чтобы подчеркнуть, что инертная масса m зависит от скорости, ее называют иногда «релятивистской» массой: она оказывается различной с точки зрения различных наблюдателей, если эти наблюдатели движутся друг относительно друга. Однако существует выделенное значение инертной массы, именно, значение, которое наблюдает неподвижный относительно тела наблюдатель. Другими словами, масса покоя является выделенным значением инертной массы. Такое свойство инертной массы аналогично свойству времени: одни и те же часы имеют разную скорость хода с точки зрения различных наблюдателей. Однако существует собственная скорость хода часов.

При желании проверить формулу (6) вы должны измерить скорость v тела, а потом измерить импульс тела. Для этого следует затормозить тело некоторой преградой, все время замеряя силу F(t), с которой при торможении тело будет действовать на преграду, а потом проинтегрировать. Импульс, как известно, равен

     (7)

Эта процедура, по сути, задает операционное определение инертной массы.

Заметим, что формулы (5) и (6) остаются справедливыми и для объекта, у которого нет массы покоя, m₀ = 0, например, для фотона или нейтрино (если предположить, что масса покоя нейтрино равна нулю).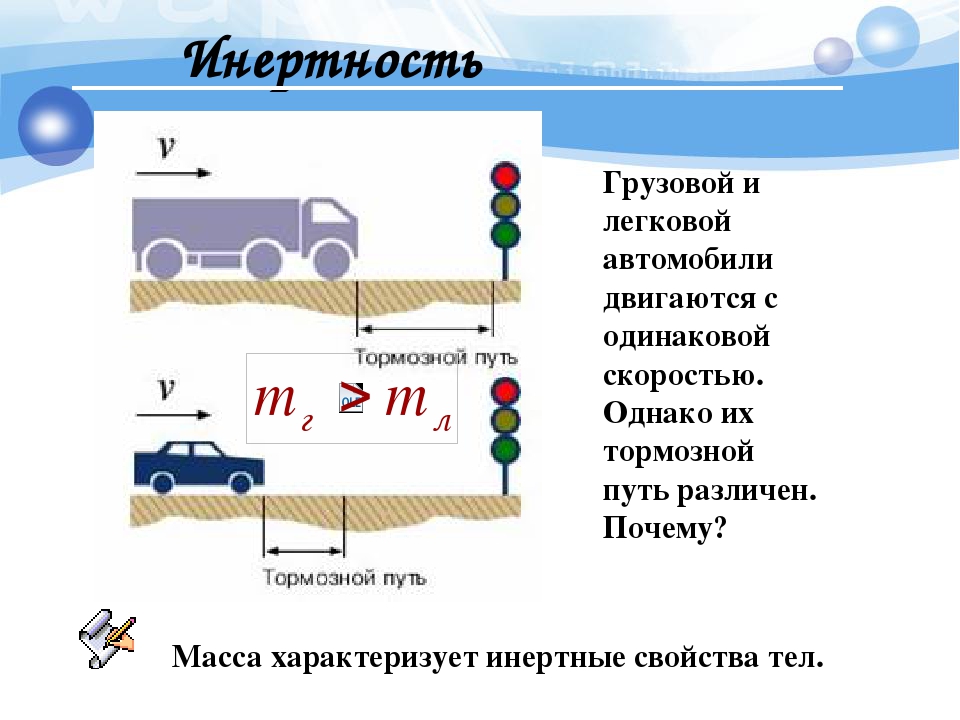 Такие объекты обладают инертной массой и импульсом, но должны двигаться со скоростью света, их нельзя остановить, они исчезают при остановке. Тем не менее, несмотря на постоянство скорости движения, величина их инертной массы оказывается различной с точки зрения различных наблюдателей. Однако в этом случае не существует какого либо выделенного значения инертной массы. Либо, можно сказать, выделенное значение равно нулю.

Увеличение инертности тела при больших скоростях мы объяснили уменьшением ускорения при большой скорости. При этом мы сослались на формулу (2). И это допустимо. Однако именно в силу увеличения инертной массы с ростом скорости тела формула (2) при некоторых условиях изменяет свой вид. Это объясняется тем, что при фиксированном ускорении сила, если она имеет составляющую вдоль скорости, должна обеспечить не только возрастание скорости уже имеющейся массы

,      (5)

она должна обеспечить возрастание самой массы:

.      (8)

Коэффициент

называют иногда продольной массой [3] .

Если сила перпендикулярна скорости и, значит, не изменяет величину скорости и инертной массы, то формула F = ma сохраняет свой вид:

.      (9)

Последнее обстоятельство позволило Р. Фейнману предложить простой способ операционного определения инертной массы, основанный на формуле (9) и справедливый для любой скорости. «Массу можно измерить так: просто привязать предмет на веревочке, крутить его с определенной скоростью и измерять ту силу, которая необходима, чтобы удержать его.» [4]

При произвольном направлении силы относительно скорости тела коэффициент пропорциональности в формуле (2) следует рассматривать как некий оператор (тензор), превращающий вектор a в вектор F: F = a. Оператор зависит от величины и направления скорости тела и, вообще говоря, изменяет направление вектора. Это нетрудно принять. Ведь скорость v тела является его свойством, а сила F, действующая на тело — это внешний по отношению к телу фактор. Понятно, что результат воздействия силы, то есть ускорение a тела, может зависеть от соотношения направлений векторов F и v.

3. Гравитационная масса

Одновременно теория относительности показала, что не только инертность тела, но и его вес увеличивается с ростом скорости, причем по тому же закону (5) в соответствии с эквивалентностью инертной и гравитационной массы. Поэтому формула (8) для тела, падающего вниз со скоростью v, выглядит, грубо говоря, так:

= .

Точная формула для ускорения может быть получена в рамках общей теории относительности, как показано в конце статьи:

, .     (10)

Эта формула является релятивистским аналогом формулы (4).

4. Энергия

Теория относительности показала далее, что прирост инертной массы, m — m₀, умноженный на квадрат скорости света, равен как раз кинетической энергии тела:

(m √ m₀)c² = E_k.      (11)

Поэтому, если приписать покоящемуся телу энергию покоя E₀ = m₀c², то полная энергия E = E₀ + E_k тела оказывается пропорциональной инертной массе:

E = mc²     (12)

Эта знаменитая формула Эйнштейна провозглашает эквивалентность инертной массы и энергии. Два, доселе различных понятия, соединяются в одно.

Заметим, что формула (12), как и формулы (5) и (6) остается справедлива и для объекта, у которого нет массы и энергии покоя, m₀ = 0.

При желании проверить формулу (11) и одновременно убедиться в справедливости теории относительности вы должны измерить инертную массу и массу покоя тела как было объяснено выше, и, кроме того, измерить кинетическую энергию тела. Для этого следует при торможении тела упомянутой преградой все время замерять силу, с которой тело будет действовать на преграду в процессе торможения в функции перемещения l преграды, F(l), а потом проинтегрировать.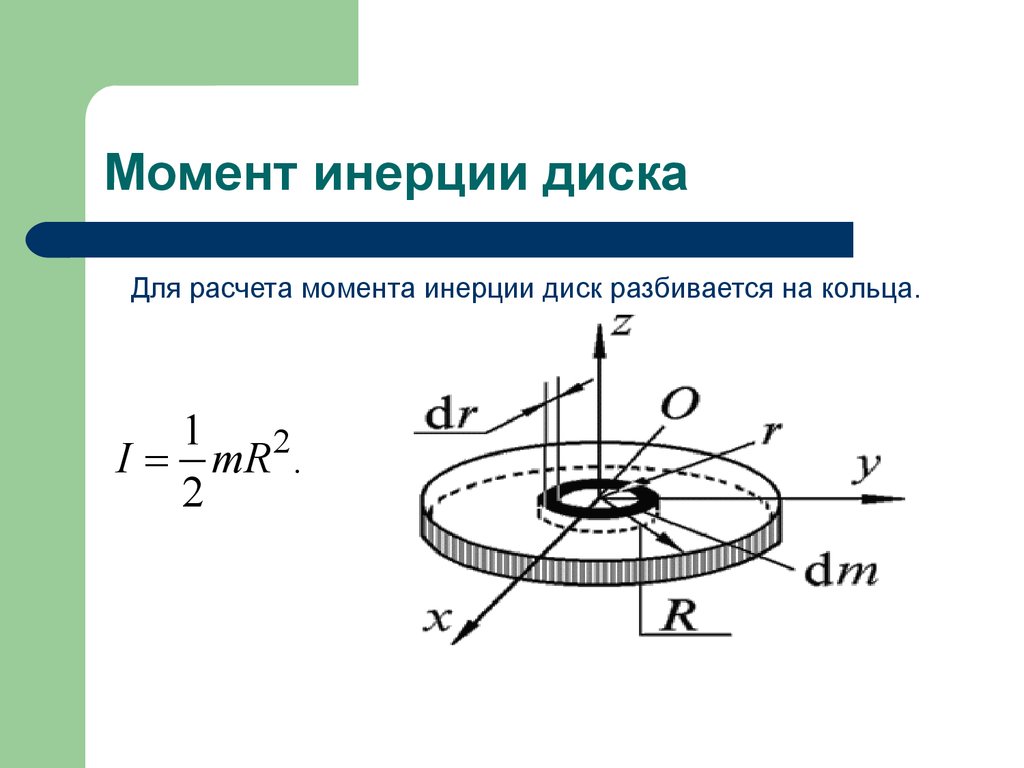 Кинетическая энергия, равная, как известно, в данном случае работе, вычисляется по формуле

.

Здесь F(l)dl — скалярное произведение силы на инфинитезимальный вектор смещения преграды. Все это рассказано в [5] .

Формула (11) связывает инертную массу, массу покоя и кинетическую энергию. Используя формулу (6) для вычисления разности m² √ P²/c², легко связать инертную массу, массу покоя и импульс:

.      (13)

Для частиц с нулевой массой покоя получаем mc = P или E = Pc.

5. Система тел

При объединении нескольких тел в систему тел, как известно, их импульсы и их инертные массы складываются. Для двух тел это выглядит так:

P = P₁ + P₂, m = m₁ + m₂.     (14)

Другими словами, импульс и инертная масса аддитивны. Не так обстоит дело с массой покоя. Из формул (13), (14) следует, что масса покоя пары тел с массами покоя m₀₁, m₀₂ равна не сумме m₀₁ + m₀₂, а сложному выражению, зависящему от импульсов P₁, P₂:

.      (15)

Таким образом, масса покоя, вообще говоря, не аддитивна. Например, пара фотонов, не имеющих массу покоя, имеет массу покоя, если фотоны летят в разные стороны, и не имеет массу покоя, если фотоны летят в одну и ту же сторону.

Тем не менее, все три величины, P, m, m₀, подчиняются закону сохранения, то есть не изменяются со временем для замкнутой системы.

Однако ввиду неаддитивности массы покоя, на наш взгляд, нецелесообразно рассматривать массу покоя системы тел. Имеет смысл говорить лишь о сумме масс покоя отдельных тел системы. В действительности именно так поступают на практике. Когда говорят, что при неупругих соударениях увеличивается масса покоя, имеют ввиду не массу покоя системы, которая удивительным образом сохраняется неизменной при соударениях благодаря неаддитивности, а сравнивают именно сумму масс покоя тел до столкновения и массу покоя после столкновения. Точно так же, когда говорят о дефекте массы покоя при ядерных реакциях, имеют в виду не массу покоя, определяемую формулой (15), а сумму масс покоя частей системы.

6. Сравнение масс

Теперь уместно задать вопрос. Какую из двух масс, массу покоя или инертную массу следует назвать простым словом масса, обозначить буквой m без индексов и тем самым признать «главной» массой. Это — не терминологическая проблема. Здесь имеется серьезная психологическая подоплека.

Чтобы решить, какая из масс — главная, перечислим еще раз свойства обеих масс.

Масса покоя является постоянной величиной для данного тела и выражает «количество вещества тела». Она соответствует привычному дорелятивисткому ньютоновскому представлению о массе. Но она не эквивалентна энергии, не эквивалентна гравитационной массе, она не аддитивна и поэтому не используется как характеристика системы тел или частиц. Это последнее обстоятельство вызывает путаницу (см. [1] , стр. 1365) и мешает проявлению закона сохранения массы покоя. Фотоны и частицы, движущиеся со скоростью света, не обладают массой покоя. Операционное определение массы покоя частицы предполагает торможение ее до малой скорости без использования информации о текущем состоянии частицы.

Инертная масса это — релятивистская масса. Она принимает различное значение для различных наблюдателей, аналогично тому, как скорость хода часов оказывается различной относительно различных наблюдателей. Инертная масса эквивалентна энергии и гравитационной массе, она аддитивна и подчиняется закону сохранения. Инертной массой обладают частицы, не имеющие массы покоя. Операционное определение инертной массы основано на простой формуле P = mv.

На наш взгляд, инертную массу следует называть массой и обозначать m, как это и делалось в настоящей статье.

7. Психологическая подоплека

К сожалению, большое количество физиков считает массу покоя главной и обозначает ее m а не m₀, а инертную массу дискриминирует и оставляет без обозначения, что вносит дополнительную путаницу, поскольку из-за этого порой бывает трудно понять, о какой массе идет речь.

Эти физики соглашаются, например, с тем, что масса газа увеличивается при нагревании, потому что увеличивается содержащаяся в нем энергия, но психологический барьер мешает им попросту объяснить это увеличение ростом массы отдельных молекул вследствие увеличения их тепловой скорости.

Эти физики жертвуют представлением о массе как мере инертности в пользу ярлыка, прикрепляемого к каждой частице с информацией о неизменном «количестве вещества», потому что ярлык соответствует их привычному ньютоновскому представлению о массе. Они считают, например, что излучение, которое, согласно Эйнштейну [6] , «переносит инерцию между излучающими и поглощающими телами», не имеет массы, поскольку к излучению невозможно прикрепить ярлык.

Инертная масса отсутствует в издаваемых сейчас стандартных учебниках физики в России (И.В.Савельев) и за рубежом [7,8], а также в популярной литературе [9] . Этот факт, однако, скрыт тем обстоятельством, что сторонники массы покоя настойчиво называют массу покоя не массой покоя, а просто массой, словом, которое ассоциируется с мерой инерции.

Главная психологическая трудность заключается в том, чтобы отождествить массу и энергию (которая изменяется), чтобы принять эти две сущности, как одну. Легко принять формулу E₀ = m₀c² для покоящегося тела. Труднее принять справедливость формулы E = mc² для любой скорости. Замечательная формула E= mc² представляется, например, Л.Б. Окуню «безобразной» [10] .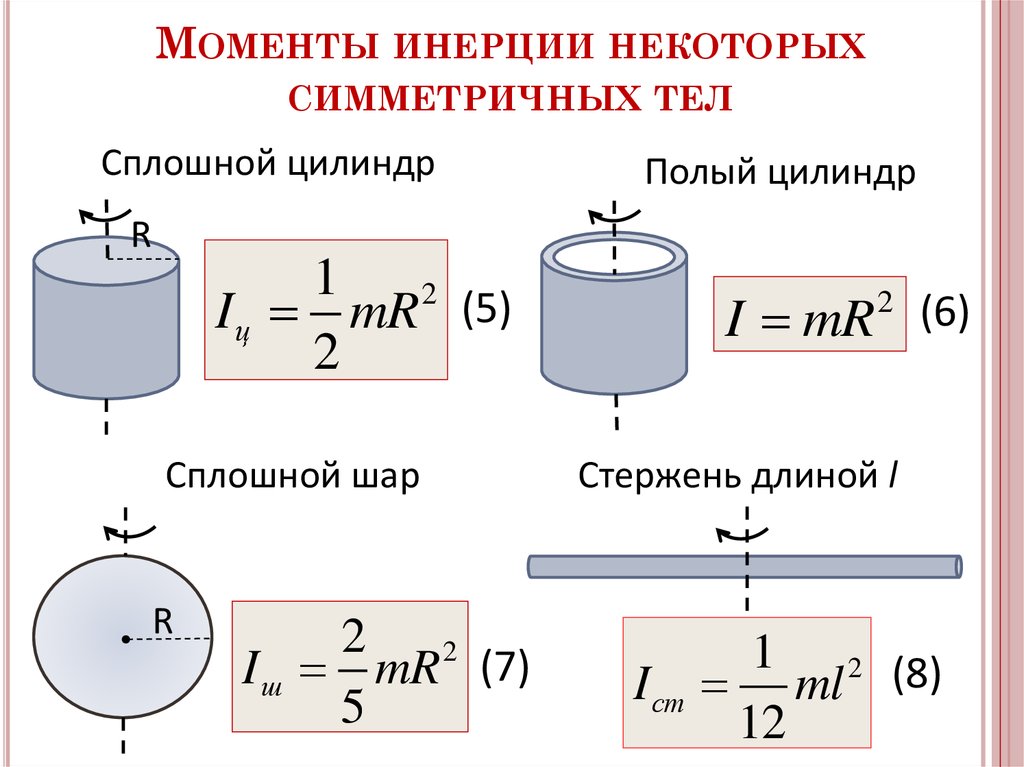

Сторонники массы покоя, видимо, не в состоянии принять идею инертной, релятивистской массы так же, как ранее противники теории относительности не могли принять относительность времени. Ведь время жизни астронавта или нестабильной частицы изменяется так же, как изменяется их инертная масса: . Здесь уместно процитировать М. Планка: «Великая научная идея редко внедряется путем постепенного убеждения и обращения своих противников, редко бывает, что Савл становится Павлом. В действительности дело происходит так, что оппоненты постепенно вымирают, а растущее поколение с самого начала осваивается с новой идеей.» [11] К сожалению, великая идея релятивистской массы тщательно изолируется от молодежи. На данный момент статья [1, 2] отклонена редакциями следующих журналов: «Известия вузов. Физика», «Квант», «American Journal of Physics», «Physics Education» (Bristol), «Physics Today».

8. Шварцшильдовское пространство

Мы получим здесь формулу (10), рассмотрев пространство-время Шварцшильда общей теории относительности с выражением для интервала s [12] :

.

Уравнения радиальной геодезической линии могут быть получены по общей формуле, использующей коэффициенты связности :

,      (16)

.      (17)

Первый интеграл уравнения (16) легко находится:

.      (18)

Запишем теперь выражение для ускорения a, учитывая (18) и то, что соотношения между расстоянием l и временем , с одной стороны, и координатами r, t, с другой, даются формулами

, :

.

Выразив таким образом ускорение a через , мы можем теперь воспользоваться уравнением (17), а затем, вернувшись к l и , получить окончательно

, .     (10)

Список литературы

1. Храпко Р. И. Что есть масса? // Успехи физических наук. — 2000, N12. √ с.1363-1366.

2. Храпко Р. И. Что есть масса? — http://www.mai.ru. Труды МАИ, Вып.2.

3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. — М. : ГИТТЛ, 1951.- 547 с.

4. Фейнман Р. и др. Фейнмановские лекции по физике. Т. 1. — М.: Мир, 1965. √ 232 с.

5. Храпко Р. И., Спирин Г.Г., Разоренов В. М. Механика. — М.: МАИ, 1993. √ 89 с.

6. Эйнштейн А. Зависит ли инерция тела от содержащейся в нем энергии. // Принцип относительности. — ОНТИ, 1935.- с.175-178.

7. Resnick R., Halliday D., Krane K. S. Physics. V.1 — N.Y.: J. Wiley, 1992.-592p.

8. Alonso M., Finn E. J. Physics — N.Y.: Addison-Wesley, 1995.-496p.

9. Taylor E. F., Wheeler J. A. Spacetime Physics. √ San Francisco: Freeman, 1966.- 631c. Русский перевод: Тейлор Э. Ф., Уилер Дж. А. Физика пространства-времени. √ М.: Мир, 1971.- 612c.

10. Окунь Л. Б. Понятие массы. // Успехи физических наук. — 1989, т. 158. — с.512-530.

11. Планк М. Происхождение научных идей и влияние их на развитие науки./ М. Планк.// Сборник статей к столетию со дня рождения Макса Планка. — М.: АНСССР, 1958.- с.52.

12. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука, 1973.- 504с.

Science Journals — 404 СТРАНИЦА НЕ НАЙДЕНА

Вся истина проходит через три этапа. Во-первых, это высмеивается. Во-вторых, яростно противится. В-третьих, это принимается как само собой разумеющееся: Артур Шопенгауэр. В вопросах науки авторитет тысячи не стоит скромных рассуждений одного человека. Галилео Галилей. зарабатывайте этим на жизнь: Альберт Эйнштейн. Когда вы устраните невозможное, то, что когда-либо останется, каким бы невероятным оно ни было, должно быть правдой: Сэр Артур Конан Дойл. Мы все согласны с тем, что ваша теория безумна, но достаточно ли она безумна? Нильс Бор — Всякий раз, когда появляется истинная теория, она будет ее собственным доказательством. Его проверка состоит в том, что он объяснит все явления: Ральф Уолдо Эмерсон — С тех пор как математики вторглись в теорию относительности, я и сам ее больше не понимаю: Альберт Эйнштейн — Я бы сказал, что эфир – это среда, изобретенная человеком для распространения его заблуждения из одного места в другое: W. F.G. Суонн: — Большинство фундаментальных идей науки по существу просты и, как правило, могут быть выражены на языке, понятном каждому: Альберт Эйнштейн — Физика является математической не потому, что мы так много знаем о физическом мире, а потому что мы так мало знаем: Бертран Рассел. Если бы я мог объяснить это обычному человеку, я не был бы достоин Нобелевской премии. Р. П. Фейнман. Я не чувствую себя обязанным верить, что тот же самый Бог, который наделил нас чувство, разум и интеллект предназначили нам отказаться от их использования: Галилео Галилей. Как смеем мы говорить о законах случая? Разве случайность не является антитезой всему закону?: Бертран Рассел — Только две вещи бесконечны, вселенная и человеческая глупость, и я не уверен в первом: Альберт Эйнштейн — Слава математики в том, что вы не должен сказать, о чем вы говорите: Ричард Фейнман — Все возможно, если вы не знаете, о чем говорите: Автор неизвестен — В жизни все относительно — кроме теории Эйнштейна: Леонид С. Сухоруков — — Не беспокойтесь о том, что люди украдут ваши идеи. Если ваши идеи хоть сколько-нибудь хороши, вам придется вбивать их людям в глотки: Говард Эйкен. Несомненно, придет день, когда эфир будет отброшен как бесполезный: А. Пуанкаре. Сначала вам скажут, что вы неправильно, и они могут это доказать; тогда они говорят вам, что вы правы, но это не важно; тогда они говорят вам, что это важно, но они всегда знали это: Чарльз Кеттеринг — Не раз и не два, а бесчисленное количество раз одни и те же идеи появляются в мире: Аристотель — Противоположностью истинному утверждению является ложное утверждение. Противоположностью глубокой истине вполне может быть другая глубокая истина: Нильс Бор — Новая научная истина торжествует не потому, что убеждает своих противников и заставляет их увидеть свет, а скорее потому, что ее противники в конце концов умирают, и новое поколение вырастает, знаком с ним: Макс Планк — Евклид научил меня, что без допущений нет доказательств. Поэтому в любом споре исследуйте предположения: Эрик Темпл Белл. Половина этой игры на девяносто процентов ментальная: Йоги Берра

Похоже, мы не можем найти эту страницу. Если вы использовали закладку или прямую ссылку, возможно, содержимое было перемещено.

Благородный газ | Определение, элементы, свойства, характеристики и факты

аргоновая изоляция

Посмотреть все носители

Ключевые сотрудники:

сэр Уильям Рамзи Фридрих Адольф Панет

Похожие темы:

ксенон гелий криптон радон аргон

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

благородный газ , любой из семи химических элементов, составляющих группу 18 (VIIIa) периодической таблицы. Элементами являются гелий (He), неон (Ne), аргон (Ar), криптон (Kr), ксенон (Xe), радон (Rn) и оганесон (Og). Благородные газы бесцветные, без запаха, без вкуса, негорючие газы. Их традиционно относят к группе 0 в периодической таблице, потому что в течение десятилетий после их открытия считалось, что они не могут связываться с другими атомами; то есть их атомы не могли соединяться с атомами других элементов с образованием химических соединений. Их электронная структура и обнаружение того, что некоторые из них действительно образуют соединения, привели к более подходящему обозначению — Группа 18.

Когда члены группы были обнаружены и идентифицированы, они считались чрезвычайно редкими, а также химически инертными, и поэтому их называли редкими или инертными газами. Однако теперь известно, что некоторые из этих элементов довольно распространены на Земле и в остальной части Вселенной, поэтому обозначение редкого вводит в заблуждение. Точно так же использование термина инертный имеет недостаток, заключающийся в том, что он подразумевает химическую пассивность, предполагая, что соединения группы 18 не могут быть образованы. В химии и алхимии слово благородный долгое время обозначал нежелание металлов, таких как золото и платина, вступать в химическую реакцию; это относится в том же смысле к рассматриваемой здесь группе газов.

Содержание инертных газов уменьшается по мере увеличения их атомных номеров. Гелий — самый распространенный элемент во Вселенной, кроме водорода. Все благородные газы присутствуют в атмосфере Земли, и, кроме гелия и радона, их основным коммерческим источником является воздух, из которого их получают сжижением и фракционной перегонкой. Большая часть гелия производится в коммерческих целях из определенных скважин природного газа. Радон обычно выделяют как продукт радиоактивного разложения соединений радия. Ядра атомов радия самопроизвольно распадаются, испуская энергию и частицы, ядра гелия (альфа-частицы) и атомы радона. Некоторые свойства благородных газов приведены в таблице.

Некоторые свойства благородных газов

	гелий	неон	аргон	криптон	ксенон	радон	уноктий
*При 25,05 атм.
**ГПУ = гексагональная плотноупакованная, ГЦК = гранецентрированная кубическая (кубическая плотноупакованная).
***Самый стабильный изотоп.
атомный номер	2	10	18	36	54	86	118
атомный вес	4.003	20.18	39.948	83,8	131.293	222	294***
температура плавления (°С)	−272,2*	−248,59	−189,3	−157,36	−111,7	−71	—
температура кипения (°С)	−268,93	−246,08	−185,8	−153,22	−108	−61,7	—
плотность при 0 °C, 1 атмосфера (грамм на литр)	0,17847	0,899	1,784	3,75	5. 881	9,73	—
растворимость в воде при 20 °C (куб. сантиметры газа на 1000 граммов воды)	8,61	10,5	33,6	59,4	108.1	230	—
изотопное содержание (земное, в процентах)	3 (0,000137), 4 (99,999863)	20 (90,48), 21 (0,27), 22 (9,25)	36 (0,3365), 40 (99,6003)	78 (0,35), 80 (2,28), 82 (11,58), 83 (11,49), 84 (57), 86 (17,3)	124 (0,09), 126 (0,09), 128 (1,92), 129 (26,44), 130 (4,08), 131 (21,18), 132 (26,89), 134 (10,44), 136 (8,87)	—	—
радиоактивные изотопы (массовые числа)	5–10	16–19, 23–34	30–35, 37, 39, 41–53	69–77, 79, 81, 85, 87–100	110–125, 127, 133, 135–147	195–228	294
цвет света, излучаемого газоразрядной трубкой	желтый	красный	красный или синий	желто-зеленый	от синего к зеленому	—	—
теплота плавления (килоджоулей на моль)	0,02	0,34	1,18	1,64	2. 3	3	—
теплота парообразования (калории на моль)	0,083	1,75	6,5	9.02	12,64	17	—
удельная теплоемкость (Джоули на грамм Кельвина)	5.1931	1,03	0,52033	0,24805	0,15832	0,09365	—
критическая температура (К)	5.19	44,4	150,87	209,41	289,77	377	—
критическое давление (атмосферы)	2,24	27,2	48,34	54,3	57,65	62	—
критическая плотность (грамм на кубический сантиметр)	0,0696	0,4819	0,5356	0,9092	1. 103	—	—
теплопроводность (ватт на метр Кельвина)	0,1513	0,0491	0,0177	0,0094	0,0057	0,0036	—
магнитная восприимчивость (единицы СГС на моль)	−0,0000019	−0,0000072	−0,0000194	−0,000028	−0,000043	—	—
Кристальная структура**	hcp	ФКК	ФКК	ФКК	ФКК	ФКК	—
радиус: атомный (ангстрем)	0,31	0,38	0,71	0,88	1,08	1,2	—
радиус: ковалентный (кристаллический) оценочный (ангстрем)	0,32	0,69	0,97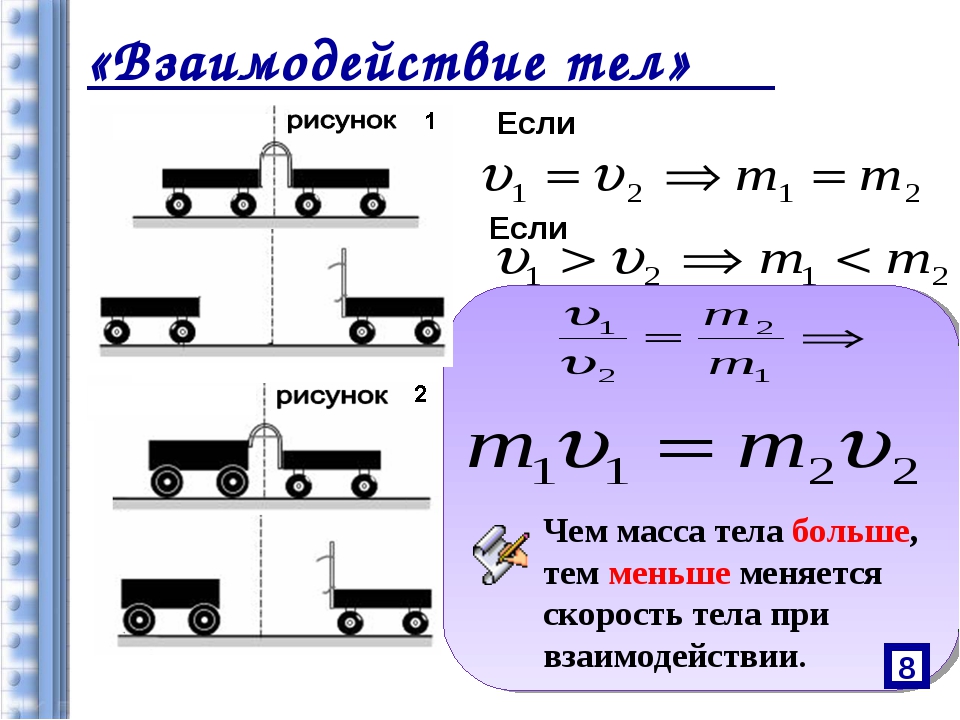	1. 1	1,3	1,45	—
статическая поляризуемость (куб. ангстрем)	0,204	0,392	1,63	2,465	4.01	—	—
потенциал ионизации (первый, электрон-вольты)	24.587	21,565	15.759	13.999	12.129	10.747	—
электроотрицательность (Полинг)	4,5	4. 0	2,9	2,6	2,25	2.0	—

В 1785 году Генри Кавендиш, английский химик и физик, обнаружил, что воздух содержит небольшую долю (чуть меньше 1 процента) вещества, химически менее активного, чем азот. Столетие спустя лорд Рэлей, английский физик, выделил из воздуха газ, который, как он думал, был чистым азотом, но обнаружил, что он тяжелее азота, полученного путем высвобождения его из соединений. Он рассудил, что его воздушный азот должен содержать небольшое количество более плотного газа. В 1894, сэр Уильям Рэмзи, шотландский химик, сотрудничал с Рэлеем в выделении этого газа, который оказался новым элементом — аргоном.

После открытия аргона и по наущению других ученых в 1895 году Рамзи исследовал газ, выделяющийся при нагревании минерала клевита, который считался источником аргона. Вместо этого газом был гелий, который в 1868 году был обнаружен спектроскопически на Солнце, но не был обнаружен на Земле. Рамзи и его коллеги искали родственные газы и путем фракционной перегонки жидкого воздуха открыли криптон, неон и ксенон в 189 году.8. Впервые радон был обнаружен в 1900 г. немецким химиком Фридрихом Э. Дорном; он был основан как член группы по благородным газам в 1904 году. Рэлей и Рамзи получили Нобелевскую премию в 1904 году за свою работу.

В 1895 году французский химик Анри Муассан, открывший элементарный фтор в 1886 году и получивший за это открытие Нобелевскую премию в 1906 году, потерпел неудачу в попытке вызвать реакцию между фтором и аргоном. Этот результат был значительным, потому что фтор является наиболее реакционноспособным элементом в периодической таблице. На самом деле все поздние 19Попытки получить химические соединения аргона в начале 20 века потерпели неудачу. Отсутствие химической реактивности, обусловленное этими неудачами, имело большое значение для развития теорий строения атома. В 1913 году датский физик Нильс Бор предположил, что электроны в атомах расположены в последовательных оболочках, имеющих характерные энергии и емкости, и что емкости оболочек для электронов определяют количество элементов в строках периодической таблицы. На основании экспериментальных данных, связывающих химические свойства с распределением электронов, было высказано предположение, что в атомах благородных газов тяжелее гелия электроны расположены в этих оболочках таким образом, что самая внешняя оболочка всегда содержит восемь электронов, независимо от сколько других (в случае с радоном 78 других) расположены внутри внутренних оболочек.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

В теории химической связи, разработанной американским химиком Гилбертом Н. Льюисом и немецким химиком Вальтером Косселем в 1916 году, этот октет электронов считался наиболее стабильным расположением самой внешней оболочки любого атома. Хотя таким расположением обладали только атомы инертных газов, именно к этому состоянию стремились атомы всех других элементов в своих химических связях. Некоторые элементы удовлетворили эту тенденцию, либо сразу приобретя, либо потеряв электроны, становясь, таким образом, ионами; другие элементы делили электроны, образуя устойчивые комбинации, связанные между собой ковалентными связями. Таким образом, пропорции, в которых атомы элементов объединялись, образуя ионные или ковалентные соединения (их «валентности»), контролировались поведением их самых внешних электронов, которые — по этой причине — назывались валентными электронами. Эта теория объясняла химическую связь активных элементов, а также относительную неактивность инертных газов, которую стали рассматривать как их главную химическую характеристику. ( См. также химическая связь: связи между атомами.)

Экранированные от ядра промежуточными электронами внешние (валентные) электроны атомов более тяжелых благородных газов удерживаются менее прочно и могут быть легче удалены (ионизированы) из атомы, чем электроны более легких благородных газов.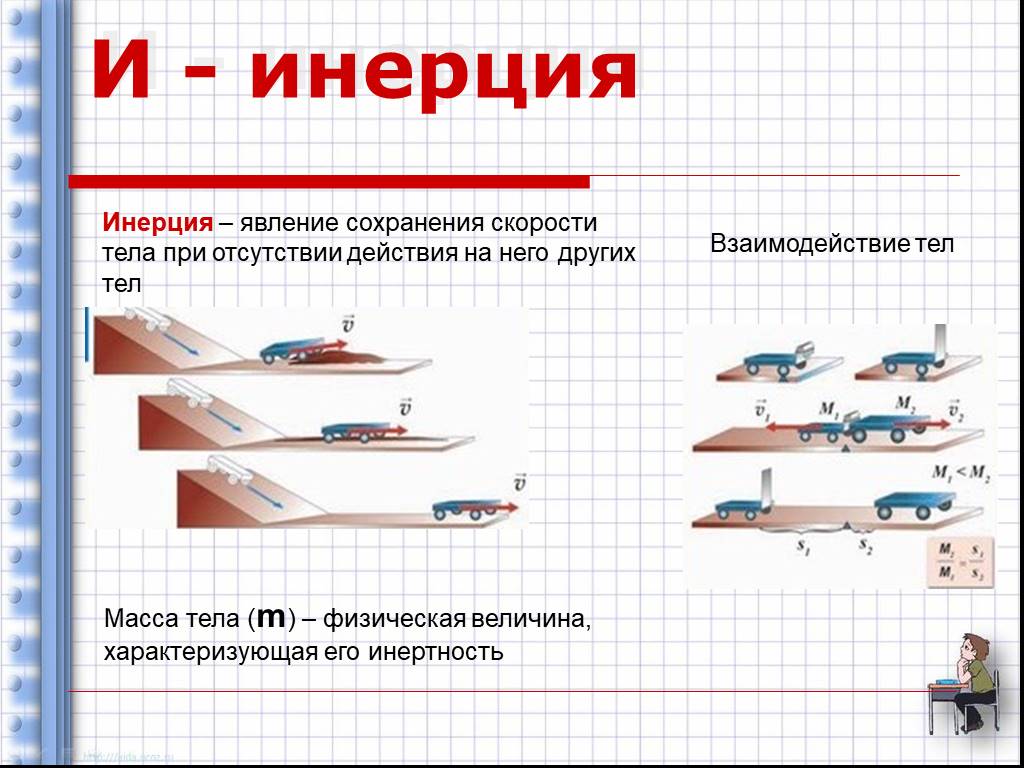 Энергия, необходимая для удаления одного электрона, называется первой энергией ионизации. В 1962 году, работая в Университете Британской Колумбии, британский химик Нил Бартлетт обнаружил, что гексафторид платины удаляет электрон из (окисляет) молекулярный кислород с образованием соли [O ₂ ⁺ ][ПтФ ₆ ⁻ ]. Первая энергия ионизации ксенона очень близка к энергии кислорода; таким образом, Бартлетт думал, что соль ксенона может быть образована аналогичным образом. В том же году Бартлетт установил, что химическим путем действительно можно удалять электроны из ксенона. Он показал, что взаимодействие паров PtF ₆ в присутствии газообразного ксенона при комнатной температуре приводит к образованию желто-оранжевого твердого соединения, которое формулируется как [Xe ⁺ ][ПтФ ₆ ⁻ ]. (Теперь известно, что это соединение представляет собой смесь [XeF ⁺ ][PtF ₆ ^— ], [XeF ⁺ ] [Pt ₂ F ₁₁ ^— ] и 0514 ] 5 .