Инерция моменті: формулалар, теңдеулер және есептеу мысалдары — Ғылым
Вызшақ: Инерция құбылысы. Күш. 7 сынып.Мазмұны
- Есептеу мысалдары
- Жіңішке штанганың центрінен өтетін оське қатысты инерция моменті
- Дискінің центрінен өтетін оське қатысты инерция моменті
- Диаметрі шамасындағы қатты шардың инерция моменті
- Қатты цилиндрдің осьтік осіне қатысты инерция моменті
- Тік бұрышты парақтың оның центрінен өтетін оське қатысты инерция моменті
- Төртбұрышты парақтың оның центрінен өтетін оське қатысты инерция моменті
- Инерция теоремаларының сәті
- Штайнер теоремасы
- Перпендикуляр осьтер теоремасы
- Жаттығу шешілді
- Әдебиеттер тізімі
The инерция моменті қатты дененің белгілі бір айналу осіне қатысты, оның осьтің айналасындағы бұрыштық жылдамдығын өзгертуге қарсылығын білдіреді. Бұл массаға, сонымен қатар айналу осінің орналасуына пропорционалды, өйткені дене геометриясына байланысты белгілі бір осьтер айналасында басқаларға қарағанда оңай айнала алады.
Бұл массаға, сонымен қатар айналу осінің орналасуына пропорционалды, өйткені дене геометриясына байланысты белгілі бір осьтер айналасында басқаларға қарағанда оңай айнала алады.
Айталық, осьтің айналасында айнала алатын үлкен объект (көптеген бөлшектерден тұрады) делік. Күш әсер етеді делік F, массаның элементіне тангенциалды қолданылады Δмменберілген, айналу моментін немесе моментін шығарады τтор = ∑рмен х Fмен. Векторлық рмен позициясы болып табылады Δммен(2-суретті қараңыз).
Бұл момент айналу жазықтығына перпендикуляр (бағыт +k = қағаздан шығу). Күш пен радиалды позиция векторы әрқашан перпендикуляр болғандықтан, көлденең көбейтінді қалады:
τтор = ∑ Fмен рменк = ∑ (Δммен дейінмен) рмен к = ∑ Δmмен (дейінмен рмен ) к
Дейін үдеумен үдеудің тангенциалды компонентін білдіреді, өйткені радиалды үдеу моментке ықпал етпейді.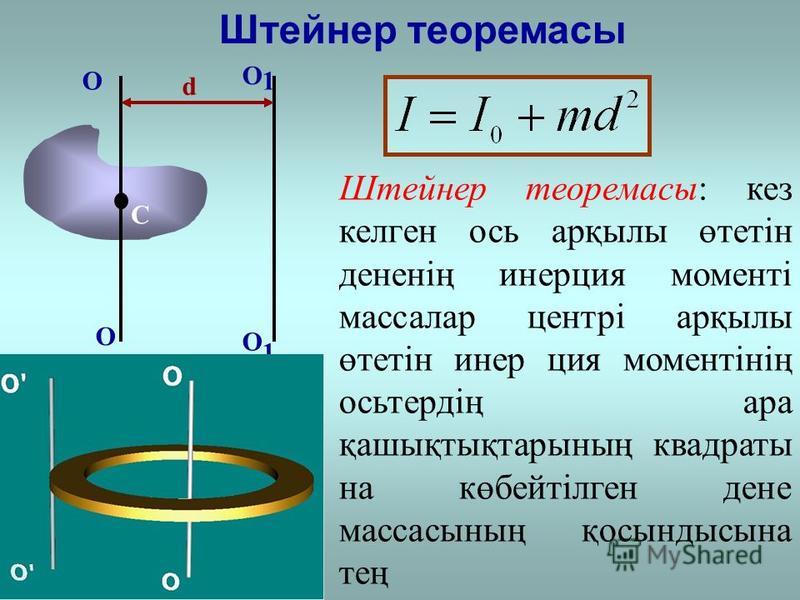 Α бұрыштық үдеуінің функциясы ретінде мынаны көрсетуге болады:
Α бұрыштық үдеуінің функциясы ретінде мынаны көрсетуге болады:
дейінмен = α rмен
Сондықтан таза момент келесідей:
τтор = ∑ Δmмен (α rмен2) k = (∑ рмен2 Δммен)α к
Α бұрыштық үдеуі бүкіл объект үшін бірдей, сондықтан оған «i» подпискасы әсер етпейді және қосындысын қалдыра алады, бұл дәл сол заттың I әрпімен бейнеленген инерция моменті:
I = ∑ rмен2 Δммен
Бұл массаның дискретті үлестірімінің инерция моменті. Тарату үздіксіз болған кезде, қосынды интегралмен ауыстырылады Δм жаппай дифференциалға айналады дм. Интеграл бүкіл объект бойынша жүзеге асырылады:
I = ∫М(р2) дм
SI халықаралық жүйесіндегі инерция моментінің өлшем бірліктері кг х м2. Бұл массаның және арақашықтықтың квадратының көбейтіндісі болғандықтан, скаляр және оң шама.
Бұл массаның және арақашықтықтың квадратының көбейтіндісі болғандықтан, скаляр және оң шама.
Тығыздығы бар жолақ, диск, шар немесе басқа сияқты кеңейтілген объект ρ тұрақты және тығыздықтың масса — көлем қатынасы, масса дифференциал екенін біле отырып дм былай жазылады:
ρ = dm / dV → dm = ρdV
Инерциалдық моментті интегралға ауыстыра отырып, бізде:
I = ∫r2 ρdV = ρ ∫r2dV
Бұл көлемді объект үшін жарамды жалпы өрнек V және позиция р кеңістіктік координаталардың функциялары болып табылады х, Y Y з. Тығыздық интегралдан тыс болатынына назар аударыңыз.
Тығыздығы ρ Ол сондай-ақ көлемдік тығыздық деп аталады, бірақ егер зат парақ тәрізді өте тегіс болса немесе таяқша тәрізді өте жұқа және тар болса, басқа тығыздық түрлерін қолдануға болады:
— Өте жұқа парақ үшін тығыздық σ, беттік тығыздық (аудан бірлігіне шаққандағы масса) және береді — бұл аймақтық дифференциал.
— Ал егер бұл тек ұзындығы сәйкес келетін жіңішке штрих болса, сызықтық массаның тығыздығы қолданылады λ және анықтамалық ретінде пайдаланылатын оське сәйкес ұзындықтың дифференциалды.
Келесі мысалдарда барлық объектілер қатты (деформацияланбайтын) болып саналады және біркелкі тығыздыққа ие.
Жіңішке штанганың центрінен өтетін оське қатысты инерция моментіМұнда L және массасы M ұзындықтағы жіңішке, қатты, біртекті штрихтың ортасынан өтетін оське қатысты инерция моментін есептейміз.
Біріншіден, координаттар жүйесін құру керек және сәйкес геометриямен фигураны салу керек:
The X осі бардың бойымен және Ось у айналу осі ретінде. Интегралды құру процедурасы сонымен қатар штангаға қатысты жаппай дифференциалды таңдауды талап етеді дм, оның дифференциалды ұзындығы бар dx және позицияда орналасқан х орталыққа қатысты ерікті x = 0.
Сызықтық тығыздықтың анықтамасына сәйкес According:
λ = M / L
Тығыздық M және L үшін жарамды біркелкі болғандықтан, dm және dx үшін де жарамды:
λ = dm / dx → dm = λdx.
Екінші жағынан, масса элементі өз орнындах, содан кейін анықтамада осы геометрияны ауыстыра отырып, бізде белгілі бір интеграл болады, оның шектері координаттар жүйесі бойынша штрихтың ұштары болып табылады:
Сызықтық тығыздықты ауыстыру λ = M / L:
Штанганың басқа айналу осіне қатысты инерция моментін табу үшін, мысалы оның ұштарының бірінен өтетін штейнер теоремасын қолдануға болады (соңында шешілген жаттығуды қараңыз) немесе көрсетілгенге ұқсас тікелей есептеулер жүргізе аласыз. мұнда, бірақ геометрияны тиісті түрде өзгерту.
Дискінің центрінен өтетін оське қатысты инерция моментіЕлеусіз қалыңдықтағы өте жұқа диск — бұл жалпақ фигура. Егер масса А ауданының бүкіл бетіне біркелкі таралса, σ масса тығыздығы:
σ = M / A
Өте қатты дм сияқты береді Олар суретте көрсетілген дифференциалды сақинаның массасына және ауданына сәйкес келеді. Бүкіл жиынтық осінің айналасында айналады деп ойлаймыз.
Диск радиустың көптеген концентрлі сақиналарынан тұрады деп елестете аласыз р, әрқайсысы сәйкес инерция моментімен. Барлық сақиналардың жарналарын радиусқа жеткенше қосу R, бізде дискінің жалпы инерция моменті болады.
σ= dm / dA → dm = σбереді
Мұнда M дискінің бүкіл массасын көрсетеді. Дисктің ауданы оның радиусына тәуелді r:
A = π.р2
R-ге қатысты:
dA / dr = 2 = 2π.r → dA = 2π.rdr
I анықтамасында жоғарыда айтылғандарды ауыстыру:
Σ = M / (π.R) ауыстыру2 ) қалады:
Диаметрі шамасындағы қатты шардың инерция моментіR радиусы сферасын шексіз аз массаның әр дискісі орналасқан бірінің үстіне бірі қойылған дискілер қатары деп санауға болады. дм, радио р және қалыңдығы dz, инерция моментіне ие:
бердідиск = (½) r2дм
Осы дифференциалды табу үшін біз алдыңғы бөліктен формуланы алып, орнына қойдық М Y R арқылы дм Y r, сәйкесінше. Осындай дискіні 5-суреттің геометриясында көруге болады.
Осындай дискіні 5-суреттің геометриясында көруге болады.
Жинақталған дискілердің барлық шексіз инерция моменттерін қосу арқылы сфераның жалпы инерция моменті алынады:
Менсфера = ∫dIдиск
Бұл қайсысына тең:
I = ∫сфера (½) r2дм
Интегралды шешу үшін мәнерлеу керекдм дұрыс. Әдеттегідей, оған тығыздықтан қол жеткізіледі:
ρ = M / V = dm / dV → dm = ρ.dV
Дифференциалды дискінің көлемі:
dV = Табанның биіктігі ауданы
Дискінің биіктігі — қалыңдығы dz, ал базаның ауданы .r2, Осылайша:
dV = πr2dz
Ұсынылған интегралға ауыстыру келесідей болады:
I = ∫сфера(½) r2dm = ∫ (½) r2(ρπr2dz)
Бірақ интегралдамас бұрын r — дискінің радиусы z және R — сфераның радиусына тәуелді болатындығын байқау керек, оны 5 суреттен көруге болады: Пифагор теоремасын қолдану:
R2 = r2 + z2 → r2 = R2 — з2
Бұл бізді:
I = ∫сфера(½) ρ r2(. r2dz) = ∫сфера(½) ρ π r4dz= ∫сфера(½) ρ π (R2 — з2)2 dz
r2dz) = ∫сфера(½) ρ π r4dz= ∫сфера(½) ρ π (R2 — з2)2 dz
Бүкіл сфераға интеграциялану үшін z –R мен R аралығында өзгеретінін ескереміз, сондықтан:
Мұны білу ρ = M / V = M / [(4/3) πR3] ақырында ол жеңілдетілгеннен кейін алынады:
Қатты цилиндрдің осьтік осіне қатысты инерция моментіБұл объект үшін сфераға қолданылатын әдіс қолданылады, тек егер бұл цилиндрді радиустың цилиндрлік қабықшалары жасайды деп елестетсе, бұл жолы оңайырақ р, қалыңдық доктор және биіктігі H, олар пияздың қабаттары сияқты.
Дыбыс деңгейі dV цилиндрлік қабат:
dV = 2π.rL.dr
Сондықтан қабықтың массасы:
dm = ρ.dV = ρ. 2π.r.L.dr
Бұл өрнек инерция моментінің анықтамасында ауыстырылады:
Жоғарыда келтірілген теңдеу цилиндрдің инерция моменті оның ұзындығына емес, тек массасы мен радиусына тәуелді екенін көрсетеді. Иә L өзгерді, осьтік оське қатысты инерция моменті өзгеріссіз қалады. Осы себеппен, Мен цилиндр бұрын есептелген жұқа дискімен сәйкес келеді.
Иә L өзгерді, осьтік оське қатысты инерция моменті өзгеріссіз қалады. Осы себеппен, Мен цилиндр бұрын есептелген жұқа дискімен сәйкес келеді.
The Ось у көлденең айналу осі. Төмендегі суретте интеграциялауға қажетті геометрия көрсетілген:
Қызылмен белгіленген аймақ элементі тікбұрышты. Оның ауданы x x биіктігі, сондықтан:
dA = a.dz
Сондықтан масса дифференциал:
dm = σ.dA = σ. (a.dz)
Аймақ элементінен айналу осіне дейінгі қашықтыққа қатысты ол әрдайым болады з. Мұның бәрін инерция моментінің интегралына ауыстырамыз:
Енді беткі массаның тығыздығы σ келесіге ауыстырылады:
σ = M / ab
Әрине, бұл келесідей:
Бұл жіңішке штангамен ұқсас екеніне назар аударыңыз.
Төртбұрышты парақтың оның центрінен өтетін оське қатысты инерция моментіБүйір квадрат үшін L, тіктөртбұрыш үшін жарамды алдыңғы өрнекте жай мәнін ауыстырыңыз б сол үшін L:
Инерция теоремаларының сәтіБасқа осьтерге қатысты инерция моменттерін есептеуді жеңілдетуге арналған екі ерекше пайдалы теорема бар, оларды симметрия болмағандықтан табу қиын болуы мүмкін.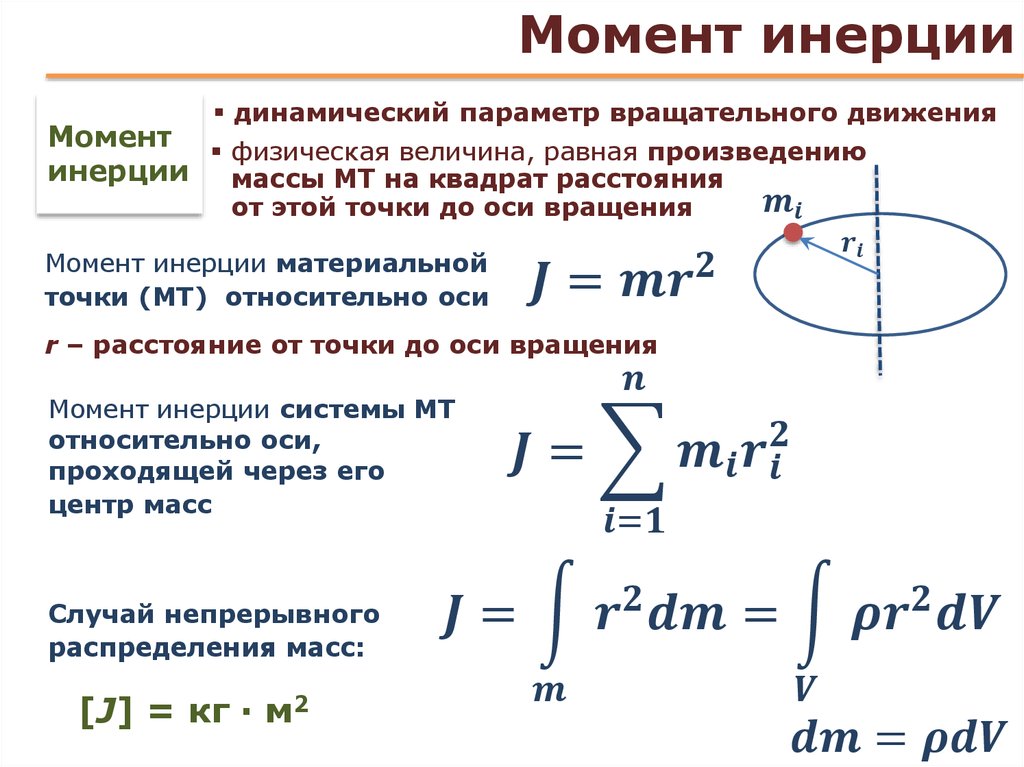 Бұл теоремалар:
Бұл теоремалар:
Сондай-ақ шақырылды параллель осьтер теоремасы, осьтерге қатысты инерция моментін осьтер параллель болғанша, заттың масса центрі арқылы өтетін екіншісімен байланыстырады. Оны қолдану үшін екі осьтің арасындағы қашықтықты және әрине объектінің М массасын білу керек.
Болуы Мензқатысты кеңейтілген объектінің инерция моменті z осі, IСМаталған заттың масса центрі (СМ) арқылы өтетін оське қатысты инерция моменті, онда:
Менз = МенСМ + М.ғ.д.2
Немесе келесі суреттің белгісінде:Менz ’ = Менз + Мд2
Перпендикуляр осьтер теоремасыБұл теорема жазықтық беттеріне қолданылады және осылай жүреді: жазық заттың оған перпендикуляр осьтің айналасындағы инерция моменті дегеніміз бірінші осіне перпендикуляр екі осьтің айналасындағы инерция моменттерінің қосындысы:
Менз = Менх + МенY
Егер объектінің симметриясы болса Менх және МенY тең болса, онда:
Менз = 2Iх
Жаттығу шешілді1-суретте көрсетілгендей (төменде және оң жақта) және 10-суретте көрсетілгендей, штанганың бір ұшынан өтетін оське қатысты инерция моментін табыңыз.
Шешім:
Бізде оның геометриялық центрі арқылы өтетін осьтің айналасындағы инерция моменті бар. Бар біртекті болғандықтан, оның масса центрі сол жерде орналасқан, сондықтан бұл біздікі болады МенСМ Штайнер теоремасын қолдану.
Егер жолақтың ұзындығы L, z осі D = L / 2 қашықтықта орналасқан, сондықтан:
Менз = МенСМ + М.ғ.д.2= (1/12) ML2+ M (L / 2)2= (1/3) ML2
Әдебиеттер тізімі- Бауэр, В. 2011. Инженерия мен ғылымдарға арналған физика. Том 1. Mc Graw Hill. 313-340
- Рекс, А. 2011. Физика негіздері. Пирсон. 190-200.
- Параллель ось теоремасы. Қалпына келтірілді: гиперфизика.phy-astr.gsu.edu.
- Serway, R. 2018. Физика ғылым мен техникаға арналған. 1-том.
- Севилья университеті. Қатты денелердің инерция моменті. Laplace.us.es сайтынан қалпына келтірілді.
- Севилья университеті. Бөлшектер жүйесінің инерция моменті.
 Laplace.us.es сайтынан қалпына келтірілді.
Laplace.us.es сайтынан қалпына келтірілді. - Википедия. Параллель ось теоремасы. Қалпына келтірілді: en.wikipedia.org
Момент инерции цилиндра Формула и его производные
Выражение момента инерции цилиндра дано здесь, чтобы помочь учащимся знать правильные формулы для решения различных задач, основанных на концепции. На этом уроке они найдут уравнения моментов инерции как для сплошного, так и для полого цилиндров.
Цельный цилиндр
Момент инерции сплошного цилиндра можно определить по следующей формуле;
| I = ½ MR 2 |
Здесь M = общая масса и R = радиус цилиндра, а ось проходит относительно его центра.
Чтобы понять полный вывод уравнения сплошного цилиндра, учащиеся могут перейти по ссылке.
Полый цилиндр
Момент инерции полого цилиндра, вращающегося вокруг оси, проходящей через центр цилиндра, можно определить по данной формуле;
| I = ½ M (R 2 2 + Р 1 2 ) |
Здесь цилиндр будет состоять из внутреннего радиуса R 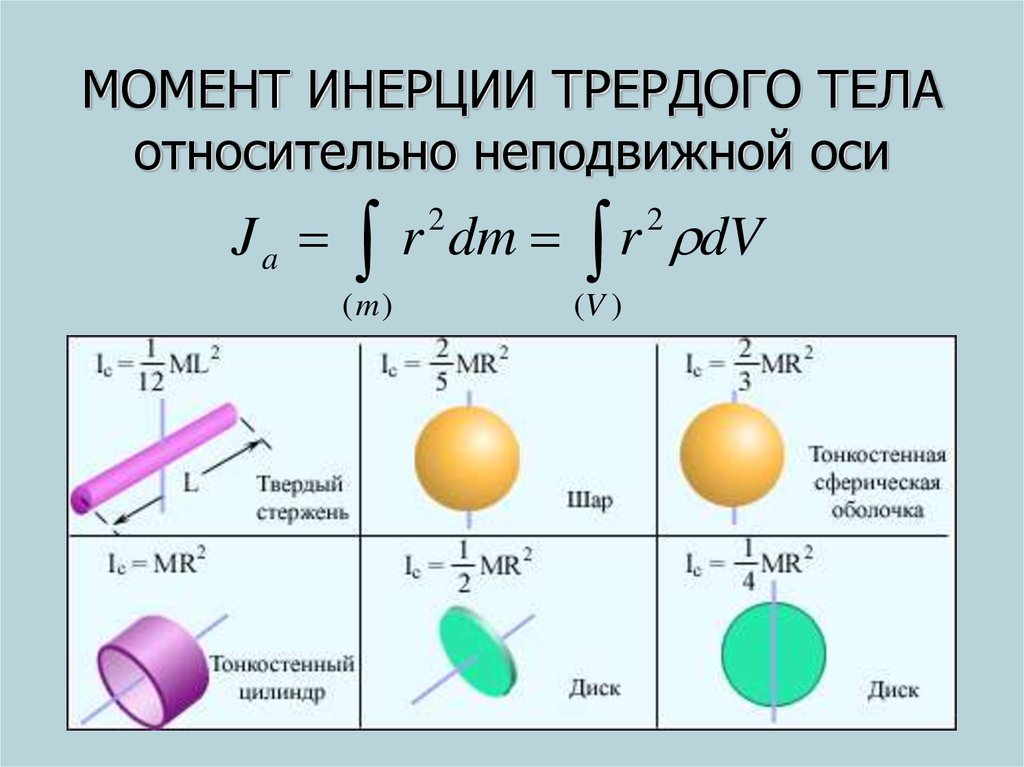
Полый цилиндр с тонкой стенкой можно выразить с помощью следующего уравнения момента инерции;
| I = МР 2 |
В этом случае ось проходит через центр цилиндра. M = масса и R = радиус.
Учащиеся могут изучить вывод выражения полого цилиндра, перейдя по ссылке.
Момент инерции цилиндра относительно перпендикулярной оси
Момент инерции цилиндра относительно перпендикулярной оси, проходящей через его центр, определяется по формуле;
I x = ¼ (MR
Ниже мы рассмотрим вывод этой формулы.
Как правило, вывод включает 3 основных этапа. Оно включает;
- Разбиение цилиндра на бесконечно малые диски и определение момента инерции.
- Использование теорем о параллельных и перпендикулярных осях для определения выражения.
- Интегрирование по длине цилиндра.
1.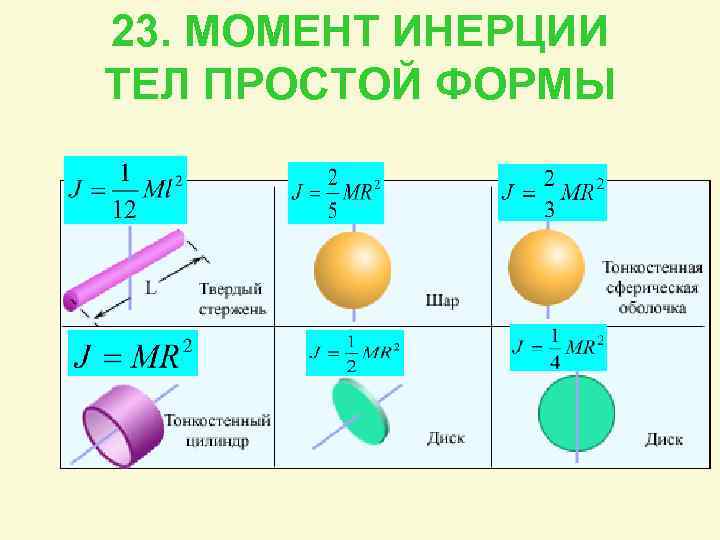 Разрезание цилиндра на бесконечно малые диски
Разрезание цилиндра на бесконечно малые диски
Рассмотрим цилиндр, имеющий массу M, радиус R, длину L и ось z, проходящую через центральную ось.
Здесь,
Плотность ρ = М/В
Далее рассмотрим момент инерции бесконечно малого диска толщиной dz.
Сначала примем, что dm — масса каждого диска, Получим;
дм = ρ x Объем диска
дм = (М/В) х (πr 2 .dz)
Возьмем V = площадь круглой грани x длина, которая равна ( πr 2 L).
Теперь получаем;
дм = (M / πr 2 L) x (πr 2 .dz)
дм = (м/л) дз
Момент инерции относительно центральной оси определяется как;
dl z = ½ dmR 2
2. Использование теоремы о перпендикулярной оси
Теперь мы применяем теорему об перпендикулярных осях, которая дает нам;
dl z = dl x + dl y
Здесь, если нам нужно учесть, что оба момента инерции x и y равны по симметрии.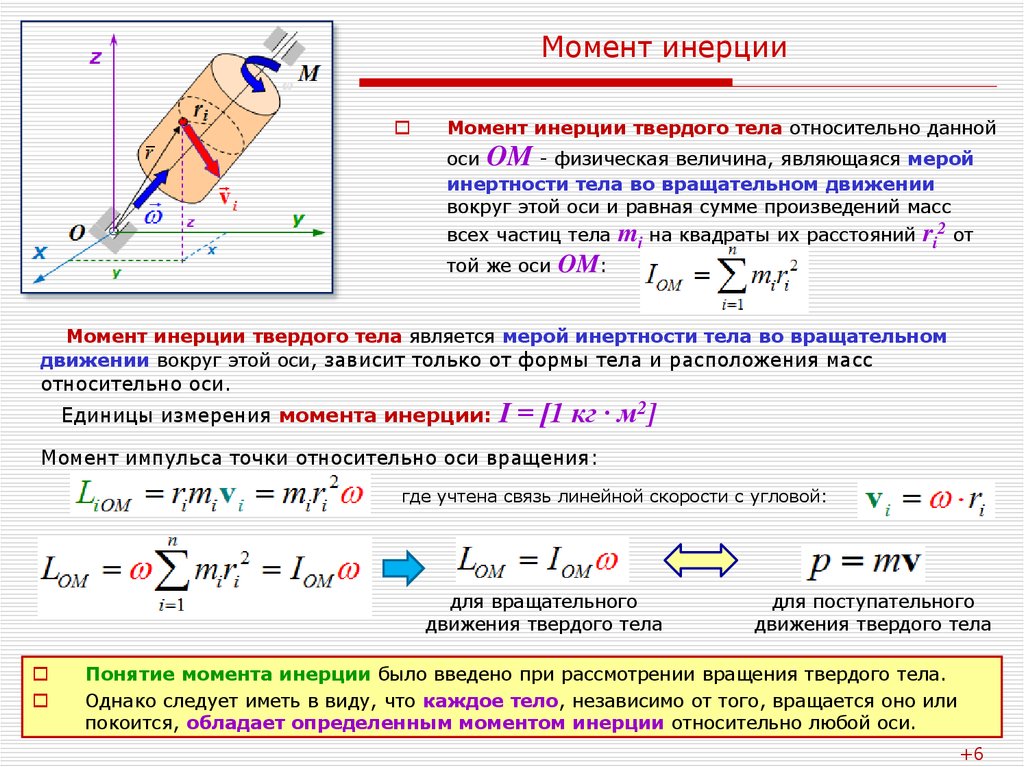
дл х = дл у
Нам нужно объединить уравнения теоремы перпендикулярной оси и симметрии. Мы получаем;
дл x = дл z / 2
Теперь подставляем l z из приведенного выше уравнения.
dl x = ½ x [½ dmR 2 ]
В качестве альтернативы, для оси x мы используем теорему о параллельности осей, чтобы найти момент инерции. Мы получаем;
dl x = ¼ dmR 2 + дмз 2
3. Интеграция
Теперь проинтегрируем по длине цилиндра, чтобы выразить элемент массы dm через z. Возьмем интеграл от z=0 до z=L.
I x = o ∫ L dl x
I x = o ∫ L ¼ (M / L) R 2 dz+ o ∫ L 9z 13 0 z 2 3M 900 I х = [¼ (М / Д) R 2 z + (M / L) z 3 / 3] Поскольку это определенная форма интеграла, мы игнорируем константу. I x = ¼ (M / L) R 2 L + ML 3 / 3 I x = MR 2 /4+ ML 2 /3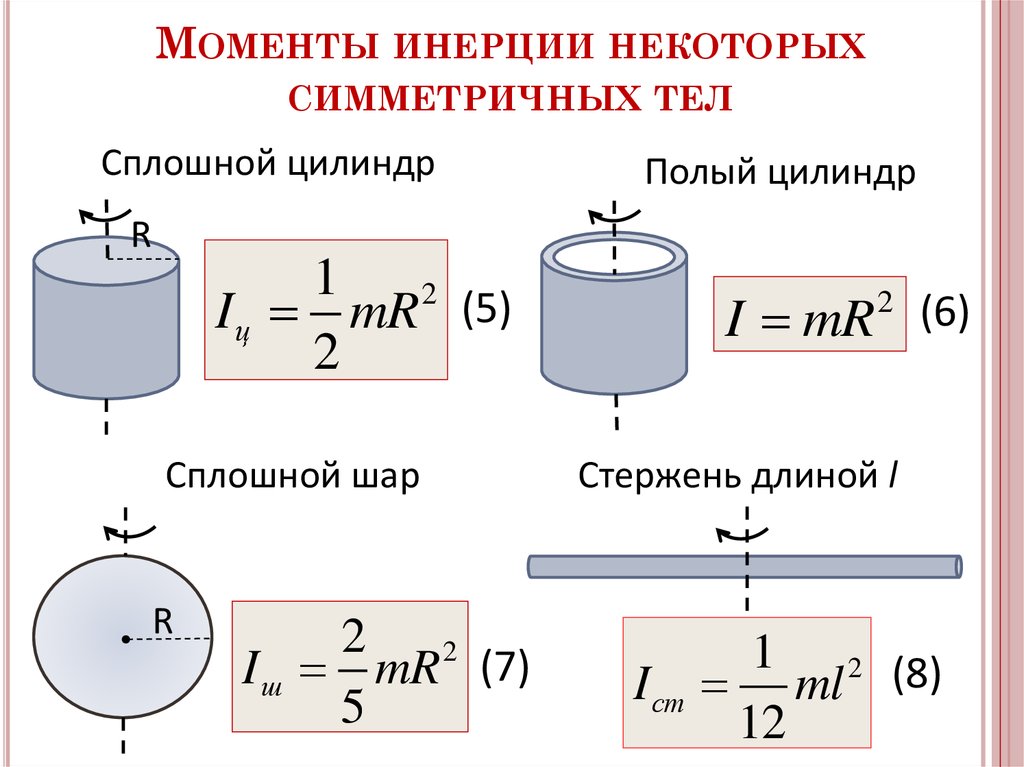 Теперь у нас будет;
Теперь у нас будет; ⇒ Проверить момент инерции другого объекта:
Теорема о параллельных осях
Момент инерции площади – формулы, расчеты и теоремы произвольная ось в плоскости поперечного сечения. Это свойство в основном характеризует прогиб плоской формы под действием некоторой нагрузки.
Момент инерции площади обычно обозначается буквой 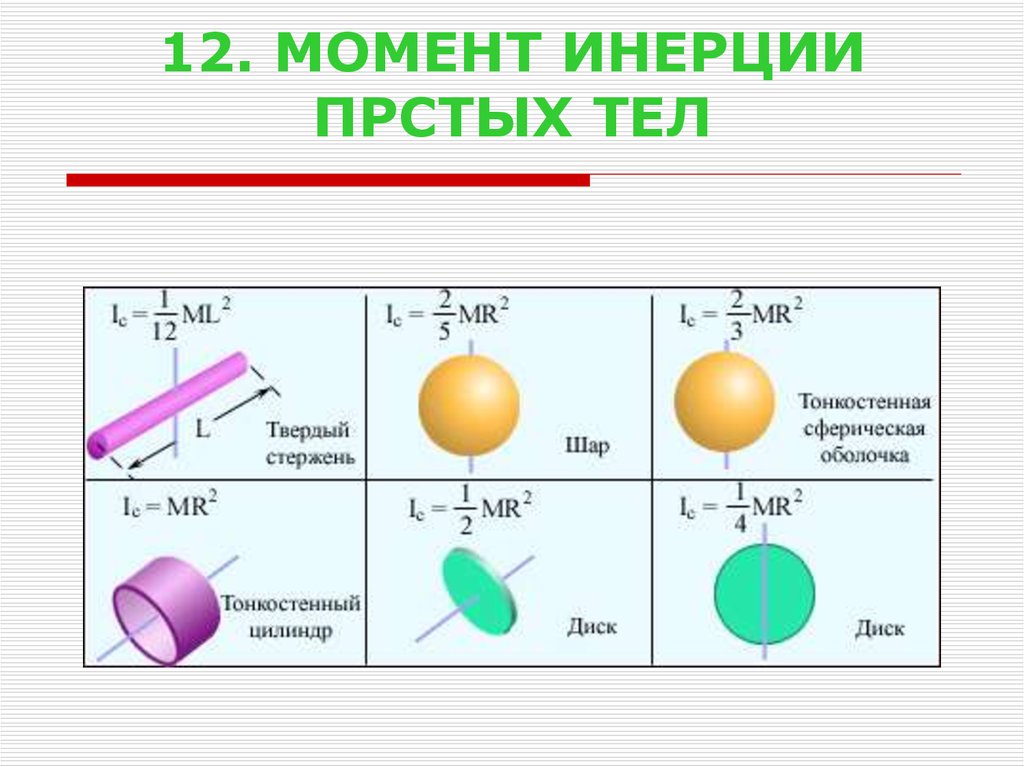 Если мы возьмем имперскую систему единиц, это может быть дюйм в четвертой степени, в 4 .
Если мы возьмем имперскую систему единиц, это может быть дюйм в четвертой степени, в 4 .
Мы часто сталкиваемся с этим понятием в области проектирования конструкций. Здесь говорят, что момент инерции площади является мерой изгибной жесткости балки. Это важное свойство, которое используется для измерения сопротивления балки изгибу или при расчете прогиба балки. Здесь мы должны рассмотреть два случая.
- Во-первых, сопротивление балки изгибу может быть легко описано или определено плоским вторым моментом площади, где сила направлена перпендикулярно нейтральной оси. 9{2}dxdy\конец{массив} \)
Между тем, «произведенный» момент площади определяется
\(\begin{array}{l}I_{xy}=\int xydxdy\end{массив} \)
Определение момента инерции площади
Теорема о параллельных осях
Момент инерции тела относительно любой оси равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс, и произведения его массы на квадрат расстояния между двумя линии.



 Laplace.us.es сайтынан қалпына келтірілді.
Laplace.us.es сайтынан қалпына келтірілді.