Инерция моменті — Студопедия
Денені? массасы мен оны? айналу центрінен денеге дейінгі ара ?ашы?ты?ыны? квадратыны? к?бейтіндісіне те? шаманы инерция моменті деп атайды.
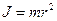
Денені? инерция моменті, ол денені? ?андай оське ?атысты айнал?анына ж?не денені? массасыны? к?леміне ?алай орналас?анына байланысты. Инерция моменті ?р т?рлі пішіндегі денелерде ?рт?рлі болады.
Массасы барлы? к?лемге бірдей орналас?ан ж?не д?рыс геометриялы?
пішіні бар массасы m біртекті денелерді? инерция моменттері
Бір инерция моментінен екіншісіне ?ту Штейнер-Гюйгенс теоремасы бойынша орындалады, кез келген айналыс осіне ?атысты инерция моменті, сол оське ?атысты ауырлы? центрі ар?ылы ?тетін инерция моменті мен дене массасыны? осьтерді? ара ?ашы?ты?ыны? квадратына к?бейтіндісіне ?осындысын айтады: 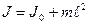
Айналмалы ?оз?алыста?ы ?атты денені? кинетикалы? энергиясы: 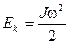
Егер дене ?рі ілгерлемелі, ?рі айналмалы ?оз?алыста болса, онда толы? кинетикалы? энергия:
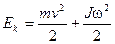
Айналмалы ?атты денені? динамикасыны? негізгі те?деуі.
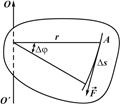
Дене Dj б?рыш?а б?рыл?анда к?ш т?сірілген А н?ктесі DS до?асыны? ?зынды?ына жылжиды, сонда F к?шіні? істеген ж?мысы: 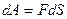
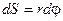 ; сонда
; сонда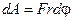 болады.
болады.
 Егер M=Fr , болса
Егер M=Fr , болса 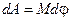 ; б?дан денені? айналдыру ж?мысы кинетикалы? энергияны ?л?айту?а кетеді:
; б?дан денені? айналдыру ж?мысы кинетикалы? энергияны ?л?айту?а кетеді:
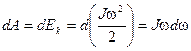 ; я?ни ?орыта келгенде мына т?рдегі те?деу шы?ады: M=Je.
; я?ни ?орыта келгенде мына т?рдегі те?деу шы?ады: M=Je.
б?л те?деу айналмалы ?атты денені? ?оз?алыс динамикасыны? негізгі те?деуі болып табылады.
Импульс моменті ж?не са?талу за?дары.
Импульс моменті, ол 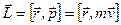 векторлы? к?бейтіндісімен аны?талатын шама
векторлы? к?бейтіндісімен аны?талатын шама
?оз?алмайтын осьтен айнал?ан абсолют ?атты денені? ?рбір н?ктесіні? жылдамды?ы vi, импульс моменті 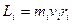 болса, барлы? денені? импульс моменті:
болса, барлы? денені? импульс моменті:

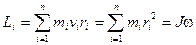
ал к?ш моменті импульс моментіні? уа?ыт бойынша бірінші туындысы:
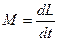
Т?йы? ж?йе ?шін импульс моменті уа?ыт а?ынымен ?згермейді: 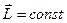
Денені? ілгерлемелі ?оз?алысы мен ?атты денені?
айналмалы ?оз?алысын салыстырайы?:
?атты денені? деформациясы.
?атты денелерді? сырт?ы к?шті? ?серінен пішіні мен ?лшемін ?згертуін деформация деп атайды.
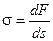
Денені? б?лшектеріні? бір-бірімен ?серлесуі н?тижесінде серіппені? барлы? к?лемі ?згеріске ?шырайды. Егер ?сер ететін к?ш бетке нормаль ба?ыттал?ан болса, кернеуді ?алыпты немесе нормаль кернеу деп атайды.
Егер к?ш бетке жанама ба?ыттал?ан болса, онда кернеу тангенсиал деп аталады.
Серіппені? деформациядан кейінгі ?заруын Dl, деформация?а дейінгі ?зынды?ына б?лсек, денені? салыстырмалы деформациясы шы?ады:
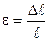
немесе салыстырмалы деформация кернеуге тура пропорционал: 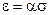 .
.
Материалды? серпімді ?асиеттерін ?арастыр?анда: 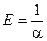 деген шама ?олданылады, б?л шама серпімді модулі немесе Юнг модулі деп аталады.
деген шама ?олданылады, б?л шама серпімді модулі немесе Юнг модулі деп аталады.
Юнг модулін ?олданып салыстырмалы деформацияны мына т?рде жазу?а болады: 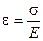
м?нда?ы a — материалды? таби?атына байланысты пропорционалды? коэффициенті, ол Пуассон коэффициенті
Юнг модуліні? ?лшем бірлігі – (Па)
Енді те?деуді те?естіре отырып, былай жазу?а болады:
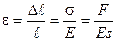 б?дан
б?дан 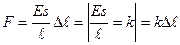 — б?л Гук за?ы болып табылады.
— б?л Гук за?ы болып табылады.
Б?дан серпімді деформация кезінде серппені? ?заруы ?сер етуші к?шке тура пропорционал екендігі шы?ады, м?нда?ы k – пропорционалды? коэффициент немесе серпімділік коэффициенті деп аталады
Б?кіл?лемдік тартылыс за?ы.
Таби?атта барлы? денелер бірін-бірі тартады. Осы тартылу за?ын Ньютон аш?ан ж?не б?кіл?лемдік тартылыс за?ы
Б?л за? бойынша: екі материалды? н?ктені? тартылыс к?ші, осы н?ктені? массаларына тура пропорционал ж?не ара ?ашы?ты?ыны? квадратына кері пропорционал.
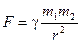
м?нда?ы g — пропорционалды? коэффициент, гравитациялы? т?ра?ты деп аталады, оны? шамасы g=6.672·10-11 H·м2/кг2, m1 ж?не m2 – денелерді? массалары, r – денелерді? ара ?ашы?ты?ы.
Космосты? жылдамды?тар.
Жерді айналып ?шу ?шін денені? ?зіндік жылдамды?ы болуы керек.
Бірінші космосты? жылдамды?: 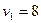 км/с
км/с
Екінші космосты? жылдамды?: 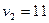 км/с
км/с
?шінші космосты? жылдамды?: 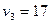 км/с,
км/с,
Инерция моменттерi — Студопедия
1. Жұқа дискiнiң: 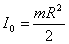
2. Стерженнiң: 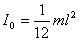
3. Цилиндрдiң: 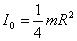
4. Шардың: 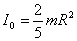
5. Материялық нүктенiң айналу осiне қатысты инерция моментi:
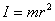 .
.
Дененiң кез-келген оське қатысты инерция моментi Штейнер теоремасы бойынша анықталады: 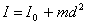
мұндағы: 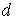 — ауырлық центрiмен айналу осі арасындағы ара қашықтық.
— ауырлық центрiмен айналу осі арасындағы ара қашықтық.
Айналмалы қозғалыстағы дененiң кинетикалық энергиясы:
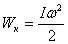 .
.
Айналмалы қозғалыс кезiнде қатты дененiң кинетикалық энергиясы- оның инерция моментi мен бұрыштық жылдамдығының квадратының көбейтiндiсiнiң жартысына тең.
Жазық қозғалыстағы дененiң кинетикалық энергиясы- дененiң iлгерiлемелi және айналмалы қозғалыс кезiндегi кинетикалық энергияларының қосындысына тең болады.
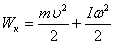
Тұтас орта механикасы
Газдар мен сұйықтардың тепе-теңдiгiн және қозғалысын зерттегенде оларды үздiксiз тұтас орта түрiнде қарастырады.
Сұйықтардың тепе-теңдiгiн қарастыратын механиканың бөлiмiн – гидростатикадеп атайды.
Сұйықтар мен газдардың серпiмдi қасиетi мынадан байқалады: олардың жеке бөлiктерi бiр-бiрiне немесе олармен жанасатын денеге сұйық пен газдардың сығылу дәрежесiне тәуелдi болатын күшпен әсер етедi. Мұндай әсер қысыммен сипатталады.
Сөйтiп, сұйықтар мен газдарды сипаттайтын ең негiзгi шамалардың бiрi — қысым.
Қысым деп бетке түсетiн күштiң осы беттiң ауданына қатынасына тең шаманы айтады. Өлшем бірлігі 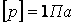 .
.
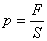 .
.
Паскаль заңы.
Сұйық ішіне түсiрілген қысым барлық бағытқа бiрдей берiледi.
Сұйық iшiндегi қысым: 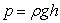 .
.
Бұл қысымды кейде гидростатикалық қысым деп атайды.
Сұйықтардың қозғалысын зерттейтiн механиканың бөлiмiн – гидродинамикадеп атайды.
Сұйық бөлшектерiнiң қозғалысын зерттеудiң екі тәсiлi бар.
1.Лагранж тәсiлi
Бұл тәсiлде әрбiр жеке сұйық бөлшегiнiң кеңiстiктегi қозғалыс заңдылығы зерттеледi.
2.Эйлер тәсiлi
Бұл тәсiлде кеңiстiктiң белгiлi бiр нүктесiнен өтетiн сұйық бөлшектерiнiң жылдамдығы қарастырылады.
Сұйық бөлшектерiнiң қозғалысы — ағыс, ал сұйықтың қозғалысы- ағындеп аталады.
Кез келген нүктесiнде жүргiзiлген жанама сол нүктедегi сұйық бөлшегiнiң жылдамдықтарымен сәйкес келетiн сызықтарды ағын сызықтарыдеп атайды. Ағын сызықтарының жиiлiгi сол жерде сұйықтың жылдамдығын көрсетедi (сурет).
Мысалы суреттегi А нүктесiндегi сұйықтың жылдамдығы В нүктесiндегi сұйықтың жылдамдығынан үлкен болады. Ағын сызықтарымен шектелген сұйық бөлiгiн ағын сорғысыдеп атайды.
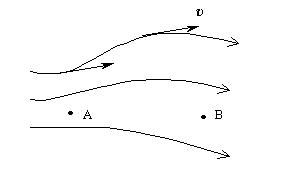
Кез келген нүктесiндегi сұйықтың жылдамдығының шамасы мен бағыты өзгермейтiн ағысты стационар ағысдеп атайды.
Ағыс сипатына байланысты екіге бөлiнедi.
Егер сұйық қабаттары бiр-бiрiмен араласпай, бiр-бiрiне параллель қозғалатын болса, мұндай ағыс – ламинар(қабатты) ағысдеп аталады.
Егер сұйық қабаттары бiр-бiрiмен араласып иiрiлiп қозғалатын болса, мұндай ағыс – турбуленттi (иiрiмдi)депаталады. Сығылмайтын тұтқыр емес сұйықты идеал сұйық деп, ал сығылатын тұтқыр сұйық реал сұйық деп аталады.
Ағынның үздiксiздiк теңдеуi
төменгi ыдыс толсын. Сұйық сығылмайды және үзiлмейдi деп есептесек, нда жоғарғы ыдыстан ағып кеткен сұйық көлемi мен төменгi ыдысқа құйылған сұйық көлемi тең болады:
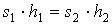 ,
,
мұндағы: 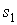 — жоғарғы ыдыстың көлденең қимасы,
— жоғарғы ыдыстың көлденең қимасы, 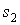 — төменгi ыдыстың көлденең қимасы, бұл формуланың екi жағын
— төменгi ыдыстың көлденең қимасы, бұл формуланың екi жағын 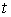 -¹а бөлсек:
-¹а бөлсек: 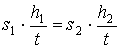 немесе
немесе 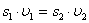 ,
,
мұндағы 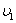 — жоғарғы ыдыстағы сұйық ағысының жылдамдығы,
— жоғарғы ыдыстағы сұйық ағысының жылдамдығы, 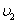 — төменгi ыдыстағы сұйық ағысының жылдамдығы. Сонда
— төменгi ыдыстағы сұйық ағысының жылдамдығы. Сонда
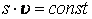 .
.
Осы өрнектi ағынның үздiксiздiк теңдеуiдеп атайды. Ыдыстың көлденең қимасының сұйық ағысының жылдамдығына көбейтiндiсi тұрақты шама болады.
Сұйық ағысының жылдамдығы ыдыстың көлденең қимасына керi пропорционал.
Бернулли теңдеуi
Идеал сұйықтың қозғалысын (ағысын) сипаттайтын өрнектi 1738 жылы Д.Бернулли (1700-1782) тұжырымдады. Бернулли энергияның сақталу заңын пайдалана отырып, сұйық қысымының жылдамдыққа тәуелдiлiгiн анықтады. Бұл формуланы қорытып шығару үшiн көлденең қимасы әр түрлi түтiкшедегi идеал сұйықтың қозғалысын қарастырайық (сурет).
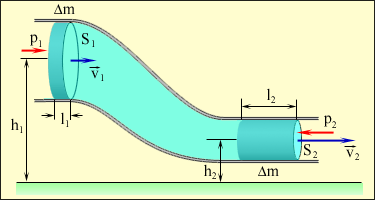
1 және 2 қималардың арасындағы сұйық массасының қозғалуын бақылайық. 1-ден кейiн, 2 қиманың алдында ағын болмаса да екi қима арасындағы сұйық массасы өз салмағы әсерiнен қозғала бастайды. Алайда, екi қима арасындағы сұйық өз массасымен ғана қозғалып қоймай, ол 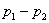 айырмасының әсерiнен де қозғалысқа келетiнiн айта кеткен жөн. Сонымен сыртқы күш
айырмасының әсерiнен де қозғалысқа келетiнiн айта кеткен жөн. Сонымен сыртқы күш 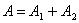 жұмыс iстейдi. Мұндағы
жұмыс iстейдi. Мұндағы 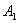 — 1 қимада iстелетiн жұмыс.
— 1 қимада iстелетiн жұмыс. 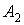 — 2 қимада iстелетiн жұмыс
— 2 қимада iстелетiн жұмыс 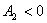 . Энергияның сақталу заңы бойынша қималар энергияларының айырымы сұйықты қозғалысқа келтiру үшiн iстелетiн жұмыстардың айырымына тең болады:
. Энергияның сақталу заңы бойынша қималар энергияларының айырымы сұйықты қозғалысқа келтiру үшiн iстелетiн жұмыстардың айырымына тең болады: 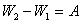 немесе
немесе
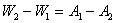 ,
,
мұндағы: 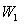 ,
, 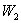 — 1 мен 2 қималардағы сұйықтардың толық энергиялары.
— 1 мен 2 қималардағы сұйықтардың толық энергиялары.
Толық энергия кинетикалық және потенциалдық энергиялардың қосындысына тең:
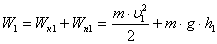 ,
,
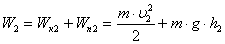 ,
,
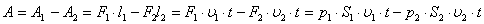 .
.
 ,
,  және
және 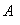 -ның мәндерiн алғашқы формулаға апарып қойсақ, табатынымыз
-ның мәндерiн алғашқы формулаға апарып қойсақ, табатынымыз
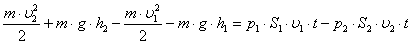 .
.
Ағыстың үздiксiздiк теңдеуiнен 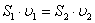 екенiн бiлемiз, олай болса:
екенiн бiлемiз, олай болса:
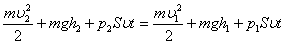 .
.
Екiншi жағынан, 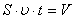
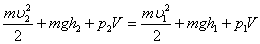 ,
,
бұл өрнектiң екi жағын да көлемге 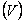 бөлсек:
бөлсек:
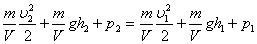 .
.
Ал 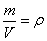 сұйықтың тығыздығы екенiн ескерсек:
сұйықтың тығыздығы екенiн ескерсек:
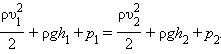
Жалпы түрде алғанда
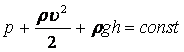 .
.
Бұл теңдеу Бернулли теңдеуi деп аталады.
мұндағы: 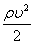 — динамикалық қысым,
— динамикалық қысым, 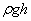 -гидравликалық қысым, р — статикалық қысым.
-гидравликалық қысым, р — статикалық қысым.
Статикалық қысым (р) сұйықтың қозғалысына тәуелсiз, ал динамикалық қысым сұйық қозғалысына тәуелдi болады. Ол сұйық тежелгенде айқын бiлiнедi. Гидравликалық қысым салмақсыздық кезiнде жойылады да, асқын салмақ кезiнде өсе түседi.
Горизанталь құбыр үшiн Бернулли теңдеуi:
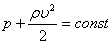 .
.
Сұйықтың жылдамдығы артқанда қысымы кемидi.
Автор Aleks На чтение 12 мин. Просмотров 114 Опубликовано
История понятия «инерция»
До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.
 Бюст Аристотеля. Римская копия греческого бронзового оригинала
Бюст Аристотеля. Римская копия греческого бронзового оригиналаЭто утверждение закономерно вытекало из реальных наблюдений. При этом Аристотель объяснял движение снарядов, выпущенных из орудия, невидимым действием окружающей среды, которая каким-то образом продолжает двигать снаряд. При этом философ пришел к выводу, что такое движение в пустоте невозможно.
Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.
Эта теория движения неоднократно оспаривалась. Например, в 6 веке византийский филолог Иоанн Александрийский (Иоанн Грамматик) раскритиковал тезисы Аристотеля, что среда поддерживает движения тела и что тело остановится в пустоте. В 11 веке персидский исламский врач, астроном, философ и писатель Ибн Сина [Авиценна] (980 – 1037 гг.) сделал вывод, что снаряд при отсутствии действия внешних сил, то есть в пустоте, не остановится.
Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.
 Портрет Кеплера в 1610 году
Портрет Кеплера в 1610 годуТермин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.
 Юстус Сустерманс. Портрет Галилея Галилея. 1636
Юстус Сустерманс. Портрет Галилея Галилея. 1636Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».
Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов. Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.
 Мысленный эксперимент Галилея
Мысленный эксперимент ГалилеяГалилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».
 Готфрид Кнеллер. Портрет Исаака Ньютона. 1689
Готфрид Кнеллер. Портрет Исаака Ньютона. 1689Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.
Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.
 Три закона Ньютона
Три закона Ньютона  Инерция: взгляды от Аристотеля до Ньютона
Инерция: взгляды от Аристотеля до НьютонаОговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.
Посмотрим на второй закон Ньютона.

Чаще его записывают в виде:

так как в инерциальной системе отсчета сила является причиной ускорения тела.
Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).
Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).
Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.

Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).
 Тормозной путь грузовика и легковушки
Тормозной путь грузовика и легковушкиИз-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.
Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.
Инерция, кинетическая энергия, работа
Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.
 Силачи тянут Ил-76
Силачи тянут Ил-76А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.
 Трюк со скатертью
Трюк со скатертьюЭнергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.

Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):

Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).
Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.
Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:

Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.
Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.
При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?
Момент инерции
Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.
Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?
 Вращение на фигурном катании
Вращение на фигурном катанииМногие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.
Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:
 Скорость вращающегося тела
Скорость вращающегося телаПри этом кинетическая энергия вращающегося тела примет вид:

Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.
Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.
Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.
 Некоторые формулы для расчета момента инерции для тел разной формы
Некоторые формулы для расчета момента инерции для тел разной формыПример.
Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r1 < r2), скатываются с горки высотой h. Какой цилиндр скатится быстрее? Какое из тел обладает меньшей инертностью?
 Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h
Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой hВ верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.
 Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точке
Потенциальная и кинетическая энергия 1 и 2 цилиндра верхней точкеПри скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.
 Кинетическая энергия первого и второго цилиндра в нижней точке
Кинетическая энергия первого и второго цилиндра в нижней точкеНо так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

Тогда для кинетической энергии поступательного движения будет справедливо отношение:

Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.
Вопросы
1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i
 Маховик автомобиля
Маховик автомобиля2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?

3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?

Видео:
- Инерция. GetAClass
- Момент инерции. GetAClass
- Момент инерции вращающихся тел. Эксперимент. Зависимость момента инерции от распределения массы
- Момент инерции вращающихся тел. Эксперимент. Скатывание цилиндров с наклонной плоскости одинаковой массы и размера
- Момент инерции вращающихся тел. Фигурное катание. Юлия Липницкая, вращение
- Момент инерции. Работа двигателя с маховиком и без него
Статьи:
- Первый закон Ньютона и инерциальные системы отсчёта
- Второй закон Ньютона
- Равнодействующая
- Третий закон Ньютона
- Неинерциальные системы отсчёта
Момент инерции — Студопедия
Рассмотрим материальную точку массой m, которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:
J = mr2 (75)
Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:
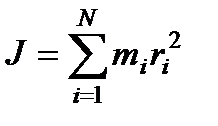 (76)
(76)
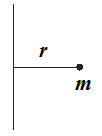
Рис. 26.
К определению момента инерции точки.
Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.
В результате получается следующее выражение:
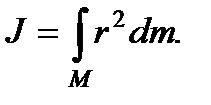 (77)
(77)
Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:
dm = ρdv, преобразуем формулу (70) следующим образом:
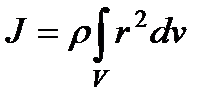 (78)
(78)
Размерность момента инерции – кг*м2.
Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.
Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.
Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.
В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.
Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:
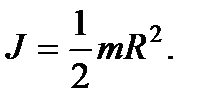
Момент инерции шара радиуса R:
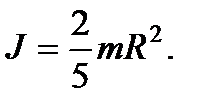
Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:
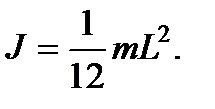
Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:
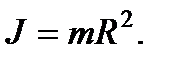
Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.
Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).
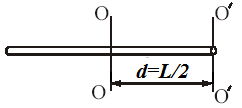
Рис. 27.
К расчету момента инерции стержня
Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md2. Отсюда получаем:
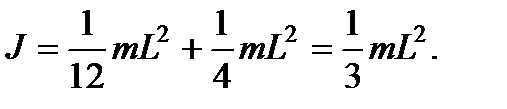
Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
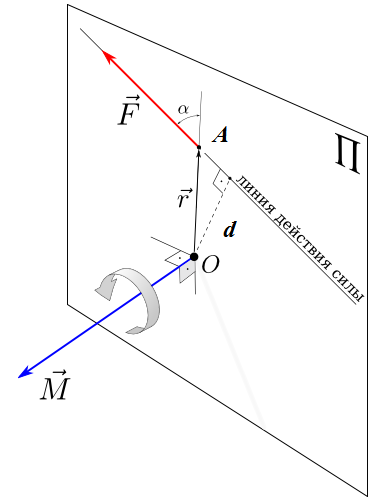
Рис. 28.
Момент силы F относительно точки O
Из повседневного опыта мы можем подтвердить следующее умозаключение: скорость и направление движения тела могут меняться лишь во время его взаимодействия с другим телом. Это порождает явление инерции, о котором мы и поговорим в этой статье.
Что такое инерция? Пример жизненных наблюдений
Рассмотрим случаи, когда какое-нибудь тело на начальном этапе эксперимента уже пребывает в движении. Позже мы увидим, что уменьшение скорости и остановка тела не могут происходить самовольно, ведь причиной тому является действие на него другого тела.
Вы, наверное, не единожды наблюдали, как пассажиры, которые едут в транспорте, вдруг наклоняются вперед во время торможения или прижимаются на бок на крутом повороте. Почему? Объясним далее. Когда, к примеру, спортсмены пробегают определенную дистанцию, они пытаются развить максимальную скорость. Пробежав финишную черту, уже можно и не бежать, однако нельзя резко остановиться, а поэтому спортсмен пробегает еще несколько метров, то есть совершает движение по инерции.
 Из вышеперечисленных примеров можно сделать вывод, что все тела имеют особенность сохранять скорость и направление движения, не будучи в состоянии при этом мгновенно их изменить впоследствии действия иного тела. Можно предположить, что при отсутствии внешнего действия тело сохранит и скорость, и направление движения как угодно долго. Итак, что такое инерция? Это явление сохранения скорости движения тела при отсутствии воздействия на него других тел.
Из вышеперечисленных примеров можно сделать вывод, что все тела имеют особенность сохранять скорость и направление движения, не будучи в состоянии при этом мгновенно их изменить впоследствии действия иного тела. Можно предположить, что при отсутствии внешнего действия тело сохранит и скорость, и направление движения как угодно долго. Итак, что такое инерция? Это явление сохранения скорости движения тела при отсутствии воздействия на него других тел.Открытие инерции
Такое свойство тел открыл итальянский ученый Галилео Галилей. На основе своих экспериментов и рассуждений он утверждал: ежели тело не взаимодействует с иными телами, то оно либо пребывает в состоянии спокойствия, либо движется прямолинейно и равномерно. Его открытия вошли в науку как Закон инерции, однако более детально сформулировал его Рене Декарт, а уж Исаак Ньютон внедрил в свою систему законов.
Интересный факт: инерция, определение которой привел нам Галилей, рассматривалась еще в Древней Греции Аристотелем, но из-за недостаточного развития науки, точной формулировки приведено не было. Первый закон Ньютона гласит: существуют такие
системы отсчета, относительно которых тело, которое движется поступательно, сохраняет свою скорость постоянной, если на него не действуют иные тела. Формула инерции в едином и обобщенном виде отсутствует, но ниже мы приведем множество иных формул, раскрывающих ее особенности.
Инертность тел
Все мы знаем, что скорость человека, автомобиля, поезда, корабля или других тел увеличивается постепенно, когда они начинают двигаться. Все вы видели запуск ракет по телевизору или взлет самолетов в аэропорту — они увеличивают скорость не рывками, а постепенно. Наблюдения, а также повседневная практика говорят о том, что все тела имеют общую особенность: скорость движения тел в процессе их взаимодействия меняется постепенно, а поэтому для их изменения необходимо некоторое время. Эта особенность тел получила название инертности.
Все тела инертны, но не у всех инертность одинакова. Из двух взаимодействующих тел она будет выше у того, которое обретет меньшее ускорение. Так, к примеру, при выстреле ружье приобретает меньшее ускорение, чем патрон. При взаимном отталкивании взрослого конькобежца и ребенка взрослый получает меньшее ускорение, чем ребенок. Это свидетельствует о том, что инертность взрослого человека больше.
Для характеристики инертности тел ввели особенную величину — массу тела, ее принято обозначать буквой m. Дабы иметь возможность сравнивать массы различных тел, массу кого-нибудь из них необходимо учесть за единицу. Ее выбор может быть произвольным, однако она должна быть удобной для практического употребления. В системе СИ за единицу взяли массу специального эталона, изготовленного из твердого сплава платины и иридия. Она носит всем нам известное название — килограмм. Следует отметить, что инерция твердого тела бывает 2-х видов: поступательная и вращательная. В первом случае мерой инерции является масса, во втором — момент инерции, о котором мы поговорим позже.
Момент инерции
Так называют скалярную физическую величину. В системе СИ единицей измерения момента инерции является кг*м2. Обобщенная формула следующая:
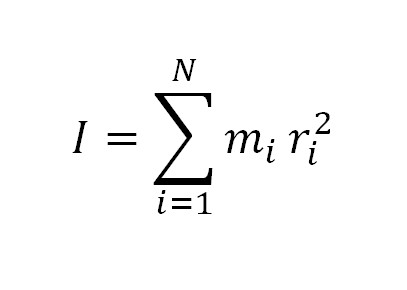
Здесь mi — это масса точек тела, ri — это расстояние от точек тела до оси z в пространственной системе координат. В словесной интерпретации можно сказать так: момент инерции определяется суммой произведений элементарных масс, умноженных на квадрат расстояния до базового множества.
Есть и другая формула, характеризующая определение момента инерции:
Здесь dm — масса элемента, r — расстояние от элемента dm до оси z. Словесно можно сформулировать так: момент инерции системы материальных точек или тела относительно полюса (точки) — это алгебраическая сумма произведения масс материальных точек, составляющих тело, на квадрат расстояния их до полюса 0.
Стоит упомянуть, что существует 2 вида моментов инерции — осевые и центробежные. Есть также такое понятие, как главные моменты инерции (ГМИ) (относительно главных осей). Как правило, они всегда различны между собой. Ныне можно рассчитать моменты инерции для многих тел (цилиндра, диска, шара, конуса, сферы и проч.), однако не будем углубляться в уточнение всех формул.
Системы отсчета
В 1-ом законе Ньютона шла речь о равномерном прямолинейном движении, которое можно рассматривать только в определенной системе отсчета. Даже приближенный анализ механических явлений показывает, что закон инерции выполняется далеко не во всех системах отсчета.
Рассмотрим простой эксперимент: положим мяч на горизонтальный столик в вагоне и понаблюдаем за его движением. Если поезд будет находиться в состоянии спокойствия относительно Земли, то и мяч сохранит спокойствие до тех пор, пока мы не подействуем на него иным телом (например, рукой). Следовательно, в системе отсчета, что связана с Землей, закон инерции выполняется.
Представим, что поезд будет ехать относительно Земли равномерно и прямолинейно. Тогда в системе отсчета, что связана с поездом, мяч сохранит состояние спокойствия, а в той, что связана с Землей, — состояние равномерного и прямолинейного движения. Следовательно, закон инерции выполняется не только в системе отсчета, связанной с Землей, но и во всех других, движущихся относительно Земли равномерно и прямолинейно.
Теперь представим, что поезд быстро набирает скорость либо круто поворачивает (во всех случаях он движется с ускорением относительно Земли). Тогда, как и раньше, мяч сохраняет равномерное и прямолинейное движение, которое он имел до начала ускорения поезда. Однако относительно поезда мяч сам по себе выходит из состояния спокойствия, хотя и нет тел, которые бы выводили его из него. Это значит, что в системе отсчета, связанной с ускорением движения поезда относительно Земли, закон инерции нарушается.
Итак, системы отсчета, в которых выполняется закон инерции, получили название инерциальных. А те, в которых не выполняется, — неинерциальных. Определить их просто: если тело движется равномерно и прямолинейно (в отдельных случаях — это спокойствие), то система инерциальная; если движение неравномерное — неинерциальная.
Сила инерции
Это довольно многозначное понятие, а поэтому попытаемся как можно более детально его рассмотреть. Приведем пример. Вы спокойно стоите в автобусе. Внезапно он начинает двигаться, а значит, набирает ускорение. Вы мимо воли отклонитесь назад. Но почему? Кто вас потянул? С точки зрения наблюдателя на Земле (инерциальная система отсчета) вы остаетесь на месте, при этом выполняется 1-ый закон Ньютона. С точки зрения наблюдателя в самом автобусе, вы начинаете двигаться назад, будто под какой-либо силой. На самом деле ваши ноги, которые связаны силами трения с полом автобуса, поехали вперед вместе с ним, а вам,
теряя равновесие, пришлось падать назад. Таким образом, для описания движения тела в неинерциальной системе отсчета необходимо вводить и учитывать дополнительные силы, что действуют со стороны связей тела с такой системой. Эти силы и есть силы инерции.
Необходимо учесть, что они фиктивны, ибо нет ни единого тела либо поля, под действием которого вы начали двигаться в автобусе. Законы Ньютона на силы инерции не распространяются, однако их использование наряду с «настоящими» силами позволяет описывать движение у произвольных неинерциальных систем отсчета при помощи различных инструментов. В этом состоит весь смысл ввода сил инерции.
Итак, теперь вы знаете, что такое инерция, момент инерции и инерциальные системы, силы инерции. Двигаемся далее.
Поступательное движение систем
Пусть на некое тело, находящееся в неинерциальной системе отсчета, движущееся с ускорением а0 относительно инерциальной, действует сила F. Для такой неинерциальной системы уравнение-аналог второго закона Ньютона имеет вид:
Где а0 – это ускорение тела с массой m, что вызвано действием силы F относительно неинерциальной системы отсчета; Fін — сила инерции. Сила F в правой части является «настоящей» в том понимании, что это результирующая взаимодействия тел, зависящая только от разности координат и скоростей взаимодействующих материальных точек, которые не меняются при переходе от одной системы отсчета к другой, движущейся поступательно. Поэтому не меняется и сила F. Она инвариантна относительно такого перехода. А вот Fін возникает не по причине взаимодействия тел, а из-за ускоренного движения системы отсчета, из-за чего она меняется при переходе к другой ускоренной системе, поэтому не является инвариантной.
Центробежная сила инерции
Рассмотрим поведение тел в неинерциальной системе отсчета. XOY вращается относительно инерциальной системы, коей будем считать Землю, с постоянной угловой скоростью ω. Примером может послужить система на рисунке ниже.
Выше изображен диск, где закреплен радиально направленный стержень, а также надет синий шарик, «привязанный» к оси диска эластичной веревкой. Пока диск не вращается, веревка не деформируется. Однако при раскручивании диска шарик понемногу растягивает веревку до тех пор, пока сила упругости Fср не станет такой, что равна произведению массы шарика m на ее нормальное ускорение aп = -ω2R, то есть Fср = -mω2R, где R — это радиус круга, который описывает шарик при вращении вокруг системы.
Ежели угловая скорость ω диска останется постоянной, то и шарик прекратит движение относительно оси OX. В этом случае относительно системы отсчета XOY, которая связана с диском, шарик будет находиться в состоянии спокойствия. Это объяснится тем, что в этой системе, помимо силы Fср, на шарик действует сила инерции Fcf, которая направлена вдоль радиуса от оси вращения диска. Сила, имеющая вид, как в формуле, представленной ниже, называется центробежной силой инерции. Возникать она может только во вращающихся системах отсчета.
Сила Кориолиса
Оказывается, когда тела двигаются относительно вращающихся систем отсчета, на них, помимо центробежной силы инерции, действует еще одна сила — Кориолиса. Она всегда перпендикулярна к вектору скорости тела V, а это означает, что она не выполняет никакой работы над этим телом. Подчеркнем, что сила Кориолиса проявляет себя лишь тогда, когда тело движется относительно неинерциальной системы отсчета, которая осуществляет вращение. Ее формула выглядит следующим образом:
Поскольку выражение (v*ω) является векторным произведением приведенных в скобках векторов, то можно прийти к выводу, что направление силы Кориолиса определяется правилом буравчика по отношению к ним. Ее модуль равен:
Здесь Ө – это угол между векторами v и ω.
В заключение
Инерция — это удивительное явление, которое ежедневно преследует каждого человека сотни раз, пусть мы и сами не замечаем этого. Думаем, что статья дала вам важные ответы на вопросы о том, что такое инерция, что такое сила и моменты инерции, кто открыл явление инерции. Уверены, вам было интересно.
- Главная
- О сайте
- Политика защиты авторских прав
- Контакты
Advertisements
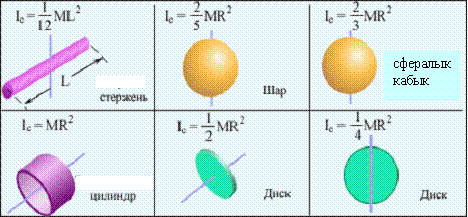
Кейбір бір текті денелердің инерция моменттері
Дене түрі
Дене формасы
Инерция моменті
Жіңішке стержень
left0
Тік төртбұрыш
эллипс
Тік бұрышты параллелепипед
Тік бұрышты пирамида
Дөнгелек цилиндр
Дөңгелек конус
эллипсоид
Инерция моменті скалярлық шама, айналмалы қозғалған дененің инерттілігінің өлшеуші материялық нүктелердің массасы мен айналу осінде қашыұтығы квадратының көбейтіндісінің қосындыларына тең. немесе бүдан инерция моменті дененің тығыздығына, пігшініне және оске қатысты орналасуына байланысты.
Аиналмалы қозғалыс кезінде қатты дененің нүктелеріцентрлері айналу осі деп аталатын түзу бойында жататын концентрлі шеңбер сызады. Айналыс шапшандығын уақыт бірлігіндегі дененің б.рылу бүрышымен сипаттауғв болады. Айналмалы қозғалыстын бүрыштық жылдамдығы .
Қатты дененің бекітілген оське қатысты айналмалы қозғалысы
Күштің берілген осьтен айналдыра алу қабілетін сипаттау үшін оське қатысты күш моменті деген ұғым енгізіледі.
Оське қатысты күш моментін күштің оське перпендикуляр жазықтықта жатқан құраушысы ғана тудыра алады.
Сондықтан қатты дененің массасы mі, оған әсер етуші сыртқы күш Fі , ал Fі күші mі массасының тракториясына жүргізілген жанамамен αі бұрыш жасайды және ол бұрыш сүйір болады (19-сурет). Сонда бұл элемент үшін теңдік былай жазылады:
мұндағы εі — массасы mі элементтің бұрыштық үдеуі. Тұтас дененің барлық элементі үшін оның қосындысын аламыз:
бұдан абсолют қатты дененің барлық элементтері үшін оның бұрыштық үдеуі тұрақты , олай болса:
мұндағы — қатты дененің барлық элементтеріне әсер ететін күш моменттерінің қосындысы, басқаша айтқанда қатты денеге әсер етуші күштердің ОО’ айналыс осіне қатысты М толық моменті болады. Дененің жеке элементтерінің қосындысы болатын шама ОО’ оське қатысты дененің инерция моменті деп аталады. Сонда күштің толық моментін (М) және инерция моментін (І) енгізіп мына теңдікті жазуға болады: M=Іε
яғни қатты дене үшін (5.21.3)- теңдікпен салыстырғанда дәл келетіндігін көрдік. Жоғарыда айтылғандай, күш моменті бұрыштық үдеумен бағыттас болғандықтан (5.21.3) — теңдікті векторлық түрде жазуға болады: (5.22.1)
Сонымен осы формула қатты дененің айналмалы қозғалысының негізгі теңдеуі болып табылады. Бұдан қатты дененің бұрыштық үдеуі мынаған тең болатынын көреміз: (5.22.2)
Сонда бұрыштық үдеу түсірілген күш моментіне тура пропорционал, ал инерция моментіне кері пропорционал болады. (5.21.3)-теңдікті Ньютонның екінші заңына өрнектейтін (ілгерілемелі қозғалыс үшін) теңдеумен салыстырсақ, онда ол қатты дене жылжымайтын осьтен айналғандығы Ньютон заңының формуласына ұқсас теңдік екендігін көреміз, бірақ мұнда сызықтық үдеудің ролін бұрыштық үдеу, күштің ролін күш моменті, массаның ролін инерция моменті атқарады. (5.21.3)- теңдікке қарағанда, егер денеге әсер ететін күштер моменті нөлге тең болса, онда бұрыштық үдеу ε=0 болады, яғни дененің инерция моменті І өзгермесе, ол дене тұрақты бұрыштық жылдамдықпен (ω) айналады.
ω =0 дербес жағдайда дене тыныштық күйде болады.
Бір инерция моментінен екінші иенрция моментіне көшу Штейнер-Гюйгенс теоремасы бойынша орындалады, яғни кез келген айналыс осіне қатысты инерция моменті, сол оське параллель ауырлық центрінен өтетін оське қатысты инерция моменті мен дене массасының сол осьтің ауырлық центрінің айналыс осінен қашықтығының квадратына көбейтісінің қосындысына тең болады (20-сурет)
(5.22.2)
мұндағы І-l қашықтықтағы дененің массалар центрінен өтетін оське параллель ОО’ оське қатысты дененің инерция моменті , І0 – ОО’ оське параллель және берілген дененің массалар центрі арқылы өтетін ОО’осіне қатысты дененің инерция моменті.
Инерция моментінің өлшемділігі мына теңдік бойынша тағайындалады: І=mR2
Бұдан Инерция моментінің өлшем бірілігі — кг*м2.
Момент инерции ?
Инерция в физике — это способность тел поддерживать состояние движения в течение определенного времени в отсутствие внешних сил.Однако понятие инерции часто используется не только в физике, но и в нашей повседневной жизни. Например, инертный человек — это человек, который вообще не проявляет никакой инициативы. Инертные люди делают только то, что им говорят другие, и делают это очень медленно, без какого-либо энтузиазма. «Он движется по инерции», — говорим мы, когда хотим подчеркнуть, что что-то делается без какого-либо смысла, а просто из-за привычки, приобретенной за эти годы. Благодаря таким повседневным примерам концепция инерции ясна, но термин «момент инерции» требует более подробного объяснения.
Момент инерции Определение
Мы хорошо знаем, что масса тела является мерой его инертности. Например, если в супермаркете давят две тележки, одна из которых будет пустой, а вторая загружена различными товарами, то позже будет сложнее остановить тележку, загруженную товарами, из-за ее большей массы. Другими словами, чем больше масса тела, тем больше влияние на него инерции и тем больше сил требуется для изменения движения такого тяжелого тела.

В приведенном выше примере тележка движется по прямой линии и выполняет поступательное движение. Если при поступательном движении какого-либо тела его масса является мерой его инерции, то при вращательном движении тела вокруг его оси мерой его инерции будет величина, которая называется моментом инерции.
Момент инерции — это скалярная физическая величина, мера инерции тела, когда оно вращается вокруг оси. Обычно обозначается буквой J и измеряется в килограммах, умноженных на квадратный метр.
Формула момента инерции
Как рассчитать момент инерции? Существует общее уравнение, которое помогает физикам определить момент инерции любого тела. Если тело разбить на бесконечно маленькие кусочки с массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения. Формула будет выглядеть следующим образом:

J — момент инерции, r — расстояние до оси вращения.
Для материальной точки массы m, которая вращается вокруг оси на расстоянии r, эта формула будет иметь следующий вид:

Теорема Гюйгенса-Штейнера
Говоря о моменте инерции, нельзя упомянуть теорему двух математиков Гюйгенса и Штейнера, которые дали формулировку к определению характеристики параллельных осей.
Теорема Гюйгенса-Штейнера гласит: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельный произвольной оси и произведению массы тела на квадрат расстояния между осями.
Если вы запишите вышеупомянутую математическую формулу, вы получите следующее:

Где d — расстояние между осями
Эта теорема значительно облегчает решение многих физических проблем, связанных с инерцией. Например, у вас есть объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, мы можем рассчитать момент инерции тела относительно любой оси параллельной линии, проходящей через середину фигуры.
Моменты инерции простейших объектов
Несмотря на свою простоту, расчет моментов инерции для различных объектов требует знания интегралов, этих важных инструментов высшей математики. Чтобы упростить задачу, была создана таблица с расчетами инерции для простых геометрических фигур: круг, квадрат, цилиндр и т. Д.

Момент инерции для круга рассчитывается таким образом.
Момент инерции цилиндра будет рассчитываться аналогично.
Предлагаем вашему вниманию более подробные таблицы с формулами для расчета момента инерции для основных геометрических фигур: диска, треугольника, сплошного цилиндра и т. Д.


Ссылки и дальнейшее чтение
- Marion, JB; Торнтон, ST (1995). Классическая динамика частиц и систем (4-е изд.). Thomson. ISBN 0-03-097302-3.
- Перейти к: a b Symon, KR (1971). Механика (3-е изд.). Addison-Wesley. ISBN 0-201-07392-7.
- Перейти к: a b Тененбаум, РА (2004). Основы прикладной динамики. Springer. ISBN 0-387-00887-X.
- Перейти к: a b c d e f g h Kane, T. R .; Левинсон, Д. А. (1985). Динамика, теория и приложения. Нью-Йорк: Макгроу-Хилл.
- Перейти к: a b Winn, Will (2010). Введение в понятную физику: Том I — Механика. AuthorHouse. п. 10,10. ISBN 1449063330.
Момент инерции, видео

При написании этой статьи я пытался сделать ее настолько интересной и полезно, насколько это возможно.Буду благодарен за любые отзывы и конструктивную критику в виде комментариев к статье. Вы также можете написать свое пожелание / вопрос / предложение на мою почту [email protected] или в Facebook.
Список формул момента инерции для разных форм
 Формулы момента инерции
Формулы момента инерции В этом посте Вы узнаете список формул момента инерции для различных форм с примерами.
Содержание:
- Моменты инерции Определение
- Формула момента инерции
- Уравнение
- Единица
- Гораздо больше
Продолжайте читать…
Что такое момент инерции?
Момент инерции ( I ) определяется как сумма произведений массы каждой частицы тела и квадрата ее перпендикулярного расстояния от оси.Это также известно как инерция вращения. Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но он не зависит от сил, задействованных в движении.
Момент инерции отражает распределение массы тела или системы вращающихся частиц относительно оси вращения. Момент инерции зависит только от геометрии тела и положения оси вращения, но он не зависит от сил, задействованных в движении.
Момент инерции играет роль, аналогичную моменту инерционной массы в случае прямолинейного и равномерного движения. Это скалярное значение продольного момента импульса твердого тела.
I = mr²
Для твердого тела, движущегося вокруг неподвижной оси, законы движения имеют ту же форму, что и законы прямолинейного движения, с моментом инерции, заменяющим массу, угловой заменой, линейной скоростью, угловым моментом, заменяющим линейным импульс и т. д. Следовательно, кинетическая энергия тела, вращающегося вокруг неподвижной оси с угловой скоростью ω, равна ½ω², что соответствует ½mv² для кинетической энергии тела массы m, переведенной со скоростью v.Смотрите также правило Рауса; теорема о параллельных осях.
Уравнение момента инерции
Рассмотрим массу m, прикрепленную к концу безмассового стержня. Предположим, что подшипник в точке поворота O не имеет трения. Пусть система будет в горизонтальной плоскости. Сила F действует на массу, перпендикулярную стержню, и, следовательно, она будет ускорять массу в соответствии с:
F = ma
При этом сила будет заставлять массу вращаться вокруг O. Поскольку тангенциальное ускорение связано до углового ускорения
по уравнению.
угловое ускорение = rα
Поскольку эффект поворота создается крутящим моментом τ, поэтому было бы лучше написать уравнение для поворота в терминах крутящего момента. Это можно сделать, умножив обе части вышеприведенного уравнения на r. Таким образом,
rF = τ = крутящий момент = м.р.α
Какой вращательный аналог второго закона движения Ньютона?
Здесь F заменяется на τ, a на α, а m на mr². Величина mr² известна как момент инерции и представлена как I.
Важность момента инерции
Момент инерции играет ту же роль в угловом движении, что и масса в линейном движении. Можно отметить, что момент инерции зависит не только от массы m, но и от r².
Формулы момента инерции
Вот список формул момента инерции различных форм:
Момент инерции обруча
 Момент инерции гильзы цилиндра
Момент инерции гильзы цилиндраМомент инерции а диск
 Момент инерции диска
Момент инерции дискаМомент инерции твердой сферы
 Момент инерции твердого цилиндра
Момент инерции твердого цилиндраМомент инерции полого цилиндра
 Момент инерции инерции полый цилиндр
Момент инерции инерции полый цилиндрмомент инерции тонкого стержня
 момент инерции длинного тонкого стержня
момент инерции длинного тонкого стержнямомент инерции прямоугольника
 момент инерции прямоугольника
момент инерции прямоугольника- Момент инерции длинного тонкого стержня
 Момент инерции тонкого стержня
Момент инерции тонкого стержняMome момент инерции сферической оболочки
 момент инерции тонкой сферической оболочки
момент инерции тонкой сферической оболочки Момент инерции (видео)
Похожие темы:
. Момент инерции — это значение, которое измеряет, насколько сложно изменить состояние вращения объекта. Момент инерции зависит от массы и формы объекта, а также от оси, вокруг которой он вращается. Моменты инерции для некоторых распространенных форм можно найти с помощью следующих формул. Момент инерции объекта, состоящего из ряда этих общих форм, является суммой моментов инерции его компонентов. Единицей для момента инерции является килограммометр в квадрате, 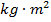 .
.
I = момент инерции (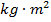 )
)
M = общая масса вращающегося объекта (кг)
L = общая длина стержня (м)
а = длина двух сторон пластины (м)
b = длина двух других сторон пластины (м)
R 1 = внутренний радиус цилиндра (м)
R 2 = внешний радиус цилиндра (м)
R = радиус цилиндра или сферы (м)
Формула момента инерции Вопросы:
1) Что такое момент инерции твердой сферы массой 55.0 кг, а радиус 0,120 м?
Ответ: Первый шаг — определить правильную формулу момента инерции. Момент инерции для твердой сферы приведен в таблице как:
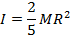
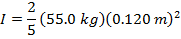
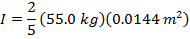
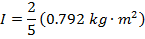
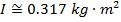
Момент инерции твердой сферы 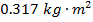 .
.
2) Пустая суповая банка с удаленными обеими крышками имеет массу 0,0580 кг, внутренний радиус 0,0320 м и внешний радиус 0.0330 м Каков момент инерции банки?
Ответ: Первый шаг — определить правильную формулу момента инерции. Суповая банка со снятыми крышками — это цилиндр. Поскольку дан внутренний и внешний радиус, формула для использования — это момент инерции для полого цилиндра с толщиной стенки:
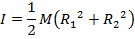
Масса банки составляет M = 0,0580 кг, внутренний радиус R 1 = 0,0320 м, а внешний радиус R 2 = 0,0330 м. Момент инерции банки:
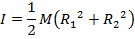
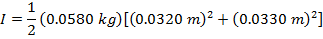
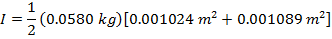
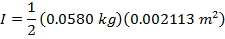
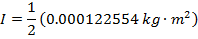
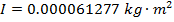
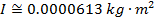
Момент инерции пустой суповой банки составляет примерно 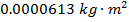 .
.
При вращательном движении крутящий момент необходим для создания углового ускорения объекта. Величина крутящего момента, необходимого для создания углового ускорения, зависит от распределения массы объекта. Момент инерции — это значение, которое описывает распределение. Это может быть найдено путем интегрирования по массе всех частей объекта и их расстояний до центра вращения, но также можно искать моменты инерции для общих форм.Крутящий момент на данной оси является произведением момента инерции и углового ускорения. Единицы крутящего момента — Ньютон-метры (Н ∙ м).
крутящий момент = (момент инерции) (угловое ускорение)
τ = Iα
τ = крутящий момент вокруг определенной оси (Н ∙ м)
I = момент инерции (кг 900 м 2 )
α = угловое ускорение (радианы / с 2 )
Формула крутящего момента Вопросы:
1) Момент инерции твердого диска равен 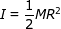 , где М — масса диска, а R — радиус.Колеса игрушечной машины имеют массу 0,100 кг и радиус 20,0 см. Если угловое ускорение колеса составляет 1,00 радиан / с 2 , каков крутящий момент?
, где М — масса диска, а R — радиус.Колеса игрушечной машины имеют массу 0,100 кг и радиус 20,0 см. Если угловое ускорение колеса составляет 1,00 радиан / с 2 , каков крутящий момент?
Ответ: Крутящий момент можно найти, используя формулу крутящего момента и момент инерции твердого диска. Крутящий момент:
τ = Iα
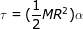
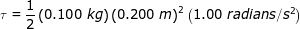
τ = 0,0020 Нм м
Крутящий момент, приложенный к одному колесу, составляет 0,0020 Н · м.
2) Момент инерции тонкого стержня, вращающегося на оси через его центр, равен 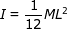 , где М — масса, а L — длина стержня.Предположим, что лопасть вертолета представляет собой тонкий стержень, массой 150,0 кг и длиной 8,00 м. Какой крутящий момент необходим для достижения углового ускорения 18,00 радиан / с 2 ?
, где М — масса, а L — длина стержня.Предположим, что лопасть вертолета представляет собой тонкий стержень, массой 150,0 кг и длиной 8,00 м. Какой крутящий момент необходим для достижения углового ускорения 18,00 радиан / с 2 ?
Ответ: Крутящий момент можно найти, используя формулу крутящего момента и момент инерции тонкого стержня. Крутящий момент:
τ = Iα
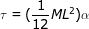
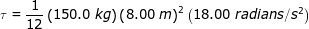
τ = 14 400 Н ∙ м
Необходимый крутящий момент составляет 14 400 Н ∙ м.

