Катушка индуктивности. устройство и принцип работы
Катушка индуктивности в цепи переменного тока
- Подробности
- Просмотров: 352
«Физика – 11 класс»
Индуктивность в цепи влияет на силу переменного тока.
Есть цепь из катушки с большой индуктивностью и электрической лампы накаливания.
При подключении с помощью переключателя цепи к источнику постоянного напряжения или к источнику переменного напряжения постоянное напряжение и действующее значение переменного напряжения будут равны.
Однако лампа светится ярче при постоянном напряжении.
Значит действующее значение силы переменного тока в цепи меньше силы постоянного тока.
Это объясняется явлением самоиндукции.
При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно.
Возникающее при этом вихревое электрическое поле тормозит движение электронов.
По прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.
Максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю.
Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля i, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля
Из равенства i = –к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
е. ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Так как удельная работа кулоновского поля равна напряжению на концах катушки, можно записать:
ei = —u
При изменении силы тока по гармоническому закону
i = Im sin ωt
ЭДС самоиндукции равна:
еi = —Li’ = —LωIm cos ωt
Так как u = —ei напряжение на концах катушки оказывается равным
гдеUm = LωIm — амплитуда напряжения.
Колебания напряжения на катушке опережают по фазе колебания силы тока на , или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на .
Амплитуда силы тока в катушке равна:
Если ввести обозначение
ωL = ХL
и действующие значения силы тока и напряжения, то получим:
Величину XL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω.
Постоянный ток вообще «не замечает» индуктивности катушки.
При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.
Итак,
Катушка индуктивности оказывает сопротивление переменному току.
Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.
Следующая страница «Резонанс в электрической цепи»
Назад в раздел «Физика – 11 класс, учебник Мякишев, Буховцев, Чаругин»
Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Аналогия между механическими и электромагнитными колебаниями —
Уравнение, описывающее процессы в колебательном контуре.
Переменный электрический ток —
Активное сопротивление. Действующие значения силы тока и напряжения —
Конденсатор в цепи переменного тока —
Катушка индуктивности в цепи переменного тока —
Резонанс в электрической цепи —
Генератор на транзисторе. Автоколебания —
Краткие итоги главы
Основные параметры катушек индуктивности
Свойства катушек могут быть охарактеризованы четырьмя основными параметрами: индуктивностью, добротностью, собственной емкостью и стабильностью.
1. Индуктивность.
Индуктивность (коэффициент самоиндукции) является основным электрическим параметром и характеризует величину энергии, запасаемой катушкой при протекании по ней электрического тока. Чем больше индуктивность катушки, тем больше энергии она запасает в своем магнитном поле.
Индуктивность зависит от размеров каркаса, формы, числа витков катушки, диаметра и марки провода, а также от формы и материала магнитопровода (сердечника).
В радиолюбительских схемах, как правило, величину индуктивности не указывают, так как радиолюбителя интересует не эта величина, а количество витков провода в катушке, диаметр и марка провода, способ намотки (внавал, виток к витку, крест на крест, секционная намотка) и размеры каркаса катушки.
2. Добротность.
Добротность (Q) характеризуется качеством работы катушки индуктивности в цепях переменного тока и определяется как отношение реактивного сопротивления катушки к ее активному сопротивлению потерь.
Активное сопротивление включает в себя сопротивление провода обмотки катушки; сопротивление, вносимое диэлектрическими потерями в каркасе; сопротивление, вносимое собственной емкостью и сопротивления, вносимые потери в экраны и сердечники.
Чем меньше активное сопротивление, тем выше добротность катушки и ее качество. В большинстве случаев добротность катушки определяют резонансные свойства и к.п.д. контура. Современные катушки средних размеров имеют добротность около 50 – 300.
3. Собственная емкость.
Катушки индуктивности обладают собственной емкостью, которая увеличивается по мере увеличения числа витков и размеров катушки. Между соседними витками существует межвитковая емкость, из-за которой некоторая часть тока проходит не по проводу, а через емкость между витками, отчего сопротивление между выводами катушки уменьшается.
Все дело в том, что общее напряжение, приложенное к катушке, разделяется на межвитковые напряжения из-за чего между витками образуется электрическое поле, вызывающее скопление зарядов. Витки, разделенные слоями изоляции, образуют обкладки множества маленьких конденсаторов, через которые протекает часть тока, из общей емкости которых и складывается собственная емкость катушки. Таким образом катушка обладает не только индуктивными но и емкостными свойствами.
Собственная емкость является вредным параметром и ее стремятся уменьшить применением специальных форм каркаса и способом намотки провода.
4.
 Стабильность.
Стабильность.Стабильность катушки характеризуется изменением ее параметров под воздействием температуры, влажности и во времени.
Изменение индуктивности под влиянием температуры характеризуют температурным коэффициентом индуктивности (ТКИ), равным относительному изменению индуктивности при изменении температуры на 1°С. ТКИ катушки определяется способом намотки и качеством диэлектрика каркаса.
Влажность вызывает увеличение собственной емкости и диэлектрических потерь, а также понижает стабильность катушки. Для защиты от действия влажности применяется герметизация или пропитка и обволакивание обмотки негигроскопичными составами.
Такие катушки обладают более низкой добротностью и большой собственной емкостью, но при этом они более устойчивы к воздействию влаги.
Мощность катушки
Треугольники напряжений, сопротивлений, мощностей
Цепь с реальной катушкой индуктивности
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид.
В цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р
, а изменение энергии в магнитном поле — реактивной мощностью. В реальной катушке имеют место оба процесса, т.е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
Приложенное к катушке напряжение состоит из двух слагаемых, одно из которых uR
равно падению напряжения в активном сопротивлении, а другоеuL уравновешивает ЭДС самоиндукции.
Поэтому катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно.
Несовпадение по фазе слагаемых в выражении затрудняет определение амплитуды и действующего значения приложенного к цепи напряжения U.
Поэтому воспользуемся векторным способом сложения синусоидальных величин. За исходный вектор диаграммы принимаем вектор тока I.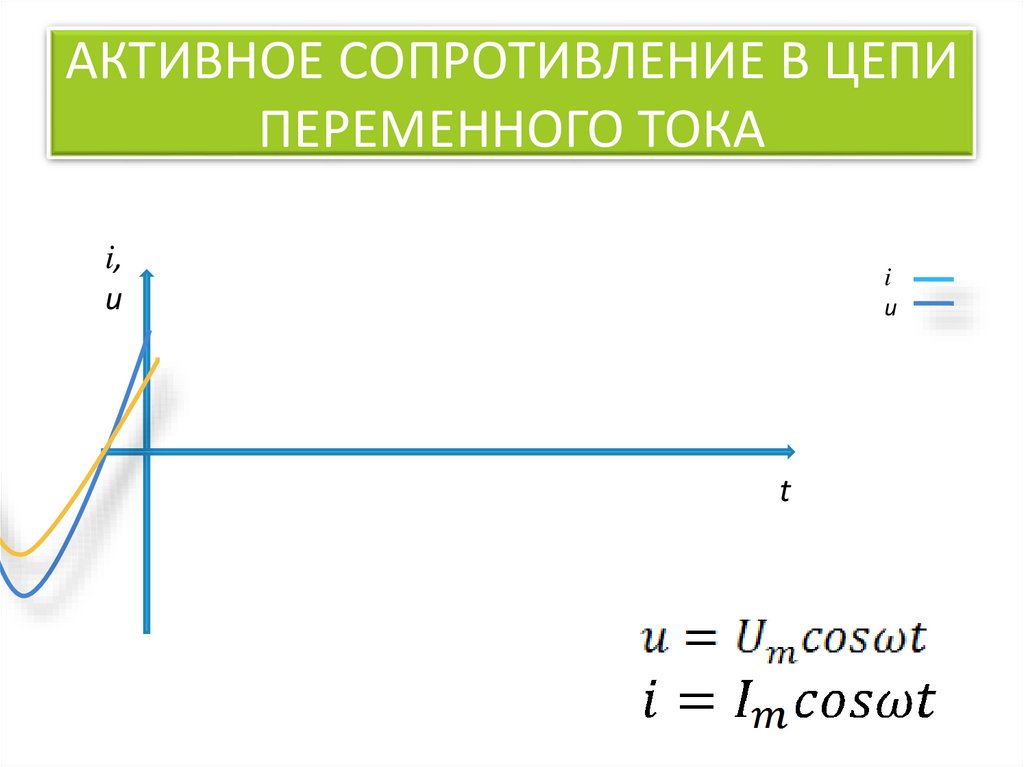 Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы. ВекторU Rпо направлению совпадает с вектором тока I, а вектор ULнаправлен перпендикулярно вектору I с положительным углом.Из диаграммы видно, что вектор общего напряжения Uопережает вектор тока I на угол ψ> 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях.
Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы. ВекторU Rпо направлению совпадает с вектором тока I, а вектор ULнаправлен перпендикулярно вектору I с положительным углом.Из диаграммы видно, что вектор общего напряжения Uопережает вектор тока I на угол ψ> 0, но <90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях.
Проекция вектора напряжения Uна направление вектора тока называется активной составляющей вектора напряжения и обозначается UR.
Проекция вектора напряжения Uна направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения.
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений,катетами которого являются активное ииндуктивное сопротивления, а гипотенузой — величина Z. ; ;
; ;
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Из графика мгновенной мощности видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
Активная мощность всей цепи равна активной мощности в сопротивлении R,
а реактивная — реактивной мощности в индуктивном сопротивленииXL.,
Коэффициент мощности — показывает, какая часть полной мощности является активной, т.е. потребляемой.
Схема замещения катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G
и индуктивнойBL проводимостями.
Покажем, что схемы эквивалентны, то есть при одинаковом напряжении сохраняются неизменнымиток в неразветвленной части цепи, активная и реактивная мощности.
; ;
Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Ia.
Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр=
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U
и получить подобный треугольник проводимостей, катетами которого являются активнаяG ииндуктивнаяBL проводимости, а гипотенузой — величинаY= I/U, называемая полной проводимостью цепи.
Индуктивность и емкость в цепи переменного тока
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
i = Iм sin ωt
u = Uм sin (ϕ + ωt),
e = Ɛm sin (ψ + ωt).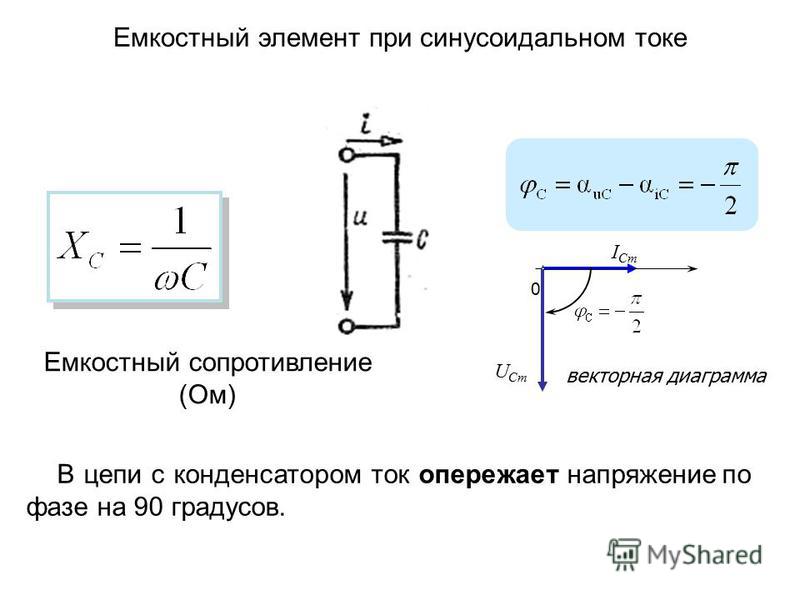
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:
R=(pl/S)(1 + at).
В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
График и схема подключения
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:
Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:
ХL = ωL.
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Катушки индуктивности
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;
Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;
Хс = 1/ωС
Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:
Будет интересно Что такое короткое замыкание
X = XL—XC
и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.
В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:
P = IU cos ϕ.
Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:
Р = I2R
Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)
Индуктивность
Катушка индуктивности в цепи переменного тока
В цепи переменного тока в катушке индуктивности происходит следующий процесс:
- ток возбуждает в катушке электромагнитное поле. Поскольку он переменный, то и параметры электромагнитного поля во времени меняются, то есть оно тоже переменное;
- переменное магнитное поле в соответствии с законом электромагнитной индукции возбуждает в самой катушке ЭДС. Ее так и называют — ЭДС самоиндукции. Она всегда идет против направления изменения силы тока. Следовательно, в первой половине полупериода, когда сила тока возрастает, катушка это нарастание сдерживает. При этом часть энергии электричества накапливается в формируемом катушкой магнитном поле;
- во второй половине полупериода, катушка, наоборот, противостоит снижению силы тока, возвращая в цепь накопленную в виде магнитного поля энергию.

Таким образом, катушка индукции оказывает сопротивление источнику переменного тока. Это сопротивление имеет иную природу, нежели активное, преобразующее электрическую энергию в тепло.
Сопротивление катушки энергию не потребляет, а лишь аккумулирует ее и затем снова возвращает в цепь, меняя характер протекания в ней тока. Его называют индуктивным. В противоположность активному, оно, как и емкостное сопротивление конденсатора, является реактивным.
Эффект проявляется тем сильнее, чем выше частота переменного тока, то подтверждается формулой расчета индуктивного сопротивления: XL = w*L = 2 π * f * L, где:
- XL — индуктивное сопротивление, Ом;
- W — круговая частота переменного тока, рад/с;
- F — частота переменного тока, Гц;
- L — индуктивность катушки, Гн.
Индуктивное сопротивление, несмотря на иной принцип действия, измеряется в тех же единицах, что и активное — Омах. Таким образом, в цепях переменного тока катушка индуктивности выступает ограничителем силы тока и нагрузку, в отличие от цепи постоянного, вводить не требуется.
Зависимость индуктивного сопротивления катушки от частоты тока позволяет использовать данный элемент помимо прочего, для фильтрации высокочастотных помех или сигналов. Например, при установке его в схеме динамика, последний воспроизводит только низкие частоты, то есть играет роль сабвуфера.
На преодоление индуктивного сопротивления источник расходует часть мощности — это реактивная мощность (Wр). Остальное называют активной или полезной мощностью (Wа) — она производит полезную работу. Вместе реактивная и активная мощности образуют полную: Wр + Wа = Wпол.
График происходящих процессов в катушке индуктивности
Доля активной мощности характеризуется параметром cosϕ: cosϕ = Wа / W пол. Полную мощность принято измерять в вольт-амперах (ВА). Именно эти единицы указываются в характеристике источников бесперебойного питания (ИБП) и дизельных электрогенераторов. Активная мощность измеряется в привычных ваттах (Вт).
Все сказанное имеет отношение к потребителям с электродвигателями и трансформаторами, поскольку обмотки этих элементов по сути, являются катушками индуктивности.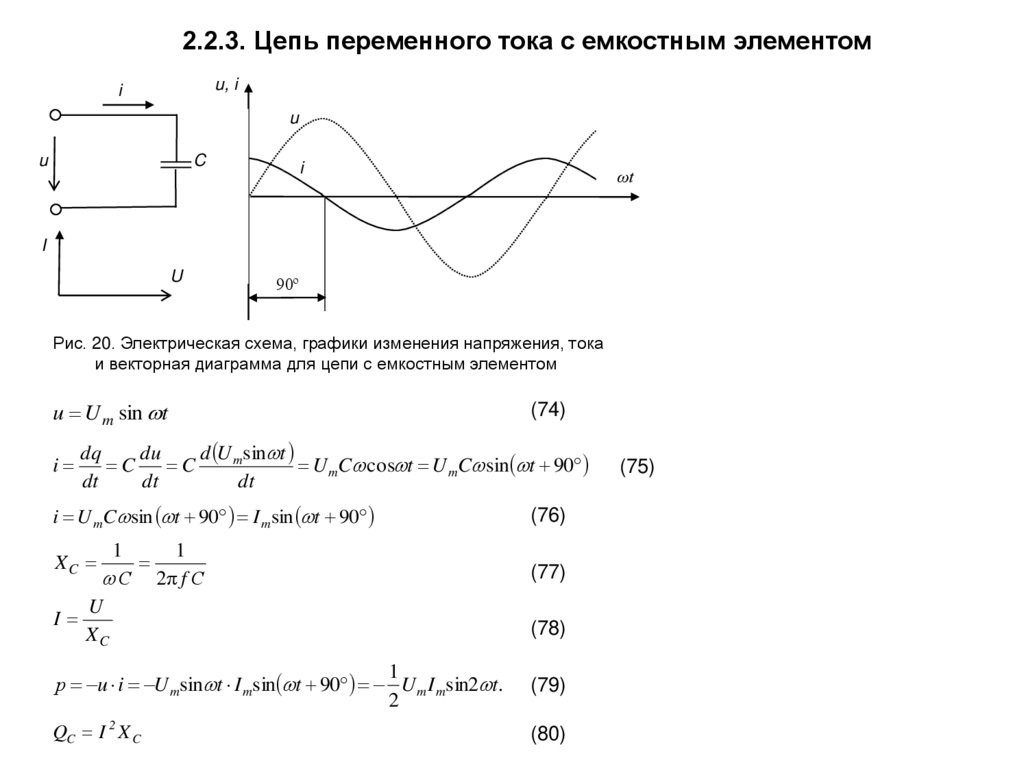 То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.
То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.
При большом количестве подобных потребителей, затраты на реактивную мощность существенно перегружают генераторы электростанций, ввиду чего в энергосетях применяют установки компенсации реактивной мощности (УКРМ).
При включении катушки индуктивности в цепь постоянного тока процесс, описанный в пунктах 1-3, также имеет место, только не все время, а в момент включения/отключения.
Если собрать простейшую цепь из последовательно установленных выключателя, катушки и лампы, можно видеть, что лампочка загорается при замыкании цепи с запаздыванием и также с запаздыванием гаснет после размыкания.
Объясняется это тем, что ток в момент включения меняется от нулевого значения до максимума, также в момент отключения его значение меняется, хоть и очень быстро, от максимума до нуля. В первом случае катушка накапливает в себе часть энергии в виде магнитного поля, во втором — отдает ее лампе, отчего та и горит после размыкания цепи.
В первом случае катушка накапливает в себе часть энергии в виде магнитного поля, во втором — отдает ее лампе, отчего та и горит после размыкания цепи.
Магнитопроводы для катушек
Важным параметром, характеризующим качество катушек, является добротность, численно равная отношению ее индуктивного сопротивления переменному току данной частоты к сопротивлению постоянному току. Чтобы увеличить добротность, пользуются разными конструктивными приемами, но наибольший эффект дает введение в катушку магнитопровода (сердечника) из специального магнитного материала. При внесении магнитопровода в катушку силовые линии магнитного поля концентрируются в магнитопроводе, так как его сопротивление магнитному потоку значительно меньше, чем воздуха.
Маркировка катушек.
В результате магнитный поток, а следовательно, и индуктивность катушки увеличиваются в несколько раз, что позволяет уменьшить число витков, а значит, и сопротивление катушки постоянному току. Кроме того, используя магнитолроводы, удается значительно уменьшить размеры катушек и очень простым способом (перемещением магнитопровода) осуществить регулировку их индуктивности. Поскольку катушки с магнитопроводами обычно работают в цепях переменного тока (исключение — катушки электромагнитных реле и некоторые другие), применять оплошные магнитопроводы из обычных магнитных материалов нельзя.
Кроме того, используя магнитолроводы, удается значительно уменьшить размеры катушек и очень простым способом (перемещением магнитопровода) осуществить регулировку их индуктивности. Поскольку катушки с магнитопроводами обычно работают в цепях переменного тока (исключение — катушки электромагнитных реле и некоторые другие), применять оплошные магнитопроводы из обычных магнитных материалов нельзя.
Будет интересно Дроссели в электрике: что это и где используются?
Под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, возникают так называемые вихревые токи, которые нагревают магнитапровол, бесполезно потребляя часть энергии магнитного поля. Чтобы уменьшить эти потери, магнитопроводы катушек, работающих в диапазоне звуковых частот, набирают из отдельных тонких изолированных пластин, изготовленных из специальных электромеханических сталей или пермаллоя. В области радиочастот стальные магнитопроводы, даже набранные из очень тонких пластин, неприменимы, так как потери на вихревые тоКи в них недопустимо велики. Магнитопроводы для катушек, предназначенных для работы на радиочастотах, изготовляют из специальных материалов: маг-нитодиэлектриков и ферритов.
Магнитопроводы для катушек, предназначенных для работы на радиочастотах, изготовляют из специальных материалов: маг-нитодиэлектриков и ферритов.
В магнитодиэлектриках мельчайшие частички вещества, содержащего в своем составе железо, равномерно распределены в массе какого-либо диэлектрика (бакелита, стирола, амино-пласта). Наиболее широко применяют магнитопроводы из альсифера (сплав алюминия, кремния и железа) и карбонильного железа.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. {-7}\medspace\frac{Гн}{м}
{-7}\medspace\frac{Гн}{м}
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Обозначение катушек с отводами и начала обмотки
В радио и электротехнической аппаратуре, например, в приемниках или импульсных преобразователях напряжения, иногда используют не всю индуктивность катушки, а только некоторую ее часть. Для таких случаев катушки изготавливают с отводом или отводами.
При разработке некоторых конструкций иногда необходимо строго соблюсти начало и конец обмотки катушки или трансформатора. Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.
Для подстройки катушек на частотах свыше 15…20 МГц часто применяют магнитопроводы из немагнитных материалов (меди, алюминия и т.п.). Возникающие в таком магнитопроводе под действием магнитного поля катушки вихревые токи создают свое поле, противодействующее основному, в результате чего индуктивность катушки уменьшается.
Немагнитный магнитопровод-подстроечник обозначают так же, как и ферритовый, но рядом указывают химический символ металла, из которого он изготовлен. На рисунке изображен подстроечник, изготовленный из меди.
Вот и все, что хотел рассказать о катушках индуктивности. Удачи!
Литература: 1. В. А. Волгов «Детали и узлы радиоэлектронной аппаратуры». 2. В. В. Фролов «Язык радиосхем». 3. М. А. Сгут «Условные обозначения и радиосхемы».
Источник
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 7 из 17Следующая ⇒ Рассмотрим цепь переменного тока, в которую включена катушка индуктивностьюL ( Рис.3,а). Пусть напряжение в цепи изменяется по закону u=Umsinwt . При протекании переменного тока через катушку на концах катушки возникает ЭДС самоиндукции εi = — L. Если активное сопротивление катушки принять равным нулю, то внешнее приложенное напряжение U, согласно закону Ома для цепи, содержащей ЭДС, по величине равно и по направлению противоположно ЭДС самоиндукции, то есть U=- εi = L, или Umsinwt= L, откуда sinwt и di = sinwtdt . Интегрируя последнее выражение получим: i = — coswt = sin (wt — ), где — амплитуда тока. Тогда по аналогии с законом Ома для участка цепи можно записать, что Im=, где величину можно рассматривать как индуктивное сопротивление. При оценке фазовых соотношений между током и напряжением на индуктивности видно, что ток в цепи, подобно напряжению, имеет синусоидальный характер, но по фазе отстает на угол p¤ 2, то есть в момент, когда напряжение на катушке достигает максимума, сила тока равна нулю, а в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Графики тока и напряжения, а также векторная диаграмма цепи переменного тока, содержащей индуктивность, представлены на рис . 3 (б, в).
Емкость в цепи переменного тока Рассмотрим цепь переменного тока, в которую включен конденсатор С( Рис.4,а).
Пусть напряжение в цепи изменяется по закону u = Um sin wt. Периодическое изменение U вызывает периодическое изменение q, и возникает емкостный ток: i= . Продифференцировав это выражение ,получим: i=wCUmcoswt = wCUmsin ( wt + p/2), где wСUm=Im — амплитуда тока. Cравнивая с законом Ома для участка цепи Im=Um/XC , получаем wСUm = Um / XC , отсюда XC = 1 / w C . Видно, что величина XC=1/wC играет роль сопротивления конденсатора переменному току, она называется емкостным сопротивлением. Из сравнения фазы тока и напряжения видно, что ток в цепи конденсатора, подобно напряжению, имеет синусоидальный характер, но по фазе опережает напряжение на угол p / 2. Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями Рассмотрим основные соотношения электрических величин в цепи переменного тока с индуктивностью, емкостью и активным сопротивлением, соединенными последовательно ( рис .5, а ). При последовательном соединении проводников, ток, протекающий через сопротивление одинаков iL=iC=iR=Imsinwt. Полное напряжение цепи будет складываться из падений напряжения на индуктивности, емкости и активном сопротивлении. Составим векторную диаграмму цепи, пользуясь результатами, полученными выше.
В произвольном масштабе отложим вектор амплитуды тока, одинаковый для всех сопротивлений и укажем направление его вращения ( Рис. 5,б). Вектор амплитуды напряжения на активном сопротивлении UmR=ImR отложим по направлению вектора тока, так как эти величины совпадают по фазе. Вектор амплитуды напряжения на индуктивном сопротивлении UmL=ImwL отложим вверх под углом p/2 к вектору токаIm , так как это напряжение опережает ток по фазе на уголp/2. Вектор амплитуды напряжения на емкости UmC=ImwC отложим вниз под углом p/2 к вектору Im, так как это напряжение отстает от тока на угол p/2. Сложив геометрически векторы UmL, UmCи UmR, получим вектор полного напряжения Um, приложенного ко всей цепи ( Рис. 5,б).
Применив теорему Пифагора, найдем Um= = = = Отсюда Im= . Последняя формула представляет собой закон Ома для полной цепи переменного тока для амплитудных значений. Полным сопротивлением или импедансом цепи называется величина Z = Закон Ома справедлив и для мгновенных значений тока и напряжения. Угол сдвига фаз между током и напряжением ( угол j на рис. 5,б) может быть определен из соотношений tgj = .
Импеданс тканей организма Ткани организма представляют собой по электрическим свойствам разнородную среду. Органические вещества ( белки, жиры, углеводы и др.), из которых состоят плотные части тканей, являются диэлектриками. Однако все ткани и клетки в организме содержат жидкости или омываются ими ( кровь, лимфа, различные тканевые жидкости ), в состав этих жидкостей кроме органических коллоидов входят также растворы электролитов, и поэтому они являются хорошими проводниками. Наилучшую электропроводность имеют спинно-мозговая жидкость, сыворотка крови, несколько меньшую — цельная кровь и мышечная ткань. Значительно меньше электропроводность тканей внутренних органов, а также нервной, жировой и соединительной тканей. Плохими проводниками являются роговой слой кожи, связки и сухожилия, костная ткань без надкостницы. В ряде случаев их можно отнести даже к диэлектрикам. Ткани организма состоят из структурных организмов — клеток, омываемых тканевой жидкостью. Цитоплазма клетки отделена от тканевой жидкости клеточной мембраной. Тканевая жидкость и цитоплазма — хорошие проводники. Клеточная мембрана проводит электрический ток плохо. Такая система напоминает конденсатор и обладает электрической емкостью. В тканях встречаются и макроскопические образования, состоящие из различных соединительных оболочек и перегородок, по обе стороны которых находятся ткани, обильно снабженные тканевой жидкостью. Все это придает тканям емкостные свойства. Как показывает опыт, ткани организма не имеют практически заметной индуктивности, но обладают емкостью и активным сопротивлением. Поэтому при прохождении переменного тока через ткани организма следует учитывать их полное сопротивление, или импеданс. Электрические параметры участка тканей организма, находящиеся между наложенными на поверхность тела электродами, можно представить в виде эквивалентных электрических схем.
В наиболее упрощенном виде эта схема для слоя кожи и подкожной клетчатки может быть представлена как значительная емкость C ( Рис.6,а), шунтированная большим сопротивлением R и включенная последовательно со значительно меньшим сопротивлением R*, а для глубоко лежащих тканей — это включенные параллельно сопротивление и емкость ( Рис.6,б). Импеданс тканей организма зависит от множества физиологических условий, основным из которых является состояние кровообращения, в частности кровонаполнение сосудов. На этом основан один из способов исследования периферического кровообращения — РЕОГРАФИЯ. При этом в течение цикла сердечной деятельности регистрируется изменение импеданса определенного участка тканей, на границах которого накладываются электроды. При реографии применяется переменный ток частотой 20 — 30 кГц. Этим методом получают реограммы головного мозга — реоэнцефалограммы, печени, легких, магистральных сосудов и т. Зависимость импеданса тканей организма от частоты переменного тока позволяет оценить жизнеспособность этих тканей, что важно знать, например, при пересадке (трансплантации) тканей и органов. На рис.7 представлены частотная зависимость импеданса здоровой ткани (1) и мертвой (2) , убитой кипячением в воде .
В мертвой ткани мембраны клеток разрушены и ткань обладает лишь активным сопротивлением, в то время как импеданс живой ткани складывается из активного и емкостного сопротивлений. Различие в частотных зависимостях импеданса получается и у здоровой, и у больной ткани.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1. Определение индуктивности катушки 1. Проверить электрическую цепь (рис.8), состоящую из последовательно соединенных катушки индуктивности L, батареи конденсаторов C, амперметра A и реостата R. 2. Подключить вольтметр для измерения напряжения на катушке. 3. Поставить движок реостата в среднее положение. 4. Включить цепь и, изменяя сопротивление реостата, получить пять различных значений тока ( в пределах от 0,1 до 0,3 A) и напряжения. 5. Вычислить индуктивное сопротивление катушки по формуле XL= , где R — активное сопротивление катушки (указано на катушке). 6. Найти среднее значение XL и рассчитать индуктивность катушки: , где w=2pn=2×50p =314 Гц. 7. Результаты измерений и вычислений занести в таблицу.
Сумма _________ Среднее _________ Упражнение 2. 1. Переключить вольтметр для измерения напряжения на конденсаторе C. 2. Поставить движок реостата в среднее положение. 3. Включить цепь и, изменяя сопротивление реостата, получить пять различных значений силы тока и напряжения. 4. Вычислить емкостное сопротивление по формуле . 5. Найти среднее значение и рассчитать емкость конденсатора: . 6. Результаты измерений и вычислений записать в таблицу.
Cумма __________ Среднее ___________ Упражнение 3.
1. Переключить вольтметр для измерения напряжения на участке АВ, состоящем из последовательно включенных активного, индуктивного и емкостного сопротивлений. 2. Включить цепь и измерить одно значение напряжения и силы тока (в пределах 0,1 — 0,3 A) на этом участке. 3. Вычислить полное сопротивление участка АВ: . 4. Рассчитать полное сопротивление участка АВ через средние значения индуктивного, емкостного и активного сопротивлений по формуле и сравнить с результатом, полученным в пункте 3. 5. Результаты измерений и вычислений занести в протокол. Контрольные вопросы. 1. Переменный ток. 2. Уравнение и график гармонического тока. 3. Мгновенное, амплитудное и эффективное значение силы переменного тока и ЭДС. 4. Цепь переменного тока с активным сопротивлением R. 5. Цепь переменного тока с емкостным сопротивлением XC. 6. Цепь переменного тока с индуктивным сопротивлением XL. 7. Вывод закона Ома для полной цепи переменного тока. Импеданс цепи. 8. Понятие о сдвиге фаз в цепи переменного тока с XL, XC и в цепи с полным сопротивлением. В каких случаях сдвиг фаз равен нулю? 9. Понятие о резонансе напряжений. 10. Импеданс тканей организма. Эквивалентные схемы тканей. 11. Понятие о реографии, ее виды. Частотная зависимость импеданса тканей, ее использование в медицине.
Лабораторная работа №7 ⇐ Предыдущая234567891011Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 712; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Измерение параметров индуктивности в цепи переменного тока
Физика \ Физика
Страницы работы
7 страниц (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
Санкт-Петербургский государственный горный институт
(технический университет)
Кафедра общей и технической физики
Лабораторная работа №5
Измерение параметров индуктивности в цепи переменного тока
Рис. 1. Экспериментальная установка для исследования импеданса (сопротивления по
переменному
току) катушки.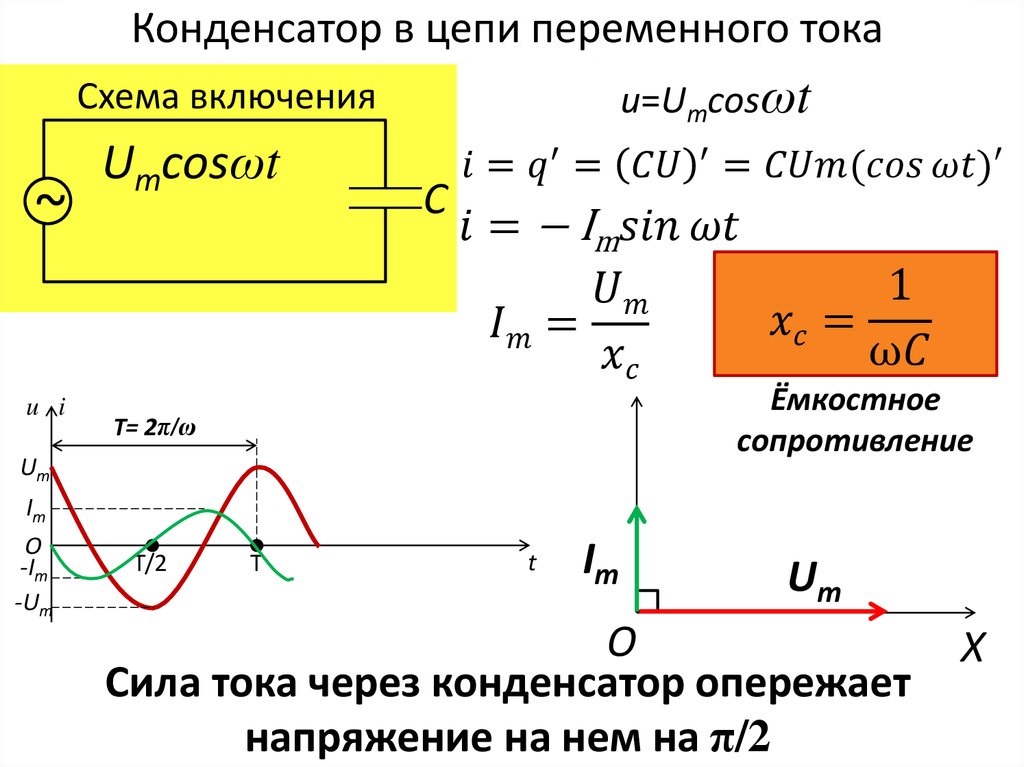
Санкт-Петербург
2008
Цель работы: Определение импеданса, сдвига фаз и измерение индуктивности на разных частотах в резистивно-индуктивной цепи.
Общие сведения
Переменный ток – это электрический ток, изменяющийся во времени. В общем понимании к переменному току относят различные виды импульсных, пульсирующих, периодических и квазипериодических токов. В технике под переменным током обычно подразумевают периодические или почти периодические токи переменного направления. Наиболее употребителен переменный ток, сила которого меняется во времени по гармоническому закону.
Если к активному сопротивлению R приложено переменное напряжение U = Umcos(wt), то текущий ток через это сопротивление по закону Ома будет равен
. (1)
Следовательно, между амплитудами силы тока и напряжения на резисторе можно записать соотношение:
. (2)
(2)
Изображая синфазные колебания напряжения и тока на резисторе методом векторной диаграммы (рис. 2), в данном случае векторы тока и напряжения будут параллельны.
Если переменное напряжение, изменяющееся по гармоническому закону, подано на концы катушки индуктивности L, не обладающей ни емкостью, ни сопротивлением, то в этой элементарной цепи с индуктивностью должна возникнуть ЭДС самоиндукции E i = –LdI/dt, направленная против ЭДС источника тока. Поскольку активное сопротивление катушки равно нулю (или пренебрежимо мало), закон Ома в этом случае запишется в виде
U + E i = RI = 0, или . (3)
Решение этого дифференциального уравнения имеет вид
. (4)
Поскольку в цепи действует лишь переменное напряжение и нет другого источника, его постоянная составляющая равна нулю:
, (5)
где Um/wL = Im.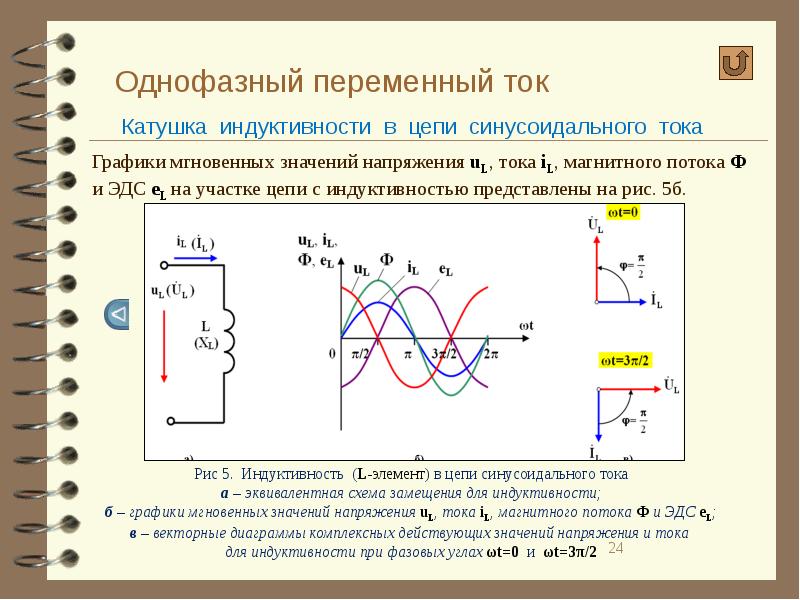 Сопоставляя полученное выражение с законом Ома для постоянного тока, нетрудно
видеть, что роль сопротивления играет произведение wL. Эта
величина называется индуктивным сопротивление (импедансом) и обозначается XL.
Сопоставляя полученное выражение с законом Ома для постоянного тока, нетрудно
видеть, что роль сопротивления играет произведение wL. Эта
величина называется индуктивным сопротивление (импедансом) и обозначается XL.
XL = wL. (6)
Следовательно, индуктивное сопротивление растет с частотой. Постоянному току, т.е. у которого w = 0, индуктивность сопротивления не оказывает. В данном случае напряжение UL на индуктивности совпадает с напряжением, вырабатываемым источником тока. На векторной диаграмме (рис. 3) видно, что напряжение опережает по фазе на p/2 ток через индуктивность.
В
данной работе упрощенная электрическая схема может быть представлена в виде
последовательно соединенных резистора R и
катушки индуктивности L, замкнутых на источнике
переменного тока Uрегулируемой
частоты. А с учетом подключенных к этой схеме измерительных приборов
окончательный вид схемы представлен на рис. 4, где через дифференциальный
усилитель выход А идёт с резистора в осциллограф на канал CH1, а выход В – общее напряжение в RL-цепи, – на канал CH2 осциллографа. К источнику переменного тока (функциональному генератору)
параллельно подключен цифровой счетчик.
4, где через дифференциальный
усилитель выход А идёт с резистора в осциллограф на канал CH1, а выход В – общее напряжение в RL-цепи, – на канал CH2 осциллографа. К источнику переменного тока (функциональному генератору)
параллельно подключен цифровой счетчик.
Поскольку обычные вольтметры и амперметры измеряют только среднеквадратичное (действующее) значение напряжения и тока, и не фиксируют соотношений фаз между ними, в данном эксперименте предпочтительней использовать осциллограф. Эксперимент будет выполнен с синусоидальными напряжениями, поэтому (если необходимо) для получения действующих значений величины, ее размахи на осциллографе (от нижнего до верхнего пика) Up—p должны быть разделены на .
В соответствии с законом Ома ток может быть
рассчитан через сопротивление путем измерения напряжения на осциллографе
(амплитудное значение синусоиды на канале Ch2). Схема, показанная на рис. 4, позволяет одновременно наблюдать полный ток и
напряжение в RL-цепи (амплитудное
значение синусоиды на канале Ch3). В этом
случае, если катушка индуктивности L и резистор сопротивления R соединены по схеме, показанной на рис. 4, сумма
падений напряжений на каждом из элементов равна напряжению питания U
Схема, показанная на рис. 4, позволяет одновременно наблюдать полный ток и
напряжение в RL-цепи (амплитудное
значение синусоиды на канале Ch3). В этом
случае, если катушка индуктивности L и резистор сопротивления R соединены по схеме, показанной на рис. 4, сумма
падений напряжений на каждом из элементов равна напряжению питания U
, (7)
где U – полное напряжение RL-цепи, IR = UR – напряжение на резисторе,
– напряжение на катушке.
Так как напряжения на последовательно соединенных резисторе и катушке отличаются по фазе на 90°, то выражение 7, исходя из векторной диаграммы, можно представить в следующем виде (теорема Пифагора):
. (8)
Откуда следует , (9)
А с учетом закона Ома для катушки (формула 6):
, (10)
где по определению циклическая частота
, (11)
где f – частота выходного сигнала, устанавливаемая на
функциональном генераторе, Гц.
Таким образом, можно определить индуктивность катушки:
, (12)
где UR/R = I – сила тока в цепи.
Однако расчет по этой формуле будет давать не точное значение индуктивности (особенно на малых частотах), т.к. не учтено омическое сопротивление катушки. Чтобы его учесть, в формуле 12 величину UR в квадрате под корнем надо понимать как напряжение на последовательно соединенных активных сопротивлений известного резистора R и катушки индуктивности RL (указано на самой катушке). Таким образом, формула 12 может быть представлена в более достоверном качестве:
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Индуктивность в цепях переменного тока — Цепи переменного тока
Цепи переменного тока
Индуктивность определялась как свойство цепи сопротивляться изменению в текущем. Это противодействие приводит к индуцированной ЭДС. Индуцированная ЭДС равна пропорциональна скорости изменения тока, а также величина индуктивности. Эта связь может быть представлена уравнением
Если в индуктивности, показанной на рисунке ниже, протекает синусоидальный ток, индуцированное напряжение на индуктивности можно изобразить в зависимости от времени.
Чистая индуктивная цепь.
График тока на рисунке ниже увеличивается от времени t 0 до т 1 . Ток растет с убывающей скоростью, и
в момент времени t 1 мгновенная скорость изменения тока равна
нуль. Следовательно, v L равно нулю в момент времени t 1 .
От времени t 1 до t 2 ток
уменьшение; скорость изменения тока отрицательна и v L отрицательный. В момент времени т 2 , ставка
изменения тока максимально, и, таким образом, v L максимально в
негативное направление. В момент времени t 3 скорость изменения
ток равен нулю, и, таким образом, v L снова равно нулю. Из t 3 до t 4 , ток увеличивается,
скорость изменения положительна, а v L положительна, достигая
максимум в t 4 , где скорость изменения максимальна.
Ток растет с убывающей скоростью, и
в момент времени t 1 мгновенная скорость изменения тока равна
нуль. Следовательно, v L равно нулю в момент времени t 1 .
От времени t 1 до t 2 ток
уменьшение; скорость изменения тока отрицательна и v L отрицательный. В момент времени т 2 , ставка
изменения тока максимально, и, таким образом, v L максимально в
негативное направление. В момент времени t 3 скорость изменения
ток равен нулю, и, таким образом, v L снова равно нулю. Из t 3 до t 4 , ток увеличивается,
скорость изменения положительна, а v L положительна, достигая
максимум в t 4 , где скорость изменения максимальна.
Зависимость напряжения от тока в чисто индуктивной цепи.
Максимальное положительное значение напряжения возникает на 90° впереди максимального
положительное значение тока. Говорят, что ток отстает от напряжения на
90 градусов. Это фазовое соотношение можно вывести математически, применив
исчисление.
Говорят, что ток отстает от напряжения на
90 градусов. Это фазовое соотношение можно вывести математически, применив
исчисление.
Из предыдущего уравнения, которое
куда
дифференцированием найдено d i /d t .
но
Следовательно
По общему виду периодической функции (т. е. В м sin ( ωt + θ)),
а также
Поскольку отношение вольта к амперу определяется как противодействие току в омах, величина ωL измеряется в омах. Количество ωL называется индуктивным сопротивлением и обозначается как X L
Если В м = 1,414 В и I м = 1,414 I подставляем в уравнение ωL = В м / I м , видно что отношение действующих значений напряжения и тока также равно индуктивное сопротивление
Обратная величина индуктивного сопротивления называется индуктивная проводимость и имеет обозначение B L .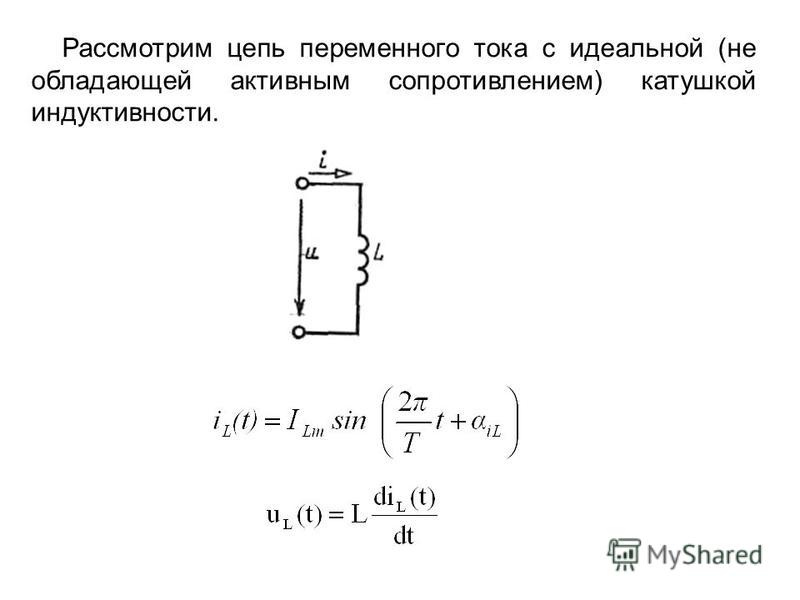 Единица индуктивности
восприимчивость — это mho (или сименс S), когда частота в герцах и
индуктивность в генри.
Единица индуктивности
восприимчивость — это mho (или сименс S), когда частота в герцах и
индуктивность в генри.
Пример 1: Переменный ток с частотой 2 кГц и максимальным значением 0,15 А протекает в катушке с индуктивностью 175 мГн. (1) Найдите максимум напряжение, развивающееся на индуктивности. (2) Найдите эффективное значение напряжение на индуктивности. (3) Запишите периодические функции, представляющие напряжение и ток.
Решение:
1.
2.
Действующее значение напряжения также можно найти, вычислив сначала эффективное значение тока
затем
3. Если в качестве эталона берется ток,
Напряжение опережает ток в индуктивной цепи
Пример 2: Напряжение на индуктивности составляет 40 В, когда ток 120 мА. Частота тока и напряжения 400 Гц. Найдите индуктивность.
Решение: Величину индуктивного сопротивления можно найти
Теперь можно рассчитать индуктивность.
Соотношение мощностей в индуктивной цепи можно проанализировать, написав уравнение для мощности с мгновенными значениями
Применяя это уравнение к рисунку выше, мы видим, что мгновенная мощность равна
положительный от t 0 до t 1 , отрицательный от t 1 до t 2 , положительный от t 2 до t 3 , и минус от т 3 до т 4 . Мгновенная мощность
изображен на рисунке ниже. Положительная мощность указывает, что энергия
берется из источника, и отрицательная мощность , в которую возвращается энергия
источник. Так как за один полный цикл, от t 0 до t 4 , возвращается столько энергии, сколько забирается из
источник, чистая энергия, полученная от источника, равна нулю. Власть над
поэтому полный цикл равен нулю. Это поддерживает определение, что
Индуктивность – это свойство цепи запасать энергию в виде
магнитное поле. Таким образом, при увеличении силы тока
магнитное поле накапливает и накапливает энергию от источника. Когда
ток уменьшается по величине, магнитное поле разрушается и
возврат энергии к источнику.
Таким образом, при увеличении силы тока
магнитное поле накапливает и накапливает энергию от источника. Когда
ток уменьшается по величине, магнитное поле разрушается и
возврат энергии к источнику.
Мощность в чисто индуктивной цепи.
Полезная мощность также определяется уравнением P = В I cos θ :
Цепи переменного тока
Цепи переменного токаДалее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия Цепи переменного тока (AC) состоят из э.д.с. источники и три различные типы пассивных элементов: резисторы, катушки индуктивности, и конденсаторы, резисторы удовлетворяют закону Ома:
| (968) |
где — сопротивление, ток, протекающий через резистор, и падение напряжения на резисторе (в направлении, в котором ток течет).
 Катушки индуктивности удовлетворяют
Катушки индуктивности удовлетворяют | (969) |
где индуктивность. Наконец, конденсаторы подчиняются
| (970) |
где — емкость, — заряд, накопленный на пластине с наибольшим положительный потенциал, а для . Обратите внимание, что любой пассивный компонент реального электрического Цепь всегда можно представить как комбинацию идеальных резисторов, катушек индуктивности и конденсаторы.
Рассмотрим классическую схему LCR, состоящую из катушки индуктивности,
конденсатор , и резистор , соединенные последовательно с ЭДС источник,
. Уравнение схемы получается путем установки входного напряжения равным
сумма падений напряжения на трех пассивных элементах цепи. Таким образом,
Таким образом,
| (971) |
Это интегро-дифференциальное уравнение, которое, вообще говоря, довольно сложно решить. решать. Предположим, однако, что и напряжение, и ток колебаться с некоторой фиксированной угловой частотой, так что
| (972) | |||
| (973) |
где под физическим решением понимается действительная часть приведенные выше выражения. Предполагаемое поведение напряжения и тока явно относится к электрике схемы питаются от сетевого напряжения (которое колеблется с частотой 60 герц).
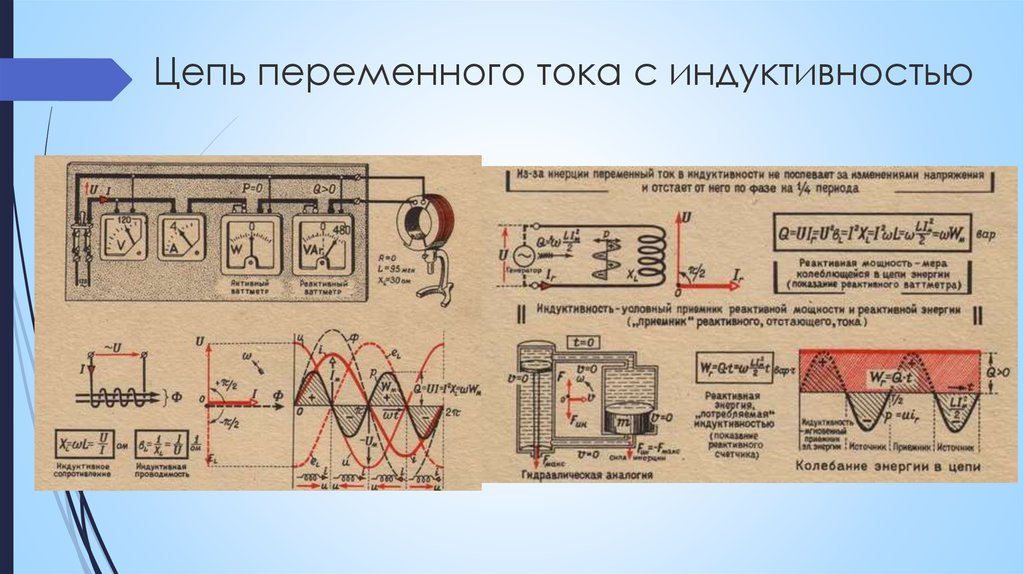
Уравнения (971)–(973) дают результат
| (974) |
давать
| (975) |
Полезно определить импеданс схемы:
| (976) |
Импеданс является обобщением понятия сопротивления. В общем случае импеданс цепи переменного тока составляет сложных величин.
Средняя выходная мощность Э.Д.С. источник
| (977) |
где среднее значение берется за один период колебаний.
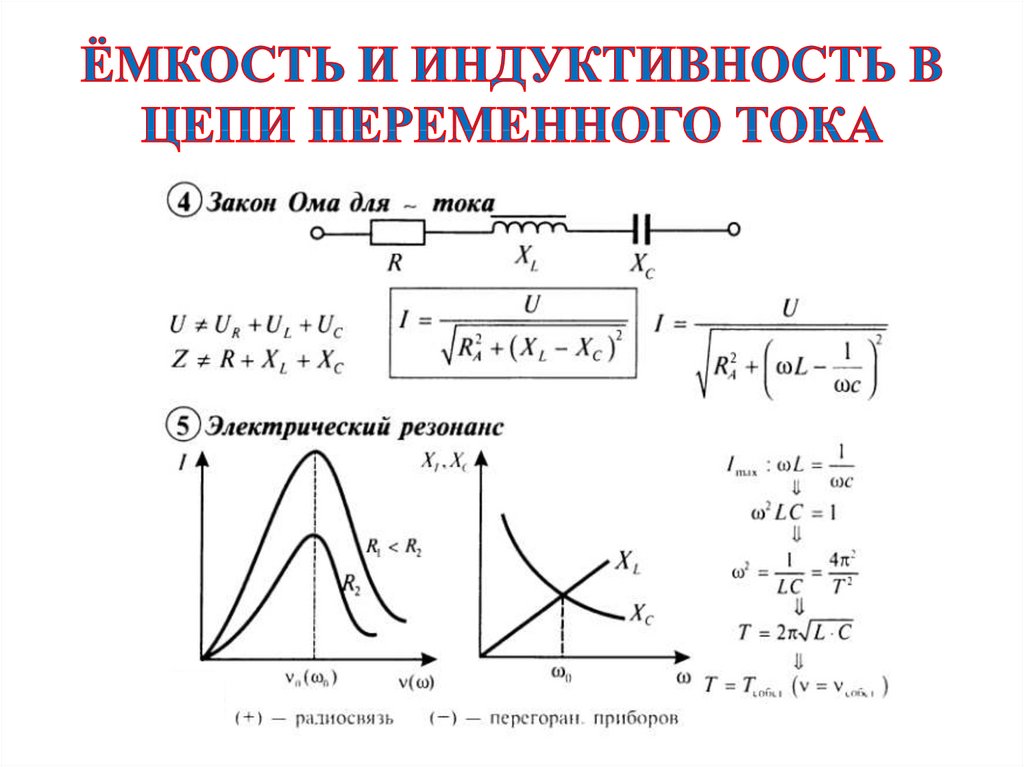 Давайте, прежде всего,
вычислить мощность, используя реальные (а не комплексные) напряжения и токи.
Мы можем написать
Давайте, прежде всего,
вычислить мощность, используя реальные (а не комплексные) напряжения и токи.
Мы можем написать | (978) | |||
| (979) |
где — фазовое отставание тока по отношению к напряжению. Это следует из того
| (980) |
давать
| (981) |
поскольку а также .
 В комплексном представлении напряжение и ток записываются
В комплексном представлении напряжение и ток записываются | (982) | |||
| (983) |
Обратите внимание, что
| (984) |
Это следует из того
| (985) |
Используя уравнение (976), мы находим, что
| (986) |
Обратите внимание, что рассеиваемая мощность связана с действительной частью импеданса.
 Для частного случая схемы LCR,
Для частного случая схемы LCR, | (987) |
Понятно, что только резистор рассеивает энергию в этой цепи. Индуктор и конденсатор накапливает энергию, но в конечном итоге возвращает ее в цепь без рассеивания.
Согласно уравнению. (976), амплитуда тока, протекающего в цепи LCR
для заданной амплитуды входного напряжения
данный
| (988) |
Ответ цепи четко резонансный , достигая пика в , и достижение пикового значения в (при условии, что ). На самом деле схемы LCR используются в радиотюнерах для фильтрации сигналы, частоты которых выходят за пределы заданного диапазона.
Отставание по фазе тока по отношению к напряжению определяется выражением
| (989) |
Отставание по фазе изменяется от для частот значительно ниже резонансной частоты, к нулю на резонансной частоте ( ), к для частот значительно выше резонансной частоты.
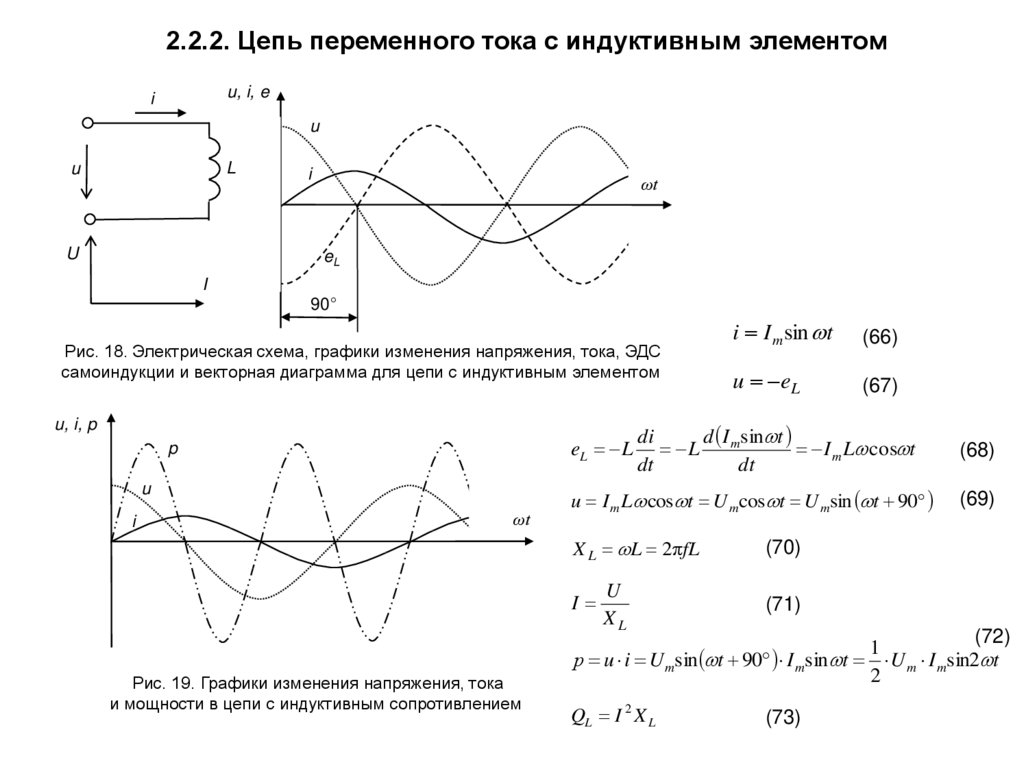
Понятно, что в обычных цепях переменного тока уравнение цепи сводится к простое алгебраическое уравнение, и поведение схемы суммируется по комплексному импедансу. Действительная часть говорит нам о мощности, рассеиваемой в цепи, величина дает отношение пикового тока к пиковое напряжение, а аргумент дает отставание по фазе тока относительно напряжения.
Далее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия Ричард Фицпатрик 2006-02-02
Катушки индуктивности
Google Ads
- Раздел 3.1 Электромагнитная индукция.
- • Магнитные поля вокруг проводников.
- • Соленоид.
- Раздел 3.2 Индуктивность и противоэ.д.с.
- • Единица индуктивности.
- • Факторы, влияющие на индуктивность.
- • Напряжение и ЭДС.
- • Обратная э.д.
 с.
с. - • Самоиндукция.
- Раздел 3.3 Практические катушки индуктивности.
- • Соленоид.
- • Типичные области применения катушек индуктивности.
- • Схематические символы индуктора.
- Раздел 3.4 Цветовые коды индукторов.
- • Коды 4-диапазонных индукторов EIA.
- • Коды катушек индуктивности для 5-диапазонных военных спецификаций (Mil Spec).
- • Коды индуктивностей для устройств поверхностного монтажа (SMD).
- Тест по разделу 3.5 Катушки индуктивности.
Введение
Катушки индуктивности представляют собой простые по конструкции компоненты, состоящие из катушек с изолированным медным проводом, намотанных на каркас, в центре которого имеется сердечник определенного типа. Этот сердечник может быть металлом, таким как железо, которое легко намагничивается; или в высокочастотных индукторах это, скорее всего, будет просто воздух.
Индукторы зависят от своего действия на магнитное поле, которое присутствует вокруг любого проводника, когда он несет ток. Если проволочная катушка намотана на сердечник из материала, который легко намагничивается, например из железа, то магнитное поле вокруг катушки сосредоточено внутри сердечника; это значительно увеличивает эффективность индуктора.
Катушки индуктивности в цепях переменного тока.
Катушки индуктивности широко используются в приложениях переменного тока (AC), таких как радио, телевидение и оборудование связи, и в этих системах очень важно, как катушки индуктивности реагируют на сигналы переменного тока различных частот.
Дроссели.
Другое название катушки индуктивности — «дроссель». Катушки индуктивности, представляющие собой просто катушки из медной проволоки, позволяют легко проходить постоянному току, но когда применяется переменный ток, катушки индуктивности создают сопротивление протеканию тока, которое увеличивается по мере увеличения частоты переменного тока. Следовательно, переменный ток не может течь или «запирается», в то время как постоянному току разрешено проходить. Этот эффект используется в цепях электропитания, где сеть переменного тока общего пользования должна быть преобразована в источник постоянного тока, пригодный для питания электронных схем.
Следовательно, переменный ток не может течь или «запирается», в то время как постоянному току разрешено проходить. Этот эффект используется в цепях электропитания, где сеть переменного тока общего пользования должна быть преобразована в источник постоянного тока, пригодный для питания электронных схем.
Аккумулятор энергии в цепи постоянного тока.
Рис. 3.0.1 Обратная ЭДС в индукторе.
Когда к катушке индуктивности подается постоянное напряжение, через катушку индуктивности течет ток. Поскольку этот ток увеличивается при включении, вокруг катушек проволоки создается возрастающее магнитное поле. Таким образом, электрическая энергия, используемая для создания магнитного поля, хранится в виде магнитной энергии. Кроме того, когда энергия в магнитном поле изменяется, это индуцирует напряжение в тех же самых катушках, которые создают магнитное поле.
Однако индуцированное напряжение, называемое «электромагнитной силой самоиндукции», будет иметь противоположную полярность приложенному напряжению, создающему магнитное поле; поэтому эта наведенная Э. Д.С. также обычно называют «обратной ЭДС». и его эффект заключается в замедлении быстрого изменения тока, которое происходит при включении.
Д.С. также обычно называют «обратной ЭДС». и его эффект заключается в замедлении быстрого изменения тока, которое происходит при включении.
По мере того, как ток через индуктор нарастает, скорость изменения тока уменьшается из-за противо-ЭДС, а также противо-ЭДС из-за уменьшения скорости изменения тока. Электрическая энергия, подаваемая на индуктор, теперь преобразуется в магнитную энергию и хранится в магнитном поле, созданном вокруг индуктора.
Если напряжение, приложенное к индуктору, теперь отключено, энергия, запасенная в магнитном поле, высвобождается обратно в катушки индуктора, на этот раз нет приложенного противоположного напряжения питания, поэтому все магнитное поле мгновенно разрушается, и накопленная энергия, теперь в виде напряжения на индукторе, но с полярностью, противоположной исходному приложенному напряжению.
Однако теперь это напряжение будет намного больше исходного напряжения питания; это связано с тем, что амплитуда напряжения, индуцированного в проводнике, пропорциональна (среди прочего) скорости изменения магнитного поля. При включении из-за изменения двух противоположных напряжений напряжение питания увеличивалось, а противо-Э.Д.С. снижается, скорость изменений замедляется. Однако при выключении напряжения питания нет, поэтому магнитное поле чрезвычайно быстро разрушается, вызывая очень высокую скорость изменения и, следовательно, создавая очень большой импульс напряжения.
При включении из-за изменения двух противоположных напряжений напряжение питания увеличивалось, а противо-Э.Д.С. снижается, скорость изменений замедляется. Однако при выключении напряжения питания нет, поэтому магнитное поле чрезвычайно быстро разрушается, вызывая очень высокую скорость изменения и, следовательно, создавая очень большой импульс напряжения.
Амплитуда этого импульса может составлять десятки, сотни или тысячи вольт, что может быть очень полезно, например. при образовании искры зажигания в бензиновом двигателе или очень опасно, например. не приятно трогать! Он также может очень легко разрушить другие компоненты, такие как полупроводники, и может стать источником серьезных радиопомех.
Узнайте больше о противоэ.д.с. здесь.
Катушки индуктивности многих типов.
Физические размеры катушек индуктивности сильно различаются в зависимости от обрабатываемой мощности и частоты используемого переменного тока; от огромных силовых трансформаторов на электростанциях и в сетях электроснабжения до крошечных катушек индуктивности в радиооборудовании, состоящих из нескольких витков провода и всего несколько миллиметров в поперечнике.




 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления





 д.
д.
 Определение емкости конденсатора
Определение емкости конденсатора Проверка закона Ома для полной цепи переменного тока
Проверка закона Ома для полной цепи переменного тока
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.018 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.018 с.) Даля 166
Даля 166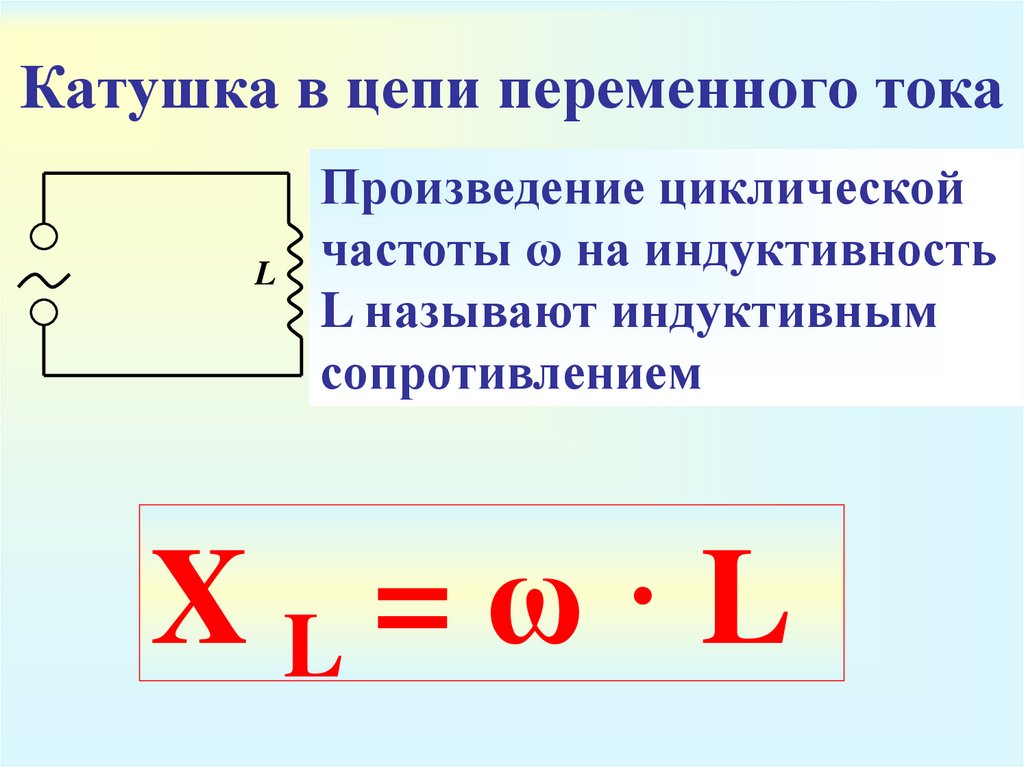 Дегтярева 174
Дегтярева 174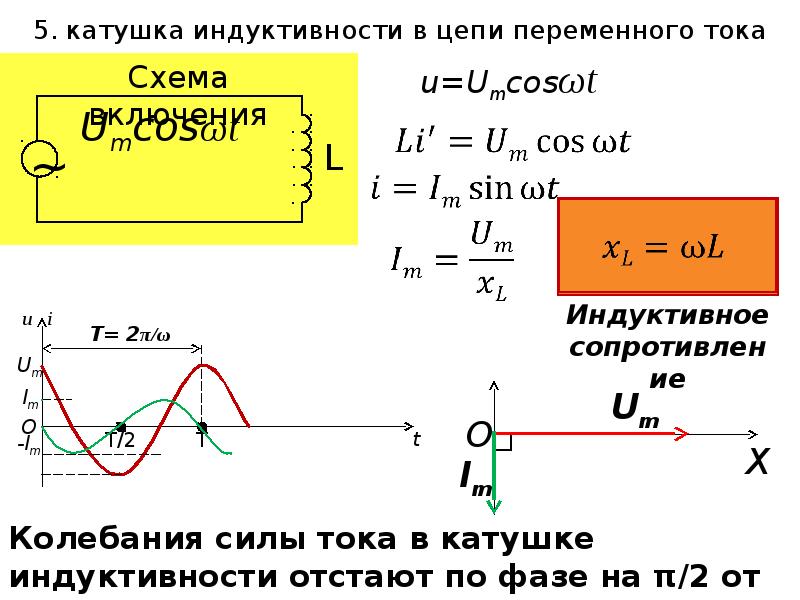 Макарова 543
Макарова 543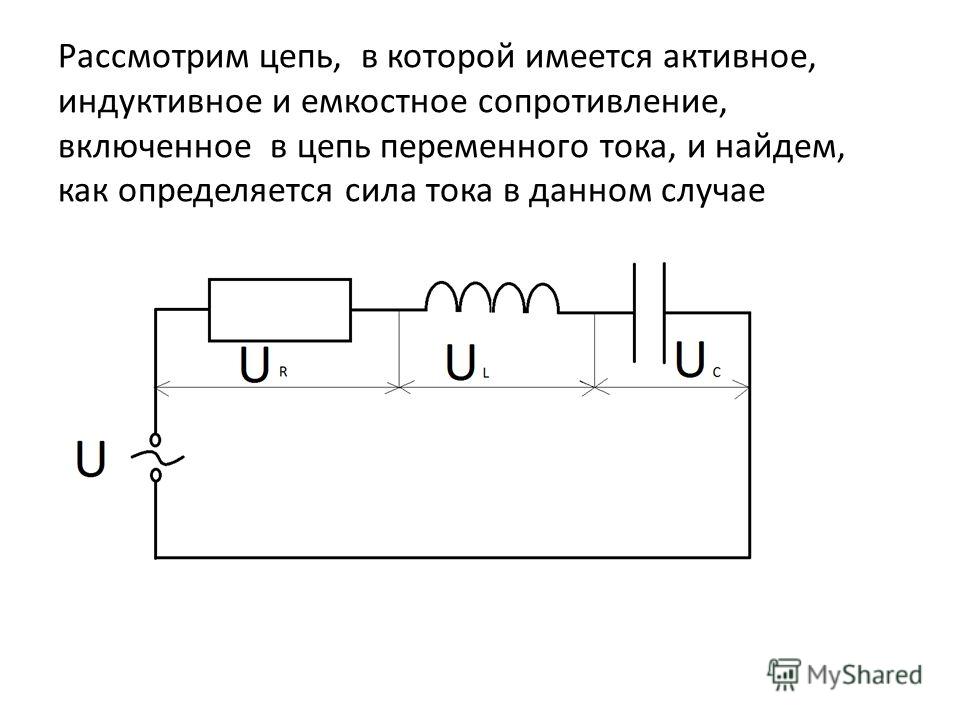 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 с.
с.