Соединение катушек — Основы электроники

Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.

Последовательное соединение катушек индуктивности.

Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.

Рисунок 1. Последовательное соединение катушект индуктивности.

Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:

где L1, L2 и L3 — индуктивности отдельных катушек.

Параллельное соединение катушек индуктивности.

Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же усло­вия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:

Рисунок 2. Параллельное соединение катушек индуктивности.

Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:

Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или парал­лельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопро­тивления цепи при последовательном и параллельном соеди­нении резисторов.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, распо­ложены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше фор­мула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

1. Магнитные потоки обеих катушек имеют одинаковые на­правления
2. Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений то­ков в них.

Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответство­вать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направ­лены в одну сторону. Очевидно, при этих условиях витки каж­дой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в дру­гой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых состав­лена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по фор­муле:

В первом случае ставится знак + (плюс), а во втором слу­чае знак — (минус).

Величина М, называемая коэффициентом взаим­ной индукции, представляет собой добавочную индук­тивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство варио­метров. Вариометр состоит из двух катушек, общая индуктив­ность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передат­чиков.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Параллельное соединение индуктивно связанных катушек

Рассмотрим параллельное соединение индуктивно связанных катушек (рис 5.9)

Рис 5.9

Запишем уравнения для каждой из ветвей цепи в комплексной форме:

Знак (+) перед соответствует согласному включению, знак (–) – встречному.

Введем обозначения

, , и перепишем последнюю систему уравнений в виде :

Определим из этих уравнений токи в ветвях

Из последнего соотношения определим входное сопротивление параллельно соединенных индуктивно связанных катушек:

При отсутствии индуктивной связи, т.е при Z_M

=0 входное сопротивление преобразуется к известному выражению

Полагая в предыдущем выражении r₁=0, r₂=0, получим выражение для полной индуктивности при согласном включении:

или в встречном включении

5.6 Расчет цепей со взаимной индуктивностью.

Расчет разветвленных ветвей при наличии взаимной индуктивности можно вести по уравнениям составленным по первому и второму законам Кирхгофа или методом контурных токов. Метод узловых потенциалов непосредственно не применим. Объясняется это тем, что ток в ветви зависит не только от разности потенциалов на зажимах ветви и от ЭДС, находящихся в ветви, но и от токов других ветвей с которым рассматриваемая ветвь индуктивно связана.

Ограниченное применение находит метод эквивалентного генератора. Его можно применить в том случае, если ветвь, в которой требуется определить ток, индуктивно не связанна с другими ветвями.

В противном случае исключение этой ветви привело бы к потере индуктивной связи.

В качестве примера запишем уравнения по законах Кирхгофа для цепи, изображенной на рис 5.10

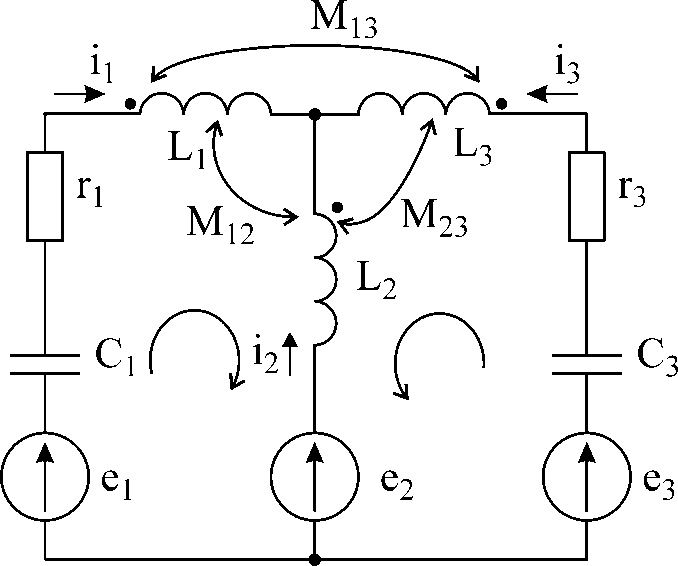
Рис 5.10

Направления обхода контуров обозначим стрелками.

В полученной системе трех уравнений неизвестными являются токи .

Решая систему, получаем их численные значения.

Развязка индуктивных связей

Выше было сказано, что не все методы пригодны для расчета индуктивно связанных цепей. Анализ и расчет цепи упрощается, если часть цепи содержащую индуктивные связи заменить эквивалентной схемой без индуктивных связей. Эта замена является называется развязкой индуктивных связей.

Рассмотрим часть цепи с индуктивной связью (рис 5.11)

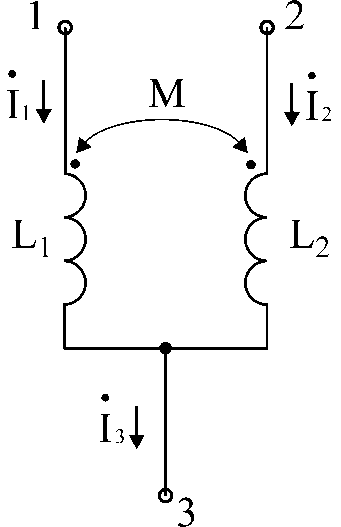
Рис 5.11

Запишем для нее уравнения в комплексной форме

где знак (+) перед

соответствует согласному включению индуктивностей, а знак (–) встречному. Выразив из первого уравнения токи подставив в выражение для, получим

, а выразив

и подставив в

, получим:

.

Полученным уравнениям для исоответствует электрическая цепь, изображенная на рис 5.12

Рис 5.12

В цепи на рис 5.12 отсутствует индуктивные связи, однако изменились величины индуктивностей и появился дополнительный элемент. Верхний знак перед М соответствует согласному включению, а нижний знак –встречное включение индуктивностей.

Для расчета цепи преобразованной таким образом можно использовать любые методы расчета цепей без ограничения.

Воздушный трансформатор

Трансформатор слово латинского происхождения и переводится как преобразователь. Этим определяется его назначение. Трансформатор служит для преобразования переменного напряжения, когда требуется изменить величину напряжения или осуществить передачу электрической энергии между контурами лишенными гальванической связи.

Конструктивно трансформатор представляет собой две или несколько индуктивно связных катушек, называемых обмотками трансформатора. Обмотки трансформатора могут быть помещены на общий ферромагнитный сердечник. Однако сердечник может отсутствовать. Тогда трансформатор называется воздушным трансформатором или трансформатором без сердечника.

Рассмотрим простейший воздушный трансформатор, состоящий из 2-х обмоток.

Такие трансформаторы находят широкое применение в устройствах работающих на высоких частотах, например, в радиоприемных устройствах. Схема трансформатора представлена на рис 5.13

Рис 5.13

Обмотка трансформатора, подключаемая к источнику переменного напряжения, называется первичной. На рис 5.13 она представлена индуктивностью L₁ и активным сопротивлением проводника r₁, из которого она изготовлена. Вторичная обмотка, к которой подключается нагрузка Z_Н, представлена индуктивностью L₂ и активным сопротивлением r₂. Между обмотками трансформатора имеется индуктивная связь, характеризуемая взаимной индуктивностью M.

Уравнения по второму закону Кирхгофа для первичной и вторичной цепи трансформатора запишутся в виде:

Векторные диаграммы трансформатора для случаев активно-индуктивной и активно-емкостнойнагрузки, построенные по уравнениям приведены на рис. 5.14 а, б соответственно :

Рис. 5.14

Порядок построения векторной диаграммы трансформатора проследим на рисунке 5.14а. Зададимся положительным направлением тока во вторичной обмотке трансформатора. Напряжение на активном сопротивлении вторичной обмотки трансформаторасовпадает по фазе стоком. Напряжение на индуктивности вторичной катушкиопережает токна 90⁰. Совмещаем начало вектора концом вектора. Напряжение на активной составляющей сопротивления нагрузкесовпадает по фазе с током. Откладываем векторпараллельно вектору токас конца вектора. Вектор напряжения на индуктивной составляющей сопротивления нагрузкиопережает токна 90⁰, откладываем с конца вектора под углом 90⁰ к вектору . Векторная суммаравна вектору напряжения, возникающего за счёт индуктивной связи между первичной и вторичной катушками. Вектор токаотносительносдвинут на –90⁰. Определив таким образом направление тока строим векторы напряжений на элементах первичной цепи трансформатора согласно первому уравнению трансформатора.

Вектор напряжения на активном сопротивлении первичной катушки совпадает с током. Вектор напряжения на индуктивности первой катушкиопережает токна 90⁰. Совмещаем начало вектора с концом вектора. Падение напряжения, вызванное в первичной цепи токомвторичной цепи имеет сдвиг фазы – 90⁰ по отношению к току . Откладываем векторс конца векторапод углом –90⁰ к току . Сумма векторовдаёт вектор входного напряжения трансформатора.

Определим входное сопротивление трансформатора. Уравнения описывающие воздушный трансформатор запишем в виде

где — реактивное сопротивление первичной цепи

— активное сопротивление вторичной цепи

— реактивное сопротивление вторичной цепи трансформатора. Из системы уравнений определим ток.

Разделим числитель и знаменатель последнего выражения на

Полученное соотношение

выражает закон Ома для первичной цепи. Следовательно, знаменатель представляет собой выражение для входного сопротивления трансформатора.

Выделим в выражении для входного сопротивления трансформатора действительную и мнимую часть, умножив числитель и знаменатель третьего слагаемого на число комплексно — сопряженное знаменателю

Таким образом, входное сопротивление трансформатора представлено в виде последовательного соединения двух активных и двух реактивных сопротивлений. Входное сопротивление трансформатора может быть изображено в виде двухполюсника на рис 5.15

Рис 5.15

где активное сопротивление, вносимое из вторичной цепи в первичной.

x_1вн=реактивное сопротивление, вносимое в первичную цепь из вторичной .

Следует заметить, что вносимое реактивное сопротивление имеет знак противоположный знаку собственного реактивного сопротивления вторичного контура x₂₂.

Из представления воздушного трансформатора в виде двухполюсника следует условие передачи максимальной мощности в нагрузку Z_ист=Z_H^*.

Другой подход к анализу трансформатора предполагает исключение индуктивной связи между обмотками и получения эквивалентной схемы замещения трансформатора.

Запишем уравнения трансформатора в виде

Добавим и вычтем к левой части первого уравнения слагаемое , а к левой части второго уравнения

Преобразуем полученные уравнения

Из последних уравнений следует, что цепь описываемая ими состоит из 2-х контуров, имеющих общее сопротивление . В первом контуре протекает токво втором – ток. Схема цепи , описываемая этими уравнениями приведена на рис 5.16

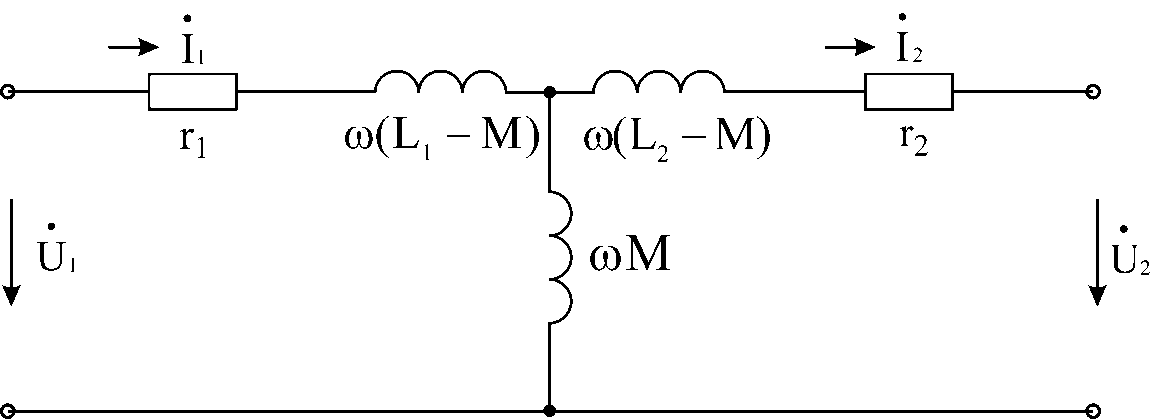
Рис 5.16

Полученная схема цепи может рассматриваться как эквивалентная исходной в отношении напряжений ии токови.

Как отмечалось выше, основное назначение трансформатора – повышение или понижение в некоторое число раз напряжения и тока. В идеальном случае такое преобразование не должно завесить ни от частоты приложенного напряжения ни от величины нагрузки. Рассмотрим ,при каких условиях это возможно.

Введём понятия функции передачи тока и функции передачи напряжения, и, соответственно.

Из второго уравнения системы 5.1 выразим .

Разделив левую и правую части полученного соотношения на получим

Из последнего выражения с учётом 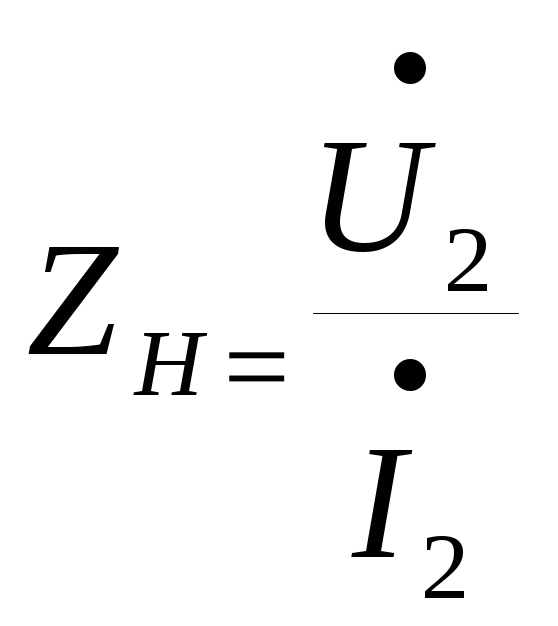, получим функцию передачи тока.

Функцию передачи напряжения получим как отношение второго уравнения к первому из системы 5.1

Разделив числитель и знаменатель последнего выражения на , получим соотношение

включающее в себя функцию передачи тока .Подставив значение, окончательно получим функцию передачи напряжения в виде

Как следует из выражений для функции передачи тока и напряжения, они зависят от многих величин.

Если можно пренебречь потерями в обмотках трансформатора, т. е. если r₁=r₂=0, то функция передачи напряжения запишется в виде

Полагая, что потоки рассеяния отсутствуют, т.е. коэффициент связи ,получим

Индуктивность обмотки трансформатора пропорциональна квадрату витков обмотки , где-магнитная проводимость пути, по которому протекает поток.

Выразив величины индуктивностей ичерез число виткови, получим функцию передачи напряжения в виде

Отношение назовем коэффициентом трансформации и обозначим буквойn.

Таким образом независимость от частоты и нагрузки функции передачи напряжения обеспечивается при нулевом активном сопротивлении и коэффициенте связи .

Рассмотрим условие независимости от частоты функции передачи тока

Если индуктивное сопротивление вторичной цепи значительно больше сопротивления нагрузки и активного сопротивления и,, то

Идеальным трансформатором называется идеализированный элемент электрической цепи с двумя парами зажимов –первичных и вторичных , обладающий следующими свойствами : при любых условиях отношение первичного и вторичного комплексных токов равны постоянному числу

n-коэффициенту трансформации.

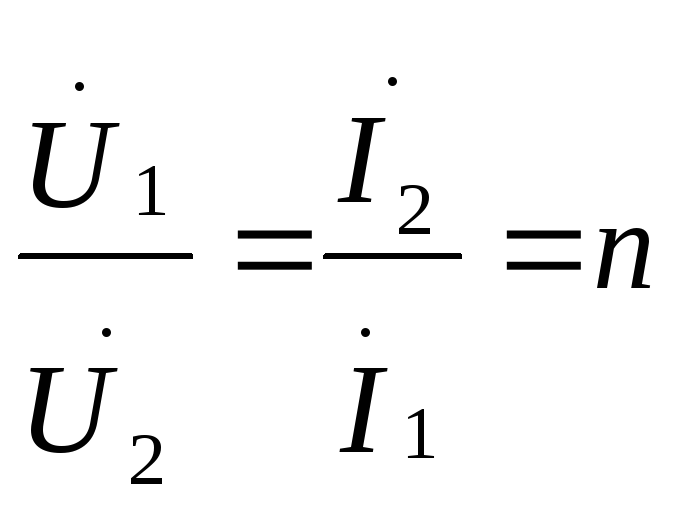
Если n>1, то трансформатор называется понижающим, если n<1, то трансформатор – повышающий.

Рассмотрим свойства идеального трансформатора.

Пусть ко вторичным зажимам подключена нагрузка с комплексным сопротивлением . Тогда входное сопротивление будет равным :

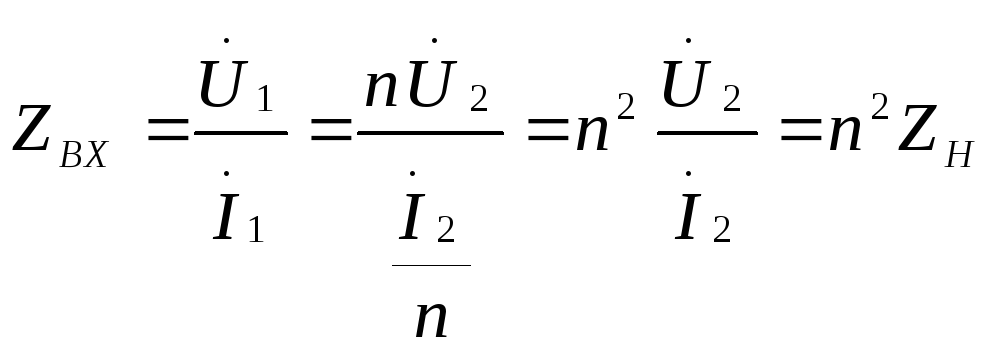
Т.е входное сопротивление изменилось в n² раз. Это позволяет применять трансформатор для согласования источника и нагрузки , например, по условию передачи в нагрузку максимальной мощности .

Например, если сопротивление источника равно r_i, а сопротивление нагрузки – r_H, то входное сопротивление относительно первичной обмотки равно и условие согласования запишется в виде

откуда

Установим связь между мощностью на входе и выходе идеального трансформатора.

–мощность на входе трансформатора

–мощность на выходе трансформатора

Таким образом, идеальный трансформатор передает энергию с входа на выход цепи без потерь.

Сформулируем условия, которые должны выполнятся для того, что бы трансформатор был идеальным:

1.Должны отсутствовать потоки рассеяния, т. е .

2. Должны отсутствовать потери, т.е

3. Должны быть великими индуктивности обмоток, т.е

Реальные трансформаторы могут обеспечить выполнение условий лишь приближенно за счет технических решений:

1. Для отсутствия потока рассеяния обмотки трансформатора помещают на замкнутом сердечнике , выполненном из материала с высокой магнитной проводимостью.

2. Второе условие обеспечивает выбором обмоточного проводника , обладающего низким удельным сопротивлением .

3. Для выполнения условия ,обмотки должны иметь большое число витковии высокую магнитную проводимость материала сердечника.

По своим свойствам к идеальному трансформатору приближается трансформатор с ферромагнитным сердечником . Трансформатор с ферромагнитным сердечником может рассматриваться как линейный элемент , если магнитный поток не насыщает сердечника . Это условие обычно выполняется за исключением приборов , где насыщение принципиально необходимо.

Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

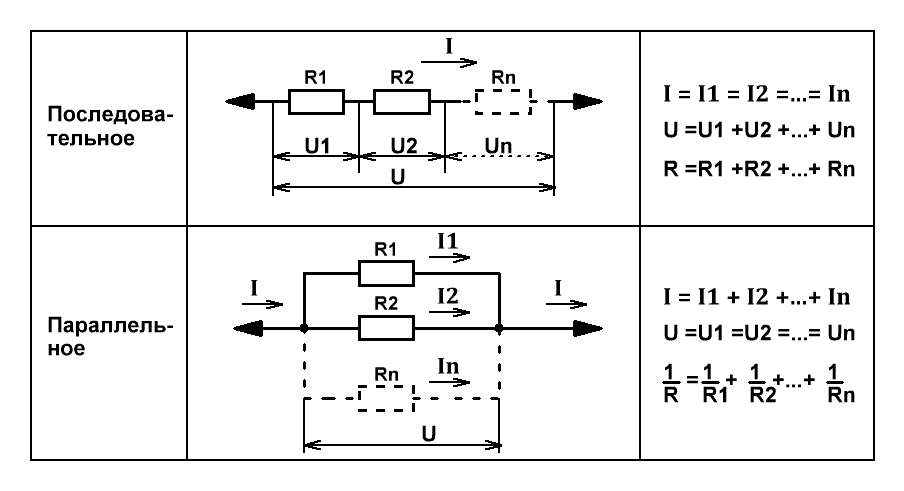
Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С₁+ С₂+….+ С_n   и   1/L = 1/L₁+ 1/L₂ +…+ 1/L_n    для параллельных цепей и
L = L₁ + L₂ +….+ L_n   и   1/С = 1/С₁+ 1/С₂+…+ 1/С_n    для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

 

2.13. Параллельное соединение активного сопротивления, индуктивности и емкости

Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).

Требуется по известным G, В_L, В_C, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.

1. М е т о д в е к т о р н ы х д и а г р а м м.

Токи ветвей находятся сразу: , , .

Для определения общего тока необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем

или ,

где – полная проводимость цепи, равная

.

Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи .

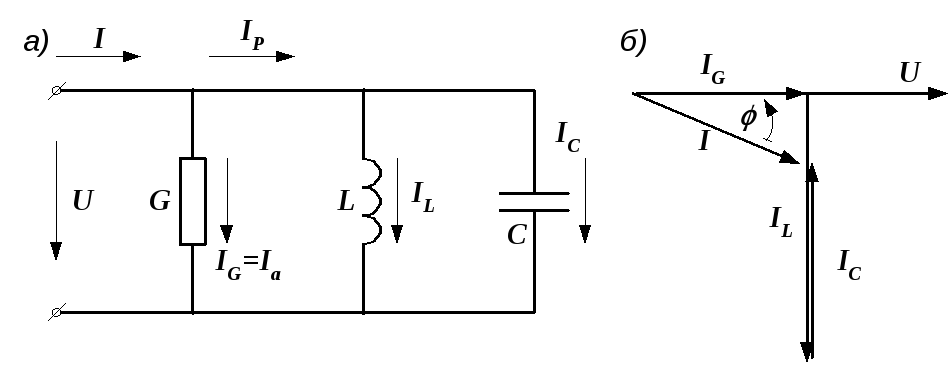Рис. 2.31. Электрическая цепь и ее векторная диаграмма

Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи: (рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов и определяется как разность длин векторов: (см. рис. 2.31,б и 2.32, а).

Рис. 2.32. Треугольники токов и проводимостей

Разделив все стороны треугольника токов на , получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:

, , , . (2.29)

2. С и м в о л и ч е с к и й м е т о д.

Раньше были получены следующие формулы:

, , .

Подставляя их в уравнение первого закона Кирхгофа, получаем:

или ,

где – комплексная проводимость цепи, равная

Пример 2.12. Для цепи, показанной на рис. 2.33, а, рассчитать токи, угол сдвига фаз между током и напряжением на входе цепи, построить векторную диаграмму. Числовые значения параметров цепи: В, Ом, мкФ, с^-1.

Рис. 2.33. Электрическая цепь и ее векторная диаграмма

Р е ш е н и е.

А, Ом,

А, А.

Векторная диаграмма приведена на рис. 2.33, б.

Угол сдвига фаз .

Величину общего тока можно найти иначе:

См, См,

См, А.

Пример 2.13. Начертить цепь, векторная диаграмма которой изображена на рис. 2.34, а.

Р е ш е н и е задачи показано на рис. 2.34, б.

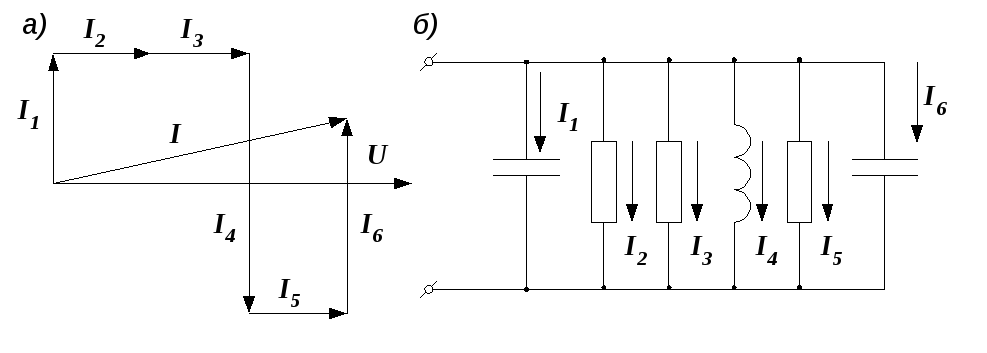
Рис. 2.34. Векторная диаграмма и соответствующая ей электрическая цепь

Пример 2.14. Чему равно показание амперметра А на входе цепи в схемах рис. 2.35, если амперметры А₁ и А₂ во всех случаях показывают соответственно 4 и 3 А?

Рис. 2.35. Измерение тока в электрической цепи

Предлагаем для каждого случая самостоятельно построить векторную диаграмму и убедиться в правильности приведенных ответов: а) 5А, б) 7А, в) 1А.

2.14. Пассивный двухполюсник в цепи синусоидального тока.Эквивалентные сопротивления и проводимости

На рис. 2.36 показан пассивный двухполюсник, состоящий из активных и реактивных элементов. Действующие значения напряжения , тока и угол сдвига фаз между ними известны.

Рис. 2.36. Пассивный двухполюсник

Построим по этим значениям векторную диаграмму и, спроектировав вектор напряжения на вектор тока и перпендикулярное к нему направление, получим треугольник напряжений, образованный сторонами , и (рис. 2.37, а).

Как и раньше, и будем называть активной и реактивной составляющими напряжения. Изображенная в таком виде диаграмма соответствует схеме, показанной на рис. 2.37, б. Действительно, для нее , и . Схема называется последовательной схемой замещения или последовательной эквивалентной схемой пассивного двухполюсника, а ее параметры , и – эквивалентными сопротивлениями двухполюсника.

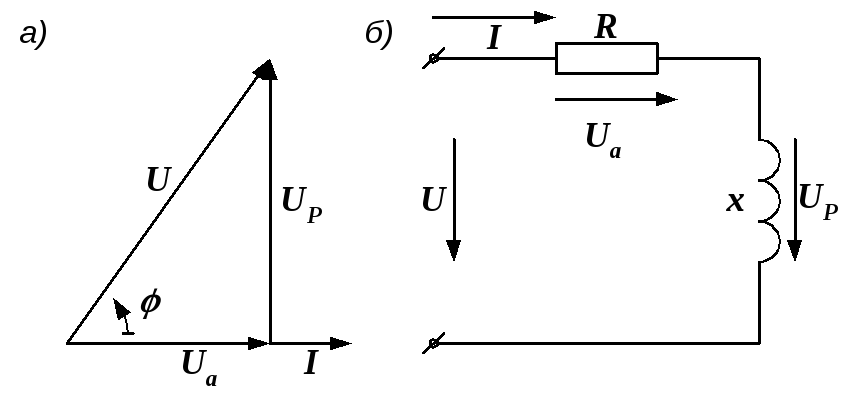
Рис. 2.37. Векторная диаграмма и соответствующая ей последовательная эквивалентная схема

Треугольник, образованный сторонами , и и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).

Теперь разложим в е к т о р т о к а на две составляющие – активную , направленную по вектору напряжения, и реактивную , перпендикулярную к нему (рис. 2.38, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 2.38, б). Ее параметры , и называются эквивалентными проводимостями. Токи в элементах и мы и представляем как активную и реактивную составляющие общего тока: , . Из треугольника токов (рис. 2.38, а) получается треугольник проводимостей (рис. 2.32, б), стороны которого связаны между собой формулами (2.29).

а) б)

Рис. 2.38. Параллельная эквивалентная схема и ее векторная диаграмма

Получим условия эквивалентности приведенных схем.

Для последовательной цепи , для параллельной , а так как токи и напряжения в обеих схемах одинаковы, то

и , (2.30)

т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.

Из сопоставления формул (2.27) и (2.29) можно записать:

и .

Рассматривая последние выражения совместно с (2.30), можно получить две группы формул:

Формулы перехода от последовательной эквивалентной схемы к параллельной:	Формулы перехода от параллельной эквивалентной схемы к последовательной:
(2.31)	(2.32)

Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного. В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1/R и B = 1/x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.

Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.

Пример 2.15. Найти общее сопротивление цепи, состоящей из параллельно соединенных активного R = 30 Ом и индуктивного х = 40 Ом сопротивлений (рис. 2.39, а).

Рис. 2.39. Схемы к примерам 2.15–2.17

Р е ш е н и е. Так как в левой ветви реактивного сопротивления нет, то ее проводимость в соответствии с (2.31) равна G = 1/R. Аналогично, во второй ветви B = 1/x. Полная проводимость цепи . В соответствии с (2.30) полное сопротивление цепи

Ом.

Пример 2.16. Рассчитать общее сопротивление цепи, состоящей из параллельно соединенных индуктивности L = 0,478 Гн и емкости С = 31,85 мкФ (рис. 2.39, б). Частота питающего напряжения f = 50 Гц.

Р е ш е н и е. Определяем сопротивления ветвей:

Ом,

Ом.

Так как в ветвях отсутствуют активные сопротивления, то их проводимости соответственно равны B_L = 1/x_L и B_C = 1/x_С. Полная эквивалентная проводимость цепи не содержит активной составляющей и равна

.

Полное эквивалентное сопротивление

Ом.

В рассматриваемой цепи активных элементов нет, она носит чисто реактивный характер. Он может быть индуктивным или емкостным. Знак минус в ответе свидетельствует о последнем, т.е. вся цепь может быть заменена конденсатором емкостью

мкФ.

Пример 2.17. Амперметр А, вольтметр V и фазометр , включенные в цепь катушки (рис. 2.39, в), дали следующие показания: U = 220 В, I = 4,4 А, cos  = 0,8. Частота питающего напряжения 50 Гц. Определить параметры последовательной и параллельной схем замещения катушки.

Р е ш е н и е. Находим параметры последовательной эквивалентной схемы:

Ом, Ом,

Ом.

Рассчитываем элементы параллельной эквивалентной схемы:

См, См,

См.

После определения эквивалентных сопротивлений эквивалентные проводимости можно было найти иначе, по формулам (2.31):

См, См,

См.

Рис. 2.40. Расчетная схема

Пример 2.18. Рассчитать токи в схеме, приведенной на рис. 2.40.

В,

Ом,

Ом,

Ом,

Ом,

Ом,

Ом,

Ом.

Р е ш е н и е. Определяем полные сопротивления второй и третьей ветвей:

Ом, Ом.

Преобразуем эти ветви в эквивалентные параллельные (рис. 2.41, а).

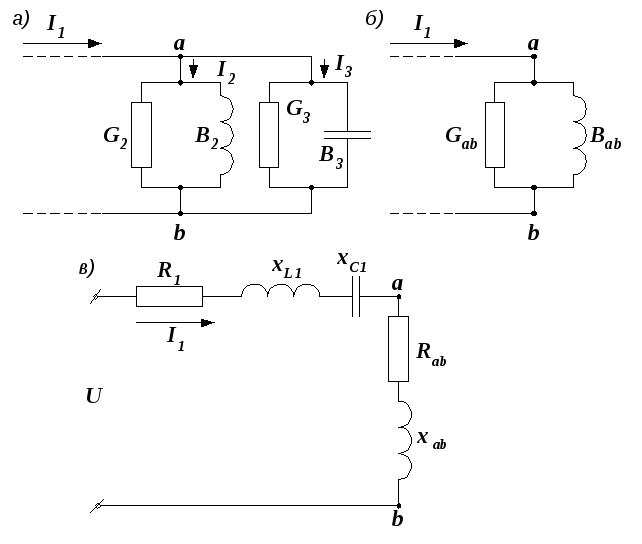
Рис. 2.41. Преобразования электрической цепи

Их проводимости:

См, См,

См, См.

Суммируем активные и реактивные проводимости параллельных ветвей: См, См (см. рис. 2.41, б).

Определяем эквивалентные сопротивления участка (рис. 2.41, в):

Ом, Ом,

Ом,

и полное сопротивление цепи:

Ом.

Ток на входе цепи I₁ = U/z = 220/41,53 = 5,297 A.

Напряжение на участке U_ab= I₁z_ab= 119,7 В.

Токи второй и третьей ветвей:

А, А.

Еще раз напоминаем, что для численных значений токов и напряжений законы Кирхгофа неприменимы: .

57. Параллельное соединение двух катушек. Определение входного сопротивления.

Пусть две индуктивно связанные катушки с параметрамииM соединены параллельно (рис. 3.5). Оба вида соединения будем рассматривать одновременно. Согласное соединение получается при подключении к одному и тому же узлу одноименных зажимов, встречное — разноименных. Первый случай отмечен на схеме звездочками, второй -точками. Запишем уравнения Кирхгофа для рассматриваемой цепи и решая их, получим выражения, определяющие токи:

Рис. 3.5. Параллельное соединение индуктивно связанных элементов

.

    В этих уравнениях ,,.

    Входное комплексное сопротивление цепи равно отношению напряжения к току на ее зажимах:

.

    При отсутствии магнитной связи между катушками, полагая , получаем известную формулу для определения общего сопротивления двух параллельных ветвей:

Во всех приведенных выражениях у слагаемых с двойным знаком верхний знак относится к согласному соединению, нижний к встречному.

58. Коэффициент индуктивной связи.

Степень индуктивной связи двух катушек характеризуется коэффициентом связи k, который равен среднегеометрическому из отношения потока взаимной индукции ко всему потоку катушки

 

Коэффициент связи всегда ниже 1.

Увеличение коэффициента связи можно получить за счет применения ферромагнитного сердечника, который имеет большую величину магнитной проницаемости. Доля потоков рассеяния в этом случае уменьшается. Коэффициент связи изменяется при изменении положения осей катушек. Так при перпендикулярном положении он обращается в ноль. Перемещая одну катушку относительно другой, можно плавно изменять k в широких пределах, т.е. при последовательном соединении катушек менять их результирующую индуктивность. Такое устройство называется вариометром.

59. Цепи со взаимной индуктивностью. Согласное и встречное включение индуктивно связанных катушек (последовательное включение). Векторные диаграммы.

60. Расчет цепей с периодическими несинусоидальными источниками (показать на примере).

Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. На рис. 2.1 представлена такая кривая, период повторения которой Т. Эта кривая может быть описана функцией

,                                   (2.1)

где  n=0, 1, 2 и т.д.

Причины появления несинусои­дальных сигналов:

1.   Источник тока или источник напряжения генерируют несинусоидальный ток или несинусоидальную ЭДС, а все элементы цепи (R, L, C) линейны, т.е. от величины тока не зависят.

2.   Источник тока или источник напряжения генерируют синусоидальный ток или синусоидальную ЭДС, но один или несколько элементов цепи нелинейны (вентиль, электрическая дуга, катушка со стальным магнитопроводом).

3.   Воздействие периодических помех на синусоидальный сигнал.

4.   Использование генераторов сигналов специальной формы (пилообразной, ступенчатой, прямоугольной) в автоматике, вычислительной технике, в различных устройствах радиосвязи.

Существует два пути расчета линейной электрической цепи при воздействии сигналов такой формы:

1. Применение специальных математических приемов, отражающих состояние цепи в каждый момент времени, что приводит к сложной системе дифференциальных уравнений. Поэтому он не нашел применения в инженерных расчетах.

2. Сведение сложной задачи к совокупности более простых и применение известных методов расчета их с учетом особенностей воздействующего сигнала.

60. Расчет линейных электрических цепей при воздействии несинусоидальных периодических сигналов.

.

Параллельное соединение катушки и конденсатора

Для рассмотрения параллельного соединения катушки и конденсатора представим их на схеме активными и реактивными проводимостями (рис. 14.11, а).

На схеме рис. 14.1.1, б те же катушки и конденсатор представлены активными и реактивными сопротивлениями. Первая схема имеет некоторое преимущество, так как в ней все элементы соединены параллельно, а в другой они соединены смешанно.

Считая известными параметры катушки G₁, B_L и конденсатора G₂, B_C, а также напряжение u = U_msinωt, определим токи в цепи и ее мощность.

Векторная диаграмма цепи. Полная проводимость цепи

Согласно первому закону Кирхгофа, мгновенная величина общего тока равна сумме мгновенных токов отдельных ветвей:

Имея в виду несовпадение по фазе активных и реактивных токов, величину общего тока найдем векторным сложением:

Для построения векторной диаграммы находим:

В зависимости от соотношения величин реактивных проводимостей ветвей с индуктивностью и емкостью можно отметить три случая.

1. B_L> B_C. Для этого случая векторная диаграмма представлена на рис. 14.12, а. На диаграмме построены треугольники токов для катушки и конденсатора и найдены векторы токов I₁ и I₂ в этих элементах:

Векторная сумма токов l₁ + I₂ = I дает общий ток в цепи. Вместе с тем вектор I является гипотенузой прямоугольного треугольника токов, катеты которого — составляющие вектора тока по двум взаимно перпендикулярным осям:

I_а = I_1G + I_2G — активная составляющая;
I_p = I_L + I_C — реактивная составляющая.

Векторы активных составляющих токов направлены в одну сторону, поэтому их численные значения складываются. Векторы реактивных составляющих токов направлены перпендикулярно вектору напряжения в противоположные стороны, поэтому им даются разные знаки: индуктивные токи считаются положительными, а емкостные — отрицательными. При одинаковом напряжении на всех элементах цепи I_L > I_C. Общий ток отстает от общего напряжения по фазе на угол ф.

Из треугольника токов следует

где G = G1 + G2 и В = BL — Bc — общие активная и реактивная проводимости цепи;

 

 полная проводимость цепи. Эти три проводимости графически можно изобразить сторонами прямоугольного треугольника проводимостей, который получается уже известным способом’ из треугольника токов.

Полная проводимость цепи У является коэффициентом пропорциональности между действующими величинами общего тока и напряжения цепи:

Из треугольников токов и проводимостей определяют величины:

Угол сдвига по фазе между напряжением и общим током в цепи положительный(ф> 0).

2. В_L<В_C. Векторная диаграмма изображена на рис. 14.12,б. Так как I_L<I_с. то напряжение отстает от общего тока на угол ф<0.

Реактивная проводимость цепи имеет емкостный характер. Расчетные формулы, полученные для случая 1, действительны и для этого случая.

3. B_L = В_C. В этом случае реактивные составляющие токов катушки и конденсатора равны по величине: I_L = I_C. Реактивная составляющая общего тока и общая реактивная проводимость равны нулю. Общий ток совпадает по фазе с напряжением и равен по величине активной составляющей тока. Угол ф сдвига фаз между общим током и напряжением равен нулю.

Общий ток в цепи и напряжение связаны формулой

I = UG, или U = I/G.

В случае В_L = В_C в цепи имеет место резонанс токов.

Энергетический процесс в цепи

Из векторной диаграммы токов легко получить треугольник мощностей, из которого следуют те же формулы (14.2), которые были получены для последовательного соединения катушки и конденсатора.

Реактивные мощности индуктивности и емкости входят в расчет с разными знаками: реактивная мощность индуктивности положительна, а реактивная мощность емкости отрицательна. В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует из формул (14.2).

Если ф> 0, то Q> 0; при ф< 0  Q< 0.

Активная мощность положительна при любом значении угла. Полная мощность тоже всегда положительна.

В рассматриваемой цепи активная мощность имеет определенную величину (Р ≠ 0), следовательно, имеет место преобразование электрической энергии в другой вид.

Кроме того, часть энергии, полученной от генератора, возвращается обратно в генератор (Q ≠ 0 при ф ≠ 0).

Обмен энергией совершается также между катушкой и конденсатором.

Соединение элементов в цепи переменного напряжения и тока

Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Последовательное соединение элементов цепи при переменном напряжении

Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.

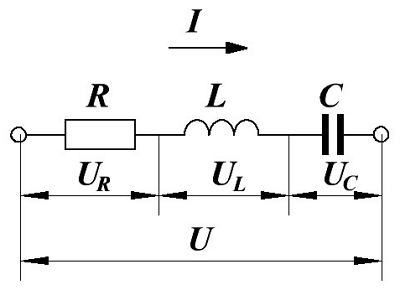
Последовательное соединение элементов цепи.

В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах

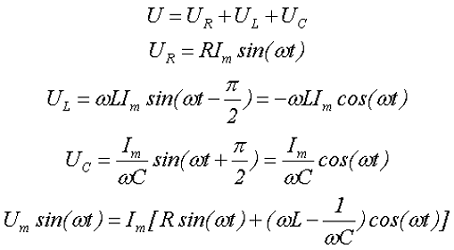
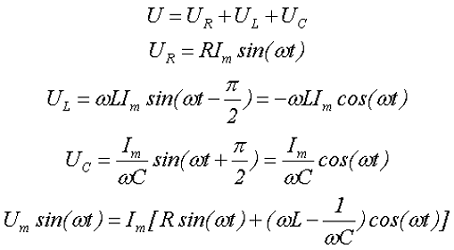
где U_R, U_L, U_C – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,

I_m­ – амплитудное значение переменного тока.

Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже

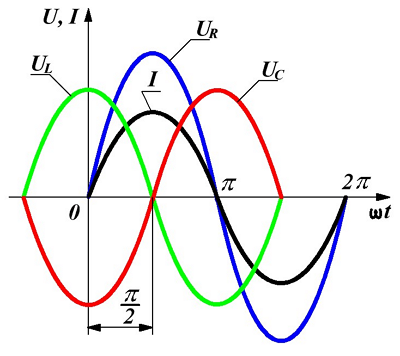
Напряжения и токи при последовательном соединении.

Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде

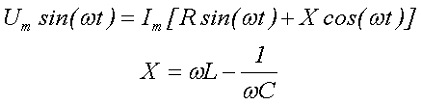
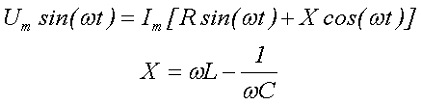
где R – активное сопротивление,

Х – реактивное сопротивление.

Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.

В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений

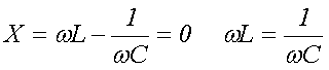
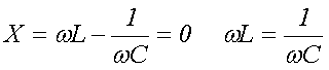
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.

При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение

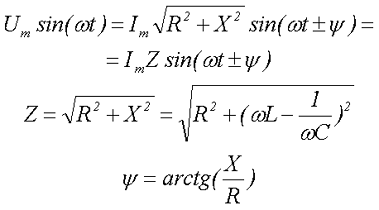
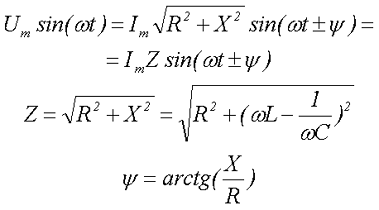
где Z – полное сопротивление цепи,

ψ – разность фаз между напряжением и током.

Таким образом, амплитудное значение напряжения U_m и амплитудное значение тока I_m связаны между собой следующим соотношением

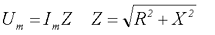
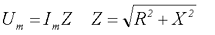
где U_m­ – амплитудное значение переменного напряжения,

I_m­ – амплитудное значение переменного тока,

Z – полное сопротивление цепи.

Параллельное соединение элементов цепи при переменном напряжении

Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.

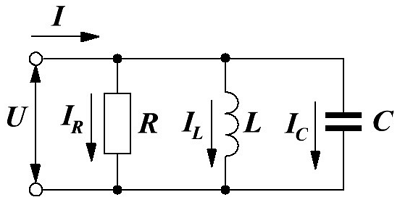
Параллельно соединение элементов цепи.

Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи

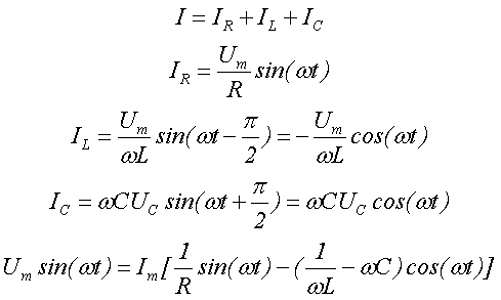
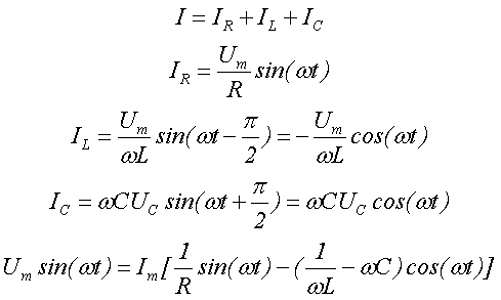
I_R, I_L, I_C – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,

U_m­ – амплитудное значение переменного тока.

Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже

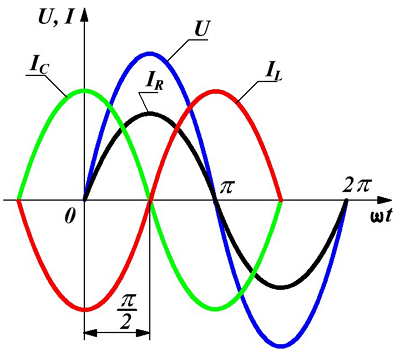
Напряжение и токи при параллельном соединении.

Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения

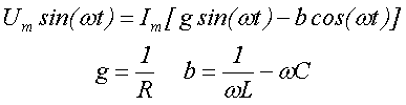
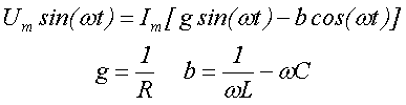
где g – активная проводимость, b – реактивная проводимость.

Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.

Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы

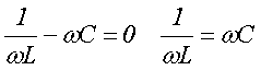
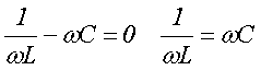
Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.

Определим зависимость между напряжением и силой тока в параллельной цепи

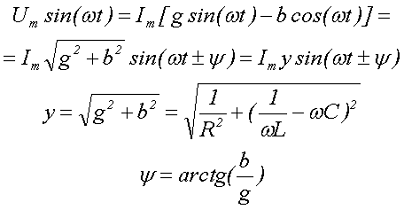
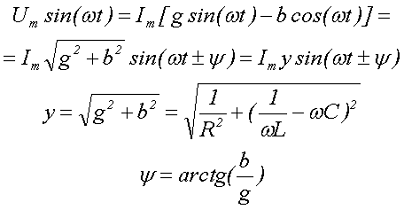
где y – полная проводимость,

ψ – разность фаз между напряжением и током в цепи.

Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид

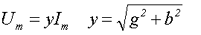
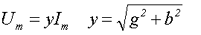
где U_m­ – амплитудное значение переменного напряжения,

I_m­ – амплитудное значение переменного тока,

y – полная проводимость цепи.

Чему равна мощность в цепи при синусоидальном напряжении?

Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения. Мгновенная мощность в цепи будет равна

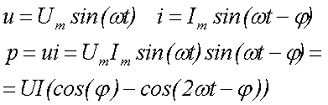
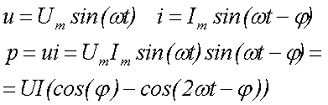
Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).

Теперь определим среднее значение мощности за период или активную мощность, которая будет равна

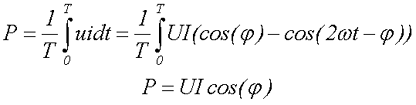
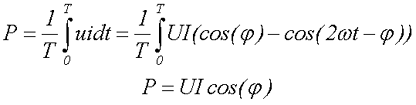
где U – действующее значение переменного напряжения,

I – действующее значение переменного тока,

cos(φ) – коэффициент мощности.

Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.

При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.