Катушки индуктивности последовательно и параллельно
Содержание : Катушки индуктивности последовательно и параллельноЧто такое индукторы?ИндукторыИндукторы — это не что иное, как магнитные накопители энергии. Физически это катушка из проводящего провода, намотанная на твердый сердечник или без сердечника. Последний называется индуктор с воздушным сердечником.
Когда ток течет через индуктор, он создает магнитное поле. Скручивание большого количества проволоки увеличивает силу магнитного поля. Направление магнитного поля определяется с помощью правило большого пальца правой руки.
Когда ток впервые начинает течь через катушку, магнитное поле начинает расширяться, затем через некоторое время оно стабилизируется и сохраняет некоторое количество магнитной энергии. Когда поле постепенно схлопывается, магнитная энергия снова превращается в электрическую. {2}A}{l}[/Latex] ( Отвечать )
{2}A}{l}[/Latex] ( Отвечать )
Как рассчитать катушки индуктивности последовательно?Добавление индукторов последовательно | Два индуктора последовательноа Катушки индуктивности в последовательной цепиВ случае двух катушек изменение тока в одной катушке вызывает ЭДС в соседней катушке. Этот инцидент известен как взаимная индукция, а это свойство первичной катушки называется взаимной индуктивностью.
При последовательном соединении катушек индуктивности из диаграммы видно, что ток в каждой катушке индуктивности одинаков. Таким образом, полное падение напряжения на катушках индуктивности является суммой падений напряжения на каждой отдельной катушке индуктивности. Предположим, L — полная индуктивность цепи. Итак, полное падение напряжения VВсего будет
VВсего V =1 + V2
V1 и V2 — это падение напряжения через отдельный индуктор соответственно.
По правилу Кирхгофа мы можем написать,
[Латекс] V_ {Всего} — (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} t} = 0 [/Latex]
[Латекс] V_ {Всего} = (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/Latex]
[Латекс] L \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2}) \ frac {\ mathrm {d} i} {\ mathrm {d} т}[/латекс]
L = L1+L2
( Отвечать )
Эквивалентная индуктивность последовательно включенных индукторов | Формула для последовательного индуктораПодобно ранее найденному уравнению для двух индукторов, если мы соединим последовательно n индукторов с собственной индуктивностью L1, L2, L3,… ..Ln при последовательном включении эквивалентная индуктивность для катушек индуктивности в последовательной цепи будет,
Leq = л1 + L2 + L3 +… .. + Ln
( Отвечать )
Как рассчитать индукторы параллельно?Катушки индуктивности параллельно Катушки индуктивности параллельноПри параллельном подключении из диаграммы можно сделать вывод, что полный ток, протекающий по цепи, является суммой тока отдельной катушки. {-1}[/Latex] ( Отвечать )
{-1}[/Latex] ( Отвечать )
Для приведенных выше выводов мы предположили, что между индукторами нет взаимной индуктивности. Теперь, если индукторы соединены таким образом, что магнитное поле, создаваемое одним, влияет на индуктивность других, говорят, что индукторы «связаны между собой».
Связанные индукторы последовательноМагнитные поля индукторов могут либо помогать, либо противодействовать друг другу в зависимости от ориентации катушек. Муфты можно разделить на два типа:
Серийный вспомогательный тип муфты :В этом типе связи магнитные поля индукторов имеют одинаковое направление. Таким образом, токи, протекающие через индукторы, также имеют одинаковое направление. Для двух индукторов с самоиндукцией L1 и я2 и взаимной индуктивности M можно записать
Общая наведенная ЭДС = Самоиндуцированные ЭДС в L1 и я2 + наведенная ЭДС в одной катушке из-за изменения тока в другой для взаимной индуктивности
[Латекс] V = V_ {1} + V_ {2} + V_ {M_ {12}} + V_ {M_ {21}} = L_ {1} \ frac {\ mathrm {d} i} {\ mathrm {d } t} + L_ {2} \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} + M \ frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2} + 2M) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/ Латекс]
Следовательно,
Компания эквивалентная индуктивность = L1+ L2 + 2M
Последовательно противоположный тип сцепления:В этом типе связи магнитные поля индукторов имеют противоположное направление. Таким образом, направления токов противоположны друг другу. Для двух катушек индуктивности с собственной индуктивностью L1 и L2 и взаимное индуктивность M, мы можем написать,
Таким образом, направления токов противоположны друг другу. Для двух катушек индуктивности с собственной индуктивностью L1 и L2 и взаимное индуктивность M, мы можем написать,
Общая наведенная ЭДС = Самоиндуцированные ЭДС в L1 и я2 + наведенная ЭДС в одной катушке из-за изменения тока в другой для взаимной индуктивности
[Латекс] V = V_ {1} + V_ {2} + V_ {M_ {12}} + V_ {M_ {21}} = L_ {1} \ frac {\ mathrm {d} i} {\ mathrm {d } t} + L_{2}\frac{\mathrm{d} i}{\mathrm{d} t} — M\frac{\mathrm{d} i}{\mathrm{d} t} — M\frac {\ mathrm {d} i} {\ mathrm {d} t} = (L_ {1} + L_ {2} — 2M) \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/ Латекс]
Следовательно, эквивалентная индуктивность = L1+ L2 -2M
Каким будет импеданс конденсатора и катушки индуктивности в последовательной LC-цепи?Импеданс конденсатора и катушки индуктивности в последовательном LC-контуре:последовательная LC-цепьДля вышеуказанного конденсатора и катушек индуктивности в последовательная схема, будем считать, что сопротивления нет. {2}}{2C}][/Latex]
{2}}{2C}][/Latex]
Для вышеуказанного конденсатора и катушек индуктивности в последовательная схема
Полный импеданс LC-цепи XLC=XL-XC если XL>XC
=XC-XL если XL<XC
Последовательные и параллельные индукторыКатушка индуктивности и конденсатор подключены к источнику переменного тока 120 В, 60 Гц. Для следующей LC-цепи найдите полное сопротивление и ток, протекающий по цепи.
Схема LCДанный:
L = 300 мГн C = 50 мкФ V = 120 В f = 50 Гц
Мы знаем, XL= 2πfL и XC= 1 / 2πfC
Подставляя данное значение L и C, получаем,
XL = 113 Ом
XC= 53 Ом
Следовательно, полное сопротивление Z = XL — ИКСC = 113 — 53 = 60 Ом
Ток в цепи, i = V / Z = 120/60 = 2 А
- LC-цепь состоит из индуктора L = 20 мГн и конденсатора C = 50 мкФ.
 Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.
Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.
Данный:
L = 20 мГн C = 50 мкФ Q0 = 10 мкКл
Полная энергия E = Q02/ 2C = (10 x 001) 2 / 2x 0.00005 = 1 Дж
Частота резонанса f = 1 / 2√LC = 1 / (2 x 3.14 x √ (20 x 0.001 x 0.00005)) = 159 Гц ( Отвечать )
Резистор и катушка индуктивности в последовательной цепи LRсерия LR цепьЦепи, содержащие резисторы и индукторы, известны как цепи LR. Когда мы подключаем источник напряжения, по цепи начинает течь ток. Теперь, если мы применим закон Кирхгофа, мы получим,
[Latex]V_{0}-iR – L\frac{\mathrm{d} i}{\mathrm{d} t}=0[/Latex] ( V0 напряжение источника)
[Латекс] V_ {0} = iR + L \ frac {\ mathrm {d} i} {\ mathrm {d} t} [/Latex]
[Латекс]\frac{di}{V_{0}-iR}=\frac{dt}{L}[/Latex]
Интегрируя обе стороны с пределом от i = 0 до I и t = 0 до t, получаем,
[Латекс]\frac{-\ln (V_{0}-iR) + \ln (V_{0})}{R}=\frac{t}{L}[/Latex]
[Латекс]\ln (\frac{V_{0}-iR}{V_{0}})=\frac{-Rt}{L}[/Latex]
[Латекс]\frac{V_{0}-iR}{V_{0}}=e^{\frac{-Rt}{L}}[/Latex]
Следовательно, [Latex]i=\frac{V_{0}}{R}(1-e^{\frac{-Rt}{L}})[/Latex] ( Отвечать )
Постоянная времени цепи LR? = L / R называется постоянной времени цепи LR
Импеданс катушки индуктивности и резистора последовательно | Импеданс цепи LRСопротивление и индуктивность — это компоненты, ответственные за полное сопротивление цепи LR. {2}}[/Latex] ( Отвечать )
{2}}[/Latex] ( Отвечать )
Батарея на 24 В удаляется из цепи, состоящей из резистора с сопротивлением 2 Ом и катушки индуктивности с индуктивностью 0.03 Н. Рассчитайте начальный ток при t = 0 секунд. Узнайте, сколько времени нужно, чтобы ток снизился до 50% от начального.
Если батарею внезапно вынуть из цепи, то потребуется некоторое время, прежде чем ток упадет до нуля.
При t = 0, i = V0/ R = 24/2 = 12 А
Постоянная времени ? = L / R = 0.03 / 2 = 0.015 секунды
я = я0e-t /? где я0 начальный ток перед замыканием переключателя
0.5 = е-t / 0.015
т / 0.015 = -ln (0.5)
t = 0.01 с ( Отвечать )
Резистор 2 Ом и катушка индуктивности 8 мГн соединены последовательно с источником питания 6 вольт. Сколько времени потребуется, чтобы ток стал 99.9% конечного тока?
Постоянная времени контура = L / R = 8 x 0. {2}}[/Latex] ( Отвечать )
{2}}[/Latex] ( Отвечать )
Последовательная цепь RLC состоит из резистора 30 Ом, катушки индуктивности 80 мГн и конденсатора 40 мкФ. На него подается напряжение питания переменного тока 120 В и 50 Гц. Узнайте ток в цепи.
решение:
Индуктивное сопротивление XL= 2πfL = 2 x 3.14 x 80 x 0.001 x 50 = 25.13 Ом
Емкостное реактивное сопротивление XC = 1 / 2πfC = 79.58 Ом
Полный импеданс, Z = √ {R2 + (XC — ИКСL)2} = √ {(30)2 + (79.58-25.13)2} = 62.17 Ом
Следовательно, ток в цепи, i = 120 / 62.17 = 1.93 А
- Выведите уравнение для тока в приведенной ниже схеме, где V = sin4t
Применяя к схеме закон Кирхгофа, можно записать
Sin4t — 3i — 2di / dt + Q / 0.5 = 0
Sin4t = 3i + 2di / dt + 2Q
Принимая дифференциацию с обеих сторон,
4cos4t = 3di / dt + 2d2i / dt2 +2 я (т)
я (t) + 3/2 (di / dt) + d2i / dt2 = 2cos4t Это необходимое уравнение для тока. ( Отвечать )
( Отвечать )
1. LC-цепь хранит полную энергию E. Максимальный заряд конденсатора составляет Q. Энергия, запасенная в катушке индуктивности, пока заряд конденсатора составляет Q / 2, составляет
- E
- Е / 2
- Е / 4
- 3E / 4 (ответ)
Решение: Общая энергия = E = Q2/ 2C
Общая энергия = EC + Ei
Когда заряд конденсатора составляет Q / 2, полная энергия,
Q2/ 2C = (Q / 2)2/ 2C + Ei
Ei = Q2/ 2C х (1-¼) = 3E / 4 ( Отвечать )
2. Если ток в одной катушке станет постоянным, какой ток будет протекать через соседнюю катушку?
- Двойник первой катушки
- Половина первой катушки
- Ноль (ответ)
- Бесконечность
Решение: ток индуцируется при изменении магнитного потока в катушке. Следовательно, если в одной катушке постоянный ток, поток не будет генерироваться, и ток в соседней катушке будет равен нулю.
Следовательно, если в одной катушке постоянный ток, поток не будет генерироваться, и ток в соседней катушке будет равен нулю.
3. Резистор на 7 Ом соединен последовательно с индуктором 32 мГн в индукторах в последовательной цепи. Если напряжение питания составляет 100 В, 50 Гц, рассчитайте падение напряжения на катушке индуктивности.
- 67 V
- 82 V (Отвечать)
- 54 V
- 100 V
Подробное решение проблемы:
Индуктивное сопротивление XL для схемы = 2 x 3.14 x 50 x 0.032 = 10 Ом
Полный импеданс Z = √(R2 + XL2) = √(72 + 102) = 12.2 Ом
Следовательно, ток в цепи = 100 / 12.2 = 8.2 А
Падение напряжения на катушке индуктивности = iXL = 8.2 х 10 = 82 В (Отвечать)
4. Найдите эквивалентный импеданс для бесконечной лестничной цепи, показанной ниже.
- j4 Ом
- j8 Ом
- j4 (√2 — 1) Ом
- j4 (√2 + 1) Ом (Отвечать)
Решение: для указанной выше бесконечной схемы предположим, что,
Z1 = j8 Ом и Z2 = j4 — j2 = j2 Ом
Если эквивалентный импеданс равен Z, то мы можем написать
Z = Z1 + (Я2 || Z) = Z1 + ЗЗ2/ Z + Z2
Z (Z + Z2 ) = Z1Z2 + ЗЗ1 + ЗЗ2
Z2 + j2Z = -16 + j8Z + j2Z
Z2 — j8Z + 16 = 0
Решая квадратное уравнение, получаем,
Z = j4 (√2 + 1) Ом (Отвечать)
5.
 Собственная индуктивность соленоида 5 мГн. Катушка имеет 10 витков. Какой будет индуктивность катушки, если количество витков увеличится вдвое?
Собственная индуктивность соленоида 5 мГн. Катушка имеет 10 витков. Какой будет индуктивность катушки, если количество витков увеличится вдвое?- 10 мГн
- 5 мГн
- 20 мГн (Отвечать)
- 30 мГн
Решение: Собственная индуктивность соленоида с N витками и площадью поперечного сечения равна = μ.0N2А / л
Здесь μ0 х 100 х А / л = 5
μ0А / л = 1/20
Если количество витков удвоить, то новая собственная индуктивность = μ0A / лк N ‘2 = 1/20 x (20) 2 = 20 мГн (Отвечать)
Часто задаваемые вопросы | Краткое примечаниеКак добавить катушки индуктивности последовательно и параллельно? | Катушки индуктивности последовательно и параллельно:
Ответ :
Последовательно сумма собственной индуктивности всех катушек индуктивности является общей индуктивностью цепи. При параллельном подключении сумма, обратная величине всех собственных индуктивностей, является обратной величиной полной индуктивности.
При параллельном подключении сумма, обратная величине всех собственных индуктивностей, является обратной величиной полной индуктивности.
Как добавление катушек индуктивности в цепь влияет на ток?
Ответ :
Катушки индуктивности, добавленные последовательно, имеют один и тот же ток. Таким образом, общая напряжение цепи выше, чем напряжения отдельных катушек индуктивности.
Что такое индукторы с дифференциальной связью?
Ответ :
Это другое название серии встречных индукторов, в которых магнитные потоки, создаваемые индукторами, противоположны по направлению. Общая индуктивность индукторов этого типа равна сумме собственной индуктивности индукторов — 2 x взаимной индуктивности.
Какова взаимная индуктивность двух последовательно соединенных катушек?
Ответ :
Взаимная индуктивность двух катушек с железным сердечником с витками N1 и н2, площадь поперечного сечения A, длина L и проницаемость μr [Latex]M = \frac{\mu {0}\mu {r}N_{1}N_{2}A}{L}[/Latex]
Что такое серийный индукционный фильтр?
Ответ :
Серийный индуктор фильтр Катушка индуктивности, включенная последовательно между нагрузкой и выпрямителем. Он называется фильтром, так как блокирует переменный ток и пропускает постоянный ток.
Он называется фильтром, так как блокирует переменный ток и пропускает постоянный ток.
Индуктор на 1 генри включен последовательно с конденсатором на 1 мкФ. Найдите сопротивление при частоте 50 Гц и 1000 Гц.
Ответ :
Импеданс, Z = XL — ИКСC
XC при частоте 50 Гц = 1 / 2πf1C = 3183 Ом
XC при частоте 1000 Гц = 1 / 2πf2C = 159 Ом
XL при частоте 50 Гц = 2πf1L = 314 Ом
XL при частоте 1000 Гц = 2πf1L = 6283 Ом
Следовательно, импеданс Z1 при частоте 50 Гц = 6283 — 159 = 6124 Ом
сопротивление Z2 при частоте 1000 Гц = | 314 — 3183 | = 2869 Ом.
Радио для всех — Индуктивности
Основные понятия.
Индуктивность — это способность извлекать энергию из источника и сохранять ее в виде магнитного поля. Это свойство проводника, предотвращающее резкие изменения текущего через него тока. Например, если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется. Если ток в катушке уменьшается, магнитное поле сжимается. Однако сжатие магнитного поля индуцирует в катушке напряжение, которое поддерживает ток. Таким образом, индуктивность позволяет энергии сохраняться в виде магнитного поля, зависящего от тока. Когда ток уменьшается, уменьшается и магнитное поле, возвращая в цепь запасенную энергию.
Например, если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется. Если ток в катушке уменьшается, магнитное поле сжимается. Однако сжатие магнитного поля индуцирует в катушке напряжение, которое поддерживает ток. Таким образом, индуктивность позволяет энергии сохраняться в виде магнитного поля, зависящего от тока. Когда ток уменьшается, уменьшается и магнитное поле, возвращая в цепь запасенную энергию.
Правило:
ЭДС самоиндукции имеет такое направление, что в любой момент оно противодействует приложенному извне напряжению.
Закон электромагнитной индукции мы расматривали в статье о магнетизме Важно понимать, что по этому закону в проводнике возникает ЭДС самоиндукции. Ленц первый изучил это явление и сформулировал правило. При увеличении тока силовые магнитные линии как будто „выходят» из оси проводника и концентрическими окружностями распространяются наружу, а ЭДС самоиндукции имеет направление, противоположное увеличивающемуся току.
Эмилий Ленц
(1804-1865)
Российский физик и электротехник.
Один из основоположников руcской геофизики
При уменьшении тока силовые магнитные линии концентрическими окружностями возвращаются к оси проводника, а ЭДС самоиндукции имеет направление согласно уменьшающемуся току.
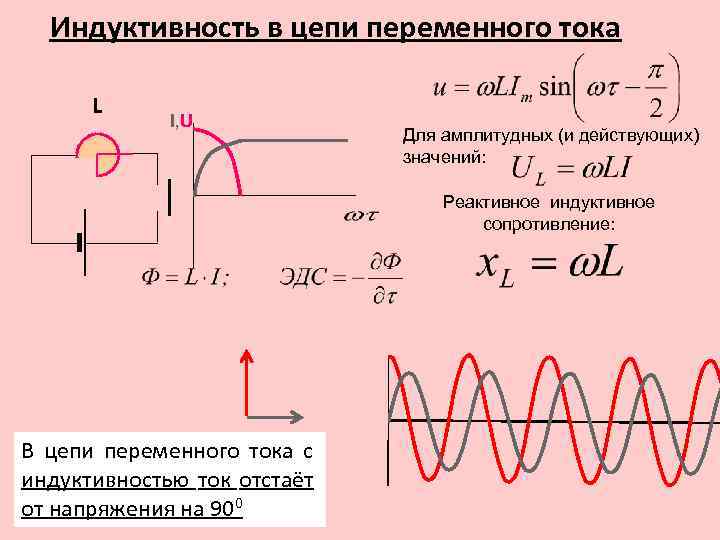
С помощью известных величин попробуем найти индуктивность. Магнитная индукция (В) создаваемая током, пропорциональна силе тока. Магнитный поток(Ф) пропорционален (В).
Значит
и можно утверждать, что
искомая индуктивность.
Подробнее
Единица, которой измеряется индуктивность называется генри (Гн). Она названа в честь американского физика Джозефа Генри.
Джозеф Генри
(1797-1878)
Американский физик.
Установил колебательный характер
разряда конденсатора
Генри — это такая индуктивность, которая требуется для индуцирования электродвижущей силы в 1 вольт при изменении тока в проводнике со скоростью 1 ампер в секунду. Это большая единица, значительно чаще используются миллигенри (мГн) и микрогенри (мкГн).
Это большая единица, значительно чаще используются миллигенри (мГн) и микрогенри (мкГн).
1мГ= 1 миллигенри = 0,001Г
1мкГ=1 микрогенри = 0,000001Г
Катушки индуктивности.
В радиолюбительской и профессиональной практике широкое применение приобрели катушки индуктивности. Катушка индуктивности — это устройство, имеющее определенную индуктивность. Состоит из провода, намотанного на сердечник, и классифицируется по материалу сердечника. Сердечник катушки может быть либо магнитным, либо немагнитным.
Катушки могут иметь как постоянную, так и изменяемую индуктивность. Катушки с переменной индуктивностью содержат подстроечный сердечник. Максимальная индуктивность регистрируется, когда сердечник полностью введен в катушку.
Катушка индуктивности.
Безкаркасные катушки (без сердечника), используются в тех случаях, когда индуктивность не превышает 2-5 миллигенри. Они наматываются на керамические или композитные сердечники. Сердечники из феррита или порошкообразного железа используются для индуктивностей до 200 миллигенри. Тороидальные сердечники имеют кольцеобразную форму и позволяют получить высокую индуктивность при малых размерах. Магнитное поле сосредоточено внутри сердечника. Экранированные индуктивности заключены в корпус (экран), сделанный из магнитного материала для защиты их от влияния внешних полей.
Условное обозначение катушек.
Обозначение | Реальный вид |
Дополнительные символы
Основные размеры катушек.
В однослойной катушке диаметр D представляет собой диаметр окружности, образуемой осевой линией активного сечения провода. На высоких частотах этот диаметр принимают равным внутреннему диаметру витков (диаметр каркаса или d1).
На высоких частотах этот диаметр принимают равным внутреннему диаметру витков (диаметр каркаса или d1).
Длина катушки l является расстоянием между осевыми линиями крайних витков. Обычно d0— диаметр провода в изоляции. Шаг намотки τ— расстояние между осевыми линиями смежных витков. Из-за неплотности, для расчетов вводится поправочный коэффициент. α — коэффициент неплотности. Он помогает найти длину l катушки с намотанным проводом.Значения коэффициента смотрим в табличке.
Значения размеров многослойной катушки определяются величиной наружного диаметра D, внутреннего D0. Радиальной глубиной t и длиной намотки l. Dср — средний диаметр катушки. N — число витков.
Все размеры выражаются в миллиметрах.
более точно
Типы намоток катушек.
| Применяемые виды намотки можно разделить на однослойные и многослойные. При однослойной намотке витки располагаются на цилиндрической поверхности каркаса в один слой. При плотном расположении витков, получается сплошная однослойная намотка. При некотором расстоянии витков друг от друга — намотка с «шагом». Многослойные намотки могут быть разделены на простые и сложные. К простым относятся рядовая (витки на каркас укладываются правильными рядами) и «внавал» (мотаются без определенной закономерности). К сложным многослойным намоткам можно отнести универсальные, секционированные и пирамидальные. При универсалной намотке витки не располагаются параллельно друг к другу, а идут попеременно от одного края к другому, пересекаясь под некоторым углом. такое расположение дает катушке высокую механическую прочность без специальных каркасов. Виток — угол намотки провода вокруг оси катушки. Повторяемость процесса намотки универсальных катушек характеризуется циклом. он соответствует такому углу намотки провода вокруг оси катушки, за который провод возвращается в свое исходное положение на край катушки. Так как витки располагаются параллельно друг другу, то каждый последующий виток не может точно возратиться в свое исходное положение, а приходит в него или несколько позже, или несколько раньше. Пирамидальная намотка отличается малой собственной емкостью. Объясняется это тем, что в данной намотке смежными являются витки с наибольшей разностью потенциалов 9между ними). Выполняется с любым числом слоев. Чаще используется двухслойная намотка (для прочности). |
Далее материалы по теме
Характеристики и маркировка индуктивностей
8.
 8 Индуктивность – Колледж Дугласа, физика 1207
8 Индуктивность – Колледж Дугласа, физика 1207Глава 8 Электромагнитная индукция, цепи переменного тока и электрические технологии
Резюме
- Расчет индуктивности катушки индуктивности.
- Рассчитайте энергию, запасенную в катушке индуктивности.
- Рассчитайте ЭДС, создаваемую катушкой индуктивности.
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9.0017 индуктивность .
Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе.
Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, ΔI/Δt, , как на причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в форме уравнения как
,
, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют меньшее значение M по сравнению с катушками трансформатора в главе 23.7. (H), после Джозефа Генри. То есть 1 Гн = 1 Ом•с.
Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют меньшее значение M по сравнению с катушками трансформатора в главе 23.7. (H), после Джозефа Генри. То есть 1 Гн = 1 Ом•с.
Природа здесь симметрична. Если мы изменим ток I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, которая определяется как
,
, где M то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью M .
Большая взаимная индуктивность M может быть желательной или нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)
Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)
Самоиндукция , действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока ΔI через прибор. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается
,
, где L — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.
Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.
Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшой L , например, путем встречной обмотки катушек, как показано на рис. 2.
Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 H , через которое протекает ток 10 A . Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная emf = -L (Δ I/Δ t) , будет противодействовать изменению. Таким образом, будет индуцироваться ЭДС, равная ЭДС = -L (ΔI/Δt) = (1,0 Гн)[(10 А)/(1,0 мс) ] = 10 000 В. Положительный знак означает, что это большое напряжение в том же направлении, что и ток, против его уменьшения. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.
Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная emf = -L (Δ I/Δ t) , будет противодействовать изменению. Таким образом, будет индуцироваться ЭДС, равная ЭДС = -L (ΔI/Δt) = (1,0 Гн)[(10 А)/(1,0 мс) ] = 10 000 В. Положительный знак означает, что это большое напряжение в том же направлении, что и ток, против его уменьшения. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.
Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)
(Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)
Можно рассчитать L для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность L обычно заданное количество. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется по закону индукции Фарадея как ЭДС = -N (Δφ/Δt) , а по определению самоиндукции как ЭДС = – (Δφ/Δt) . Приравнивание этих результатов дает
Приравнивание этих результатов дает
.
Решение для L дает
.
Это уравнение для собственной индуктивности L устройства всегда справедливо. Это означает, что собственная индуктивность L зависит от того, насколько эффективен ток в создании потока; чем эффективнее, тем больше Δφ/ΔI .
Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь соленоида A фиксирована, изменение потока равно Δφ = ΔAB = A ΔB . Чтобы найти ΔB , заметим, что магнитное поле соленоида определяется выражением . (Здесь , где N — количество витков и длина соленоида.) Изменяется только ток, так что . Замена Δφ на дает
.
Это упрощается до
(соленоид)
Это собственная индуктивность соленоида с площадью поперечного сечения A и длиной . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.
Пример 1. Расчет собственной индуктивности соленоида среднего размера
Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.
Стратегия
Это прямое применение , поскольку все величины в уравнении, кроме L , известны.
Решение
Используйте следующее выражение для собственной индуктивности соленоида:
Площадь поперечного сечения в этом примере равна , N дается 200, а длина 0,100 м. Мы знаем, что проницаемость свободного пространства равна . Подстановка их в выражение для L дает
.
Обсуждение
Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определять, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье». ) См. рис. 5.
) См. рис. 5.
Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что энергия, запасенная в катушке индуктивности E ind равна
Это выражение похоже на выражение для энергии, запасенной в конденсаторе.
Пример 2. Расчет энергии, запасенной в поле соленоида
Сколько энергии хранится в катушке индуктивности 0,632 мГн из предыдущего примера, когда через нее протекает ток 30,0 А?
Стратегия
Энергия определяется уравнением и всеми величинами, кроме E ind известны.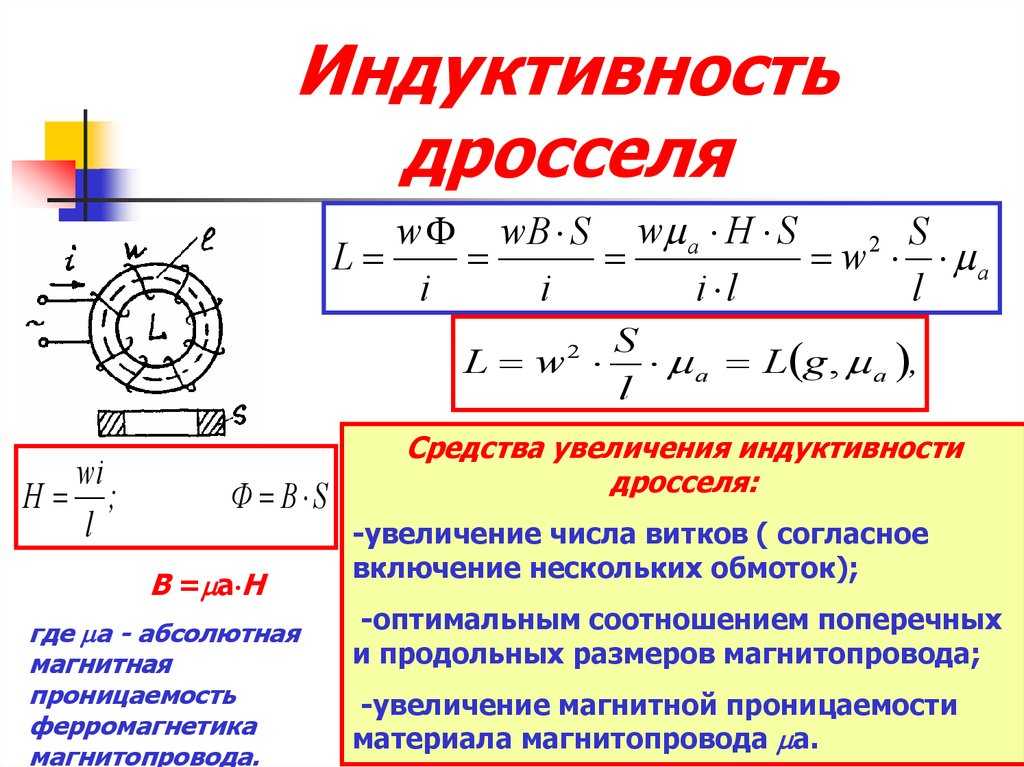
Решение
Подстановка значения L из предыдущего примера и заданного тока в дает
Обсуждение
Этого количества энергии, безусловно, достаточно, чтобы вызвать искру при внезапном отключении тока . Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.
- Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
- Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
- Изменение тока ΔI/Δt в одном индуцирует ЭДС эдс 2 во втором:
,
, где M определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.
- Симметрично, изменение тока ΔI/Δt через второе устройство индуцирует ЭДС ЭДС 1 в первом:
,
, где M — та же взаимная индуктивность, что и в обратном процессе.

- Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
- Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
- Устройство называется катушкой индуктивности, а ЭДС, индуцируемая в нем изменением тока через него, равна
,
, где L — собственная индуктивность катушки индуктивности, а ΔI/Δt — скорость изменения тока через него. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.
- Единицей собственной и взаимной индуктивности является генри (Гн), где .
- Собственная индуктивность L катушки индуктивности пропорциональна степени изменения магнитного потока в зависимости от тока. Для катушки индуктивности N-витка ,
- Самоиндукция соленоида
(соленоид)
где N — число витков в соленоиде, A — площадь поперечного сечения, длина и проницаемость свободного пространства.

- Энергия, запасенная в катушке индуктивности E ind
.
Задачи и упражнения
1: Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?
2: Если две катушки, расположенные рядом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?
3: Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?
4: Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?
5: Начиная с , покажите, что единицы индуктивности равны .
6: Фотовспышки заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?
7: Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?
8: (a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?
9: Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?
а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?
10: Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?
11: Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению. Каково значение собственной индуктивности?
12: Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?
13: Integrated Concepts
Очень большой сверхпроводящий соленоид, такой как тот, который используется в МРТ, хранит 1,00 МДж энергии в своем магнитном поле, когда 100 А течет. а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какой прирост температуры произойдёт, если вся накопленная энергия пойдет на нагрев 1000 кг магнит, учитывая его среднюю удельную теплоемкость 200 Дж/кг • o C ?
а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какой прирост температуры произойдёт, если вся накопленная энергия пойдет на нагрев 1000 кг магнит, учитывая его среднюю удельную теплоемкость 200 Дж/кг • o C ?
14: необоснованные результаты
A 25,0 Г дроссель имеет 100 A тока, отключенного через 1,00 мс. (а) Какое напряжение индуцируется, чтобы противостоять этому? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
- индуктивность
- свойство устройства, описывающее, насколько эффективно оно создает ЭДС в другом устройстве
- взаимная индуктивность
- насколько эффективно пара устройств индуцирует ЭДС друг в друге
- Генри
- единица индуктивности; 1 Гн = 1 Ом•с
- самоиндукция
- насколько эффективно устройство создает ЭДС само по себе
- индуктор
- устройство со значительной собственной индуктивностью
- энергия, запасенная в катушке индуктивности
- не требует пояснений; рассчитано по
Электроника | Бесплатный полнотекстовый | Расчет индуктивности однослойной планарной спиральной катушки
1.
 Введение
ВведениеБлагодаря простоте реализации спиральная катушка нашла широкое применение во многих электромагнитных приложениях, начиная от высокочастотной радиочастотной идентификации (RFID) [1] и заканчивая относительно низкочастотная беспроводная передача энергии [2,3,4]. Для успешного применения в этих приложениях требуется точное моделирование спиральной катушки. Для решения этой проблемы было проделано много работ. Некоторые из них кратко рассмотрены в этой статье.
В [5,6,7] собственная индуктивность плоской спиральной катушки вычисляется путем рассмотрения ее как группы концентрических окружностей. Поэтому всегда существует некоторая погрешность между вычисленным и результатом измерения. Кроме того, для получения собственной индуктивности плоской спиральной катушки требуется вычисление индуктивностей каждой окружности и взаимных индуктивностей между ними. Следовательно, вычислительная сложность увеличивается.
Самоиндукция спиральной катушки аппроксимируется с помощью формулы Уилера или ее модифицированной формы [8,9]. Однако в этих формулах не учитывался один из параметров, влияющих на индуктивность: диаметр провода. Поэтому точность формул снижается при изменении диаметра проволоки спирального витка. Более того, точная деталь их вывода не установлена, и вместо аналитического метода индуктивность вычисляется эмпирически.
Однако в этих формулах не учитывался один из параметров, влияющих на индуктивность: диаметр провода. Поэтому точность формул снижается при изменении диаметра проволоки спирального витка. Более того, точная деталь их вывода не установлена, и вместо аналитического метода индуктивность вычисляется эмпирически.
Программное обеспечение ANSYS Maxwell 3-D — один из лучших методов определения собственной индуктивности спиральной катушки любой формы; однако моделирование требует значительного времени расчета.
Для решения этого вопроса в статье предложено точное выражение собственной индуктивности плоской спиральной катушки, включающее все параметры, влияющие на индуктивность. Кроме того, используя интегральную формулу Неймана, этот метод вычисляет индуктивность плоской спиральной катушки, рассматривая всю спираль, не предполагая ее как группу концентрических окружностей. В результате вычислительная сложность формулы снижается.
Для проверки точности предложенного метода результаты расчета сравниваются с результатом моделирования и общепринятыми формулами, которые показывают хорошее совпадение. Для экспериментальной проверки несколько катушек с разными геометрическими параметрами изготавливаются на бобине, специально разработанной с помощью 3D-принтера. Наконец, сравнение результатов расчета и измерений подтверждает точность предложенного метода.
Для экспериментальной проверки несколько катушек с разными геометрическими параметрами изготавливаются на бобине, специально разработанной с помощью 3D-принтера. Наконец, сравнение результатов расчета и измерений подтверждает точность предложенного метода.
Структура документа следующая: Расчет собственной индуктивности плоской катушки обсуждается в Разделе 2. Раздел 3 проверяет результаты расчета с помощью другого традиционного метода и моделирования с использованием метода конечных элементов (МКЭ). Экспериментальная проверка результата расчета показана в разделе 4. Наконец, в разделе 5 подводятся итоги.
2. Расчет собственной индуктивности плоской спиральной катушки
Самоиндукцию круглой плоской спиральной катушки можно рассчитать, решив интегральную формулу Неймана для взаимной индуктивности между двумя катушками [10]. Геометрические параметры плоской спирали, лежащие в плоскости x–y, показаны на рис. 1. Предполагается, что по спиральной катушке течет постоянный ток.
На рис. 1 R — внешний радиус спиральной катушки. θ — угол поворота R относительно оси x. w показывает диаметр провода, а s — расстояние между витками.
Внешний радиус R определяется с помощью уравнения плоской спиральной катушки.
где R i — внутренний радиус катушки, а — коэффициент шага, влияющий на расстояние между каждым витком.
Н – количество витков спиральной катушки.
Когда радиус кривизны спиральной катушки с одинаковой площадью поперечного сечения больше радиуса проводника катушки, самоиндукция плоской спиральной катушки будет равна взаимной индуктивности между исходной спиральной катушкой и ее фиктивной катушка размещена на расстоянии среднего геометрического расстояния (GMD) проводника [11]. Среднее геометрическое расстояние для литцендрата круглого сечения приведено в уравнении (4)
g представляет собой среднее геометрическое расстояние, а r — радиус проводника.
Радиус кривизны (внешний радиус) исходного R 1 и его фиктивного спирального витка R 2 показан в уравнениях (5) и (6).
θ 1 и θ 2 — угол поворота исходного и фиктивного витков спирали соответственно.
Интегральная формула Неймана может быть представлена уравнением (7).
где μ 0 — вакуумная проницаемость, dl 1 и dl 2 — составляющие линии, а R — расстояние между dl 1 и dl 2 . Индуктивность плоской катушки можно рассчитать, оценив параметры в уравнении (7).
Скалярное произведение между dl 1 и dl 2 дано в уравнении (10).
Расстояние R можно представить с помощью формулы косинуса.
Подставив уравнения (10) и (11) в уравнение (7), получим точное уравнение собственной индуктивности плоской спиральной катушки, как показано в уравнении (12)
Уравнение (11) содержит все параметры, влияющие на индуктивность, такие как внутренний и внешний радиус спиральной катушки, число витков, диаметр провода и расстояние между витками. Влияние каждого параметра на индуктивность подробно обсуждается в следующих разделах.
Влияние каждого параметра на индуктивность подробно обсуждается в следующих разделах.
3. Сравнение с моделированием и обычными методами
Для проверки предлагаемого метода индуктивности нескольких спиральных катушек с различными геометрическими параметрами рассчитываются с использованием уравнения (12). Индуктивности также рассчитываются с использованием обычного метода и метода конечных элементов (МКЭ). По отношению к результату моделирования вычисляются погрешность расчета и условные результаты. Ошибка вычисляется как RFem-RcRFem×100, где R Fem представляет результат моделирования, а R c показывает расчетный или обычный результат.
Моделирование МКЭ проводится с использованием программного обеспечения ANSYS Maxwell 15. Тип решения — магнетостатический. Сетка назначается как длина на основе катушки и ее границы. Длина элемента является значением по умолчанию. Ток назначается равномерно по поперечному сечению катушки для простоты. Существует множество традиционных методов расчета спиральной катушки [8,9].,12]. В большинстве этих методов использовалась модифицированная формула Уилера для расчета собственной индуктивности спиральной катушки. Некоторые из этих формул были выбраны для сравнения в данной работе и обсуждаются ниже.
Существует множество традиционных методов расчета спиральной катушки [8,9].,12]. В большинстве этих методов использовалась модифицированная формула Уилера для расчета собственной индуктивности спиральной катушки. Некоторые из этих формул были выбраны для сравнения в данной работе и обсуждаются ниже.
В [8] собственная индуктивность спиральной катушки аппроксимирована с использованием концепции среднего диаметра катушки, как показано в уравнении (13).
Собственная индуктивность спиральной катушки определяется исходя из эквивалентных плотностей тока и аппроксимации спирали [9]. Уравнение этого метода аппроксимации индуктивности спиральной катушки приведено в уравнении (16).
C i – зависимый коэффициент. Для спиральной катушки круглой формы значение C 1 равно 1, C 2 равно 2,46, C 3 равно 0,00 и C 4 равно 0,20.
Методом приближения Уилера вычисляется собственная индуктивность спиральной катушки [12]. Эта формула недействительна, когда расстояние между витками меньше диаметра проволоки и катушка имеет меньшее количество витков. Эта формула аппроксимации математически обозначена в уравнении (17) и представлена графически на рисунке 2.
Эта формула недействительна, когда расстояние между витками меньше диаметра проволоки и катушка имеет меньшее количество витков. Эта формула аппроксимации математически обозначена в уравнении (17) и представлена графически на рисунке 2.
Для расчета индуктивности однослойной круглой спиральной катушки в уравнении (18) используется модифицированная формула Гарольда А. Уилера.
где N — общее количество витков, w — диаметр провода, s — зазор между витками, а d в и d из — внутренний и внешний диаметр провода соответственно.
Уравнения (13), (16)–(18) получены с использованием формулы Уилера или ее модифицированной формы для расчета индуктивности спиральной катушки. Следовательно, собственная индуктивность плоской спиральной катушки будет одинаковой при использовании любой из этих формул, а значит, и их погрешность относительно предлагаемого метода будет одинаковой. Любая из этих формул может быть выбрана для сравнения с предлагаемым методом.
Сравнение индуктивности путем изменения каждого геометрического параметра обсуждается в следующем подразделе.
3.1. Изменение внешнего радиуса
Для различных внешних радиусов сравнивается поведение самоиндукции спирали для провода радиусом r = 1,8 мм, числом витков N = 10 и зазором между витками s = 4 мм. . Подробное сравнение показано на рисунке 3. На приведенном выше рисунке показано, что индуктивность катушки увеличивается, когда увеличивается внешний радиус или внешний диаметр катушки. Это можно объяснить определением индуктивности катушки.
Одним из факторов, от которых зависит индуктивность, является размер катушки. С увеличением размера катушки увеличивается и индуктивность. Индуктивность, полученная традиционным методом, ниже, чем результат расчета и моделирования. Таким образом, относительно результата моделирования ошибка традиционного метода выше, которая составляет около 16 %, по сравнению с ошибкой результата расчета, которая составляет менее 4 %. Таким образом, предлагаемый метод обеспечивает хорошую точность в отношении изменения внешнего радиуса.
Таким образом, предлагаемый метод обеспечивает хорошую точность в отношении изменения внешнего радиуса.
3.2. Изменение диаметра провода
На рис. 4 показано поведение индуктивности для диаметров провода 3 мм и 3,6 мм. Значения остальных параметров такие же, как показано в разделе 3.1. По сравнению с проводом большого диаметра индуктивность катушки меньшего диаметра выше в результате расчета и моделирования. Однако индуктивность остается постоянной при изменении диаметра провода во многих традиционных формулах, потому что эти формулы не учитывают диаметр провода. При использовании обычного метода для расчета индуктивности ошибка составляет менее 17 % для диаметра провода 3,6 мм и 20 % для w = 3,0 мм по сравнению с результатом моделирования, и ошибка увеличивается по мере уменьшения диаметра провода. Однако погрешность результата расчета для всех случаев составляет менее 4%, что подтверждает его точность.
3.3. Изменение числа витков
На рис. 5 показано сравнение расчета собственной индуктивности и обычных результатов при различном числе витков для R i = 10 мм, s = 4 мм и w = 3,6 мм. При увеличении числа витков катушки индуктивность возрастает. В обычных методах ошибка увеличивается с увеличением числа витков; однако он показал лучшую точность для меньшего количества витков по сравнению с результатом расчета. Можно сделать вывод, что обычная формула подходит для приложений, где требуется катушка с меньшим количеством витков. С другой стороны, погрешность результата расчета относительно результата МКЭ составляет менее 6 %, и точность сохраняется для всех случаев.
5 показано сравнение расчета собственной индуктивности и обычных результатов при различном числе витков для R i = 10 мм, s = 4 мм и w = 3,6 мм. При увеличении числа витков катушки индуктивность возрастает. В обычных методах ошибка увеличивается с увеличением числа витков; однако он показал лучшую точность для меньшего количества витков по сравнению с результатом расчета. Можно сделать вывод, что обычная формула подходит для приложений, где требуется катушка с меньшим количеством витков. С другой стороны, погрешность результата расчета относительно результата МКЭ составляет менее 6 %, и точность сохраняется для всех случаев.
3.4. Изменение зазора между витками
На рис. 6 показано поведение индуктивности спиральной катушки при различных зазорах между витками при w = 3,6 мм, R i = 10 мм и N = 10. Геометрия катушка расходуется с увеличением зазора между витками, увеличивая таким образом индуктивность. Погрешность резко возрастает с увеличением зазора между витками при использовании обычного метода. Однако результат расчета имеет погрешность менее 5% для увеличения зазора между витками. Таким образом, эти сравнения подтверждают справедливость результата расчета при различных вариациях геометрического параметра спирального витка.
Однако результат расчета имеет погрешность менее 5% для увеличения зазора между витками. Таким образом, эти сравнения подтверждают справедливость результата расчета при различных вариациях геометрического параметра спирального витка.
4. Экспериментальная проверка
Для экспериментальной проверки предложенного метода необходимо рассчитать некоторые параметры изготовления спиральной катушки, такие как длина провода и сопротивления постоянному току. Кроме того, необходимо учитывать тип проволоки, качество пайки и катушку для удержания проволоки. Каждый из этих факторов кратко обсуждается в следующем подразделе.
4.1. Выбор провода
Различные типы проводов используются для изготовления катушки, но в этом исследовании выбран литцендратный провод из-за его огромных преимуществ и многократного использования во многих приложениях, таких как кристаллическое радио, рамочная антенна, высокодобротные катушки, коммутация. электроснабжение и индукционное нагревательное оборудование. Литцендрат изготавливается путем соединения нескольких жил тонкой изолированной проволоки рядом друг с другом. Каждая изолированная жила несет часть тока, уменьшая воздействие на кожу и близость. Благодаря этим эффектам литцендраты уменьшают увеличение сопротивления на более высоких частотах [13]. Этот провод можно использовать примерно до 1 МГц. В этой работе для изготовления спиральных катушек используется 500 прядей литцендрата, каждая прядь диаметром 0,1 мм. Диаметр проволоки составляет около 3,6 мм, что определяется эмпирическим путем по уравнению (19).).
электроснабжение и индукционное нагревательное оборудование. Литцендрат изготавливается путем соединения нескольких жил тонкой изолированной проволоки рядом друг с другом. Каждая изолированная жила несет часть тока, уменьшая воздействие на кожу и близость. Благодаря этим эффектам литцендраты уменьшают увеличение сопротивления на более высоких частотах [13]. Этот провод можно использовать примерно до 1 МГц. В этой работе для изготовления спиральных катушек используется 500 прядей литцендрата, каждая прядь диаметром 0,1 мм. Диаметр проволоки составляет около 3,6 мм, что определяется эмпирическим путем по уравнению (19).).
где D e — расчетный диаметр литцендрата, D s — диаметр одной жилы, а N s — общее количество прядей.
4.2. Качество пайки
Диаметр провода, который является одним из факторов, влияющих на индуктивность, может быть уменьшен во время пайки. Поэтому для качественной пайки необходимы надлежащий процесс и меры предосторожности. Температура припоя (свинца) должна равномерно распределяться внутри паяльной ванны, при этом лучше выбирать припой с меньшим количеством примесей. Температура пайки зависит от типа и ширины проволоки. Таким образом, температуру следует регулировать и проверять термометром. Наконец, требуется специальное приспособление и соответствующий набор для пайки, как показано на рис. 7.
Температура припоя (свинца) должна равномерно распределяться внутри паяльной ванны, при этом лучше выбирать припой с меньшим количеством примесей. Температура пайки зависит от типа и ширины проволоки. Таким образом, температуру следует регулировать и проверять термометром. Наконец, требуется специальное приспособление и соответствующий набор для пайки, как показано на рис. 7.
4.3. Расчет длины провода и сопротивления провода
Длина провода пропорциональна его сопротивлению постоянному току. Поэтому важно рассчитать длину провода и сопротивление. Общая длина и сопротивление провода могут быть рассчитаны по уравнениям (20) и (21). Кроме того, расчетная и фактическая длина и сопротивление постоянному току провода показаны на рис. 8а,б. Сопротивление постоянному току измеряется с помощью Gwinstek LCR-6020.
где l длина провода; σ постоянная, ее значение равно 58 000; n — количество прядей; r — радиус одной нити.
4.4. Бобина
Для удержания проволоки спиральной катушки с помощью 3D-принтера изготавливаются различные бобины с разным диаметром проволоки, количеством витков, расстоянием между витками и внешним радиусом. Нить для печати была PLA (полимолочная кислота). На рис. 9а,б показаны катушка и спиральная катушка с катушкой.
4.5. Экспериментальный результат
Для проверки предлагаемого метода изготавливаются три случайные катушки разных размеров, и их индуктивность измеряется с помощью Gwinstek LCR-6020 m. Частота тестирования для этого измерения составляет 20 кГц. Наконец, результаты измерений сравниваются с результатом расчета, и их результаты представлены в таблице 1. Кроме того, результаты измерений также показаны на рисунке 10.
Из таблицы 1 видно, что результаты расчета хорошо согласуются с результатом измерений. Относительная ошибка составляет менее 5%.
5. Выводы
В статье представлен новый способ вычисления индуктивности однослойной плоской спирали. Используя принцип среднего геометрического расстояния, предлагаемый метод определяется путем решения формулы Неймана для взаимной индуктивности между двумя катушками. Численно рассчитаны индуктивности различных размеров спиральных катушек с различными внешними радиусами, числом витков, диаметром проволоки и зазором между витками. Результаты расчетов проверяются моделированием, экспериментальными и общепринятыми формулами. Погрешность результатов расчета составляет менее 5 % для всех случаев по сравнению с общепринятой формулой, которая составляла более 20 %. Более того, предлагаемый метод содержит все параметры, влияющие на индуктивность. Однако традиционные формулы не учитывали все параметры, что приводило к ошибочным результатам.
Используя принцип среднего геометрического расстояния, предлагаемый метод определяется путем решения формулы Неймана для взаимной индуктивности между двумя катушками. Численно рассчитаны индуктивности различных размеров спиральных катушек с различными внешними радиусами, числом витков, диаметром проволоки и зазором между витками. Результаты расчетов проверяются моделированием, экспериментальными и общепринятыми формулами. Погрешность результатов расчета составляет менее 5 % для всех случаев по сравнению с общепринятой формулой, которая составляла более 20 %. Более того, предлагаемый метод содержит все параметры, влияющие на индуктивность. Однако традиционные формулы не учитывали все параметры, что приводило к ошибочным результатам.
В этом исследовании индуктивность однослойной спиральной катушки рассчитывается для равномерного протекания тока в проводе. Однако индуктивность может быть разной для неоднородных токов. В этом случае она требует дальнейшего исследования и может быть учтена в дальнейшей работе.
Вклад авторов
И.Х. предложил теоретическую модель и провел эксперимент; Д.-К.В. пересмотрела проект и дала указания. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Это исследование не получило внешнего финансирования.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Ссылки
- Liu, Y.; Терри, Т.Ю. Антенна с сопряженной планарной катушкой (CPC) в качестве датчика смещения для меток NFC или HF RFID. В материалах Международной конференции IEEE по RFID (RFID) 2020 г., Орландо, Флорида, США, 5–9 октября 2020 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2020 г.; стр. 1–6. [Google Scholar]
- Ифтихар Х.; Ву, Д.-К. Упрощенный расчет взаимной индуктивности плоской спиральной катушки для беспроводных приложений питания. Датчики 2022 , 22, 1537. [Google Scholar] [CrossRef] [PubMed]
- Шахид, Х.
 ; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Energies 2020 , 13, 3119. [Google Scholar] [CrossRef]
; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Energies 2020 , 13, 3119. [Google Scholar] [CrossRef] - Young, D.J. Беспроводное питание и телеметрия данных для биомедицинских имплантатов. В материалах ежегодной международной конференции IEEE Engineering in Medicine and Biology Society 2009 г., Миннеаполис, Миннесота, США, 3–6 сентября 2009 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2009 г.; стр. 3221–3224. [Google Scholar]
- Чан, Х.Л.; Ченг, KWE; Сутанто, Д. Упрощенная формула Неймана для расчета индуктивности спиральной катушки. В материалах Восьмой международной конференции по силовой электронике и приводам с регулируемой скоростью 2000 г. (публикация IEE Conf. No.475), Лондон, Великобритания, 18–19 сентября 2000 г.; стр. 69–73. [Google Scholar]
- Рам Рахьяни, А.К.; Шахриар, М .; Mu, C.
 Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed] - Li, X.; Ханру, З .; Фей, П.; Ян, Л .; Тяньян, Ю .; Поклон.; Dongming, F. Беспроводная магнитно-резонансная система передачи энергии для микроимплантируемых медицинских датчиков. Датчики 2012 , 12, 10292–10308. [Google Scholar] [CrossRef] [PubMed]
- Jie, L.; Костинетт, Д. Анализ и разработка последовательной саморезонансной катушки для беспроводной передачи энергии. В материалах конференции и выставки IEEE Applied Power Electronics Conference and Exposition (APEC) 2018 г., Сан-Антонио, Техас, США, 4–8 марта 2018 г.; стр. 1052–1059.. [Google Scholar]
- Тао, Л.; Вэй, З .; Чи, Х .; Инь, Б. Расчет индуктивности многослойных круглых печатных спиральных катушек. Дж. Физ. конф. сер. 2019 , 1176, 062045.
 [Google Scholar]
[Google Scholar] - Инан, Инженерная электромагнетика США; Pearson Education: Noida, India, 1998. [Google Scholar]
- Калантаров П.Л. расчет индуктивности; National Power Press: Москва, Россия, 1955. [Google Scholar]
- Чаттерджи, С.; Айер, А .; Бхаратираджа, К.; Вагасия, И.; Валивети, Р. Оптимизация конструкции эффективной беспроводной системы передачи энергии для электромобилей. Энергетическая процедура 2017 , 117, 1015–1023. [Google Scholar] [CrossRef]
- Вяйсянен, В.; Хилтунен, Дж.; Нерг, Дж.; Сильвентойнен, П. Методы расчета сопротивления переменному току и практические соображения по проектированию при использовании литцендрата. В материалах IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Вена, Австрия, 10–13 ноября 2013 г.; стр. 368–375. [Google Scholar]
Рисунок 1. Плоская спиральная катушка.
Рисунок 1. Плоская спиральная катушка.
Плоская спиральная катушка.
Рисунок 2. Поперечный разрез спиральной катушки.
Рисунок 2. Поперечный разрез спиральной катушки.
Рисунок 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.
Рис. 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.
Рисунок 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.
Рис. 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.
Рисунок 5. Влияние изменения числа витков на индуктивность спиральной катушки.
Рисунок 5. Влияние изменения числа витков на индуктивность спиральной катушки.
Рисунок 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.
Рисунок 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.
Рисунок 7. Настройка пайки.
Рис. 7. Настройка пайки.
Рисунок 8. Сравнение расчетной и измеренной длины и DCR. ( a ) Сравнение длины. ( b ) Сравнение DCR.
Рис. 8. Сравнение расчетной и измеренной длины и DCR. ( а ) Сравнение длины. ( b ) Сравнение DCR.
Рисунок 9. Спиральная катушка и бобина. ( a ) Бобина. ( b ) Спиральная катушка, намотанная на бобины.
Рис. 9. Спиральная катушка и бобина. ( a ) Бобина. ( b ) Спиральная катушка, намотанная на бобины.
Рисунок 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( с ) 16 витков.
Рис. 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( c ) 16 витков.
Таблица 1. Сравнение результата расчета и измерения.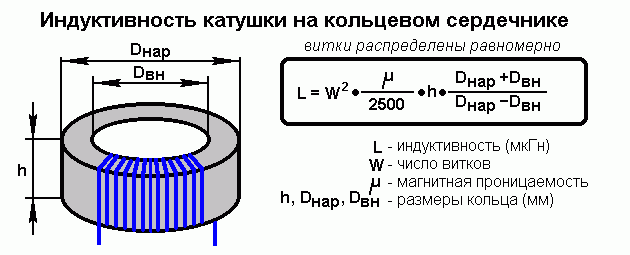
Таблица 1. Сравнение результата расчета и измерения.
| Параметры | Результаты | ||||||
|---|---|---|---|---|---|---|---|
| N | R i (mm) | s (mm) | w (mm) | R o (mm) | Inductance (μH) (Calculated) | Inductance (μH) (Measured) | Error (%) |
| 7 | 12 | 4 | 3.6 | 40 | 2. | ||


 Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.
Начальный заряд обкладки конденсатора составляет 10 мКл. Какая полная энергия? Также узнайте резонансную частоту.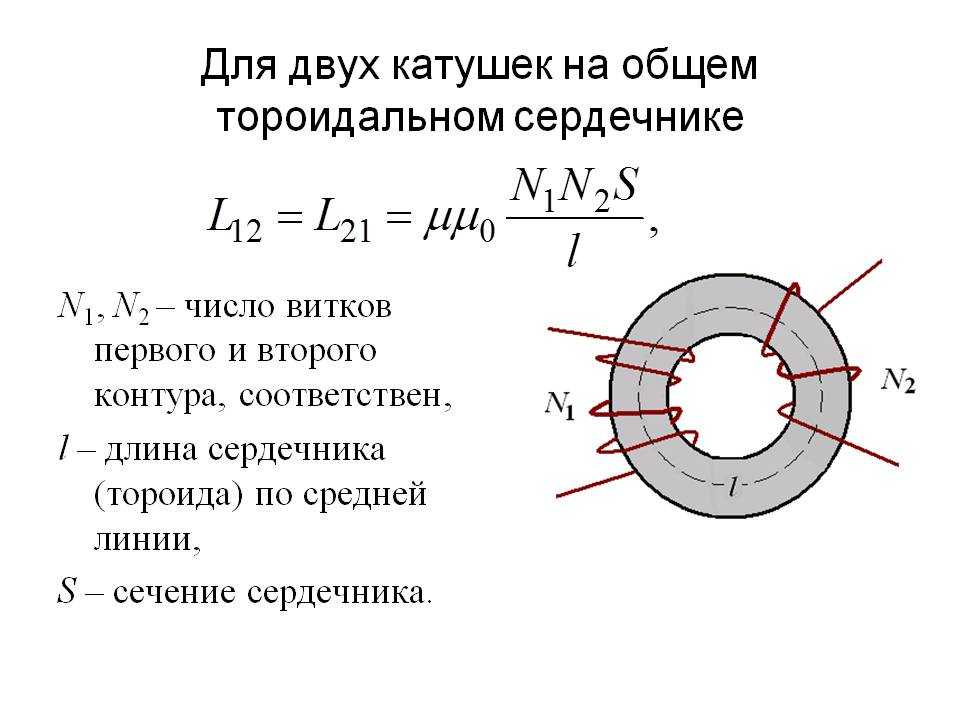


 ; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Energies 2020 , 13, 3119. [Google Scholar] [CrossRef]
; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Energies 2020 , 13, 3119. [Google Scholar] [CrossRef] Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed] [Google Scholar]
[Google Scholar]