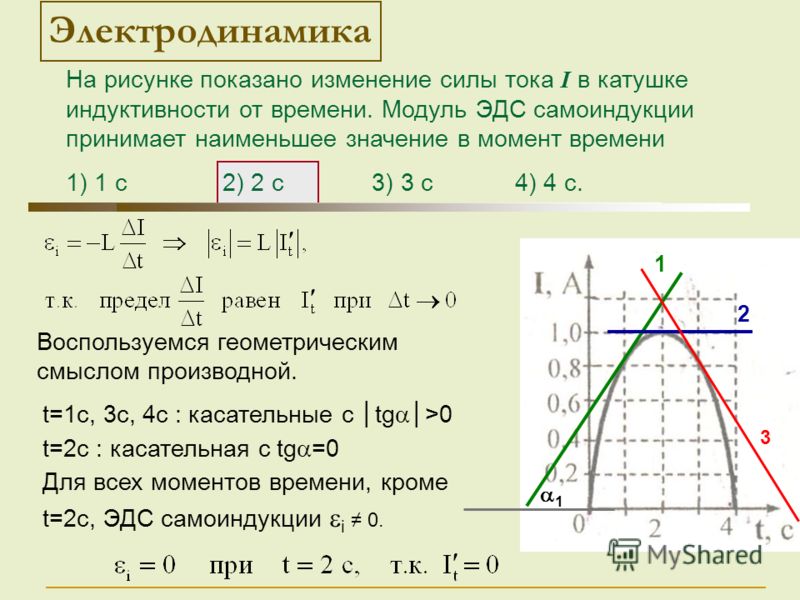
Сборник задач абитуриенту. МАГНЕТИЗМ. Индуктивность. ЭДС самоиндукции. Тема 23-7
Опубликовано ср, 07/24/2019 — 11:14 пользователем fizportal.ru
МАГНЕТИЗМ. Индуктивность. ЭДС самоиндукции. Тема 23-7
23.54. При пропускании через катушку тока силой 5 А в ней возникает магнитное поле с индукцией 3 Тл Определите индуктивность катушки, если площадь ее поперечного сечения 100 см2, а число витков 2500.
Ответ23.55. Магнитный поток через площадь контура, создаваемый током 10 А, текущим по контуру равен 0,9 мВб Определите ЭДС самоиндукции (в мВ), возникшую в контуре при равномерном убывании силы тока до 5 А за 1 мс.
Ответ23.56. Замкнутый виток площадью 20 см2 с индуктивностью 0,1 мГн помещают в однородное магнитное поле с индукцией 2 мТл перпендикулярно линиям индукции, затем охлаждают его до сверхпроводящего состояния и выключают поле.
23.57. По замкнутому проводнику протекает ток силой 1,5 А. Магнитное поле этого тока создает поток через площадь контура, равный 6 мВб Найдите индуктивность (в мГн) проводника.
Ответ23.58. Сила тока, протекающего по обмотке катушки, равномерно изменяется на 5 А за 0,25 с При этом возбуждается ЭДС самоиндукции 200 В. Определите индуктивность катушки.
Ответ23.59. Определите индуктивность катушки, если при равномерном изменении в ней силы тока от 5 до 10 А за 1 с возникает ЭДС самоиндукции 60 В.
Ответ23.60. При равномерном изменении силы тока в катушке индуктивностью 6 мГн в ней возникает ЭДС самоиндукции 8 мВ. На какую величину изменяется сила тока за 3 с?
23.61. В катушке индуктивностью 0,2 мГн с помощью реостата равномерно увеличивают силу тока со скоростью 100 А/с. Какова абсолютная величина ЭДС самоиндукции (в мВ), возникающей в катушке?
Ответ23. 62. В катушке с индуктивностью 6 мГн при равномерном увеличении силы тока на 40 А возникла ЭДС самоиндукции 8 В Сколько миллисекунд длилось увеличение тока?
62. В катушке с индуктивностью 6 мГн при равномерном увеличении силы тока на 40 А возникла ЭДС самоиндукции 8 В Сколько миллисекунд длилось увеличение тока?
23.63. Катушку с индуктивностью 2 Гн, содержащей 200 витков площадью 50 см2, помещают в однородное магнитное поле с индукцией 60 мТл, параллельной оси катушки Обмотку катушки охлаждают до сверхпроводящего состояния, а затем поворачивают катушку на 60°. Какой силы ток (в мА) возникнет в катушке?
23.64. Соленоид, содержащий 1000 витков провода, находится в однородном магнитном поле, индукция которого изменяется со скоростью 20 мТл/с. Ось соленоида составляет с вектором индукции магнитного поля угол 60°. Радиус соленоида 2 см. Определить ЭДС индукции, возникающей в соленоиде.
Ответ23.65. Найти индуктивность проводника, в котором равномерное изменение силы тока на 2 А в течение 0,5 с возбуждается ЭДС самоиндукции 20 мВ.
Ответ23.66. В однородном магнитном поле находится катушка из сверхпроводника.
Tags:
Абитуриенту
магнетизм
индуктивность
самоиндукция
Домашняя работа 10 класс. 13 Электростатика. Соединение конденсаторв fizportal.ru | ||
Домашняя работа 8 класс. Повторение. ДУ №37 Электричество fizportal.ru | ||
Домашняя работа 10 класс. 12 Электростатика. Плоский конденсатор fizportal.ru | ||
9 класс. Тема 1. СТАТИКА. Равновесие материальной точки fizportal.ru | ||
Домашняя работа 8 класс. Повторение. ДУ №36 Электричество fizportal.ru | ||
Домашняя работа 8 класс. Повторение. ДУ №33 Электричество fizportal.ru | ||
Домашняя работа 8 класс. fizportal.ru | ||
9 класс. Тема 7. ДИНАМИКА. Движение материальной точки по окружности — 2 fizportal.ru | ||
Домашняя работа 10 класс. 8 Электростатика. Проводники в электростатическом поле fizportal.ru | ||
Домашняя работа 10 класс. 7 Электростатика. Потенциальная энергия поля точечного заряда fizportal.ru |
Определите индуктивность катушки и изменение энергии магнитного поля. Физика, 11 класс, параграф 8-17, 6 задача. Мякишев и Буховцев – Рамблер/класс
Определите индуктивность катушки и изменение энергии магнитного поля. Физика, 11 класс, параграф 8-17, 6 задача. Мякишев и Буховцев – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Прива, кто решал эту задачу?
Сила тока в катушке изменяется от 1 А до 4 А за время, равное 3 с.
Лучший ответ
Привет. Мы уже решали ее
I1 = 1A
I2 = 4 A
= 0,1 В
Δ t = 3 c
L, Δ W — ?
Решение:
ЭДС самоиндукции
Из этого выражения находим индуктивность
Изменение энергии магнитного поля
Произведение индуктивности на изменение силы тока равно ЭДС самоиндукции, умноженной на промежуток времени, в течение которого это изменение произошло:
Тогда
Ответ: 0,1 Гн, 0,75 Дж
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
Компьютерные игры
похожие вопросы 5
Какой высоты должно быть плоское зеркало Физика 11 класс Мякишев Г. Я. 52-8
Я. 52-8
Ребята подскажите кто сможет:
Какой высоты должно быть плоское зеркало, висящее вертикально, чтобы человек, рост которого Н, видел (Подробнее…)
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Какой был проходной балл в вузы в 2017 году?
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
6.9 Индуктивность | Шлюз Техаса
Катушки индуктивности
Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с эффективностью данного устройства? Ответ положительный, и эта физическая величина называется индуктивностью.
Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 6.39, где простые катушки наводят друг в друге ЭДС.
Рис. 6.39 Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что E2E2 индуцируемая представляет ЭДС индукции в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, ΔI/Δt, ΔI/Δt, величине 12{ΔI} {} как на причине индукции. Изменение тока I1I1 размера 12{I rSub { размера 8{1} } } {} в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС2ЭДС2 размера 12{«ЭДС» rSub {размер 8{2} } } { } в другом.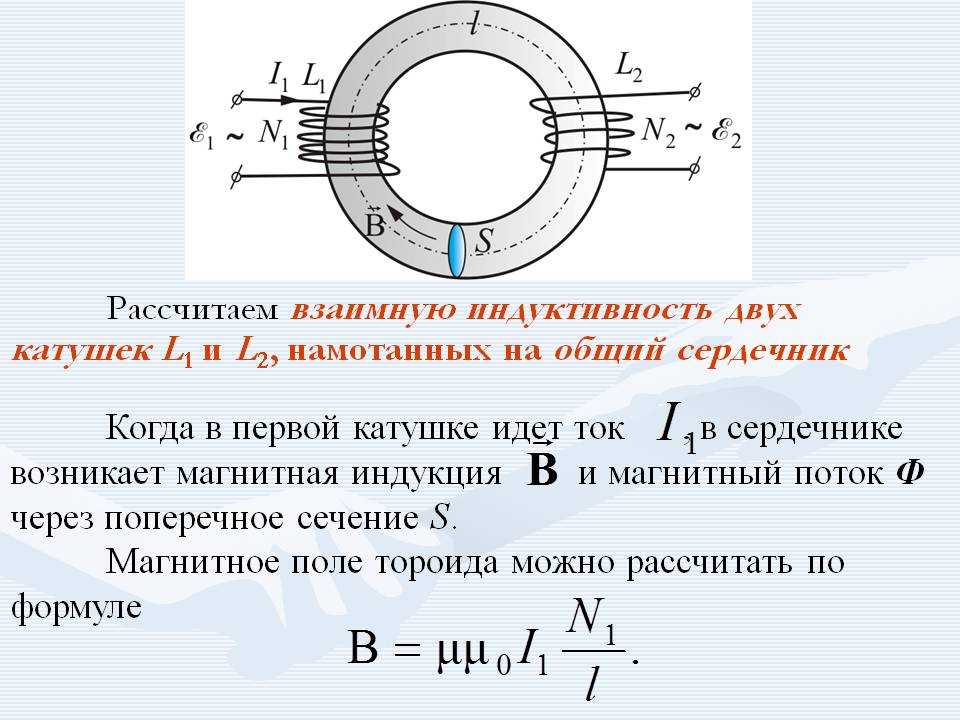 Мы выражаем это в форме уравнения как {Δt} } } {}
Мы выражаем это в форме уравнения как {Δt} } } {}
, где размер MM 12{M} {} определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M,M, размер 12{M}{}, тем эффективнее связь. Например, катушки на рис. 6.39 имеют малый размер ММ 12{M} {} по сравнению с катушками трансформатора на рис. 6.28. Единицы измерения ММ: (В⋅с)/A=Ω⋅с, (В⋅с)/A=Ω⋅с, что называется Генри (H), в честь Джозефа Генри. То есть 1 H=1Ω⋅s.1 H=1Ω⋅s.
Природа здесь симметрична. Если мы изменим текущий размер I2I2 12{I rSub { размер 8{2} } } {} в катушке 2, мы индуцируем ЭДС1emf1 размера 12{«ЭДС» rSub { размер 8{1} } } {} в катушке 1, что дается
6,35 ЭДС1=-MΔI2Δt, ЭДС1=-MΔI2Δt, размер 12{«ЭДС» rSub { размер 8{1} } = — M {{ΔI rSub {размер 8{2} } } свыше {Δt} } } {}
, где размер MM 12{M} {} такой же, как и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью, или взаимная индуктивность М. М. размер 12{М} {}
М. размер 12{М} {}
Большая взаимная индуктивность MM размера 12{M} {} может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшения взаимной индуктивности ММ типоразмера 12{M} {} — встречные катушки, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 6.40.)
Рис. 6.40 Нагревательные спирали электрической сушилки для белья могут быть намотаны встречно, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.
Самоиндукция, действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца.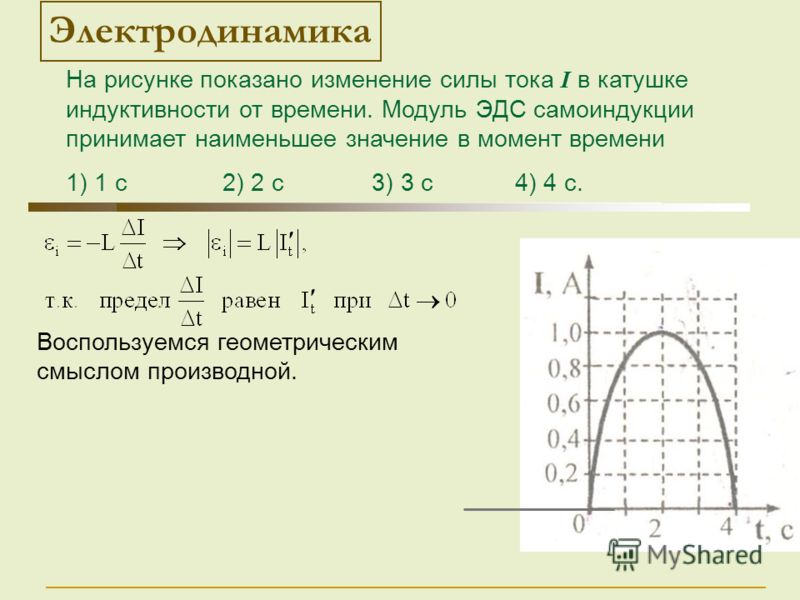 И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью обусловлено изменением тока ΔIΔI размером 12{ΔI} {} через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается
И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью обусловлено изменением тока ΔIΔI размером 12{ΔI} {} через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается
6,36 ЭДС=-L∆I∆t, ЭДС=-L∆I∆t, размер 12{«ЭДС»= — L { {∆I} над {∆t} } } {}
, где размер LL 12{L} {} — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется индуктором и обозначается символом на рис. 6.41.
Рис. 6.41
Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше величина собственной индуктивности LL 12{L}{} устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой размер LL 12{L}{} и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12{L} {}, например, путем встречной обмотки катушек, как показано на рис. 6.40.
Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12{L} {}, например, путем встречной обмотки катушек, как показано на рис. 6.40.
Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L=1,0 HL=1,0 H размером 12{L=1 «.» 0`H} {}, через который протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная эЭДС=-L(ΔI/Δt), будет против изменений. Таким образом, ЭДС будет индуцироваться по формуле eemf=-L(ΔI/Δt)=(1,0 H)[(10 A)/(1,0 мс)]=10 000 В. . Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.
Такое большое наведенное напряжение может быть использовано. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 6.42.)
(Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 6.42.)
Рис. 6.42 Благодаря быстрому переключению катушки индуктивности батареи на 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.
Можно рассчитать размер LL 12{L} {} для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в данном тексте индуктивность LL размером 12{L}{} обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как
эЭДС=-N(ΔΦ/Δt)
и, по определению собственной индуктивности, как
эЭДС=-L(ΔI/Δt).
Приравнивая эти выходы
Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется законом индукции Фарадея как
эЭДС=-N(ΔΦ/Δt)
и, по определению собственной индуктивности, как
эЭДС=-L(ΔI/Δt).
Приравнивая эти выходы
6,37 ЭДС=-NΔΦΔt=-LΔIΔt.ЭДС=-NΔΦΔt=-LΔIΔt. размер 12{«ЭДС»= — N {{ΔΦ} над {Δt} } = — L {{ΔI} над {Δt} } } {}
Решение для размера LL 12{L} {} дает
6,38 L=NΔΦΔI.L=NΔΦΔI. размер 12{L=N {{ΔΦ} свыше {ΔI} } } {}
Это уравнение для собственной индуктивности LL размера 12{L} {} устройства всегда справедливо. Это означает, что величина собственной индуктивности LL 12{L} {} зависит от того, насколько эффективно ток создает поток; чем эффективнее, тем больше ΔΔΦ/ΔI является.
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь соленоида AA фиксирована, изменение потока равно
ΔΦ=Δ(BA)=AΔB.ΔΦ=Δ(BA)=AΔB.
Найти
ΔB, ΔB, заметим, что магнитное поле соленоида задается как B=μ0nI=μ0NIℓ.B=μ0nI=μ0NIℓ.size 12{B=μ rSub { size 8{0} } ital «nI»=μ rSub { размер 8{0} } { { ital «NI»} более {ℓ} } } {} (Здесь,
nn=N/л,
куда
NN – количество витков и
ℓℓ — длина соленоида.) Изменяется только ток, так что более {ℓ} } } {}
ΔΦΔΦ в L=NΔΦΔIL=NΔΦΔI размера 12{L=N {{ΔΦ} над {ΔI}} } {} дает
Поскольку площадь соленоида AA фиксирована, изменение потока равно
ΔΦ=Δ(BA)=AΔB.ΔΦ=Δ(BA)=AΔB.
Найти
ΔB, ΔB, заметим, что магнитное поле соленоида задается как B=μ0nI=μ0NIℓ.B=μ0nI=μ0NIℓ.size 12{B=μ rSub { size 8{0} } ital «nI»=μ rSub { размер 8{0} } { { ital «NI»} более {ℓ} } } {} (Здесь,
nn=N/л,
куда
NN – количество витков и
ℓℓ — длина соленоида.) Изменяется только ток, так что более {ℓ} } } {}
ΔΦΔΦ в L=NΔΦΔIL=NΔΦΔI размера 12{L=N {{ΔΦ} над {ΔI}} } {} дает
6,39 L=NΔΦΔI=Nμ0NAΔIℓΔI.L=NΔΦΔI=Nμ0NAΔIℓΔI. размер 12 {L = N { {ΔΦ} над {ΔI} } = N { {μ rSub { размер 8 {0} } ital «NA» { {ΔI} над {ℓ} } } над {ΔI} } } {}
Это упрощается до
6,40 L=μ0N2Aℓ(соленоид).L=μ0N2Aℓ(соленоид). размер 12{L= { {μ rSub { размер 8{0} } N rSup { размер 8{2} } A} свыше {ℓ} } } {}
Это собственная индуктивность соленоида поперечного сечения площадь АА и длина
ℓ,ℓ, Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.
Пример 6.7 Расчет собственной индуктивности соленоида среднего размера
Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.
Стратегия
Это прямое применение L=µ0N2Aℓ,L=µ0N2Aℓ,размер 12{L= { {µ rSub { размер 8{0} } N rSup { размер 8{2} } A} более {ℓ} } } { }, так как все величины в уравнении, кроме размера LL 12{L} {}, известны.
Решение
Используйте следующее выражение для собственной индуктивности соленоида:
6,41 L=μ0N2AℓL=μ0N2Aℓ размер 12{L= { {µ rSub { размер 8{0} } N rSup { размер 8{2} } A} более {ℓ} } } {}
Площадь поперечного сечения в этом примере равна A=πr2=(3,14 …)(0,0200 м)2=1,26 × 10-3 м2, A=πr2=(3,14 …)(0,0200 м)2=1,26 × 10-3 м2, NN задается как быть 200, а длина ℓℓ равна 0,100 м. Мы знаем, что проницаемость свободного пространства равна μ0=4π×10−7T⋅м/A.μ0=4π×10−7T⋅m/A. Подставляя их в выражение для ЛЛ дает
6,42 L=(4π×10–7 Т⋅м/А)(200)2(1,26×10–3 м2)0,100 м=0,632 м вод. л.=(4π×10–7 Т⋅м/А)( 200)2(1,26×10-3 м2)0,100 м=0,632 мГн.
л.=(4π×10–7 Т⋅м/А)( 200)2(1,26×10-3 м2)0,100 м=0,632 мГн.
Обсуждение
Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных приложений индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. См. Рисунок 6.43.
См. Рисунок 6.43.
Рис. 6.43 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Alexbuirds, Wikimedia Commons)
Характеристики и контроль резонанса в электродвижущей силе электромагнитной индукции
Журнал электромагнитного анализа и приложений
Том 5 № 8 (2013 г.), идентификатор статьи: 35486, 5 страниц DOI :10.4236/jemaa.2013.58049
Характеристики и контроль резонанса в электродвижущей силе электромагнитной индукции
Санг Дон Бу, Джин Кю Хан, Джин Ён Хён, Ги Гван Ким Университет, Чонджу, Южная Корея.
Электронная почта: [email protected]
Copyright © 2013 Sang Don Bu et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Поступила в редакцию 25 апреля -го -го, 2013 г.; пересмотрено 28 мая th , 2013; принят 30 июня -й , 2013
Ключевые слова: Электромагнитная индукция; Электродвижущая сила; Резонатор, резонансная/антирезонансная частота
АННОТАЦИЯ
Принципы электромагнитной индукции применяются во многих устройствах и системах, включая индукционные плиты, трансформаторы и беспроводную передачу энергии; однако мало данных о резонансе в электродвижущей силе (ЭДС) электромагнитной индукции. Мы изучали электромагнитную индукцию между двумя круглыми катушками провода: одна является катушкой источника, а другая катушкой датчика (или индукции). Измеренные графики зависимости ЭДС от частоты показывают наличие резонанса/антирезонанса в ЭДС электромагнитной индукции в свободном пространстве. Мы обнаружили, что можно управлять резонансными и антирезонансными частотами системы. В некоторых устройствах желаемая резонансная или антирезонансная частота достигается за счет изменения размера резонатора. Здесь, напротив, наши экспериментальные результаты показывают, что резонансную и антирезонансную частоты системы можно регулировать, изменяя расстояние между двумя катушками или число витков индукционной катушки.
Здесь, напротив, наши экспериментальные результаты показывают, что резонансную и антирезонансную частоты системы можно регулировать, изменяя расстояние между двумя катушками или число витков индукционной катушки.
1. Введение
1.1. Резонанс
Резонанс широко распространен в природе и используется во многих искусственных устройствах. Электрический резонанс используется во многих схемах [1-5]; например, радио и телевизоры используют резонансные цепи для настройки на станции. В этих устройствах через антенну в цепь одновременно попадают многие частоты, но значительный ток индуцируется только частотами, близкими к резонансной частоте цепи. Изменяя индуктивность или емкость, устройство можно настроить на разные станции. В физике резонанс — это тенденция системы колебаться с большей амплитудой на резонансных частотах системы, чем на других. На этих частотах даже небольшие периодические движущие силы могут вызывать колебания большой амплитуды, поскольку система накапливает энергию колебаний. В этой работе мы изучили электромагнитную индукцию между двумя круглыми катушками провода: одна является катушкой источника, а другая — катушкой датчика (или индукции), и сообщаем о характеристиках и контроле над резонансом и антирезонансом в электродвижущая сила (ЭДС) электромагнитной индукции через свободное пространство.
В этой работе мы изучили электромагнитную индукцию между двумя круглыми катушками провода: одна является катушкой источника, а другая — катушкой датчика (или индукции), и сообщаем о характеристиках и контроле над резонансом и антирезонансом в электродвижущая сила (ЭДС) электромагнитной индукции через свободное пространство.
1.2. Как ведет себя величина электродвижущей силы при увеличении частоты, подаваемой на катушку источника?
Эксперимент проводился по закону Фарадея:
. (1)
где и – ЭДС, индуцируемая в индукционной катушке, и магнитный поток, проходящий через индукционную катушку, соответственно [1,6]. Экспериментальная установка состоит из двух круглых катушек провода, состоящего из электропроводящего медного провода с радиусом поперечного сечения 0,35 мм, туго намотанного в виде ряда петель из 5-320 витков радиусом 7 см и высотой 2 см, как показано на рисунке 1. ● Одна катушка (источник) подключена к генератору сигналов (AFG3021B, Tektronix), а другая (датчик или индукционная катушка) подключена к осциллографу (DSO 5012A, Agilent Technologies). Генератор сигналов подает синусоидальное напряжение на катушку источника, создавая синусоидальное магнитное поле. Магнитное поле переменного тока распространяется в свободном пространстве и достигает приемной катушки. Согласно закону Фарадея, электрическое поле индуцируется в любой области пространства, в которой магнитное поле изменяется
Генератор сигналов подает синусоидальное напряжение на катушку источника, создавая синусоидальное магнитное поле. Магнитное поле переменного тока распространяется в свободном пространстве и достигает приемной катушки. Согласно закону Фарадея, электрическое поле индуцируется в любой области пространства, в которой магнитное поле изменяется
Рис. 1. Схема экспериментальной установки. Экспериментальная установка состоит из двух катушек. Катушка А является катушкой-источником, передающей электромагнитную волну через свободное пространство. Катушка B — это приемная (или индукционная) катушка, которая регистрирует наведенную ЭДС. Катушки А и В выровнены коаксиально, так что расстояние d между двумя катушками можно регулировать от 10 мм до 1000 мм. Катушки неподвижны во время работы.
со временем. Таким образом, в приемной катушке индуцируется ЭДС. Если магнитный поток, проходящий через катушку датчика, равен, то ЭДС индукции равна . Поскольку увеличивается, увеличивается, и величина пропорциональна скорости изменения магнитного потока во времени, так что более быстрые изменения дают более сильные. Здесь наш вопрос: как ведет себя величина при увеличении, особенно в диапазоне высоких частот от 10 кГц до нескольких МГц?
Здесь наш вопрос: как ведет себя величина при увеличении, особенно в диапазоне высоких частот от 10 кГц до нескольких МГц?
2. Простота использования Свойства электромагнитной индукции
2.1. Сравнение экспериментальной и прогнозируемой электродвижущих сил
На рисунках 2(a) и (b) показаны типичные характеристики 1) среднеквадратичного значения катушки датчика и 2) разности фаз между приложенным напряжением (к катушке источника) и генерируемой (в приемной катушке) соответственно в зависимости от приложенной частоты (к катушке источника). Мы ожидали, что согласно закону Фарадея и радиационному сопротивлению катушки оно будет увеличиваться с ростом и затем, наконец, достигнет нового равновесия, как показано черной пунктирной линией на рис. 2(а). Такой отклик можно смоделировать с помощью функции Ланжевена [7],
. (2)
Однако экспериментальные данные продемонстрировали совсем другое поведение, как показано красными сплошными кружками на рисунке 2(а). Резонансное поведение наблюдалось на высоких частотах, а релаксационное — на низких частотах. Резонансные и антирезонансные пики отчетливо наблюдались на частотах 87 кГц и 285 кГц соответственно.
Резонансные и антирезонансные пики отчетливо наблюдались на частотах 87 кГц и 285 кГц соответственно.
На рис. 2(b) показано, что при частоте 10 Гц катушка звукоснимателя была сдвинута по фазе на 78˚ по отношению к волне, подаваемой на катушку источника. По мере увеличения разность фаз уменьшалась до тех пор, пока фазы не совпадали, где фазовое согласование означает, что разность фаз составляет менее 5˚. Между тем, разность фаз сильно изменилась, когда катушка звукоснимателя стала резонансной. Катушка звукоснимателя была сдвинута по фазе на 176˚ на частотах между резонансным и антирезонансным пиками, то есть в диапазоне частот 87 — 285 кГц.
Резкое изменение разности фаз могло быть вызвано движением зарядов в приемной катушке. Если разность фаз возникла из-за ускорения проводящих электронов, вызванного электромагнитным излучением (генерируемым катушкой источника), разность фаз может быть фактически независимой на высоких частотах. Однако, если бы разность фаз возникала из-за колебаний в электрических/магнитных диполях или тороидальных диполях 1 [8-14], индуцированных электромагнитным излучением, можно было бы ожидать, что разность фаз будет зависеть от на высоких частотах.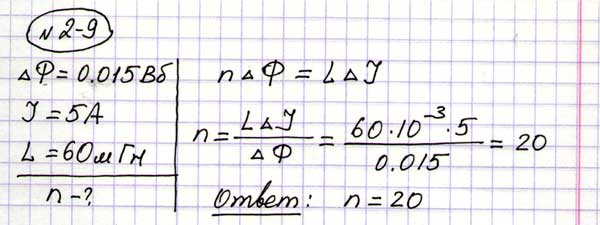
Радиационное сопротивление в катушке с витками, состоящими из электропроводящего медного провода, можно смоделировать следующим образом. Для катушки радиусом 7 см и высотой 2 см, используемой здесь (см. рис. 1), составляющая электрического дипольного излучения в сопротивлении излучения меньше, чем составляющая магнитного дипольного излучения, если предположить, что расстояние от катушки составляет, где скорость света, например; первое порядка, второе порядка, где и — угловая частота и скорость света соответственно. Резонансные частоты, полученные в наших экспериментах, были значительно ниже резонансных частот валентных электронов или электрических/магнитных диполей [6,7]. Следовательно, в рассматриваемой здесь конкретной геометрии резкие изменения разности фаз могли быть преимущественно вызваны колебаниями тороидальных диполей [13,14] в индукционной катушке.
2.2. Настройка резонансной и антирезонансной частот
Для определения резонансной частоты и
Рис. 2. Сравнение экспериментальных и расчетных значений и. Экспериментальные измерения и показаны на (а) и (б) соответственно, обозначены красными и синими сплошными кружками. Амплитуда сигнала, подаваемого на катушку источника, и расстояние между источником и индукционной катушкой затем фиксировались на уровне 14 В и 3 см соответственно. Прогнозируемые значения и показаны на (а) и (б) соответственно черными пунктирными линиями.
2. Сравнение экспериментальных и расчетных значений и. Экспериментальные измерения и показаны на (а) и (б) соответственно, обозначены красными и синими сплошными кружками. Амплитуда сигнала, подаваемого на катушку источника, и расстояние между источником и индукционной катушкой затем фиксировались на уровне 14 В и 3 см соответственно. Прогнозируемые значения и показаны на (а) и (б) соответственно черными пунктирными линиями.
антирезонансную частоту можно было регулировать, мы исследовали влияние трех экспериментальных параметров на и. На рисунках 3(a)-(c) показаны зависимости для различных 1) напряжений, подаваемых на катушку источника (= 2, 6, 10 и 14 В), 2) расстояний между двумя катушками (d = 10, 30, 100 В). и 1000 мм) и 3) количество витков приемной катушки (= 5, 50, 150, 250 и 320) соответственно. На рисунках 4(a)-(c) показаны изменения и for и n B соответственно, полученные из рисунка 3. Резонансные и антирезонансные пики отчетливо видны на большинстве кривых на рисунке 3. или, как показано черными квадратами на рисунках 4(a)-(b). Интервал между и существенно не менялся при увеличении (рис. 4(а)), тогда как резко уменьшался при увеличении (рис. 4(б)). Эти результаты показывают, что можно было контролировать независимо от. С другой стороны, как увеличилось, так и уменьшилось вместе, как показано на рисунке 4(c).
или, как показано черными квадратами на рисунках 4(a)-(b). Интервал между и существенно не менялся при увеличении (рис. 4(а)), тогда как резко уменьшался при увеличении (рис. 4(б)). Эти результаты показывают, что можно было контролировать независимо от. С другой стороны, как увеличилось, так и уменьшилось вместе, как показано на рисунке 4(c).
, и каждый из них ведет себя по-своему. Кривые и , показанные на рисунке 4 (b), показывают, что это не зависит от и может быть описано уравнением, включающим логарифм. График в зависимости от давал прямую линию, как показано красной линией на вставке к рисунку 4(b). Таким образом, может иметь вид «», где и – константы пропорциональности и точки пересечения вертикальной оси (или бессмысленные константы), re
Рисунок 3. Графики зависимости от f A . была измерена как функция напряжения, подаваемого на катушку источника (V A ), расстояния между двумя катушками (d) и числа витков приемной катушки (n B ), где количество витков катушки источника (n A ) было зафиксировано на уровне 320. (a) Графики зависимости f A для V A на 2, 6, 10 и 14 В, с d и n B , фиксированными на 30 мм и 320 соответственно; (b) Графики зависимости f A для d 10, 30, 100 и 1000 мм при V A и n B фиксируются на 14 В и 320 В соответственно; (c) Графики зависимости f A от n B , равные 5, 50, 150, 250 и 320, с V A и d, зафиксированными на уровне 14 В и 100 мм соответственно.
(a) Графики зависимости f A для V A на 2, 6, 10 и 14 В, с d и n B , фиксированными на 30 мм и 320 соответственно; (b) Графики зависимости f A для d 10, 30, 100 и 1000 мм при V A и n B фиксируются на 14 В и 320 В соответственно; (c) Графики зависимости f A от n B , равные 5, 50, 150, 250 и 320, с V A и d, зафиксированными на уровне 14 В и 100 мм соответственно.
соответственно. Согласно рисунку 4(c), может иметь вид «», а не «», а также может иметь вид «». Экспериментальные результаты, полученные для различных комбинаций и показывают, что можно было описать уравнением вида «» с условием, а можно было описать уравнением вида «» с условием. Отмечено, что в условиях различных поворотов все поведение и с было похоже на результаты, показанные на рисунке 4(b), что указывает на то, что перекрестный член «» может быть незначительным.
Экспериментально мы показали, что катушки звукоснимателя с разными резонансными/антирезонансными частотами можно получить, выбрав соответствующую катушку для заданного размера. Эти результаты предполагают возможность «беспроводной станции передачи энергии», которая передает мощность от катушки источника на большое количество приемных катушек
Эти результаты предполагают возможность «беспроводной станции передачи энергии», которая передает мощность от катушки источника на большое количество приемных катушек
Рис. 4. f R и f AR в зависимости от (a) V A , (b) d и (c) n B .
через свободное пространство. Если несколько приемных катушек (с разными резонансными/антирезонансными частотами) расположить вокруг катушки-источника (т. е. системы энергоснабжения ближнего действия), мощность можно будет передавать от катушки-источника к приемным катушкам путем модуляции скорости изменения (с течением времени) магнитного потока, проходящего через каждую катушку датчика. Станции беспроводной передачи энергии, аналогичные радиостанциям, могут быть реализованы в ближайшем будущем, чтобы каждый мог использовать энергию в любом месте без необходимости проводной передачи энергии.
3. Заключение
Таким образом, мы изучили электромагнитную индукцию между двумя круглыми витками проволоки и ясно показали наличие резонанса/антирезонанса в ЭДС электромагнитной индукции через свободное пространство. Мы считаем, что наши результаты могут обеспечить конкурентоспособный подход к разработке высокоэффективных систем в устройствах индукционных плит, силовых трансформаторов и беспроводной передачи энергии.
Мы считаем, что наши результаты могут обеспечить конкурентоспособный подход к разработке высокоэффективных систем в устройствах индукционных плит, силовых трансформаторов и беспроводной передачи энергии.
4. Благодарности
Это исследование было поддержано Программой фундаментальных научных исследований через Национальный исследовательский фонд Кореи (NRF), финансируемый Министерством образования, науки и технологий (номер гранта 2012R1A1A 2042743).
ССЫЛКИ
- Д. К. Джанколи, «Физика: принципы с приложениями», Prentice Hall, Upper Saddle River, 2005, стр. 584–608.
- А. Курс, А. Каралис, Р. Моффатт, Дж. Д. Джоаннопулос, П. Фишер и М. Солячич, «Беспроводная передача энергии с помощью сильно связанных магнитных резонансов», Science, Vol. 317, № 5834, 2007, стр. 83-86. doi:10.1126/science.1143254
- Т. Имура, Т. Учида и Ю. Хори, «Гибкость бесконтактной передачи энергии с использованием магнитно-резонансной связи с воздушным зазором и несоосностью для электромобилей», World Electric Vehicle Journal, Vol.
 3, 2009 г., стр. 1-10.
3, 2009 г., стр. 1-10. - С. А. Хакворт, X. Лю, К. Ли и М. Сан, «Беспроводная солнечная энергия для дома: магнитно-резонансный подход», Международный журнал инноваций в энергетических системах и энергетике, Vol. 5, № 1, 2010. С. 40-44.
- Б. Ван, Т. Нишино и К. Х. Тео, «Повышение эффективности беспроводной передачи энергии с помощью метаматериалов», Материалы Международной конференции IEEE 2010 г. по беспроводным информационным технологиям и системам, Гонолулу, 28 августа — 3 сентября 2010 г., стр. 1–4. . Дои: 10.1109/ICWITS.2010.5612284
- Джексон Дж.Д. Классическая электродинамика // Wiley. -73.
- В. М. Дубовик, М. А. Марценюк и Б. Саха, «Материальные уравнения для электромагнетизма с тороидальными поляризациями», Physics Review E, Vol. 61, № 6, 2000, стр. 7087-7097. doi:10.1103/PhysRevE.61.7087
- В. М. Дубовик, Б. Саха и Дж. Л. Рубин, «Преобразование Лоренца тороидальной поляризации», Секция писем по ферроэлектрикам, Vol. 27, № 1-2, 2000, стр.
 1-6. дои: 10.1080/07315170008204647
1-6. дои: 10.1080/07315170008204647 - Г. Н. Афанасьев, «Простейшие источники электромагнитных полей как инструмент для проверки теорем взаимности», Journal of Physics D: Applied Physics, Vol. 34, № 4, 2001, стр. 539-559. doi:10.1088/0022-3727/34/4/316
- Дубовик В.М., Тугушев В.В. Тороидальные моменты в электродинамике и физике твердого тела // Physics Reports. 187, № 4, 1990, стр. 145-202. doi:10.1016/0370-1573(90)-Z
- Маринов К., Бордман А.Д., Федотов В.А., Желудев Н. Тороидальный метаматериал // Новый журнал физики. 9, № 9, 2007, стр. 324-202. doi:10.1088/1367-2630/9/9/324
- А.А. Горбацевич, Ю.А. Копаев В. Тороидальный порядок в кристаллах // Сегнетоэлектрики. 161, № 1, 1994, стр. 321-334. doi: 10.1080/00150199408213381
- Х. Шмид, «Тороидальные моменты в спин-упорядоченных кристаллах», Труды однодневного международного исследовательского семинара по супертороидальной электродинамике, Саутгемптонский университет, Саутгемптон, 2004 г., стр.



 Повторение. ДУ №35 Электричество
Повторение. ДУ №35 Электричество 3, 2009 г., стр. 1-10.
3, 2009 г., стр. 1-10.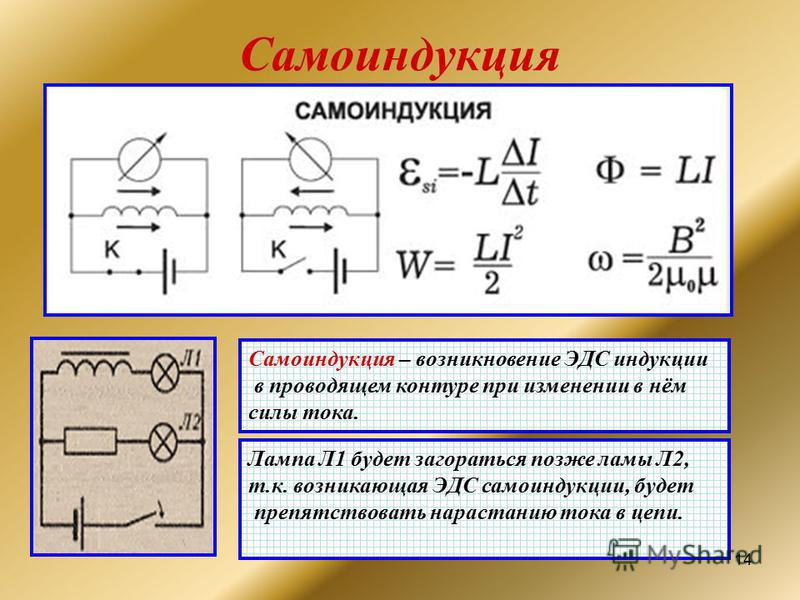 1-6. дои: 10.1080/07315170008204647
1-6. дои: 10.1080/07315170008204647