Курс физики (Грабовский Р.И.)

Курс физики (Грабовский Р.И.)

Грабовский Р.И. Курс физики. Учеб. пособие для с/х ин-тов. Изд. 4-е, перераб. и доп. М., «Высш. школа», 1974. — 552 с. Учебник составлен в соответствии с программой по физике для сельскохозяйственных институтов. В нем приводится достаточное количество примеров, связанных с агробиологическими науками и сельскохозяйственным производством. Настоящее издание (3-е вышло в 1970 г.) отличается от предыдущих некоторыми (небольшими по объему) дополнениями и изменениями, способствующими улучшению содержания. Предназначается для студентов неинженерных факультетов сельскохозяйственных вузов. Многие разделы учебника могут быть использованы и студентами инженерных факультетов. Оглавление Предисловие Введение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 10. Силы упругости § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 43. О числе степеней свободы. Внутренняя энергия газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. 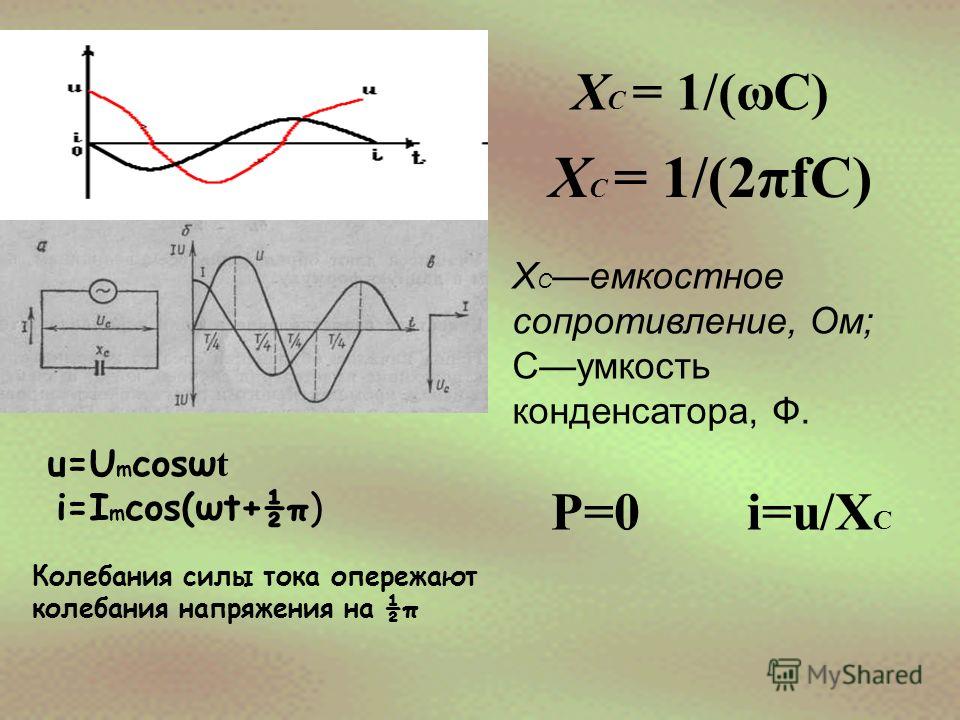Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. Тепловое расширение твердых и жидких тел § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. 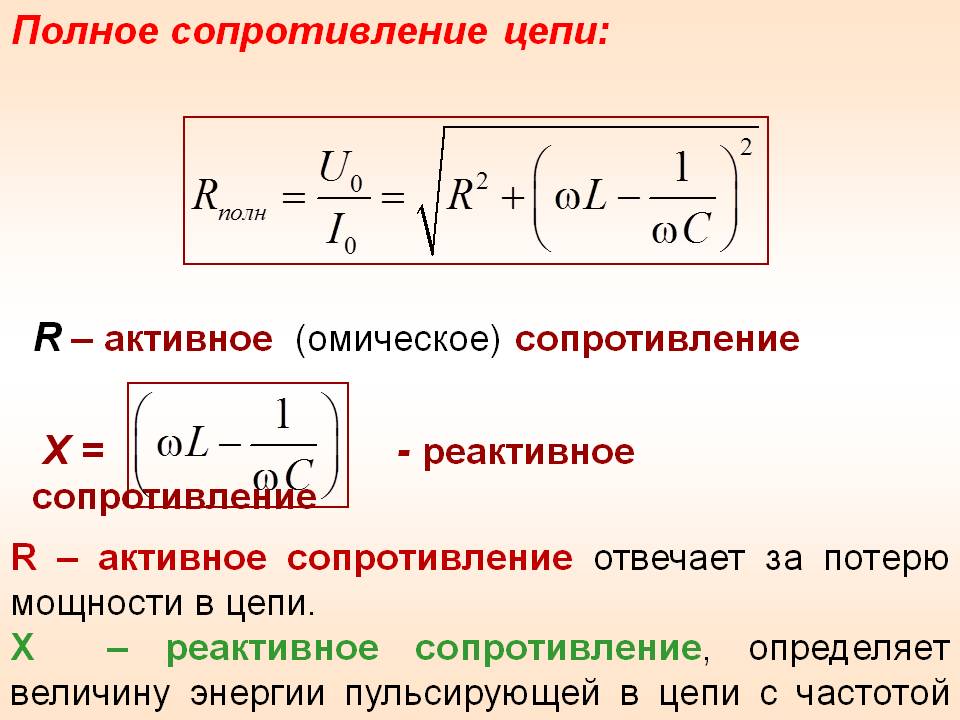Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии

37.

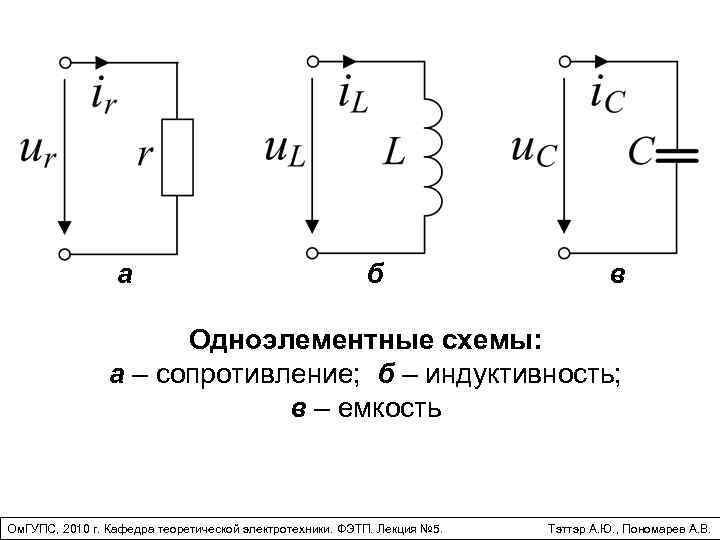
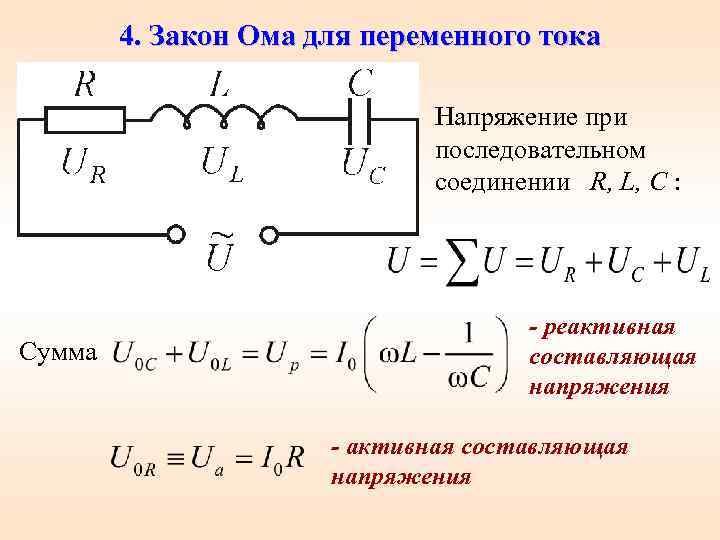Активное, индуктивное и емкостное сопротивления в цепи синусоидального тока.

Активное электрическое сопротивление – параметр пассивного двухполюсника, равный отношению активной мощности, поглощаемой в этом двухполюснике, к квадрату действующего значения тока через этот двухполюсник.

Пусть к активному сопротивлению приложено синусоидальное напряжение u=U_msin(ωt + ψ_u) с начальной фазой ψ_u=0. Тогда по закону Ома u=iR, iR=U_msinωt, i=sinωt*U_m/R, ψ_i=0. Значит, φ= ψ_u — ψ_i=0.

На участке цепи с активным сопротивлением ток совпадает по фазе с напряжением на этом участке.

I_m=U_m/R; I=U/R; I_ср=U_ср/R.

Индуктивность в цепи синусоидального тока. Пусть в ветви с индуктивностью L ток синусоидален с начальной фазой ψ_i=0: I=I_msinωt.

где U_m – модуль амплитудного значения напряжения, U_m=ωLI_m, [В]; X_L – индуктивное сопротивление, X_L=ωL=2πfL, [Ом]. ψ_u = π/2, ψ_i = 0, φ= ψ_u — ψ_i= π/2.

Ток в индуктивности отстает от приложенного напряжения на угол π/2.

I_m=U_m/X_L=U_m/ωL; I=U/X_L=U/ωL; I_ср=U_ср/X_L=U_ср/ωL.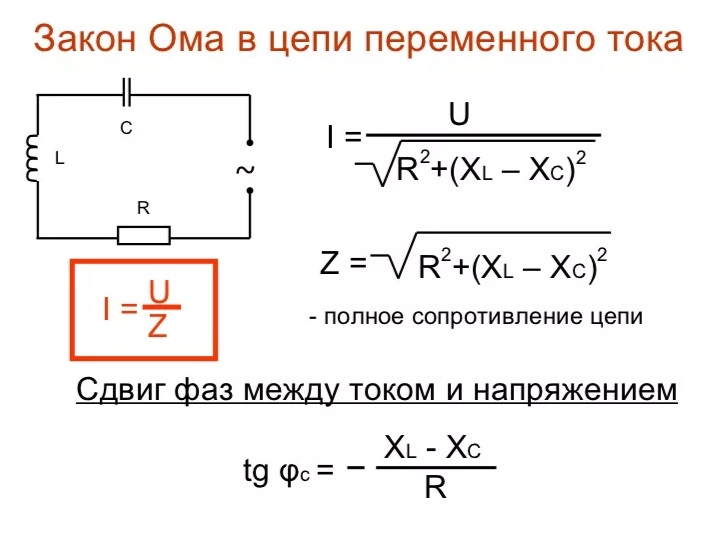

Емкость в цепи синусоидального тока. Пусть к емкости С приложено синусоидальное напряжение с начальной фазой ψ_u = 0: U=U_msinωt.

где I_m – модуль амплитудного значения тока; Х_С – емкостное сопротивление. Х_С=1/ωC=1/2πfC [Ом]. ψ_u = 0, ψ_i = π/2, φ= ψ_u — ψ_i= —π/2. В емкости ток опережает напряжение на угол π/2.

I_m=U_m/X_c=ωCU_m; I=U/X_C=ωCU; I_ср=U_ср/X_C=ωCU_ср.

18. 25.

Метод контурных токов. Алгоритм расчета с источниками тока

I₁=I₁₁, I₂=I₂₂—I₁₁, I₃=I₃₃—I₁₁, I₄=-I₂₂, I₅=I₃₃—I₂₂, I₆=I₃₃.

Запишем уравнение по второму закону Кирхгофа для первого контура, считая направление обхода контура совпадающим с направлением контурного тока I₁₁: I₁R₁ – I₃R₃ – I₂R₂ = E₁ – E₃. Заменим реальные токи I₁, I₂, I₃ на контурные, тогда: I₁₁R₁ – I₃₃R₃ + I₁₁R₃ – I₂₂R₂ + I₁₁R₂ = E₁ – E₃. Сгруппируем. Аналогично, для второго и третьего контуров можно записать два других уравнения. Получим систему трех уравнений:

Из системы уравнений находят контурные токи, по которым определяют реальные токи. Общее выражение для случая n-го количества независимых контуров можно записать:

где R₁₁, R₂₂, R_nn – собственные сопротивления соотв-но первого, второго и n-го контуров, равные сумме всех сопротивлений, входящих в рассматриваемый контур; R₁₂, R₂₃, …, R_km – взаимное сопротивление м/у соответственно первым и вторым, вторым и третьим, к-м и m –м контурами; E₁₁, E₂₂, …, E_nn – контурная ЭДС n-го контура, равная алгебраической сумме ЭДС, входящих в рассматриваемый контур.

Запись уравнений по методу контурных токов в цепях с источниками тока может быть осуществлена из условия, что один из контурных токов известен и равен току источника тока:

Другой способ заключается в том, что можно составить уравнения после эквивалентного преобразования источника тока в источник ЭДС:

24.

Резонанс напряжений в цепи с последовательным соединением r, l, c, её частотные хар-ки.

Явление в электрической цепи, содержащей участки, имеющие индуктивный и емкостной характер, при котором разность фаз синусоидального электрического напряжения и синусоидального электрического тока на входе цепи равна нулю, называют резонансом.

Резонансом напряжений называют явление резонанса в участке электрической цепи, содержащей последовательно соединенные индуктивный и емкостной элементы.

Определим полное комплексное сопротивление R,L,C цепи:

Условие φ=0 выполнимо, если соблюдается ωL-1/ωC=0 или ω²LC=1. Следовательно, резонанса можно достичь изменением частоты, индуктивности, емкости: ω₀ = 1/√LC; L₀ = 1/ω²C; C₀ = 1/ω²L.

Условие ωL-1/ωC=0 справедливое для цепи с последова-тельно соединенными R, L, С элементами, может быть представлено в виде условия резонанса напряжений для любой цепи: Jm{Z}=0

Если реактивные сопротивления Х_с = X_L при резонансе превосходят по значению активное сопротивление R, то напряжения на индуктивности и емкости могут значительно превысить напряжение на сопротивлении и, следовательно, на входе цепи. Поэтому резонанс при последовательном соединении называют резонансом напряжений.

Зависимости полного, реактивного, активного сопротивлений или проводимостей цепи, угла разности фаз φ от частоты называют частотными характеристиками.

R(ω) = R, X_L(ω) = ωL, X_C(ω) = 1/ωC, X(ω) = ωL-1/ωC, Z(ω) = √R²+X²(ω), φ(ω) = arctg((ωL-1/ωC)/R).

Частотные характеристики I(ω), U_R(ω), U_L(ω), U_C(ω) называют резонансными кривыми:

где d=1/Q – затухание (безразмерная величина, обратная добротности)

При ω = 0 I = 0, так как конденсатор не пропускает постоянный ток. При ω = ∞ I = 0, так как сопротивление катушки бесконечно большое. Максимум тока наблюдается при ω = ω₀, так как Z имеет мин-ое значение, равное R. При ω = 0 все входное напряжение приложено к конденсатору, напряжения на катушке нет, так как Х_С → ∞, при ω → ∞ Х_С → 0 напряжение на конденсаторе стремится к нулю, все напряжение на катушке.

Индуктивное реактивное сопротивление и емкостное реактивное сопротивление – определение и примеры решения

Емкостное реактивное сопротивление можно определить как реактивное сопротивление, создаваемое емкостными элементами (конденсаторами). Мы можем обозначить его как. Емкостное реактивное сопротивление представляет собой противодействие напряжения на емкостном элементе, которое временно используется для накопления электрической энергии в виде электрического поля. Емкостное сопротивление создает разность фаз между током и напряжением.

 

В емкостной цепи напряжение опережает ток. Для идеальной емкостной цепи напряжение опережает ток. Благодаря емкостному реактивному сопротивлению, из-за которого коэффициент мощности системы или цепи опережает. Ниже показана векторная диаграмма идеальной емкостной цепи.

 

(Изображение будет загружено в ближайшее время)

 

Разница между реактивным сопротивлением и сопротивлением

1. Реактивное сопротивление является составляющей импеданса, а сопротивление является постоянной составляющей сопротивления.

2. Значение реактивного сопротивления всегда является комплексным числом, тогда как значение сопротивления должно быть действительным числом.

3. В чисто индуктивной или емкостной цепи сопротивление будет равно нулю, а в чисто резистивной цепи реактивное сопротивление будет равно нулю.

4. Из-за реактивного сопротивления будет изменяться как амплитуда, так и фаза тока. Из-за сопротивления ток и напряжение всегда будут оставаться в фазе.

5. Значение реактивного сопротивления зависит от частоты сети, тогда как значение сопротивления не зависит от частоты сети.

6. Для источника постоянного тока индуктивное сопротивление должно быть равно нулю, а емкостное сопротивление будет бесконечно. Для питания постоянным током сопротивление останется прежним.

7. Реактивные сопротивления обозначаются как и. Сопротивление обозначается как.

8. Коэффициент мощности в реактивном сопротивлении опережает или отстает из-за элемента реактивного сопротивления. В сопротивлении мощность равна единице, когда реактивное сопротивление равно нулю.

Решенные примеры Индуктивное реактивное сопротивление и емкостное реактивное сопротивление

Что такое реактивное электрическое сопротивление?
Электрическое реактивное сопротивление можно определить как поток, противоположный направлению тока в элементе цепи из-за его индуктивности и емкости. Если реактивное сопротивление больше, то ток будет меньше при том же приложенном напряжении. Реактивное сопротивление, почти аналогичное электрическому сопротивлению, также имеет несколько отличий от него. Когда переменный ток проходит через электрическую цепь или элемент, изменяется как фаза, так и амплитуда тока. Кроме того, энергия запасается в элементе, содержащем реактивное сопротивление.

Таким образом, энергия высвобождается либо в форме электрического поля, либо в форме магнитного поля. Реактивное сопротивление в магнитном поле сопротивляется изменению тока, тогда как в электрическом поле реактивное сопротивление будет сопротивляться изменению напряжения. Если реактивное сопротивление высвобождает энергию в виде магнитного поля, оно называется индуктивным реактивным сопротивлением, тогда как если реактивное сопротивление высвобождает энергию в форме электрического поля, оно называется емкостным реактивным сопротивлением. С увеличением частоты емкостное сопротивление уменьшается, а индуктивное сопротивление увеличивается. Идеальный резистор будет иметь нулевое реактивное сопротивление, тогда как идеальные катушки индуктивности и конденсаторы будут иметь нулевое сопротивление.

Что такое индуктивное сопротивление?

Индуктивное сопротивление – это реактивное сопротивление, создаваемое индуктивным элементом (индуктивностью). Его можно обозначить как. С помощью индуктивных элементов электрическая энергия может храниться в виде магнитного поля. Когда через цепь пропускают переменный ток, вокруг нее образуется магнитное поле, которое может изменяться под действием тока. Изменения в магнитном поле могут индуцировать другой электрический ток в той же цепи. Закон Ленца гласит, что направление этого тока противоположно основному току. Следовательно, мы можем сказать, что индуктивное сопротивление фактически препятствует изменению тока через элемент.

 

Протекание тока из-за индуктивного реактивного сопротивления приводит к задержке, которая может привести к созданию разности фаз между сигналами тока и напряжения. Ток индуктивной цепи может отставать от напряжения. В идеальной индуктивной цепи ток отстает от напряжения на . Индуктивное сопротивление также является причиной отставания коэффициента мощности. Ниже показана векторная диаграмма идеальной индуктивной цепи.

 

(Изображение скоро будет загружено)

 

Векторная диаграмма идеальной индуктивной цепи

Когда учащиеся готовятся к ЕГЭ, вопросы могут быть сложными, но определенно не невозможно решить. Помните, что будучи студентами, вы находитесь на пути к построению светлого будущего, поэтому о чем беспокоиться? Дайте экзаменам все возможное!

Чтобы помочь учащимся лучше учиться и стараться изо всех сил, Веданту дает определения и решенные примеры, чтобы лучше всего проиллюстрировать тему индуктивного реактивного сопротивления и емкостного реактивного сопротивления. Этот ресурс особенно полезен, когда учащиеся хотят быстро ознакомиться с темами и решить свои сомнения относительно вопросов, которые могут быть заданы в JEE Mains. Студенты должны знать, что каждая тема важна не только для экзамена, но и для их будущей карьеры.

Что такое электрическое, индуктивное и емкостное сопротивление?

1. Электрическое реактивное сопротивление – определяется как поток, который течет в направлении, противоположном течению тока в электрической цепи. Чем больше реактивное сопротивление, тем меньше ток будет для этого приложенного напряжения. Реактивное сопротивление ведет себя по-разному в магнитном и электрическом полях. В магнитном поле реактивное сопротивление будет сопротивляться изменению тока, в то время как оно сопротивляется изменению напряжения в электрическом поле.

2. Индуктивное реактивное сопротивление — Обозначается символом X _L , создается за счет наличия индуктивного элемента, т.е. индуктора. Одним из применений индуктивного элемента является то, что его можно использовать для хранения электрической энергии в виде магнитного поля. Конкретный закон, называемый законом Ленца, ясно гласит, что направление тока, создаваемого индуктивным реактивным сопротивлением, противоположно направлению основного тока. Это может привести к задержке мощности между формами сигналов напряжения и тока.

3. Емкостное реактивное сопротивление — Обозначается символом X _C , создается за счет наличия емкостного элемента, т.е. конденсаторов. Емкостной элемент помогает хранить электрическую энергию в виде электрического поля, в отличие от индуктивного элемента. Емкостное реактивное сопротивление возникает из-за противоположности напряжения на конденсаторах. Это также создает отставание между током и напряжением. Идеальное отставание в индуктивной цепи и идеальное опережение напряжения по току в емкостной цепи равны 90 градусов.

Реактивное, индуктивное и емкостное сопротивление | Физика

Цели обучения

К концу этого раздела вы сможете:

• Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное реактивное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Катушки индуктивности и индуктивное реактивное сопротивление

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что это оказывает незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности с пренебрежимо малым сопротивлением. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рис. 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:

Напряжение переменного тока в катушке индуктивности

Когда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − L (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L задается версией закона Ома:

[латекс]I=\frac{V}{{X}_{L}}\\[/latex],

, где В — среднеквадратичное значение напряжения. через индуктор и X _L определяется как

[латекс]{X}_{L}=2\pi{fL}\\[/латекс],

с f частотой источника переменного напряжения в герцах (анализ схемы с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). Х _Д называется индуктивным сопротивлением , потому что индуктор препятствует протеканию тока. X _L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в (циклах/с)(Ом ⋅ с)=Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X _L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X _L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I / Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения X _L   = 2πf L . Как только X _L найдены для каждой частоты, можно использовать закон Ома, как указано в уравнении I = V / X _L , чтобы найти ток на каждой частоте.

Решение для (a)

Ввод частоты и индуктивности в уравнение  x _L = 2πf L Приведена

x _L = 2πf L = 6.28 (60,0/с) (3,00 м) = 1,13 №.

Аналогично, на частоте 10 кГц

X _L   = 2πf L = 6,28(1,00 × 10 ^{4 кОм, 1 8,0 мГн) при 10 90,0 мГн при}

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I  =  В / X _L , при условии, что приложенное среднеквадратичное значение напряжения составляет 120 В. Для первой частоты это дает

[латекс]I=\frac{V}{{X}_{L }}=\frac{120\text{ V}}{1,13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\\[/latex].

Аналогично, на частоте 10 кГц

[латекс]I=\frac{V}{{X}_{L}}=\frac{120\text{ V}}{188\text{ }\Omega}= 0,637\text { A at } 10\text{ кГц}\\[/latex].

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Конденсаторы и емкостное реактивное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и так что можно предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( Q = 0 на нем) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четвертую периода или на угол сдвига фаз 90º.

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C , по другой версии закона Ома определяется как

[latex]I=\frac{V}{{X}_{C}}\\[/latex] ,

, где V является среднеквадратичным напряжением и определено x _C (как с x _L , эта экспрессия для x 9082 . схема с использованием правил Кирхгофа и исчисления) будет

[латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex],

, где X _C называется емкостным реактивным сопротивлением , потому что конденсатор препятствует протеканию тока. X _C измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). X _C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X}_{C}=\frac{1}{2\pi fC}\\[/latex]. Однажды 9Для каждой частоты было найдено 0114 X _C . Для определения тока на каждой частоте можно использовать закон Ома:

Решение для (a)

Ввод частоты и емкости в [латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex], дает

[ латекс]\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{1}{6.28\left(60.0/\text {s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ at }60\text{ Гц}\end{массив}\ \[/латекс]. 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\[/латекс].

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = В / X _{В действующее значение C 9008 Для первой частоты это дает}

[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{531\text{ }\Omega}=0,226 \text{ A при }60\text{ Гц}\\[/latex].

Аналогично, на частоте 10 кГц

[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{3.18\text{ }\Omega}= 3,37 \text{ А при }10 \text{ Гц}\\[/latex].

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают противоположное воздействие на цепи переменного тока по сравнению с катушками индуктивности .

Резисторы в цепи переменного тока

В качестве напоминания рассмотрим рис. 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Переменное напряжение на резисторе

Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.

Резюме раздела

• Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
• Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
• Закон Ома для катушки индуктивности

  [латекс]I=\frac{V}{{X}_{L}}\\[/латекс],

  , где В — среднеквадратичное напряжение на катушке индуктивности.

• X _L определяется как индуктивное реактивное сопротивление, определяемое формулой

  [латекс]{X}_{L}=2\pi fL\\[/латекс],

  с f частотой источника переменного напряжения в герцах.

• Индуктивное сопротивление  X _L выражается в омах и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

  [латекс]I=\frac{V}{{X}_{C}}\\[/латекс],

  , где В — среднеквадратичное напряжение на конденсаторе.

• Х _С  определяется как емкостное реактивное сопротивление, определяемое выражением

  [латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex].

• X _C измеряется в омах и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1. Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.

2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул частотой 100 Гц в звуковой системе? Объяснять.

3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?

5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.

Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.

6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?

Задачи и упражнения

1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?

2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?

3. Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?

4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?

5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?

6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?

7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?

8. Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?

9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]\текст{10,0 м\Омега}[/латекс] для сигнала частотой 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12. Необоснованные результаты  При записи напряжений, вызванных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

13. Создайте свою собственную задачу  Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.