Математическая индукция — Википедия
Материал из Википедии — свободной энциклопедии

Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: P1,P2,…,Pn,Pn+1,…{\displaystyle P_{1},P_{2},\ldots ,P_{n},P_{n+1},\ldots }.
Допустим, что
Тогда все утверждения нашей последовательности верны. |
Логическим основанием для этого метода доказательства служит так называемая
Принцип полной математической индукции[править | править код]
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }. Если для любого натурального n{\displaystyle n} из того, что истинны все P1{\displaystyle P_{1}}, P2{\displaystyle P_{2}}, P3{\displaystyle P_{3}}, …{\displaystyle \ldots }, Pn−1{\displaystyle P_{n-1}}, следует также истинность Pn{\displaystyle P_{n}}, то все утверждения в этой последовательности истинны, то есть (∀n∈N)((∀i∈{1;…;n−1})Pi⟶Pn)⟶(∀n∈N)Pn{\displaystyle (\forall n\in {\mathbb {N} }){\Big (}(\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}{\Big )}\longrightarrow (\forall n\in {\mathbb {N} })P_{n}}. |
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при n=1{\displaystyle n=1} импликация (∀i∈{1;…;n−1})Pi⟶Pn{\displaystyle (\forall i\in \{1;\dots ;n-1\})P_{i}\longrightarrow P_{n}} эквивалентна P1{\displaystyle P_{1}}. Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида[1]. Современное название метода было введено де Морганом в 1838 году.
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
- 1+q+q2+⋯+qn=1−qn+11−q.{\displaystyle 1+q+q^{2}+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
Доказательство. Индукция по n.
База, n = 1:
- 1+q=(1−q)(1+q)1−q=1−q1+11−q.{\displaystyle 1+q={\frac {(1-q)(1+q)}{1-q}}={\frac {1-q^{1+1}}{1-q}}.}
Переход: предположим, что
- 1+q+⋯+qn=1−qn+11−q,{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}},}
тогда
- 1+q+⋯+qn+qn+1=1−qn+11−q+qn+1={\displaystyle 1+q+\cdots +q^{n}+q^{n+1}={\frac {1-q^{n+1}}{1-q}}+q^{n+1}=}
- =1−qn+1+(1−q)qn+11−q=1−qn+1+qn+1−q(n+1)+11−q=1−q(n+1)+11−q{\displaystyle ={\frac {1-q^{n+1}+(1-q)q^{n+1}}{1-q}}={\frac {1-q^{n+1}+q^{n+1}-q^{(n+1)+1}}{1-q}}={\frac {1-q^{(n+1)+1}}{1-q}}},
что и требовалось доказать.
Комментарий: истинность утверждения Pn{\displaystyle P_{n}} в этом доказательстве — то же, что истинность равенства
- 1+q+⋯+qn=1−qn+11−q.{\displaystyle 1+q+\cdots +q^{n}={\frac {1-q^{n+1}}{1-q}}.}
- ↑ Nachum L. Rabinovih. Раби Леви бен Гершом и происхождение метода математической индукции = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — Вып. 6. — С. 237-248.
- Видео по методу математической индукции
ИНДУКЦИЯ — Новейший философский словарь
ИНДУКЦИЯ (лат. inductio — наведение) — метод познания, связанный с обобщением наблюдений и экспериментов. В логическом плане И. представляет собой умозаключение, при котором общее суждение по особым правилам получается на основе единичных или частных посылок. В науке и повседневной жизни многие положения общего характера появляются в результате освоения отдельных фактов. Происходит мысленный переход от единичного и частного к общему. Например, в начале 17 в. И. Кеплер сформулировал утверждение: «Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце» (позже оно получило известность под названием первого закона Кеплера). Это обобщение было получено на основе изучения движения отдельных планет — Земли, Марса, Венеры и др. Затем было выяснено, что и другие небесные тела под воздействием притяжения Солнца могут описывать вокруг него конические сечения: окружности, эллипсы, параболы и гиперболы. Вследствие этого первоначальная формулировка первого закона Кеплера была изменена и получила следующий вид: «Всякое тело, движущееся вокруг Солнца, описывает коническое сечение, в одном из фокусов которого находится Солнце». Объективной основой для получения общих положений с помощью И. является повторяемость событий, объединенных общей закономерной связью, благодаря чему по части фактов можно устанавливать общий закон. Вместе с тем, повторение может быть характерно для более узкого круга событий, чем тот, на который претендует обобщение, или может свидетельствовать о случайных совпадениях. Игнорирование данных обстоятельств приводит к ошибкам в процессе применения И., носящих названия «поспешное обобщение» и «после этого значит по причине этого». Вывод с помощью И. имеет вероятностный характер. Он будет более надежным, если а) число предметов, о которых говорится в посылках, будет большим; б) эти предметы будут более разнообразны; в) они будут характерными, типичными представителями того класса предметов, о котором говорится в заключении; г) субъект заключения будет возможно меньшим, а предикат возможно большим по объему; д) признак, переносимый на совокупность предметов, о которых речь идет в заключении, будет более существенным для них. Раздел современной логики, связанный с изучением индуктивных выводов, с применением к ним математических методов, с построением дедуктивных теорий об индуктивных процессах, называется индуктивной логикой.
Источник: Новейший философский словарь на Gufo.me
Значения в других словарях
- индукция — Заимств. в начале XIX в. из франц. яз., где induction < лат. inductio, суф. производного от inducere «вводить, проводить, выводить». Этимологический словарь Шанского
- индукция — ИНДУКЦИЯ (от лат. inductio — выведение; возбуждение) — этот термин в современной логике используется как синоним более точного, но более громоздкого, термина «индуктивное рассуждение». Энциклопедия эпистемологии и философии науки
- Индукция — I (греч. hypothesis — основание, предположение, от hypó — под, внизу и thésis — положение) то, что лежит в основе, — причина или сущность. Например, «атомы» Демокрита, «идеи» Платона, «перводвигатель» Аристотеля. В современном словоупотреблении… Большая советская энциклопедия
- индукция — ИНДУКЦИЯ, и, ж. 1. Способ рассуждения от частных фактов, положений к общим выводам; противоп. дедукция (книжн.). 2. Возбуждение электрического тока в каком-н. проводнике при движении его в магнитном поле или изменении вокруг него магнитного поля (спец.). Толковый словарь Ожегова
- индукция — I. ИНДУКЦИЯ I и, ж. induction f., нем. Induction <�лат. inductio выведение. 1. Логическое умозаключение от частного к общему, от отдельных фактов к обобщениям. Крысин 1998. 2. мат. Словарь галлицизмов русского языка
- индукция — сущ., кол-во синонимов: 5 возбуждение 58 индуктирование 1 наведение 12 умозаключение 17 электроиндукция 1 Словарь синонимов русского языка
- индукция — ИНДУКЦИЯ — 1. Один из механизмов регуляции биосинтеза белка. И. представляет собой активацию синтеза какого-нибудь фермента посредством проникновения в клетку определенного вещества (индуктора). 2. Развитие клеток под влиянием веществ, выделяемых другими клетками. Ботаника. Словарь терминов
- ИНДУКЦИЯ — ИНДУКЦИЯ — в биологии -1) взаимодействие процессов возбуждения и торможения; торможение в группе нейронов вызывает (индуцирует) возбуждение (положительная индукция) — которое индуцирует торможение (отрицательная индукция)… Большой энциклопедический словарь
- индукция — Индукция, индукции, индукции, индукций, индукции, индукциям, индукцию, индукции, индукцией, индукциею, индукциями, индукции, индукциях Грамматический словарь Зализняка
- индукция — ИНД’УКЦИЯ, индукции, ·жен. (·лат. inductio — наведение). 1. Метод мышления, при котором из частных суждений выводится общее (филос.). Толковый словарь Ушакова
- ИНДУКЦИЯ — ИНДУКЦИЯ (от лат. inductio — введение) — англ. induction; нем. Induktion. 1. Форма умозаключения, способ рассуждения, означающие движение познания от частного к общему, обобщение отдельных факторов… Социологический словарь
- индукция — индукция I ж. 1. Логическое умозаключение от частного к общему, от единичного наблюдения к обобщению, от фактов к некоторой гипотезе. || противоп. дедукция… Толковый словарь Ефремовой
- индукция — ИНДУКЦИЯ -и; ж. [лат. inductio] 1. Лог. Способ рассуждения от отдельных частных фактов и положений к общим выводам, обобщениям (противоп.: дедукция). И. — основной метод обучения. 2. Физ. Возбуждение электродвижущей силы в каком-л. Толковый словарь Кузнецова
- индукция — Индукции, ж. [латин. inductio – наведение]. 1. Метод мышления, при к-ром из частных суждений выводится общее (филос.). 2. Возбуждение электрической и магнитной энергии под влиянием магнитного поля или приближением заряженного электрического тела (физ.). Магнитная и электрическая индукция. Большой словарь иностранных слов
- индукция — орф. индукция, -и Орфографический словарь Лопатина
- ИНДУКЦИЯ — ИНДУКЦИЯ – познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение. Идея индукции обсуждалась Сократом и Аристотелем… Новая философская энциклопедия
- Индукция — (лат. inductio введение, наведение) в физиологии — функциональное взаимодействие нервных центров, характеризующееся изменением их возбудимости. Индукция взаимная —… Медицинская энциклопедия
- ИНДУКЦИЯ — ИНДУКЦИЯ, в физике, процесс электризации или намагничивания. В случае ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ электрический ток вызывается при помещении ПРОВОДНИКА в переменное МАГНИТНОЕ ПОЛЕ. Величина тока пропорциональна скорости изменения МАГНИТНОГО ПОТОКА. Научно-технический словарь
- индукция — Французское – induction. Латинское – inducere (вводить, проводить). Слово было заимствовано русским языком из французского в начале XIX в. Индукция – логическое умозаключение от частного к общему; взаимодействие нервных процессов возбуждения и торможения. Этимологический словарь Семёнова
- индукция — Инду́кц/и/я [й/а]. Морфемно-орфографический словарь
- Индукция — (от лат. inductio — наведение) переход от единичного знания об отдельных предметах данного класса к общему выводу о всех предметах данного класса; один из методов познания. Основой И. являются данные, полученные путём наблюдения и эксперимента. Педагогический терминологический словарь

ИНДУКЦИОННЫЙ — это… Что такое ИНДУКЦИОННЫЙ?
индукционный — индуктивный, наведенный, высокочастотный Словарь русских синонимов. индукционный прил., кол во синонимов: 4 • высокочастотный (2) • … Словарь синонимов
индукционный — ИНДУК ИЯ, и, ж. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
индукционный — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN induction instrument … Справочник технического переводчика
индукционный — относящийся к индукции2, и ная катушка состоит из двух обмоток на сердечнике из магнитного материала; служит для возбуждения путем индукции токов высокого напряжения; и. у с коритель электронов то же, что бетатрон. Новый словарь иностранных слов … Словарь иностранных слов русского языка
Индукционный — I прил. соотн. с сущ. индукция I, связанный с ним II прил. соотн. с сущ. индукция II, связанный с ним III прил. соотн. с сущ. индукция III, связанный с ним Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Индукционный — I прил. соотн. с сущ. индукция I, связанный с ним II прил. соотн. с сущ. индукция II, связанный с ним III прил. соотн. с сущ. индукция III, связанный с ним Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
индукционный — индукционный, индукционная, индукционное, индукционные, индукционного, индукционной, индукционного, индукционных, индукционному, индукционной, индукционному, индукционным, индукционный, индукционную, индукционное, индукционные, индукционного,… … Формы слов
индукционный — индукци онный … Русский орфографический словарь
индукционный — … Орфографический словарь русского языка
ИНДУКЦИОННЫЙ — [см. индукция] прил. от сл. индукция; относящийся к индукции (см., напр., Индукционное торможение) … Психомоторика: cловарь-справочник
ИНДУКТИВНЫЙ — это… Что такое ИНДУКТИВНЫЙ?
ИНДУКТИВНЫЙ — ИНДУКТИВНЫЙ, индуктивная, индуктивное (книжн.). 1. прил. к индукция в 1 знач.; основанный на индукции (филос.). Индуктивный метод. Индуктивное доказательство. 2. прил. к индукция во 2 знач.; производимый индукцией. Индуктивная связь. Индуктивное… … Толковый словарь Ушакова
Индуктивный — метод. Различают двоякую И.: полную (inductio completa) инеполную (ипductHo incompleta или per enumerationern simplicern). Впервой мы заключаем от полного перечисления видов известного рода ковсему роду; очевидно, что при подобном способе… … Энциклопедия Брокгауза и Ефрона
индуктивный — ая, ое. inductif, ive adj. 1. Основанный на индукции, пользующийся методом индукции. СИС 1985. Индуктивное доказательство. Уш. 1934. Индуктивный метод. БАС 1. 2. Отн. к индукции <в элетротехнике>. БАС 1. Индуктивная связь. Индуктивное… … Исторический словарь галлицизмов русского языка
индуктивный — ИНДУК ИЯ, и, ж. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
индуктивный — прил., кол во синонимов: 2 • индукционный (4) • электроиндуктивный (2) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
индуктивный — [IEV number 151 15 53] EN inductive, adj qualifies an electric device or an electric circuit the predominant quantity of which, under given conditions, is an inductance [IEV number 151 15 53] FR inductif, adj qualifie un dispositif… … Справочник технического переводчика
Индуктивный — I прил. соотн. с сущ. индукция I, связанный с ним II прил. соотн. с сущ. индукция II, связанный с ним III прил. соотн. с сущ. индукция III, связанный с ним Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Индуктивный — I прил. соотн. с сущ. индукция I, связанный с ним II прил. соотн. с сущ. индукция II, связанный с ним III прил. соотн. с сущ. индукция III, связанный с ним Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
индуктивный — индуктивный, индуктивная, индуктивное, индуктивные, индуктивного, индуктивной, индуктивного, индуктивных, индуктивному, индуктивной, индуктивному, индуктивным, индуктивный, индуктивную, индуктивное, индуктивные, индуктивного, индуктивную,… … Формы слов
Индуктивный — English: Inductive Термин, применяемый к устройству или цепи, у которого индуктивность в определенных условиях является преобладающей (по СТ МЭК 50(151) 78) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
Электромагнитная индукция — это… Что такое Электромагнитная индукция?
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа[источник не указан 100 дней] 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
- — электродвижущая сила, действующая вдоль произвольно выбранного контура,
- — магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
- Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
- — электродвижущая сила,
- — число витков,
- — магнитный поток через один виток,
- — потокосцепление катушки.
Векторная форма
В дифференциальной форме закон Фарадея можно записать в следующем виде:
- (в системе СИ)
или
- (в системе СГС).
В интегральной форме (эквивалентной):
- (СИ)
или
- (СГС)
Здесь — напряжённость электрического поля, — магнитная индукция, — произвольная поверхность, — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
- В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[1].
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство продолжает соблюдаться, но ЭДС в левой части теперь не сводится к (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
- Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[2] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[3]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
- Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определенных ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединенным к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчета, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчета, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчета мы ее рассчитали.
Потенциальная форма
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
- (в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
История
В 1820 г. Ганс Христиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 г. в своём дневнике. Многие годы настойчиво ставил он различные опыты, но безуспешно, и только 29 августа 1831 г. наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, заключалась в том, что Фарадей изготовил кольцо из мягкого железа примерно 2 см шириной и 15 см диаметром и намотал много витков медной проволоки на каждой половине кольца. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
См. также
Примечания
- ↑ Это уравнение Максвелла может быть переписано в эквивалентном виде
- ↑ М. Лившиц Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.
Ссылки
Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия
Метод математической индукции — это… Что такое Метод математической индукции?
- Метод математической индукции
-

Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами:

Допустим, что
- Установлено, что P1 верно. (Это утверждение называется базой индукции.)
- Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений
 . Допустим, что
. Допустим, что- Установлено, что P1 верно.
- Для любого натурального n доказано, что если верны все
 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда

 ,
,
что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
См. также
Вариации и обобщения
Литература
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
Wikimedia Foundation. 2010.
- Метод лактационной аменореи
- Метод реплик
Смотреть что такое «Метод математической индукции» в других словарях:
Принцип математической индукции — Математическая индукция в математике один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 база индукции, а затем… … Википедия
Метод индукции — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Индуктивный метод — Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не столько через законы логики, а скорее через некоторые… … Википедия
ГЕНЕТИЧЕСКИЙ МЕТОД — способ задания содержания и сущности исследуемого предмета не путем конвенции, идеализации или логического вывода, а с помощью изучения его происхождения (опираясь на изучение причин, приведших к его возникновению, механизм становления). Широко… … Философия науки: Словарь основных терминов
Аксиоматический метод — способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) аксиомы (См. Аксиома), или Постулаты, из которых все остальные утверждения этой науки (теоремы (См. Теорема)) должны выводиться… … Большая советская энциклопедия
аксиоматический метод — АКСИОМАТИЧЕСКИЙ МЕТОД (от греч. axioma) принятое положение способ построения научной теории, при котором в доказательствах пользуются лишь аксиомами, постулатами и ранее выведенными из них утверждениями. Впервые ярко продемонстрирован… … Энциклопедия эпистемологии и философии науки
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается … Математическая энциклопедия
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Индуктивное умозаключение — У этого термина существуют и другие значения, см. Индукция. Индукция (лат. inductio наведение) процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки… … Википедия



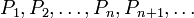
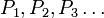 . Допустим, что
. Допустим, что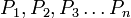 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)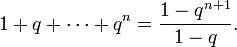
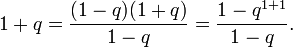
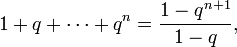
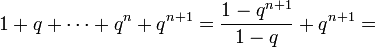
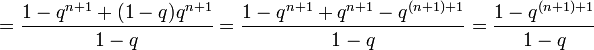 ,
,
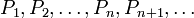
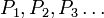 . Допустим, что
. Допустим, что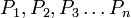 , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
, то верно и Pn + 1. (Это утверждение называется индукционным переходом.)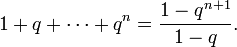
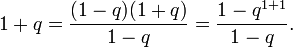
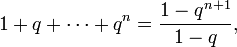
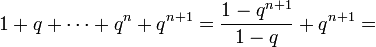
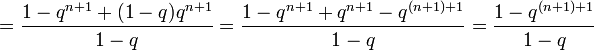 ,
,