Логическое «или» — это… Что такое Логическое «или»?

Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».

Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи: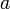
|| | .

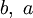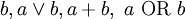Булева алгебра

В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен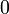

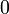, если оба операнда равны ; во всех остальных случаях результат равен .

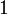Многозначная логика

В многозначной логике операция дизъюнкции может определяться другими способами. Чаще всего применяется схема: 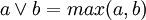, где

. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов .

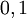Классическая логика

В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространенных вариантов включает 3 аксиомы для дизъюнкции: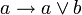

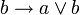
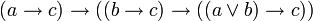
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Программирование

В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++ логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|».

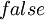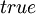Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата или . Например:

if (a || b) 
{
    /* какие-то действия */
};

Результат будет равен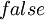

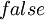, если оба операнда равны или 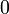. В любом другом случае результат будет равен .

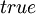При этом применяется стандартное соглашение: если значение левого операнда равно 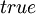, то значение правого операнда не вычисляется (вместо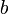

может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:

if (a == NULL || a->x == 0) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет разыменования нулевого указателя.

Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =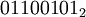
b =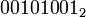
то
a ИЛИ b =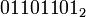

Связь с естественным языком

Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.

Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ».

См. также

Wikimedia Foundation. 2010.

Введение, Или что такое логика и зачем она нужна?. Логика. Учебное пособие

Введение, Или что такое логика и зачем она нужна?

Начиная знакомиться с какой-либо наукой, мы прежде всего отвечаем на вопрос о том, что она изучает, чему посвящена, чем занимается. Логика – это наука о мышлении. Но ведь мышлением занимаются и психология, и педагогика, и многие другие науки. Значит, логика занимается не всеми вопросами и проблемами, связанными с мышлением, не всеми его областями или сторонами, а только какими-то из них. Что же интересует логику в мышлении?

Каждый из нас хорошо знает, что по содержанию человеческое мышление бесконечно многообразно, ведь мыслить (думать) можно о чем угодно, например, – об устройстве мира и происхождении жизни на Земле, о прошлом человечества и его будущем, о прочитанных книгах и просмотренных фильмах, о сегодняшних занятиях и завтрашнем отдыхе и т. д. и т. п.

Но самое главное заключается в том, что наши мысли возникают и строятся по одним и тем же законам, подчиняются одним и тем же принципам, укладываются в одни и те же схемы или формы. Причем, если содержание нашего мышления, как уже было сказано, бесконечно разнообразно, то форм, в которых выражается это разнообразие совсем немного.

Для пояснения этой мысли приведем простой пример. Рассмотрим три совершенно различных по содержанию высказывания:

1. Все караси – это рыбы;

2. Все треугольники – это геометрические фигуры;

3. Все стулья – это предметы мебели.

Несмотря на различное содержание, у этих трех высказываний есть нечто общее, что-то их объединяет. Что? Их объединяет не содержание, а форма. Отличаясь по содержанию, они сходны по форме: ведь каждое из этих трех высказываний строится по схеме или по форме – «Все А – это В», где А и В – это какие-либо предметы. Понятно, что само высказывание «Все А – это В» лишено всякого содержания (О чем конкретно оно говорит? Ни о чем!). Это высказывание представляет собой чистую форму, которую, как вы догадываетесь, можно наполнить любым содержанием, например: Все сосны – это деревья; Все города – это населенные пункты; Все школы – это учебные заведения; Все тигры – это хищники

и т. д. и т. п.

Приведем другой пример. Возьмем три различных по содержанию высказывания:

1. Если наступает осень, то опадают листья;

2. Если завтра будет дождь, то на улице будут стоять лужи;

3. Если вещество – металл, то оно электропроводно.

Будучи непохожими друг на друга по содержанию, эти три высказывания сходны между собой тем, что строятся по одной и той же форме: «Если А, то В». Понятно, что к этой форме можно подобрать огромное количество различных содержательных высказываний, например: Если не подготовиться к контрольной работе, то можно получить двойку; Если взлетная полоса покрыта льдом, то самолеты не могут взлетать; Если слово стоит в начале предложения, то его надо писать с большой буквы

и т. д. и т. п.

Итак, мы заметили, что по содержанию наше мышление бесконечно разнообразно, но все это разнообразие укладывается всего в несколько форм. Так вот логика не интересуется содержанием мышления (им занимаются другие науки), она изучает только формы мышления, ее интересует не то, что мы мыслим, а то, как мы мыслим, поэтому она также часто называется формальной логикой. Так, например, если по содержанию высказывание Все комары – это насекомые является нормальным, понятным, осмысленным, а высказывание Все Чебурашки – это инопланетяне является бессмысленным, нелепым, абсурдным, то для логики эти два высказывания равноценны: ведь она занимается формами мышления, а форма у этих двух высказываний была одной и той же – «Все А – это В».

Таким образом, форма мышления – это способ, которым мы выражаем наши мысли, или схема, по которой они строятся. Существует три формы мышления.

1. Понятие – это форма мышления, которая обозначает какой-либо объект или признак объекта (примеры понятий: карандаш, растение, небесное тело, химический элемент, мужество, глупость, нерадивость и т. п.).

2. Суждение – это форма мышления, которая состоит из понятий, связанных между собой и что-либо утверждает или отрицает (примеры суждений: Все планеты являются небесными телами; Некоторые школьники – это двоечники; Все треугольники не являются квадратами и т. п.).

3. Умозаключение – это форма мышления, в которой из двух или нескольких исходных суждений вытекает новое суждение или вывод. Примеры умозаключений:

Все планеты движутся.

Юпитер – это планета.

Юпитер движется.

или

Железо электропроводно.

Медь электропроводна.

Ртуть электропроводна.

Железо, медь, ртуть – это металлы.

Все металлы электропроводны.

Весь бесконечный мир наших мыслей выражается в понятиях, суждениях и умозаключениях. Об этих трех формах мышления мы будем подробно говорить на других страницах книги.

Помимо форм мышления логика также занимается законами мышления, то есть – такими правилами, соблюдение которых всегда приводит рассуждение, независимо от его содержания, к истинным выводам и предохраняет от ложных (при условии истинности исходных суждений). Основных законов мышления (или законов логики) четыре. Здесь только перечислим (назовем) их, а подробно рассмотрим каждый из них после того, как рассмотрим все формы мышления.

1. Закон тождества.

2. Закон противоречия.

3. Закон исключенного третьего.

4. Закон достаточного основания.

Нарушение этих законов приводит к различным логическим ошибкам, как правило, – к ложным выводам. Иногда эти законы нарушают непроизвольно, не нарочно, по незнанию. Возникающие при этом ошибки называются паралогизмами. Однако иногда это делают преднамеренно, с целью запутать собеседника, сбить его с толка и доказать ему какую-нибудь ложную мысль. Такие преднамеренные нарушения логических законов для внешне правильного доказательства ложных мыслей называются софизмами, о которых речь впереди.

Итак, логика – это наука о формах и законах правильного мышления.

Логика появилась приблизительно в V в. до н. э. в Древней Греции. Ее создателем считается знаменитый древнегреческий философ и ученый Аристотель (384–322 гг. до н. э.). Как видим, логике 2,5 тысячи лет, однако она до сих пор сохраняет свое практическое значение. Многие науки и искусства Древнего мира навсегда ушли в прошлое и представляют для нас только «музейное» значение, интересны нам исключительно как памятники старины. Но некоторые немногие создания древних пережили века, и в настоящее время мы продолжаем ими пользоваться. К их числу относится геометрия Евклида (в школе мы изучаем именно ее) и логика Аристотеля, которая также часто называется традиционной логикой.

В XIX веке появилась и стала быстро развиваться символическая или математическая, или современная логика, в основе которой лежат идеи, выдвинутые задолго до Х1Х в. немецким математиком и философом Готфридом Лейбницем (1646–1716 гг.), об осуществлении полного перехода к идеальной (т. е. совершенно освобожденной от содержания) логической форме при помощи универсального символического языка, аналогичного языку алгебры. Лейбниц говорил о возможности представить доказательство как математическое вычисление. Ирландский логик и математик Джордж Буль (1815–1864 гг.) истолковал умозаключение как результат решения логических равенств, в результате чего теория умозаключений приняла вид своеобразной алгебры, отличающейся от обычной алгебры лишь отсутствием численных коэффициентов и степеней. Таким образом, одно из основных отличий символической логики от традиционной заключается в том, что в последней при описании правильного мышления используется обычный, или естественный язык; а символическая логика исследует тот же предмет (правильное мышление) с помощью построения искусственных, специальных, формализованных языков, или, как их еще называют, исчислений.

Традиционная и смволическая логика не являются, как может показаться, различными науками, а представляют собой два последовательных периода в развитии одной и той же науки: основное содержание традиционной логики вошло в символическую, было в ней уточнено и расширено, хотя многое при этом оказалось переосмысленным.

Теперь ответим на вопрос, зачем нам нужна логика, какую роль она играет в нашей жизни. Логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше их понимать, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях. Конечно же, без логики вполне можно обойтись: одного здравого смысла и жизненного опыта часто бывает достаточно для решения каких-либо задач. Например, любой человек, не знакомый с логикой, сможет найти подвох в следующем рассуждении:

Движение вечно.

Хождение в школу – это движение.

Следовательно, хождение в школу вечно.

Каждый заметит, что ложный вывод получается из-за употребления слова «движение» в разных смыслах (в первом исходном суждении оно употребляется в широком, философском смысле, а во втором – в узком, механическом смысле). Однако найти ошибку в рассуждении не всегда просто. Рассмотрим такой пример:

Все мои друзья знают английский язык.

Нынешний президент Америки тоже знает английский язык.

Следовательно, нынешний президент Америки – мой друг.

Любой человек увидит, что в этом рассуждении есть какой-то подвох, что-то в нем не то или не так. Но что? Тот, кто не знаком с логикой, скорее всего, не сможет точно определить, какая ошибка здесь допущена. Тот, кто знаком с логикой сразу же скажет, что в данном случае допущена ошибка – «нераспределенность среднего термина в простом силлогизме». Или такой пример:

Во всех городах за полярным кругом бывают белые ночи.

Петербург не находится за полярным кругом.

Следовательно, в Петербурге не бывает белых ночей.

Как видим, из двух истинных суждений вытекает ложный вывод. Понятно, что в этом рассуждении тоже что-то не то, есть некая ошибка. Но какая? Вряд ли не знакомый с логикой человек сможет сразу же ее найти. А тот, кто владеет логической культурой, немедленно установит данную ошибку – «расширение большего термина в простом силлогизме».

Прочитав эту книгу, вы узнаете, не только то, как нарушаются логические законы в подобных рассуждениях, но и много другой интересной и полезной информации.

Итак, здравого смысла и жизненного опыта, как правило, достаточно для того, чтобы ориентироваться в различных затруднительных ситуациях. Но если к нашему здравому смыслу и жизненному опыту добавить еще и логическую культуру, то мы от этого нисколько не проиграем, а даже, наоборот, выиграем. Конечно же, логика никогда не решит всех проблем, но помочь в жизни она, несомненно, может.

Здравый смысл часто называют практической, или интуитивной логикой. Она формируется стихийно в процессе жизненного опыта, примерно к 6–7 годам, т. е. к школьному возрасту или даже раньше, и все мы ей владеем. Так, например, само слово «логика», скорее всего, было знакомо вам задолго до того, как вы начали читать эту книгу. В жизни мы часто сталкиваемся с такими выражениями, как «логичное рассуждение», «нелогичный поступок», «железная логика» и т. п. Даже если мы никогда не изучали логику, то все равно вполне понимаем, о чем идет речь, когда говорят о логике, логичном или нелогичном.

Рассмотрим такой пример: любой человек, не знакомый с логикой, заметит логическую некорректность и даже нелепость высказывания: Я иду в новых брюках, а ты идешь в гимназию. И каждый скажет, что корректным и осмысленным было бы такое высказывание: Я иду в брюках, а ты идешь в шортах или: Я иду в гимназию, а ты идешь в лицей. Когда мы изучаем логику, то узнаем, что в приведенном примере нарушается логический закон тождества, так как в нем смешиваются две различные (неравные или нетождественные друг другу) ситуации: идти в какой-то одежде и идти куда-то. Получается, что еще до знакомства с законом тождества мы уже им практически пользуемся, знаем о нем, только неявно, интуитивно. Точно так же закон тождества нарушается в высказывании: Сегодня будем копать траншею от этого столба и до обеда. Даже если человек ничего не знает о законе тождества и о его разнообразных и многочисленных нарушениях, он, тем не менее, обязательно обратит внимание на то, что в данном высказывании присутствует какая-то логическая ошибка (хотя бы он и не мог определить, какая именно).

Точно так же любой человек, скорее всего, не сможет не заметить некое логическое нарушение в следующих высказываниях: Он не взял устного разрешения в письменной форме; Поедем завтра вечером на рассвете; Она была юной девушкой преклонного возраста и т. п. Далеко не каждый сможет квалифицировать данную ошибку как нарушение логического закона противоречия. Однако, даже если мы ничего не знаем об этом законе, мы чувствуем, или ощущаем его нарушение.

Наконец, в повседневной жизни каждый из нас часто слышит и сам употребляет такие выражения, как: Почему я должен тебе верить? Чем ты это докажешь? На каком основании? Обоснуй! Мотивируй! и т. п. Когда мы так говорим, то используем логический закон достаточного основания. Тот, кто не изучал логику, скорее всего, не знаком с этим законом и ничего о нем не слышал. Однако, как видим, незнание данного логического закона не мешает нам практически, или интуитивно им пользоваться.

Данные примеры свидетельствуют в пользу того, что все люди владеют логикой, независимо от того, изучали они ее или нет. Таким образом, мы практически используем логику задолго до того, как начинаем ее теоретически изучать Возникает вопрос: зачем нужно изучать логику, если мы и так ей владеем?

Отвечая на этот вопрос, можно отметить, что то же самое происходит с родным языком: практически мы начинаем им пользоваться в 2,5–3 года своей жизни, а изучать его начинаем только со школьного возраста. Для чего же мы изучаем родной язык в школе, если задолго до нее и так хорошо им владеем? В 2,5–3 года мы пользуемся языком интуитивно, или бессознательно: практически владея им, мы ничего не знаем не только о склонениях и спряжениях, но также – о словах и буквах и даже – о самом факте того, что в жизни мы постоянно используем язык. Обо всем этом мы узнаем только тогда, когда начинаем изучать его в школьном (или старшем дошкольном) возрасте, в результате чего наше интуитивное использование языка постепенно превращается в осознанное – мы начинаем владеть им намного лучше.

Так и с логикой: владея ей интуитивно и практически повседневно ее используя, мы изучаем ее как науку для того, чтобы превратить стихийное использование логики в осознанное, владеть ей еще лучше и пользоваться более эффективно.

Поделитесь на страничке

Следующая глава >

ЛОГИКА — это… Что такое ЛОГИКА?

        (греч. , от — построенный на рассуждении, от — слово, понятие, рассуждение, разум) формальная, наука об общезначимых формах и средствах мысли, необходимых для рационального познания в любой области знания. К общезначимым формам мысли относятся понятия, суждения, умозаключения, а к общезначимым средствам мысли — определения, правила (принципы) образования понятий, суждений и умозаключений, правила перехода от одних суждений или умозаключений к другим как следствиям из первых (правила рассуждений), законы мысли, оправдывающие такие правила, правила связи законов мысли и умозаключений в системы, способы формализации таких систем и т. п. Представляя общие основания для корректности мысли (в ходе рассуждений, выводов, доказательств, опровержений и пр.), Л. является наукой о мышлении — и как метод анализа дедуктивных и индуктивных процессов мышления, и как метод (норма) мышления, постигающего истину. Задача Л., которую вслед за Кантом обычно наз. формальной Л., исторически сводилась к каталогизации правильных способов рассуждений (способов «обращений с посылками»), позволяющих из истинных суждений-посылок всегда получать истинные суждениязаключения. Известным набором таких способов рассуждений однозначно определялся процесс дедукции, характерный для т. н. традиционной Л., ядро которой составляла силлогистика, созданная Аристотелем. По мере изучения особенностей умозаключений и демонстративного (доказывающего) мышления вообще предмет традиционной Л. постепенно расширялся за счёт не-силлогистич., хотя и дедуктивных способов рассуждений, а также за счёт индукции. Поскольку последняя выпадала из рамок Л. как дедуктивной теории, она стала предметом особой теории — индуктивной логики.         Совр. формальная Л.— историч. преемник традиционной Л. Для неё характерно разнообразие теорий, в которых изучаются способы рассуждений, приемлемые с т. зр. каждой такой теории, а также их формализация, т. е. отображение в логич. исчислениях (формализмах). Логич. исчисления — это системы символов (знаков), заданные объединением двух порождающих процессов: процесса индуктивного порождения грамматически правильных выражений исчисления — его слов и фраз (языка исчисления), и процесса дедуктивного порождения (дедукции) потенциально значимых (истинных) фраз (теорем) исчисления — его фразеологии. Заданием алфавита исходных символов, правил образования в нём языка (его структурных свойств) и правил преобразования его фразеологии (аксиом и правил вывода) логич. исчисление однозначно определяется как синтаксич. система (формальная структура символов). Выбор этой системы как представителя определ. логич. идей и соответственно приписывание её символам значений (интерпретация, или рассмотрение, её как семантич. системы) превращают логич. исчисление в оп-редел. теорию приемлемых способов рассуждений — теорию логич. вывода. Сообразно тому, каков синтаксис логич. теории (её правила преобразования) и её семантика, различают классические, интуиционистские, конструктивные, модальные, многозначные и др. теории логич. вывода.         Классич. теории исходят из предположения, что любое утверждение можно уточнить таким образом, что к нему будет применим исключённого третьего принцип. Опираясь на этот принцип (см. также Двузначности принцип), в классич. Л. отвлекаются от гносеология, ограничений, вытекающих из невозможности общего (рекурсивного) метода для классич. оценки суждений, согласно которой относительно любого объекта универсума вопрос о принадлежности ему («да») или отсутствии у него («нет») некоторого свойства решается всегда положительно. Интуиционистские (см. Интуиционизм) и конструктивные (см. Конструктивное направление) теории, напротив, придают эффективности (в частности, в смысле общерекурсивности) доказательств (установления свойств) решающее значение. Поэтому в общем случае (для бесконечных универсумов) в этих теориях отказываются от принципа исключённого третьего, исходя из др. предпосылки: чтобы утверждать, надо иметь возможность эффективно проверять свои знания и утверждения. Последнее существенно зависит от возможности восполнения утверждений алгоритмом подтверждения их истинности. Поэтому идея приемлемости рассуждений сопряжена в этих теориях с широко понимаемым (в смысле абстракции потенциальной осуществимости) эмпирич. познанием. Близкую к конструктивной идейную основу имеет и модальная логика, изучающая свойства модальностей — разновидностей отношения субъекта логич. деятельности к характеру его целевой активности или к содержанию высказываемой им мысли (напр., степени убеждённости в сказанном). В свою очередь, исчисления многозначной логики формализуют ещё более широкий подход к оценкам высказываний и объективных событий. Допуская множественность, в частности бесконечную, истинностных оценок (степеней подтверждения, правдоподобия, вероятности), теории многозначной Л. являются обобщениями классич. и модальных теорий, напр. на область индуктивных (статистич.) умозаключений, оставаясь в то же время дедуктивными логич. теориями.         Каждая из этих логич. теорий включает, как правило, два осн. раздела: логику высказываний и логику предикатов. В Л. высказываний учитываются не все смысловые связи фраз естеств. языка, а только такие, которые не создают косвенных контекстов и позволяют, рассматривая сколь угодно сложные высказывания как функции истинности простых (атомарных), выделять в множестве высказываний всегда истинные — тавтологии, или логические законы. В Л. высказываний отвлекаются от понятийного состава высказываний (их субъ-ектно-предикатной структуры). Сохраняя характер смысловых связей Л. высказываний, в Л. предикатов, напротив, анализируют и субъектнопредикатную структуру высказываний, и то, как она влияет на структуру и методы логич. вывода. Классич. вариант Л. предикатов является непосредств. продолжением традиц. силлогистики (Л. свойств), но в различных исчислениях предикатов субъектно-предикатная структура суждений анализируется с большей глубиной, чем в силлогистике: помимо свойств («одноместных» предикатов), в них формализуются и отношения («многоместные» предикаты; см. Предикат).

        В многообразии логич. теорий выражается многообразие требований, предъявляемых к Л. совр. наукой и практикой. Важнейшим из них является требование в содействии точной постановке и формулировке науч.-технич. задач и разысканию возможных путей их разрешения. Предлагая строгие методы анализа определ. аспектов реальных процессов рассуждений, логич. теории одновременно содействуют и объективному анализу положения вещей в той области знания, которая отражается в соответств. процессах мысли. Т. о., логич. теории не субъективны и не произвольны, а представляют собой глубокое и адекватное отображение посредством символов объективной «логики вещей» на ступени абстрактного мышления.

        По мере использования логич. исчислений в качестве необходимой «техники мышления» собств. идейное содержание логич. теорий совершенствуется и обогащается, а растущие потребности решения науч. и прак-тич. задач стимулируют развитие старых и создание новых разделов Л. Примером может служить обусловленное задачей обоснования математики возникновение метатеории (теории доказательств) — в узком смысле как теории формальных систем, ограниченной рамками финитизма, и в широком — как металогики, воплощающей взаимодействие формальных (синтак-сич.), содержат. (семантич.) и деятельностных (прагма-тич.) аспектов познания. Мн. результаты, относящиеся к взаимоотношению формальных логич. систем и их моделей, а потому имеющие и общенауч. значение, получены как металогич. теоремы (напр., о полноте Л. предикатов первого порядка, о наличии счётной модели у любой непротиворечивой теории, формализуемой в языке предикатов первого порядка, о неполноте формальных систем, включающих арифметику, и ряд др.), раскрывающие гносеологич. подтекст самой Л.         История логики. Первые учения о формах и способах рассуждений возникли в странах Др. Востока (Китай, Индия), но в основе совр. Л. лежат учения, созданные в 4 в. до н. э. др.-греч. мыслителями (Аристотель, ме-гарская школа). Аристотелю принадлежит исторически первое отделение логич. формы речи от её содержания. Он открыл атрибутивную форму оказывания как утверждения или отрицания «чего-то о чём-то», определил простое суждение (высказывание) как атрибутивное отношение двух терминов, описал осн. виды атрибутивных суждений и правильных способов их обращения, ввёл понятия о доказывающих силлогизмах как общезначимых формах связи атрибутивных суждений, о фигурах силлогизмов и их модусах, а также изучил условия построения всех силлогистич. законов (доказывающих силлогизмов). Аристотель создал законченную теорию дедукции — силлогистику, реализующую в рамках полуформальных представлений идею выведения логич. следствий при помощи некоторого механич. приёма — алгоритма. Он дал первую классификацию логич. ошибок, первую математич. модель атрибутивных отношений, указав на изоморфизм этих и объёмных отношений, и заложил основы учения о логич. доказательстве (логич. обосновании истинности). Ученики Аристотеля (Теофраст, Евдем) продолжили его теорию применительно к условным и разделит. силлогизмам.         Потребность в обобщениях силлогистики в целях полноты учения о доказательстве привела мегариков к анализу связей между высказываниями. Диодор Крон и его ученик Филон из Мегары предложили параллельные уточнения отношения логич. следования посредством понятия импликации. Диодор толковал импликацию как модальную (необходимую) условную связь, а Филон — как материальную.         Логич. идеи мегарской школы восприняли стоики. Хрисипп принял критерий Филона для импликации и принцип двузначности как онтологич. предпосылку Л. Идею дедукции стоики формулировали более чётко, чем мегарики: высказывание логически следует из посылок, если оно является консеквентом всегда истинной импликации, имеющей в качестве антецендента конъюнкцию этих посылок. Это исторически первая формулировка т. н. теоремы дедукции, дающей общий метод формального доказательства средствами логики. Аргументы, основанные только на правильной форме дедукции и не исключающие ложность посылок, стоики наз. формальными. Если же привлекалась содержат. истинность посылок, аргументы наз. истинными. Наконец, если посылки и заключения в истинных аргументах относились соответственно как причины и следствия, аргументы наз. доказывающими. Последние предполагали понятие о естеств. законах, которые стоики считали аналитическими, отрицая возможность их обоснования посредством аналогии и индукции. Стоич. учение о доказательстве выходило за пределы собственно Л.— в область теории познания, и здесь дедукти-визм стоиков встретил филос. противника в лице радикального эмпиризма школы Эпикура, которая в споре со стоиками защищала опыт, аналогию и индукцию. Эпикурейцы положили начало индуктивной Л., указав, в частности, на роль противоречащего примера в проблеме обоснования индукции, и сформулировали ряд правил индуктивного обобщения (Филодем из Гадары).         На смену логич. мысли ранней античности пришла антич. схоластика, сочетавшая аристотелизм со стоицизмом и заменившая искусство свободного исследования искусством экзегезы (истолкования авторитетных текстов), популярной и в «языч.» школе поздних перипатетиков, и в христ. школах неоплатоников. Из нововведений эллино-римских логиков заслуживают внимания: логич. квадрат (quadrata formula) Апулея из Медавры, реформированный позднее Боэцием; полисиллогизмы и силлогизмы отношений, введённые Га леном; дихотомич. деление понятий и учение о видах и родах, встречающиеся у Порфирия; зачатки истории Л. у Секста Эмпирика и Диогена Лаэртия; наконец, ставшая с тех пор общепринятой латинизированная логич. терминология, восходящая к соч. Цицерона и лат. переводам из аристотелевского «Органона», выполненных Боэцием. В этот период Л. входит в число семи свободных искусств, которые Марциан Капелла наз. энциклопедией гуманитарного образования.         Логич. мысль раннего европ. средневековья беднее эллино-римской. Самостоят. значение Л. сохраняет лишь в странах арабоязычной культуры (аль-Фараби, Ибн Сина, Ибн Рушд), где философия остаётся относительно независимой от теологии. В Европе же складывается в основном схоластич. Л.— церковно-школьная дисциплина, приспособившая элементы перипатетич. Л. к нуждам христ. вероучения. Только после того, как все произв. Аристотеля канонизируются церк. ортодоксией, возникает оригинальная (несхоластич.) ср. век. Л., известная под назв. logica modernorum. Контуры её намечены «Диалектикой» Абеляра, но окончательно она оформляется к кон. 13 — сер. 14 вв. в соч. У. Шервуда, Петра Испанского, Иоанна Дунса Скота, В. Бурлея (Бёрли), У. Оккама, Ж. Буридана, Альберта Саксонского и др. Именно здесь логич. и фактич. истинность строго разделяются и Л. понимается как формальная дисциплина о принципах всякого знания (modi scientiarum omnium), предметом которой являются не эмпирич., а абстрактные объекты — универсалии. Учение о дедукции основывается на явном различении материальной и формальной, или тавтологичной, импликаций: для первой имеется контрпример, для второй — нет. Поэтому материальная импликация выражает фактическое, а формальная — логич. следование, с которым естественно связывается понятие о логич. законах. У ср.-век. логиков этой эпохи встречается и первая попытка аксиоматизации Л. высказываний, включая модальности. При этом Л. высказываний, как и у стоиков, признаётся более общей теорией дедукции, чем силлогистика. В этот же период, хотя и вне связи с общим течением модернизации логич. мысли, зарождается идея «машинизации» процессов дедукции (Р. Луллий, «Великое искусство» — «Ars magna», 1480).         Эпоха Возрождения для дедуктивной Л. была эпохой кризиса. Её воспринимали как опору мыслит. привычек схоластики, как Л. «искусственного мышления», освящающую схематизм умозаключений, в которых посылки устанавливаются авторитетом веры, а не знания. Руководствуясь общим лозунгом эпохи: «вместо абстракций — опыт», дедуктивной Л. стали противопоставлять Л. «естественного мышления» (П. Раме), под которой обычно подразумевались интуиция и воображение. Леонардо да Винчи и Ф. Бэкон возрождают антич. идею индукции и индуктивного метода, выступая с резкой критикой силлогизма. Лишь немногие, подобно падуанцу Я. Дзабарелле («Логич. труды» — «Opera logica», 1578), отстаивают формальную дедукцию как основу науч. метода вообще.         В нач. 17 в. положение Л. меняется. Г. Галилей вводит в науч. обиход понятие о гипотетикодедуктивном методе: он восстанавливает права абстракции, обосновывает потребность в абстракциях, которые «восполняли» бы данные опытных наблюдений, и указывает на необходимость введения этих абстракций в систему логич. дедукции в качестве гипотез, или постулатов (аксиом), с последующим сравнением результатов дедукции с результатами наблюдений. Т. Гоббс истолковывает аристотелевскую силлогистику как основанное на соглашениях исчисление истинностных функций — суждений именования, заменяя, по примеру стоиков, атрибутивные связи пропозицивнальными. П. Гассен-ди пишет историю Л., а картезианцы А. Арно и Н. Ни-коль — «Логику, или Искусство мыслить» («La logique ou L’art de penser», 1662), т. н. логику Пор-Рояля, в крой Л. представлена как рабочий инструмент всех др. наук и практики, поскольку она принуждает к строгим формулировкам мысли. Сам Декарт реабилитирует дедукцию (из аксиом) как «верный путь» к познанию, подчиняя её более точному методу всеобщей науки о «порядке и мере» — mathesis universalis, простейшими примерами которой он считал алгебру и геометрию. В том же духе работали И. Юнг («Гамбургская логика» — «Logica Hamburgiensis», 1638), В. Паскаль («О геометрич. разуме» — «De l’esprit geometrique»), А. Гейлинкс («Логика…» — «Logica…», ?662), Дж. Сак-кери («Наглядная логика» — «Logica demonstrative», 1697) и в особенности Г. Лейбниц, который идею mathesis universalis доводит до идеи calculus rationator — универсального искусств. языка, формализующего рассуждения подобно тому, как в алгебре формализованы вычисления. Этим путём Лейбниц надеялся расширить границы демонстративного познания, которые до тех пор, по его мнению, почти совпадали с границами математики. Он отмечал важность тождеств. истин («бессодержат. предложений») Л. для мышления, а в универсальном языке видел возможность «общей Л.», частными случаями которой считал силлогистику и Л. евклидовских «Начал». Лейбниц не осуществил своего замысла, но он дал арифметизацию силлогистики, разрешив тем самым совершенно новый для Л. вопрос — о её непротиворечивости относительно арифметики.         Программа Лейбница не вызвала всеобщего признания, хотя её поддержали Дж. Валлис («Логическое учение» — «Institutio logicae», 1729), Г. Плуке («Филос. и теоретич. описания» — «Expositiones pliilo-sophiae theoreticae», 1782), И. Ламберт («Новый органон» — «Neues Organon», 1764). Благодаря их трудам внутри филос. Л., не связанной с точными методами анализа рассуждений и носящей преим. описат. характер, сложились реальные предпосылки для развития математич. Л. Однако это развитие до сер. 19 в. было приостановлено авторитетами Канта и Гегеля, считавших, что формальная Л.— это не алгебра, с помощью которой можно обнаруживать скрытые истины, что она не нуждается ни в каких новых изобретениях, а потому оценивших математич. направление как не имеющее существ. применения.         Между тем запросы развивающегося естествознания оживили почти забытое индуктивное направление в Л,— т. н. Л. науки. Инициаторами этого направления стали Дж. Гершель (1830), У. Уэвелл (1840), Дж. С. Милль (1843). Последний, по примеру Ф. Бэкона, сделал индукцию отправной точкой критики дедукции, приписав всякому умозаключению (в основе) индуктивный характер и противопоставив силлогизму свои методы анализа причинных связей (т. н. каноны Бэкона — Милля). Критика эта, однако, не повлияла на то направление логич. мысли, которое наследовало идеи Лейбница. Напротив, скорее как ответ на эту критику (и, в частности, на критику идей У. Гамильтона о логич. уравнениях) почти одновременно появились обобщённая силлогистика О. де Моргана (1847), включившая Л. отношений и понятие о вероятностном выводе, и «Математич. анализ логики» («The mathematical analysis of logic», 1847) Дж. Буля, в котором автор переводит силлогизм на язык алгебры, а совершенство дедуктивного метода Л. рассматривает как свидетельство истинности её принципов. Позднее Буль («Исследование законов мысли» — «An investigation of the laws of thought…», 1854), С. Джевонс («Чистая логика» — «Pure logic», 1864), Ч. Пирс («Об алгебре логики» — «On the algebra of logic», 1880), Дж. Венн («Сим-волич. логика» — «Symbolic logic», 1881), П. С. Порецкий («О способах решения логич. равенств…», 1884) и Э. Шредер («Лекции по алгебре логики» — «Vorlesungen uber die Algebra der Logik», 1890—1905) окончательно опровергли тезис о неалгебраич. характере форм мысли, создав теорию «законов мысли» как вид нечисловой алгебры. Эта реформация в Л. коснулась не только силлогистики (логики классов). В 1877 X. Мак-Колл впервые после схоластов обращается к теории критериев логич. следования и к Л. высказываний, а Г. Фреге («Исчисление понятий» — «Begriffsschrift», 1879) создаёт первое исчисление высказываний в строго аксиоматич. форме. Он обобщает тра-диц. понятие предиката до понятия пропозициональной функции, существенно расширяющего возможности отображения смысловой структуры фраз естеств. языка в формализме субъектно-нредикатного типа и одновременно сближающего этот формализм с функциональным языком математики. Опираясь на идеи предшественников, Фреге предложил реконструкцию традиц. теории дедукции на основе искусств. языка (исчисления), обеспечивающего полное выявление логич. структуры мысли, всех элементарных шагов рассуждения, требуемых исчерпывающим доказательством, и полного перечня осн. принципов: определений, постулатов, аксиом, положенных в основу дедукции. Фреге использует созданный им язык Л. для формализации арифметики. Ту же задачу, но на основе более простого языка, осуществляют Дж. Пеано и его школа («Формуляр математики» — «Formulaire de mathematique», t. 1—2, 1895—97).         Очевидным успехом движения за математизацию Л. явилось его признание на 2-м Филос. конгрессе в Женеве (1904), хотя в обществ. мнении оно утвердилось не сразу. Гл. идейным противником применения мате-матич. методов к системе логич. понятий был психологизм в логике, который воспринимал математизацию Л. как своего рода возрождение схоластики, менее всего способное поставить логические исследования на научный фундамент. Однако именно в этом своём пункте психологизм оказался антиисторичен. Борьба за математизацию Л. привела к мощному развитию этой науки.         После «Principle Mathematica» (1910—13) Б. Рассела и А. Уайтхеда — трёхтомного труда, систематизировавшего дедуктивно-аксиоматич. построение классич. Л. (см. Логицизм), создаётся многозначная Л. (Я. Лу-касевич, Э. Пост, 1921), аксиоматизируются модальная (К. Льюис, 1918) и интуиционистская Л. (В. Гливенко, 1928; А. Гейтинг, 1930). Но главные исследования переносятся в область теории доказательств: уточняются правила и способы построения исчислений и изучаются их осн. свойства — независимость постулатов (П. Бер-найс, 1918; К. Гёдель, 1930), непротиворечивость (Пост, 1920; Д. Гильберт и В. Аккерман, 1928; Ж. Эр-бран, 1930) и полнота (Пост, 1920; Гёдель, 1930), появляются классические работы по логической семантике (А. Тарский, 1931) и теории моделей (Л. Лёвенхейм, 1915; Т. Скулем, 1919; Гёдель, 1930; А.И.Мальцев, 1936).

        Начиная с 1930-х гг. закладываются основы изучения «машинного мышления» (теория алгоритмов — Гёдель, Эрбран, С. Клини, А. Тьюринг, А. Чёрч, Пост, А. А. Марков, А. Н. Колмогоров и другие). И хотя выясняется ограниченность этого мышления, проявляющаяся, напр., в алгоритмич. неразрешимости ряда логич. проблем (Гёдель, 1931; П. С. Новиков, 1952), в невыразимости всех содержат, истин в к.-л. едином формальном языке (Гёдель, 1931), а тем самым и невыполнимость лейбницевской идеи создания каталога всех истин вместе с их формальными доказательствами, всё же растёт сирое на применение Л. в вычислит. математике, кибернетике, технике (первоначально в форме алгеб-раич. теории релейно-контактных схем, а затем в форме более общей теории анализа и синтеза конечных автоматов, теории алгоритмов и пр.), а также в гуманитарных науках: психологии, лингвистике, экономике. Совр. Л.— это не только инструмент точной мысли, но и «мысль» первого точного инструмента, электронного автомата, непосредственно в роли партнёра включённого человеком в сферу решения интеллектуальных задач но обработке (хранению, анализу, вычислению, моделированию, классификации) и передаче информации в любой, области знания и практики.

        Аристотель, Соч., т. 2, М., 1978; Лукасевич Я., Аристотелевская силлогистика с т. зр. совр. формальной Л., пер. с англ., М., 1959; M и л л ь Д ж. С., Система Л. силлогистической и индуктивной, пер. с англ., М., 19142; Гильберт Д.,Аккерман В., Основы теоретич. Л., пер. с нем., М., 1947; Тарский А., Введение в Л. и методологию дедуктивных наук, пер. с англ., М., 1948; Чёрч А., Введение в ма-тематич. Л., пер. с англ., т. 1, М., 1960; Попов П. С., История Л. нового времени, М., 1960; Маковельский А. О., История Л., М., 1967; С т я ж к и н Н. И., Формирование математич. Л., М., 1967; Математич. теория логич. вывода. Сб. переводов, М., 1967; Карри X. Б., Основания математич. Л., пер. с англ., М., 1969; Марков А. А.,О логике конструктивной математики, М., 1972; Н о в и к о в П. С., Элементы математич. Л., M., 19732; К л и н н С. К., Математич. Л., пер, с англ., М., 1973; ? ей с Р., Модальная Л., пер. с англ., М., 1974; Попов П. С., Стяжкин Н. И., Развитие логич. идей от античности до эпохи Возрождения, М., 1974; Философия в совр. мире. Философия и Л., М., 1974; Ш е н ф и л д Д ж. Р., Математич. Л., пер. с англ., М., 1975; Т а к е у т и Г., Теория доказательств, пер. с англ., М., 1978; Драгалин А. Г., Математич. интуиционизм. Введение в теорию доказательств, ?., 1979; Крайзель Г., Исследования по теории доказательств, пер. с англ., М., 1981; В е г k а К., К г е i s е г L., Logik — Texte. Kommentierte Auswahl zur Geschichte der modernen Logik, B., 1971; Risse W., Bibliographie logica, Bd 1—4, Hildesheim — N. Y., 1965 — 79.

        M. M. Новосёлов.

Философский энциклопедический словарь. — М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983.

как научиться правильно рассуждать — Нож

Логика: бытовое и точное значение

Значение термина «логика» слишком размылось в повседневной речевой практике, а ведь на деле логика — одна из старейших наук. Долгое время она воспринималась как инструмент для правильного научного познания. Корпус посвященных логике работ Аристотеля — создателя первой логической теории — называли термином «органон» («инструмент» на древнегреческом).

В основном логику изучают на математических и философских факультетах, а также на факультетах, где занимаются компьютерными науками и всем, что связано с созданием искусственного интеллекта (здесь ее изучают наиболее фундаментально).

Но не обязательно быть математическим гением, чтобы заниматься логикой. Она берет свое начало в философии и до сих пор остается одной из самых активно развивающихся именно философских наук — несмотря на то, что на определенном этапе своей долгой истории обогатилась значительным числом математических методов.

Так что логика — одна из важнейших гуманитарных дисциплин, которая входит в образовательные стандарты и по многим другим специальностям в высших учебных заведениях: юриспруденция, психология, политология, журналистика, социология, история, лингвистика и т. д.

Чем занимается логика как наука

Логика изучает, какие рассуждения правильные, а какие нет. Кроме того, в ней вырабатываются критерии правильного рассуждения, то есть она может рассказать как надо рассуждать. Почти все используемые нами рассуждения уже давно классифицированы и изучены профессиональными логиками. Известны границы применимости многих методов, изучена степень правдоподобности различных видов рассуждений. Все это систематизировано, но большинство людей абсолютно не владеет этими знаниями.

Как логика смотрит на обобщения

Вы возвращаетесь вечером домой, по дороге вспоминаете, что у вас закончилось молоко и идете в ближайший супермаркет. Перед вами — большой холодильник, все полки которого заставлены бутылками с молоком. Вы подходите к полкам и начинаете выбирать.

Допустим, что там две такие полки и на них выставлено в общей сложности сорок бутылок. Обычно мы ищем максимально свежее молоко, то есть такое, у которого дата производства максимально приближена к дню покупки.

Если сегодня 20-е число, а вы достаете одну бутылку и видите, что оно было произведено 18-го, то достаете другую бутылку — и опять 18-е. «Наверное, на второй полке может быть посвежее», — и вы берете бутылку со второй полки — 17-е число, еще одну — 17-е, еще — 18-е. Потом вы протягиваете руку вглубь полки и достаете еще одну бутылку, и она тоже произведена 18-го числа. После этого вы, скорее всего, сделаете вывод, что молоко, которое произвели 18-го числа — это самое свежее молоко из представленных и пойдете на кассу с ним.

Этот пример иллюстрирует применение не самого достоверного рассуждения: так называемой неполной индукции. Ваш вывод о том, что молоко, произведенное 18-го числа — самое свежее из представленных, носит лишь вероятностный характер, поскольку вы не перебрали все бутылки, а осуществили вывод, основываясь только на некоторой минимальной выборке, которую посчитали достаточной, после чего совершили так называемое индуктивное обобщение. И даже если вы оказались правы, и там действительно не было более свежего молока, это неважно. Само рассуждение, сам способ, при помощи которого вы пришли к такому заключению, считается логикой ненадежным.

Это весело и забавно, когда речь идет о выборе молока в магазине, но так ли это весело и забавно, когда люди, используя похожие рассуждения, анализируют результаты каких-нибудь экономических реформ и на этом основании планируют новые или выявляют общественное мнение по какому-то важному вопросу?

Каждый раз, когда по телевизору или в интернете вы натыкаетесь на результаты очередного социологического опроса, скажем, с выводом «россияне считают, что США представляют для них угрозу», — вы имеете дело с результатом такой же индукции, которая основана точно не на мнении всех россиян, и, более того, не на мнении большинства россиян. В подобных исследованиях количество участников вообще не играет почти никакой роли. Эти рассуждения основаны на характере той выборки людей, которые проходят данный опрос; в качестве основания принимается их возраст, пол, род деятельности, сексуальная ориентация и всё, что угодно. Само число участников зачастую в сотни тысяч раз меньше, чем реальное число россиян. Чтобы в этом убедиться, достаточно открыть любой отчет по статистике.

А теперь вы можете сравнить степень правдоподобности такого метода рассуждений и того, как полученные таким способом результаты влияют на общественное мнение, циркулируя в топах информационных агентств, новостных лент и т. п. Именно поэтому логику и стоит изучать.

Главные правила логики

Самое главное — осознать, что существует два основных вида рассуждений: одни из них — самые надежные, а другие — не очень. Первые называют дедуктивными рассуждениями, вторые — правдоподобными. Как ни парадоксально, обычные люди почему-то больше предпочитают использовать правдоподобные, а не дедуктивные рассуждения.

Есть ряд дедуктивных рассуждений, которые просто необходимо усвоить.

1. Условно-категорические умозаключения

К условно-категорическому типу рассуждений относятся два правильных: modus ponens и modus tollens.

Modus ponens. Такое рассуждение имеет следующую структуру:

«если А, то B»;

«А» значит «B».

Логиков интересует именно сама структура этих рассуждений, в реальности же они не всегда предстают перед нами именно в таком обличии и могут принимать разные языковые и риторические формы. На человеческом языке оно может выглядеть так:

«если сборная России выиграет у Испании, то я сделаю татуировку»;

«сборная России выиграла у Испании» — значит «я сделаю татуировку».

Modus tollens. Это рассуждение выглядит так:

«если А, то B»;

«не-B» значит «не-А».

Опять переведем:

«если сборная России выиграет у Испании, то я сделаю татуировку»,

«я не сделал татуировку» — значит «сборная России не выиграла у Испании».

Оно может выглядеть и немного по-другому: «если А, то B» — значит «если не-B, то не-А». В таком виде его называют «контрапозицией».

Вот для примера на недавнем Международном экономическом форуме в Санкт-Петербурге во время панельной дискуссии Алексей Кудрин использовал упомянутый modus tollens для демонстрации того, что антироссийские санкции — один из существенных факторов, влияющих на темп экономического роста российской экономики, притом что правительство ставит достаточно амбициозные задачи по его увеличению. Кудрин замечает: «Сейчас после последней волны санкций их влияние увеличилось примерно до 0,5 % ВВП. Здесь мы тоже должны видеть, что наши задачи и планы уменьшаются вот такими внешнеполитическими рисками». В рамках этой реплики можно реконструировать пресловутую «контрапозицию», благодаря которой Кудрин пришел к такому мнению: если экономические санкции применяются в отношении к России, то рост ее экономики снижается; следовательно, если экономическая политика направлена на увеличение экономического роста, то экономические санкции не должны применяться в отношении к России. И правильно сделал!

Очень часто многие из нас ошибаются и используют следующие неправильные условно-категорические рассуждения:

«если А, то B»; «B», следовательно, «А». И «если А, то B»; «не-А», следовательно, «не-B».

В качестве примера можно привести ошибочное рассуждение Алексея Венедиктова во время выпуска его программы «Особое мнение», в рамках которого он дискутировал с Ксенией Собчак. В этом фрагменте Собчак рассказывает о том, какие реформы судебной власти она будет проводить в случае своей победы на президентских выборах. В ответ на это Венедиктов утверждает, что после этого выступления электорат в лице «судей и членов их семей» не проголосует за Собчак.

Рассуждение Венедиктова можно реконструировать в следующем виде: «если Ксения Собчак выступает с привлекательными для избирателей предложениями, то эти избиратели проголосуют за Собчак»; «Собчак выступает не с привлекательными для избирателей предложениями», следовательно, «эти избиратели за нее не проголосуют».

На первый взгляд может показаться, что это рассуждение не противоречит никакой логике, однако это не так.

Дело в том, что дедуктивные рассуждения имеют существенную характеристику, которая и делает их очень надежными: в них из истинных посылок с необходимостью следует истинное заключение. Другими словами, для правильного дедуктивного рассуждения не существует такой ситуации, при которой его посылки окажутся истинными, а заключение — ложным. Для того типа рассуждения, которое в данном случае использует Венедиктов, такая ситуация с истинными посылками и ложным заключением существует.

Чтобы в этом удостовериться, нам нужно привести контрпример. Например, вот две посылки: «если сборная России выиграет у Хорватии, то я сделаю татуировку», «сборная России не выиграла у Хорватии» — из этих двух посылок совершенно не следует, что «я не сделал татуировку», поскольку я мог сделать эту татуировку совершенно по другим причинам: из гордости за ногу Акинфеева, из сожаления за его правую руку, которая чуть было не отбила один из одиннадцатиметровых ударов и т. п. Действительно, обе посылки являются истинными высказываниями, однако заключение в таком случае оказывается ложным.

У многих могут возникнуть сомнения, выдержат ли подобную проверку на вшивость уже упомянутые правильные типы рассуждений: modus ponens и modus tollens. Что ж, попробуйте подобрать к ним контрпримеры (в логике есть более точные и удобные методы для проверки правильности рассуждений, но, к сожалению, их невозможно рассмотреть в рамках этой статьи).

2. Сведение к абсурду и рассуждение «от противного»

В логике существуют и другие способы рассуждений: это так называемые непрямые умозаключения. Среди них есть две классные техники, они называются «сведение к абсурду» и «доказательство от противного» (они фактически представляют собой одно и то же).

Сведение к абсурду. Мы хотим опровергнуть некоторое утверждение «А». Вооружившись техникой «сведения к абсурду», мы должны предположить, что утверждение «А» является истинным — и затем стараться использовать какие-то рассуждения, чтобы продемонстрировать, что это предположение приводит к противоречию. Если нам удается прийти к противоречию, значит, наше исходное предположение было неверным. Таким образом, мы опровергаем утверждение «А».

Доказательство «от противного». Оно строится немного иначе: первоначальной целью является не опровергнуть «А», а обосновать «А». Для достижения этой цели сначала предполагается, что «А» является ложным, а дальше всё то же самое: выводится противоречие, которое позволяет обосновать неправильность исходного предположения.

Люди частенько используют эти две техники рассуждения. Рассмотрим например метод «от противного».

Будем считать, что вы допрашиваете подозреваемого в убийстве человека. Преступление было совершено при помощи пистолета, который был найден в квартире у подозреваемого.

Последний, естественно, отрицает свою причастность и понятия не имеет, кто на самом деле был убийцей. Кроме того, он утверждает, что весь тот злополучный день он провел дома. С целью усилить свою аргументацию в пользу вины подозреваемого, вы предполагаете, что пистолет действительно не его. Из этого допущения можно заключить, что пистолет ему подкинули. Но в таком случае подозреваемый должен быть знаком с убийцей или отсутствовать дома в какой-то момент времени в день убийства. Обе эти альтернативы противоречат показаниям подозреваемого, значит, ваше допущение о том, что пистолет ему не принадлежит, неверное. Следовательно, пистолет все-таки принадлежит подозреваемому.

Как изучить логику

К сожалению, число хороших учебников по логике, которые нацелены на широкую аудиторию и написаны простым для всех языком, очень мало. Зачастую этот «простой для всех язык» сразу сказывается на качестве теоретической составляющей.

Учебники либо доступные и некачественные — либо очень специализированные, но качественные. В такой ситуации лучше сделать выбор в пользу вторых, потому что главное — это качество образования:

1. Бочаров В.А., Маркин В.И. Введение в логику. М., 2011.
2. Бочаров В.А., Маркин В.И. Основы логики. М., 2008.
3. Войшвилло Е.К. Понятие как форма мышления. М., 1989.

Что касается интернет-ресурсов, то здесь тоже надо быть избирательными, однако есть и очень ценные экспонаты. Серия видеороликов, созданных силами БФУ им. И. Канта совместно со специалистами из других российских научных и учебных центров:

1. Серия бесед двух профессоров логики — Д. В. Зайцева (МГУ) и И. Б. Микиртумова (СПбГУ).
2. Серия бесед двух специалистов по теории аргументации — Д. В. Зайцева (МГУ) и Д. В. Хизанишвили (БФУ).

В открытом доступе лежат полноформатные видеозаписи курса лекций по дедуктивной логике, который периодически читается на философском факультете МГУ. Там есть специальная практика под названием «межфакультетский курс»: преподаватели на разных факультетах предлагают свои учебные курсы, на которые в соответствии со своим выбором записываются студенты с других факультетов. Это очень интересная практика, которая стимулирует появление учебных курсов на доступном для студентов разных направленностей языке.

Кроме того, существуют различные открытые научно-популярные мероприятия, например ежегодный Фестиваль науки, который проходит в том числе и на философском факультете МГУ, где логическая проблематика всегда представлена. Приходите, интересуйтесь и спрашивайте.

---

Логика научит вас точнее выражать свои мысли, и это в целом скажется на вашем стиле общения с людьми и умении разбираться в людях.

Когда вы начнете требовать от людей такой же точности, то обнаружите, что далеко не все способны общаться подобным образом. Но если вы увидите человека, который может грамотно излагать свои мысли и вести корректную полемику, то это многое скажет вам об уровне его логической культуры — да и вообще о личности в целом.