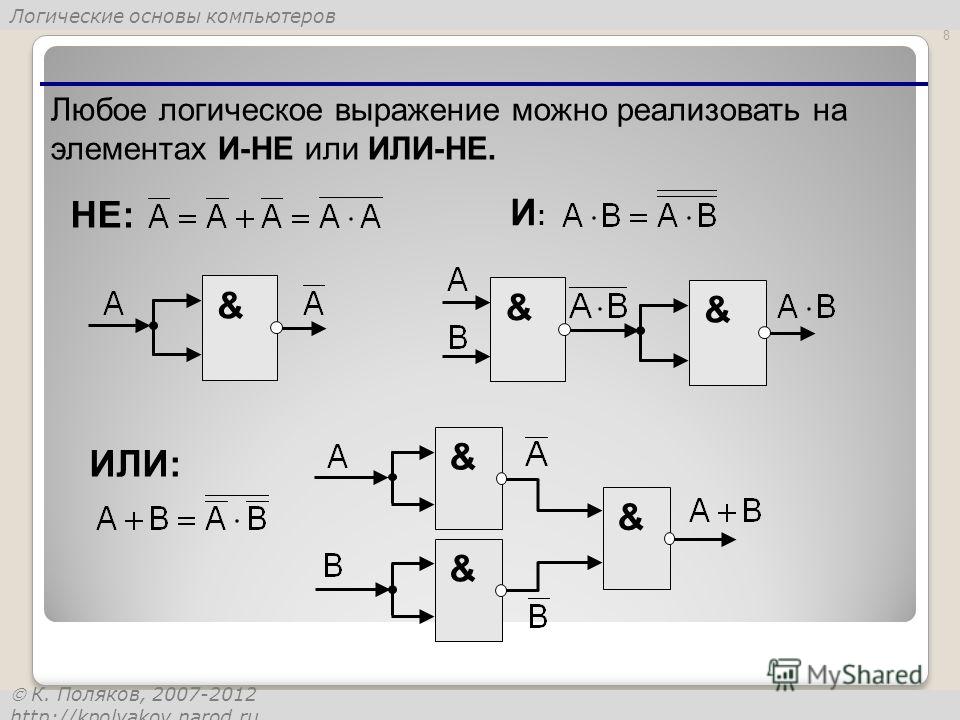
Логические элементы Electronics Workbench | EWB
EWB
Логическое НЕ
Элемент логическое НЕ или инвертор изменяет состояние входного сигнала на противоположное. Уровень логической единицы появляется на его выходе, когда на входе не единица, и наоборот.
Таблица истинности
|
Вход А |
Выход Y |
|
0 |
1 |
|
1 |
0 |
Выражение
булевой алгебры: Y=Ā.
Логическое И
Элемент И реализует функцию логического умножения. Уровень логической единицы на его выходе появляется в случае, когда на оба входа подается уровень логической единицы.
Таблица истинности
|
Вход А |
Вход В |
Выход Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Выражение
булевой алгебры: Y=А × В.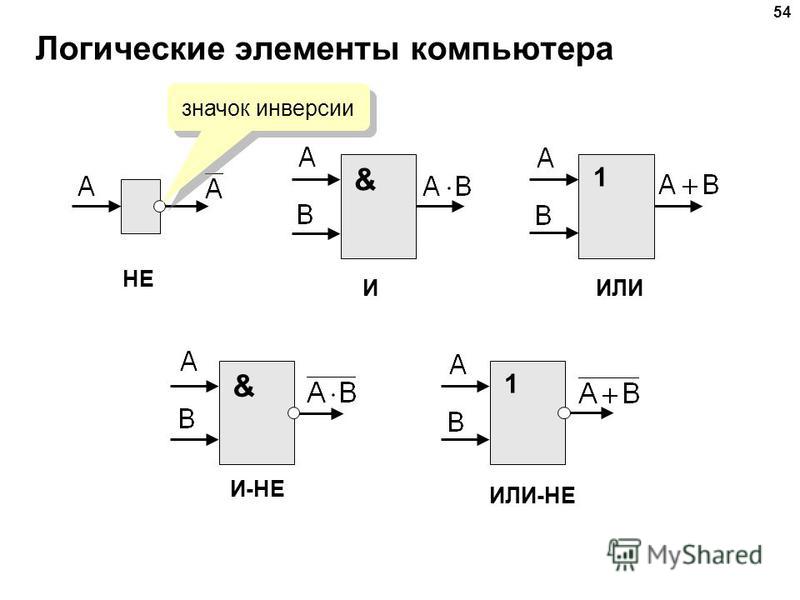
Логическое ИЛИ
Элемент ИЛИ реализует функцию логического сложения. Уровень логической единицы на его выходе появляется в случае, когда на один или на другой вход подается уровень логической единицы.
Таблица истинности
|
Вход А |
Вход В |
Выход Y |
|
0 |
0 |
0 |
|
0 |
1 |
|
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Выражение булевой
алгебры: Y=A V B.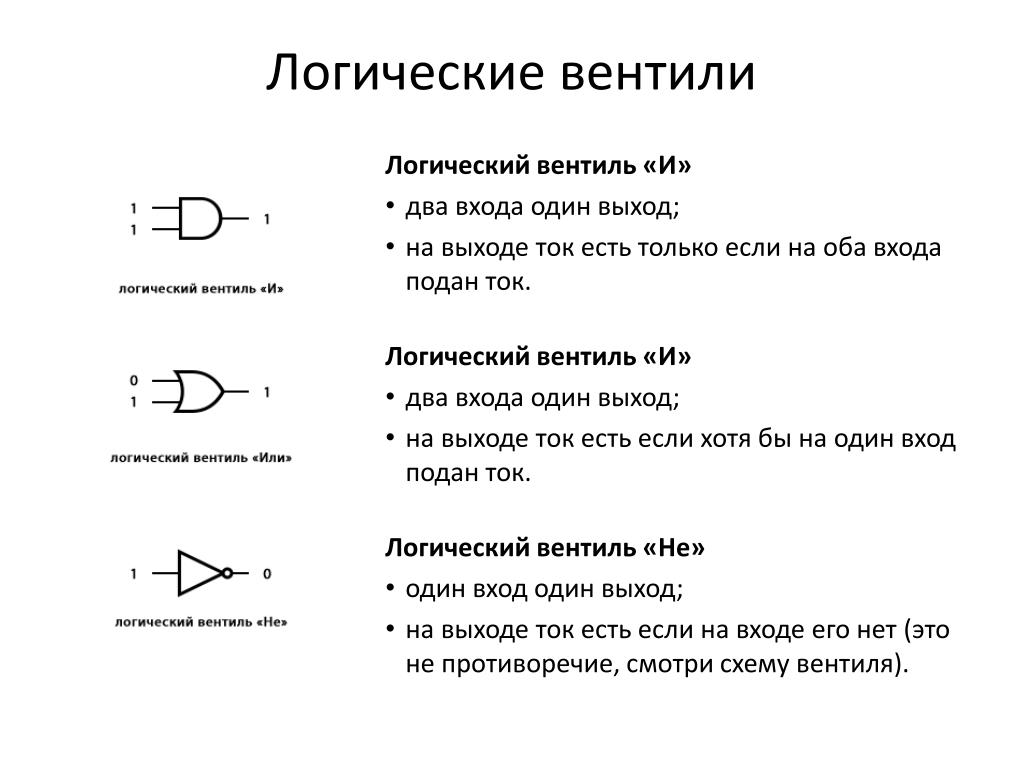
Исключающее ИЛИ
Двоичное число на выходе элемента, исключающее ИЛИ, является младшим разрядом суммы двоичных чисел на его входах.
Таблица истинности
|
Вход А |
Вход В |
Выход Y |
|
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Выражения булевой алгебры:
Элемент
И-НЕ реализует функцию логического умножения с последующей инверсией
результата.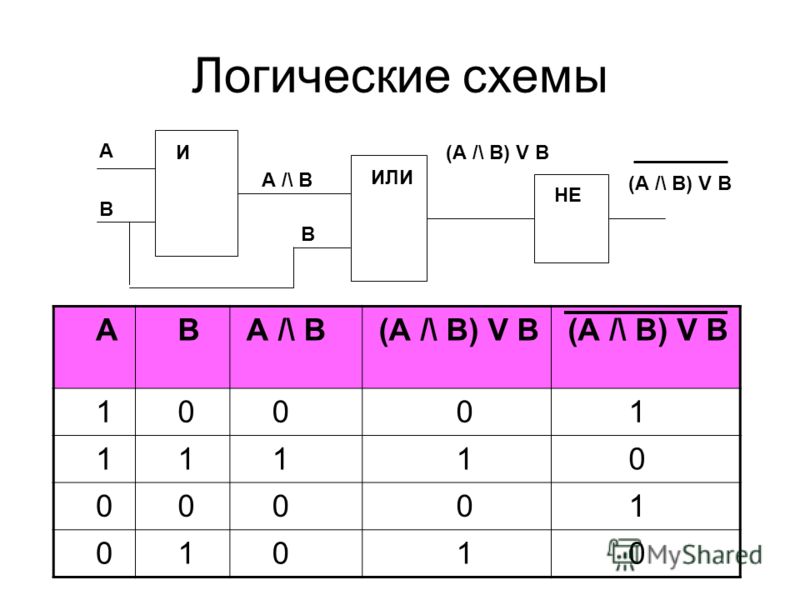 Он представляется моделью из последовательно включенных элементов И
и НЕ.
Он представляется моделью из последовательно включенных элементов И
и НЕ.
Таблица истинности элемента получается из таблицы истинности элемента И путем инверсии результата.
Таблица истинности
|
Вход А |
|
Выход Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Выражение булевой алгебры:
Элемент ИЛИ – НЕ
Элемент
ИЛИ-НЕ реализует функцию логического сложения с последующей инверсией
результата. Он представляется моделью из последовательно включенных элементов ИЛИ
и НЕ.
Он представляется моделью из последовательно включенных элементов ИЛИ
и НЕ.
Его таблица истинности получается из таблицы истинности элемента ИЛИ путем инверсии результата.
Таблица истинности
|
Вход А |
Вход В |
Выход Y |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Выражение булевой алгебры:
Данный
элемент реализует функцию «исключающее ИЛИ» с последующей инверсией результата.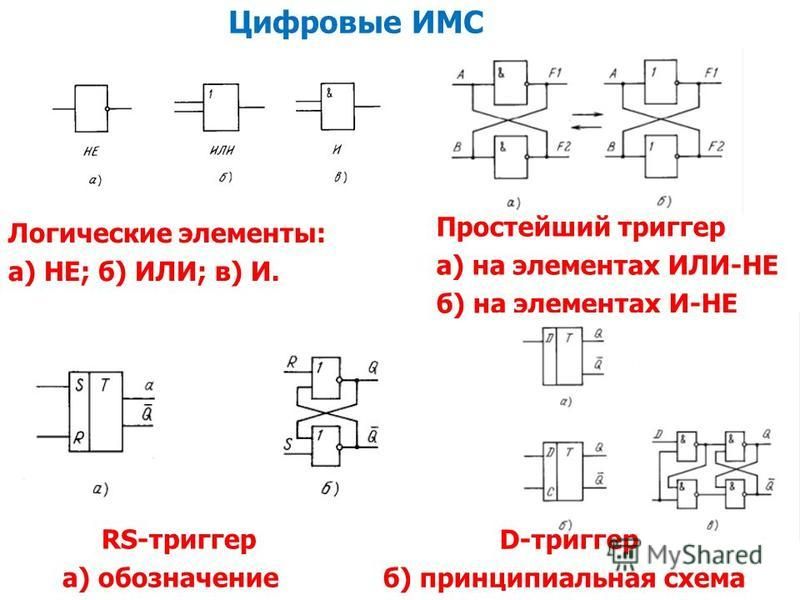 Он представляется моделью из двух последовательно соединенных элементов
исключающее ИЛИ и НЕ.
Он представляется моделью из двух последовательно соединенных элементов
исключающее ИЛИ и НЕ.
Таблица истинности
|
Вход А |
Вход В |
Выход Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Выражение булевой алгебры:
Логические вентили.
 Взаимозаменяемость. — Elektrolife
Взаимозаменяемость. — ElektrolifeСущность цифровой электроники — выработка выходных цифровых сигналов в соответствии с входными. Например, сумматор может принять на свои входы два 16-разрядных числа и сформировать на выходе 16-разрядную сумму (плюс перенос). Можно сделать также схему для умножения двух чисел. Такого типа операции должен уметь выполнять процессор.
Другая задача — сравнение двух чисел с целью удостовериться в том, что «все системы действуют нормально». Если дополнить паритетным битом число, подлежащее передаче по каналу связи, таким образом, чтобы общее количество «единиц» в нем стало четным, то проверка паритета на приемной стороне обеспечивает простой контроль правильности передачи.
Еще одна типичная задача заключается в том, чтобы взять какие-либо числа, выраженные в двоичном коде, а затем воспроизвести их на экране или отпечатать в виде десятичных знаков. Состояние выхода или выходов во всех этих задачах предопределено состоянием входа или входов. Задачи, относящиеся к этому классу, называются «комбинационными». Они могут быть решены с помощью вентилей — устройств, которые выполняют операции булевой алгебры в системах с двумя состояниями (двоичных).
Задачи, относящиеся к этому классу, называются «комбинационными». Они могут быть решены с помощью вентилей — устройств, которые выполняют операции булевой алгебры в системах с двумя состояниями (двоичных).
Существует другой класс задач, которые требуют знания прежнего состояния входных сигналов. Для решения этих задач необходимо применять «последовательные» схемы.
К задачам такого типа относится:
— преобразование строки двоичных разрядов из последовательной формы (один разряд следует за другим во времени) в параллельную группу разрядов
— подсчет числа единиц
— распознавание заданной определенной кодовой комбинации и последовательности битов, или, например, формирование одного выходного импульса после поступления четырех входных.
Для решения всех этих задач требуется в какой-либо форме цифровая память. Основным устройством для построения этой памяти служит триггер (или мультивибратор с двумя устойчивыми состояниями).
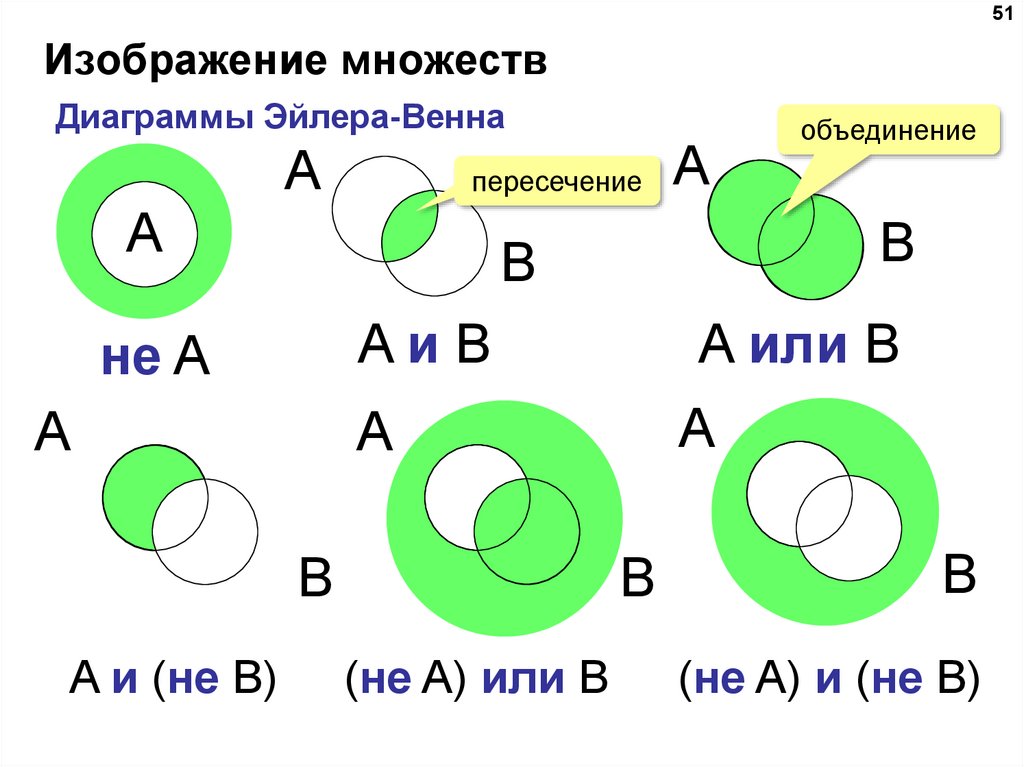
Логические вентили и комбинационная логика являются основой для построения любых цифровых схем.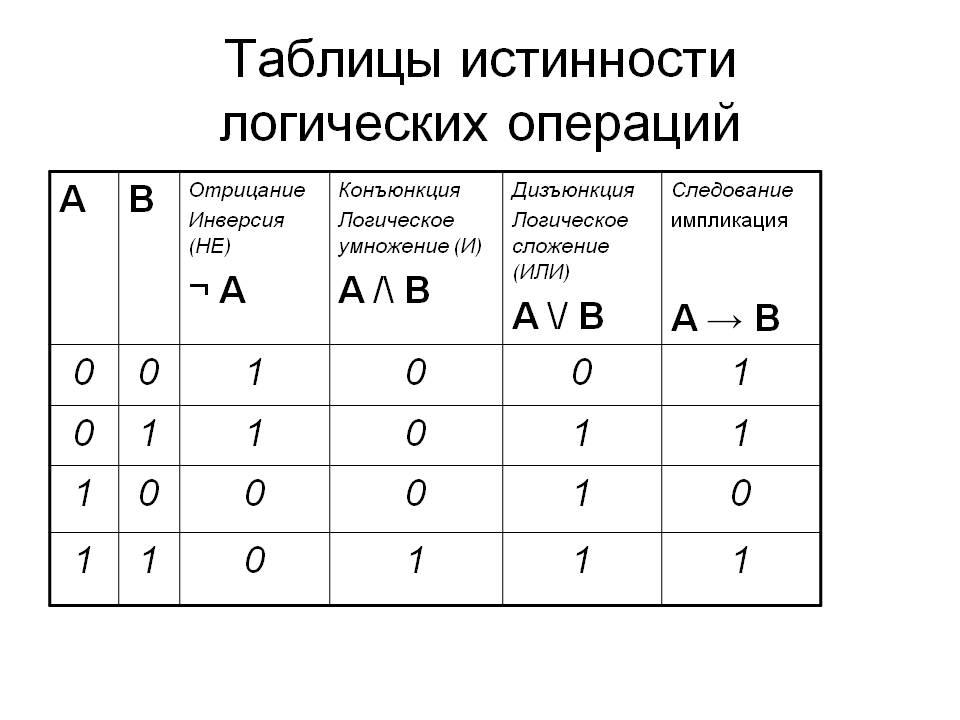
Вентиль ИЛИ
Выход вентиля ИЛИ имеет ВЫСОКИЙ уровень, если хотя бы на одном из его входов присутствует ВЫСОКИЙ уровень. Это можно выразить с помощью «таблицы истинности», представленной на рисунке ниже, где показан вентиль ИЛИ на 2 входа.К задачам такого типа относится:
Вентиль ИЛИВ общем случае число входов не ограничено, однако в стандартном корпусе микросхемы обычно размещаются четыре 2-входовых вентиля, три 3-входовых или два 4-входовых. Например, на выходе 4-входового вентиля ИЛИ «ВЫСОКИЙ» уровень будет присутствовать в том случае, если он подан на любой из его входов. Для обозначения операции ИЛИ в булевой алгебре используется символ +. Функция «А ИЛИ В» записывается как А+В.
Вентиль И
Выход вентиля И имеет высокий уровень только в том случае, если ВЫСОКИЙ уровень присутствует на обоих его входах. Схематическое изображение вентиля и его таблица истинности показаны на рисунке ниже.
Вентили И, выпускаемые промышленностью также как и вентили ИЛИ, могут иметь 3, 4, а иногда и большее число входов. Например, 8-входовой вентиль И вырабатывает на выходе ВЫСОКИЙ уровень только в том случае, если на всех его входах действует ВЫСОКИЙ уровень.
Для обозначения операции И в булевой алгебре используется точка (•), которая может быть опущена, функция «А и В» записывается как А•В или просто АВ.
Функция НЕ (инвертор)
Иногда бывает нужно получить дополнение (инверсию) логического сигнала. Эту функцию выполняет инвертор — вентиль, который имеет только один вход (рисунок ниже).
ИнверторДля обозначения операции НЕ в булевой алгебре используется черта над символом или апостроф. «НЕ А» записывается как или А’. Для удобства вместо черты над буквой для указания отрицания часто используются символы /, *, —, ‘. Таким образом, «НЕ А» можно записать любым из следующих способов: А’, —А, *А, /А, А*, А/.
Вентили И-НЕ и ИЛИ-HE
Вентили могут совмещать инвертирование с выполнением функций
И и ИЛИВентиль И-НЕВентиль ИЛИ-НЕТакие вентили имеют более широкое распространение, чем просто И и ИЛИ
Исключающее ИЛИ
Большой интерес представляет логическая функция «Исключающее ИЛИ», хотя она не относится к числу основных (см. рисунок).
ИСКЛЮЧАЮЩЕЕ ИЛИНа выходе вентиля «Исключающее ИЛИ» ВЫСОКИЙ уровень сформируется в том случае, если он будет подан на один из его входов (но не на оба одновременно). Другими словами, ВЫСОКИЙ уровень действует на выходе тогда, когда входы имеют различное состояние. Этот вентиль может иметь только два входа. Операция «Исключающее ИЛИ» подобна сложению двух бит по модулю 2.
Схемы вентилей на дискретных элементах
На рисунке показан диодный вентиль И
Диодный вентиль ИЕсли на каком-либо его входе действует НИЗКИЙ уровень, то он будет действовать и на выходе, а ВЫСОКИЙ уровень на выходе возникает только в том случае, если он будет присутствовать на обоих входах.
Эта схема обладает рядом недостатков:
а) НИЗКИЙ уровень на выходе выше НИЗКОГО уровня на входе на величину падения на диоде. Естественно, слишком много диодов ставить нельзя.
б) отсутствует «разветвление по выходу», т. е. возможность питать одним выходом несколько входов, так как выходная нагрузка действует на входной сигнал
в) низкое быстродействие, обусловленное резисторной нагрузкой.
Вообще логические схемы, построенные на дискретных элементах, не обладают теми свойствами, которые присущи интегральным микросхемам. Преимущества логических схем на микросхемах связаны отчасти с применением специальной технологии (например, ионная имплантация), которая позволяет получать хорошие характеристики.
Простейшая схема транзисторного вентиля
ИЛИ-HE показана на рисункеЭта схема использовалась в семействе логических элементов РТЛ (резисторно-транзисторная логика), которые из-за низкой стоимости были популярны в 1960-х годах, но в настоящее время они совершенно не употребляются.
 ВЫСОКИЙ уровень, действующий по любому входу (или по обоим одновременно), откроет хотя бы один транзистор и на выходе возникнет НИЗКИЙ уровень. Поскольку по своей сути такой вентиль является инвертирующим, то для того, чтобы получить из него вентиль ИЛИ, к нему нужно добавить инвертор.
ВЫСОКИЙ уровень, действующий по любому входу (или по обоим одновременно), откроет хотя бы один транзистор и на выходе возникнет НИЗКИЙ уровень. Поскольку по своей сути такой вентиль является инвертирующим, то для того, чтобы получить из него вентиль ИЛИ, к нему нужно добавить инвертор.Взаимозаменяемость вентилей
При построении цифровых схем надо помнить, что из вентиля одного типа можно получить вентиль другого типа. Например, если вам нужен вентиль
И, а у вас есть половина стандартной интегральной микросхемы серии 7400 (4 И-НЕ на два входа), то можно произвести замену, как показано на рисункеВторой вентиль используется в качестве инвентора, в результате этого получается функция И.
Путем многократного использования инвентируемого вентиля (например, И-НЕ) одного типа можно реализовать любую комбинационную функцию. Однако это не относится к неинвентирующему вентилю, так как с его помощью функцию НЕ получить нельзя.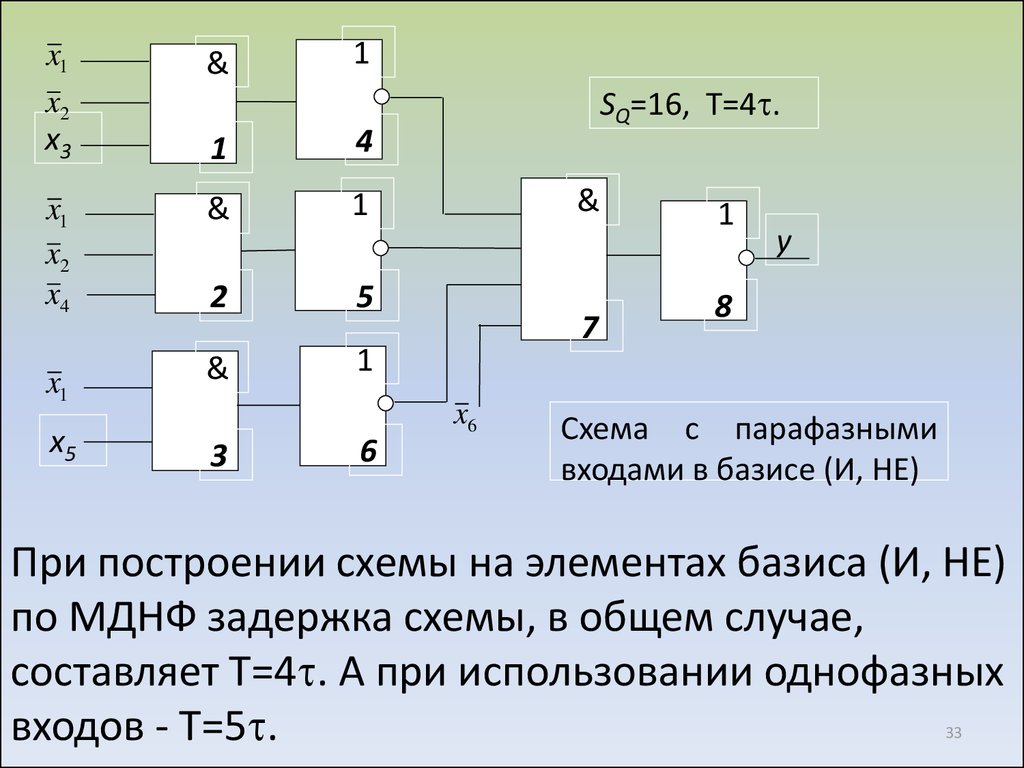 Именно по этой причине скорее всего вентили И-НЕ получили наибольшее распространение в логических схемах.
Именно по этой причине скорее всего вентили И-НЕ получили наибольшее распространение в логических схемах.
Логические обозначения при заданных уровнях
Вентиль
И будет иметь ВЫСОКИЙ уровень на выходе, когда ВЫСОКИЙ уровень будет действовать на обоих его входах. Если ВЫСОКИЙ уровень обозначает «истину», то «истина» будет на выходе в том случае, если она присутствует на всех входах. Другими словами, при использовании положительной логики вентиль И выполняет логическую функцию И. То же самое касается и вентиля ИЛИ.Что произойдет, если «истину» будет обозначать НИЗКИЙ уровень. Вентиль И даст на выходе НИЗКИЙ уровень, если на любом из его входов была «истина» (НИЗКИЙ уровень), но это функция ИЛИ. С другой стороны, вентиль ИЛИ сформирует НИЗКИЙ уровень лишь в том случае, если «истина» будет на обоих его входах. Но это функция И.
Существует два пути для разрешения этой проблемы. Первый заключается в том, что разработчик выбирает такой тип вентиля, который позволит получить требуемый выход.
Первый заключается в том, что разработчик выбирает такой тип вентиля, который позволит получить требуемый выход.
Например, если нужно определить, имеет ли один из трех входов НИЗКИЙ уровень, необходимо использовать 3-входовой вентиль И-НЕ. По всей вероятности, этим методом пользуется большинство разработчиков цифровых схем. Следуя этим путем, начертим вентиль И-НЕ, даже если по отношению к своим входам он выполняет функцию ИЛИ-HE (при отрицательной логике). При этом обозначим входы, как показано на рисунке
В данном примере сигналы сброса — СБРОС’ (CLEAR’), ОС’-ОБЩИЙ СБРОС, MR’ (master reset) и УСТАНОВКА В «0» (RESET’), поступающие из различных точек схемы, будут иметь уровни отрицательной логики. Выходной сигнал СБРОС, представленный в положительной логике, будет подаваться на различные устройства, которые должны сбрасываться, если любой из сигналов установки в исходное состояние имеет НИЗКИЙ уровень («истина»).
Другой способ решения задачи сигналов отрицательной логики состоит в использовании метода «заданных уровней». Если вентиль И выполняет функцию ИЛИ, используя на входах отрицательную логику, то изобразим его, как показано на рисунке.
Если вентиль И выполняет функцию ИЛИ, используя на входах отрицательную логику, то изобразим его, как показано на рисунке.
Вентиль ИЛИ на 3 входа с отрицательными входными сигналами аналогичен по выполняемой функции 3-входовому вентилю И-НЕ. Эта эквивалентность представляет собой важный принцип — свойство логических цепей, который называется теоремой Моргана.
Таким образом можно менять И на ИЛИ и наоборот, проинвертировав при этом выход и все входы.
Следует отметить два важных момента:1. Термин «отрицательная логика» не означает, что логические уровни имеют отрицательную полярность. Он лишь говорит, что «истинное» утверждение определяется тем из двух состояний, которое имеет меньший уровень (НИЗКИЙ).
2. При символическом изображении вентиля предполагается, что он использует положительную логику. Выполняющий функцию ИЛИ для сигналов отрицательной логики вентиль И-НЕ, может изображаться либо как И-НЕ, либо с использованием логики заданных уровней с обозначением в форме ИЛИ с символами инверсии на входах (маленькие кружки). В последнем случае эти кружки обозначают инверсию входных сигналов, которые поступают на вентиль ИЛИ, работающий при положительной логике, согласно первоначальному определению.
В последнем случае эти кружки обозначают инверсию входных сигналов, которые поступают на вентиль ИЛИ, работающий при положительной логике, согласно первоначальному определению.
Смотрите также:
Общие сведения о логических операторах C++ | Udacity
Простые союзы, такие как «и» и «или», позволяют нам связать наши идеи — даже самые сложные.
Эти два мощных слова могут играть не меньшую роль в языке программирования C++, где они используются в качестве логических операторов.
Логические операторы необходимы для создания более сложного и динамичного потока управления программой. В этой статье рассказывается, как создавать логические операторы и когда их использовать.
Что такое операторы в C++?
Операторы — это символы, используемые в C++ для выполнения вычислений над переменными и значениями. Когда вы будете учиться, чтобы стать разработчиком C++, вы быстро увидите, что операторы играют важную роль в таких областях, как арифметические, реляционные и логические (истинные или ложные) утверждения в коде.
C++ использует логические значения для проверки истинности или ложности операторов отношения. Логические значения могут возвращать только 1 (истина) или 0 (ложь) в зависимости от результата сравнения. Как мы увидим ниже, мы можем использовать эти операторы несколькими способами, чтобы привести программу к определенному результату.
Во-первых, давайте рассмотрим, как мы можем использовать реляционные операторы для получения истинных или ложных выходных данных.
Реляционные операторы
Реляционные операторы, как кратко упоминалось выше, работают с переменными с определенными значениями и дают логический результат. Они используют такие символы, как ==, !=, <= и >, чтобы проверить, являются ли два операнда одинаковыми, разными, больше или меньше друг друга. Эти операторы выводят 1, если утверждение истинно, и 0, если ложно.
Логические операторы
Логические операторы работают только с логическими значениями (или выражениями, подобными реляционным операторам, которые возвращают логические значения) и дают собственный логический результат. В C++ для логических вычислений используются операторы !, && и ||.
В C++ для логических вычислений используются операторы !, && и ||.
Использование логических операторов в C++?
Как мы увидим, логические операторы хорошо подходят для проверки правильности двух (или более) сравнительных операций. Затем операторы выводят конкретный ответ, основанный на характере оператора и истинности одного или обоих операндов. В C++ мы часто видим это в форме оператора if/else.
Прежде чем мы сможем подробнее рассмотреть, где в коде часто встречаются логические операторы, нам сначала нужно понять синтаксис, стоящий за ними. Всего имеется три логических оператора:
Оператор «и» (&&)
Логический оператор «и» просматривает операнды на любой из своих сторон и возвращает «истина», только если оба утверждения истинны. Если хотя бы одно из двух утверждений ложно, логическое «и» вернет ложь.
Ниже приведен практический пример использования оператора && в C++:
#include |
Выше мы просим пользователя указать номер. Наш логический оператор «и» проверяет, является ли число больше 0, а также меньше или равно 10. Если оба эти утверждения верны, число должно быть между 1 и 10, и мы можем вывести, что это число кейс.
Наш логический оператор «и» проверяет, является ли число больше 0, а также меньше или равно 10. Если оба эти утверждения верны, число должно быть между 1 и 10, и мы можем вывести, что это число кейс.
Если введено число 0 или меньше или число больше 10, программа объявит результат «ложным», отрицая оператор if и вместо этого выводя, что число не находится в диапазоне от 1 до 10.
Оператор «или» (||)
Логический оператор «или» работает аналогично оператору «и» выше. Разница в том, что «или» вернет «истина», если левый или правый операнд истинен. || оператор вернет ложное значение только в том случае, если оба операнда ложны.
Рассмотрим сценарий, в котором выигрыш одного из двух счастливых чисел от 1 до 10 в игре принесет нам приз. В этом примере мы установим счастливые числа на четыре и восемь. Нам нужно написать программу на C++ для проверки победителей:
#include |
Когда пользователь приходит играть в нашу игру, его просят ввести число. Если они правильно угадывают четыре или восемь, им сообщают, что они выбрали выигрышный номер. Если пользователь вводит любое другое целочисленное значение, ему придется повторить попытку в другой раз.
Оператор «не» (!)
Логический оператор «не» используется для преобразования значения из истинного в ложное или из ложного в истинное. Точно так же, если операнд оценивается как истина, логическое «нет» заставит его оценить как ложь. Если операнд оценивается как ложный, его логический эквивалент «не» будет истинным.
В следующем примере показано одно возможное использование логического оператора «не»:
#include |
Эта программа настроена на возврат значения true в любое время, когда переменная x не равна нулю. Оператор if проверяет, равен ли x 0, что возвращает false для всех чисел, кроме нуля. ! оператор переворачивает результат с false на true, в результате чего программа выводит истинный результат оператора if:
Оператор if проверяет, равен ли x 0, что возвращает false для всех чисел, кроме нуля. ! оператор переворачивает результат с false на true, в результате чего программа выводит истинный результат оператора if:
Введите число: 786 Вы ввели число, отличное от 0 |
При использовании логического оператора «не» важно помнить, что он имеет очень высокий уровень приоритета в C++. Логическое «не» выполняется перед операторами сравнения, такими как «равно» (==) и «больше чем» ( > ). При кодировании с логическим «не» программист должен убедиться, что программа настроена на выполнение операторов в правильном порядке.
В приведенном ниже примере мы видим, как невыполнение этого требования приводит к проблеме:
#include |
В этом примере программа сначала выполнит логическое ! перед выполнением сравнения. При этом программа ошибочно возвращает следующее:
При этом программа ошибочно возвращает следующее:
3 больше 11 |
Чтобы все исправить, нам нужно изменить наш оператор if следующим образом:
если (!(число1 > число2)) |
Таким образом, программа сначала выполняет реляционную операцию, а затем логическое «не», чтобы привести нас к правильному выводу.
Таблица истинности логических операций
Каким бы обширным ни было логическое выражение, при оценке все сводится к двоичному значению истинности или ложности.
Принимая во внимание только результат операнда «a», операнда «b» и логического оператора, мы можем построить следующую таблицу, которая показывает результат данной логической операции.
| и | б | а && б | а || б | !а |
| правда | правда | правда | правда | ложь |
| правда | ложь | ложь | правда | ложь |
| ложный | ложь | ложь | ложь | правда |
| ложный | правда | ложь | правда | правда |
Эта таблица дает хороший способ проверить свою работу с логическими операциями. Программа, которая не возвращает перечисленный результат для предоставленных критериев, будет иметь ошибку, которую необходимо устранить.
Программа, которая не возвращает перечисленный результат для предоставленных критериев, будет иметь ошибку, которую необходимо устранить.
Битовые операторы в сравнении с логическими операторами
Битовые операторы выглядят и функционируют аналогично логическим операторам, но работают только со значениями целочисленного типа, а не с логическими значениями. Побитовые операторы сравнивают два целых числа побитно и выводят 1 или 0 в зависимости от результата операции.
Для сравнения, побитовое «и» (&) очень похоже на логическое «и» (&&). Аналогично, побитовое «или» (|) следует тому же соглашению, что и логическое «или» (||). К счастью, побитовое «не» (~) выглядит существенно иначе, чем логическое «не» (!).
Смешение этих операторов приведет к ошибкам компиляции в вашей программе.
Изучайте C++ с помощью Udacity
Теперь, когда вы лучше понимаете логические операторы, вы готовы взяться за новые возможности C++.
В Udacity мы предлагаем интерактивную программу под руководством экспертов, которая выводит начинающих разработчиков C++ на новый уровень. Вы даже проверите свои навыки, написав пять реальных проектов.
Вы даже проверите свои навыки, написав пять реальных проектов.
Зарегистрируйтесь в нашей программе C++ Nanodegree уже сегодня!
Сравнение и логические операторы | Codecademy
Перейти к содержимомуМини-значок со стрелкой внизFavicon IconCodecademy Team
Мини-значок с круглым кружкомИспользуйте эту статью в качестве справочного листа для сравнения JavaScript и логических операторов.
Используйте эту статью в качестве справочного материала для сравнения JavaScript и логических операторов.
- Операторы сравнения — операторы, сравнивающие значения и возвращающие
trueилиfalse. Операторы включают:>,<,>=,<=,===и!==. - Логические операторы — операторы, которые объединяют несколько логических выражений или значений и обеспечивают один логический вывод.
 Среди операторов:
Среди операторов: &&,||и!.
Операторы сравнения
Возможно, вы знакомы с операторами сравнения по математике. Убедитесь, что в ваших знаниях нет пробелов.
- Меньше чем (
<) — возвращаетtrue, если значение слева меньше значения справа, в противном случае возвращаетfalse. - Больше, чем (
>) — возвращаетtrue, если значение слева больше значения справа, в противном случае возвращаетсяложь. - Меньше или равно (
<=) — возвращаетtrue, если значение слева меньше или равно значению справа, в противном случае возвращаетfalse. - Больше или равно (
>=) — возвращаетtrue, если значение слева больше или равно значению справа, в противном случае возвращаетfalse. - Equal to (
===) — возвращаетtrue, если значение слева равно значению справа, иначе возвращаетложь.


 ";
возврат 0;
}
";
возврат 0;
}  Среди операторов:
Среди операторов: