Гравитация
Не смотря на то, что гравитация – это слабейшее взаимодействие между объектами во Вселенной, ее значение в физике и астрономии огромно, так как она способна оказывать влияние на физические объекты на любом расстоянии в космосе.
Содержание:
- 1 Общие сведения
- 2 Материалы по теме
- 3 Гравитационные поля
- 4 Гравитационное излучение
- 5 Интересные эффекты гравитации
- 6 Материалы по теме
- 7 Теории гравитации
- 8 Интересные факты
Общие сведения
Если вы увлекаетесь астрономией, вы наверняка задумывались над вопросом, что собой представляет такое понятие, как гравитация или закон всемирного тяготения. Гравитация – это универсальное фундаментальное взаимодействие между всеми объектами во Вселенной.
Материалы по теме
Открытие закона гравитации приписывают знаменитому английскому физику Исааку Ньютону. Наверное, многим из вас известна история с яблоком, упавшим на голову знаменитому ученому. Тем не менее, если заглянуть вглубь истории, можно увидеть, что о наличии гравитации задумывались еще задолго до его эпохи философы и ученые древности, например, Эпикур. Тем не менее, именно Ньютон впервые описал гравитационное взаимодействие между физическими телами в рамках классической механики. Его теорию развил другой знаменитый ученый – Альберт Эйнштейн, который в своей общей теории относительности более точно описал влияние гравитации в космосе, а также ее роль в пространственно-временном континууме.
Тем не менее, если заглянуть вглубь истории, можно увидеть, что о наличии гравитации задумывались еще задолго до его эпохи философы и ученые древности, например, Эпикур. Тем не менее, именно Ньютон впервые описал гравитационное взаимодействие между физическими телами в рамках классической механики. Его теорию развил другой знаменитый ученый – Альберт Эйнштейн, который в своей общей теории относительности более точно описал влияние гравитации в космосе, а также ее роль в пространственно-временном континууме.
Закон всемирного тяготения Ньютона говорит, что сила гравитационного притяжения между двумя точками массы, разделенными расстоянием обратно пропорциональна квадрату расстояния и прямо пропорциональна обеим массам. Сила гравитации является дальнодействующей. То есть, в независимости от того, как будет двигаться тело, обладающее массой, в классической механике его гравитационный потенциал будет зависеть сугубо от положения этого объекта в данный момент времени. Чем больше масса объекта, тем больше его гравитационное поле – тем более мощной гравитационной силой он обладает. Такие космически объекты, как галактики, звезды и планеты обладают наибольшей силой притяжения и соответственно достаточно сильными гравитационными полями.
Такие космически объекты, как галактики, звезды и планеты обладают наибольшей силой притяжения и соответственно достаточно сильными гравитационными полями.
Гравитационные поля
Гравитационное поле Земли
Гравитационное поле – это расстояние, в пределах которого осуществляется гравитационное взаимодействие между объектами во Вселенной. Чем больше масса объекта, тем сильнее его гравитационное поле – тем ощутимее его воздействие на другие физические тела в пределах определенного пространства. Гравитационное поле объекта потенциально. Суть предыдущего утверждения заключается в том, что если ввести потенциальную энергию притяжения между двумя телами, то она не изменится после перемещения последних по замкнутому контуру. Отсюда выплывает еще один знаменитый закон сохранения суммы потенциальной и кинетической энергии в замкнутом контуре.
В материальном мире гравитационное поле имеет огромное значения. Им обладают все материальные объекты во Вселенной, у которых есть масса. Гравитационное поле способно влиять не только на материю, но и на энергию. Именно за счет влияния гравитационных полей таких крупных космических объектов, как черные дыры, квазары и сверхмассивные звезды, образуются солнечные системы, галактики и другие астрономические скопления, которым свойственна логическая структура.
Гравитационное поле способно влиять не только на материю, но и на энергию. Именно за счет влияния гравитационных полей таких крупных космических объектов, как черные дыры, квазары и сверхмассивные звезды, образуются солнечные системы, галактики и другие астрономические скопления, которым свойственна логическая структура.
Последние научные данные показывают, что знаменитый эффект расширения Вселенной так же основан на законах гравитационного взаимодействия. В частности расширению Вселенной способствуют мощные гравитационные поля, как небольших, так и самых крупных ее объектов.
Гравитационное излучение
Гравитационное излучение в двойной системе
Гравитационное излучение или гравитационная волна – термин, впервые введенный в физику и космологии известным ученым Альбертом Эйнштейном. Гравитационное излучение в теории гравитации порождается движением материальных объектов с переменным ускорением. Во время ускорения объекта гравитационная волна как бы «отрывается» от него, что приводит к колебаниям гравитационного поля в окружающем пространстве. Это и называют эффектом гравитационной волны.
Это и называют эффектом гравитационной волны.
Хотя гравитационные волны предсказаны общей теорией относительности Эйнштейна, а также другими теориями гравитации, они еще ни разу не были обнаружены напрямую. Связано это в первую очередь с их чрезвычайной малостью. Однако в астрономии существуют косвенные свидетельства, способные подтвердить данный эффект. Так, эффект гравитационной волны можно наблюдать на примере сближения двойных звезд. Наблюдения подтверждают, что темпы сближения двойных звезд в некоторой степени зависят от потери энергии этих космических объектов, которая предположительно затрачивается на гравитационное излучение. Достоверно подтвердить эту гипотезу ученые смогут в ближайшее время при помощи нового поколения телескопов Advanced LIGO и VIRGO.
Интересные эффекты гравитации
Материалы по теме
В современной физике существует два понятия механики: классическая и квантовая. Квантовая механика была выведена относительно недавно и принципиально отличается от механики классической. В квантовой механике у объектов (квантов) нет определенных положений и скоростей, все здесь базируется на вероятности. То есть, объект может занимать определенное место в пространстве в определенный момент времени. Куда переместиться он дальше, достоверно определить нельзя, а только с высокой долей вероятности.
В квантовой механике у объектов (квантов) нет определенных положений и скоростей, все здесь базируется на вероятности. То есть, объект может занимать определенное место в пространстве в определенный момент времени. Куда переместиться он дальше, достоверно определить нельзя, а только с высокой долей вероятности.
Интересный эффект гравитации заключается в том, что она способна искривлять пространственно-временной континуум. Теория Эйнштейна гласит, что в пространстве вокруг сгустка энергии или любого материального вещества пространство-время искривляется. Соответственно меняется траектория частиц, которые попадают под воздействие гравитационного поля этого вещества, что позволяет с высокой долей вероятности предсказать траекторию их движения.
Теории гравитации
Сегодня ученым известно свыше десятка различных теорий гравитации. Их подразделяют на классические и альтернативные теории. Наиболее известными представителем первых является классическая теория гравитации Исаака Ньютона, которая была придумана известным британским физиком еще в 1666 году. Суть ее заключается в том, что массивное тело в механике порождает вокруг себя гравитационное поле, которое притягивает к себе менее крупные объекты. В свою очередь последние также обладают гравитационным полем, как и любые другие материальные объекты во Вселенной.
Суть ее заключается в том, что массивное тело в механике порождает вокруг себя гравитационное поле, которое притягивает к себе менее крупные объекты. В свою очередь последние также обладают гравитационным полем, как и любые другие материальные объекты во Вселенной.
Следующая популярная теория гравитации была придумана всемирно известным германским ученым Альбертом Эйнштейном в начале XX века. Эйнштейну удалось более точно описать гравитацию, как явление, а также объяснить ее действие не только в классической механике, но и в квантовом мире. Его общая теория относительности описывает способность такой силы, как гравитация, влиять на пространственно-временной континуум, а также на траекторию движения элементарных частиц в пространстве.
Самая точная гравитационная карта Земли
Среди альтернативных теорий гравитации наибольшего внимания, пожалуй, заслуживает релятивистская теория, которая была придумана нашим соотечественником, знаменитым физиком А.А. Логуновым. В отличие от Эйнштейна, Логунов утверждал, что гравитация – это не геометрическое, а реальное, достаточно сильное физическое силовое поле. Среди альтернативных теорий гравитации известны также скалярная, биметрическая, квазилинейная и другие.
Среди альтернативных теорий гравитации известны также скалярная, биметрическая, квазилинейная и другие.
Интересные факты
- Людям, побывавшим в космосе и возвратившимся на Землю, достаточно трудно на первых порах привыкнуть к силе гравитационного воздействия нашей планеты. Иногда на это уходит несколько недель.
- Доказано, что человеческое тело в состоянии невесомости может терять до 1% массы костного мозга в месяц.
- Наименьшей силой притяжения в Солнечной системе среди планет обладает Марс, а наибольшей – Юпитер.
- Известные бактерии сальмонеллы, которые являются причиной кишечных заболеваний, в состоянии невесомости ведут себя активнее и способны причинить человеческому организму намного больший вред.
- Среди всех известных астрономических объектов во Вселенной наибольшей силой гравитации обладают черные дыры. Черная дыра размером с мячик для гольфа, может обладать той же гравитационной силой, что и вся наша планета.
- Сила гравитации на Земле одинакова не во всех уголках нашей планеты.
 К примеру, в области Гудзонова залива в Канаде она ниже, чем в других регионах земного шара.
К примеру, в области Гудзонова залива в Канаде она ниже, чем в других регионах земного шара.
Понравилась запись? Расскажи о ней друзьям!
Просмотров записи: 26394
Запись опубликована: 14.09.2015
Автор: Максим Заболоцкий
Напряжённость гравитационного поля
Из проекта Викизнание
Напряжённость гравитацио́нного по́ля — векторная физическая величина, характеризующая гравитационное поле в данной точке и численно равная отношению гравитационной силы , действующей на неподвижную пробную частицу, помещённую в данную точку поля, к гравитационной массе этой частицы:
Данное определение сводит
напряжённость поля к гравитационной силе, действующей на единичную массу.
Существует и другое определение, когда напряжённость поля находится через
пространственные и временные производные от потенциалов гравитационного поля
либо через компоненты тензора гравитационного
поля. [1] Поскольку гравитационное поле представляет собой
векторное поле, его напряжённость зависит от времени и координат той точки
пространства, где измеряется напряжённость поля:
[1] Поскольку гравитационное поле представляет собой
векторное поле, его напряжённость зависит от времени и координат той точки
пространства, где измеряется напряжённость поля:
Напряжённость гравитационного поля вместе с полем кручения описывают гравитационное поле в лоренц-инвариантной теории гравитации и подчиняются максвеллоподобным гравитационным уравнениям.
В общей теории относительности напряжённость гравитационного поля называется напряжённостью гравитоэлектрического поля, а поле кручения соответствует гравитомагнитному полю. В пределе слабого гравитационного поля указанные величины входят в уравнения гравитоэлектромагнетизма.
Напряжённость гравитационного поля в международной системе единиц измеряется в метрах на секунду в квадрате [м/с2] или в ньютонах на килограмм [Н/кг].
Оглавление
|
Напряжённость гравитационного поля в лоренц-инвариантной теории гравитации
Если записывать соотношения лоренц-инвариантной теории гравитации (ЛИТГ) на
языке 4-векторов и тензоров, то оказывается, что вектор напряжённости
гравитационного поля и вектор поля кручения составляют в совокупности тензор гравитационного поля, входят в тензор энергии-импульса гравитационного поля
и в функцию Лагранжа для частицы в
гравитационном поле, а скалярный и векторный потенциалы гравитационного поля
образуют гравитационный 4-потенциал.
где – скорость распространения гравитационного воздействия, – гравитационная постоянная.
Гравитационная сила
Полная сила, с которой гравитационное поле действует на пробную частицу, выражается следующей формулой:
где: – масса частицы, – скорость частицы, – вектор поля кручения.
В данной формуле первый член силы пропорционален напряжённости
гравитационного поля, а второй член силы зависит от скорости движения частицы и
от поля кручения, действующего на частицу. При этом предполагается, что и являются усреднёнными по объёму частицы напряжённостью
и полем кручения от внешнего гравитационного поля, а полем от самой частицы
можно пренебречь ввиду его малости.
Для расчёта полной силы, действующей на протяжённое тело, в пределах которого напряжённость и кручение гравитационного поля изменяются в значительных размерах, осуществляют разбиение тела на небольшие части, подсчитывают для каждой части свою силу и затем производят векторное суммирование всех таких сил.
Плотность вектора силы , понимаемая как гравитационная сила, действующая на единицу движущегося объёма, входит в пространственноподобную компоненту 4-вектора плотности гравитационной силы (смотри 4-сила). В ковариантной теории гравитации этот 4-вектор выражается так:
где – метрический тензор, – тензор гравитационного поля, есть 4-вектор плотности массового тока, – тензор энергии-импульса гравитационного поля.
Выражение для 4-вектора плотности гравитационной силы в лоренц-инвариантной теории гравитации можно представить через напряжённость гравитационного поля:
где – плотность тока массы, плотность гравитационной силы выражается формулой
– фактор Лоренца, есть плотность вещества в сопутствующей
системе отсчёта.
Из формулы видно, что произведение равно мощности работы, совершаемой гравитационной силой в единице объёма, причём поле кручения не входит в это произведение и не совершает работу над веществом.
Уравнения Хевисайда
Лоренц-ковариантные уравнения гравитации в инерциальных системах отсчёта
можно найти в работах Оливера Хевисайда.
где: – плотность тока массы, – плотность движущейся массы, – скорость движения потока массы, создающего гравитационное поле и кручение.
Данные четыре уравнения полностью описывают гравитационное поле для тех
случаев, когда поле не настолько велико, чтобы влиять на распространение
электромагнитных волн, на их скорость и частоту.
Если же гравитационное поле значительно по величине, то его влияние на
электромагнитные процессы приводит к гравитационному красному смещению,
замедлению времени, отклонению движения электромагнитных волн вблизи источников
гравитационного поля, и к другим эффектам. Поскольку измерения времени и
пространственных расстояний осуществляются с помощью электромагнитных волн, то
в гравитационном поле для наблюдателя размеры тел могут оказаться меньше, а
скорость течения времени замедлиться. Подобные эффекты учитываются путём
введения метрики пространства-времени, зависящей от координат и времени.
Поэтому в случае сильного гравитационного поля вместо указанных выше уравнений
используются более общие уравнения ковариантной
теории гравитации, либо уравнения общей
теории относительности, в которых присутствует метрический тензор.
Если от первого уравнения Хевисайда взять градиент, а от четвёртого уравнения частную производную по времени, то в результате можно получить неоднородное волновое уравнение для напряжённости гравитационного поля:
Повторяя те же действия для второго и третьего уравнений, приходим к волновому уравнению для поля кручения:
Наличие волновых уравнений говорит о том, что напряжённость и кручение гравитационного поля в каждой точке могут быть найдены как суммы (интегралы) множества отдельных простых волн, делающих свой вклад в общее поле, при этом каждый вклад должен быть подсчитан с учётом запаздывания влияния источников поля за счёт ограниченности скорости передачи гравитационного воздействия.
Третье уравнение Хевисайда приводит к возможности гравитационной индукции, когда изменяющееся
во времени поле кручения, проходящее через некоторый контур, или изменение
площади контура при неизменном поле кручения, генерируют круговую напряжённость
гравитационного поля вдоль окружности этого контура.
Потенциалы гравитационного поля
Напряжённость гравитационного поля выражается как через скалярный потенциал , так и через векторный потенциал гравитационного поля по формуле:
Поле кручения зависит только от векторного потенциала, поскольку:
Гравистатика
Наиболее простым случаем для исследования свойств гравитации является случай взаимодействия неподвижных либо движущихся с достаточно малой скоростью тел. В гравистатике пренебрегают векторным потенциалом гравитационного поля из-за отсутствия или малости поступательного или вращательного движения масс, создающих поле, поскольку пропорционален скорости движения масс. В результате становится малым и поле кручения, вычисляемое как ротор от векторного потенциала. В таком приближении можно записать:
где называется гравистатический потенциал, чтобы подчеркнуть статический
случай гравитационного поля. В гравистатике
напряжённость гравитационного поля становится потенциальным векторным полем, то
есть полем, зависящим только от градиента от некоторой функции, в данном случае
от скалярного потенциала.
В гравистатике
напряжённость гравитационного поля становится потенциальным векторным полем, то
есть полем, зависящим только от градиента от некоторой функции, в данном случае
от скалярного потенциала.
При условии, что в рассматриваемой физической системе нет массовых токов и потому напряжённость гравитационного поля не зависит от времени, равны нулю векторный потенциал и поле кручения в уравнениях Хевисайда остаётся одно уравнение:
Если в (1) использовать соотношение то получается уравнение, которое имеет форму уравнения Пуассона:
За пределами тел плотность покоящегося вещества равна нулю, и уравнение для гравистатического потенциала становится уравнением Лапласа:
Уравнения Пуассона и Лапласа справедливы как для потенциала точечной
частицы, так и для суммы потенциалов множества частиц, что приводит к
возможности использовать принцип суперпозиции для расчёта суммарного потенциала
и напряжённости общего гравитационного поля в любой точке системы. Однако в достаточно
сильных полях из модернизированной теории
гравитации Лесажа следует, что принцип суперпозиции нарушается из-за
экспоненциальной зависимости потоков гравитонов в веществе от пройденного
расстояния. [4]
Однако в достаточно
сильных полях из модернизированной теории
гравитации Лесажа следует, что принцип суперпозиции нарушается из-за
экспоненциальной зависимости потоков гравитонов в веществе от пройденного
расстояния. [4]
Применение формулы Гаусса—Остроградского
Уравнение (1) можно проинтегрировать по произвольному объёму пространства и затем применить формулу Гаусса—Остроградского, заменяющую интеграл от дивергенции векторной функции по некоторому объёму на интеграл потока этой векторной функции по замкнутой поверхности вокруг данного объёма:
где есть суммарная масса вещества внутри поверхности.
Во многих случаях оказывается, что поток напряжённости гравитационного поля на поверхности неизменен, что позволяет вынести напряжённость поля за знак интеграла и затем интегрировать только площадь поверхности. В частности, площадь сферической поверхности , и для напряжённости поля на расстоянии от центра сферы (и от центра тела сферической формы с собственным радиусом, не превышающим радиус поверхности ) получается:
Данная формула остаётся справедливой независимо от радиуса тела сферической
формы, пока этот радиус не превышает , то есть
когда напряжённость поля ищется за пределами тела. Для тела массы в виде материальной точки можно считать, что
расстояние отсчитывается от этой точки.
Для тела массы в виде материальной точки можно считать, что
расстояние отсчитывается от этой точки.
В случае, когда формула Гаусса—Остроградского применяется к сферической поверхности внутри тела со сферически симметричным расположением массы, из формулы следует, что напряжённость гравитационного поля внутри тела зависит только от массы тела находящейся внутри сферической поверхности радиуса :
Для сферы с однородной плотностью вещества масса что даёт для напряжённости поля:
В центре сферы, где напряжённость поля равна нулю, а при радиусе где есть радиус сферы, напряжённость достигает максимальной амплитуды.
Классическая теория тяготения
Выражение для напряжённости гравитационного поля материальной точки можно получить также из закона Ньютона для силы гравитации, действующей на частицу с массой . Если источником гравитационного поля является однородное тело сферической формы с гравитационной массой , то согласно классической теории тяготения Ньютона за пределами тела:
где: – радиус-вектор от центра тела до точки в
пространстве, где определяется напряжённость гравитационного поля ,
а знак минус показывает, что сила и напряжённость поля направлены против
направления радиус-вектора .
В классической теории скалярный потенциал гравитационного поля за пределами тела сферической формы равен:
Применяя формулу находим напряжённость гравитационного поля в векторном виде:
Если считать справедливым принцип эквивалентности, при котором гравитационная масса пробной частицы равна инертной массе этой частицы во втором законе Ньютона, то получается следующее:
то есть напряжённость гравитационного поля численно (и по размерности) равна ускорению свободного падения пробной частицы в этом поле.
См. также
- Поле кручения
- Максвеллоподобные гравитационные уравнения
- Гравитоэлектромагнетизм
- Лоренц-инвариантная теория гравитации
- Ковариантная теория гравитации
- Тензор гравитационного поля
- Вектор Хевисайда
- Тензор энергии-импульса гравитационного поля
- Гравитационный 4-потенциал
- Напряжённость электрического поля
Ссылки
- Fedosin
S.
 G. Electromagnetic and
Gravitational Pictures of the World. Apeiron, 2007, Vol. 14, No. 4, P. 385 –
413; статья на русском языке: Электромагнитная
и гравитационная картины мира.
G. Electromagnetic and
Gravitational Pictures of the World. Apeiron, 2007, Vol. 14, No. 4, P. 385 –
413; статья на русском языке: Электромагнитная
и гравитационная картины мира. - Федосин С.Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1. 544 стр., Табл.66, Ил.93, Библ. 377 назв.
- Oliver Heaviside. A Gravitational and Electromagnetic Analogy, Part I, The Electrician, 31, 281-282 (1893).
- Fedosin S.G. Model of Gravitational Interaction in the Concept of Gravitons. Journal of Vectorial Relativity, March 2009, Vol. 4, No. 1, P.1 – 24, статья на русском языке: Модель гравитационного взаимодействия в концепции гравитонов.
Внешние ссылки
· Gravitational field strength
Источник: http://sergf. ru/ngp.htm
ru/ngp.htm
На список страниц
Магнитные, электрические и гравитационные поля. Интерстеллар: наука за кадром
Магнитные, электрические и гравитационные поля. Интерстеллар: наука за кадромВикиЧтение
Интерстеллар: наука за кадром
Торн Кип Стивен
Содержание
Магнитные, электрические и гравитационные поля
Силовые линии магнитных полей играют большую роль во Вселенной и очень важны для понимания «Интерстеллар», поэтому стоит поговорить о них, прежде чем углубиться в научные аспекты фильма.
Наверное, на уроках физики вам уже приходилось иметь дело с силовыми линиями магнитного поля, когда вы ставили простой, но очень эффектный опыт. Помните, берешь листок бумаги, накрываешь им магнитный брусок и сыпешь сверху железные опилки? Опилки при этом складываются в узор, как на рис. 2.6. Они выстраиваются вдоль силовых линий магнитного поля, которые сами по себе невидимы. Эти линии исходят от одного из полюсов магнита, огибают магнит и достигают другого полюса. Магнитное поле – это совокупность всех магнитных силовых линий.
Эти линии исходят от одного из полюсов магнита, огибают магнит и достигают другого полюса. Магнитное поле – это совокупность всех магнитных силовых линий.
Рис. 2.6. Силовые линии магнитного поля вокруг магнитного бруска видны благодаря рассыпанным по листу бумаги железным опилкам (Рисунок Мэтта Зимета по моему наброску; из моей книги «Черные дыры и складки времени: дерзкое наследие Эйнштейна» [Торн 2009].)
Если вы возьмете два магнита и поднесете их северными полюсами друг к другу, их силовые линии будут отталкиваться. При этом в пространстве между магнитами вы ничего не увидите, но силу магнитного поля почувствуете. Этот эффект можно использовать для удержания в воздухе намагниченных объектов, каковым может быть даже железнодорожный поезд (рис. 2.7).
Рис. 2.7. Первый в мире коммерческий поезд на магнитной подушке в Шанхае, Китай
У Земли тоже есть два полюса, Северный и Южный. Силовые линии магнитного поля выходят из Южного полюса, огибают Землю и достигают Северного полюса (рис. 2.8). Эти линии воздействуют на стрелку компаса таким же образом, как и на железные опилки: стрелка не успокоится, пока не встанет вдоль линий настолько точно, насколько это возможно. Таков принцип работы компаса.
2.8). Эти линии воздействуют на стрелку компаса таким же образом, как и на железные опилки: стрелка не успокоится, пока не встанет вдоль линий настолько точно, насколько это возможно. Таков принцип работы компаса.
Рис. 2.8. Силовые линии магнитного поля Земли
Силовые линии магнитного поля Земли можно увидеть, наблюдая полярное (иначе – северное) сияние (рис. 2.9). Силовые линии захватывают летящие от Солнца протоны, и те входят в земную атмосферу. Там протоны сталкиваются с молекулами кислорода и азота, заставляя их флуоресцировать[14]. Это свечение и есть полярное сияние.
Рис. 2.9. Полярное сияние над Хаммерфестом, Норвегия
Магнитное поле нейтронных звезд очень мощное. Его силовые линии, так же как и земные, образуют фигуру, напоминающую пончик. Быстро движущиеся частицы, пойманные в магнитное поле нейтронной звезды, подсвечивают его силовые линии (голубые кольца на рис. 2.10). Некоторые частицы освобождаются и отлетают от полюсов, образуя конусообразные струи – джеты[15] (на рис. 2.10 показаны фиолетовым). Джеты состоят из самых разных излучений: гамма-лучей, рентгеновских лучей, ультрафиолета, видимого излучения, инфракрасного излучения, а также радиоволн. По мере того как звезда вращается, излучающие джеты движутся по небосводу подобно прожекторам. Каждый раз, когда джет поворачивается в сторону Земли, астрономы наблюдают импульс излучения; из-за периодичности импульсов такие звезды и прозвали пульсарами.
2.10 показаны фиолетовым). Джеты состоят из самых разных излучений: гамма-лучей, рентгеновских лучей, ультрафиолета, видимого излучения, инфракрасного излучения, а также радиоволн. По мере того как звезда вращается, излучающие джеты движутся по небосводу подобно прожекторам. Каждый раз, когда джет поворачивается в сторону Земли, астрономы наблюдают импульс излучения; из-за периодичности импульсов такие звезды и прозвали пульсарами.
Рис. 2.10. Условное изображение нейтронной звезды с магнитным полем в форме пончика и джетами
Во Вселенной есть и другие поля (совокупности силовых линий) помимо магнитных. Это среди прочих электрические поля (совокупности силовых линий, благодаря которым электрический ток движется по проводам). Еще один пример – гравитационные поля (совокупности силовых линий, которые, в частности, притягивают нас к земной поверхности).
Силовые линии гравитационного поля Земли направлены радиально, к ее центру, и притягивают объекты к Земле. Сила гравитационного притяжения пропорциональна плотности силовых линий (количеству линий, которые проходят через заданную площадь). По мере того как линии приближаются к Земле и проходят через воображаемые сферы все меньшей и меньшей площади (окружности из красного пунктира на рис. 2.11), плотность линий увеличивается обратно пропорционально площади сфер, а следовательно, гравитация возрастает по мере приближения к Земле – обратно пропорционально площади воображаемой сферы. Поскольку площадь каждой сферы пропорциональна квадрату ее удаленности от центра Земли r, сила притяжения Земли возрастает как 1/r2. Это ньютоновский закон обратных квадратов для гравитации – один из фундаментальных законов физики, которыми так страстно увлечен профессор Брэнд и знакомство с которыми – наша следующая веха на пути освоения научных аспектов «Интерстеллар».
Сила гравитационного притяжения пропорциональна плотности силовых линий (количеству линий, которые проходят через заданную площадь). По мере того как линии приближаются к Земле и проходят через воображаемые сферы все меньшей и меньшей площади (окружности из красного пунктира на рис. 2.11), плотность линий увеличивается обратно пропорционально площади сфер, а следовательно, гравитация возрастает по мере приближения к Земле – обратно пропорционально площади воображаемой сферы. Поскольку площадь каждой сферы пропорциональна квадрату ее удаленности от центра Земли r, сила притяжения Земли возрастает как 1/r2. Это ньютоновский закон обратных квадратов для гравитации – один из фундаментальных законов физики, которыми так страстно увлечен профессор Брэнд и знакомство с которыми – наша следующая веха на пути освоения научных аспектов «Интерстеллар».
Рис. 2.11. Силовые линии гравитационного поля Земли
Данный текст является ознакомительным фрагментом.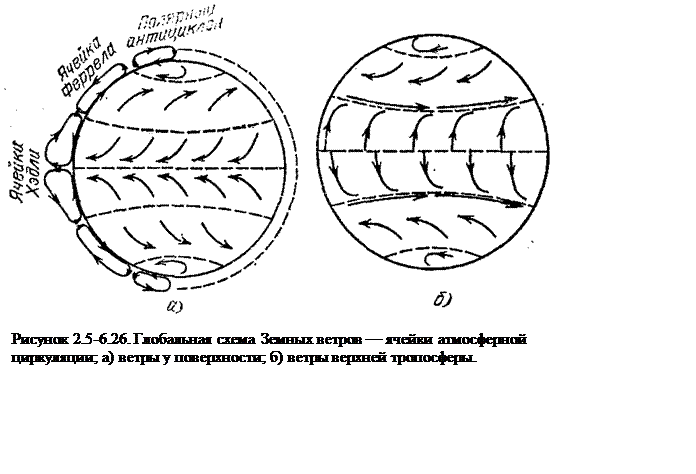
Глава 37 МАГНИТНЫЕ МАТЕРИАЛЫ
Глава 37 МАГНИТНЫЕ МАТЕРИАЛЫ § 1.Сущность ферромагнетизма§ 2.Термодинамические свойства§ 3. Петля гистерезиса§ 4.Ферромагнитные материалы§ 5.Необычные магнитные материалы§ 1. Сущность ферромагнетизмаВ этой главе мы поговорим об особенностях и поведении ферромагнетиков и
1. Тонкая структура и магнитные аномалии
1. Тонкая структура и магнитные аномалии Мы изложили принципы волновой механики электрона. Теперь мы должны показать, почему, несмотря на ее успехи, эта механика в своей первоначальной форме оказалась все же несовершенной и должна претерпеть еще существенные изменения.
ЭЛЕКТРИЧЕСКИЕ ОСЦИЛЛЯТОРЫ*
ЭЛЕКТРИЧЕСКИЕ ОСЦИЛЛЯТОРЫ*
Мало было открыто таких областей, которые оказались столь урожайными как токи высокой частоты. Их необыкновенные свойства и эффектность демонстрируемых ими явлений сразу же вызвали всеобщее внимание. Научные люди заинтересовались
Их необыкновенные свойства и эффектность демонстрируемых ими явлений сразу же вызвали всеобщее внимание. Научные люди заинтересовались
ЭЛЕКТРИЧЕСКИЕ ВОЗМОЖНОСТИ, СКРЫТЫЕ В УГЛЕ И ЖЕЛЕЗЕ
ЭЛЕКТРИЧЕСКИЕ ВОЗМОЖНОСТИ, СКРЫТЫЕ В УГЛЕ И ЖЕЛЕЗЕ Многие «вот-если-бы» исследователи, терпя неудачу в своих попытках, чувствовали досаду от того, что родились в то время, когда все уже создано и не осталось ничего, что нужно сделать. Это ложное ощущение, что по мере нашего
ВОЕННЫЕ ЭЛЕКТРИЧЕСКИЕ ИЗОБРЕТЕНИЯ
ВОЕННЫЕ ЭЛЕКТРИЧЕСКИЕ ИЗОБРЕТЕНИЯ Нынешний международный конфликт — это мощный стимул к изобретению устройств и орудий войны. Скоро сделают электрическую пушку. Удивительно, что ее не сделали давным- давно. Дирижабли и аэропланы будут оборудоваться небольшими
Две электрические жидкости
Две электрические жидкости
Последующие страницы содержат скучный отчет о некоторых очень простых экспериментах. Отчет будет скучным не только потому, что описание экспериментов неинтересно по сравнению с самим осуществлением их, но и потому, что самый смысл
Отчет будет скучным не только потому, что описание экспериментов неинтересно по сравнению с самим осуществлением их, но и потому, что самый смысл
Магнитные жидкости
Магнитные жидкости Мы будем поступать здесь так же, как и раньше: начинать с очень простых фактов, а затем отыскивать их теоретическое объяснение. Рис. 321. Пусть у нас имеются два длинных магнита; один из них уравновешен так, что он занимает горизонтальное положение, а
1.4. Магнитные ppm
1.4. Магнитные ppm Первым известным магнитным ppm была машина Петра Пилигрима (1269 г.), уже описанная в начале этой главы (рис. 1.4).Новые виды магнитных вечных двигателей, появившиеся позже, основывались, так же как и первый, на аналогии между силой тяжести и силой притяжения
Магнитные поля в галактиках
Магнитные поля в галактиках
В 1945 году известный уже нам английский астроном Ф. Хойл опубликовал свою гипотезу, согласно которой диффузная первоматерия Галактики сконцентрировалась под воздействием магнитного поля в два рукава, отходящие от центральной части,
Хойл опубликовал свою гипотезу, согласно которой диффузная первоматерия Галактики сконцентрировалась под воздействием магнитного поля в два рукава, отходящие от центральной части,
97 Магнитные поля на бумаге
97 Магнитные поля на бумаге Для опыта нам потребуются: железные опилки (придется напилить из гвоздей), обычный маленький бытовой магнит, плотный лист бумаги, банка с подсолнечным маслом. Этот опыт потребовал от меня взять напильник и напилить из гвоздей, зажав их в тисках,
Глава седьмая Электрические опыты
Глава седьмая Электрические опыты Наэлектризованный гребень Если вы еще даже ничего не знаете из науки об электричестве, не знакомы даже с первыми буквами ее азбуки, вы и в таком случае можете проделать ряд электрических опытов, любопытных и во всяком случае полезных
Электрические опыты с газетой
Электрические опыты с газетой
Гораздо более разнообразные опыты, чем с «кошачьим» электричеством, можно проделывать с электричеством «газетным», извлекаемым из газетного листа. В детстве меня забавлял ими старший брат; я поделюсь с читателем этими
В детстве меня забавлял ими старший брат; я поделюсь с читателем этими
Гравитационные волны
Гравитационные волны В 1919 г. Эйнштейн предсказал, что движущиеся массы производят гравитационные волны, распространяющиеся со скоростью света. К сожалению, амплитуда такого гравитационного излучения, испускаемого любым источником, созданным в лаборатории, слишком
7. Гравитационные пращи
7. Гравитационные пращи Управлять космическим кораблем вблизи Гаргантюа нелегко – из-за очень больших скоростей. Чтобы не погибнуть, планета, звезда или космический корабль должны противопоставить огромной гравитации Гаргантюа центробежную силу сравнимой величины.
24. Гравитационные аномалии
24. Гравитационные аномалии Гравитационная аномалия – это нечто такое, что связано с гравитацией и не укладывается в наши представления о Вселенной или не соответствует нашему пониманию законов физики, управляющих Вселенной: например падения книг
Модель гравитационного поля планеты в системе гравитирующих стержней
Автор: Хромова Ирина Викторовна
Рубрика: Физика
Опубликовано в
Молодой учёный
№15 (119) август-1 2016 г.
Дата публикации: 31.07.2016 2016-07-31
Статья просмотрена: 284 раза
Скачать электронную версию
Скачать Часть 1 (pdf)
Библиографическое описание:Хромова, И. В. Модель гравитационного поля планеты в системе гравитирующих стержней / И. В. Хромова. — Текст : непосредственный // Молодой ученый. — 2016. — № 15 (119). — С. 116-118. — URL: https://moluch.ru/archive/119/32974/ (дата обращения: 24.09.2022).
Моделирование внешнего гравитационного поля Земли важно для вычисления траекторий естественных и искусственных тел. Простейшую модель центрального поля шара построил Ньютон. Учет несферичности Земли привел к использованию разложения потенциала по сферическим функциям. Значения параметров разложения приближенно определяются по наблюдениям Луны, ИСЗ и по гравиметрическим и геодезическим измерениям. Известный набор значений получил название «Стандартная Земля». Перечисленные сведения можно найти в книге Аксенова Е. П. [1]. Хорошее приближение дает модель двух неподвижных центров [1]. Обобщением является построение системы из многих материальных точек [5]. В нашей задаче используется модель из нескольких гравитирующих стержней, жестко связанных с Землей [4], а также модели, состоящие из «зубцов» и из «кочек». Введем геоцентрическую цилиндрическую систему координат R, θ, z. Ось z направим вдоль оси вращения Земли. Перейдем к безразмерным величинам. Для этого введем новую систему единиц. Пусть одна единица длины — 6371 км, единица массы — 5,9726·1024 кг, гравитационная постоянная G = 1. На этой оси поместим набор симметричных относительно начала СК однородных бесконечно тонких стержней, умещающихся на отрезке [-1,1].
Значения параметров разложения приближенно определяются по наблюдениям Луны, ИСЗ и по гравиметрическим и геодезическим измерениям. Известный набор значений получил название «Стандартная Земля». Перечисленные сведения можно найти в книге Аксенова Е. П. [1]. Хорошее приближение дает модель двух неподвижных центров [1]. Обобщением является построение системы из многих материальных точек [5]. В нашей задаче используется модель из нескольких гравитирующих стержней, жестко связанных с Землей [4], а также модели, состоящие из «зубцов» и из «кочек». Введем геоцентрическую цилиндрическую систему координат R, θ, z. Ось z направим вдоль оси вращения Земли. Перейдем к безразмерным величинам. Для этого введем новую систему единиц. Пусть одна единица длины — 6371 км, единица массы — 5,9726·1024 кг, гравитационная постоянная G = 1. На этой оси поместим набор симметричных относительно начала СК однородных бесконечно тонких стержней, умещающихся на отрезке [-1,1]. Плотность каждого стержня равна . Полагаем, что концы отрезка находятся внутри Земли.
Плотность каждого стержня равна . Полагаем, что концы отрезка находятся внутри Земли.
Постановка задачи
Будем строить варианты моделей с одинаковой безразмерной массой, равной единице, которые помещаются в сферу единичного радиуса. Вариант модели обозначим M (S, D, N). Параметр Sописывает структуру — дискретная модель из материальных точек, из кусочно-непрерывных стержней, из точек и стержней соответственно. При этом гладкость линейной плотности стержней может быть различной — на концах стержней может испытывать скачок сама плотность и/либо ее производная, а могут быть непрерывны и плотность и производная (случаи пенька , зубца, кочки). D = 1, 2, 3 означает размерность модели, то есть количество осей, на которых расположены точки и стержни. N — это число элементов модели. Массы, размеры элементов также могут различаться. Простейшим случаем является модель M (point, 1, 1), состоящая из одной материальной точки.
Введем декартову систему координат с началом в центре масс системы. Размазав модель равномерно по оси, получим варианты M (segment(s), 1, 1) с пеньком либо с зубцом, либо с кочкой. Далее, добавляя распределения масс вдоль осей получим варианты M (point, 2, N), M (point, 3, N), M (segment(s), 2, N), M (segment(s), 3, N). Аналогично можно поступить с вариантами M (point & segment(s), D, N), располагая вперемежку точки и стержни. Ограничимся моделями с зеркальной симметрией относительно плоскости , но при этом будем строить модели с ротационной симметрией. В этом случае можно рассматривать вращение системы.
Размазав модель равномерно по оси, получим варианты M (segment(s), 1, 1) с пеньком либо с зубцом, либо с кочкой. Далее, добавляя распределения масс вдоль осей получим варианты M (point, 2, N), M (point, 3, N), M (segment(s), 2, N), M (segment(s), 3, N). Аналогично можно поступить с вариантами M (point & segment(s), D, N), располагая вперемежку точки и стержни. Ограничимся моделями с зеркальной симметрией относительно плоскости , но при этом будем строить модели с ротационной симметрией. В этом случае можно рассматривать вращение системы.
Введем новую характеристику гравитационного поля системы — квазикруговую скорость (ККС) с помощью скалярного произведения:
В системе с ротационной симметрией относительно оси и зеркальной симметрией она совпадает с обычной круговой скоростью при:
Нужно построить для рассматриваемого потенциала изолинии ККС в трех координатных плоскостях — экваториальной двух меридиональных — и . В случае сферической модели все изолинии будут окружностями.
В случае сферической модели все изолинии будут окружностями.
Типы рассматриваемых распределений масс:
- Разрывное кусочно-постоянное распределение
- Непрерывное кусочно–линейное пилообразное распределение
Построим кусочно-линейное распределение масс, график которого имеет пилообразный вид. Расположим нечетное количество зубцов n симметрично относительно начала СК на оси z. Зубцы образуют равнобедренные треугольники с основаниями 2и высотой , где k — номер зубца. Зубцу приписываем массу [4]. Считаем, что зубцы не пересекаются друг с другом, а крайние зубцы не выходят за интервал [-1,1].
- Гладкое кусочно-параболическое распределение
Построим гладкое кусочно-параболическое распределение, график которого имеет вид «кочек». Функция плотности одного элемента состоит из 3 частей, каждая из которых является частью параболы. Масса «кочки» равна , основание 2, середину основания обозначим .
Масса «кочки» равна , основание 2, середину основания обозначим .
При получаем дельта-функцию, которая отображает точечную массу величиной . Положение материальной точки совпадает с координатой .
Гравитационное поле
Введем новую характеристику гравитационного поля системы — квазикруговую скорость (ККС). Рассмотрим изолинии ККС для каждого вида потенциала. ККСвводим с помощью скалярного произведения:
(1)
Это выражение является вириалом. Вириал для системы точек массами имеет вид [6]:
.(2)
Так как — потенциал модели, то уравнения движения будут иметь вид:
(3)
Выразив из (3) и подставив в выражение (2), получим выражение (1). Теорема вириала гласит, что усредненная по бесконечному интервалу времени кинетическая энергия механической системы равна усредненному по тому же интервалу вириалу сил. Следовательно, введенная ККС является характеристикой гравитационного поля.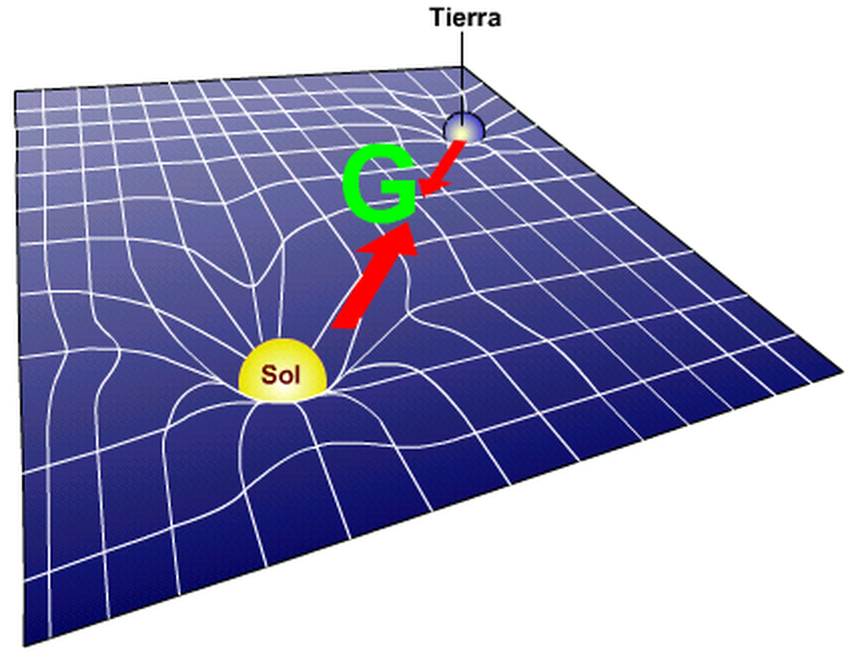
Рассмотрим изолинии ККС для различных моделей. Сначала исследуем модель двух стержней постоянной плотности на оси (Рис.1).
Рис. 1. Изолинии ККС в меридиональной плоскости
Рис. 2. Изолинии ККС. Слева , справа
В экваториальной плоскости изолинии будут окружностями, так как влияние стержней одинаковое в любой момент времени, потому что располагаются они на оси . Из-за ротационной симметричности модели график изолинии в любой меридиональной плоскости будет одинаковым. Изолинии ККС вытягиваются вдоль оси , округляясь по мере отдаления от центра. При изменении типа распределения стержня на зубчатый, изолинии отдаляются от центра (Рис. 2).
Исследуем, как изменение гладкости распределения отразится на виде изолиний. На рис. 3 сравнены две модели — с зубчатым и кочкообразным распределением. Как видно из рисунка, увеличение порядка гладкости отражается незаметно, вид изолиний идентичен.
Рис. 3. Изолинии ККС Слева , справа
Заключение
Предлагаемая модель внешнего гравитационного поля Земли является довольно гибкой благодаря наличию большого числа параметров.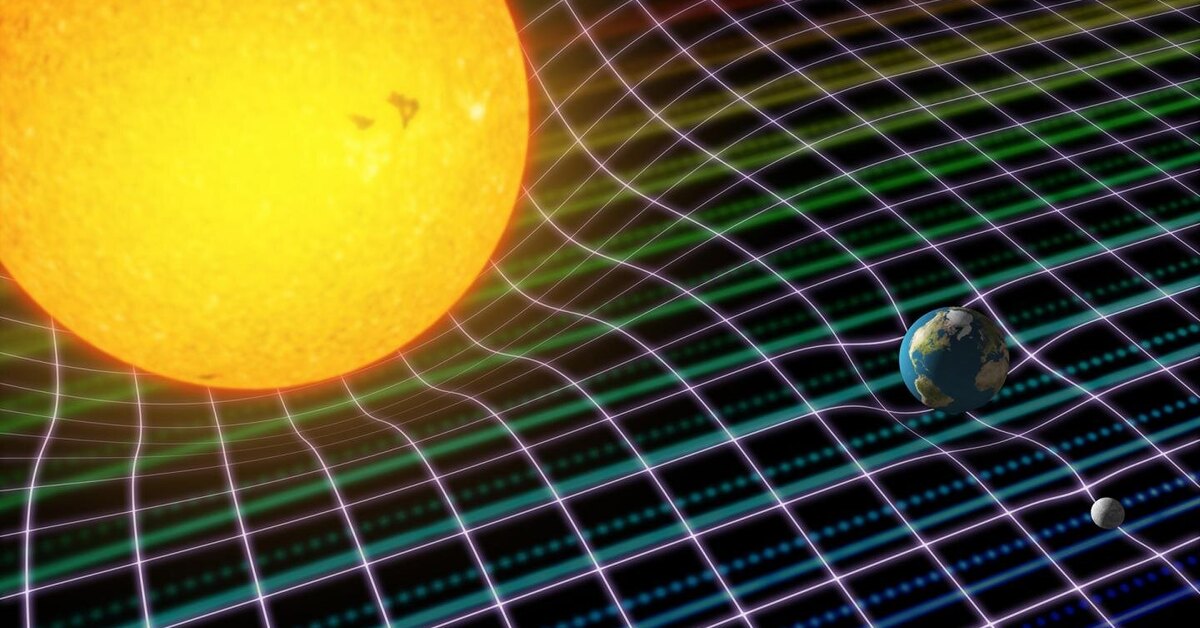 Изменяя вид распределения можно достичь хорошего приближения к выражению внешнего потенциала Земли как суммы кеплерова потенциала и возмущающей части.
Изменяя вид распределения можно достичь хорошего приближения к выражению внешнего потенциала Земли как суммы кеплерова потенциала и возмущающей части.
Модели такого рода можно строить и для других планет Солнечной системы. Значения параметров могут приближенно определяться по известным данным о некоторых планетах.
Литература:
- Аксенов Е. П. Теория движения искусственных спутников Земли. М.: Наука, 1977. 360 с.
- Кутузов С. А. Математическое описание астрономических систем. Учеб. пособие.-СПб.: Изд. СПбГУ, 2004. 244 с.
- Антонов В. А., Никифоров И. И., Холшевников К. В. Элементы теории гравитационного потенциала и некоторые случаи его явного выражения. СПб.: Изд-во С.-Петерб. ун-та, 2008. 208 с.
- Кодрик В. В., Кутузов С. А. Моделирование внешнего поля Земли с помощью гравитирующих стержней //Труды XLII международной научной конференции аспирантов и студентов «Процессы управления и устойчивость» / Под ред. А.
 С. Еремина, Н. В. Смирнова.-СПб, издат. дом СПбГУ, 2011. 588с. с. 145–150.
С. Еремина, Н. В. Смирнова.-СПб, издат. дом СПбГУ, 2011. 588с. с. 145–150. - Антонов В. А., Тимошкова Е. И., Холшевников К. В. Введение в теорию ньютоновского потенциала. М.: Наука, 1988. 272 с.
- Огородников К. Ф. Динамика звездных систем, М: Физматгиз, 1958. 644 с.
Основные термины (генерируются автоматически): модель, изолиния, ось, внешнее гравитационное поле, гладкое кусочно-параболическое распределение, гравитационное поле, зеркальная симметрия, меридиональная плоскость, ротационная симметрия, скалярное произведение.
Похожие статьи
Геометрические свойства
гравитационного поляПоэтому гравитационное поле любого тела искривляет не просто пространство, а меняющееся гравитационное поле определенного интервала центральной массы.
Центральная симметрия гравитационного поля позволяет оценивать самое простое движение – динамику. ..
..
Гипотеза механизма закономерности Тициуса-Боде
В поле Солнца расположение орбит образует закономерную последовательность, в которой характеристики движения внешних
Тогда большая часть пространства гравитационного поля Солнца для каждой орбиты делится горизонтальными плоскостями на 2…
Математическое моделирование взаимодействия ионов…
С этой целью предложена математическая модель движения большого числа таких частиц во внешнем поле.
Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .
О проблемах геометрического моделирования рельефа
поля для…Планировка поля для оптимального орошения требует наиболее плоской планировки. При этом микрорельеф местности не всегда идеален.
При этом микрорельеф местности не всегда идеален.
Но проблема в том, что поверхности между горизонталями принимаются за ровные плоскости или за линейные поверхности, что видно…
Создание цифровой геологической
модели для уточнения…В основе метода оценки распределения водонасыщенности по мощности нефтяного пласта лежит классическая теория равновесия между гравитационными и капиллярными силами. Так как нефтенасыщенность обратная величина водонасыщенности, то она также зависит от…
Системный подход в изучении начертательной геометрии
– способам изображения пространственных фигур на плоскости
5 Шантаренко, В. Г. Системный подход к обучению студентов математике на основе моделирования в визуальном информационном поле как способ реализации когнитивно-визуального подхода / В. Г…
Г…
Исследование свойств
поверхностей вращения с использованием…Приводятся методики разработки 3D моделей поверхностей и реальных сооружений в САПР «Компас», а также натурных моделей с помощью 3D-печати.
– плоскостной симметрией относительно всех координатных плоскостей. 3) В сечении плоскостью, ортогональной оси…
Обработка и сегментация тепловизионных изображений
Сегментацией изображения — это распределение множества пикселей изображения на объекты и области
Также контур может быть внутренний или внешний. Точки контура, в сравнении с
Далее высчитывается сумма, где слагаемыми являются произведения значений пикселей на…
Геометрические свойства
гравитационного поляПоэтому гравитационное поле любого тела искривляет не просто пространство, а меняющееся гравитационное поле определенного интервала центральной массы.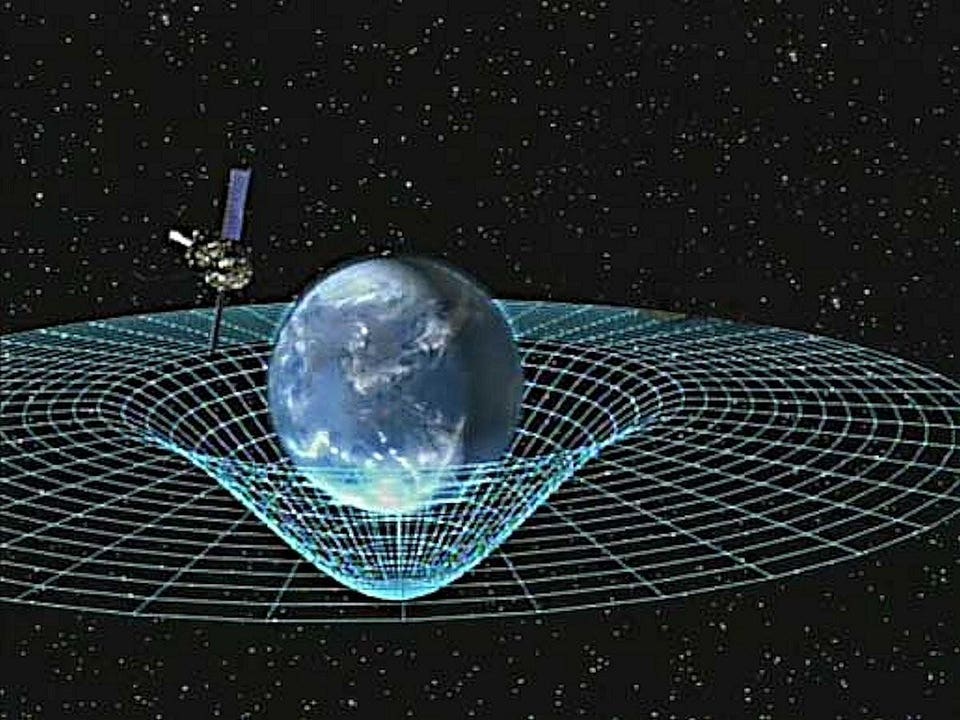
Центральная симметрия гравитационного поля позволяет оценивать самое простое движение – динамику…
Гипотеза механизма закономерности Тициуса-Боде
В поле Солнца расположение орбит образует закономерную последовательность, в которой характеристики движения внешних
Тогда большая часть пространства гравитационного поля Солнца для каждой орбиты делится горизонтальными плоскостями на 2…
Математическое моделирование взаимодействия ионов…
С этой целью предложена математическая модель движения большого числа таких частиц во внешнем поле.
Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .
О проблемах геометрического моделирования рельефа
поля для. ..
..Планировка поля для оптимального орошения требует наиболее плоской планировки. При этом микрорельеф местности не всегда идеален.
Но проблема в том, что поверхности между горизонталями принимаются за ровные плоскости или за линейные поверхности, что видно…
Создание цифровой геологической
модели для уточнения…В основе метода оценки распределения водонасыщенности по мощности нефтяного пласта лежит классическая теория равновесия между гравитационными и капиллярными силами. Так как нефтенасыщенность обратная величина водонасыщенности, то она также зависит от…
Системный подход в изучении начертательной геометрии
– способам изображения пространственных фигур на плоскости
5 Шантаренко, В. Г. Системный подход к обучению студентов математике на основе моделирования в визуальном информационном поле как способ реализации когнитивно-визуального подхода / В. Г…
Г…
Исследование свойств
поверхностей вращения с использованием…Приводятся методики разработки 3D моделей поверхностей и реальных сооружений в САПР «Компас», а также натурных моделей с помощью 3D-печати.
– плоскостной симметрией относительно всех координатных плоскостей. 3) В сечении плоскостью, ортогональной оси…
Обработка и сегментация тепловизионных изображений
Сегментацией изображения — это распределение множества пикселей изображения на объекты и области
Также контур может быть внутренний или внешний. Точки контура, в сравнении с
Далее высчитывается сумма, где слагаемыми являются произведения значений пикселей на…
Похожие статьи
Геометрические свойства
гравитационного поляПоэтому гравитационное поле любого тела искривляет не просто пространство, а меняющееся гравитационное поле определенного интервала центральной массы.
Центральная симметрия гравитационного поля позволяет оценивать самое простое движение – динамику…
Гипотеза механизма закономерности Тициуса-Боде
В поле Солнца расположение орбит образует закономерную последовательность, в которой характеристики движения внешних
Тогда большая часть пространства гравитационного поля Солнца для каждой орбиты делится горизонтальными плоскостями на 2…
Математическое моделирование взаимодействия ионов…
С этой целью предложена математическая модель движения большого числа таких частиц во внешнем поле.
Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .
О проблемах геометрического моделирования рельефа
поля для. ..
..Планировка поля для оптимального орошения требует наиболее плоской планировки. При этом микрорельеф местности не всегда идеален.
Но проблема в том, что поверхности между горизонталями принимаются за ровные плоскости или за линейные поверхности, что видно…
Создание цифровой геологической
модели для уточнения…В основе метода оценки распределения водонасыщенности по мощности нефтяного пласта лежит классическая теория равновесия между гравитационными и капиллярными силами. Так как нефтенасыщенность обратная величина водонасыщенности, то она также зависит от…
Системный подход в изучении начертательной геометрии
– способам изображения пространственных фигур на плоскости
5 Шантаренко, В. Г. Системный подход к обучению студентов математике на основе моделирования в визуальном информационном поле как способ реализации когнитивно-визуального подхода / В.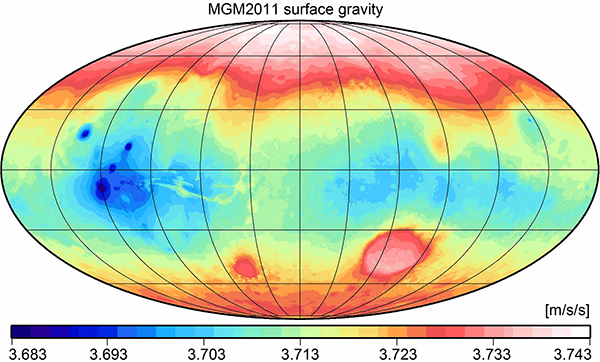 Г…
Г…
Исследование свойств
поверхностей вращения с использованием…Приводятся методики разработки 3D моделей поверхностей и реальных сооружений в САПР «Компас», а также натурных моделей с помощью 3D-печати.
– плоскостной симметрией относительно всех координатных плоскостей. 3) В сечении плоскостью, ортогональной оси…
Обработка и сегментация тепловизионных изображений
Сегментацией изображения — это распределение множества пикселей изображения на объекты и области
Также контур может быть внутренний или внешний. Точки контура, в сравнении с
Далее высчитывается сумма, где слагаемыми являются произведения значений пикселей на…
Геометрические свойства
гравитационного поляПоэтому гравитационное поле любого тела искривляет не просто пространство, а меняющееся гравитационное поле определенного интервала центральной массы.
Центральная симметрия гравитационного поля позволяет оценивать самое простое движение – динамику…
Гипотеза механизма закономерности Тициуса-Боде
В поле Солнца расположение орбит образует закономерную последовательность, в которой характеристики движения внешних
Тогда большая часть пространства гравитационного поля Солнца для каждой орбиты делится горизонтальными плоскостями на 2…
Математическое моделирование взаимодействия ионов…
С этой целью предложена математическая модель движения большого числа таких частиц во внешнем поле.
Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .
О проблемах геометрического моделирования рельефа
поля для. ..
..Планировка поля для оптимального орошения требует наиболее плоской планировки. При этом микрорельеф местности не всегда идеален.
Но проблема в том, что поверхности между горизонталями принимаются за ровные плоскости или за линейные поверхности, что видно…
Создание цифровой геологической
модели для уточнения…В основе метода оценки распределения водонасыщенности по мощности нефтяного пласта лежит классическая теория равновесия между гравитационными и капиллярными силами. Так как нефтенасыщенность обратная величина водонасыщенности, то она также зависит от…
Системный подход в изучении начертательной геометрии
– способам изображения пространственных фигур на плоскости
5 Шантаренко, В. Г. Системный подход к обучению студентов математике на основе моделирования в визуальном информационном поле как способ реализации когнитивно-визуального подхода / В. Г…
Г…
Исследование свойств
поверхностей вращения с использованием…Приводятся методики разработки 3D моделей поверхностей и реальных сооружений в САПР «Компас», а также натурных моделей с помощью 3D-печати.
– плоскостной симметрией относительно всех координатных плоскостей. 3) В сечении плоскостью, ортогональной оси…
Обработка и сегментация тепловизионных изображений
Сегментацией изображения — это распределение множества пикселей изображения на объекты и области
Также контур может быть внутренний или внешний. Точки контура, в сравнении с
Далее высчитывается сумма, где слагаемыми являются произведения значений пикселей на…
Ловцы гравитации: ученые составят космический прогноз землетрясений | Статьи
Российско-китайский космический проект по созданию четырех исследовательских спутников позволит в 10 раз повысить точность мониторинга гравитационного поля Земли. В результате будут улучшены долгосрочные прогнозы погоды и открыты возможности для предсказания землетрясений. Если проект окажется успешным, в дальнейшем появится также гравитационная навигация, которая станет аналогом GPS и ГЛОНАСС. Запустить аппараты на орбиту планируется через три года.
В результате будут улучшены долгосрочные прогнозы погоды и открыты возможности для предсказания землетрясений. Если проект окажется успешным, в дальнейшем появится также гравитационная навигация, которая станет аналогом GPS и ГЛОНАСС. Запустить аппараты на орбиту планируется через три года.
Создание и регулярное обновление карты гравитационного поля Земли — важная научная задача, решение которой позволяет оценивать и прогнозировать множество природных явлений. При этом ключевую роль в исследованиях играет работа специальных спутников, измерения которых дают возможность актуализировать данные с периодичностью в один месяц. Новый российско-китайский космический проект должен ускорить мониторинг, предоставив ученым более точную информацию.
Гравитация_1
Спутник GRACE Follow On во время испытаний
Фото: Airbus DS GmbH/A. Ruttloff
Справка «Известий»Существование гравитационного поля Земли обусловлено массой планеты и центробежной силой, которая вызвана ее вращением.
При этом сила тяготения в различных областях различается из-за неоднородности распределения масс и особенностей рельефа поверхности. Для того чтобы отразить ее величину в различных точках Земли, были созданы гравитационные карты, которые используются для прогнозирования климатических явлений.
— В настоящее время для исследования гравитационного поля используются два спутника проекта GRACE Follow On — оно проводится с помощью постоянного измерения расстояния между ними, изменение которого говорит о перемене характеристик поля, — отметил заведующий лабораторией лазерных интерферометрических измерений Астрономического института им. Штернберга МГУ Вадим Милюков. — Этот способ обеспечивает точность до одного микрометра. В нашем же проекте мы планируем увеличить ее на порядок за счет применения более совершенных лазерных дальномеров, погрешность которых составляет всего около 100 нанометров.
Гравитация_2
3D-модель работы спутников GRACE Follow On на орбите
Фото: NASA
По словам ученого, сейчас подразумевается оснащение лазерами сразу четырех спутников — они составят две группировки, одна из которых будет двигаться по полярной орбите (с наклонением в 90 градусов), а другая — по орбите с наклонением 70 градусов. Это решение позволит ученым еженедельно обновлять гравитационную карту Земли. В качестве базового аппарата планируется взять российскую платформу «Карат», созданную специалистами НПО им. Лавочкина.
Это решение позволит ученым еженедельно обновлять гравитационную карту Земли. В качестве базового аппарата планируется взять российскую платформу «Карат», созданную специалистами НПО им. Лавочкина.
Также для правильной работы лазеров на спутниках будет необходимо использовать новую систему стабилизации движения. Она необходима для компенсации их увода с траектории при контакте с остаточной атмосферой, которая еще присутствует на целевой 500-километровой высоте рабочей орбиты.
Фото: laspace.ru
Малая космическая платформа «Карат» с полезной нагрузкой
— Для этого на аппараты планируется установить акселерометры, в их конструкции будет использовано специальное зеркало с электростатическим подвесом, который предназначен для отражения лазерного луча, — пояснил начальник отдела перспективных исследований НПО им. Лавочкина Валентин Сысоев. — Конструкция позволит прибору детектировать все микроколебания спутника, которые способны помешать наблюдениям.
В дальнейшем сигналы от акселерометра будут направляться на электрические микродвигатели, работа которых возвратит спутник на идеальную траекторию.
Информация о гравитационном поле, полученная в результате работы новых спутников, позволит следить за распределением и перемещением различных веществ под землей и в атмосфере.
— В частности, новые данные могут открыть возможности для предсказания мест будущих крупных землетрясений, поскольку на обновленной гравитационной карте будут отражены зоны напряжений в земной коре, — считает Вадим Милюков.
Перспективы проекта прокомментировали в Институте физики Земли (ИФЗ) им. О.Ю. Шмидта РАН.
Гравитация_3
Изображение гравитационного поля Земли
Фото: NASA/JPL-Caltech
— Во время крупных землетрясений происходят заметные изменения гравитационного поля Земли, которые можно зафиксировать с помощью орбитальных наблюдений, — рассказал заведующий лабораторией комплексной интерпретации геофизических данных ИФЗ РАН, член-корреспондент РАН Валентин Михайлов. — Если же с помощью новой спутниковой системы удастся значительно повысить точность мониторинга изменений гравитационного поля, то можно будет находить крупные зоны, где накапливаются напряжения и деформации, например по периферии Тихого океана. Это позволит увидеть области, где готовятся сильные землетрясения.
Это позволит увидеть области, где готовятся сильные землетрясения.
Повлияет проект и на предсказание погодных явлений.
— Детальные данные о гравитационном поле необходимы для численного моделирования циркуляции Мирового океана, — пояснил Валентин Михайлов. — Характер океанических течений оказывает значительное влияние на климат и учитывается в моделях, использующихся для среднесрочных и долгосрочных прогнозов погоды.
Также гравитационный мониторинг позволит следить и за состоянием крупных ледников. Дело в том, что их таяние из-за глобального потепления приводит к значительному уменьшению массы, что должно отразиться на составляемой карте.
Гравитационный маршрутПо словам разработчиков, если информацию со спутников получится дополнить результатами систематических наблюдений оснащенных гравиметрами беспилотников, то высокоточная гравитационная карта может использоваться и в качестве основы для новых систем навигации. Ожидается, что они обеспечат точность позиционирования до нескольких метров и будут работать независимо от спутниковых систем GPS и ГЛОНАСС.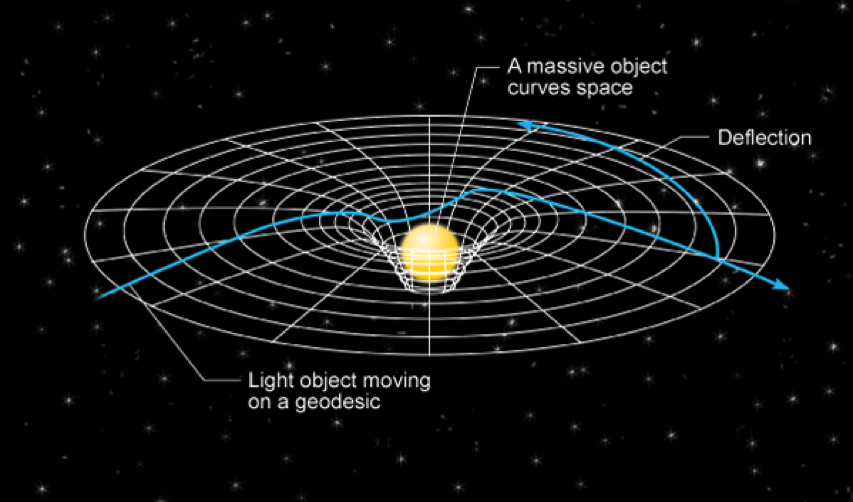
Гравитация_4
Фото: Global Look Press/Ivan Damanik
Сейчас проект по созданию научных аппаратов развивается в рамках соглашения о сотрудничестве между МГУ им. Ломоносова и Университетом Сунь Ятсена (Гуанчжоу, Китай). Кроме того, к его подготовке готовится присоединиться НПО им. Лавочкина — это может произойти после заключения соответствующего договора с госкорпорацией «Роскосмос».
Ожидается, что спутники для мониторинга гравитационного поля Земли будут отправлены на орбиту уже через три года. Для этих целей может быть использована российская ракета-носитель «Союз».
ЧИТАЙТЕ ТАКЖЕ
Аномалии гравитационного поля
Изучение гравитационного поля Земли имеет не только научное, но и большое практическое значение для многих отраслей народного хозяйства России. Являясь самостоятельным научным направлением, гравиметрия одновременно входит составной частью в другие комплексные науки о Земле, такие, как физика Земли, геология, геодезия и космонавтика, океанография и навигация, сейсмология и прогноз землетрясений.
Все исходные понятия гравиметрии основываются на положениях классической ньютоновой механики. Под действием силы тяжести все массы Земли испытывают ускорение g Обычно имеют дело не с силой тяжести, а с её ускорением, численно равным напряженности поля в данной точке. Изменения силы тяжести зависят от распределения масс в Земле. Под действием этой силы создалась современная форма (фигура) Земли и продолжается ее дифференциация на разные по составу и плотности геосферы. Это явление используется в гравиметрии для изучения геологического строения Земли. Изменения силы тяжести, связанные с плотностными неоднородностями земной коры, не имеющие явной, видимой закономерности и обусловливающие отклонение значений силы тяжести от нормального, называются аномалиями силы тяжести. Аномалии эти не велики. Их значения колеблются в пределах нескольких единиц 10-3 м/с 2 что составляет 0,05% полного значения силы тяжести и на порядок меньше нормального изменения её. Однако именно эти изменения представляют интерес для изучения земной коры и для поиска полезных ископаемых.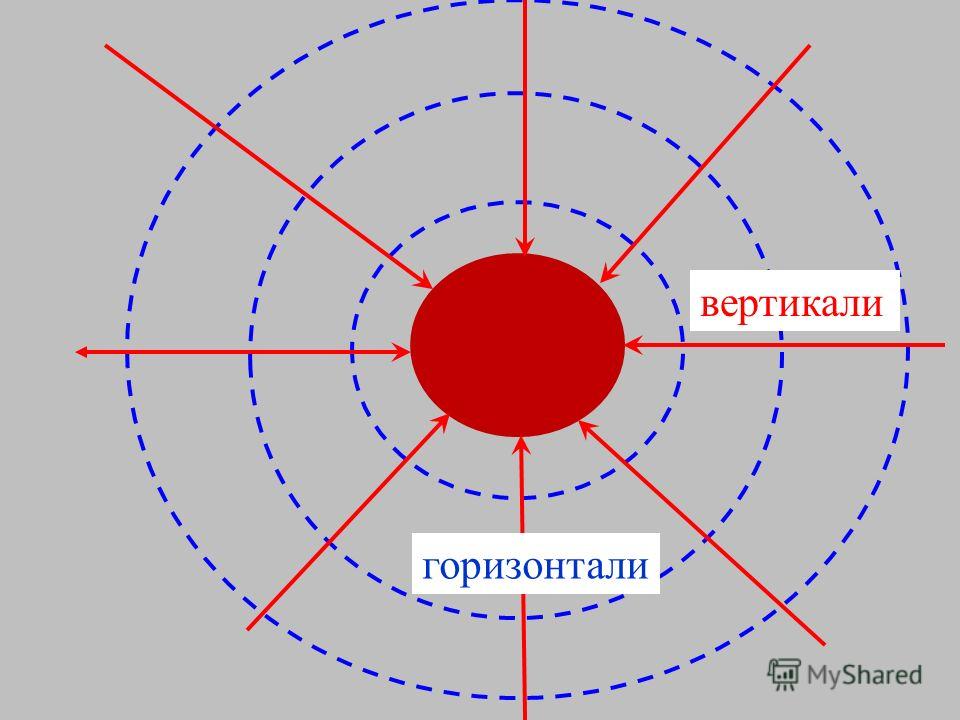
Гравитационные аномалии вызываются как выступающими на поверхность массами (горами), так и различием плотностей масс внутри Земли. Влияние внешних видимых масс рассчитывается исключением из полученных аномалий поправок на рельеф местности. Изменение плотностей может происходить как за счёт поднятия и опускания слоёв, так и за счёт изменения плотностей внутри самих слоёв. Поэтому в аномалиях силы тяжести отражаются как структурные формы, так и петрографический состав пород различных слоёв земной коры. Дифференциация плотностей в коре идёт как по вертикали, так и по горизонтали. Плотность с глубиной увеличивается от 1,9–2,3 г/см 3 на поверхности до 2,7–2,8 г/см 3 на уровне нижней границы коры и достигает 3,0–3,3 г/см 3 в области верхней мантии.
Особо важную роль приобретает интерпретация аномалий силы тяжести в геологии. Прямо или косвенно сила тяжести участвует во всех тектонических движениях. Наконец, аномалии силы тяжести, ввиду их физической природы и применяемых способов их вычисления, позволяют одновременно изучать любые плотностные неоднородности Земли, где бы и на какой глубине они ни находились. Это обусловливает возможность использования гравитационных данных для решения весьма разнообразных по масштабам и глубинности геологических задач. Гравиметрическая съёмка широко применяется при поисках и разведке рудных месторождений и нефтегазоносных структур.
Это обусловливает возможность использования гравитационных данных для решения весьма разнообразных по масштабам и глубинности геологических задач. Гравиметрическая съёмка широко применяется при поисках и разведке рудных месторождений и нефтегазоносных структур.
Роль и значение гравитационных данных в изучении глубинных недр Земли особенно возросли за последние годы, когда не только Кольская, но и другие глубокие и сверхглубокие скважины, в том числе зарубежные (Оберпфальц в Германии, Гравберг в Швеции и др.) не подтвердили результаты геологической интерпретации данных глубинной сейсмики, положенные в основу проектирования этих скважин.
Для геологического истолкования гравитационных аномалий геоморфологически резко различных регионов особую роль приобретает выбор наиболее обоснованной редукции силы тяжести так как, например, в горных областях аномалии Фая и Буге резко различаются не только по интенсивности, но даже и по знаку. Для континентальных территорий наиболее признанной является редукция Буге с плотностью промежуточного слоя 2,67 г/см 3 и с поправкой на влияние рельефа поверхности в радиусе 200 км
Превышения земной поверхности, а также глубины дна морей и океанов измеряются от поверхности квазигеоида (уровня моря). Поэтому для полного учета гравитационного влияния формы Земли необходимо вводить две поправки: поправку Брунса за отклонения фигуры Земли от нормального земного эллипсоида либо сфероида вращения, а также топографическую и гидротопографическую поправки за отклонения твердой земной поверхности от уровня моря.
Поэтому для полного учета гравитационного влияния формы Земли необходимо вводить две поправки: поправку Брунса за отклонения фигуры Земли от нормального земного эллипсоида либо сфероида вращения, а также топографическую и гидротопографическую поправки за отклонения твердой земной поверхности от уровня моря.
Аномалии силы тяжести широко используются при решении разнообразных геологических задач. Представления о глубинной геологической природе гравитационных аномалий столь большой и разнородной по геологическому строению территории России будут во многом меняться в зависимости от того, какие теоретические концепции образования и тектонической эволюции Земли были положены в их основу. Отчетливая связь гравитационных аномалий в редукциях Буге и гидротопографической с дневным рельефом и с глубинами моря, когда горным сооружениям соответствуют интенсивные минимумы, а морям — максимумы силы тяжести, давно уже отмечалась исследователями и широко применялась для изучения изостазии, корреляции гравитационных аномалий с данными глубинного сейсмического зондирования и использования ее для вычисления “мощности” земной коры на сейсмически не изученных территориях.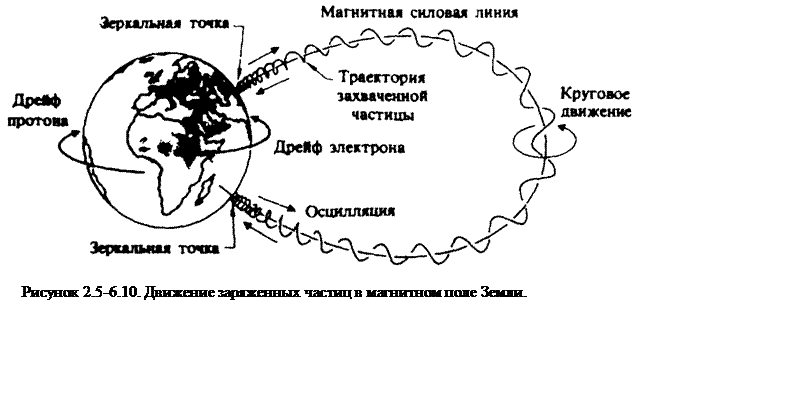 Редукции Буге и гидротопографическая позволяют убрать влияние известных плотностных неоднородностей Земли и тем самым выделить более глубинные составляющие поля. Наблюдаемая корреляционная связь с дневным рельефом аномалий силы тяжести подчеркивает, что именно изостазия как физическое явление и служит причиной того, что не только рельеф, но и все плотностные неоднородности Земли взаимно уравновешены в виде зон относительно повышенной и пониженной плотности, часто неоднократно чере-дующихся с глубиной и взаимно компенсирующих друг друга. Современные данные о реологических свойствах Земли с ее лито- и астеносферой, резко различных по своей упругости и, соответственно, подвижности, а также тектоническая расслоенность зем-ной коры, с возможным наличием в ней многоярусной конвекции глубинного вещества Земли, свидетельствуют о геологически мгновенной релаксации нагрузок. Поэтому в Земле как сейчас, так и раньше все аномальные массы любых размеров и глубины залегания были и продолжают оставаться изостатически скомпенсированными, независимо от того, где бы они ни находились и в какой бы форме ни проявлялись.
Редукции Буге и гидротопографическая позволяют убрать влияние известных плотностных неоднородностей Земли и тем самым выделить более глубинные составляющие поля. Наблюдаемая корреляционная связь с дневным рельефом аномалий силы тяжести подчеркивает, что именно изостазия как физическое явление и служит причиной того, что не только рельеф, но и все плотностные неоднородности Земли взаимно уравновешены в виде зон относительно повышенной и пониженной плотности, часто неоднократно чере-дующихся с глубиной и взаимно компенсирующих друг друга. Современные данные о реологических свойствах Земли с ее лито- и астеносферой, резко различных по своей упругости и, соответственно, подвижности, а также тектоническая расслоенность зем-ной коры, с возможным наличием в ней многоярусной конвекции глубинного вещества Земли, свидетельствуют о геологически мгновенной релаксации нагрузок. Поэтому в Земле как сейчас, так и раньше все аномальные массы любых размеров и глубины залегания были и продолжают оставаться изостатически скомпенсированными, независимо от того, где бы они ни находились и в какой бы форме ни проявлялись.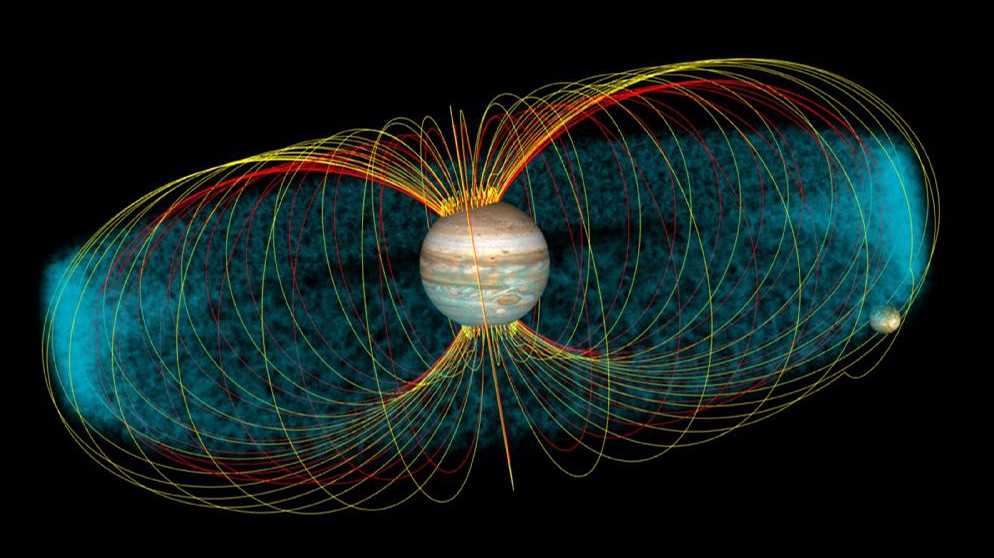 И если раньше амплитуды и знаки гравитационных аномалий пытались объяснить лишь изменениями общей мощности земной коры и вычисляли для этой цели коэффициенты ее корреляционной связи с дневным рельефом либо с гравитационными аномалиями, то последующее все более детальное сейсмическое изучение земной коры и верхней мантии, применение методов сейсмической томографии показали, что латеральные сейсмические, а следовательно, и плотностные неоднородности свойственны всем уровням дифференциации глубинных масс Земли, т. е. не только земной коре, но и верхней, и нижней мантии, и даже ядру Земли.
И если раньше амплитуды и знаки гравитационных аномалий пытались объяснить лишь изменениями общей мощности земной коры и вычисляли для этой цели коэффициенты ее корреляционной связи с дневным рельефом либо с гравитационными аномалиями, то последующее все более детальное сейсмическое изучение земной коры и верхней мантии, применение методов сейсмической томографии показали, что латеральные сейсмические, а следовательно, и плотностные неоднородности свойственны всем уровням дифференциации глубинных масс Земли, т. е. не только земной коре, но и верхней, и нижней мантии, и даже ядру Земли.
Поле аномалий силы тяжести изменяется на громадную величину — свыше 500 мГал — от –245 до +265 мГал, образуя систему разных по размерам и интенсивности глобальных, региональных и более локальных гравитационных аномалий, характеризующих собой коровые, коро-мантийные и собственно мантийные уровни латеральных плотностных неоднородностей Земли. Аномальное гравитационное поле отражает суммарное действие гравитирующих масс, расположенных на различных глубинах в земной коре и верхней мантии. Так, строение осадочных бассейнов лучше проявляется в аномальном гравитационном поле при наличии достаточной плотностной дифференциации в областях, где породы кристаллического фундамента залегают на больших глубинах. Гравитационный эффект осадочных пород в районах с неглубоким залеганием фундамента наблюдать значительно труднее, поскольку его затушёвывают влияния особенностей фундамента. Участки с большой мощностью «гранитного слоя» выделяются отрицательными аномалиями силы тяжести. Выходы гранитных массивов на поверхность характеризуются минимумами силы тяжести. В аномальном гравитационном поле зонами больших градиентов и полосовыми максимумами силы тяжести чётко вырисовываются границы отдельных блоков. В пределах платформ и складчатых областей выделяются более мелкие структуры, впадины, валы, краевые прогибы.
Так, строение осадочных бассейнов лучше проявляется в аномальном гравитационном поле при наличии достаточной плотностной дифференциации в областях, где породы кристаллического фундамента залегают на больших глубинах. Гравитационный эффект осадочных пород в районах с неглубоким залеганием фундамента наблюдать значительно труднее, поскольку его затушёвывают влияния особенностей фундамента. Участки с большой мощностью «гранитного слоя» выделяются отрицательными аномалиями силы тяжести. Выходы гранитных массивов на поверхность характеризуются минимумами силы тяжести. В аномальном гравитационном поле зонами больших градиентов и полосовыми максимумами силы тяжести чётко вырисовываются границы отдельных блоков. В пределах платформ и складчатых областей выделяются более мелкие структуры, впадины, валы, краевые прогибы.
Наиболее глобальные аномалии силы тяжести, характеризующие неоднородности собственно мантийного (астеносферного) уровня, столь велики, что лишь своими краевыми частями заходят в пределы рассматриваемой территории России, прослеживаясь далеко за ее пределы, где их интенсивность существенно возрастает. Единая зона Средиземноморского максимума силы тяжести совпадает с бассейном Средиземного моря и ограничена с севера небольшим Альпийским минимумом силы тяжести, а на востоке — единым очень интенсивным и громадным по площади Азиатским минимумом силы тяжести, соответствующим в целом Азиатскому мегавздутию Земли, охватывающему горные сооружения Средней и Высокой Азии от Забайкалья до Гималаев и, соответственно, от Тянь-Шаня до северо-восточной системы впадин внутреннего Китая (Ордосской, Сычуанской и др.). Этот глобальный Азиатский минимум силы тяжести уменьшается в своей интенсивности и прослеживается далее на территорию Северо-Востока России (горные сооружения Алтая, Забайкалья, Верхояно-Чукотской области), а его ответвление охватывает практически всю область активизированной в новейшее время Сибирской докембрийской платформы в виде в целом незначительно приподнятого (до 500–1000 м) Сибирского плоскогорья.
Единая зона Средиземноморского максимума силы тяжести совпадает с бассейном Средиземного моря и ограничена с севера небольшим Альпийским минимумом силы тяжести, а на востоке — единым очень интенсивным и громадным по площади Азиатским минимумом силы тяжести, соответствующим в целом Азиатскому мегавздутию Земли, охватывающему горные сооружения Средней и Высокой Азии от Забайкалья до Гималаев и, соответственно, от Тянь-Шаня до северо-восточной системы впадин внутреннего Китая (Ордосской, Сычуанской и др.). Этот глобальный Азиатский минимум силы тяжести уменьшается в своей интенсивности и прослеживается далее на территорию Северо-Востока России (горные сооружения Алтая, Забайкалья, Верхояно-Чукотской области), а его ответвление охватывает практически всю область активизированной в новейшее время Сибирской докембрийской платформы в виде в целом незначительно приподнятого (до 500–1000 м) Сибирского плоскогорья.
Крайняя северная часть Эгейского максимума частично попадает в пределы территории России, где после небольшого пережима начинается новый максимум, косо пересекающий Русскую платформу, Урал, Западную Сибирь и уходящий на севере в Северный Ледовитый океан. На крайнем востоке и северо-востоке, также лишь частично заходя на территорию России, располагается еще один — Тихоокеанский гигантский максимум силы тяжести, краевая часть которого протягивается в виде интенсивной линейной зоны гравитационного градиента от Шантарских островов до Берингова пролива через всю окраину Евразийского континента и омывающие его моря.
На крайнем востоке и северо-востоке, также лишь частично заходя на территорию России, располагается еще один — Тихоокеанский гигантский максимум силы тяжести, краевая часть которого протягивается в виде интенсивной линейной зоны гравитационного градиента от Шантарских островов до Берингова пролива через всю окраину Евразийского континента и омывающие его моря.
Находят логическое объяснение и разные знаки этих аномалий, если учесть, что зонная плавка, по мере подъема к поверхности астенолита, оставляет за собой на каждом уровне переплавленные породы, относительно более плотные, чем вмещающие их по латерали толщи. Поэтому в гравитационном поле вся сумма таких переплавленных пород создаёт единый суммарный максимум силы тяжести, и даже наличие в нем расплавленных “слоев” (зон инверсии скорости и плотности) не изменит общей его характеристики, как это и наблюдается в попадающих в пределы карты краевых частях Арктическо-Атлантического и Тихоокеанского глобальных максимумов силы тяжести.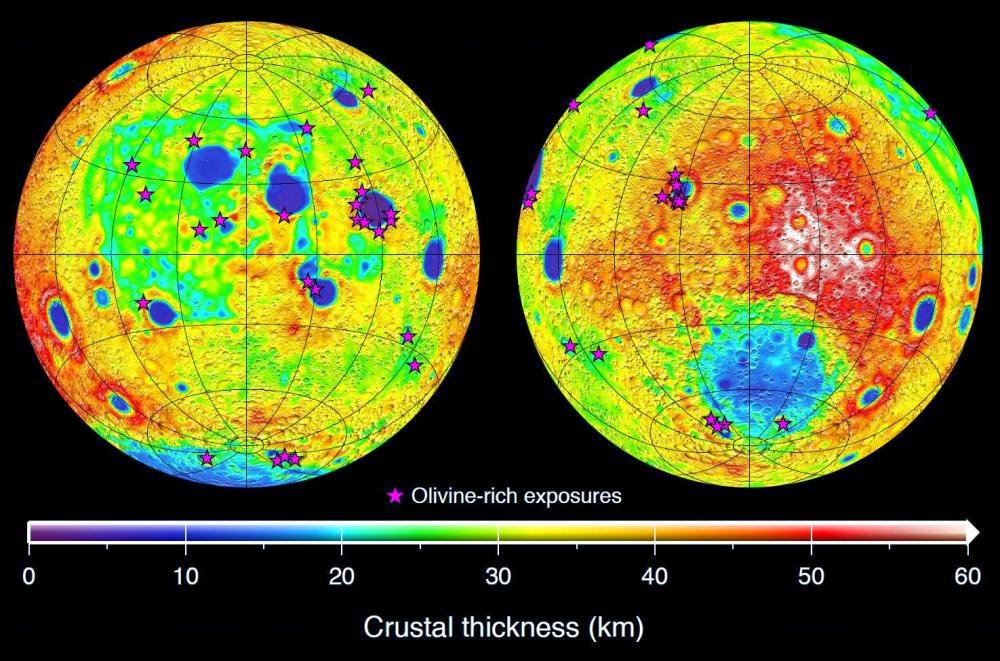
Аномальные массы, создающие Среднеазиатский глобальный минимум, вероятно, находятся на еще большой глубине, в результате чего образовавшаяся зона расплава привела к увеличению объема лишь глубинных масс и, соответственно, к образованию на поверхности единого гигантского Азиатского мегавздутия Земли, а наличие расплавленной линзы на глубине, видимо, обусловило небольшой по объемам и рассеянный по всей этой территории базальтоидный магматизм, мезозойские трубки взрыва в Тянь-Шане, потухшие четвертичные вулканы в Алтае-Саянской области, наконец, более интенсивный базальтоидный магматизм Байкало-Патомского нагорья, далеко уходящий за пределы самого Байкальского рифта.
Большая глубинность глобальных максимумов и минимумов силы тяжести, попадающих в пределы территории России, находит свое подтверждение и при интерпретации высот геоида.
Гравитационное поле Определение и значение
- Основные определения
- Тест
- Примеры
- Британский
Показывает уровень сложности слова.
Сохрани это слово!
Показывает уровень сложности слова.
сущ. Физика.
притяжение, рассматриваемое как распространяющееся по всему пространству воздействие материи на другую материю.
область, окружающая астрономическое тело, в которой сила гравитации сильна.
ВИКТОРИНА
Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Должны ли вы пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Происхождение гравитационного поля
Впервые записано в 1915–1920 гг. радиус
Dictionary.com Полный текст Основано на словаре Random House Unabridged Dictionary, © Random House, Inc. 2022
Как использовать гравитационное поле в предложении
Нахождение в таком тесном контакте с Солнцем также означает, что 2021 Ph37 действительно ощущает воздействие массивности нашей звезды.
 гравитационное поле.
гравитационное поле.Этот скоростной космический камень — самый быстрый астероид в нашей Солнечной системе|Ханна Сео|24 августа 2021 г.|Popular-Science слабые гравитационные поля, сообщают физики в журнале Nature от 11 марта.
Крошечный золотой шарик — самый маленький объект, гравитация которого была измерена|Эмили Коновер|10 марта 2021|Новости науки
Космический корабль НАСА «Юнона» находится на орбите Юпитера с июля 2016 года, предоставляя наши лучшие данные об атмосфере Юпитера. , гравитационное поле, магнитное поле и геология.
11 крупнейших космических миссий 2021 года (и их шансы на успех)|Нил Патель|4 января 2021|MIT Technology Review
Однако проблема трех тел — он имел в виду землю, солнце и Луна, движущаяся в их взаимных гравитационных полях, вызывала у него головную боль.
Время течет к порядку — Выпуск 93: Предтечи|Джулиан Барбур|2 декабря 2020|Наутилус
Эти струи воды вырываются из больших трещин на поверхности и, учитывая слабое гравитационное поле Энцелада, разбрызгиваются в пространство.

Четыре самых многообещающих мира для инопланетной жизни в Солнечной системе|Гарет Дорриан|24 сентября 2020 г.|Центр Singularity
Мнения о расстройствах пищевого поведения по-прежнему расходятся во мнениях относительно потенциальной эффективности таких мер.
Насколько худая слишком худая? Израиль запрещает «худощавые» модели|Кэрри Арнольд|8 января 2015 г.|DAILY BEAST
«Он был храбрым полевым командиром и экспертом в разведке, а также в организации народных и племенных сил», — сказал хвалебный человек.
Что иранские похороны говорят нам о войнах в Ираке|IranWire|6 января 2015|DAILY BEAST
Во всяком случае, обучение офицеров и методы работы полиции на местах укрепляют эти убеждения.
Что произойдет, если я попаду в лицо белому полицейскому?|Голди Тейлор|30 декабря 2014 г.|DAILY BEAST
Затем к этому переполненному полю присоединились коммерческие бегемоты по снижению веса Weight Watchers и Jenny Craig.

Почему ваша новогодняя диета не сработает|Кэрри Арнольд|30 декабря 2014|DAILY BEAST
Так и было, у нас должна быть команда, правильные мячи, большое поле, и все должно выглядеть правильно и быть правым.
Стена напряженности Тима Ховарда|Уильям О’Коннор|22 декабря 2014 г.|DAILY BEAST
Он отличился в нескольких кампаниях, особенно в войне на полуострове, и был повышен до звания фельдмаршала.
Книга истории и хронологии на каждый день|Джоэл Манселл
У нас было шесть полевых орудий, но мы взяли только четыре, запряженных вдвое большим количеством лошадей.
Эдинбургский журнал Blackwood, № CCCXXXIX. Январь 1844 г. Том. LV.|Разные
Было два батальона, всего около тысячи человек; и они принесли полевое орудие с ними.
Эдинбургский журнал Blackwood, № CCCXXXIX. Январь 1844 г. Том. LV.|Разные
Пробуждением спящих мексиканцев стал разряд наших двух полевых орудий, заряженных канистрой.

Эдинбургский журнал Blackwood, № CCCXXXIX. Январь 1844 г. Том. LV.|Various
Затем вражеские гаубицы и полевые орудия действовали по-своему, вынуждая атаку уступать много территории.
Дневник Галлиполи, том I|Ян Гамильтон
Определения Британского словаря для гравитационного поля
гравитационное поле
сущ.
силовое поле, окружающее тело конечной массы, в котором другое тело испытывает силу притяжения, пропорциональную произведению масс и обратно пропорциональную квадрату расстояния между ними
Словарь английского языка Коллинза — Полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Издательства 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
гравитация | Определение, физика и факты
гравитационная линза
Посмотреть все медиа
- Ключевые люди:
- Кип Торн Исаак Ньютон Галилео Джон Арчибальд Уилер Саймон Стевин
- Похожие темы:
- супергравитация масса точка Лагранжа Радиус Шварцшильда гравитационная аномалия
Просмотреть весь связанный контент →
Сводка
Прочтите краткий обзор этой темы
гравитация , также называемая гравитацией , в механике универсальная сила притяжения, действующая между всей материей. Это, безусловно, самая слабая из известных сил в природе, и поэтому она не играет никакой роли в определении внутренних свойств повседневного вещества. С другой стороны, благодаря своему большому охвату и универсальному действию он контролирует траектории тел в Солнечной системе и других местах во Вселенной, а также структуру и эволюцию звезд, галактик и всего космоса. На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
Это, безусловно, самая слабая из известных сил в природе, и поэтому она не играет никакой роли в определении внутренних свойств повседневного вещества. С другой стороны, благодаря своему большому охвату и универсальному действию он контролирует траектории тел в Солнечной системе и других местах во Вселенной, а также структуру и эволюцию звезд, галактик и всего космоса. На Земле все тела имеют вес или направленную вниз силу тяжести, пропорциональную их массе, которую оказывает на них масса Земли. Гравитация измеряется ускорением, которое она сообщает свободно падающим телам. У поверхности Земли ускорение свободного падения составляет около 90,8 метра (32 фута) в секунду за секунду. Таким образом, за каждую секунду нахождения объекта в свободном падении его скорость увеличивается примерно на 9,8 метра в секунду. На поверхности Луны ускорение свободно падающего тела составляет около 1,6 метра в секунду за секунду.
Понять концепцию гравитационной силы, используя теорию гравитации Ньютона
Посмотреть все видео к этой статье Работы Исаака Ньютона и Альберта Эйнштейна доминируют в развитии теории гравитации. Классическая теория силы тяготения Ньютона господствовала с его 9 лет.0185 Principia , опубликованной в 1687 году, до работы Эйнштейна в начале 20 века. Теории Ньютона достаточно даже сегодня для всех приложений, кроме самых точных. Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Классическая теория силы тяготения Ньютона господствовала с его 9 лет.0185 Principia , опубликованной в 1687 году, до работы Эйнштейна в начале 20 века. Теории Ньютона достаточно даже сегодня для всех приложений, кроме самых точных. Общая теория относительности Эйнштейна предсказывает лишь незначительные количественные отличия от ньютоновской теории, за исключением нескольких особых случаев. Основное значение теории Эйнштейна заключается в ее радикальном концептуальном отходе от классической теории и ее последствиях для дальнейшего развития физической мысли.
Запуск космических аппаратов и развитие исследований на них привели к значительным улучшениям в измерениях гравитации вокруг Земли, других планет и Луны, а также в экспериментах по изучению природы гравитации.
Развитие теории гравитации
Ранние концепции
Ньютон утверждал, что движения небесных тел и свободное падение объектов на Земле определяются одной и той же силой. Классические греческие философы, с другой стороны, не считали, что небесные тела подвержены влиянию гравитации, поскольку наблюдалось, что тела следуют постоянно повторяющимся ненисходящим траекториям в небе. Таким образом, Аристотель считал, что каждое небесное тело следует определенному «естественному» движению, не подверженному влиянию внешних причин или факторов. Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Таким образом, Аристотель считал, что каждое небесное тело следует определенному «естественному» движению, не подверженному влиянию внешних причин или факторов. Аристотель также считал, что массивные земные объекты обладают естественной тенденцией двигаться к центру Земли. Эти аристотелевские концепции преобладали на протяжении столетий вместе с двумя другими: что тело, движущееся с постоянной скоростью, требует постоянной силы, действующей на него, и эта сила должна быть приложена посредством контакта, а не взаимодействия на расстоянии. Эти идеи в основном держались до 16 и начала 17 веков, тем самым препятствуя пониманию истинных принципов движения и препятствуя развитию представлений о всемирном тяготении. Этот тупик начал меняться с появлением нескольких научных работ, посвященных проблеме земного и небесного движения, которые, в свою очередь, подготовили почву для более поздней теории тяготения Ньютона.
Тест «Британника»
Физика и законы природы
Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.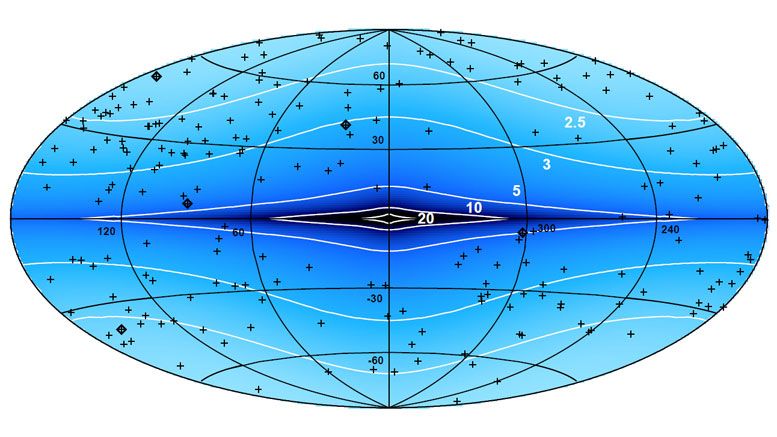
Немецкий астроном XVII века Иоганн Кеплер принял аргумент Николая Коперника (который восходит к Аристарху Самосскому) о том, что планеты вращаются вокруг Солнца, а не Земли. Используя улучшенные измерения движения планет, сделанные датским астрономом Тихо Браге в 16 веке, Кеплер описал планетарные орбиты с помощью простых геометрических и арифметических соотношений. Три количественных закона движения планет Кеплера таковы:
Планеты описывают эллиптические орбиты, один из фокусов которых занимает Солнце (фокус — это одна из двух точек внутри эллипса; любой луч, исходящий из одной из них, отражается от стороны эллипса и проходит через другой фокус) .
Линия, соединяющая планету с Солнцем, заметает равные площади за равные промежутки времени.
Квадрат периода обращения планеты пропорционален кубу ее среднего расстояния от Солнца.
В этот же период итальянский астроном и естествоиспытатель Галилео Галилей добился прогресса в понимании «естественного» движения и простого ускоренного движения земных объектов. Он понял, что тела, на которые не действуют силы, продолжают двигаться бесконечно и что сила необходима для изменения движения, а не для поддержания постоянного движения. Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Он понял, что тела, на которые не действуют силы, продолжают двигаться бесконечно и что сила необходима для изменения движения, а не для поддержания постоянного движения. Изучая, как объекты падают на Землю, Галилей обнаружил, что движение происходит с постоянным ускорением. Он продемонстрировал, что расстояние, которое падающее тело проходит таким образом из состояния покоя, изменяется пропорционально квадрату времени. Как отмечалось выше, ускорение свободного падения на поверхности Земли составляет около 90,8 метра в секунду в секунду. Галилей был также первым, кто экспериментально показал, что тела падают с одинаковым ускорением независимо от их состава (слабый принцип эквивалентности).
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Гравитационное поле — обзор
ScienceDirectЗарегистрироватьсяВойти
Гравитационное поле удобнее всего определять с точки зрения гравитационного потенциала U. Потенциал U, связанный с точечной массой m в заданной точке P на расстоянии r от m, определяется как работа, необходимая гравитационной силе для перемещения единицы массы из бесконечности в конечное положение P. Единицей измерения является Гал (см/с2), то есть напряженность гравитационного поля или единица ускорения, которая будет действовать на массу 1 г с силой 1 дин.
Единицей измерения является Гал (см/с2), то есть напряженность гравитационного поля или единица ускорения, которая будет действовать на массу 1 г с силой 1 дин.
Из: Mineral Exploration, 2013
PlusAdd to Mendeley Свапан Кумар Халдар, Mineral Exploration (Second Edition), 2018
6.3.3 Единица силы тяжести определяется гравитационным потенциалом
U. Потенциал U, связанный с точечной массой «m» в данной точке «P» на расстоянии «r» от m, определяется как работа, необходимая силе тяжести для перемещения единицы массы из бесконечности в конечное положение P Единица измерения Гал (по Галилею) (г/см 3 ), который представляет собой силу гравитационного поля или единицу ускорения, которое будет действовать на массу 1 г с силой 1 дина. Величина силы тяжести (90 185 г 90 186) составляет в среднем по всему миру 980 галлонов на поверхности Земли с вариацией 5,17 галлонов от экватора к полюсу. Используемая единица измерения поля — миллигал (мГал 90 185) 90 186, а единица силы тяжести = 0,1 мГал. 1 гал равен 0,01 м/с 2 .
1 гал равен 0,01 м/с 2 .
Гравитационные аномалии возникают из-за разницы в плотности или контраста плотности между телом скалы и его окружением. Контраст плотности Δρ определяется выражением Δρ = ρ 1 –ρ 2 , для тела плотностью ρ 1 , погруженного в материал плотностью ρ 2 .
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B978012814022200006X
S.K. Haldar, in Mineral Exploration, 2013
5.3.3 Единица силы тяжести
Гравитационное поле наиболее удобно определять с точки зрения гравитационного потенциала У . Потенциал U , обусловленный точечной массой м в данной точке P , на расстоянии r от м , определяется как работа, необходимая силе тяжести для перемещения единицы массы из бесконечности в конечная позиция P . Единицей измерения является гал (см/с 2 ), то есть напряженность гравитационного поля или единица ускорения, которое будет действовать на массу 1 г с силой 1 дина. Значение силы тяжести ( г ) имеет в среднем около 980 галлонов на поверхности Земли с разницей в 5,17 галлонов от экватора к полюсу. Единицей измерения поля, обычно используемой для измерения, является миллигал (мГал), а единица силы тяжести = 0,1 мГал; 1 гал точно равен 0,01 м/с 2 .
Единицей измерения является гал (см/с 2 ), то есть напряженность гравитационного поля или единица ускорения, которое будет действовать на массу 1 г с силой 1 дина. Значение силы тяжести ( г ) имеет в среднем около 980 галлонов на поверхности Земли с разницей в 5,17 галлонов от экватора к полюсу. Единицей измерения поля, обычно используемой для измерения, является миллигал (мГал), а единица силы тяжести = 0,1 мГал; 1 гал точно равен 0,01 м/с 2 .
Гравитационные аномалии возникают из-за разницы в плотности или контраста плотности между телом скалы и его окружением. Для тела плотностью ρ 1 , погруженного в материал плотностью ρ 2 , контраст плотности ▵ρ определяется выражением ▵ρ = ρ 1 − ρ 2.
View chapterPurchase book
Read full chapter
URL: https://www.sciencedirect.com/science/article/pii/B9780124160057000052
In Thermal Physics of the Atmosphere (Второе издание), 2021 г.
Abstract
Гравитационная потенциальная энергия воздушной посылки значительно изменяется по глубине атмосферы по сравнению с изменениями внутренней энергии. Это означает, что гравитационная потенциальная энергия должна быть частью баланса термодинамической энергии при рассмотрении вертикальной структуры атмосферы.
Гидростатическое равновесие является первым проявлением гравитационной потенциальной энергии в жидкостных системах. Он отражает тот факт, что давление в любой точке статической жидкости определяется весом жидкости над ней. В этой главе мы даем общий термодинамический вывод гидростатического равновесия.
Когда воздух находится в движении, гидростатический баланс действителен только в качестве приближения. С точки зрения динамики, гидростатический баланс требует, чтобы вертикальное ускорение воздушных посылок было намного меньше, чем ускорение свободного падения. С точки зрения термодинамики гидростатический баланс требует, чтобы изменения кинетической энергии были намного меньше, чем изменения потенциальной энергии или внутренней энергии.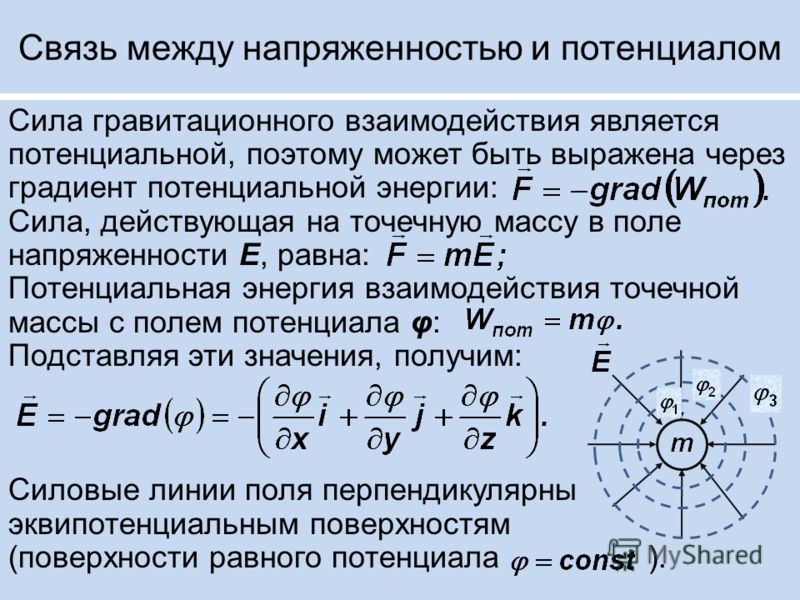 Эти условия по существу эквивалентны и обычно выполняются в атмосфере. Только при сильных восходящих или нисходящих потоках нельзя предполагать гидростатическое равновесие.
Эти условия по существу эквивалентны и обычно выполняются в атмосфере. Только при сильных восходящих или нисходящих потоках нельзя предполагать гидростатическое равновесие.
Оставшаяся часть главы посвящена изучению того, что предположение о гидростатическом равновесии подразумевает для вертикальной структуры атмосферы.
Глава завершается обсуждением вертикальной структуры изотермической атмосферы в контексте статистической механики. Вводятся некоторые ключевые понятия статистической механики, иллюстрирующие способ использования статистической механики для связи микроскопического мира молекул с макроскопическим миром термодинамики.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780128244982000112
M.B. Киркхэм, в принципах связей с водой почвы и растения (второе издание), 2014
4.
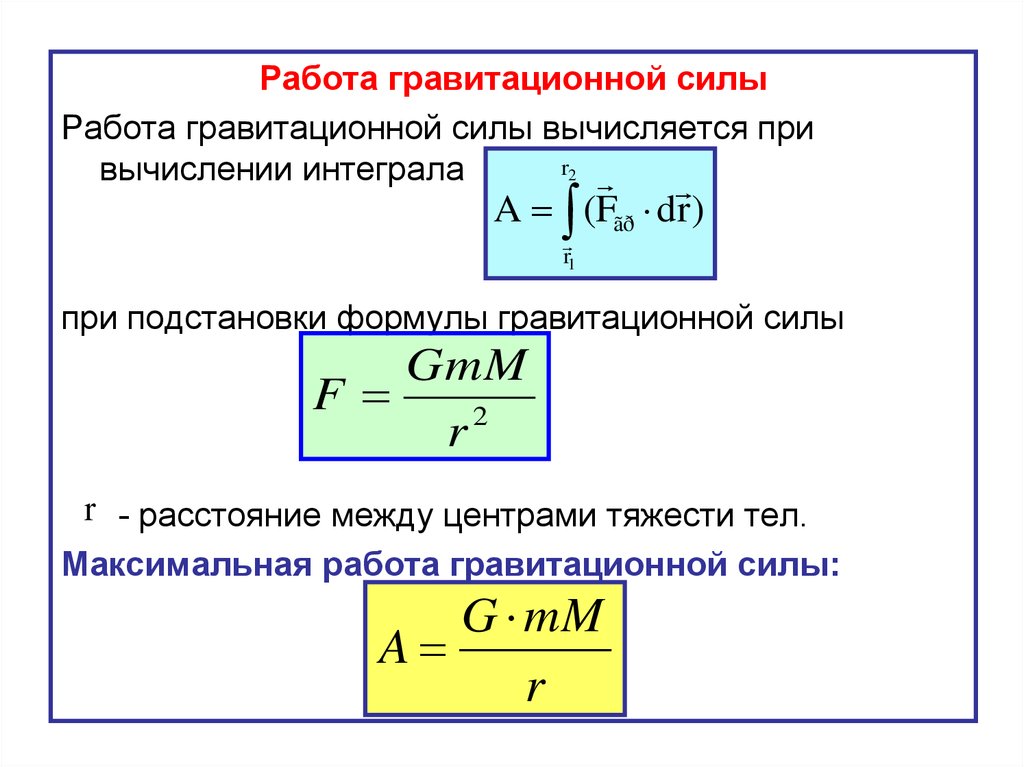 2.2 Гравитационный потенциал, ψ G или ψ Z
2.2 Гравитационный потенциал, ψ G или ψ Z потенциальная энергия потенциальная энергия 55555 . — это потенциальная энергия, связанная с вертикальным положением. Назначенная опорная высота или исходная точка могут варьироваться в зависимости от необходимости и часто основаны на полезности. Обычно удобно поддерживать достаточно низкий опорный уровень, чтобы не получить отрицательных значений. Решения задач подвержены ошибкам, когда используются отрицательные числа. Геодезисты берут свои данные на уровне ниже самого низкого уровня, который они ожидают встретить в своей съемке, чтобы гарантировать, что все их уровни будут положительными. В качестве исходного уровня почвоведы часто принимают либо поверхность почвы, либо уровень грунтовых вод. Референтный уровень обычно зависит от направления движения воды: восходящего или инфильтрационного. Если контрольный уровень находится ниже рассматриваемой точки, над водой должна быть совершена работа, а гравитационный потенциал положителен; если уровень выше рассматриваемой точки, вода совершает работу, а гравитационный потенциал отрицателен (Бейвер и др. Просмотреть главуКнига покупок Прочитать главу полностью URL: https://www.sciencedirect.com/science/article/pii/B9780124200227000045 ), 2014 Гравитационное поле Луны дает важную информацию о пространственном распределении массы на поверхности и в недрах Луны. Исследования гравитационного поля обычно основаны на измерениях доплеровского сдвига сигнала радиослежения, вызванного ускорениями, действующими на орбитальные космические аппараты, и дополняются наземными наблюдениями лунного лазера. Ранние модели гравитационного поля Lunar Orbiter выявили большие концентрации массы (масконы) на ближней стороне Луны, а измерения Аполлона 15 и 16 согласуются с более толстой корой на дальней стороне полушария по сравнению с ближней. Первые надежные глобальные характеристики высоты поверхности Луны и гравитации были основаны на топографических и гравитационных картах Клементины, а также на радиоотслеживании космического корабля Lunar Prospector. РИСУНОК 23.7. Лунное гравитационное поле GRAIL. Красные цвета соответствуют излишкам массы, которые создают области с более высокой локальной гравитацией; синие цвета представляют дефицит массы, что приводит к областям с более низкой местной гравитацией. Гравитационные данные показывают смещение центра масс относительно центра фигуры Луны в направлении к Земле на 1,9 км. Это смещение объясняется ярко выраженной дихотомией между ближней и дальней земной корой, возможно, установленной на стадии магматического океана. Анализ глобальных гравитационных и топографических данных показывает, что толщина дальней коры превышает толщину ближней в среднем примерно на 15 км. Волнистости современного лунного геоида (или селеноида) превышают 500 м и, следовательно, намного грубее, чем геоид Земли (200 м). Лунные нагорья кажутся почти изостатически компенсированными, однако структуры бассейнов демонстрируют широкий диапазон состояний компенсации, которые не зависят от их размеров или возраста. Круглые моря во многих случаях демонстрируют большие положительные гравитационные аномалии (масконы) в несколько 100 мГал, что указывает на избыток массы, тогда как некоторые бассейны окружены концентрическими гравитационными минимумами. Масконы лучше всего объясняются суперизостатическим поднятием границы коры и мантии под бассейнами и размещением плотных морских базальтов внутри бассейнов. Просмотреть книгу Глава покупки Читать полная глава URL: https://www. .r. Smallwow Форма и ее гравитационное поле Гравитационный потенциал совершенно однородной сферы был бы одинаковым во всех точках на ее поверхности. Однако Земля не является идеальной сферой; это сплюснутый сфероид с меньшим радиусом на полюсах, чем на экваторе. Исследования в начале восемнадцатого века, проведенные под руководством Ш.-М. де Ла Кондамина и М. де Мопертиуса, показали, что градус меридиана, измеренный в Кито, Эквадор, недалеко от экватора, был примерно на 1500 м длиннее, чем градус меридиана возле Торнио, Финляндия. недалеко от полярного круга. Впоследствии различные стандартные эталонные сфероиды или эллипсоиды были предложены в качестве приближений первого порядка к форме Земли, таких как Всемирная геодезическая система 19.84 (табл. 1). Имея такой эллипсоид, гравитационное поле можно вычислить аналитически как функцию широты. Например, эталонная гравитационная формула была принята Международной геодезической ассоциацией в 1967 г. Средняя плотность Земли, имеющая фундаментальное значение для расчета гравитационного притяжения, была впервые оценена после эксперимента в 1775 году преподобным Невиллом Маскелином с использованием метода, предложенного Ньютоном. Если бы Земля была идеально сферической и имела одинаковую плотность, то отвес указывал бы вниз к центру Земли из-за силы тяжести, действующей на груз. Однако любая близлежащая масса отклонит отвес от этой «вертикали». Маскелин и его коллеги измерили отклонения отвеса на шотландской горе Шихаллион (рис. 1). Они обнаружили, что гравитационное притяжение горы отклонило отвес на 11,7 угловых секунды. Это позволило Чарльзу Хаттону сообщить в 1778 году, что средняя плотность Земли составляет примерно 4500 кг м 9 .0239 −3 . Это значение плотности приводит к оценке массы Земли примерно в 5 × 10 90 239 24 90 240 кг, что недалеко от принятого в настоящее время значения 5,97 × 10 90 239 24 90 240 кг. Рис. 1. Схематическая карта местности вокруг Шихаллиона, Шотландия, составленная Чарльзом Хаттоном. Отклонения отвеса, измеренные на станциях к северу и югу от горы, позволили впервые оценить плотность земли. (По Р. М. Силлито с разрешения Хаттона (1778 г.) © Королевское общество.) Поскольку масса Земли распределена неравномерно, реальное гравитационное поле не соответствует рассчитанному для эллипсоида однородной плотности. «Геоид» — это поверхность, которая определяется точками с равным гравитационным потенциалом или эквипотенциалом (таблица 1), которая выбрана так, чтобы в среднем совпадать со средним уровнем моря. Геоид не является идеальным эллипсоидом, поскольку локальные и региональные массовые аномалии возмущают поверхность гравитационного потенциала в их окрестностях на несколько десятков метров. View chapterPurchase book Read full chapter URL: https://www.sciencedirect.com/science/article/pii/B01236939688 M.A. Wieczorek, in Treatise on Geophysics, 2007 Гравитационное поле Земли было нанесено на карту несколькими методами, включая анализ данных спутникового слежения, кампании наземных измерений и спутниковую альтиметрию поверхности океана (наклоны геоида пропорциональны гравитационному полю в спектральной области (см. В отличие от модели EGM96, основанной на данных спутникового слежения с наземных станций, текущие миссии CHAMP (Reigber и др. , 2004) и GRACE (Tapley et al. , 2004) основаны на непрерывных данных спутникового слежения за GPS (глобальная система позиционирования). В то время как CHAMP представляет собой один спутник, GRACE состоит из двух спутников на одинаковых орбитах, расстояние между которыми измеряется с высокой точностью с помощью микроволновой линии связи. Две самые последние модели гравитационного поля Земли с высоким разрешением, полученные на основе этих данных, включают GGM02C (Tapley и др. , 19).72, с. 296).
, 19).72, с. 296). 6.2 Гравитация
 Первое надежное определение гравитационного поля обратной стороны Луны было выполнено SELENE (Кагуя), что также значительно улучшило пространственное разрешение данных лунного гравитационного поля. Недавно космический аппарат GRAIL получил глобальные гравитационные данные с самым высоким разрешением (рис. 23.7).
Первое надежное определение гравитационного поля обратной стороны Луны было выполнено SELENE (Кагуя), что также значительно улучшило пространственное разрешение данных лунного гравитационного поля. Недавно космический аппарат GRAIL получил глобальные гравитационные данные с самым высоким разрешением (рис. 23.7).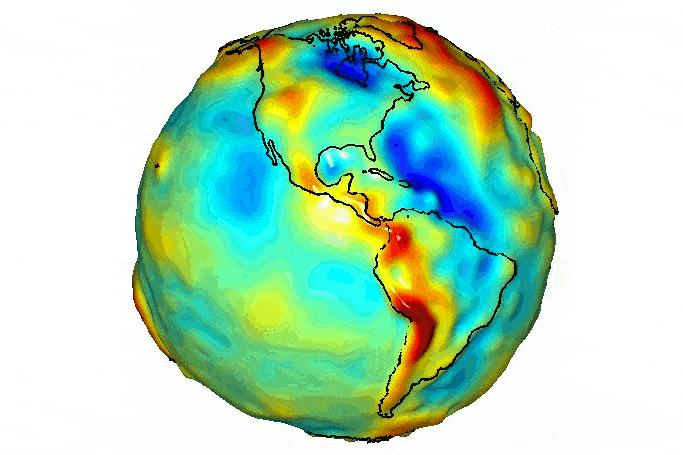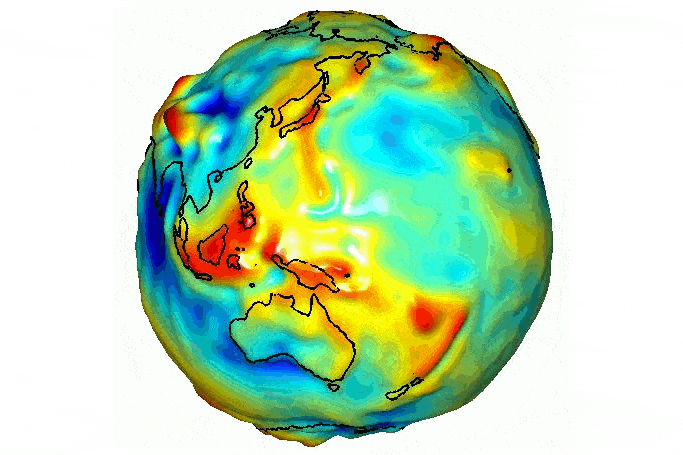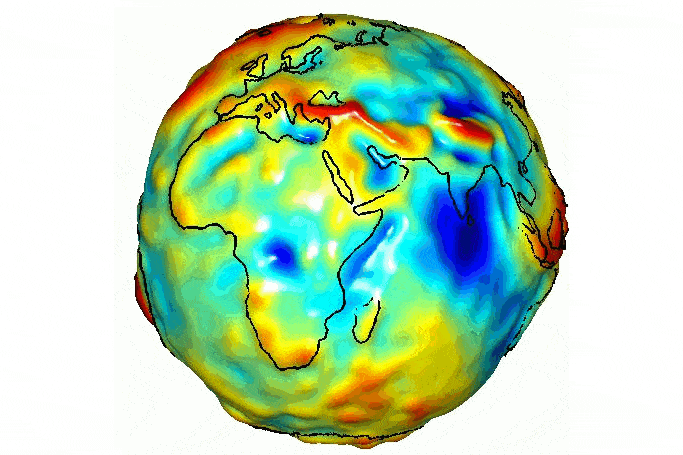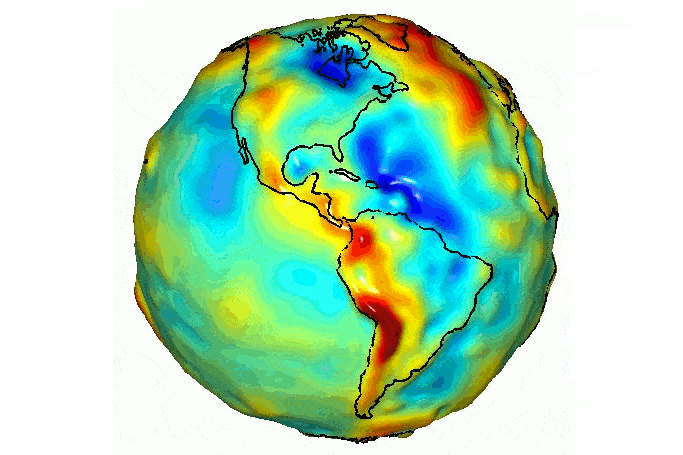 Однако результаты, основанные на гравитации, зависят от модели; состав земной коры, меняющийся по латерали, также является частью дихотомии и может способствовать смещению.
Однако результаты, основанные на гравитации, зависят от модели; состав земной коры, меняющийся по латерали, также является частью дихотомии и может способствовать смещению.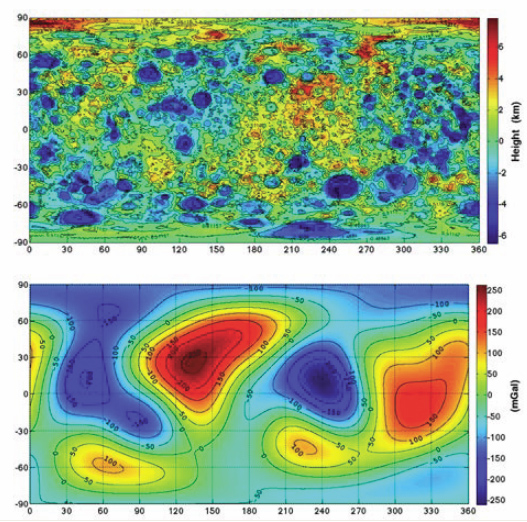 sciencedirect.com/science/article/pii/b9780124158450000232
sciencedirect.com/science/article/pii/b9780124158450000232 (IGF67, таблица 1), а другая введена в 1984 г. (WGS84, таблица 1).
(IGF67, таблица 1), а другая введена в 1984 г. (WGS84, таблица 1). Эксперимент Шихаллона имел еще одно отличие: для расчета массы и центра тяжести горы была проведена подробная съемка, и Хаттон изобрел контурную карту для представления данных.
Эксперимент Шихаллона имел еще одно отличие: для расчета массы и центра тяжести горы была проведена подробная съемка, и Хаттон изобрел контурную карту для представления данных. Например, подводная гора на дне океана, более плотная, чем окружающая морская вода, будет отклонять геоид вниз над собой. «Аномалии геоида» определяются как смещения геоида выше или ниже выбранного эллипсоида. Концепция геоида как глобальной поверхности среднего уровня моря может быть распространена на территории, занятые сушей. Это обеспечивает как горизонтальную исходную точку, так и определение направления вертикали, поскольку отвес будет висеть перпендикулярно геоиду.
Например, подводная гора на дне океана, более плотная, чем окружающая морская вода, будет отклонять геоид вниз над собой. «Аномалии геоида» определяются как смещения геоида выше или ниже выбранного эллипсоида. Концепция геоида как глобальной поверхности среднего уровня моря может быть распространена на территории, занятые сушей. Это обеспечивает как горизонтальную исходную точку, так и определение направления вертикали, поскольку отвес будет висеть перпендикулярно геоиду. 10.05. 3.1.2 Гравитация
 , среди прочего, Hwang and Parsons, 1996; Сандвелл и Смит, 1997)). Построение глобальных моделей с высоким разрешением обычно состоит из объединения длинноволновой информации из данных спутникового слежения с коротковолновой информацией наземных и океанических съемок высотомеров. Модель EGM96 (Lemoine et al. , 1998) была стандартным эталоном на протяжении большей части последнего десятилетия, но она была заменена данными, полученными в ходе недавних миссий CHAMP и GRACE.
, среди прочего, Hwang and Parsons, 1996; Сандвелл и Смит, 1997)). Построение глобальных моделей с высоким разрешением обычно состоит из объединения длинноволновой информации из данных спутникового слежения с коротковолновой информацией наземных и океанических съемок высотомеров. Модель EGM96 (Lemoine et al. , 1998) была стандартным эталоном на протяжении большей части последнего десятилетия, но она была заменена данными, полученными в ходе недавних миссий CHAMP и GRACE. , 2005 г.) и EIGEN-GL04C (см. Reigber 9).0185 и др.
, 2005 г.) и EIGEN-GL04C (см. Reigber 9).0185 и др.
Изображения радиальной гравитационной аномалии и геоида, определенные по уравнениям [21] и [22] соответственно, показаны на Рисунок 1 для модели EIGEN-GL04C. Для обоих изображений зональный член степени 2, который в первую очередь является результатом ротационного выравнивания, был установлен равным нулю, а поля были оценены на эталонном радиусе 6378,1 км. (Форма и потенциал сплющенного эллипсоида хорошо аппроксимируются зональной гармоникой степени 2.) Видно, что самые большие гравитационные аномалии коррелируют с топографией (такими как впадины и подводные горы), а высота геоида изменяется примерно на 200 м.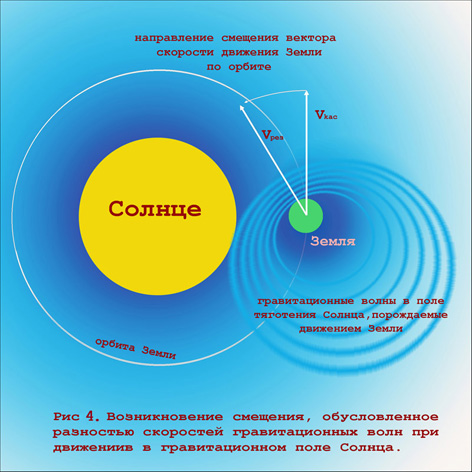 Погрешности геоида и гравитационного поля оцениваются примерно в 30 см и 8 мГал соответственно.
Погрешности геоида и гравитационного поля оцениваются примерно в 30 см и 8 мГал соответственно.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B9780444527486001565
C. Jekeli, in Treatise13 Edition (9 0 Secon13 on Geophysics),
3.02.1.3 Предварительные определения и концепции
Гравитационный потенциал Земли, В , создается распределением ее полной плотности массы. Для приложений на поверхности Земли полезно включить потенциал-аналогичную функцию ϕ , связанное с центробежным ускорением из-за вращения Земли. Сумма, Вт = В + ϕ , известна в геодезической терминологии как гравитационный потенциал, отличный от гравитационного потенциала. Однако центробежный потенциал не является ньютоновским потенциалом и введен только для удобства. Кроме того, полезно определить относительно простой эталонный потенциал, или нормальный потенциал, который объясняет большую часть гравитационного потенциала (9). 0177 Раздел 3.02.5.2 ). Нормальный гравитационный потенциал, U , определяется как гравитационный потенциал, связанный с наиболее подходящим эллипсоидом, нормальным эллипсоидом, который вращается вместе с Землей и также является поверхностью с постоянным потенциалом в этом поле. Разница между действительным и нормальным гравитационными потенциалами известна как возмущающий потенциал: T = W − U ; таким образом, он исключает центробежный потенциал. Нормальный гравитационный потенциал составляет примерно 99,9995% от общего потенциала.
0177 Раздел 3.02.5.2 ). Нормальный гравитационный потенциал, U , определяется как гравитационный потенциал, связанный с наиболее подходящим эллипсоидом, нормальным эллипсоидом, который вращается вместе с Землей и также является поверхностью с постоянным потенциалом в этом поле. Разница между действительным и нормальным гравитационными потенциалами известна как возмущающий потенциал: T = W − U ; таким образом, он исключает центробежный потенциал. Нормальный гравитационный потенциал составляет примерно 99,9995% от общего потенциала.
Градиент потенциала представляет собой ускорение, гравитационное или гравитационное ускорение, в зависимости от того, включает ли оно центробежное ускорение. Нормальная сила тяжести, γ , обычно составляет около 99,995% от общей силы тяжести, g , хотя разница в величинах, гравитационное возмущение, δ g , может достигать нескольких частей в 10 4 . Разность особого рода, называемая гравитационной аномалией, Δ г , определяется как разница между силой тяжести в точке, P , и нормальной силой тяжести в соответствующей точке, Q , где W P = U 8 8 9 P и Q находятся на одном перпендикуляре к нормальному эллипсоиду.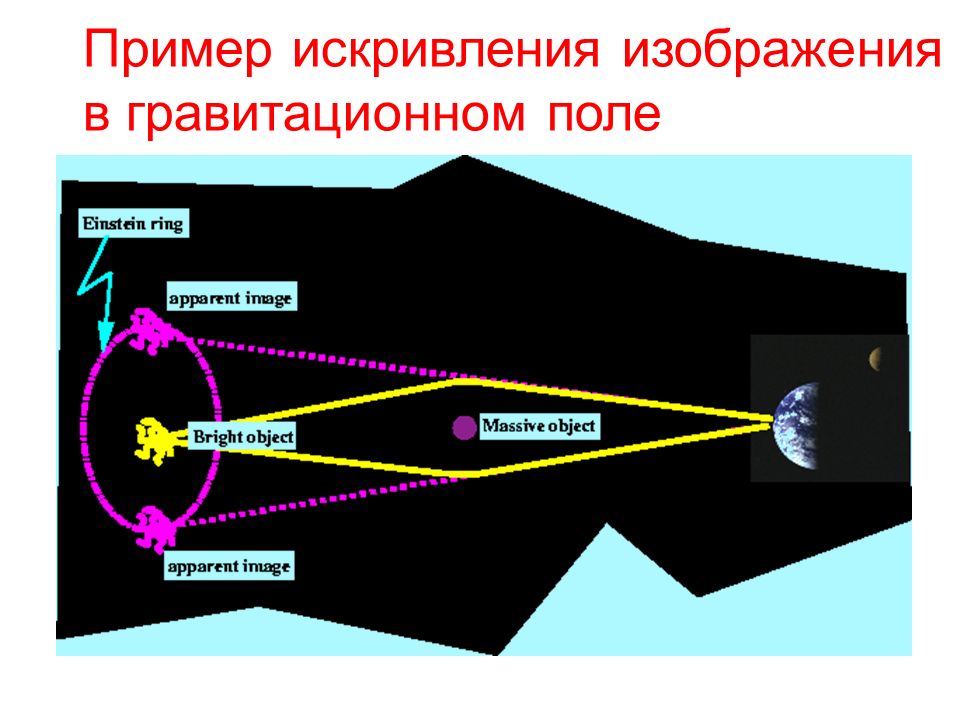
Поверхность с постоянным гравитационным потенциалом, W 0 , которая близко соответствует среднему уровню моря, известна как геоид. Если постоянный нормальный гравитационный потенциал, U 0 , на нормальном эллипсоиде равна постоянному гравитационному потенциалу геоида, то гравитационная аномалия на геоиде есть разность между гравитацией на геоиде и нормальной гравитацией на эллипсоиде в соответствующих точках, P 0 и Q 0 , имеющие один и тот же перпендикуляр к эллипсоиду. Разделение между геоидом и эллипсоидом известно как волнистость геоида, N , или также высота геоида ( Рисунок 3 ). Простое разложение Тейлора нормального гравитационного потенциала вдоль перпендикуляра эллипсоида дает следующую важную формулу:
Рис. 3. Относительная геометрия геоида и эллипсоида.
[3]N=Tγ
Это уравнение Брунса (Hofmann-Wellenhof and Moritz, 2005), которое имеет точность до нескольких миллиметров в N и может быть расширено до N = T / γ — ( W 0 — U 0 )/ γ для общего случая, W 0 ≠ U 0 . Аномалия силы тяжести (на геоиде) представляет собой возмущение силы тяжести, скорректированное для оценки нормальной силы тяжести на эллипсоиде, а не на геоиде. Эта поправка равна N ∂ γ /∂ h = (∂ γ /∂ h )( T / γ )( T / γ ) вдоль перпендикуляра 1 эллипсоида 90 , У нас примерно δ г = − ∂ T /∂ h и, следовательно,
Аномалия силы тяжести (на геоиде) представляет собой возмущение силы тяжести, скорректированное для оценки нормальной силы тяжести на эллипсоиде, а не на геоиде. Эта поправка равна N ∂ γ /∂ h = (∂ γ /∂ h )( T / γ )( T / γ ) вдоль перпендикуляра 1 эллипсоида 90 , У нас примерно δ г = − ∂ T /∂ h и, следовательно,
[4] Δg=−∂T∂h+1γ∂γ∂hT
, известное как фундаментальное уравнение физической геодезии (Hofmann-Wellenhof and Moritz, 2005).
Наклон геоида по отношению к эллипсоиду также является углом между соответствующими перпендикулярами к этим поверхностям. Этот угол известен как отклонение вертикали, то есть отклонение отвесной линии (перпендикуляра к геоиду) относительно перпендикуляра к нормальному эллипсоиду. Угол отклонения имеет составляющие, ξ и η соответственно в северном и восточном направлениях. Сферические аппроксимации гравитационного возмущения, гравитационной аномалии и отклонения вертикали даются формулами (Hofmann-Wellenhof and Moritz, 2005)
[5] δg=−∂T∂r, Δg=−∂T∂r −2rT,ξ=1γ∂Tr∂θ,η=−1γ∂Trsinθ∂λ,
, где знаки производных условны.
Посмотреть главуКнига покупок
Прочитать всю главу
URL: https://www.sciencedirect.com/science/article/pii/B9780444538024000567
M.A. Wieczorek, в трактате по геофизике (второе издание), 2015
10.05.9. лунные «масконы» Мюллера и Шегрена в 1968 году. В то время как ранние наборы данных были довольно скудными, постепенное накопление данных с каждой последующей космической миссией привело к появлению почти глобальных гравитационных и топографических моделей сферических гармоник. Некоторые модели гравитации теперь обладают шириной полосы сферических гармоник более 900, и будущие миссии, безусловно, приведут к дальнейшим улучшениям.
Не только разрешение планетарных наборов данных продолжало улучшаться со временем, но и методы анализа. Ранние исследования часто ограничивались анализом отдельных одномерных профилей гравитационного ускорения на линии прямой видимости. По мере того, как покрытие данных становилось более плотным, были разработаны двумерные региональные модели, которые чаще всего анализировались с использованием декартовых методов, разработанных для Земли. Из-за небольшого размера некоторых планетарных тел предположение о декартовой геометрии не всегда оправдано, и методы сферического анализа оказались более эффективными. Для сферы был разработан полный набор декартовых методов гравитационно-топографического анализа, включая многоконусный спектральный анализ, вейвлет-анализ, быстрый расчет гравитационных аномалий на основе топографического рельефа конечной амплитуды и реалистичные модели проводимости, учитывающие поверхностную и подповерхностную нагрузку. . Хотя аппроксимация декартовой геометрии может не давать больших ошибок для некоторых мелкомасштабных исследований, столь же легко использовать сферический метод, обладающий сравнимой скоростью вычислений.
По мере того, как покрытие данных становилось более плотным, были разработаны двумерные региональные модели, которые чаще всего анализировались с использованием декартовых методов, разработанных для Земли. Из-за небольшого размера некоторых планетарных тел предположение о декартовой геометрии не всегда оправдано, и методы сферического анализа оказались более эффективными. Для сферы был разработан полный набор декартовых методов гравитационно-топографического анализа, включая многоконусный спектральный анализ, вейвлет-анализ, быстрый расчет гравитационных аномалий на основе топографического рельефа конечной амплитуды и реалистичные модели проводимости, учитывающие поверхностную и подповерхностную нагрузку. . Хотя аппроксимация декартовой геометрии может не давать больших ошибок для некоторых мелкомасштабных исследований, столь же легко использовать сферический метод, обладающий сравнимой скоростью вычислений.
Многое известно о строении земной коры и литосферы планет земной группы, но многое еще предстоит сделать. В частности, теперь, оглядываясь назад, становится ясно, что во многих гравитопографических исследованиях допускной способности и когерентности использовались методы анализа, надежность которых иногда трудно оценить. Недостатки включают неправильное применение метода многоконусного спектрального анализа, игнорирование функции проводимости или корреляционной функции, а также использование теоретической модели проводимости, которая может быть чрезмерным упрощением реальности. Немногие исследования, даже для Земли, провели этот анализ полностью правильно, и следует критически оценивать каждую из оценок упругой толщины, которые были опубликованы для регионов, где важна подповерхностная нагрузка.
В частности, теперь, оглядываясь назад, становится ясно, что во многих гравитопографических исследованиях допускной способности и когерентности использовались методы анализа, надежность которых иногда трудно оценить. Недостатки включают неправильное применение метода многоконусного спектрального анализа, игнорирование функции проводимости или корреляционной функции, а также использование теоретической модели проводимости, которая может быть чрезмерным упрощением реальности. Немногие исследования, даже для Земли, провели этот анализ полностью правильно, и следует критически оценивать каждую из оценок упругой толщины, которые были опубликованы для регионов, где важна подповерхностная нагрузка.
Важно также отметить, что концепция упругой литосферы, часто используемая в гравитационном анализе, на самом деле является грубым упрощением реальности. Из-за простоты создания неизменного во времени профиля изгиба от нагрузки, приложенной к упругой пластине, хотелось бы надеяться, что полученная «эффективная упругая толщина» имеет некоторый физический смысл. Хотя это может иметь место в регионах, где величина поверхностной и подповерхностной нагрузки невелика и где силы в плоскости отсутствуют, было продемонстрировано, что использование более реалистичной реологии может привести к получению изгибных профилей, которые иногда сильно отличаются. К сожалению, наиболее реалистичные модели EVP являются дорогостоящими в вычислительном отношении и в настоящее время не поддаются надежной процедуре инверсии, использующей гравитацию и топографию в качестве ограничений. В такой инверсии можно было бы использовать более простую эластично-пластическую формулу, но в этой реологической модели используются допущения, которые все же могут оказаться слишком упрощенными. Несмотря на это, было бы уместно разработать модель упругопластического нагружения, подобную упругой модели, описанной в 9.0177 Секция 10.05.7 для сферы. Одним из преимуществ такой модели является возможность инвертирования регионального теплового потока. Дополнительным направлением будущих исследований является сравнение мест поверхностных разломов с теми, которые были предсказаны с помощью моделей упругой, упруго-пластической и EVP.
Хотя это может иметь место в регионах, где величина поверхностной и подповерхностной нагрузки невелика и где силы в плоскости отсутствуют, было продемонстрировано, что использование более реалистичной реологии может привести к получению изгибных профилей, которые иногда сильно отличаются. К сожалению, наиболее реалистичные модели EVP являются дорогостоящими в вычислительном отношении и в настоящее время не поддаются надежной процедуре инверсии, использующей гравитацию и топографию в качестве ограничений. В такой инверсии можно было бы использовать более простую эластично-пластическую формулу, но в этой реологической модели используются допущения, которые все же могут оказаться слишком упрощенными. Несмотря на это, было бы уместно разработать модель упругопластического нагружения, подобную упругой модели, описанной в 9.0177 Секция 10.05.7 для сферы. Одним из преимуществ такой модели является возможность инвертирования регионального теплового потока. Дополнительным направлением будущих исследований является сравнение мест поверхностных разломов с теми, которые были предсказаны с помощью моделей упругой, упруго-пластической и EVP.
Наконец, стоит отметить, что в будущем можно ожидать значительных улучшений в наших знаниях о гравитационных полях и топографии планет земной группы. В частности, несмотря на то, что наземная топография Земли в настоящее время известна с высокой точностью, вблизи полярных регионов все еще существуют пробелы, которые можно было бы заполнить данными, полученными с помощью лазерного высотомера орбитальной системы лазерного альтиметра (GLAS) (например, Abshire). и др., 2005; Шуц и др., 2005; Шуман и др., 2006). Данные, полученные в ходе наземной миссии GOCE, в состав которой входит гравиградиометр, позволили разработать улучшенные модели гравитационного поля Земли. Областью активных исследований Земли, а также и других планет в более ограниченном смысле, является измерение и моделирование переменных во времени гравитационных сигнатур, являющихся результатом гидрологических процессов и приливной деформации.
Что касается других планет, то топография и гравитационное поле Меркурия продолжают характеризоваться данными, собранными космическим аппаратом MESSENGER (Solomon et al.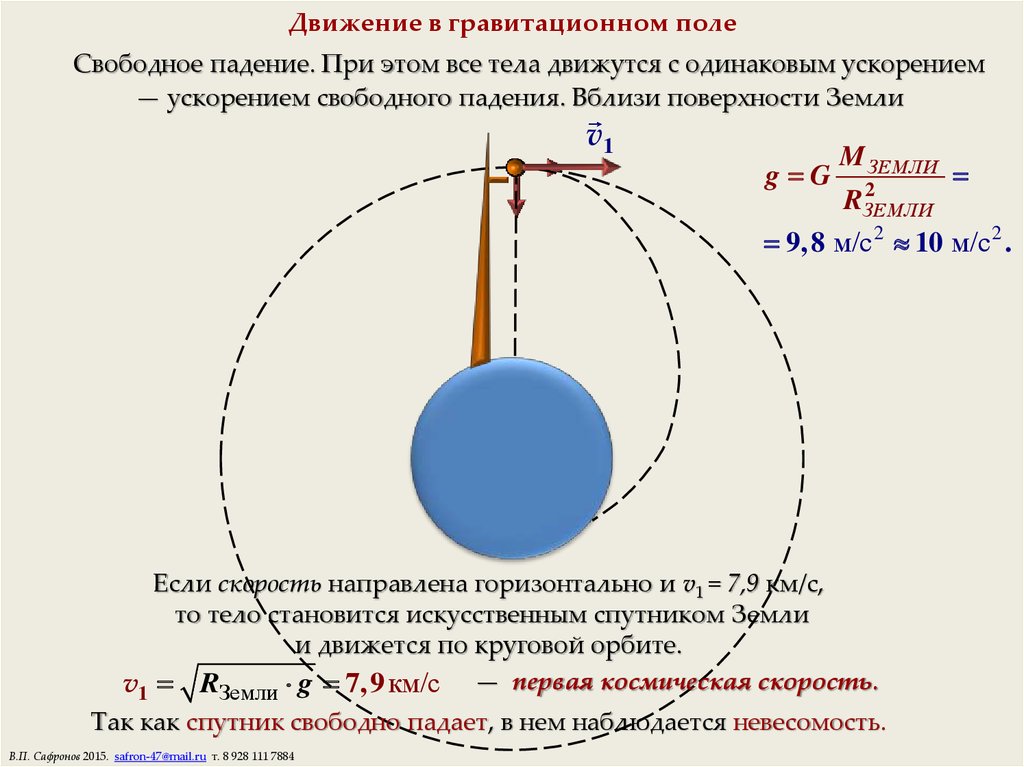 , 2001), и они будут дополнены данными, которые будут собраны будущая миссия BepiColombo (Spohn et al., 2001). JUpiter ICy moons Explorer (JUICE) будет собирать альтиметрические и гравиметрические данные для ледяного спутника Ганимеда и, в ограниченной степени, для Европы и Ганимеда. Ограниченные гравитационные данные будут также собраны в конце миссии Venus Express и во время миссии MAVEN на Марс.
, 2001), и они будут дополнены данными, которые будут собраны будущая миссия BepiColombo (Spohn et al., 2001). JUpiter ICy moons Explorer (JUICE) будет собирать альтиметрические и гравиметрические данные для ледяного спутника Ганимеда и, в ограниченной степени, для Европы и Ганимеда. Ограниченные гравитационные данные будут также собраны в конце миссии Venus Express и во время миссии MAVEN на Марс.
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/B978044453802400169X
Alessandro M. Forte, Richard Peltiers in Geophysics, W. 1994
4.6 Негидростатический геоид
Возмущения гравитационного потенциала, возникающие над конвективной мантией, представляют собой сумму возмущений потенциала из-за внутренних возмущений плотности, которые управляют потоком, и потенциальных возмущений из-за вызванных потоком отклонений границы ( например, Пекерис, 19 лет35; Ричардс и Хагер, 1984 г.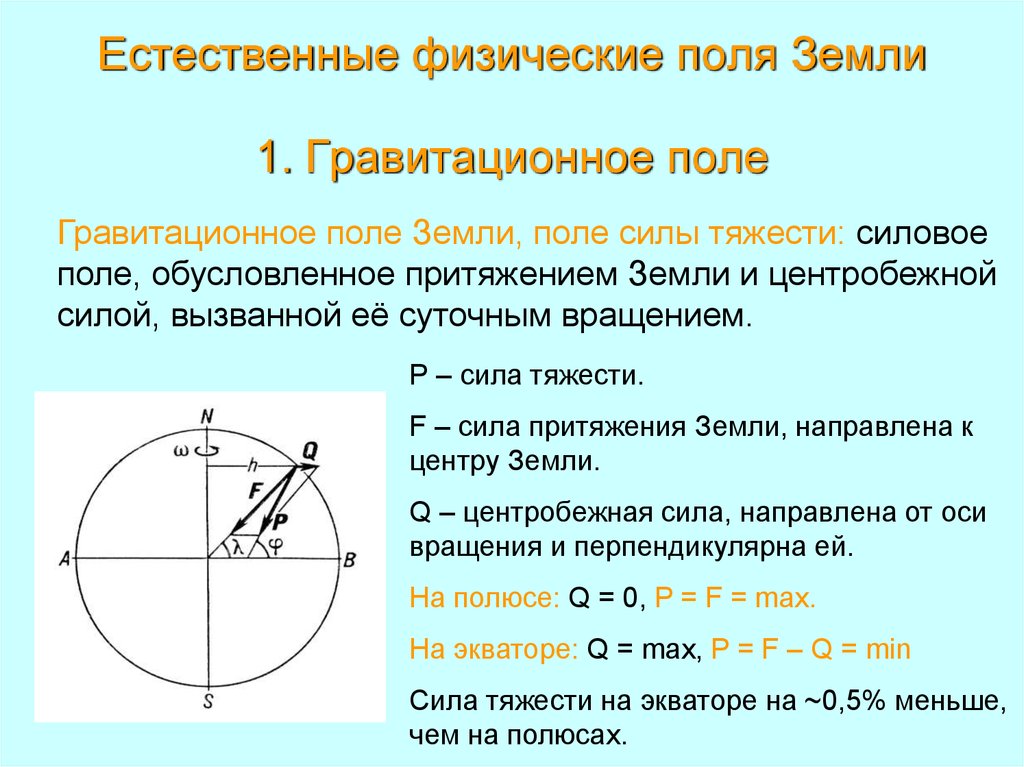 ; Рикард и др. , 1984; Форте и Пельтье, 1987). Поверхностные гравитационные возмущения в значительной степени контролируются взаимно компенсирующими гравитационными вкладами топографии поверхности, вызванной потоками (при r = a ) и аномалиями внутренней плотности. В предыдущем разделе мы наблюдали, что хотя изменение вязкости мантии на глубине оказывает сильное влияние на амплитуду и, следовательно, на гравитационный эффект волнистости поверхности, присутствие очень сильных 0185 боковых вариаций вязкости оказывает гораздо меньшее влияние на амплитуду и характер рельефа поверхности. Поэтому мы ожидаем, что негидростатический геоид проявит аналогичную нечувствительность к латеральным вариациям вязкости и, следовательно, будет преимущественно чувствителен только к радиальным вариациям вязкости. Ниже мы демонстрируем это явно. В Приложении VII мы приводим явные выражения для негидростатического геоида в самогравитирующей мантии.
; Рикард и др. , 1984; Форте и Пельтье, 1987). Поверхностные гравитационные возмущения в значительной степени контролируются взаимно компенсирующими гравитационными вкладами топографии поверхности, вызванной потоками (при r = a ) и аномалиями внутренней плотности. В предыдущем разделе мы наблюдали, что хотя изменение вязкости мантии на глубине оказывает сильное влияние на амплитуду и, следовательно, на гравитационный эффект волнистости поверхности, присутствие очень сильных 0185 боковых вариаций вязкости оказывает гораздо меньшее влияние на амплитуду и характер рельефа поверхности. Поэтому мы ожидаем, что негидростатический геоид проявит аналогичную нечувствительность к латеральным вариациям вязкости и, следовательно, будет преимущественно чувствителен только к радиальным вариациям вязкости. Ниже мы демонстрируем это явно. В Приложении VII мы приводим явные выражения для негидростатического геоида в самогравитирующей мантии.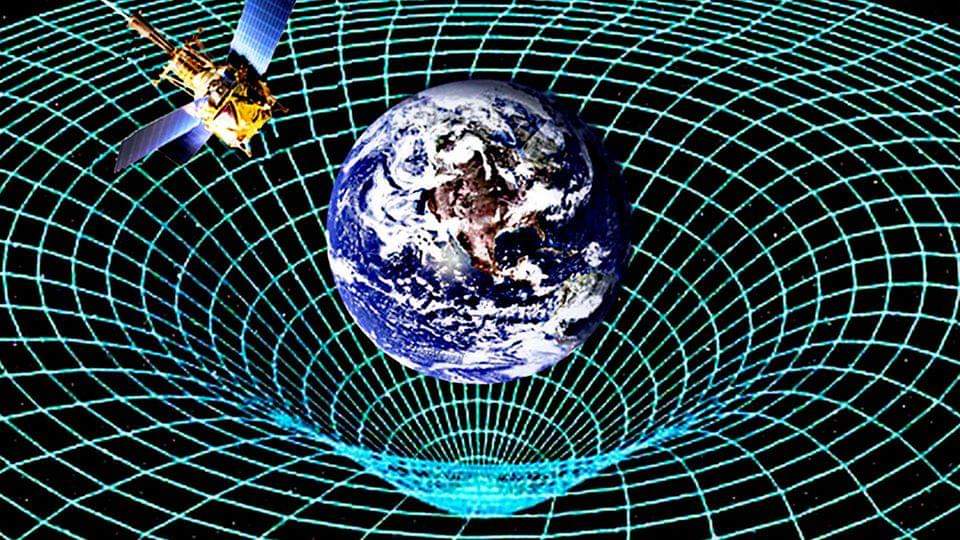
На рис. 38а показан прогноз негидростатического геоида л = 2–3 для изовязкой мантии η00r=η0 с использованием неоднородности плотности л = 2–3, полученной по модели SH8/WM13 и δ5 9016 ln ρ/δ ln v s на рис. 6б. Негидростатический геоид степени 1–6, образовавшийся при взаимодействии аномалий плотности л = 2–3 с вариациями вязкости степени 1–5 на рис. 25, опять же с η00r=η0, показан на рис. 38b. За исключением небольшого уменьшения амплитуды максимумов геоида в южной части Тихого океана и на юге Африки, рис. 38b почти идентичен изовязкому прогнозу на рис. 38a. Карта различий между этими двумя предсказаниями представлена на рис. 38c, где мы видим, что пиковое различие локализовано в южной части Тихого океана. Среднеквадратическая амплитуда разностного поля составляет 12 м по сравнению со среднеквадратичной амплитудой 100 м на рис. 38а (т. е. относительное влияние латеральных вариаций вязкости составляет всего 12%).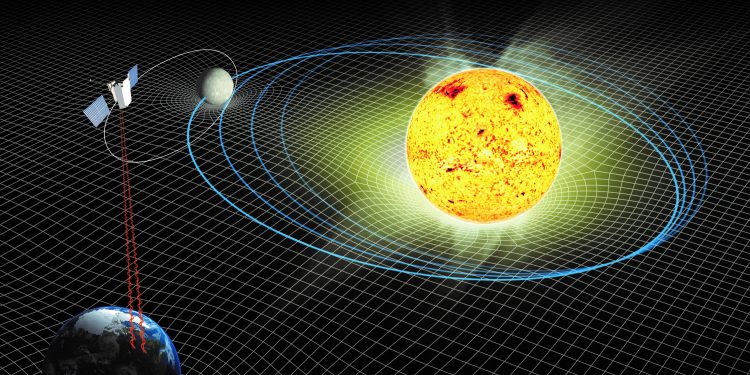 Отметим, что разностное поле на рис. 38c в значительной степени отражает небольшое влияние латеральных вариаций вязкости на топографию поверхности, вызванную течением (см. рис. 32c). Подробная сводка прогнозов геоида на рис. 38 представлена на рис. 39..
Отметим, что разностное поле на рис. 38c в значительной степени отражает небольшое влияние латеральных вариаций вязкости на топографию поверхности, вызванную течением (см. рис. 32c). Подробная сводка прогнозов геоида на рис. 38 представлена на рис. 39..
Рис. 38. (a) Степень ℓ = 2–3 негидростатического геоидного прогноза для изовиско -мантии [т.е. η ( R , θ , r , θ , r ) ) ) ) ) ) ) ) ) ) ) ) ) ) = 1], рассчитанный на основе возмущений плотности степени 2–3, полученных по модели SH8/WM13 [с использованием δ ln ρ/δ ln v s на рис. 6[. (б) Степень ℓ = 1–6 прогноза негидростатического геоида для мантии с трехмерной вязкостью η ( r , θ , ϕ ) /η 0 = 1+ V ( vd 1+ V ( ven 1+ V ( vd 1+ V ( vd 1+ V ( vd 1+ V ( = 1+ V ( = 1+. представляет собой изменение вязкости в степени 1–5 на рис. 25. Возмущения плотности такие же, как в (a), (c). Разность геоида в диапазоне 90 185 ℓ 90 186 = 1–6, полученная путем вычитания геоида на (b) из пункта (а). Единицами измерения на всех линейках шкалы являются метры.
представляет собой изменение вязкости в степени 1–5 на рис. 25. Возмущения плотности такие же, как в (a), (c). Разность геоида в диапазоне 90 185 ℓ 90 186 = 1–6, полученная путем вычитания геоида на (b) из пункта (а). Единицами измерения на всех линейках шкалы являются метры.
Рис. 39. (а) Взаимная корреляция для каждой степени ℓ , между предсказаниями негидростатического геоида на рис. 38а и 38б. (b) Среднеквадратическая амплитуда при каждом градусе 90 185 ℓ 90 186 прогнозируемого геоида на рис. 38a (o, без латеральной вязкости), прогнозируемого геоида на рис. . 38c (Δ, разница).
На рис. 40а мы теперь показываем прогноз негидростатического геоида ℓ = 2–3 для латерально-однородной вязкости с изменением глубины η 0 ( a/r ) 10 дано в уравнении. (165). Это предсказание геоида изменило знак по сравнению с предсказанием изовязкости на рис. 38а, потому что сильное увеличение вязкости с глубиной сильно уменьшило амплитуду топографии поверхности (сравните рис. 32а и 35а), что позволяет внутренним возмущениям плотности доминировать над сигнал геоида. Прогноз геоида степени 1–6, рассчитанный при введении вариаций вязкости степени 1–5 [с η00r=η0a/r10], показан на рис. 40b. Снова мы наблюдаем, что влияние очень больших боковых вариаций вязкости невелико, и это подтверждается малой амплитудой разностного поля на рис. 40c. Среднеквадратическая амплитуда этого разностного поля составляет 14 м по сравнению со среднеквадратичной амплитудой 108 м на рис. 40а (т.е. относительная разница составляет всего 13%). Мы снова отмечаем, что разностное поле на рис. 40c является отражением небольшого влияния латеральных вариаций вязкости на топографию поверхности, вызванную потоком (см. рис. 35c). Количественная сводка прогнозов геоида на рис. 40 представлена на рис. 41.
32а и 35а), что позволяет внутренним возмущениям плотности доминировать над сигнал геоида. Прогноз геоида степени 1–6, рассчитанный при введении вариаций вязкости степени 1–5 [с η00r=η0a/r10], показан на рис. 40b. Снова мы наблюдаем, что влияние очень больших боковых вариаций вязкости невелико, и это подтверждается малой амплитудой разностного поля на рис. 40c. Среднеквадратическая амплитуда этого разностного поля составляет 14 м по сравнению со среднеквадратичной амплитудой 108 м на рис. 40а (т.е. относительная разница составляет всего 13%). Мы снова отмечаем, что разностное поле на рис. 40c является отражением небольшого влияния латеральных вариаций вязкости на топографию поверхности, вызванную потоком (см. рис. 35c). Количественная сводка прогнозов геоида на рис. 40 представлена на рис. 41.
Рис. 40. (а) Степень ℓ = 2–3 прогноз негидростатического геоида для сферически-симметричной мантии с переменной вязкостью по глубине = ( a/r ) 10 , рассчитанное на основе возмущений плотности степени 2–3, полученных по модели SH8/WM13 (с использованием Рис. 6). (б) Степень ℓ = 1–6 предсказание негидростатического геоида для мантии с трехмерной вязкостью η ( r , θ , ϕ ) /η 0 = ( a / r ) 10 [1 + v ( θ, ϕ )] , где v ( θ , ϕ ) – изменение вязкости в степени 1–5 на рис. 25. = 1–6. полученный путем вычитания геоида в (б) из геоида в (а). Единицами измерения на всех линейках шкалы являются метры.
6). (б) Степень ℓ = 1–6 предсказание негидростатического геоида для мантии с трехмерной вязкостью η ( r , θ , ϕ ) /η 0 = ( a / r ) 10 [1 + v ( θ, ϕ )] , где v ( θ , ϕ ) – изменение вязкости в степени 1–5 на рис. 25. = 1–6. полученный путем вычитания геоида в (б) из геоида в (а). Единицами измерения на всех линейках шкалы являются метры.
Рис. 41. (a) Взаимная корреляция для каждого градуса 90 185 ℓ 90 186 между предсказаниями негидростатического геоида на рис. 40а и 40б. (b) Среднеквадратическая амплитуда при каждом градусе ℓ предсказанного геоида на рис. 40a (○, без латеральной вязкости), предсказанного геоида на рис. . 40c (Δ, разница).
При рассмотрении выводов, полученных в этом разделе и в разделе 4.5, стоит напомнить, что во всех наших демонстрациях использовались идеализированные не зависящие от глубины боковые вариации вязкости. Мы ожидаем, что наложение крупноамплитудных латеральных вариаций на рис. 23 на всех глубинах мантии, вероятно, завышает реально существующие крупномасштабные вариации, особенно в глубокой мантии (например, Zhang and Christensen, 1993). ). Окончательное подтверждение наших выводов станет возможным, когда мы сможем надежно картировать амплитуду вариаций латеральной вязкости по всей мантии. Благодаря недавним экспериментам по плавлению под высоким давлением (Zerr and Boehler, 19) в настоящее время достигнут обнадеживающий прогресс.93), а также в результате недавних выводов о латеральных вариациях сейсмических Q в глубинной мантии (Romanowicz and LeStunff, 1993).
Мы ожидаем, что наложение крупноамплитудных латеральных вариаций на рис. 23 на всех глубинах мантии, вероятно, завышает реально существующие крупномасштабные вариации, особенно в глубокой мантии (например, Zhang and Christensen, 1993). ). Окончательное подтверждение наших выводов станет возможным, когда мы сможем надежно картировать амплитуду вариаций латеральной вязкости по всей мантии. Благодаря недавним экспериментам по плавлению под высоким давлением (Zerr and Boehler, 19) в настоящее время достигнут обнадеживающий прогресс.93), а также в результате недавних выводов о латеральных вариациях сейсмических Q в глубинной мантии (Romanowicz and LeStunff, 1993).
Просмотреть главуКнига покупок
Прочитать главу полностью
URL: https://www.sciencedirect.com/science/article/pii/S0065268708605373
5: Гравитационное поле и потенциал
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6818
- Джереми Татум
- Университет Виктории
Эта глава посвящена расчету гравитационных полей и потенциалов вблизи массивных тел различных форм и размеров. Читатель, изучавший электростатику, поймет, что все это просто повторение того, что он или она уже знает.
Читатель, изучавший электростатику, поймет, что все это просто повторение того, что он или она уже знает.
- 5.1: Введение
- 5.2: Гравитационное поле
- Область вокруг гравитирующего тела (под которой я подразумеваю массу, которая будет притягивать другие массы поблизости) является гравитационным полем. Хотя я употребил слова «вокруг» и «около него», на самом деле поле простирается до бесконечности. Все массивные тела (а под «массивным» я подразумеваю любое тело, обладающее свойством массы, пусть и незначительное) окружены гравитационным полем, и все мы погружены в гравитационное поле.
- 5.3: Закон тяготения Ньютона
- Ньютон заметил, что отношение центростремительного ускорения Луны на ее орбите вокруг Земли к ускорению яблока, падающего на поверхность Земли, обратно пропорционально квадратам расстояний Луны и яблока от центра Земли.
 Вместе с другими доказательствами это привело Ньютона к предложению его универсального закона тяготения:
Вместе с другими доказательствами это привело Ньютона к предложению его универсального закона тяготения:
- 5.4: Гравитационные поля различных тел
- 5.4.1: Поле точечной массы
- 5.4.2: Поле на оси кольца
- 5.4.3: Плоские диски
- 5.4.4: Бесконечные плоские пластинки 5 9.0404 5: Полово полушария
- 5.4.6: стержни
- 5.4.7: сплошной цилиндр
- 5.4.8: Полая сферическая раковина
- 5.4.9: сплошная сфера
- 5.4.10: пузырь внутри универсальной сферы
- 5.5: Теорема Гаусса
- Полный нормальный направленный наружу гравитационный поток через замкнутую поверхность равен \(−4 \pi G\), умноженному на общую массу, заключенную в этой поверхности.
- 5.6: Расчет поверхностных интегралов
- Хотя понятие поверхностного интеграла звучит достаточно просто, как его вычислить на практике?
- 5.
 7: Потенциал
7: Потенциал - Мы определили только разность потенциалов между двумя точками. Если мы хотим определить потенциал в точке, необходимо произвольно определить потенциал в конкретной точке равным нулю. Мы могли бы, например, определить потенциал на уровне пола равным нулю, и в этом случае потенциал на высоте h над полом равен gh; равным образом мы можем определить потенциал на уровне поверхности лабораторного стола равным нулю, тогда как потенциал на высоте z над поверхностью стола равен gz.
- 5,8: Гравитационные потенциалы вблизи различных тел
- 5,8,1: Потенциал вблизи массы точки
- 5,8,2: Потенциал на оси на кольце
- 5,8.3: плоскость 444.
- 5.8.4: Бесконечная плоская пластинка
- 5.8.5: Полая полусфера
- 5.8.6: Стержни
- 5.8.7: Сплошной цилиндр
- 5.8.8: Полая сферическая оболочка
4
- : Сплошная сфера
- 5.
 9: Работа, необходимая для сборки однородной сферы
9: Работа, необходимая для сборки однородной сферы
- 5.10: Набла, градиент и дивергенция
- В этом разделе мы встретимся с символом ∇ . В Северной Америке оно обычно произносится как «дел», хотя в Соединенном Королевстве и других местах иногда можно услышать альтернативное произношение «набла», названное в честь древнего ассирийского инструмента, похожего на арфу, примерно такой формы.
- 5.11: Полиномы Лежандра
- В этом разделе мы рассказываем о многочленах Лежандра ровно столько, чтобы быть полезными в следующем разделе.
- 5.12: гравитационный потенциал любого массивного тела р?
Миниатюра: Линии гравитационного поля вокруг Земли. (Общественное достояние; Sjlegg).
Эта страница под названием 5: Gravitational Field and Potential распространяется под лицензией CC BY-NC 4. 0 и была создана, изменена и/или курирована Джереми Татумом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Джереми Татумом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- Джереми Татум
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Метки
- источник@http://orca.
 phys.uvic.ca/~tatum/celmechs.html
phys.uvic.ca/~tatum/celmechs.html
- источник@http://orca.
Обнаружено сверхслабое гравитационное поле
- НОВОСТИ И МНЕНИЯ
Эксперимент показывает, что закон всемирного тяготения Ньютона выполняется даже для двух масс всего около 90 миллиграммов. Полученные данные приближают нас к измерению гравитационных полей, которые настолько слабы, что могут войти в квантовый режим.
- Кристиан Ротлейтнер 0
- Кристиан Ротлейтнер
Кристиан Ротляйтнер работает в отделе механики и акустики, Physikalisch-Technische Bundesanstalt, 38116 Брауншвейг, Германия.

Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google ученый
В физике известны четыре фундаментальные силы: слабое и сильное взаимодействия, а также электромагнитная и гравитационная силы. Гравитационная сила является самой слабой из этих четырех. По этой причине, а также из-за того, что эксперименты не могут быть защищены от земного притяжения, измерения гравитационного поля тестируемого объекта трудно проводить в лаборатории — даже для объектов, имеющих многокилограммовые массы. Но писать в Природа , Вестфаль и др. . 1 сообщают об обнаружении гравитационной связи между двумя массами всего около 90 миллиграммов.
Но писать в Природа , Вестфаль и др. . 1 сообщают об обнаружении гравитационной связи между двумя массами всего около 90 миллиграммов.
Варианты доступа
Подписаться на журнал
Получить полный доступ к журналу на 1 год
199,00 €
всего 3,90 € за выпуск
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Природа 591 , 209-210 (2021)
doi: https://doi.org/10.1038/d41586-021-00591-1
Ссылки
Westphal, T., Hepach, H., Pfaff, J. & Aspelmeyer, M. Nature 591 , 225–228 (2021).

Артикул Google ученый
Ньютон, И. Philosophiae Naturalis Principia Mathematica (sumptibus Societatis, 1687).
Google ученый
Нибауэр, Т. М., Сасагава, Г. С., Фаллер, Дж. Э., Хилт, Р. и Клоппинг, Ф. Metrologia 32 , 159–180 (1995).
Артикул Google ученый
Оорт, Дж. Х. Bull. Астрон. Инст. Нет. 6 , 249–287 (1932).
Google ученый
Рис, М. Дж. Фил. Транс. Р. Соц. Лонд. А 361 , 2427–2434 (2003).
Артикул Google ученый
Де Сварт, Дж. Г., Бертоне, Г. и ван Донген, Дж. Nature Astron. 1 , 0059 (2017).

Артикул Google ученый
Милгром М. Астрофиз. J. 270 , 365–370 (1983).
Артикул Google ученый
Двали Г. в Проц. 2011 ЦЕРН – Латиноамериканская школа физики высоких энергий (под редакцией Грожан, К., Малдерс, М. и Спиропулу, М.) 145–156 (ЦЕРН, 2013).
Google ученый
Аркани-Хамед, Н., Димопулос, С. и Двали, Г. физ. лат. B 429 , 263–272 (1998).
Артикул Google ученый
Rothleitner, C. & Schlamminger, S. Rev. Sci. Инструм. 88 , 111101 (2017).
ПабМед Статья Google ученый
Вуд, Б. М. Фил. Транс. Р. Соц.
 Лонд. А 372 , 20140029 (2014).
Лонд. А 372 , 20140029 (2014).Артикул Google ученый
Кляйн, Дж. Р. и Рудман, А. Annu. Преподобный Нукл. Часть. науч. 55 , 141–163 (2005).
Артикул Google ученый
Кавендиш, Х. Фил. Транс. Р. Соц. Лонд. 88 , 469–526 (1798).
Артикул Google ученый
Li, Q. и др. Природа 560 , 582–588 (2018).
ПабМед Статья Google ученый
Philips, K.G., Jacques, S.L. & McCarty, O.J.T. Phys. Преподобный Летт. 109 , 118105 (2012).
ПабМед Статья Google ученый
Скачать ссылки
Прочтите статью: Измерение гравитационного взаимодействия между массами миллиметрового размера.

Гравитация измерена с рекордной точностью
Классный способ измерить большой G
Просмотреть все новости и просмотры
Субъекты
- Физика
Последнее:
Работа
Базовый научный сотрудник факультета визуализации
Станфордское отделение радиологии
Пало-Альто, Калифорния, США
Председатель (W3) железнодорожных операций
Технический университет Дрездена (TU Dresden)
01069 Дрезден, Германия
Заведующая отделением акушерства и гинекологии
Университет Британской Колумбии (UBC)
Ванкувер, Канада
Кандидат наук — Исследовательский проект Метаболическая регуляция ответов макрофагов при хронической обструктивной болезни легких (ф/м/х)
Гельмгольц Мюнхен
Мюнхен, Германия
физиков измерили наименьшее гравитационное поле – Physics World
Точные весы Исследователи измерили гравитационное поле между двумя золотыми массами радиусом 1 мм каждая, которые были сближены. (С любезного разрешения: Тобиас Вестфаль, Венский университет)
(С любезного разрешения: Тобиас Вестфаль, Венский университет)Физики из Австрии измерили гравитационное поле самого маленького из когда-либо существовавших объектов: золотой сферы диаметром всего 2 мм. Проведенное с помощью миниатюрных торсионных весов измерение прокладывает путь к еще более чувствительным гравитационным зондам, которые могли бы выявить квантовую природу гравитации.
В течение многих лет общая теория относительности Эйнштейна и универсальный закон всемирного тяготения Ньютона подвергались все более строгим проверкам. Эти испытания включали как астрономические наблюдения, так и лабораторные эксперименты. Обычно массы, обеспечивающие гравитационное поле в последних, представляют собой крупные объекты в несколько килограммов и более, такова необходимость компенсации присущей гравитации слабости.
В последней работе, напротив, используется золотой шар массой всего 92 мг в качестве источника. Маркус Аспельмейер и Тобиас Вестфаль из Института квантовой оптики и квантовой информации в Вене и их коллеги поместили эту массу в нескольких миллиметрах от другой крошечной золотой сферы с примерно такой же массой, расположенной на одном конце стеклянного стержня длиной 4 см. Стержень был подвешен в центре на кварцевом волокне, а третья сфера на дальнем конце стержня действовала как противовес.
Стержень был подвешен в центре на кварцевом волокне, а третья сфера на дальнем конце стержня действовала как противовес.
Такие «крутильные весы» уже более 200 лет используются для точных измерений силы тяжести. Идея состоит в том, что исходная масса притягивает ближний конец стержня к себе, заставляя подвешенное волокно или проволоку вращаться. Измеряя это вращение и балансируя его с жесткостью проволоки, можно рассчитать силу гравитационного взаимодействия. Тот факт, что полоса движется горизонтально, означает, что она меньше подвергается воздействию гораздо большего гравитационного поля Земли.
Стратегии снижения уровня шума
Основной проблемой таких экспериментов является отсеивание шума. Аспельмейер и его коллеги сделали это, поместив весы в вакуум, чтобы ограничить акустические и тепловые помехи, а также заземлив исходную массу и поместив экран Фарадея между ней и тестовой массой, чтобы уменьшить электромагнитные взаимодействия. Кроме того, они в основном собирали данные ночью, чтобы свести к минимуму внешние источники гравитации. Это важно, поскольку гравитационное притяжение исходной массы эквивалентно притяжению человека, стоящего в 2,5 м от эксперимента, или венского трамвая в 50 м от него.
Это важно, поскольку гравитационное притяжение исходной массы эквивалентно притяжению человека, стоящего в 2,5 м от эксперимента, или венского трамвая в 50 м от него.
Чтобы генерировать сигналы выше оставшегося шума, исследователи использовали изгибающееся пьезоэлектрическое устройство для циклического перемещения источника к тестовой массе и от нее. Выполнение этого на фиксированной частоте (12,7 мГц) позволило им найти соответствующее изменение вращения баланса, которое они измерили, отражая лазерный луч от зеркала под кварцевым волокном.
Повторив этот процесс сотни раз в течение 13,5 часов, а затем преобразовав данные временного ряда в частотный спектр, Аспельмейер и его коллеги определили два четких сигнала над фоном. Это были основные колебания на частоте 12,7 мГц и вторая гармоника на частоте 25,4 мГц, генерируемая нелинейным изменением гравитационного поля в пространстве. Как отмечают исследователи, обе гармоники были значительно выше резонансной частоты качающихся весов и ниже частот шума считывания.
Как отмечают исследователи, обе гармоники были значительно выше резонансной частоты качающихся весов и ниже частот шума считывания.
Ньютоновский результат – пока
Используя камеру для регистрации изменения расстояния между источником и тестовой массой, физики также построили график изменения гравитационной силы в пространстве. Они говорят, что их данные — плавная кривая, убывающая как квадрат расстояния — однозначно свидетельствуют о ньютоновской гравитации. Более того, они также рассчитали собственное значение гравитационной постоянной G. Эта величина остается головной болью для метрологов, учитывая очень точные, но взаимно противоречивые ее измерения, сделанные разными группами. Результат группы – средневзвешенное значение на основе 29измерения во время сейсмически спокойного рождественского периода 2019 г. — вряд ли решат эти споры, поскольку они примерно на 9,5% меньше официального значения CODATA 6,674 × 10 −11 м 3 кг −1 с −2 . Однако исследователи отмечают, что этот запас находится в пределах примерно 10% неопределенности, которую они получают, суммируя все известные источники систематической ошибки в своем эксперименте.
Однако исследователи отмечают, что этот запас находится в пределах примерно 10% неопределенности, которую они получают, суммируя все известные источники систематической ошибки в своем эксперименте.
Забегая вперед, Аспельмейер и его коллеги утверждают, что их экспериментальный подход в принципе может быть распространен на еще меньшие массы источников. В частности, они говорят, что можно значительно снизить тепловой шум, увеличив добротность волокна. Повышение текущего значения примерно с 5 до более чем 20 000 может позволить получить массу источника ниже планковской массы 22 мкг, тем самым повысив перспективы исследования квантовой гравитации.
Подробнее
Квантовая гравитация вскоре может быть проверена с использованием ультрахолодных атомов
Чтобы достичь этого, они предупреждают, что потребуется уменьшить влияние других источников шума. Однако они считают, что эти проблемы решаемы. Например, низкочастотный шум от человеческих источников можно уменьшить, перенеся эксперимент в подходящее удаленное место.


 К примеру, в области Гудзонова залива в Канаде она ниже, чем в других регионах земного шара.
К примеру, в области Гудзонова залива в Канаде она ниже, чем в других регионах земного шара. 1 Гравитационная
сила
1 Гравитационная
сила С. Еремина, Н. В. Смирнова.-СПб, издат. дом СПбГУ, 2011. 588с. с. 145–150.
С. Еремина, Н. В. Смирнова.-СПб, издат. дом СПбГУ, 2011. 588с. с. 145–150.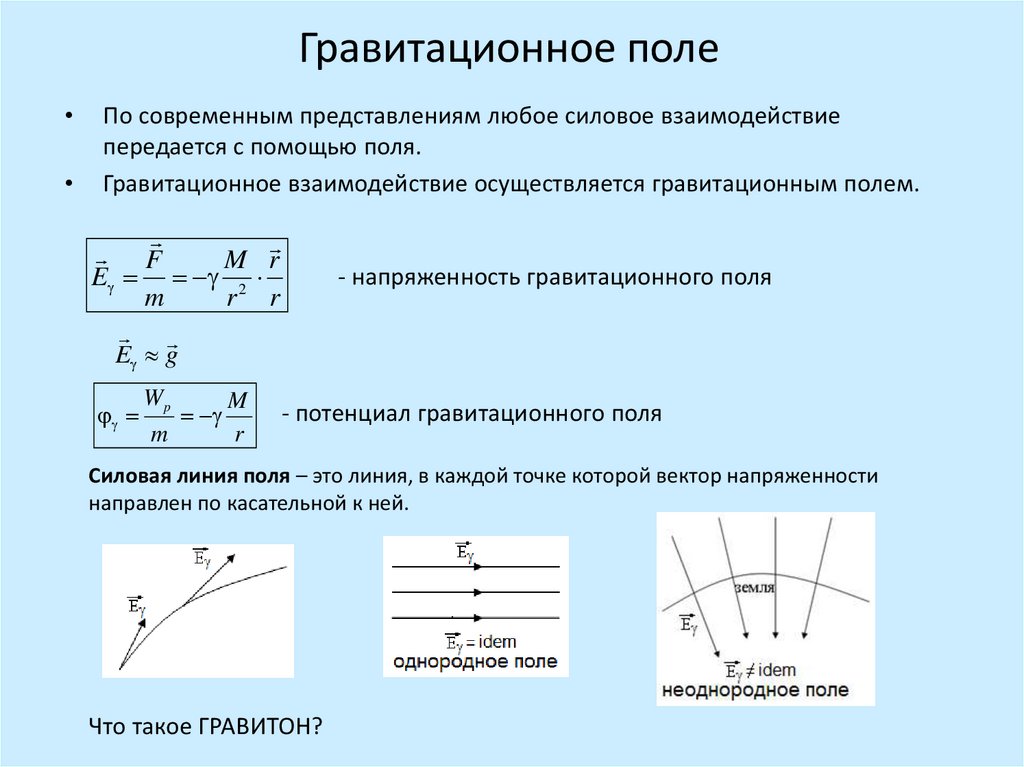 гравитационное поле.
гравитационное поле.
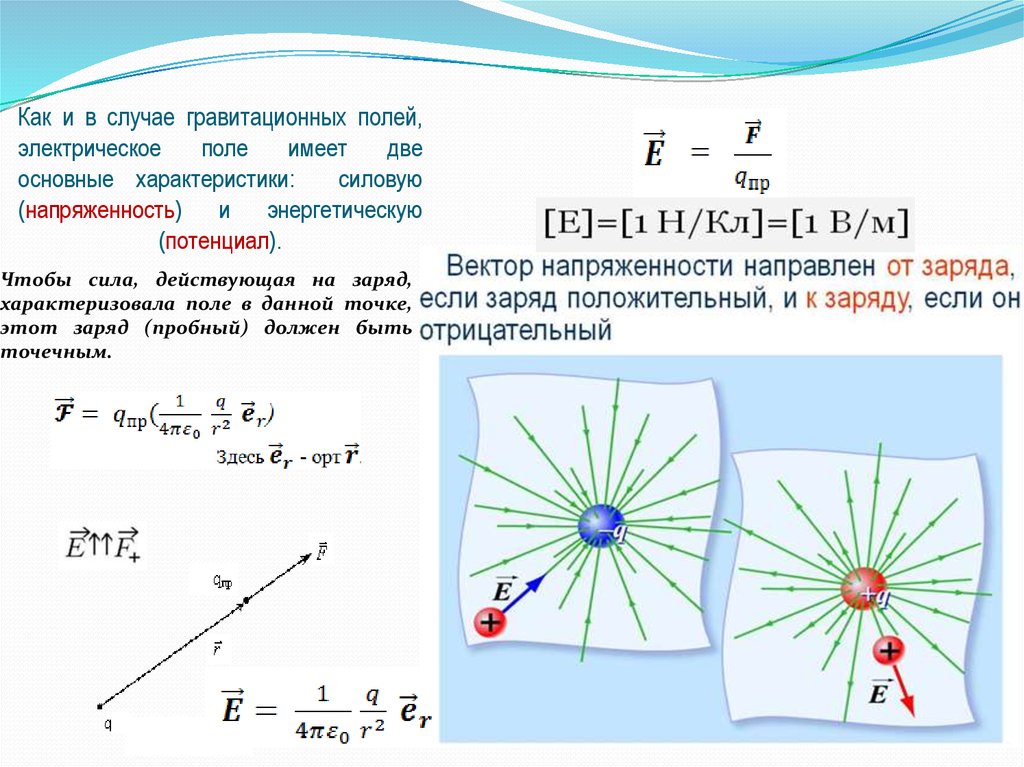

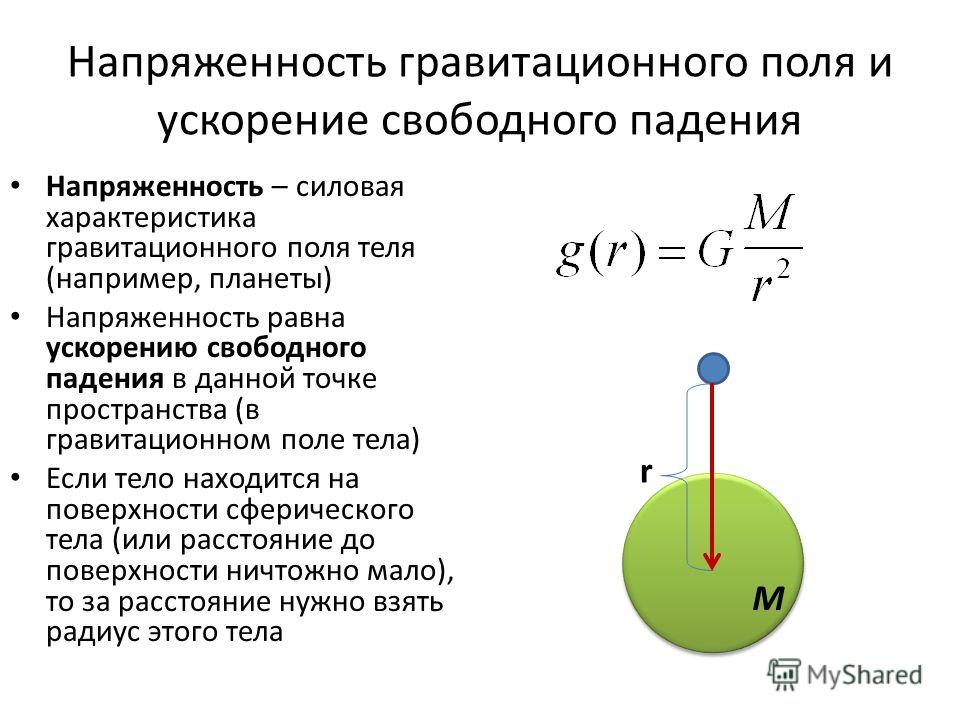 Вместе с другими доказательствами это привело Ньютона к предложению его универсального закона тяготения:
Вместе с другими доказательствами это привело Ньютона к предложению его универсального закона тяготения: 7: Потенциал
7: Потенциал 9: Работа, необходимая для сборки однородной сферы
9: Работа, необходимая для сборки однородной сферы phys.uvic.ca/~tatum/celmechs.html
phys.uvic.ca/~tatum/celmechs.html


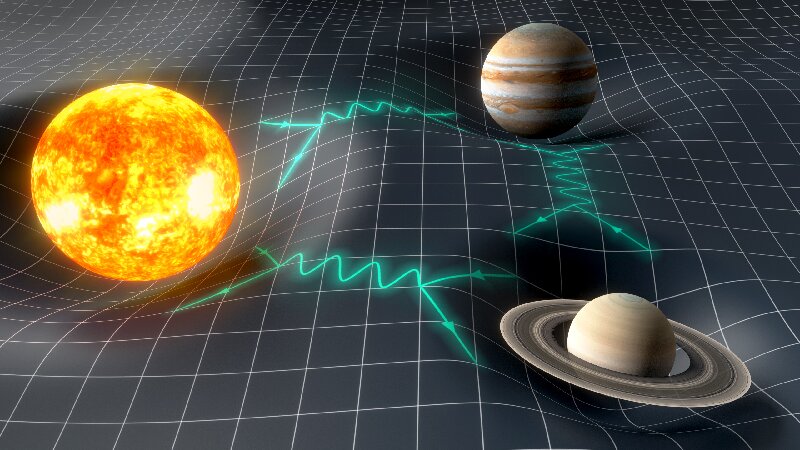 Лонд. А 372 , 20140029 (2014).
Лонд. А 372 , 20140029 (2014).