Векторное произведение. Геометрический смысл векторного произведения.
Тройка векторов , , (некомпланарных) называется правой, если она ориентирована по правилу правого винта.
Правило левого винта
Под векторным произведением двух векторов и понимается вектор = * , для которого:
1)Модуль равен площади параллелограмма, построенного на данных векторах, т.е. модуль = * *sinϕ, где ϕ угол между векторами
2)Вектор одновременно ⊥и и
3)если векторынеколлинеарны, то вектора , , образуют правую тройку векторов
Свойства векторного произведения:
1. * =- *
2. * =0
3.(λ )* =λ( * )= *(λ ), где λ-const
4.( + )* = * + *
5. // , если * =0
= + +
= + +
* =
* =
Из определения векторного произведения ,построенного на векторах и равна
Геометрический смысл векторного произведения:
По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки. Другими словами,
13. Смешанное произведение. Условие компланарности векторов.
Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .
Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Смешанное произведение векторов = {ax; ay; az}, = {bx; by; bz} и = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:
· [ х ] =
Свойства:
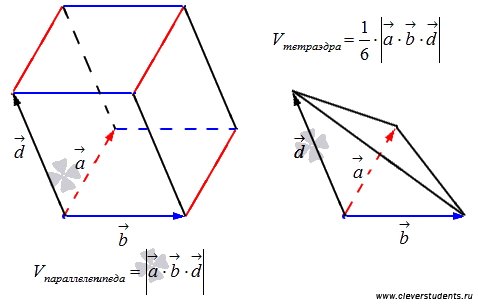
1)Геометр. смысл смешанного произведения. Модуль смешанного произведения 3х векторов вектора , и равен объёму параллелепипеда, образованного этими векторами:
Vпарал = · [ × ]
2) Геометрич.смысл смешанного произведения. Объем пирамиды образованной 3мя векторами , и равен 1/6 части от модуля смешанного произведения этих векторов:
Vпир = 1/6*| · [ × ]|
3) Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
4) · [ × ] = · ( · ) — · ( · )
5) · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ]
Условия компланарности векторов:
Для 3-х векторов:
Три вектора компланарны если их смешанное произведение равно нулю.
Для 3-х векторов:
Три вектора компланарны если они линейно зависимы.
Для n векторов:
Вектора компланарны если среди них не более двух линейно независимых векторов.
14. Прямая на плоскости. Виды уравнений прямой линии.Взаимное расположение прямых на плоскости.
Определение. Любая прямая на плоскости может быть задана уравнением 1 порядка: Ах + Ву + С = 0, (А ≠0, В ≠ 0). Это уравнение 1 порядка называется общим уравнением прям. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
1)Уравнение прямой по точке и вектору нормали:
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
2) Уравнение прямой, проходящая через 2 точки:
Пусть в пространстве заданы 2 точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой, проходящая через эти точки: X-X1/X2-X1=Y-Y1/Y2-Y1=Z-Z1/Z2-Z1. Если какой- либо из знаменателяравен0, следует приравнять 0 соответ. числитель. На плоскости записанное выше уравнение прямой упрощается: Y-Y1=Y2-Y1/X2-X1*(X-X1), если х
3)Уравнение прямой по точке и угловому коэффициенту:
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: Y=-A/B*X-C/B, и обозначить –A/B=k, -C/B=b, т.еy=kx+b, то полученное уравнение называется уравнением прямой с угловым коэффициентомk.
4)Уравнение прямой по точке и направляющему вектору:
по аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Опр.: Каждый ненулевой вектор ( α
5)Уравнение прямой в отрезках:
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: -A/C*X-B/C*Y=1 или x/a+y/b=1, где a= -C/A, b= -C/B. Геометрический смысл коэффициентов в том, что коэффициент аявляется координатой точки пересечения прямой с осью Ох, а b– координатой точки пересечения прямой с осью Оу.
6)Нормальное уравнение прямой: Если обе части уравнения Ах + Ву + С = 0 разделить на число µ= , которое называется нормирующем множителем
Взаимное расположение прямых на плоскости:
Возможны 3 варианта взаимного расположения прямой и плоскости:
1)Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.
2)Прямая пересекает плоскость, если она имеет с плоскостью ровно 1 общую точку.
3)Прямая лежит в плоскости, если каждая точка прямой принадлежит этой плоскости.
Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости. Важным частным случаем пересечения прямой и плоскости является их перпендикулярность.
Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Геометрические свойства векторного произведения
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
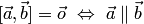 ,
в частности,
,
в частности, 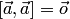 .
.
Первое
свойство следует из определения. Докажем
второе свойство. Равенство 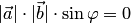 возможно
в трех случаях:
возможно
в трех случаях: 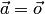
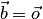 ,
или
,
или 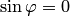 .
В каждом из этих случаев
векторы
.
В каждом из этих случаев
векторы 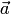 и
и 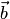 коллинеарны
(см. разд. 1.1).
коллинеарны
(см. разд. 1.1). Пример
1.19. Вычислить
площади параллелограмма и треугольника,
построенных на векторах 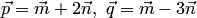 ,
где ,
угол между векторами
,
где ,
угол между векторами 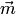
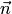 равен
равен 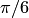 (рис.
1.44).
(рис.
1.44).Решение. Используя алгебраические свойства, найдем сначала векторное произведение
а затем его модуль .
По
первому геометрическому свойству
векторного произведения искомая площадь
параллелограмма равна 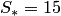 ,
а площадь треугольника в 2 раза меньше:
,
а площадь треугольника в 2 раза меньше: 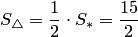 .
.
Выражение векторного произведения через координаты векторов
 .
Векторные произведения базисных векторов
находятся по определению:
.
Векторные произведения базисных векторов
находятся по определению:Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).
Найдем
выражение векторного произведения
через координаты множителей. Пусть в
стандартном базисе 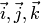 векторы
векторы 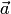 и имеют
координаты
и имеют
координаты 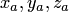 и
и 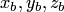 соответственно.
Тогда, используя линейность векторного
произведения по любому множителю (см.
пункт 2 замечаний 1.12) и формулы (1.14),
получаем
соответственно.
Тогда, используя линейность векторного
произведения по любому множителю (см.
пункт 2 замечаний 1.12) и формулы (1.14),
получаем
Запишем это равенство при помощи определителей второго порядка:
Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке
Формула вычисления векторного произведения
Теорема
1.8 (формула вычисления векторного
произведения). Если
векторы 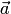 и
и 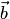 в
правом ортонормированием базисе
в
правом ортонормированием базисе 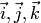 имеют
координаты
имеют
координаты 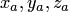 и
и 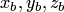 соответственно,
то векторное произведение этих векторов
находится по формуле (1.15), которую принято
записывать в виде
соответственно,
то векторное произведение этих векторов
находится по формуле (1.15), которую принято
записывать в виде
Если 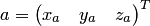 и
и 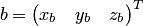 —
координатные столбцы векторов
—
координатные столбцы векторов 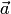 и
и 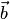 в
стандартном базисе, то координатный
столбец
в
стандартном базисе, то координатный
столбец 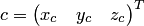 векторного
произведения
векторного
произведения 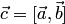 находится
по формуле
находится
по формуле
В самом деле, выполняя умножение матрицы на столбец, получаем
Тогда , что совпадает с (1.15).
Пример
1.20. Параллелограмм 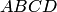 построен
на векторах (рис.
1.46). Найти:
построен
на векторах (рис.
1.46). Найти:
а)
векторные произведения 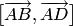 и
и 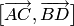 ;
б)
площадь параллелограмма
;
б)
площадь параллелограмма 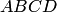 ;
в)
направляющие косинусы такого вектора
;
в)
направляющие косинусы такого вектора 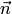 ,
перпендикулярного плоскости
параллелограмма
,
перпендикулярного плоскости
параллелограмма 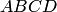 ,
,
для
которого тройка 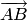 ,
, 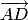 ,
, 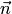 —
левая.
—
левая.
Решение. а)
Векторное произведение 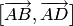 находим
по формуле (1.16):
находим
по формуле (1.16):
Для
нахождения векторного произведения
можно использовать матричную запись
формулы (1.15) (см. теорему 1.8).
Векторам 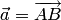 и
и 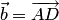 соответствуют
координатные столбцы
соответствуют
координатные столбцы 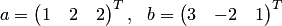 .
.
По
указанной формуле получаем координатный
столбец  вектора
вектора 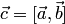 :
:
то
есть 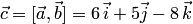 .
Результаты совпадают.
.
Результаты совпадают.
Векторное
произведение 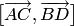 находим,
используя алгебраические свойства:
находим,
используя алгебраические свойства:
Следовательно, .
б)
Площадь параллелограмма 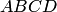 находим
как модуль векторного произведения
находим
как модуль векторного произведения 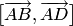 :
:
в)
Вектор, противоположный вектору 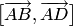 ,
удовлетворяет перечисленным в условии
требованиям, поэтому
,
удовлетворяет перечисленным в условии
требованиям, поэтому
Разделив
этот вектор на его длину 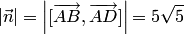 ,
получим единичныи вектор:
,
получим единичныи вектор:
Согласно его координатами служат направляющие косинусы
Мішаний добуток векторів, його властивості та геометричний зміст. Необхідна та достатня умова компланарності векторів. Обчислення мішаного добутку.
Геометрические свойства векторного произведения
1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
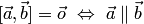 ,
в частности,
,
в частности, 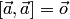 .
.
Первое
свойство следует из определения. Докажем
второе свойство. Равенство 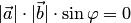 возможно
в трех случаях:
возможно
в трех случаях: 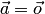 ,
или
,
или 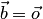 ,
или
,
или 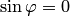 .
В каждом из этих случаев
векторы
.
В каждом из этих случаев
векторы 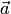 и
и 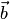 коллинеарны
(см. разд. 1.1).
коллинеарны
(см. разд. 1.1).
Пример
1.19. Вычислить
площади параллелограмма и треугольника,
построенных на векторах 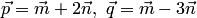 ,
где
,
где 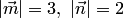 ,
угол между векторами
,
угол между векторами 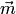 и
и 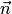 равен
равен 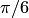 (рис.
1.44).
(рис.
1.44).
Решение. Используя алгебраические свойства, найдем сначала векторное произведение
а затем его модуль .
По
первому геометрическому свойству
векторного произведения искомая площадь
параллелограмма равна 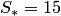 ,
а площадь треугольника в 2 раза меньше:
,
а площадь треугольника в 2 раза меньше: 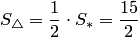 .
.
Выражение векторного произведения через координаты векторов
Пусть
в пространстве задан ортонормированный
(стандартный) базис 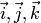 .
Векторные произведения базисных векторов
находятся по определению:
.
Векторные произведения базисных векторов
находятся по определению:
Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).
Найдем
выражение векторного произведения
через координаты множителей. Пусть в
стандартном базисе 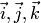 векторы
векторы 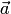 и
и 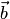 имеют
координаты
имеют
координаты 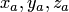 и
и 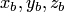 соответственно.
Тогда, используя линейность векторного
произведения по любому множителю (см.
пункт 2 замечаний 1.12) и формулы (1.14),
получаем
соответственно.
Тогда, используя линейность векторного
произведения по любому множителю (см.
пункт 2 замечаний 1.12) и формулы (1.14),
получаем
Запишем это равенство при помощи определителей второго порядка:
Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке
Формула вычисления векторного произведения
Теорема
1.8 (формула вычисления векторного
произведения). Если
векторы 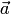 и
и 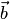 в
правом ортонормированием базисе
в
правом ортонормированием базисе 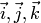 имеют
координаты
имеют
координаты 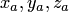 и
и 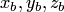 соответственно,
то векторное произведение этих векторов
находится по формуле (1.15), которую принято
записывать в виде
соответственно,
то векторное произведение этих векторов
находится по формуле (1.15), которую принято
записывать в виде
Если 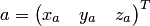 и
и 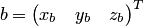 —
координатные столбцы векторов
—
координатные столбцы векторов 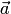 и
и 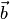 в
стандартном базисе, то координатный
столбец
в
стандартном базисе, то координатный
столбец 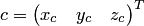 векторного
произведения
векторного
произведения 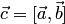 находится
по формуле
находится
по формуле
В самом деле, выполняя умножение матрицы на столбец, получаем
Тогда , что совпадает с (1.15).
Пример
1.20. Параллелограмм 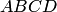 построен
на векторах (рис.
1.46). Найти:
построен
на векторах (рис.
1.46). Найти:
а)
векторные произведения 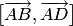 и
и 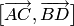 ;
б)
площадь параллелограмма
;
б)
площадь параллелограмма 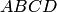 ;
в)
направляющие косинусы такого вектора
;
в)
направляющие косинусы такого вектора 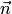 ,
перпендикулярного плоскости
параллелограмма
,
перпендикулярного плоскости
параллелограмма 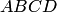 ,
,
для
которого тройка 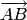 ,
, 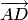 ,
, 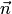 —
левая.
—
левая.
Решение. а)
Векторное произведение 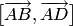 находим
по формуле (1.16):
находим
по формуле (1.16):
Для
нахождения векторного произведения
можно использовать матричную запись
формулы (1.15) (см. теорему 1.8).
Векторам 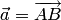 и
и 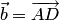 соответствуют
координатные столбцы
соответствуют
координатные столбцы 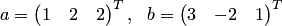 .
.
По
указанной формуле получаем координатный
столбец  вектора
вектора 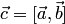 :
:
то
есть 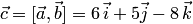 .
Результаты совпадают.
.
Результаты совпадают.
Векторное
произведение 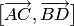 находим,
используя алгебраические свойства:
находим,
используя алгебраические свойства:
Следовательно, .
б)
Площадь параллелограмма 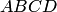 находим
как модуль векторного произведения
находим
как модуль векторного произведения 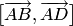 :
:
в)
Вектор, противоположный вектору 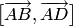 ,
удовлетворяет перечисленным в условии
требованиям, поэтому
,
удовлетворяет перечисленным в условии
требованиям, поэтому
Разделив
этот вектор на его длину 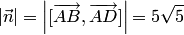 ,
получим единичныи вектор:
,
получим единичныи вектор:
Согласно его координатами служат направляющие косинусы
Мішаний добуток векторів, його властивості та геометричний зміст. Необхідна та достатня умова компланарності векторів. Обчислення мішаного добутку.
Геометрический смысл смешанного произведения.
Выясним
геометрический смысл смешанного
произведения векторов  и
и 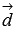 .
.
Отложим
векторы  и
и 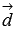 от
одной точки и построим параллелепипед
на этих векторах как на сторонах.
от
одной точки и построим параллелепипед
на этих векторах как на сторонах.
Обозначим 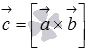 .
В этом случае смешанное произведение
можно записать как
.
В этом случае смешанное произведение
можно записать как 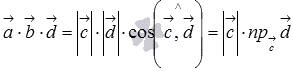 ,
где
,
где 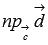 — числовая
проекция вектора
— числовая
проекция вектора 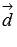 на
направление вектора
на
направление вектора 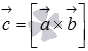 .
.
Абсолютная
величина числовой проекции 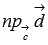 равна
высоте параллелепипеда, построенного
на векторах
равна
высоте параллелепипеда, построенного
на векторах  и
и 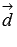 ,
так как вектор
,
так как вектор 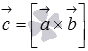 перпендикулярен
и вектору
перпендикулярен
и вектору 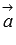 и
вектору
и
вектору  по
определению векторного произведения.
А в разделе геометрический
смысл векторного произведения мы
выяснили, что величина
по
определению векторного произведения.
А в разделе геометрический
смысл векторного произведения мы
выяснили, что величина 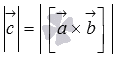 представляет
собой площадь параллелограмма,
построенного на векторах
представляет
собой площадь параллелограмма,
построенного на векторах 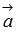 и
и 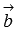 .
Таким образом, модуль смешанного
произведения
.
Таким образом, модуль смешанного
произведения 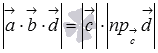 —
это произведение площади основания на
высоту параллелепипеда, построенного
на векторах
—
это произведение площади основания на
высоту параллелепипеда, построенного
на векторах  и
и 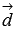 .
.
Следовательно, абсолютная
величина смешанного произведения
векторов представляет собой объем
параллелепипеда:  .
В этом заключается геометрический смысл
смешанного произведения векторов.
.
В этом заключается геометрический смысл
смешанного произведения векторов.
Объем
тетраэдра, построенного на векторах  и
и 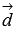 ,
равен одной шестой объема соответствующего
параллелепипеда, таким образом,
,
равен одной шестой объема соответствующего
параллелепипеда, таким образом,  .
.
Рассмотрим решения нескольких примеров.
Пример.
Вычислите
объем параллелепипеда, построенного
на векторах 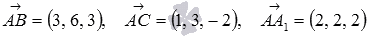 ,
заданных в прямоугольной системе
координат.
,
заданных в прямоугольной системе
координат.
Решение.
Искомый
объем параллелепипеда равен абсолютной
величине смешанного произведения
заданный векторов. Находим смешанное
произведение: 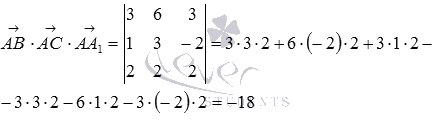
Тогда, 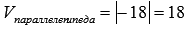 .
.
Ответ:
.
Пример.
В
прямоугольной декартовой системе
координат даны четыре точки 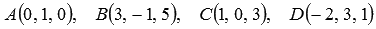 .
Найдите объем тетраэдра АВСD.
.
Найдите объем тетраэдра АВСD.
Решение.
Объем
тетраэдра АВСD мы
можем вычислить с использованием
смешанного произведения векторов по
формуле 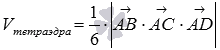 .
.
Найдем координаты
векторов по координатам точек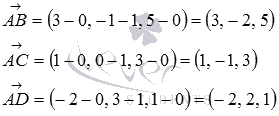
Вычисляем
смешанное произведение 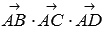 по
координатам векторов:
по
координатам векторов: 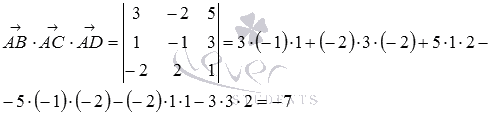
Таким
образом, искомый объем тетраэдра равен 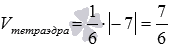 .
.
Ответ:
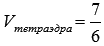 .
.
Необходимое и достаточное условие компланарности трех векторов.
Напомним определение компланарных векторов.
Определение.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Два
вектора 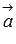 и
и 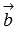 трехмерного
пространства всегда компланарны. Это
утверждение легко доказать. Пусть a и b –
прямые, на которых лежат
векторы
трехмерного
пространства всегда компланарны. Это
утверждение легко доказать. Пусть a и b –
прямые, на которых лежат
векторы 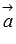 и
и 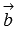 соответственно.
Проведем через начало вектора
соответственно.
Проведем через начало вектора 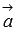 прямую b1,
параллельную прямой b,
а через начало вектора
прямую b1,
параллельную прямой b,
а через начало вектора 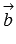 прямуюa1,
праллельную прямой a.
Плоскости, образуемые прямыми a и b1,
а так же прямыми b и a1,
параллельны по построению, а
векторы
прямуюa1,
праллельную прямой a.
Плоскости, образуемые прямыми a и b1,
а так же прямыми b и a1,
параллельны по построению, а
векторы 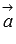 и
и 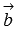 принадлежат
им. Следовательно, векторы
принадлежат
им. Следовательно, векторы 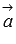 и
и 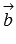 компланарны.
компланарны.
А как же определить, являются ли три вектора компланарными?
Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.
Теорема.
Для
компланарности трех векторов 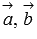 и
и 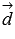 трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
Доказательство.
Пусть 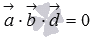 ,
докажем что векторы
,
докажем что векторы 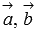 и
и 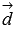 компланарны.
компланарны.
Так
как 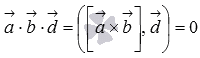 ,
то векторы
,
то векторы 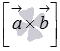 и
и 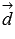 перпендикулярны
в силу необходимого и достаточного условия
перпендикулярности двух векторов. С
другой стороны, по определению
векторного произведения вектор
перпендикулярны
в силу необходимого и достаточного условия
перпендикулярности двух векторов. С
другой стороны, по определению
векторного произведения вектор 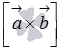 перпендикулярен
и вектору
перпендикулярен
и вектору 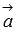 и
вектору
и
вектору 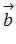 .
Следовательно, векторы
.
Следовательно, векторы 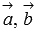 и
и 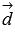 компланарны,
так как перпендикулярны одному вектору
компланарны,
так как перпендикулярны одному вектору 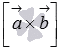 .
.
Пусть
теперь векторы 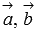 и
и 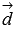 компланарны,
докажем равенство нулю смешанного
произведения
компланарны,
докажем равенство нулю смешанного
произведения 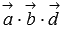 .
.
Так
как векторы 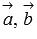 и
и 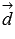 компланарны,
то вектор
компланарны,
то вектор 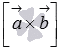 перпендикулярен
каждому из них, следовательно, скалярное
произведение вектора
перпендикулярен
каждому из них, следовательно, скалярное
произведение вектора 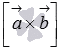 на
на 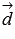 равно
нулю, что означает равенство нулю
смешанного произведения
равно
нулю, что означает равенство нулю
смешанного произведения 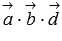 .
.
Итак, теорема полностью доказана.
Покажем применение доказанного условия компланарности трех векторов к решению задач.
Пример.
Компланарны
ли векторы 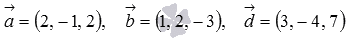 ,
заданные в прямоугольной системе
координат.
,
заданные в прямоугольной системе
координат.
Решение.
Вычислим
их смешанное произведение по координатам: 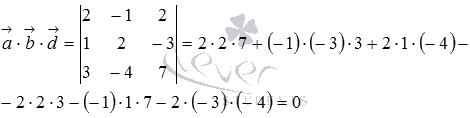
Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.
Ответ:
векторы компланарны.
Необходимое
и достаточное условие компланарности
векторов можно использовать для проверки
принадлежности четырех точек
пространства А,
В, С и D одной
плоскости. Для этого находим координаты
векторов  и
вычисляем их смешанное произведение.
Если оно равно нулю, то точки лежат в
одной плоскости, в противном случае –
не лежат в одной плоскости.
и
вычисляем их смешанное произведение.
Если оно равно нулю, то точки лежат в
одной плоскости, в противном случае –
не лежат в одной плоскости.
Пример.
Принадлежат
ли точки  одной
плоскости?
одной
плоскости?
Решение.
Найдем
координаты векторов  (при
необходимости смотрите статьюнахождение
координат вектора по координатам точек
его начала и конца):
(при
необходимости смотрите статьюнахождение
координат вектора по координатам точек
его начала и конца):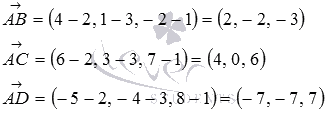
Теперь
вычисляем смешанное произведение этих
векторов 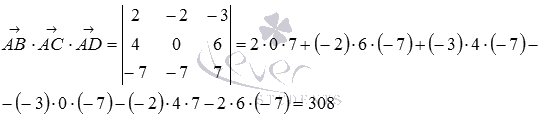
Так
как смешанное произведение векторов
отлично от нуля, то векторы  не
компланарны, следовательно, точки А,
В, С и D не
лежат в одной плоскости.
не
компланарны, следовательно, точки А,
В, С и D не
лежат в одной плоскости.
Ответ:
не принадлежат.
К началу страницы
Рівняння поверхні у просторі. Різні рівняння площин: загальне, неповні рівняння площин, у відрізках, рівняння площини, що проходить через три задані точки, нормальне рівняння площини.

