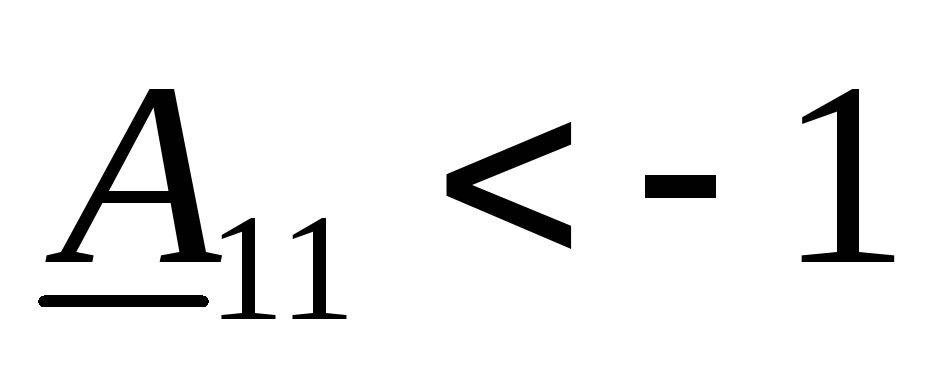Полосовые фильтры
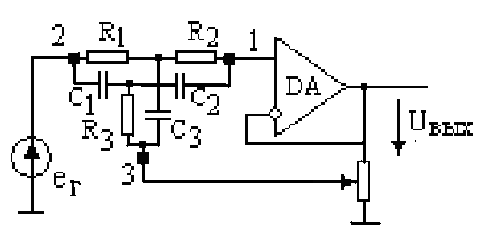
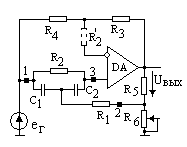
При создании активных полосовых (Рис. 7.1) фильтров (пропускающих (ПП) и заграждающих (ПЗ)) в качестве цепи ОС используют частотно-зависимые цепи, имеющие на определенной частоте максимум, либо минимум пропускания. Это и создает изменение глубины ОС с частотой и формирует полосовую АЧХ усилителя. Наиболее часто в качестве частотно-зависимого звена ОС используют такие цепи, как Т-мост, мост Вина, 2Т-мост (см. табл.7.1).
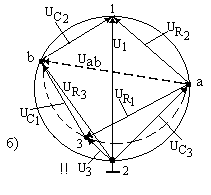
Расмотрим ПФ с симметричным 2Т-мостом (табл.7.3, строка 1). Для такого моста (табл. 7.1, строка 2) в идеальном случае должны соблюдаться условия:
R1=R2=R, R3=R/2, C1=C2=C, C3=2C.
Коэффициент передачи моста по напряжению между точками 1-3 (точка 2 заземлена) описывается выражением
К1-3= u3/u1= jx / (4+jx),
а между точками 2-3 (точка 1 заземлена) – выражением
К2-3 = u3/u2 = 4 / (4+jx).
Здесь x = (w/w0 – w0/w) является относительной расстройкой.
Если использовать параметр Р=jw/w0, то
К1-3 = (Р2+1) / (Р2+4Р+1), и К2-3 = 4P / (P2+4P+1).
Как видно, цепь ОС является фильтром II порядка. На частоте w = w0= = 1/RC при включении точками 1-3 фильтр имеет минимум пропускания (К1-3= 0).
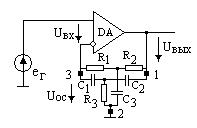
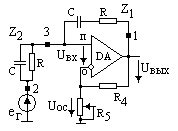
В схеме АФ 2Т-мост точками 1, 3 включается в качестве цепи ООС. Источник сигнала подключается к неинвертирующему входу ОУ (табл. 7.3, сх. № 1). Возможно включение источника сигнала в точку 2 моста. В последнем случае требуется малое выходное сопротивление источника сигнала.
Поскольку на частоте w0 отрицательная ОС отсутствует (КОС = К1-3= 0), то усилитель на данной частоте имеет максимальный коэффициент усиления
Расчет АЧХ проводим при тех же условиях, что и ранее. Поскольку ООС последовательная, то можно записать
еГ = uВХ + uОС = uВЫХ / KU0 + uВЫХK
После преобразований получаем
КU = КU0 / (1+ jx KU0 / (4+jx)) , или
KU = (KU0 / (1+KU0)) · ((P2+4P+1) / (P2+(1/QP) P+1)).
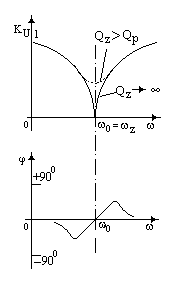
Эти две записи эквивалентны. Как видно, АФ является фильтром второго порядка, имеет два комплексно-сопряженных корня (полюса) в знаменателе. Их собственная частота и добротность соответственно равны
w0=1/RC
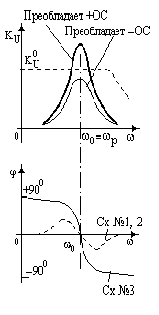
Имеются два действительных корня в числителе (нули), которые определяют частоты перегибов АЧХ. Численной подстановкой Р=jw/w0 можно вычислить модуль | КU |(w) и построить АЧХ фильтра, либо j(w) – построить ФЧХ фильтра. Активный фильтр имеет КU= КU0 при w= w0 = = 1/RC, а при w®0 или w®¥ – КU ®1. Вид АЧХ (ФЧХ) АФ приведен в Табл.7.3.
Важным параметром полосового фильтра является его полоса пропускания (Пd = wВ
 ) и полоса обозначается как П
) и полоса обозначается как П .
По аналогии с LC цепями фильтр принято характеризовать
добротностью
.
По аналогии с LC цепями фильтр принято характеризовать
добротностью Q = w0 / П ,
,
что позволяет определять полосу пропускания фильтра. Математически добротность фильтра оценивается по величине коэффициента перед членом
2Т-мост
критичен к подбору своих элементов.
Отклонение в номиналах резисторов и
конденсаторов от идеала приводит к
неполному подавлению сигнала на частоте
w0.
Это можно показать в первом приближении,
анализируя мост с использованием
круговых диаграмм (рис. 7.2). Вектор
выходного напряжения в точке 3 моста
конечен и может принимать различное
положение. На частоте w
|
|
Рис. 7.2. а – 2Т-мост; б – векторная диаграмма моста | |
Подбором резистора R3 в определенных пределах удается компенсировать
Таблица 7.3
АЧХ и ФЧХ полосовых пропускающих фильтров
№ сх
Фильтр
Схема активного фильтра
Передаточная характеристика
АЧХ и ФЧХ фильтров
1
2Т-мост
ПФ-ПП



Мост Вина
ПФ-ПП


3
Т-мост
ПФ-ПП


Принято: p=j, P=j/0 ; Ku оу =KU0, r вх оу, r вых оу 0.
Окончание таблицы 7.3
АЧХ и ФЧХ полосовых заграждающих фильтров
№ сх
Фильтр
Схема фильтра
Передаточная характеристика
АЧХ и ФЧХ фильтров
4
2Т — мост
ПФ-ПЗ



5
Мост Вина
ПФ-ПЗ


6
Т-мост
ПФ-ПЗ


Принято: p=j, P=j/0 ; Ku оу =KU0, r вх оу, r вых оу 0.
разбаланс моста. При R3>R/2 на выходе моста формируется сигнал противофазный входному и возможно возникновение положительной обратной связи. При R3<R/2 преобладает отрицательная обратная связь. Регулируя R3, можно изменять КU(w) и добротность всего ПФ. Надо иметь в виду, что при изменении резисторов (и емкостей) моста изменяется его частота резонанса w0. При значительной положительной ОС в схеме возникают гармонические колебания на частоте близкой к w0. Усилитель превратится в генератор!!!
На основе 2Т-моста можно построить полосовой заграждающий АФ-ПЗ-фильтр – режектор для частот в окрестности w0 (табл. 7.3, сх. № 4). Схема фильтра построена на усилителе с КU~ 1. 2Т-мост включен последовательно в цепь сигнала и на частоте w0 имеет нулевой коэффициент передачи сигнала. Коэффициент передачи такого АФ определяется уравнением
Т = К (P2+1) / (P2+(1/QP) P+1).
Видно, что добротность корня числителя (нуля) равна бесконечности. Варьируя положение (g) движка резистора R, мы изменяем глубину положительной ОС и таким образом изменяем добротность полюса. Это определяет глубину подавления сигнала на частоте w0 и узость полосы режекции. Вид АЧХ представлен в табл. 7.3. Реально (в зависимости от настройки) удается ослабить сигнал на частоте w0 приблизительно на 40 дБ.
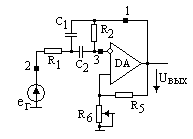
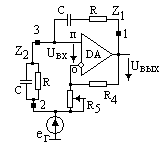
Рассмотрим активный ПФ на основе моста Вина (табл.7.3, сх. № 2). В схеме ПФ-ПП усилителя частотно-зависимое плечо моста Вина включено в цепь положительной ОС. Данная цепь является слабо избирательной и имеет коэффициент передачи (табл.7.1, сх.№ 3)
К1-3 = КОС = 1 / (3+jx), или КОС= P / (P2+3P+1).
На частоте w0 = 1/RC цепь положительной ОС имеет максимум КОС=1/3 при фазовом сдвиге равном нулю, т.е. на этой частоте мост проявляет себя как чисто омический делитель.
Во избежание генерации усилитель имеет цепь последовательной отрицательной ОС (ООС) – второе плечо моста Вина, коэффициент передачи которой (КООС=R2 / (R1+R2)) не зависит от частоты в рабочем диапазоне частот. На частоте настройки w0 глубина отрицательной ОС выбирается равной глубине положительной ОС, и усиление АФ максимально. При отклонении частоты сигнала, как в область нижних, так и верхних частот, глубина положительной ОС уменьшается, и в схеме преобладает отрицательная ОС, что ведет к уменьшению коэффициента передачи усилителя. Так формируется АЧХ полосового фильтра (табл. 7.3).
Расчет уравнения АЧХ фильтра проводится так же, и с теми же предположениями, что и в предыдущих случаях. Записываются условия на
входе усилителя:
(eГ – jп) / Z2 = (jп – uВЫХ) / Z1,
jо = uВЫХR2 / (R1 +R2),
jп – jо = uВХ = uВЫХ / KU0 ,
где Z1 =R +1/pC, Z2 = R / (1+pCR).
Решение системы уравнений с подстановкой P=jw/w0 дает
КU = uВЫХ / eГ= (KU0/ (1+KU0KООС)) (P2+2P+1) / (P2+(3 – K) P+1),
где K = KU0KООС/ (1+KU0KООС).
Как видно, АФ – полосовой усилитель. Он имеет два комплексно-сопряженных корня (полюса) с собственной частотой w0 = 1/RC и два действительных корня – (нуля). Добротность полюса, а следовательно, и ПФ (QP = 1/(3–К)) зависит от величины К, т.е. от глубины ООС. Если КООС= 1/3 и КU0 КООС> 1, то QP = КU0 / 9, КU(w0) = 2КU0/3.
Если К 3, то усилитель превращается в генератор колебаний близких к гармоническим на частоте w0. В таком качестве схема весьма популярна как генератор, частоту колебаний которого легко перестраивать в значительных пределах, изменяя одновременно и в одинаковых пределах величины резисторов R, либо конденсаторов C.
Заграждающий АФ – полосовой фильтр на основе моста Вина можно осуществить по схеме (табл. 7.3, сх. № 5). Сигнал (eГ – uВЫХ) подается одновременно на оба плеча моста – частотно-зависимое и частотно-независимое. Коэффициент передачи частотно-зависимого плеча от точки 2 к точке 3 (K2-3) имеет неярко выраженный минимум K2-3 = 2/3 на частоте резонанса w0 при фазовом сдвиге равном нулю (см. табл. 7.1). Можно подобрать частотно-независимый делитель R4–R5 (см. табл. 7.3, сх. № 5) так, что на частоте w0 на инвертирующий и неинвертирующий входы операционного усилителя будут приходить сигналы равные по амплитуде и по фазе. Результирующий сигнал на выходе усилителя будет существенно ослаблен (КUсинф !) и стремится к нулю.
При отклонении частоты от резонанса сигнал на неинвертирующем входе ОУ будет возрастать по сравнению с сигналом на инвертирующем входе. Это вызовет увеличение напряжения на выходе ОУ. Благодаря действию положительной ОС слабо выраженный минимум исходной АЧХ моста Вина превращается в достаточно узкий минимум АЧХ всего АФ.
Математическое описание АФ-ПЗ представлено в табл. 7.3, а способ решения аналогичен ранее примененному. Данный фильтр является фильтром II порядка с бесконечной добротностью нуля. Реальное ослабление сигнала достигает 40 дБ.
Для построения полосовых фильтров очень часто используют Т-мост (табл. 7.1, cх. № 4), при этом удобно выбирать С1 = С2. На частоте w0 = = 1/(R1R2C1C2)0.5 мост имеет максимум коэффициента передачи сигнала К2-3 = u3/u2, одновременно К1-3 = u3/u1 на этой частоте имеет минимум. При организации АФ-ПП (табл. 7.3, сх. № 3) Т-мост точками 1, 3 включается в цепь отрицательной обратной связи, в точку 2 включен источник сигнала. В цепи положительной обратной связи используется частотно-независимое звено – делитель R5–R6. Варьируя глубину положительной ОС с помощью делителя R5–R6 можно изменять коэффициент усиления АФ и его добротность. АФ с Т-мостом является фильтром II порядка. Его АЧХ представлена в табл. 7.3.
Заграждающий полосовой фильтр на основе Т-моста (см. табл. 7.3, сх. № 6) строят по аналогии с ПЗ активным фильтром на основе моста Вина путем подачи сигнала через частотно-зависимое и частотно-независимое плечи на неинвертирующий и инвертирующий входы ОУ. На частоте резонанса w0 сигналы на обоих входах ОУ идентичны, что и приводит к существенному ослаблению сигнала на выходе усилителя. Ослабление может достигать 40 дБ. Варьируя с помощью делителя R5–R6 глубину положительной обратной связи, можно изменять ширину полосы заграждения и степень подавления сигнала. Фильтр является фильтром II порядка, его уравнение приведено в табл. 7.3.
Классификация фильтров по виду их амплитудно-частотных характеристик
 Рассмотрим основные типы фильтров, классифицируемых по виду амплитудно-частотных характеристик.
Рассмотрим основные типы фильтров, классифицируемых по виду амплитудно-частотных характеристик.
Фильтры нижних частот.
Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются.
Приведем примеры амплитудно-частотных характеристик фильтров нижних частот. На рис. 2.52, а показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров. 
Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ωс. Обычно частоту среза определяют как частоту, на которой величина А(ω) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3 дБ).
Полоса задерживания (подавления) начинается от частоты задерживания ωз и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(ω) меньше максимального значения на 40 дБ (т. е. меньше в 100 раз).
Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная полоса отсутствует.
Фильтры верхних частот.
Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.
Частотные характеристики фильтров верхних частот, как и характеристики фильтров нижних частот, многообразны в своих деталях.
Изобразим для иллюстрации две характеристики: идеальную, нереализуемую (рис. 2.53, а), и одну из типичных реальных (рис. 2.53, б). Через ωс и ωз обозначены частоты среза и задерживания. 
Полосовые фильтры (полосно-пропускающие).
Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.
Изобразим амплитудно-частотную характеристику для идеального (нереализуемого) фильтра (рис. 2.54, а) и одну из типичных реальных характеристик (рис. 2.54, б). 
Через ωс1 и ωс2 обозначены две частоты среза, ω0 — средняя частота. Она определяется выражением
ω0 = √ (ωс1 · ωс2)
Режекторные фильтры (полосно-заграждающие).
Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами. Изобразим амплитудно-частотную характеристику для идеального (нереализуемого) фильтра (рис. 2.55, а) и одну из типичных реальных характеристик (рис. 2.55, б). 
Всепропускающие фильтры (фазовые корректоры).
Эти фильтры пропускают сигналы любой частоты. Построим соответствующую амплитудно-частотную характеристику (рис. 2.56). 
Такие фильтры используются в некоторой электронной системе для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы.
Исходя из приведенного математического описания фильтров, нетрудно сделать вывод, что ход амплитудно-частотной характеристики на достаточном удалении от полосы пропускания прямо определяется порядком фильтра. Этот факт хорошо иллюстрируют амплитудно-частотные характеристики, выполненные в логарифмическом масштабе. Рассмотрим указанные характеристики для некоторых фильтров различного порядка, имеющих одинаковые коэффициенты усиления на нулевой частоте, равные 100 (рис. 2.57). 
Из математического описания следует, что на достаточном расстоянии от полосы пропускания наклон характеристики равен − 20n дБ/дек, где
n
— порядок фильтра. Наклон − 20 дБ/дек означает, что увеличение частоты в 10 раз приводит к уменьшению коэффициента усиления в 10 раз, а наклон − 40 дБ/дек означает, что увеличение частоты в 10 раз приводит к уменьшению коэффициента усиления в 100 раз.
Из изложенного следует, что если необходимо обеспечить более быстрое изменение коэффициента усиления на удалении от полосы пропускания, то следует увеличить порядок фильтра (но при этом схема фильтра усложняется).
1.2. Частотные параметры полосовых фильтров
Чаще всего объектом измерения АЧХ являются частотно-избира-тельные цепи и устройства, в частности фильтры. Определим их частотные параметры на примере полосовых фильтров (ПФ), исследуемых в данной работе.
На рис. 1.2 представлены типичные частотные характеристики полосовых фильтров: АЧХ (а) и затухание (б). Основными частотными параметрами реального ПФ являются:
Коэффициент передачи по напряжению K(f)=UВЫХ/UВХ.
Коэффициент передачи является функцией частоты. Его значение, соответствующее максимуму АЧХ, обозначают K0:
K(f)/K0, Дб

 1
1

 0
0


3
f0
 2
2

f0.1
 20
20


fН fВ f
а

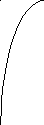


 d,
Дб f0.1
d,
Дб f0.1
20
f0
 3
3
 0
0
fН fВf
б
Рис. 1.2. Частотные характеристики полосовых фильтров:
а АЧХ идеального (1) и реального (2) ПФ;
б частотная характеристика затухания фильтра.
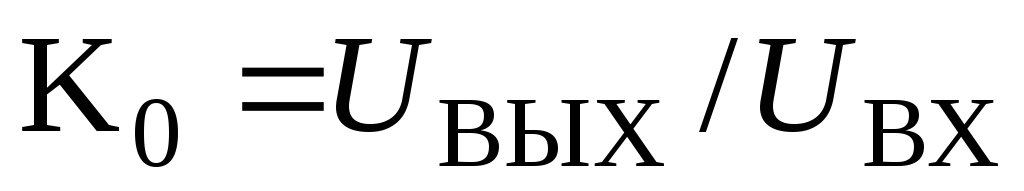 ,
, 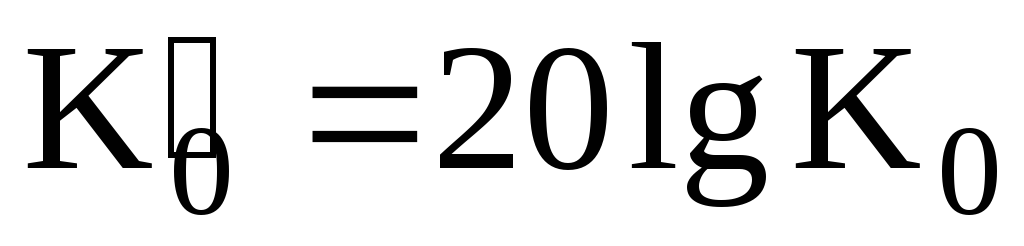 ,
(1.1)
,
(1.1)
где 
значение K0,
выраженное в децибелах.
значение K0,
выраженное в децибелах.
2) Коэффициент затухания D(f) =
1/K(f)
и минимальный коэффициент затухания D0 = 1/K0.
Обычно при исследовании фильтров строят
зависимость d(f) =
K0/K(f),
представляющую собой “перевернутую”
АЧХ (рис. 1.2, б).
Выраженное в децибелах значение 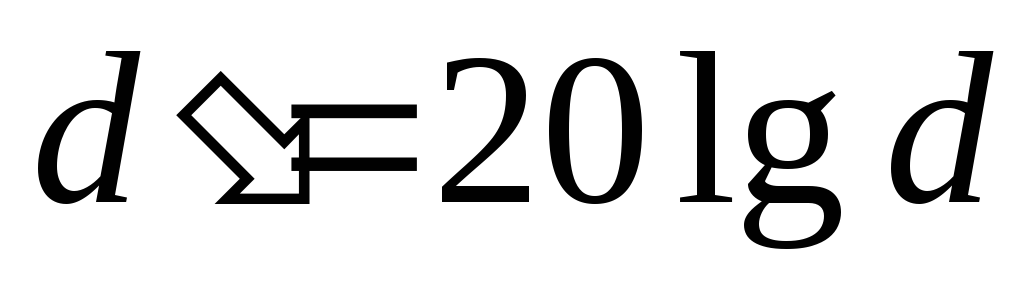 называют затуханием передачи, а его
зависимость от частоты
частотной характеристикой затухания
фильтра. Частоту, на которой D=D0,
называют частотой
минимального затухания.
называют затуханием передачи, а его
зависимость от частоты
частотной характеристикой затухания
фильтра. Частоту, на которой D=D0,
называют частотой
минимального затухания.
3) Полоса пропускания f полоса частот, в которой затухание передачи не превышает заданного значения. Ширину полосы пропускания, измеренную по уровню 3 дБ (K(f)/K0 = 0,707), обозначают f0. Нижняя и верхняя частоты среза фильтра fН и fВ соответствуют границам полосы пропускания.
4) Коэффициент прямоугольности отношение ширины полосы пропускания, измеренной по одному заданному уровню d1, к ширине полосы пропускания, измеренной по другому уровню d2. Обычно уровни d1и d2 принимаются равными 20 и 3 дБ, что соответствует значениям K(f)/K0, равным 0,1 и 0,707 соответственно. Тогда коэффициент прямоугольности
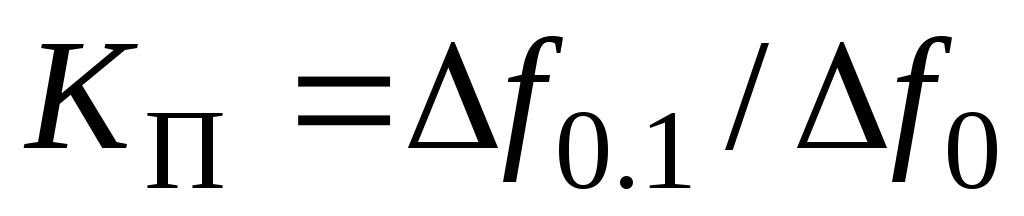 .
(1.2)
.
(1.2)
Коэффициент прямоугольности показывает степень приближения АЧХ реального фильтра к АЧХ идеального.
5) Крутизна скатов АЧХ за пределами полосы пропускания SАЧХ=d[d(f)]/df . Этот параметр позволяет оценить степень подавления мешающего сигнала в зависимости от его удаленности по частоте от границ полосы пропускания фильтра в случаях, когда закон убывания АЧХ от расстройки является монотонным. На практике измеряют усредненное значение SАЧХ = d(f)/f, вычисленное как модуль отношения разности некоторых выбранных значений затухания d1 и d2 (например, 10 и 20 дБ) к разности соответствующих им частот [f(d1) f(d2)] и выраженное в дБ/кГц:
SАЧХ
СР =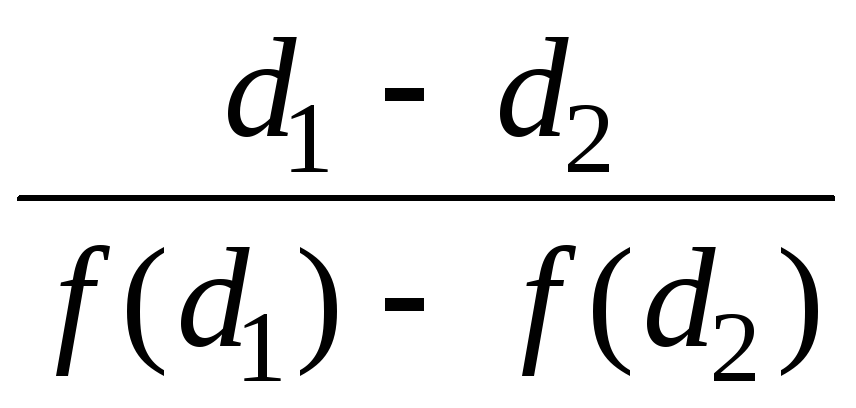 .
(1.3)
.
(1.3)
Удобнее пользоваться значениямиSАЧХ СР, выраженными в дБ/окт или в дБ/дек. Октавой (или декадой) называют частотный интервал, соответствующий двукратной (или десятикратной) частотной расстройке fd= f(d) f0, где f0 частота минимального затухания фильтра; f(d) частота, соответствующая выбранному затуханию d. Тогда:
SАЧХ
СР [дБ/окт]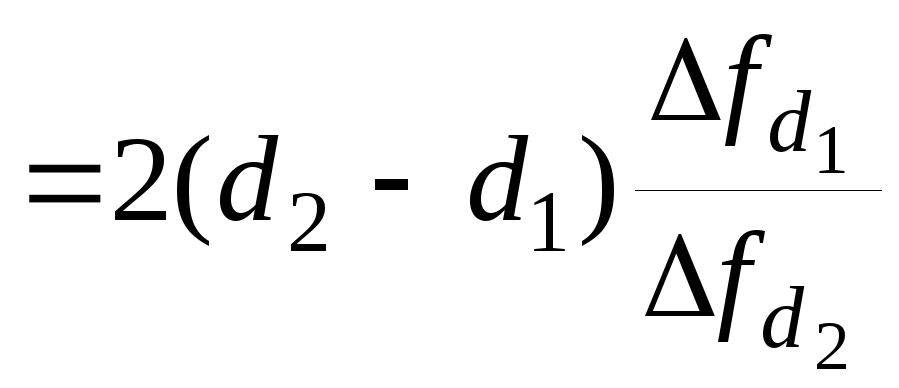 ,
(1.4)
,
(1.4)
SАЧХ
СР [дБ/дек]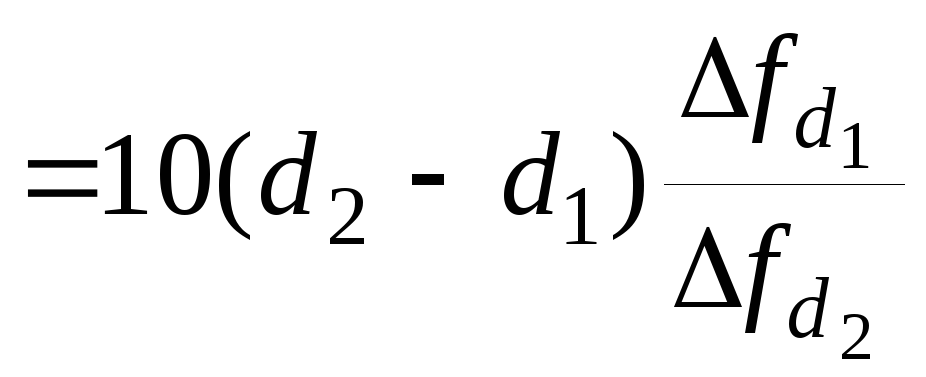 .
(1.5)
.
(1.5)
Примером полосового фильтра является одиночный колебательный контур. Его АЧХ существенно отличается от АЧХ идеального ПФ, однако ввиду своей простоты колебательный контур широко применяется в качестве частотно-избирательной цепи.
Классификация фильтров по виду их амплитудно-частотных характеристик
Фильтры нижних частот. Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются. На рис. 12.1,а показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров.
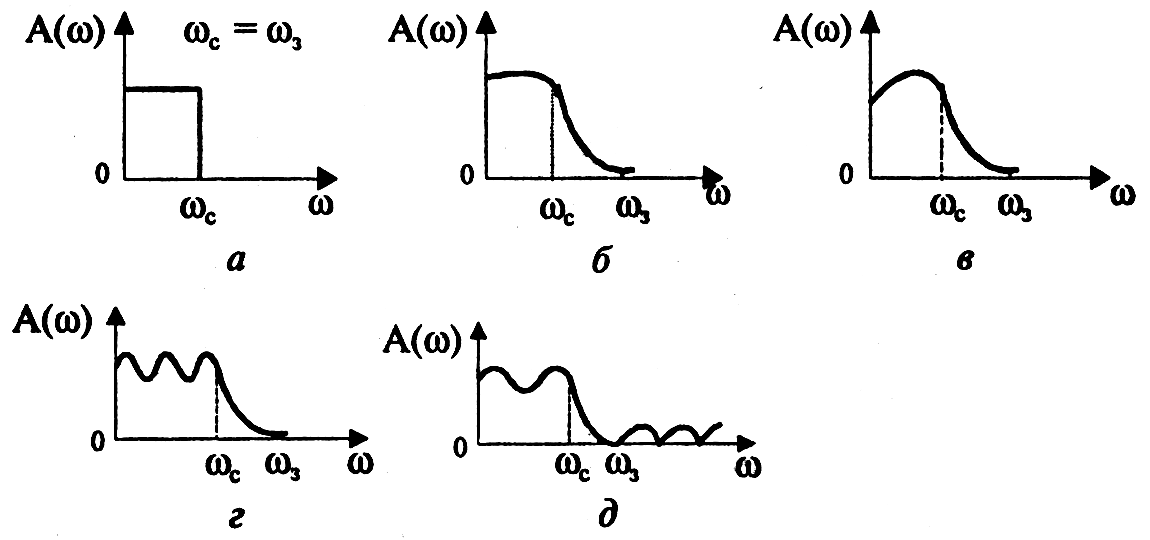
Рис. 12.1.Амплитудно-частотные характеристики
фильтров нижних частот
Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ωс. Обычно частоту среза определяют как частоту, на которой величина А(ω) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3 дБ).
Полоса задерживания (подавления) начинается от частоты задерживания ωз и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(ω) меньше максимального значения на 40 дБ (т. е. меньше в 100 раз).
Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная частота отсутствует.
Фильтры верхних частот. Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.
На рис. 12.2,а приведена идеальная (нереализуемая) амплитудно-частотная характеристика фильтра нижних частот, а на рис. 12.2,б – одна из типичных реальных. Через ωс и ωз обозначены частоты среза и задерживания.
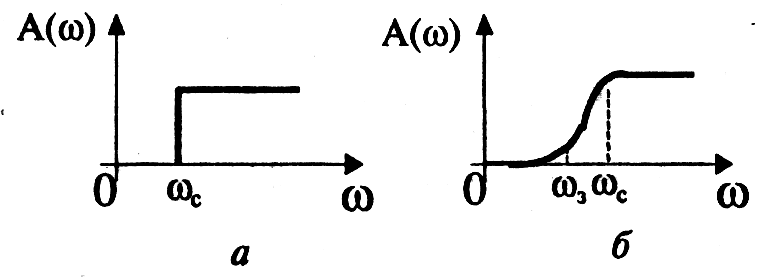
Рис. 12.2. Амплитудно-частотные характеристики
фильтров верхних частот
Полосовые фильтры (полосно-пропускающие). Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.
На рис. 12.3,а приведена амплитудно-частотная характеристика идеального (нереализуемого) фильтра и одна из типичных реальных характеристик (рис. 12.3,б). Через ωс1 и ωс2 обозначены две частоты среза, ω0 – средняя частота. Она определяется выражением
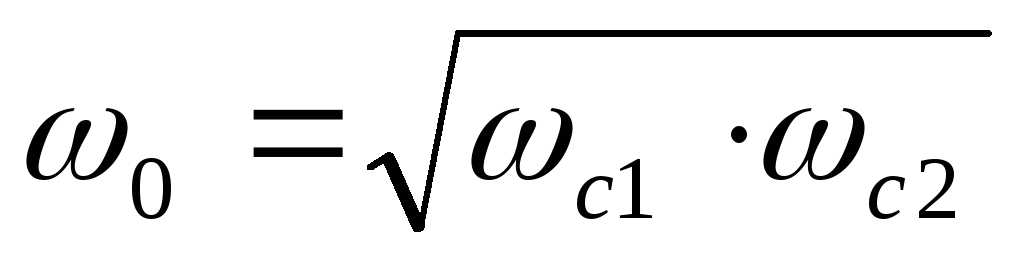 .
.
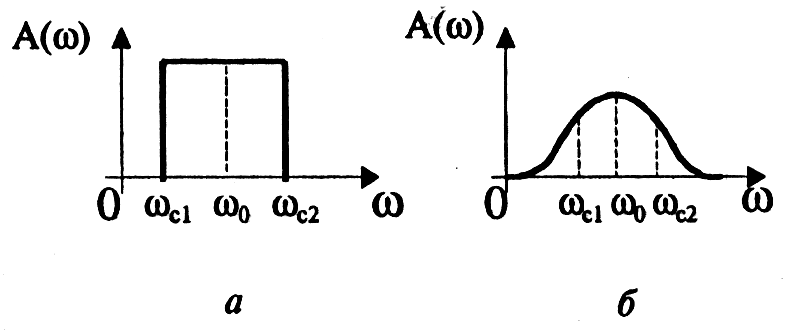
Рис. 12.3. Амплитудно-частотные характеристики полосового фильтра
а-идеальная характеристика; б-реальная характеристика
Режекторные фильтры (полосно-заграждающие). Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами.
Амплитудно-частотная характеристика идеального (нереализуемого) фильтра приведена на рис. 12.4,а. На рис. 12.4,б показана одна из типичных реальных характеристик.
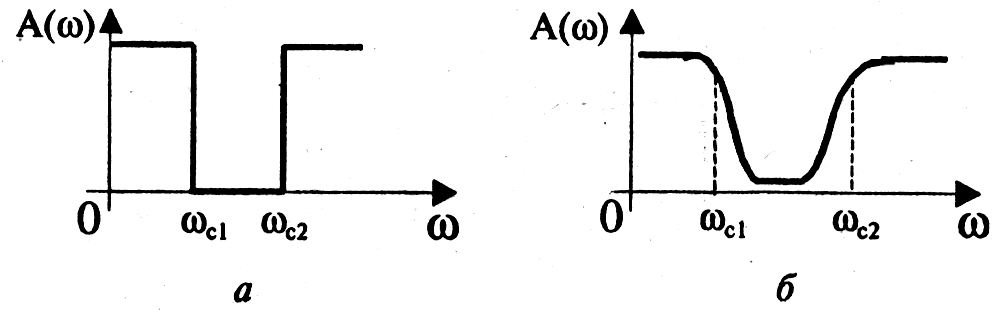
Рис. 12.4. Амплитудно-частотные характеристики
режекторного фильтра
Всепропускающие фильтры (фазовые корректоры). Эти фильтры пропускают сигналы любой частоты. Такие фильтры используются в некоторых электронных системах для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы (рис. 12.5).
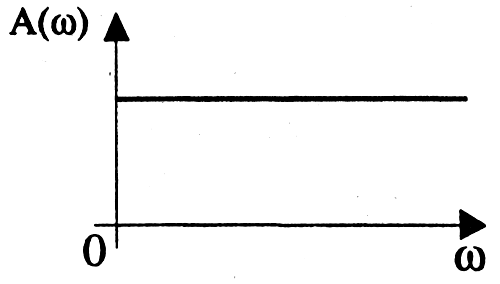
Рис. 12.5. Амплитудно-частотная характеристика
всепропускающего фильтра
6.5. Исследование влияния разброса параметров элементов на ачх активного полосового фильтра (пф)
6.5.1 Определение рабочего диапазона частот схемы активного пф
С помощью программы EWBполучим АЧХ ПФ (рис. 6.22) и определим нижнюю и верхнюю граничные частоты диапазона по уровню 0,707 от максимального значения АЧХ. Это соответствует спаду усиления на -3дБ. Максимальный коэффициент передачи в полосе частот рабочего диапазона равен 32,35 дБ.
Вычтем 3дБ и определим нижнюю и верхнюю частоты рабочего диапазона частот ПФ по пересечению уровня 29,35 дБ с линией АЧХ: fн=15,75 Гц;fв=16,23 Гц.
Таким образом, рабочий диапазон частот активного ПФ составляет 15,75…16,23 Гц.
Зная частоту, при которой коэффициент передачи в полосе частот фильтра максимален и равен 32,35 дБ (f0=15,94 Гц), и рабочий диапазон частот ПФ, можно определить добротностьQ полосового фильтра по формуле:
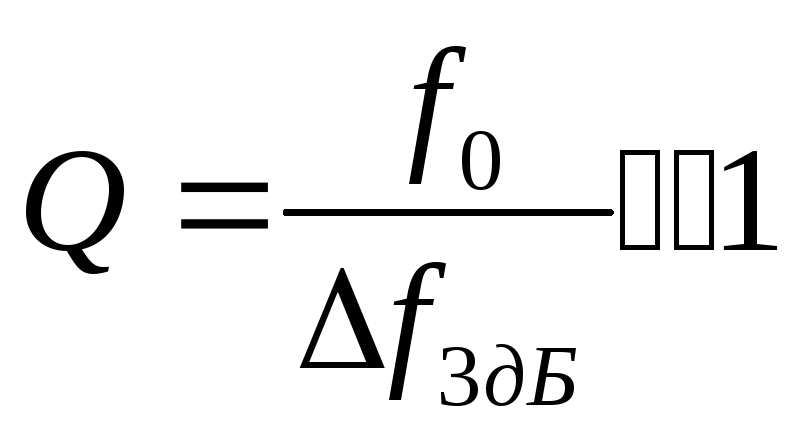 (6.4)
(6.4)
где f0=15,93 Гц – значение частоты, при которой коэффициент передачи равен 32,35 дБ;
Δf3дБ – разность нижней и верхней границ рабочего частотного диапазона ПФ по уровню 0,707.
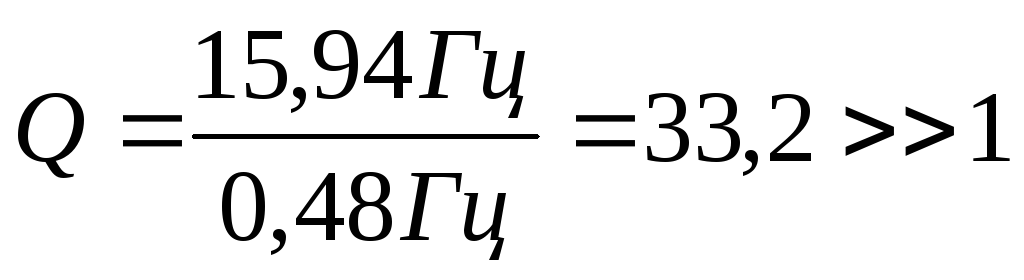 (6.5)
(6.5)

6.5.2. Исследование чувствительности активного пф к общему 20% разбросу параметров всех элементов схемы
С помощью программы EWBпроведено исследование, результаты которого представлены на рис.6.23. По графику АЧХ (рис. 3.23) определяем изменение коэффициента передачи, которое в результате разброса параметров всех элементов схемы составляет 22,1 дБ. Разброс параметров сильно повлиял и на значения нижней и верхней границ рабочего диапазона ПФ.
3.5.3. Исследование чувствительности активного пф к 20% разбросу параметров отдельных элементов схемы
С помощью программы EWBпроведено исследование, результаты которого приведены на рис. 6.24, 6.25, 6.26. По графикам АЧХ (рис. 6.24, 6.25, 6.26) определяем изменение коэффициента передачи в результате разброса сопротивленияR2(изменение составило 10,89 дБ), сопротивленияR2– 23,68 дБ.
Разброс емкости C1привел к значительному изменению нижней границы полосы пропускания ПФ. Остальные элементы слабо влияют на АЧХ ПФ, таким образом, выявлены элементы, к которым схема ПФ наиболее чувствительна (R2,R2,C1).
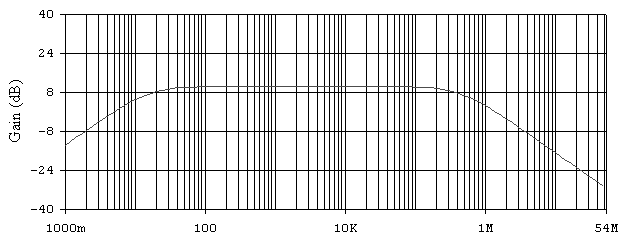
Рис. 6.2. АЧХ не инвертирующего усилителя.
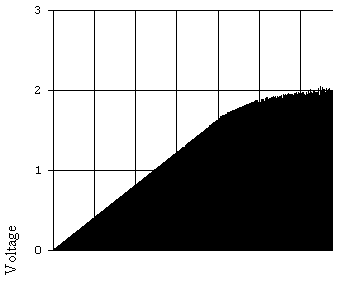
Рис. 6.3. Амплитудная характеристика не инвертирующего усилителя.
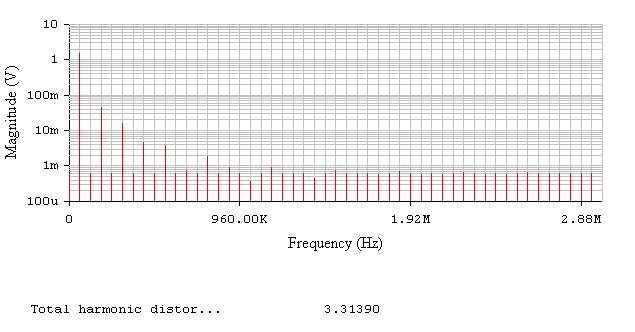
Рис. 6.4. Спектр сигнала. Нелинейные искажения.
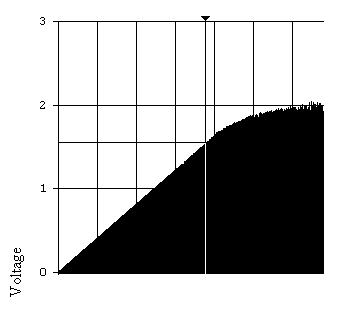
Рис. 6.5. Амплитудная характеристика не инвертирующего усилителя с рабочей точкой U=1,5В, где нелинейные искажения не превышают 3%.
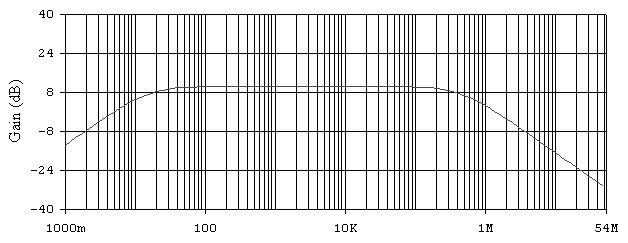
Рис. 6.6. АЧХ не инвертирующего усилителя при Rос = 5.1 кОм.
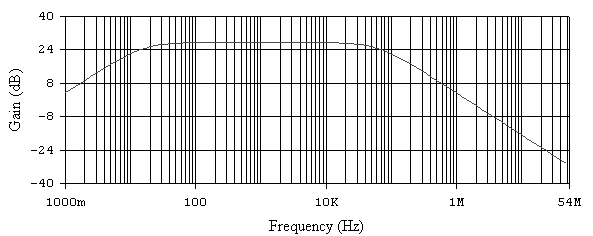
Рис. 6.7. АЧХ не инвертирующего усилителя при Rос= 50 кОм.
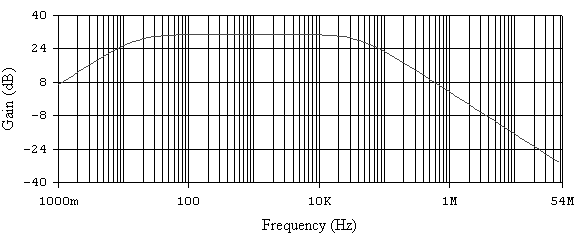
Рис. 6.8. АЧХ не инвертирующего усилителя при Rос= 75 кОм.
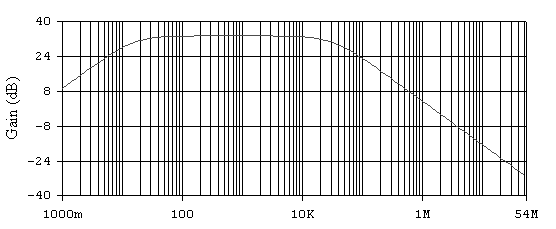
Рис. 6.9. АЧХ не инвертирующего усилителя при Rос = 100 кОм.
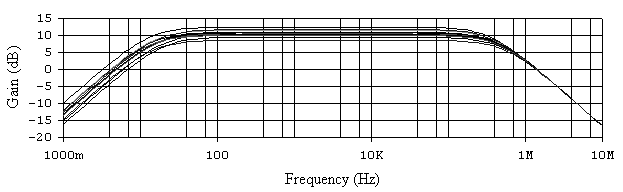
Рис. 6.10. АЧХ не инвертирующего усилителя при общем 20% разбросе
параметров всех элементов схемы
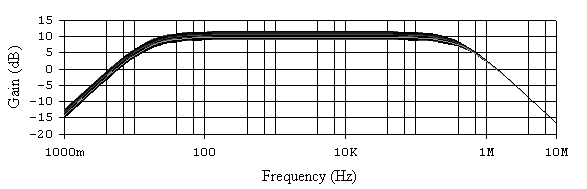
Рис. 6.11. АЧХ не инвертирующего усилителя при 20% разбросе RОС.
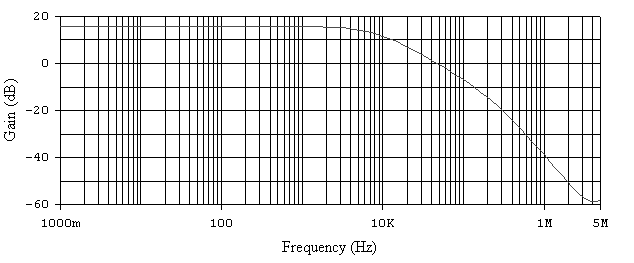
Рис. 6.12. АЧХ активного ФНЧ.
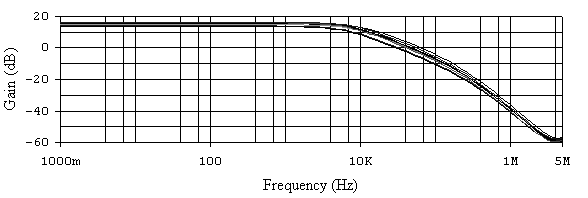
Рис. 6.13. АЧХ активного ФНЧ при общем 20% разбросе параметров
всех элементов схемы
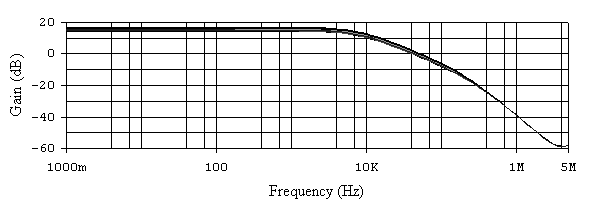
Рис. 6.14. АЧХ активного ФНЧ при 20% разбросе сопротивления R2.
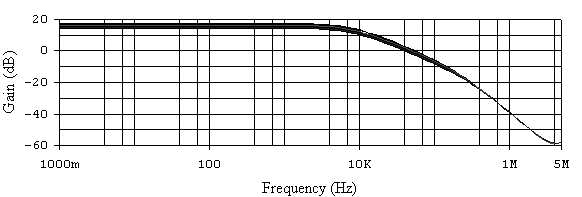
Рис. 6.15. АЧХ активного ФНЧ при 20% разбросе сопротивления R1.
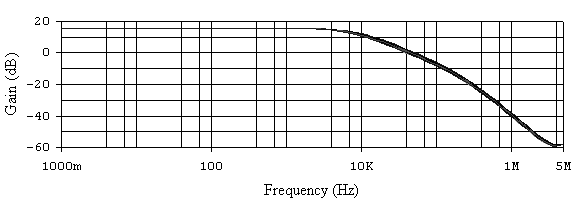
Рис. 6.16. АЧХ активного ФНЧ при 20% разбросе емкости С2.
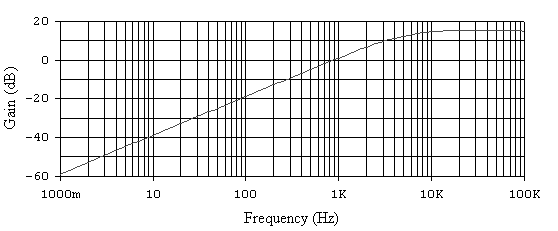
Рис. 6.17. АЧХ активного ФВЧ.
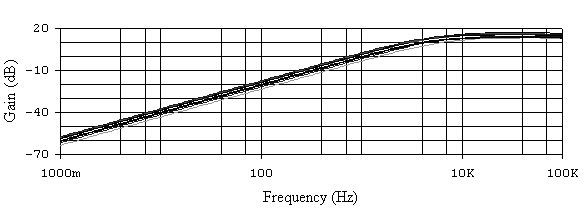
Рис. 6.18. АЧХ активного ФВЧ при 20% разбросе параметров
всех элементов схемы.
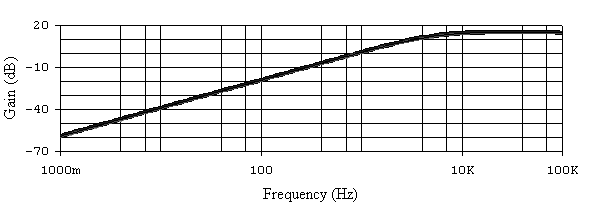
Рис.6.19. АЧХ активного ФВЧ при 20% разбросе сопротивления R2.
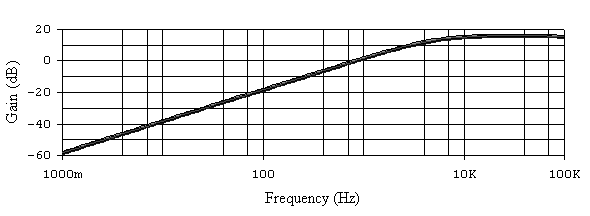
Рис. 6.20. АЧХ активного ФВЧ при 20% разбросе сопротивления R1.
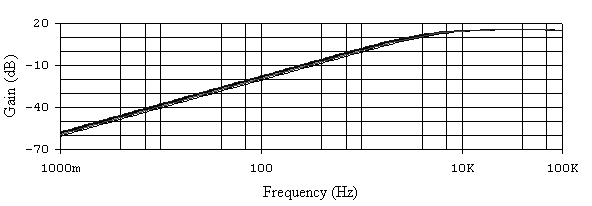
Рис. 6.21. АЧХ активного ФВЧ при 20% разбросе сопротивления R4.
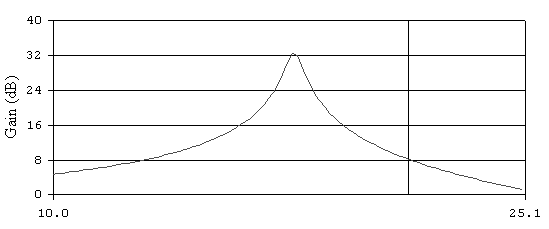
Рис. 6..22. АЧХ активного ПФ.
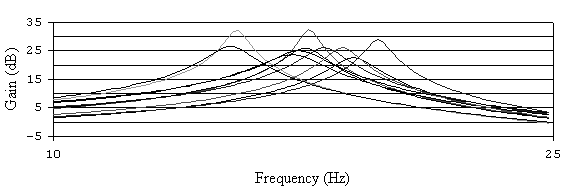
Рис. 6.23. АЧХ активного ПФ при 20% разбросе параметров
всех элементов схемы
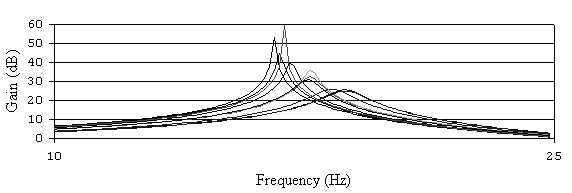
Рис. 6.24. АЧХ активного ПФ при 20% разбросе сопротивления R2.
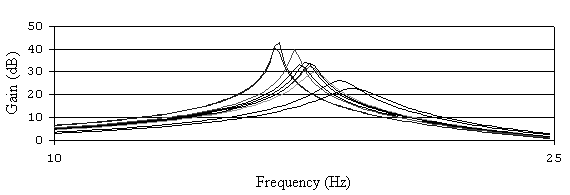
Рис. 6..25. АЧХ активного ПФ при 20% разбросе сопротивления R1.
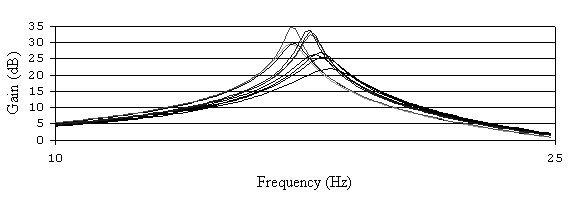
Рис. 6.26. АЧХ активного полосового фильтра при 20% разбросе емкости C1.
4. Частотные характеристики фильтров
Электрические фильтры имеют следующие частотные характеристики:
Частотная характеристика затухания (ЧХЗ) – зависимость коэффициента затухания о частоты:
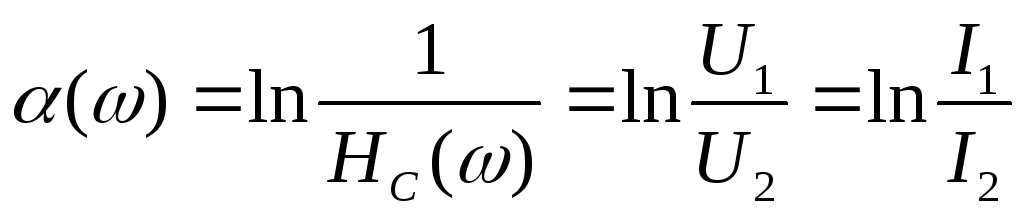 (9.10)
(9.10)
Частотная характеристика фазы (ЧХФ) – зависимость коэффициента фазы от частоты.
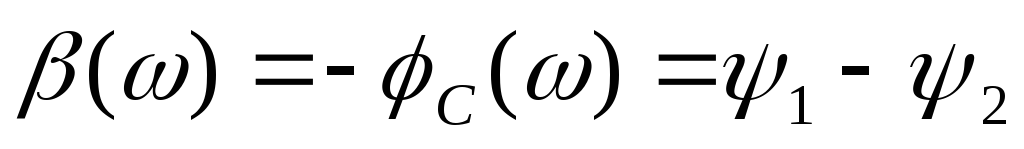 ,
(9.11)
,
(9.11)
где 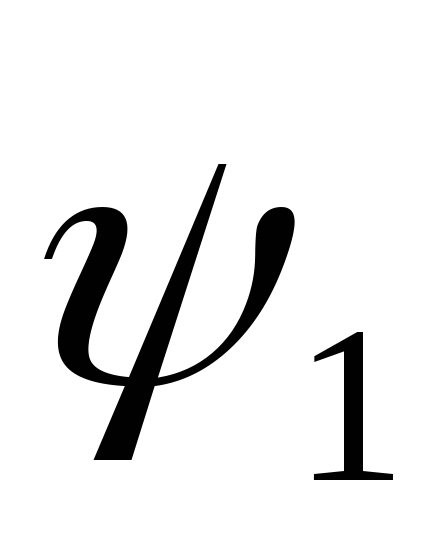 и
и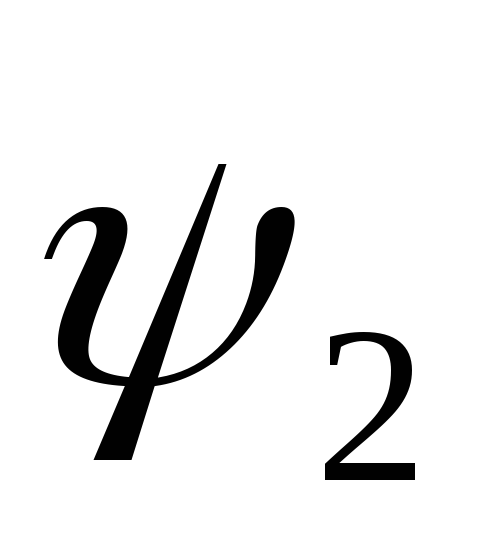 — фазы напряжения (тока) на входе и выходе
фильтра.
— фазы напряжения (тока) на входе и выходе
фильтра.
Напомним, что соотношения (9.10) и (9.11) получены на основании физического смысла меры передачи Г четырехполюсника:
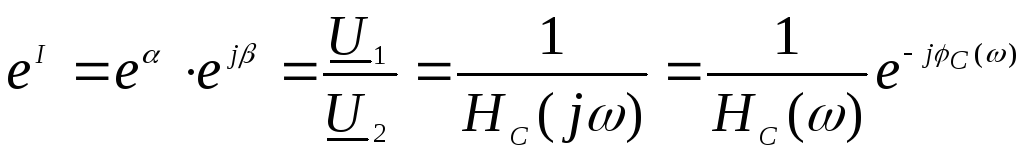 , (9.12)
, (9.12)
где 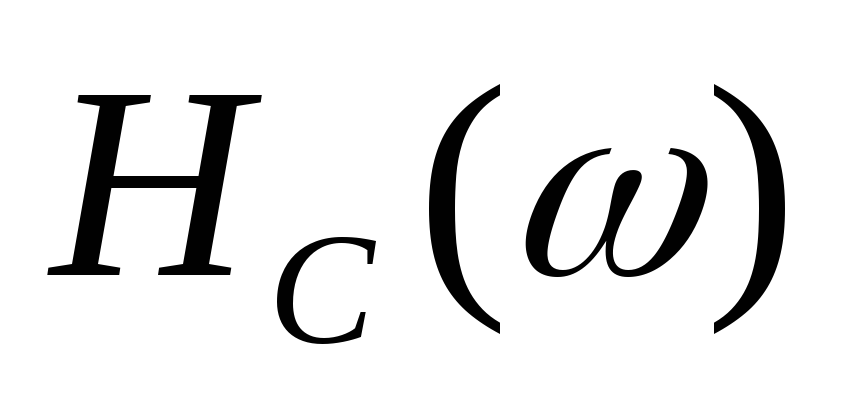 и
и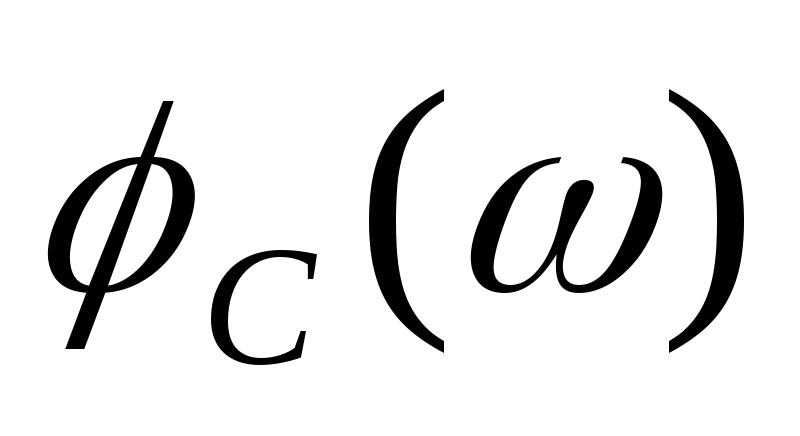 —
АЧХ и ФЧХ симметричного фильтра
—
АЧХ и ФЧХ симметричного фильтра
Для Т-образного и П-образного фильтров мера передачи выражается следующим образом:
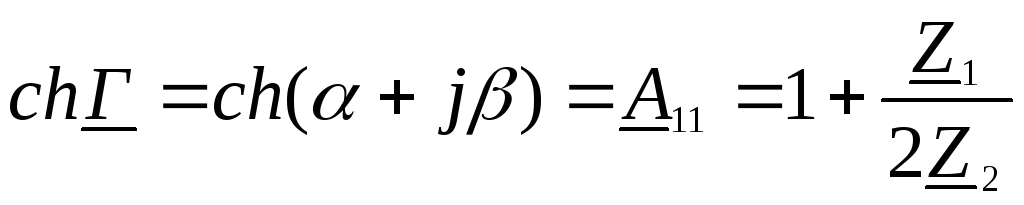 (9.13)
(9.13)
Гиперболический косинус комплексного числа можно выразить через гиперболические и тригонометрические функции:
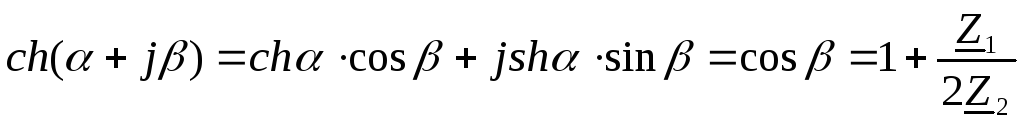
отношение мнимых
величин  и
и – число вещественное, следовательно
сумма
– число вещественное, следовательно
сумма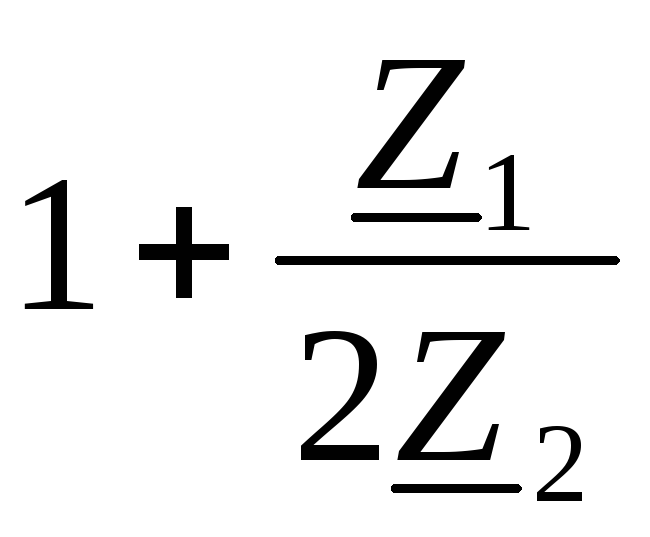 не имеет мнимой составляющей, т.е.
не имеет мнимой составляющей, т.е. 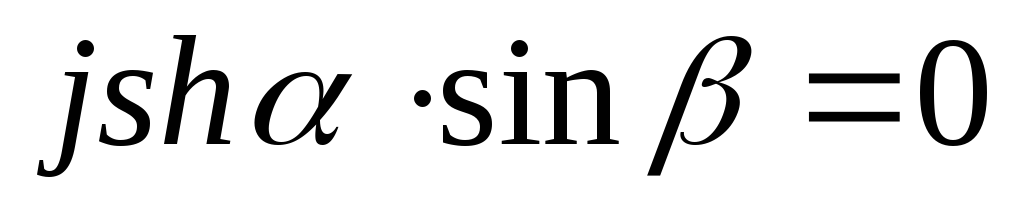 .
Тогда в полосе затухания (при
.
Тогда в полосе затухания (при 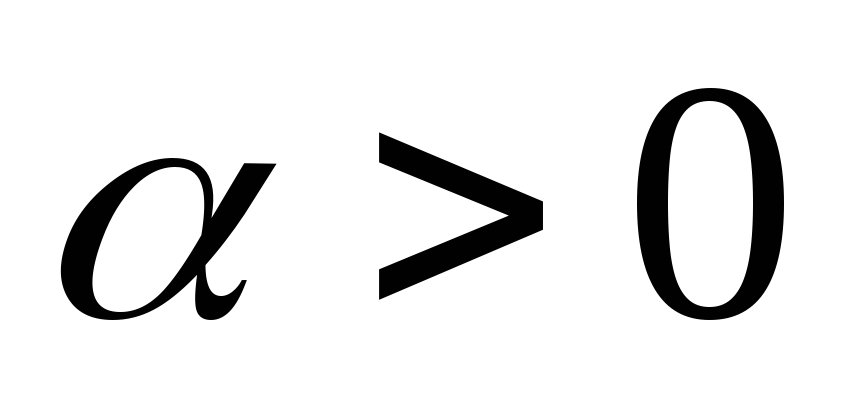 )
) 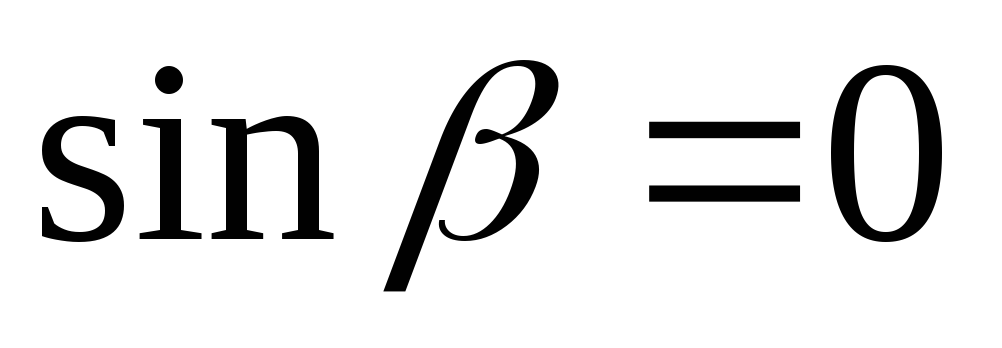 ,
т.е.
,
т.е.  равен 0 или
равен 0 или .
.
Окончательное выражение для ЧХЗ в полосе затухания:
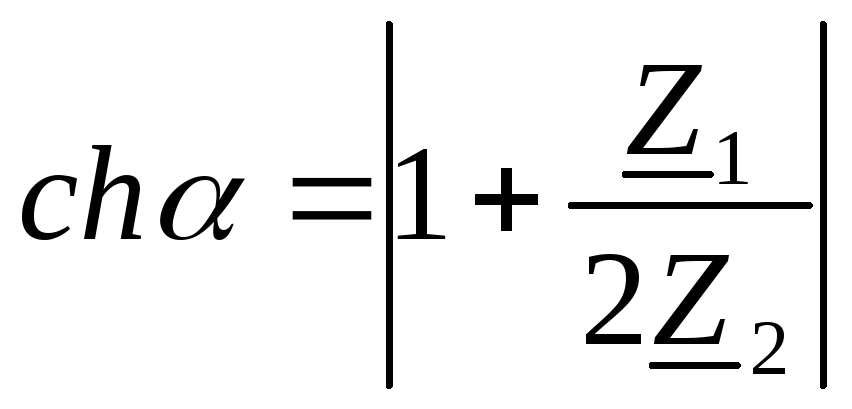
или
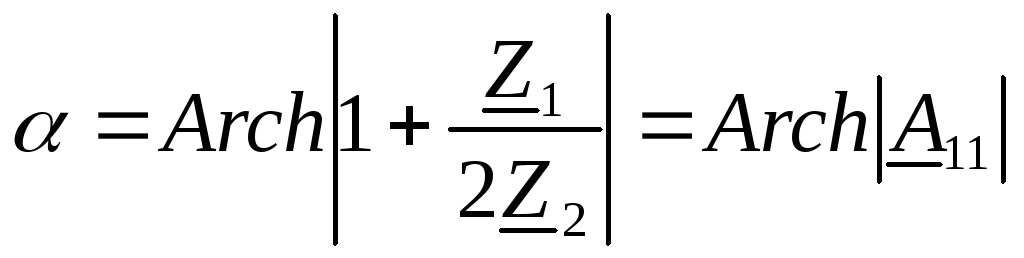 (9.14)
(9.14)
В полосе пропускания
затухание  .
.
ЧХФ в полосе
затухания не зависит от частоты и
принимает постоянные значения 0 или  ,
а в полосе пропускания определяется
соотношением:
,
а в полосе пропускания определяется
соотношением:
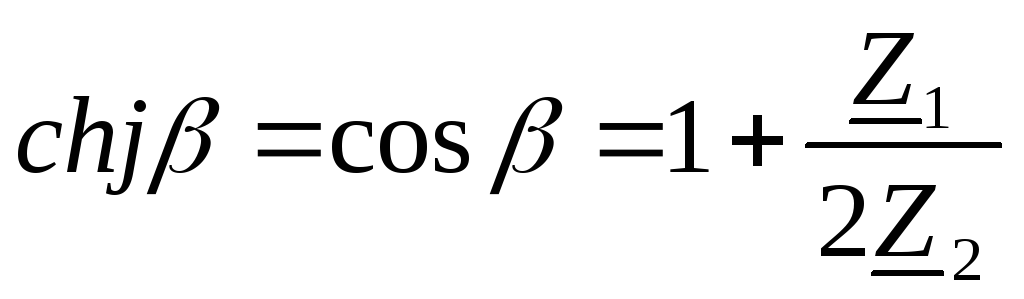
или
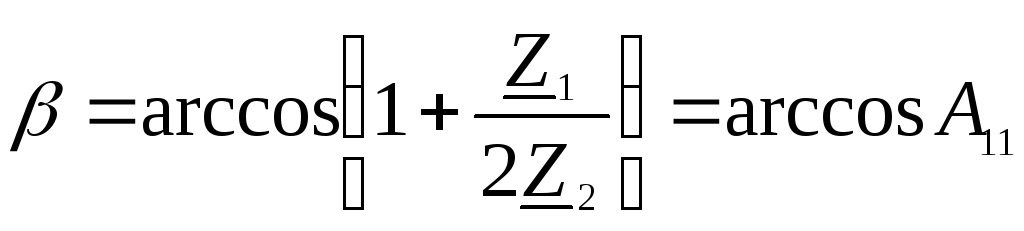 (9.15)
(9.15)
Таким образом, расчетные формулы для ЧХЗ и ЧХФ реактивных фильтров можно представить в таблице 9.1
Таблица 9.1
В полосе прозрачности | В полосе затухания |
| |
| |
5. Физические процессы в электрических фильтрах типа k.
Фильтр нижних частот.
Фильтр нижних частот (ФНЧ) предназначен для пропускания постоянного тока и всех колебаний с частотами ниже частоты среза и подавления колебаний с частотами выше частоты среза.
Последовательные
(продольные) ветви фильтра должны иметь
малое сопротивление для токов нижних
частот (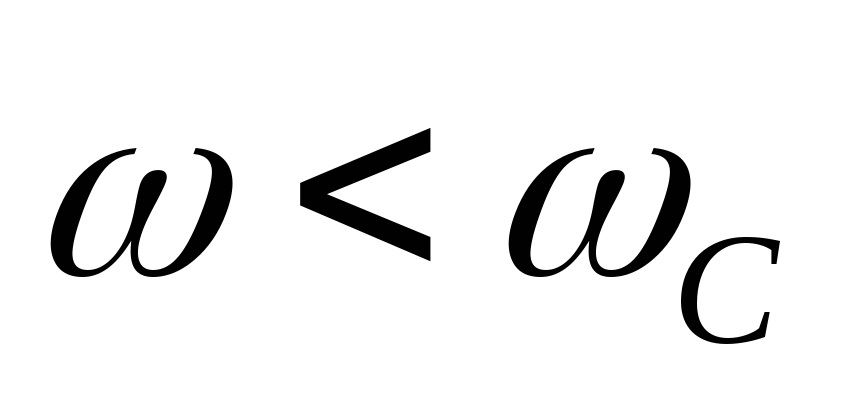 )
и большое сопротивление для токов
высоких частот (
)
и большое сопротивление для токов
высоких частот (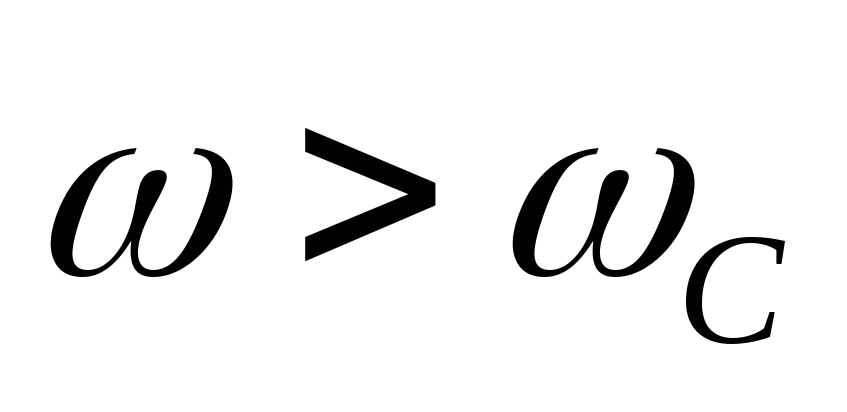 ).
Эти требования будут удовлетворены,
если в качестве последовательных ветвей
использовать индуктивности, сопротивление
которых пропорционально частоте (
).
Эти требования будут удовлетворены,
если в качестве последовательных ветвей
использовать индуктивности, сопротивление
которых пропорционально частоте (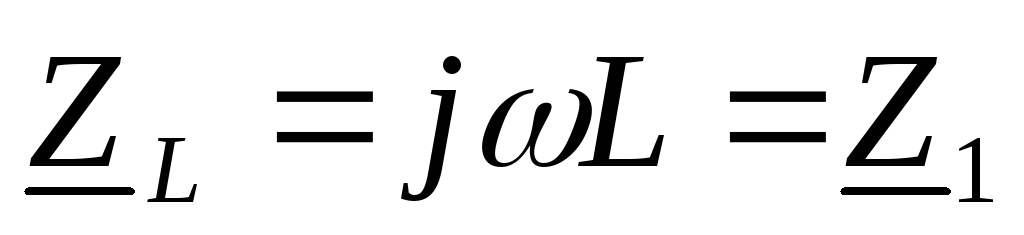 ).
).
Параллельные
(поперечные) ветви фильтра должны иметь
большое сопротивление для токов нужных
частот и малое сопротивление для токов
высоких частот (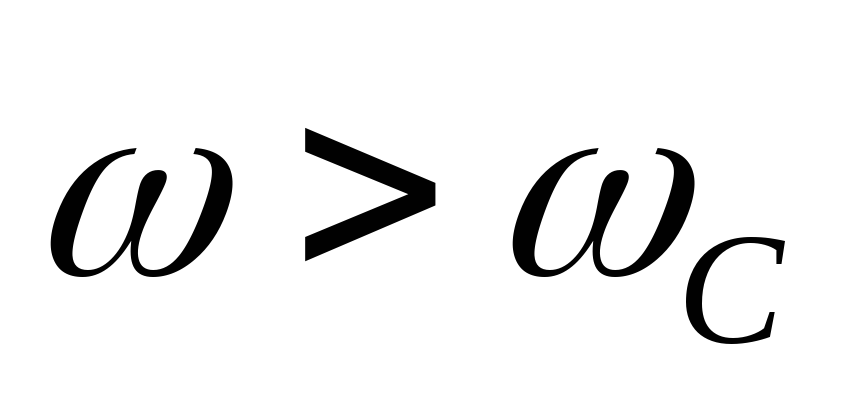 ).
Этим требованиям удовлетворяет емкость,
сопротивление которой падает с ростом
частоты (
).
Этим требованиям удовлетворяет емкость,
сопротивление которой падает с ростом
частоты (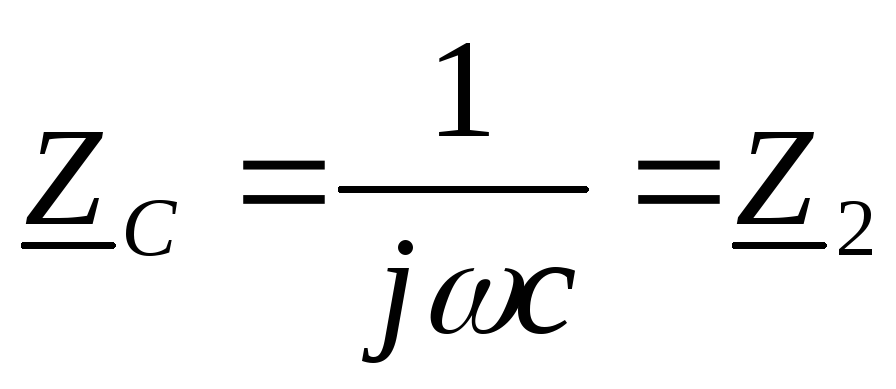 ).
).
В соответствии с произведенным выбором элементов для последовательных и параллельных ветвей Т- и П-образные схемы фильтров нижних частот имеют вид, представленный на рис. 9.5.
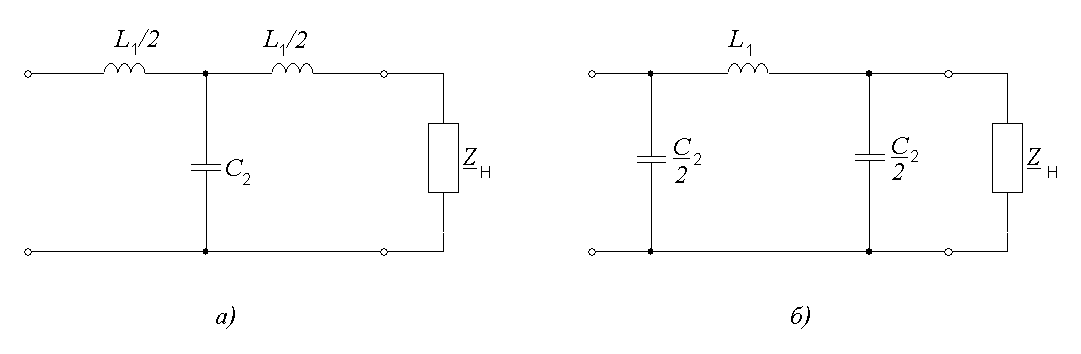
Рис. 9.5
Произведение
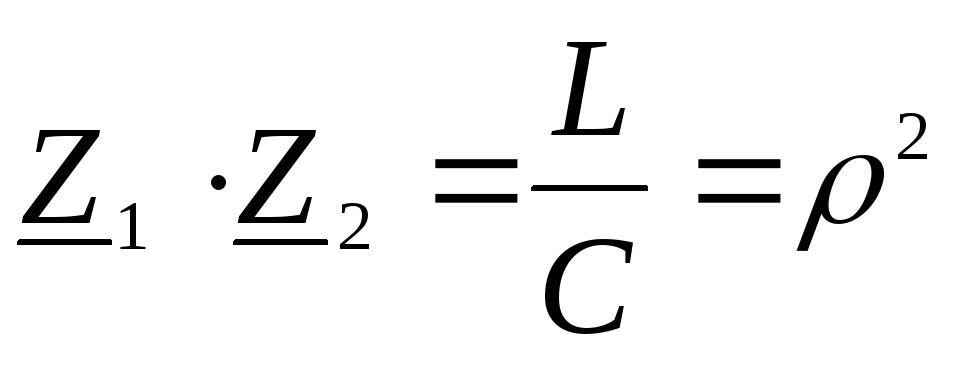 (9.16)
(9.16)
где 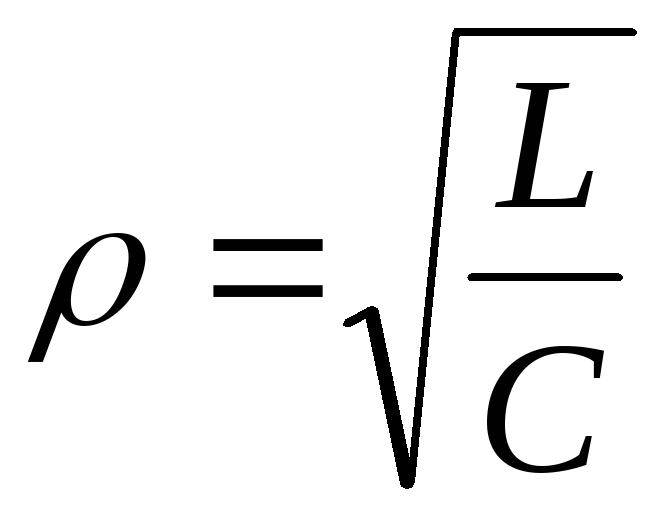 – характеристическое сопротивление
колебательного контура, который мог бы
быть составлен из индуктивностиL и емкости C.
Из формулы (9.16) видно, что фильтры,
изображенные на рис. 9.5, являются фильтрами
типа k.
– характеристическое сопротивление
колебательного контура, который мог бы
быть составлен из индуктивностиL и емкости C.
Из формулы (9.16) видно, что фильтры,
изображенные на рис. 9.5, являются фильтрами
типа k.
Сущность физических
процессов в этих фильтрах становится
ясной при  и
и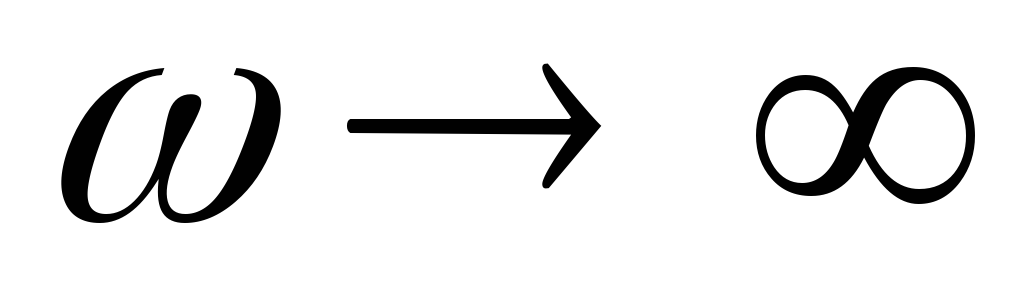 .
Так, на рисунке 9.6, а приведена эквивалентная
схема замещения ФНЧ, изображенного на
рисунке 9.5 а, при
.
Так, на рисунке 9.6, а приведена эквивалентная
схема замещения ФНЧ, изображенного на
рисунке 9.5 а, при ,
а на рисунке 9.6, б – при
,
а на рисунке 9.6, б – при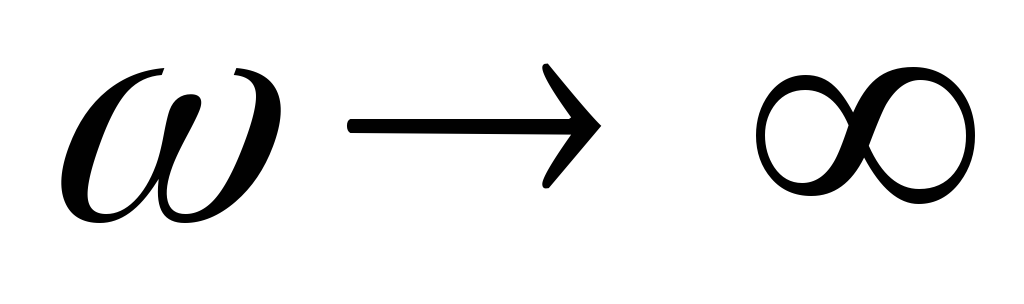 .
.
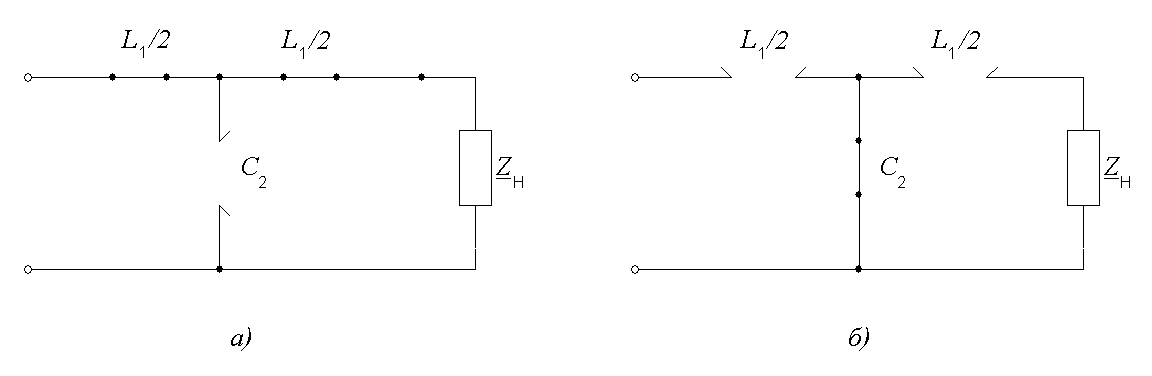
Рис. 9.6
Как видно, при  сигналы к нагрузкеZН проходят без затухания, а при
сигналы к нагрузкеZН проходят без затухания, а при 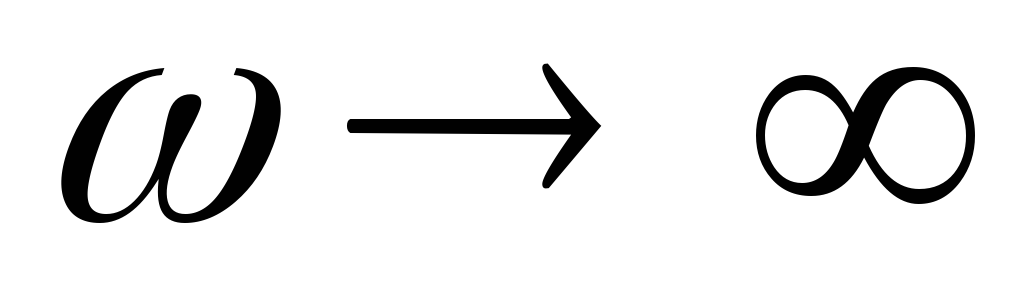 сигналы к нагрузке не проходят.
сигналы к нагрузке не проходят.
На основе соотношений (9.10), (9.14) и (9.15) могут быть построены АЧХ, ЧХЗ и ЧХФ рассматриваемого ФНЧ (рис. 9.7)
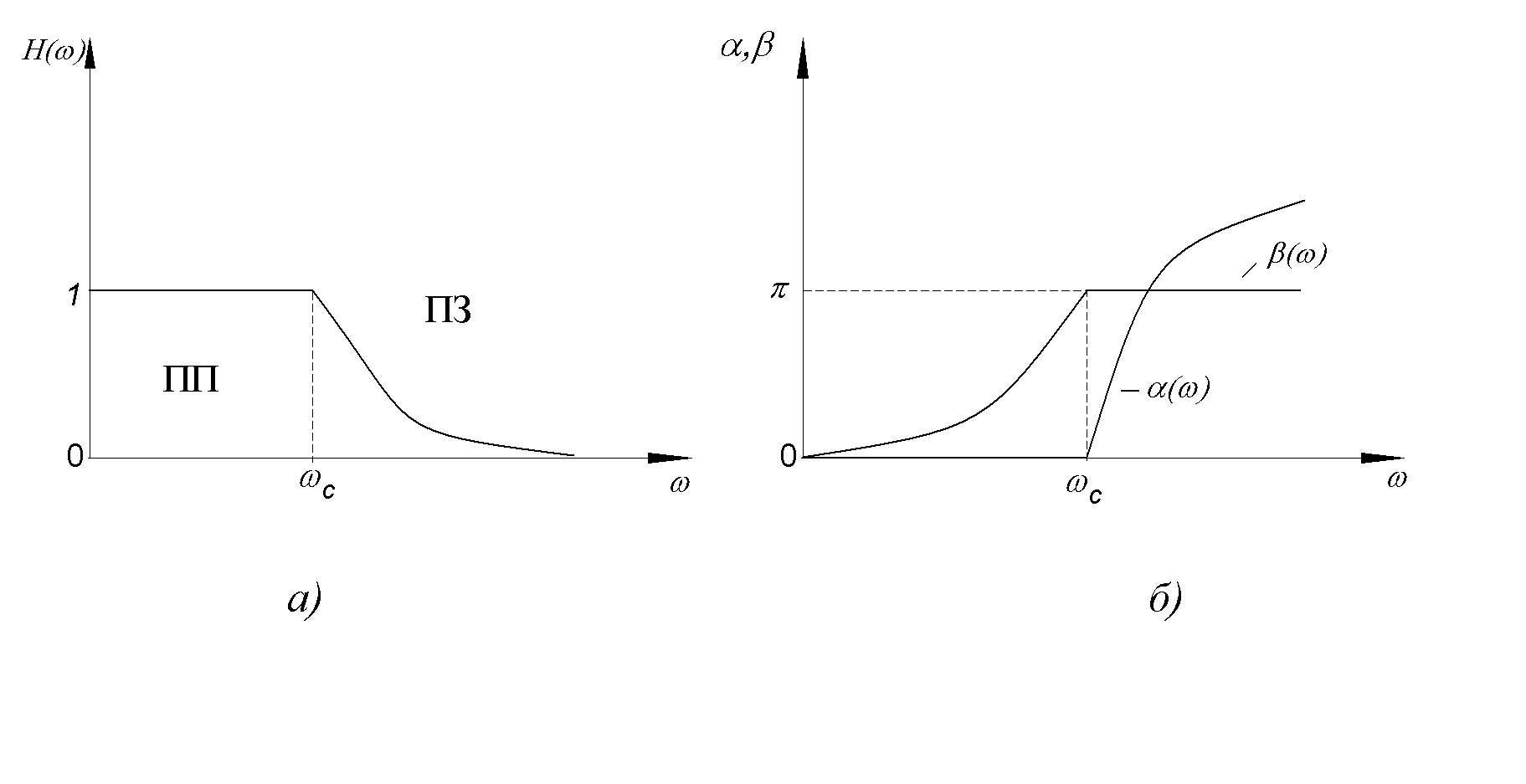
Рис. 9.7
Таким образом ФНЧ
имеют полосу пропускания в области
низких частот 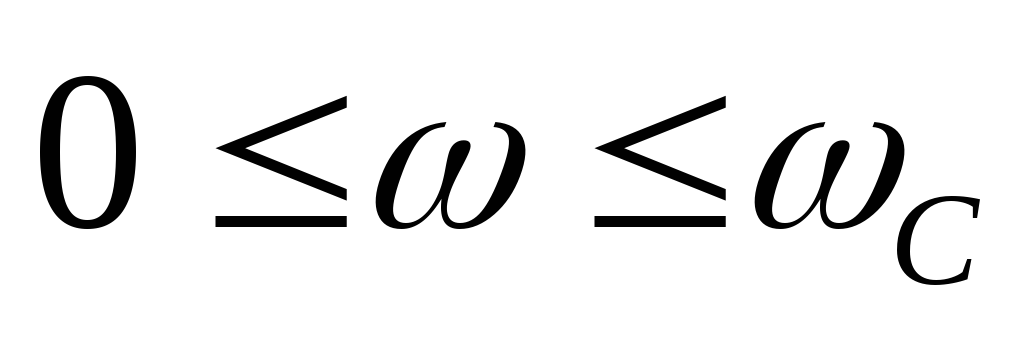 ,
а полосу затухания – в области высоких
частот
,
а полосу затухания – в области высоких
частот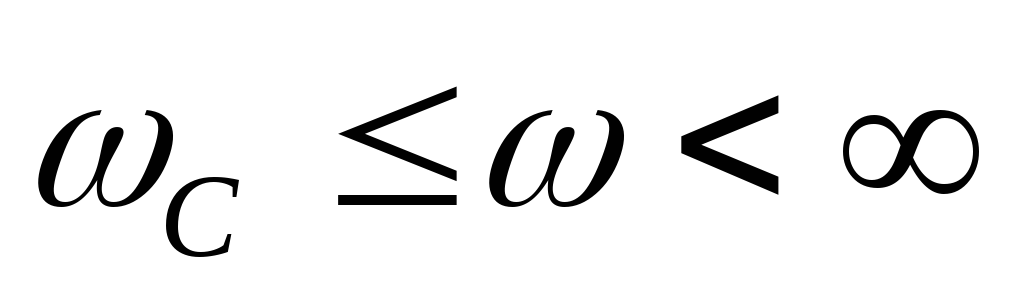 .
.
Фильтры верхних частот (ФВЧ) имеют полосу пропускания на высоких частотах, а полосу затухания – на низких частотах.
На рисунке 9.8, а
приведена Т-образная схема ФВЧ, а на
рисунке 9.8, б, в – эквивалентные схемы
замещения ФВЧ при  и при
и при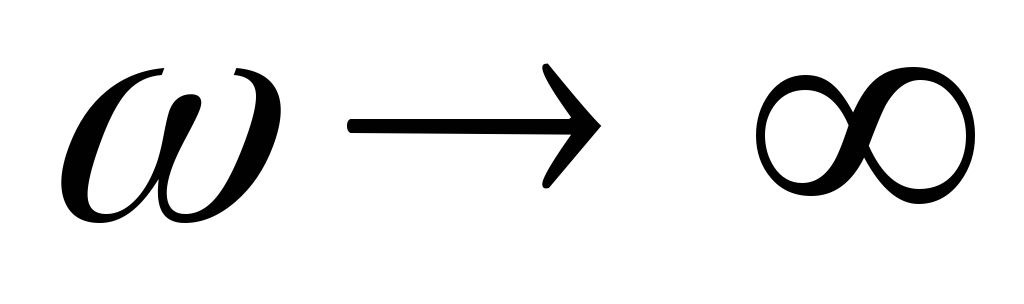 .
.
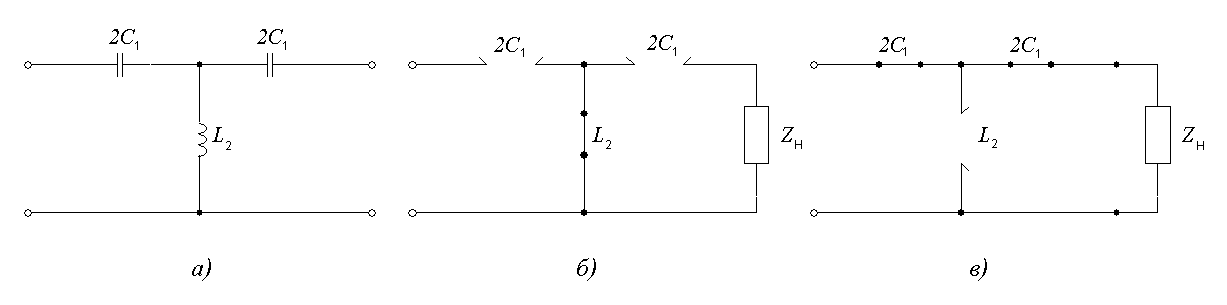
Рис 9.8
Аналогичным образом могут быть построены АЧХ, ЧХЗ и ЧХФ для ФВЧ (рис 9.10)
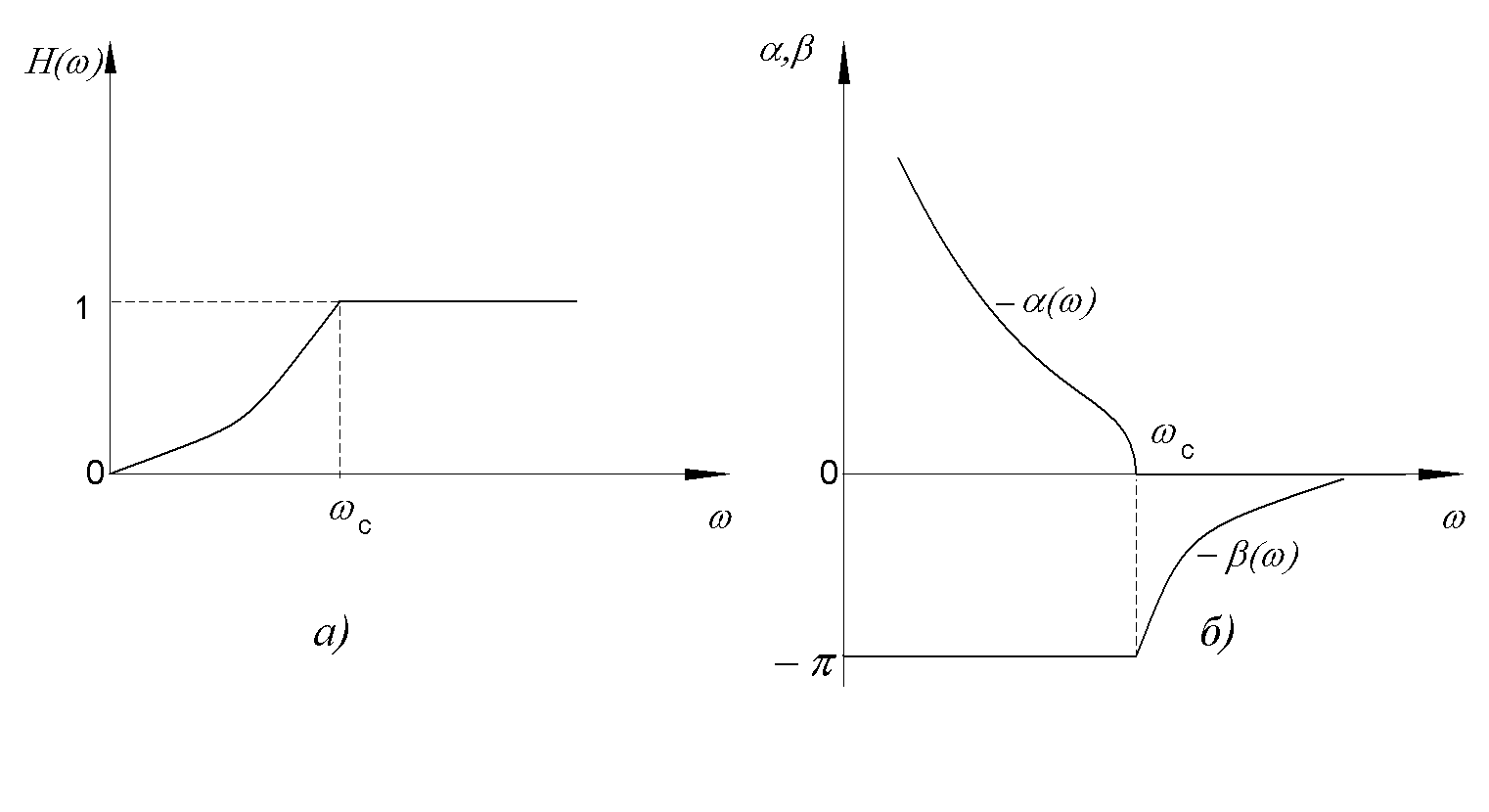
Рис 9.10
Полосовой
пропускной фильтр (ППФ) пропускает сигналы в некоторой полосе
между частотами среза 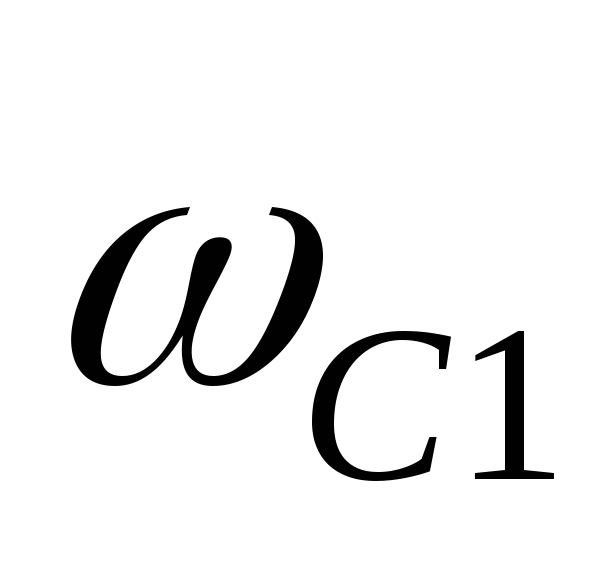 и
и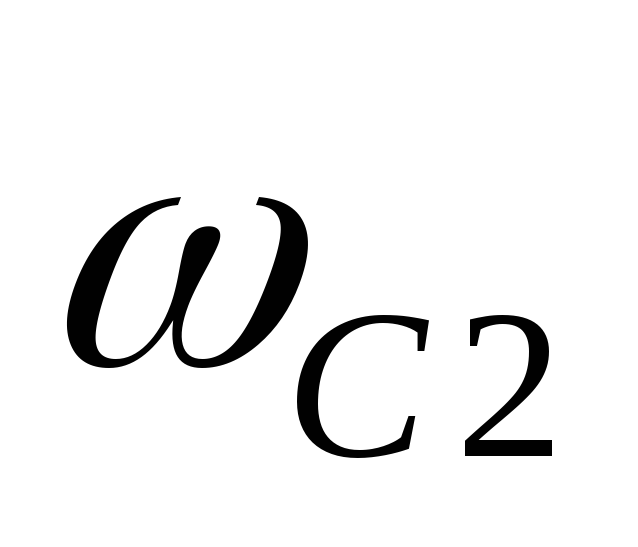 .
.
АЧХ идеального ППФ приведена на рисунке 9.11, а, ЧХЗ ППФ типа k – на рисунке 9.11, б.
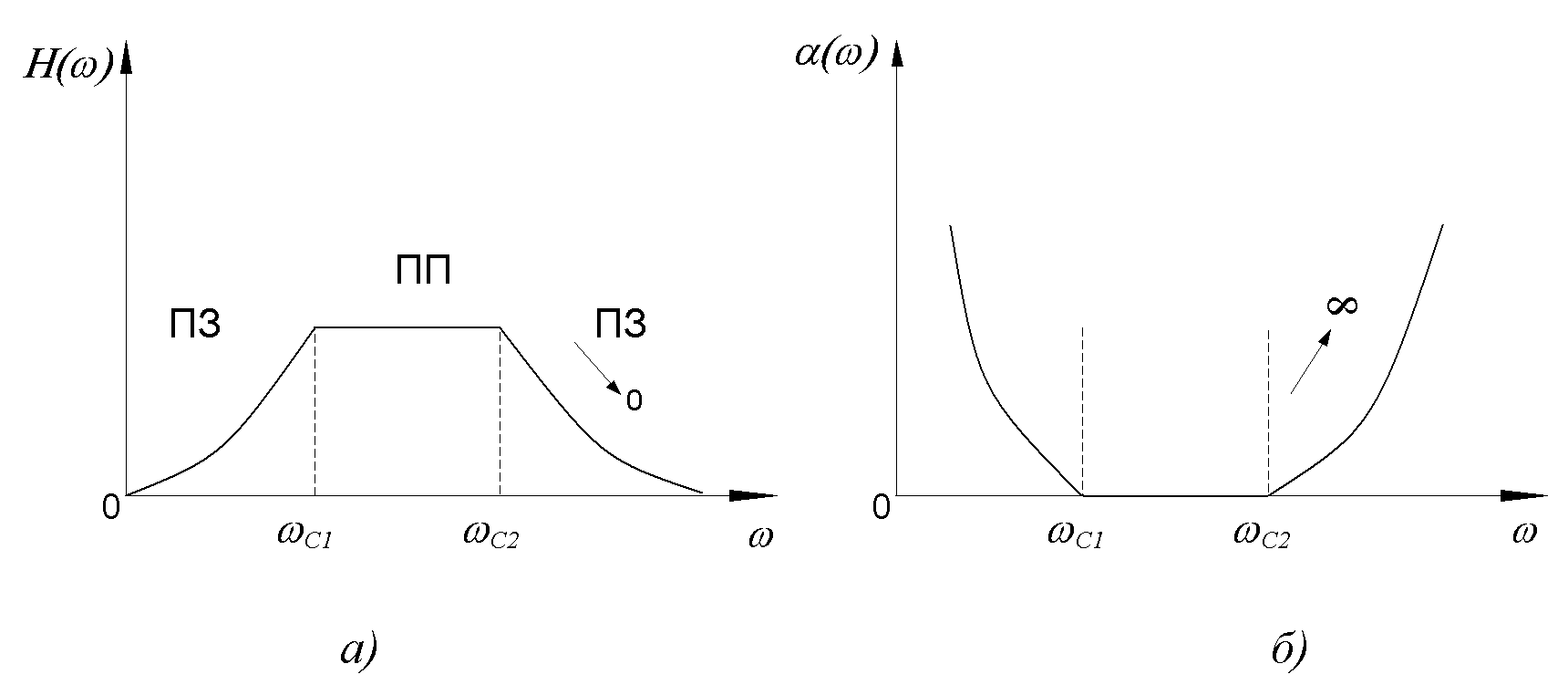
Рис 9.11
Т-образная схема
ППФ типа k изображена на рисунке 9.12, а, причем
резонансные частоты «продольного» и
«поперечного» плеч ППФ одинаковы: 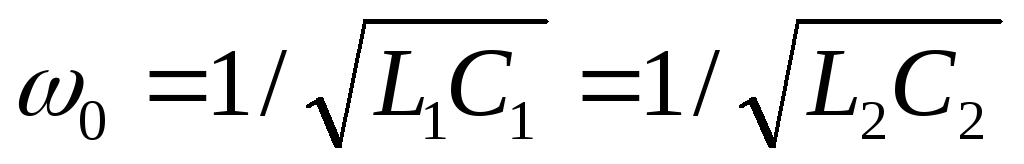 .
.
Эквивалентные
схемы замещения ППФ при  ,
, ,
,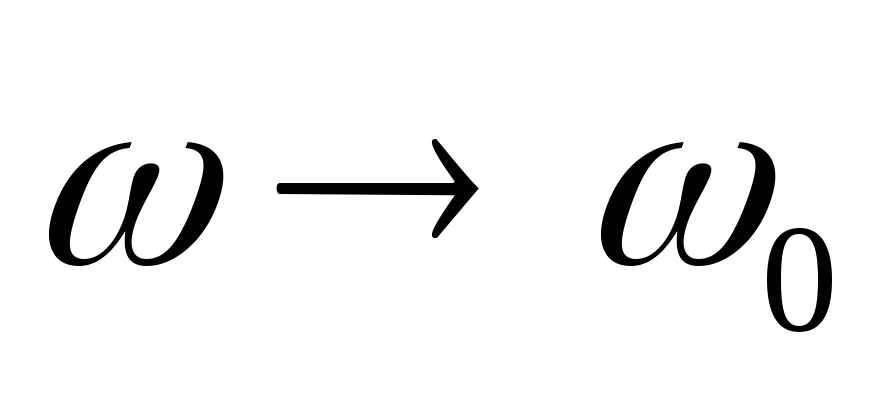 изображены соответственно на рисунках
9.12, б, в, г.
изображены соответственно на рисунках
9.12, б, в, г.
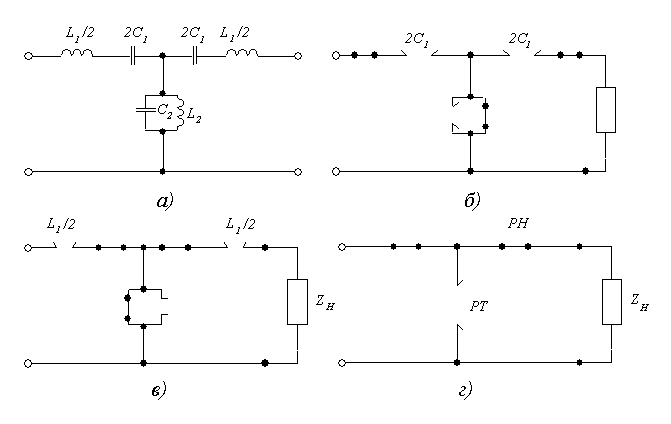
Рис 9.12
Полосовой
заграждающий фильтр (ПЗФ) не пропускает сигналы в некоторой
области частот между 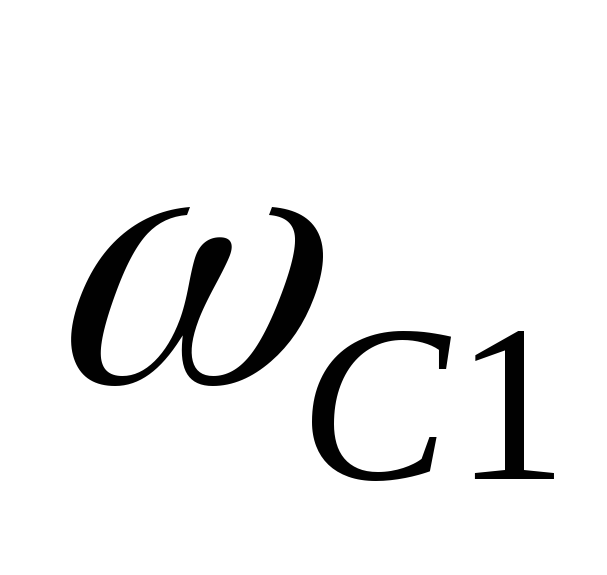 и
и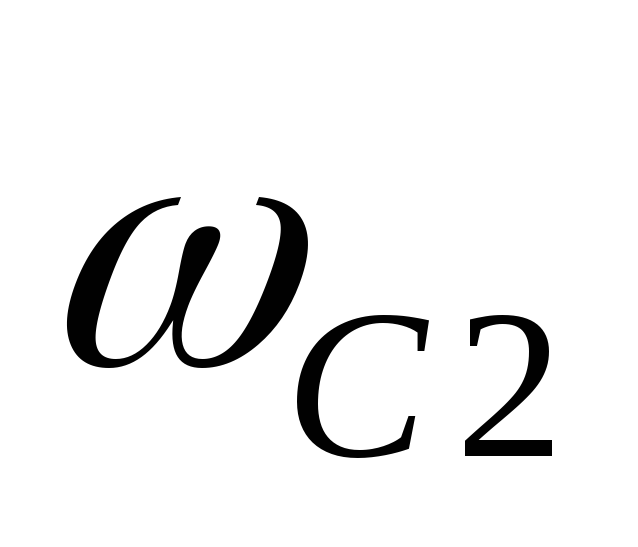 (см. рис. 9.13, а).
(см. рис. 9.13, а).
Характеристика затухания ПЗФ типа k приведена на рисунке 9.13, б, а схема на рисунке 9.14.
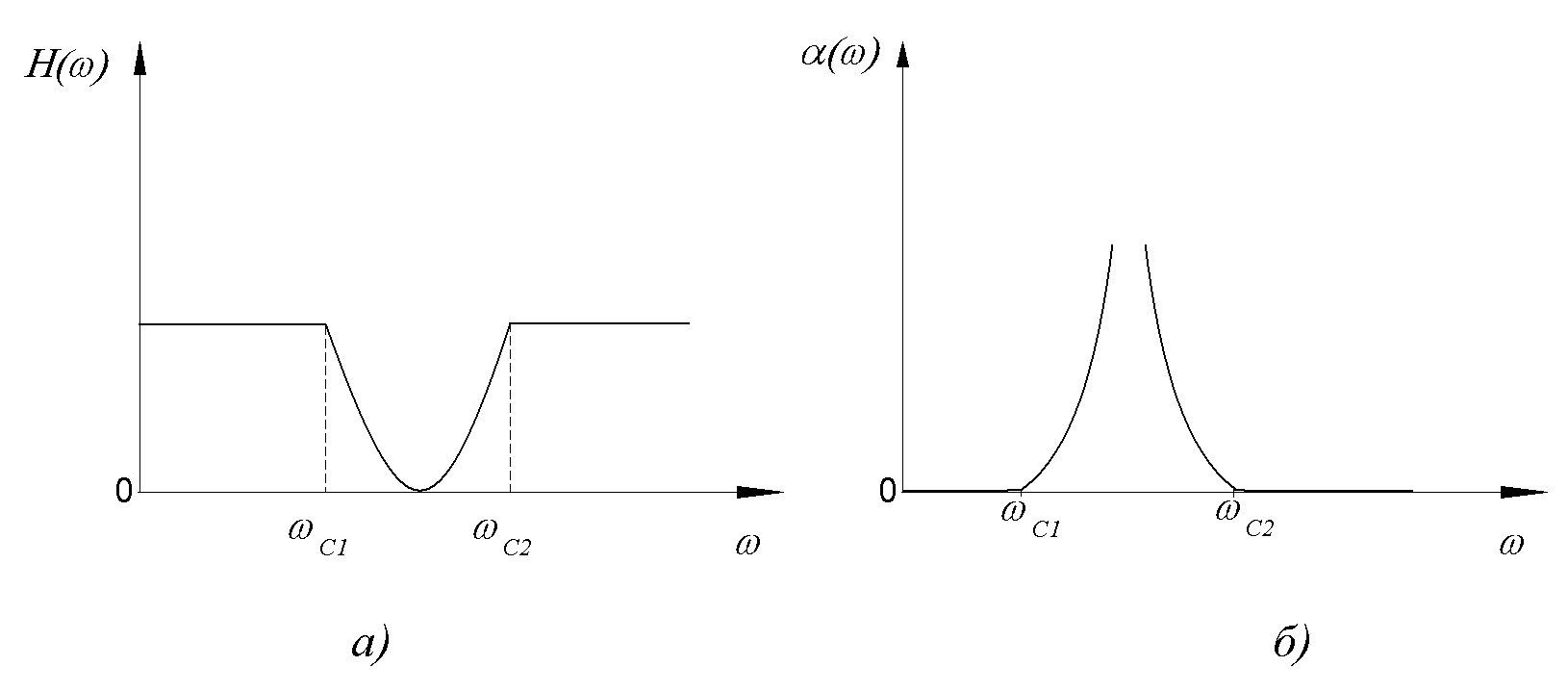
рис. 9.13
причем резонансные частоты одинаковы
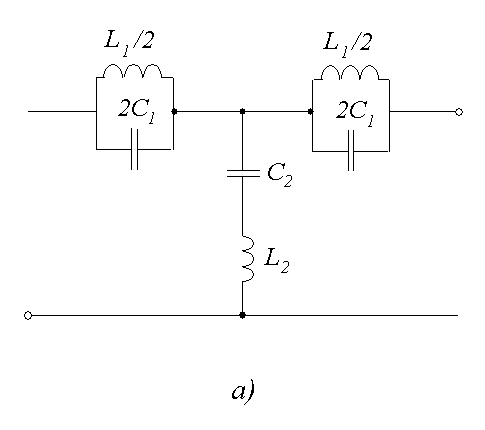
Рис 9.14
Сравнительно
медленное нарастание коэффициента
затухания  за пределами полосы пропускания и ярко
выраженная зависимость характеристического
сопротивления от частоты в пределах
этой полосы является существенным
недостатком фильтров типаk.
за пределами полосы пропускания и ярко
выраженная зависимость характеристического
сопротивления от частоты в пределах
этой полосы является существенным
недостатком фильтров типаk.
Достоинством фильтров типа k является их простота и обеспечение монотонного затухания в полосе затухания.
Необходимые теоретические сведения
ЛАБОРАТОРНАЯ РАБОТА №4
ФИЛЬТРЫ-ПРОТОТИПЫ
Цель работы: получение практических навыков расчета коэффициентов фильтра; изучение их временных и частотных характеристик.
Фильтром называется устройство, устанавливаемое между выводами электрической цепи с целью изменения соотношения между частотными со-ставляющими спектра проходящего через него сигнала.
Фильтры могут работать в диапазоне частот от 0 до 10 ГГц. Они различаются по типу, форме амплитудно-частотной характеристики и диапазону частот. Ниже приведены основные определения, используемые в практике проектирования аналоговых и цифровых фильтров.
Крутизна АЧХ — термин, используемый для описания наклона амплитудно—частотной характеристики в переходной полосе, расположенной между полосами пропускания и задерживания. Можно сказать, что АЧХ фильтра имеет крутизну 12 дБ/октаву. Это значит, что сигналы, частота которых отличается на две октавы, будут ослаблены на 24 дБ, а отстоящие по частоте на три октавы – на 36 дБ и т.д.
Неравномерность АЧХ в полосе пропускания — размер флуктуации АЧХ от пика до пика в полосе пропускания.
Ослабление — уменьшение амплитуды сигнала, обычно измеряемое в дБ, после прохождения через аналоговый (цифровой) фильтр. Ослабление фильтра представляет собой отношение амплитуды выходного сигнала фильтра к амплитуде входного сигнала на некоторой частоте.
Если на заданной частоте амплитуда выходного сигнала фильтра меньше амплитуды входного сигнала, то отношение меньше единицы, а ослабление выражается отрицательным числом.
Относительное ослабление — ослабление, измеренное по отношению к наибольшему значению амплитуды. Наибольшему уровню сигнала обычно присваивается опорный уровень 0 дБ, в результате чего все остальные значения АЧХ оказываются отрицательными.
Передаточная функция — математическое выражение, получаемое как отношение z-преобразования (для аналоговых фильтров — преобразования Лапласа) выходного сигнала фильтра к преобразованию входного сигнала. По заданной передаточной функции мы можем определить АЧХ и ФЧХ фильтра.
Переходная полоса — диапазон частот, в котором АЧХ фильтра переходит от полосы пропускания к полосе задерживания.
Полоса задерживания — диапазон частот, в котором фильтр ослабляет сигналы.
Полоса пропускания — диапазон частот сигнала, в котором фильтр пропускает энергию сигнала на выход с минимальным ослаблением. Обычно определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности.
Порядок фильтра — число, определяющее наибольшую степень числителя или знаменателя передаточной функции фильтра в z-области. В общем случае, чем больше порядок фильтра, тем лучше его частотная характеристика.
Пульсации — флуктуации (величина которых измеряется в дБ) АЧХ в полосе пропускания или задерживания. Эллиптические фильтры и фильтры Чебышева имеют АЧХ с равноволновыми пульсациями, т.е. амплитуда их пульсаций не меняется в пределах полосы пропускания. АЧХ фильтров Бесселя и Баттерворта не имеют пульсаций. Пульсации в полосе задерживания иногда называют внеполосными пульсациями.
Центральная частота (f0) — частота, лежащая в центре полосы пропускания полосового фильтра.
Частота среза — наивысшая частота полосы пропускания для ФНЧ (и наименьшая частота полосы пропускания ФВЧ), на которой АЧХ еще не выходит за пределы пульсаций полосы пропускания.
Фазо-частотная характеристика (ФЧХ) — разность фаз входного и выходного синусоидальных сигналов фильтра в зависимости от частоты сигнала. ФЧХ, которую иногда называют характеристикой фазовой задержки, обычно изображается кривой, показывающей сдвиг фаз фильтра в зависимости от частоты.
Ширина полосы фильтра — ширина полосы пропускания фильтра. Для ФНЧ ширина полосы равна частоте среза. Для полосового фильтра ширина полосы обычно определяется как разность верхней и нижней частот, на которых АЧХ уменьшается на 3 дБ.
По своему предназначению фильтры служат для обработки сигналов с целью получения требуемых характеристик этих сигналов.
В зависимости от формы амплитудно-частотной характеристики (АЧХ) имеется четыре основных класса фильтров:
1) фильтр нижних частот (ФНЧ). Он пропускает только низкочастотные составляющие спектра сигнала – обычно от постоянной составляющей и до частоты, которая называется частотой среза и определяется в исходных данных для расчета фильтра. Все спектральные составляющие сигнала с частотой выше частоты среза ФНЧ подавляет;
2) фильтр верхних частот (ФВЧ). Фильтры этого класса подавляют в спектре сигнала все компоненты с частотой от 0 до частоты среза. Спектраль-ные составляющие с частотой выше частоты среза пропускаются ФВЧ без ис-кажений;
3) полосовой фильтр (ПФ). Он пропускает без искажений все спектральные компоненты только в пределах заданной полосы частот и подавляет все компоненты вне ее;
4) режекторный фильтр (РФ). Он подавляет компоненты спектра внутри заданной полосы, называемой полосой задержания, и пропускает без искажений частоты вне этой полосы.
Для создания обобщенных фильтрующих систем, обычно представленных своей передаточной функцией H(s), используются аналоговые фильтры-прототипы. С помощью фильтров-прототипов в последующем удобно рассчитать реальный аналоговый или цифровой фильтр с заданными свойствами.
Рассмотрим класс фильтров нижних частот.
Все ФНЧ в зависимости от вида АЧХ делятся на две категории – полюсные и эллиптические. Их различие заключается в том, что в передаточной функции полюсных фильтров содержатся только полюса, а у эллиптических — кроме полюсов имеются еще и нули. К полюсным фильтрам относятся фильтры Баттерворта, Чебышева и Бесселя.


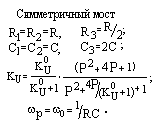
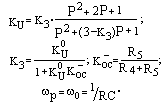
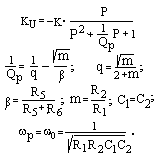
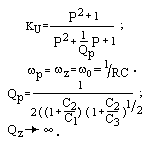
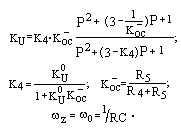
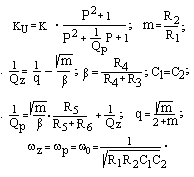
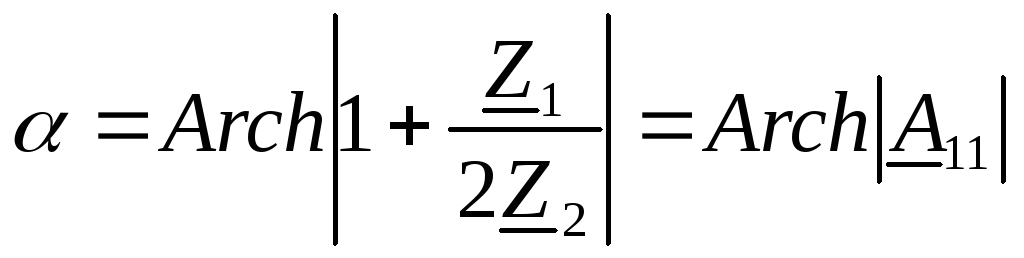
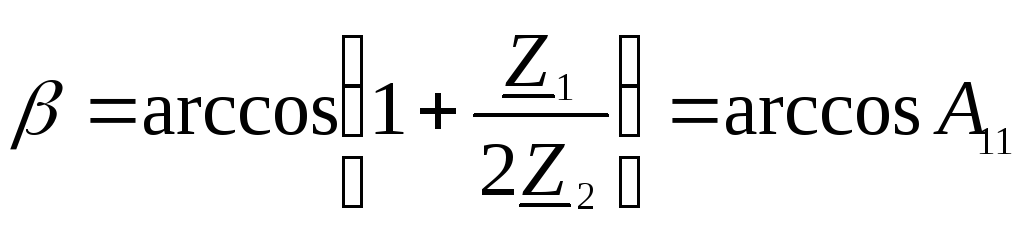
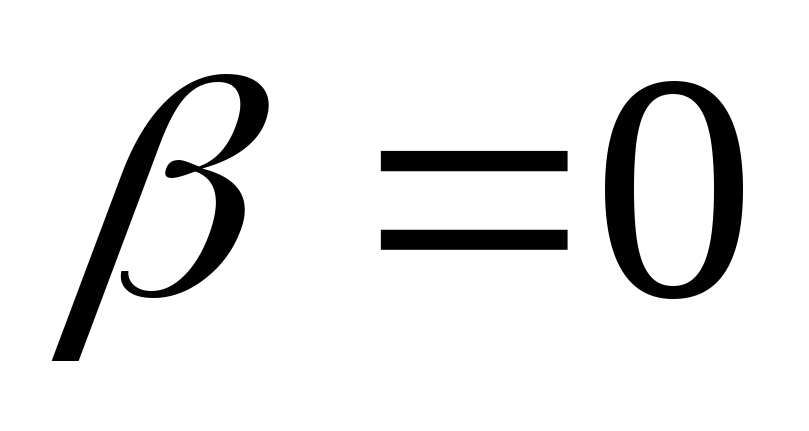 при
при 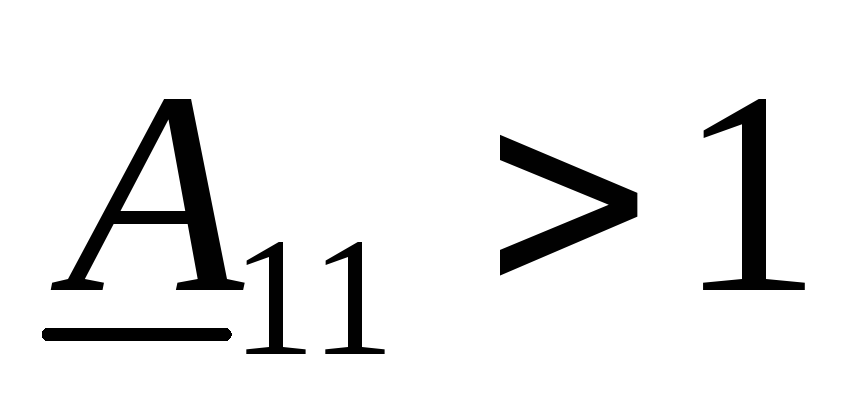
 при
при