Геометрический смысл векторное произведение: Векторное Произведение Векторов. Свойства, определение — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Векторное Произведение Векторов. Свойства, определение

Определение векторного произведения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов.

Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

он является нулевым, если векторы →a и →b коллинеарны;
он перпендикулярен и вектору →a и вектору →b;
длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.

В прямоугольной системе координат трехмерного пространства

векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

, где

→i, →j, →k — координатные векторы.

Это определение показывает нам векторное произведение в координатной форме.

Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:

Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

Антикоммутативность
Свойство дистрибутивности
или
Сочетательное свойство
или

, где λ произвольное действительное число.

Для большей ясности докажем свойство антикоммутативности векторного произведения.

По определению

Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому

что доказывает свойство антикоммутативности векторного произведения.

Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.

Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Примеры решения задач

Пример 1

а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.

Как решаем:

а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:

Ответ:

Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.

б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:

Ответ:

Пример 2

Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.

Как решаем:

По условию снова нужно найти длину векторного произведения. Используем нашу формулу:

Согласно ассоциативным законам, выносим константы за переделы векторного произведения.

Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.

Ответ:

Пример 3

Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.

Как решаем:

Сначала найдём векторы:

Затем векторное произведение:

Вычислим его длину:

Подставим данные в формулы площадей параллелограмма и треугольника:

Ответ:

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна

А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].

Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart.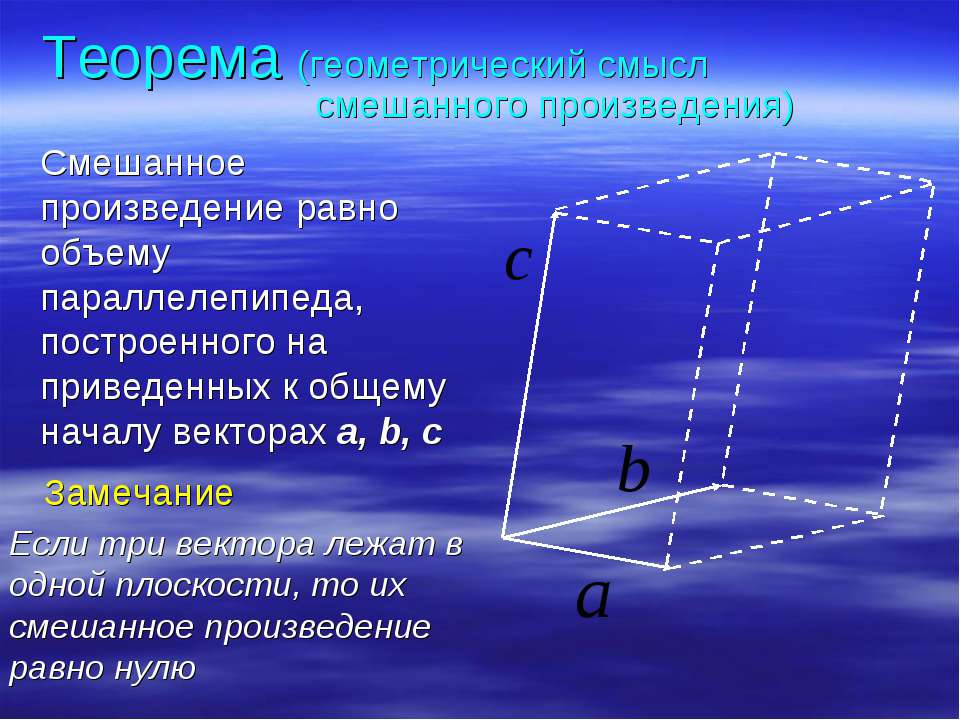 Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!

Векторное произведение векторов.

Навигация по странице:

Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).

рис. 1

Формулы вычисления векторного произведения векторов

Векторное произведение двух векторов a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:

a × b =	i	j	k	= i(a_yb_z — a_zb_y) — j(a_xb_z — a_zb_x) + k(a_xb_y — a_yb_x)
	a_x	a_y	a_z
	b_x	b_y	b_z

a × b = {a_yb_z — a_zb_y; a_zb_x — a_xb_z; a_xb_y — a_yb_x}

Свойства векторного произведения векторов

Геометрический смысл векторного произведения.
Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
S_парал = [a × b]
Геометрический смысл векторного произведения.
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c

Примеры задач на вычисления векторного произведения векторов

Пример 1. Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.

Решение:

a × b =	i	j	k	=
	1	2	3
	2	1	-2

= i(2 · (-2) — 3 · 1) — j(1 · (-2) — 2 · 3) + k(1 · 1 — 2 · 2) =

= i(-4 — 3) — j(-2 — 6) + k(1 — 4) = -7i + 8j — 3k = {-7; 8; -3}

Пример 2.

Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.

Решение: Найдем векторное произведение этих векторов:

a × b =	i	j	k	=
	-1	2	-2
	2	1	-1

= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =

= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}

Из свойств векторного произведения:

SΔ =	1	\|a × b\| =	1	√0² + 5² + 5² =	1	√25 + 25 =	1	√50 =	5√2
	2		2		2		2		2

Ответ: SΔ = 2. b)

2) его направление перпендикулярно к плоскости упомянутого параллелограмма;
3) при этом направление вектора с выбирается (из двух возможных) так, чтобы векторы a, b, с составляли правую систему.

Геометрический смысл векторного произведения

Модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на этих векторах, т.е.

$\left| {\vec a \times \vec b} \right| = {S_{параллелограмма}}$

Векторное произведение двух трехмерных векторов a={x₁,y₁,z₁} и b={x₂,y₂,z₂}, заданных в координатной форме определяется по формуле:

Пример 1

Найти векторное произведение двух векторов a={x₁,y₁,z₁} и b={x₂,y₂,z₂}, заданных в координатной форме

Решение

Подставляя в формулу выше, находим векторное произведение векторов

$\vec a \times \vec b = \left| {\begin{array}{*{20}{c}} {\vec i}&{\vec j}&{\vec k} \\ 2&{ — 1}&1 \\ { — 3}&4&1 \end{array}} \right| =$

$= — 5i — 5j + 5k$

Пример 2
Векторы а и b имеют длины, соответственно равные 20 см и 30 см, и образуют угол в 30⁰. b)=20·30·sin30⁰=

=20·30·0.5=600·0.5=300 см²

Лекция Векторное произведение векторов. Смешанное произведение векторов.

Скачать с Depositfiles

Лекция № 6. Тема 3 : Векторное произведение

3.1. Векторное произведение двух векторов и его основные свойства

Определение 1. Векторным произведением двух векторов и называется вектор , удовлетворяющий следующим условиям:

2. вектор перпендикулярен векторам и .

3. вектора образуют правую тройку, т.е. из конца третьего вектора кратчайший поворот от вектора ко второму вектору виден против часовой стрелки.

В противном случае тройка векторов называется левой.

а) правая б) левая

Обозначается векторное произведение: или

Из определения векторного произведения следуют его свойства и геометрический смысл:

Модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.

Основные свойства векторного произведения:

1.  векторное произведение антикоммутативно.

2. , где , если и коллинеарные или по крайней мере один из сомножителей является нулевым вектором.

Замечание 1. Тройка базисных векторов является правой.

3.2. Векторное произведение векторов, заданных своими координатами

Из определения векторного произведения следует, что:

(1)

Тогда с учетом формул (1) и свойств векторного произведения получаем

(2)

Пример 1. Заданы векторы и Найти площадь параллелограмма, построенного на этих векторах.

Исходя из геометрического смысла векторного произведения, получим

Тогда

Замечание 2. Площадь треугольника, построенного на векторах и будет равна .

3.3.* Механический смысл векторного произведения

Если  радиус-вектор точки , к которой при-ложена сила , то момент этой силы относительно точки вычисляется по формуле

(3)

При этом  моменты силы относительно координатных осей. z

Рассмотрим задачу из механики: 3 M

В точке приложена сила

. Требуется найти моменты

этой силы относительно координатных осей. 2 y

По формуле (3) получаем х

Полезно отметить тот факт, что значения этих моментов совпадают со школьным определением – «Момент равен произведению силы на плечо». См. рисунок!

Тема 4 : Смешанное произведение

4.1. Смешанное произведение и его основные свойства

Определение 2. Векторно–скалярное произведение называется смешанным и обозначается

Рассмотрим его геометрический смысл.

Построим параллелепипед на векторах

Его объем равен в

его основании лежит параллелограмм с h

площадью

Его высота поэтому имеем

(4)

Знак в выражении совпадает со знаком и поэтому смешанное произведение положительно, если вектора образуют правую тройку.

Таким образом, приходим к следующему правилу:

Смешанное произведение некомпланарных векторов по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.

Рассмотрим основные свойства смешанного произведения:

1. Если смешанное произведение равно нулю, то векторы компланарны.

Верно и обратное, т.е., если сомножители компланарны, то смешанное произведение равно нулю.

Равенство возможно в следую-щих случаях:

а) хотя бы один из векторов является нулевым, то векторы компланарны;

б) и коллинеарны  компланарны;

в)  компланарны.

Аналогично доказывается обратное утверждение.

2. , т.е. при циклической перестановке сомножителей смешанное произведение знак не меняется. Это следует из того, что в данном случае ориентация тройки этих векторов сохраняется. В остальных случаях перестановки сомножителей ориентация векторов меняется и тогда

3. где А и В константы.

Это свойство следует из свойств векторного и скалярного произведений.

4.2. Смешанное произведение векторов, заданных своими координатами

Пусть заданы векторы . Требуется найти их смешанное произведение.

Из определения скалярного и векторного произведений следует

Таким образом, получаем формулу

(5)

Пример 2: Проверить – лежат ли векторы , и в одной плоскости, т. е. являются ли они компланарными.

По формуле смешанного произведения векторов имеем:

Поскольку , то данные векторы , и лежат в одной плоскости, т.е. являются компланарными.

Пример 3. Пирамида задана координатами своих вершин Найти высоту, проведённую из вершины D на грань АВС. D

Построим векторы

Н С

Из геометрии известно, что объем пирамиды равен трети произведения А площади основания на ее высоту Н, т.е. В

, (6)

поскольку основанием пирамиды является треугольник (его площадь равна половине площади параллелограмма ), а высота пирамиды равна высоте соответствующего параллелепипеда.

Используя геометрический смысл смешанного произведения и форму-лы (5) и (6), получим

Из формулы (2) и геометрического смысла векторного произведения следуют

Снова воспользуемся известной из геометрии формулой

и тогда окончательно получим

Скачать с Depositfiles

Векторное произведение векторов и его свойства (Лекция №18)

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ И ЕГО СВОЙСТВА

Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .
Таким образом, и .

Доказательство. Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что . По определению скалярного произведения

. Предполагая, что и обозначив через h высоту параллелепипеда, находим .

Таким образом, при

Если же , то и . Следовательно, .

Объединяя оба эти случая, получаем или .

Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .
Для любых векторов , , справедливо равенство
.

Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки «+» и «–» берутся одновременно, т.к. углы между векторами и и и одновременно острые или тупые.
При перестановке любых двух сомножителей смешанное произведение меняет знак.
Действительно, если рассмотрим смешанное произведение , то, например, или

.
Смешанное произведение тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.
Доказательство.
1. Предположим, что , т.е. , тогда или или .
  Если , то или или . Поэтому – компланарны.
  
  Если , то , , — компланарны.
2. Пусть векторы – компланарны и α – плоскость, которой они параллельны , т. е. и . Тогда , а значит , поэтому или .
Т. о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

.

Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Примеры.
1. Показать, что векторы образуют базис в пространстве.
  , т.е. векторы – базис.
2. Найти объём пирамиды с вершинами в точках A(2; -2; 0), B(-1; 4; -4), C(4; -8; 5), D(1; -7; 0). Правую или левую тройку образуют векторы и ?
  
  Т. к. , то тройка векторов левая.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Уравнение F(x, y, z) = 0 определяет в пространстве Oxyz некоторую поверхность, т. е. геометрическое место точек, координаты которых x, y, z удовлетворяют этому уравнению. Это уравнение называется уравнением поверхности, а x, y, z – текущими координатами.

Однако, часто поверхность задаётся не уравнением, а как множество точек пространства, обладающих тем или иным свойством. В этом случае требуется найти уравнение поверхности, исходя из её геометрических свойств.

ПЛОСКОСТЬ.

НОРМАЛЬНЫЙ ВЕКТОР ПЛОСКОСТИ.

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДАННУЮ ТОЧКУ

Рассмотрим в пространстве произвольную плоскостьσ. Её положение определяется заданием вектора , перпендикулярного этой плоскости, и некоторой фиксированной точки M₀(x₀, y₀, z₀), лежащей в плоскости σ.

Вектор перпендикулярный плоскости σ, называется нормальным вектором этой плоскости. Пусть вектор имеет координаты .

Выведем уравнение плоскости σ, проходящей через данную точку M₀ и имеющей нормальный вектор . Для этого возьмём на плоскости σ произвольную точку M(x, y, z) и рассмотрим вектор .

Для любой точки MÎ σ вектор .Поэтому их скалярное произведение равно нулю . Это равенство – условие того, что точка MÎ σ. Оно справедливо для всех точек этой плоскости и нарушается, как только точка M окажется вне плоскости σ.

Если обозначить через радиус-вектор точки M, – радиус-вектор точкиM₀, то и уравнение можно записать в виде

Это уравнение называется векторным уравнением плоскости. Запишем его в координатной форме. Так как , то

Итак, мы получили уравнение плоскости, проходящей через данную точку. Таким образом, для того чтобы составить уравнение плоскости, нужно знать координаты нормального вектора и координаты некоторой точки, лежащей на плоскости.

Заметим, что уравнение плоскости является уравнением 1-ой степени относительно текущих координат x, y и z.

Примеры.

Составить уравнение плоскости, проходящей через точку М(1;-2;3) перпендикулярно вектору .
Используя выведенное уравнение, получим 2(x-1)+0(y+2)+4(z-3)=0 или x+2z-7=0.
Составить уравнение плоскости, проходящей через точки A(1;2;3), B(-1;0;0), C(3;0;1).
Чтобы составить требуемое уравнение, нужно найти вектор перпендикулярный плоскости. Заметим, что таким вектором будет вектор . Найдем это вектор. . Тогда

.

Взяв в качестве точки, через которую проходит плоскость точку A, получим уравнение –2(x-1)-10(y-2)+8(z-3)=0 или x+5y-4z+1=0.

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости.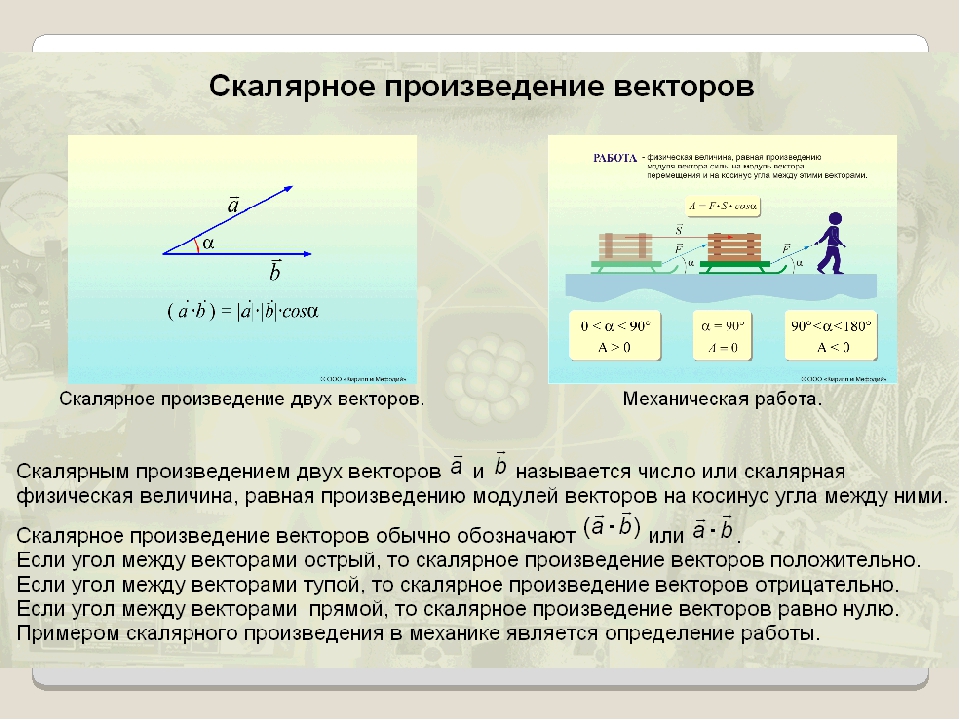 Это уравнение записывается в виде:

Ax+By+Cz+D=0

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

Свободный член равен нулю D= 0.
В этом случае уравнение плоскости принимает вид Ax+Cy+Bz=0. Т.к. числа x=0, y=0, z=0 удовлетворяют уравнению плоскости, то она проходит через начало координат.

Один из коэффициентов при текущих координатах равен нулю. Пусть например A =0. В этом случае уравнение плоскости имеет вид By+Cz+D=0. Нормальный вектор плоскости имеет координаты и перпендикулярен оси Ox. Следовательно, плоскость параллельна оси Ox.
Аналогично, если B= 0, то плоскость параллельна оси Oy и C= 0 – плоскость параллельна оси Oz.

Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси.
Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox. Следовательно, плоскость проходит через ось Ox.

Аналогично, при B=D=0 плоскость Ax+Cz=0 проходит через ось Oy. При C=D=0 плоскость проходит через ось Oz.
Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B=0. Тогда плоскость Cz+D=0 в силу п. 2 будет параллельна осям Ox и Oy, а следовательно параллельна координатной плоскости xOy.
Аналогично, уравнениям Ax+D=0 и By+D=0 соответствуют плоскости, параллельные координатным плоскостям yOz и xOz.
Два коэффициента при текущих координатах и свободный член равны нулю. Пусть, например, A=B=D=0. Тогда уравнение плоскости имеет вид Cz=0 или z=0. Эта плоскость проходит через начало координат и параллельна осям Ox и Oy, т. е. уравнение определяет координатнуюплоскость xOy. Аналогично, x=0 – уравнение координатной плоскости yOz и y=0 – плоскость xOz.

Примеры.

Составить уравнение плоскости, проходящей параллельно оси Oy, через точки M₁(1; 0; -1), M₂(-1; 2;0).
Так как ось Oy параллельна , то уравнение плоскости Ax+Cy+D=0. Учитывая, что M₁Î α, M₂Î α, подставим координаты этих точек в уравнение и получим систему из двух линейных уравнений с тремя неизвестными

Положив D=1, найдем A= 1 и C= 2. Следовательно, уравнение плоскости имеет видx+2z+1=0.
Составить уравнение плоскости, проходящей через точку M(2;3;-4) параллельно плоскости yOz (перпендикулярно оси Ox).
Так как yOz||α, то уравнениеплоскости будет Ax+D=0. С другой стороны MÎ α, поэтому 2A+D=0, D=-2A. Поэтому плоскость имеет уравнениеx-2=0.

УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ.

ПОСТРОЕНИЕ ПЛОСКОСТЕЙ

Рассмотрим плоскость, пересекающую все три координатные оси и не проходящую через начало координат. Пусть плоскость задана своим общим уравнением Ax+By+Cz+D=0, где ни один из коэффициентов не равен нулю.

Преобразуем это уравнение.

Ax+By+Cz=-D. Поделим полученное равенство на –D и запишем его в виде:

Тогда, обозначив , приходим к уравнению . Это уравнение и называется уравнением плоскости в отрезках.

Выясним геометрический смысл чисел a, b и c. Если положим y=z=0, то изуравнения x=a. Т.е. данному уравнению удовлетворяет точка с координатами (0; 0; 0). Следовательно, a – это длина отрезка, отсекаемого плоскостью на оси Ox. Аналогично, можно показать, что b и c – длины отрезков, отсекаемых рассматриваемой плоскостью на осях Oy и Oz.

Уравнением плоскости в отрезках удобно пользоваться для построения плоскостей.

Примеры.

Построить плоскость 2x+3y+6z-6=0. Приведём это уравнение к уравнению плоскости в отрезках: .

2x—y-4z-4=0. Рассмотрим еще один способ построения плоскостей. Для построения плоскости достаточно найти три какие-либо её точки, не лежащие на одной прямой. Удобнее всего определять точки пересечения плоскости с осями координат.
2x+5z-10=0. Плоскость параллельна оси Oy. Найдём точки пересечения с осями Ox и Oz.

Плоскость 3x+2y=0 проходит через ось Oz.

2z+5=0, z=-5/2.

Механический смысл векторного произведения — Мегаобучалка

П. 7. Векторное произведение векторов

Определение. Тройкой векторов называется три вектора с общим началом, перечисленных в определенном порядке ( — первый, — второй, — третий) и не лежащих в одной плоскости (некомпланарных).

Определение.Тройка векторов называется «правой», если кратчайший поворот от вектора к вектору , когда смотрим с конца вектора , происходит против часовой стрелки. Если же этот поворот кажется происходящим по часовой стрелке, то тройка векторов называется «левой».

Происхождение названия: если векторы совпадают соответственно с большим, указательным и средним пальцами правой руки – тройка правая, если левой руки – тройка левая.

Смысл декартовой тройки всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.

Определение. Векторным произведением векторов и называется вектор , удовлетворяющий условиям:

1) , 2) , 3) образуют правую тройку. (1)

Обозначение или . Это вектор.

Геометрический смысл векторного произведения

Модуль векторного произведения равен площади параллелограмма, построенного на векторах и . . (2)

Механический смысл векторного произведения

Пусть сила приложена к точке В. Тогда моментом силы относительно точки А называется вектор такой, что , где вектор — плечо АВ, .

2) Пусть материальная точка движется по окружности с центром в точке О,

— линейная скорость движения точки, — радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор такой, что .

Свойства векторного произведения.

1. – коллинеарные векторы. (3)

Доказательство.

Доказательство необходимости: 1) Пусть – ненулевые векторы. Тогда длина векторного произведения тогда и только тогда, когда , т.е. когда . 2) Пусть среди векторов может быть нулевой вектор (или оба нулевые). По определению -вектор можно считать параллельным любому вектору, т.е. пусть .

Доказательство достаточности: 1) Пусть , причем – ненулевые векторы. Тогда длина векторного произведения , так как . 2) Пусть , причем среди векторов может быть нулевой вектор (или оба нулевые). Тогда длина векторного произведения равна нулю, так как длина — вектора равна 0. (что и треб. доказать).

Частный случай:

2. (Пояснение: из-за смены троек)

3. Скалярный квадрат векторного произведения равен квадрату модуля векторного произведения: (следует из 2-го свойства скалярного произведения)

4. Если – действительное число, то

(Пояснение: если одну из сторон параллелограмма увеличить в λ раз, не меняя ее направление, то и площадь увеличиться в λ раз).

5. ,

Перемножаем, строго соблюдая порядок.

Таблица векторного умножения ортов

Углы , , , , ,

; тогда ; длины ортов равны .

Следовательно, исходя из определения векторного произведения, можем записать, что

, , ,

Смешанное произведение векторов, его геометрический смысл и свойства

Содержание:

Смешанное произведение векторов, его геометрический смысл и свойства

Смешанная работа вектора, его геометрический смысл, природа Рассмотрим произведение векторов a, b и c, построенных следующим образом: (Топор б) -с. Где первые два вектора умножаются на вектор, а результатом является скаляр для третьего вектора. Такое произведение называется векторно-скалярным или смешанным произведением трех векторов. Есть явно ряд смешанных продуктов. Проверьте геометрический смысл выражения (а х 6) • стр.

c = —I для слева, где I — высота поля. (A x b) • c = S • (± H), т. Е. (A x b) • c = ± Vy, где V — объем параллелепипеда, образованного векторами a, b и c.

Создает параллелепипед с векторами a, S, c и вектором d = a x b в качестве ребер. Людмила Фирмаль

Следовательно, смешанное произведение трех векторов равно объему параллелепипеда, построенного на основе этих векторов, и, если эти векторы образуют правильную тройку, используйте знак плюс \ VS IS но Знак минус, чтобы сформировать левую тройку. Смешанные рабочие свойства

1. Смешанный продукт имеет циклическую перестановку своих факторов, то есть (a x b) • c = (b x c) • a = (c x a) • 6. Фактически в этом случае не изменяется ни объем параллелепипеда, ни направление ребра. 2. Если знак векторного умножения и скалярного умножения обратный, то есть (a x b) • c = a- (bxc), произведение смеси не изменяется.

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Фактически, (a x b) • c = ■ ± V и a ■ (b × c) — (b × c) • a = ± K. Поскольку тройки векторов a, b, c и b, c, -re находятся в одном и том же направлении, знаки в правой части этих уравнений одинаковы. Следовательно, (a x 6) • c = a (6 x c). Это позволяет записывать смешанные произведения векторов (a x 6) в формате abc без знака векторного скалярного умножения. 3. Смешанные продукты меняют знак при изменении местоположения любых двух векторов фактора. То есть abc = –acb, abc = –bass, abc ––cba.

Фактически такая перестановка эквивалентна перестановке факторов в векторном произведении и меняет знак произведения. 4. Смешанное произведение неплоских векторов a, 6 и c равно нулю, только если они находятся в одной плоскости. Если <abc = 0, a, 6 и c находятся в одной плоскости. Предположим, что это не так. Можно было бы построить параллелепипед с объемом V f 0.

Однако, поскольку abc- ± V}, abc f 0 получается. Людмила Фирмаль

Это противоречит условию, что abc = 0. И наоборот, предположим, что векторы a, 5 и c находятся в одной плоскости. Далее, вектор d-ax b равен d L c, потому что он перпендикулярен плоскости , где существуют векторы a, b и c. Следовательно, d-c = 0, то есть abc = 0. ►

Понимание перекрестного продукта — лучшее объяснение

Взяв два вектора, мы можем записать каждую комбинацию компонентов в сетку:

Эта заполненная сетка представляет собой внешний продукт , который можно разделить на:

Точечное произведение , взаимодействие между аналогичными размерами ( x * x , y * y , z * z )
Перекрестное произведение , взаимодействие между различными измерениями ( x * y , y * z , z * x и т. Д.)

Точечное произведение ($ \ vec {a} \ cdot \ vec {b} $) измеряет сходство, потому что оно накапливает взаимодействия только в совпадающих измерениях. Это простой расчет, состоящий из трех компонентов.

Перекрестное произведение (обозначаемое как $ \ vec {a} \ times \ vec {b} $) должно измерять полдюжины «перекрестных взаимодействий». Расчет выглядит сложным, но концепция проста: накопите 6 индивидуальных различий для получения общей разницы.

Вместо того, чтобы думать: «Когда мне нужно кросс-произведение?» подумайте: «Когда мне нужно взаимодействие между разными измерениями?».

Площадь, например, образована векторами, указывающими в разных направлениях (чем больше ортогональность, тем лучше). Действительно, перекрестное произведение измеряет площадь, охватываемую двумя трехмерными векторами (источник):

(«Перекрестное произведение» предполагает трехмерные векторы, но концепция распространяется на более высокие измерения.)

Щелкнула ли ключевая интуиция? Давайте углубимся в детали.

Определение перекрестного произведения

Скалярное произведение представляет сходство между векторами как одно число:

Например, мы можем сказать, что север и восток на 0% похожи, поскольку $ (0, 1) \ cdot (1, 0) = 0 $.Или что север и северо-восток на 70% похожи ($ \ cos (45) = 0,707 $, помните, что триггерные функции — это проценты). Сходство показывает количество одного вектора, который «проявляется» в другом.

Должно ли перекрестное произведение, разность векторов, тоже быть одним числом?

Давай попробуем. Синус — это процентная разница, поэтому мы могли бы написать:

К сожалению, мы упускаем некоторые детали. Допустим, мы смотрим вниз по оси x: обе точки y и z на 100% от нас.Число вроде «100%» говорит нам о большой разнице, но мы не знаем, что это такое! Нам нужна дополнительная информация, чтобы сказать нам: «разница между $ \ vec {x} $ и $ \ vec {y} $ составляет против » и «разница между $ \ vec {x} $ и $ \ vec {z} $ , что “.

Итак, представим кросс-произведение в виде вектора:

Размер перекрестного произведения — это числовая «величина разницы» (с $ \ sin (\ theta) $ в процентах). Само по себе это не отличает $ \ vec {x} \ times \ vec {y} $ от $ \ vec {x} \ times \ vec {z} $.
Направление перекрестного произведения основано на обоих входных данных: это направление, ортогональное обоим (т. Е. Не благоприятное ни для одного).

Теперь $ \ vec {x} \ times \ vec {y} $ и $ \ vec {x} \ times \ vec {z} $ имеют разные результаты, каждый с величиной, указывающей, что они на «100%» отличаются от $ \ vec {x} $.

(Должно ли скалярное произведение быть векторным результатом? Ну, мы отслеживаем сходство между $ \ vec {a} $ и $ \ vec {b} $. Сходство измеряет перекрытие между исходными векторными направлениями, которое мы уже есть.)

Геометрическая интерпретация

Два вектора определяют плоскость, и векторное произведение указывает в направлении, отличном от обоих (источник):

Вот проблема: есть два перпендикулярных направления. Условно мы предполагаем «правостороннюю систему» (источник):

Если вы держите первые два пальца, как показано на схеме, большой палец будет указывать в направлении перекрестного произведения. Я проверяю правильность ориентации, проводя указательным пальцем от $ \ vec {a} $ до $ \ vec {b} $.Когда направление выяснено, величина перекрестного произведения равна $ | a | | б | \ sin (\ theta) $, который пропорционален величине каждого вектора и «проценту разницы» (синус).

Крестное произведение для ортогональных векторов

Чтобы запомнить правило правой руки, напишите порядок xyz дважды: xyzxyz . Затем найдите узор, который вы ищете:

xy => z ( x крест y — z )
yz => x ( y cross z is x ; мы зациклились на: y to z to x )
zx => y

Теперь, xy и yx имеют противоположные знаки, потому что в нашей установке xyzxyz они идут вперед и назад.

Итак, без формулы вы сможете вычислить:

Опять же, это потому, что пересечение x y положительно z в правой системе координат. Я использовал единичные векторы, но мы могли масштабировать термины:

Расчет перекрестного произведения

Один вектор можно разложить на 3 ортогональные части:

Когда векторы пересекаются, каждая пара ортогональных компонентов (например, $ a_x \ times b_y $) голосует за то, куда должен указывать ортогональный вектор.6 компонентов, 6 голосов, и их сумма является перекрестным произведением. (Подобно градиенту, где каждая ось голосует за направление наибольшего увеличения.)

xy => z и yx => -z (предположим, что $ \ vec {a} $ стоит первым, поэтому xy означает $ a_x b_y $)
yz => x и zy => -x
zx => y и xz => -y

xy и yx борются с ним в направлении z .Если эти члены равны, например, в $ (2, 1, 0) \ times (2, 1, 1) $, то в направлении z отсутствует компонент кросс-произведения (2 — 2 = 0).

Окончательная комбинация:

, где $ \ vec {n} $ — единичный вектор, нормальный к $ \ vec {a} $ и $ \ vec {b} $.

Пусть вас это не пугает:

Всего 6 членов, 3 положительных и 3 отрицательных
Два измерения голосуют за третье (поэтому член z должен иметь только компоненты y и x )
Положительный / отрицательный порядок основан на шаблоне xyzxyz

Если хотите, существует алгебраическое доказательство того, что формула одновременно ортогональна и имеет размер $ | a | | б | \ sin (\ theta) $, но мне нравится интуиция «пропорционального голосования».

Пример времени

Опять же, мы должны делать простые перекрестные произведения в уме:

Почему? Мы пересекли оси x и y , получив z (или $ \ vec {i} \ times \ vec {j} = \ vec {k} $, используя эти единичные векторы). Переход в другую сторону дает $ — \ vec {k} $.

Вот как я рассмотрю более сложные примеры:

Давайте займемся последним членом, z-компонентом. Это (1) (5) минус (4) (2), или 5-8 = -3.Сначала я сделал z , потому что он использует x и y , первые два члена. Попробуйте рассматривать (1) (5) как «вперед» при сканировании от первого вектора ко второму, и (4) (2) как «назад» при перемещении от второго вектора к первому.
Теперь компонент y : (3) (4) — (6) (1) = 12-6 = 6
Теперь компонент x : (2) (6) — (5) (3) = 12-15 = -3

Итак, общая сумма $ (- 3, 6, -3) $, которую мы можем проверить с помощью Wolfram Alpha.

Вкратце:

Перекрестное произведение отслеживает все «перекрестные взаимодействия» между измерениями
Имеется 6 взаимодействий (по 2 в каждом измерении) со знаками на основе порядка xyzxyz

Приложение

Связь с определителем

Вы можете вычислить перекрестное произведение, используя определитель этой матрицы:

Здесь есть четкая связь, поскольку определитель («подписанная площадь / объем») отслеживает вклады от ортогональных компонентов.

Существуют теоретические причины, по которым векторное произведение (как ортогональный вектор) доступно только в 0, 1, 3 или 7 измерениях. Однако перекрестное произведение в виде единственного числа по сути является определяющим фактором (площадь со знаком, объем или гиперобъем в виде скаляра).

Соединение с Curl

Curl измеряет скручивающую силу, которую векторное поле прикладывает к точке, и измеряется вектором, перпендикулярным поверхности. Всякий раз, когда вы слышите «перпендикулярный вектор», начинайте думать «кросс-произведение».

Возьмем «определитель» этой матрицы:

Вместо умножения взаимодействие принимает частную производную. Как и раньше, $ \ vec {i} $ компонент curl основан на векторах и производных в направлениях $ \ vec {j} $ и $ \ vec {k} $.

Связь с теоремой Пифагора

Крест и скалярное произведение подобны ортогональным сторонам треугольника:

Для единичных векторов, где $ | a | = | b | = 1 $, имеем:

Я немного схитрил в сеточной диаграмме, так как мы должны отслеживать квадраты величин (как это сделано в теореме Пифагора).

Продвинутая математика

Перекрестное произведение и друзья расширяются в алгебре Клиффорда и геометрической алгебре. Я все еще изучаю это.

Перекрестные произведения перекрестных продуктов

Иногда бывает такой сценарий:

Во-первых, перекрестное произведение не ассоциативно: порядок имеет значение.

Затем вспомните, что делает кросс-произведение: нахождение ортогональных векторов. Если любые два компонента параллельны ($ \ vec {a} $ параллельно $ \ vec {b} $), то никакие измерения не влияют друг на друга, и перекрестное произведение равно нулю (что переносится на $ 0 \ times \ vec {c} $).

Но это нормально для $ \ vec {a} $ и $ \ vec {c} $ быть параллельными, поскольку они никогда не участвуют напрямую в перекрестном произведении, например:

Ух ты! Как нам вернуться к $ \ vec {j} $? Мы запросили направление, перпендикулярное как $ \ vec {i} $, так и $ \ vec {j} $, и снова сделали это направление перпендикулярным $ \ vec {i} $. «Двойная перпендикулярность» означает, что вы вернулись на исходную ось.

Точечное произведение перекрестных произведений

Теперь возьмем

что происходит? Мы вынуждены сначала выполнить $ \ vec {a} \ times \ vec {b} $, потому что $ \ vec {b} \ cdot \ vec {c} $ возвращает скаляр (одно число), которое нельзя использовать в перекрестном произведении.

Если $ \ vec {a} $ и $ \ vec {c} $ параллельны, что произойдет? Итак, $ \ vec {a} \ times \ vec {b} $ перпендикулярно $ \ vec {a} $, что означает, что оно перпендикулярно $ \ vec {c} $, поэтому скалярное произведение с $ \ vec {c } $ будет нулем.

Я никогда особо не запоминал эти правила, я должен продумывать взаимодействия.

Другие системы координат

Движок Unity — левша, OpenGL (и большинство математических / физических инструментов) — правша. Почему?

В компьютерной игре x идет горизонтально, y идет вертикально, а z идет «в экран».Это приводит к левосторонней системе. (Попробуйте: правой рукой вы увидите, что крест x y должен выходить за пределы экрана).

Приложения перекрестного продукта

Найдите направление, перпендикулярное двум заданным векторам.
Найдите площадь со знаком, охватываемую двумя векторами.
Определите, ортогональны ли два вектора (хотя проверка скалярного произведения 0, вероятно, быстрее).
«Умножьте» два вектора, когда вклад вносят только перпендикулярные поперечные члены (например, определение крутящего момента).
С кватернионами (4d комплексные числа) перекрестное произведение выполняет работу по вращению одного вектора вокруг другого (еще одна статья в разработке!).

Счастливая математика.

Другие сообщения этой серии

Векторное исчисление: понимание точечного произведения
Векторное исчисление: понимание кросс-произведения
Векторное исчисление: понимание потока
Векторное исчисление: понимание расходимости
Векторное исчисление: понимание циркуляции и изгиба
Векторное исчисление: понимание градиента
Пифагорейское расстояние и градиент

geometry — Что представляет собой скалярное произведение двух векторов?

Как указывали другие ответы, скалярное произведение $ \ vec {a} \ cdot \ vec {b} $ связано с углом $ \ theta $ между $ \ vec {a} $ и $ \ vec {b} $ через:

$$ \ vec a \ cdot \ vec b = \ Vert \ vec a \ Vert_2 \, \ Vert \ vec b \ Vert_2 \, \ cos \ theta $$

Предполагая, что $ a $ и $ b $ указывают в одинаковых направлениях, i.е., $ \ theta \ leq 90 ° $, мы можем визуализировать, что означает эта связь (с этого момента пропуская векторные стрелки и индекс евклидовой нормы):

$ p $ — вектор, полученный в результате ортогональной проекции $ a $ на $ b $. Поскольку $ \ cos $ — это отношение между соседним катетом ($ p $) и гипотенузой ($ a $) в прямоугольном треугольнике, то есть

$$ \ cos \ theta = \ frac {\ Vert p \ Vert} {\ Vert a \ Vert}, $$

получаем за внутренний продукт:

$$ a \ cdot b = \ Vert a \ Vert \, \ Vert b \ Vert \, \ frac {\ Vert p \ Vert} {\ Vert a \ Vert} = \ Vert p \ Vert \ Vert b \ Vert $ $

Итак, внутреннее произведение — это длина вектора $ p $, проекция $ a $ на $ b $, умноженная на длину $ b $.Если $ a $ и $ b $ указывают в противоположных направлениях, то есть $ 90 ° <\ theta \ leq 180 ° $, точечное произведение будет отрицательным: $ a \ cdot b = - \ Vert p \ Vert \ Vert b \ Верт $

Проблема в том, что соотношение между скалярным произведением и углом $ \ theta $ по сути не задано. По определению:

$$ a \ cdot b = \ sum_i a_i b_i $$

Итак, нам нужно найти связь между этим и косинусом. Из определения скалярного произведения мы видим, что он масштабируется пропорционально входным векторам, поэтому для неединичных векторов $ u $ и $ v $ с соответствующими единичными векторами $ \ hat {u} $ и $ \ hat { v} $:

$$ u \ cdot v = \ Vert u \ Vert \ cdot \ Vert v \ Vert \ cdot \ hat {u} \ cdot \ hat {v} $$

Для простоты предположим, что $ a $ и $ b $ являются единичными векторами.2 \\ & = 2 — (2-2 \ sum_i b_i a_i) \\ & = 2 \ sum_i b_i a_i \\ \ Vert p \ Vert & = \ sum_i b_i a_i \ end {align}

q.e.d.

Перекрестное произведение | Brilliant Math & Science Wiki

Все эти свойства могут быть выведены из определения перекрестного произведения и оставлены читателям в качестве упражнений для проверки.

Для двух векторов v⃗ = 3i − 2j − k \ vec {v} = 3i-2j-kv = 3i − 2j − k и w⃗ = 4i + 3j + 2k \ vec {w} = 4i + 3j + 2kw = 4i + 3j + 2к, найти

A) v⃗ × w⃗ \ \ vec {v} \ times \ vec {w} v × w
B) w⃗ × v⃗ \ \ vec {w} \ times \ vec {v} w × v.

A) v⃗ × w⃗: \ \ vec {v} \ times \ vec {w}: v × w:
Мы можем получить векторное произведение, вычислив определитель: ∣ijk3−2−1432∣ = (- 2 (2) −3 (−1)) i− (3 (2) −4 (−1)) j + (3 (3) −4 (−2)) k = −i − 10j + 17k. \ Begin {align} \ begin {vmatrix} i & j & k \\ 3 & -2 & -1 \\ 4 & 3 & 2 \ end {vmatrix} & = \ big (-2 (2) -3 (-1) \ big) i- \ big (3 (2) -4 (-1) \ big) j + \ big (3 (3) -4 (-2 ) \ большой) к \\ & = — i-10j + 17к. \ end {align} ∣∣∣∣∣∣ i34 j − 23 k − 12 ∣∣∣∣∣∣ = (- 2 (2) −3 (−1)) i− (3 (2 ) −4 (−1)) j + (3 (3) −4 (−2)) k = −i − 10j + 17k.

B) w⃗ × v⃗: \ \ vec {w} \ times \ vec {v}: w × v:
Мы могли бы просто выполнить те же шаги, но более быстрым способом было бы использовать теорему 1 выше: w⃗ × v⃗ = — (v⃗ × w⃗) = — (- i − 10j + 17k) = i + 10j − 17k.□ \ begin {align} \ vec {w} \ times \ vec {v} & = — (\ vec {v} \ times \ vec {w}) \\ & = — (- i-10j + 17k) \\ & = i + 10j-17k. \ _ \ квадрат \ end {align} w × v = — (v × w) = — (- i − 10j + 17k) = i + 10j − 17k. □

Есть также некоторые свойства, которые связывают перекрестное произведение и скалярное произведение:

Первые два свойства легко понять, если мы поймем, что перекрестное произведение выводит вектор, перпендикулярный обоим векторам, и что скалярное произведение перпендикулярных векторов равно нулю. Остальные похожи на первые два из-за свойств скалярных и перекрестных произведений, и читатель должен их доказать.

Для векторов a⃗ = (- 1,2,2), b⃗ = (0,3,4), c⃗ = (1, −2,0), \ vec {a} = (- 1,2,2), \ vec {b} = (0,3,4), \ vec {c} = (1, -2,0), a = (- 1,2,2), b = (0,3,4), c = (1, −2,0), покажем, что они действительно удовлетворяют указанным выше четырем свойствам с A) по D).

A) a⃗⋅ (a⃗ × b⃗): \ \ vec {a} \ cdot \ big (\ vec {a} \ times \ vec {b} \ big): a⋅ (a × b):
У нас есть a⃗ × b⃗ = [ijk − 122034] = (2,4, −3) ⟹ a⃗⋅ (a⃗ × b⃗) = (- 1) (2) +2 (4) +2 (−3) = 0. \ begin {выровнено} \ vec {a} \ times \ vec {b} = \ begin {bmatrix} i & j & k \\ -1 \ quad & 2 \ quad & 2 \ quad \\ 0 & 3 & 4 \ end { bmatrix} = (2,4, -3) \ подразумевает \ vec {a} \ cdot \ big (\ vec {a} \ times \ vec {b} \ big) = (- 1) (2) +2 (4) +2 (-3) = 0.\ end {align} a × b = ⎣⎡ i − 10 j23 k24 ⎦⎤ = (2,4, −3) ⟹a⋅ (a × b) = (- 1) (2) +2 (4) +2 (−3) = 0,

B) b⃗⋅ (a⃗ × b⃗): \ \ vec {b} \ cdot \ big (\ vec {a} \ times \ vec {b} \ big): b⋅ (a × b):
Мы имеют a⃗ × b⃗ = [ijk − 122034] = (2,4, −3) ⟹ b⃗⋅ (a⃗ × b⃗) = 0 (2) +3 (4) +4 (−3) = 0. \ begin {align} \ vec {a} \ times \ vec {b} = \ begin {bmatrix} i & j & k \\ -1 \ quad & 2 \ quad & 2 \ quad \\ 0 & 3 & 4 \ end {bmatrix} = (2,4, -3) \ подразумевает \ vec {b} \ cdot \ big (\ vec {a} \ times \ vec {b} \ big) = 0 (2) +3 (4) +4 (-3) = 0.\ end {align} a × b = ⎣⎡ i − 10 j23 k24 ⎦⎤ = (2,4, −3) ⟹b⋅ (a × b) = 0 (2) +3 (4) +4 (−3) = 0,

C) a⃗ × (b⃗ × c⃗) = (a⃗⋅c⃗) b⃗− (a⃗⋅b⃗) c⃗: \ \ vec {a} \ times \ big (\ vec {b} \ times \ vec {c} \ big) = (\ vec {a} \ cdot \ vec {c}) \ vec {b} — \ big (\ vec {a} \ cdot \ vec {b} \ big) \ vec {c}: a × (b × c) = (a⋅c) b− (a⋅b) c:
Имеем a⃗ × (b⃗ × c⃗) = (- 14,13, −20) \ vec {a} \ times \ big ( \ vec {b} \ times \ vec {c} \ big) = (- 14,13, -20) a × (b × c) = (- 14,13, −20), что останется для читателей чтобы показать, как. потом a⃗⋅c⃗ = −1 (1) +2 (−2) +2 (0) = — 5a⃗⋅b⃗ = −1 (0) +2 (3) +2 (4) = 14a⃗ × (b⃗ × c⃗) = (a⃗⋅c⃗) b⃗− (a⃗⋅b⃗) c⃗⇒ (−14,13, −20) = — 5 (0,3,4) −14 (1, −2,0) = (0,15, — 20) — (14, −28,0) = (- 14,13, −20).\ begin {выровнено} \ vec {a} \ cdot \ vec {c} & = — 1 (1) +2 (-2) +2 (0) \\ & = — 5 \\ \ vec {a} \ cdot \ vec {b} & = — 1 (0) +2 (3) +2 (4) \\ & = 14 \\ \ vec {a} \ times \ big (\ vec {b} \ times \ vec {c} \ big) & = (\ vec {a} \ cdot \ vec {c}) \ vec {b} — \ big (\ vec {a} \ cdot \ vec {b} \ big) \ vec {c} \\ \ Rightarrow (-14,13, -20) & = — 5 (0,3,4) -14 (1, -2,0) \\ & = (0,15, -20) — (14, -28,0) \\ & = (- 14,13, -20). \ end {align} a⋅ca⋅ba × (b × c) ⇒ (−14,13, −20) = −1 (1) +2 (−2) +2 (0) = — 5 = −1 (0) +2 (3) +2 (4) = 14 = (a⋅c) b− (a⋅b) c = −5 (0,3,4) −14 (1, −2,0) = (0,15, −20) — (14, −28,0) = (- 14,13, −20).

D) (a⃗ × b⃗) × c⃗ = (a⃗⋅c⃗) b⃗− (b⃗⋅c⃗) a⃗: \ \ big (\ vec {a} \ times \ vec {b} \ big) \ times \ vec {c} = (\ vec {a} \ cdot \ vec {c}) \ vec {b} — \ big (\ vec {b} \ cdot \ vec {c} \ big) \ vec {a}: (a × b) × c = (a⋅c) b− (b⋅c) a:
Имеем a⃗⋅c⃗ = −1 (1) +2 (−2) +2 (0) = — 5b⃗⋅c⃗ = 0 (1) +3 (−2) +4 (0) = — 6 (a⃗ × b⃗) × c⃗ = (a⃗⋅c⃗) b⃗− (b⃗⋅c⃗) a⃗⇒ (−6, −3, −8) = — 5 (0,3,4) — (- 6) (- 1,2,2) = (0, −15,20) — (6, −12, −12) = (- 6, −3, −8). □ \ begin {align} \ vec {a} \ cdot \ vec {c} & = — 1 (1) +2 (-2) +2 (0) \\ & = — 5 \\ \ vec {b} \ cdot \ vec {c} & = 0 (1) +3 (-2) +4 (0) \\ & = — 6 \\ \ big (\ vec {a} \ times \ vec {b} \ big) \ times \ vec {c} & = (\ vec {a} \ cdot \ vec {c}) \ vec {b} — \ big (\ vec {b} \ cdot \ vec {c} \ big) \ vec {a} \\ \ Rightarrow (-6, -3, -8) & = — 5 (0,3,4) — (- 6) (- 1,2,2) \\ & = (0, -15,20) — (6, -12, -12) \\ & = (- 6, -3, -8).\ _\квадратный \ end {align} acb⋅c (a × b) × c⇒ (−6, −3, −8) = −1 (1) +2 (−2) +2 (0) = — 5 = 0 (1) +3 (−2) +4 (0) = — 6 = (a⋅c) b− (b⋅c) a = −5 (0,3,4) — (- 6) (- 1 , 2,2) = (0, −15,20) — (6, −12, −12) = (- 6, −3, −8). □

Перекрестный продукт — Викиверситет

Перекрестное произведение , также известное как «векторное произведение», представляет собой вектор, связанный с парой векторов в трехмерном пространстве.

Перекрестное произведение перпендикулярно векторам a и b и указывает в направлении большого пальца правой руки, когда пальцы сгибаются в направлении движения от a к b.Если бы порядок векторов был обратным, пальцы загибались бы в противоположном направлении, поэтому перекрестное произведение будет указывать в противоположном направлении.

Перекрестное произведение пишется со знаком времени ^[1] между векторами. Если C → {\ displaystyle {\ vec {C}}} быть перекрестным произведением A → {\ displaystyle {\ vec {A}}} умноженное на B → {\ displaystyle {\ vec {B}}}, мы имеют:

C → = A → × B → {\ displaystyle {\ vec {C}} = {\ vec {A}} \ times {\ vec {B}}}

Величина C → {\ displaystyle {\ vec {C}}} — произведение длин двух векторов, умноженное на синус угла между ними:

|| A → × B → || = ABsin⁡θ {\ displaystyle || {\ vec {A}} \ times {\ vec {B}} || = AB \ sin \ theta},

, где A = || A → || {\ displaystyle A = || {\ vec {A}} ||} и B = || B → || {\ displaystyle B = || {\ vec {B }} ||} и указывая в направлении, перпендикулярном плоскости, образованной двумя векторами:

Это оставляет двусмысленность — он может указывать в любом из двух противоположных направлений.Неоднозначность разрешается «правилом правой руки» — если пальцы правой руки (кроме большого пальца) согнуты, как будто изображая вращение первого вектора во вторую (следуя угловому направлению наименьшего угла между ними), затем большой палец указывает в направлении перекрестного произведения.

Из этого определения можно вывести несколько свойств:

Это однородных в каждом аргументе: (λA →) × B → = A → × (λB →) = λ (A → × B →) {\ displaystyle (\ lambda {\ vec {A}}) \ раз {\ vec {B}} = {\ vec {A}} \ times (\ lambda {\ vec {B}}) = \ lambda ({\ vec {A}} \ times {\ vec {B}}) \,}.
Если два вектора указывают в одном или противоположных направлениях, их векторное произведение равно нулю. Это потому, что синус 0 ° или 180 ° равен нулю. К счастью, это так, потому что в этом случае нельзя было применить правило правой руки.
Перекрестное произведение двух векторов перпендикулярно каждому из этих векторов.
Это антикоммутативно: A → × B → = −B → × A → {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = — {\ vec {B}} \ times {\ vec {A}}}.
Перекрестное произведение имеет внутреннюю «правоту» или хиральность из-за использования правила правой руки.Если посмотреть в зеркало на два вектора и их перекрестное произведение, будет казаться, что перекрестное произведение указывает в неправильном направлении.

Перекрестное произведение имеет замечательную, удобную и элегантную алгебраическую формулировку. Если компоненты вектора в трехмерном декартовом пространстве заданы с индексами: Ax {\ displaystyle A_ {x}}, Ay {\ displaystyle A_ {y}} и Az {\ displaystyle A_ {z}}, то перекрестное произведение векторов A → {\ displaystyle {\ vec {A}}} и B → {\ displaystyle {\ vec {B}}} дается следующим образом:

(A → × B →) x = (AyBz − AzBy) {\ displaystyle ({\ vec {A}} \ times {\ vec {B}}) _ {x} = (A_ {y} B_ {z} -A_ {z} B_ {y})}

(A → × B →) y = (AzBx − AxBz) {\ displaystyle ({\ vec {A}} \ times { \ vec {B}}) _ {y} = (A_ {z} B_ {x} -A_ {x} B_ {z})}

(A → × B →) z = ( AxBy − AyBx) {\ displaystyle ({\ vec {A}} \ times {\ vec {B}}) _ {z} = (A_ {x} B_ {y} -A_ {y} B_ {x})}

Следует подчеркнуть, что эта формула работает только в том случае, если компоненты векторов описаны в декартовом пространстве.AxAyAzBxByBz | {\ displaystyle {\ vec {A}} \ times {\ vec {B}} = {\ begin {vmatrix} {\ hat {x}} & {\ hat {y}} & {\ hat {z} } \\ A_ {x} & A_ {y} & A_ {z} \\ B_ {x} & B_ {y} & B_ {z} \ end {vmatrix}}}

Теория определителей говорит нам, что определитель меняет знак, если любые две строки матрицы меняются местами, поэтому при замене двух векторов знак меняется — перекрестное произведение антикоммутативно. Теория детерминанты также говорят нам, что он однороден. Также можно разобраться, что это дистрибутив:

(A → + B →) × C → = (A → × C →) + (B → × C →) {\ displaystyle ({\ vec {A}} + {\ vec {B}}) \ times {\ vec {C}} = ({\ vec {A}} \ times {\ vec {C}}) + ({\ vec {B}} \ times {\ vec {C}})}

Эквивалентность двух определений [править | править источник]

Фигура 1.Операция «звезда» — это проекция вектора на плоскость P {\ displaystyle P \,}.
Важно доказать, что геометрическое и алгебраическое определения перекрестного произведения совпадают. {*}}, как показано на рисунке 5.{*} \ times {\ vec {C}}}
И по лемме 1 это становится
A → × C → + B → × C → = (A → + B →) × C → {\ displaystyle {\ vec {A}} \ times {\ vec {C}} + {\ vec { B}} \ times {\ vec {C}} = ({\ vec {A}} + {\ vec {B}}) \ times {\ vec {C}}}
QED
Из-за антисимметрии перекрестного произведения оно также является дистрибутивным во втором аргументе:
C → × (A → + B →) = (C → × A →) + (C → × B →) {\ displaystyle {\ vec {C}} \ times ({\ vec {A}} + {\ vec {B}}) = ({\ vec {C}} \ times {\ vec {A}}) + ({\ vec {C}} \ times {\ vec {B}})}
Теорема: геометрическое и алгебраическое определения перекрестного произведения совпадают.{\ displaystyle {\ vec {A}} \ times {\ vec {B}} = (A_ {y} B_ {z} -A_ {z} B_ {y}) \ {\ hat {x}} + (A_ {z} B_ {x} -A_ {x} B_ {z}) \ {\ hat {y}} + (A_ {x} B_ {y} -A_ {y} B_ {x}) \ {\ hat { z}}}
, что совпадает с алгебраическим определением.
Q.E.D.
↑ Настоящая, старомодная, временная вывеска. Не звездочка.
Кросс-произведение векторов — обзор
1.3 Основные концепции релятивистской квантовой механики
Третий вопрос, заданный выше: «Как нужно модифицировать квантовую теорию, изучаемую на курсах химии бакалавриата, чтобы учесть релятивистские эффекты?», требует несколько более подробного ответа.Рассмотрим нерелятивистский не зависящий от времени SE для электрона с потенциальной энергией V ,
(11) hˆnrelψnrel = V + Tˆψnrel = V + 12mepˆ⋅pˆψnrel = ψnrelEnrel
Как уже упоминалось, член кинетической энергии получается путем квантования нерелятивистская кинетическая энергия T = p ² / (2 m _e ), используя pˆ = −iℏ∇. Проблема с релятивистским случаем заключается в следующем: как квантовать выражение квадратного корня (6) для релятивистской энергии? Одна из возможностей — использовать расширение корня в c ^{— 2}, как в уравнении.(7), а затем квантовать импульс. Однако это приводит к сильно сингулярным операторам, и спин, естественно, не возникает из этого подхода. Другая возможность — квантовать Вт ² уравнения. (5) и решим уравнение типа Hˆ2ψ = ψE2. Это действительно представляет собой релятивистское квантово-теоретическое уравнение (названное в честь Клейна и Гордона). Оказалось, что это неправильное уравнение для частиц со спином 1/2 (таких как электроны), и есть другие проблемы, связанные с уравнением, связанным с тем фактом, что в его зависящей от времени версии производные по времени имеют второй заказ [11].
Дирак утверждал, что релятивистский квантовый гамильтониан должен быть линейным по импульсу, так что временные и пространственные производные появляются в первом порядке в зависящем от времени волновом уравнении. ⁹ Соответственно, он предложил линеаризацию квадратного корня выражения (6) в виде
(12) W = me2c4 + c2p2 = mec2β + cα · p
Это приводит к гамильтониану Дирака при квантовании
(13 ) hˆD = V + mec2β + cα⋅pˆ
Тогда возникает вопрос: что такое β и вектор ¹⁰ α = ( α _x , α _y , α _z )? Взяв квадрат с обеих сторон уравнения.(12) и предполагая, что p коммутирует с β и α , дает ( u , v ∈ { x , y , z })
(14 ) m2c4 + c2p2 = me2c4β4 + c2∑u, vpupvαuαv + mec3∑upuβαu + αuβ
Отсюда следует, что ¹¹
(15) β2 = 1, αuαv + αvαu = 2δuv, βα0 9 + αuβ000, такое, что правая часть уравнения. (14) равна левой части. Эти условия не могут быть выполнены, если β и α _u являются числами.Вместо этого можно удовлетворить условиям с набором матриц 4 × 4 (или с матрицами более высокой четной размерности), потому что матричные произведения, в отличие от чисел, обычно не коммутируют. Стандартное представление матриц Дирака:
(16) β = 1000010000−10000−1, αx = 0001001001001000, αy = 000 − i00i00 − i00i000, αz = 0010000−110000−100
В уравнении. (15), тогда «0» следует интерпретировать как матрицу, заполненную нулями, а «1» соответствует единичной матрице 4 × 4 (1 на диагонали, ноль в другом месте).См. Также упражнение 2.
Возможно, читатель заметил, что недиагональные блоки 2 × 2 из α -матриц являются спиновыми матрицами Паули
(17) σx = 0110, σy = 0 − ii0, σz = 100−1
, которые можно сгруппировать в векторный оператор σ = ( σ _x , σ _y , σ _z ). Оператор электронного спина Sˆ = 1 / 2σℏ. Существует удобное обозначение матриц Дирака в виде блоков 2 × 2, в которых используются матрицы Паули:
(18) β = 100-1, α = 0σσ0
Каждый элемент матриц в уравнении.(18) представляет собой блок 2 × 2, где «0» представляет блок нулей, а «1» представляет единичную матрицу (а не блок 2 × 2, заполненный единицей). В этих разделенных обозначениях одноэлектронный гамильтониан Дирака уравнения (13) читается как
(19) hˆD = V + mec2β + cα · pˆ = V + mec2cσ · pˆcσ⋅pˆV − mec2
Этот вид сильно отличается от нерелятивистской SE. Более того, поскольку гамильтониан Дирака имеет матричную структуру 4 × 4, волновая функция должна быть четырехкомпонентным объектом
(20) ψD = ψ1ψ2ψ3ψ4 = ψUψL, ψU = ψ1ψ2, ψL = ψ3ψ4
Каждый из ψ _i — это функция трехмерного пространства.Квадратные скобки указывают разделение обозначений, соответствующих формуле. (19), где U обозначает два верхних, а L обозначает два нижних из четырех компонентов волновой функции. Обозначения, обозначающие «большой» и «малый» компоненты, чаще используются в соответствующей литературе, при этом малым компонентом является ψ ^L для электронных состояний. Волновая функция нормирована,
(21) 1 = ∫ψ † ψdV = ∫ (ψ1, ψ2, ψ3, ψ4) ⁎ψ1ψ2ψ3ψ4dV = ∫ψU † ψU + ψL † ψLdV
ψ _i не являются независимыми. друг от друга, но взаимосвязаны пространственной и спиновой симметрией физической задачи и матричной структурой hˆD.Наличие оператора спина в hˆD указывает на то, что многокомпонентный характер оператора и волновой функции так или иначе связан со спиновыми степенями свободы электрона. Поэтому четырехкомпонентная волновая функция Дирака также называется четырехспинором. Верхний и нижний компоненты, ψ ^U , ψ ^L , являются двухспинорами.
Прежде чем продолжить, мы установили нуль шкалы энергии на + mc ², как в уравнении.(8). Для согласованности нам нужно вычесть mc ² из потенциальной энергии в уравнении. (19), что эквивалентно замене
(22) β = 100−1 → β ′ = 000−2
в уравнении. (19). В конечном итоге ДЭ для электрона имеет вид
(23) hˆDψD = Vcσ · pˆcσ · pˆV − 2mec2ψUψL = ψUψLE
Это уравнение может не иметь четко определенного нерелятивистского предела, c → ∞, потому что не фигурируют в знаменателях. Похоже, что весь оператор просто уходит в бесконечность при c → ∞.Однако нерелятивистский предел действительно содержится в формуле. (23). Сначала запишем два уравнения для ψ ^U и ψ ^L явно:
(24a) VψU + cσ · pˆψL = ψUE
(24b) cσ · pˆψU + V − 2mec2ψL = ψL3
Из второго уравнения получаем
(25) ψL = XˆψU, ψU = Xˆ − 1ψL, где Xˆ = 12meckσ · pˆ
, где
(26) k = 1 − V − E2mec2−1 = 1 + ∑n = 1∞V − E2mec2n
Из-за множителя 1 / (2 c ) в уравнении. (25), ψ ^L традиционно называют «малым» компонентом.Это действительно обычно намного меньше, чем верхний компонент ψ ^U . Мы подставляем уравнение. (25) в уравнение. (24a) и получить релятивистское уравнение для верхних компонент
(27) hˆESCψU = V + 12meσ · pˆkcσ · pˆψU = ψUE
Исключаются нижние (малые) компоненты четырехкомпонентной волновой функции. Поэтому процедуру часто называют удалением мелких компонентов (ESC). Процедура показывает, что в принципе можно проводить релятивистские квантовые вычисления только с одной из двухспинорных компонент, ψ ^U или ψ ^L , поскольку другая компонента может быть создана с помощью оператора Xˆ или Xˆ − 1, как в уравнении.(25). Уравнение ESC не имеет большого практического значения, поскольку оператор зависит от энергии. Кроме того, нормализация волновой функции требует учета вкладов от обоих компонентов в уравнение. (21).
В последние годы был достигнут огромный прогресс в разработке процедур, позволяющих строить не зависящие от энергии формально точные двухкомпонентные релятивистские одноэлектронные гамильтонианы, которые можно использовать для релятивистских вычислений. Этот маршрут может быть более эффективным при четырехкомпонентных вычислениях, потому что нужно оптимизировать и хранить только две компоненты волновой функции вместо четырех, хотя четырехкомпонентные методы также становятся очень быстрыми.¹² Кроме того, существует множество вычислительно эффективных приближенных («квазирелятивистских») двухкомпонентных гамильтонианов, доступных в пакетах квантово-химического программного обеспечения, которые позволяют исследователям выполнять достаточно точные релятивистские вычисления для атомов и молекул. Как это часто бывает, эффективность достигается за счет введения приближений.
Для конечного потенциала В (конечные ядра) k переходит в 1, когда скорость света стремится к бесконечности.Позже мы можем взять предел точечного ядра, что оставляет k → 1 в качестве нерелятивистского предела. Из уравнения. (27), тогда получаем
(28) hˆnrelψ = V + 12meσ⋅pˆσ⋅pˆψ = ψE
Читателю предлагается (Упражнение 3) использовать определение матриц Паули, чтобы подтвердить, что
(29) σ ⋅pˆσ⋅pˆ = 1001pˆ⋅pˆ
Следовательно, уравнение. (28) во многом эквивалентно нерелятивистской СЭ. Волновые функции могут быть выбраны в качестве собственных функций σ _z или любой другой линейной комбинации матриц Паули, а двухспинорная природа имеет значение только для спиновых факторов.С σ _z собственных функций,
ψr, «спин» = ψrtimes10or01
, где ψ ( r ) является решением уравнения. (11). Следовательно, ДЭ действительно включает нерелятивистский предел, хотя и не очевидным образом. Спин электрона естественным образом возникает из релятивистской теории электрона и входит в нерелятивистский предел по формуле (2). (28).
Вместо того, чтобы идти за нерелятивистским пределом, сохраняя некоторые члены в разложении k в уравнении.(26) дает приближенные двухкомпонентные релятивистские гамильтонианы. Например, в порядке c ^{— 2} получается (см. Упражнения 4 и 5) ¹³
(30) hˆrel = hˆnrel + 14me2c2pˆV − Epˆ + i4me2c2σ⋅pˆV × pˆ
. заказ c ^{— 2} представляет собой скалярные релятивистские поправки. Последний член, зависящий от спина, отвечает за спин-орбитальное взаимодействие. Приближенный гамильтониан зависит от энергии и поэтому не имеет большого практического применения.Однако можно подумать об использовании его для теории возмущений, где сначала вычисляется нормализованная нерелятивистская волновая функция, а затем используется уравнение. (30) с нерелятивистской энергией E для вычисления младшего порядка c ^{— 2} поправки к энергии. В порядке возмущения выше, чем самый низкий, необходимо учитывать как расширения c ^{— 2} из ψ ^L и ψ ^U , так и члены более высокого порядка в операторе.
С учетом перенормировки верхних компонент волновой функции (см. [12], глава 17) релятивистский двухкомпонентный гамильтониан порядка c ^{— 2} превращается в оператор Паули
(31 ) hˆPauli = hˆnrel − pˆ48me3c2 + ℏ2∇2V8mec2 + i4me2c2σ⋅pˆV × pˆ
Энергия возмущения первого порядка, взятая с нерелятивистской волновой функцией, 〈ψnrel | hˆrel − hˆnrel | ψnrel | . (30) и (31) (операторы SO идентичны).Стоит выделить несколько особенностей оператора Pauli. Первый член, называемый членом массы-скорости, может рассматриваться как квантованная версия члена квадратного корня разложения в уравнении ( p ⁴). (7). Этот термин обычно интерпретируется как поправка к кинетической энергии, связанной с релятивистским увеличением массы электрона (член массы-скорости). Второй оператор в правой части уравнения. (31) можно рассматривать как поправку к потенциальной энергии, которая возникает из-за того факта, что электростатическое взаимодействие между электроном и ядром не является мгновенным (термин Дарвина).Последний член — это оператор связи SO. Оператор Паули содержит сильно сингулярные члены, которые приводят к вариационному коллапсу и вызывают проблемы также при расчетах по теории возмущений, за исключением низшего порядка. Поэтому его использование не рекомендуется. Однако он имеет характерные компоненты двухкомпонентных релятивистских гамильтонианов, которые часто используются: есть скалярные релятивистские (бессиновые) члены и есть SO-связь. Для многоэлектронных систем есть дополнительные члены, похожие на члены одноэлектронного гамильтониана, но с потенциалом отталкивания электронов, заменяющим V , и новые спин-зависимые члены, которые возникают из релятивистских поправок к электрон-электронному взаимодействию.
Пример для вариационно устойчивого приближенного двухкомпонентного оператора получается следующим образом: Переписывая безразмерный объект k уравнения. (26) как
(32) k = 1 − V − E2mec2−1 = 2mec22mec2 − V1 + E2mec2 − V − 1
и приблизительно k как
(33) K = 2mec22mec2 − V≈k
взяв только нулевой порядок разложения правой части уравнения. (32) дает гамильтониан, который часто используется для релятивистских расчетов ЯМР. Это называется регулярным приближением нулевого порядка (ZORA) или гамильтонианом Чанга – Пелисье – Дюрана [13,14].Его версия без полей ¹⁴ читает
(34a) hˆZORA = V + 12meσ⋅pˆKσ⋅pˆ
(34b) = V + 12mepˆ⋅Kpˆ + i2meσ⋅pˆK × pˆ
Как и другие двухкомпонентные релятивистские операторы, гамильтониан ZORA можно разделить на скалярную и SO-часть (переход от формул 34a к 34b, см. упражнение 4). Нерелятивистский предел дается K → 1. Поскольку в выражении присутствует потенциал V , K зависит от положения. На рис. 3 показан график Kr для атома Hg. Видно, что K сильно отличается от K в областях, близких к ядру, где потенциал достигает сравнимых величин, как mc ².Для точечного ядра K → 0 при r → 0. Для конечного ядра K остается конечным, но небольшим, вблизи и внутри ядра. Видно, что электронный потенциал, экранирующий ядерный заряд, имеет значение для значений r , соответствующих внутреннему и внешнему ядру, валентной оболочке и далее. ¹⁵
Рис. 3. Кинематический фактор ZORA K для атома Hg как функция расстояния от ядра. Синий (сплошной): используется V ( r ) из численного расчета DFT с конечным ядром.Красный (пунктир): Использование В ( r ) = потенциал только ядра для точечного ядра с зарядом Z = 80 в выражении для K. Среднеквадратичный радиус ядра составляет 5,5 × 10 ^{— 5} Å. [4].
ZORA, как известно, является хорошим приближением для валентных орбиталей в HAs, а также для связывания и орбиталей неподеленных пар в молекулах с HAs. Из уравнения. (32) обрезание правой части нулевого порядка оправдано, пока E мало. Это верно для валентных орбиталей, даже в HAs, но не верно для глубоких ядерных орбиталей в тяжелых элементах.Для расчетов молекулярных свойств, которые являются «химическими» в том смысле, что они определяются валентными орбиталями, ZORA является подходящим приближенным релятивистским методом. Существуют и другие вариационно устойчивые приближенные, а также формально точные двухкомпонентные подходы, которые используются для расчетов ЯМР (избранные ссылки см. В разделе 2.2). Эти операторы, как правило, не имеют компактных простых операторных представлений, в частности, для членов, зависящих от магнитного поля. Поэтому для целей этой главы структура ZORA, хотя и приблизительная, используется для иллюстрации различий между четырехкомпонентными, двухкомпонентными релятивистскими и нерелятивистскими операторами.
Прежде чем перейти к обсуждению параметров ЯМР, мы кратко обсудим еще несколько аспектов одноэлектронного оператора SO. Для сферически-симметричного ядерного потенциала В ( r ) = — Ze ² / (4 πε ₀ r ) (т.е. для атомов ¹⁶), в операторе Паули СО
pˆV = −iℏ∇V = iℏZe24πε0rr3
(см. Упражнение 6). Напомним, что оператор углового момента имеет вид Lˆ = r × pˆ. Кроме того, σℏ = 2Sˆ.Таким образом, SO-оператор электрона для атома может быть записан как
(35) hˆSO = Ze28πε0me2c2Sˆ⋅Lˆr3 = Ze28πε0me2c2Lˆ⋅Sˆr3
В упражнениях 7 и 8 свойства этого оператора исследуются более подробно. В упражнении 9 читатель может рассчитать влияние взаимодействия SO на энергию атомизации молекулы TlH. Как уже упоминалось в разделе 1.2, оператор SO приводит к расщеплению вырожденных состояний в атомной оболочке с заданным угловым моментом ℓ . Собственные функции больше не являются проекциями чистого спина, а смешивают α (↑) со спином β (↓).SO-взаимодействие в атомах также смешивает состояния с разными магнитными квантовыми числами m _ℓ . Как будет показано ниже, сочетание SO может иметь сильное влияние на химические сдвиги ЯМР в системах с тяжелыми элементами.
Наконец, необходимо отметить, что рассмотрение электронной корреляции в теории релятивистской электронной структуры является очень активной областью исследований (см. [15] и обзоры, перечисленные в разделе 6), как и расчет спектроскопические свойства, такие как параметры ЯМР с помощью методов релятивистской квантовой химии.В тематических исследованиях, представленных в этой главе, использовалась некоторая форма приближения к проблеме электронной корреляции. Для выбранных примеров этому способствовало использование ДПФ, а приближенный двухкомпонентный гамильтониан использовался для учета релятивистских эффектов в расчетах. Относительно конкретных вопросов ДПФ в релятивистских вычислениях, в частности, общего использования нерелятивистских функционалов в сочетании с релятивистскими плотностями, см. [16].
Подводя итог этому разделу:
•
Релятивистское квантовое уравнение для электрона, разработанное Дираком, является четырехкомпонентным уравнением.Электронный спин естественно возникает из релятивистской теории.
•
Уравнения можно преобразовать в двухкомпонентную форму. Для релятивистских квантово-химических расчетов доступны приближенные и (в принципе) точные двухкомпонентные гамильтонианы.
•
Для c → ∞ решения DE и его двухкомпонентные версии становятся эквивалентными решениям SE (со спином).
•
Для многоэлектронных систем необходимо также учитывать релятивистские эффекты для электрон-электронного взаимодействия.Это активный объект исследований, наряду с разработкой точных и эффективных четырех- и двухкомпонентных релятивистских методов для расчета спектроскопических свойств, таких как параметры ЯМР.
•
Обычно существует различие между скалярными релятивистскими эффектами (от операторов без спина) и SO-связью. Часто для квантово-химических расчетов используются приближенные скалярно-релятивистские методы (без учета SO-связи). В этом случае вычислительная установка очень похожа на обычные нерелятивистские вычисления с реальными «однокомпонентными» спиновыми орбиталями.К этой категории также относятся расчеты со свободными от спина эффективными остовными потенциалами, которые имитируют скалярные релятивистские эффекты на валентных оболочках.
Математика — Векторы — Мартин Бейкер
Как и многие математические концепции, векторы можно понимать и исследовать по-разному.
Есть как минимум два способа смотреть на векторы:
Алгебраический — обрабатывает вектор как набор скалярных значений как единое целое с добавлением, вычитанием и скалярным умножением, которые работают со всем вектором.
Геометрический — вектор представляет величину, имеющую как величину, так и направление.
Мы можем абстрагироваться от различий в этих подходах и просто посмотреть, что всегда верно для векторов, когда мы это делаем, мы получаем набор аксиом, обычно в форме уравнений. Примером аксиомы для векторов является «закон распределенности»:
c (v ₁ + v ₂) = c v ₁ + c v ₂
, где v ₁ и v ₂ — векторы, а c — скаляр.
Эта аксиома важна, потому что она описывает линейное свойство векторов
Геометрические свойства
Вектор — это величина, имеющая как величину, так и направление, есть две операции, определенные с векторами, и обе имеют очень прямую геометрическую интерпретацию. Мы рисуем вектор как линию со стрелкой, а пока я назову конец без стрелки «началом» вектора, а конец со стрелкой — «концом» вектора.
Сложение вектора: чтобы сложить два вектора, мы берем начало второго вектора и перемещаем его в конец первого вектора.Сложение этих двух векторов представляет собой вектор от начала первого вектора до конца второго вектора.
Скалярное умножение изменяет длину вектора без изменения его направления. То есть мы «масштабируем» его на коэффициент умножения. Итак, скалярное умножение включает в себя умножение скаляра (одного числа) на вектор, чтобы получить другое число.
Эти две операции: сложение векторов и скалярное умножение можно рассматривать как определение линейного пространства (см. Евклидово пространство).
Итак, как вообще получить векторы? Мы могли бы принять уже существующую систему координат и определить все наши векторы в этой системе координат, или мы могли бы начать с набора базисных векторов и представить векторы как линейную комбинацию этих базисных векторов, то есть скалярным умножением и сложением базисные векторы мы можем создать любой вектор в пространстве при условии, что:
Базовых векторов столько, сколько измерений в пространстве.
Все базисные векторы независимы (не более двух в любой данной плоскости).
Таким образом, любая точка может быть идентифицирована по:
α V _a + β V _b
где:
α, β = скалярные множители
V _a, V _b = базисные векторы.
Итак, два скалярных множителя (α, β) могут представлять положение точки в терминах наших базисных векторов. Это приводит к способу работы с векторами чисто алгебраическим способом.
Алгебраические свойства
Алгебраический подход и его операции объяснены на этой странице, поэтому здесь мы просто дадим обзор.
Мы можем думать о векторе как о концепции массива на компьютерном языке, например,
Векторы имеют размер, равный количеству элементов в массиве.
Все элементы в векторе должны быть одного типа.
Вектор может отображаться в виде одного столбца
или рядом
Однако есть отличие от компьютерного массива, потому что в случае компьютера элементы массива могут быть любыми допустимыми объектами, при условии, что все они одного типа.В случае векторов элементы должны иметь определенные математические свойства, в частности, для них должны быть определены операции сложения и умножения с определенными свойствами. Свойства, необходимые для элементов вектора, заключаются в том, что они должны образовывать математическую структуру, известную как поле (см. Рамку справа). В математической терминологии это известно как вектор над полем, другими словами вектор, элементами которого являются поля.
операция обозначение объяснение
добавление В (а + б) = В (а) + В (б) сложение двух векторов выполняется путем сложения соответствующих элементов двух векторов.
скалярное умножение В (с * а) = с * В (а) скалярное произведение вектора получается путем умножения скалярного произведения на каждый из его членов по отдельности.
Эти операции взаимодействуют согласно свойству распределенности:
с * (b + c) = s * b + s * c
Что придает векторам линейное свойство. Теперь мы можем составить набор аксиом для векторов:
аксиома дополнение скалярное умножение
ассоциативность (a + b) + c = a + (b + c) (s1 s2) a = s1 (s2 a)
коммутативность а + Ь = Ь + а
распределение s * (b + c) = s * b + s * c
(s1 + s2) * a = s1 * a + s2 * a
идентификация а + 0 = а
0 + а = а 1 а = а
обратное а + (- а) = 0
(-а) + а = 0
Где:
a, b, c — векторы
0 — это тождественный вектор
s, s1, s2 — скаляры
1 — скаляр идентичности
Сравните это с аксиомами поля (на этой странице)
Векторы также могут иметь дополнительную структуру, определенную в терминах других определенных для них умножений, таких как скалярные произведения и перекрестные произведения, как мы увидим позже.Это необязательные операции, единственными обязательными операциями являются сложение и скалярное умножение.
Векторное обозначение
До сих пор мы показывали вектор как набор значений в сетке, так как это более удобно на веб-странице html, но обычное обозначение вектора — это помещать значения в квадратные скобки:
Где:
x = компонент в измерении x.
y = составляющая в измерении y.
z = компонент по оси z.
Иногда, когда мы представляем весь вектор как символ, мы можем поместить стрелку над символом (в данном случае v ), чтобы подчеркнуть, что это вектор.
Или альтернативно, мы можем использовать следующие обозначения:
= a ₁ x + a ₂ y + a ₃ z
Где:
x = единичный вектор в измерении x.
y = единичный вектор в измерении y.
z = единичный вектор в измерении z.
Первая форма удобнее при работе с матрицами, а вторая форму легче написать в текстовой форме.
Здесь «x», «y» и «z» — операторы, они часто могут использоваться в уравнениях аналогично переменным, но у них могут быть разные законы (например, умножение может не коммутировать). Это может быть удобным способом кодирования законов комбинирования векторов в обычной алгебре поиска.
Связь с другими математическими величинами
Мы можем расширить концепцию векторов (обычно добавляя дополнительные типы умножения для добавления к встроенному сложению и скалярному умножению), чтобы сформировать более сложные математические структуры, в качестве альтернативы мы можем рассматривать векторы как подмножества этих структур, например :
Как подмножество матрицы или тензора (матрица 1 на n или n на 1).Матрица — это двумерный массив с скалярным произведением.
Как подмножество мультивекторов (алгебра Клиффорда). Например, комплексные числа — это двухэлементные векторы с добавлением определенного типа умножения.
Чего мы не можем сделать, так это иметь вектор, элементы которого сами являются векторами. Это связано с тем, что элементы вектора должны быть математической структурой, известной как «поле», а вектор сам по себе не является полем, потому что он не обязательно имеет коммутативное умножение и другие свойства, необходимые для поля.
Тем не менее, было бы неплохо, если бы мы могли построить матрицу из вектора (нарисованного в виде столбца), элементы которого сами являются векторами (нарисованными в виде строки):
Чтобы создать матрицу путем объединения векторных структур, нам нужно сделать две вещи с «внутренним вектором»:
Нам нужно сделать транспонирование так, чтобы это была строка, а не столбец.
Нам нужна операция умножения, которая сделает его полем.
Для этого мы создаем «двойник» вектора, это называется ковектором, как описано на этой странице.
Векторы могут быть умножены на скаляры, даже если они являются отдельными объектами, векторы и скаляры не могут быть добавлены, например (только когда мы дойдем до алгебры Клиффорда), но мы можем определить тип умножения, называемый скалярным умножением, обычно обозначаемый ‘* ‘или скаляр может быть записан рядом с вектором с подразумеваемым умножением. Этот тип умножения требует одного вектора и одного скаляра. Скалярное умножение умножает величину вектора, но не меняет его направления, поэтому:
если есть,
vOut = 2 * vIn
где:
тогда vOut будет вдвое больше vIn, но в том же направлении.
Квадратичная структура на линейном пространстве
Однако этих линейных свойств самих по себе недостаточно, чтобы определить свойства евклидова пространства, используя только алгебру. Чтобы иметь возможность определять такие понятия, как расстояние и угол, мы должны определить квадратичную структуру.
Например, пифагор:
r ² = x ² + y ² + z ²
в алгебраических терминах,
, если a — трехмерный вектор с основаниями e ₁, _{e ₂, _{e ₃}}
a = a ₁ e ₁ + a ₂ e ₂ + a ₃ e ₃
так,
a • a = a ₁ ² + a ₂ ² + a ₃ ²
Другие векторные алгебры
В уже обсуждаемой векторной алгебре квадрат вектора всегда является положительным числом:
а х а = 0
a • a = положительное скалярное число
Однако мы могли бы определить одинаково действительную и непротиворечивую векторную алгебру, которая возводит в квадрат отрицательное число:
а × а = 0
a • a = отрицательное скалярное число
Мы также могли бы определить алгебру, в которой мы смешиваем измерения: квадрат с положительным, другой квадрат с отрицательным.Примером этого является квадрат Эйнштейна пространства-времени, пространства и времени в квадрате с разными значениями, если пространство квадратов в положительное значение, то квадрат времени в отрицательное и наоборот.
Приложения векторов
Для 3D программирования (тематика этого сайта) нас больше всего интересует с векторами из 2 или 3 чисел.
Вектор размерности 3 может представлять физическую величину, которая является направленной. например положение, скорость, ускорение, сила, импульс, и т.п.
Например, если вектор представляет точку в пространстве, эти 3 числа представляют положение в координатах x, y и z (см. системы координат). Где x, y и z — взаимно перпендикулярные оси в какое-то согласованное направление и единицы.
Трехмерный вектор может также представлять смещение в пространстве, например перевод в каком-то направлении. В случае библиотеки Java Vecmath эти это два класса: Point3f и Vector3f, оба производные от Tuple3f.(Обратите внимание на эти использовать числа с плавающей запятой, существуют также классы, оканчивающиеся на d, которые содержат двойные значения). Класс Point3f используется для представления абсолютных точек и Класс Vector3f представляет смещение. В большинстве случаев поведение этих классы такие же, насколько я знаю, разница между этими классами когда они преобразуются матрицей Point3f будет транслироваться матрицей но Vector3f не будет.
Здесь мы разрабатываем следующие классы для хранения вектора и инкапсуляции операции, описанные здесь,
Можно было бы построить векторный класс, который мог бы содержать вектор любого измерение, но класс переменного измерения будет менее эффективным.Поскольку мы когда речь идет об объектах в трехмерном пространстве, важнее работать с двухмерными и трехмерными объектами. векторы эффективно.
Другие векторные величины
Альтернативная интерпретация векторов
До сих пор мы думали о векторе как о позиции на 2,3- или n-мерном пространстве. сетка. Однако для некоторых физических ситуаций может не быть готово определенного Декартова система координат. Альтернативой может быть представление вектора как линейная комбинация из 3-х базисов:
σ ₁
σ ₂
σ ₃
Эти основания не обязательно должны быть взаимно перпендикулярными (хотя в большинстве случаев они, вероятно, будут), но они должны быть независимыми друг от друга, другими словами, они не должны быть параллельны друг другу, и все 3 не должны быть в одной плоскости.
Таким образом, вектор в 3 измерениях может быть представлен как [a, b, c], где a, b и c представляют масштабирование 3-х базисов, чтобы сделать вектор следующим образом:
а σ ₁ + б σ ₂ + c σ ₃
Обратите внимание, что если этот вектор представляет положение, то это будет относительное положение, т.е. относительно некоторой другой точки, если мы хотим определить абсолютную точку, мы еще нужно определить происхождение.
Итак, остается проблема, как определить основу, могут быть некоторые естественные определение их в проблемной области.В качестве альтернативы мы могли бы определить базируются как трехмерные векторы с использованием системы координат. Но зачем беспокоиться сделайте это, если у нас есть система координат, почему бы просто не представить векторы в это система координат? Что ж, мы могли бы захотеть изменить систему координат или перевести все векторы каким-либо образом (см. здесь). Например, мы могли бы захотеть представить точки на твердом объекте в некотором локальном системе координат, но твердый объект может сам двигаться относительно некоторого абсолютная система координат.
Дополнительная литература
Векторы могут управляться с помощью матриц, для пример переведен, повернут, масштабирован, отражен.
Есть математические объекты, известные мультивекторами, их можно использовать для выполнения многих задач, которые выполняют векторы, но у них нет некоторые ограничения (например, векторное векторное произведение ограничено 3-мя измерениями и не имеет обратного).
Существует также более общее семейство алгебр (меньше ограничений), чем «векторные пространства над полем», это «модули над кольцом».
Векторная геометрия — линейная алгебра с приложениями
В этой главе мы изучаем геометрию трехмерного пространства. Мы рассматриваем точку в 3-м пространстве как стрелку от начала координат к этой точке. Так вы получите «картину», которая действительно стоит тысячи слов.
Векторы в
Представьте систему координат в трехмерном пространстве обычным способом. Сначала выберите точку, которая называется, затем выберите три взаимно перпендикулярные линии, называемые, и, и установите числовую шкалу на каждой оси с нулем в начале координат.Данной точке в -пространстве мы связываем три числа, и, как показано на рисунке 4.1.1.
Эти числа называются of, и мы обозначаем точку как, или, чтобы подчеркнуть этикетку. Результат называется системой координат для 3-мерного пространства, а получившееся описание 3-пространства называется.
Как и на плоскости, мы вводим векторы, идентифицируя каждую точку с вектором
in, представленным от начала координат до, как показано на рисунке 4.1.1. Неформально мы говорим, что у точки есть вектор, а у этого вектора есть точка.Таким образом, 3-пробел отождествляется с, и это отождествление будет происходить на протяжении всей главы, часто без комментариев. В частности, термины «вектор» и «точка» взаимозаменяемы. Получившееся описание 3-мерного пространства называется. Обратите внимание, что происхождение.
Длина и направление
Мы собираемся обсудить два основных геометрических свойства векторов в: длину и направление. Во-первых, если это вектор с точкой, вектор определяется как расстояние от начала координат до, то есть длина представляющей стрелки.Следующие свойства длины будут использоваться часто.
Проба:
Пусть есть точка.
На рис. 4.1.2 — гипотенуза прямоугольного треугольника, и так по теореме Пифагора. Но это гипотенуза прямоугольного треугольника, так что. Теперь (1) следует путем исключения и извлечения положительных квадратных корней.
Если = 0, то по (1). Поскольку квадраты действительных чисел неотрицательны, отсюда следует то, а значит, и то. Обратное потому, что.
У нас так (1) дает
Значит, и мы закончили, потому что для любого действительного числа.
Если
, то. Аналогично, если
в 2-м пространстве, то.
Когда мы рассматриваем два ненулевых вектора как стрелки, исходящие из начала координат, с геометрической точки зрения становится ясно, что мы имеем в виду, говоря, что они имеют одинаковое или противоположное значение. Это приводит к принципиально новому описанию векторов.
Проба:
Если, они явно имеют одинаковое направление и длину. Наоборот, позвольте и быть векторами с точками и соответственно.Если и имеют одинаковую длину и направление, то геометрически и должна быть одна и та же точка.
Следовательно, и, то есть.
Обратите внимание, что длина и направление вектора зависят от выбора системы координат в. Такие описания важны в приложениях, потому что физические законы часто формулируются в терминах векторов, и эти законы не могут зависеть от конкретной системы координат, используемой для описания ситуации.
Геометрические векторы
Если и — разные точки в пространстве, стрелка от до имеет длину и направление.
Следовательно,
Обратите внимание, что если любой вектор в точке с точкой, то сам является геометрическим вектором, где находится начало координат. Ссылка на «вектор» кажется оправданной теоремой 4.1.2, потому что у него есть направление (от до) и длина. Однако возникает проблема, потому что два геометрических вектора могут иметь одинаковую длину и направление, даже если концы и хвосты разные.
Например, и на рис. 4.1.5 имеют одинаковую длину и одинаковое направление (1 единица влево и 2 единицы вверх), поэтому по теореме 4.1.2 они же вектора! Лучший способ понять этот очевидный парадокс — увидеть один и тот же базовый вектор как разные. Как только он будет прояснен, это явление станет большим преимуществом, потому что, благодаря теореме 4.1.2, оно означает, что один и тот же геометрический вектор может быть расположен где угодно в пространстве; важны длина и направление, а не расположение кончика и хвоста. Эта способность перемещать геометрические векторы очень полезна.
Закон параллелограмма
Теперь мы даем внутреннее описание суммы двух векторов и in, то есть описание, которое зависит только от длины и направления, а не от выбора системы координат.Используя теорему 4.1.2, мы можем думать, что эти векторы имеют общий хвост. Если их кончики имеют размер и соответственно, то они оба лежат в плоскости, содержащей, и, как показано на рисунке 4.1.6. Векторы и образуют параллелограмм в, заштрихованный на рис. 4.1.6, который называется параллелограммом с помощью и.
Если мы теперь выберем систему координат на плоскости с началом координат, то закон параллелограмма на плоскости показывает, что их сумма равна диагонали параллелограмма, который они определяют с хвостом.Это внутреннее описание суммы, поскольку оно не ссылается на координаты. Это обсуждение доказывает:
Поскольку вектор может быть расположен хвостом в любой точке, закон параллелограмма приводит к другому способу рассмотрения сложения векторов. На рис. 4.1.7 (а) сумма двух векторов и показана как заданная законом параллелограмма. Если его передвинуть так, чтобы его хвост совпадал с концом (показано на (b)), тогда сумма будет выглядеть как «сначала, а затем». Точно так же перемещение хвоста к кончику показывает в (c), что «сначала, а потом.Он будет называться, и он дает графическую иллюстрацию того, почему.
Так как обозначает вектор от точки к точке, правило кончика к хвосту принимает легко запоминаемую форму
для любых точек,, и.
Одна из причин важности правила «кончик к хвосту» состоит в том, что оно означает, что два или более вектора могут быть добавлены путем последовательного размещения их «кончик к хвосту». Это дает полезную «картину» суммы нескольких векторов, которая проиллюстрирована для трех векторов на рисунке 4.1.8 где сначала рассматривается, потом, потом.
Существует простой геометрический способ визуализировать (матрицу) двух векторов. Если и расположены так, что у них общий хвост, и если и являются их соответствующими кончиками, тогда действует правило кончика к хвосту. Отсюда вектор от кончика к кончику. Таким образом, оба и появляются в виде диагоналей в параллелограмме, определяемом и (см. Рисунок 4.1.9.
Одним из наиболее полезных приложений вычитания векторов является то, что оно дает простую формулу для вектора от одной точки к другой и для расстояния между точками.
Можете ли вы доказать эти результаты?
Следующая теорема говорит нам, что происходит с длиной и направлением скалярного кратного данного вектора.
Если a — действительное число и вектор, то:
Проба:
Первое утверждение верно в силу теоремы 4.1.1.
Чтобы доказать второе утверждение, позвольте обозначить начало координат в Let have point и выбрать любую плоскость, содержащую и. Если мы настроим систему координат в этой плоскости с началом координат, тогда результат будет следовать из скалярного закона множественных чисел на плоскости.
Вектор называется if. Тогда
, и
— это единичные векторы, называемые векторами.
Если показать, что это уникальный единичный вектор в том же направлении, что и
Решение:
Векторы в том же направлении, что и скалярные кратные где. Но когда, то есть единичный вектор тогда и только тогда, когда.
Два ненулевых вектора вызываются, если они имеют одинаковое или противоположное направление.
Два ненулевых вектора и параллельны тогда и только тогда, когда один является скалярным кратным другому.
Решение:
По теореме 4.1.3, и. Если
то, значит и, что невозможно. Следовательно, является скалярным кратным, поэтому эти векторы не параллельны по теореме 4.1.5.
Линии в космосе
Эти векторные методы можно использовать для очень простого описания прямых линий в пространстве. Для этого нам сначала нужен способ
указать ориентацию такой линии.
Мы называем ненулевой вектор вектором направления для линии, если он параллелен некоторой паре различных точек и на прямой.
Обратите внимание, что любое ненулевое скалярное кратное также будет служить вектором направления линии.
Мы используем тот факт, что есть ровно одна линия, которая проходит через конкретную точку и имеет заданный вектор направления
. Мы хотим описать эту линию, задав условие, и что точка лежит на этой линии. Обозначим

и векторы из и соответственно.
Рисунок 4.1.10
Затем
Следовательно, лежит на прямой тогда и только тогда, когда она параллельна, то есть тогда и только тогда, когда для некоторого скаляра по теореме 4.1.5. Таким образом является вектор точки на прямой тогда и только тогда, когда для некоторого скаляра.
В компонентной форме векторное уравнение принимает вид
Приравнивание компонентов дает другое описание линии.
Найдите уравнения прямой, проходящей через точки и.
Решение:
Пусть

обозначает вектор от до. Затем он параллелен линии (и на линии ), поэтому служит вектором направления для линии.Использование точки на линии приводит к параметрическим уравнениям
Обратите внимание, что если используется (а не), уравнения равны
Они отличаются от предыдущих уравнений, но это просто результат изменения параметра. По факту, .
Определите, пересекаются ли следующие линии, и, если да, найдите точку пересечения.
Решение:
Пусть вектор лежит на обеих линиях.Тогда
, где первое (второе) уравнение находится в первой (второй) строке. Следовательно, прямые пересекаются тогда и только тогда, когда три уравнения
есть решение. В этом случае и удовлетворить все три уравнения, так что линии действительно пересекаются, а точка пересечения равна
.
с использованием. Конечно, эту точку можно найти и из
, используя.
Предположим, что заданы точка и плоскость и требуется найти точку, которая лежит на плоскости и является ближайшей к ней, как показано на рисунке 4.2.1.
Рисунок 4.2.1
Очевидно, что требуется найти прямую, проходящую через которую перпендикулярно плоскости, а затем получить точку пересечения этой прямой с плоскостью. Чтобы найти прямую , перпендикулярную плоскости, требуется способ определить, когда два вектора перпендикулярны. Это можно сделать, используя идею скалярного произведения двух векторов.
Точечное произведение и углы
Для векторов
и
их скалярное произведение представляет собой определенное число
Поскольку это число, его иногда называют скалярным произведением и
.
Читателям предлагается доказать эти свойства, используя определение скалярных произведений.
Проверить, что когда, и.
Решение:
Применим теорему 4.2.1 несколько раз:
Существует внутреннее описание скалярного произведения двух ненулевых векторов в. Чтобы понять это, нам потребуется следующий результат из тригонометрии.
Рисунок 4.2.2
Проба:
Мы доказываем это, когда остро, то есть; тупой случай аналогичен. На рисунке 4.2.2 у нас есть и.
Следовательно, теорема Пифагора дает
Закон косинусов следует, потому что для любого угла.
Обратите внимание, что закон косинусов сводится к теореме Пифагора, если угол прямой (потому что).
Пусть теперь и — ненулевые векторы, расположенные с общим хвостом. Затем они определяют уникальный угол в диапазоне
.
Этот угол будет называться углом между и. Ясно и параллельны, если есть или. Обратите внимание, что мы не определяем угол между и, если один из этих векторов.
Следующий результат дает простой способ вычислить угол между двумя ненулевыми векторами с помощью скалярного произведения.
Рисунок 4.2.4
Проба:
Рассчитываем двумя способами. Сначала примените закон косинусов к треугольнику на рисунке 4.2.4, чтобы получить:
С другой стороны, мы используем теорему 4.2.1:
Сравнивая их, мы видим это, и результат следует.
Если и — ненулевые векторы, теорема 4.2.2 дает внутреннее описание, потому что, и угол между и не зависят от выбора системы координат.Более того, поскольку и отличны от нуля (и являются ненулевыми векторами), это дает формулу для косинуса угла:
Так как это можно использовать для поиска.
Вычислите угол между
и
.
Решение:
Вычислить. Теперь напомним, что и определены так, что (,) — это точка на единичной окружности, определяемая углом (проведенным против часовой стрелки, начиная с положительной оси). В данном случае мы знаем то и то.Потому что из этого следует.
Если и отличны от нуля, предыдущий пример показывает, что имеет тот же знак, что и, поэтому
В этом последнем случае (ненулевые) векторы перпендикулярны. В линейной алгебре используется следующая терминология:
Так как если либо, либо, то справедлива следующая теорема:
Два вектора и ортогональны тогда и только тогда, когда.
Покажите, что точки, и являются вершинами прямоугольного треугольника.
Решение:
Векторов по сторонам треугольника равны
.
Очевидно, так и являются ортогональными векторами. Это означает, что стороны и перпендикулярны, то есть угол при прямой.
Проекции
В приложениях векторов часто бывает полезно записать вектор как сумму двух ортогональных векторов.
Рисунок 4.2.5
Если указан ненулевой вектор, основная идея состоит в том, чтобы иметь возможность записать произвольный вектор как сумму двух векторов,
, где параллельно и ортогонально.Предположим, что и происходит из общего хвоста (см. Рис. 4.2.5). Позвольте быть вершиной, и позвольте обозначить основание перпендикуляра от к линии, проходящей параллельно к.
Тогда имеет необходимые свойства:
1. параллельно .
2. ортогонален .
3..
Вектор на рисунке 4.2.6 называется проекцией на.
Обозначается
На рисунке 4.2.5 (а) вектор имеет то же направление, что и; однако, и имеют противоположные направления, если угол между и больше чем (см. Рисунок 4.2.5 (b)). Обратите внимание, что проекция равна нулю тогда и только тогда, когда и ортогональны.
Вычислить проекцию на очень просто.
Проба:
Вектор параллелен некоторому скаляру и поэтому имеет вид. Требование ортогональности и определяет. Фактически это означает, что по теореме 4.2.3. Если здесь подставлено, то условие будет
Отсюда следует, что, где предположение, которое гарантирует, что.
Решение:
Проекция на
Следовательно, и это ортогонально по теореме 4.2.4 (в качестве альтернативы, заметим, что). Так как мы закончили.
Обратите внимание, что идея проекций может использоваться для нахождения кратчайшего расстояния от точки до прямой линии, в которой длина вектора ортогональна вектору направления линии.
Самолеты
Ненулевой вектор называется нормалью для плоскости, если он ортогонален каждому вектору на плоскости.
Например, единичный вектор является нормальным вектором для плоскости.
Рис. 4.2.6
Для точки и ненулевого вектора имеется уникальная сквозная плоскость с нормалью, заштрихованная на рис. 4.2.6. Точка лежит на этой плоскости тогда и только тогда, когда вектор ортогонален, то есть тогда и только тогда. Потому что это дает следующий результат:
Найдите уравнение плоскости через
как обычно.
Решение:
Здесь общее скалярное уравнение принимает вид
Это упрощает до.
Если мы напишем, скалярное уравнение показывает, что каждая плоскость с нормалью
имеет линейное уравнение вида
(4,2)
для некоторой константы. И наоборот, график этого уравнения представляет собой плоскость с вектором нормали (при условии, что, и не все равны нулю).
Найдите уравнение плоскости, проходящей через параллельную плоскости с уравнением.
Решение:
Плоскость с уравнением имеет нормаль. Поскольку две плоскости параллельны, она служит нормалью к плоскости, которую мы ищем, поэтому уравнение для некоторых соответствует (4.2). Настаивая на том, что лежит в плоскости, определяет; это, . Следовательно, уравнение есть.
Рассмотрим точки и с векторами
и
.
Для ненулевого вектора скалярное уравнение сквозной плоскости с нормалью принимает векторную форму:
Кроме того, уравнение (4.2) переводится следующим образом:
Каждая плоскость с нормалью имеет векторное уравнение для некоторого числа.
Найдите кратчайшее расстояние от точки до плоскости с помощью уравнения. Также найдите точку на этой плоскости, ближайшую к.
Решение:
У рассматриваемого самолета нормальный. Выберите любую точку на плоскости, скажем, и пусть это будет ближайшая к ней точка на плоскости (см. Диаграмму). Вектор от до есть. Теперь прямо хвостиком. Тогда и является проекцией на:
Значит расстояние есть. Чтобы вычислить точку, пусть
и

будут векторами и. Тогда
Это дает координаты.
Перекрестное произведение
Если, и — три различные точки в, не все на какой-либо прямой, геометрически ясно, что существует единственная плоскость, содержащая все три.Векторы и оба лежат в этой плоскости, поэтому нахождение нормали сводится к нахождению ненулевого вектора, ортогонального обоим и. Перекрестное произведение обеспечивает систематический способ сделать это.
Учитывая векторы и, определите перекрестное произведение на
Поскольку это вектор, его часто называют векторным произведением . Есть простой способ запомнить это определение с помощью векторов координат :
Это векторы длины, направленные вдоль положительных осей, и.Причина названия в том, что любой вектор можно записать как
Таким образом, перекрестное произведение можно описать следующим образом:
Если и — два вектора, то
, где определитель раскрывается по первому столбцу.
Обратите внимание, что он ортогонален обоим и в Примере 4.2.11. В общем, это верно, что можно проверить напрямую, вычислив и, и записано как первая часть следующей теоремы.Это будет следовать из более общего результата, который вместе со второй частью будет доказан позже.
Напомним, что
Найдите уравнение плоскости через, и.
Решение:
Векторы
и

лежат в плоскости, поэтому
— нормаль к плоскости (ортогональна обоим и). Следовательно, плоскость имеет уравнение
Так как лежит в самолете у нас.Отсюда и уравнение. Можете ли вы проверить, что то же уравнение можно получить, если использовать и, или, в качестве векторов на плоскости?
Перекрестное произведение двух -векторов и
было определено в разделе 4.2, где мы заметили, что его лучше всего запомнить с помощью определителя:
(4,3)
Здесь, и
— векторы координат, а определитель развернут по первому столбцу.Мы наблюдали (но не доказали) в теореме 4.2.5, которая ортогональна обоим и. Это легко следует из следующего результата.
Проба:
Напомним, что вычисляется путем умножения соответствующих компонентов и последующего сложения. Используя уравнение (4.3), получаем:
, где последний определитель раскрывается по столбцу 1.
Результат теоремы 4.3.1 можно кратко сформулировать следующим образом: Если, и — три вектора в, то
где обозначает матрицу с, и в качестве столбцов.Теперь ясно, что он ортогонален обоим и потому, что определитель матрицы равен нулю, если два столбца идентичны.
В силу (4.3) и теоремы 4.3.1 некоторые из следующих свойств перекрестного произведения вытекают из
свойств определителей (они также могут быть проверены напрямую).
Мы видели некоторые из этих результатов в прошлом; вы можете доказать 6,7 и 8?
Теперь мы подошли к фундаментальной взаимосвязи между скалярными и перекрестными произведениями.
Если и — любые два вектора в, то
Проба:
Учитывая и, введите систему координат и запишите
и
в форме компонентов. Тогда все члены тождества могут быть вычислены в терминах компонентов.
Выражение для величины вектора может быть легко получено из тождества Лагранжа. Если — угол между и, подстановка в тождество Лагранжа дает
с учетом того, что.Но является неотрицательным в диапазоне, поэтому извлечение положительного квадратного корня из обеих частей дает
.
Рисунок 4.3.1
Это выражение для не ссылается на систему координат и, более того, имеет красивую геометрическую интерпретацию. Параллелограмм определяется векторами и имеет длину основания и высоту. Следовательно, площадь параллелограмма, образованного и равна
.
Доказательство 2:
По (1) тогда и только тогда, когда площадь параллелограмма равна нулю.Площадь исчезает тогда и только тогда, когда они имеют одинаковое или противоположное направление, то есть тогда и только тогда, когда они параллельны.
Найдите площадь треугольника с вершинами, и.
Решение:
У нас
и. Площадь треугольника равна половине площади параллелограмма, образованного этими векторами, и поэтому равна. У нас
, поэтому площадь треугольника
Рисунок 4.3.2
Если заданы три вектора, и, они определяют «сжатое» прямоугольное тело, называемое параллелепипедом (рисунок 4.3.2), и часто бывает полезно найти объем такого твердого тела. Основание твердого тела — это параллелограмм, определяемый знаком и, поэтому у него есть площадь. Высота твердого тела равна длине выступа на. Следовательно,
Таким образом, объем параллелепипеда равен. Это доказывает
Объем параллелепипеда определяется тремя векторами, и определяется выражением.
Найдите объем параллелепипеда, определяемый векторами
Решение:
По теореме 4.3.1,.
Следовательно, объем равен теореме 4.3.5.
Теперь мы можем дать внутреннее описание перекрестного произведения.
Чтобы указать, почему это так, введите координаты следующим образом: Пусть и имеют общий хвост, выберите начало координат, выберите ось так, чтобы она указывала в положительном направлении, а затем выберите ось так, чтобы она находилась в плоскости — и положительная ось находится с той же стороны от оси, что и. Тогда в этой системе и есть компоненты формы
и
, где и.Можете ли вы нарисовать график на основе приведенного здесь описания?
Правило правой руки утверждает, что это должно указывать в положительном направлении.

	Вектор может отображаться в виде одного столбца
	или рядом

операция	обозначение	объяснение
добавление	В (а + б) = В (а) + В (б)	сложение двух векторов выполняется путем сложения соответствующих элементов двух векторов.
скалярное умножение	В (с * а) = с * В (а)	скалярное произведение вектора получается путем умножения скалярного произведения на каждый из его членов по отдельности.

аксиома	дополнение	скалярное умножение
ассоциативность	(a + b) + c = a + (b + c)	(s1 s2) a = s1 (s2 a)
коммутативность	а + Ь = Ь + а
распределение		s * (b + c) = s * b + s * c (s1 + s2) * a = s1 * a + s2 * a
идентификация	а + 0 = а 0 + а = а	1 а = а
обратное	а + (- а) = 0 (-а) + а = 0

Векторное Произведение Векторов. Свойства, определение

Определение векторного произведения

Координаты векторного произведения

Свойства векторного произведения

Примеры решения задач

Пример 1

Пример 2

Пример 3

Геометрический смысл векторного произведения

Физический смысл векторного произведения

Векторное произведение векторов.

Формулы вычисления векторного произведения векторов

Свойства векторного произведения векторов

Примеры задач на вычисления векторного произведения векторов

Лекция Векторное произведение векторов. Смешанное произведение векторов.

Векторное произведение векторов и его свойства (Лекция №18)

Механический смысл векторного произведения — Мегаобучалка

Смешанное произведение векторов, его геометрический смысл и свойства

Содержание:

Смешанное произведение векторов, его геометрический смысл и свойства

Примеры решения и задачи с методическими указаниями

Понимание перекрестного продукта — лучшее объяснение

Определение перекрестного произведения

Геометрическая интерпретация

Крестное произведение для ортогональных векторов

Расчет перекрестного произведения

Пример времени

Приложение

Другие сообщения этой серии

geometry — Что представляет собой скалярное произведение двух векторов?

Перекрестное произведение | Brilliant Math & Science Wiki

Перекрестный продукт — Викиверситет

Эквивалентность двух определений [править | править источник]

Кросс-произведение векторов — обзор

1.3 Основные концепции релятивистской квантовой механики

Математика — Векторы — Мартин Бейкер

Геометрические свойства

Алгебраические свойства

Векторное обозначение

Связь с другими математическими величинами

Квадратичная структура на линейном пространстве

Другие векторные алгебры

Приложения векторов

Другие векторные величины

Альтернативная интерпретация векторов

Дополнительная литература

Векторная геометрия — линейная алгебра с приложениями

Векторы в

Длина и направление

Геометрические векторы

Закон параллелограмма

Линии в космосе

Точечное произведение и углы

Проекции

Самолеты

Перекрестное произведение

alexxlab

Добавить комментарий Отменить ответ

Рубрики