Калькулятор Крутящий момент | Преобразование единиц крутящего момента
Крутящий момент, момент силы — направленность сил на осуществление поворота объекта вокруг оси или точки опоры. В математике крутящий момент определяется как векторное производное расстояния и силы, которой свойственно производить вращение. Проще говоря, крутящий момент — это мера силы вращения объекта, такого как маховик или болт. Как правило, символ — греческая буква Тау (Т) или иногда обозначается буквой «М», от слова «момент». Единицей СИ для крутящего момента является ньютон-метр (Н•м). Единицы фунт-сила-фут, фунт-сила-дюйм и унция-сила-фут также используются для крутящего момента. Для всех этих величин слово «сила» часто выпадает, к примеру, фунт-сила-дюйм сокращается до «фунт-дюйм».
Конвертер крутящего момента
Переводим из
Переводим в
| Основные единицы | |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
| Килоньютон на метр | кН·м |
| Ньютон на метр | Н·м |
| Фунт-Сила-Дюйм | lbf∙in |
| Другие единицы | |
| Дина-сантиметр | дин·см |
| Дина-Метр | дин·м |
| Дина-Миллиметр | дин·мм |
| Грамм-Сила-Сантиметр | гс·см |
| Грамм-Сила-Метр | гс·м |
| Грамм-Сила-Миллиметр | гс·мм |
| Килограмм-Сила-Сантиметр | кгс∙см |
| Килограмм-Сила-Метр | кгс∙м |
| Килограмм-Сила-Миллиметр | кгс∙мм |
| Ньютон сантиметр | Н∙cм |
| Ньютон-Миллиметр | Н∙мм |
| Унция-Сила-Дюйм | ozf∙in |
Результат конвертации:
Единицы измерения крутящего момента двигателей — OneKu
Содержание статьи:В технических характеристиках двигателей и конструкций, оснащенных двигателями, постоянно фигурирует загадочный показатель нм, как единица измерения крутящего момента. Если с мощностью в лошадиных силах все понятно даже на интуитивном уровне, лошадь – она и есть лошадь, то здесь могут возникнуть некоторые затруднения.
Архимедов рычаг
Широко известный ученый Архимед как-то изрек знаменитую фразу: «Дайте мне рычаг, и я переверну Землю». Можно сказать, что именно эта фраза и послужила началом рождения показателя единицы измерения крутящего момента. Как известно, планета Земля несколько тяжеловата для того, чтобы человек, даже такой уважаемый и известный, как Архимед, мог ее перевернуть. Ключ – это использование рычага, позволяющего на порядки увеличивать силу воздействия на объект. Рычаг представляет собой фактически любой предмет, способный свободно вращаться вокруг точки опоры. Если точка опоры находится ровно в середине рычага, при приложении одинаковых усилий с каждого конца рычага вся конструкция будет стоять на месте. Ситуация изменится лишь при смещении точки опоры в одну из сторон. Лучше всего это видно на приведенном ниже рисунке.
Вам будет интересно:Краткая история педагогики: этапы развития, значение и цели
Оно крутится
Как видно, рычаг крутится вокруг точки опоры, совершая неполный оборот. Соотношение прикладываемой силы к длинному плечу рычага и получаемого усилия на коротком плече составляет основу единиц измерения крутящего момента. Соотношение это очень простое: усилия, помноженные на длину соответствующего плеча рычага, должны быть равны. Закон сохранения энергии работает всегда. Этот принцип действия можно распространить и на пару шестеренок разного диаметра, и вообще на любые взаимодействующие при помощи вращения агрегаты механизмов разных диаметров, представляющие собой, по сути, плечи условных рычагов.
Крутящий момент
Теперь можно взять вращающийся вал двигателя. Радиус вала двигателя – это условный рычаг, а при его вращении возникает сила, направленная перпендикулярно к оси вращения. Схематично это показано на следующем рисунке.
Здесь R – это радиус вала, а F – вектор силы, образуемой при вращении вала. Как и при обычном рычаге, их произведение (R*F) и будет моментом силы, или крутящим моментом. Поскольку, в соответствии с международной системой единиц, сила измеряется в ньютонах, а расстояние – в метрах, единицей измерения крутящего момента является ньютон-метр, или сокращенно – нм.
Однако имеются и другие обозначения. Иногда для измерения силы используют не ньютоны, а килограммы (кгс), тогда эту величину можно пересчитать в «классику» при помощи коэффициента. 1 кгс на метр равен 9,81 нм. В странах, не использующих метрическую систему, в качестве единицы измерения крутящего момента электродвигателя применяют фунтофут. Звучит непривычно, но тем не менее. 1 фунтофут равен 1,36 нм. Существует зависимость между мощностью, частотой оборотов и создаваемым крутящим моментом. Она очень простая. Мощность равна произведению частоты оборотов на крутящий момент, деленную на коэффициент. Коэффициент зависит от единиц измерения крутящего момента и других указанных величин.
Если речь идет о лошадиных силах, кгс на метр и оборотах в минуту, этот коэффициент равен 716,2, для нм и киловатт – 9549. В открытом доступе имеются соответствующие калькуляторы. В технических характеристиках обычно указывают крутящий момент, измеренный непосредственно на валу двигателя.
Источник
Единицы измерения крутящего момента двигателей
В технических характеристиках двигателей и конструкций, оснащенных двигателями, постоянно фигурирует загадочный показатель нм, как единица измерения крутящего момента. Если с мощностью в лошадиных силах все понятно даже на интуитивном уровне, лошадь – она и есть лошадь, то здесь могут возникнуть некоторые затруднения.
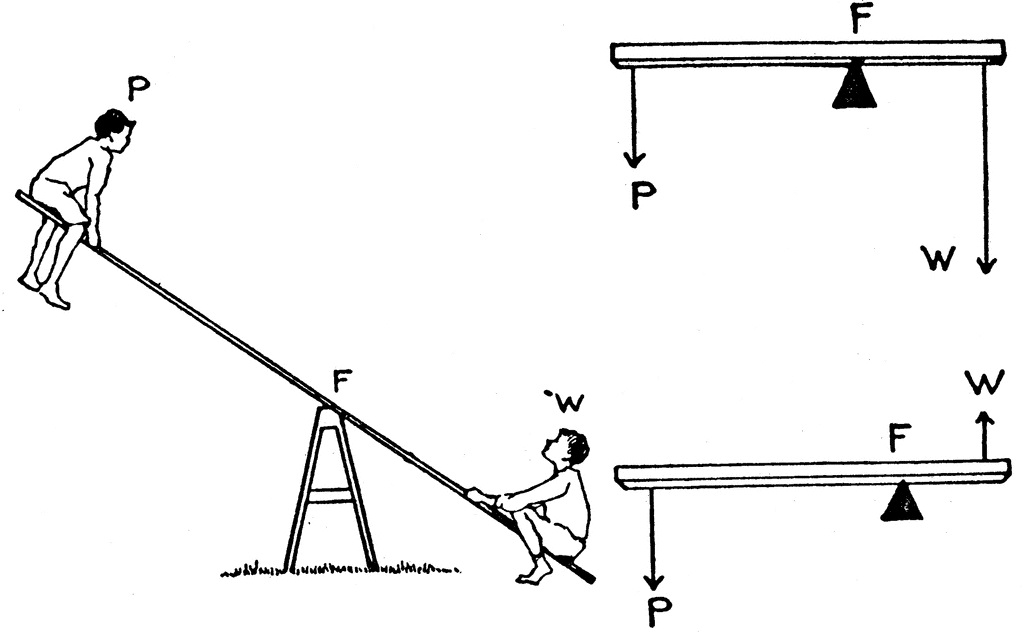
Архимедов рычаг

Оно крутится
Как видно, рычаг крутится вокруг точки опоры, совершая неполный оборот. Соотношение прикладываемой силы к длинному плечу рычага и получаемого усилия на коротком плече составляет основу единиц измерения крутящего момента. Соотношение это очень простое: усилия, помноженные на длину соответствующего плеча рычага, должны быть равны. Закон сохранения энергии работает всегда. Этот принцип действия можно распространить и на пару шестеренок разного диаметра, и вообще на любые взаимодействующие при помощи вращения агрегаты механизмов разных диаметров, представляющие собой, по сути, плечи условных рычагов.
Крутящий момент
Теперь можно взять вращающийся вал двигателя. Радиус вала двигателя – это условный рычаг, а при его вращении возникает сила, направленная перпендикулярно к оси вращения. Схематично это показано на следующем рисунке.
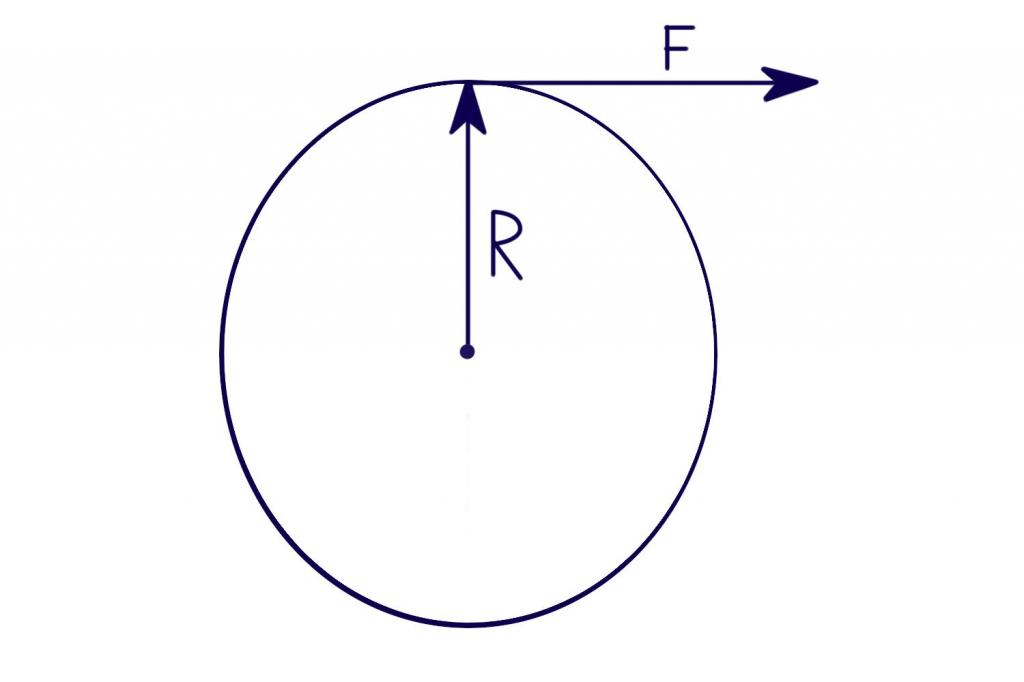
Здесь R – это радиус вала, а F – вектор силы, образуемой при вращении вала. Как и при обычном рычаге, их произведение (R*F) и будет моментом силы, или крутящим моментом. Поскольку, в соответствии с международной системой единиц, сила измеряется в ньютонах, а расстояние – в метрах, единицей измерения крутящего момента является ньютон-метр, или сокращенно – нм.
Однако имеются и другие обозначения. Иногда для измерения силы используют не ньютоны, а килограммы (кгс), тогда эту величину можно пересчитать в «классику» при помощи коэффициента. 1 кгс на метр равен 9,81 нм. В странах, не использующих метрическую систему, в качестве единицы измерения крутящего момента электродвигателя применяют фунтофут. Звучит непривычно, но тем не менее. 1 фунтофут равен 1,36 нм. Существует зависимость между мощностью, частотой оборотов и создаваемым крутящим моментом. Она очень простая. Мощность равна произведению частоты оборотов на крутящий момент, деленную на коэффициент. Коэффициент зависит от единиц измерения крутящего момента и других указанных величин.
Если речь идет о лошадиных силах, кгс на метр и оборотах в минуту, этот коэффициент равен 716,2, для нм и киловатт – 9549. В открытом доступе имеются соответствующие калькуляторы. В технических характеристиках обычно указывают крутящий момент, измеренный непосредственно на валу двигателя.
Крутящий момент — это… Что такое Крутящий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу
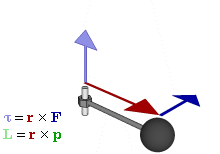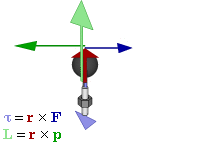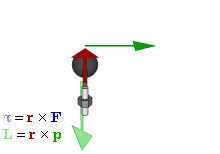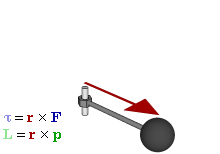
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
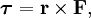
где  — сила, действующая на частицу, а
— сила, действующая на частицу, а 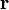 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 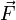 на рычаг
на рычаг 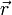 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 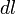 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 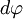 . Обозначим через
. Обозначим через 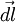 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 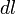 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 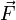 и вектором
и вектором 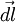 равен
равен 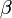 , а угол
, а угол 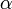
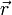 и вектором силы
и вектором силы 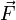 .
.
Следовательно, бесконечно малая работа 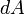 , совершаемая силой
, совершаемая силой 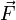 на бесконечно малом участке
на бесконечно малом участке 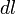 равна скалярному произведению вектора
равна скалярному произведению вектора 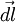 и вектора силы, то есть
и вектора силы, то есть 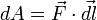 .
.
Теперь попытаемся выразить модуль вектора 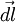 через радиус вектор
через радиус вектор 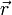 , а проекцию вектора силы
, а проекцию вектора силы 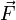 на вектор
на вектор 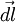 , через угол
, через угол 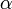 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 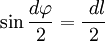 , где в случае малого угла справедливо
, где в случае малого угла справедливо 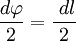 и следовательно
и следовательно 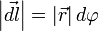
Для проекции вектора силы 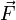 на вектор
на вектор 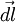 , видно, что угол
, видно, что угол 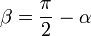 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 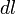 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 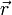 , а так как
, а так как 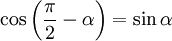 , получаем, что
, получаем, что 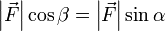 .
.
Теперь запишем бесконечно малую работу через новые равенства 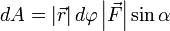 или
или 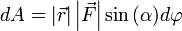 .
.
Теперь видно, что произведение 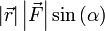 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 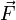 и
и 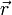 , то есть
, то есть 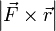 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 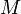 или модуля вектора момента силы
или модуля вектора момента силы 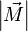 .
.
И теперь полная работа записывается очень просто 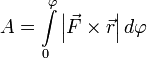 или
или 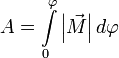 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
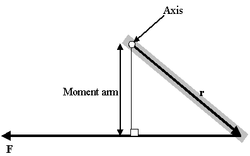
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 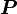 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 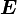 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 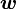 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 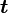 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 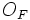 , к которой приложена сила
, к которой приложена сила 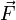 , то момент силы относительно точки
, то момент силы относительно точки 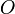 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 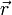 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 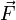 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/biograf.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
что такое крутящий момент и в чём его измеряют?
Крутящий момент — это сила, умноженная на плечо ее приложения, которую может “предоставить” двигатель автомобилю для преодоления тех или иных сопротивлений движению. Обычно измеряется в «ньютонах на метр» (н * м) .
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Крутящий момент — это сила, умноженная на плечо ее приложения, которую может предоставить двигатель автомобилю для преодоления тех или иных сопротивлений движению. Обычно измеряется в «ньютонах на метр» (н/м).
Крутящий момент — это сила, умноженная на плечо ее приложения, которую может “предоставить” двигатель автомобилю для преодоления тех или иных сопротивлений движению. Обычно измеряется в «ньютонах на метр» (н * м) . Максимальный крутящий момент обычно достигается при 3400-4500 оборотах коленчатого вала в минуту (эта величина обычно указывается при написании крутящего момента двигателя автомобиля) . Максимальный крутящий момент и максимальное значение мощности достигаются при различных оборотах двигателя (и, соответственно, скоростях).
Крутящий момент двигателя — что это за характеристика и на какие параметры влияет
 Контакты
Menu Menu
Контакты
Menu Menu- Главная
- Авто
 Audi
Audi BMW
BMW Cadillac
Cadillac Chevrolet
Chevrolet Citroen
Citroen Ford
Ford Geely
Geely
 Honda
Honda Hyundai
Hyundai Infiniti
Infiniti Jaguar
Jaguar Kia
Kia Lada
Lada Land Rover
Land Rover
 Lexus
Lexus Mazda
Mazda Mercedes
Mercedes Mitsubishi
Mitsubishi
Вращающий момент — это… Что такое Вращающий момент?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
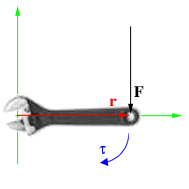
Момент силы приложенный к гаечному ключу
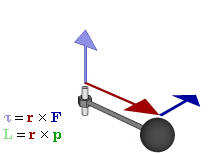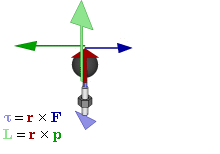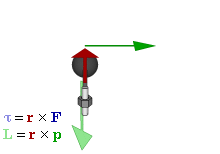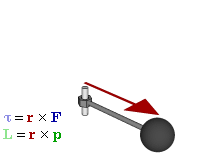
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
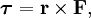
где 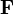 — сила, действующая на частицу, а
— сила, действующая на частицу, а 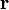 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 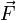 на рычаг
на рычаг 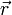 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 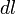 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 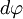 . Обозначим через
. Обозначим через 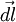 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 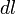 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 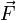 и вектором
и вектором 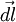 равен
равен 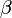 , а угол
, а угол 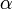
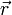 и вектором силы
и вектором силы 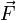 .
.
Следовательно, бесконечно малая работа 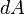 , совершаемая силой
, совершаемая силой 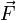 на бесконечно малом участке
на бесконечно малом участке 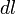 равна скалярному произведению вектора
равна скалярному произведению вектора 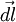 и вектора силы, то есть
и вектора силы, то есть 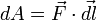 .
.
Теперь попытаемся выразить модуль вектора 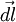 через радиус вектор
через радиус вектор 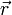 , а проекцию вектора силы
, а проекцию вектора силы 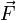 на вектор
на вектор 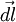 , через угол
, через угол 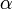 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 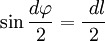 , где в случае малого угла справедливо
, где в случае малого угла справедливо 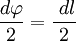 и следовательно
и следовательно 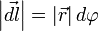
Для проекции вектора силы 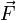 на вектор
на вектор 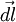 , видно, что угол
, видно, что угол 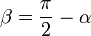 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 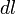 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 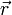 , а так как
, а так как 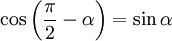 , получаем, что
, получаем, что 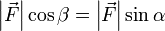 .
.
Теперь запишем бесконечно малую работу через новые равенства 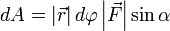 или
или 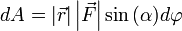 .
.
Теперь видно, что произведение 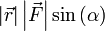 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 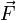 и
и 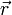 , то есть
, то есть 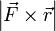 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 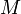 или модуля вектора момента силы
или модуля вектора момента силы 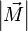 .
.
И теперь полная работа записывается очень просто 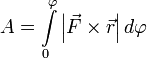 или
или 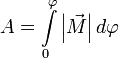 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
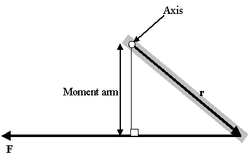
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 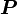 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 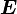 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 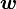 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 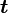 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 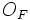 , к которой приложена сила
, к которой приложена сила 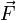 , то момент силы относительно точки
, то момент силы относительно точки 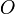 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 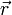 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 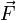 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dikc.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.


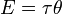 ,
,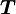 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ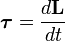 ,
,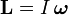 ,
,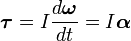 ,
, Audi
Audi BMW
BMW Cadillac
Cadillac Chevrolet
Chevrolet Citroen
Citroen Ford
Ford Geely
Geely Honda
Honda Hyundai
Hyundai Infiniti
Infiniti Jaguar
Jaguar Kia
Kia Lada
Lada Land Rover
Land Rover Lexus
Lexus Mazda
Mazda Mercedes
Mercedes Mitsubishi
Mitsubishi
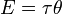 ,
,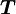 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ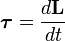 ,
,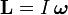 ,
,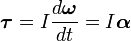 ,
,