Джо Вулфи / Joe Wolfe (Австралия) Перевод статьи публикуется с разрешения автора, оригинал размещен по адресу: http://www.phys.unsw.edu.au/jw/strings.html
Чтобы вызвать звук необходимо произвести колебания. Чтобы получить музыкальный звук необходимо, чтобы колебания имели постоянную частоту, т.е. стабильную высотность, которой исполнитель мог бы легко управлять. В электроинструментах стабильные и управляемые колебания получают с помощью электроники, у неэлектрических — за счет стоячих волн. Мы будем рассматривать колебания на примере струн, поскольку здесь они более наглядны, чем колебания воздуха в духовых инструментах, и менее сложны по сравнению с колебаниями дощечек и кожи ударных инструментов.
Натянутые струны скрипки, фортепиано и т.д. колеблются столь быстро, что разглядеть что-либо невозможно. Однако, можно провести несколько любопытных экспериментов, позволяющих понять работу струн с помощью нескольких метров гибкого резинового шланга. Садовый поливной шланг для этого недостаточно гибок, лучше всего взять резиновый шланг или длинную бельевую веревку. Привяжите или прижмите один конец шланга, а другой слегка натяните одной рукой (сильно натягивать не нужно, небольшой прогиб не страшен). Теперь другой рукой оттяните шланг в сторону, чтобы образовался выступ, и, отпустив его, вы увидите в замедленном темпе то, что происходит при щипке струны. Можно наблюдать, как выступ пробежит вдоль «струны» и вернется обратно. При возврате он толкнет Вашу руку, но если Вы держите «струну» крепко, произойдет новое отражение.
Первое, что Вы должны заметить, это то, что скорость движения волны по струне возрастает с увеличением ее натяжения. Это свойство используется при настройке инструментов, но сейчас мы не будем на этом останавливаться. Скорость движения волны зависит и от «веса» струны — в более толстой, тяжелой струне (при равной длине и натяжении) она будет медленнее, чем в легкой.
Теперь остановимся на отражении, которое происходит на закрепленном конце. Заметьте, что если оттягивать струну влево, то выступ побежит с левой стороны, но при возврате будет расположен справа — при отражении происходит инвертирование. Этот эффект наблюдается не только в струнах, но и в духовых и ударных. Волна инвертируется в момент, когда сталкивается с какой-либо неподвижной или трудно преодолимой преградой.
Несмотря на то, что струны музыкального инструмента закреплены с обоих концов, наблюдаемые процессы при щипке струны в них будут аналогичными. Сперва струна оттягивается в некой точке, а затем отпускается, как показано на рисунке. Если приглядеться, можно различить форму, которую образует бегущий выступ (показано тонкой линией на рисунках ниже), движущийся вдоль струны в обоих направлениях. Для наблюдений лучше использовать басовые струны, оттягивая их в нескольких миллиметрах от точки крепления. Фигура, образованная бегущим выступом, видна лучше, чем сама струна, потому что точку покоя, в которой происходит смена направлений, выступ проходит мгновенно, а к краям его движение замедляется.
Схема движения выступа, образованного при щипке струны. Жирной линией показана сама струна, тонкой — фигура, образованная движением выступа. В фазах, отмеченных буквами (d) и (j), струна представляет прямую линию. В эти моменты потенциальная энергия ее колебаний исчерпана, а кинетическая энергия максимальна. Заметим, что в момент отражения положение выступа меняется на 180 градусов с верхнего на нижний или наоборот. Обратите внимание на проход выступов одного «сквозь» другой в момент, когда они встречаются посередине.
Схема, показывающая отражение движущихся выступов, при возбуждении струны смычком.
Отчего при отражении происходит инвертирование? Поскольку струна закреплена на неподвижном объекте, то и точка отражения является неподвижной. Теперь посмотрите на движение струны на левых рисунках, отражающих ее положение в разное время. Видно как часть струны позади выступа возвращается к своему первоначальному состоянию (на рисунках — вниз). Чем ближе выступ к концу струны, тем он становится меньше, и при его достижении он исчезает — в этот момент струна становится прямой. Однако движение струны вниз не прекращается, и, пройдя точку покоя, она образует обратный выступ, который начинает движение в обратном направлении.
Если раскачивать вверх-вниз незакрепленный конец струны, можно наблюдать один интересный эффект. С помощью резинового шланга можно проделать этот опыт самостоятельно. Если такой возможности у Вас нет, то взгляните на представленную ниже диаграмму.
Мы опять видим инвертирование отраженной волны, из-за чего после отражения мы получаем уже две волны (с одинаковой частотой и амплитудой), которые движутся в противоположных направлениях. В точке крепления струны, где они складываются, движение прекращается, т.е. имеет место нулевое перемещение, благодаря которому и возникает инвертированное отражение. Но если вы посмотрите на сплошную линию на диаграмме (представляющую собой результат суммирования двух волн), то увидите, что на струне есть и другие неподвижные точки. Эти равноудаленные друг от друга точки, играющие важнейшую роль в функционировании любого музыкального инструмента, называются «узлами» (node) вибрации. Посередине между узлами располагаются «пучности» (antinode) — зоны максимального движения. Обратите внимание, что эти выступающие зоны не движутся по струне. При сложении двух волн, бегущих в противоположных направлениях, образуется стоячая волна.
Две движущиеся волны при слиянии образуют стоячие волны.
Посмотрите на рисунок, который представляет последовательность фаз движения волн во времени (время течет сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии — при наложении). Отмечены положения (узлы/nodes) в которых обе движущиеся волны нейтрализуют друг друга и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой. Можно сказать, что приведенная выше диаграмма представляет колебание 5-й гармоники струны, длина которой равна ширине диаграммы. Здесь мы коснулись темы, которая будет освещена в следующей главе.
Гармоники и моды (типы) колебаний
На музыкальном инструменте струна закреплена с обоих концов, которые ограничивают возможные колебания и на которых во время колебаний расположены узлы. Струна, имеющая длину L, образует стоячую волну, длина которой равна удвоенной длине струны (длина волны = 2L), что демонстрируется на первом из рисунков следующей серии. При этом узлы расположены на концах струны, а пучность посередине между ними. Это одна из мод («мода» — тип колебаний струны). Какие еще моды встречаются на струне, закрепленной с обоих концов? Ниже приводятся примеры таких стоячих волн.
Рисунки демонстрируют первые четыре моды колебаний идеальной* закрепленной струны (увеличено по вертикали).
В каком соотношении находятся моды колебаний? Частота колебаний волны равна отношению ее скорости к длине: f=v/длина волны. Таким образом, для струны длиной L, длины волн составят 2L, L, 2L/3, L/2, что можно записать так 2L/n, где n — номер гармоники.
Базовая частота или 1-я мода имеет частоту f1= v/длина волны = v/2L
Частота 2-й гармоники f2= v/l2 = 2v/2L = 2f1
Частота 3-й гармоники f3= v/l3 = 3v/2L = 3f1
Частота 4-й гармоники f4= v/l4 = 4v/2L = 4f1 …
fn= v/ln = nv/2L = nf1
Все волны движутся по струне с одинаковой скоростью, поэтому волны с различными длинами имеют разные частоты, как показано на рисунках. Мода самой нижней частоты (f1) называется базовой. Частота n-ной моды будет в n раз больше базовой. Все эти моды (как и звуки, которые они образуют) называются гармониками струны. Частоты f, 2f, 3f, 4f и т.д. называется последовательностью гармоник. Музыканты хорошо знакомы с этими последовательностями, особенно те, кто играют на натуральных горнах или знакомы с флажолетами. Если для примера мы возьмем базовую частоту соответствующую ноте С3, т.е. альтовой До (частота = 131Гц), то ее гармоники будут иметь высотности, показанные на следующем рисунке. Высотность нот дана в приближении до четверти тона. При этом октавы являются чистыми, а вот другие интервалы не совсем соответствуют равномерно темперированному строю.
Нотное написание первых 12-ти гармоник (флажолетов) на примере ноты До. При прослушивании звукового файла (записанного в форматах au и wav) обратите внимание на высотность звуков.
Седьмая и одиннадцатая гармоники приходятся почти посередине между нотами равномерно темперированного строя, поэтому обозначены с половинками диезов.
Вы сами можете получить эти звуки на струнах. Проще это сделать на басовых струнах гитары, виолончели или контрабаса*. Для этого коснитесь слегка струны в точке, которая отстоит на длину =1/n от ее конца (где n = 1,2,3 и т.д.), а затем проведите смычком. Или слегка коснитесь струны в точке, которая приходится на длину =1/n от ее конца, ударьте по струне недалеко от подставки и мгновенно отдерните прижатый палец. Благодаря касанию, в точке произойдет образование узла, который образует моду, имеющую узел в данной точке. Вы легко сможете найти на струне от двух до шести флажолетов (если Вы только что проделали этот эксперимент, то, наверное, обратили внимание, на то, что двенадцатый лад, отвечающий за получение октавы, расположен менее, чем на половине длины струны, поэтому то место, где Вы касались струны для получения 2-й гармоники, находится не совсем точно над этим ладом).
* «Идеальной» я называю струну, которая, обладая абсолютной гибкостью, позволяет оттягивать ее без усилий в любом месте. Но поскольку реальные струны обладают жесткостью, их рабочая длина (которую мы обозначали в формулах буквой L) немного меньше физической длины, и это одна из причин, почему на басовых струнах применяется обмотка, а голая струна G (соль) классической гитары плохо строит в верхних позициях.
Упражнение для гитаристов
На настроенной гитаре струна В(си) и верхняя Е(ми) настроены примерно на 3-ю и 4-ю гармоники нижней струны Е(ми). Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/3, струна В(си) начнет колебаться, возбуждаясь через колебания подставки от гармоники 1-й струны. Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/4, отзовется верхняя струна Е(ми). Гитаристы обычно начинают настройку следующим образом: настраивают в унисон 4-ю гармонику басовой Е(ми), 3-ю у струны А(ля) и верхнюю струну Е(ми), затем струну В(си) строят по 3-й гармонике верхней Е(ми), а затем по 4-й гармонике А(ля) 3-ю гармонику струны D(ре). Настроить струну G(соль) по гармоникам не получится, в связи с невозможностью получения верхних гармоник, что связано с физическими параметрами толщины и жесткости самой струны, поэтому ее настраивают октавами, используя лады. По некоторым причинам (о которых будет сказано в конце главы), данный метод настройки достаточно приблизителен и требует дальнейшей подстройки при помощи ладов. Самой точной настройкой все-таки является компромиссная, которая осуществляется по аккордам, которые исполнитель собирается брать на грифе инструмента.
Гармоники (флажолеты) в музыке
Композиторы часто применяют гармоники/флажолеты на струнных инструментах, при этом наиболее часто используют «четвертую касательную». Одним пальцем музыкант зажимает струну, получая ноту за счет отрезка определенной длины, а другим легко касается струны там, где располагается нота на 4 тона выше (отсюда и название). Данная точка лежит на четверти длины отрезка струны, поэтому образуется 4-я гармоника базовой частоты в четыре раза больше базовой, т.е. получается интервал в две октавы. Струнные гармоники/флажолеты называются «натуральными» если они образованы от открытых струн и «искусственными» если струна прижимается. Ниже на рисунке показано, как берется натуральный флажолет. Для наглядности рисунок вытянут по вертикали.
Прослушайте фрагмент. Сначала звучит открытая струна А(ля), затем ее четвертая касательная (4-я гармоника).
Так обозначается на нотном стане «четвертая касательная» на скрипичной струне А(ля)
Немного технической информации для струнников
Несмотря на то, что «четвертая касательная» наиболее часто встречающийся флажолет, это не вполне удачный пример, поскольку получить четвертую гармонику гораздо проще, нежели «две четверки». Как известно, касание струны на отрезке 1/n (где n — целое число) дает n-ую гармонику, и для низких гармоник правило соблюдается, но для высших гармоник особое значение играет толщина струны, и здесь формула перестает работать. Таким образом, гармоники выше 8-й практически не берутся.
Если взять на струне подряд пять полутонов, то мы получим точку, соответствующую 1/3 длины струны, то есть «пятая касательная» даст нам третью гармонику. Гармоники расположены в следующем порядке:
| интервал на грифе | часть струны | номер гармоники | интервал от базовой ноты |
| октава | 1/2 | 2 | октава |
| квинта | 1/3 | 3 | октава + квинта (дуодецима) |
| кварта | 1/4 | 4 | две октавы |
| большая терция | 1/5 | 5 | 2 октавы + б. терция |
| малая терция | 1/6 | 6 | 2 октавы + квинта |
| ув. кварта | 2/7 | 7 | 2 октавы + м. секста повышенная |
| малая секста | 3/8 | 8 | 3 октавы |
| большая секунда | 1/9 | 9 | 3 октавы + б. секунда |
Положения нот звукоряда соответствуют чистому строю. Касание струны на 2/9 ее длины предпочтительней, чем на 1/9, хотя данная точка расположена не над нотой гаммы, а немного выше малой терции. Буду рад, если альтисты или виолончелисты исполняющие «Практикующая бесконечность» Радулески (Radulescu’s «Practicing Infinity») пришлют мне свои предложения о способах исполнения высоких флажолетов.
Несовершенство настройки по гармоникам (флажолетам)
Есть несколько проблем при настройке любой гитары, в том числе при использовании флажолетов, о чем говорилось выше. Приблизительность настройки инструмента очевидно связана с равномерной темперацией. Даже если бы струны были идеальны, а положение ладов на грифе идеально отвечало равномерной темперации, при настройке по четвертой гармонике струн E-A (ми-ля), и A-D (ля-ре), октава между открытой нижней E(ми) и нотой ми на 2-м ладу струны D(ре) отклонялась бы приблизительно на 4 цента ((4/3)222/12=1.996), что приводило бы к появлению одного интерференционного биения в несколько секунд.
Другая проблема заключается в том, что в зоне верхнего порожка и подставки струны не могут обеспечить абсолютную гибкость (что было отмечено выше). В результате 1-й обертон на струне всегда будет чуть выше октавы, второй выше чем дуодецима (октава + квинта), и так далее. Так настройка в унисон 4-ой «гармоники» струны Е(ми) и 3-ей гармоники струны А(ля) при сравнении открытых струн даст интервал несколько больший, чем кварта, отчего приходится исправлять настройку, чтобы иметь равномерную темперацию.
Еще один отрицательный момент относится к расположению ладов и подставки. При прижиме струны на двенадцатом ладу увеличивается и ее длина (это уже не самое короткое расстояние между верхним порожком и подставкой), и ее натяжение. Вследствие этого, а также из-за выгиба конца струны, будь 12-й лад точно посередине между верхним порожком и подставкой, мы бы имели интервал больше октавы. Поэтому расстояние от подставки до 12-ого лада делают несколько большим, чем до верхнего порожка. Необходимо отметить, что в зависимости от вида струн эффект может быть различен. На электрогитарах есть возможность регулировать положение каждой подставки струны, на некоторых гитарах подставку поворачивают под углом, а в случае с классической гитарой прямая подставка ведет к определенному компромиссу в настройке.
Вышеописанные моменты сложно отследить с большой точностью, поскольку при анализе звука струны, возбуждаемой щипком, неточности составляют лишь несколько центов, что не намного больше разрешающей способности слуха или приборов настройки. Настройка колками также не позволяет достичь точности менее двух центов. С другой стороны, если Вам удастся интонировать мелодию с точностью в пределах двух центов, это будет большая удача — большинству музыкантов такое не по силам!
Определенная часть проблем настройки касается старения струн. Там, где Вы касаетесь их пальцами левой руки, они вбирают в себя пот и становятся более тяжелыми (хотя может иметь место и износ материала в местах, которые трутся об лады). Струны также изнашиваются под пальцами правой руки. Неоднородность струн ведет к невозможности их точной настройки. Мойка струн может помочь лишь отчасти.
Конечно, на безладовом инструменте большинство этих проблем можно обойти, но аккордная техника при этом сильно страдает.
На рисунке показаны гармоники открытой струны СОЛЬ контрабаса или виолончели. (Ноты для контрабаса записываются октавой выше его звучания.) Над нотами указаны номера гармоник, а под ними записаны приблизительные частоты в Герцах, причем для наглядности сделано округление чисел. Данный пример демонстрирует закон изменения высотности гармоник, и, хотя реальные частоты составляют пропорционально несколько меньшие значения, динамика возрастания частот от значения в 100Гц отражена абсолютно точно. (Приведенные значения частоты ноты СОЛЬ и ее гармоник могли бы иметь место при камертоне Ля=449Гц. Примечание переводчика).
Перепечатка статьи возможна только с согласия автора Джо Вулфи J.Wolfe()unsw.edu.au, а также фирмы ГОСПОДИН МУЗЫКАНТ®, осуществлявшей ее перевод.
Гармоническая волна — согласно наиболее общему определению — волна, каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания[1]. В разных случаях при необходимости особо выделяется интересующий класс гармонических волн, например, плоская гармоническая волна, стоячая гармоническая волна итд (см. ниже).
Слово ‘гармоническая’ тут является синонимом слова ‘монохроматическая’, однако, по-видимому, не совсем точным; во всяком случае, обычные области применения того и другого термина обычно несколько различаются.
Источниками гармонических волн могут быть гармонические колебания, они также могут возбуждаться в какой-либо системе при взаимодействии ее с гармонической волной.
Одномерный случай
Случай одномерного однородного пространства (или одномерной однородной среды)[2] — наиболее прост.
В этом случае все виды гармонических волн сводятся к:
- синусоидальным (косинусоидальным) бегущим волнам:
- или бегущим волнам виде мнимой экспоненты:
а также к конечным линейным комбинациям волн такого вида (для выражения произвольной действительной гармонической волн в этом случае достаточно смешать две волны первого вида или четыре второго; в случае более многомерного u добавляется по два таких слагаемых на каждую поляризацию).
- Может быть также использовано понятие гармонической стоячей волны, сводящейся к сумме двух гармонических бегущих (бегущих в противоположных направлениях) волн, описанных выше:
Здесь A — постоянный (не зависящий от x и t) коэффициент, природа и размерность которого свпадает с природой и размерностью поля u; k, ω и φ0 — также постоянные параметры, в рассматриваемом одномерном случае все они — действительные числа (в отличие от более многомерных, где k становится векторным — для плоских волн). A — есть амплитуда волны, k — волновое число, ω — (циклическая) частота и φ0 — начальная фаза — то есть фаза волны при x = t = 0.
Во второй формуле A — (обычно) комплексное, амплитуду волны определяет его модуль |A|, а начальная фаза спрятана также в A в качестве его аргумента, поскольку
Так же, как стоячая волна выражается (как записано здесь) через две бегущих, так же и бегущая может быть выражена через две стоячих. Поэтому можно выбрать один из двух равноправных способов выражения произвольной гармонической волны в случае одномерного однородного пространства: через линейную комбинацию бегущих или линейную комбинацию стоячих волн. Это верно и для всех других случаев, хотя базисные волны, через линейную комбинацию которых выражается произвольная гармоническая волна, могут оказаться сложнее.
- случай неоднородного одномерного пространства (неоднородной среды) оказывается значительно сложнее. В этом случае зависимость гармонических волн от пространственной координаты x становится не синусоидальной, а в общем — и наиболее типичном — случае и вовсе не выражается через элементарные функции. Тем не менее, и в этом случае остается верным утверждение о возможности выразить произвольную гамоническую волну через конечное (для определенной частоты) количество базисных гармонических волн.
Случаи пространства размерностью больше единицы
В случаях пространства размерностью больше единицы, даже если оно однородно, в принципе разнообразие возможных гармонических волн очень сильно возрастает. Однако есть два типа гармонических волн, которым следует уделить главное отдельное внимание.
Плоские гармонические волны
наиболее важным и часто встречающимся типом гармонических волн являются плоские гармонические волны. (Одномерные гармонические волны являются их одномерным частным случаем.)
- Бегущая плоская волна — это волна такого вида:
или
где, в отличие от одномерной волны — уже не действительное число, а вектор, называемый волновым вектором, размерность которого равна размерности пространства, а выражение означает скалярное произведения этого вектора с вектором[3] , характеризующим точку пространства: .
Легко видеть, что если выбрать ось координат вдоль волнового вектора, плоская многомерная волна сводится к одномерной (u вообще перестает зависеть от остальных координат, а от первой — зависит как одномерная гармоническая волна).
- Стоячая плоская волна:
Так же, как и в одномерном случае, стоячие и бегущие гармонические волны одной частоты с одинаковым (быть может, с точностью до знака) волновым вектором, элементарно линейно выражаются друг через друга.
Поскольку с помощью преобразования Фурье (в текущем параграфе подразумевается, конечно, многомерное преобразование Фурье) практически любую[4] функцию пространственных координат можно представить как сумму (интеграл) функций, представляющих каждая плоскую волну, а зависимость от времени в тогда для случая однородного пространства будет тоже очевидно гармонической, то очевидно удобство разложения любой гармонической (да и не только гармонической) волны по плоским гармоническим волнам. В каких-то случаях и в какой-то мере это может быть полезным и в случаях неоднородности пространства, хотя в этом случае это вполне может и не дать ожидаемых преимуществ, или извлечение этих преимуществ может потребовать особого искусства.
Сферические гармонические волны
Сферические гармонические волны несколько менее универсальны и просты (их гораздо труднее даже выписать в явном виде, если не выражать просто через бесконечные суммы/интегралы плоских волн; например, для двумерного пространства гармонические сферические волны выражаются через функции Бесселя, то есть не выражаются через элементарные функции).
Тем не менее они бывают очень полезны, когда сами условия задачи склоняют к попытке рассмотрения сферических волн, то есть, в особенности при исследовании волн, порождаемых точечным источником или когда задача в целом имеет сферическую симметрию (последнее лучше всего для попытки искать решение просто в виде только сферических волн).
Для трехмерного однородного пространства гармонические сферические волны имеют вид:
или
или (в виде, удобном в качестве для разложения):
Значение и теоретическое применение
Общий линейный случай
Любое линейное дифференциальное уравнение вида
где порядок дифференцирования по времени n может быть любым (чаще интересны n = 1 или 2), а L любой линейный дифференциальный оператор, не зависящий от t (правда, если u должно быть действительным одномерным, а L -эрмитов, то нечетные n придется исключить), будет иметь решением гармоническую волну.
Действительно, подставим , где x — точка пространства любой размерности. Получаем тогда:
а экспонента сокращается. Сделав такую же подстановку с -ω, получим, при оговоренных выше условиях подходящего K, получить и действительное v как сумму этих двух решений.
Примечания
- ↑ См. определение по ГОСТу: http://www.rgost.ru/index.php?option=com_content&task=view&id=1680&Itemid=33
- ↑ Так же, конечно, как и сводящиеся к нему многомерные случаи
- ↑ Многоточие означает, что количество координат, определяющих вектор равно размерности пространства; если эта размерность равна 2, то количество компонент вектора, естественно, также должно быть усечено до 2.
- ↑ Математические условия, накладываемые на класс функций, для которых возможно преобразование Фурье и для которых обратное преобразование восстанавливает исходную функцию, можно считать удовлетворенными для любой функции, интересной сточки зрения физики волн, а случаи, когда то не совсем так, как правило, не очень важны с принципиальной точки зрения, во-вторых же достаточно успешно исправляются достаточно простой регуляризацией.
См. также
1.3 Гармоническая волна и ее параметры
Гармоническая волна – волна, изменяющаяся во времени по гармоническому (синусоидальному) закону. Для этой волны также употребляется термин монохроматическая (одноцветная) волна, заимствованный из оптики. Любой волновой процесс можно представить с помощью преобразований Фурье через гармонические волны.
Кратко остановимся на основных определениях и понятиях гармонической волны. Уравнения плоской гармонической волны, распространяющейся, например, вдоль оси zв среде без потерь записывается в следующем виде
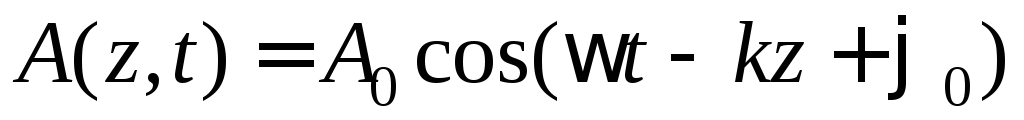(1.1)
Под
величиной A понимается физическая
величина, определяющая волновой процесс.
Максимальное значение этой величины
называется амплитудой, обозначенной в
(1.1) через
.
Размерность амплитуды определяется
природой волнового процесса. Например,
в звуковых волнах амплитуда измеряется
в единицах давления паскалях (Па), в
электромагнитных волнах амплитуда
напряженности электрического поля
измеряется в вольтах на метр (В/м), а
магнитного поля – в амперах на метр
(А/м).
Выражение, стоящее в скобках (1.1), называется фазой колебания, через которую определяется значение физической величины в данный момент времени и в данной точке пространства. Константа j0называется начальной фазой, использование которой имеет смысл при сравнении двух и более волн одной частоты в данной точке пространства и в фиксированный момент времени. Круговая частотаwсвязана с частотойf(число колебаний в единицу времени) соотношением
(1.2)
Частота wизмеряется в радианах в секунду, частотаfв герцах (1Гц – одно колебание в секунду). При известной частотеf период колебания находится из соотношения
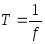. (1.3)
Из периодичности волнового процесса в пространстве определяется длина волны
. (1.4)
Таким
образом, длина волны – пространственный
интервал, по прохождению которого фаза
волны меняется на 
вдоль направления распространения.
Число длин волн, укладывающихся на
расстоянии
метров, называется волновым числом и
обозначаетсяk.
Поверхность, на которой волновой процесс имеет одинаковую фазу колебания, называется поверхностью равных фаз или фронтом волны. По форме фронта волны можно выделить плоские, цилиндрические и сферические волны. Поверхность, на которой амплитуда волнового процесса постоянна, называется поверхностью равных амплитуд. Волна называется однородной, если у нее поверхности равных амплитуд и равных фаз совпадают, то есть на поверхности фронта не меняется амплитуда волнового процесса. В неоднородной волне амплитуда на поверхности фронта изменяется.
Плотность потока энергии (или интенсивность) волны – это энергия, переносимая волной через единицу перпендикулярно ориентированной поверхности за единицу времени. Плотность потока энергии пропорциональна квадратуре амплитуды волны
, (1.5)
где p– коэффициент пропорциональности, зависящий от свойств среды и типа волны;
– единичный вектор, показывающий
направление распространения энергии.
Вектор плотности потока энергии в единицу времени (плотности потока мощности) принято называть вектором Умова-Пойнтинга.
Распространение
волны происходит в направлении,
перпендикулярном поверхности фронта
волны. Плоская волна идет в одном
направлении по нормали к ее фронту.
Цилиндрическая волна расходится по
радиусу в плоскости, перпендикулярной
оси цилиндра. Сферическая волна расходится
по радиусу перпендикулярно сферическому
фронту. Элемент поверхности цилиндрического
фронта 
возрастает прямо пропорционально
расстоянию, при этом плотность потока
мощности убывает обратно пропорционально
расстоянию, а амплитуда цилиндрической
волны убывает обратно пропорционально
корню квадратному из расстояния. Элемент
поверхности сферического фронта
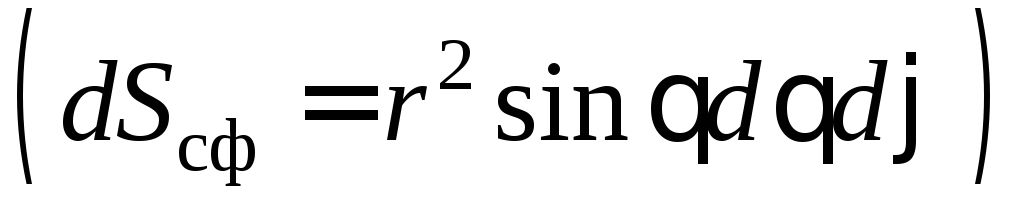возрастает пропорционально квадрату
расстояния, плотность потока мощности
уменьшается обратно пропорционально
квадрату расстояния, а амплитуда
сферической волны убывает обратно
пропорционально расстоянию. В среде с
потерями распространяющиеся волны
теряют часть своей энергии и их амплитуды
убывают по экспоненциальному закону
вдоль направления распространения.
Что такое гармоники или обертона
В этой статье я хочу рассказать о том, что такое гармоники или обертона.
Любой музыкальный звук состоит из основного тона и дополнительных гармоник (обертонов).
Основной тон – это основа звука, отправная точка строения обертонов. Мы воспринимаем именно этот тон с точки зрения его высотности.
Гармоники – это производные основного тона. Причем, кратные производные.
Это значит, что если основной тон ноты «до» малой октавы имеет частоту приблизительно 130 Гц, то его обертона будут иметь частоту 260 Гц, 390 Гц, 520 Гц и т.д. То есть все эти гармоники можно разделить на 130 и получится целое число. Поэтому говорят вторая гармоника, третья гармоника и т.д. За счет этих гармоник и формируется окраска звука. Мы не можем воспринимать каждую гармонику разрозненно. Мы лишь слышим результат сочетания гармоник с основным тоном.
Основной тон всегда лежит ниже гармоник и является более громким, что и определяет его выраженность.
Гармоники – это основа окраски звука. Любой инструмент имеет свой неповторимый тембр, порождённый гармониками. Поэтому мы и слышим различия в звучании фортепиано, гитары и саксофона. Всё дело в гармониках.
Что такое гармоники
Для того чтобы наглядно продемонстрировать вам гармоники, я проведу один простой эксперимент. Для этого мне понадобятся синтезатор Sylenth2 в комплексе с плагином iZotope Ozone 4. C помощью синтезатора я буду генерировать различные звуки и анализировать результаты используя анализатор спектра в iZotope Ozone 4.
Итак, приступим!
1. Выберу пустой пресет, включу один осциллятор, выберу синусоидальную форму волны и сгенерирую звук ноты «Ля» большой октавы.
Как видно из скриншота, я сгенерировал основной тон ноты «Ля» 110 Гц. Кроме него никаких гармоник в сигнале нет.
2. Изменю форму волны на пилообразную.
Из скриншота видно, что у основного тона ноты «Ля» появились гармоники кратные 110.
3. Теперь выберу какой-нибудь пресет. Например, 44. LD Cello.
На скриншоте отчётливо видно, что тембр этого звука сформирован большим количеством дополнительных обертонов.
Из всего вышесказанного следует, что гармоники являются неотъемлемой составляющей любого звука. Без наличия обертонов музыка бы потеряла всю свою колоритность. Все инструменты звучали бы одинаково и примитивно.
Благодаря гармоникам мы имеем огромную палитру разнообразных тембров. Их число бесконечно велико. Это даёт возможность музыкантам и саунд продюсерам постоянно экспериментировать и синтезировать новые более интересные и насыщенные тембры.
В этой статье я рассказал о том, что такое гармоники.
Если есть вопросы, задавайте их в комментариях.
Понравилась статья? Поделись с друзьями.
Читайте также:
Автор: Александр Коваленко
В 1747 г. Жан ле Рон Д’Аламбер (1717 — 1783), французский математик, философ, писатель, один из создателей знаменитой «Энциклопедии наук, искусств и ремесел», член Парижской и Петербургской Академий, опубликовал статью «Исследование по вопросам о кривой, которую образует натянутая струна, приведенная в колебание», где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных, названного волновым уравнением:
Здесь t — время; x — координата струны в положении равновесия;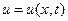 
— неизвестная функция, выражающая отклонение точки с координатой x в момент времени t от положения равновесия; 
— коэффициент пропорциональности, характеризующий упругие свойства струны (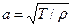 
; T — сила натяжения струны; ρ — плотность однородной струны). Символы 
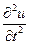и 
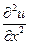обозначают частную производную второго порядка, которая определяется как производная от производной ( 
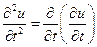).·Частные производные 
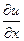и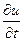 
, как и обыкновенная производная 
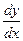, характеризуют скорость изменения функции 
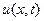по каждой из переменных x или t в отдельности при условии, что другая переменная не изменяется. Предполагается, что струна совершает малые колебания, происходящие в одной плоскости.
Еще через полвека другой соотечественник Д’Аламбера Жан Батист Жозеф Фурье (1768 — 1830), выдающийся математик и сподвижник императора Наполеона, изобрел новый метод, позволивший получить общее решение задачи о колебании конечной струны. Эта задача формулируется так: найти решение волнового уравнения (3.3.1), удовлетворяющее начальным и граничным условиям:
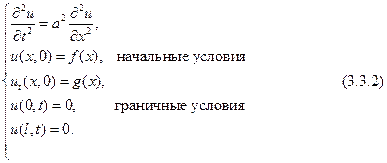
Начальные условия означают, что в момент времени 
струне придали некоторую форму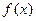 
и сообщили ускорение 
. Граничные условия показывают, что на концах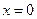 
или 
струна жестко закреплена.
Опуская промежуточные выкладки, выпишем решение Фурье задачи о колебании конечной струны, которое представляет собой бесконечную сумму слагаемых, или, как говорят, разложение функции 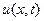в ряд:
Выясним физический смысл решения (3.3.3), и прежде всего функций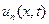 
, составляющих это решение. Для этого выполним искусственное преобразование:
Итак,
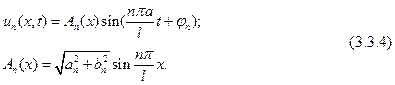
Из формулы (3.3.4) видно, что каждое решение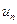 
представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой 
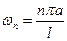и фазой 
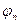. Амплитуда же колебаний 
для разных точек струны разная. Ясно также, что пр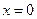и и 
, т. е. на концах струна неподвижна. Итак, во времени колебания струны происходят с постоянной частотой 
, но с переменной по координате x амплитудой. При этом все точки струны одновременно достигают своего максимального отклонения в одну или другую сторону и одновременно проходят положения равновесия. Такие колебания называют стоячими волнами. Пользуясь выражением для амплитуды стоячей волны (3.3.4) и учитывая, что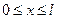 
, найдем неподвижные точки стоячих волн:
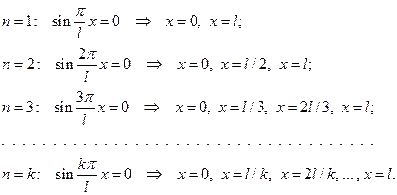
Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.
Сделаем общий вывод: колебание конечной струны представляет собой бесконечную сумму стоячих волн 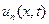, каждая из которых имеет постоянную частоту колебания 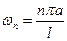и переменную по длине струны амплитуду 
. В k-й стоячей волне имеется k пучностей и 
узлов. На рисунке 77 показаны четыре первые стоячие волны струны.
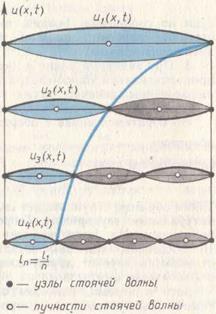
Рис. 77. Четыре первые стоячие волны (гармоники) колеблющейся струны.
Перейдем теперь к «музыкальному содержанию» решения (3.3.3). Мы пришли к выводу, что струна колеблется не только всей своей длиной, но одновременно и отдельными частями: половинками, третями, четвертями и т. д. Следовательно, струна издает звук не только основной частоты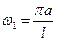 
, но и призвуки частот 
, 
, … , 
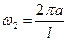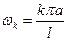, … . Тон основной частоты струны 
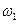называется основным тоном струны, а остальные тона, соответствующие частотам 
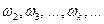, называются обертонами (верхними тонами) или гармониками. Основной тон струны принимается за первый обертон. Именно обертоны, сливаясь в общем звучании с основным тоном, который имеет наибольшую амплитуду и потому наиболее заметен, придают звуку музыкальную окраску, называемую тембром.
Различие тембров музыкальных звуков прежде всего объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, «богаче» он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизводимые на скрипке или фортепьяно, голосом или на флейте.
Рассмотрим подробнее основной тон струны. Вспоминая, что 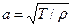, получим формулу для частоты основного тона:
откуда легко увидеть законы колебания струны, которые экспериментально пытались обнаружить на монохорде пифагорейцы. А именно:
1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это в точности пифагорейский закон (3.1.2)).
2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения (этот закон, судя по сообщению Боэция, пифагорейцы знали только качественно, ошибочно полагая высоту тона пропорциональной натяжению струны).
3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности (этот закон пифагорейцы, конечно, также могли знать только качественно: чем толще струна, тем ниже издаваемый ею звук).
Но обратимся вновь к обертонам. Легко видеть, что частоты обертонов 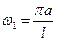, , 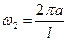… , , … 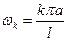относятся как числа натурального ряда:
Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение лишь первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.
Зато в первых, наиболее сильных обертонах мы находим замечательное свойство: второй обертон с основным тоном образует интервал октавы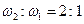 
, третий и второй обертоны—интервал квинты 
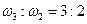, четвертый и третий — кварты 
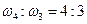. Но ведь это есть не что иное, как набор совершенных консонансов! Причем у второй гармоники с первой совпадает каждый второй узел стоячей волны, у третьей с первой — каждый третий, а у четвертой с первой — каждый четвертый (рис. 77). Ясно, что, чем больше узлов у двух стоячих волн совпадает, тем они «больше похожи» друг на друга, т. е. тем созвучнее образуемый ими интервал. Следовательно, с ростом номера гармоники степень консонантности интервала убывает.
Итак, мы приходим к разгадке закона целочисленных отношений консонансов (3.1.1), который, по преданию, был экспериментально открыт самим Пифагором. Все совершенные консонансы, т. е. интервалы с отношением частот вида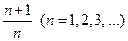 
, определены самой природой колебания струны. Все совершенные консонансы заключены в первых четырех, наиболее мощных гармониках колеблющейся струны, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Этот «закон консонансов» является следствием математического решения задачи о колебании конечной струны (3.3.3).
Со временем в теории музыки стали различать и несовершенные консонансы: большую и малую терции. Эти интервалы как среднее арифметическое и среднее гармоническое основного тона (1) и квинты (3/2) нашел еще Архит. В самом деле, для интервального коэффициента большой терции имеем
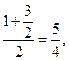
а для интервального коэффициента малой терции:
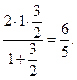
Легко видеть, что несовершенные консонансы определяются следующими — пятой и шестой — гармониками колеблющейся струны. По этому поводу еще в XVIII в. французский музыкальный теоретик Балльер с присущей французу легкостью писал: «Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го».
Но почему именно шесть гармоник определяют все консонансы? Почему знаменитый «фальшивый», седьмой, обертон не входит ни в какие музыкальные созвучия, тогда как девятый и восьмой образуют основу всей музыкальной гаммы — известный нам тон-интервал (9/8)? Эти и немало других вопросов все еще остаются тайнами гармонии.
В заключение заметим, что пифагорейцы имели практически такое же объяснение явлению консонансов, которое следует из решения (3.3.3). Начиная с Архита греки представляли звук как совокупность множества отдельных ритмических ударов струны по воздуху и таких же колебаний воздуха. Тогда в консонансе октавы отдельные удары верхнего тона происходят в два раза чаще, чем у более низкого основного тона. Следовательно, каждый второй удар верхнего тона достигает нашего уха одновременно с одним ударом основного тона, при этом основной тон как бы целиком переходит в верхний и сливается с ним в едином звучании. В консонансе квинты каждый третий удар верхнего тона совпадает с каждым вторым ударом основного тона, и поэтому квинта звучит менее слитно, чем октава. И так далее. Но совпадение числа ударов струны по воздуху эквивалентно совпадению числа узлов в стоячей волне, которые и определяют число таких ударов в единицу времени, т. е. частоту колебания струны.
Таким образом, пифагорейцы совершенно правильно представляли себе физические основы явления консонанса! Мы же имеем еще одну возможность убедиться в блестящей интуиции и глубоком проникновении пифагорейцев в суть физических явлений.
Начиная с Пифагора теории музыки посвящали глубокие исследования такие прославленные ученые, как Архит и Евклид, Клавдий Птолемей и Северин Боэций, а впоследствии Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер. Не всегда эти изыскания приносили желанные плоды (так, о математической теории музыки Эйлера говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов), но всегда они служили развитию как науки математики, так и искусства музыки. И в математике, и в музыке продолжали звучать могучие аккорды, некогда взятые Пифагором.
На этом мы расстаемся с пифагорейской теорией музыки. Но расстаемся ненадолго, ибо пифагорейская музыка продолжала звучать в… пифагорейской астрономии.
Общая физика. Оптика и волны
1. Спектр колебаний. Тембр звука, речь и пение
Причудливое изменение формы струны со временем мало что говорит нам о составе колебаний. Поэтому самой, быть может, важной характеристикой колебания является его спектр: диаграмма, показывающая относительный вклад каждой гармоники в полную интенсивность (энергию) колебаний, то есть функция
Спектр колебания также зависит от способа возбуждения струны. На рис. 2.13 приведен численный расчет спектра колебаний струны для обоих наших случаев. Темные столбики соответствуют «треугольной» начальной форме струны, а светлыми показан спектр колебаний струны, начальная форма которой составлена из кусков разных синусоид. По горизонтальной оси отложены номера гармоник, а высота столбиков по вертикальной оси дает относительную интенсивность соответствующих колебаний (то есть долю каждой из гармоник в полной интенсивности издаваемого струной звука).
Рис. 2.13. Спектр колебаний струны (первые восемь гармоник) при разных способах возбуждения колебаний.
Синими столбиками показаны амплитуды обертонов при «треугольной» начальной форме струны,
а фиолетовыми — при «кусочно-синусоидальной» форме
Видно, что в первом случае наибольший вклад вносят первые четыре гармоники — на них приходится 97.9 % интенсивности звука, вклад следующих четырех гармоник уже невелик (2%), а на все остальные приходится лишь около 0.1% интенсивности. Конкретные числа здесь зависят от способа возбуждения струны, при ином методе они могут измениться. Например, при оттягивании струны за середину все четные гармоники просто отсутствуют в спектре, на долю первой приходится 98.55 %, на долю третьей — 1.22 %, пятой — 0.16 %, а оставшиеся 0.07 % — на долю всех остальных.
Во втором случае вклад второй гармоники даже больше вклада основ ной, заметны третья и, в меньшей степени, четвертая гармоники. В сумме вклад первых четырех гармоник составляет около 99.97 %, так что на все остальные приходится лишь 0.03 %.
Эти примеры демонстрируют общее правило: обычно возбуждаются низшие гармоники колебаний, а влияние высших уменьшается с ростом их номера. От наличия дополнительных гармоник в спектре колебаний (их называют обертонами) зависит окраска, тембр звука. По-разному воспринимается одна и та же нота, сыгранная на флейте, скрипке или гобое. Если бы звучала чистая нота, то никакого отличия одного инструмента от другого не было бы. Разнообразию музыкальных звуков мы обязаны обертонам. Степень их присутствия, помимо способа возбуждения вибратора, зависит также (и даже в гораздо большей степени) от резонатора инструмента. Так, при игре на скрипке в образовании звука принимает участие корпус инструмента, колеблющийся под действием колебаний струн, и объем воздуха внутри корпуса. Во-первых, тем самым усиливается звук инструмента: основной источник звука — тонкая струна, и сама по себе она не может привести в движение большую массу воздуха, чтобы звук дошел до слушателя. Во-вторых, на верхней деке скрипки возникают колебания, причем благодаря резонансу некоторые обертоны исходных колебаний струн усиливаются, а другие — гасятся. Резонаторы музыкальных инструментов выступают, таким образом, как преобразователи тембра исходного звука. Всем известно, что ценность инструмента, будь то скрипка или рояль, зависит не от качества натянутых в нем струн, а от особенностей строения их корпуса, дек. Искусство старых итальянских мастеров Страдивари, Амати, Гварнери, изготовивших прекрасные скрипки, альты и виолончели, состояло, в частности, в том, что они умели на практике добиваться оптимального спектра колебаний, что мы воспринимаем как божественного звучание их инструментов.
Области усиления высших обертонов называются формантами, и они определяют тембр того или иного инструмента. На рис. 2.14 показано разложение в спектр звуков рояля и кларнета.
|
Рояль |
Кларнет |
Рис. 2.14. Спектр звука различных музыкальных инструментов
На спектре отчетливо видны форманты: скажем, шестая гармоника для рояля и восьмая–десятая — для кларнета. Именно они создают отличия в звучании этих инструментов.
Если перейти к голосу человека, то источником исходного звука является голосовая щель, колебания голосовых связок (то есть в сущности — тех же струн). На слух этот звук резко отличается от нормального, выходящего изо рта. Он носит «пищащий» характер и не имеет формы того или иного гласного звука, как не имеет его простая гитарная струна: музыкальные инструменты говорить не умеют. Исходный тембр голосовой щели приобретает характер речевого звука при прохождении по рото-глоточному каналу. Со времен исследований Гельмгольца по акустике известно, что каждый гласный звук содержит в своем спектре две основные, относительно усиленные области частот — форманты гласных, или характеристические тоны Гельмгольца. По ним наше ухо отличает один гласный звук от другого. Одна из частот связана с резонансом глотки, вторая — с резонансом ротовой полости. Ротовая полость меньше по объему, и потому объем воздуха в ней резонирует на более высокие частоты — порядка килогерц, глоточная полость по размеру больше, и резонирует она на частоты порядка нескольких сот герц. (Зависимость резонансной частоты от размера полости резонатора такая же, как для частот на струне — чем короче струна, тем выше извлекаемая на ней частота.) Изменение относительных размеров этих полостей производится артикуляцией языка, перемещение которого создает в ротовой и глоточной полостях нужные для образования формант объемы воздуха. В старые времена преступникам вырезали язык, и они лишались возможности произносить гласные звуки, лишались дара речи, хотя голос у них и сохранялся. Форманты для гласных русского языка имеют примерно следующие значения: и – 240 Гц и 2 250 Гц, у – 300 Гц и 650 Гц, е – 440 Гц и 1 800 Гц, о – 535 Гц и 780 Гц, а – 700 Гц и 1 000 Гц. У женщин и детей формантные области несколько смещены в сторону более высоких частот, и благодаря этому мы различаем, кто говорит с нами, даже если частота основного звука будет одной и той же. Важно, что формантные области остаются постоянными, несмотря на изменение высоты основного тона: человек может произнести гласную е басом или тенорком, но формантные частоты будут теми же самыми (рис. 2.15). Некоторые отличия в числах между приведенными данными и рисунком связаны с тем, что измерения слегка отличаются у разных групп исследователей.
Рис. 2.15. Спектр гортани, состоящий из равномерно убывающих по амплитуде обертонов (1) и спектры звука е,
взятого на частоте 100 Гц (2) и 200 Гц (3). Формантные области n = 700 Гц и n = 1 400 Гц
остаются неизменными, несмотря на изменение высоты основного тона
При изучении не речи, но уже пения, были открыты еще две области обертонов — так называемые певческие форманты. В 20–30-е гг. было обнаружено, что в спектре хорошо поставленного мужского голоса всегда присутствуют усиленные обертоны с частотой в области 500 Гц. Наличие этой низкой певческой форманты придает голосу округлое, полное и мягкое звучание. Высокая певческая форманта лежит в области 3 000 Гц, она привносит в звук яркость, блеск, создает серебристость тембра. У мастеров вокального искусства в области высокой певческой форманты сосредоточено до 30–35 % всей звуковой энергии голоса, в речи же, даже поставленной (у дикторов и актеров) — только 5–7 %. Чем интенсивнее звук, тем более выражены певческие форманты по сравнению с формантами гласных. Поэтому при большой мощности звука гласные становятся плохо различимыми, и мы узнаем их скорее по контексту, в начальный момент формирования звука. На рис. 2.16 показан спектр голоса Ф. Шаляпина.
Рис. 2.16. Спектр голоса Ф. Шаляпина. Основной тон у Шаляпина в общем спектре роли не играет.
Его амплитуда принята на рисунке за единицу. Основная энергия заключена в низкой певческой форманте — 2–4 обертонах.
Высокая певческая форманта возникает в гортани человека — в надсвязочной полости между голосовыми связками и входом в гортань. Эта полость имеет размеры порядка 3 см, что при скорости звука v = 340 м/с приводит к резонансу на частоте
(основной тон закрытой трубы, который мы обсуждали выше), то есть как раз в области высокой певческой форманты. Место возникновения низкой певческой форманты точно не определено: данные указывают, скорее всего на резонанс трахеальной трубки.
С тембром голоса, в присутствии в его спектре высоких обертонов, связано качество «полетности». Существуют певческие голоса, летящие в зал и «пробивающие» звучание оркестра, причем иногда они не имеют большой силы. И наоборот, есть голоса необыкновенной мощи, теряющиеся в больших помещениях, заглушаемые звучанием оркестра. Качество полетности оказалось связанным с особенностями нашего слуха, который наиболее восприимчив к области частот 2 500 – 3 000 Гц. На эти частоты резонирует наружный слуховой проход уха, и такие звуки субъективно воспринимаются как более громкие. Как мы уже знаем, это — область высокой певческой форманты. Голоса, в которых большой процент энергии концентрируется в высокой певческой форманте, обладают способностью «лететь через оркестр», они хорошо слышны в большом зале.
2. Высота звука и устройство музыкальной шкалы
Равномерная темперация
Одной из важнейших характеристик музыкального звука является его высота, количественной мерой которой служит частота n колебаний соответствующего вибратора (столбика воздуха в духовых инструментах, струны — в струнных и т. п.). Частота колебаний может принимать любые значения, но с точки зрения восприятия музыкального звука наблюдается известная периодичность: два звука воспринимаются как аналогичные, если частота одного из них ровно в два раза превышает частоту другого. Эту аксиому эквивалентности звуков провозгласил в 1722 г. французский композитор Жан Филипп Рамо. Таким двум звукам соответствует одна и та же нота, и, как говорят, их разделяет интервал, называемый октавой.
Международным стандартом для ноты «ля» первой октавы установлена частота Гц. Нота «ля» следующей, второй октавы, имеет частоту, ровно в два раза большую — Гц. В европейской системе октава делится на двенадцать разных звуков (вспомните, например, семь белых и пять черных клавиш в каждой октаве фортепиано). Интервал между соседними звуками называется полутоном. Как же настроить соответствующие вибраторы, исходя из стандартной частоты ? Один из способов — равномерный строй (как говорят музыканты – равномерная темперация), когда отношение между частотами соседних звуков постоянно. Это отношение, как легко понять, равно
Именно это число, будучи умноженным само на себя 12 раз, дает в результате удвоение частоты для той же ноты в следующей октаве:
Приняв равномерно-темперированный строй, мы можем рассчитать частоты любых нот. Так, нота «ля» первой октавы и нота «до» второй октавы разделены тремя полутонами, то есть частота последней должна равняться
Соответственно, частота Гц ноты «до» первой октавы получается отсюда делением на двойку. Нота «соль» первой октавы отстоит от «до» той же октавы на семь полутонов, то есть ее частота равна
Результаты подобных расчетов для четырех октав приведены в таблице 2.2.
Таблица 2.2.
Высота музыкальных звуков при равномерно-темперированном строе: для каждой ноты указаны ее международное (латинское) обозначение и частота в герцах
|
Большая октава |
|||||||||||
|
до |
до |
ре |
ре диез |
ми |
фа |
фа диез |
соль |
соль диез |
ля |
си бемоль |
си |
|
С |
Cis |
D |
Dis |
Е |
F |
Fis |
G |
Gis |
А |
В |
Н |
|
65.4 |
69.3 |
73.4 |
77.8 |
82.4 |
87.3 |
92.5 |
98.0 |
103.8 |
110 |
116.5 |
123.5 |
|
Малая октава |
|||||||||||
|
до |
до |
ре |
ре диез |
ми |
фа |
фа диез |
соль |
соль диез |
ля |
си бемоль |
си |
|
с |
cis |
d |
dis |
е |
f |
lis |
g |
gis |
а |
b |
h |
|
130.8 |
138.6 |
146.8 |
155.6 |
164.8 |
174.6 |
185.0 |
196.0 |
207.6 |
220 |
233.1 |
246.9 |
|
Первая октава |
|||||||||||
|
до |
до |
ре |
ре диез |
ми |
фа |
фа диез |
соль |
соль диез |
ля |
си бемоль |
си |
|
с1 |
cis1 |
d1 |
dis1 |
е1 |
f1 |
lis1 |
g1 |
gis1 |
а1 |
Ь1 |
h1 |
|
261.6 |
277.2 |
293.7 |
311.1 |
329.6 |
349.2 |
370.0 |
392.0 |
415.3 |
440 |
466.2 |
493.9 |
|
Вторая октава |
|||||||||||
|
до |
до |
ре |
ре диез |
ми |
фа |
фа диез |
соль |
соль диез |
ля |
си бемоль |
си |
|
с2 |
cis2 |
d2 |
dis2 |
е2 |
f2 |
lis2 |
g2 |
gis2 |
а2 |
Ь2 |
h2 |
|
523.3 |
554.4 |
587.3 |
622.3 |
659.3 |
698.5 |
740.0 |
784.0 |
830.6 |
880 |
932.3 |
987.8 |
Заметим, кстати, что эти октавы выбраны для примера не случайно: именно в этом диапазоне лежит голос человека. Самый высокий женский певческий голос — сопрано, для которого характерен диапазон с1–e3 (редко — до g3). На несколько тонов ниже лежит диапазон меццо-сопрано: а–h2. Самый низкий женский голос — контральто, его типичный диапазон — f–а2. Особо надо упомянуть контратеноров — современных исполнителей произведений, написанных некогда для певцов-кастратов. Но диапазон последних был необычайно широк, и немногие из нынешних певцов в полной мере могут воспроизвести некогда популярные произведения. «Типичные» контратеноры (если можно говорить о типичности столь редких голосов) поют в диапазоне (c–e2), отличаясь от контральто тембром.
Самый высокий из обычных мужских голосов — тенор, для него типичен диапазон с–с2. Далее следуют баритон (А–f1) и бас (С–е1). Таким образом, «вокальные» частоты простираются от примерно 70 Гц до 1 400 Гц (здесь идет речь об основной ноте, а не о примеси обертонов). Примерные диапазоны певческих голосов показаны на рис. 2.17 вместе с диапазонами струнных инструментов — скрипки, альта, виолончели и контрабаса. Король инструментов — концертный рояль — содержит обычно 7.25 октав: от А2 (27.5 Гц) до с5 (4 186 Гц).
Рис. 2.17. Примерные диапазоны струнных инструментов и человеческих голосов
Идея равномерной темперации родилась в Германии на рубеже XVII–XVIII веков. Приведенная музыкальная шкала поначалу встретила сопротивление, но после сочинения И.С. Бахом в 1722–1744 гг. «Хорошо темперированного клавира» — сборника прелюдий и фуг, по одной на каждую из существующих 24 тональностей, – жизнеспособность новой шкалы была доказана. С тех пор она и стала общепринятой. Основное достоинство равномерно темперированной шкалы — это возможность транспонировать мелодию в другой диапазон без ее искажения. Например, мелодия «Чижика» (ми1 – до1 – ми1 – до1 – фа1 – ми1 – ре1), играемая в первой октаве, соответствует последовательности частот (в Гц): 330–262–330–262–349–330–294 (мы округлили значения, приведенные в таблице 3.2). Предположим, мы хотим сыграть ее, перенеся начало на три клавиши выше — с ноты «си», которой соответствует частота 494 Гц. Отношение первых нот оригинальной и транспонированной мелодий равно 493.7/329.6=1.4983=27/12 (показатель степени соответствует семи полутонам, разделяющий ноты «ми» и «си» — см. рис. 3.17). Таким же должно быть отношение вторых и всех последующих нот мелодии. Стало быть, последовательность частот транспонированной мелодии должна иметь вид 494–392–494–392–523–494–440, то есть транспонированная мелодия прозвучит как си1 – соль1 – си1 – соль1 – до2 – си1 – ля1.
Почему же равномерно темперированная музыкальная шкала вызывала возражения? Дело в том, что еще в древности, со времен Пифагора, было известно, что некоторые ноты, взятые одновременно, звучат в консонанс, благозвучно, не вступают в противоречие друг с другом. К таким двузвучиям Пифагор относил октаву (отношение частот 2:1), квинту (3:2) и кварту (4:3)— так называемые совершенные консонансы. Позже к ним причислили еще большую и малую терции (5:4 и 6:5). Что же общего между консонансом двузвучия и отношением первых шести целых чисел?
Разберемся, что происходит, когда одновременно берутся две ноты. Нижний по высоте звук называется основанием интервала, верхний — его вершиной. Пусть основанию соответствует частота v1 при звучании струны на этой ноте неизбежно будут возбуждаться и первые обертоны с частотами v2 = 2v1, v3 = 3v1, v4 = 4v1. Если теперь одновременно с первой нотой взять другую, образующую с первой интервал в октаву (соответствующая ей частота равна v2 = 2v1), то на ней тоже будут возникать обертоны с частотами v4=2v2 = 4v1, v6 = 3v2 = 6v1 и т. д. Мы видим, что состав созвучия, в сущности, не изменился — добавление новой ноты не прибавило новых обертонов. Поэтому октава и звучит почти как одна нота, абсолютный консонанс.
«Примесь» второй гармоники всегда существует при колебании любого вибратора, и, может, это и есть причина того, что наше ухо воспринимает одинаковые ноты в разных октавах как звучащие в унисон, как, в сущности, ту же самую ноту. В этом, видимо, заключена физическая основа аксиомы эквивалентности Рамо, само понятие октавы как некой меры периодичности музыкального звука, когда начинают повторяться те же самые ноты.
Попутно мы установили, что нота, соответствующая частоте v3 = 3v1 тесно связана с первоначально взятой нотой — так или иначе, но этот звук уже присутствует в изначальном как его третья гармоника. Но по теореме эквивалентности этой ноте в предыдущей октаве соответствует частота v1quint=3v1/2. Таким образом, интервал, где основанию соответствует частота v1, а вершине — частота vquint = 3n1/2, будет благозвучным. Такой интервал называется, напомним, квинтой, и отношение частот вершины и основания в квинте в точности равно 3/2.
Возьмем теперь благозвучную квинту — двузвучие с частотами v1 и vquint = 3v1/2, — и добавим к нему третью ноту, составляющую октаву с основанием. Ее частота равна 2v1. По теореме эквивалентности, благозвучие этого созвучия не нарушится. Но если благозвучен интервал между основанием и третьей нотой (октава) и благозвучен интервал между основанием и вершиной двузвучия (квинта), то должен быть благозвучен и интервал между вершиной и третьей нотой. Соответствующее отношение частот равно v2/vquint = 2v1/(3v1/2) = 4:3. Такой интервал называется, как мы помним, квартой. Если за основание интервала взять все ту же ноту с частотой v1, то кварту с ней образует нота, звучащая на частоте vquart = 4v1/3.
В принципе, эти отношения целых чисел можно было бы положить в основу построения музыкальной шкалы. Но тогда возникнет проблема с транспонированием мелодии.
Попробуем построить одну октаву гипотетической музыкальной шкалы, а) основанной на отношении целых чисел и б) допускающей транспонирование мелодии. Пусть эта шкала содержит какую-то ноту с частотой v. Тогда в ней должна содержаться также и нота, образующая с исходной интервал в октаву (2v). Пусть также в шкале имеется еще одна нота, образующая с первой, например, чистую квинту (3v/2). Тогда шкала должна содержать и ноту, отстоящую от первой на две квинты: ее частота равна (3/2)2v = 9v/4, а понижение на октаву дает нам ноту 9v/8. Понижение на октаву комбинации трех квинт приводит к ноте с частотой v/(3/2)3/2 = 27v/16, понижение на две октавы комбинации четырех квинт приводит к частоте 81v/64 и т. д. Продолжая этот процесс, мы получим бесконечное число нот в пределах одной октавы, ибо никакая степень тройки не станет равной какой-то степени двойки (нечетное число не может быть равным четному). Значит, описанная процедура будет приводить все к новым и новым нотам, которые необходимо включить в шкалу. Тот же результат получается, если строить шкалу на основе кварт, а не квинт. Таким образом, требования а) и б) к музыкальной шкале оказываются несовместимыми. Надо отказаться от одного из них, и проще пожертвовать отношением целых чисел для совершенных консонансов, приобретая свободу выбора тональностей и легкость транспонирования мелодий.
Поэтому музыканты отказались от настройки своих инструментов по закону отношения целых чисел, и перешли к равномерной темперации. При этом частоты совершенных консонансов воспроизводятся приблизительно. Например, в равномерно темперированной шкале квинте соответствует интервал в 7 полутонов: 27/12 = 1.4983, что лишь на 0.1 % отличается от чистой квинты (отношения 1.5). Таков интервал, например, между нотами «до» и «соль». Кварте соответствует интервал в 5 полутонов: 25/12 = 1.3348, что отличается от чистой кварты (1.3333) также на 0.1 % (опытному уху слышны даже столь малые отличия от идеальных интервалов).
Было бы интересно обсудить физические принципы, лежащие в основе мажорного (до–ми–соль) и минорного (до–ми бемоль–соль) трезвучий, но это увело бы нас слишком далеко от физики, к которой пора возвращаться. Мы надеемся, однако, что музыкальные примеры помогли усвоить важные понятия высших гармоник и спектра колебаний, с которыми нам еще предстоит встретиться.
Дополнительная информация
http://physbook.ru/index.php/Kvant._%D0%9C%D1%83%D0%B7%D1%8B%D0%BA%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B3%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%8F – О музыкальной гармонии.
http://dic.academic.ru/dic.nsf/enc_physics/404/%D0%92%D0%BE%D0%BB%D0%BD%D1%8B – Волны. Материал из физической энциклопедии.
http://koi.tspu.ru/waves/ch5_1.htm – Основные определения для волн.
http://allphysics.ru/feynman/volni – Фейнмановские лекции по физике. Волны.
http://physbook.ru/index.php/Kvant._%D0%92%D0%BE%D0%BB%D0%BD%D1%8B_%D0%BD%D0%B0_%D0%BF%D0%BB%D1%8F%D0%B6%D0%B5 – Волны на пляже, солнце в небе и многое другое.
http://physbook.ru/index.php/Kvant._%D0%92%D0%BE%D0%BB%D0%BD%D0%B0 – Хорошо ли вам знакомо понятие волна? Вопросы с ответами.
http://www.phyzika.ru/waves.html – Кратко о волнах.
Гармоническое искажение было дано в мире аналоговой записи и помогло создать волнение в аналоговых записях: получить советы о том, как этого добиться в готовом виде.
Гармоническое искажение — это термин, который мы часто слышим при обсуждении спецификаций аналоговых компонентов, но что именно? И как это полезно в нашей повседневной работе со звуком?
Существует множество цифровых инструментов для хирургического и эффективного добавления глубины гармоник, возбуждения, более сильных искажений или где-то между ними (i.е. Vitamin Sonic Enhancer, кобальтовая сапфира). В этой статье мы сосредоточимся на стиле гармонического тепла и волнения, присущего аналоговым компонентам .
Окраска цифровой записи оставляет нам сравнительно чистую гармоническую палитру, поэтому, если мы хотим насладиться теплом записывающего оборудования прошлых лет, мы должны сознательно принять решение добавить его в микс.
Здесь мы рассмотрим некоторые из вариантов и много использования аналоговых инструментов для цифрового производства:
Гармоники: определения
Гармоники представляют собой целые числа, кратные основной частоте звука, которые психоакустически возбуждают общий тембр, добавляя глубину, цвет, присутствие, характер или теплоту к звуку.Любой звук, который является более сложным, чем простая синусоида, имеет внутреннее гармоническое содержание выше основного тона, делая тембральное различие между звуком скрипки и флейты, фортепиано или гитары, играющих одну и ту же ноту.
Существует два простых типа гармоник: четные и нечетные . Четные гармоники являются результатом умножения четных чисел (2, 4, 6, 8 и т. Д.), А нечетные гармоники являются результатом умножения нечетных чисел (3, 5, 7, 9 и т. Д.)) основной частоты. Например, если ваш основной тон представляет собой синусоидальную волну 1 кГц, 2 кГц будет четной гармоникой, а 3 кГц будет нечетной гармоникой. Каждый набор имеет четкое результирующее чувство и имеет важное значение для возбуждения звука.
Те же самые аддитивные принципы действуют при передаче звука через аналоговое оборудование, поскольку компоненты добавляют артефакты к сигналу, изменяя и добавляя к оригинальному звуку. Эти искажения создаются физическими ограничениями электрических компонентов, которые вместе изменяют источник звука.
Некоторые компоненты, такие как вакуумные лампы и трансформаторы , искажают звук в музыкальном плане, когда они хорошо продуманы. Магнитные среды, подобные аналоговой ленте, также будут искажать сигнал в виде гармонических искажений, искажений модуляции и сжатия. Степень, в которой мы определяем ограничения этих компонентов, определяет, насколько распространенным будет искажение.
Давайте рассмотрим некоторые из многих способов, которыми мы можем использовать характеристики гармонических искажений для нашего преимущества:
1.Добавьте искажение предусилителя: первая стадия окраски
Наиболее очевидными примерами различий в характеристиках гармонических искажений были различные звуки аналоговых консолей разных производителей. Если у вас нет опыта работы с несколькими винтажными консолями, может быть трудно понять совокупность различных характеристик. Каждая консоль поддерживает уникальную звуковую подпись как побочный продукт тщательного проектирования.
Все это начинается со стадии предварительного усиления .Будь то ламповое питание, как в эмуляциях предусилителя REDD-консолей Abbey Road Studios, или твердотельное в виде консолей TG12345, Helios и Neve, ступень предусилителя задает характерный тон, на котором формируется остальная часть звука ,
Гелиос
.