Струны ГОСПОДИН МУЗЫКАНТ® (GMstrings®) / Производство музыкальных струн

Джо Вулфи / Joe Wolfe (Австралия) Перевод статьи публикуется с разрешения автора, оригинал размещен по адресу: http://www.phys.unsw.edu.au/jw/strings.html

Чтобы вызвать звук необходимо произвести колебания. Чтобы получить музыкальный звук необходимо, чтобы колебания имели постоянную частоту, т.е. стабильную высотность, которой исполнитель мог бы легко управлять. В электроинструментах стабильные и управляемые колебания получают с помощью электроники, у неэлектрических — за счет стоячих волн. Мы будем рассматривать колебания на примере струн, поскольку здесь они более наглядны, чем колебания воздуха в духовых инструментах, и менее сложны по сравнению с колебаниями дощечек и кожи ударных инструментов.

Натянутые струны скрипки, фортепиано и т.д. колеблются столь быстро, что разглядеть что-либо невозможно. Однако, можно провести несколько любопытных экспериментов, позволяющих понять работу струн с помощью нескольких метров гибкого резинового шланга.

Садовый поливной шланг для этого недостаточно гибок, лучше всего взять резиновый шланг или длинную бельевую веревку. Привяжите или прижмите один конец шланга, а другой слегка натяните одной рукой (сильно натягивать не нужно, небольшой прогиб не страшен). Теперь другой рукой оттяните шланг в сторону, чтобы образовался выступ, и, отпустив его, вы увидите в замедленном темпе то, что происходит при щипке струны. Можно наблюдать, как выступ пробежит вдоль «струны» и вернется обратно. При возврате он толкнет Вашу руку, но если Вы держите «струну» крепко, произойдет новое отражение.

Первое, что Вы должны заметить, это то, что скорость движения волны по струне возрастает с увеличением ее натяжения. Это свойство используется при настройке инструментов, но сейчас мы не будем на этом останавливаться. Скорость движения волны зависит и от «веса» струны — в более толстой, тяжелой струне (при равной длине и натяжении) она будет медленнее, чем в легкой.

Теперь остановимся на отражении, которое происходит на закрепленном конце. Заметьте, что если оттягивать струну влево, то выступ побежит с левой стороны, но при возврате будет расположен справа — при отражении происходит инвертирование. Этот эффект наблюдается не только в струнах, но и в духовых и ударных. Волна инвертируется в момент, когда сталкивается с какой-либо неподвижной или трудно преодолимой преградой.

Несмотря на то, что струны музыкального инструмента закреплены с обоих концов, наблюдаемые процессы при щипке струны в них будут аналогичными. Сперва струна оттягивается в некой точке, а затем отпускается, как показано на рисунке. Если приглядеться, можно различить форму, которую образует бегущий выступ (показано тонкой линией на рисунках ниже), движущийся вдоль струны в обоих направлениях. Для наблюдений лучше использовать басовые струны, оттягивая их в нескольких миллиметрах от точки крепления. Фигура, образованная бегущим выступом, видна лучше, чем сама струна, потому что точку покоя, в которой происходит смена направлений, выступ проходит мгновенно, а к краям его движение замедляется.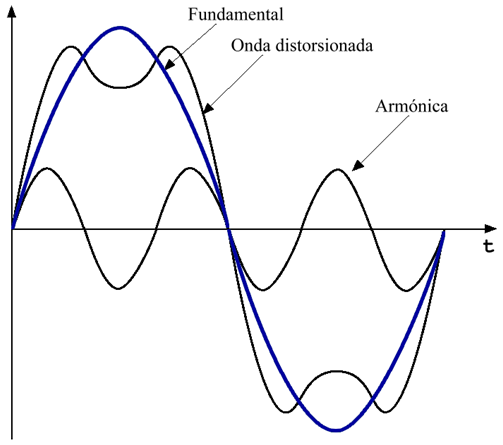

Схема движения выступа, образованного при щипке струны. Жирной линией показана сама струна, тонкой — фигура, образованная движением выступа. В фазах, отмеченных буквами (d) и (j), струна представляет прямую линию. В эти моменты потенциальная энергия ее колебаний исчерпана, а кинетическая энергия максимальна. Заметим, что в момент отражения положение выступа меняется на 180 градусов с верхнего на нижний или наоборот. Обратите внимание на проход выступов одного «сквозь» другой в момент, когда они встречаются посередине.

Схема, показывающая отражение движущихся выступов, при возбуждении струны смычком.

Отчего при отражении происходит инвертирование? Поскольку струна закреплена на неподвижном объекте, то и точка отражения является неподвижной. Теперь посмотрите на движение струны на левых рисунках, отражающих ее положение в разное время. Видно как часть струны позади выступа возвращается к своему первоначальному состоянию (на рисунках — вниз). Чем ближе выступ к концу струны, тем он становится меньше, и при его достижении он исчезает — в этот момент струна становится прямой. Однако движение струны вниз не прекращается, и, пройдя точку покоя, она образует обратный выступ, который начинает движение в обратном направлении.

Если раскачивать вверх-вниз незакрепленный конец струны, можно наблюдать один интересный эффект. С помощью резинового шланга можно проделать этот опыт самостоятельно. Если такой возможности у Вас нет, то взгляните на представленную ниже диаграмму.

Мы опять видим инвертирование отраженной волны, из-за чего после отражения мы получаем уже две волны (с одинаковой частотой и амплитудой), которые движутся в противоположных направлениях. В точке крепления струны, где они складываются, движение прекращается, т.е. имеет место нулевое перемещение, благодаря которому и возникает инвертированное отражение. Но если вы посмотрите на сплошную линию на диаграмме (представляющую собой результат суммирования двух волн), то увидите, что на струне есть и другие неподвижные точки.

Эти равноудаленные друг от друга точки, играющие важнейшую роль в функционировании любого музыкального инструмента, называются «узлами» (node) вибрации. Посередине между узлами располагаются «пучности» (antinode) — зоны максимального движения. Обратите внимание, что эти выступающие зоны не движутся по струне. При сложении двух волн, бегущих в противоположных направлениях, образуется стоячая волна.

Две движущиеся волны при слиянии образуют стоячие волны.

Посмотрите на рисунок, который представляет последовательность фаз движения волн во времени (время течет сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии — при наложении). Отмечены положения (узлы/nodes) в которых обе движущиеся волны нейтрализуют друг друга и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой.

Можно сказать, что приведенная выше диаграмма представляет колебание 5-й гармоники струны, длина которой равна ширине диаграммы. Здесь мы коснулись темы, которая будет освещена в следующей главе.

Гармоники и моды (типы) колебаний

На музыкальном инструменте струна закреплена с обоих концов, которые ограничивают возможные колебания и на которых во время колебаний расположены узлы. Струна, имеющая длину L, образует стоячую волну, длина которой равна удвоенной длине струны (длина волны = 2L), что демонстрируется на первом из рисунков следующей серии. При этом узлы расположены на концах струны, а пучность посередине между ними. Это одна из мод («мода» — тип колебаний струны). Какие еще моды встречаются на струне, закрепленной с обоих концов? Ниже приводятся примеры таких стоячих волн.

Рисунки демонстрируют первые четыре моды колебаний идеальной* закрепленной струны (увеличено по вертикали).

В каком соотношении находятся моды колебаний? Частота колебаний волны равна отношению ее скорости к длине: f=v/длина волны.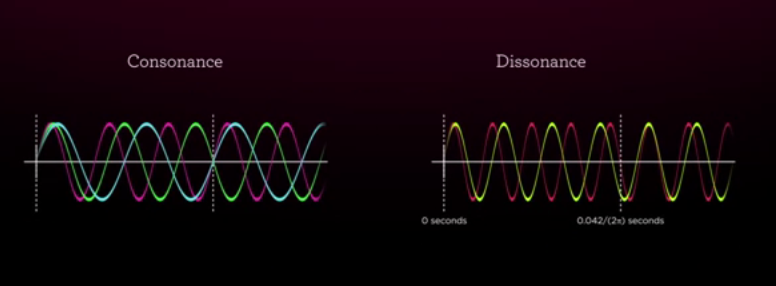 Таким образом, для струны длиной L, длины волн составят 2L, L, 2L/3, L/2, что можно записать так 2L/n, где n — номер гармоники.

Базовая частота или 1-я мода имеет частоту f1= v/длина волны = v/2L
Частота 2-й гармоники f2= v/l2 = 2v/2L = 2f1
Частота 3-й гармоники f3= v/l3 = 3v/2L = 3f1
Частота 4-й гармоники f4= v/l4 = 4v/2L = 4f1 …
 
fn= v/ln = nv/2L = nf1

Все волны движутся по струне с одинаковой скоростью, поэтому волны с различными длинами имеют разные частоты, как показано на рисунках. Мода самой нижней частоты (f1) называется базовой. Частота n-ной моды будет в n раз больше базовой. Все эти моды (как и звуки, которые они образуют) называются гармониками струны. Частоты f, 2f, 3f, 4f и т.д. называется последовательностью гармоник. Музыканты хорошо знакомы с этими последовательностями, особенно те, кто играют на натуральных горнах или знакомы с флажолетами. Если для примера мы возьмем базовую частоту соответствующую ноте С3, т.

е. альтовой До (частота = 131Гц), то ее гармоники будут иметь высотности, показанные на следующем рисунке. Высотность нот дана в приближении до четверти тона. При этом октавы являются чистыми, а вот другие интервалы не совсем соответствуют равномерно темперированному строю.

Нотное написание первых 12-ти гармоник (флажолетов) на примере ноты До. При прослушивании звукового файла (записанного в форматах au и wav) обратите внимание на высотность звуков.

Седьмая и одиннадцатая гармоники приходятся почти посередине между нотами равномерно темперированного строя, поэтому обозначены с половинками диезов.

Вы сами можете получить эти звуки на струнах. Проще это сделать на басовых струнах гитары, виолончели или контрабаса*. Для этого коснитесь слегка струны в точке, которая отстоит на длину =1/n от ее конца (где n = 1,2,3 и т.д.), а затем проведите смычком. Или слегка коснитесь струны в точке, которая приходится на длину =1/n от ее конца, ударьте по струне недалеко от подставки и мгновенно отдерните прижатый палец. Благодаря касанию, в точке произойдет образование узла, который образует моду, имеющую узел в данной точке. Вы легко сможете найти на струне от двух до шести флажолетов (если Вы только что проделали этот эксперимент, то, наверное, обратили внимание, на то, что двенадцатый лад, отвечающий за получение октавы, расположен менее, чем на половине длины струны, поэтому то место, где Вы касались струны для получения 2-й гармоники, находится не совсем точно над этим ладом).

---

* «Идеальной» я называю струну, которая, обладая абсолютной гибкостью, позволяет оттягивать ее без усилий в любом месте. Но поскольку реальные струны обладают жесткостью, их рабочая длина (которую мы обозначали в формулах буквой L) немного меньше физической длины, и это одна из причин, почему на басовых струнах применяется обмотка, а голая струна G (соль) классической гитары плохо строит в верхних позициях.

Упражнение для гитаристов

На настроенной гитаре струна В(си) и верхняя Е(ми) настроены примерно на 3-ю и 4-ю гармоники нижней струны Е(ми).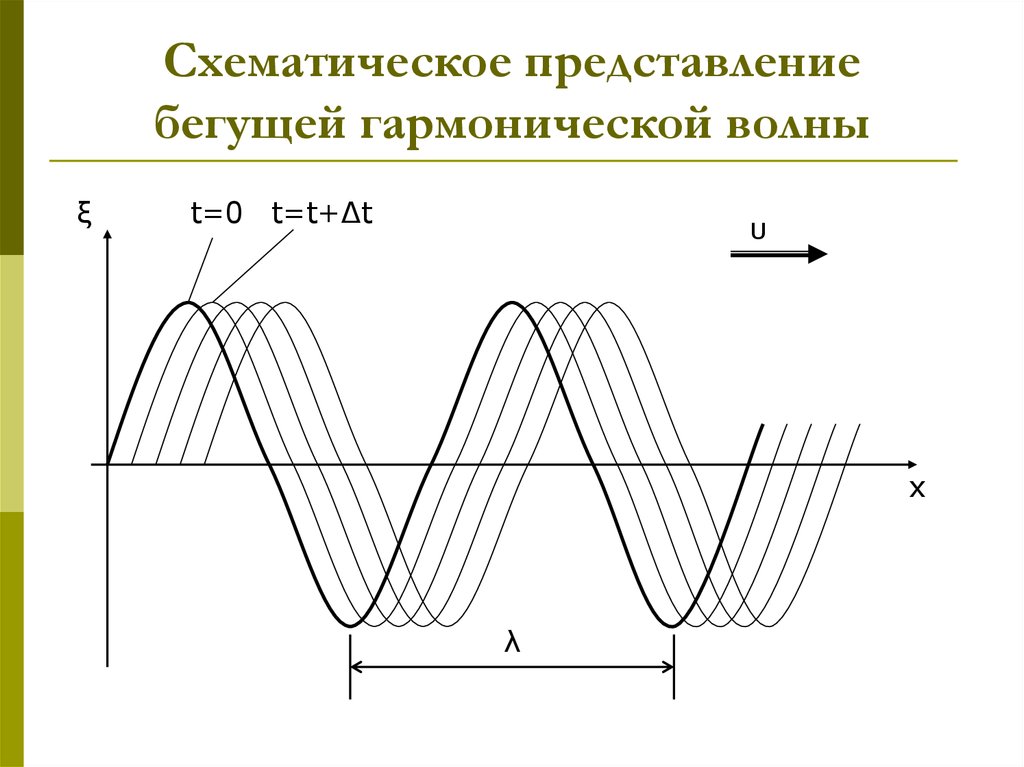 Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/3, струна В(си) начнет колебаться, возбуждаясь через колебания подставки от гармоники 1-й струны. Если взять на щипок басовую струну Е(ми) в любой точке кроме ее 1/4, отзовется верхняя струна Е(ми). Гитаристы обычно начинают настройку следующим образом: настраивают в унисон 4-ю гармонику басовой Е(ми), 3-ю у струны А(ля) и верхнюю струну Е(ми), затем струну В(си) строят по 3-й гармонике верхней Е(ми), а затем по 4-й гармонике А(ля) 3-ю гармонику струны D(ре). Настроить струну G(соль) по гармоникам не получится, в связи с невозможностью получения верхних гармоник, что связано с физическими параметрами толщины и жесткости самой струны, поэтому ее настраивают октавами, используя лады. По некоторым причинам (о которых будет сказано в конце главы), данный метод настройки достаточно приблизителен и требует дальнейшей подстройки при помощи ладов. Самой точной настройкой все-таки является компромиссная, которая осуществляется по аккордам, которые исполнитель собирается брать на грифе инструмента.

Гармоники (флажолеты) в музыке

Композиторы часто применяют гармоники/флажолеты на струнных инструментах, при этом наиболее часто используют «четвертую касательную». Одним пальцем музыкант зажимает струну, получая ноту за счет отрезка определенной длины, а другим легко касается струны там, где располагается нота на 4 тона выше (отсюда и название). Данная точка лежит на четверти длины отрезка струны, поэтому образуется 4-я гармоника базовой частоты в четыре раза больше базовой, т.е. получается интервал в две октавы. Струнные гармоники/флажолеты называются «натуральными» если они образованы от открытых струн и «искусственными» если струна прижимается. Ниже на рисунке показано, как берется натуральный флажолет. Для наглядности рисунок вытянут по вертикали.

Прослушайте фрагмент. Сначала звучит открытая струна А(ля), затем ее четвертая касательная (4-я гармоника).

Так обозначается на нотном стане «четвертая касательная» на скрипичной струне А(ля)

Немного технической информации для струнников

Несмотря на то, что «четвертая касательная» наиболее часто встречающийся флажолет, это не вполне удачный пример, поскольку получить четвертую гармонику гораздо проще, нежели «две четверки». Как известно, касание струны на отрезке 1/n (где n — целое число) дает n-ую гармонику, и для низких гармоник правило соблюдается, но для высших гармоник особое значение играет толщина струны, и здесь формула перестает работать. Таким образом, гармоники выше 8-й практически не берутся.

Если взять на струне подряд пять полутонов, то мы получим точку, соответствующую 1/3 длины струны, то есть «пятая касательная» даст нам третью гармонику. Гармоники расположены в следующем порядке:

интервал на грифе	часть струны	номер гармоники	интервал от базовой ноты
октава	1/2	2	октава
квинта	1/3	3	октава + квинта (дуодецима)
кварта	1/4	4	две октавы
большая терция	1/5	5	2 октавы + б. терция
малая терция	1/6	6	2 октавы + квинта
ув. кварта	2/7	7	2 октавы + м. секста повышенная
малая секста	3/8	8	3 октавы
большая секунда	1/9	9	3 октавы + б. секунда

Положения нот звукоряда соответствуют чистому строю. Касание струны на 2/9 ее длины предпочтительней, чем на 1/9, хотя данная точка расположена не над нотой гаммы, а немного выше малой терции. Буду рад, если альтисты или виолончелисты исполняющие «Практикующая бесконечность» Радулески (Radulescu’s «Practicing Infinity») пришлют мне свои предложения о способах исполнения высоких флажолетов.

Несовершенство настройки по гармоникам (флажолетам)

Есть несколько проблем при настройке любой гитары, в том числе при использовании флажолетов, о чем говорилось выше. Приблизительность настройки инструмента очевидно связана с равномерной темперацией. Даже если бы струны были идеальны, а положение ладов на грифе идеально отвечало равномерной темперации, при настройке по четвертой гармонике струн E-A (ми-ля), и A-D (ля-ре), октава между открытой нижней E(ми) и нотой ми на 2-м ладу струны D(ре) отклонялась бы приблизительно на 4 цента ((4/3)222/12=1.996), что приводило бы к появлению одного интерференционного биения в несколько секунд.

Другая проблема заключается в том, что в зоне верхнего порожка и подставки струны не могут обеспечить абсолютную гибкость (что было отмечено выше). В результате 1-й обертон на струне всегда будет чуть выше октавы, второй выше чем дуодецима (октава + квинта), и так далее. Так настройка в унисон 4-ой «гармоники» струны Е(ми) и 3-ей гармоники струны А(ля) при сравнении открытых струн даст интервал несколько больший, чем кварта, отчего приходится исправлять настройку, чтобы иметь равномерную темперацию.

Еще один отрицательный момент относится к расположению ладов и подставки. При прижиме струны на двенадцатом ладу увеличивается и ее длина (это уже не самое короткое расстояние между верхним порожком и подставкой), и ее натяжение. Вследствие этого, а также из-за выгиба конца струны, будь 12-й лад точно посередине между верхним порожком и подставкой, мы бы имели интервал больше октавы. Поэтому расстояние от подставки до 12-ого лада делают несколько большим, чем до верхнего порожка. Необходимо отметить, что в зависимости от вида струн эффект может быть различен. На электрогитарах есть возможность регулировать положение каждой подставки струны, на некоторых гитарах подставку поворачивают под углом, а в случае с классической гитарой прямая подставка ведет к определенному компромиссу в настройке.

Вышеописанные моменты сложно отследить с большой точностью, поскольку при анализе звука струны, возбуждаемой щипком, неточности составляют лишь несколько центов, что не намного больше разрешающей способности слуха или приборов настройки. Настройка колками также не позволяет достичь точности менее двух центов. С другой стороны, если Вам удастся интонировать мелодию с точностью в пределах двух центов, это будет большая удача — большинству музыкантов такое не по силам!

Определенная часть проблем настройки касается старения струн. Там, где Вы касаетесь их пальцами левой руки, они вбирают в себя пот и становятся более тяжелыми (хотя может иметь место и износ материала в местах, которые трутся об лады). Струны также изнашиваются под пальцами правой руки. Неоднородность струн ведет к невозможности их точной настройки. Мойка струн может помочь лишь отчасти.

Конечно, на безладовом инструменте большинство этих проблем можно обойти, но аккордная техника при этом сильно страдает.

На рисунке показаны гармоники открытой струны СОЛЬ контрабаса или виолончели. (Ноты для контрабаса записываются октавой выше его звучания.) Над нотами указаны номера гармоник, а под ними записаны приблизительные частоты в Герцах, причем для наглядности сделано округление чисел. Данный пример демонстрирует закон изменения высотности гармоник, и, хотя реальные частоты составляют пропорционально несколько меньшие значения, динамика возрастания частот от значения в 100Гц отражена абсолютно точно. (Приведенные значения частоты ноты СОЛЬ и ее гармоник могли бы иметь место при камертоне Ля=449Гц. Примечание переводчика).

Перепечатка статьи возможна только с согласия автора Джо Вулфи J.Wolfe()unsw.edu.au, а также фирмы ГОСПОДИН МУЗЫКАНТ®, осуществлявшей ее перевод.

© 2002

Третья гармоника – Наука – Коммерсантъ

Физики из МГУ имени Ломоносова и Института ядерных исследований сделали важный экспериментальный шаг в работе над теорией, выдвинутой 85 лет назад немецкими учеными. Заодно они подтвердили результат работы шведских коллег 20-летней давности.

Фото: Анатолий Жданов, Коммерсантъ

Фото: Анатолий Жданов, Коммерсантъ

Согласно классической электродинамике, теории, сформулированной еще в XIX веке Джеймсом Максвеллом на основе обобщения экспериментальных данных, лучи света в вакууме не взаимодействуют друг с другом. То есть два световых луча, пересекаясь, не отклоняются друг от друга и не рассеиваются, рождая электромагнитное излучение других частот. Но что произойдет, если учесть квантовые поправки, вызванные взаимодействием света с виртуальными электронами?

Поправки еще в 1936 году посчитали лауреат Нобелевской премии по физике 1932 года Вернер Гейзенберг и его ученик Ганс Эйлер (погиб 23 июня 1941 года, участвуя в разведывательном полете над Азовским морем). Они описали вызванное квантовыми поправками нелинейное взаимодействие четырех фотонов, которое часто называют нелинейностью вакуума. Это взаимодействие чрезвычайно мало, и уровень технологий только в последнее десятилетие вплотную приблизился к возможности его экспериментальной проверки. Какие же эффекты появляются в такой нелинейной теории, с помощью которых можно попробовать ее проверить?

Для ответа на этот вопрос у ученых есть хорошая подсказка. Похожая нелинейная теория возникает при описании распространении света в веществе, в так называемых нелинейных кристаллах. Один из характерных эффектов здесь — генерация второй гармоники. То есть лазерный луч (красный), проходя через такой кристалл, рождает слабый луч удвоенной частоты (ближний ультрафиолет). Это широко известный в оптике кристаллов эффект, который был экспериментально открыт еще в 1960-е годы.

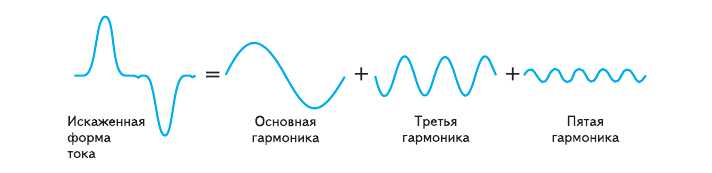
Тот же эффект рождения высшей гармоники (только третьей, то есть волны с утроенной частотой), но гораздо более слабый можно было бы наивно ожидать и в отсутствие всякого кристалла — из-за нелинейности вакуума. Эффект в 2001 году предложили искать три шведских ученых: Герт Бродин, Маттиас Марклунд и Леннарт Стенфло — с помощью сверхпроводящих радиочастотных резонаторов.

Чем хороши такие резонаторы? Своим исчезающе малым затуханием — прежде чем амплитуда электромагнитной волны внутри него уменьшится в два раза, волна отразится от стенок такого резонатора более 10 млрд раз! Чрезвычайно слабую третью гармонику в таком резонаторе можно попытаться зарегистрировать до того, как она затухнет.

В 2004 году Бродин и его коллеги, решив соответствующие нелинейные уравнения в частном случае, показали, что при возбуждении двух определенных мод различных частот w1 и w2 можно подобрать параметры резонатора так, чтобы из-за нелинейности вакуума резонансно появлялась мода с частотой (2w1 – w2). Но ответа, что произойдет с подобной частотой со знаком плюс и с третьей гармоникой (3w1), они не дали.

Оптика кристаллов. Возникновение резонанса

Оптика кристаллов. Возникновение резонанса

Задачу решили физики из МГУ им. М. В. Ломоносова и Института ядерных исследований (ИЯИ) РАН Илья Копчинский и Петр Сатунин в свежей работе, которая опубликована в январе 2022 года в международном журнале Physical Review A и отмечена в нем как выбор редактора. Работа была поддержана фондом РНФ по гранту 21-72-10151.

Копчинский и Сатунин записали нелинейные уравнения, решения которых должны описывать резонансное рождение сигнальных мод новой частоты, сформулировали два критерия наличия резонансного решения в общем виде, и аналитически решили эти уравнения для двух произвольных электромагнитных мод, помещенных как в одномерный резонатор — «отрезок», так и в реалистичный резонатор формы прямоугольного параллелепипеда с произвольным соотношением сторон.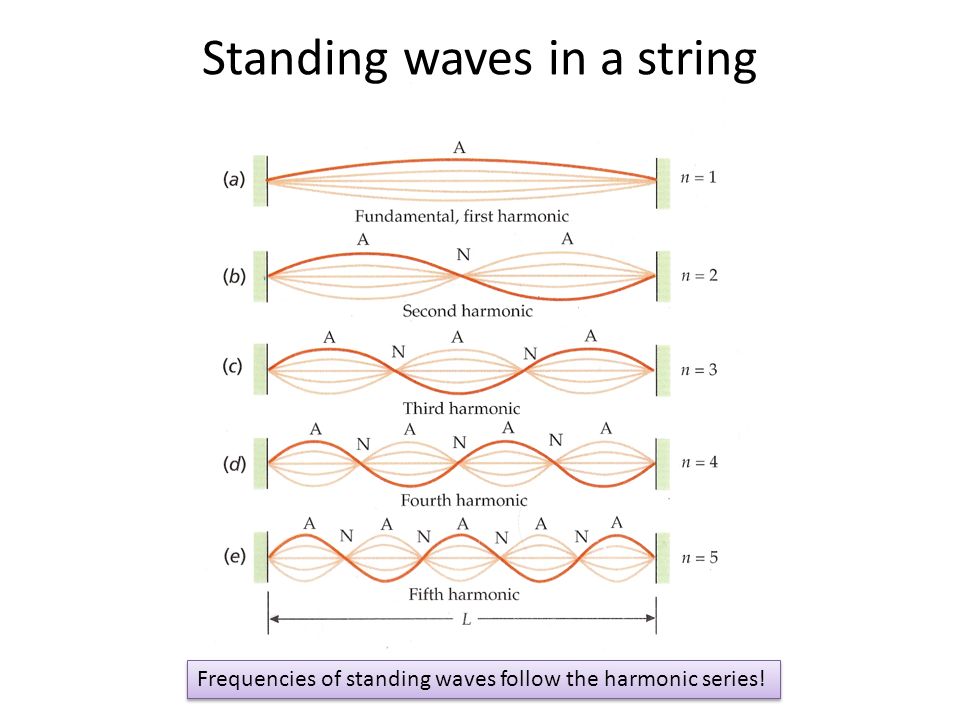 Для нахождения очень громоздких в общем виде аналитических решений ученые использовали систему компьютерной алгебры с открытым кодом Maxima.

«Неожиданно для нас оказалось, что та наивная идея, с которой все началось,— генерация гармоники утроенной частоты по аналогии с нелинейным кристаллом — на самом деле не реализуется. Не выполняются условия резонанса в этом случае из-за векторной природы электромагнитного поля. Нет резонанса также и для комбинационной моды со знаком плюс, частотой 2w1+w2»,— комментирует Петр Сатунин.

Оказалось, что резонанс может возникать только при генерации частоты 2w1 – w2 при определенном соотношении сторон резонатора, то есть как раз в том случае, который рассмотрели Бродин и его коллеги. Их результаты таким образом были подтверждены российскими физиками.

Можно надеяться, что в ближайшем будущем будет построена подобная установка по поиску нелинейности вакуума и предсказание Эйлера и Гейзенберга, сделанное более 80 лет назад, наконец будет экспериментально проверено.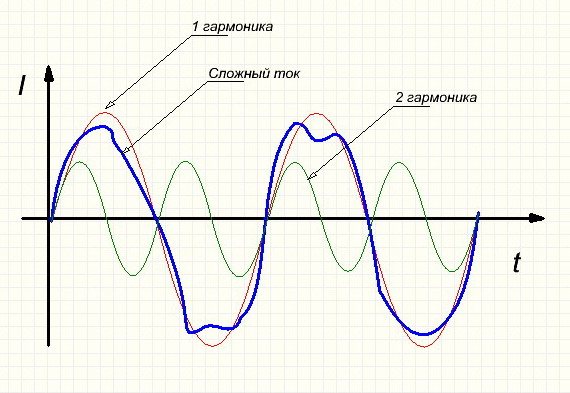

Или опровергнуто, что может вести к открытиям в новой физике.

Полина Юдина

Гордон Рид. «Что скрывает звук?»

В первой из 63-х частей серии, исследующей мир субтрактивного синтеза (subtractive synthesis), Гордон Рид объясняет читателю основы физики звука. Что такое звуковая волна (Waveform) и гармоники (Harmonics), откуда они берутся и как теория связана с практикой?

Далее, перевод текста статьи. В скобках указаны термины на языке оригинала.

↓

Я рассмотрю основные принципы наиболее распространенной формы звукового синтеза — субтрактивного синтеза (принципы хорошо известные), а затем в последующих частях серии — как эти принципы применяются на конкретных синтезаторах, звуковом дизайне и музыке в целом. Если у вас есть синтезатор, который работает на основе субтрактивных принципов, и вы знаете, как получить из него звуки, которые вам нравятся, но не понимаете, почему или как получаются эти звуки, эта серия заполнит некоторые теоретические пробелы. Теперь: что такое субтрактивный синтез?

Название «субтрактивный синтез» происходит от самого метода, в котором вы ослабляете (делаете заметно тише) или удаляете гармонии из гармонически насыщенных сигналов для создания новых звуков. Это можно делать статично, чтобы создавать простые тоны, или использовать средства, предлагаемые фильтрами (filters), генераторами огибающей (envelope generators) и модуляторами (modulators) в вашем синтезаторе или программном обеспечении для создания динамических звуков, которые изменяются относительно времени своего звучания. Но… Возможно, я уже вас запутал. Что такое гармоники? Что за звуковые волны? Откуда они берутся в природе? В этой статье я отвечу на эти три вопроса.

Во всем виноваты греки

Чтобы ответить на такие фундаментальные вопросы, мы должны запрыгнуть в нашу машину времени и отправиться в темные недра истории человечества. Задолго до искусственного моделирования звуков, до сэмплеров, до аналоговых полифонических синтезаторов, даже до появления клавишных инструментов…

Тут мы нагло врываемся на территорию Доктора Кто, потому что нам нужно вернуться аж на 2500 лет назад и познакомиться с парнем из Ионии по имени Пифагор. Пифагор был, пожалуй, первым в мире профессиональным математиком, но мы относительно мало знаем о нем и его достижениях (большая часть того, что мы знаем не более чем легенды: то, что каждый школьник воспринимает как теорему Пифагора — задолго до его рождения уже было известно в Вавилоне) Но речь не об этом.

Одним из менее известных открытий, приписываемых Пифагору, было то, что две одинаково натянутые струны дают приятный уху звук при щипке, если их длины соотносятся с простыми числами (то есть целыми числами) Простыми словами: Пифагор открыл законы музыкальной гармонии.

Легенда гласит, что учитель однажды прогуливался и услышал звуки молотов из кузницы, которые ковали железо; прислушавшись к ним, он понял, что их стук создает гармонию. Позже, опытным путем Пифагор установил, что различие звуков зависит только от массы молотка, а не от других характеристик. Потом философ сделал из струн устройство с различным количеством гирек; струны крепились к гвоздю, который был вбит в стену его дома. Ударяя по струнам, он вывел понятие октавы, и то, что её соотношение равно 2:1, открыл квинту и кварту. Затем Пифагор сделал устройство с параллельными струнами, которые натягивались колками. С помощью этого инструмента он установил, что определенные созвучия и законы есть во многих инструментах: флейтах, цимбалах, лирах и других устройствах, с помощью которых можно производить ритм и мелодию.

Например, если одна струна в два раза длиннее другой (в соотношении 1:2), звучало довольно красиво. Соотношение 2: 3 — тоже приятно ласкает ухо.

Пифагор был настолько поражен своим открытием, что возвел цифры в культ. Нумерология станет основой его философии. Музыкальная гармония в учении Пифагора является моделью вселенской гармонии, которая состоит из нот — различных аспектов Мироздания. К сожалению, он и его последователи затем немного слетели с катушек, пытаясь определить аналогичные числовые соотношения для астрономических явлений и орбит пяти известных в то время планет планет, солнца и луны, что породило мифическую «музыку сфер».

Но почему струны у Пифагора имеют целочисленные отношения? Почему приятный уху звук не возникает, если, например, одна из струн в 1,21346706544 раза длиннее другой?

Давайте дернем струну

Чтобы начать отвечать на этот вопрос, взгляните на натянутую струну: она зафиксирована на обоих концах, но свободно вибрирует по всей своей длине.

↓

Рис. 1-6 (сверху-вниз)

(На рисунке 1 показана такая строка в состоянии покоя)

Теперь представьте, что мы аккуратно щипаем струну ровно посередине. Как вы уже догадались: это заставляет её вибрировать так, как показано на рисунке 2.

Это пример «стоячей волны» (Standing wave). Если вибрация (или «колебание» (oscillation)) так же проста, как показано на рисунке 2, точка в центре струны перемещается по простой повторяющейся схеме, называемой синусоидальной волной (см. Рисунок 3). Такое колебание принято называть звуковой волной (waveform), а частота, с которой звуковая волна завершает один «цикл» за одну секунду, называется «фундаментальной» частотой струны.

Фундаментальная частота не единственное состояние вибрации струны — хотя из–за того, что она зафиксирована на обоих концах, количество вибраций строго ограничено её длинной. Представьте себе, что вы помещаете палец на центр струны, щипая ее по обе стороны от пальца (так, чтобы струна все еще вибрировала по всей своей длине). На рисунке 4 видно, что вибрация в половину длины оригинальной волны возможна. Точно так же будет если вы отсчитаете пальцем одну треть длины струны (рисунок 5) и так далее.

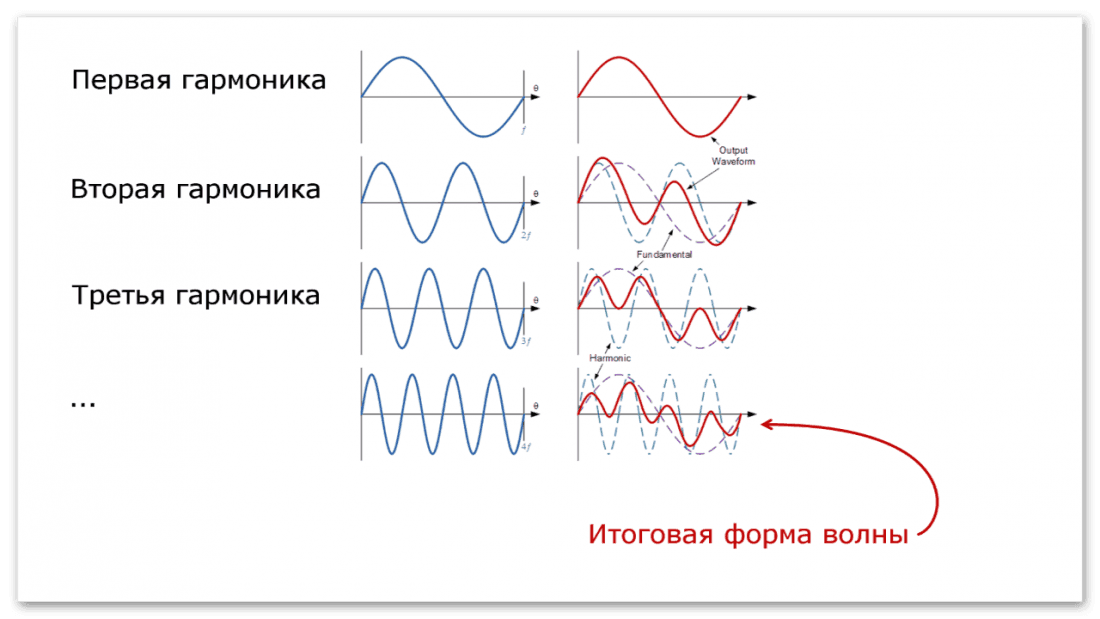
Такие волны (standing waves) возможны во всех целочисленных соотношениях, показанных на рисунке 2. Их и называют «гармониками» основной частоты.

Если серьезно озаботиться математикой стоячих волн, обнаружим, что такую волну можно представить как две «бегущие» волны, движущиеся вдоль струны в противоположных направлениях (нет, не спрашивайте почему, или мы будем здесь вечно). Знание этого, однако, приводит нас к простому выводу: если вы уменьшите длину волны пополам, частота требуемых «бегущих» волн удвоится.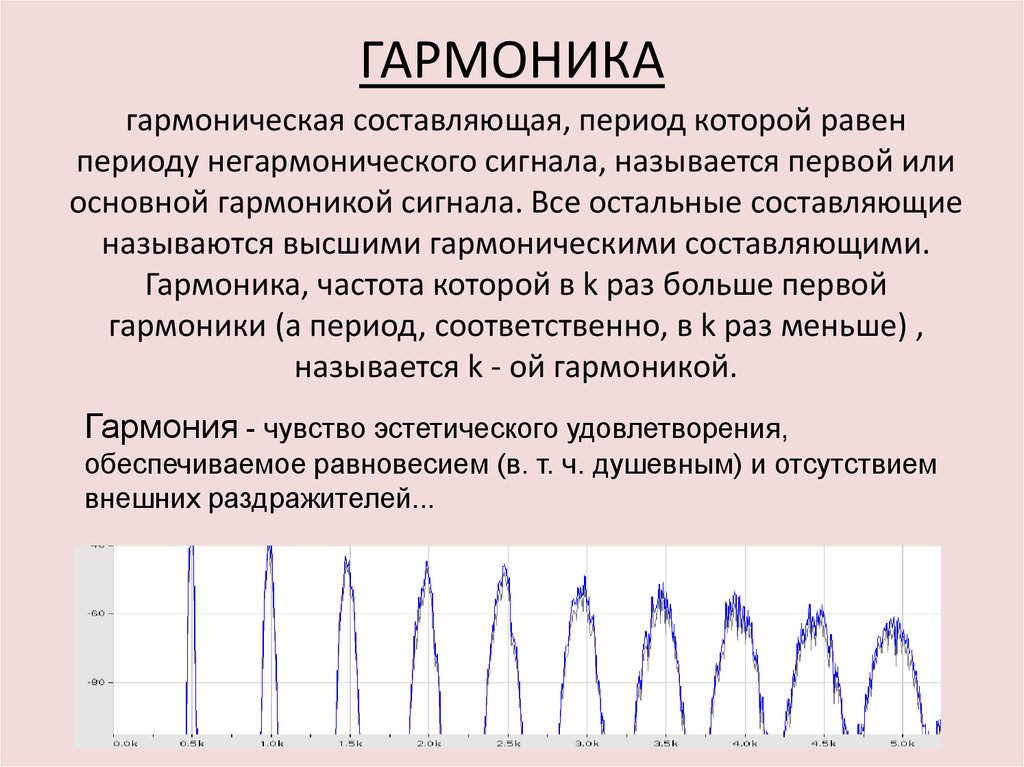 Точно так же, если вы разделите длину волны в три раза, вы утроите частоту; четверть длины волны — и вы умножаете частоту на четыре, и так далее…

Так или иначе, мы теперь ответили на наш первый вопрос: что такое гармоники — это меньшие вибрации «поверх» друг друга в целочисленных соотношениях к фундаментальной частоте, которые возникают в процессе колебания струны. Конечно, этот анализ относится не только к вибрирующей струне. Например, воздух в комнате. На мгновение, забывая о любых мелочах, таких как, мебель, воздух может вибрировать в любом месте комнаты кроме стен, пола и потолка. Другими словами, вибрации воздуха в комнате ограничены так же, как вибрации струны (своими нулевыми отметками). Вот почему обычные комнаты имеют «резонансы» — они являются гармоническими частотами самой комнаты. И именно поэтому органы в соборах имеют характерный звук: их трубы — это тоже простые гармонические осцилляторы.

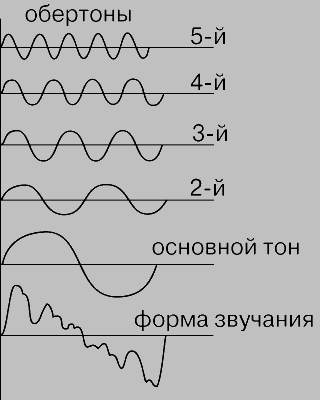
Во всех случаях, кроме некоторых эзотерических, первая гармоника (фундаментальная, называемая f) — это тон, который вы определяете, когда слушаете звук. Вторая гармоника (также называемая первый «обертон») составляет половину длины волны основной частоты и, следовательно, в два раза больше по своей частоте. В изоляции мы воспринимаем это как тон , который на одну октаву выше основного.

Третья гармоника имеет частоту 3f (которая является чистой квинтой, на полторы октавы выше основного тона), а четвертая гармоника с частотой 4f определяет вторую октаву. Следующие три гармоники лежат в следующей октаве, а восьмая гармоника определяет третью октаву выше основного тона. И так далее.

↓

4ая гармоника

Это та информация, которая нам необходима для понимания наблюдения Пифагора. В соотношении 1:2 короткая струна имеет фундаментальную частоту равную второй гармонике длинной струны. Это ровно на октаву выше. В примере струн в соотношении 2:3 третья гармоника длинной струны имеет ту же частоту, что и вторая гармоника короткой. Другими словами, гармонические структуры двух струн тесно связаны друг с другом, и мы воспринимаем такой звук, как музыкально «приятный».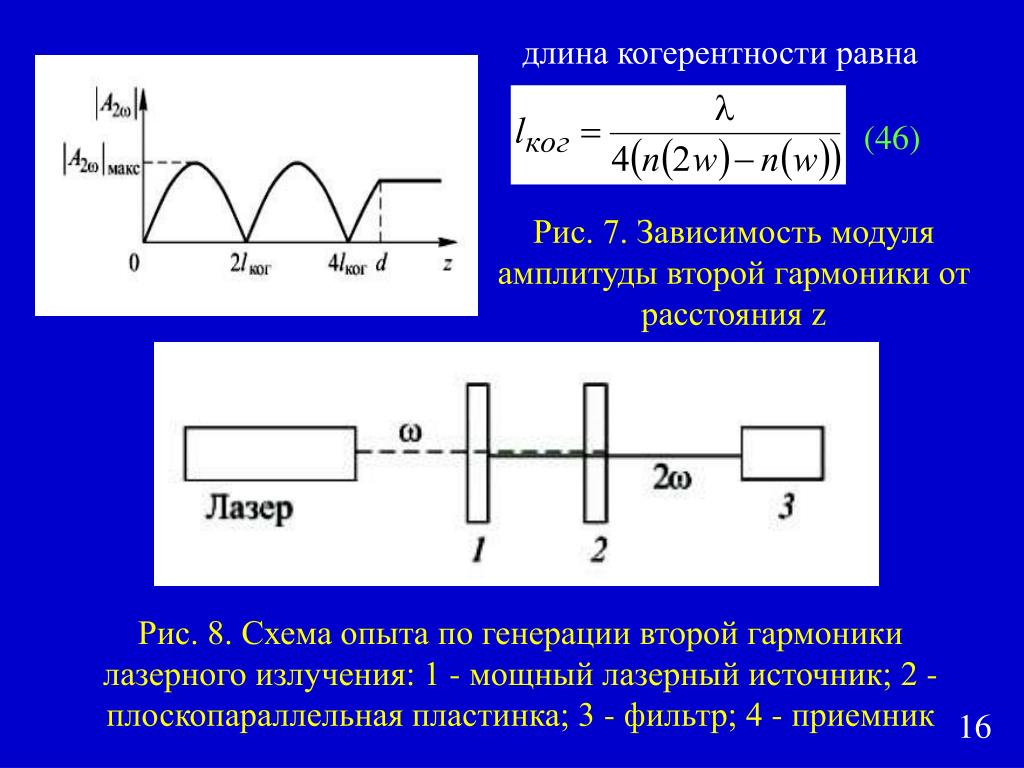

Природа звука

Теперь разберем: когда вы дергаете струну, вы не слышите звук лишь одной гармоники. Условия для создания такого чистого тона — в реальном мире — почти невозможны, поэтому любой естественный тон, вероятно, будет состоять из множества гармоник, присутствующих в разных количествах. В любой момент именно их комбинация определяет форму волны звука, и из–за количества присутствующих гармоник звуковая волна будет гораздо сложнее, чем простая синусоида, показанную на рисунке 3 (выше). Вам нужно только взглянуть на образец звука гитары или человеческого голоса в аудиоредакторе, чтобы увидеть, насколько сложной может быть реальная звуковая волна.

Синтез звука был бы невозможным, если бы не французский математик Жан Батист Жозеф Фурье. Парень с яркой жизнью, Фурье был учителем, тайным полицейским, политзаключенным, губернатором Египта, префектом и другом Наполеона. Несмотря на это, он все же нашел время, чтобы определить, что любое периодическое движение, независимо от того, насколько оно сложное, можно разбить на его гармонические составляющие. Эта процедура называется анализом Фурье. Кроме того, анализ Фурье также показывает, что при наличии набора гармоник вы можете получить уникальный звук.

↓

Подожди секунду… Звуковые волны определяют гармоники, а гармоники определяют звуковые волны? Очевидно, что гармоники и формы волны — это всего лишь два способа выразить одно и то же. Это ключевой момент: природа музыкальных тонов определяется количеством и амплитудой гармоник, содержащихся в них, и любой данный набор гармоник дает нам заданную форму волны. Поэтому, когда мы смотрим на генераторы на синтезаторе и видим такие вещи, как «квадратные» волны или «пилообразные» волны, это просто сокращенный способ сказать: «Этот параметр генерирует определенный набор гармоник с амплитудами x, y и z…»

Субтрактивный Синтез

↓

Рис. 7,8,9 (сверху-вниз)

Итак, давайте применим эти идеи к синтезатору. Посмотрите на форму волны на рисунке 6 (выше). Вы найдете ее почти на каждом синтезаторе, когда-либо созданном. Это идеальная пилообразная волна, названная так из–за своей формы.

Такая звуковая волна имеет простые гармонические отношения, выраженные следующим образом:

Каждая гармоника присутствует, а амплитуда n-й гармоники в 1 / n раз больше основной.

на рисунке 7 показаны первые 10 гармоник в пилообразной волне. Можно увидеть, как они уменьшаются на более высоких частотах.

Но что произойдет, если вы удалите эту серию гармоник? Допустим, вы удалили все кроме первых пяти из них (для которых вам нужно устройство, называемое «фильтром»). На рисунке 8 показан этот спектр, а на рисунке 9 показана форма волны, которой он соответствует.

Как видите, новая форма волны отличается от пилообразной волны. Она звучит по-другому. Различие между ними состоит в том, что вы обрезали гармонический ряд пилообразного зуба так, чтобы осталась только первая горстка гармоник. Другими словами, вы использовали «фильтр» для «вычитания» гармоник, создавая новую форму волны и, следовательно, новый звук.

Добро пожаловать в мир субтрактивного синтеза!

Переведено для проекта «Бык на крыше»

Оригинал статьи

Эскимо Губная гармоника и наука о звуке

Что такое звук?

Эскимо (рукодельная палочка) губная гармошка — отличный способ продемонстрировать науку о звуке, потому что все звуки производятся определенным движением. Когда вы растягиваете резинку, а затем дергаете ее, резинка двигается вперед и назад так быстро, что ее движения кажутся размытыми. Звук, который вы слышите, исходит от его движения. Это очень быстрое возвратно-поступательное движение называется вибрацией . Вибрации являются источником всех звуков.

Представьте себе камень, брошенный в неподвижную воду. Кольца волн расширяются до бесконечности. То же самое верно для звука и того, что происходит с губной гармошкой эскимо. Нерегулярно повторяющиеся звуковые волны создают шум, а регулярно повторяющиеся волны производят музыкальные ноты.

Человеческое ухо улавливает звуковых волн . Кроме того, звуковые волны обладают особыми характеристиками, которые делают их уникальными.

Наука о звуке: Вибрирующий воздух проникает в ваши уши и ударяется о барабанные перепонки, заставляя их вибрировать.

Ваши уши вибрируют так же, как первоначальный источник вибрации. Затем это посылает сообщение в ваш мозг, и мозг слышит звук, позволяя вам слышать много разных звуков.

Не все вибрации создают звуки, которые может слышать человек. Человеческие уши воспринимают вибрации со скоростью от 20 до 20 000 полуколебаний в секунду. Если вибрация слишком быстрая или слишком медленная, люди не услышат ее как «звук». Одна вибрация, слишком быстрая для человеческого слуха, — это ультразвуковой сигнал, излучаемый летучими мышами для эхолокации. Вибрации, которые слишком медленны для человеческого слуха, включают океанские волны и землетрясения. Мы обнаруживаем эти вибрации, видя и чувствуя их, но мы их не слышим.

Знаете ли вы? Собаки могут слышать звук на более высокой частоте, чем люди, что позволяет им слышать звуки, которые мы не можем слышать.

Как движется звук?

Материя, передающая звук, называется средой . Звуковые волны могут проходить через все виды сред. Вы можете слышать звуковые волны, прошедшие через воздух, но звук также может проходить через твердое тело или жидкость. Вода, дерево и земля — вот некоторые примеры сред.

Если нет среды для передачи звука в уши, вы не услышите звук. В глубоком космосе нет звука. В больших пустых пространствах между звездами и планетами нет молекул, которые могли бы вибрировать, производя звук. Там нет звука.

Вы когда-нибудь пробовали что-то услышать в ванной, когда опускаете голову под воду или в бассейн? Звук может показаться приглушенным, но вы, вероятно, услышите много звука, которого не услышите, сидя в ванне. На самом деле звук движется в четыре раза быстрее, когда он распространяется через воду, чем когда он распространяется по воздуху.

Материалы для изготовления губной гармошки:

• 2 палочки для эскимо
• 1 широкая резинка
• 2 маленькие резинки
• 2 листа бумаги: шириной 2 см и длиной 6 см
• Скотч

Процедура изготовления губной гармошки от эскимо:

1. Положите одну палочку поверх другой так, чтобы полоски бумаги были внизу и на расстоянии друг от друга.

2. Сложите оба листа бумаги по обеим сторонам палочек.

3. Закрепите бумагу лентой, убедившись, что лента не касается палочек.

4. Осторожно извлеките рукоятку снизу. Затем натяните длинную резинку вокруг верхней палочки. Поместите нижнюю палку прямо под. затем закрепите их обе двумя меньшими резинками.

5. Вуаля! Великолепная губная гармошка для эскимо, сделанная специально ВАМИ! Затем сожмите губы, а затем осторожно подуйте, чтобы издать заводные звуки губной гармошки и музыку!

Когда дуешь на губную гармошку, воздух заставляет резиновую ленту вибрировать и издавать заводной звук.

Эскимо Губная гармоника Безопасность для STEM-специалистов

Для всех действий на нашем веб-сайте требуется присмотр и помощь взрослых.

Палочки для рукоделия могут иметь небольшие осколки. Обязательно осмотрите каждую палочку, чтобы убедиться, что она безопасна для ребенка.

Если вы раскрасите губную гармошку маркерами, чернила или другие материалы могут оторваться от губ ребенка или попасть в рот ребенка.

Акустика

/əˈko͞ostik/ сущ.
раздел физики, изучающий звук и звуковые волны.

Звук

/звук/ сущ.
вибрации, которые путешествуют и могут быть услышаны, когда достигают уха человека или животного.

Наука о звуке Факты

• Скорость звука составляет около 1230 километров в час (км/ч)

• Громкий звук, создаваемый кнутом, возникает из-за того, что его кончик движется так быстро, что превышает скорость звука!

• Летучие мыши могут видеть в темноте с помощью эхолокации. Они отражают свои звуковые волны от объектов, чтобы найти свой путь. Дельфины также используют эхолокацию под водой.

• Хотя музыку трудно определить, ее часто описывают как приятную или осмысленную аранжировку звуков.

Если ваши STEM-специалисты увлечены наукой о звуке, ознакомьтесь с нашей отдельной коробкой «Хорошие вибрации» сегодня!

Также в блоге: 4 увлекательных упражнения для обучения вибрации и звуковой энергии

Для более сложной игры попробуйте ежемесячную тематику  Groovy Lab in a Box .   Нет лучшего способа обучить ваших STEM-специалистов, чем держать их умы свободными от экрана, проектировать, учиться создавать и решать в процессе инженерного проектирования и деятельности, связанной с STEM. Кроме того, наша ежемесячная коробка активизирует мышление, вопросы, исследования и оригинальное творчество, поскольку мы направляем детей в процессе научных исследований и инженерного проектирования.

Поделись!

18 акции

Наука о звуке: сделай свою губную гармошку!

• Share on Facebook

• Share on Twitter

• Share on Reddit

• Share on LinkedIn

• Share via Email

• Print

Ring in the New Year with this забавный самодельный инструмент, основанный на физике! Авторы и права: Джордж Рецек

Ключевые концепции
Физика
Звуковая волна
Частота
Шаг
Герц

Введение
Можете ли вы назвать самый продаваемый музыкальный инструмент в мире? Если вы сказали… губная гармошка, вы правы! Гармошку запатентовал в 1821 году 16-летний немецкий мальчик. С тех пор он стал самым продаваемым инструментом в мире и предметом домашнего обихода во многих местах. Легко воспринимать инструменты (и музыку, которую они создают) как должное, но создание красивого шума — это не просто искусство, это еще и наука! В этом упражнении вы создадите и исследуете свой собственный инструмент, похожий на гармонику, сделанный из предметов домашнего обихода. Время настроиться!

Фон
Звуки, которые мы слышим каждый день, представляют собой звуковые волны, распространяющиеся по воздуху и достигающие наших ушей. Как и океанская волна, звуковые волны генерируются вибрацией или движением объекта в среде. В случае океана средой является вода, тогда как звуковые волны чаще всего достигают нас, путешествуя по воздуху. Звуковая волна исходит от вибрирующего объекта, такого как голосовые связки, и проходит через среду (например, воздух), заставляя все частицы воздуха вибрировать с частотой голосовых связок. Частота этого движения обычно измеряется в герцах (Гц), где один герц равен одному колебанию в секунду.

Чтобы лучше понять это, представьте двух людей, держащих между собой веревку. Если один человек осторожно покачивает веревку вверх и вниз один раз в секунду, по веревке будет проходить волна с частотой один герц. Если человек увеличивает свою скорость так, что он двигает веревку вверх и вниз два раза в секунду, волна будет проходить по веревке с частотой два Гц.

Звук распространяется по воздуху аналогичным образом. Скрипач проводит смычком по струнам скрипки, заставляя струны вибрировать. Вибрирующая струна сталкивается с частицами воздуха вокруг себя. Эти частицы воздуха впоследствии сталкиваются с частицами воздуха рядом с ними и так далее, поэтому волна распространяется от частицы воздуха к частице воздуха — и все это с той же частотой, что и вибрация струны скрипки.

В этом упражнении вы создадите свой собственный звучащий инструмент и исследуете виды звуковых волн, которые он генерирует.

Материалы

• Две большие палочки для рукоделия (длиной не менее шести дюймов)
• Две широкие резинки (хорошо подойдет размер #64)
• Одна пластиковая соломинка для питья
• Четыре маленькие резинки
• Линейка
• Ножницы
• Взрослый помощник
• Лист бумаги
• Ручка или карандаш
  

Подготовка

• Натяните широкую резинку вдоль одной из палочек для рукоделия.
• Отрежьте ножницами четыре кусочка соломы, каждый длиной до полутора дюймов.
• Поместите одну из соломинок под резинку перпендикулярно палочке. Переместите эту соломинку так, чтобы она находилась примерно в двух дюймах от конца палочки. Это Соломинка 1.
• Отойдя от конца палочки, поместите еще одну соломинку поверх резинки рядом с соломинкой 1. Это соломинка 2.
• Поместите третью соломинку рядом с соломинкой 2 под резинку. Это Соломинка 3.
• Поместите последнюю соломинку рядом с соломинкой 3 поверх резинки. Это Соломинка 4.
• Соломинки 1 и 4 должны располагаться ближе всего к концам палочки для рукоделия, а соломинки 2 и 3 – посередине.
• С помощью взрослого, который поможет вам удерживать соломинки на месте, положите вторую палочку для рукоделия поверх первой, создав бутерброд с соломинками между палочками для рукоделия.
• Закрепите этот бутерброд, обернув небольшую резинку примерно на полдюйма с каждого конца палочки. Концы палочек должны быть зажаты вместе с небольшим пространством между ними, созданным соломинками.
• С помощью бумаги и карандаша нарисуйте таблицу с двумя столбцами и пятью строками. Назовите первый столбец «расстояние между средними соломинками» и заполните каждое место ниже: «2,5 дюйма», «2 дюйма», «1,5 дюйма» и «1 дюйм». Назовите вторую колонку «тон звука».
  

Процедура

• Для начала переместите соломинки 1 и 4 как можно ближе к концам палочки. Вы можете двигать соломинки, осторожно двигая их вперед и назад, стараясь не вытащить их из бутерброда!
• Сдвиньте соломинки 2 и 3 друг от друга так, чтобы между ними было расстояние 2,5 дюйма.
• Держите инструмент так, как если бы это был бутерброд, одной рукой осторожно держась за каждый конец открытой частью к себе. Убедитесь, что палочка с резинкой находится на дне бутерброда, и старайтесь держать пальцы на маленькой резинке. Убедитесь, что вы не нажимаете на широкую резинку.
• Продуйте в отверстие между палочками для рукоделия, как будто это губная гармошка (не дуйте через соломинку!). Какой звук ты слышишь? Чувствуете ли вы что-нибудь в своих руках, когда дуете в инструмент? Вибрируют ли ремесленные палочки или ощущаются ли они иначе, когда вы воспроизводите звук?
• Переместите соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние 2 дюйма.
• Снова продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Звучит иначе, чем когда вы играли в первый раз? Если да, то каким образом? Отличается ли вибрация инструмента?
• Снова переместите соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние 1,5 дюйма.
• Продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Это звучит иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
• Наконец, снова сдвиньте соломинки 2 и 3 ближе друг к другу, чтобы между ними было расстояние в 1 дюйм.
• Еще раз продуйте свой инструмент. Обратите внимание на звук и ощущение в ваших руках. Это звучит иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
• Верните соломинки 2 и 3 в исходное положение на расстоянии 2,5 дюйма между ними. Повторите описанные выше шаги — на этот раз запишите свои наблюдения о тоне звука в таблицу. Чтобы вам было легче сравнивать звуки, оцените самый низкий звук в 1, а самый высокий звук в 4.
• Рассмотрите результаты в своей таблице. Замечаете ли вы какие-либо закономерности в тоне звука? Менялся ли тон, когда вы передвигали соломинку? Если да, то смещение соломинок ближе друг к другу повышало или понижало тон?
• Переверните инструмент так, чтобы широкая резинка оказалась сверху. Держите инструмент так, чтобы пальцы нажимали на широкую резинку. Продуйте инструмент, как и в предыдущих шагах. Изменяет ли что-нибудь ношение резинки в вашем инструменте? Как бы вы объяснили наблюдаемые вами различия?
• Переверните прибор так, чтобы резинка снова оказалась внизу. Удалите все соломинки, кроме соломинки 1. Попробуйте продуть инструмент. Это звучит иначе, чем в прошлые разы? Если да, то каким образом? Отличается ли вибрация инструмента?
• Попробуйте передвинуть оставшуюся соломинку и посмотреть, как это повлияет на тон звука. Можно ли изменить тон звука, передвигая соломинку?
• Дополнительно: Проверьте большие и/или меньшие палочки для рукоделия и другие материалы, кроме соломинок. Сколько различных инструментов вы можете сделать?
  

Наблюдения и результаты
Звук, издаваемый вашим инструментом, на самом деле является звуком, создаваемым большой резиновой лентой, вибрирующей, когда вы дуете через нее, так же, как скрипичная струна вибрирует, когда играет скрипач. Когда вы дули в свой инструмент, вы, возможно, заметили, что чувствуете вибрацию резиновой ленты через ремесленную палочку. Кроме того, когда вы перевернули инструмент и нажали на резиновую ленту, вы, вероятно, обнаружили, что не можете произвести никакого звука, когда дуете через нее. Из этого вы можете заметить, что звук создается резинкой, и когда вы препятствуете движению резинки, вы не можете производить никакого звука.

Кроме того, в этом упражнении вы должны были заметить, что можете менять тон звука, передвигая соломинки. Когда вы передвигали соломинки 2 и 3 ближе друг к другу, вибрирующая часть резинки становилась короче. В результате тональность звука стала выше. Более короткая резинка вибрирует быстрее, и наши уши улавливают эти более высокие частоты как более высокие звуки. Более тонкие струны на скрипке издают более высокий звук, потому что они могут вибрировать быстрее, чем более толстые струны. Точно так же у мужчин, как правило, более длинные голосовые связки, чем у женщин, и поэтому их голоса обычно ниже, чем у женщин.

Когда вы убрали все, кроме одной соломинки, вы должны были обнаружить, что звук инструмента стал тише. Только с одной соломинкой резиновая лента была длиннее, а звук, издаваемый ею при вибрации, был ниже. Перемещая оставшуюся соломинку, вы могли менять тон, так как резинка становилась все короче и длиннее.

Еще для изучения
Поющие бокалы для вина, от Science Buddies
Разговор по струнному телефону, от Scientific American
Выдувание крышек бутылок: Создание музыки с помощью бутылок, от Science Buddies
Научные мероприятия для всех возрастов! от Science Buddies

Это задание предоставлено вам в сотрудничестве с Science Buddies

ОБ АВТОРАХ

20 забавных песен на губной гармошке для игры в тональности C

Гармошка – невероятно интересный и уникальный инструмент. На губной гармошке можно играть практически в каждой песне; задача состоит в том, чтобы выбрать идеальные, которые обеспечат веселое обучение и игровой опыт.

Когда дело доходит до выбора и исполнения правильных песен на губной гармошке, приоритетом является поиск самых веселых и тех, которые сделают процесс обучения приятным. По этой причине я составил список из 20 забавных песен для губной гармошки в тональности C именно для того, чтобы вы могли учиться и получать удовольствие одновременно.

Начинаем!

Содержание

• 1. Представьте – Джон Леннон
• 2. Пусть будет – The Beatles
• 3. No Woman No Cry – Боб Марли
• 4. Привет – The Lumineers
• 5. Не оглядывайся в гневе – Oasis
• 6. Пианист – Билли Джоэл
• 7. Я хочу тебя – Боб Дилан
• 8. Наверное, поэтому они называют это блюзом – Элтон Джон
• 9. Будешь ли ты любить меня завтра? – Кэрол Кинг
• 10. Капли Юпитера – Поезд
• 11. Плохой до костей – Джордж Торогуд и Разрушители
• 12. Аллилуйя – Леонард Коэн
• 13. Ла Бамба – Ричи Валенс
• 14. Люби меня нежно – Элвис Пресли
• 15. Где-то над радугой – Гарольд Арлен
• 16. Останься со мной – Бен Э. Кинг
• 17. Отвези меня домой, проселочные дороги – Джон Денвер
• 18. Мысли вслух – Эд Ширан
• 19. Какой чудесный мир – Луи Армстронг
• 20. Лестница в небо – Led Zeppelin
• Резюме

1. Представьте себе – Джон Леннон

«Imagine» Джона Леннона — идеальное начало этого списка. Песня вышла в 1971 под одноименным альбомом. Применение этих прекрасных мелодий на губной гармошке — привилегия и удовольствие для любого игрока на губной гармошке.

Что касается сложности, то она довольно проста и подходит для игроков среднего уровня. Если вы хотите сыграть ее в тональности C, приведенная выше ссылка покажет вам, как именно выучить и сыграть эту прекрасную песню.

2. Пусть будет – Битлз

Кто не знает Let It Be группы The Beatles? Эта песня была выпущена в 19 году70. Она была написана Ленноном-Маккартни, а также спета Джоном Ленноном и Полом Маккартни. Эта песня была включена в альбом Let It Be и дает интересный опыт для изучения и использования.

Представьте, как весело было бы достать губную гармошку и показать этот шедевр семье и друзьям. Для получения более подробной информации о том, как его изучить, ссылка выше предоставит все, что вам нужно.

3. No Woman No Cry – Боб Марли

No Woman No Cry на данный момент хорошо известна всем. Легендарный Боб Марли выпустил эту песню в 19 году.74. Представляете, как эта песня будет звучать на губной гармошке? Одно слово — Удивительно!

Когда вы почувствуете, как песня звучит на губной гармошке в тональности C, вы просто ухватитесь за возможность выучить ее. Получайте удовольствие, изучая и выполняя это перед друзьями и семьей, а также на других собраниях.

4. Хо Эй – Люминиры

The Lumineers долгое время были источником веселых песен и энергии. Их песня Ho Hey вышла в 2012 году и засела у всех в голове.

Как заядлый меломан, я не могу вспомнить ни одной вечеринки, фестиваля или тусовки, на которой хотя бы раз не играли Ho Hey из The Lumineers. Разучивание этой песни на губной гармошке обязательно привлечет внимание, где бы вы ни находились.

Попробуй и засунь себе в руки как можно скорее.

5. Не оглядывайся в гневе – Oasis

Don’t Look Back In Anger, пожалуй, одна из самых узнаваемых песен в этом списке. Oasis выпустили этот в 1996, и с тех пор он стал основным продуктом на радио, в барах и на вечеринках.

Если вы просто посмотрите кавер, ссылка на который приведена выше, вы сразу же увидите, что эта песня хорошо звучит практически на любом инструменте, не говоря уже о красиво звучащей губной гармошке.

Имея его в своем арсенале, вы, несомненно, сможете произвести впечатление на своего партнера, семью и друзей.

6. Человек-пианист – Билли Джоэл

«Человек-пианист Билли Джоэла» — это просто классика по определенной причине. Эта песня была выпущена в 1973, и это песня, в которой на самом деле есть губная гармошка, в отличие от большинства в списке, которые являются каверами.

Изучение фирменного звучания, которое делает эту песню такой блестящей, будет достойным хвастовства для всех. Возможность исполнить это или просто факт того, что вы умеете играть, определенно обогатит ваш музыкальный опыт.

7. Я хочу тебя – Боб Дилан

Не может быть губной гармошки в предложении и не упомянуть Боба Дилана. Его песня I Want You была выпущена в 1966, и на видном месте играла губная гармошка. После записи этой песни у Дилана случился приступ астмы, но это не помешало ему в дальнейшем играть на инструменте.

Когда он выступал вживую в Manchester Free Trade Hall в 1966 году, громкость его гармоники была слышна на большинстве инструментов. Это, несомненно, вызовет интерес у любителей губной гармошки узнать об этом, если вы еще этого не сделали. Это гарантированный веселый опыт, а также музыкальное развитие.

8. Наверное, поэтому они называют это блюзом – Элтон Джон

Думаю, именно поэтому они называют это блюзом — это вечная классика Элтона Джона, которую любой начинает петь, как только слышит. Песня была выпущена в 1983 году на альбоме Too Low For Zero.

Эта песня о том, как ты скучаешь по тому, кого любил, но был вынужден расстаться. Нет ничего лучше, чем взять в руки губную гармошку и погрузиться в блюзовую природу песни, которая просто поможет вам выразить себя еще больше.

На самом деле, эту песню действительно интересно разучить, и она наверняка пригодится для будущих посиделок.

9. Будешь ли ты любить меня завтра? – Кэрол Кинг

Кэрол Кинг «Любишь ли ты меня завтра?» была выпущена в 1960 году. Это была одна из первых песен, в которых мужчина и женщина выразили беспокойство по поводу физических отношений. Чтобы иметь возможность играть это на губной гармошке, вам нужно освоить некоторые ключевые изменения.

Тем не менее, это сделает вас лучшим игроком и даст вам забавную песню для игры. Вы будете выражать свои эмоции с помощью прекрасно звучащих мелодий губной гармошки.

10. Капли Юпитера – Поезд

Drops Of Jupiter — песня группы Train, выпущенная в 2001 году как первый сингл с их альбома Drops Of Jupiter. Песня эмоционально обусловлена ​​стремлением к более простым временам и является отражением жизни вокалиста Патрика Монахана.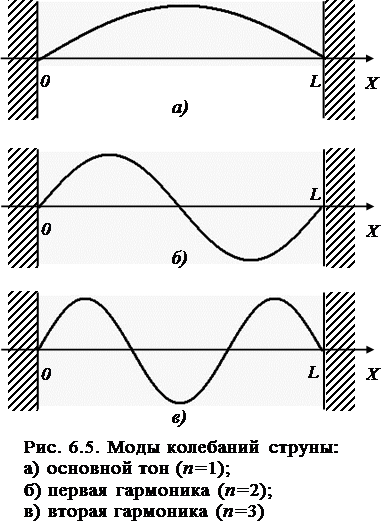

Представьте, что вы играете на губной гармошке и можете воспроизводить звуки пышного оркестра, используя всего лишь мундштук и пару отверстий. Такова магия гармоники! Без сомнения, вам понравится учиться этому и играть в него еще больше.

11. Bad To The Bone – Джордж Торогуд и The Destroyers

Давайте будем честными, мы все хотели играть на губной гармошке в Bad To The Bone. Джордж Торогуд и The Destroyers выпустили эту песню в 1982 году, и она часто звучала на классическом рок-радио.

Вы не можете отрицать привлекательность солирования этой песни, особенно если вы играете на губной гармошке. С Bad To The Bone нет ничего более впечатляющего, чем звучание крутого гармониста. Когда и где бы вы в нее ни играли, она, несомненно, привлечет внимание.

12. Аллилуйя – Леонард Коэн

Hallelujah Леонарда Коэна звучит потрясающе в любой обстановке. Песня была выпущена в 1984 году и стала одной из самых популярных песен в современной музыке. Это важная песня, которую все ценят.

Играть ее на губной гармошке — это действительно большой вызов и большое достижение. Наличие этого в вашем арсенале пригодится, когда вы попытаетесь исполнить серенаду своему партнеру и даже устроить веселое представление для семьи и друзей!

13. Ла Бамба – Ричи Валенс

La Bamba известен во всем мире благодаря Los Lobos, но настоящую аккредитацию должен получить Ричи Валенс. Он выпустил эту песню в 1958 году, и в настоящее время она входит в список 500 величайших песен всех времен по версии журнала Rolling Stone.

Быстрая мелодия, которую будет непросто освоить на губной гармошке, но взамен она даст вам прекрасно звучащий продукт. Представьте себе следующую домашнюю вечеринку, которую вы посещаете, вы можете вытащить губную гармошку и подарить всем незабываемые впечатления.

14. Люби меня нежно – Элвис Пресли

Love Me Tender — еще одна вечная классика, которую мы все знаем и любим.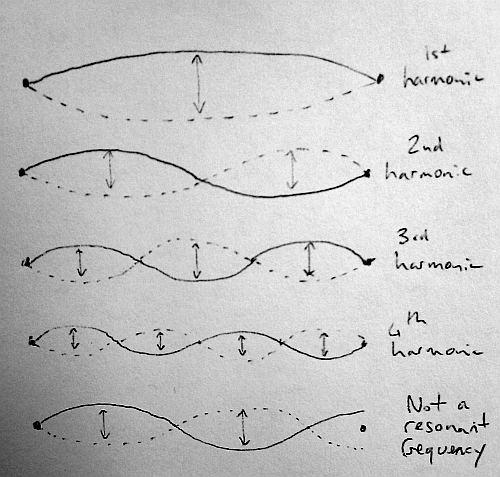 Элвис выпустил эту песню в 1956 году, и она быстро поднялась в чартах. Песня действительно захватывает дух, а слова очень романтичны.

Представьте, что это звучит на губной гармошке, поскольку песня приобретает совершенно новый смысл, когда вы ее играете. Это обязательно пригодится, когда вы захотите произвести впечатление на кого-то особенного в своей жизни. Что может быть лучше, чем песня Элвиса.

15. Где-то над радугой — Гарольд Арлен

Somewhere Over The Rainbow дарит всем нам тепло внутри. Гарольд Арлен выпустил эту песню в 1939 году и имел огромный успех. Он был выпущен для фильма «Волшебник страны Оз» и с тех пор стал основным продуктом для многих любителей музыки.

Эта красивая песня становится еще красивее, когда ее играют на губной гармошке. Гармошка выводит песню на новый уровень и обеспечивает незабываемое звучание для всех, кто ее слышит. Итак, приступайте к обучению!

16. Останься со мной – Бен Э. Кинг

Вы же не думали, что я не включу Stand By Me? Шедевр Бена Э. Кинга был выпущен в США в 1961 году и с тех пор стал частью американской культуры. Песня по сей день имеет культурное, историческое и эстетическое значение.

Обучение игре на губной гармошке даст вам возможность играть всю оставшуюся жизнь, которую вы сможете играть где угодно и когда угодно. Я знаю, что вам это понравится вашей семье и друзьям! Я знаю, у тебя это хорошо получится.

17. Отвези меня домой, проселочные дороги – Джон Денвер

«Отвези меня домой, проселочные дороги» Джона Денвера — это, мягко говоря, вечнозеленое растение. Песня была выпущена в 1971 году и мгновенно стала хитом, поэтому она стала любимой песней для караоке для всех, кто хочет выразить своего мальчика (или девушку) из глубинки страны.

Эта песня на губной гармошке тоже звучит потрясающе. Изучение этого будет еще более впечатляющим и, безусловно, будет полезным, когда вы захотите устроить вечеринку в стиле кантри и поиграть для семьи и друзей.

18. Мысли вслух – Эд Ширан

Мы все знаем «Мысли вслух» Эда Ширана, потому что когда он вышел, он был практически везде. Песня была выпущена в декабре 2014 года и с тех пор стала очень популярной, а со временем еще больше.

Что может быть лучше, чтобы произвести впечатление или исполнить серенаду для этого особенного человека, чем с губной гармошкой в ​​руке и позволяя эмоциям выплескиваться через инструмент. Выучить его довольно легко, и он очень хорошо подойдет вам для любого будущего события или момента.

19. Какой чудесный мир – Луи Армстронг

Это точно возвращает нас в более прекрасное время в нашей жизни. «Какой чудесный мир» Луи Армстронга был выпущен в 1967 году. Он не был очень хорошо принят в Англии и Франции, но ему удалось мгновенно стать хитом №1 в США.

Эту мелодию, наверное, знает каждый второй человек. Учиться игре на губной гармошке на самом деле не так уж и сложно — это простой 12-тактовый блюз. Взамен у вас будет песня для любого случая, которая произведет впечатление практически на любого.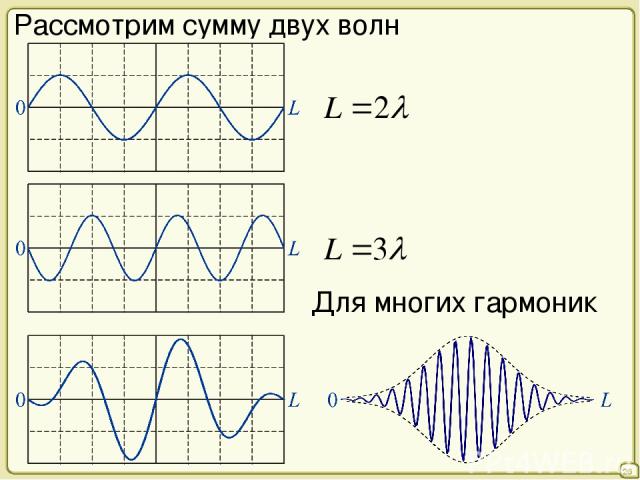

20. Лестница в небо – Led Zeppelin

Что может быть лучше, чтобы закрыть этот список, чем Stairway To Heaven. Led Zeppelin выпустили ее в 1971 году, и я почти уверен, что почти все ее слышали. Эта мягкая и наполненная эмоциями песня определенно станет хорошим дополнением к вашему репертуару игры на губной гармошке.

Игра на губной гармошке того стоит. Песня впечатляет независимо от того, какой инструмент вы выберете, но губная гармошка просто придает ей совершенно новое звучание и лишит вас дара речи.

Сводка

Губная гармошка – прекрасный инструмент, который придает причудливое и впечатляющее звучание любой музыке. Играть на губной гармошке достаточно просто в освоении — всего за несколько дней упорной практики вы сможете создать песню для особых случаев.

Этот список представляет собой прекрасное сочетание блюза, рок-н-ролла, поп-музыки и кантри-песен, которые должен уметь играть каждый.