Гармонические и периодические колебания это одно и тоже?

Тут налицо подмена понятий. Гармоническая — это функция, непрерывная и дважды дифференцируемая в рассматриваемой области, удовлетворяющая уравнению Лапласа. Некоторые (далеко не все) из гармонических функций являются периодическими. Периодической называется функция, для которой выполняется f(t) = f(t+kT), где k — целое число, Т -период. Есть еще понятие гармоники — это синусоидальная функция — член функционального ряда Фурье. Тоже очень интересно, тем более, что в контексте многих задач математической физики гармоники являются частью решения, то есть — входят в гармонические функции. Например: f(x,t)=Ak*sin(ax)*sin(wt) — член двумерного ряда, описывающего колебания струны. При этом в данном контексте эта функция — решение гиперболического уравнения, а не уравнения Лапласа. Но — это гармоника, хотя она может быть и решением уравнения Лапласа, а значит -гармонической функцией.

Гармонические -это частный случай периодических, которые описываются синусоидами.

Нет. Но гармонические всегда периодические.

Гармонические — постоянные. Периодические — возникающие периодически.

Слово «гармонический» вообще пришло в современные языки из греческого. По ходу заимствования в естественные науки оно оказалось связано с музыкой, с уравнениями колебаний музыкальных инструментов и прочих объектов. А там достаточно часто всё состоит из синусоид с кратными частотами. Но у классических гармонических колебаний в физике синусоида ровно одна для описания состояния системы во времени используется, это иначе называется «математический маятник» или «гармонические колебания». Матфиз и гармонические ф-ции Вам пока не нужны. Так что гармонические колебания — частный случай периодических, да.

ГАРМОНИКА — это… Что такое ГАРМОНИКА?

ГАРМОНИКА — (лат., от греч. harmonia согласие, созвучие). Музыкальный инструмент, состоящий из ящика, в котором располагается валик с колокольчиками, звук извлекается посредством клавиш; изобретен Делавалем и усовершенствован Франклином; впоследствии стали… …   Словарь иностранных слов русского языка

ГАРМОНИКА — ГАРМОНИКА, гармоники, жен. (нем. Harmonika). 1. Духовой музыкальный инструмент, состоящий из двух дощечек с клавиатурой, соединенных раздвижными мехами. «Гармоника, гармоника, эй, пой, визжи и жги!» А.Блок. 2. Раздвижной складчатый кожух,… …   Толковый словарь Ушакова

гармоника — гармония, гармонь, гармошка; колебание, частота; концертина, субгармоника, хромка, инструмент, фисгармония, лушэн, тальянка, аккордеон, баян Словарь русских синонимов. гармоника / однорядовая: тальянка ) Словарь синонимов русского языка.… …   Словарь синонимов

гармоника — Гармоническая составляющая периодических колебаний. Примечание Частоты гармоник кратны частоте анализируемых периодических колебаний. [ГОСТ 24346 80] гармоника Гармонический сигнал с амплитудой и начальной фазой, равными соответственно значениям… …   Справочник технического переводчика

ГАРМОНИКА — ГАРМОНИКА, и, жен. 1. Духовой язычковый музыкальный инструмент подвижные меха с двумя дощечками, снабжёнными клавиатурой. 2. перен. Ряд частых расходящихся параллельных складок (разг.). Сложить бумагу гармоникой. • Губная гармоника музыкальный… …   Толковый словарь Ожегова

гармоника — периодических колебаний; гармоника Каждое слагаемое периодических колебаний, представляемых в виде суммы гармонических колебаний …   Политехнический терминологический толковый словарь

ГАРМОНИКА — (гармонь) (от греч. harmonikos созвучный стройный), клавишно пневматический духовой музыкальный инструмент с проскакивающими язычками. Изобретена немецким мастером К. Ф. Л. Бушманом (1822). Распространилась у многих народов Европы, в т. ч. в… …   Большой Энциклопедический словарь

ГАРМОНИКА — (см. ОБЕРТОН). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 …   Физическая энциклопедия

гармоника — и, ж. harmonique. устаревающ. Батарея отопления. Глупые ненужные предметы нелепой комнаты каждый посылали ему какой либо очередной упрек, словно только затем эти шифоньерки, кронштейны и пуфы и были сюда понапиханы, подтяжки висели на гармонике… …   Исторический словарь галлицизмов русского языка

ГАРМОНИКА — синусоидальная (гармоническая) составляющая периодического процесса с частотой, кратной его основной частоте колебания …   Большая политехническая энциклопедия

Гармонические колебания — это… Что такое Гармонические колебания?

Графики функций f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.

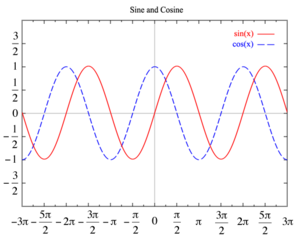
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия;

ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд  — полная фаза колебаний,  — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )

Виды колебаний

Эволюция во времени перемещения, скорости и ускорения при гармоническом движении

• Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).
• Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Применение

Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:

• Очень часто^[2] малые колебания, как свободные, так и вынужденные, которые происходят в реальных системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.
• Широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов. Другими словами, любое колебание может быть представлено как сумма гармонических колебаний.
• Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. С учётом предыдущего свойства это позволяет исследовать прохождение колебаний произвольной формы через системы.

См. также

Примечания

1. ↑ То есть не равное тождественно нулю.
2. ↑ Подразумеваемым условием здесь является то, что свойства системы должны быть постоянны во времени (что в реальности достаточно часто выполняется, по крайней мере, приближенно).

Литература

• Физика. Элементарный учебник физики / Под ред. Г. С. Лансберга. — 3 изд. — М., 1962. — Т. 3.
• Хайкин С. Э. Физические основы механики. — М., 1963.
• А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
• Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Физматлит, 1959. — 572 с.

Гармоника (колебания) Википедия

Запрос «Гармоника (колебания)» перенаправляется сюда; также см. Гармоника. Колебания струны: 1 — колебание по всей длине образует основной тон, 2 — колебание половинок образует первый обертон, 3 — колебание третей — второй обертон и т. д. 15 обертонов от ноты До большой октавы (16 гармоник), озвученные как нажатие клавиш фортепиано

Оберто́ны (нем. ober — высокий, Ton — звук^[1]) в акустике — призвуки, входящие в спектр музыкального звука; высота обертонов выше основного тона (отсюда название). Наличие обертонов обусловлено сложной картиной колебаний звучащего тела (струны, столба воздуха, мембраны, голосовых связок и т. д.): частоты обертонов соответствуют частотам колебания его частей.

Обертоны бывают гармоническими и негармоническими. Частоты гармонических обертонов больше частоты основного тона в 2, 3, 4, 5 и т. д. раз (кратность равна натуральному числу). Гармонические обертоны вместе с основным тоном называются гармониками и образуют натуральный звукоряд:

В реальных физических ситуациях (например, при колебаниях массивной и жесткой струны) частоты обертонов могут заметно отклоняться от величин, кратных частоте основного тона — такие обертоны называются негармоническими. Присутствие негармонических обертонов в колебаниях струн музыкальных инструментов приводит к феномену неточного равенства между рассчитанными частотами равномерно темперированного строя и реальными частотами правильно настроенного фортепиано (см. Кривые Рейлсбека).

Ввиду исключительной важности для музыки именно гармонических обертонов (и относительной малозначимости негармонических) вместо «гармонический обертон» в музыкально-теоретической (но не в физической) литературе часто пишут «обертон» без каких-либо уточнений.

Обертон может быть колебанием частей звучащего тела, выраженных как аликвотными дробями (¹/₂, ¹/₃, ¹/₄ и т. д.), так и неаликвотными (например, при колебании звучащего элемента ударного инструмента с неопределённой высотой звука, такого как там-там). Количество и характер обертонов влияют на тембр инструмента. Каждый обертон имеет порядковый номер, обозначающий, какая часть струны колеблется. Звукоряд, состоящий из основного тона и его гармонических обертонов, называется натуральным (обертоновым) звукорядом.

Начальные 10 обертонов прослушиваются по высоте и сливаются друг с другом в аккорды. Остальные прослушиваются плохо или не прослушиваются вообще.

Использование обертонов в музыке

Обертоны (как гармонические, так и негармонические) стали основным звуковым материалом для ряда экспериментальных сочинений (чаще электронных «реализаций») последней трети XX века, обобщённо именуемых тембральной, или спектральной музыкой.

Примечания

Литература

• Обертоны // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1976. — Т. 3. — С. 1066—1067. — 1104 с.
• Обертоны // Музыкальный энциклопедический словарь. — М.: Советская энциклопедия, 1990. — С. 389. — 672 с.

Гармонические колебания

Определение 1

Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.

Колебательные движения. Формулы

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Определение 2

Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Определение 3

Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.

Функция x=f(t) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2.1.1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

Рисунок 2.1.1. Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Определение 4

Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.

Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x=xmcos (

Обертон — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 марта 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 марта 2019; проверки требует 1 правка. Запрос «Гармоника (колебания)» перенаправляется сюда; также см. Гармоника.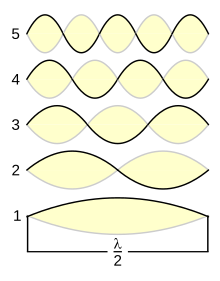 Колебания струны: 1 — колебание по всей длине образует основной тон, 2 — колебание половинок образует первый обертон, 3 — колебание третей — второй обертон и т. д. 15 обертонов от ноты До большой октавы (16 гармоник), озвученные как нажатие клавиш фортепиано

Оберто́ны (нем. ober — высокий, Ton — звук^[1]) в акустике — призвуки, входящие в спектр музыкального звука; высота обертонов выше основного тона (отсюда название). Наличие обертонов обусловлено сложной картиной колебаний звучащего тела (струны, столба воздуха, мембраны, голосовых связок и т. д.): частоты обертонов соответствуют частотам колебания его частей.

Обертоны бывают гармоническими и негармоническими. Частоты гармонических обертонов больше частоты основного тона в 2, 3, 4, 5 и т. д. раз (кратность равна натуральному числу). Гармонические обертоны вместе с основным тоном называются гармониками и образуют натуральный звукоряд:

В реальных физических ситуациях (например, при колебаниях массивной и жесткой струны) частоты обертонов могут заметно отклоняться от величин, кратных частоте основного тона — такие обертоны называются негармоническими. Присутствие негармонических обертонов в колебаниях струн музыкальных инструментов приводит к феномену неточного равенства между рассчитанными частотами равномерно темперированного строя и реальными частотами правильно настроенного фортепиано (см. Кривые Рейлсбека).

Ввиду исключительной важности для музыки именно гармонических обертонов (и относительной малозначимости негармонических) вместо «гармонический обертон» в музыкально-теоретической (но не в физической) литературе часто пишут «обертон» без каких-либо уточнений.

Обертон может быть колебанием частей звучащего тела, выраженных как аликвотными дробями (¹/₂, ¹/₃, ¹/₄ и т. д.), так и неаликвотными (например, при колебании звучащего элемента ударного инструмента с неопределённой высотой звука, такого как там-там). Количество и характер обертонов влияют на тембр инструмента. Каждый обертон имеет порядковый номер, обозначающий, какая часть струны колеблется. Звукоряд, состоящий из основного тона и его гармонических обертонов, называется натуральным (обертоновым) звукорядом.

Начальные 10 обертонов прослушиваются по высоте и сливаются друг с другом в аккорды. Остальные прослушиваются плохо или не прослушиваются вообще.

Обертоны (как гармонические, так и негармонические) стали основным звуковым материалом для ряда экспериментальных сочинений (чаще электронных «реализаций») последней трети XX века, обобщённо именуемых тембральной, или спектральной музыкой.

• Обертоны // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1976. — Т. 3. — С. 1066—1067. — 1104 с.
• Обертоны // Музыкальный энциклопедический словарь. — М.: Советская энциклопедия, 1990. — С. 389. — 672 с.

Гармоника (наука) — Википедия

У этого термина существуют и другие значения, см. Гармоника.

Гармо́ника (др.-греч. ἁρμονική <подразумевается ἐπιστήμη или πραγματεία>, лат. harmonica) в античности, в Средние века, в эпоху Возрождения, реже в Новое время — наука и учение о звуковысотной структуре музыки, т.е. о гармонии. Античная гармоника — прообраз современной научной и учебной дисциплины гармонии (отрасли музыкознания).

Обязательные отделы (части) гармоники установил в IV в. до н. э. Аристоксен: о звуках (понимаемых музыкально-логически, т.е. как материал для «гармоничного»), об интервалах, о родах, о звукорядах («системах»), о тонах (т.е. о ладах), о метаболах, о мелопее. Таким образом, гармоника охватывала все необходимые аспекты звуковысотности, от акустико-математических до музыкально-логических категорий. Сохранились учебные гармоники Клеонида, Никомаха, Гауденция, Алипия, анонимов Беллермана; исследования гармонии (в т.ч. в позднейших пересказах) оставили Адраст Афродисийский, Птолемей и др.

Рассмотрение ритма в музыке, стихе и танце не входило в проблематику гармоники. Этой области знания была посвящена другая мусическая наука — «ритмика» (сохранились фрагменты трактата Аристоксена «Элементы ритмики»; ей посвящена часть девятой книги трактата Марциана Капеллы «О бракосочетании Филологии и Меркурия» и т.д.).

В латинской литературе гармонику также называли «музыкой» (musica), подразумевая не музыкальное искусство (в том смысле, как его принято понимать в Новое время), а науку о звуковысотном строении музыки. В этом смысле, например, название трактата «Основы музыки» (Institutio musica) Боэция нужно понимать как основы гармоники, т.е. учения о гармонии (в античном понимании этого слова). В таком же смысле следует понимать и многочисленные средневековые трактаты-«Музыки» (например, «Musica enchiriadis» Псевдо-Хукбальда, «Музыка» Германа Расслабленного и др.), исследующие не этос музыкального искусства и подавно не практические навыки музицирования (музыкального исполнительства), а излагающие учение о музыкальной гармонии. Как и в греческой античности, в средневековых гармониках (например, в трактате «De harmonica institutione» Регино Прюмского) трактуется звуковысотная структура монодии (григорианский хорал), а не многоголосия.

В эпоху Возрождения «гармониками» называли свои учения авторы, демонстрирующие свою приверженность античным идеалам. Например, Царлино называет свой трактат (написанный уже на итальянском языке) «Основы гармоники» (Le istitutioni harmoniche). Слово «гармоника» у Царлино и в других ренессансных трактатах (при всём уважении к античности) относят не только к монодии, но и к многоголосию. Таким образом, «гармоника» постепенно приближается к современному основному пониманию гармонии как звуковысотной структуры многоголосной музыки.

В России понимание гармоники как «науки гармонии» прослеживается вплоть до XIX века, оно зафиксировано в первой русской универсальной энциклопедии Плюшара^[1].

Объект изучения старинной гармоники — звук определённой высоты, для которого в ряде трактатов использовался специальный термин др.-греч. φθόγγος (в латинской транслитерации — лат. phthongos), и связи разновысотных звуков такого рода. Звуки (звучания) неопределённой высоты (как, например, вой волка, мычание коровы и т.п., а также речь человека), которые обобщённо именовались экмелическими, нельзя точно измерить, и потому они не могут быть объектом изучения в гармонике. Современная гармония по преимуществу занимается звуками определённой высоты, но также изучает и слитные звучания (как, например, в сонорной музыке).

Старинная гармоника изучает только эммелические звуки, т.е. звуки, пригодные для мелодии. Современная гармония включает в сферу своего рассмотрения любые звуки, например, «грязные ноты» (dirty tones) в джазе, отгласы и другие экмелические явления в музыкальном фольклоре.

Старинная (особенно античная) гармоника изучает звуковысотность одноголосной музыки (склад античной музыки представляет собой по преимуществу монодию). Школьная гармония, ориентирующаяся на классическую мажорно-минорную тональность, изучает преимущественно многоголосную музыку гомофонного склада. Гармоника изучает интервалы и многоразличные монодические лады, школьная гармония изучает (терцовые) аккорды и их закономерные связи на основе лишь двух многоголосных ладов — мажора и минора.

Предмет изучения современной гармонии (например, в учении о гармонии Ю.Н. Холопова) — любая звуковысотная структура любого склада, музыка как одноголосная, так и многоголосная.

1. ↑ Т. 13. Спб. 1838, с. 317.

• Ван дер Варден Б.Л. Пифагорейское учение о гармонии // Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматлит, 1959. (Репринт: М.: КомКнига, 2006), сс. 393-434.
• Музыкально-теоретические системы. Учебник для историко-теоретических и композиторских факультетов музыкальных вузов. М., 2006.
• Geschichte der Musiktheorie. Bd. 2: Vom Mythos zur Fachdisziplin. Antike und Byzanz, hrsg. v. F.Zaminer u.a. Darmstadt, 2006.
• Barker A. The science of harmonics in classical Greece. Cambridge: Cambridge University Press, 2007. ISBN 9780521289955.