Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Как поступить в БелГУТ:

дневное, заочное полное,
заочное сокращенное

Как получить место

в общежитии БелГУТа

Как поступить иностранному гражданину

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
					1	2
3	4 Дата : 2022-10-04	5	6 Дата : 2022-10-06	7	8	9
10	11 Дата : 2022-10-11	12	13 Дата : 2022-10-13	14 Дата : 2022-10-14	15	16
17	18	19	20 Дата : 2022-10-20	21	22	23
24	25	26 Дата : 2022-10-26	27 Дата : 2022-10-27	28	29 Дата : 2022-10-29	30
31

Все анонсы

• I международная научно-техническая конференция сту. ..
• 29 октября — ДЕНЬ ОТКРЫТЫХ ДВЕРЕЙ ФАКУЛЬТЕТА ПГС…
• Вакцинация от гриппа
• 1 тур серии игр «ЧТО? ГДЕ? КОГДА?» среди студентов…
• Открытая лекция Евдокимовича Владислава Евгеньевич…
• Лига дебатов в БелГУТе
• Курсы самообороны
• Заседание совета университета …
• С Днем отца!
• С Днем отца! Поздравляет Студенческий совет БелГУТ…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

I международная научно-техническая конференция сту…

29 октября — ДЕНЬ ОТКРЫТЫХ ДВЕРЕЙ ФАКУЛЬТЕТА ПГС…

Вакцинация от гриппа

1 тур серии игр «ЧТО? ГДЕ? КОГДА?» среди студентов…

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений



• Университет

СИЛА ЗАКОНА
27 октября 2022

• Университет

Поздравляем с присвоением степени кандидата технических наук. ..
27 октября 2022

• Воспитательная работа

Студенты на телепрограмме «Черное и белое» Беларусь-4…
27 октября 2022

• Спорт

Встреча школьников-таможенников со студентами-спортсменами сборной Бел…
27 октября 2022

• Университет

Встреча с представителями силового блока…
27 октября 2022

• Студенческая жизнь

«Крылья надежды» в КСУП «Брилево»
27 октября 2022

• Университет

Волшебная неделя ФРАНЦУЗСКОГО ЯЗЫКА
26 октября 2022

• Университет

К 30-летнему юбилею специальности «АВТОМОБИЛЬНЫЕ ДОРОГИ» в УО «БЕЛОРУ. ..
26 октября 2022

• Университет

Диалоговая площадка с представителями Гомельской таможни…
26 октября 2022

Другие новости

• Волейбольная встреча БелГУТа и БТЭУ
• Неделя родительской любви глазами участников автопоезда #Беларусь.Моло…
• Курсы самообороны
• В гостях «Золотой голос БелГУТа» Дмитрий Даниленко — выпускник нашего …
• Победа за нами!
• Первый визит Второго секретаря Центрального комитета ОО «БРСМ» Прохоро…
• III Международная научно-практическая конференция «Тихомировские чтени…
• Открытие портрета профессора Н.В. Правдина в галерее ученых-эксплуатац…
• Дневник участников проекта «Автопоезд #Беларусь.Молодежь.Традиции»…
• Встреча Елены Алексиной с первокурсниками БелГУТа…
• Открытый диалог в Гомельском колледже

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Гармонические колебания | это.

.. Что такое Гармонические колебания?

Графики функций

f(x) = sin(x) и g(x) = cos(x) на декартовой плоскости.

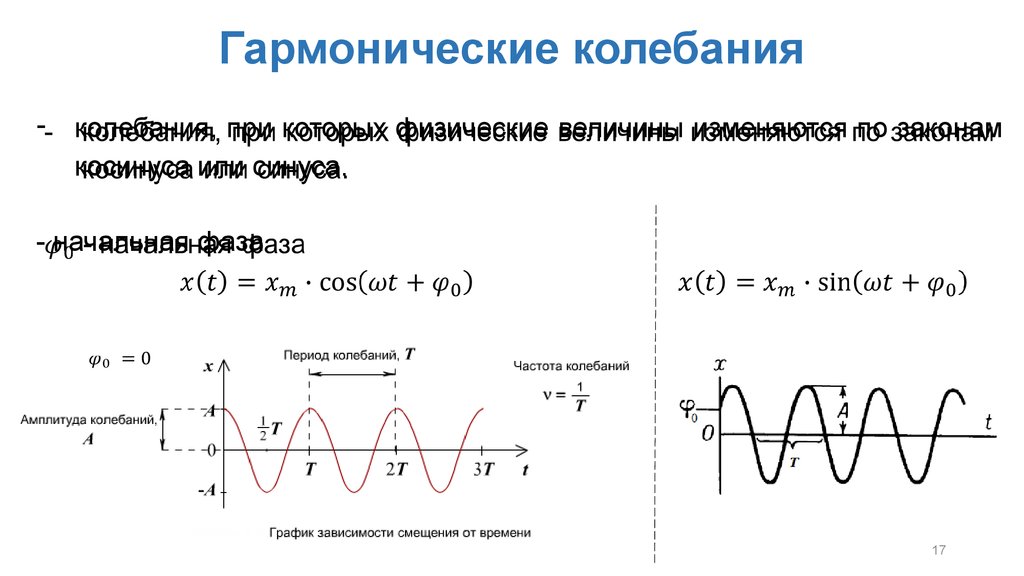
Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд  — полная фаза колебаний,  — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )

Содержание 1 Виды колебаний 2 Применение 3 См. также 4 Примечания 5 Литература

Виды колебаний

Эволюция во времени перемещения, скорости и ускорения при гармоническом движении

• Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).
• Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Применение

Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:

• Очень часто^[2] малые колебания, как свободные, так и вынужденные, которые происходят в реальных системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.
• Широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов. Другими словами, любое колебание может быть представлено как сумма гармонических колебаний.
• Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. С учётом предыдущего свойства это позволяет исследовать прохождение колебаний произвольной формы через системы.

См. также

• Гармонический осциллятор
• Математический маятник
• Физический маятник
• Псевдогармонические колебания

Примечания

1. ↑ То есть не равное тождественно нулю.
2. ↑ Подразумеваемым условием здесь является то, что свойства системы должны быть постоянны во времени (что в реальности достаточно часто выполняется, по крайней мере, приближенно).

Литература

• Физика. Элементарный учебник физики / Под ред. Г. С. Лансберга. — 3 изд. — М., 1962. — Т. 3.
• Хайкин С. Э. Физические основы механики. — М., 1963.
• А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
• Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Физматлит, 1959. — 572 с.

Что трясет мои фонарные столбы?

Опубликовано 25 октября 2015 г.

Что такое гармоническая вибрация?

Проще говоря, гармоническая вибрация — это когда механический объект вибрирует на гармонических частотах. Есть два разных вида вибрации; бесплатно и принудительно. Свободные вибрации — это те, которые вы вызываете и позволяете произойти. Обычно они желательны, как камертон. Вынужденные вибрации возникают, когда в механической системе возникает отклонение во времени, подобное тряске, производимой стиральной машиной. Любая из этих вибраций может быть гармонической или негармонической.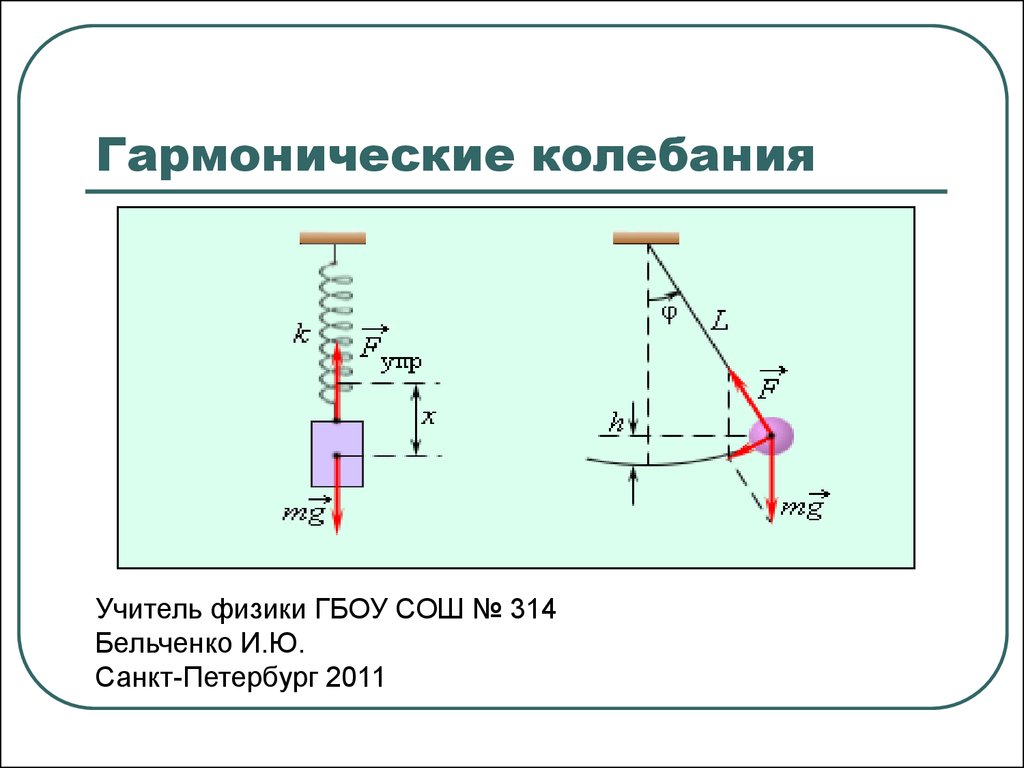 Ради нашего обсуждения мы будем продолжать использовать термин гармоническая вибрация.

С какими типами вибрации вы сталкиваетесь при работе с фонарными столбами?

Вы можете столкнуться с одним из двух движений с фонарными столбами. Колебания первой или второй формы. Первая мода возникает в верхней части стойки с низкими частотами, которые мало вредят стойке. Вторая мода возникает вблизи середины полюса с высокими частотами и обычно вызывается ветровым вихрем. Это возмущение может повредить конструкцию опоры и светильника.

Как узнать, испытывает ли фонарный столб вибрацию второй моды?

• Преждевременный отказ лампы
• Отсутствующие или ослабленные винты и принадлежности
• Звуки «тиканья/щелчка»
• Гармонические частоты слышимого гудения

Все нижеперечисленное является возможными индикаторами гармонической вибрации, происходящей в ваших фонарных столбах. Чтобы дополнительно подтвердить любые вибрации, поищите волосяные трещины возле сварного шва и в любых других местах. Если вы что-то подозреваете, проконсультируйтесь с лицензированным инженером-строителем или производителем освещения.

Как предотвратить гармоническую вибрацию?

Невозможно полностью предотвратить гармоническую вибрацию фонарных столбов. Правильная установка и использование подходящих деталей — первый шаг. Виброгасители также можно использовать для минимизации разрушительной силы второй моды вибрации. Обычно они устанавливаются внутри конструкции полюса, но также могут быть в виде чего-то, что крепится и снаружи.

Также почти невозможно предсказать места, которые могут вызвать вредную гармоническую вибрацию. Хотя наиболее уязвимыми средами являются широкие открытые площадки без ветрозащитных экранов, такие как здания; т.е. мосты, большие парковки, аэропорты.

---

Свяжитесь с WLS Lighting Systems сегодня, чтобы узнать больше об обновлении освещения вашей парковки — [email protected]

Рубрика: Часто задаваемые вопросы по освещению, Технология освещения С тегами: Гармоническая вибрация, важность, Обслуживание светодиодов, Освещение, Обслуживание освещения, Обслуживание, техническое обслуживание металлогалогенных ламп, тряска опор, вибрация, воздействие ветра

Наша цель — предоставить вам лучшие решения по освещению и управлению, отвечающие вашим требованиям дизайна и бюджета.

9{я \ омега т } ], $$

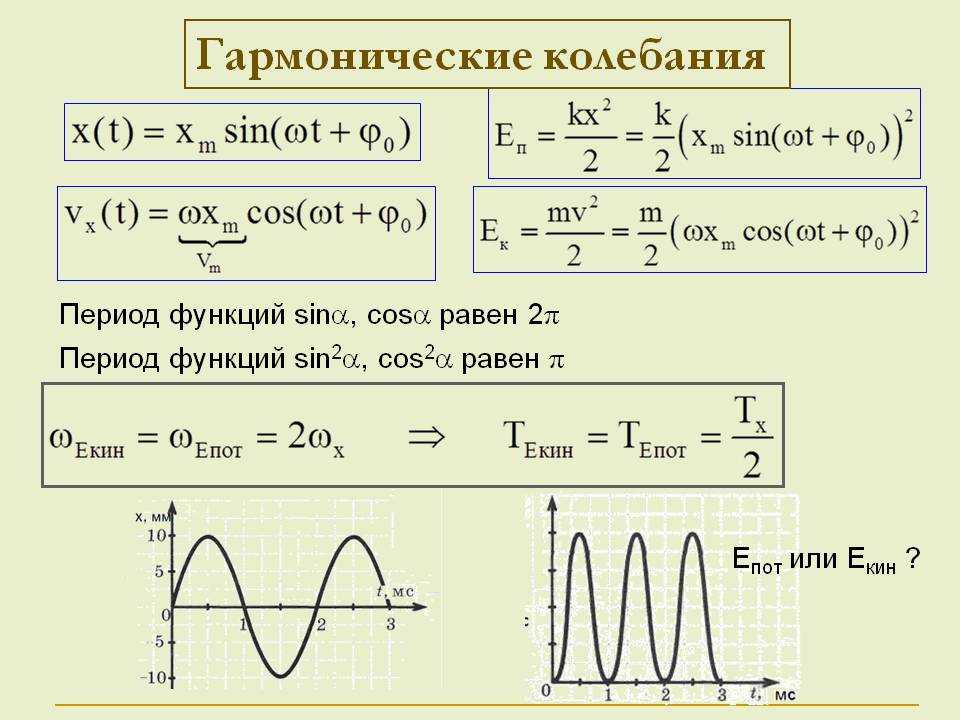
где $ х = х( т) $ — значение вибрационной амплитуды в момент времени $t$, $ | А | = | Б | $ – амплитуда, $ \omega $ – периодическая (круговая) частота, а $\alpha$ является начальной фазой вибрации. Длительность одного полного колебания $ T = 2 \pi / \omega $ называется периодом гармонического колебания, при этом $\nu = 1/T$, число полных колебаний, совершаемых в единицу времени, известно как частота гармонических колебаний ($\omega=2\pi\nu$). Период гармонического колебания не зависит от его амплитуды. Скорость, ускорение и все высшие производные величины вибрации изменяются гармонически на одной и той же частоте. Гармоническое колебание представляется в виде эллипса на фазовой плоскости $(x,\dot{x})$. Из-за диссипации энергии совершенные гармонические колебания в природе не встречаются, но многие процессы близки к гармоническим колебаниям. К ним относятся небольшие колебания механических систем относительно их положения равновесия. Результирующие частоты (так называемые собственные частоты) колебаний не зависят от начальных условий движения и определяются характером самой колебательной системы. Например, малые колебания (под действием силы тяжести) математического маятника на нити длиной $ l $ описываются дифференциальным уравнением

$$ мл \dot{x} точка = — мгх, $$

где $ г $ – ускорение свободного падения и $ x( t) $ угол между вертикалью и нитью маятника. Общее решение этого уравнения имеет вид $ x = A \cos ( \omega t — \alpha )$, где собственная частота колебаний, $ \omega = \sqrt g/l $, зависит от $g$ и $л$ только, а амплитуда $ A $ и фаза $\alpha$ – константы интегрирования, выбранные в соответствии с начальными условиями. 9{- в т } дт $$

определяет амплитуду $ ( | a _ {n} | ) $ и фазовый сдвиг $ ( \mathop{\rm arg} a _ {n} ) $ гармонического колебания с частотой $n$. Совокупность всех коэффициентов Фурье определяет спектр $ x( t) $ и показывает гармонические колебания, которые действительно участвуют в $ x( t) $, а также амплитуды и начальные фазы этих колебаний. Знание спектра эквивалентно знанию функции $x(t)$.

Функция $ x( t) $ определено на $ ( — \infty , \infty ) $ больше нельзя построить из гармонических колебаний с целыми частотами. В его построении участвуют колебания всех частот: Функция $ x( t) $ можно представить интегралом Фурье: 9{- в т} дт $$

— спектральная плотность $x(t)$.

Эти представления функций составляют основу метода Фурье для решения различных задач теории дифференциальных и интегральных уравнений.

References

[1]	G.S. Gorelik, «Oscillations and waves» , Moscow-Leningrad (1950) (In Russian)

Comments

References

[a1]	Дж.В.С. Рэлей, «Теория звука» , 1 , Дувр, переиздание (1945)

Как цитировать эту запись:
Гармонические вибрации.