Физический смысл функции тока

П

ψ_n+Δψ

одсчитаем расход несжимаемой жидкости в плоском канале единичной ширины между линиями токаина плоскостиXOY. В данном случае сечение S будет криволинейным; выберем на нём элемент dS и заменим его составным, состоящим из двух прямолинейных отрезков AO=dy и OB=-dx – проекций dS на оси XOY. Очевидно, что расход через dS и расход через составное сечения равны одной и той же величине (рис. Д.2.2)

.

ψ_n

Рис. Д.2.2

Если учесть, что

и что

,

то получим окончательно

.

Итак, разность есть объемный расход жидкости через площадку единичной высоты, расположенную между линиями тока и.

Пример Д.2.1. Рассмотрим плоское прямолинейное и равномерное установившееся течение несжимаемой невязкой жидкости с одинаковой во всём потоке (в любой точке) скоростью, направленной вдоль оси Оy. В этом случае

,

Тогда уравнение неразрывности удовлетворяется, и течение является потенциальным.

Тогда

–

линии равных потенциалов представляют собой прямые, параллельные оси абсцисс, рис. Д.2.3. Ось Оy (x=0) также является одной из эквипотенциальных линий; обозначим её через .

Рис. Д.2.3

М

Рис Д.2.2

ожно допустить, что, следовательно

Рис. Д.2.2

.

Для функции тока найдём аналогично

.

Линии тока представляют прямые, параллельные оси Оy.

Задача Д. 2.2. Найти потенциали функцию токаплоского поступательного потока, направленного под углом к оси абсцисс.

Решение. Такой поток может быть образован в результате наложения плоского однородного поступательного потока, параллельного оси абсцисс на плоский однородный поступательный поток вдоль оси ординат.

, .

Пример Д.2.2. Предположим, что невязкая несжимаемая жидкость непрерывно подводится к некоторой точке плоскости и растекается по ней с одинаковой интенсивностью по всем направлениям, рис. Д.2.4; такое течение называется плоским источником.

Проведём из центра источника несколько концентрических окружностей различного радиуса. Уравнение постоянства расхода через цилиндрическую поверхность, построенную на любой окружности и имеющую высоту, равную единице, будет иметь вид (при =const)

.

С

Рис. Д.2.4

корость, как следует из последнего равенства, выразится так

,

где .

Поэтому

.

Аналогично

;

окончательно полный дифференциал потенциала скорости

.

Интегрируя это выражение, найдём потенциал скорости для источника

,

где С – константа интегрирования, которую можно принять равной нулю, если положить, что при круге r=1 функция и тогда

, (Д.2.10)

Для определения функции тока учтём, что

, ,

.

После интегрирования

.

Из рис. Д.2.4 видно, что , где– угол, образованный одной из линий тока. Принимая, приy=0 получаем c=0 и, следовательно, для функций тока можно записать

. (Д.2.11)

Эта зависимость выражает функцию тока источника. Из выражений (Д.2.10) и (Д.2.11) следует, что потенциал скорости источника может быть представлен семейством концентрических окружностей различного радиуса, а функция токапредставляется пучком прямых, исходящих из центра.

Потенциал скорости и функция тока для стока будут иметь вид, аналогичный (Д.2.10) и (Д.2.11), но с обратным знаком, т.е.

, .

П

Рис. Д.2.5

ример Д.2.3. Рассмотрим течение, которое получается при одновременном существовании (наложении) на некотором расстоянии друг от друга источника и стока равной интенсивности (равного радиуса). Начало координат поместим в точку, делящую расстояние между центрами источника и стока пополам. Допустим, что источник располагается в точке , а сток в точке, рис. Д.2.5. В этом случае потенциалы скорости и функции тока для источника и стока определяются следующими зависимостями

, ; (Д. 2.12)

, . (Д.2.13)

Будем теперь сближать источник и сток, т.е. величина стремится к нулю. В пределе присток поглотит источник и всякое движение будет отсутствовать. Если одновременно со сближением центров источника и стока будем увеличивать их расход так, чтобы

,

то получим в процессе течение, которое называется диполем. Постоянная М, характеризующая этот поток, называется моментом диполя, а ось Оx – осью диполя. На основании зависимостей (Д.2.12) и (Д.2.13) определяем потенциал скорости и функцию тока рассматриваемого течения (диполя) так, как будет показано ниже.

=

.

Умножим числитель и знаменатель последнего равенства на ; в числителе получим, т.е.

.

В последнем выражении – предел отношения приращения функции к приращению аргумента по координате х, что является частной производной по х; поэтому выражение для может быть записано так

.

Аналогично для функции тока диполя получается выражение

.

Выполняя операции дифференцирования, приходим к окончательным выражениям

,

.

А

Рис. Д.2.6

нализ последних уравнений показывает следующее: линии тока диполя есть окружности, проходящие через начало координат и имеющие центры на оси Оу, рис. Д.2.6; эквипотенциальные линии также представляют собой окружности, проходящие через начало координат, но с центрами, расположенными на оси ОХ. Жидкость движется из начала координат в сторону отрицательного направления оси Ох и, описав окружность, снова попадает в начало координат. Течение жидкости в диполе – идеализированное, не встречающееся на практике, но изучение его позволяет построить схемы течений некоторых реальных потоков.

Пример Д.2.4. Бесциркуляционное обтекание круглого цилиндра плоским прямолинейным потоком.

Рассмотрим цилиндр бесконечной длины, который обтекается безграничным прямолинейным плоским потоком идеальной жидкости перпендикулярно его оси и так, что скорость набегающего потока направлена вдоль оси Ох; начало координат поместим на оси цилиндра. Произведём сложение двух течений: одного – диполя, помещённого в начале координат, а второго – прямолинейного со скоростью, параллельной оси ОХ. Произведём суммирование функций тока

. (Д.2.14)

Из этого равенства следует, что при у=0, а также на окружности радиуса , определяемого условием

, (Д.2.15)

функция тока равна нулю, т.е. постоянна и, следовательно, названные линии являются линиями тока. Картина линий тока приведена на рис. Д.2.7.

Ψ=0

Ψ=0

Ψ=0

Ψ=0

Рис. Д.2.7

Ψ=0

Ψ=0

Так называемая «нулевая» линия тока состоит из отрезка отрицательной оси абсцисс от бесконечности до точки А, из окружности радиуса(ACBD) и из отрезка положительной оси абсцисс от точки В до бесконечности. Эта «нулевая» линия тока разграничивает две области течения жидкости: «внешний поток» (вне окружности радиуса ) и «внутренний поток», замыкающийся внутри окружности радиуса. Этот «внутренний поток» не влияет на поведение внешнего потока и ,следовательно, картина обтекания не изменится, если предположить, что потоком обтекается жесткий цилиндр радиуса. Такое течение носит название бесциркуляционного обтекания цилиндра. Исключая с помощью (Д.2.15) момент диполя из (Д.2.14), найдём выражение для функции тока (при)

.

Потенциал скорости такого течения будет иметь вид

.

Формулы перехода от прямоугольных координат (х,у) к полярным имеют вид

,

и, следовательно, функции имогут быть представлены в полярных координатах

, (Д. 2.16)

. (Д.2.17)

Найдём распределение скоростей по контуру цилиндра. Для этого достаточно найти тангенциальную составляющую , так как скорость направлена по касательной к линии тока, а радиальная составляющая скорости на контуре цилиндра равна нулю. Поэтому

.

Знак «минус» указывает, что скорость направлена в сторону, противоположную направлению отсчёта углов . Распределение скоростей по развёртке полуокружности (верхней и нижней) имеет вид отрезка синусоиды. Скорости в точках А и В – так называемых точках разветвления (критических точках) – прииравны нулю. Максимум скорости достигается на пересечении поверхности цилиндра с осью ординат

,

. (Д.2.18)

Задача Д.2.3. применяя зависимость (Д.2.16), построить линии тока для случая обтекания цилиндра при следующих данных: r=3 см,см/с. Построить кривую распределения скоростина осевом сечении цилиндра от его поверхности (по вертикали от точкиС, рис. Д.2.6).

6.2. Функция тока и потенциал скорости

Уравнение линии тока. Вектор скорости частицы w направлен по касательной к линии тока S; для плоского течения это показано на рис. 53. Пусть w_x, w_y — проекции вектора скорости на координатные оси. Из рис. 53 следует, что

, ,

где ds – элемент дуги линии тока. Составим производные пропорции:

, ,

откуда

. (6.5)

Мы получили уравнение линии тока для плоского течения. В слу­чае трехмерного (пространственного) потока уравнения линии тока выводятся аналогично и имеют вид:

. (6.5а)

Функция тока для двухмер­ного течения. Дифференциальное уравнение линии тока плоского течения (6.5) может быть пред­ставлено в виде:

. (6.5б)

Введем такую «функцию тока» ψ(x, y), полный дифференциал которой равен левой части выражения (6.5б):

. (6.6)

Поскольку на линии тока согласно формуле (6.5б) dψ = 0, оче­видно, что функция тока сохраняет вдоль линии тока постоянное значение.

Полный дифференциал функции двух переменных ψ имеет вид:

Рис. 53

.

Сравнивая это выражение с формулой (6.6), получаем, что про­изводные функции тока определяются зависимостями:

, . (6.7)

Сама функция тока может быть определена интегрированием вы­ражения (6.7).

Рис. 54

К онтур поверхности тела, обтекаемого потоком идеальной жид­кости, сам является линией тока: в некоторой «критической» точке набегающий поток раздваивается и огибает тело. Следовательно, на обтекаемой поверхности функция тока постоянна. Но можно, наоборот, рас­сматривать любую линию тока как контур сечения твердого тела. Действи­тельно, если заменить об­ласть, ограниченную ли­нией тока твердым телом, то остальные линии тока не изменятся (так как жидкость мы считаем иде­альной, трение отсут­ствует). Они дают картину обтекания такого тела. В этом состоит принцип отвердения линий тока, широко применяемый в гидродинамике идеальной жидкости. Если, напри­мер, считать отвердевшими линии тока, проходящие на рис. 54 по координатным осям х, у, то получится картина течения внутри прямого угла.

Потенциал скорости. Функцией скоростного потенциала или — сокращенно — потенциалом скорости φ (х, у, z) называется та­кая функция, частные производные которой равны составляющим вектора скорости по соответствующим координатным осям:

, , . (6.8)

Полный дифференциал функции φ равен

. (6.9)

Сама функция скоростного потенциала определяется интегрирова­нием выражения (6. 9).

Рис. 55

В ведение потенциала скорости позволяет заменить вектор­ное поле скорости течения, для изучения которого нужно знать три компоненты по координатным осям, распределением в про­странстве одной скалярной функции φ, что значительно упрощает исследование. В механике твердого тела вводится ана­логичное понятие «потенциала силы»; это скалярная функция, про­изводные от которой равны составляющим силы по координатным осям. Такую же природу имеет в электротехнике понятие потен­циала электрического поля: вместо задания в пространстве вектор­ной величины напряженности поля вводится скалярная функция потенциала V, производные от которой по координатным осям равны соответствующим компонентам вектора напряженности.

Придавая функции φ определенные значения, получаем уравне­ния поверхностей равного потенциала, или эквипотенци­альных поверхностей (в случае двухмерного течения — линий равного потенциала, или эквипотенциалей).

Рассмотрим связь потенциала скорости и функции тока. В слу­чае плоского (двухмерного) течения w_z = 0; дифференциал функ­ции тока выражается формулой (6. 6), дифференциал функции ско­ростного потенциала, из равенства (6. 9), формулой

.

Пусть линия тока ψ = const такого течения представлена на рис. 55 сплошной линией, эквипотенциаль φ = const — пунктир­ной линией.

Проведем к этим линиям касательные в точке их пересечения А. Угол наклона прямой АВ к оси абсцисс определится согласно урав­нению (6. 5б) выражением

;

угол наклона прямой AD выражением

.

Очевидно, что и угол β между касательными равен 90º.

Таким образом, функция тока ψ и потенциал скорости φ взаимно ортогональны; линии тока и эквипотенциали пе­ресекаются всегда под прямым углом. Это позволяет по известным эквипотенциалям строить линии тока и наоборот. Семейства линий ψ (х, у) = const и φ (х, у) = const, нанесенные на один чертеж, на­зываются гидродинамической сеткой течения. Пример такой сетки был приведен на рис. 54.

Сравнивая выражения для составляющих скорости плоского течения w_x и w_y через функцию тока ψ (6.7) и функцию скорост­ного потенциала φ (6.8), видим, что функции ψ и φ связаны усло­виями:

, . (6.10)

В математике эти условия называются условиями Коши—Римана. При их соблюдении оказывается возможным использовать для ис­следования функций ψ и φ математический аппарат теории функций комплексной переменной, который широко применяется в теории потенциального обтекания геометрически правильных тел.

В § 18 указывалось, что угловая скорость вращения жидкой частицы в плоском потоке определяется формулой (6. 6). Если те­чение потенциально, т. е. существует некоторая функция скорост­ного потенциала φ, производные которой равны соответствующим компонентам вектора скорости, то согласно выражению (6.8) имеем

.

Равенство нулю угловой скорости вращения свидетельствует о том, что потенциальное течение — безвихре­вое, т. е. вращение частиц в нем отсутствует. Как будет показано в дальнейшем, у твердых поверхностей, ограничивающих поток, вследствие вязкости всегда формируются зоны вращательных дви­жений, поэтому вблизи стенок теория потенциального обтекания неприменима. Однако для изучения внешнего потока теория по­тенциала используется с большим успехом.

Применим к потенциальному течению несжимаемой жидкости уравнение неразрывности (2.7):

.

Подставляя в него выражения для компонентов скорости через функцию скоростного потенциала (6.8), получаем

. (6. 11)

Это уравнение известно в математической физике под названием уравнения Лапласа. Таким образом, для нахождения функции φ, полностью определяющей кинематику потенциального потока, необходимо решить уравнение Лапласа.

Дифференциальное уравнение в частных производных (6. 11) имеет бесчисленное множество решений, поэтому должны быть за­даны дополнительные (граничные) условия для данной конкретной задачи. Как уже говорилось в § 2.2, к таким условиям относятся за­дание скорости в удалении от обтекаемого тела w_∞ и условие ра­венства нулю на поверхности тела нормальной составляющей ско­рости. При этом предполагается, что жидкость обтекает тело без отрывов. У поверхности тела скорость направлена по касательной (имеет место «скольжение» жидкости).

В силу того, что сумма любого числа частных решений уравне­ния Лапласа является также его решением, оказывается возмож­ным суммировать потенциалы скорости простейших течений для получения картины сложного течения. В этом состоит идея метода наложения потенциальных потоков.

Моделирование потенциальных течений. Исследование обтека­ния реальных тел аналитическими методами представляет в общем случае большую математическую сложность. Отыскание функции скоростного потенциала или функции тока, например, для лопа­точных профилей наперед заданной формы оказывается весьма трудным. Эта задача существенно упрощается с использованием метода аналогий. Наибольшее развитие к настоящему времени по­лучило исследование потенциальных потоков методом электрогид­родинамической аналогии (ЭГДА). Он базируется на следующих положениях.

Согласно выводам теоретической электротехники распределение электрического потенциала в проводнике, как и распределение по­тенциала в безвихревом потоке идеальной жидкости, подчиняется уравнению Лапласа. Действительно, закон Ома, связывающий силу тока с распределением потенциала электрического поля, записы­вается в дифференциальной форме следующим образом:

; ; . (6. 12)

Здесь i — плотность тока, т. е. количество электричества, проте­кающее в 1 сек, через единицу площади проводника; V — электри­ческий потенциал; С — коэффициент электропроводности (вели­чина, обратная удельному сопротивлению).

По закону Кирхгофа, уравнение сплошности электрического тока имеет вид:

,

т. е. оно аналогично уравнению неразрывности (2.7). Подставим в него значение i из системы (6.12). При постоянной электропро­водности среды C уравнение сплош­ности принимает вид:

, (6.11а)

т . е. мы опять получили уравнение Лапласа.

Рис. 56

Таким образом, электрический потенциал V аналогичен потен­циалу скорости φ, удельная плот­ность электрического тока — ана­логична скорости течения w. По­этому, если область распростране­ния электрического тока геомет­рически подобна области течения жидкости, а граничные условия для V и φ аналогичны, интегралы уравнения Лапласа (6. 11) и (6.11a) будут отличаться лишь про­извольными постоянными. Эквипотенциальные поверхности в элек­трическом поле V (х, у, z) = const в этом случае соответствуют эк­випотенциальным поверхностям в потоке жидкости φ (х, у, z) = const, а силовые линии в электрическом поле соответствуют ли­ниям тока в жидкости. Практическое использование этой аналогии состоит в том, что уравнение Лапласа решается на установке ЭГДА, а результаты решения переносятся на поток жидкости.

Для решения задач плоского потенциального обтекания сейчас преимущественно используются модели, в которых в качестве элек­тропроводного материала применяется бумага с графитовым по­крытием. Для измерения потенциалов в различных точках модели измерительная цепь собирается по мостовой схеме (рис. 56). По­стоянный или переменный ток от источника тока подводится к ши­нам Ш1 и Ш2. Параллельно шинам подключен потенциометр R, на скользящем контакте К которого можно задавать любые проме­жуточные значения электрического потенциала между потенциа­лами шин Ш1 и Ш2. Указателем равновесия моста является гальва­нометр Г, включенный в цепь щупа Щ. Прикасаясь щупом Щ к какой-либо точке графитированной бумаги, мы подаем на щуп элек­трический потенциал данной точки.

Граничные условия в моделируемом потоке жидкости таковы:

1. Вдали от обтекаемого тела на линиях, перпендикулярных вектору скорости (им соответствуют линии установки шин на модели, рис. 56), потенциал скорости φ сохраняет постоянное значение: φ = const.

2. На поверхности обтекаемого тела (ей соответствует вырезанный участок на электропроводной бумаге) .

Задавая на потенциометре различные значения электрического потенциала V, с помощью щупа находят на модели точки, принад­лежащие линиям равного потенциала. В этих точках ток в цепи щупа равен нулю, стрелка гальванометра не отклоняется. В этом состоит «аналогия А», позволяющая построить эквипотенциали пло­ского потока.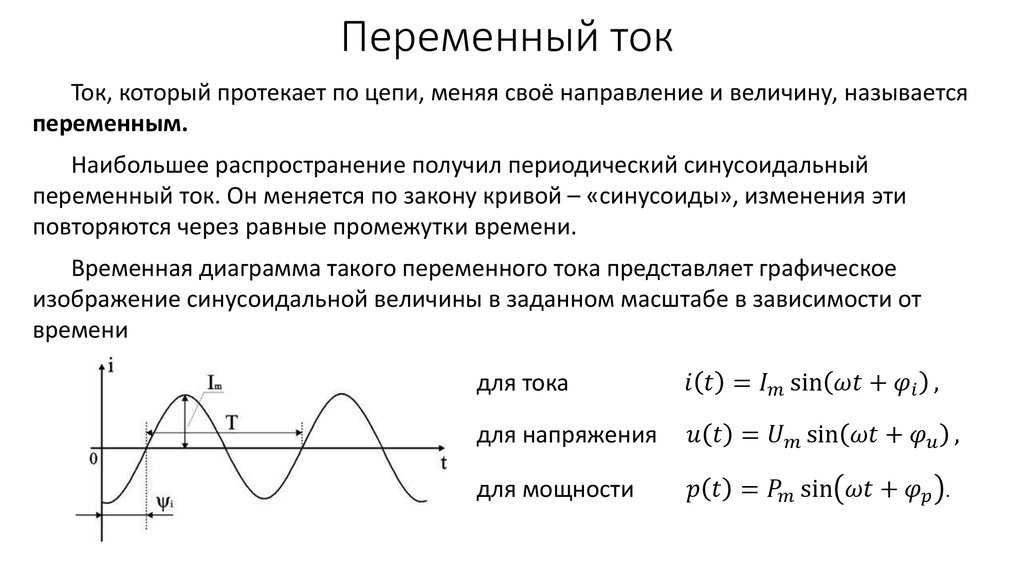

В силу взаимной ортогональности функций скоростного потен­циала φ и тока ψ на установке ЭГДА можно также смоделировать течение таким образом, чтобы линии равного потенциала электри­ческого поля соответствовали линиям тока в жидкости, силовые линии — эквипотенциалям в потоке жидкости. В этом случае на участок модели, соответствующий обтекаемому телу, наклеивается электропроводным клеем модель сечения тела, вырезанная из ма­териала, электропроводность которого во много раз превосходит электропроводность бумаги. Шины размещаются по сторонам модели вдоль потока. Построив с помощью щупа эквипотенциали элек­трического поля, мы получим картину линий тока в потоке жидко­сти. Этот способ получил название «аналогии B».

Построение гидродинамической сетки течения методом ЭГДА осуществляется быстро, не требует высокой квалификации испол­нителей или сложного оборудования и в то же время обеспечивает высокую точность решения. Этим объясняется его широкое приме­нение.

Примеры функции Current() — английский язык

оцените помощь 29 июля 2021 г., 10:42

#1

Привет всем, недавно мне представили новую функцию под названием CURRENT(), и мне интересно, может ли кто-нибудь привести пример/объяснение того, как она работает.

Также любые ссылки на видео уроки были бы замечательными. Спрашиваю, потому что не нашел никакой информации ни в руководстве по Calc, ни в интернете, как ни странно.

анон73440385 29 июля 2021 г., 11:25

#2

Здравствуйте,

со ссылкой на решение, которое было представлено вам:
=СЛУЧМЕЖДУ(1;7)+(ТЕКУЩИЙ()>=A2) (в вопросе Ошибка 502, созданная несовместимо с Randbetween/Выбрать вложенную функцию)

Если ввести эту формулу в ячейку, произойдет следующее:

• Формула читается/вычисляется слева направо
• Вычисляет =СЛУЧМЕЖДУ(1;7) (и результат сохраняется в некоторой внутренней переменной/регистре)
• Теперь появляется операция плюс + , указывающая на то, что к текущему значению нужно что-то добавить (а вот и модное слово и почему функция названа так, как она названа)
• Функция CURRENT() обеспечивает доступ к сохраненному значению =RANDBETWEEN(1;7) на шаге выше и фактически (CURRENT()>=A2) оценивает

либо ИСТИНА ( 1 ), если выполняется условие (т. е. условие =СЛУЧМЕЖДУ(1;7)>=A2 выполнено) и по существу вычисляется =СЛУЧМЕЖДУ(1;7) + 1 ,

или ЛОЖЬ ( 0 ), если условие не выполнено (т.е. условие =СЛУЧМЕЖДУ(1;7)>=A2 равно а не выполнено) и по существу вычисляет 900 22 =СЛУЧМЕЖДУ(1; 7) + 0 .

Очень кратко: Функция CURRENT() возвращает текущее значение оценки ячейки, как это было непосредственно перед вызовом CURRENT() (очень простой случай: 1+CURRENT() дает 2 ).

Ref.: LibreOffice Help — CURRENT (что действительно немного искаженное объяснение, но примеры вполне понятны)

Надеюсь, это объясняет, что происходит.

благодарю за помощь 29 июля, 2021, 14:18

#3

Спасибо, это было очень подробно. Было приятно видеть это и в контексте вопроса.

Таким образом, ТЕКУЩЕЕ в основном представляет любое значение, которое в настоящее время встречается в вычислении, в котором оно используется, а не результат вычисления постфактум, позволяя пользователю ссылаться на текущий результат вычисления в середине формулы. Хорошо.

благодарю за помощь 29 июля, 2021, 14:21

#4

Другими словами, ТЕКУЩИЙ раздел формулы оценивает, является ли результат СЛУЧМЕЖДУ большим или равным A2. Если это не так, логический результат равен 0, и он добавляется к числу СЛУЧМЕЖДУ, чтобы не изменять его, так как никаких изменений не требуется, чтобы избежать двух последовательных итераций одного и того же числа; они уже не те.

Однако, если результат СЛУЧМЕЖДУ БОЛЬШЕ или равен A2, это приводит к логическому значению 1, которое добавляется к результату СЛУЧМЕЖДУ, чтобы изменить его, чтобы избежать двух итераций одного и того же числа.

Следовательно, =СЛУЧМЕЖДУ(1;7)+(ТЕКУЩИЙ()=A2) недостаточно, так как случайные числа, которые уже больше, чем число в A2, не нуждаются в модификации, чтобы избежать двух соответствующих итераций одного и того же число в каждой ячейке, точно так же, как рандом между числами, которые меньше A2, не требуют изменения?

Микекагански 30 июля 2021 г., 9:29

#5

, чтобы изменить его, чтобы избежать двух итераций одного и того же номера.

Это полная неверная интерпретация. Мы добавляем 1 не к , чтобы избежать двух итераций одного и того же числа , а чтобы получить случайное число из отфильтрованного набора из 7 чисел: (возьмем 3 в A2 ) 1,2,4,5, 6,7,8 .

Моя формула дает эти результаты для различных результатов RANDBETWEEN :

 1 -> 1 + 0 -> 1
2 -> 2 + 0 -> 2
3 -> 3 + 1 -> 4
4 -> 4 + 1 -> 5
5 -> 5 + 1 -> 6
6 -> 6 + 1 -> 7
7 -> 7 + 1 -> 8
 

Все дела покрываются ровно один раз, без пропусков.

микекагански 30 июля 2021 г., 11:10

#6

не будет =СЛУЧМЕЖДУ(1;7)+(ТЕКУЩИЙ()=A2) достаточно

Ваша модификация приведет к неправильному результирующему набору:

 1 -> 1 + 0 -> 1
2 -> 2 + 0 -> 2
3 -> 3 + 1 -> 4
4 -> 4 + 0 -> 4
5 -> 5 + 0 -> 5
6 -> 6 + 0 -> 6
7 -> 7 + 0 -> 7
 

Вы никогда не получите 8 ; вы получаете 4 в два раза чаще, чем любой другой результат (поэтому у вас не случайный результат, и вы можете смело ставить на A1+1 , чтобы всегда иметь лучшие шансы — 2/7 против 1/7 для любого другого возможного результата). номер, за исключением случаев, когда A2 равен 7 или 8 ).

Вы можете предложить изменить его на =СЛУЧМЕЖДУ(1;8)+(ТЕКУЩИЙ()=A2) — но тогда у вас будут две проблемы: иногда это будет давать вам 9 ; и все равно даст в два раза больше 9Результат 0022 A2+1 аналогичен любому другому результату.

anon73440385 30 июля 2021 г., 11:13

#7

Хмм — это все о этом вопросе , или это скорее не вопрос Ошибка 502, созданная несовместимо с вложенной функцией Randbetween/Choose?

микекагански 30 июля 2021 г., 11:48

#8

@ anon73440385: действительно, вы правы, и я согласен, что ОП должен был прокомментировать это.

go — Как получить текущее имя функции

спросил 8 лет, 9 месяцев назад

Изменено 5 месяцев назад

Просмотрено 48 тысяч раз

Для отслеживания я хотел бы распечатать имя текущей функции, например __FUNCTION__ макрос в gcc.

Так что, когда у меня есть функция

 func foo () {
   след()
}
 

он автоматически распечатает Entering foo()... или что-то в этом роде.

1

[Примечание. Go 1.7+ рекомендует использовать среду выполнения .CallersFrames вместо среды выполнения .FuncForPC ; другой ответ имеет обновленный пример].

Среда выполнения пакета вам в помощь:

 функция трассировки () {
    pc := make([]uintptr, 10) // требуется как минимум 1 запись
    runtime.Callers(2, ПК)
    f := время выполнения.FuncForPC(pc[0])
    файл, строка := f.FileLine(pc[0])
    fmt.Printf("%s:%d %s\n", файл, строка, f.Name())
}
 

3

В Go 1.7 добавлены некоторые функции среды выполнения для улучшения доступа к информации о кадрах стека.

From the Go Примечания к выпуску 1.7:

Новая функция CallersFrames переводит слайс ПК, полученный от вызывающих абонентов, в последовательность кадров, соответствующую стеку вызовов. Этот новый API следует предпочесть прямому использованию FuncForPC, поскольку последовательность кадров может более точно описывать стеки вызовов с помощью встроенных вызовов функций.

Улучшенный пример:

 func trace2() {
    пк := сделать([]uintptr, 15)
    n := runtime.Callers(2, pc)
    кадры: = время выполнения.CallersFrames(pc[:n])
    кадр, _ := кадры.Следующий()
    fmt.Printf("%s:%d %s\n", frame.File, frame.Line, frame.Function)
}
 

Игровая площадка: https://play.golang.org/p/YkEN5mmbRld

Вот более простая версия, в которой не нужно выделять массив.

 func trace() (строка, целое число, строка) {
    ПК, файл, строка, ок := runtime.Caller(1)
    если !ok { вернуть "?", 0, "?" }
    fn := время выполнения.FuncForPC(ПК)
    if fn == nil { вернуть файл, строку, "?" }
    возвращаемый файл, строка, fn.Name()
}
 

1

шт, _, _, _ := время выполнения. Вызывающий(0)
log.Println(runtime.