Правда ли что векторное умножение векторов это умножение двух матриц размерностью два и имеет геометрический смысл площади параллелограмма?
Математика и математики
Популярное
Сообщества
Правда ли что векторное умножение векторов идентично умножение двух матриц с размерностью два и имеет геометрический смысл площади параллелограмма?
МатематикаДомашние задания+3
igor simchanko
Математика и математики·
4,4 K
ОтветитьУточнитьAndronick Arutyunov
Математика
1,0 K
к.ф.м.н., преподаватель Свободного Университета, доцент МФТИ, с.н.с. Института Проблем… · 20 дек 2022
Нет, это неправда. Прежде всего векторное умножение это операция, которая определена в трехмерном пространстве R^3. 3. Иными словами, если у нас имеется два трехмерных вектора a,b, то их векторное произведение [a,b] это снова трехмерный вектор.
3. Иными словами, если у нас имеется два трехмерных вектора a,b, то их векторное произведение [a,b] это снова трехмерный вектор.
При этом, конечно, для векторного произведения в ортнормированном базисе i, j. k справедлива формула
Более подробно про формулы в других базисах можно почитать в википедии. Так что умножение двумерных матриц (т.е. видимо матриц 2х2) тут ни при чём.
В тоже время, есть и геометрические свойства. Прежде всего модуль векторного произведения |[a,b]| действительно численно равен площади параллелограмма «натянутого» на векторы a,b. Кроме того, векторное произведение ортогонально плоскости векторов a,b. Эти два свойства определяют два противоположных вектора (советую проверить это). По этому для определённости говорят, что векторы a,b, [a,b] образуют «правую тройку», это позволяет выбрать из двух векторов один.
Вообще, векторное произведение очень интересная штука: позволяет не только решать многие стереометрические задачи (например с их помощью очень просто доказывается теорема косинусов для трехранного угла), но они ещё и тесно связаны с кватернионами (см.
А значит трехмерные векторы с операцией векторного произведения образуют алгебру Ли, это очень интересный и важный пример такой алгебраической структуры.
Математика, политика, высшая школа и хейт спич
Перейти на t.me/forodirchNEWS1 эксперт согласен
igor simchanko
24 декабря 2022
Почему в двумерном пространстве нельзя произвести векторное умножение двух векторов? Результирующий вектор будет… Читать дальше
Комментировать ответ…Комментировать…
Топ-20
Александр Рябцев
Математика
215
Бог Царь Отечество · 20 дек 2022
Похоже, автор вопроса слышал что-то о векторной и тензорной алгебре, но особо не вникал.
Речь здесь должна идти об антисимметричных тензорах ранга два. Векторное произведение — это антисимметризация тензорного произведения векторов. Ранг и размерность — независимые характеристики, но антисимметричные тензоры ранга два и размерности три (и только такой) имеют три… Читать далее
Векторное произведение — это антисимметризация тензорного произведения векторов. Ранг и размерность — независимые характеристики, но антисимметричные тензоры ранга два и размерности три (и только такой) имеют три… Читать далее
igor simchanko
20 декабря 2022
Какой физический смысл имеет векторное произведение векторов . Напишите расчетные примеры примеры.
Комментировать ответ…Комментировать…
Faris Mekhdi-Zadeh
14
Digital marketer, researcher and data analyst · 20 дек 2022
Векторное умножение векторов, также известное как векторное произведение, это операция, которая применяется к двум векторам и возвращает вектор, который является перпендикуляром к плоскости, в которой расположены исходные векторы. Векторное произведение векторов не может быть выражено как умножение двух матриц размерностью два, так как это операция, которая имеет.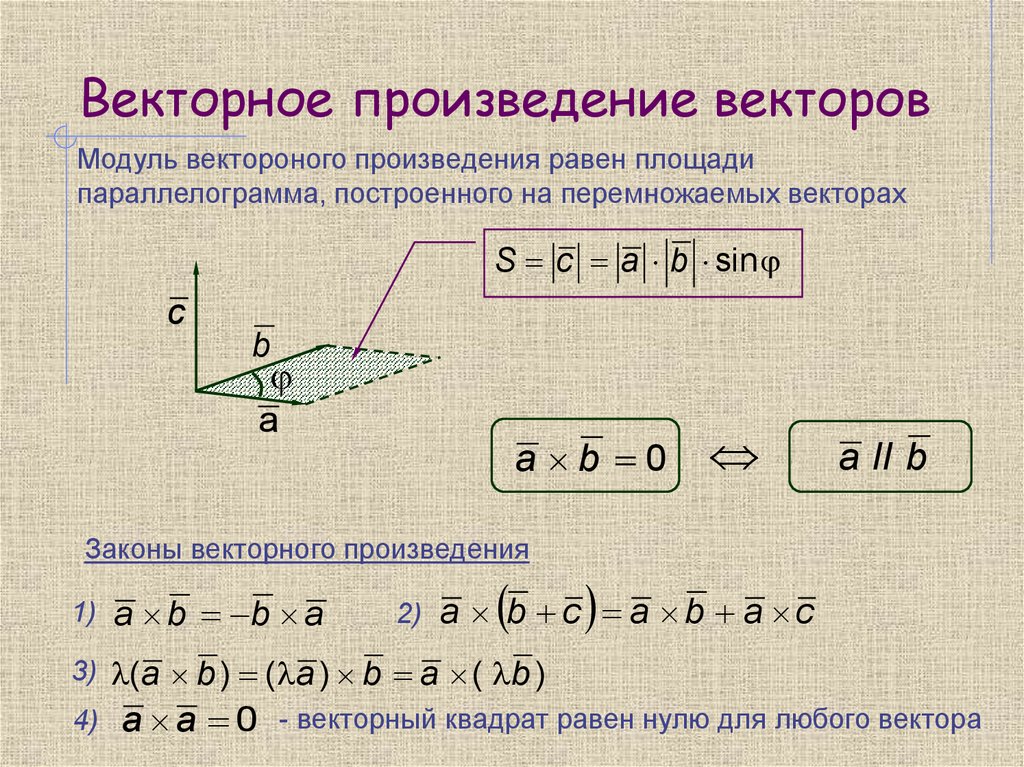
Леонид Коганов
20 декабря 2022
Полагаю, что глагол «возвращает» в первой фразе несёт смысл «доставляет в конечном итоге операции (векторного… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
О сообществе
Математика и математики
Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!
Свойства, химическая структура и применение
Площадь между любыми двумя векторами можно рассчитать с помощью формулы перекрестного произведения . Площадь параллелограмма, натянутого на два вектора, определяется величиной результирующего вектора, который определяется формулой перекрестного произведения .
Двоичная операция над двумя векторами в трех измерениях называется формулой перекрестного произведения . Еще раз, он создает вектор, который перпендикулярен обоим векторам. Правило правой руки используется для вычисления векторного произведения двух векторов.
Еще раз, он создает вектор, который перпендикулярен обоим векторам. Правило правой руки используется для вычисления векторного произведения двух векторов.
Правило правой руки гласит, что любые два вектора должны давать результат, перпендикулярный двум другим векторам. Можно также определить размер результирующего вектора, используя формулу перекрестного произведения .
Различные типы векторов определены в векторной алгебре, и над этими векторами можно выполнять различные операции, такие как сложение, вычитание, произведение и т. д. Формула перекрестного произведения двух векторов описана вместе с общими Cross Product Formula , свойства и примеры на веб-сайте Extramarks и в мобильном приложении.
В трех измерениях формула перекрестного произведения
 Результирующий вектор параллелен и a, и b. Взаимные товары — это другое название векторных продуктов. Когда два вектора являются векторными произведениями, создается вектор, который можно вычислить с помощью правила правой руки.
Результирующий вектор параллелен и a, и b. Взаимные товары — это другое название векторных продуктов. Когда два вектора являются векторными произведениями, создается вектор, который можно вычислить с помощью правила правой руки.Учащиеся должны обратить внимание на плоскости, в которых они живут, и на уравнения, необходимые для вычисления векторного произведения для определенного набора векторных уравнений. Учащиеся могут ознакомиться с примерами, приведенными на веб-сайте Extramarks и в мобильном приложении, чтобы улучшить свое понимание основ этой формулы перекрестного произведения
Ниже приведены области применения формулы перекрестного произведения :
A Формула перекрестного произведения в основном используется в физике и астрологии для работы с вращающимися телами.
- Формулу перекрестного произведения также можно использовать для определения вектора, перпендикулярного другим предоставленным векторам.

- Формула перекрестного произведения дает представление о направлении, размере и иногда скорости объекта, приводимого в движение.
- Они, как и другие формулы, используются в исчислении. Детерминанты могут быть получены через перекрестные произведения.
- Формула перекрестного произведения описывает направление и силу объекта.
- Иногда для определения направления гравитационного поля можно использовать векторное произведение двух векторов.
Учащиеся могут использовать правило большого пальца правой руки, чтобы определить направление векторного произведения двух ненулевых параллельных векторов a и b. Большой палец правой руки указывает направление векторного произведения, когда учащиеся указывают указательным пальцем вдоль вектора а, а средним пальцем — вдоль вектора b.
Три вектора используются для формирования тройного креста. Другими словами, перекрестное произведение двух дополнительных векторов и одного вектора.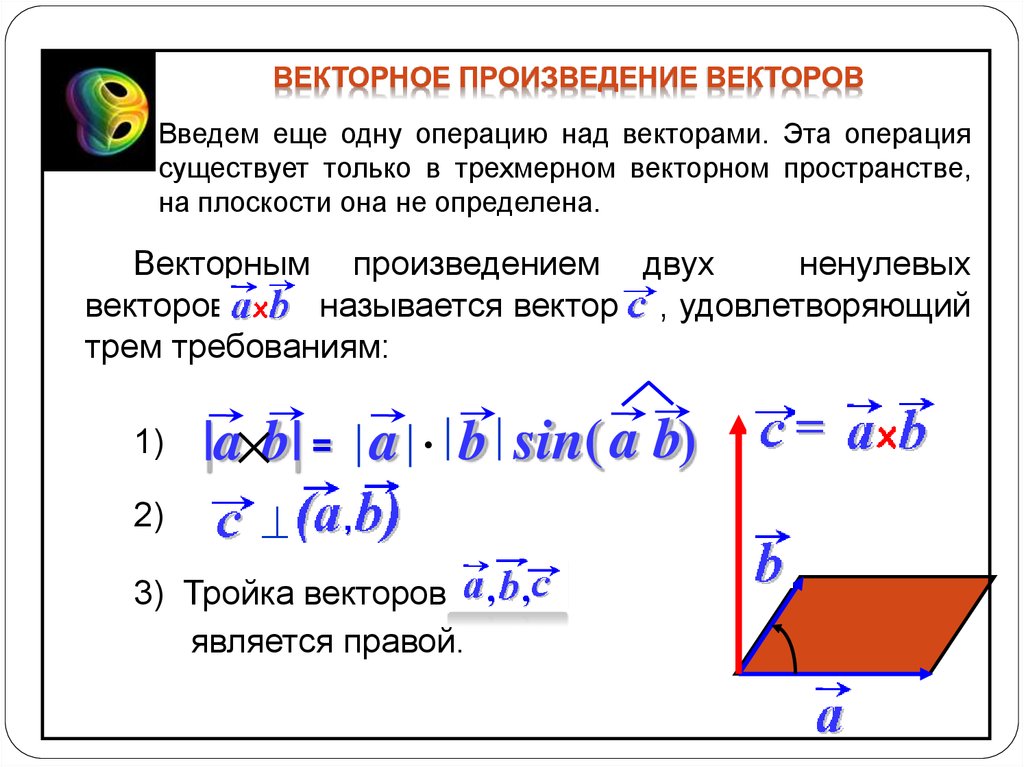
Векторное произведение или векторное произведение двух векторов
A→ и B → обозначается A → × B →, и его результирующий вектор перпендикулярен векторам.
A→ и B →
Ниже приведены несколько моментов, которые следует помнить в случае формулы перекрестного произведения :
- Каждый раз, когда пересекаются два вектора, получается векторная величина.
- Если порядок векторов изменяется в векторном произведении, результирующий вектор имеет отрицательный знак.
- путь:
A → × B → всегда параллелен плоскости, содержащей
A → и B →
- Любое перекрестное произведение двух линейных векторов всегда является нулевым вектором.
Процесс умножения двух векторов называется Формула перекрестного произведения . Знак умножения (x) между двумя векторами указывает на перекрестное произведение. Формула перекрестного произведения имеет трехмерное определение и представляет собой двоичную векторную операцию. Третий вектор, параллельный двум исходным векторам, представляет собой перекрестное произведение двух исходных векторов. Площадь параллелограмма, которая их разделяет, дает информацию о его величине, и правило большого пальца правой руки можно использовать для определения его направления. Поскольку результатом перекрестного произведения векторов является векторная величина, Формула перекрестного произведения двух векторов также называется векторным произведением. Учащиеся получат более глубокое представление о формуле перекрестного произведения двух векторов на веб-сайте Extramarks и в мобильном приложении.
Знак умножения (x) между двумя векторами указывает на перекрестное произведение. Формула перекрестного произведения имеет трехмерное определение и представляет собой двоичную векторную операцию. Третий вектор, параллельный двум исходным векторам, представляет собой перекрестное произведение двух исходных векторов. Площадь параллелограмма, которая их разделяет, дает информацию о его величине, и правило большого пальца правой руки можно использовать для определения его направления. Поскольку результатом перекрестного произведения векторов является векторная величина, Формула перекрестного произведения двух векторов также называется векторным произведением. Учащиеся получат более глубокое представление о формуле перекрестного произведения двух векторов на веб-сайте Extramarks и в мобильном приложении.
AB обозначает векторное произведение или перекрестное произведение двух векторов A и B, при этом результирующий вектор перпендикулярен двум исходным. В то время как скалярное произведение используется для определения длины вектора или угла между двумя векторами, формула перекрестного произведения обычно используется для определения вектора, который перпендикулярен плоской поверхности, натянутой на два вектора. В трех измерениях перекрестное произведение двух векторов, таких как AB, равно вектору, расположенному под прямым углом к обоим.
В трех измерениях перекрестное произведение двух векторов, таких как AB, равно вектору, расположенному под прямым углом к обоим.
Перекрестное произведение — это тип векторного умножения, которое выполняется между двумя векторами различной формы или природы. Вектор имеет направление и величину. Формула перекрестного произведения и скалярное произведение могут использоваться для умножения двух или более векторов. Результирующий вектор известен как Формула перекрестного произведения двух векторов или векторного произведения, когда два вектора перемножаются, а произведение векторов также является векторной переменной. Результирующий вектор параллелен плоскости, в которой расположены два предоставленных вектора.
Два вектора разного типа или природы умножаются в перекрестном произведении, своего рода умножении векторов. Вектор имеет направление и величину. Два или более вектора могут быть перемножены с помощью векторного произведения или скалярного произведения. Результирующая векторная величина от умножения двух векторов также является векторной величиной. Конечным векторным произведением является перекрестное произведение двух векторов, часто называемое «вектором». Два предоставленных вектора содержатся в плоскости, и результирующий вектор перпендикулярен этой плоскости.
Результирующая векторная величина от умножения двух векторов также является векторной величиной. Конечным векторным произведением является перекрестное произведение двух векторов, часто называемое «вектором». Два предоставленных вектора содержатся в плоскости, и результирующий вектор перпендикулярен этой плоскости.
Если A и B — два отдельных вектора, то их векторное произведение (AxB) будет перпендикулярно им обоим и перпендикулярно плоскости, в которую они оба включены. Это показано уравнением A x B= |A| |Б| sin θ
Учащиеся смогут понять это, используя пример, что если у них есть два вектора, расположенные в плоскости X-Y, их векторное произведение даст результирующий вектор, который расположен перпендикулярно плоскости X-Y вдоль ось Z.
Символ × используется между исходными векторами. Векторное произведение или формула перекрестного произведения двух векторов отображается как:
→a×→b=→ca→×b→=c→
Где→aa→ и →bb→ два вектора.
→cc→ результирующий вектор.
Правило правой руки – векторное произведение двух векторовУчащиеся также могут определить направление вектора, применив правило правой руки к формуле
- Наведите указательный палец в направлении первого вектора (A A).
- Поместите средний палец в направлении второго вектора (BB).
- В настоящее время большой палец указывает в направлении формулы перекрестного произведения двух векторов.
Правило правой руки может помочь учащимся определить направление единичного вектора.
Учащиеся могут использовать это правило, вытянув правую руку так, чтобы средний палец указывал в направлении второго вектора, а указательный палец указывал в направлении первого вектора.
Функции Формула перекрестного произведения полезны для четкого понимания умножения векторов и для быстрого решения любых проблем, которые могут возникнуть при выполнении векторных вычислений. Следующие характеристики формулы перекрестного произведения двух векторов подробно обсуждаются и объясняются на веб-сайте Extramarks и в мобильном приложении.
Учащиеся могут использовать свойства для определения векторного произведения двух векторов. Нахождение перекрестного произведения двух векторов сильно зависит от таких свойств, как свойство антикоммутативности и свойство нулевого вектора. Другие свойства, кроме этих, включают свойство Якоби и распределительное свойство. На веб-сайте и в мобильном приложении Extramarks перечислены свойства перекрестного продукта.
Другие свойства, кроме этих, включают свойство Якоби и распределительное свойство. На веб-сайте и в мобильном приложении Extramarks перечислены свойства перекрестного продукта.
Площадь прямоугольника со сторонами X и Y представлена Формулой перекрестного произведения двух векторов, которая равна произведению их величин. Формула перекрестного произведения становится: = 90 градусов, когда два вектора перпендикулярны друг другу. Как известно учащимся, sin 90° = 1.
Формула перекрестного произведения — это математическая операция, используемая для умножения двух векторов. Это бинарная векторная операция в трех измерениях. Формула перекрестного произведения двух векторов создает третий вектор, который параллелен первым двум векторам. Площадь параллелограмма, который их разделяет, определяет его величину, а правило большого пальца правой руки определяет его направление. Поскольку результат перекрестного произведения двух векторов является векторной величиной, перекрестное произведение двух векторов часто называют «векторным произведением». В качестве иллюстрации попробуйте скрутить болт с помощью гаечного ключа: длина гаечного ключа — это один вектор. Другой вектор — это направление, в котором мы крутим гаечный ключ, чтобы затянуть или ослабить болт. Результирующая ориентация поворота параллельна обоим векторам.
В качестве иллюстрации попробуйте скрутить болт с помощью гаечного ключа: длина гаечного ключа — это один вектор. Другой вектор — это направление, в котором мы крутим гаечный ключ, чтобы затянуть или ослабить болт. Результирующая ориентация поворота параллельна обоим векторам.
Тройное перекрестное произведение векторов — это перекрестное произведение вектора и формулы перекрестного произведения двух других векторов. Вектор — это результат тройного перекрестного произведения. Равнодействующая вектора тройного пересечения расположена в плоскости, образованной первыми тремя векторами. Тройное векторное произведение этих векторов будет иметь определенную форму, если векторы a, b и c. Студенты могут получить подробное объяснение формы на веб-сайте Extramarks и в мобильном приложении.
Здесь используются значения u, v и w. Подумайте об уравнении u x (v x w). u x v x w u x v x w Имейте в виду, что (u x v) x w параллельно (u x v). U и V определяют эту нормальную плоскость.
U и V определяют эту нормальную плоскость.
Векторы должны быть компланарными, если тройное произведение векторов равно нулю.
Вектор тройного произведения представляет объем параллелепипеда. Любой из трех векторов идентифицируется и отображает нулевую величину, если он равен нулю. Его перпендикулярное отношение к плоскости может служить индикатором для векторов a и b. Если вектор c также лежит в той же плоскости, что и равнодействующая, то скалярное произведение равнодействующей на c также будет равно нулю.
Тройное векторное произведение является подполем векторной алгебры. Студенты могут узнать о векторном произведении трех векторов, посмотрев на векторное тройное произведение.
Если они практикуют перекрестное произведение вектора вместе с перекрестными произведениями двух других векторов, они могут вычислить количество векторного тройного произведения.
В результате перекрестного произведения получается векторная величина. Результатом упрощения векторного тройного произведения является тождественное имя BAC – CAB.
Формула перекрестного произведения важна во многих областях науки и техники. Следующие два примера довольно просты.
Пример 1: Приложение равных и противоположных сил к двум диаметрально противоположным концам крана приведет к его открытию. В этом случае используется крутящий момент. В векторной форме крутящий момент представляет собой векторное произведение вектора силы и радиус-вектора, который измеряет расстояние от оси вращения до точки приложения силы.
Пример 2. Использование гаечного ключа для поворота болта. Длина гаечного ключа равна одному вектору. При затягивании или ослаблении болта мы прикладываем усилие к гаечному ключу в этом направлении. Ориентация полученного поворота параллельна обоим векторам.
Вектор, ортогональный двум предоставленным векторам, создается, когда два вектора являются векторными произведениями.
- Правило большого пальца правой руки определяет направление векторного произведения двух векторов, а площадь параллелограмма, созданного двумя исходными векторами, a и b b, определяет величину.

- Нулевой вектор получается в результате перекрестного произведения двух параллельных или линейных векторов.
Часто задаваемые вопросы (Часто задаваемые вопросы)
1. Формула векторного произведения двух векторов равна?
Третий вектор, перпендикулярный первым двум векторам, получается путем умножения векторного произведения первых двух векторов. Площадь параллелограмма, образованного между ними, дает величину результирующего вектора, и правило большого пальца правой руки можно использовать для определения его направления. При пересечении двух векторов a и b получается a = b = c.
2. Что достигается формулой перекрестного произведения?
Когда учащиеся вычисляют векторное произведение двух векторов, мы получаем новый вектор, который перпендикулярен плоскости, в которой находились исходные два вектора. Произведение модулей векторов на синус угла между ними дает величину результирующего вектора. а × б = | а | |б| грех θ.
3. Что такое скалярное произведение двух векторов и формула перекрестного произведения?
Скалярный продукт и Формула перекрестного произведения — это два альтернативных способа умножения векторов. Оба этих умножения векторов дают разные результаты. В результате перекрестное произведение дает векторную величину, а скалярное произведение дает скалярную величину. Формула перекрестного произведения двух векторов — это векторное произведение двух векторов, а скалярное произведение — скалярное произведение двух векторов. Формулу перекрестного произведения иногда называют «векторным произведением», а скалярное произведение также называют «скалярным произведением».
4. Что такое векторное произведение двух векторов Правило большого пальца правой руки?
Направление результирующего вектора можно определить с помощью правила правой руки для векторного произведения двух векторов. Их большие пальцы укажут в направлении векторного произведения двух векторов, если учащиеся укажут правой рукой в направлении первой стрелки, а пальцы согнут в направлении второй.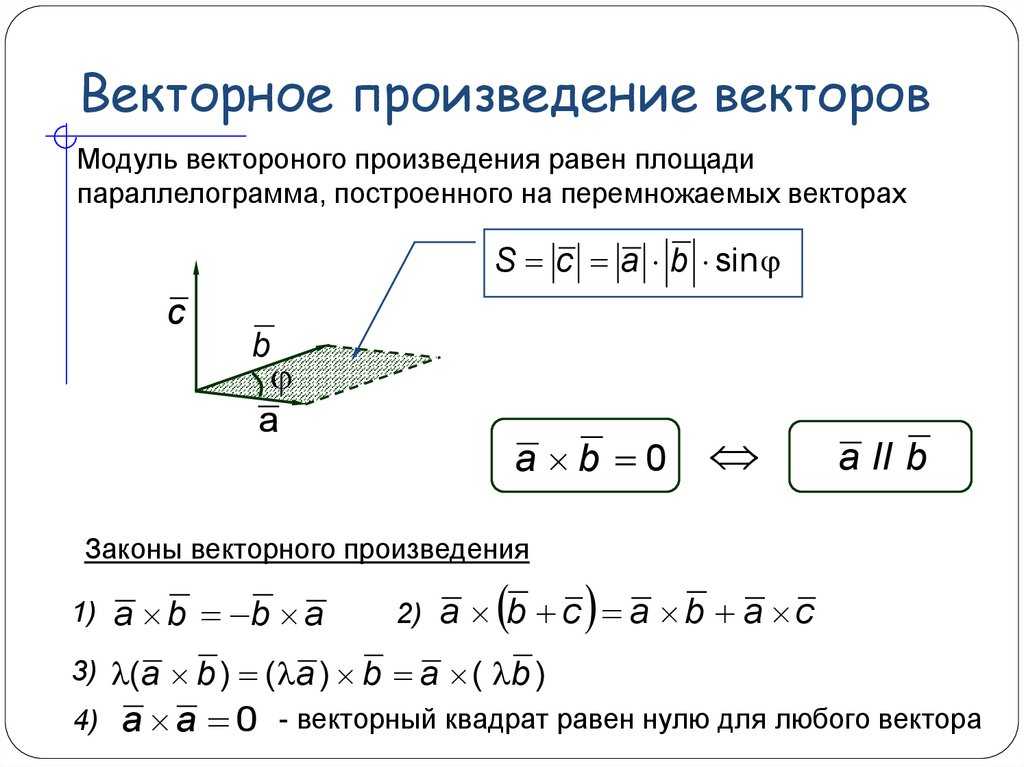 Формула перекрестного произведения для определения направления результирующего вектора обеспечивается правилом большого пальца правой руки.
Формула перекрестного произведения для определения направления результирующего вектора обеспечивается правилом большого пальца правой руки.
5. Почему перекрестное произведение является синусоидальным?
Поскольку площадь параллелограмма определяется перекрестным произведением двух векторов, используется синус, поскольку он представляет собой угол между двумя исходными векторами.
√ Перекрестное произведение (формула, правило и примеры)
от администратора
Содержание
Что такое перекрестное произведениеПерекрестное произведение является одним из видов. Его также называют векторным произведением. Это потому, что векторное произведение работает в векторном случае.
Результат: длина и направление. Чтобы получить результат (длину и направление), нужно умножить два вектора (вектор a и b).
Длина (величина) описывает площадь векторов (вектора a и b). Форма представляет собой параллелограмм и вектора a и b в качестве сторон.
Форма представляет собой параллелограмм и вектора a и b в качестве сторон.
Другими словами, если вектора a и b имеют прямой угол, то длина (величина) результата векторного произведения векторов a и b такая же, как умножение их обоих.
Направление результата перекрестного произведения описывает направление как произведение векторов a и b. По правилу правой руки будет легче определить направление.
Есть случай, когда результат перекрестного произведения равен нулю. Это если два вектора имеют одинаковое направление или векторы имеют прямо противоположное направление.
Другой случай, если длина одного из векторов равна нулю. Но если векторы a и b имеют прямой угол, он будет иметь максимальную длину.
Формула перекрестного произведения Перекрестное произведение двух векторов описывается в трехмерном пространстве. Обозначается как a x б.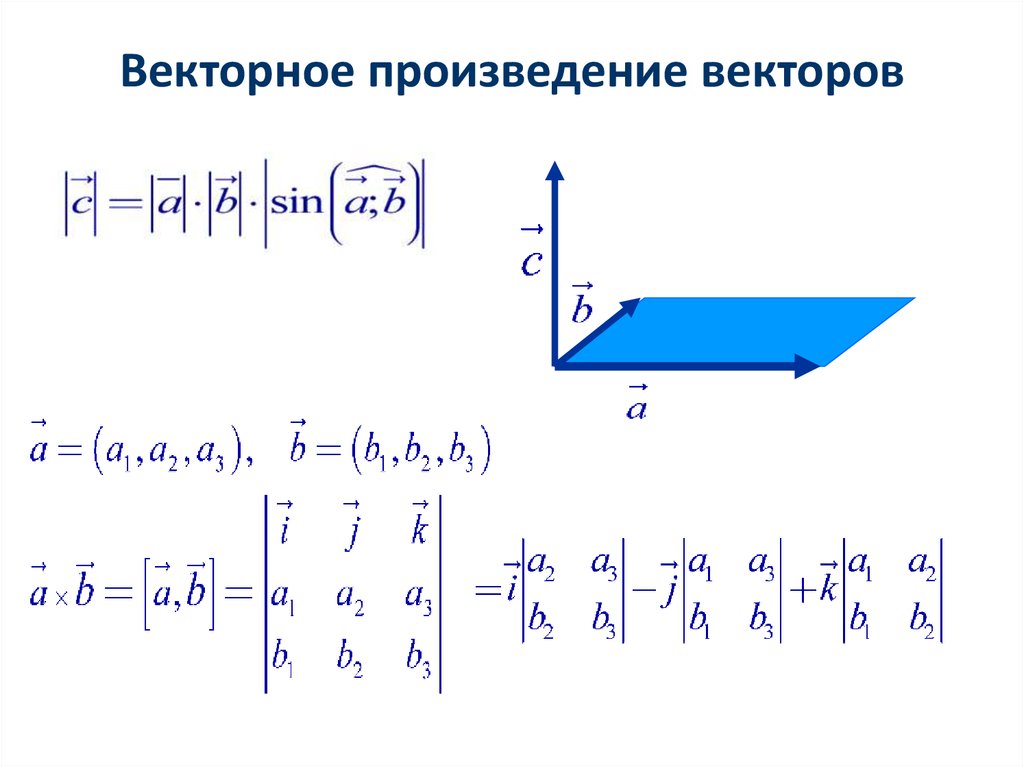
Формула перекрестного произведения:
|a| × |б| × sin(a) × n
Где:
- a и b : векторы
- α : угол между векторами a и b (между 0°-180°) :
- n единичный вектор под прямым углом к а и b.
Если есть вектор a (x a , y a , z a ) и вектор b (x b , y b , z b ), которые начинаются с исходной точки (0,0,0), тогда векторным произведением является вектор c (x c , y c , z c ). Вектор C также можно определить с помощью:
x C = Y A .Z B — Z A .Y B
Y C = Z . . б – х а .z б
z в = х а .b у – у а х .б 0266 Правило правой руки
Правило правой руки описывает векторное произведение двух векторов (векторы a и b) и результат (вектор c). Он находится в трехмерном пространстве.
Он находится в трехмерном пространстве.
В частности, правило правой руки описывает направление результата. Используя указательный палец в качестве вектора a и средний палец в качестве вектора b, мы получаем направление большого пальца.
Примеры1. Вектор a имеет модуль 4, вектор b имеет модуль 5, угол между ними a и b составляет 30°, а n – единичный вектор под прямым углом к обоим a и b. Определить a × b
Пример
Известно, что
|a| = 4
|б| = 5
α = 30 o
Используя формулу перекрестного произведения, мы получаем
|a| х |б| x sin(a) x n = 4.5.sin(30˚) x n = 10n
2. Чему равно произведение a (1,3,-2) и b (-2,1,3)? И определить величину результата.
Пример
x a = 1; у а = 3; z a = -2
x b = -2; у б = 1; z b = 3
, тогда, если результатом является вектор c,
x c = 3,3 – (-2).



